Adaptive Genetic Algorithm Based on Fuzzy Reasoning for the Multilevel Capacitated Lot-Sizing Problem with Energy Consumption in Synchronizer Production
Abstract
1. Introduction
2. Literature Review—Existing Approaches for the MLCLSP
2.1. Decomposition-Based Approaches
2.2. Traditional Heuristic Methods
2.3. Bionic Algorithms
2.4. A Brief Summary
3. The Proposed Fuzzy-GA for MLCLSP
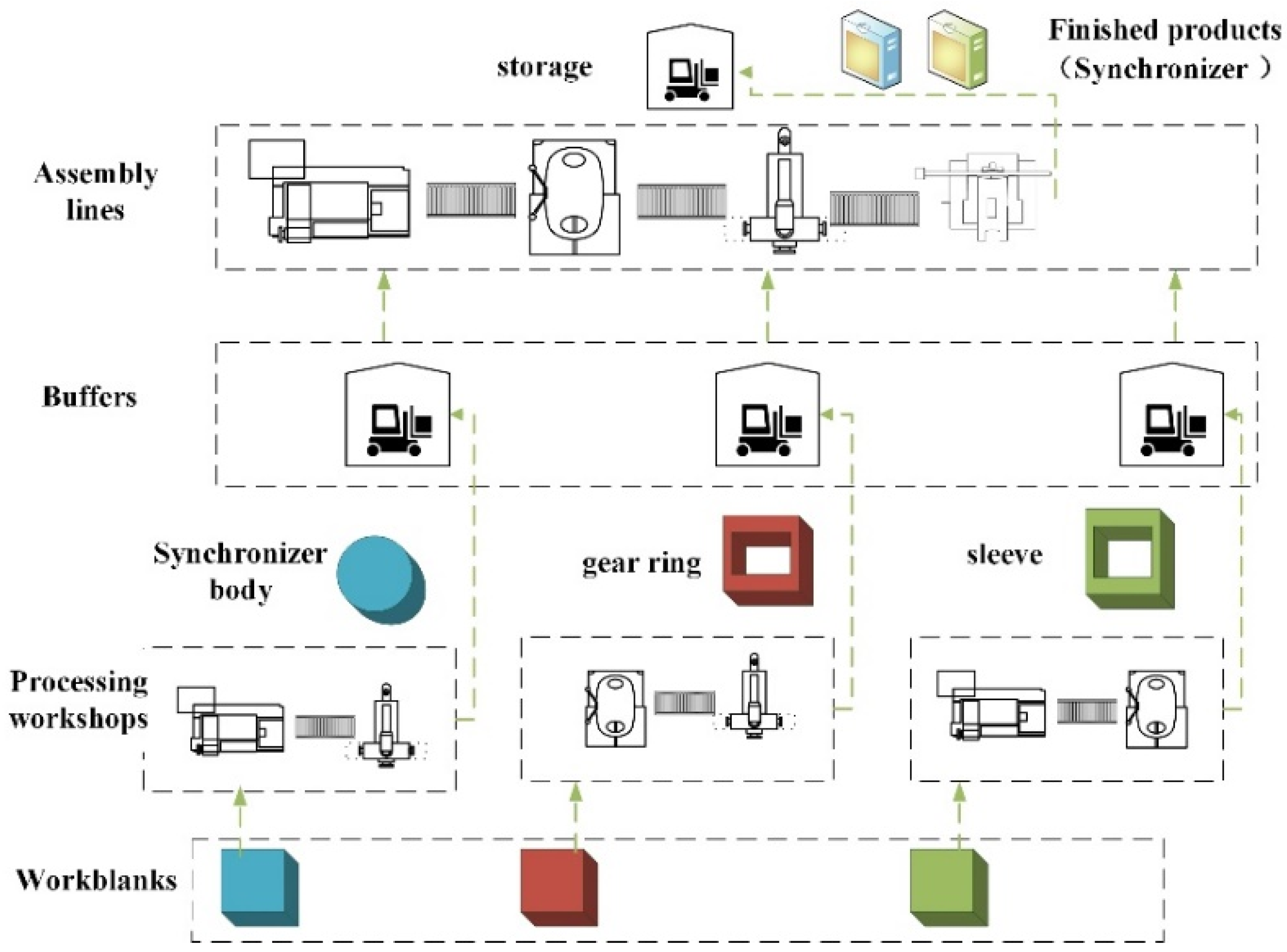
3.1. Problem Statement
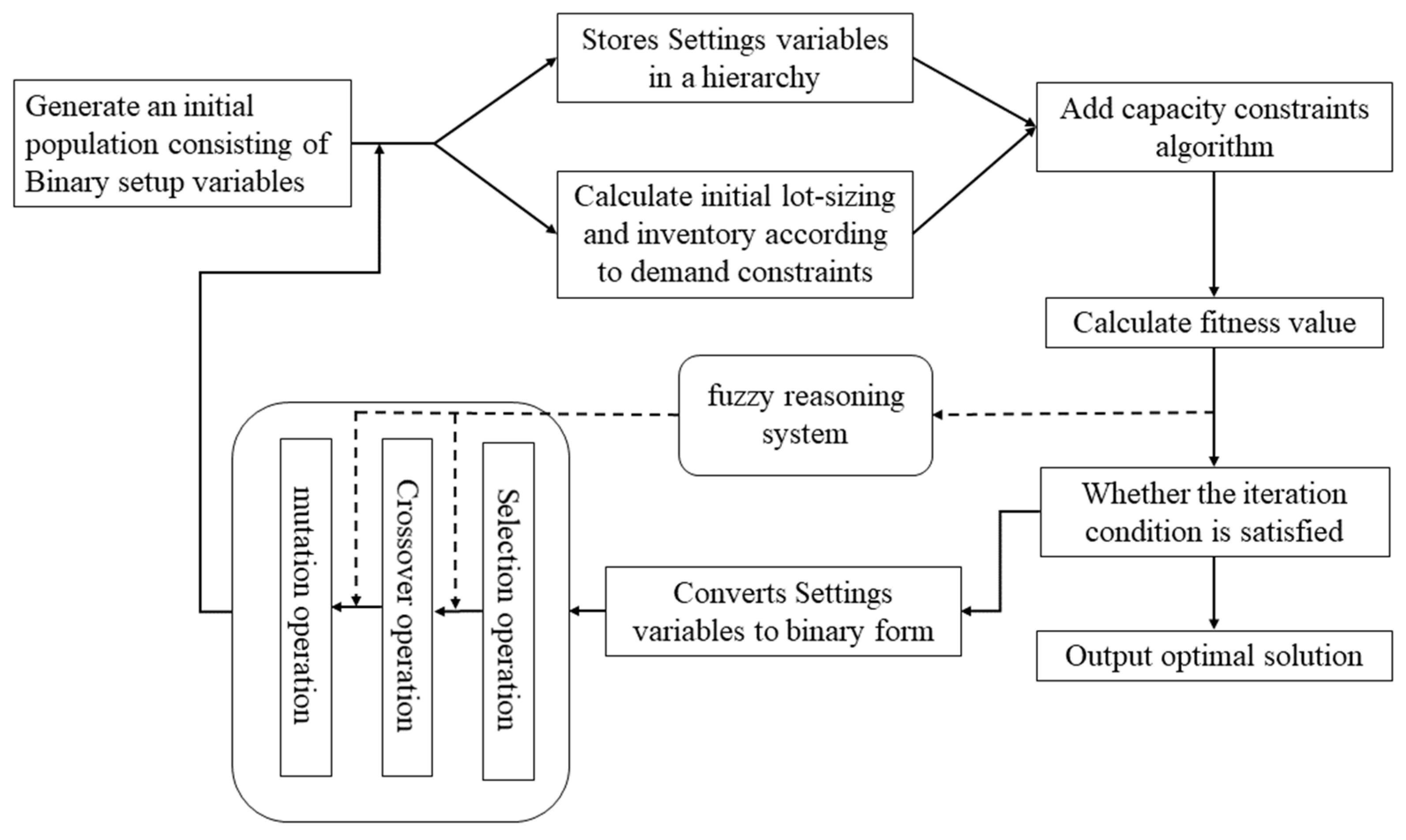
3.2. Solving Model of MLCLSP with the Fuzzy-GA
| Algorithm1 Capacity constraint algorithm |
| Input: xit, ; output: xit |
|
| {production lot size of period t is obtained without capacity constraints sort in ascending order . Then, find the minimum lot size . Calculate , Else calculate if . End this cycle and jump to Step 5 for the next cycle. End End |
|
| {the corresponding lot-sizing of is transferred to the production lot-sizing of . Set the corresponding binary variable to zero. Cyclic variable . Calculate }. |
|
| End |
|
|
If , jump to Step 4. Else, update . If , output updated lot-sizing, setup variable as result, and end the whole procedure; Else, the solution cannot satisfy the capacity constraint and end the whole procedure. End End |
| Algorithm 2 Algorithm of solving fitness value |
| Input: production lot-sizing x_it, inventory I_it, and setup variable Y_it; output: fitness value: f |
|
3.3. Encoder Based on Hierarchical Structure
| Algorithm 3 Algorithm of a lot-sizing solution according to the demand constraints |
| Input: setup variable, product demand, and material quantity relationship , , ; output: production lot-sizing |
|
| Use demand balance relation and solve production lot-sizing of product i at different planning periods. Else, use demand balance relation and solve production lot-sizing . End |
|
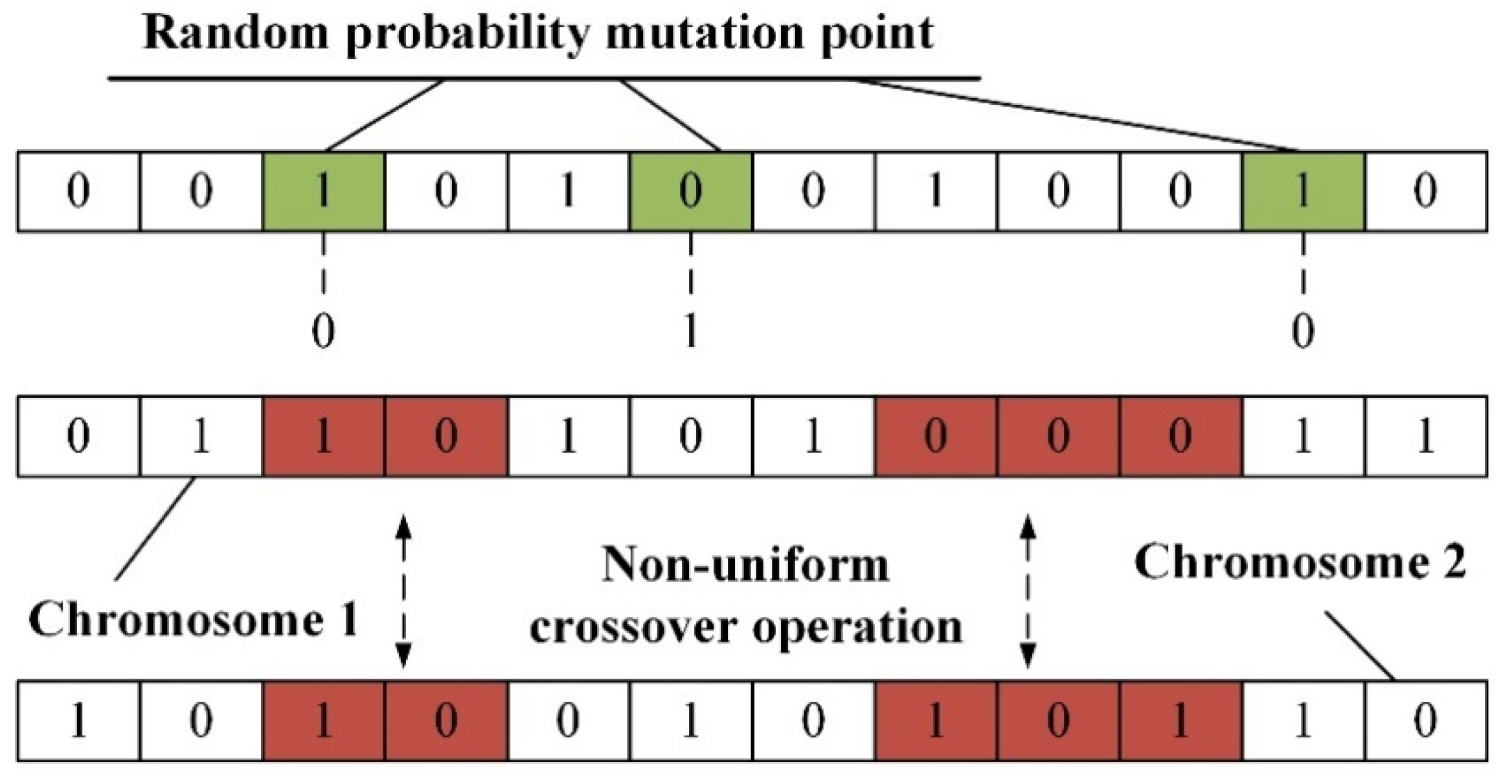
3.4. Adaptive Optimization Process of Parameters Based on Fuzzy Theory
4. Experimental Setup
4.1. Experimental Data and Design Hypothesis
4.1.1. Experiment 1 Validation of Fuzzy-GA in Solving MLCLSP
4.1.2. Experiment 2 Adaptive Parameters of the Fuzzy-GA
4.1.3. Experiment 3 Performance of Fuzzy-GA in Solving MLCLSP
4.2. Performance Evaluation Metrics
5. Results and Discussion
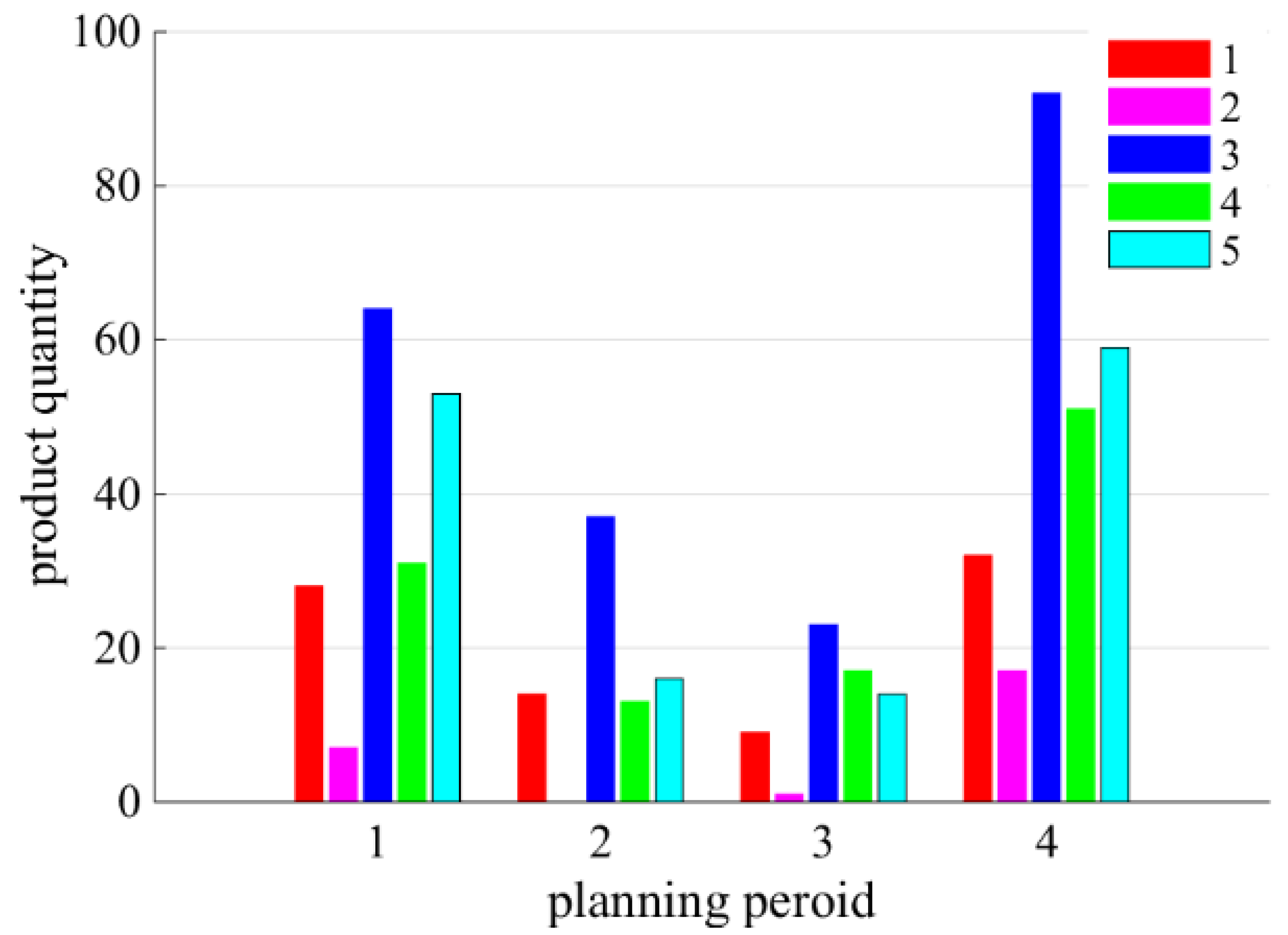
5.1. Results and Discussion for Experiment 1
5.2. Results and Discussion for Experiment 2
5.3. Results and Discussion for Experiment 3
6. Conclusions and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Awad, M.I.; Hassan, N.M. Joint decisions of machining process parameters setting and lot-size determination with environmental and quality cost consideration. J. Manuf. Syst. 2018, 46, 79–92. [Google Scholar] [CrossRef]
- Jia, S.; Yuan, Q.; Cai, W.; Li, M.; Li, Z. Energy modeling method of machine-operator system for sustainable machining. Energy Convers. Manag. 2018, 172, 265–276. [Google Scholar] [CrossRef]
- Klement, N.; Abdeljaouad, M.A.; Porto, L.; Silva, C. Lot-Sizing and Scheduling for the Plastic Injection Molding Industry—A Hybrid Optimization Approach. Appl. Sci. 2021, 11, 1202. [Google Scholar] [CrossRef]
- Boonmee, A.; Sethanan, K. A GLNPSO for multi-level capacitated lot-sizing and scheduling problem in the poultry industry. Eur. J. Oper. Res. 2016, 250, 652–665. [Google Scholar] [CrossRef]
- Berretta, R.; Rodrigues, L.F. A memetic algorithm for a multistage capacitated lot-sizing problem. Int. J. Prod. Econ. 2004, 87, 67–81. [Google Scholar] [CrossRef]
- Buschkühl, L.; Sahling, F.; Helber, S.; Tempelmeier, H. Dynamic capacitated lot-sizing problems: A classification and review of solution approaches. Or Spectr. 2010, 32, 231–261. [Google Scholar] [CrossRef]
- Duda, J.; Stawowy, A. Optimization Methods for Lot-Sizing Problem in an Automated Foundry. Arch. Metall. Mater. 2013, 58, 863–866. [Google Scholar] [CrossRef][Green Version]
- Jia, S.; Yuan, Q.; Lv, J.; Liu, Y.; Ren, D.; Zhang, Z. Therblig-embedded value stream mapping method for lean energy machining. Energy 2017, 138, 1081–1098. [Google Scholar] [CrossRef]
- Jinxing, X.; Jiefang, D. Heuristic genetic algorithms for general capacitated lot-sizing problems. Comput. Math. Appl. 2002, 44, 263–276. [Google Scholar]
- Yijun, L.; David, L. Self-adaptive randomized constructive heuristics for the multi-item capacitated lot-sizing problem. arXiv 2021, arXiv:2103.04199. [Google Scholar]
- Furlan, M.M.; Santos, M.O. BFO: A hybrid bees algorithm for the multi-level capacitated lot-sizing problem. J. Intell. Manuf. 2017, 28, 929–944. [Google Scholar] [CrossRef]
- Kirschstein, T.; Meisel, F. A dynamic multi-commodity lot-sizing problem with supplier selection storage selection and discounts for the process industry. Eur. J. Oper. Res. 2019, 279, 393–406. [Google Scholar] [CrossRef]
- Cunha, J.O.; Kramer, H.H.; Melo, R.A. On the computational complexity of uncapacitated multi-plant lot-sizing problems. Optim. Lett. 2021, 15, 803–812. [Google Scholar] [CrossRef]
- Han, Y.; Kaku, I.; Tang, J.; Dellaert, N.; Cai, J.; Li, Y. A Comparison of Particle Swarm Optimizations for Uncapacitated Multilevel Lot-sizing Problems(Theory and Methodology). J. Jpn. Ind. Manag. Assoc. 2010, 61, 203–213. [Google Scholar]
- Seeanner, F. Multi-Stage Simultaneous Lot-Sizing and Scheduling—Planning of Flow Lines with Shifting Bottlenecks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Jia, S.; Yuan, Q.; Cai, W.; Lv, J.; Hu, L. Establishing prediction models for feeding power and material drilling power to support sustainable machining. Int. J. Adv. Manuf. Technol. 2019, 100, 2243–2253. [Google Scholar] [CrossRef]
- Jia, S.; Cai, W.; Liu, C.; Zhang, Z.; Bai, S.; Wang, Q.; Li, S.; Hu, L. Energy modeling and visualization analysis method of drilling processes in the manufacturing industry. Energy 2021, 228, 120567. [Google Scholar] [CrossRef]
- Zohali, H.; Naderi, B.; Mohammadi, M. The economic lot scheduling problem in limited-buffer flexible flow shops: Mathematical models and a discrete fruit fly algorithm. Appl. Soft Comput. 2019, 80, 904–919. [Google Scholar] [CrossRef]
- Farooq, B.; Bao, J.; Raza, H.; Sun, Y.; Ma, Q. Flow-shop path planning for multi-automated guided vehicles in intelligent textile spinning cyber-physical production systems dynamic environment. J. Manuf. Syst. 2021, 59, 98–116. [Google Scholar] [CrossRef]
- Che, Z.H.; Chiang, T.A.; Lin, T.T. A multi-objective genetic algorithm for assembly planning and supplier selection with capacity constraints. Appl. Soft Comput. 2021, 101, 107030. [Google Scholar] [CrossRef]
- Hadi, A.S.; Mehdi, R.B. Solving a flexible job shop lot sizing problem with shared operations using a self-adaptive COA. Int. J. Prod. Res. 2021, 59, 483–515. [Google Scholar]
- Andrés, A.; Mingyuan, C. Multi-level lot-sizing with raw-material perishability, deterioration, and lot-sizing ordering: An application of production planning in advanced composite manufacturing. Comput. Ind. Eng. 2020, 145, 106484. [Google Scholar]
- Sikora, R. A genetic algorithm for integrating lot-sizing and sequencing in scheduling a capacitated flow line. Comput. Ind. Eng. 1996, 30, 969–981. [Google Scholar] [CrossRef]
- Soltanali, H.; Rohani, A.; Tabasizadeh, M.; Abbaspour-Fard, M.H.; Parida, A. An improved fuzzy inference system-based risk analysis approach with application to automotive production line. Neural Comput. Appl. 2020, 32, 10573–10591. [Google Scholar] [CrossRef]
- Tempelmeier, H.; Helber, S. A heuristic for dynamic multi-item multi-level capacitated lot-sizing for general product structures. Eur. J. Oper. Res. 1984, 75, 296–311. [Google Scholar] [CrossRef]
- Boctor, F.F.; Poulin, P. Heuristics for N-product, M-stage, economic lot sizing and scheduling problem with dynamic demand. Int. J. Prod. Res. 2005, 43, 2809–2828. [Google Scholar] [CrossRef]
- Miller, A.J.; Nemhauser, G.L.; Savelsbergh, M. Solving Multi-Item Capacitated Lot-Sizing Problems with Setup Times by Branch-and-Cut; CORE Discussion Papers; Université Catholique de Louvain: Ottignies-Louvain-la-Neuve, Belgium, 2000. [Google Scholar]
- Zhang, C.; Zhang, D.; Wu, T. Data-driven Branching and Selection for Lot-sizing and Scheduling Problems with Sequence-dependent Setups and Setup Carryover. Comput. Oper. Res. 2021, 132, 105289. [Google Scholar] [CrossRef]
- Ramezanian, R.; Saidi-Mehrabad, M.; Fattahi, P. MIP formulation and heuristics for multi-stage capacitated lot-sizing and scheduling problem with availability constraints. J. Manuf. Syst. 2013, 32, 392–401. [Google Scholar] [CrossRef]
- Verma, M.; Sharma, R. Lagrangian relaxation and bounded variable linear programs to solve a two-level capacitated lot sizing problem. In Proceedings of the 2011 3rd International Conference on Electronics Computer Technology, Kanyakumari, India, 8–10 April 2011; Volume 6, pp. 188–192. [Google Scholar]
- Tempelmeier, H.; Buschkühl, L. A heuristic for the dynamic multi-level capacitated lot-sizing problem with linked lot-sizes for general product structures. Or Spectr. 2009, 31, 385–404. [Google Scholar] [CrossRef]
- Wu, T.; Shi, L.; Geunes, J.; Akartunalı, K. An optimization framework for solving capacitated multi-level lot-sizing problems with backlogging. Eur. J. Oper. Res. 2011, 214, 428–441. [Google Scholar] [CrossRef]
- Zhao, Q.; Xie, C.; Xiao, Y. A variable neighborhood decomposition search algorithm for multi-level capacitated lot-sizing problems. Electron. Notes Discret. Math. 2012, 39, 129–135. [Google Scholar] [CrossRef]
- Chen, H. Fix-and-optimize and variable neighborhood search approaches for multi-level capacitated lot sizing problems. Omega 2015, 56, 25–36. [Google Scholar] [CrossRef]
- Mohammadi, M.; Fatemi Ghomi SM, T.; Karimi, B.; Torabi, S.A. Rolling-horizon and fix-and-relax heuristics for the multi-product multi-level capacitated lot-sizing problem with sequence-dependent setups. J. Intell. Manuf. 2010, 21, 501–510. [Google Scholar] [CrossRef]
- Pitakaso, R.; Almeder, C.; Doerner, K.F.; Hartl, R.F. Combining exact and population-based methods for the constrained multi-level lot-sizing problem. Int. J. Prod. Res. 2006, 44, 4755–4771. [Google Scholar] [CrossRef]
- Toledo, C.F.M.; De Oliveira, R.R.R.; França, P.M. A Hybrid Multi-Population Genetic Algorithm Applied to Solve the Multi-Level Capacitated Lot Sizing Problem with Backlogging; Elsevier Science Ltd.: Amsterdam, The Netherlands, 2013; Volume 40, pp. 910–919. [Google Scholar]
- Mohammadi, M.; Ghomi, S.M.T.F. Genetic algorithm-based heuristic for capacitated lot-sizing problem in flow shops with sequence-dependent setups. Expert Syst. Appl. 2011, 38, 7201–7207. [Google Scholar] [CrossRef]
- Duda, J. A hybrid genetic algorithm and variable neighborhood search for multi-family capacitated lot-sizing problem. Electron. Notes Discret. Math. 2017, 58, 103–110. [Google Scholar] [CrossRef]
- Quadt, D.; Kuhn, H. Capacitated lot-sizing with extensions: A review. 4OR 2008, 6, 61–83. [Google Scholar] [CrossRef]


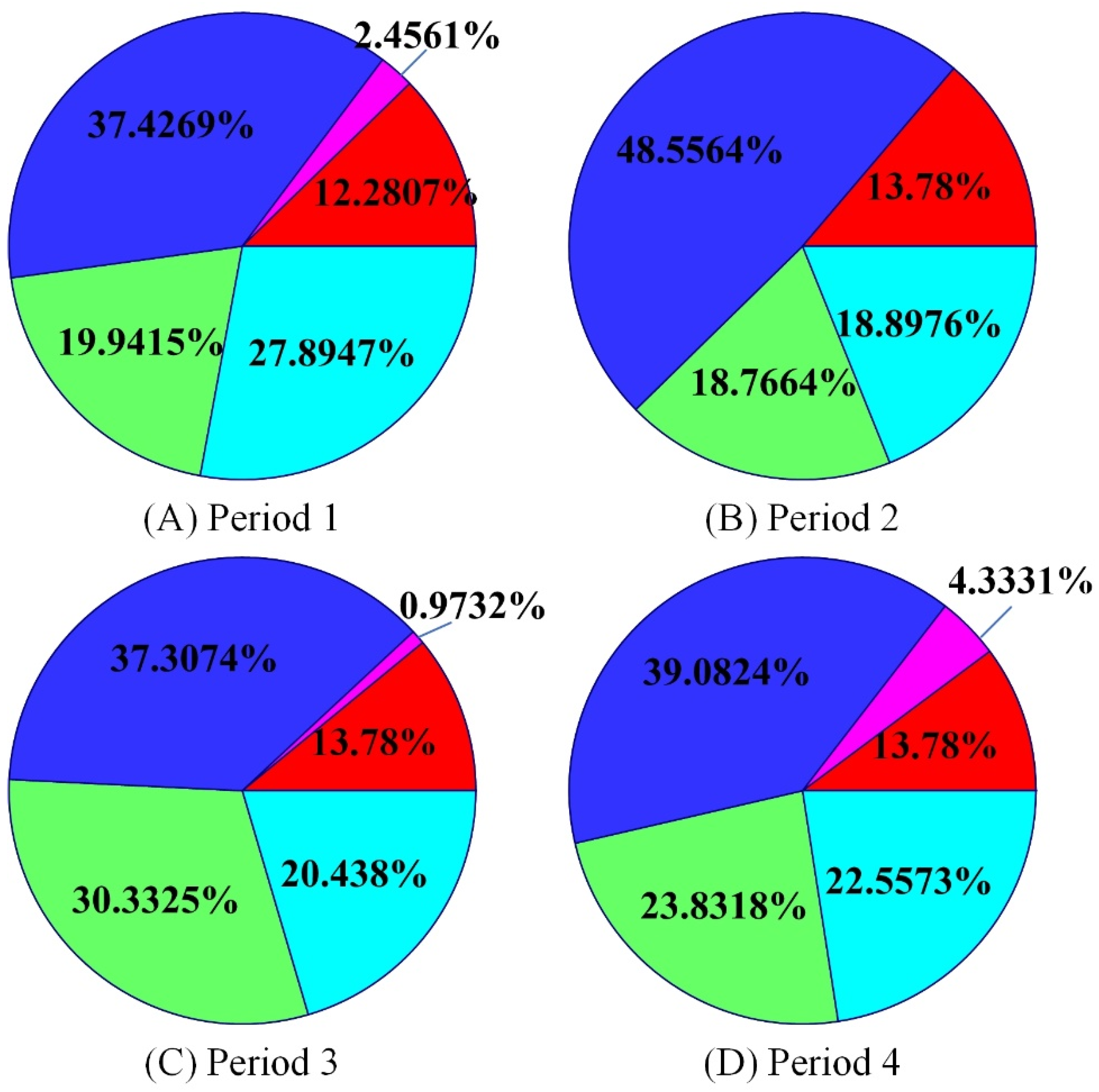
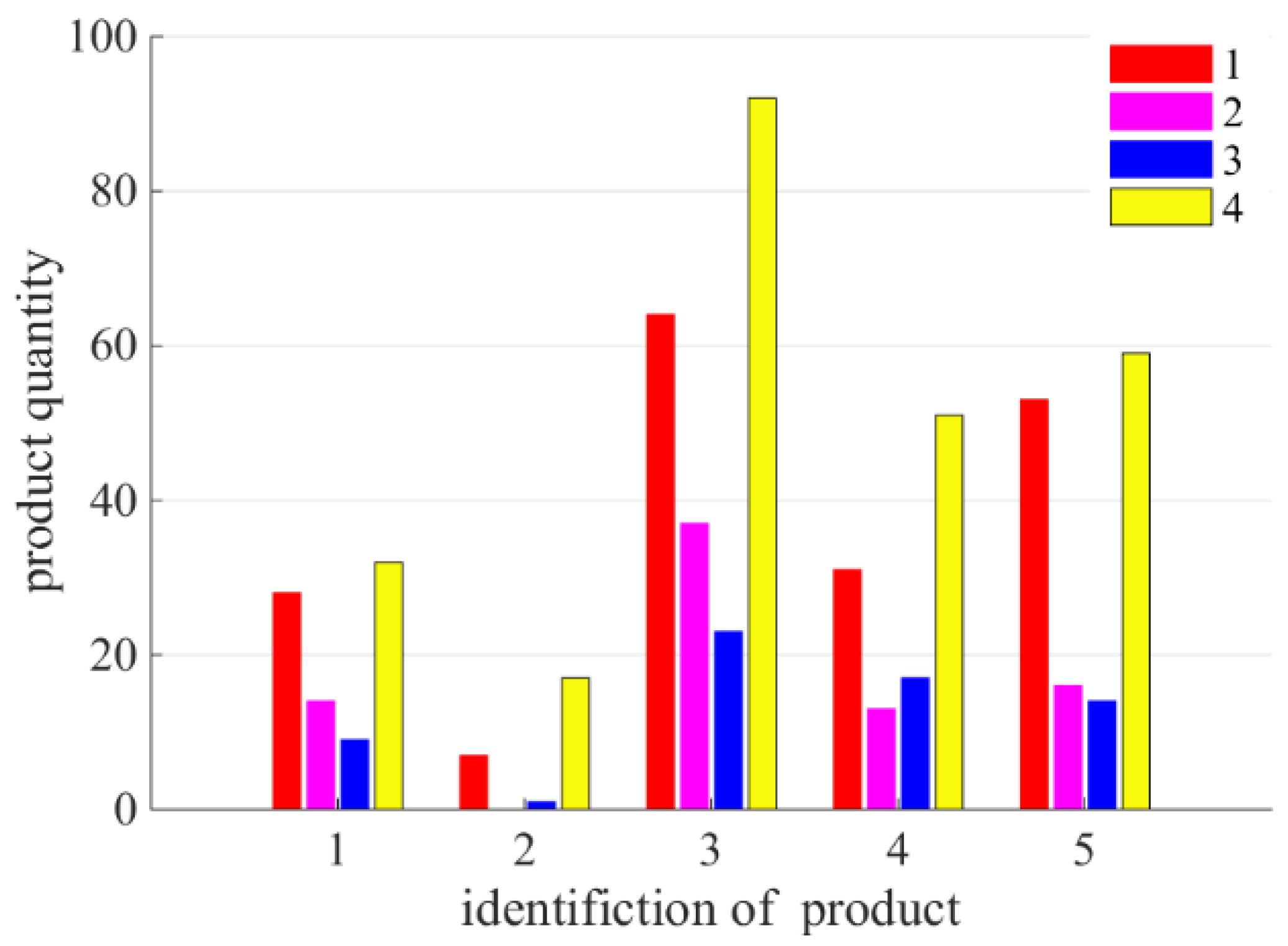

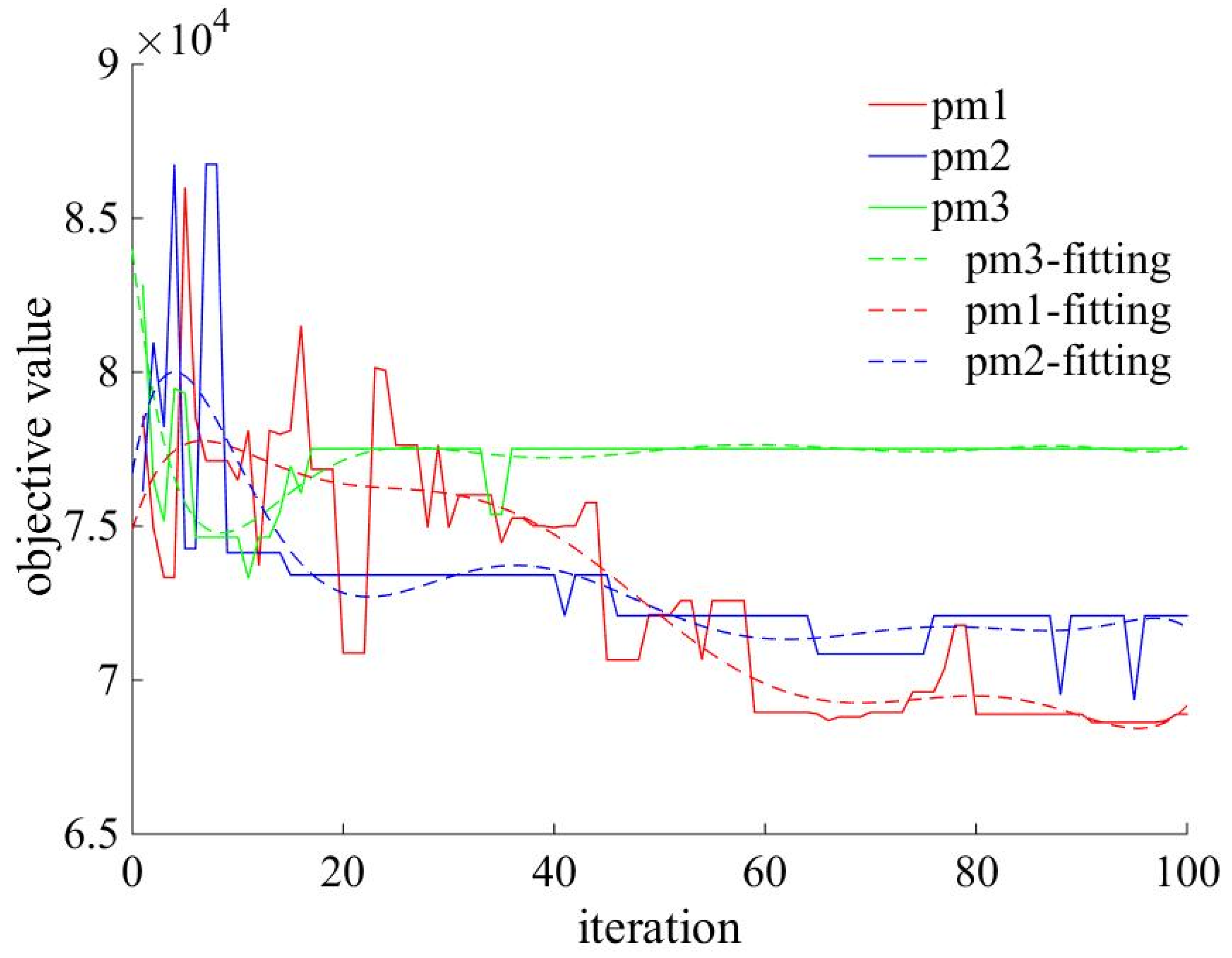
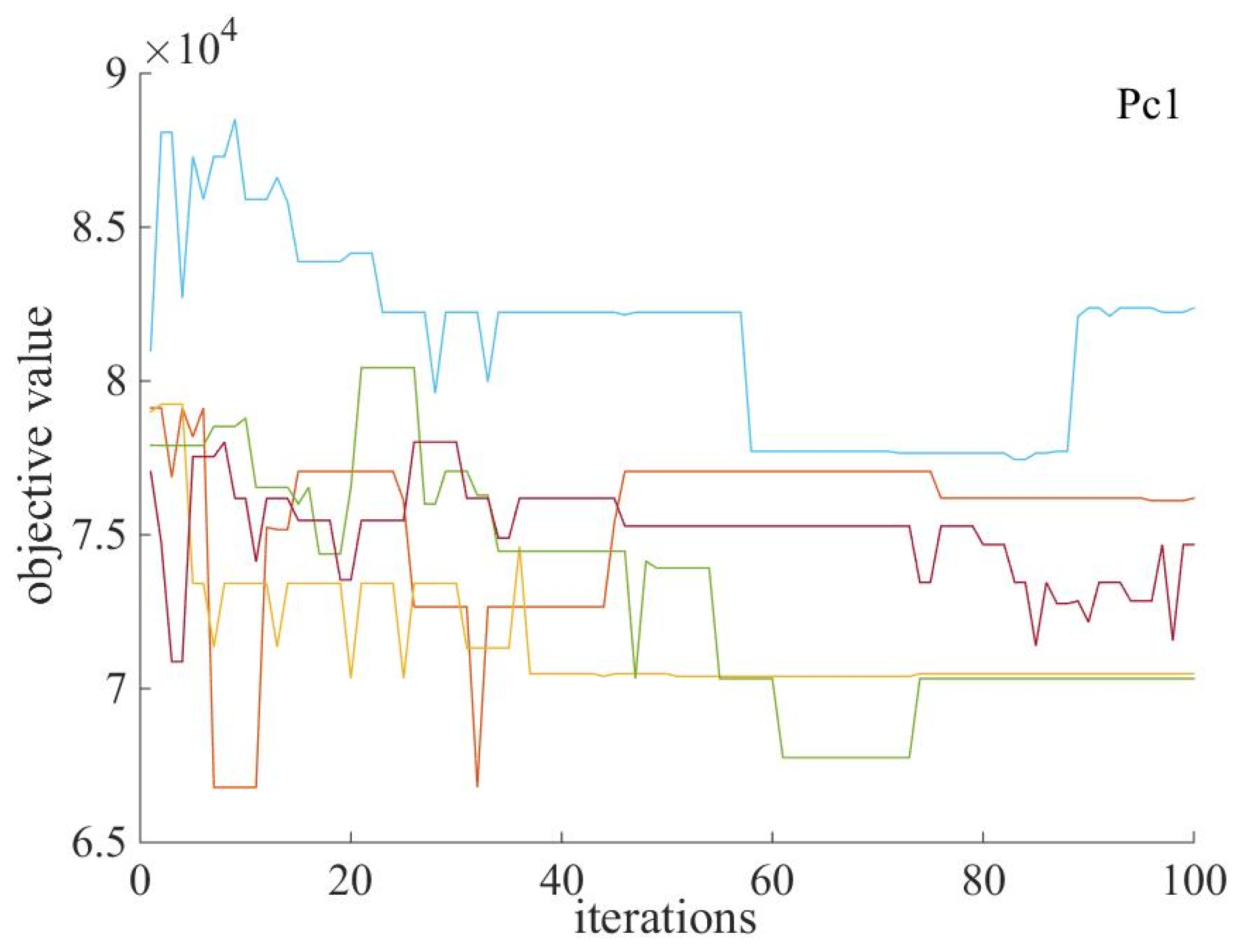
| t = 1,2, …,T: | Planning period |
| i = 1,2, …,n: | Index for product |
| k = 1,2, …,M: | Equipment number |
| E(i): | Set of next-level products that need product i in the production process |
| cit: | Production cost unit product |
| sit: | Setup cost per production of lot-sizing |
| hit: | Inventory cost unit product |
| Dit: | External demand of product i in the planning period t |
| Cakt: | Production capacity of equipment resources k in the planning period t |
| Rij: | The quantity of product i directly needed to produce one unit of product j (gozinto factor) |
| ctkit: | The time cost of unit production of the product i in the equipment resource k during the planning period t |
| stkit: | Time cost of production setup of the product i in the equipment resource k during the planning period t |
| xit: | Output of product i during the planning period t |
| Iit: | Inventory of product i during the planning period t |
| : | Whether the product i is produced in the planning period t; , if otherwise. |
| IF | |||
|---|---|---|---|
| THEN | PB (Pm) | PM (Pm) | PS (Pm) |
| THEN | PB (Pc) | PM (Pc) | PS (Pc) |
| Product Number \Planning Period | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 28 | 14 | 9 | 32 |
| 2 | 6 | 1 | 1 | 17 |
| 3 | 1 | 9 | 4 | 11 |
| 4 | 17 | 13 | 15 | 17 |
| 5 | 18 | 2 | 4 | 10 |
| Equipment Number k\Planning Period t | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 5666 | 5483 | 5427 | 5539 |
| 2 | 5332 | 5437 | 5213 | 5147 |
| 3 | 5189 | 5088 | 5711 | 5225 |
| 4 | 5891 | 5676 | 5367 | 5148 |
| 5 | 5835 | 5274 | 5249 | 5982 |
| 6 | 5442 | 5948 | 5618 | 5596 |
| 7 | 5694 | 5944 | 5902 | 5961 |
| 8 | 5498 | 5342 | 5072 | 5554 |
| 9 | 5625 | 5717 | 5492 | 5336 |
| Level 2\Level 1 Product Number | 1 | 2 |
|---|---|---|
| 3 | 2 | 1 |
| 4 | 0 | 2 |
| 5 | 1 | 1 |
| Equipment Number k | Product Number i | Planning Period t | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 1 | 34\2 | 31\4 | 32\3 | 30\8 |
| 2 | 32\9 | 33\7 | 32\6 | 35\9 | |
| 3 | 31\3 | 33\8 | 33\9 | 34\9 | |
| 4 | 31\4 | 33\5 | 31\6 | 32\8 | |
| 5 | 33\7 | 35\7 | 32\4 | 30\3 | |
| 2 | 1 | 35\8 | 31\8 | 31\4 | 30\2 |
| 2 | 30\2 | 33\5 | 33\5 | 33\6 | |
| 3 | 32\2 | 31\5 | 35\5 | 33\6 | |
| 4 | 34\4 | 34\2 | 35\2 | 35\9 | |
| 5 | 32\3 | 31\7 | 35\4 | 33\7 | |
| 3 | 1 | 33\7 | 35\4 | 34\7 | 30\3 |
| 2 | 34\3 | 30\6 | 30\2 | 32\4 | |
| 3 | 31\3 | 31\8 | 35\9 | 32\4 | |
| 4 | 30\7 | 34\4 | 31\5 | 31\2 | |
| 5 | 33\3 | 30\7 | 33\3 | 33\9 | |
| 4 | 1 | 32\5 | 32\6 | 32\7 | 33\7 |
| 2 | 34\3 | 30\4 | 30\6 | 30\7 | |
| 3 | 33\9 | 31\3 | 32\7 | 33\3 | |
| 4 | 33\3 | 33\9 | 30\9 | 34\7 | |
| 5 | 35\6 | 33\8 | 33\8 | 31\8 | |
| 5 | 1 | 33\4 | 32\6 | 32\6 | 34\8 |
| 2 | 33\8 | 31\2 | 32\2 | 33\5 | |
| 3 | 34\7 | 31\5 | 34\8 | 31\5 | |
| 4 | 31\4 | 33\4 | 34\5 | 31\9 | |
| 5 | 30\2 | 33\5 | 33\5 | 30\8 | |
| 6 | 1 | 31\6 | 32\8 | 33\8 | 34\7 |
| 2 | 31\6 | 34\5 | 31\4 | 31\4 | |
| 3 | 31\9 | 33\8 | 33\3 | 34\8 | |
| 4 | 31\3 | 31\9 | 33\3 | 34\3 | |
| 5 | 35\3 | 34\8 | 32\4 | 31\8 | |
| 7 | 1 | 31\4 | 32\5 | 31\2 | 30\9 |
| 2 | 34\5 | 33\3 | 32\3 | 32\5 | |
| 3 | 34\6 | 33\9 | 32\4 | 33\8 | |
| 4 | 32\3 | 32\3 | 35\4 | 34\3 | |
| 5 | 33\8 | 31\2 | 31\3 | 31\7 | |
| 8 | 1 | 34\5 | 34\6 | 31\3 | 31\9 |
| 2 | 33\8 | 31\7 | 32\7 | 33\6 | |
| 3 | 30\7 | 33\7 | 35\8 | 32\6 | |
| 4 | 30\2 | 32\6 | 32\6 | 31\2 | |
| 5 | 30\7 | 33\3 | 32\7 | 33\6 | |
| 9 | 1 | 30\8 | 32\4 | 30\8 | 35\2 |
| 2 | 30\5 | 34\3 | 32\4 | 35\7 | |
| 3 | 35\7 | 32\7 | 34\7 | 32\3 | |
| 4 | 33\7 | 34\5 | 31\3 | 32\5 | |
| 5 | 30\2 | 32\7 | 35\5 | 35\9 | |
| Parameters\Production Number | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Production cost | 39 | 36 | 31 | 37 | 35 |
| Inventory cost | 59 | 48 | 32 | 53 | 40 |
| Setup cost | 123 | 110 | 117 | 104 | 127 |
| Initial inventory | 5 | 18 | 18 | 1 | 22 |
| Energy costs | 1.5 | 1.2 | 2 | 2.2 | 1.8 |
| Fuzzy Sets\Magnitude | |||
|---|---|---|---|
| PS | 0.01 | 0.1 | 0.001 |
| PM | 0.02 | 0.2 | 0.002 |
| PB | 0.03 | 0.3 | 0.003 |
| Fuzzy Sets\Magnitude | |||
|---|---|---|---|
| PS | 0.1 | 0.1 | 0.1 |
| PM | 0.7 | 0.3 | 0.5 |
| PB | 0.9 | 0.9 | 0.9 |
| Product Number i \Planning Period t | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 28 | 14 | 9 | 32 |
| 2 | 7 | 0 | 1 | 17 |
| 3 | 64 | 37 | 23 | 92 |
| 4 | 31 | 13 | 17 | 51 |
| 5 | 53 | 16 | 14 | 59 |
| Product Type N | Planning Period T | Number of Devices M | Traditional GA | Fuzzy-GA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Optimal Value | Average Optimal Value | Iterations | Running Time (s) | Optimal Value | Average Optimal Value | Iterations | Running Time (s) | |||
| 5 | 5 | 9 | 90,101 | 94,619 | 95 | 4.5174 | 87,629 | 90,839 | 104 | 4.3237 |
| 10 | 5 | 9 | 256,618 | 263,514 | 111 | 5.7030 | 242,461 | 246,960 | 105 | 5.5393 |
| 20 | 5 | 9 | 999,289 | 1,061,107 | 94 | 7.0897 | 908,033 | 944,982 | 97 | 7.6957 |
| 20 | 7 | 9 | 1,406,511 | 1,457,795 | 107 | 9.8041 | 1,349,712 | 1,378,720 | 93 | 9.2876 |
| 20 | 10 | 9 | 1,950,637 | 2,115,856 | 100 | 12.7491 | 2,005,225 | 2,044,097 | 90 | 11.3101 |
| 20 | 10 | 15 | 1,985,502 | 2,020,672 | 95 | 13.3185 | 1,888,792 | 1,905,142 | 85 | 12.2024 |
| 20 | 10 | 20 | 2,515,585 | 2,596,667 | 112 | 16.4103 | 2,410,076 | 2,440,758 | 97 | 15.5662 |
| Product Type N | Planning Period T | Number of Devices M | The Proposed Iteration Condition | 100 Times | 300 Times | 500 Times | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Optimal Value | Running Time (s) | Optimal Value | Running Time (s) | Optimal Value | Running Time (s) | Optimal Value | Running Time (s) | |||
| 5 | 5 | 9 | 87,629 | 4.3237 | 88,748 | 3.3064 | 88,080 | 9.7639 | 86,276 | 16.6609 |
| 10 | 5 | 9 | 242,461 | 5.5393 | 244,647 | 4.3638 | 247,769 | 13.0195 | 241,662 | 21.7165 |
| 20 | 5 | 9 | 908,033 | 7.6957 | 975,467 | 6.4136 | 947,128 | 21.6976 | 918,993 | 33.2535 |
| 20 | 7 | 9 | 1,349,712 | 9.2876 | 1,402,439 | 8.2405 | 1,345,295 | 24.7846 | 1,214,054 | 42.3357 |
| 20 | 10 | 9 | 2,005,225 | 11.3101 | 2,081,146 | 10.7705 | 1,877,778 | 33.7112 | 2,074,800 | 54.1895 |
| 20 | 10 | 15 | 1,888,792 | 12.2024 | 2,148,849 | 11.9693 | 1,984,062 | 37.0395 | 1,977,120 | 58.4784 |
| 20 | 10 | 20 | 2,410,076 | 15.5662 | 2,663,989 | 12.7645 | 2,512,804 | 38.8569 | 2,330,056 | 66.2304 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Hui, J.; Zhu, B.; Liu, Y. Adaptive Genetic Algorithm Based on Fuzzy Reasoning for the Multilevel Capacitated Lot-Sizing Problem with Energy Consumption in Synchronizer Production. Sustainability 2022, 14, 5072. https://doi.org/10.3390/su14095072
Wang S, Hui J, Zhu B, Liu Y. Adaptive Genetic Algorithm Based on Fuzzy Reasoning for the Multilevel Capacitated Lot-Sizing Problem with Energy Consumption in Synchronizer Production. Sustainability. 2022; 14(9):5072. https://doi.org/10.3390/su14095072
Chicago/Turabian StyleWang, Shuai, Jizhuang Hui, Bin Zhu, and Ying Liu. 2022. "Adaptive Genetic Algorithm Based on Fuzzy Reasoning for the Multilevel Capacitated Lot-Sizing Problem with Energy Consumption in Synchronizer Production" Sustainability 14, no. 9: 5072. https://doi.org/10.3390/su14095072
APA StyleWang, S., Hui, J., Zhu, B., & Liu, Y. (2022). Adaptive Genetic Algorithm Based on Fuzzy Reasoning for the Multilevel Capacitated Lot-Sizing Problem with Energy Consumption in Synchronizer Production. Sustainability, 14(9), 5072. https://doi.org/10.3390/su14095072







