Multi-Asset Defect Hotspot Prediction for Highway Maintenance Management: A Risk-Based Machine Learning Approach
Abstract
1. Introduction
- Marginal Attention to the Interrelations Between Asset Classes: Due to the mutual impacts of nearby assets and similar environmental conditions in their proximity, there is a potential correlation between the condition of neighboring asset classes. A few research studies have investigated such correlations [9,10,11]. However, the majority of the developed deterioration models in the literature did not take into consideration such interrelations and investigated the condition of each asset independent from its neighbors [12,13,14,15,16,17,18]. For example, Abaza et al. [12] forecasted pavement condition only based on historical condition data of pavements. As another example, Immaneni et al. [16] developed prediction models for traffic signs only based on age and retroreflectivity data of the signs.
- Shortcomings of Predictive Frameworks in Dealing with Limited Inspection Data: Random inspection of roadways is the current practice of most transportation agencies that restrict the number of segments with adequate historical condition data of road assets. This usually results in discontinuous records of historical conditions on most road segments during all years of inspection. To overcome this limitation, most of the previous studies used the idea of grouping segments with similar deterioration characteristics (family groups) and estimating the average degradation of each group by utilizing a family deterioration model. For example, Mills et al. [19] developed family pavement performance models to help the Delaware DOT in managing road pavements. In another study, Saha et al. [20] used the family group idea to come up with pavement distress deterioration models. However, several challenges come with this approach. Firstly, the condition of specific segments in a family might be different from the average condition of the family. This is mainly attributed to the local variation of contributors to the degradation of assets such as traffic, weather, and maintenance [21]. Secondly, since the number of families highly impacts the accuracy of family deterioration models finding the optimal number of families is still challenging [22].
- Subjective Expert-based Selection of Contributing Factors to Assets Degradation: Several factors impact the condition of roadway assets and could be considered as the contributing factors to their deterioration. For example, the role of material, traffic loading, weather condition, and historical maintenance on the degradation patterns of multiple assets was highlighted in several studies [12,23,24,25,26,27,28,29,30]. For example, the study performed by Anyala et al. [23] highlighted the impacts of the thickness of flexible pavements and the binder type as two main factors on the resistance of the pavement layer against degradation. As another example, Bannour et al. [24] addressed the role of different ranges of pavements structural composition, environment, moisture and traffic conditions on the deterioration of pavements. However, most studies developed deterioration models when a selected number of contributing factors were considered based on experts’ judgment. In addition, historical maintenance activities, as a major factor that improves the condition of highway assets, have received marginal attention in building previous prediction models [31].
- Maximizing the potential of available data in building prediction models by combining machine learning and risk score generator, offering transportation agencies a practical predictive maintenance planning
- Incorporating the interrelations of defects in multiple nearby assets into a defect prediction method
- Developing a data-driven approach to identify and quantify the most significant contributors to the degradation of multiple assets among a wide range of potential candidates
- Creating a scalable learning-based algorithm to improve maintenance planning for a combination of assets by forecasting the occurrence probability of various defects on multiple asset types
2. Related Works
2.1. Machine Learning in Transportation Asset Management
2.2. Risk-Based Predictive Modelling
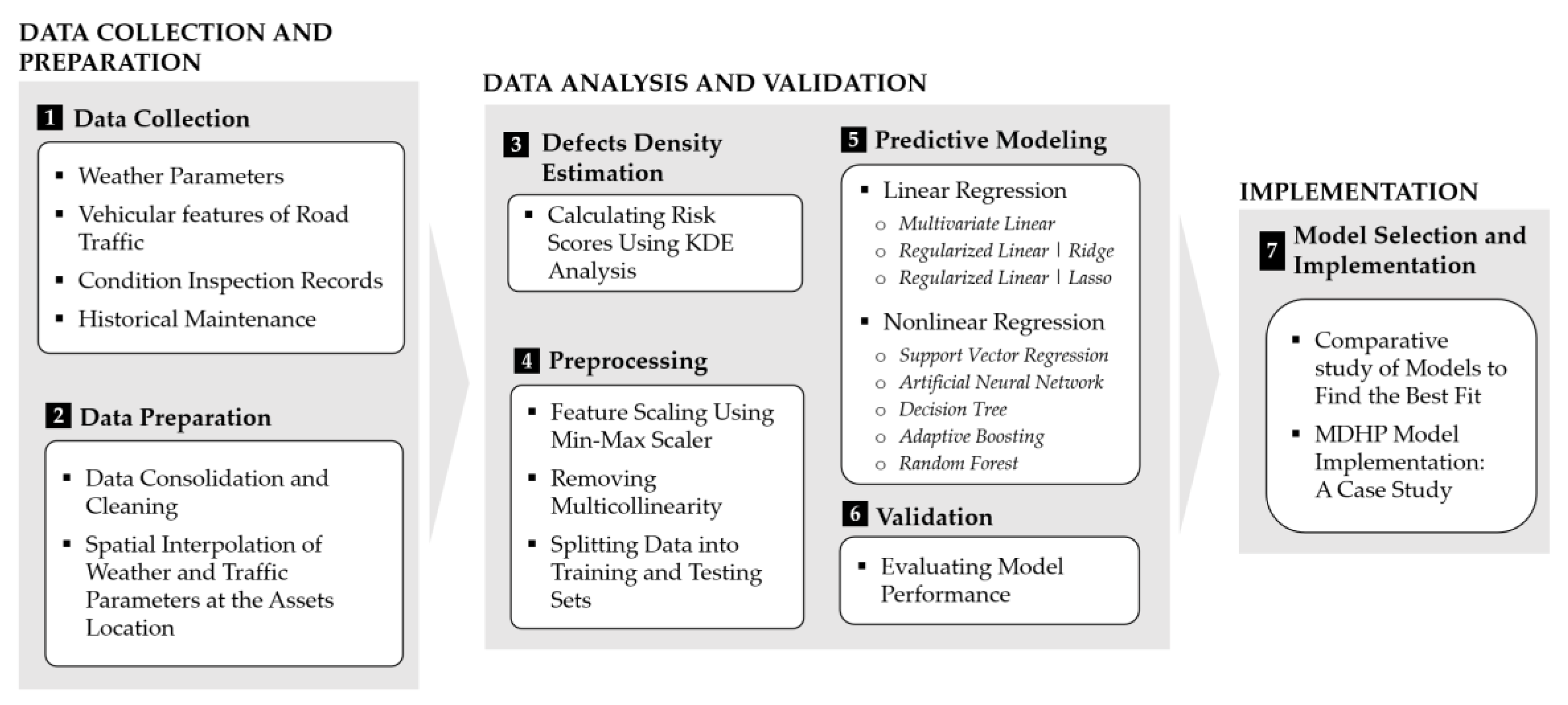
3. Methodology
3.1. Collection of Contributing Factors’ Data
3.2. Data Preparation
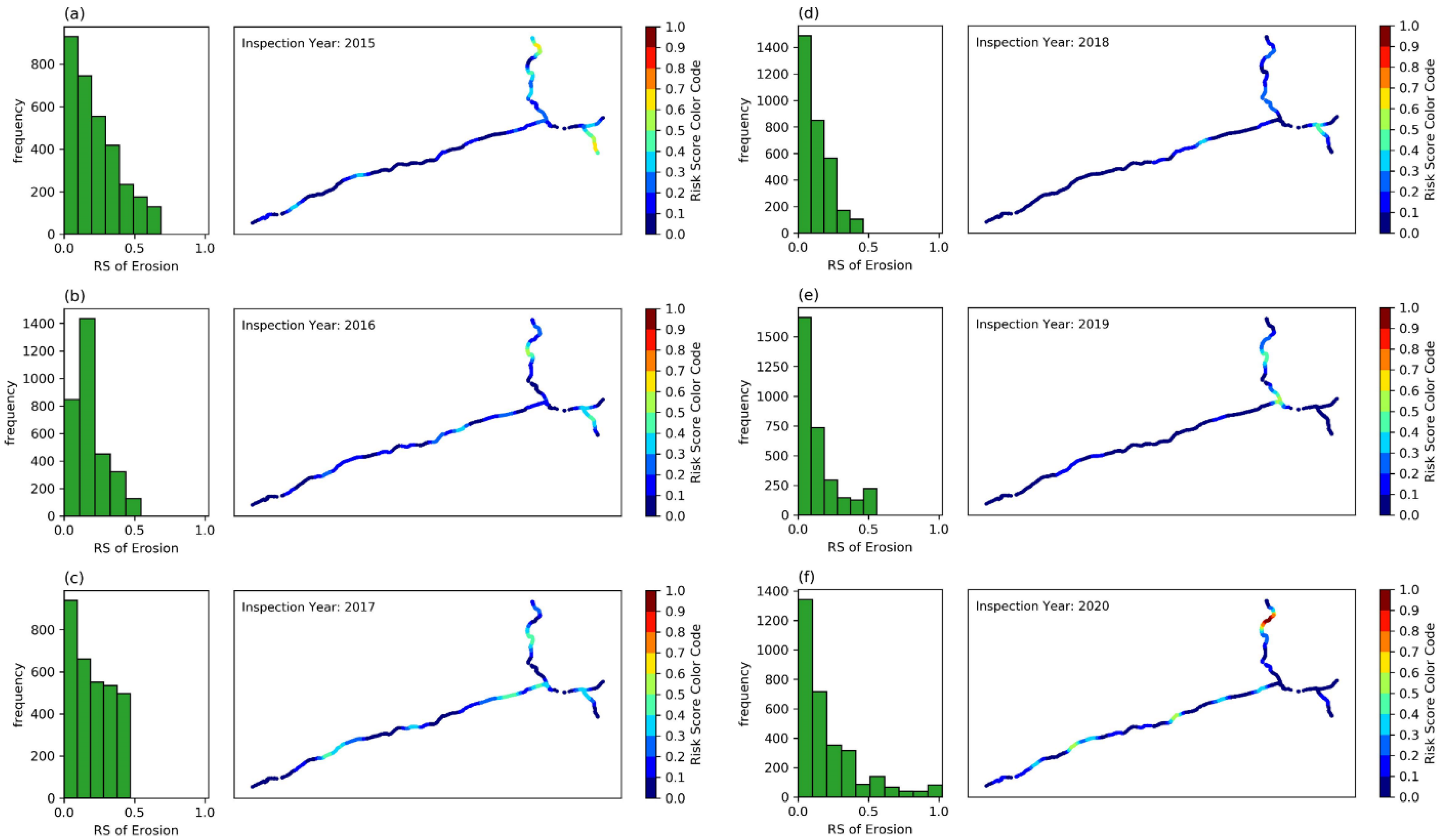
3.3. Density Estimation of Defects
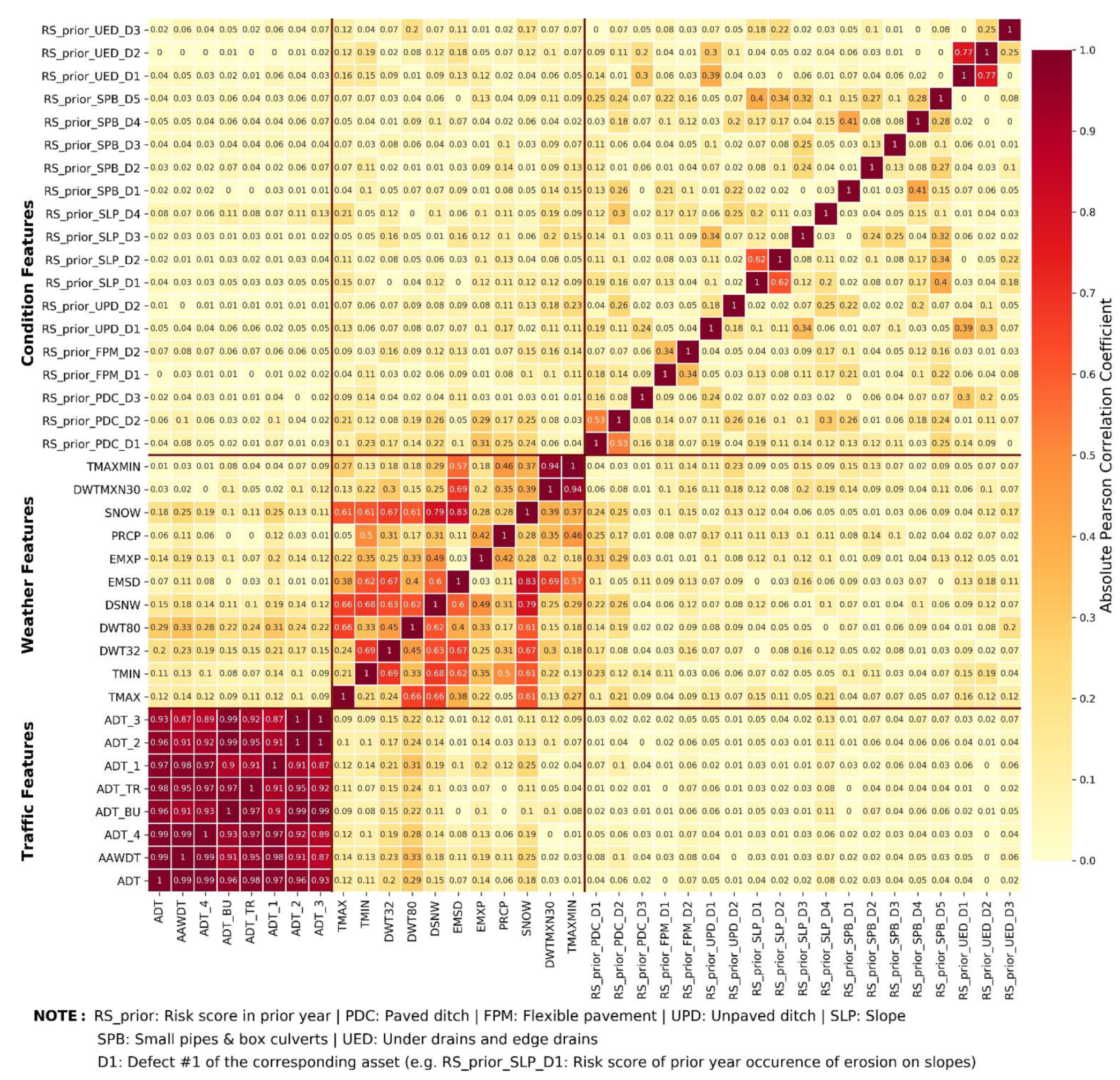
3.4. Preprocessing for Machine Learning (ML)
3.5. Predictive Modelling
3.5.1. Linear Regression
3.5.2. Nonlinear Regression
3.6. Validation
3.7. Model Selection and Implementation
4. Case Study
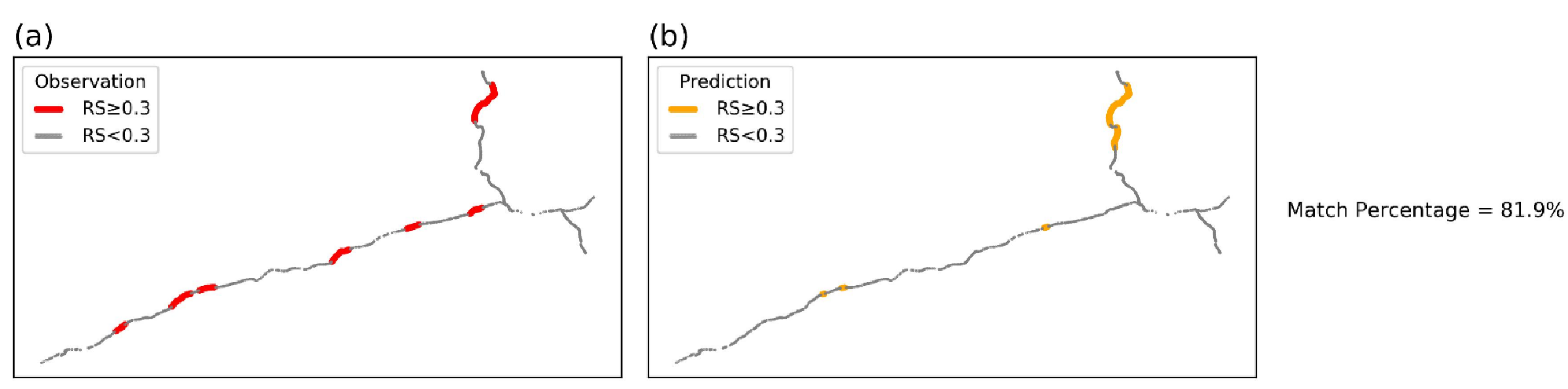
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- NASEM. Critical Issues in Transportation 2019. In The National Academies of Science, Engineering & Medicine; The National Academies Press: Washington, DC, USA, 2019. [Google Scholar]
- AASHTO. AASHTO Transportation Asset Management Guide: A Focus on Implementation; AASHTO: Washington, DC, USA, 2011. [Google Scholar]
- Frangopol, D.M.; Dong, Y.; Sabatino, S. Bridge life-cycle performance and cost: Analysis, prediction, optimization and decision-making. Struct. Infrastruct. Eng. 2017, 13, 1239–1257. [Google Scholar] [CrossRef]
- Kobayashi, K.; Kaito, K. Big data-based deterioration prediction models and infrastructure management: Towards assetmetrics. Struct. Infrastruct. Eng. 2017, 13, 84–93. [Google Scholar] [CrossRef]
- Shoghli, O.; De La Garza, J.M. A multi-objective decision-making approach for the sustainable maintenance of roadways. In Construction Research Congress; American Society of Civil Engineers: Reston, VA, USA, 2016; pp. 1424–1434. [Google Scholar]
- Piryonesi, S.M.; El-Diraby, T. Climate change impact on infrastructure: A machine learning solution for predicting pavement condition index. Constr. Build. Mater. 2021, 306, 124905. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L. A BIM-data mining integrated digital twin framework for advanced project management. Autom. Constr. 2021, 124, 103564. [Google Scholar] [CrossRef]
- Falls, L.C.; Haas, R.; Tighe, S. Asset service index as integration mechanism for civil infrastructure. Transp. Res. Rec. 2006, 1957, 1–7. [Google Scholar] [CrossRef]
- Coffey, S.; Park, S. Observational study on the pavement performance effects of shoulder rumble strip on shoulders. Int. J. Pavement Res. Technol. 2016, 9, 255–263. [Google Scholar] [CrossRef][Green Version]
- Ghabchi, R.; Zaman, M.; Khoury, N.; Kazmee, H.; Solanki, P. Effect of gradation and source properties on stability and drainability of aggregate bases: A laboratory and field study. Int. J. Pavement Eng. 2013, 14, 274–290. [Google Scholar] [CrossRef]
- Karimzadeh, A.; Sabeti, S.; Burde, A.; Tabkhi, H.; Shoghli, O. Spatial-Temporal Deterioration of Multiple Highway Assets: A Correlational Study. In Proceedings of the ASCE Construction Research Congress (CRC)—2020, Tempe, AZ, USA, 8–10 March 2020. [Google Scholar]
- Abaza, K.A. Empirical Markovian-based models for rehabilitated pavement performance used in a life cycle analysis approach. Struct. Infrastruct. Eng. 2017, 13, 625–636. [Google Scholar] [CrossRef]
- Chimba, D.; Emaasit, D.; Allen, S.; Hurst, B.; Nelson, M. Factors affecting median cable barrier crash frequency: New insights. J. Transp. Saf. Secur. 2014, 6, 62–77. [Google Scholar] [CrossRef]
- Elwakil, E.; Eweda, A.; Zayed, T. Modelling the effect of various factors on the condition of pavement marking. Struct. Infrastruct. Eng. 2014, 10, 93–105. [Google Scholar] [CrossRef]
- Halmen, C.; Trejo, D.; Folliard, K. Service Life of Corroding Galvanized Culverts Embedded in Controlled Low-Strength Materials. J. Mater. Civ. Eng. 2008, 20, 366–374. [Google Scholar] [CrossRef]
- Immaneni, V.P.; Hummer, J.E.; Rasdorf, W.J.; Harris, E.A.; Yeom, C. Synthesis of sign deterioration rates across the United States. J. Transp. Eng. 2009, 135, 94–103. [Google Scholar] [CrossRef]
- Malyuta, D.A. Analysis of Factors Affecting Pavement Markings and Pavement Marking Retroreflectivity in Tennessee Highways. University of Tennessee at Chattanooga. Ph.D. Thesis, University of Tennessee at Chattanooga, Chattanooga, TN, USA, 2015. [Google Scholar]
- Sitzabee, W.E.; White, E.D.; Dowling, A.W. Degradation modeling of polyurea pavement markings. Public Work. Manag. Policy 2012, 18, 185–199. [Google Scholar] [CrossRef]
- Mills LN, O.; Attoh-Okine, N.O.; McNeil, S. Developing pavement performance models for Delaware. Transp. Res. Rec. 2012, 2304, 97–103. [Google Scholar] [CrossRef]
- Saha, P.; Ksaibati, K.; Atadero, R. Developing Pavement Distress Deterioration Models for Pavement Management System Using Markovian Probabilistic Process. Adv. Civ. Eng. 2017, 2017, 8292056. [Google Scholar] [CrossRef]
- Pantuso, A.; Flintsch, G.W.; Katicha, S.W.; Loprencipe, G. Development of network-level pavement deterioration curves using the linear empirical Bayes approach. Int. J. Pavement Eng. 2019, 22, 780–793. [Google Scholar] [CrossRef]
- Karimzadeh, A.; Sabeti, S.; Shoghli, O. Optimal Clustering of Pavement Segments Using K-Prototype Algorithm in a High-Dimensional Mixed Feature Space. J. Manag. Eng. 2021, 37, 04021022. [Google Scholar] [CrossRef]
- Anyala, M.; Odoki, J.; Baker, C. Hierarchical asphalt pavement deterioration model for climate impact studies. Int. J. Pavement Eng. 2014, 15, 251–266. [Google Scholar] [CrossRef]
- Bannour, A.; El Omari, M.; Lakhal, E.K.; Afechkar, M.; Benamar, A.; Joubert, P. Optimization of the maintenance strategies of roads in Morocco: Calibration study of the degradations models of the highway development and management (HDM-4) for flexible pavements. Int. J. Pavement Eng. 2017, 20, 245–254. [Google Scholar] [CrossRef]
- Ford, K.M.; Arman, M.; Labi, S.; Sinha, K.C.; Thompson, P.; Shirole, A.; Li, Z. Estimating Life Expectancies of Highway Assets—Volume 2: Final Report; Transportation Research Board, National Academy of Sciences: Washington, DC, USA, 2012. [Google Scholar]
- Hong, F.; Prozzi, J.A. Roughness model accounting for heterogeneity based on in-service pavement performance data. J. Transp. Eng. 2010, 136, 205–213. [Google Scholar] [CrossRef]
- Labi, S.; Sinha, K.C. Measures of short-term effectiveness of highway pavement maintenance. J. Transp. Eng. 2003, 129, 673–683. [Google Scholar] [CrossRef]
- Prozzi, J.A.; Serigos, P.A.; Kim, M.Y.; Xu, H. Deterioration Modelling of Preventive Maintenance Treatments for Flexible Pavements; University of Texas at Austin: Austin, TX, USA, 2017. [Google Scholar]
- Ré, J.; Miles, J.; Carlson, P. Analysis of in-service traffic sign retroreflectivity and deterioration rates in Texas. Transp. Res. Rec. 2011, 2258, 88–94. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Z.; Tsai, Y.-C. Piecewise Multiple Linear Models for Pavement Marking Retroreflectivity Prediction Under Effect of Winter Weather Events. Transp. Res. Rec. 2016, 2551, 52–61. [Google Scholar] [CrossRef]
- Karimzadeh, A.; Shoghli, O. Predictive analytics for roadway maintenance: A review of current models, challenges, and opportunities. Civ. Eng. J. 2020, 6, 602–625. [Google Scholar] [CrossRef]
- Hunt, P.D.; Bunker, J.M. Study of site-specific roughness progression for a bitumen-sealed unbound granular pavement network. Transp. Res. Rec. 2003, 1819, 273–281. [Google Scholar] [CrossRef]
- Von Quintus, H.L.; Eltahan, A.; Yau, A. Smoothness models for hot-mix asphalt-surfaced pavements: Developed from long-term pavement performance program data. Transp. Res. Rec. 2001, 1764, 139–156. [Google Scholar] [CrossRef]
- Kargah-Ostadi, N.; Stoffels, S.M. Framework for development and comprehensive comparison of empirical pavement performance models. J. Transp. Eng. 2015, 141, 04015012. [Google Scholar] [CrossRef]
- Swargam, N. Development of a Neural Network Approach for the Assessment of the Performance of Traffic Sign Retroreflectivity. Master’s Thesis, Lousiana State University, Civil and Environmental Engineering, Baton Rouge, LA, USA, 2004. [Google Scholar]
- Haider, S.W.; Chatti, K. Effect of design and site factors on fatigue cracking of new flexible pavements in the LTPP SPS-1 experiment. Int. J. Pavement Eng. 2009, 10, 133–147. [Google Scholar] [CrossRef]
- Karwa, V.; Donnell, E.T. Predicting pavement marking retroreflectivity using artificial neural networks: Exploratory analysis. J. Transp. Eng. 2011, 137, 91–103. [Google Scholar] [CrossRef]
- Karlaftis, A.G.; Badr, A. Predicting asphalt pavement crack initiation following rehabilitation treatments. Transp. Res. Part C Emerg. Technol. 2015, 55, 510–517. [Google Scholar] [CrossRef]
- Marcelino, P.; de Lurdes Antunes, M.; Fortunato, E.; Gomes, M.C. Machine learning approach for pavement performance prediction. Int. J. Pavement Eng. 2021, 22, 341–354. [Google Scholar] [CrossRef]
- Wang, W.-C.; Chau, K.-W.; Qiu, L.; Chen, Y.-B. Improving forecasting accuracy of medium and long-term runoff using artificial neural network based on EEMD decomposition. Environ. Res. 2015, 139, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Chopra, T.; Parida, M.; Kwatra, N.; Chopra, P. Development of Pavement Distress Deterioration Prediction Models for Urban Road Network Using Genetic Programming. Adv. Civ. Eng. 2018, 2018, 1253108. [Google Scholar] [CrossRef]
- Sanabria, N.; Valentin, V.; Bogus, S.; Zhang, G.; Kalhor, E. Comparing Neural Networks and Ordered Probit Models for Forecasting Pavement Condition in New Mexico. In Proceedings of the Transportation Research Board 96th Annual Meeting, Washington, DC, USA, 8–12 January 2017. [Google Scholar]
- Proctor, G.; Varma, S. Risk-Based Transportation Asset Management: Evaluating Threats, Capitalizing on Opportunities: Report 1: Overview of Risk Management; National Academy of Sciences: Washington, DC, USA, 2012. [Google Scholar]
- Renn, O. Risk Governance: Coping with Uncertainty in a Complex World; Earthscan: London, UK, 2008. [Google Scholar]
- Kuter, N.; Kuter, S. Investigation of wildfire at forested landscapes: A novel contribution to nonparametric density mapping at regional scale. Appl. Ecol. Environ. Res. 2018, 16, 4701–4716. [Google Scholar] [CrossRef]
- Massada, A.B.; Radeloff, V.C.; Stewart, S.I.; Hawbaker, T.J. Wildfire risk in the wildland–urban interface: A simulation study in northwestern Wisconsin. For. Ecol. Manag. 2009, 258, 1990–1999. [Google Scholar] [CrossRef]
- Millington, J.; Romero-Calcerrada, R.; Wainwright, J.; Perry, G. An agent-based model of Mediterranean agricultural land-use/cover change for examining wildfire risk. J. Artif. Soc. Soc. Simul. 2008, 11, 4. [Google Scholar]
- Gaull, B.; Michael-Leiba, M.; Rynn, J. Probabilistic earthquake risk maps of Australia. Aust. J. Earth Sci. 1990, 37, 169–187. [Google Scholar] [CrossRef]
- Erdogan, S. Explorative spatial analysis of traffic accident statistics and road mortality among the provinces of Turkey. J. Saf. Res. 2009, 40, 341–351. [Google Scholar] [CrossRef]
- Rahman, M.K.; Crawford, T.; Schmidlin, T.W. Spatio-temporal analysis of road traffic accident fatality in Bangladesh integrating newspaper accounts and gridded population data. GeoJournal 2018, 83, 645–661. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X. An ontology-based traffic accident risk mapping framework. In Proceedings of the International Symposium on Spatial and Temporal Databases, Minneapolis, MN, USA, 24–26 August 2011. [Google Scholar]
- Hunt, R.E. Slope failure risk mapping for highways: Methodology and case history. Transp. Res. Rec. 1992, 1343, 42–51. [Google Scholar]
- Sohn, J. Evaluating the significance of highway network links under the flood damage: An accessibility approach. Transp. Res. Part A Policy Pract. 2006, 40, 491–506. [Google Scholar] [CrossRef]
- Wright, L.; Chinowsky, P.; Strzepek, K.; Jones, R.; Streeter, R.; Smith, J.B.; Mayotte, J.-M.; Powell, A.; Jantarasami, L.; Perkins, W. Estimated effects of climate change on flood vulnerability of US bridges. Mitig. Adapt. Strateg. Glob. Change 2012, 17, 939–955. [Google Scholar] [CrossRef]
- Anderson, C.J.; Claman, D.; Mantilla, R. Iowa’s Bridge and Highway Climate Change and Extreme Weather Vulnerability Assessment Pilot; Institute for Transportation: Ames, IA, USA, 2015. [Google Scholar]
- Lu, D. Pavement Flooding Risk Assessment and Management in the Changing Climate. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2020. [Google Scholar]
- da Silva AS, A.; Stosic, B.; Menezes RS, C.; Singh, V.P. Comparison of Interpolation Methods for Spatial Distribution of Monthly Precipitation in the State of Pernambuco, Brazil. J. Hydrol. Eng. 2019, 24, 04018068. [Google Scholar] [CrossRef]
- Frazier, A.G.; Giambelluca, T.W.; Diaz, H.F.; Needham, H.L. Comparison of geostatistical approaches to spatially interpolate month-year rainfall for the Hawaiian Islands. Int. J. Climatol. 2016, 36, 1459–1470. [Google Scholar] [CrossRef]
- Plouffe, C.C.; Robertson, C.; Chandrapala, L. Comparing interpolation techniques for monthly rainfall mapping using multiple evaluation criteria and auxiliary data sources: A case study of Sri Lanka. Environ. Model. Softw. 2015, 67, 57–71. [Google Scholar] [CrossRef]
- Anderson, T.K. Kernel density estimation and K-means clustering to profile road accident hotspots. Accid. Anal. Prev. 2009, 41, 359–364. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; CRC Press: Boca Raton, FL, USA, 1986; Volume 26. [Google Scholar]
- Chainey, S.; Ratcliffe, J. GIS and Crime Mapping; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Aksoy, S.; Haralick, R.M. Feature normalization and likelihood-based similarity measures for image retrieval. Pattern Recognit. Lett. 2001, 22, 563–582. [Google Scholar] [CrossRef]
- Yoo, W.; Mayberry, R.; Bae, S.; Singh, K.; He, Q.P.; Lillard, J.W., Jr. A study of effects of multicollinearity in the multivariable analysis. Int. J. Appl. Sci. Technol. 2014, 4, 9. [Google Scholar]
- Leggetter, C.; Woodland, P.C. Speaker adaptation of continuous density HMMs using multivariate linear regression. Int. Conf. Spok. Lang. Process. 1994, 94, 451–454. [Google Scholar]
- Yuan, M.; Ekici, A.; Lu, Z.; Monteiro, R. Dimension reduction and coefficient estimation in multivariate linear regression. J. R. Stat. Soc. Ser. B 2007, 69, 329–346. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning (Vol. 1): Springer Series in Statistics New York; Springer: New York, NY, USA, 2001. [Google Scholar]
- Clarke, S.M.; Griebsch, J.H.; Simpson, T.W. Analysis of support vector regression for approximation of complex engineering analyses. J. Mech. Des. 2005, 127, 1077–1087. [Google Scholar] [CrossRef]
- Wu, C.-H.; Tzeng, G.-H.; Lin, R.-H. A Novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression. Expert Syst. Appl. 2009, 36, 4725–4735. [Google Scholar] [CrossRef]
- Cohen, S.; Intrator, N. A study of ensemble of hybrid networks with strong regularization. In Proceedings of the International Workshop on Multiple Classifier Systems, Guildford, UK, 11–13 June 2003. [Google Scholar]
- Yilmaz, I.; Kaynar, O. Multiple regression, ANN (RBF, MLP) and ANFIS models for prediction of swell potential of clayey soils. Expert Syst. Appl. 2011, 38, 5958–5966. [Google Scholar] [CrossRef]
- Tso, G.K.; Yau, K.K. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Schapire, R.E. The boosting approach to machine learning: An overview. In Nonlinear Estimation and Classification; Springer: Berlin/Heidelberg, Germany, 2003; pp. 149–171. [Google Scholar]
- Karabulut, E.M.; Ibrikci, T. Analysis of cardiotocogram data for fetal distress determination by decision tree based adaptive boosting approach. J. Comput. Commun. 2014, 2, 32–37. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2019, 569, 387–408. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Suen, Y.L.; Melville, P.; Mooney, R.J. Combining bias and variance reduction techniques for regression trees. In Proceedings of the European Conference on Machine Learning, Porto, Portugal, 3–7 October 2005. [Google Scholar]
- VDOT. Bundled Interstate Maintenance Services (BIMS): Instructions, Asset and Activity Codes for Reports Manual, Virginia Department of Transportation (VDOT); ProQuest LLC: Ann Arbor, MI, USA, 2014.
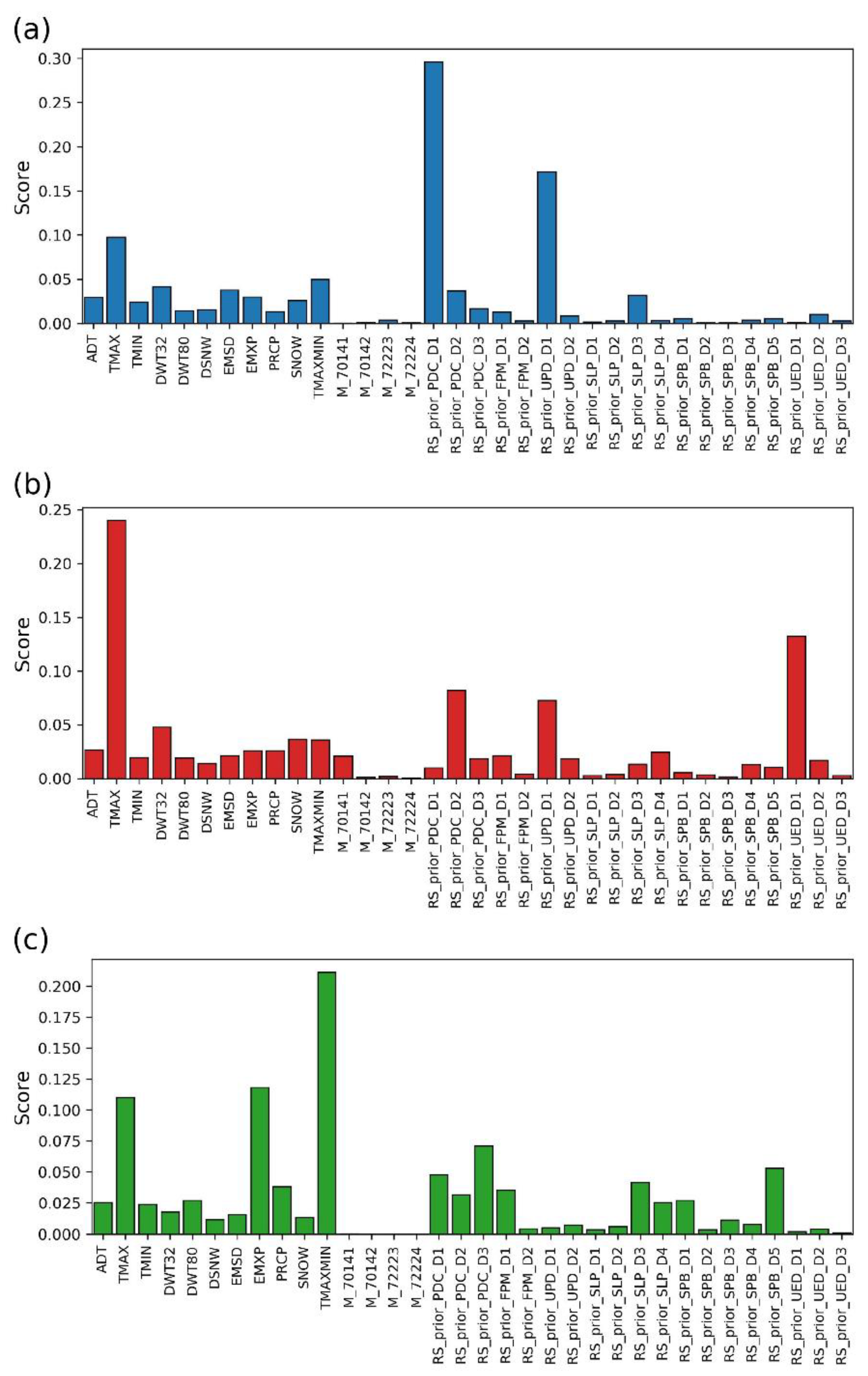
- Strobl, C.; Boulesteix, A.-L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef]
- North, M.A. A method for implementing a statistically significant number of data classes in the Jenks algorithm. In Proceedings of the 2009 Sixth International Conference on Fuzzy Systems and Knowledge Discovery, Tianjin, China, 14–16 August 2009. [Google Scholar]




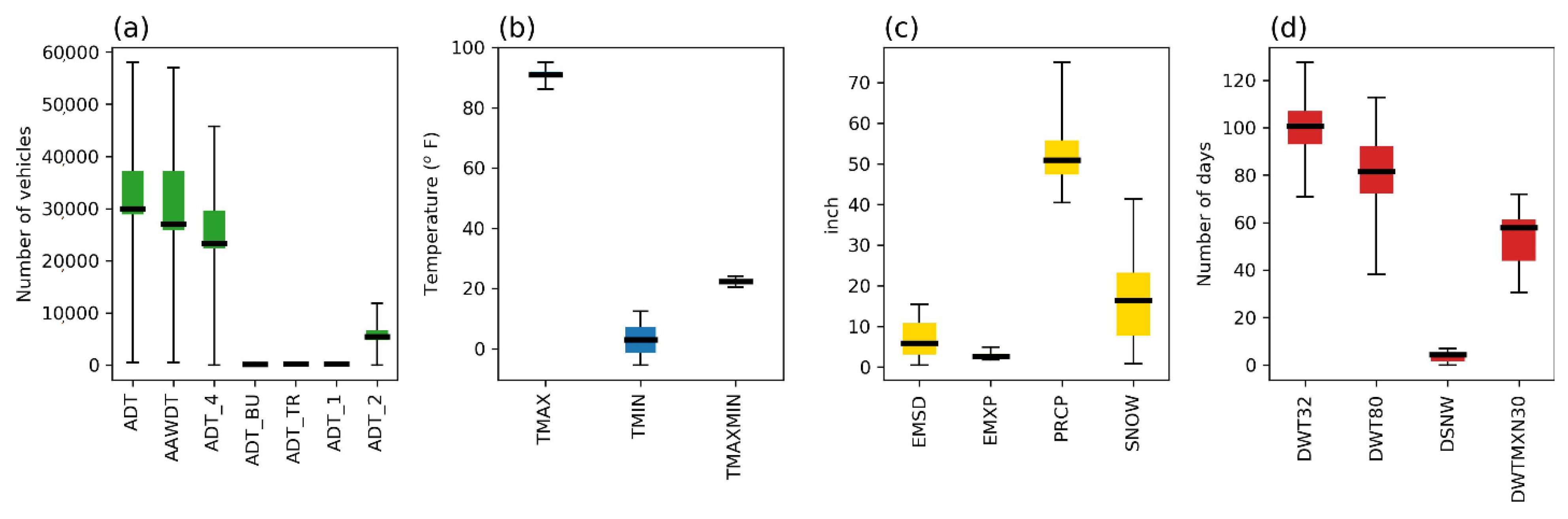




| Index | Parameter | Definition |
|---|---|---|
| 1 | TMAX | Annual maximum daily temperature (°C) |
| 2 | TMIN | Annual minimum daily temperature (°C) |
| 3 | TMAXMIN | Annual average of daily max-min temperature difference (°C) |
| 4 | DWT32 | Number of days with minimum temperature < 0 °C (32 °F) in a year |
| 5 | DWT80 | Number of days with maximum temperature > 26.7 °C (80 °F) in a year |
| 6 | DWTMXN30 | Number of days with Tmax-Tmin > 16.7 °C (30 °F) in a year |
| 7 | DSNW | Number of days with snow depth > 2.54 cm (1 inch) in a year |
| 8 | EMSD | Maximum annual daily snow depth (cm) |
| 9 | EMXP | Maximum annual daily precipitation depth (cm) |
| 10 | PRCP | Total annual precipitation (cm) |
| 11 | SNOW | Total annual snow depth (cm) |
| Index | Parameter | Definition |
|---|---|---|
| 1 | ADT | Average daily traffic (number of vehicles per day) |
| 2 | AAWDT | Average annual weekday traffic (number of vehicles per day) |
| 3 | ADT_4 | Average daily traffic of 4-tire vehicles (number of vehicles per day) |
| 4 | ADT_BU | Average daily traffic of buses (number of vehicles per day) |
| 5 | ADT_TR | Average daily traffic of trucks with 1 trailer (number of vehicles per day) |
| 6 | ADT_1 | Average daily traffic of trucks with 2 axles (number of vehicles per day) |
| 7 | ADT_2 | Average daily traffic of trucks with 2 trailers (number of vehicles per day) |
| 8 | ADT_3 | Average daily traffic of trucks with 3 axles (number of vehicles per day) |
| Index | Code | Maintenance Name | Description |
|---|---|---|---|
| 1 | M_70141 | Hand Cleaning | Hand cleaning of drainage assets, traffic control devices, shoulders, tunnels, ferries, etc. Cleaning with manual tools (shovels, pickaxes, etc.). Cleaning without the use of machinery. |
| 2 | M_70142 | Machine Cleaning/Mechanical Sweeping | Machine cleaning or sweeping of drainage assets such as pipes, ditches, etc.; tunnels; roadside assets such as sidewalks, truck ramps, pedestrian trails, walls, etc.; traffic assets such as rumble strips; pavement assets including roads, and paved shoulders, etc. Also, to be used for cleaning when using pressurized water such as power washing. |
| 3 | M_71152 | Seeding, Fertilizing, Mulching (Serv) | Seeding, fertilizing, mulching, sodding, soiling, spreading lime. The cyclical and regular replacement and maintenance of vegetation to combat erosion. |
| 4 | M_72223 | Concrete Patching/Repair-Drainage (Serv) | Patching holes, blow-ups, and other irregularities on concrete surfaces for drainage assets. This activity includes cutting and removing damaged concrete and patching concrete areas. |
| 5 | M_72224 | Concrete Joint Repair-Drainage (Serv) | Removing and replacing joint filler, pouring joints, trimming joints, joint patching, and other maintenance of drainage concrete joints. |
| Asset Type | Acronym | Defects | ||||
|---|---|---|---|---|---|---|
| D1 | D2 | D3 | D4 | D5 | ||
| Flexible Pavement | FPM | Pothole | Patch | - | - | - |
| Paved Ditch | PDC | Erosion | Obstruction | Cracking | - | - |
| Unpaved Ditch | UPD | Erosion | Obstruction | - | - | - |
| Slope | SLP | Erosion | Erosion Pattern | Lower Slope | Higher Slope | - |
| Small Pipes and Box Culverts | SPB | Pipe Obstruction | Pipe Joint | Pipe Erosion | Pipe Vegetation | End Wall |
| Under Drains and Edge Drains | UED | Drain Outlet Damage | Drain Obstruction | End Protection | - | - |
| M_71152 | M_70141 | M_70142 | M_72223 | M_72224 | |
| M_71152 | N/A | 9.08 × 10−219 | 6.60 × 10−147 | 1.04 × 10−5 | 5.22 × 10−2 |
| M_70141 | 9.08 × 10−219 | N/A | 0.00 | 9.14 × 10−260 | 8.26 × 10−25 |
| M_70142 | 6.60 × 10−147 | 0.00 | N/A | 7.22 × 10−159 | 1.99 × 10−42 |
| M_72223 | 1.04 × 10−5 | 9.14 × 10−260 | 7.22 × 10−159 | N/A | 0.00 |
| M_72224 | 5.22 × 10−2 | 8.26 × 10−25 | 1.99 × 10−42 | 0.00 | N/A |
| Utilized ML Algorithm | Erosion | Obstruction | Cracking | |||
|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | |
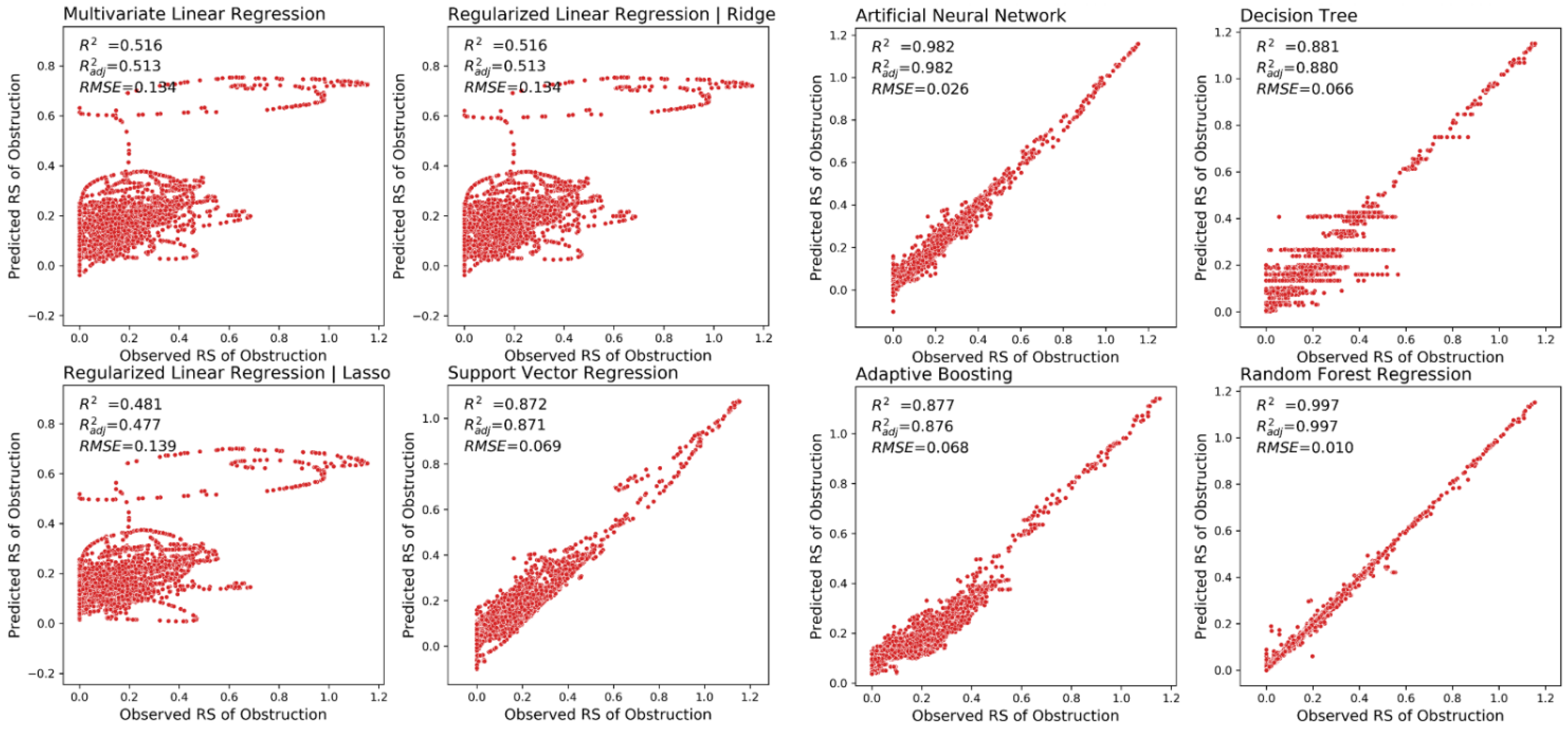
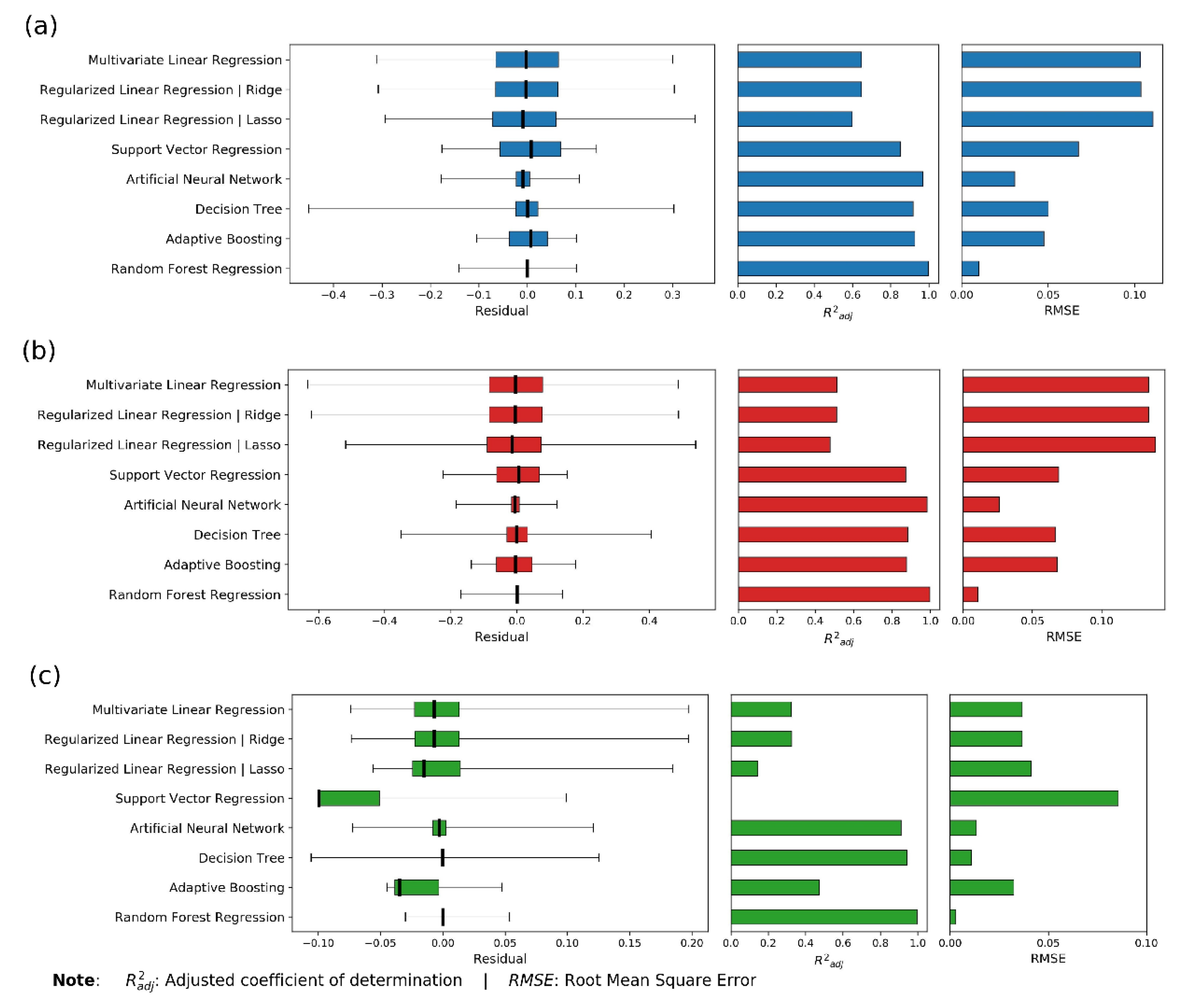
| Multivariate Linear Regression | 0.642 | 0.652 | 0.515 | 0.516 | 0.317 | 0.330 |
| Regularized Linear Regression | Ridge | 0.641 | 0.651 | 0.515 | 0.516 | 0.316 | 0.330 |
| Regularized Linear Regression | Lasso | 0.600 | 0.602 | 0.479 | 0.481 | 0.127 | 0.150 |
| Support Vector Regression | 0.845 | 0.852 | 0.871 | 0.872 | −2.575 | −2.638 |
| Artificial Neural Network | 0.968 | 0.969 | 0.982 | 0.982 | 0.919 | 0.911 |
| Decision Tree | 0.918 | 0.918 | 0.886 | 0.881 | 0.951 | 0.942 |
| Adaptive Boosting | 0.926 | 0.927 | 0.876 | 0.877 | 0.493 | 0.477 |
| Random Forest Regression | 0.999 | 0.997 | 0.999 | 0.997 | 0.999 | 0.996 |
| Algorithm | Erosion | Obstruction | Cracking | |||
|---|---|---|---|---|---|---|
| Min Score | Max Score | Min Score | Max Score | Min Score | Max Score | |
| Multivariate Linear Regression | 0.614 | 0.672 | 0.480 | 0.546 | 0.285 | 0.350 |
| Regularized Linear Regression | Ridge | 0.615 | 0.67 | 0.481 | 0.546 | 0.286 | 0.349 |
| Regularized Linear Regression | Lasso | 0.583 | 0.623 | 0.453 | 0.502 | 0.103 | 0.162 |
| Support Vector Regression | 0.834 | 0.865 | 0.873 | 0.877 | −2.997 | −2.224 |
| Artificial Neural Network | 0.973 | 0.984 | 0.984 | 0.990 | 0.914 | 0.937 |
| Decision Tree | 0.893 | 0.927 | 0.829 | 0.891 | 0.933 | 0.963 |
| Adaptive Boosting | 0.919 | 0.939 | 0.872 | 0.910 | 0.390 | 0.624 |
| Random Forest Regression | 0.996 | 0.999 | 0.998 | 0.999 | 0.997 | 0.999 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimzadeh, A.; Shoghli, O.; Sabeti, S.; Tabkhi, H. Multi-Asset Defect Hotspot Prediction for Highway Maintenance Management: A Risk-Based Machine Learning Approach. Sustainability 2022, 14, 4979. https://doi.org/10.3390/su14094979
Karimzadeh A, Shoghli O, Sabeti S, Tabkhi H. Multi-Asset Defect Hotspot Prediction for Highway Maintenance Management: A Risk-Based Machine Learning Approach. Sustainability. 2022; 14(9):4979. https://doi.org/10.3390/su14094979
Chicago/Turabian StyleKarimzadeh, Arash, Omidreza Shoghli, Sepehr Sabeti, and Hamed Tabkhi. 2022. "Multi-Asset Defect Hotspot Prediction for Highway Maintenance Management: A Risk-Based Machine Learning Approach" Sustainability 14, no. 9: 4979. https://doi.org/10.3390/su14094979
APA StyleKarimzadeh, A., Shoghli, O., Sabeti, S., & Tabkhi, H. (2022). Multi-Asset Defect Hotspot Prediction for Highway Maintenance Management: A Risk-Based Machine Learning Approach. Sustainability, 14(9), 4979. https://doi.org/10.3390/su14094979







