Application of Harris Hawks Optimization with Reservoir Simulation Model Considering Hedging Rule for Network Reservoir System

Abstract

This research aims to apply the Harris hawks optimization (HHO) technique connected with a reservoir simulation model to search optimal rule curves of the network reservoir system in Thailand. The downstream water demand from the network reservoir that required shared water discharge, hydrological data, and physical data were considered in the reservoir simulation model. A comparison of the situation of water shortage using optimal rule curves from HHO technique, genetic algorithm (GA), and wind-driven optimization (WDO) is presented. The results showed that the new rule curves derived from the HHO technique with network reservoir searching were able to alleviate the water shortage and over-flow situations better than the current rule curves. The efficiency of using rule curves from HHO technique compared to GA and WDO techniques showed that the HHO technique can provide a better solution that reduced water scarcity and average over-flow compared with the current rule curves by up to 4.80%, 4.70%, and 4.50%, respectively. In addition, HHO was efficient in converging rule curve solutions faster than GA and WDO techniques by 15.00% and 54.00%, respectively. In conclusion, the HHO technique can be used to search for optimal network reservoir rule curves solutions effectively.

1. Introduction

Water resources are considered as limited resources that are necessary for human life. At present, there is a problem with the amount of water both in flood and drought situations. Climate change and land-use change are further variables influencing input uncertainty within a basin. The growth of the economy and the population are causing a greater water requirement and producing more wastewater [1,2,3,4]. As a result, high-efficiency water resource management is urgently required.

Reservoirs were constructed to store excess water for use in downstream areas. The function of the reservoir is to handle rainfall in the rainy season to prevent flooding and to release the water according to the needs for water at the bottom of the basin in the dry season [5]. Multi-purpose reservoir is one that is built to serve multiple purposes, such as irrigation, water supply for human consumption and industry, hydroelectric power generation, flood or drought relief, water transport, and downstream water control, among others [6,7,8]. While unified reservoir management is as straightforward as managing a multi-purpose reservoir, there are a few extra variables to consider. Even yet, dealing with both types of reservoirs operating within a single reservoir is not as difficult as dealing with a reservoir that operates simultaneously. These are linked and utilized in the same system as other reservoirs. This is a difficult-to-manage system with high performance [9].

The limitations presented by a single reservoir led to the creation of a network reservoir. This is due to the difficulties of maintaining a single reservoir, such as when the water in the reservoir is inadequate to meet the required water demand or when the reservoir is unable to keep the level of water flowing into the basin until flooding occurs. In order to fulfill the demand for water at the basin’s end, networked reservoir operations can share water or even allow the flow of water from one reservoir to another to deal with the problem of water overflowing one reservoir, which is an excellent technique to deal with water management [10,11]. Therefore, optimal reservoir management is required to make full use of the reservoir. Nowadays, there are many networked reservoirs in use in many countries. The advantage is that they provide more flexibility in reservoir management in terms of flood and drought prevention. Thailand has a network of reservoirs ranging from small- to medium-sized to huge reservoirs, such as the Bhumibol and Sirikit reservoirs that operate together to supply the Chao Phraya river basin’s high water demand. In Thailand, maintaining reservoirs is a big challenge [12,13].

Reservoir management is the management of the water available in the reservoir to meet the water demand to provide a balance that reduces future water problems. To alleviate future water shortages, a balance between water supply and demand is essential. This is the main problem of reservoir management: what should be done to make water satisfactorily and sustainably available to meet the water needs at various times and to avoid flooding or water shortages? This issue arises because the amount of water remaining in the reservoir during different periods is not the same [14,15,16].

Reservoir operation is a sub-discipline of reservoir management. Simulating a reservoir system with a water-release simulation method, such as the hydropower rule, pack rule, and space rule, as well as the water release requirements, alters depending on the reservoir’s characteristic. The most common reservoir-operating regulations have been utilized to model water outflows in previous studies. They are commonly used as standard operating guidelines for water discharges. This is the criterion that allows for the release of as much water as the downstream water demand [17,18]. On the other hand, it may not be appropriate for the reservoir in times of severe water scarcity, that is, when a reservoir has only a small amount of water flowing into it, but there is high downstream water demand. As a result, it is unable to meet demand, resulting in a severe water deficit, and this may require other reservoir-operating criteria to help manage the problem [19,20].

The hedging rule (HR) is a release criterion delivering water at certain intervals to retain water for the next period although the available reservoir volume can meet the full potential of the target water demand. It can be said that the hedging rule is an attempt to reduce the severe dehydration that may arise in the future with an advanced distribution of dehydration in the present time. It is particularly suitable for systems with high water demand but faces a problem in the data variation of the amount of water flowing into the reservoir. When applied to a reservoir that works together as a system to satisfy the need for water sharing, it becomes much more complicated [21,22,23].

The reservoir’s management, on the other hand, must evaluate all of the missing aspects in order to make informed decisions. Reservoir rule curves are an essential tool for calculating how much water to allocate. These are employed in reservoir operation with the release criterion. The upper and lower boundaries for managing water release and storage are indicated by reservoir rule curves, which are made up of upper and lower bounds. Long-term reservoir management is achieved by employing rule curves in reservoir operations. After 4–5 years of usage, it is necessary to research for optimal rule curves to enhance efficiency [24,25,26]. Reservoir rule curves have also been studied in order to discover a solution to the common rule curves in various methods.

In the past, finding the optimal reservoir rule curves solutions was done by trial and error. This starts with the analysis of the reservoir system with an analysis of the minimum storage volume required by the reservoir. For example, to find the optimal monthly rule curves for a reservoir, a reservoir simulation model is built utilizing simulated research methodologies. Dynamic programming (DP) was later developed to discover the best rule curves [27] and was applied to search optimal monthly rule curves of the Bhumibol reservoir and Sirikit reservoir. DP technique is a technique for a nonlinear problem with stage search. However, DP has a limit when more state variables are used. In addition, DP is more difficult a calculation to process but provides an optimal solution because the method that can find answers precisely and efficiently [28].

Later, a genetic algorithm (GA) was used in conjunction with reservoir modeling to find the best rule curves for the Bhumibol and Sirikit reservoirs in Thailand’s Chao Phraya river basin [29]. The average annual water scarcity was employed as the search process’s goal function. The monthly discharge of water was calculated using the standard operating policy (SOP) and rule curves. GA was discovered to develop optimum rule curves that mitigated water-scarcity circumstances better than the existing reservoir rule curves. However, the criteria may not effectively adapt to perform in the present situation because water shortage is a hot issue for Bhumibol and Sirikit reservoirs. The downstream water requirement of both reservoirs increases following economic growth. Therefore, another release criteria conjunction with rule curves needs to be investigated for solving the water-shortage situation.

Subsequently, the metaheuristic algorithms, such as ant colony [30], Tabu search [31], genetic programming [32], flower pollination algorithm (FPA) [33], cuckoo search (CS), particle swarm optimization (PSO) [34], wind-driven optimization (WDO) [35], grey wolf optimizer (GWO) [36], and genetic algorithm (GA) [37], etc., have been applied to search for optimal rule curves. These methods provided the new optimal rule curves that mitigated the situation of water shortage and excess water. However, some techniques have their own set of restrictions, and some techniques cannot converge to the global optimal, while others are too complex and huge. Furthermore, some techniques contain an excessive number of parameters that make them difficult to use. As a result, researchers are trying to come up with answers to these problems.

The Harris hawks optimization (HHO) approach, which is inspired by the prey of Harris hawks, an intelligent bird, has recently been discovered to be another excellent way for determining optimal values. The birds form a team and use attack strategies [38]. HHO outperforms numerous well-known approaches, such as PSO, GWO, CS, moth-flame optimization (MFO), differential evolution (DE), bat algorithm (BA), and whale optimization algorithm (WOA), in terms of initial performance [39]. HHO has a benefit over other swarm-based optimization algorithms in that it does not need the commencement of any parameters other than the swarm’s starting population. There is no derivative equation for HHO. It is also simple to use, sturdy, and comprehensive. The balance between exploration and exploitation is HHO’s most useful feature. The exploring ability rises as the number of HHO iterations grows [40,41]. HHO and its variants have lately been widely employed for real-world situations as a result of these advantages. This approach is another rapid and efficient convergence method that has been used in the analysis of landslide susceptibility in western Iran [42], drug design and discovery [43], and fault diagnosis for rolling bearings [44]. HHO was enhanced with a long-term memory concept known as long-term memory HHO (LMHHO) and novel HHOs (HHO)-based MPPT control of PV systems, among other things [45]. The HHO has also been used in a variety of different disciplines. According to several studies, HHO is one strategy that may identify the correct answer in less time than other strategies [46,47,48]. Recently, there has been research on improving the efficiency and sustainability of distribution networks (DNs) by applying an HHO-based approach that is compared with two related well-known metaheuristic techniques, the PSO and the conditional simulated annealing algorithm (CSA). The results show that HHO outperforms the other two optimizers in terms of minimized power losses, enhanced voltage profile, and running time [49].

According to the literature study above, the HHO approach is very successful when compared to other procedures under the same conditions, and it is quite valuable when applied to other issues. Therefore, this research proposes a Harris hawks optimization (HHO) approach connected with the reservoir simulation model to search for optimal rule curves of the network reservoir system. The Bhumibol and Sirikit reservoirs located in Thailand were considered in this study. The hedging rule criteria were applied to use with rule curves in reservoir operation for searching optimal rule curves. The results of the study were divided in two main parts: (1) the effectiveness of HHO technique for searching for networked reservoir rule curves and (2) the efficiency of water-shortage mitigation using standard operating policy (SOP) and the hedging rule (HR) in terms of maximum water shortage. A comparison of the situation of water shortage using optimal rule curves from HHO technique, genetic algorithm (GA), and wind-driven optimization (WDO) technique is presented.

2. Materials and Methods

The Harris hawks optimization (HHO) technique was utilized in conjunction with a reservoir simulation model to find the best rule curves for the network reservoir system. In this study, the Bhumibol and Sirikit reservoirs in Thailand were considered as the network reservoir system. The hedging rule criteria were used to find the best rule curves for reservoir operations using rule curves as shown in Figure 1.

2.1. Research Area

Two large reservoirs, the Bhumibol and the Sirikit reservoirs, were chosen as a network reservoirs system for conducting this research. The downstream water requirement was together supplied by discharge water of the two reservoirs as shown in Figure 2. The main downstream water requirement was an irrigation project of the Chao Phraya river basin as described in GCPYIP (The Greater Chao Phraya Irrigation Project), LNIP (Lower Nan Irrigation Project), and LPIP (Lower Ping Irrigation Project) in Figure 2 and Figure 3. It receives water from sharing of two reservoirs (network systems reservoir). For the dashed line of flow, the direction is out of model consideration due to flowing in lower downstream areas of the Bhumibol and Sirikit reservoirs, which does not affect release conditions in this reservoir simulation model.

The Bhumibol reservoir is located in Tak province, in the north of Thailand, as shown in Figure 2. It located in the upper basin of the Ping river. The full storage capacity is 13,462 MCM, and dead storage capacity is 3800 MCM. The amount of inflow flowing into the Bhumibol reservoir for 57 years, during the years 1964–2020, was as shown in Figure 4.

The Sirikit reservoir is located in Uttaradit province, in the north of Thailand, as shown in Figure 2. It located in the upper basin of the Nan river. The full storage capacity is 9510 MCM, and dead storage capacity is 2850 MCM. The amount of inflow flowing into the Sirikit reservoir for 47 years, during the years 1974–2020, was as shown in Figure 4.

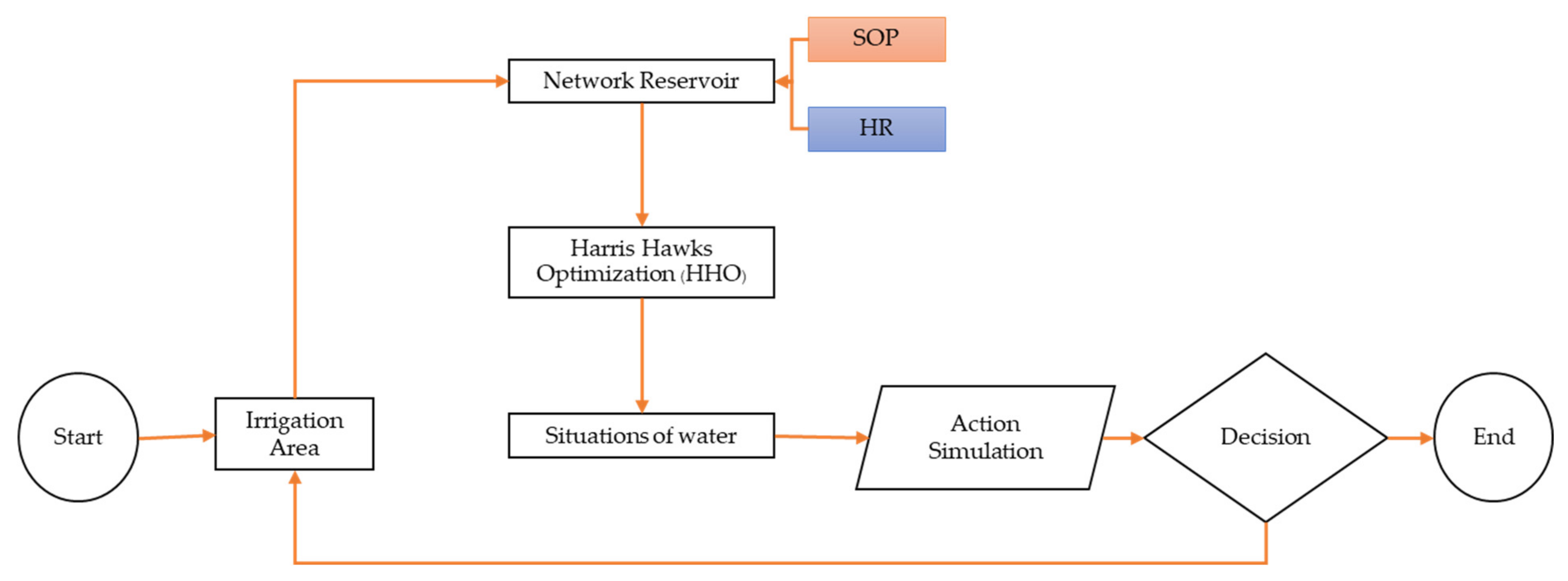
2.2. Application of HHO with the Reservoir Simulation Model for Searching Optimal Rule Curves

HHO is a population-based, nature-inspired metaheuristic algorithm, described in [38], that replicates Harris-type hawk hunting behavior. These birds are cooperative predators who are able to successfully carry out coordinated foraging actions. Hawks work together to adjust their assault approach based on the prey’s current location during the hunting phase (e.g., a rabbit). To properly seek the prey, appropriate switching between different searching conditions is required. In the same way, the HHO algorithm seeks to find the optimum solution in the search space while avoiding early convergence to undesirable locations. This is the algorithm’s key advantage over other state-of-the-art metaheuristic approaches [38]. Specifically, throughout the algorithm’s execution, the population of candidate solutions representing hawks locations is updated until the best solution is found (i.e., the near optimum of the optimization problem), representing that the rabbit position is achieved [49].

The connecting of the HHO with the network reservoir simulation model is described in Figure 5 and Algorithm 1.

• The model starts with input data and all initial necessary data, such as upper and lower bound data of reservoir and objective function.
• The HHO starts with Harris hawks track and detects the prey from a set generate initial population of Harris hawks {X1, X2, …, Xn} that is created randomly from exploration within the feasible space. The feasible space is the value between the dead storage capacity and the normal high water level of the considered reservoir.
• For this study, each decision variable represents the monthly rule curves of the reservoir, which are defined as the upper rule curves and the lower rule curves of the Bhumibol and the Sirikit reservoirs after the first set of Harris hawks in the initial population have been calculated (48 simultaneous decision variables that consist of 24 values from the upper rule curves and 24 values from lower rule curves for both reservoirs).
• The monthly release of water will be calculated by the reservoir simulation model considering those rule curves (fitness evaluations) in accordance with the criteria set forth in Section 2.3.1 and Section 2.3.2.
• Next, the released water is used to determine the objective functions that were described in the previous section procedure (update the location of each Harris hawk) [38]. After that, the reproduction process will create new values of rule curves in the next generation (exploitation). This procedure is repeated until criteria are satisfied, and optimal rule curves are then obtained.
• In this study, the objective function of the search procedure of Bhumibol reservoir and Sirikit reservoir was the minimal average shortage per year and the minimal of maximum water shortage according to the context of the reservoir.

The minimal average water shortage per year:

$$Min{H}_{(avr)}=\frac{1}{n}{\displaystyle {\sum }_{v=1}^n}S{h}_V$$

(1)

The minimal of maximum water shortage:

$$Min{H}_{(Max)}={\displaystyle {\sum }_{v=1}^n}S{h}_V$$

(2)

Algorithm1. Pseudo-code of the proposed HHO method [38].

Inputs: The population size N and maximum number of iterations T

Outputs: The location of rabbit and its fitness value

Initialize the number of hawks (N) and iteration (T) randomly Xi (i = 1, 2, …, 48)

while (stopping condition is reached) do

Evaluate the fitness value of hawks

Now, set Xrabbit as the best location of rabbit

for (several hawk (Xi)) do

update Energy (E) and its jumping strength (J)

Initial Energy (E0) = 2rand() − 1, J = 2(1 − rand())

Update E using (10)

if (|E| ≥ 1) then

Exploration phase

if (|E| < 1) then

if (r ≥ 0.5 and |E| ≥ 0.5) then

Exploitation phase

Soft siege

else if (r ≥ 0.5 and |E| < 0.5) then

Hard siege

else if (r < 0.5 and |E| ≥ 0.5) then

Soft siege

else if (r < 0.5 and |E| < 0.5) then

Hard siege

Return best location of Xrabbit (global optimal solution)

2.3. Network Reservoir-Operation Model

The reservoir-operation system consists of the available water that is calculated from the water-balance concept and water demands from downstream sites. The monthly release of water is estimated by considering the monthly available water with release criteria, operating policies. and reservoir rule curves.

$$W_{\nu ,\tau }=S_{\nu ,\tau -1}+Q_{\nu ,\tau -1}-R_{\nu ,\tau -1}-E_{\tau -1}$$

(3)

where S_ν,_τ−1 is the stored water at the end of month τ−1; Q_ν,_τ−1 is the monthly inflow to the reservoir; and E_τ−1 is the average value of the evaporation loss. The operating policy usually reserves the available water (W_ν,_τ) for mitigating the risk of water shortage in the future when 0 ≤ W_ν,_τ < x_τ—D_τ under long-term operation.

2.3.1. Standard Operating Policy

For this study, the reservoir-operation model was created following the concept of the water balance. The reservoir-operation model was operated under the standard operating policy as expressed in Equation (4) and Figure 6.

$$R_{\nu ,\tau }=\left\{\begin{array}{l}{D}_{\tau }+W_{\nu ,\tau }-y_{\tau },\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}\hspace{0.17em}{W}_{\nu ,\tau }\ge y_{\tau }+D_{\tau }\hfill \\ D_{\tau },\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}\hspace{0.17em}{x}_{\tau }\le W_{\nu ,\tau }<y_{\tau }+D_{\tau }\hfill \\ D_{\tau }+W_{\nu ,\tau }-x_{\tau },\hspace{0.17em}\hspace{0.17em}for\hspace{0.17em}\hspace{0.17em}{x}_{\tau }-D_{\tau }\le W_{\nu ,\tau }<x_{\tau }\hfill \\ 0,\hspace{0.17em}\hspace{0.17em}otherwise\hfill \end{array}\right.$$

(4)

where R_ν,_τ is the release of water during year ν and month τ (τ = 1 to 12 representing January to December), D_τ is the net water demand during month τ; x_τ is the lower rule curve of month τ; y_τ is the upper rule curve of month τ; and W_ν,_τ is the available water by calculating the water balance concept during year ν and month τ.

2.3.2. Hedging Rule

The hedging rule is a reservoir-operating criterion that attempts to reduce water supply at certain times to store water for later use although the amount of water stored in the reservoir can meet the full potential of the target water demand.

It can be said that the hedging criterion is an attempt to mitigate serious water shortages that may arise in the future by distributing the dehydration at present in advance, as expressed in Figure 7 and Equation (5).

$$R_{v,\tau }=\left\{\begin{array}{lc}W{A}_{\tau }& if W{A}_{\tau }<SW{A}_{\tau }\hfill \\ D_{\tau }+\left(SW{A}_{\tau }-D_{\tau }\right)\frac{W{A}_{\tau }-EW{A}_{\tau }}{SWA{t}_{\tau }-EW{A}_{\tau }}& \hspace{1em}if SW{A}_{\tau }\le W{A}_{\tau }EW{A}_{\tau }\hfill \\ D_{\tau }& if EW{A}_{\tau }\le W{A}_{\tau }<D\hfill \\ W{A}_{\tau }& if W{A}_{\tau }\ge D_{\tau }\hfill \\ 0,otherwise& \end{array}\right.$$

(5)

where R_τ is the total release of the aggregated reservoir at time τ; SWA_τ and EWA_τ are the starting and ending water availability of the aggregated reservoir at time τ; and D_τ is the water demand for the water-supply system at time τ [50,51,52].

From Equations (4) and (5), it can be seen that both are conditions for the release of water. This will depend on the amount of water available each month and then take into account the release under this condition. When the water volume in the basin is less than half of the basin, we can see that the two criteria are different. The criteria for considering emissions will change, affecting the lower rule curve’s optimal response.

3. Results and Discussion

3.1. Optimal Rule Curves of HHO

3.1.1. Optimal Rule Curves for Network Reservoir

The optimal rule curves of networked reservoir for the Bhumibol and Sirikit reservoirs from the HHO with reservoir simulation model incorporating the HR with both objective functions of the minimal average water shortage per year and the minimal maximum water shortage per year are shown in Figure 8 and Figure 9.

The figures show that, due to seasonal inflow effect and searching conditions, the patterns of the optimal rule curves for the Bhumibol reservoir using the minimal average water shortage per year as the objective function (BH-HHO-HRAvs) and the minimal maximum water shortage per year as the objective function (BH-HHO-HRMas) are similar to the current rule curves (BH-current). Furthermore, due to seasonal inflow effects and searching conditions, the pattern of the optimal rule curves for the Sirikit reservoir using the minimal average water shortage per year as the objective function (SK-HHO-HRAvs) and the minimal maximum water shortage per year as the objective function (SK-HHO-HRMas) are similar to the current rule curves (SK-current).

The figures also indicate that the optimal rule curves of Bhumibol and Sirikit reservoirs from the HHO approach are higher than the current rule curves for both upper and lower rule curves. These are influenced by HR criteria in the recruitment process. The new lower rule curve was derived by considering that the HR was higher than the current lower rule curve and encourages discharge of water to be less than goal demand. The new upper rule curve produced from HR throughout the rainy season is higher than the upper current rule curve, allowing for additional water storage at the end of the rainy season.

Table 1. The situations of water shortage and excess water from network reservoir (The Bhumibol reservoir and the Sirikit reservoir).

Situations	Rule Curves	Frequency (Times/Year)	Volume (Million Cubic Meters)		Time Period (Million Cubic Meters)
			Average	Maximum	Average	Maximum
Shortage	Current	0.368	182.860	1964.000	7.115	12.000
	HHO-HRAvs	0.456	174.140	1623.000	7.900	12.000
	HHO-HRMas	0.351	196.526	1451.000	8.050	12.000
Excess water	Current	0.825	1390.123	7643.000	4.915	10.000
	HHO-HRAvs	0.842	1121.877	7540.000	4.000	8.000
	HHO-HRMas	0.825	1354.298	7214.000	5.125	9.000

shows the scenarios of water scarcity and excess release in the downstream area as a result of applying the newly derived rule curves of the HHO with a reservoir simulation model that included HR for both objective functions of the network reservoirs.

It was found that when using the historic inflow under HR with the objective functions of the minimal average water-shortage rule curves (HHO-HRAvs), the average and maximum water shortages were the smallest at 174.140 MCM/year and 1,623,000 MCM/year, respectively, while the frequency of water shortage was the highest at 0.456 times/year.

These scenarios showed that when applying the historic inflow under the HR with the objective functions of the minimal average water-shortage rule curves (HHO-HRAvs), the average excess water and maximum excess water were the smallest at 1,112,877 MCM/year and 7,540,000 MCM/year, respectively.

As a result, HR criteria for releasing water during the dry season were limited in order to save more water in order to alleviate the water shortage in the next dry season. During the dry season, however, the water-release demand was satisfied using the current rule curves. As a result, the following season’s water supply was insufficient [25,26].

3.1.2. Optimal Rule Curves for Single Reservoir

Figure 10 shows the optimal rule curves for a single reservoir (The Ubolratana reservoir) from the HHO with reservoir simulation model incorporating HR with both objective functions of the lowest average and minimal–maximum water shortage per year.

Due to the seasonal inflow effect and searching conditions, it shows that the patterns of the optimal rule curves for the Ubolratana reservoir using the minimal average water shortage per year as the objective function (UB-HHO-HRAvs) and the minimal–maximum water shortage per year as the objective function (UB-HHO-HRMas) are similar to the current rule curves (UB-current).

The figure also shows that the HHO technique’s optimal rule curves for Ubolratana reservoir are higher than the current rule curves for both upper and lower rule curves. These are influenced by HR criteria in the recruitment procedure. The new lower rule curve derived by considering HR greater than the current lower rule curve encourages discharge water to be less than target demand. The new upper rule curve produced from HR throughout the rainy season is higher than the upper current rule curve, allowing for additional water storage at the end of the rainy season.

Table 2. The situations of water shortage and excess water from Single Reservoir (Ubolratana reservoir).

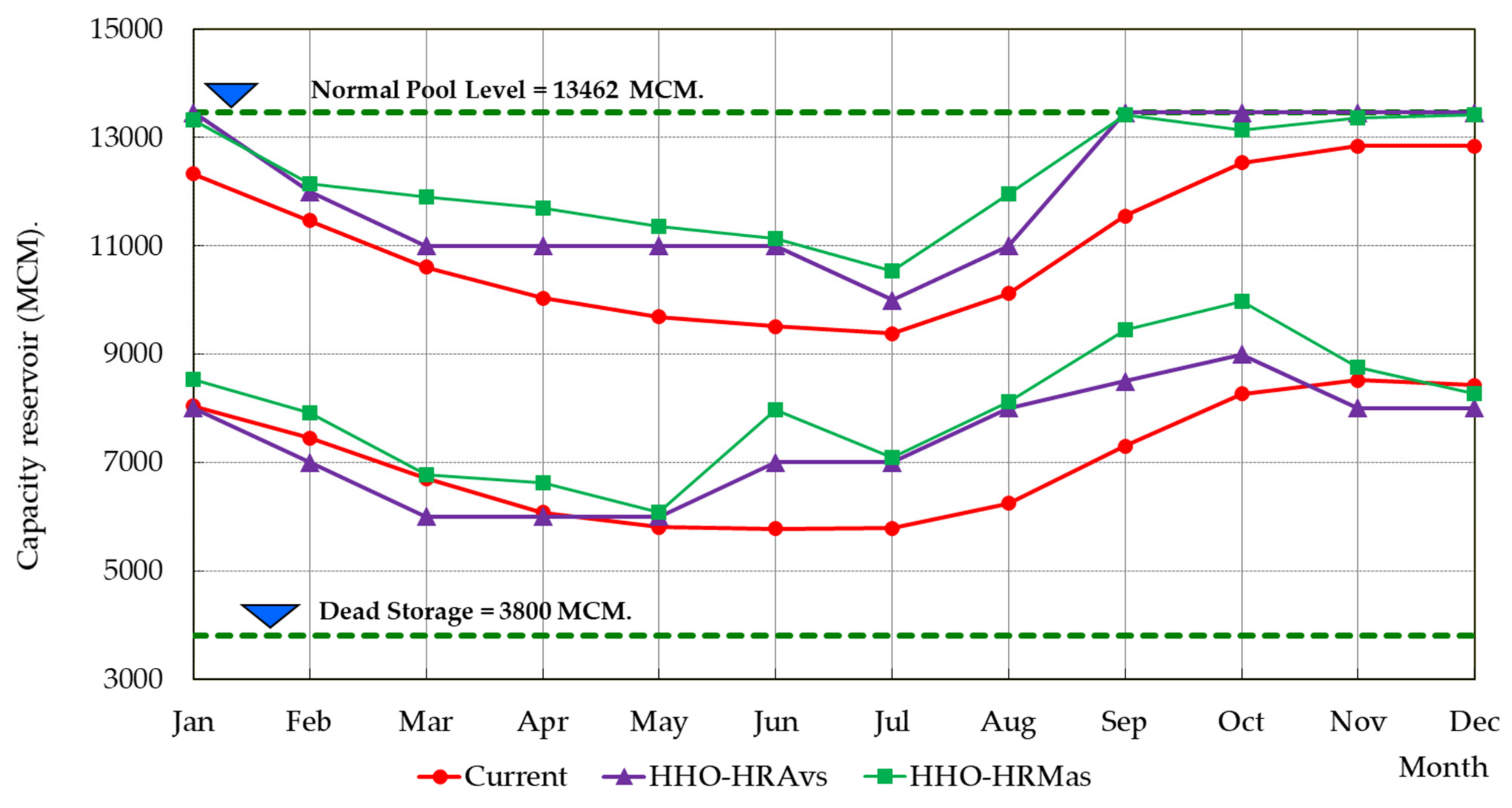
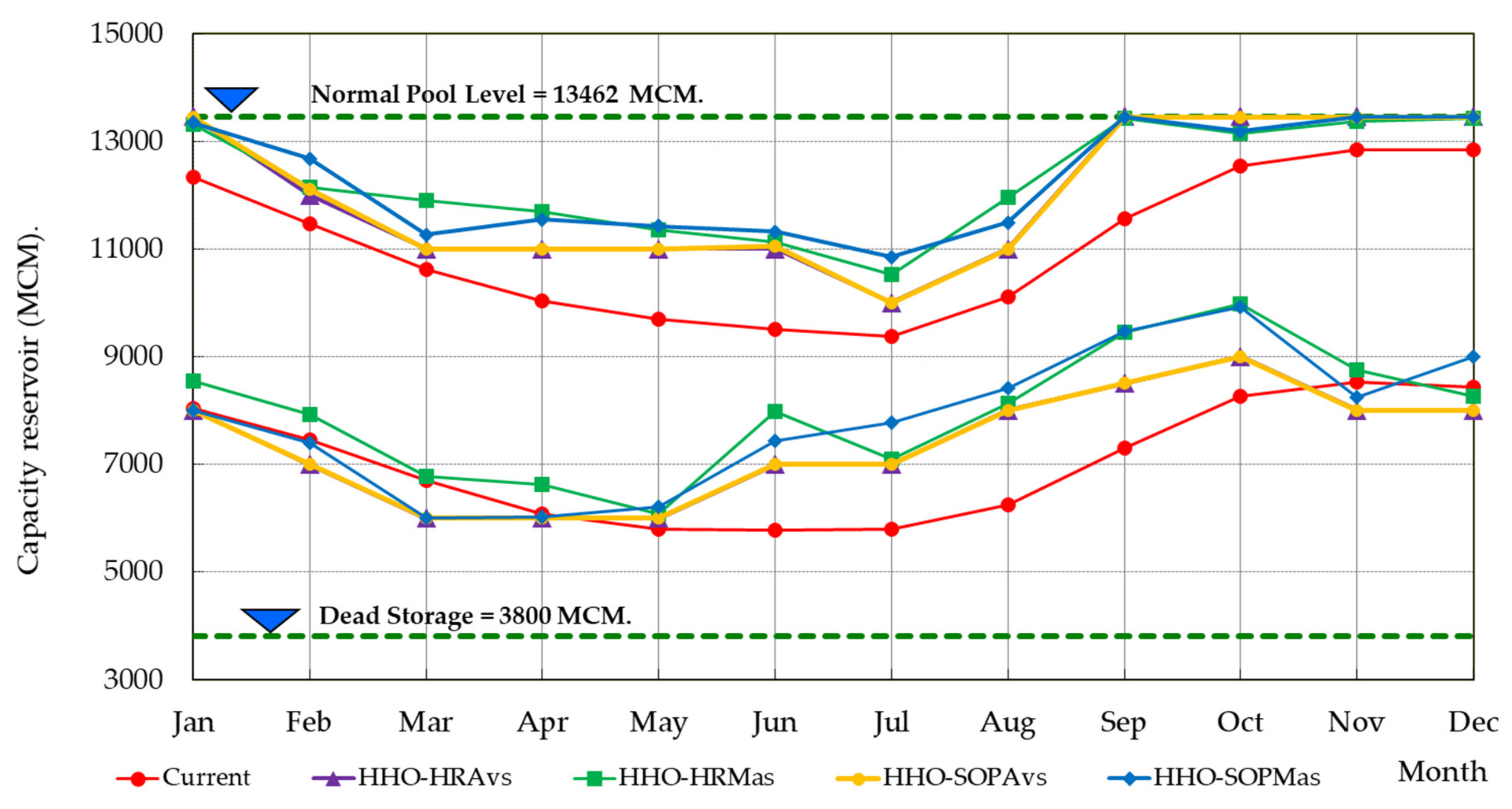
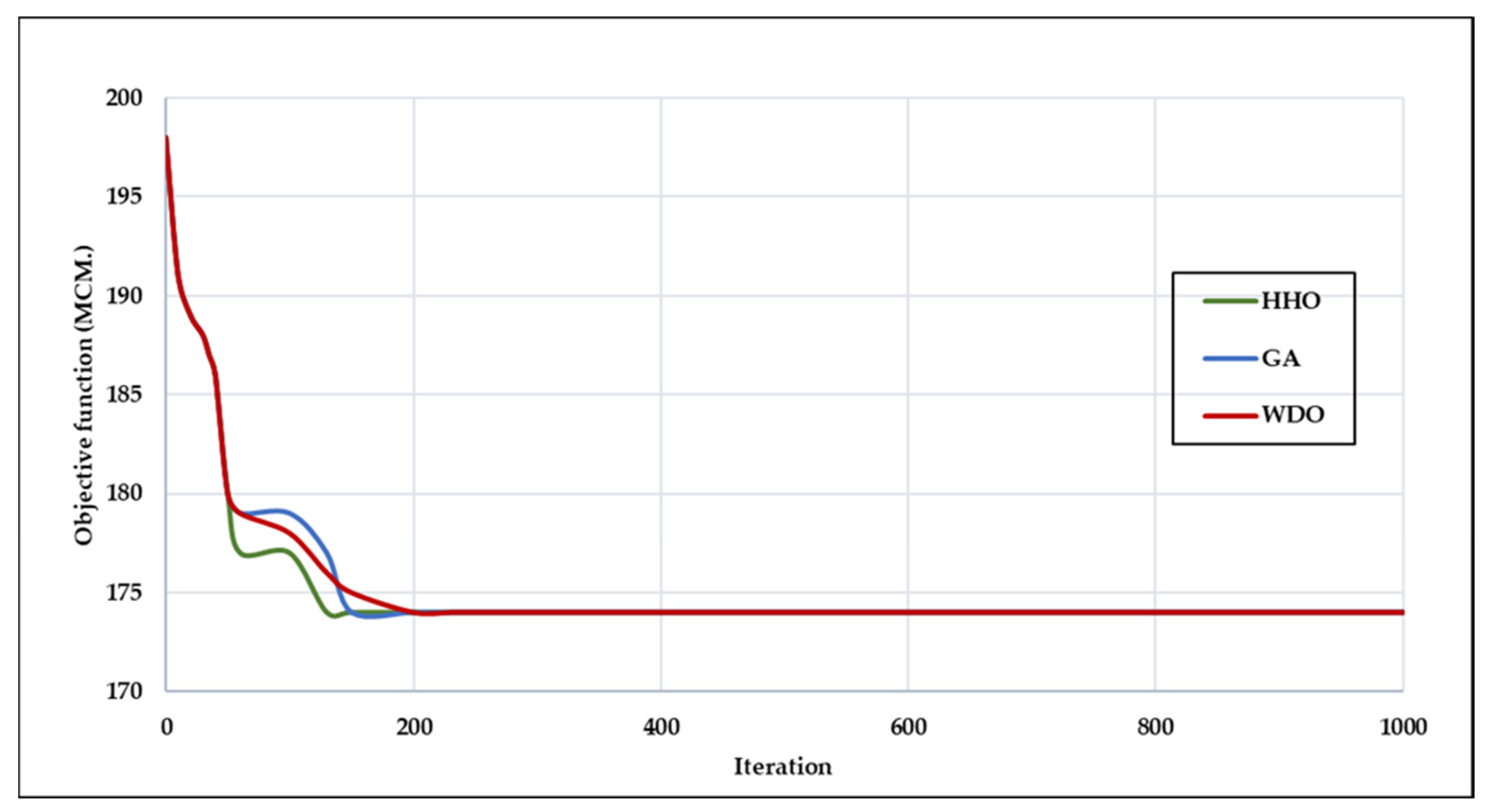
Situations	Rule Curves	Frequency (Times/Year)	Volume (Million Cubic Meters)		Time Period (Million Cubic Meters)
			Average	Maximum	Average	Maximum
Shortage	Current	0.673	204.308	865.000	3.889	8.000
	HHO-HRAvs	0.654	115.769	742.000	3.778	7.000
	HHO-HRMas	0.647	129.762	722.000	4.000	7.000
Excess water	Current	0.923	1230.310	4126.736	9.600	21.000
	HHO-HRAvs	0.865	1107.549	4113.159	6.143	10.000
	HHO-HRMas	0.832	1187.834	4011.000	9.000	13.000

shows the scenarios of water shortages and excess release in the downstream area as a result of utilizing the newly obtained rule curves of the HHO with a reservoir simulation model that included HR for both objective functions of the single reservoirs.

It was found that when using the historic inflow under HR with the objective functions of the minimal average water-shortage rule curves (HHO-HRAvs), the average and maximum water shortages were the smallest at 115.769 MCM/year and 722.000 MCM/year, respectively, while the frequency of water shortage was the highest at 0.647 times/year.

Table 2 also shows that when applying the historic inflow under the HR with the objective functions of the minimal average water-shortage rule curves (HHO-HRAvs), the average excess water and maximum excess water were the smallest at 1,107,549 MCM/year and 4,113,159 MCM/year, respectively.

As a result, HR criteria for releasing water during the dry season were narrowed in order to save more water so as to alleviate the water shortage in the next dry season. During the dry season, however, the water-release demand was satisfied using the current rule curves. As a result, the following season’s water supply was insufficient [25,26].

The HHO can be used to find optimal rule curves for both networked reservoirs and single reservoirs, as shown by the situations of water shortage and excess release in downstream areas from using the new obtained rule curves of the HHO with reservoir simulation model considering HR for both networked reservoirs and single reservoirs as mentioned above.

3.2. Comparison of Optimal Rule Cuves from HHO Considering HR and SOP for Network Reservoirs

Figure 11 and Figure 12 show the optimal rule curves of networked reservoirs for the Bhumibol reservoir and Sirikit reservoirs using the HHO with reservoir simulation model considering HR and SOP with both objective functions of the minimal average water shortage per year and the minimal–maximum water shortage per year.

The figures show that, due to seasonal in-flow effect and searching conditions, the patterns of the optimal rule curves for the Bhumibol reservoir using the minimal average water shortage per year as the objective function considering HR (BH-HHO-HRAvs) and SOP (BH-HHO-SOPAvs) and the minimal–maximum water shortage per year as the objective function considering HR (BH-HHO-HRMas) and SOP (BH-HHO-SOPMas) are similar to the current patterns. Furthermore, due to the seasonal inflow effect and searching conditions, the pattern of the optimal rule curves for the Sirikit reservoir using the minimal average water shortage per year as the objective function considering HR (SK-HHO-HRAvs) and SOP (SK-HHO-SOPAvs) and the minimal–maximum water shortage per year as the objective function considering HR (SK-HHO-HRMas) and SOP (SK-HHO-SOPMas) are similar to the current rule curves.

They show that for both reservoirs, the patterns of optimal rule curves from HHO approach considering HR are greater than the patterns of HHO technique using SOP and current rule curves. Furthermore, for both reservoirs, the lower rule curves from utilizing HR criteria are greater than the lower rule curves from using SOP criteria, especially during the dry season (January–May).

HR’s control of release water from January to May is more limited than SOP’s. This means that the best HR rule curves try to retain water by reducing water release during the dry season, which is the goal of HR. The results also show that during the wet season (August–November), upper rule curves from HR criteria are greater than those from SOP criteria. As a result, the higher optimal rule curves based on HR encourage the reservoir to save more water in order to avoid severe water shortages during the next dry season. The application of HR criteria with rule curves for reservoir operation is mainly for this purpose.

Table 3. The situations of water shortage and excess water considering historic inflow using SOP.

Situations	Rule Curves	Frequency (Times/Year)	Volume (Million Cubic Meters)		Time Period (Million Cubic Meters)
			Average	Maximum	Average	Maximum
Shortage	Current	0.303	167.737	1900.000	0.053	0.193
	HHO-HRAvs	0.333	153.789	1765.000	0.070	0.193
	HHO-HRMas	0.298	180.825	1502.000	0.158	0.228
	HHO-SOPAvs	0.333	153.982	1766.000	0.070	0.193
	HHO-SOPMas	0.298	184.842	1338.000	0.175	0.193
Excess water	Current	0.825	1379.632	7643.000	4.894	10.000
	HHO-HRAvs	0.842	1116.895	7540.000	4.000	8.000
	HHO-HRMas	0.789	1351.175	7214.000	5.146	9.000
	HHO-SOPAvs	0.842	1158.316	7365.000	3.289	7.000
	HHO-SOPMas	0.789	1349.754	7275.000	5.125	9.000

and

Table 4. The situations of water shortage and excess water considering historic inflow using HR.

Situations	Rule Curves	Frequency (Times/Year)	Volume (Million Cubic Meters)		Time Period (Million Cubic Meters)
			Average	Maximum	Average	Maximum
Shortage	Current	0.368	182.860	1964.000	7.115	12.000
	HHO-HRAvs	0.456	174.140	1623.000	7.900	12.000
	HHO-HRMas	0.351	196.526	1451.000	8.050	12.000
	HHO-SOPAvs	0.456	175.035	1619.000	7.950	12.000
	HHO-SOPMas	0.351	204.842	1472.000	7.810	12.000
Excess water	Current	0.825	1390.123	7643.000	4.915	10.000
	HHO-HRAvs	0.842	1121.877	7540.000	4.000	8.000
	HHO-HRMas	0.825	1354.298	7214.000	5.125	9.000
	HHO-SOPAvs	0.842	1162.965	7365.000	3.289	7.000
	HHO-SOPMas	0.825	1353.053	7275.000	5.104	9.000

illustrate water shortage and surplus release in the downstream area as a result of utilizing the HHO’s optimal rule curves with a reservoir simulation model that considered HR and SOP for both objective functions of the network reservoirs.

They show that when evaluating water-shortage situations using reservoir simulation of network reservoirs using historic inflow under HR with the objective functions of the minimal average water-shortage rule curves (HHO-HRAvs), the average and maximum water shortages were the smallest at 174,140 MCM/year and 1,623,000 MCM/year, respectively, while the frequency of water shortage was the highest at 0.456 times/year.

The tables also show that when applying the historic inflow under the HR with the objective functions of the minimal average water-shortage rule curves (HHO-HRAvs), the average excess water and maximum excess water were the smallest at 1,121,877 MCM/year and 7,540,000 MCM/year, respectively.

The tables also show that when utilizing the optimal rule curves from HHO when considering HR, the circumstances of water shortage and excess water are smaller than when using the generated rule curves from HHO while considering SOP. As a result, the HR criteria limit water discharge in order to avoid a water shortage during the following dry season as opposed to the situation with the SOP criteria.

The SOP criteria controls release water in order to meet target demand for all considered duration times according to many previous studies [20,21]. Hence, the SOP criteria is less inappropriately suitable for reservoirs with high frequency of drought problems than HR criteria.

3.3. Comparison of Optimal Rule Curves Performance of MPA, GA, and FPA Tecniques

By comparing iteration numbers for all approaches in searching for optimal rule curves under the same conditions, the search efficiency of HHO, GA, and WDO techniques was explored. Figure 13 shows the results of the iteration number search.

They demonstrate that the best HHO rule curves were obtained at 130 iterations, and the best GA and WDO iteration numbers were 150 and 200, respectively. In the search for reservoir rule curves, it can be concluded that the HHO approach outperforms the GA and WDO approaches.

Figure 14 and Figure 15 illustrate the optimal networked reservoir rule curves for the Bhumibol and Sirikit reservoirs using the HHO, GA, WDO reservoir simulation model with HR and both objective functions of the least average water shortage per year and the minimal–maximum water shortage per year. They indicate that the patterns from the new rule curves obtained from the HHO, GA, and WDO are similar because of the seasonal inflow effect and the same conditions. All of the methods’ upper rule curves (HHO-HRAvs, GA-HRAvs, and WDO-HRAvs, respectively) were higher than the present upper rule curves, according to the results. These methods can help to limit spill water and maintain a filled storage capacity as the rainy season finally ends. This will help avoid water shortages during the next dry season. During the dry season (January–May), however, lower rule curves obtained by all approaches were greater than current upper rule curves. According to the HR principle, they can manage water discharge by lowering the amount of water released to a level lower than the target demand.

Furthermore, the answer of rule curves will be found to be extremely similar in shape to the rule curves of all three approaches. Because the response is the best in the situation, all three approaches can find the correct answer; however, the search time may different.

The performance of mitigating water-shortage and water-surplus scenarios was evaluated using optimal rule curves from HHO, GA, and WDO approaches linked with a reservoir simulation model utilizing HR, as shown in

Table 5. The situations of water shortage and excess water of using optimal rule curves from HHO, GA, and WDO techniques using HR considering evaluation by reservoir simulation considering historic inflow.

Situations	Rule Curves	Frequency (Times/Year)	Volume (Million Cubic Meters)		Time Period (Million Cubic Meters)
			Average	Maximum	Average	Maximum
Shortage	Current	0.368	182.860	1964.000	7.115	12.000
	HHO-HRAvs	0.456	174.140	1623.000	7.900	12.000
	GA-HRAvs	0.456	174.250	1623.000	7.900	12.000
	WDO-HRAvs	0.456	174.720	1623.000	7.900	12.000
Excess	Current	0.825	1390.123	7643.000	4.915	10.000
water	HHO-HRAvs	0.842	1121.877	7540.000	4.000	8.000
	GA-HRAvs	0.842	1121.965	7540.000	4.000	8.000
	WDO-HRAvs	0.842	1121.993	7540.000	4.000	8.000

.

It was found that employing optimal rule curves from HHO, GA, and WDO approaches, the conditions of water shortage and water surplus were slightly different since their patterns were close together. The results also demonstrate that HHO’s optimal rule curves were more effective than other approaches in reducing average water shortages and overflows. The HHO approach can reduce the minimum average water shortage by up to 4.8%, 4.7%, and 4.5%, respectively, compared to the current rule curves.

It may be concluded that the HHO approach, like the GA and WDO procedures, is useful in finding networked reservoir rule curves. Nonetheless, in terms of discovering solutions, it can be claimed that, while the results are comparable, the speed of search or the complexity of the system is also considered an important part, in which HHO outperforms the other techniques [35,37].

4. Conclusions

The Bhumibol reservoir and the Sirikit reservoir are the largest network of reservoirs in Thailand, which currently faces frequent water shortages during the dry season and overflow during the rainy season. This study aimed to find the optimal reservoir rule curves under reservoir operation using the HHO technique connecting with the network reservoir simulation system of the Bhumibol reservoir and the Sirikit reservoir. The objective functions of the search procedure were the minimal average water shortage per year and the minimal of maximum water shortage. The release criteria using with rule curves in simulating network system were standard operating policy and hedging rule.

The results found that the proposed HHO model with two objective functions pro-vided the new optimal rule curves. The patterns of these new optimal rule curves from HHO were similar to the current rule curves due to seasonal inflow effects and searching conditions. The results of evaluating the efficiency of the networked reservoir rule curves and single reservoir rule curves showed that the rule curves obtained from HHO technique were able to alleviate water-shortage and overflow situations better than the current rule curves.

The optimal rule curves obtained from using the hedging rule criteria showed that the new lower rule curves from using the hedging rule are lower than the new lower rule curves from using standard operating policy and the current lower rule curves. These conditions enhance to reduce among of maximum water shortage but to increase frequency of water shortage slightly. The maximum water-shortage value when using the hedging rule criteria can be reduced to 8.05%, which is higher than when using standard operating policy.

In addition, the optimal rule curves obtained from all techniques were simulated to evaluate the efficiency, and it was found that the HHO technique can provide the better results for reducing water scarcity and average overflow than the current rule curves up to 4.80%, 4.70%, and 4.50%, respectively. The obtained rule curves from HHO technique were similar to the obtained rule curves of GA and WDO search techniques. It can be concluded that HHO technique is robustly acceptable for searching for optimal rule curves. In addition, rule curves solutions converge faster than with GA and WDO techniques by about 15% and 54%, respectively. Therefore, the newly obtained rule curves from the HHO technique can be applied effectively to operate in a network reservoir system for mitigating both drought and flood situations effectively.

The reservoir’s physical factors, water demand, evaporation, and sedimentation are the factors that need to be considered for an effective rule curves that re suitable for its management. The reservoir’s purpose searching function must be considered and applied in the reservoir simulation along with searching for the new technique that is effective, precise, and low-complexity for the suitable rule curves. These factors can help to manage other networks in the future.