Evaluation of Machine Learning versus Empirical Models for Monthly Reference Evapotranspiration Estimation in Uttar Pradesh and Uttarakhand States, India
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site and Data Information
2.2. Empirical Models
2.3. Penman-Monteith Model
2.4. Support Vector Machine
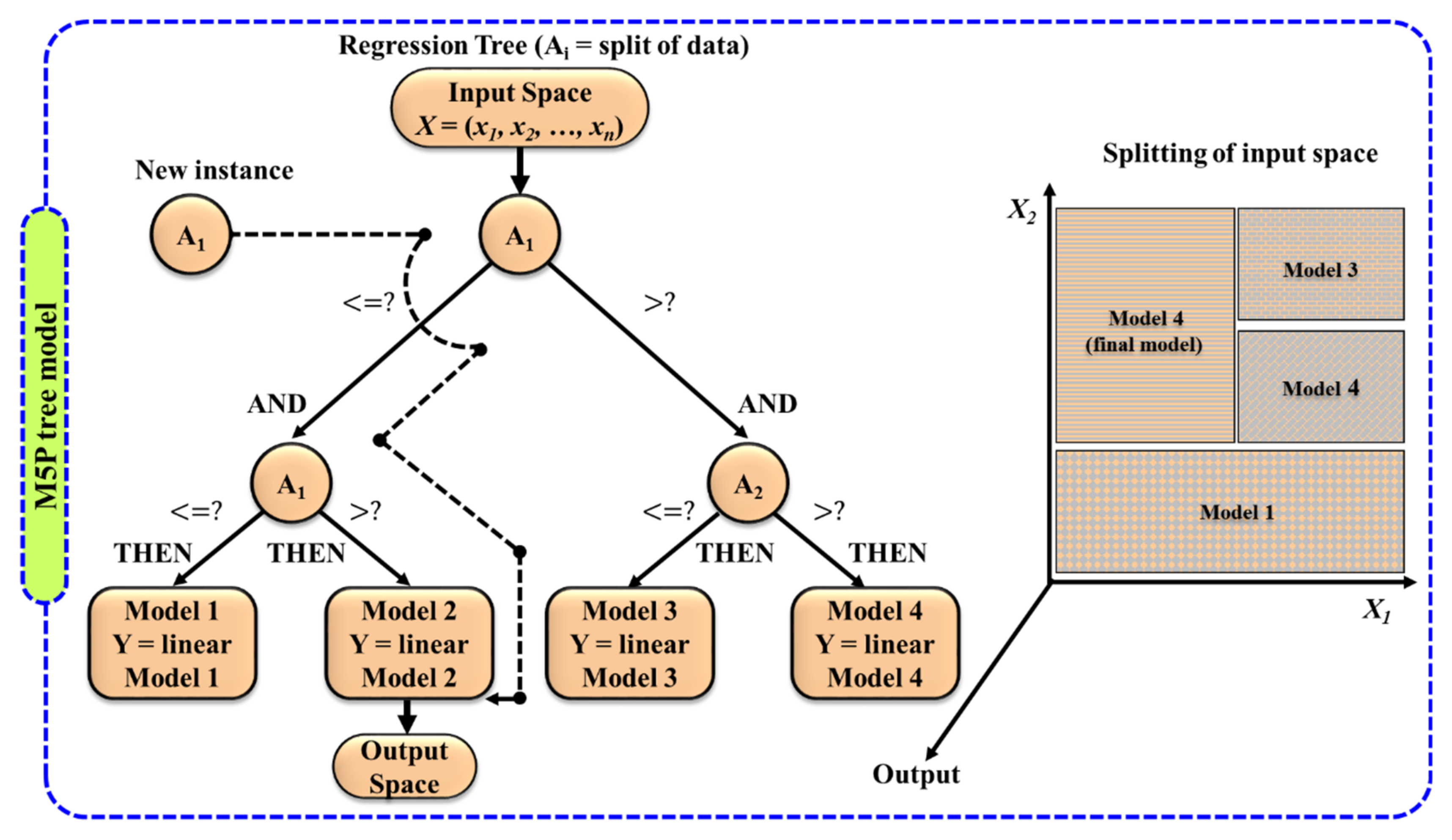
2.5. M5P Tree
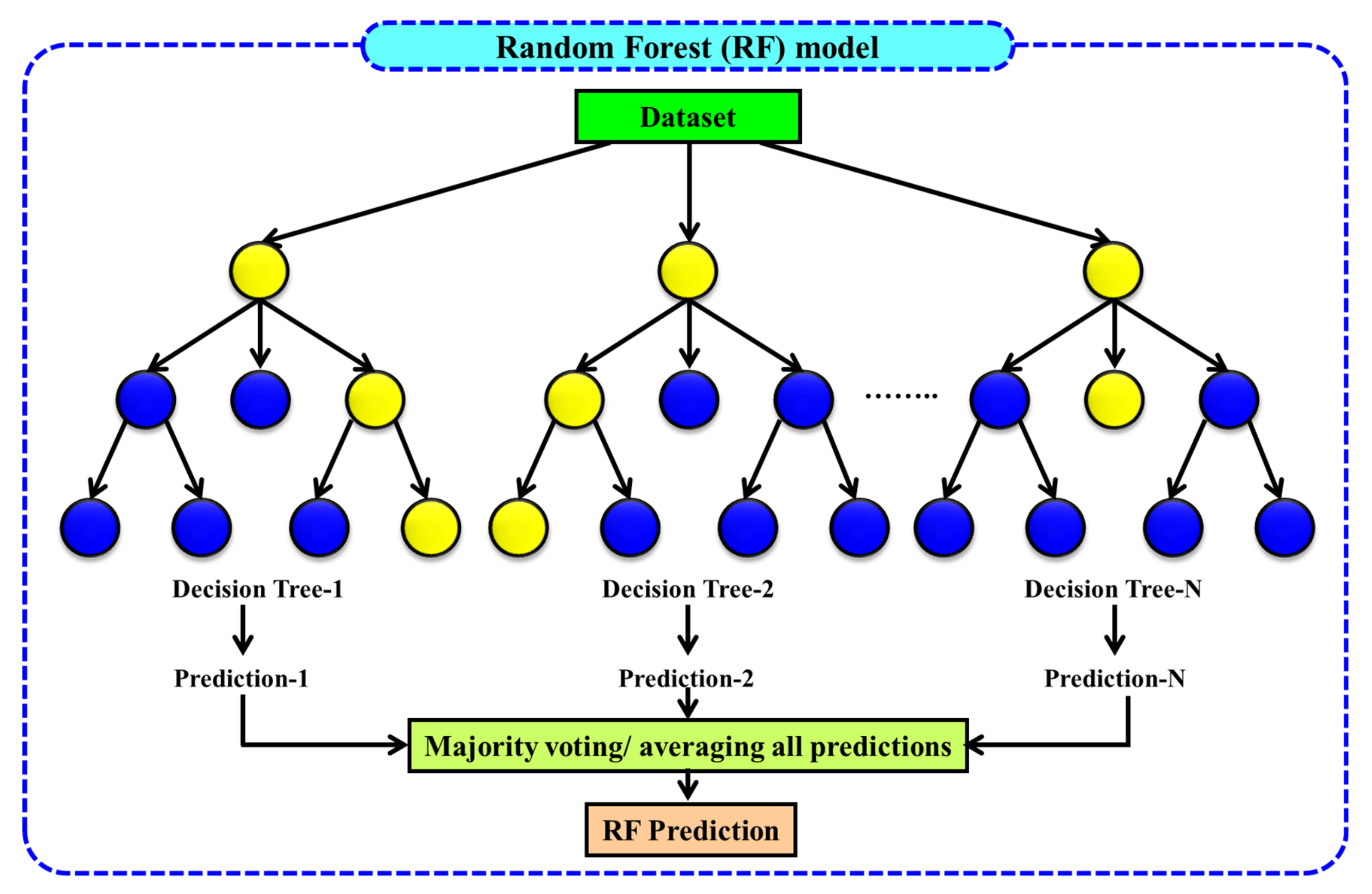
2.6. Random Forest
2.7. Model Formulation and Statistical Indicators
3. Results and Discussion
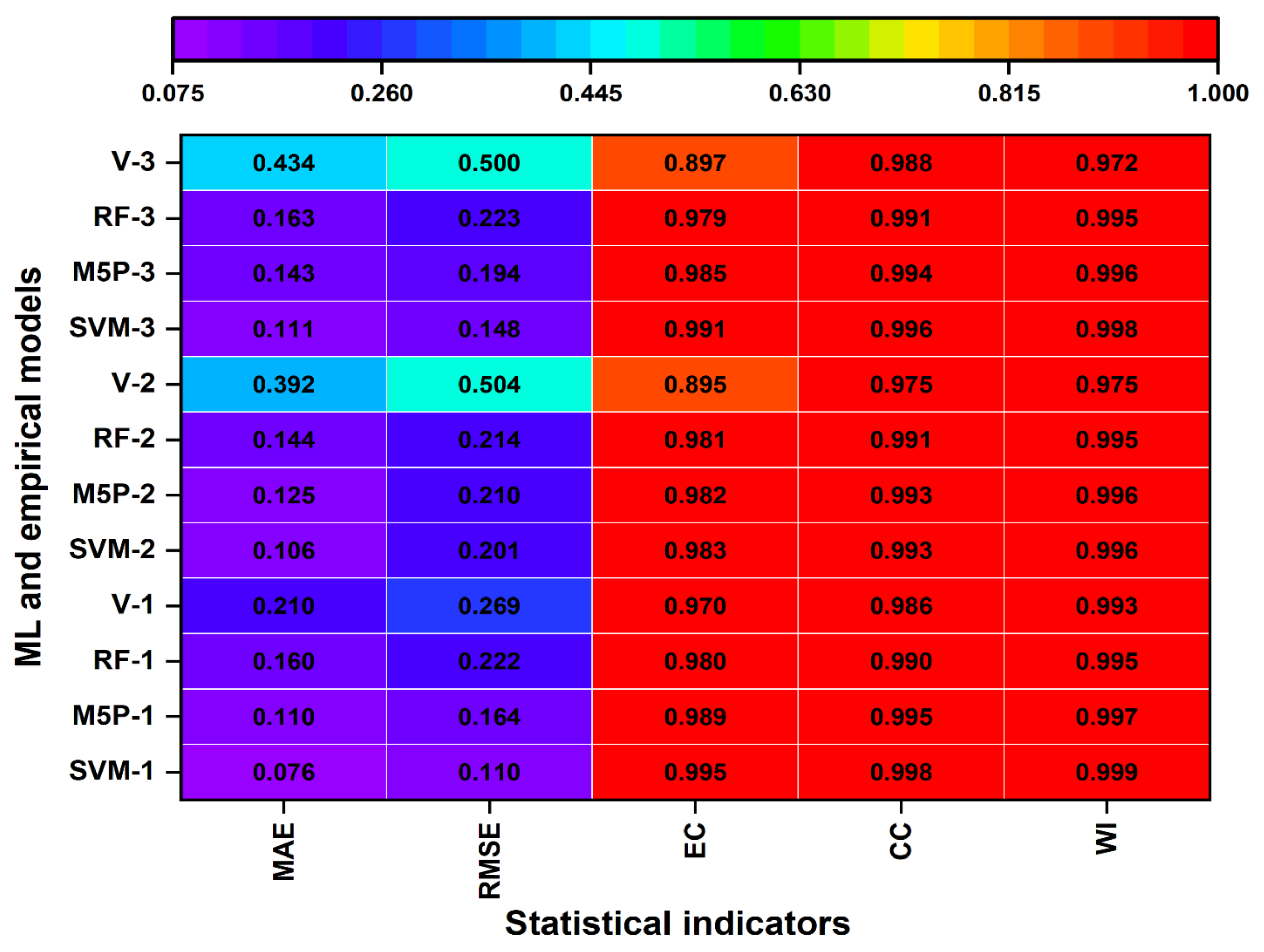
3.1. Model Evaluation Based on Statistical Indicators
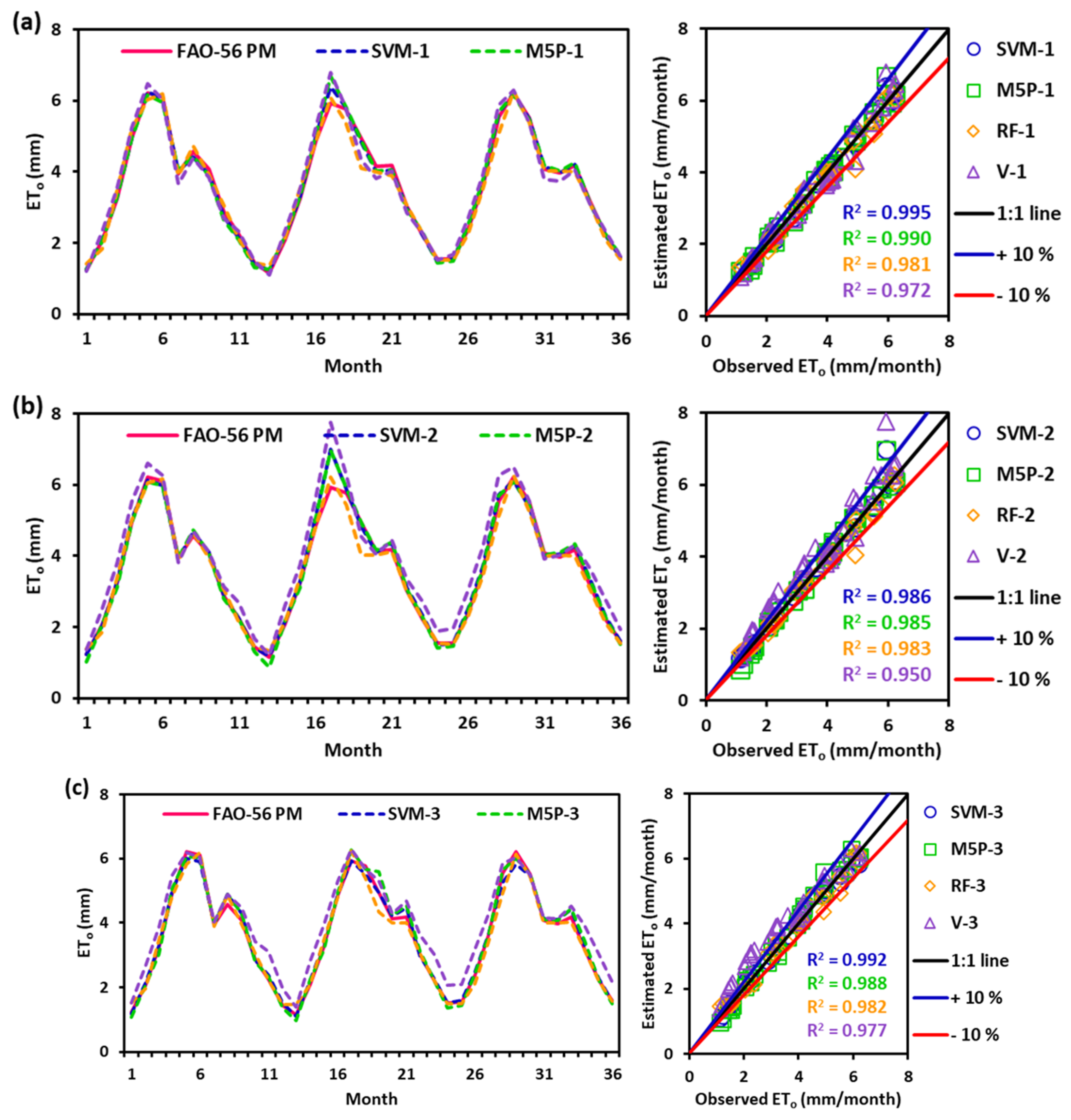
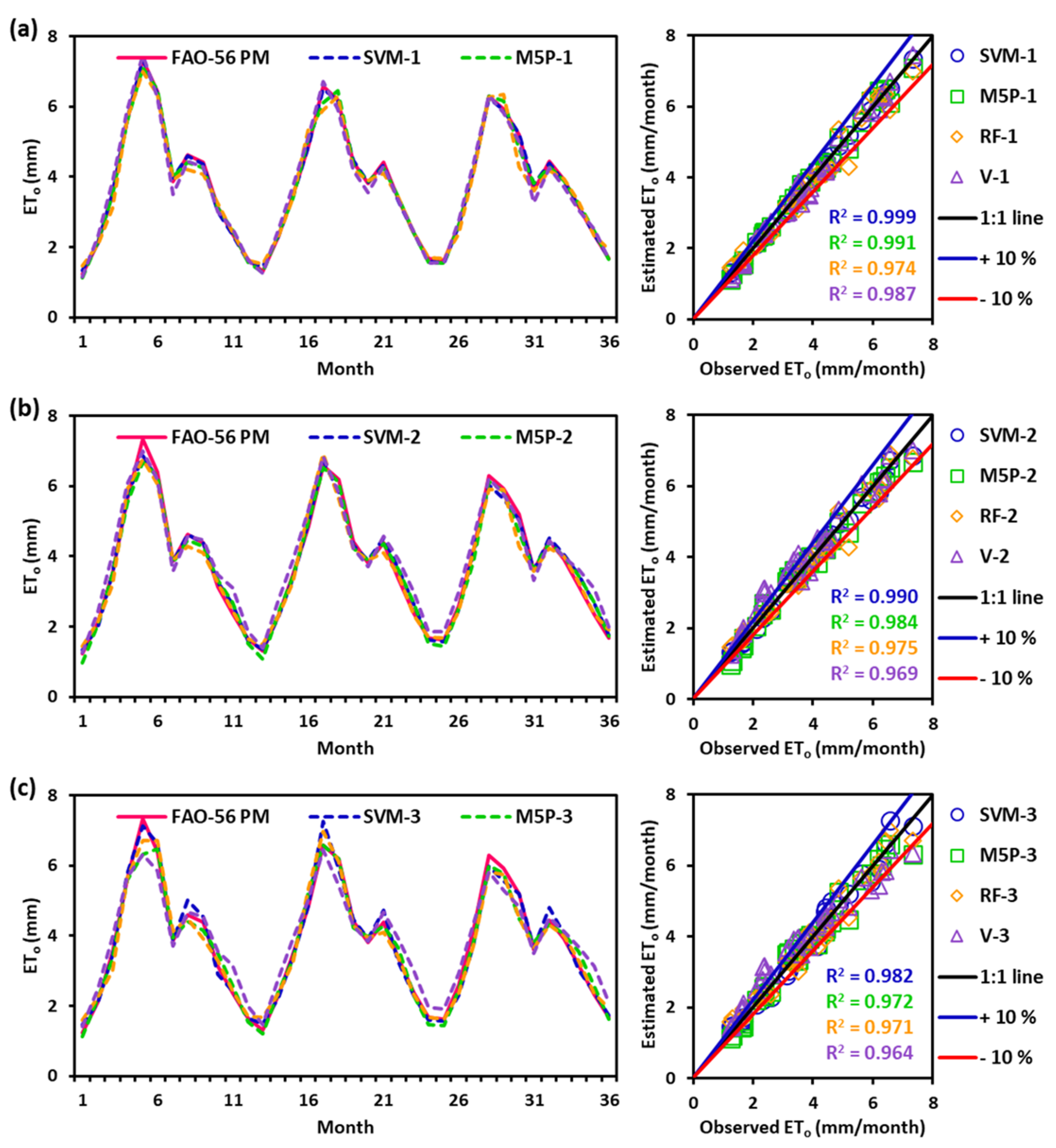
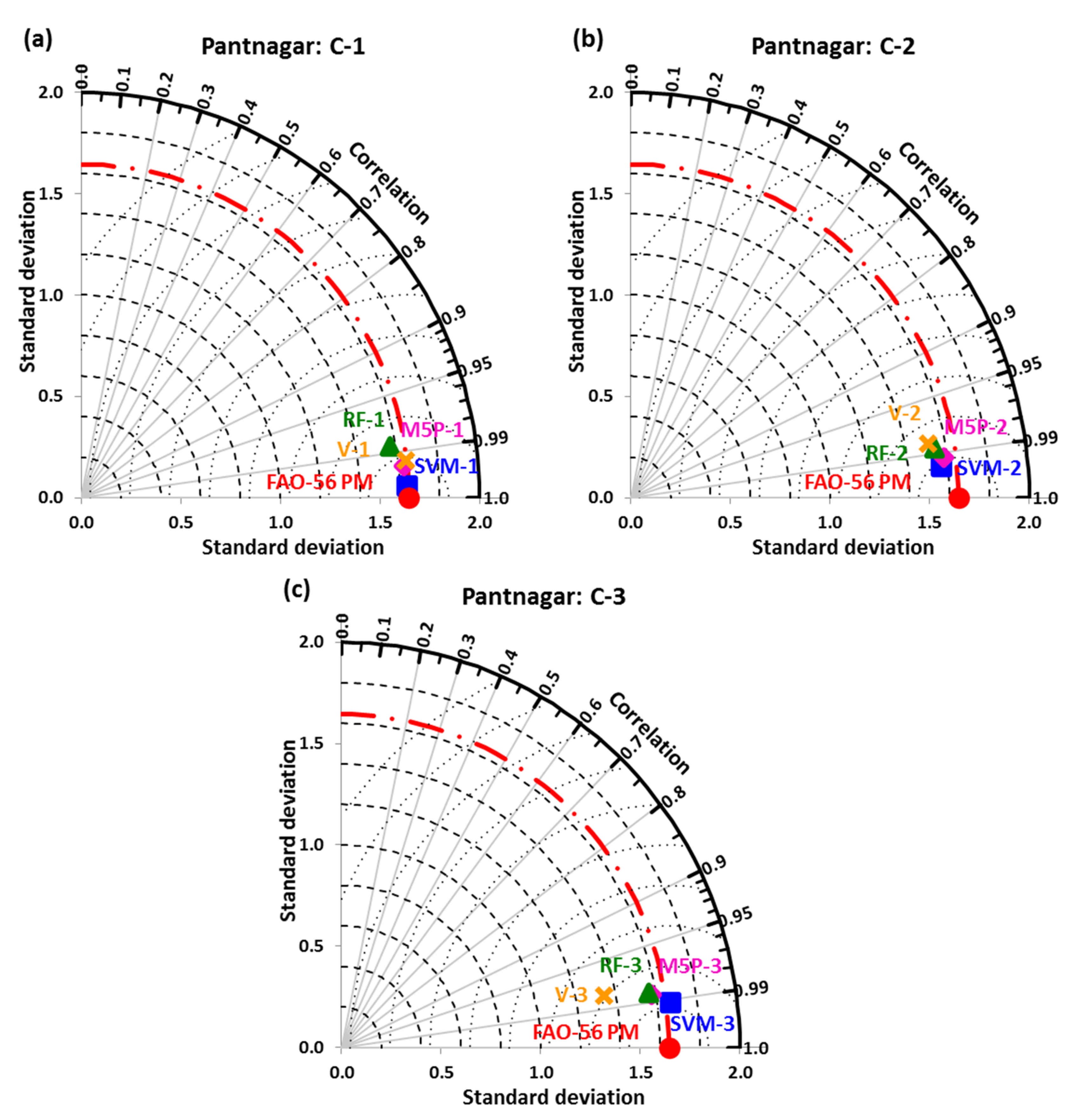
3.2. Performance Evaluation Using Graphical Inspection
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alizamir, M.; Kisi, O.; Muhammad Adnan, R.; Kuriqi, A. Modelling Reference Evapotranspiration by Combining Neuro-Fuzzy and Evolutionary Strategies. Acta Geophys. 2020, 68, 1113–1126. [Google Scholar] [CrossRef]
- Awal, R.; Habibi, H.; Fares, A.; Deb, S. Estimating Reference Crop Evapotranspiration under Limited Climate Data in West Texas. J. Hydrol. Reg. Stud. 2020, 28, 100677. [Google Scholar] [CrossRef]
- Adamala, S.; Raghuwanshi, N.S.; Mishra, A.; Singh, R. Generalized Wavelet Neural Networks for Evapotranspiration Modeling in India. ISH J. Hydraul. Eng. 2019, 25, 119–131. [Google Scholar] [CrossRef]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop Evapotranspiration Estimation with FAO56: Past and Future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Zhao, L.; Hu, X.; Gong, D. Comparison of ELM, GANN, WNN and Empirical Models for Estimating Reference Evapotranspiration in Humid Region of Southwest China Comparison of ELM, GANN, WNN and Empirical Models for Estimating Reference Evapotranspiration in Humid Region of Southwest. J. Hydrol. 2016, 536, 376–383. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Requirements. FAO Irrig. Drain. Pap. 56 1998, 300, D05109. [Google Scholar]
- Abdullah, S.S.; Malek, M.A.; Abdullah, N.S.; Kisi, O.; Yap, K.S. Extreme Learning Machines: A New Approach for Prediction of Reference Evapotranspiration. J. Hydrol. 2015, 527, 184–195. [Google Scholar] [CrossRef]
- Tabari, H.; Hosseinzadeh Talaee, P. Multilayer Perceptron for Reference Evapotranspiration Estimation in a Semiarid Region. Neural Comput. Appl. 2013, 23, 341–348. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Malik, A.; Kumar, A.; Souag-Gamane, D.; Kisi, O. Estimation of Monthly Reference Evapotranspiration Using Novel Hybrid Machine Learning Approaches. Hydrol. Sci. J. 2019, 64, 1824–1842. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, Z.; Jiang, H.; Sun, S. Estimating Daily Reference Evapotranspiration Based on Limited Meteorological Data Using Deep Learning and Classical Machine Learning Methods. J. Hydrol. 2020, 591, 125286. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Malik, A.; Pandey, K.; Sammen, S.S.; Souag-Gamane, D.; Heddam, S.; Kisi, O. Monthly Evapotranspiration Estimation Using Optimal Climatic Parameters: Efficacy of Hybrid Support Vector Regression Integrated with Whale Optimization Algorithm. Environ. Monit. Assess. 2020, 192, 696. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, L.B.; da Cunha, F.F. New Approach to Estimate Daily Reference Evapotranspiration Based on Hourly Temperature and Relative Humidity Using Machine Learning and Deep Learning. Agric. Water Manag. 2020, 234, 106113. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. Reference Evapotranspiration Estimation and Modeling of the Punjab Northern India Using Deep Learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- Khosravi, K.; Daggupati, P.; Alami, M.T.; Awadh, S.M.; Ghareb, M.I.; Panahi, M.; Pham, B.T.; Rezaie, F.; Qi, C.; Yaseen, Z.M. Meteorological Data Mining and Hybrid Data-Intelligence Models for Reference Evaporation Simulation: A Case Study in Iraq. Comput. Electron. Agric. 2019, 167, 105041. [Google Scholar] [CrossRef]
- Wu, L.; Fan, J. Comparison of Neuron-Based, Kernel-Based, Tree-Based and Curve-Based Machine Learning Models for Predicting Daily Reference Evapotranspiration. PLoS ONE 2019, 14, e0217520. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and Four Tree-Based Ensemble Models for Predicting Daily Reference Evapotranspiration Using Limited Meteorological Data in Different Climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F.; de Oliveira, R.A.; Fernandes Filho, E.I. Estimation of Reference Evapotranspiration in Brazil with Limited Meteorological Data Using ANN and SVM—A New Approach. J. Hydrol. 2019, 572, 556–570. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Behmanesh, J.; Khalili, K. Using MARS, SVM, GEP and Empirical Equations for Estimation of Monthly Mean Reference Evapotranspiration. Comput. Electron. Agric. 2017, 139, 103–114. [Google Scholar] [CrossRef]
- Wang, S.; Lian, J.; Peng, Y.; Hu, B.; Chen, H. Generalized Reference Evapotranspiration Models with Limited Climatic Data Based on Random Forest and Gene Expression Programming in Guangxi, China. Agric. Water Manag. 2019, 221, 220–230. [Google Scholar] [CrossRef]
- Sarker, S.; Veremyev, A.; Boginski, V.; Singh, A. Critical Nodes in River Networks. Sci. Rep. 2019, 9, 11178. [Google Scholar] [CrossRef] [Green Version]
- Sarker, S. Investigating Topologic and Geometric Properties of Synthetic and Natural River Networks under Changing Climate. Dr. Diss. Univ. Cent. Fla. US 2021, 2020, 965. [Google Scholar]
- Ashrafzadeh, A.; Kişi, O.; Aghelpour, P.; Biazar, S.M.; Masouleh, M.A. Comparative Study of Time Series Models, Support Vector Machines, and GMDH in Forecasting Long-Term Evapotranspiration Rates in Northern Iran. J. Irrig. Drain. Eng. 2020, 146, 04020010. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Mohammadi, B.; Pham, Q.B.; Duan, Z. Development of Boosted Machine Learning Models for Estimating Daily Reference Evapotranspiration and Comparison with Empirical Approaches. Water 2021, 13, 3489. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Islam, A.R.M.T.; Kisi, O.; Kuriqi, A.; Heddam, S. Estimating Reference Evapotranspiration Using Hybrid Adaptive Fuzzy Inferencing Coupled with Heuristic Algorithms. Comput. Electron. Agric. 2021, 191, 106541. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mehdizadeh, S. Modeling Daily Reference Evapotranspiration via a Novel Approach Based on Support Vector Regression Coupled with Whale Optimization Algorithm. Agric. Water Manag. 2020, 237, 106145. [Google Scholar] [CrossRef]
- Maroufpoor, S.; Bozorg-Haddad, O.; Maroufpoor, E. Reference Evapotranspiration Estimating Based on Optimal Input Combination and Hybrid Artificial Intelligent Model: Hybridization of Artificial Neural Network with Grey Wolf Optimizer Algorithm. J. Hydrol. 2020, 588, 125060. [Google Scholar] [CrossRef]
- Rezaabad, M.Z.; Ghazanfari, S.; Salajegheh, M. ANFIS Modeling with ICA, BBO, TLBO, and IWO Optimization Algorithms and Sensitivity Analysis for Predicting Daily Reference Evapotranspiration. J. Hydrol. Eng. 2020, 25, 04020038. [Google Scholar] [CrossRef]
- Chia, M.Y.; Huang, Y.F.; Koo, C.H. Swarm-Based Optimization as Stochastic Training Strategy for Estimation of Reference Evapotranspiration Using Extreme Learning Machine. Agric. Water Manag. 2021, 243, 106447. [Google Scholar] [CrossRef]
- Panahi, M.; Sadhasivam, N.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial Prediction of Groundwater Potential Mapping Based on Convolutional Neural Network (CNN) and Support Vector Regression (SVR). J. Hydrol. 2020, 588, 125033. [Google Scholar] [CrossRef]
- Borji, M.; Malekian, A.; Salajegheh, A.; Ghadimi, M. Multi-Time-Scale Analysis of Hydrological Drought Forecasting Using Support Vector Regression (SVR) and Artificial Neural Networks (ANN). Arab. J. Geosci. 2016, 9, 725. [Google Scholar] [CrossRef]
- Valiantzas, J.D. Simple ET0 Forms of Penman’s Equation without Wind and/or Humidity Data. I: Theoretical Development. J. Irrig. Drain. Eng. 2013, 139, 1–8. [Google Scholar] [CrossRef]
- Valiantzas, J.D. Simple ET0 Forms of Penman’s Equation without Wind and/or Humidity Data. II: Comparisons with Reduced Set-FAO and Other Methodologies. J. Irrig. Drain. Eng. 2013, 139, 9–19. [Google Scholar] [CrossRef] [Green Version]
- Afradi, A.; Ebrahimabadi, A. Comparison of Artificial Neural Networks (ANN), Support Vector Machine (SVM) and Gene Expression Programming (GEP) Approaches for Predicting TBM Penetration Rate. SN Appl. Sci. 2020, 2, 2004. [Google Scholar] [CrossRef]
- Biazar, S.M.; Rahmani, V.; Isazadeh, M.; Kisi, O.; Dinpashoh, Y. New Input Selection Procedure for Machine Learning Methods in Estimating Daily Global Solar Radiation. Arab. J. Geosci. 2020, 13, 431. [Google Scholar] [CrossRef]
- Hadi, S.J.; Tombul, M. Forecasting Daily Streamflow for Basins with Different Physical Characteristics through Data-Driven Methods. Water Resour. Manag. 2018, 32, 3405–3422. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Jebur, M.N.; Bui, D.T.; Xu, C.; Akgun, A. Spatial Prediction of Landslide Hazard at the Luxi Area (China) Using Support Vector Machines. Environ. Earth Sci. 2016, 75, 40. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Bui, D.T.; Xu, C.; Youssef, A.M.; Chen, W. Comparison of Four Kernel Functions Used in Support Vector Machines for Landslide Susceptibility Mapping: A Case Study at Suichuan Area (China). Geomat. Nat. Hazards Risk 2017, 8, 544–569. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Dixon, B. GIS-Based Groundwater Potential Mapping Using Boosted Regression Tree, Classification and Regression Tree, and Random Forest Machine Learning Models in Iran. Environ. Monit. Assess. 2016, 188, 44. [Google Scholar] [CrossRef]
- Khaledian, M.R.; Isazadeh, M.; Biazar, S.M.; Pham, Q.B. Simulating Caspian Sea Surface Water Level by Artificial Neural Network and Support Vector Machine Models. Acta Geophys. 2020, 68, 553–563. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Zhang, K. Short-Term Electric Load Forecasting Based on Singular Spectrum Analysis and Support Vector Machine Optimized by Cuckoo Search Algorithm. Electr. Power Syst. Res. 2017, 146, 270–285. [Google Scholar] [CrossRef]
- Sihag, P.; Tiwari, N.K.; Ranjan, S. Support Vector Regression-Based Modeling of Cumulative Infiltration of Sandy Soil. ISH J. Hydraul. Eng. 2018, 26, 138–152. [Google Scholar] [CrossRef]
- Sihag, P.; Singh, V.P.; Angelaki, A.; Kumar, V.; Sepahvand, A.; Golia, E. Modelling of Infiltration Using Artificial Intelligence Techniques in Semi-Arid Iran. Hydrol. Sci. J. 2019, 64, 1647–1658. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; p. 314. [Google Scholar]
- Pourghasemi, H.R.; Jirandeh, A.G.; Pradhan, B.; Xu, C.; Gokceoglu, C. Landslide Susceptibility Mapping Using Support Vector Machine and GIS at the Golestan Province, Iran. J. Earth Syst. Sci. 2013, 122, 349–369. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Li, X.; Yang, B.; Wen, Z. Wavelet Support Vector Machine-Based Prediction Model of Dam Deformation. Mech. Syst. Signal Process. 2018, 110, 412–427. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration Evaluation Models Based on Machine Learning Algorithms—A Comparative Study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. Learning with Continuous Classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Australia, 16–18 November 1992; Volume 92, pp. 343–348. [Google Scholar]
- Pal, M.; Deswal, S. M5 Model Tree Based Modelling of Reference Evapotranspiration. Hydrol. Process. 2009, 23, 1437–1443. [Google Scholar] [CrossRef]
- Ali, M.; Deo, R.C.; Downs, N.J.; Maraseni, T. An Ensemble-ANFIS Based Uncertainty Assessment Model for Forecasting Multi-Scalar Standardized Precipitation Index. Atmos. Res. 2018, 207, 155–180. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sihag, P.; Yusuf, B.; Al-Janabi, A.M.S. Modelling Infiltration Rates in Permeable Stormwater Channels Using Soft Computing Techniques. Irrig. Drain. 2020, 70, 117–130. [Google Scholar] [CrossRef]
- Kisi, O.; Khosravinia, P.; Nikpour, M.R.; Sanikhani, H. Hydrodynamics of River-Channel Confluence: Toward Modeling Separation Zone Using GEP, MARS, M5 Tree and DENFIS Techniques. Stoch. Environ. Res. Risk Assess. 2019, 33, 1089–1107. [Google Scholar] [CrossRef]
- Taghi Sattari, M.; Pal, M.; Apaydin, H.; Ozturk, F. M5 Model Tree Application in Daily River Flow Forecasting in Sohu Stream, Turkey. Water Resour. 2013, 40, 233–242. [Google Scholar] [CrossRef]
- Rahimikhoob, A. Comparison between M5 Model Tree and Neural Networks for Estimating Reference Evapotranspiration in an Arid Environment. Water Resour. Manag. 2014, 28, 657–669. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Solomatine, D.P. Neural Networks and M5 Model Trees in Modelling Water Level–Discharge Relationship. Neurocomputing 2005, 63, 381–396. [Google Scholar] [CrossRef]
- Sattari, M.T.; Mirabbasi, R.; Sushab, R.S.; Abraham, J. Prediction of Groundwater Level in Ardebil Plain Using Support Vector Regression and M5 Tree Model. Groundwater 2018, 56, 636–646. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Sarker, T. Role of Climatic and Non-Climatic Factors on Land Use and Land Cover Change in the Arctic: A Comparative Analysis of Vorkuta and Salekhard. Master’s Dissertation, The George Washington University, Washington, DC, USA, 2020. Available online: https://scholarspace.library.gwu.edu/etd/6969z1516 (accessed on 5 May 2022).
- Sihag, P.; Esmaeilbeiki, F.; Singh, B.; Pandhiani, S.M. Model-Based Soil Temperature Estimation Using Climatic Parameters: The Case of Azerbaijan Province, Iran. Geol. Ecol. Landscapes 2020, 4, 203–215. [Google Scholar] [CrossRef] [Green Version]
- Legates, D.R.; McCabe, G.J. Evaluating the Use of “Goodness-of-Fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Salih, S.Q.; Kim, S.; Kim, N.W.; Yaseen, Z.M.; Singh, V.P. Drought Index Prediction Using Advanced Fuzzy Logic Model: Regional Case Study over Kumaon in India. PLoS ONE 2020, 15, e0233280. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A. Meteorological Drought Prediction Using Heuristic Approaches Based on Effective Drought Index: A Case Study in Uttarakhand. Arab. J. Geosci. 2020, 13, 276. [Google Scholar] [CrossRef]
- Willmott, C.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Willmott, C.J. On the Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Rai, P.; Kuriqi, A. Prediction of Multi-Scalar Standardized Precipitation Index by Using Artificial Intelligence and Regression Models. Climate 2021, 9, 28. [Google Scholar] [CrossRef]
- Ye, L.; Zahra, M.M.A.; Al-Bedyry, N.K.; Yaseen, Z.M. Daily Scale Evapotranspiration Prediction over the Coastal Region of Southwest Bangladesh: New Development of Artificial Intelligence Model. Stoch. Environ. Res. Risk Assess. 2022, 36, 451–471. [Google Scholar] [CrossRef]
- Gao, Z.; He, J.; Dong, K.; Li, X. Trends in Reference Evapotranspiration and Their Causative Factors in the West Liao River Basin, China. Agric. For. Meteorol. 2017, 232, 106–117. [Google Scholar] [CrossRef]
- Sridhar, V.; Hubbard, K.G.; Wedin, D.A. Assessment of Soil Moisture Dynamics of the Nebraska Sandhills Using Long-Term Measurements and a Hydrology Model. J. Irrig. Drain. Eng. 2006, 132, 463–473. [Google Scholar] [CrossRef] [Green Version]
- Sridhar, V. Tracking the Influence of Irrigation on Land Surface Fluxes and Boundary Layer Climatology. J. Contemp. Water Res. Educ. 2013, 152, 79–93. [Google Scholar] [CrossRef]
- Seong, C.; Sridhar, V.; Billah, M.M. Implications of Potential Evapotranspiration Methods for Streamflow Estimations under Changing Climatic Conditions. Int. J. Climatol. 2018, 38, 896–914. [Google Scholar] [CrossRef]
- Kaya, Y.Z.; Zelenakova, M.; Üneş, F.; Demirci, M.; Hlavata, H.; Mesaros, P. Estimation of Daily Evapotranspiration in Košice City (Slovakia) Using Several Soft Computing Techniques. Theor. Appl. Climatol. 2021, 144, 287–298. [Google Scholar] [CrossRef]
- Kisi, O.; Keshtegar, B.; Zounemat-Kermani, M.; Heddam, S.; Trung, N.-T. Modeling Reference Evapotranspiration Using a Novel Regression-Based Method: Radial Basis M5 Model Tree. Theor. Appl. Climatol. 2021, 145, 639–659. [Google Scholar] [CrossRef]
- Adnan, R.M.; Chen, Z.; Yuan, X.; Kisi, O.; El-Shafie, A.; Kuriqi, A.; Ikram, M. Reference Evapotranspiration Modeling Using New Heuristic Methods. Entropy 2020, 22, 547. [Google Scholar] [CrossRef] [PubMed]
- Malik, A.; Kumar, A.; Ghorbani, M.A.; Kashani, M.H.; Kisi, O.; Kim, S. The Viability of Co-Active Fuzzy Inference System Model for Monthly Reference Evapotranspiration Estimation: Case Study of Uttarakhand State. Hydrol. Res. 2019, 50, 1623–1644. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez del Cerro, R.T.; Subathra, M.S.; Manoj Kumar, N.; Verrastro, S.; Thomas George, S. Modelling the Daily Reference Evapotranspiration in Semi-Arid Region of South India: A Case Study Comparing ANFIS and Empirical Models. Inf. Process. Agric. 2020, 8, 173–184. [Google Scholar] [CrossRef]
- Ahmadi, F.; Mehdizadeh, S.; Mohammadi, B.; Pham, Q.B.; DOAN, T.N.C.; Vo, N.D. Application of an Artificial Intelligence Technique Enhanced with Intelligent Water Drops for Monthly Reference Evapotranspiration Estimation. Agric. Water Manag. 2021, 244, 106622. [Google Scholar] [CrossRef]
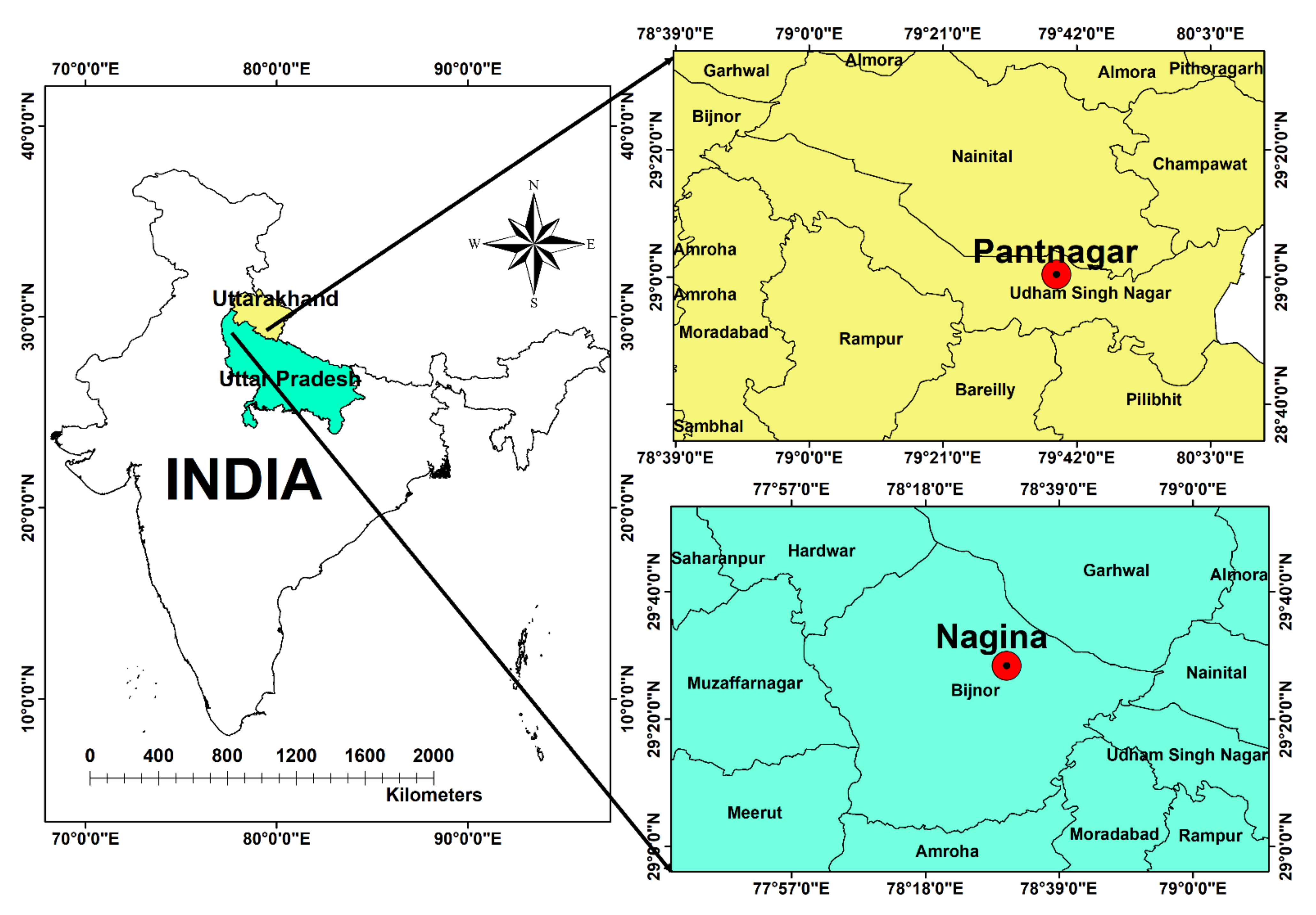



| Station | Statistical Properties | Climatic Variables | Geographical Properties | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | RH (%) | u (m/s) | Rs (MJ/m2/month) | ETo (mm/month) | Longitude (E) | Latitude (N) | Altitude (m) | Climatic Data (Year) | ||
| Nagina | Minimum | 10.900 | 24.600 | 0.278 | 8.300 | 1.140 | 78°25′59″ | 29°26′35″ | 282.0 | 2009–2016 |
| Maximum | 33.000 | 88.000 | 1.946 | 25.000 | 6.760 | |||||
| Mean | 22.994 | 71.965 | 1.049 | 17.089 | 3.572 | |||||
| Standard deviation | 6.412 | 11.891 | 0.422 | 4.611 | 1.573 | |||||
| Skewness | −0.393 | −1.235 | 0.210 | −0.035 | 0.255 | |||||
| Kurtosis | −1.274 | 1.667 | −0.925 | −0.989 | −0.958 | |||||
| Pantnagar | Minimum | 11.450 | 41.500 | 0.584 | 8.200 | 1.240 | 79°38′00″ | 29°00′00″ | 243.8 | 2009–2016 |
| Maximum | 33.000 | 86.500 | 2.752 | 24.700 | 7.680 | |||||
| Mean | 23.609 | 67.839 | 1.415 | 16.634 | 3.831 | |||||
| Standard deviation | 6.204 | 11.303 | 0.527 | 4.413 | 1.692 | |||||
| Skewness | −0.433 | −0.721 | 0.375 | −0.064 | 0.459 | |||||
| Kurtosis | −1.255 | −0.473 | −0.435 | −0.818 | −0.629 | |||||
| Model | Equation | Reference |
|---|---|---|
| V-1 | [31,32] | |
| V-2 | [31,32] | |
| V-3 | [31,32] |
| Combination | Inputs | Output | ML Models |
|---|---|---|---|
| C-1 | T, RH, u, Rs | ETo | SVM, M5P, RF |
| C-2 | T, RH, Rs | ETo | SVM, M5P, RF |
| C-3 | T, Rs | ETo | SVM, M5P, RF |
| Equation | Range | Reference |
|---|---|---|
| (0 < MAE < ∞) | [60,61] | |
| (0 < RMSE < ∞) | [62,63] | |
| (−∞ < EC < 1) | [64,65] | |
| (−1 < CC < 1) | [65,66] | |
| (0 < WI ≤ 1) | [67,68] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rai, P.; Kumar, P.; Al-Ansari, N.; Malik, A. Evaluation of Machine Learning versus Empirical Models for Monthly Reference Evapotranspiration Estimation in Uttar Pradesh and Uttarakhand States, India. Sustainability 2022, 14, 5771. https://doi.org/10.3390/su14105771
Rai P, Kumar P, Al-Ansari N, Malik A. Evaluation of Machine Learning versus Empirical Models for Monthly Reference Evapotranspiration Estimation in Uttar Pradesh and Uttarakhand States, India. Sustainability. 2022; 14(10):5771. https://doi.org/10.3390/su14105771
Chicago/Turabian StyleRai, Priya, Pravendra Kumar, Nadhir Al-Ansari, and Anurag Malik. 2022. "Evaluation of Machine Learning versus Empirical Models for Monthly Reference Evapotranspiration Estimation in Uttar Pradesh and Uttarakhand States, India" Sustainability 14, no. 10: 5771. https://doi.org/10.3390/su14105771
APA StyleRai, P., Kumar, P., Al-Ansari, N., & Malik, A. (2022). Evaluation of Machine Learning versus Empirical Models for Monthly Reference Evapotranspiration Estimation in Uttar Pradesh and Uttarakhand States, India. Sustainability, 14(10), 5771. https://doi.org/10.3390/su14105771







