Enabling Knowledge Discovery in Multi-Objective Optimizations of Worker Well-Being and Productivity
Abstract
:1. Introduction
2. Method
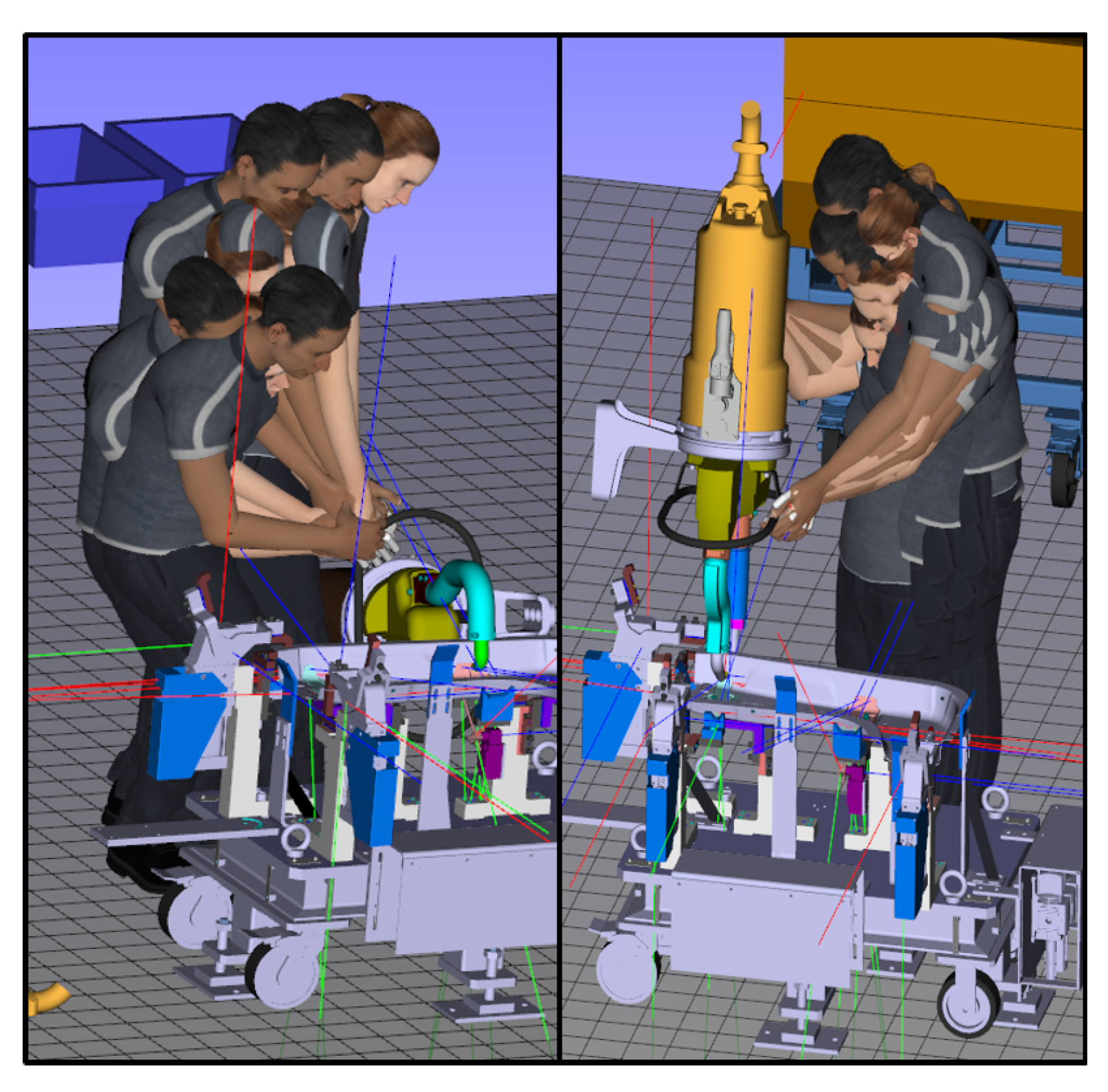
2.1. Application Study
2.1.1. Model Definition
2.1.2. Well-Being and Productivity Evaluation
2.1.3. Mathematical Modeling of Optimization
2.1.4. Optimization Method
2.2. Knowledge Discovery
2.2.1. FPM
2.2.2. InfS-R
3. Results
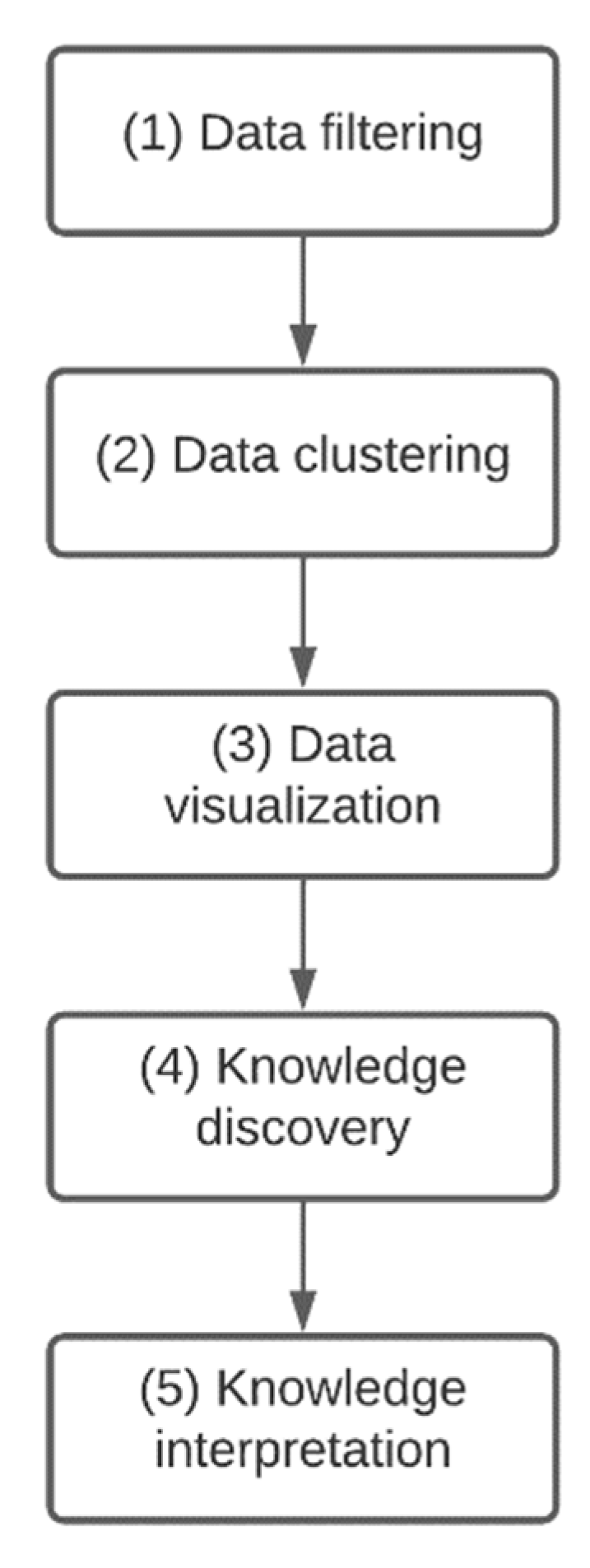
3.1. Data Filtering
3.2. Data Clustering
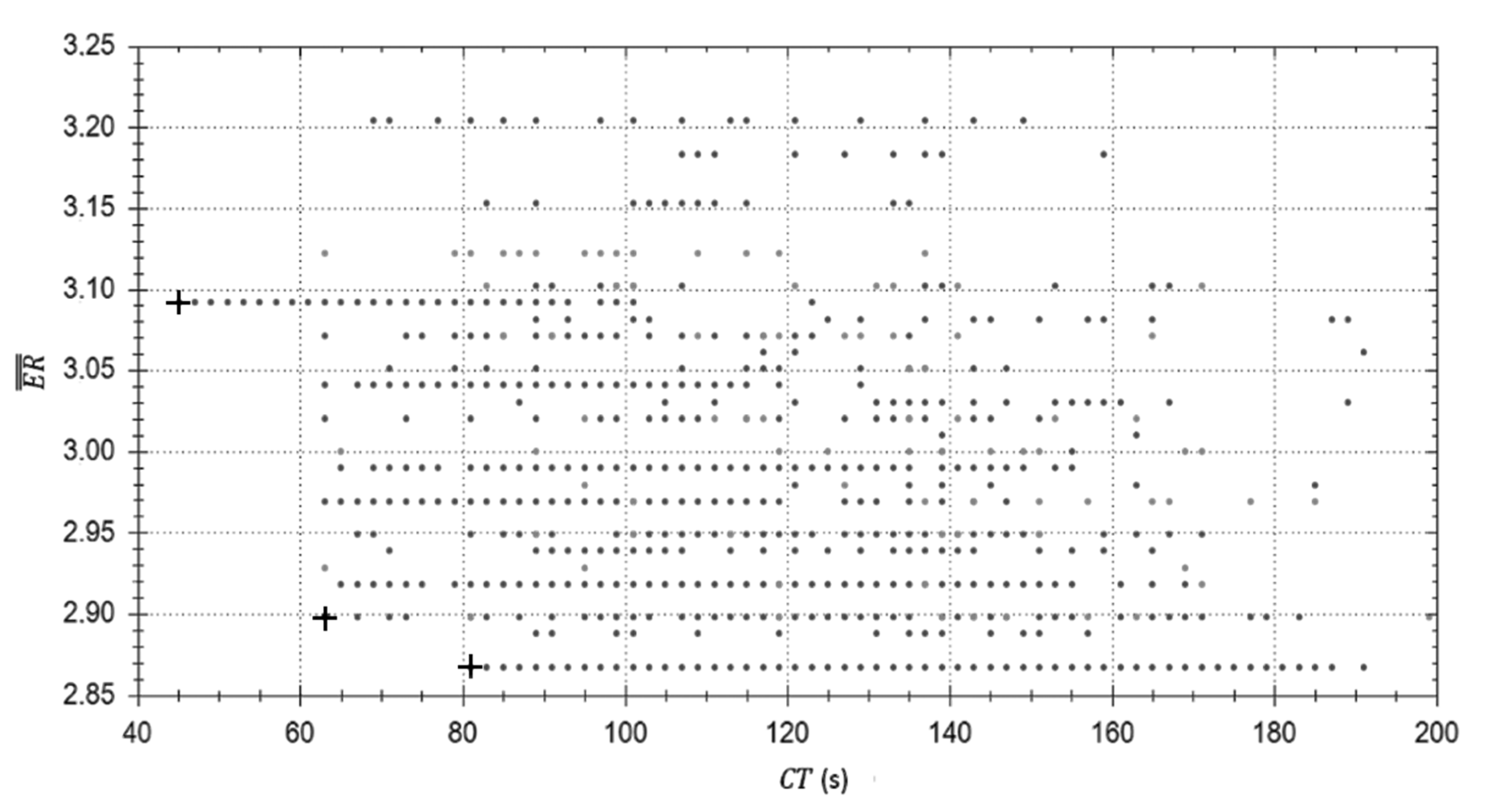
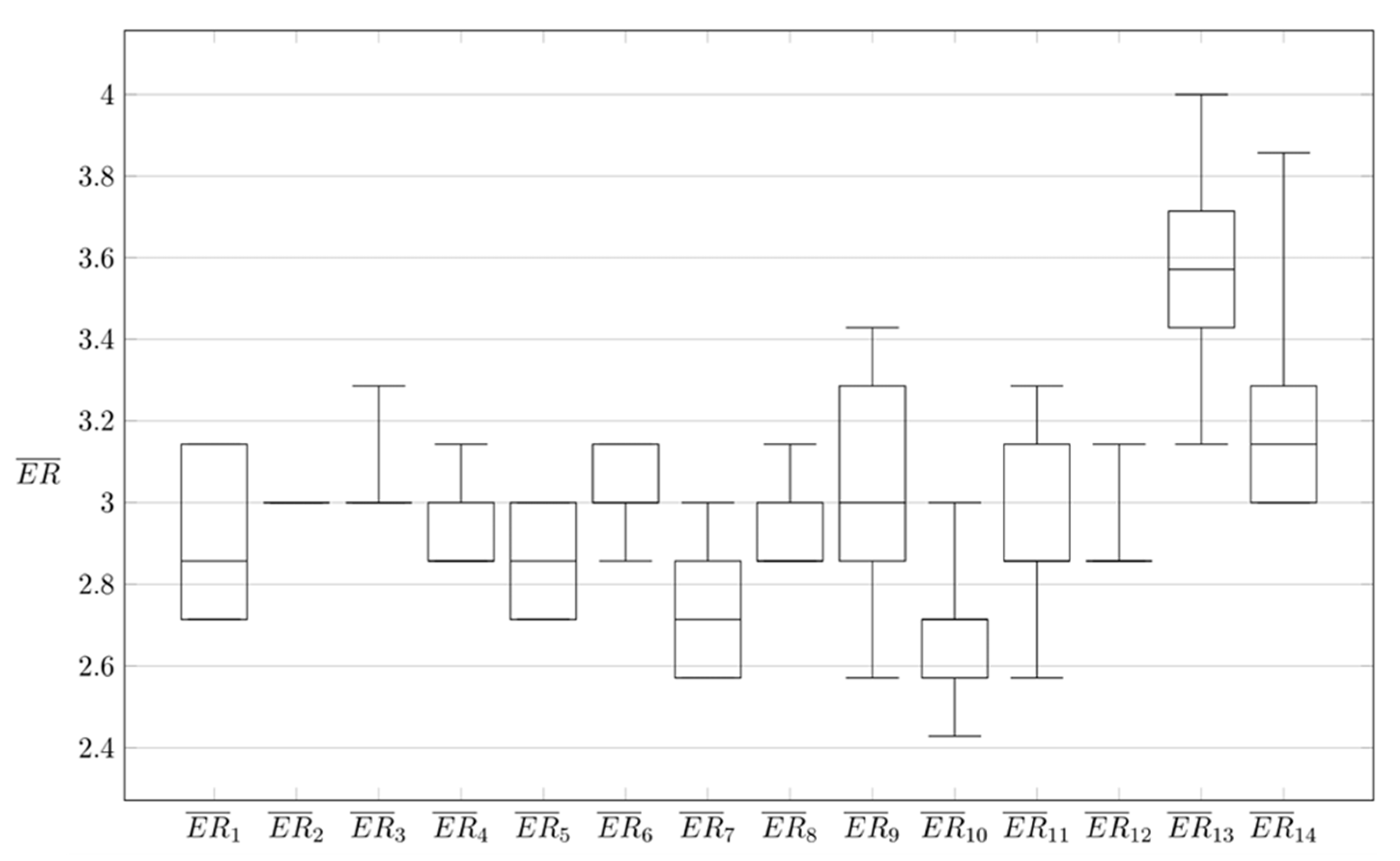
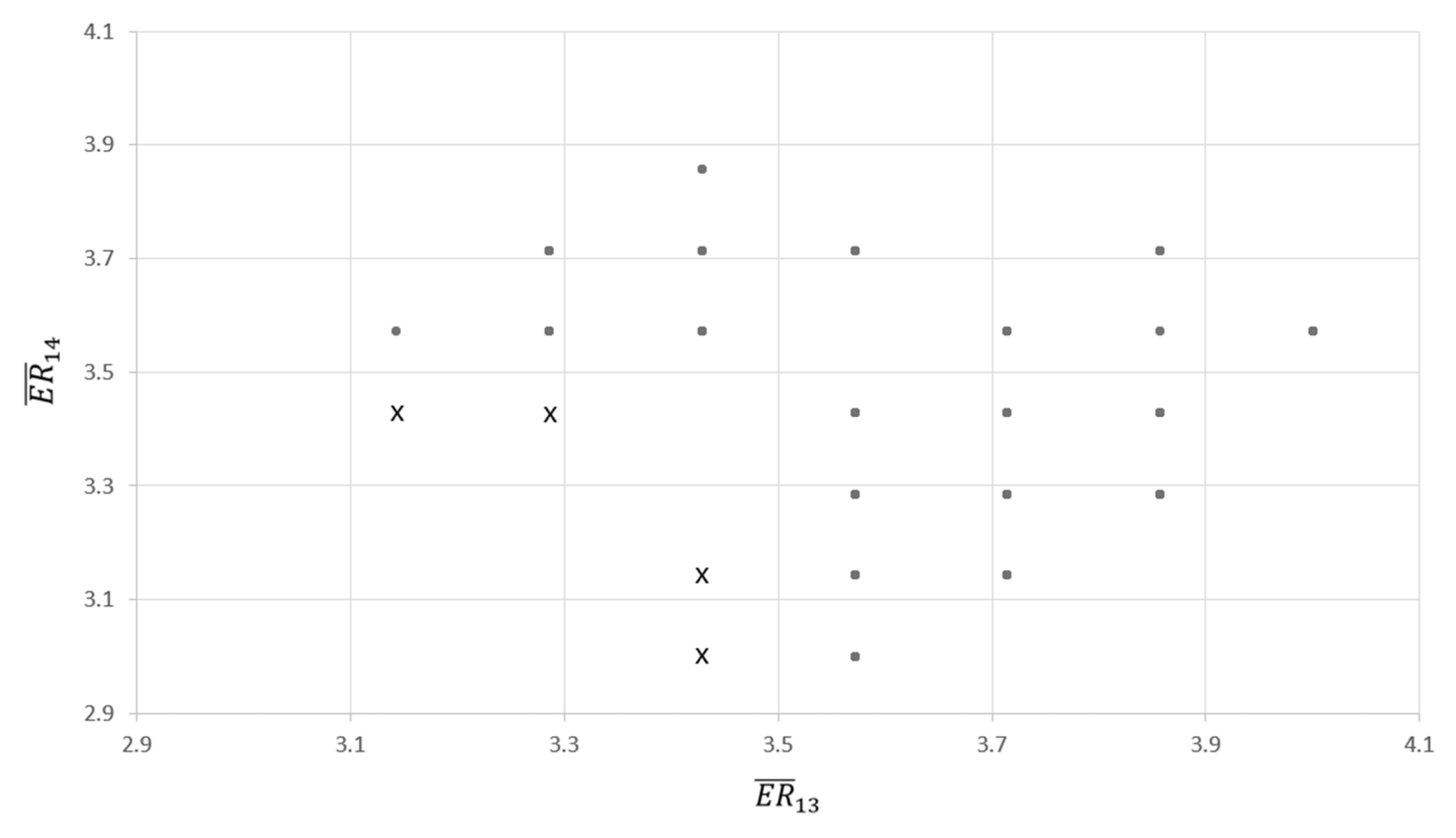
3.3. Data Visualization
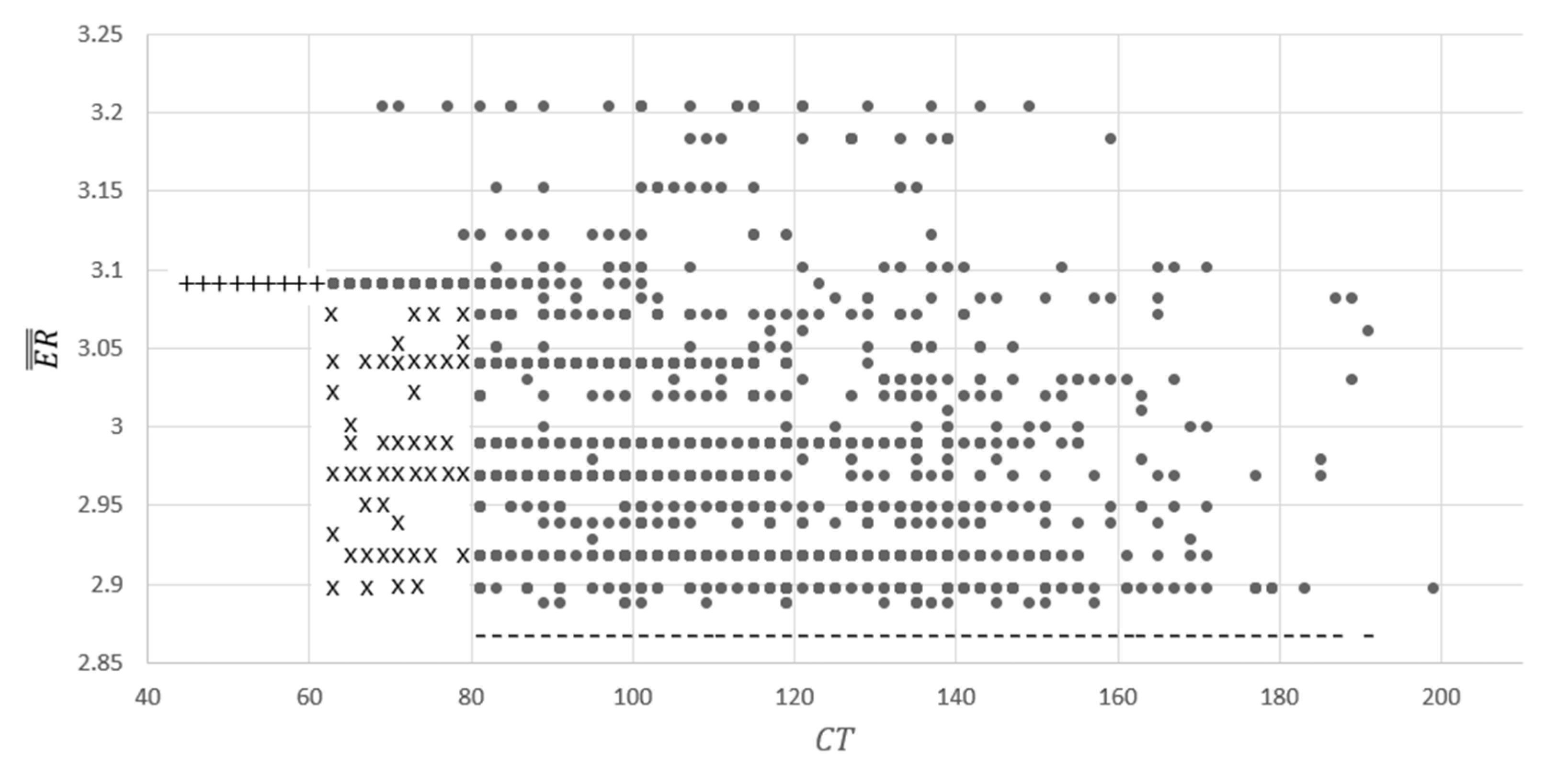
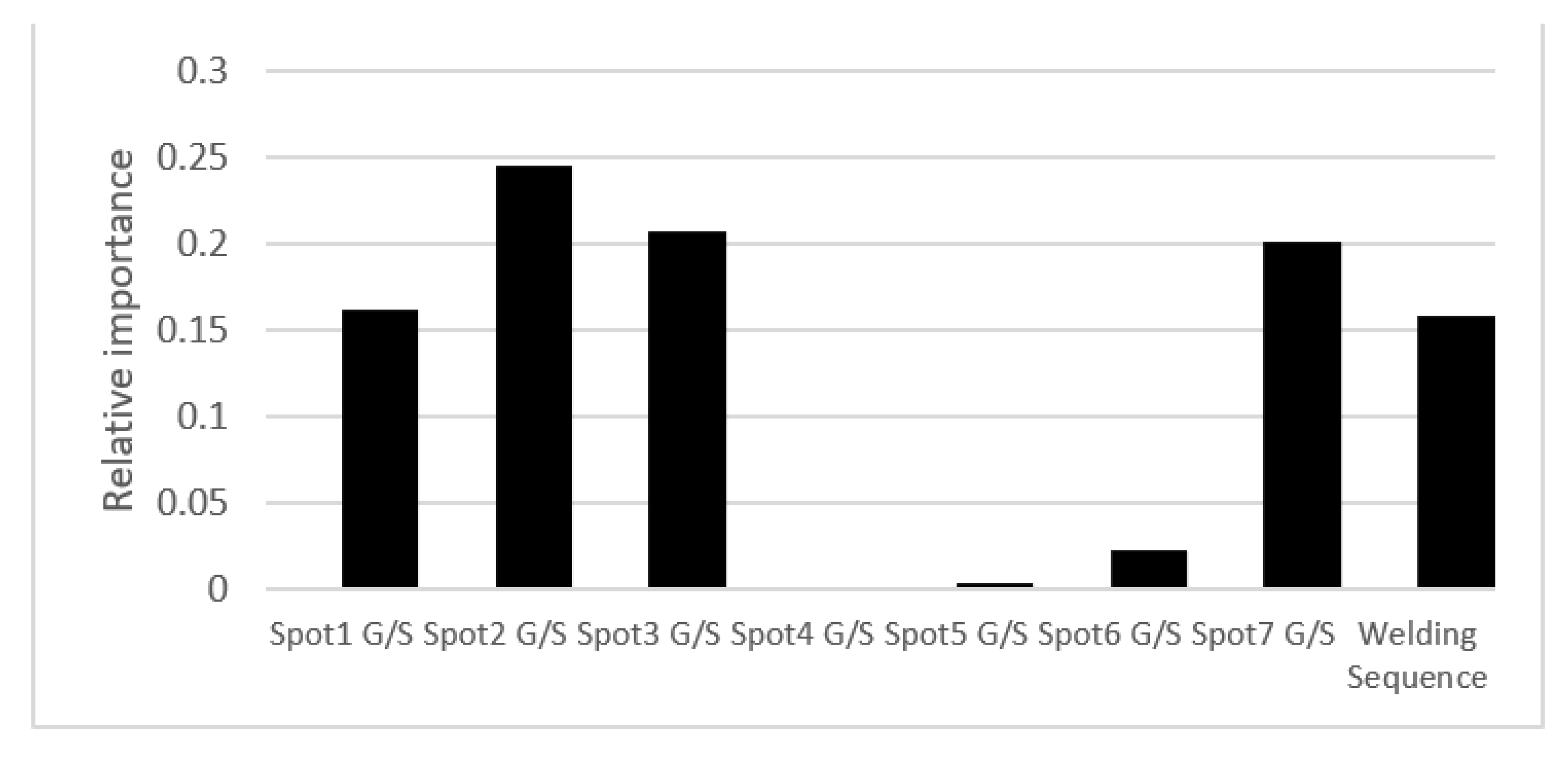
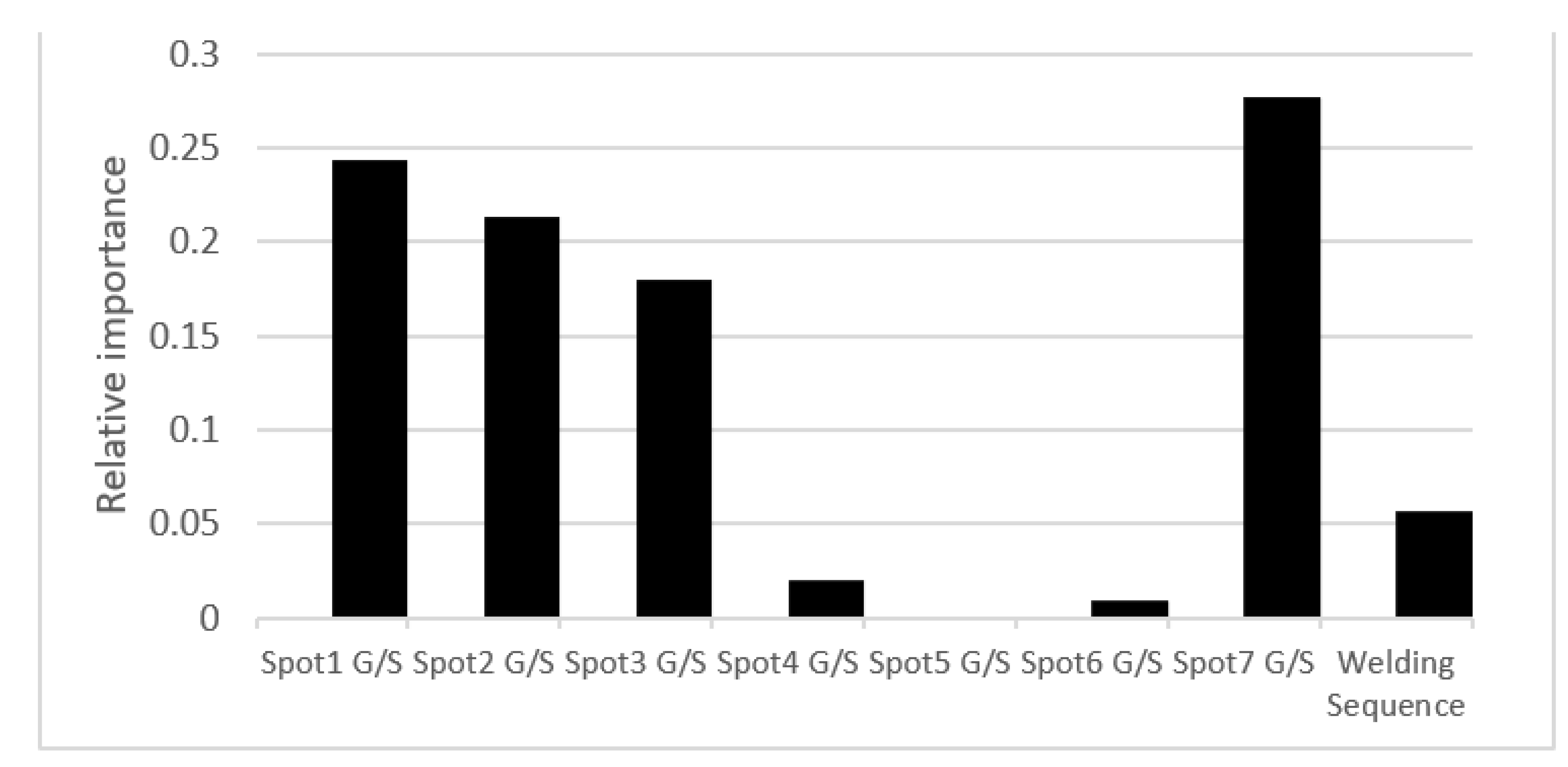
3.4. Knowledge Discovery
3.5. Knowledge Interpretation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Kuhn, W. Digital Factory—Simulation Enhancing the Product and Production Engineering Process. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; pp. 1899–1906. [Google Scholar] [CrossRef]
- Fisher, D.L.; Lee, J.D.; Rizzo, M.; Caird, J. Handbook of Driving Simulation for Engineering, Medicine, and Psychology; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Oppelt, M.; Urbas, L. Integrated virtual commissioning an essential activity in the automation engineering process: From virtual commissioning to simulation supported engineering. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 2564–2570. [Google Scholar] [CrossRef]
- Wang, Q.; Chatwin, C. Key issues and developments in modelling and simulation-based methodologies for manufacturing systems analysis, design and performance evaluation. Int. J. Adv. Manuf. Technol. 2004, 25, 1254–1265. [Google Scholar] [CrossRef]
- Ore, F.; Vemula, B.R.; Hanson, L.; Wiktorsson, M. Human—Industrial Robot Collaboration: Application of Simulation Software for Workstation Optimisation. Procedia CIRP 2016, 44, 181–186. [Google Scholar] [CrossRef] [Green Version]
- Scataglini, S.; Paul, G. DHM and Posturography; Elsevier Academic Press: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Eklund, J.A. Relationships between ergonomics and quality in assembly work. Appl. Ergon. 1995, 26, 15–20. [Google Scholar] [CrossRef]
- Vink, P.; Koningsveld, E.A.; Molenbroek, J. Positive outcomes of participatory ergonomics in terms of greater comfort and higher productivity. Appl. Ergon. 2006, 37, 537–546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Falck, A.-C.; Örtengren, R.; Högberg, D. The impact of poor assembly ergonomics on product quality: A cost-benefit analysis in car manufacturing. Hum. Factors Ergon. Manuf. Serv. Ind. 2010, 20, 24–41. [Google Scholar] [CrossRef]
- Widana, I.; Sumetri, N.W.; Sutapa, I.K. Ergonomic Work Station Design to Improve Workload Quality and Productivity of the Craffsmen. J. Phys. Conf. Ser. 2018, 953, 12091. [Google Scholar] [CrossRef]
- Green, R.F. A Generic Process for Human Model Analysis; SAE Technical Paper 2000-01–2167; SAE International: Warrendale, PA, USA, 2000. [Google Scholar] [CrossRef]
- Hanson, L.; Blomé, M.W.; Dukic, T.; Högberg, D. Guide and documentation system to support digital human modeling applications. Int. J. Ind. Ergon. 2006, 36, 17–24. [Google Scholar] [CrossRef]
- Reed, M.P.; Faraway, J.; Chaffin, D.B.; Martin, B.J. The HUMOSIM Ergonomics Framework: A New Approach to Digital Human Simulation for Ergonomic Analysis; SAE Technical Paper 2006-01–2365; SAE International: Warrendale, PA, USA, 2006. [Google Scholar] [CrossRef] [Green Version]
- Battini, D.; Faccio, M.; Persona, A.; Sgarbossa, F. New methodological framework to improve productivity and ergonomics in assembly system design. Int. J. Ind. Ergon. 2011, 41, 30–42. [Google Scholar] [CrossRef]
- Mura, M.D.; Dini, G. Optimizing ergonomics in assembly lines: A multi objective genetic algorithm. CIRP J. Manuf. Sci. Technol. 2019, 27, 31–45. [Google Scholar] [CrossRef]
- Harari, Y.; Bechar, A.; Riemer, R. Simulation-Based Optimization Methodology for a Manual Material Handling Task Design That Maximizes Productivity While Considering Ergonomic Constraints. IEEE Trans. Hum.-Mach. Syst. 2019, 49, 440–448. [Google Scholar] [CrossRef]
- Sana, S.S.; Mateus, H.O.; Arrieta, F.A.G.; Acevedo-Chedid, J. Application of genetic algorithm to job scheduling under ergonomic constraints in manufacturing industry. J. Ambient Intell. Humaniz. Comput. 2018, 10, 2063–2090. [Google Scholar] [CrossRef]
- Sato, Y.; Izui, K.; Yamada, T.; Nishiwaki, S. Data mining based on clustering and association rule analysis for knowledge discovery in multiobjective topology optimization. Expert Syst. Appl. 2019, 119, 247–261. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Javadpour, F.; Sahimi, M. Data mining and machine learning for identifying sweet spots in shale reservoirs. Expert Syst. Appl. 2017, 88, 435–447. [Google Scholar] [CrossRef]
- Pascual, A.I.; Högberg, D.; Lämkull, D.; Luque, E.P.; Syberfeldt, A.; Hanson, L. Optimization of productivity and worker well-being by using a multi-objective optimization framework. IISE Trans. Occup. Ergon. Hum. Factors 2021, 9, 143–153. [Google Scholar] [CrossRef]
- Högberg, D.; Hanson, L.; Bohlin, R.; Carlson, J.S. Creating and shaping the DHM tool IMMA for ergonomic product and production design. Int. J. Digit. Hum. 2016, 1, 132–152. [Google Scholar] [CrossRef]
- Brolin, E.; Högberg, D.; Hanson, L.; Örtengren, R. Development and evaluation of an anthropometric module for digital human modelling systems. Int. J. Hum. Factors Model. Simul. 2019, 7, 47. [Google Scholar] [CrossRef]
- McAtamney, L.; Corlett, E.N. RULA: A survey method for the investigation of work-related upper limb disorders. Appl. Ergon. 1993, 24, 91–99. [Google Scholar] [CrossRef]
- Sayin, S. Multi-objective optimization and decision support systems. In Encyclopedia of Optimization, 2nd ed.; Floudas, C.A., Pardalos, P., Eds.; Springer: Boston, MA, USA, 2009. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Smedberg, H.; Bandaru, S. Finding influential variables in multi-objective optimization problems. In Proceedings of the 2020 IEEE Symposium Series on Computational Intelligence (SSCI), Canberra, ACT, Australia, 1–4 December 2020; pp. 173–180. [Google Scholar] [CrossRef]
- Bandaru, S.; Ng, A.H.; Deb, K. Data mining methods for knowledge discovery in multi-objective optimization: Part B—New developments and applications. Expert Syst. Appl. 2017, 70, 119–138. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, R.; Srikant, R. Mining sequential patterns. In Proceedings of the Eleventh International Conference on Data Engineering, Taipei, Taiwan, 6–10 March 1995; pp. 3–14. [Google Scholar] [CrossRef]
- Kleijnen, J.P.C. Factor screening in simulation experiments: Review of sequential bifurcation. In Advancing the Frontiers of Simulation: A Festschrift in Honor of George Samuel Fishman; Alexopoulos, C., Goldsman, D., Wilson, J.R., Eds.; Springer: Boston, MA, USA, 2009; pp. 153–167. [Google Scholar] [CrossRef]
| Manikin Number | Stature (mm) | Elbow Height (mm) | Sex |
|---|---|---|---|
| 1 | 1629 | 984 | Female |
| 2 | 1755 | 1091 | Male |
| 3 | 1656 | 1020 | Female |
| 4 | 1780 | 1134 | Male |
| 5 | 1668 | 963 | Female |
| 6 | 1794 | 1068 | Male |
| 7 | 1800 | 1094 | Female |
| 8 | 1936 | 1221 | Male |
| 9 | 1602 | 949 | Female |
| 10 | 1731 | 1047 | Male |
| 11 | 1590 | 1006 | Female |
| 12 | 1717 | 1114 | Male |
| 13 | 1457 | 875 | Female |
| 14 | 1574 | 961 | Male |
| Indices | Parameters | ||
|---|---|---|---|
| Welding spots | Welding time (s) | ||
| Welding guns | Time to change welding gun (s) | ||
| Welding sides | Time to change welding side (s) | ||
| Manikins | Time to move to a far position (s) | ||
| Welding sequence | Time to move to a near position (s) | ||
| Variables | Previous gun: 1 if different, 0 if same | ||
| Welding spot sequence | Previous side: 1 if different, 0 if same | ||
| Welding gun used at each welding spot | 1 if previous spot is far, 0 if near | ||
| Welding side at each welding spot | 1 if previous spot is near, 0 if far | ||
| Objectives | RULA score for a manikin on a side with a welding gun at a welding spot | ||
| Cycle time of welding process (s) | |||
| Average RULA score per manikin in the welding process | |||
| Average RULA score of all manikins in the welding process | |||
| Optimization Algorithm | NSGA-II |
|---|---|
| Population size | 150 |
| Child population size | 150 |
| Tournament size | 2 |
| Mutation operator | Polynomial |
| Mutation probability | 0.2 |
| Crossover probability | 0.9 |
| Crossover operator | SBX |
| Maximum iterations | 25,000 |
| Result Selected | Sequence | ||
|---|---|---|---|
| 47 | 3.09 | Spot sequence: 7-1-3-2-5-4-6 Gun sequence: 3-3-3-3-3-3-3 Side sequence: 1-1-1-1-2-2-2 | |
| 63 | 2.89 | Spot sequence: 4-5-6-7-1-2-3 Gun sequence: 3-3-3-3-2-2-2 Side sequence: 2-2-2-1-1-1-1 | |
| 85 | 2.86 | Spot sequence: 4-5-6-7-1-2-3 Gun sequence: 4-5-6-7-1-2-3 Side sequence: 2-2-2-1-1-1-1 |
| X | X | |||||
| X | X | |||||
| X | X | |||||
| X | X | X | X | |||
| X | X | X | X | |||
| X | X | X | X | |||
| X | X | X | ||||
| FPM | ||||
|---|---|---|---|---|
| Case | Filtered Rules | Sig. (%) | Unsig. (%) | Ratio |
| == 4 | 91.53 | 27.07 | 3.38 | |
| > 2 | 100 | 40.85 | 2.45 | |
| == 3 | 79.1 | 28.86 | 2.74 | |
| == 3 | 75.14 | 7.58 | 9.91 | |
| < 4 | 71.29 | 68.59 | 1.03 | |
| > 2 | 64.36 | 45.51 | 1.41 | |
| > 2 | 82.18 | 69.4 | 1.18 | |
| > 2 | 52.48 | 17.38 | 3.02 | |
| == 2 | 100 | 41.86 | 2.39 | |
| == 2 | 100 | 31.93 | 3.13 | |
| == 1 | 100 | 23.45 | 4.26 | |
| == 1 | 100 | 0.73 | 136.99 | |
| Worker diversity inclusion | == 2 | 93.84 | 38.17 | 2.46 |
| == 2 | 93.84 | 26.94 | 3.48 | |
| == 1 | 82.35 | 22.73 | 3.62 | |
| == 1 | 75.95 | 0.32 | 237.34 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iriondo Pascual, A.; Smedberg, H.; Högberg, D.; Syberfeldt, A.; Lämkull, D. Enabling Knowledge Discovery in Multi-Objective Optimizations of Worker Well-Being and Productivity. Sustainability 2022, 14, 4894. https://doi.org/10.3390/su14094894
Iriondo Pascual A, Smedberg H, Högberg D, Syberfeldt A, Lämkull D. Enabling Knowledge Discovery in Multi-Objective Optimizations of Worker Well-Being and Productivity. Sustainability. 2022; 14(9):4894. https://doi.org/10.3390/su14094894
Chicago/Turabian StyleIriondo Pascual, Aitor, Henrik Smedberg, Dan Högberg, Anna Syberfeldt, and Dan Lämkull. 2022. "Enabling Knowledge Discovery in Multi-Objective Optimizations of Worker Well-Being and Productivity" Sustainability 14, no. 9: 4894. https://doi.org/10.3390/su14094894
APA StyleIriondo Pascual, A., Smedberg, H., Högberg, D., Syberfeldt, A., & Lämkull, D. (2022). Enabling Knowledge Discovery in Multi-Objective Optimizations of Worker Well-Being and Productivity. Sustainability, 14(9), 4894. https://doi.org/10.3390/su14094894







