Abstract
The study aims to adopt an artificial neural network (ANN) for modeling industrial energy demand in Taiwan related to the subsector manufacturing output and climate change. This is the first study to use the ANN technique to measure the industrial energy demand–manufacturing output–climate change nexus. The ANN model adopted in this study is a multilayer perceptron (MLP) with a feedforward backpropagation neural network. This study compares the outcomes of three ANN activation functions with multiple linear regression (MLR). According to the estimation results, ANN with a hidden layer and hyperbolic tangent activation function outperforms other techniques and has statistical solid performance values. The estimation results indicate that industrial electricity demand in Taiwan is price inelastic or has a negative value of −0.17 to −0.23, with climate change positively influencing energy demand. The relationship between manufacturing output and energy consumption is relatively diverse at the disaggregated level.
1. Introduction
Data published by the International Energy Agency (IEA) [1] illustrates that until 2019, the industrial sector was the highest energy user globally, with a total of 121 million terajoules. This number has almost doubled compared to the previous three decades. It has contributed to triggering carbon emissions caused by the industrial sector, which doubled in the same period. In addition, energy use in industry accounts for 24.2% of greenhouse gas emissions, and this number is the highest compared to other sectors [2].
At the domestic level, Taiwan is also facing a similar situation. This is due to Taiwan’s economy being highly dependent on the industrial sector [3]. From data published by the Taiwan government. Until the third quarter of 2021, the industrial sector contributed 39.87% of Taiwan’s total GDP, of which the manufacturing sector contributed 34.39%. In addition, the industrial sector also has a reasonably high growth every period, until the third quarter of 2021, the industrial sector, including the manufacturing industry, grew 13.06% compared to the previous period and contributed to Taiwan’s economic growth of 4.59 points, which is the highest contributor to Taiwan’s economic growth [4].
On the one hand, the large contribution of the industrial sector to Taiwan’s economy also causes this sector to be the largest energy user in Taiwan. In 2020, the industrial sector in Taiwan consumed 26,877.4 × 103 kiloliters of oil equivalent (KLOE) of energy, or 31.47% of total final consumption, an increase of 0.22% from the previous year. In addition, energy use in this sector is the highest compared to other sectors. Although there was a slowdown due to the pandemic impact, energy consumption in the industrial sector still increased. Examining more specifically with electricity consumption, it is identical: the industrial sector remains the most extensive electricity user in Taiwan. Until 2020, the use of electricity by the industrial sector in Taiwan was 150,742.3 gigawatts per hour (GWh) or equivalent to 59.83% of the total final consumption.
Based on the industrial subsector, it can be seen in Figure 1 that the electrical and electronic machinery industry is the highest electric consumer. Based on data from the BOE [5], the electrical and electronic machinery industry consumed 55,668 GWh of electricity, or equivalent to 36.9% of the total consumption of the industrial sector. The amount is even higher than consumption in other sectors, such as the service sector and residential sector, with consumption levels of 46,237 GWh and 50,207 GWh, respectively. Besides the high level of energy demand, Taiwan has a problem of low resources, which causes 98% of the total energy use in Taiwan to attain from imports, of which 93% are fossil fuels. This causes Taiwan to handle two problems, the risk of energy dependence from abroad and high carbon emissions.
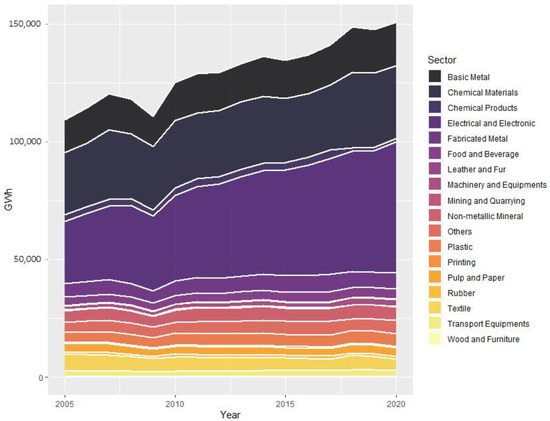
Figure 1.
Electricity consumption by industrial subsector.
It is rather crucial to comprehend the energy demand model based on the situation, especially industrial electricity demand, in Taiwan. However, there has been no research on industrial electricity demand in relation to climate change in Taiwan, to our knowledge. This is not unexpected because studies on industrial energy demand are infrequently discovered (Bernstein and Madlener [6]). One reason is that the industrial sector is one of the most challenging end-users to studying, modeling, and forecasting [7]. According to Agnolucci et al. [8], the problem lies in aggregation problems, such as high heterogeneity in the industry, lumpy investment, time lags between investment and energy consumption, and energy price diversity.
Many studies on industrial energy demand refer to the seminal paper by Berndt and Wood [9], who used a single-equation approach to model industrial energy demand with inputs of capital, labor, and intermediate materials. After that, the use of the single-equation approach certainly became prevalent in measuring industrial energy demand [10]. According to Adeyemi and Hunt [11], the popularity of the single-equation approach is due to its simplicity, straightforward interpretation, and ease of data usage.
In general, empirical assessment techniques for energy demand modeling is classified into conventional, machine learning, and deep learning methods, and it employs both parametric and nonparametric approaches [12,13,14]. Time-series methods commonly used to measure energy demand include autoregressive (AR), vector autoregressive (VAR), autoregressive moving average (ARMA), autoregressive moving average (ARIMA), and ARIMA with exogenous variables (ARIMAX). Several studies employed regression models in addition to time-series models. Some studies, such as those conducted by Ouedraogo [15] and Harris et al. [16], employed logistic regression. Multiple linear regression is another popular regression model. Kipping and Trømborg [17] employed this model to forecast electricity consumption in Norway, and Kovačič and Šarler [18] employed MLR to forecast gas consumption in Slovenia. Bianco et al. [19] analyzed the natural gas consumption in the Italian residential sector. They used MLR with a logarithmic function containing the research, which took the form of a standard dynamic constant elasticity function of consumption. Because the models are more diverse, and their applications can be found in many fields, one of which is the environmental field, parametric approaches tend to be easier [20]. They also require less data than machine learning models [13].
Furthermore, artificial neural networks (ANN), support vector machines (SVM), and long-short-term memory (LSTM) are machine learning methods that are commonly used in energy consumption modeling [21,22]. Feedforward neural network (FFNN), backpropagation neural network (BPNN), and adaptive network-based fuzzy inference system (ANFIS) are some of the ANN models used [13]. Several studies that measure energy demand using ANN include those conducted by Szoplik [23]. It estimates Poland’s energy demand using ANN and a multilayer perceptron model. Then, Soldo et al. [24] used ANN and SVM to forecast residential natural gas consumption in their study. In addition, Amber et al. [25] conducted a study that compared the estimation results of multiple regression, genetic programming, ANN, DNN, and SVM. According to the findings of their research, ANN outperforms all four other techniques. Machine learning, according to Parmezan et al. [26], has flexible structures and nonparametric procedures for capturing and identifying complex interactions and nonlinear relationships among variables.
Specifically for measuring industrial energy demand, several approaches are used, including using time-series analysis with time-varying parameters [27]. The study’s findings, based on data from Korea’s residential and industrial sectors, show that conditional factor demands in the industrial sectors are more elastic than those in the residential sector, and that those elasticities have also increased significantly. Another study that measures industrial energy demand using time-varying parameters was carried out by Wang and Mogi [28]. They employed a time-varying parameter model in conjunction with the Kalman filter. According to the findings, industrial consumers have become less price sensitive following the deregulation of electricity and the financial crisis. However, one of the drawbacks of TVP is the risk of overfitting, which increases as the number of coefficients in the model increases [29]. Another method is vector autoregressive (VAR), as used by Agnolucci, De Lipsis, and Arvanitopoulos [8], who used industrial energy demand data up to disaggregated levels in the UK. This study yielded disparate findings regarding the long-term impact of economic activity and energy prices on industrial energy consumption. In addition to TVP and VAR, the structural time-series model proposed by Harvey [30] is used for modeling industrial energy demand. Adeyemi and Hunt [11], Adeyemi and Hunt [31], and Alarenan, Gasim, and Hunt [10] are studies that use this approach. Adeyemi and Hunt [31] discovered that almost all of the preferred models for OECD industrial energy demand incorporate a stochastic underlying energy demand trend and asymmetric price responses using data on industrial energy consumption. Furthermore, Alarenan, Gasim, and Hunt [10] discovered that in Saudi Arabia’s energy demand model, both energy prices and income are inelastic.
In addition to the conventional methods above, modeling industrial energy demand using machine learning is more challenging to find than conventional methods. Several previous studies using machine learning were carried out by Kucukali and Baris [32] using fuzzy logic. Their research forecasts Turkey’s short-term gross annual electricity demand. The result shows 3.9 percent absolute relative error. According to the study findings, the advantage of this model is its ability to mimic human thinking and reasoning. Bilgili et al. [33] used ANN, linear regression, and nonlinear regression to estimate industrial energy demand in Turkey. The electricity consumption prediction was based on two different scenarios, and the results of the three methods were compared, with the ANN method producing better predictions than the LR and NLR methods. The same result is shown by Azadeh et al. [34], who compared the estimation of industrial energy demand using ANN and ANOVA. The study’s findings indicate that ANN outperforms ANOVA. Ramos et al. [35] conducted a more recent study that measured energy consumption in industrial buildings using ANN and incremental learning to improve forecast accuracy. Their study’s findings indicate that ANN is capable of predicting electricity consumption in industrial buildings. Another approach is using the cointegration panel conducted by El-Shazly [36]. Several studies also focus on the problem of asymmetric prices [37,38], which Adeyemi and Hunt [11], Adeyemi and Hunt [31], applied to the industrial energy demand sector.
In the case of Taiwan, there are several studies that measure the relationship between electricity consumption and economic growth. The study from Pao [39], with the new error-correction state space (ECSTSP) model, STSP, and SARIMA, found a strong forecasting performance through the model proposed. The study also found a unilateral short- and long-term causality from real GDP to electricity consumption. Concerning the industrial sector, compelling research was completed by Lu et al. [40], who measured the potential for energy savings in the six most energy-intensive industrial sectors in Taiwan. With the BAT approach, they found that the total energy savings in the industrial sector are estimated at 66.3 TWh or about 5.3% of national energy use. Additionally, the reduction in GHG emissions from the six industries was estimated to be around 16.2 Mt-CO2 or around 6.4% of the national GHG emissions. Another study from Lu [41], who investigated the Granger causality between electricity consumption and economic growth in 17 Taiwanese industries, found that a 1% increase in electricity consumption raises the real GDP by 1.72%.
Based on the findings of previous studies, it can be seen that machine learning methods have advantages over conventional methods in several studies. However, the application of machine learning for modeling industrial energy demand and its relationship to climate change is even more limited. Therefore, our study employs ANN to model industrial energy demand in Taiwan and its relationship to subsector manufacturing output and climate change. This work used three activation function models in the ANN analysis, and the study also measured using multiple linear regression (MLR). Thus, the study compared three activation function models in ANN and MLR.
ANN is a mathematical model consisting of interconnected neurons that process information using a computing-based connection. ANN performs the processing of the information entered into the network during the learning process. One of the advantages contained by ANN is that it cannot only process linear data but is also useful at processing nonlinear data because it can learn data flows directly [42,43,44,45,46]. ANN as an alternative to statistical modeling and forecasting has been widely used today because, in some literature, it shows better performance when compared to the regression model [45,47,48]. In addition, ANN is also used to identify, model, and predict complex systems in various cases [49,50,51,52,53], including that was recently used to forecast cryptocurrency volatility [54,55]. To the best of our knowledge, no previous studies have used the ANN approach to model industrial energy demand and its relationship to subsector manufacturing output and climate change in Taiwan.
Based on the explanation, this study aims to adopt the ANN to model industrial energy demand in Taiwan and its relation to subsector manufacturing output and climate change. Hence, this research has several contributions to the industrial energy demand literature. First, we emphasize that this paper is the first to measure industrial energy demand using an artificial neural network by assessing the climate change factor as one of the critical determinants in the industrial energy demand model. This study also uses disaggregated level data, where studies on industrial energy demand using the subsector level data are still rarely found. Thus, the method in this study can be an alternative for modeling energy demand because it has a statistically good performance. Second, this research is not only important from an academic perspective, but the study results are also essential to be input for policymakers in Taiwan concerning industrial energy demand elasticity policy.
The remainder of this paper is organized as follows. Section 2 describes the methodology and data. Section 3 explains the findings of the measurement. Section 4 provides the discussions, and Section 5 concludes the paper by providing the conclusion, research limitations, and avenues for future research.
2. Methodology and Data
2.1. Methodology
This research used a multilayer perceptron (MLP) with a feedforward backpropagation neural network [47,56,57]. The model consists of several neurons in the input layer, and the signal moves from the input layer to the hidden layer, then to the output layer [42,44]. Backpropagation has the advantage of being able to minimize the following cost function related to weights and neurons [58]. Figure 2 illustrates a multilayer perceptron anatomy [59]. This study employs R software to perform data processing and analysis, as well as to generate figures, and several figures also use Stata software.
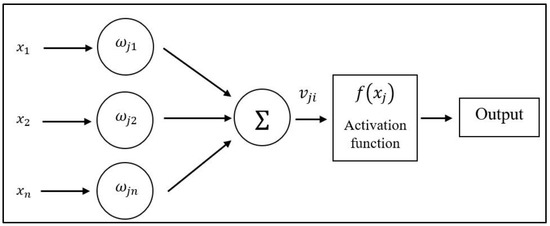
Figure 2.
MLP anatomy.
In general, there are several steps to constructing a neural network. It begins by preprocessing the data by normalizing it. Second, the data are distributed based on the training and testing data obtained. Third, the number of hidden layers and neurons used in the model is determined. The fourth stage is to evaluate the activation function in the model. The work began preprocessing the data by normalizing them, then normalizing the data using minimum–maximum normalization into a specific range between 0 and 1. This method is commonly used because it is more convenient when performing data learning [60].
where is normalization value from , if (i = 1,2,3,…,n).
The data are then divided into training and testing sets. This separation is used to validate the performance of the data used, thereby verifying the level of accuracy. According to Nefeslioglu et al. [61], the data separation does not follow strict mathematical rules in determining the size of the data used. In this study, we used a 70:30 ratio for training and testing the data set.
In the third stage, according to Heaton [62], the number of hidden layers used in the neural network does not have a tightly theoretical basis. Several basic options, including no hidden layers and up to two hidden layers, can be used empirically. One hidden layer, on the other hand, can estimate a variety of functions by continuously mapping from one finite space to another [62]. As a result, this study experimented with one and two hidden layers and compared the results. After that, in determining the number of neurons in the hidden layer, this research used 30 nodes for one hidden layer and 20:10 nodes for two hidden layers.
The next step in this study is to evaluate the model’s activation function. As a possible consequence, this research compares three types of common activation functions as displayed in Figure 3: linear (purelin) functions, the hyperbolic tangent-sigmoid (tansig) and logsigmoid (logsig). These functions are commonly applied as activation functions to solve nonlinear and linear regression problems [63].
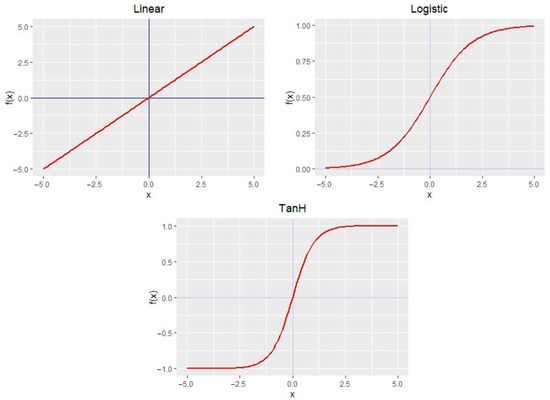
Figure 3.
Activation function used in this study.
Moreover, based on Haykin [44], the adoption of multilayer perceptron (MLP) in the study has a structure with the input and weights . Then, is the weighted sum of inputs, and b is bias. Mathematically, the description of the MLP model is following the equations:
where m is the number of inputs used by neurons j. The learning process in the perceptron is accomplished by varying the connection weight for each part of the data based on the number of errors in the output. The error can be represented by the following equation:
From the equation above, j is the output node, d is the target value, and y is the MLP value produced [46]. The sum of the weights on the hidden layer to the output layer is fixed to 1 based on Equation (2), and the output is computed by the following equation:
where f is the activation function used in the study, and k is the network’s analogous order. This study also measured the industrial energy demand model using multiple linear regression (MLR) to compare the results of the ANN estimation. The MLR model used in this study is expressed as a linear logarithmic function with the shape of a parametric persistent elasticity function of consumption [19,64]. The autocorrelation problem is one of the issues that can arise with time-series data, particularly when error terms in a regression model correlate over time. As a result, this research used the Durbin–Watson test to examine the data. The test results show that the Durbin–Watson statistic is 1.993, indicating that there is no serial correlation between the model’s residuals [25,45,46,65].
To be even more convincing, we examined the error term’s autocorrelation function (ACF) and partial autocorrelation function (PACF) plots. The ACF plot in Figure 4 shows that there is a significant spike at lag 5, indicating that there is serial autocorrelation in the residuals. Furthermore, the PACF plot shown in Figure 4 provides the same value. As a result, the estimated model violates the assumption of no autocorrelation in the errors, and our forecasts may be inefficient, based on the ACF and PACF plots. Estimates from a model with autocorrelated residuals are still unbiased, but they usually have wider prediction intervals than necessary [66]. The MLR with logarithmic function follows this equation:
where MO is manufacturing output that will be separated into disaggregate levels in our analysis. As a result, this study makes a comparison from the estimation results of the seven models used. The values of the mean absolute error (MAE), root mean squared error (RMSE), mean absolute percentage error (MAPE), and adjusted R2 will be used to compare the performance of all the methods.
where is the actual value, is the mean of actual value, is the estimated value, n is the number of observations, and p is the number of independent variables. In the investigation, this work used the trial-and-error method used by Ghasemiyeh, Moghdani, and Sana [63] to select the best model. Table 1 shows the structure of the neural network that was utilized to conduct the experiment.
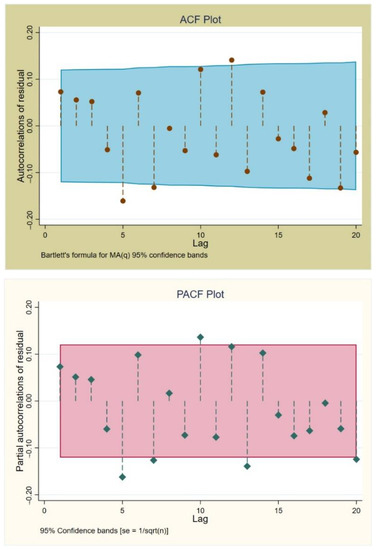
Figure 4.
ACF and PACF Plots.

Table 1.
Proposed neural network structure.
2.2. Data
The dataset used in this study consists of four main variables: electricity consumption, electricity prices, degree days to demonstrate climate change, and manufacturing output as a measure of economic activity. The variables are observed monthly between January 1998 and December 2019. Table 2 displays the descriptive statistics.

Table 2.
Descriptive statistics.
Data on electricity consumption and electricity prices were observed from the Bureau of Energy, Ministry of Economic Affairs Taiwan. In this study, manufacturing output data is used up to the subsector level, which contains 27 industrials subsectors. The data were collected from the Ministry of Economic Affairs’ Department of Statistics. Furthermore, the degree days data were derived from temperature data published by Taiwan’s Central Weather Bureau. We used a widely used formula to calculate degree days, which is to add heating degree days (HDD) and cooling degree days (CDD) [67], as follows:
where refers to the base temperature of the degree day. is the average daily temperature obtained from the daily maximum temperature and daily minimum temperature divided by two. Thus, the DD value is obtained from the sum of the HDD and CDD.
3. Results
In this section, the ANN architecture is trained using 264 observation data and 30 variables, of which 185 are training data, and 79 are testing data. This work used a trial-and-error method [63,68] to find the best model based on the activation functions used in this study. Additionally, the analysis compares the ANN results with the MLR model. According to Figure 5, the performance of the BP-FFNN model in this study is more promising than the MLR model because the distribution plot generated by ANN is more closely aligned with the ideal line. This is because the neural network produces better prediction results than the MLR model. Our findings also support the results of past researchers, who found that ANN produced better estimation results than MLR [42,46,51,61]. When comparing the three ANN functions used in our analysis (linear, sigmoid, and tansig), the hyperbolic tangent-sigmoid function (tansig) has an ideal value distribution. This is supported by nearly the same value when using one hidden layer and two hidden layers.
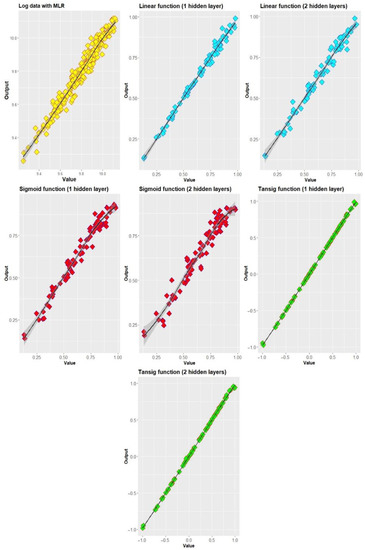
Figure 5.
Model performance.
In addition to testing the performance between the predicted and actual values, as shown in Figure 5, this study also tested each activation function’s forecasting ability. Figure 6 depicts the forecasting results of each activation function over a 12-month period using train and test datasets. The forecasting results in each model show an increasing trend in Taiwan’s industrial energy demand.
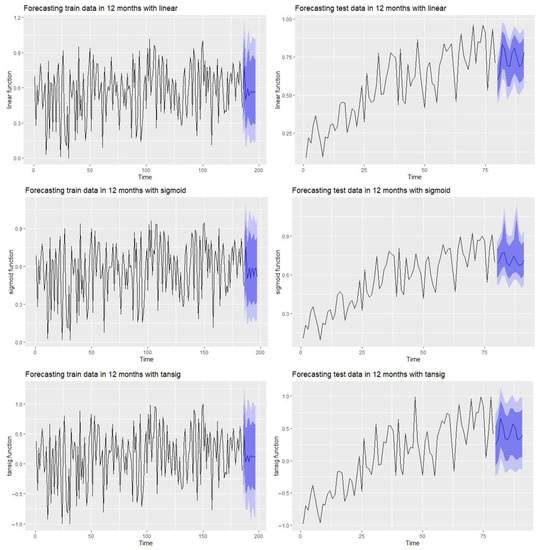
Figure 6.
Forecasting train and test data.
In this study, the best model was selected by comparing the MAE, RMSE, MAPE, and adj-R2 values. Table 3 displays that an ANN with one hidden layer and 30 nodes using a tansig activation function has the lowest MAE, RMSE, and MAPE values, as well as the highest adjusted R2 values. As a result, our experiment revealed that BP-FFNN with the hyperbolic tangent-sigmoid activation function produced the best results. In order to evaluate the model’s performance, we plotted the real value against the predicted value generated by the ANN model, as shown in Figure 5. To be confident, we performed the same plotting with MLR.

Table 3.
Model comparison.
The average rating was measured based on the validation criteria (MAE, RMSE, MAPE, and adj-R2) to determine the score for each model, as shown in Table 3. The final score results for each proposed model are shown in this table. Based on the validation criteria comparison results, it is clear that ANN with a sigmoid activation function has the poorest performance. It is primarily indicated in the model with two hidden layers because the model receives the lowest ranking with the highest MAE, RMSE, and MAPE, while the adjusted R2 value is the smallest. MLR produces better results than ANN with a sigmoid activation function in terms of MAE, RMSE, MAPE, and adjusted R2 values. Even for some criteria, such as MAE and MAPE, MLR outperforms ANN with a linear activation function. Overall, it can be seen that the ANN value with linear activation function outperforms MLR for each assessment parameter. If we look at the validation criteria for all of the estimation techniques used in this study, we can see that the ANN with hyperbolic tangent-sigmoid has the best results. When compared to the entire proposed model, the model with one hidden layer has the lowest MAE, RMSE, and MAPE values of 0.003, 0.008, and 0.829, respectively, and the highest adjusted R2 value of 99.9%.
4. Discussion
Based on a comparison of MAE, RMSE, MAPE, and adj-R2 values, the estimation results show that the hyperbolic tangent-sigmoid model is the best model. As a result, the variable importance is measured using that activation function. To calculate the variable importance, we used the method proposed by Goh [56] and Garson [69], which divides the hidden output connection weights into components associated with each input neuron based on the absolute value of the connection weights [70]. However, one of the model’s drawbacks is its use of absolute values, which do not reflect the actual value. Therefore, we modified it by using the model proposed by Olden and Jackson [71]. Figure 7 depicts the end result.
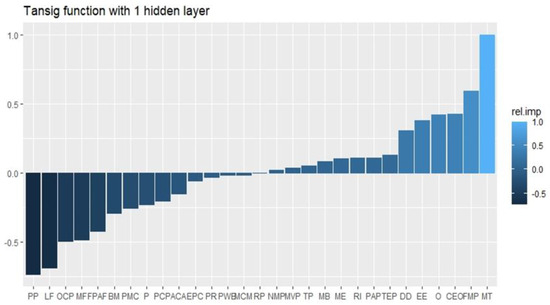
Figure 7.
Variable importance.
The results of the relative importance estimation show that the electricity price variable has a negative value of −0.17 to −0.23. In general, the negative relationship between price and industrial electricity demand indicates that the price of electricity is price inelastic. In comparison to the price elasticity of Taiwanese household electricity demand, which is −0.11 to −0.21 [42], industrial electricity demand in Taiwan is significantly more price elastic. In other words, the industrial sector, particularly the Taiwanese manufacturing industry, is more sensitive to changes in electricity prices than the household sector. However, it should be noted that the price elasticity generated by ANN will require further consideration in the future because the value generated by the ANN’s relative importance measurement is not identical to the conventional regression technique. As a result, in order to increase confidence in the value of relative importance, we compared it to the estimation results generated by MLR. Table 4 demonstrates that though. When the two models are compared, the result shows that the price elasticity of industrial energy demand in Taiwan is inelastic. According to the MLR estimation results, the coefficient value of the electricity price is negative or inelastic with a value of −0.183 and significant at 5% alpha.

Table 4.
ANN and MLR estimation.
The climate change factor indicated by the change in degree days in this study has a positive relationship with industrial energy demand in Taiwan, with a value of 0.31 in train data and 0.18 in test datasets. It suggests that the rise in climate change will increase energy demand. These findings also corroborate the findings of previous studies by numerous researchers who linked the temperature condition factor with the proclivity to increase the use of electrical energy in households [42,67,72,73,74,75,76,77]. The findings from this research show that the increase in electricity consumption caused by climate change occurs not only in households but also in the industrial sector. This positive relative importance value is supported by the MLR estimation results, which are also positive, with values of 0.08 and statistically significant at 1% alpha.
Furthermore, according to the relative importance shown in Figure 7, the variable industrial output of plastic product manufacture, with a value of −0.73, has the strongest negative relationship with electricity consumption in Taiwan, while the variable industrial output of textiles manufacture, with a value of 1, has the strongest positive relationship with electricity consumption. Additionally, the variable of rubber product manufacture has a relative importance value close to zero, indicating that this variable is not significantly related to industrial electricity consumption in Taiwan. This value, however, is most likely to have a minor impact on the response variable [48]. In addition to the manufacture of plastic products, several manufacturing companies have a negative relative importance in terms of energy demand, including the manufacture of leather and fur, other chemical products, furniture, food products, basic metals, pharmaceutical and medicine, petroleum and coal products, wearing apparel and clothing, electronic parts, printings, woods, and chemical materials. Furthermore, manufacturing of other nonmetallic mineral products has a positive relative importance relationship with industrial energy consumption, such as motor vehicles, tobacco products, beverages, machinery and equipment, repair and installation, paper, other transport equipment, electrical equipment, computers, electronic and optical products, and fabricated metal products.
Additionally, the estimates of manufacturing output at the disaggregated level show varying and disparate values for ANN and MLR. Previous research has shown that this difference in estimates is common [42,45,46,47,51,65,78]. Because, as previously stated, the relative importance of the ANN with the results of the MLR regression coefficient is calculated using a different technique [48,69]. However, based on the estimation results and statistical performance demonstrated in this study, ANN can be a viable option for modeling industrial energy demand.
5. Conclusions
Taiwan’s industrial sector is a key economic driver and contributor to the country’s GDP. On the one hand, this industry is Taiwan’s largest energy consumer and one of the highest carbon emitters. Therefore, it is critical to analyze the industrial energy demand model in order to develop the best policy. However, literature on modeling industrial energy demand in Taiwan in relation to manufacturing output and climate change remains scarce. Therefore, the main objective of this research is to use machine learning to analyze industrial energy demand models related to the manufacturing output subsector and climate change.
In this study, we used ANN as the machine learning method, and we applied three activation functions and compared the results to MLR. We used a multilayer perceptron (MLP) with a feedforward backpropagation neural network as our ANN model. We compared the performance of each model’s MAE, RMSE, MAPE, and adjusted R2 values to determine the best model among three activation functions and MLR.
Based on the data from this study’s estimation, it was discovered that ANN with one hidden layer and a hyperbolic tangent-sigmoid activation function performed the best. The statistical performance values show that the MAE, RMSE, MAPE, and adjusted R2 values are 0.003, 0.008, 0.829, and 99.9 percent, respectively. The model’s relative importance estimation result shows that industrial electricity demand in Taiwan is price inelastic or has a negative value of −0.17 to −0.23. Furthermore, the climate change factor as measured by changes in degree days has a positive relationship with Taiwan’s industrial electricity demand. It demonstrates that as global warming worsens, industrial electricity use will increase. In this study, the value-added industry as measured by manufacturing output at the disaggregated level indicates that the manufacturing industry has various important relationships with industrial energy consumption in Taiwan. According to the experimental results of this study, ANN can be used as an alternative to industrial energy demand modeling, as demonstrated by a powerful statistical performance that outperforms conventional techniques.
However, this study has several limitations. For starters, the amount of data used in this study was small. It is due to the availability of data, where data on manufacturing output at the subsector level that the government publishes only reaches the data used in this study. Additionally, collecting more comprehensive data necessitates a more complicated bureaucracy. More data are required to obtain better neural network training, testing, and validation results. Second, lack of development of the ANN model and comparison with other models. Based on the goal of this research is to use ANN as an alternative to industrial energy demand modeling, the ANN approach used is a basic model with no further development, such as the use of a hybrid model [49,52,63] or adopting more models, both parametric and nonparametric [21]. As a result, the issue for further research is to address the limitations of this study, such as using larger datasets, employing a hybrid model, and employing more diverse estimation techniques so that the estimation results obtained are much better.
Author Contributions
Conceptualization, Y.-H.S., S.-F.Y., R.A. and S.M.; methodology, S.-F.Y., R.A. and S.M.; software, R.A.; validation, Y.-H.S. and S.-F.Y.; formal analysis, S.-F.Y. and R.A.; investigation, Y.-H.S. and S.-F.Y.; resources, Y.-H.S., S.-F.Y., R.A. and S.M.; data curation, R.A. and S.M.; writing—original draft preparation, R.A.; writing—review and editing, Y.-H.S. and S.-F.Y.; visualization, R.A.; supervision, Y.-H.S. and S.-F.Y.; project administration, Y.-H.S. and S.-F.Y.; funding acquisition, Y.-H.S. and S.-F.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology, Taiwan, MOST 109-2112-M-004-001 and MOST 110-2118-M-004-001-MY2.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data can be made available upon reasonable request.
Acknowledgments
Sincere appreciation goes to the Graduate Institute of Applied Physics, Statistics Department, National Chengchi University, and Taiwan’s Ministry of Science and Technology for their generous support of this research. We are grateful to the editor Rezzy Eko Caraka and two anonymous referees for constructive comments and helpful improvements to the paper. Nonetheless, we are responsible for any errors or omissions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- IEA. Total Final Consumption (TFC) by Sector, World 1990–2019; IEA: Paris, France, 2020. [Google Scholar]
- Ritchie, H.; Roser, M. CO2 and Greenhouse Gas Emissions; OurWorldInData.org: London, UK, 2020; Available online: https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions (accessed on 24 January 2022).
- Yu-Chen, Y.; Cheng-Yih, H.; Muzayyanah, S.; Adha, R. Decomposition of Growth Factors in High-tech Industries and CO2 Emissions: After the World Financial Crisis in 2008. Int. J. Energy Econ. Policy 2020, 10, 500. [Google Scholar]
- DGBAS. Economic Indicators, Structure of Domestic Production; Yuan, D.E., Ed.; DGBAS: Taipei, Taiwan, 2021.
- Bureau of Energy (BOE). Energy Statistical Annual Reports; Bureau of Energy, Ministry of Economic Affairs: Taipei, Taiwan, 2020.
- Bernstein, R.; Madlener, R. Short- and long-run electricity demand elasticities at the subsectoral level: A cointegration analysis for German manufacturing industries. Energy Econ. 2015, 48, 178–187. [Google Scholar] [CrossRef]
- Greening, L.A.; Boyd, G.; Roop, J.M. Modeling of industrial energy consumption: An introduction and context. Energy Econ. 2007, 29, 599–608. [Google Scholar] [CrossRef]
- Agnolucci, P.; De Lipsis, V.; Arvanitopoulos, T. Modelling UK sub-sector industrial energy demand. Energy Econ. 2017, 67, 366–374. [Google Scholar] [CrossRef]
- Berndt, E.R.; Wood, D.O. Technology, Prices, and the Derived Demand for Energy. Rev. Econ. Stat. 1975, 57, 259–268. [Google Scholar] [CrossRef]
- Alarenan, S.; Gasim, A.A.; Hunt, L.C. Modelling industrial energy demand in Saudi Arabia. Energy Econ. 2019, 85, 104554. [Google Scholar] [CrossRef]
- Adeyemi, O.I.; Hunt, L.C. Modelling OECD industrial energy demand: Asymmetric price responses and energy-saving technical change. Energy Econ. 2007, 29, 693–709. [Google Scholar] [CrossRef]
- Hamdoun, H.; Sagheer, A.; Youness, H. Energy time series forecasting-analytical and empirical assessment of conventional and machine learning models. J. Intell. Fuzzy Syst. 2021, 40, 12477–12502. [Google Scholar] [CrossRef]
- Wei, N.; Li, C.; Peng, X.; Zeng, F.; Lu, X. Conventional models and artificial intelligence-based models for energy consumption forecasting: A review. J. Pet. Sci. Eng. 2019, 181, 106187. [Google Scholar] [CrossRef]
- Shah, I.; Iftikhar, H.; Ali, S.; Wang, D. Short-Term Electricity Demand Forecasting Using Components Estimation Technique. Energies 2019, 12, 2532. [Google Scholar] [CrossRef]
- Ouedraogo, N.S. Modeling sustainable long-term electricity supply-demand in Africa. Appl. Energy 2017, 190, 1047–1067. [Google Scholar] [CrossRef]
- Harris, T.M.; Devkota, J.P.; Khanna, V.; Eranki, P.L.; Landis, A.E. Logistic growth curve modeling of US energy production and consumption. Renew. Sustain. Energy Rev. 2018, 96, 46–57. [Google Scholar] [CrossRef]
- Kipping, A.; Trømborg, E. Modeling and disaggregating hourly electricity consumption in Norwegian dwellings based on smart meter data. Energy Build. 2016, 118, 350–369. [Google Scholar] [CrossRef]
- Kovačič, M.; Šarler, B. Genetic programming prediction of the natural gas consumption in a steel plant. Energy 2014, 66, 273–284. [Google Scholar] [CrossRef]
- Bianco, V.; Scarpa, F.; Tagliafico, L.A. Analysis and future outlook of natural gas consumption in the Italian residential sector. Energy Convers. Manag. 2014, 87, 754–764. [Google Scholar] [CrossRef]
- Gautam, A.; Singh, V. Parametric Versus Non-Parametric Time Series Forecasting Methods: A Review. J. Eng. Sci. Technol. Rev. 2020, 13, 165–171. [Google Scholar] [CrossRef]
- Shah, I.; Bibi, H.; Ali, S.; Wang, L.; Yue, Z. Forecasting One-Day-Ahead Electricity Prices for Italian Electricity Market Using Parametric and Nonparametric Approaches. IEEE Access 2020, 8, 123104–123113. [Google Scholar] [CrossRef]
- Shah, I.; Lisi, F. Day-ahead electricity demand forecasting with nonparametric functional models. In Proceedings of the 2015 12th International Conference on the European Energy Market (EEM), Lisbon, Portugal, 19–22 May 2015; pp. 1–5. [Google Scholar]
- Szoplik, J. Forecasting of natural gas consumption with artificial neural networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]
- Soldo, B.; Potočnik, P.; Šimunović, G.; Šarić, T.; Govekar, E. Improving the residential natural gas consumption forecasting models by using solar radiation. Energy Build. 2014, 69, 498–506. [Google Scholar] [CrossRef]
- Amber, K.P.; Ahmad, R.; Aslam, M.W.; Kousar, A.; Usman, M.; Khan, M.S. Intelligent techniques for forecasting electricity consumption of buildings. Energy 2018, 157, 886–893. [Google Scholar] [CrossRef]
- Parmezan, A.R.S.; Souza, V.M.A.; Batista, G.E.A.P.A. Evaluation of statistical and machine learning models for time series prediction: Identifying the state-of-the-art and the best conditions for the use of each model. Inf. Sci. 2019, 484, 302–337. [Google Scholar] [CrossRef]
- Chang, Y.; Kim, C.S.; Miller, J.I.; Park, J.Y.; Park, S. Time-varying Long-run Income and Output Elasticities of Electricity Demand with an Application to Korea. Energy Econ. 2014, 46, 334–347. [Google Scholar] [CrossRef]
- Wang, N.; Mogi, G. Industrial and residential electricity demand dynamics in Japan: How did price and income elasticities evolve from 1989 to 2014? Energy Policy 2017, 106, 233–243. [Google Scholar] [CrossRef]
- Bitto, A.; Frühwirth-Schnatter, S. Achieving shrinkage in a time-varying parameter model framework. J. Econ. 2019, 210, 75–97. [Google Scholar] [CrossRef]
- Harvey, A.C. Forecasting, Structural Time Series Models and the Kalman Filter; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Adeyemi, O.I.; Hunt, L.C. Accounting for asymmetric price responses and underlying energy demand trends in OECD industrial energy demand. Energy Econ. 2014, 45, 435–444. [Google Scholar] [CrossRef]
- Kucukali, S.; Baris, K. Turkey’s short-term gross annual electricity demand forecast by fuzzy logic approach. Energy Policy 2010, 38, 2438–2445. [Google Scholar] [CrossRef]
- Bilgili, M.; Sahin, B.; Yasar, A.; Simsek, E. Electric energy demands of Turkey in residential and industrial sectors. Renew. Sustain. Energy Rev. 2012, 16, 404–414. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.F.; Sohrabkhani, S. Annual electricity consumption forecasting by neural network in high energy consuming industrial sectors. Energy Convers. Manag. 2008, 49, 2272–2278. [Google Scholar] [CrossRef]
- Ramos, D.; Faria, P.; Vale, Z.; Mourinho, J.; Correia, R. Industrial Facility Electricity Consumption Forecast Using Artificial Neural Networks and Incremental Learning. Energies 2020, 13, 4774. [Google Scholar] [CrossRef]
- El-Shazly, A. Electricity demand analysis and forecasting: A panel cointegration approach. Energy Econ. 2013, 40, 251–258. [Google Scholar] [CrossRef]
- Dargay, J.; Gately, D. The imperfect price reversibility of non-transport oil demand in the OECD. Energy Econ. 1995, 17, 59–71. [Google Scholar] [CrossRef]
- Dargay, J.; Gately, D. The demand for transportation fuels: Imperfect price-reversibility? Transp. Res. Part B Methodol. 1997, 31, 71–82. [Google Scholar] [CrossRef]
- Pao, H.-T. Forecast of electricity consumption and economic growth in Taiwan by state space modeling. Energy 2009, 34, 1779–1791. [Google Scholar] [CrossRef]
- Lu, S.-M.; Lu, C.; Tseng, K.-T.; Chen, F.; Chen, C.-L. Energy-saving potential of the industrial sector of Taiwan. Renew. Sustain. Energy Rev. 2013, 21, 674–683. [Google Scholar] [CrossRef]
- Lu, W.-C. Electricity Consumption and Economic Growth: Evidence from 17 Taiwanese Industries. Sustainability 2017, 9, 50. [Google Scholar] [CrossRef]
- Adha, R.; Hong, C.-Y. How large the direct rebound effect for residential electricity consumption when the artificial neural network takes on the role? A Taiwan case study of household electricity consumption. Int. J. Energy Econ. Policy 2021, 11, 354–364. [Google Scholar] [CrossRef]
- Goyal, S.; Goyal, G.K. Shelf Life Estimation of Processed Cheese by Artificial Neural Network Expert Systems. J. Adv. Comput. Sci. Technol. 2012, 1, 32–41. [Google Scholar] [CrossRef][Green Version]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Hoboken, NJ, USA, 1998. [Google Scholar]
- Stangierski, J.; Weiss, D.; Kaczmarek, A. Multiple regression models and Artificial Neural Network (ANN) as prediction tools of changes in overall quality during the storage of spreadable processed Gouda cheese. Eur. Food Res. Technol. 2019, 245, 2539–2547. [Google Scholar] [CrossRef]
- Tsakiri, K.; Marsellos, A.; Kapetanakis, S. Artificial Neural Network and Multiple Linear Regression for Flood Prediction in Mohawk River, New York. Water 2018, 10, 1158. [Google Scholar] [CrossRef]
- Kumar, R.; Aggarwal, R.K.; Sharma, J.D. Comparison of regression and artificial neural network models for estimation of global solar radiations. Renew. Sustain. Energy Rev. 2015, 52, 1294–1299. [Google Scholar] [CrossRef]
- Zhang, Z.; Beck, M.W.; Winkler, D.A.; Huang, B.; Sibanda, W.; Goyal, H. Opening the black box of neural networks: Methods for interpreting neural network models in clinical applications. Ann. Transl. Med. 2018, 6, 216. [Google Scholar] [CrossRef] [PubMed]
- Caraka, R.E.; Chen, R.C.; Toharudin, T.; Pardamean, B.; Yasin, H.; Wu, S.H. Prediction of Status Particulate Matter 2.5 Using State Markov Chain Stochastic Process and HYBRID VAR-NN-PSO. IEEE Access 2019, 7, 161654–161665. [Google Scholar] [CrossRef]
- Li, Y.X.; Jiang, L.C. Application of ANN Algorithm in Tree Height Modeling. Appl. Mech. Mater. 2010, 20–23, 756–761. [Google Scholar] [CrossRef]
- Şahin, M.; Kaya, Y.; Uyar, M. Comparison of ANN and MLR models for estimating solar radiation in Turkey using NOAA/AVHRR data. Adv. Space Res. 2013, 51, 891–904. [Google Scholar] [CrossRef]
- Caraka, R.E.; Chen, R.C.; Yasin, H.; Suhartono, S.; Lee, Y.; Pardamean, B. Hybrid Vector Autoregression Feedforward Neural Network with Genetic Algorithm Model for Forecasting Space-Time Pollution Data. Indones. J. Sci. Technol. 2021, 6, 243–266. [Google Scholar] [CrossRef]
- Roshani, M.; Sattari, M.A.; Ali, P.J.M.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Application of GMDH neural network technique to improve measuring precision of a simplified photon attenuation based two-phase flowmeter. Flow Meas. Instrum. 2020, 75, 101804. [Google Scholar] [CrossRef]
- Charandabi, S.E.; Kamyar, K. Using A Feed Forward Neural Network Algorithm to Predict Prices of Multiple Cryptocurrencies. Eur. J. Bus. Manag. Res. 2021, 6, 15–19. [Google Scholar] [CrossRef]
- Charandabi, S.E.; Kamyar, K. Prediction of Cryptocurrency Price Index Using Artificial Neural Networks: A Survey of the Literature. Eur. J. Bus. Manag. Res. 2021, 6, 17–20. [Google Scholar] [CrossRef]
- Goh, A.T.C. Back-propagation neural networks for modeling complex systems. Artif. Intell. Eng. 1995, 9, 143–151. [Google Scholar] [CrossRef]
- Konaté, A.A.; Pan, H.; Khan, N.; Yang, J.H. Generalized regression and feed-forward back propagation neural networks in modelling porosity from geophysical well logs. J. Pet. Explor. Prod. Technol. 2014, 5, 157–166. [Google Scholar] [CrossRef]
- Fayed, M.; Elhadary, M.; Abderrahmane, H.A.; Zakher, B.N. The ability of forecasting flapping frequency of flexible filament by artificial neural network. Alex. Eng. J. 2019, 58, 1367–1374. [Google Scholar] [CrossRef]
- Nasr, M.S.; Moustafa, M.A.E.; Seif, H.A.E.; El Kobrosy, G. Application of Artificial Neural Network (ANN) for the prediction of EL-AGAMY wastewater treatment plant performance-EGYPT. Alex. Eng. J. 2012, 51, 37–43. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide susceptibility assessment and factor effect analysis: Backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modelling. Environ. Model. Softw. 2010, 25, 747–759. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Gokceoglu, C.; Sonmez, H. An assessment on the use of logistic regression and artificial neural networks with different sampling strategies for the preparation of landslide susceptibility maps. Eng. Geol. 2008, 97, 171–191. [Google Scholar] [CrossRef]
- Heaton, J. Introduction to Neural Networks for Java, 2nd ed.; Heaton Research, Inc.: Chesterfield, MO, USA, 2008. [Google Scholar]
- Ghasemiyeh, R.; Moghdani, R.; Sana, S.S. A Hybrid Artificial Neural Network with Metaheuristic Algorithms for Predicting Stock Price. Cybern. Syst. 2017, 48, 365–392. [Google Scholar] [CrossRef]
- Haas, R.; Schipper, L. Residential energy demand in OECD-countries and the role of irreversible efficiency improvements. Energy Econ. 1998, 20, 421–442. [Google Scholar] [CrossRef]
- Kalantary, S.; Jahani, A.; Jahani, R. MLR and ANN Approaches for Prediction of Synthetic/Natural Nanofibers Diameter in the Environmental and Medical Applications. Sci. Rep. 2020, 10, 8117. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Adha, R.; Hong, C.-Y.; Firmansyah, M.; Paranata, A. Rebound effect with energy efficiency determinants: A two-stage analysis of residential electricity consumption in Indonesia. Sustain. Prod. Consum. 2021, 28, 556–565. [Google Scholar] [CrossRef]
- Lin, T.Y.; Tseng, C.H. Optimum design for artificial neural networks: An example in a bicycle derailleur system. Eng. Appl. Artif. Intell. 2000, 13, 3–14. [Google Scholar] [CrossRef]
- Garson, G.D. Interpreting neural-network connection weights. AI Expert 1991, 6, 46–51. [Google Scholar]
- Olden, J.D.; Joy, M.K.; Death, R.G. An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data. Ecol. Model. 2004, 178, 389–397. [Google Scholar] [CrossRef]
- Olden, J.D.; Jackson, D.A. Illuminating the “black box”: A randomization approach for understanding variable contributions in artificial neural networks. Ecol. Model. 2002, 154, 135–150. [Google Scholar] [CrossRef]
- Alvi, S.; Mahmood, Z.; Nawaz, S.M.N. Dilemma of direct rebound effect and climate change on residential electricity consumption in Pakistan. Energy Rep. 2018, 4, 323–327. [Google Scholar] [CrossRef]
- Filippini, M.; Hunt, L.C. US residential energy demand and energy efficiency: A stochastic demand frontier approach. Energy Econ. 2012, 34, 1484–1491. [Google Scholar] [CrossRef]
- Orea, L.; Llorca, M.; Filippini, M. A new approach to measuring the rebound effect associated to energy efficiency improvements: An application to the US residential energy demand. Energy Econ. 2015, 49, 599–609. [Google Scholar] [CrossRef]
- Filippini, M.; Hunt, L.C. Measuring persistent and transient energy efficiency in the US. Energy Effic. 2016, 9, 663–675. [Google Scholar] [CrossRef]
- Filippini, M.; Zhang, L. Estimation of the energy efficiency in Chinese provinces. Energy Effic. 2016, 9, 1315–1328. [Google Scholar] [CrossRef]
- Filippini, M.; Hunt, L.C. Energy Demand and Energy Efficiency in the OECD Countries: A Stochastic Demand Frontier Approach. Energy J. 2011, 32, 59–80. [Google Scholar] [CrossRef]
- Tosun, E.; Aydin, K.; Bilgili, M. Comparison of linear regression and artificial neural network model of a diesel engine fueled with biodiesel-alcohol mixtures. Alex. Eng. J. 2016, 55, 3081–3089. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).