Predicting Demand for Shared E-Scooter Using Community Structure and Deep Learning Method
Abstract
:1. Introduction
2. Literature Review
3. Data and Methodology
3.1. Data Collection
3.2. Community Structure
3.3. Long Short-Term Memory (LSTM)
4. Results
4.1. Clustering the Community
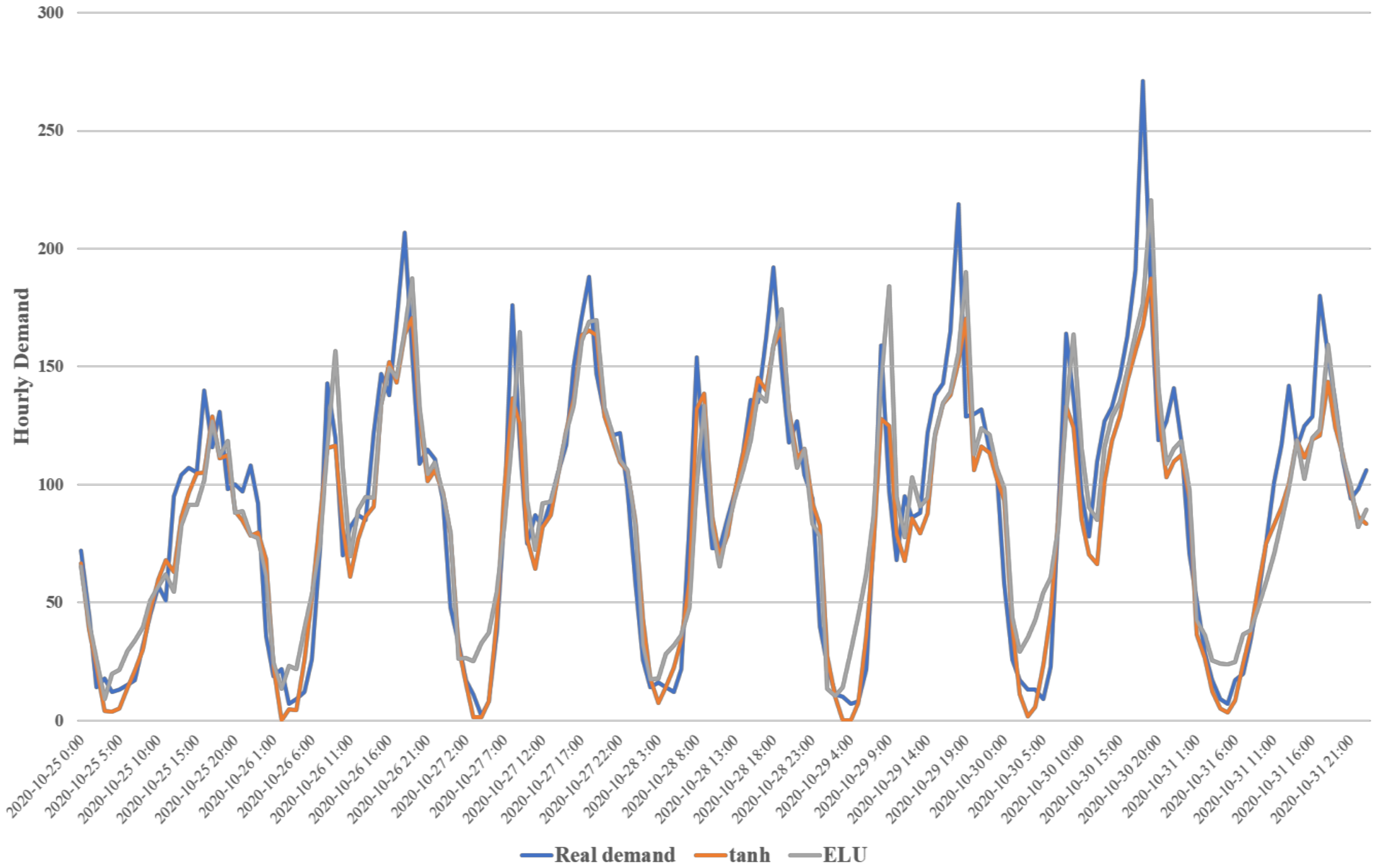
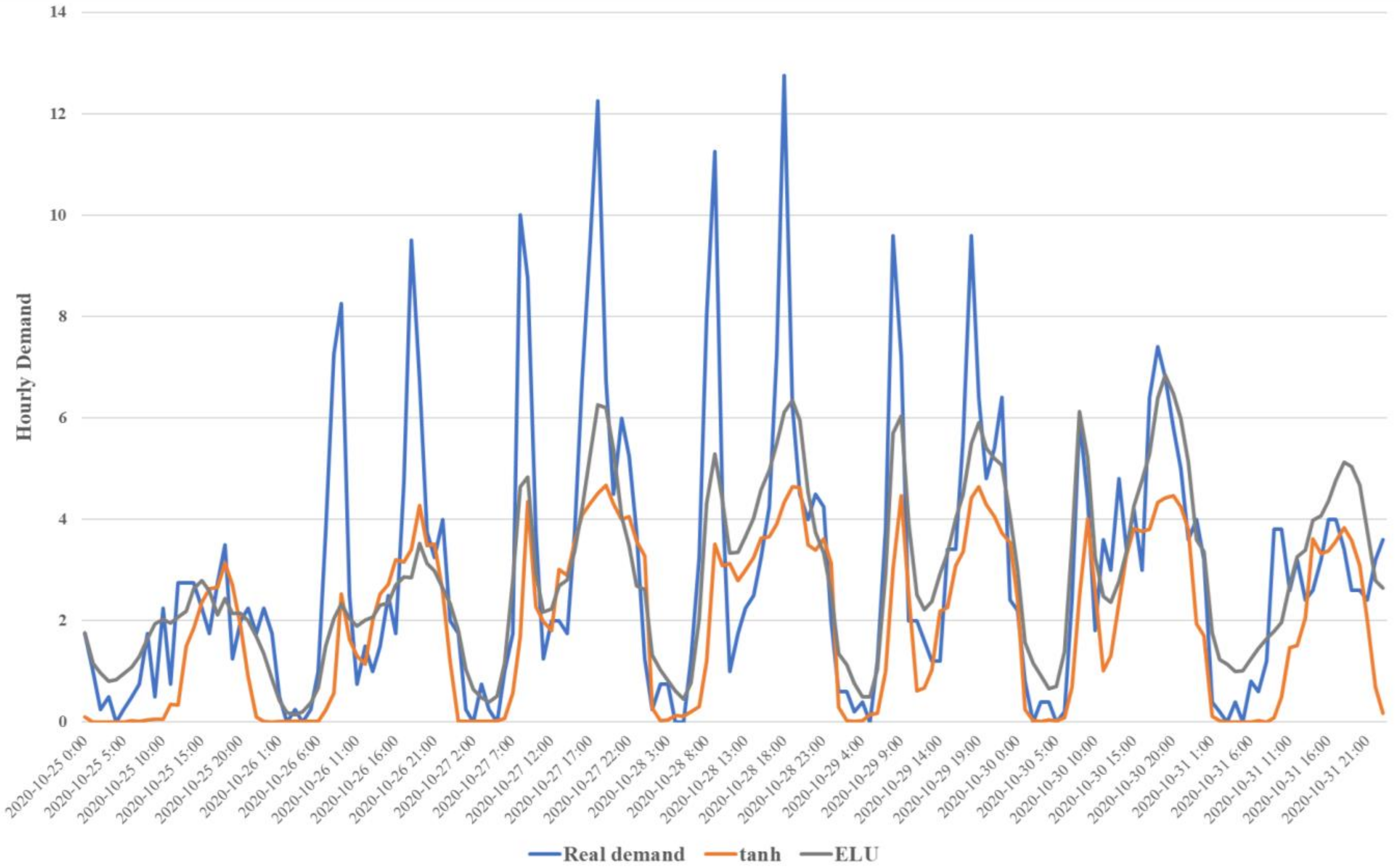
4.2. Prediction of Demand
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Clewlow, R.R. The Micro-mobility Revolution: The Introduction and Adoption of Electric Scooters in the United States. In Proceedings of the 98th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 13–17 January 2019. [Google Scholar]
- Liu, M.; Seeder, S.; Li, H. Analysis of E-scooter Trips and Their Temporal Usage Patterns. ITE J. 2019, 89, 44–49. [Google Scholar]
- Shaheen, S.; Bell, C.; Cohen, A.; Yelchuru, B. Travel Behavior: Shared Mobility and Transportation Equity; Transportation Research Board: Washington, DC, USA, 2017. [Google Scholar]
- McKenzie, G. Spatiotemporal Comparative Analysis of Scooter-share and Bike-share Usage Patterns in Washington, DC. J. Transp. Geogr. 2019, 78, 19–28. [Google Scholar] [CrossRef]
- Dias, G.; Arsenio, E.; Ribeiro, P. The role of shared E-Scooter systems in urban sustainability and resilience during the COVID-19 mobility restrictions. Sustainability 2021, 13, 7084. [Google Scholar] [CrossRef]
- Campisi, T.; Akgün-Tanbay, N.; Nahiduzzaman, M.; Dissanayake, D. Uptake of e-Scooters in Palermo, Italy: Do the Road Users Tend to Rent, Buy or Share? In International Conference on Computational Science and Its Applications; Springer: Cham, Switerland, 2021; pp. 669–682. [Google Scholar]
- Kim, S.; Koack, M.; Choo, S.; Kim, S. Analyzing Spatial Usage Characteristics of Shared E-scooter: Focused on Spatial Autocorrelation Modeling. J. Korea Inst. Intell. Transp. Syst. 2021, 20, 54–69. [Google Scholar] [CrossRef]
- Fang, K.; Agrawal, A.W.; Steele, J.; Hunter, J.J.; Hooper, A.M. Where Do Riders Park Dockless, Shared Electric Scooters? Findings from San Jose, California; Mineta Transportation Institute Publication: San Jose, CA, USA, 2018. [Google Scholar]
- James, O.; Swiderski, J.I.; Hicks, J.; Teoman, D.; Buehler, R. Pedestrians and E-scooters: An Initial Look at E-scooter Parking and Perceptions by Riders and Non-riders. Sustainability 2019, 11, 5591. [Google Scholar] [CrossRef] [Green Version]
- Zou, Z.; Younes, H.; Erdoğan, S.; Wu, J. Exploratory Analysis of Real-time E-scooter Trip Data in Washington, DC. Transp. Res. Rec. J. Transp. Res. Board 2020, 2674, 285–299. [Google Scholar] [CrossRef]
- Raptopoulou, A.; Basbas, S.; Stamatiadis, N.; Nikiforiadis, A. A first look at e-scooter users. In Conference on Sustainable Urban Mobility; Springer: Cham, Switerland, 2020; pp. 882–891. [Google Scholar]
- Bai, S.; Jiao, J. Dockless E-scooter Usage Patterns and Urban Built Environments: A Comparison Study of Austin, TX, and Minneapolis, MN. Travel Behav. Soc. 2020, 20, 264–272. [Google Scholar] [CrossRef]
- Caspi, O.; Smart, M.J.; Noland, R.B. Spatial Associations of Dockless Shared E-scooter Usage. Transp. Res. Part D Transp. Environ. 2020, 86, 102396. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.; Algomaiah, M.; Kluger, R.; Li, Z. E-scooters and Sustainability: Investigating the Relationship Between the Density of E-scooter Trips and Characteristics of Sustainable Urban Development. Sustain. Cities Soc. 2021, 66, 102624. [Google Scholar] [CrossRef]
- Lee, M.; Chow, J.Y.; Yoon, G.; Yueshuai He, B. Forecasting E-scooter Competition with Direct and Access Trips by Mode and Distance in New York City. arXiv 2019, arXiv:1908.08127. [Google Scholar]
- Ham, S.; Cho, J.; Park, S.; Kim, D. Spatiotemporal Demand Prediction Model for E-Scooter Sharing Services with Latent Feature and Deep Learning. Transp. Res. Rec. J. Transp. Res. Board 2021, 2675, 34–43. [Google Scholar] [CrossRef]
- Sikka, N.; Vila, C.; Stratton, M.; Ghassemi, M.; Pourmand, A. Sharing the Sidewalk: A Case of E-scooter Related Pedestrian Injury. Am. J. Emerg. Med. 2019, 37, 1807-e5. [Google Scholar] [CrossRef] [PubMed]
- Trivedi, B.; Kesterke, M.J.; Bhattacharjee, R.; Weber, W.; Mynar, K.; Reddy, L.V. Craniofacial Injuries Seen with the Introduction of Bicycle-share Electric Scooters in an Urban Setting. J. Oral Maxillofac. Surg. 2019, 77, 2292–2297. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campisi, T.; Skoufas, A.; Kaltsidis, A.; Basbas, S. Gender Equality and E-Scooters: Mind the Gap! A Statistical Analysis of the Sicily Region, Italy. Soc. Sci. 2021, 10, 403. [Google Scholar] [CrossRef]
- Chen, Y.W.; Cheng, C.Y.; Li, S.F.; Yu, C.H. Location Optimization for Multiple Types of Charging Stations for Electric Scooters. Appl. Soft Comput. 2018, 67, 519–528. [Google Scholar] [CrossRef]
- Espinoza, W.; Howard, M.; Lane, J.; Van Hentenryck, P. Shared E-scooters: Business, Pleasure, or Transit? arXiv 2019, arXiv:1910.05807. [Google Scholar]
- Turoń, K.; Kubik, A.; Chen, F. When, What and How to Teach about Electric Mobility? An Innovative Teaching Concept for All Stages of Education: Lessons from Poland. Energies 2021, 14, 6440. [Google Scholar] [CrossRef]
- Chang, P.C.; Wu, J.L.; Xu, Y.; Zhang, M.; Lu, X.Y. Bike Sharing Demand Prediction using Artificial Immune System and Artificial Neural Network. Soft Comput. 2019, 23, 613–626. [Google Scholar] [CrossRef]
- Xu, T.; Han, G.; Qi, X.; Du, J.; Lin, C.; Shu, L. A Hybrid Machine Learning Model for Demand Prediction of Edge-computing-based Bike-sharing System using Internet of Things. IEEE Internet Things J. 2020, 7, 7345–7356. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, L.; Zhong, R.; Tan, Y. A Markov Chain Based Demand Prediction Model for Stations in Bike Sharing Systems. Math. Probl. Eng. 2018, 2018, 8028714. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Heppenstall, A.; Turner, A.; Comber, A. using Graph Structural Information about Flows to Enhance Short-term Demand Prediction in Bike-sharing Systems. Comput. Environ. Urban Syst. 2020, 83, 101521. [Google Scholar] [CrossRef]
- Pan, Y.; Zheng, R.C.; Zhang, J.; Yao, X. Predicting Bike Sharing Demand using Recurrent Neural Networks. Procedia Comput. Sci. 2019, 147, 562–566. [Google Scholar] [CrossRef]
- Xu, C.; Ji, J.; Liu, P. The Station-free Sharing Bike Demand Forecasting with a Deep Learning Approach and Large-scale Datasets. Transp. Res. Part C Emerg. Technol. 2018, 95, 47–60. [Google Scholar] [CrossRef]
- Ai, Y.; Li, Z.; Gan, M.; Zhang, Y.; Yu, D.; Chen, W.; Ju, Y. A Deep Learning Approach on Short-term Spatiotemporal Distribution Forecasting of Dockless Bike-sharing System. Neural Comput. Appl. 2019, 31, 1665–1677. [Google Scholar] [CrossRef]
- Lin, L.; He, Z.; Peeta, S. Predicting Station-level Hourly Demand in a Large-scale Bike-sharing Network: A Graph Convolutional Neural Network Approach. Transp. Res. Part C Emerg. Technol. 2018, 97, 258–276. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Wu, Y.; Tan, H.; Dong, H.; Ding, F.; Ran, B. Understanding and modeling urban mobility dynamics via disentangled representation learning. IEEE Trans. Intell. Transp. Syst. 2020, 1–11. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community Structure in Social and Biological Networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [Green Version]
- Newman, M.E. Fast Algorithm for Detecting Community Structure in Networks. Phys. Rev. E 2004, 69, 066133. [Google Scholar] [CrossRef] [Green Version]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast Unfolding of Communities in Large Networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Meng, M.; Wang, D.Z.; Du, B. Allocation Strategies in a Dockless Bike Sharing System: A Community Structure-based Approach. Int. J. Sustain. Transp. 2022, 16, 95–104. [Google Scholar] [CrossRef]
- Olah, C. Understanding Lstm Networks. 2015. Available online: http://colah.github.io/posts/2015-08-Understanding-LSTMs (accessed on 10 June 2021).
- Huang, S.; Eichler, G.; Bar-Yam, Y.; Ingber, D.E. Cell Fates as High-dimensional Attractor States of a Complex Gene Regulatory Network. Phys. Rev. Lett. 2005, 94, 128701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaluza, P.; Kölzsch, A.; Gastner, M.T.; Blasius, B. The Complex Network of Global Cargo Ship Movements. J. R. Soc. Interface 2010, 7, 1093–1103. [Google Scholar] [CrossRef] [PubMed]
- Rubinov, M.; Sporns, O. Complex Network Measures of Brain Connectivity: Uses and Interpretations. Neuroimage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Sporns, O. The Human Connectome: A Complex Network. Ann. New York Acad. Sci. 2011, 1224, 109–125. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E. Modularity and Community Structure in Networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clauset, A.; Newman, M.E.; Moore, C. Finding Community Structure in Very Large Networks. Phys. Rev. E 2004, 70, 066111. [Google Scholar] [CrossRef] [Green Version]
- Ahn, Y.Y.; Bagrow, J.P.; Lehmann, S. Link Communities Reveal Multiscale Complexity in Networks. Nature 2010, 466, 761–764. [Google Scholar] [CrossRef] [Green Version]
- Tealab, A. Time Series Forecasting using Artificial Neural Networks Methodologies: A Systematic Review. Future Comput. Inform. J. 2018, 3, 334–340. [Google Scholar] [CrossRef]
- Sak, H.; Senior, A.; Beaufays, F. Long Short-term Memory Based Recurrent Neural Network Architectures for Large Vocabulary Speech Recognition. arXiv 2014, arXiv:1402.1128. [Google Scholar]
- Graves, A.; Liwicki, M.; Fernández, S.; Bertolami, R.; Bunke, H.; Schmidhuber, J. A Novel Connectionist System for Unconstrained Handwriting Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 855–868. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long Short-term Memory Neural Network for Traffic Speed Prediction using Remote Microwave Sensor Data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Ma, X.; Gildin, E.; Plaksina, T. Efficient Optimization Framework for Integrated Placement of Horizontal Wells and Hydraulic Fracture Stages in Unconventional Gas Reservoirs. J. Unconv. Oil Gas Resour. 2015, 9, 1–17. [Google Scholar] [CrossRef]
- Gers, F.A.; Schraudolph, N.N.; Schmidhuber, J. Learning Precise Timing with LSTM Recurrent Networks. J. Mach. Learn. Res. 2002, 3, 115–143. [Google Scholar]
- Zhao, Z.Z.; Chen, H.P.; Huang, Y.; Zhang, S.B.; Li, Z.H.; Feng, T.; Liu, J.K. Bioactive Polyketides and 8, 14-seco-ergosterol from Fruiting Bodies of the Ascomycete Daldinia Childi-ae. Phytochemistry 2017, 142, 68–75. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ese, N.; Esent, P. Long Short-Term Memory in Recurrent Neural Networks. Epfl 2001, 9, 1735–1780. [Google Scholar]
- Shewalkar, A.; Nyavanandi, D.; Ludwig, S.A. Performance evaluation of deep neural networks applied to speech recognition: RNN, LSTM and GRU. J. Artif. Intell. Soft Comput. Res. 2019, 9, 235–245. [Google Scholar] [CrossRef] [Green Version]
- Apaydin, H.; Feizi, H.; Sattari, M.T.; Colak, M.S.; Shamshirband, S.; Chau, K.W. Comparative analysis of recurrent neural network architectures for reservoir inflow forecasting. Water 2020, 12, 1500. [Google Scholar] [CrossRef]
- Elsaraiti, M.; Merabet, A. A comparative analysis of the arima and lstm predictive models and their effectiveness for predicting wind speed. Energies 2021, 14, 6782. [Google Scholar] [CrossRef]
| Variables | Type | Explanation | |
|---|---|---|---|
| Hourly demand (Pick-up) | Numeric | The number of hourly demand (pick-up) | |
| Time variables | Weekday | Binary | 1: a weekday, 0: otherwise |
| Weekend | Binary | 1: a weekend, 0: otherwise | |
| Hour of day | Numeric | Time window | |
| Weather variables | Temperature | Numeric | Temperature in Celsius |
| Wind speed | Numeric | Wind speed in meter per second | |
| Community | The Number of Grids | The Total Demands (Pick-Up) | The Demands for Each Grid | Major Facilities |
|---|---|---|---|---|
| Red | 144 | 43,384 | 301 | Sinsa-dong garosu-gil road |
| Orange | 356 | 57,512 | 162 | Residential area |
| Yellow | 199 | 39,346 | 198 | Teheran-ro |
| Green | 301 | 37,775 | 125 | Samsung-dong trade center, Residential area |
| Blue | 164 | 46,079 | 281 | Apgujeong rodeo street, Cheongdam-dong luxury shopping street |
| Total | 1164 | 224,096 | 193 |
| Evaluating Indicators | Hidden State Size (The Number of Hidden Layers Is 1) | Number of Hidden Layers (Hidden State Size Is 6) | ||||||
|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 1 | 2 | 3 | 4 | |
| MSE | 0.0134 | 0.0126 | 0.0065 | 0.0106 | 0.0065 | 0.0139 | 0.0139 | 0.0145 |
| MAE | 0.0716 | 0.0753 | 0.0608 | 0.0685 | 0.0608 | 0.0805 | 0.0749 | 0.0804 |
| Activation Function | 5 Partitions | 1164 Square Grids | |||||
|---|---|---|---|---|---|---|---|
| MSE | MAE | Computing Time | MSE | MAE | Computing Time | ||
| LSTM | Sigmoid | 0.0091 | 0.0739 | 109 | 0.0512 | 0.1707 | 5998 |
| Tanh | 0.0065 | 0.0608 | 53 | 0.0507 | 0.1700 | 6390 | |
| ReLU | 0.0085 | 0.0677 | 50 | 0.0509 | 0.1710 | 6002 | |
| ELU | 0.0066 | 0.0604 | 78 | 0.0507 | 0.1702 | 5700 | |
| HA | 0.0083 | 0.0618 | - | 0.1300 | 0.5440 | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Choo, S.; Lee, G.; Kim, S. Predicting Demand for Shared E-Scooter Using Community Structure and Deep Learning Method. Sustainability 2022, 14, 2564. https://doi.org/10.3390/su14052564
Kim S, Choo S, Lee G, Kim S. Predicting Demand for Shared E-Scooter Using Community Structure and Deep Learning Method. Sustainability. 2022; 14(5):2564. https://doi.org/10.3390/su14052564
Chicago/Turabian StyleKim, Sujae, Sangho Choo, Gyeongjae Lee, and Sanghun Kim. 2022. "Predicting Demand for Shared E-Scooter Using Community Structure and Deep Learning Method" Sustainability 14, no. 5: 2564. https://doi.org/10.3390/su14052564
APA StyleKim, S., Choo, S., Lee, G., & Kim, S. (2022). Predicting Demand for Shared E-Scooter Using Community Structure and Deep Learning Method. Sustainability, 14(5), 2564. https://doi.org/10.3390/su14052564






