Abstract
Cool road pavements contribute to mitigating urban heat islands. To evaluate the heat balance in paved surfaces and to select appropriate road construction materials that help suppress heat islands, an accurate understanding of heat transport parameters such as thermal conductivity (λ) and heat capacity (HC) is important. Recycled aggregates from construction and demolition waste, including scrap construction materials and industrial by-products, are often used for road construction; however, λ and HC of recycled aggregates especially for roadbeds are not fully understood. This study involved a series of laboratory tests to measure λ and HC of recycled concrete and clay brick aggregates (<40 mm) and their mixtures with autoclaved aerated concrete grains (<2 mm) under varied moisture conditions. The measured λ and HC increased with increasing volumetric water content (θ). Closed-form models for estimating λ(θ) were proposed using normalized thermal conductivity (λe) and effective saturation (Se). The new λe(Se) models performed well for the measured data compared to previously proposed models and would be useful to evaluate λ of recycled aggregates for roadbed materials.
1. Introduction
Natural resources have been always exploited in human activities, and the construction industry is one of the industries that uses the most natural resources [1]. The unsustainable exploitation of natural resources leads to a series of adverse consequences such as environmental degradation, climate change, and depletion of natural resources. The construction industry also releases large amounts of solid waste into the environment during the processes of construction and demolition [1]. In developing countries such as those in Southeast Asia, along with economic development, the urbanization and industrialization has led to significant generation of construction and demolition waste (CDW), scrap construction materials (e.g., autoclaved aerated concrete (AAC)), and industrial by-products such as steel slag and coal ash [2,3]. While in the developed countries such as Japan, the USA, Australia, and members of the EU, most of the CDW, scrap construction materials, and industrial by-products are being recycled [4], in the developing countries, the percentage of recycled materials is very low. For example, in Vietnam, only 1–2% of CDW is recycled [5]. Instead, CDW is usually dumped at landfills without any treatment or illegally dumped in ponds, canals, and public areas [1,2,6]. Therefore, promoting the use of recycled materials from CDW, scrap construction materials, and industrial by-products in developing countries is essential to ensure environmental safety and reduce the consumption of natural materials.
Thermal conductivity (λ) and thermal capacity (HC) of materials play important roles in a variety of engineering applications [7,8]. For example, in the field of civil construction, materials with low thermal conductivity are often selected as insulating materials for walls and roofs. In contrast, the backfill materials or soils surrounding power cables must have a high thermal conductivity for the generated heat to dissipate to ensure that the cables are not thermally overloaded [7]. To mitigate the formation of urban heat islands and to construct cooling road pavements, low thermal conductivity, high porosity, and good water retention materials are especially effective [9,10]. The surface layer along with the road base layers participate in the heat transfer process of the pavement structure. Many previous studies have investigated CDW, scrap construction materials, and industrial by-products as road base and subbase materials; however, most of them were focused largely on the mechanical properties, hydraulic conductivity, and gas transport parameters [3,11,12,13,14]. To date, few studies have investigated the thermal conductivity and heat capacity of recycled aggregates of roadbed materials from CDW, scrap construction materials, and industrial by-products.
The objectives of this study were, for recycled aggregates from concrete, clay brick, and their mixtures with autoclaved aerated concrete grains, that are often used as road base materials: (i) to evaluate the thermal conductivity and heat capacity under varied moisture conditions and (ii) to develop new models suitable for thermal conductivity of these materials.
2. Materials and Methods
2.1. Materials
CDW was collected from the Thanh Tri landfill, Hanoi, Vietnam (20°59′21.6″ N, 105°53′58.1″ E), and AAC scrap was obtained from the Viglacera Joint Stock Company in Bac Ninh province, Vietnam (21°11′50.8″ N, 106°00′42.8″ E). All materials were shipped from Vietnam to Japan then crushed, sieved, and graded to prepare samples for a series of laboratory tests. Photographs of the samples tested in this study are shown in Figure A1. Seven test samples were prepared by blending recycled concrete (RC) or recycled clay brick (RCB) with different proportions of AAC, i.e., RC100%, RCB100%, AAC100%, RC80% + AAC20%, RC60% + AAC40%, RCB80% + AAC20%, and RCB60% + AAC40%. The basic physical properties of the tested materials are given in Table 1. AAC is a material with high water absorption, and mixing AAC with RC or RCB is expected to improve the water retention property of RC or RCB mixtures compared to single materials of RC or RCB. The particle size distributions (PSDs) for the tested samples are shown in Figure 1. The upper and lower boundaries of PSDs for road base materials prescribed in the Vietnam national standards TCVN 8859:2011 [15] and TCVN 8857:2011 [16] are also plotted in the figure.

Table 1.
Basic physical properties of tested materials.
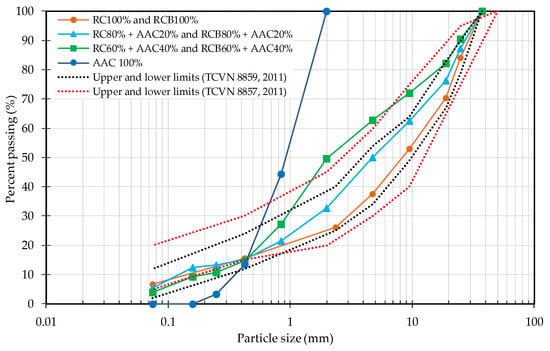
Figure 1.
Particle size distributions (PSDs) of tested samples in this study. The upper and lower boundaries of PSD for road base materials prescribed in TCVN 8859:2011 and TCVN 8857:2011, respectively, are indicated by dotted lines.
2.2. Testing Methods
2.2.1. Preparation of the Samples
The flowchart of sample preparation and measurements is shown in Figure 2. The crushed/sieved/graded samples were mixed at the above-mentioned proportions and compacted following the modified Proctor compaction method described in TCVN 12790:2020 [17] and ASTM D 1557:2012 [18]. The compaction was conducted in a cylindrical mold with an inner diameter of 150 mm and height of 120 mm by using a rammer with a weight of 4.54 kg, falling from a height of 457 mm. There were five compacted layers in each sample, and 56 blows were applied per layer (compaction energy ~2700 kJ m−3). The dry density and total porosity of the tested samples are shown in Table 2.
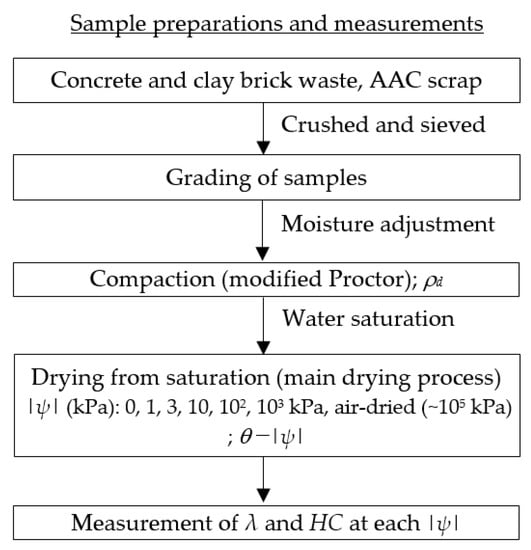
Figure 2.
Flowchart of sample preparations and measurements.

Table 2.
Dry density and total porosity of the tested samples.
2.2.2. Water Retention Curve Measurement
After compaction, the samples were saturated with water, and then the water content was reduced by stepwise drainage at different water potential energies (|ψ|, kPa). Two different methods were used to apply different |ψ|, i.e., a hanging-water column method was used for lower |ψ| (i.e., 1 and 3 kPa), and a pressure chamber method was used for higher |ψ| (i.e., 10, 100, and 1000 kPa). At the end of the drying process, the samples were placed in an oven and dried at 105 degrees to the highest |ψ| (>1000 kPa). After a few days, the dried samples were taken out of the oven and put into a temperature-controlled room for about a week. Then, |ψ| was measured using a dewpoint potential meter (WP4-T, Decagon Devices Inc., Pullman, WA, USA). At each |ψ| value, λ and HC of samples were measured as described below.
The water retention curves (WRCs) were fitted by using the van Genuchten model (the unimodal model) [19] or the Durner model (the bimodal model) [20] as Equations (1) and (2), respectively. The van Genuchten model represents the WRCs of the soils having a homogeneous pore structure, while that of Durner represents the WRCs of the soils with a heterogeneous pore structure [21].
where θ (m3 m−3), θr (m3 m−3), and θs (m3 m−3) are the volumetric water content, residual volumetric water content, and the saturated volumetric water content, respectively; k is the number of the peak pore size density or subsystems which form the total pore size distribution; wi represents the sub-curve weighting factors; and αi, ni, and mi are the parameters of the sub-curves (mi = 1 − 1/ni) that indicate fitted parameters. The equivalent pore size distributions of the tested samples were calculated by using the equation which was defined by Durner [20]:
where r (μm) is the equivalent pore radius (r = 1500/|ψ|; [22]), and C* is the specific moisture capacity (C* = dθ/dψ).
The WRCs and pore size distributions of tested samples are shown in Figure 3 with the fitted parameters for WRCs shown in Table 3. While the WRCs of RC100% and RCB100% samples were fitted well to the unimodal model [19], the WRCs of other samples were fitted well to the bimodal model [20]. This means that RC100% and RCB100% are samples with homogeneous pore structure, while other samples have heterogeneous pore structure due to the presence of AAC as high porosity material, including pores of different sizes [23,24]. The WRCs of tested samples showed that the saturated volumetric water content (θs) increased with the increased proportion of AAC grains for both blended RC and RCB samples, i.e., the θs values of samples with 20% and 40% blended AAC were 1.8 to 2.2 times higher than those of the single material for RC mixtures and 1.2 to 1.4 times higher than those of the single material for RCB mixtures. This indicated that the water retention capacities of RC and RCB were improved by blending in AAC grains as expected above. In addition, in air-dried conditions, tested samples retained a high residual volumetric water content (θr). This may be because tested materials, which were compacted before measurement, had high water absorption capacity. Compacted samples are usually very dense and contain many micropores (see Figure 3b,d), which prevent the movement of water out of the samples under air-dried conditions.
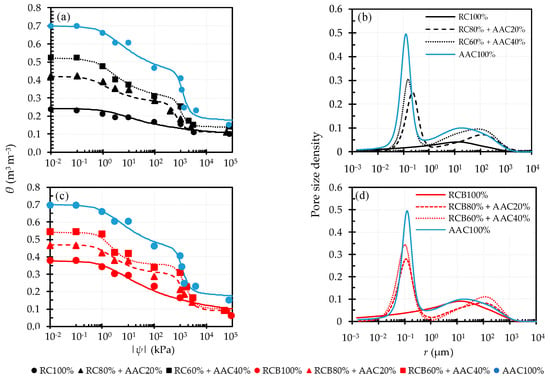
Figure 3.
Water retention curves (WRCs) (Equations (1) and (2)) and pore size density of tested samples (Equation (3)). (a,b) RC 100%, RC–AAC mixtures, and AAC100% and (c,d) RCB100%, RCB–AAC mixtures, and AAC100%. Measured values of saturated volumetric water content (θs) were plotted at |ψ| = 10−2 kPa.

Table 3.
Fitting parameters for WRCs for all tested samples (Equations (1) and (2)).
As shown in the figures, the equivalent pore size distributions of tested samples depend significantly on the proportion of AAC grains. The pore size distribution of the AAC seems more dominant than those of the RC and RCB grains. As a result, the increase in the proportion of AAC grains tends to increase the pore size density of both fine pores (ranging from 0.03 to 1 µm) and large pores (ranging from 5 to 300 µm).
2.2.3. Measurement of Thermal Properties
A variety of methods can be used to measure thermal properties of materials such as needle probe, hot-wire, hot plate, and heat-flow meter, of which needle probe and hot-wire are the widely used methods [25,26].
Figure 4 shows the comparison of thermal conductivity measurements of two samples RC100% and RCB100% by two different methods (i.e., needle probe and hot-wire methods). For the needle probe method, the KD2 Pro Thermal Analyzer (Decagon Devices, Pullman, WA, USA) with a dual needle SH-1 sensor (30 mm in length, 1.3 mm diameter, 6 mm spacing between two needles) was used. For the hot-wire probe method, a QTM-700 (Kyoto Electronics Manufacturing Co., Ltd., Japan) was used. The thermal conductivities measured by the two methods agreed closely, and the scatterplot points were all within the 95% confidence interval curves for a 1:1 line as shown by the t-test. The needle probe (dual needle probe) method is advantageous because it determines not only λ but also HC, while the hot-wire method can only determine λ. Measured HC data of recycled aggregates have been quite limited in past studies. Although the development of the models focused only on the λ–θ relationships, we took advantage of the simultaneous λ and HC measurement capability. Therefore, in this study, the needle probe method was chosen.
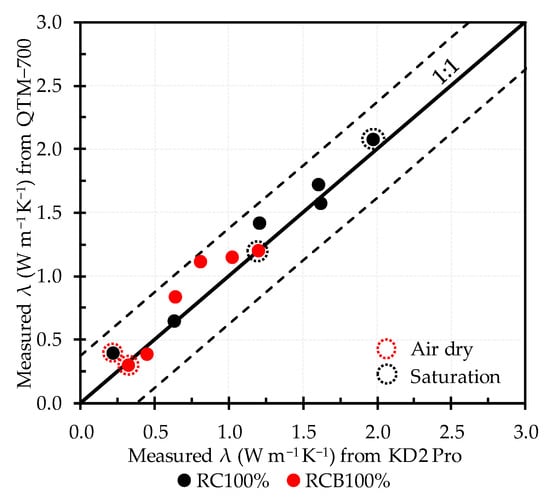
Figure 4.
Comparison of measured λ values by two different methods. The 95% confidence curves are indicated by broken lines.
The principle of heat transfer in porous materials is complicated due to the irregular microstructure [27]. Heat is transferred through these materials by thermal conduction in the solid phase, thermal conduction in the fluid phase (liquid or air), radiation, and convection of latent heat (vaporization) [7,27,28,29]. Of these, conduction and convection of latent heat play the most important role [29]; convection makes a large contribution when the gas-filled spaces (pore sizes) are over several millimeters [7,30], and radiation should be considered at a high temperature (above 200 degrees) [31]. All experiments were performed in a climate-controlled laboratory at 20 °C and relative humidity of 60%; the pore sizes of all the tested samples were less than 1 mm (see Figure 3b,d). Therefore, convection and radiation can be neglected in this study, and heat transfer is considered conduction-dominant.
2.3. Statistical Evaluation of the Model Prediction
Three statistical indexes, i.e., the root mean square error (RMSE), bias, and Akaike’s information criterion (AIC) [32,33], were used to calculate the statistical accuracy of the predictive thermal properties of the models described in the latter section. Of these, RMSE was used to evaluate the best overall fit compared with measured data, bias was used to evaluate the model overestimation (positive bias) or underestimation (negative bias) of measured thermal properties, and AIC was used to account for the number of model parameters, with smaller (or more negative) AIC indicating better model performance [34]. RMSE, bias, and AIC were calculated by the following equations:
where Δλi (W m−1 K−1) is the difference between the ith predicted and measured thermal conductivities, n is the number of measurements, and k is the number of model parameters.
3. Model Development for Estimating Thermal Conductivity
3.1. Existing Models for Estimating Thermal Conductivity
A variety of models have been used to predict the thermal conductivity of soils under varied moisture conditions. However, the number of studies conducted to predict the thermal conductivity of unbound aggregates, especially recycled aggregates, is very limited. In this study, a series of existing thermal conductivity models for soils were considered as listed below:
Lichtenecker [35] proposed the geometric mean model. Woodside and Messmer [31] used it for thermal conductivity prediction of two-phase porous material.
where λf, λs (W m−1 K−1) are thermal conductivities of pore fluid and solid phases; ϕ (m3 m−3) is the total porosity of the soil. According to Beziat [36] and Zhang et al. [37], when soil consists of three phases (solid, water, and gas), thermal conductivity can be calculated as below:
where λs and λw, and λa (W m−1 K−1) are the thermal conductivities of the solid phase, water, and air, respectively; Sr (%) is the degree of saturation:
where θ and θs (m3 m−3) are the volumetric water content and the saturated volumetric water content. Note here that water is more thermally conductive than air by a factor of >20 (λw = 0.57 W m−1 K−1 and λa = 0.025 W m−1 K−1 [38]). Thus, the higher the volumetric water content, the higher the apparent thermal conductivity.
The model that de Vries [38] proposed was also based on three phases, i.e., solid, water, and air, and had a different form. The thermal conductivity of all phases in combination with the volumetric fractions and the weighting factors were used to calculate thermal conductivity as the following equations:
where λw and λs, (W m−1 K−1) are the thermal conductivity of water and the solid phase, respectively; λapp (W m−1 K−1) is the apparent thermal conductivity of the air-filled pore space, made up partly of normal heat conduction (λa) and partly of vapor movement (λv); θ, σ, and ε (m3 m−3) are the volumetric fractions of water, solids, and air, respectively; ks and ka are the weighting factors for the solid and air phases determined by λ for each phase and geometric shape of the soil particles; and ga, gb, and gc represent the depolarization factor of the ellipsoid in the different directions, satisfying ga + gb + gc = 1. Farouki [7] suggested that and gc = 1 − 2ga.
Johansen [39] first introduced the concept of normalized thermal conductivity (λe):
where λe is normalized thermal conductivity, and λsat and λdry (W m−1 K−1) are thermal conductivities under full saturation and dry conditions, respectively. Johansen [39] proposed λe as a function of Sr:
The thermal conductivity at saturation was estimated by using the geometric mean equation:
where λw and λs (W m−1 K−1) are the thermal conductivity of water and the solid phase, respectively; ϕ (m3 m−3) is the total porosity of the soil. Note that Equation (16) is equivalent to Equation (7). Thermal conductivity in dry conditions has an empirical form:
Campbell [40] measured the thermal conductivity of a series of soils such as forest litter, silt loam soil, and sand to develop an empirical equation:
where A, B, C, D, and E are parameters dependent on soil physical properties; A = 0.65 − 0.78(ρd/1000) + 0.60(ρd/1000)2, B = 1.06(ρd/1000)θ, C = 1 + 2.6(1000mc)−0.5, D = 0.03 + 0.10(ρd/1000)2, and E = 4, where ρd (kg m−3) is the dry bulk density and mc (kg) is the clay mass fraction of the soil; θ (m3 m−3) is the volumetric water content.
Cote and Konrad [41] studied nearly 200 samples of unfrozen and frozen subbase and base materials with a variety of soil types. They proposed that normalized thermal conductivity is a function of the degree of saturation (Sr):
where κ is the parameter related to the soil type effect on the λe–Sr relationship. They suggested that κ is 4.6 for gravel and coarse sand; 3.55 for median and fine sand; and 1.9 for silt and clay. Thermal conductivity of saturated soil was calculated by Equation (16). Thermal conductivity of dry soils was predicted:
where χ and η are the coefficients accounting for the effects of soil type and grain shape on the thermal conductivity of dry soils. χ = 1.7 and η = 1.8 for well-graded gravels.
Lu et al. [42] measured thermal conductivity of 12 different soils such as sand, loam, and sandy loam and proposed the model for normalized thermal conductivity:
where Sr (%) is the degree of saturation; F is a soil texture-dependent parameter, F is suggested to be 0.96 and 0.27 for coarse and fine soils, respectively. Thermal conductivity of saturated soil was calculated by Equation (16). Lu et al. [42] presented a simple linear model for predicting the thermal conductivity of dry soils from the total porosity of the soil:
where G and H are the coefficients related to the thermal conductivity of dry soils. The suggested values are 0.56 and 0.51.
3.2. The New Models for Estimating Thermal Conductivity
3.2.1. Linear Model
The volumetric water content (θ) is an important factor that significantly affects thermal conductivity of the samples. In this study, compacted samples contained high residual volumetric water content (θr) in air-dried conditions. Therefore, to develop the model for estimating λ of tested samples with the change of θ, we suggest that λ should be a function of (θ − θr). A linear model was expected for estimating λ as:
λdry can be calculated from σ by a simple linear equation:
where a1 and b1 are empirical parameters. We assumed b1 is equal to the thermal conductivity of air, b1 = λa = 0.025 W m−1 K−1 [38]). Therefore, the linear model for thermal conductivity can be written as the equation:
3.2.2. Simple Closed-Form Model
In this study, simple closed-form models consisting of a parabolic segment (from (0,0) to (1,1) in the x–y coordinate plane) for thermal conductivity were developed by using the concept of normalized thermal conductivity, λe [39]. Previous studies proposed normalized thermal conductivity, λe, as a function of Sr [39,41,42]. In these, the λe models of Johansen [39] and Lu et al. [42] are convex curves, while Cote and Konrad’s λe model [41] is a convex curve when κ > 1 and a concave curve when κ < 1. Cote and Konrad’s λe model seems to be more general than the other two models. Therefore, the simple closed-form model for λe in this study was developed based on Cote and Konrad’s λe model (Equation (19)) [41]. As mentioned above, in air-dried conditions, the tested samples contained a significant amount of water to make the Sr values of tested samples large, which may not be expressed well by the previous λe models. Thus, we incorporated the effective saturation, Se [Se = (θ − θr)/(θs − θr); Equation (1)], into the model development. The resulting new model for estimating λe is shown by the equation below:
where κ is a material-dependent parameter.
Combining Equations (13) and (26), the new λ model labeled the Johansen–Cote–Konrad (J-CK) model can be obtained.
To estimate λsat and λdry, we applied two models: the geometric mean (GM) model [31] and the linear model. By applying the GM model for estimating λsat and λdry, modified geometric mean equations were proposed to calculate λsat and λdry of tested samples for not only single materials (i.e., RC100%, RCB100%, AAC100%) but also mixtures (i.e., RC80% + AAC20%, RC60% + AAC40%, RCB80% + AAC20%, and RCB60% + AAC40%) with the following equations:
where λs1 and λs2 (W m−1 K−1) are the thermal conductivity of the solid phase of aggregates 1 and 2 in the mixtures, respectively; f is the proportion of aggregate 1 in the mixtures; and σ (m3 m−3) is volumetric solid content. We assumed that λs values of tested materials (RC, RCB, and AAC) could be estimated from λsat based on Equation (16) and are shown in Table 4.

Table 4.
Estimated thermal conductivity of solid (λs) from saturation condition (λsat) based on geometric mean model.
From Equations (27)–(29), a new model which is labeled the Johansen–Cote–Konrad geometric mean (J-CK-GM) model could be obtained by the equation below:
Regarding the application of the linear model to estimate λsat and λdry, λdry can be calculated by Equation (24), while λsat can be calculated by substituting θ = θs in Equation (25) to obtain:
From Equations (24), (27) and (31), the new model, which is labelled the Johansen–Cote–Konrad linear (J-CK-L) model, can be written as the equation below:
4. Results and Discussion
4.1. Measured Thermal Conductivity and Heat Capacity
Figure 5 and Figure 6 showed the relationships between λ, HC, and θ of tested samples. The water states are also presented in the figures, with the boundary between capillary and hygroscopic regions assumed to be the sum of the maximum adsorbed water in fine and coarse aggregates [14]. The maximum volumetric water absorbed by coarse or fine aggregates can be calculated by θabs,c/f = [mc/f × (wabs,c/f/100)]/(1000V), where mc/f is the mass of coarse or fine aggregates in the tested sample (kg), wabs,c/f is the water absorption of coarse or fine aggregates (kg/kg in %), and V is the volume of the sample (m3). The maximum volumetric absorbed water by coarse and fine aggregates for the tested materials is shown in Table 1.
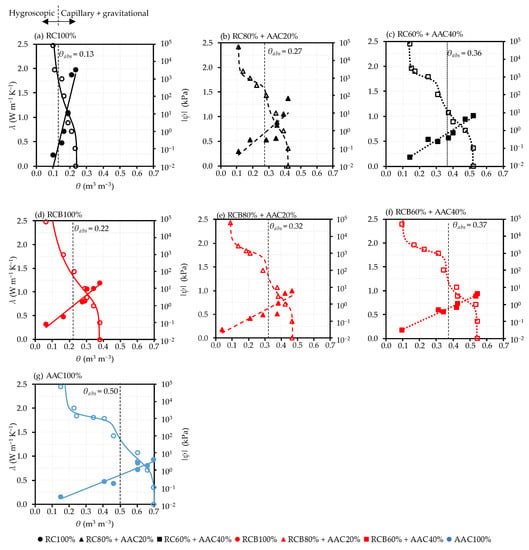
Figure 5.
Thermal conductivity as a function of volumetric water content and water retention curves of tested samples. The filled points present the data of thermal conductivity, and the unfilled points present the data of water retention curves.
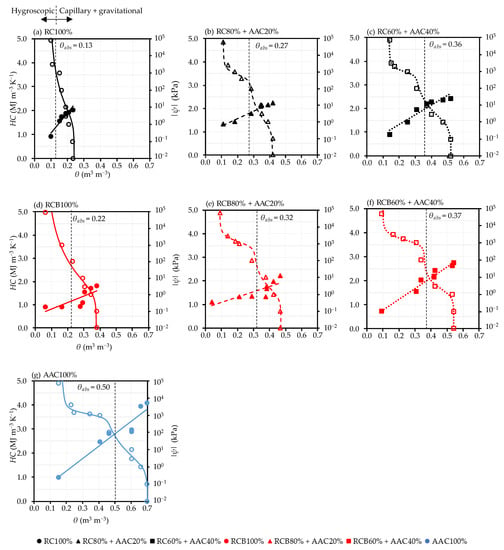
Figure 6.
Heat capacity as a function of volumetric water content and water retention curves of tested samples. The filled points present the data of heat capacity, and the unfilled points present the data of water retention curves.
Figure 5 shows that the λ values of all tested samples increased with the increase in θ for all tested samples. This can be explained by the water bridge effect. When the water content in samples increased, the particles were surrounded by the water films that bridge the gaps between the particles. These water films tended to increase the effective contact area between the particles, which caused the increase in the thermal conductivity [43,44,45,46]. As noted above, water has a significantly higher thermal conductivity than air (λw = 0.57 W m−1 K−1 and λa = 0.025 W m−1 K−1 [38]); when θ increases, water displaces air, leading to an increase in the thermal conductivity of the sample. Turning to the comparison of tested materials, at the same θ value, RC had the highest λ value followed by RCB and AAC. This may be due to the difference in the water absorption capacity of materials. AAC and RCB had a higher water absorption capacity than RC (see Table 1), which resulted in the water films surrounding the AAC and RCB particles being thinner than the water films surrounding the RC particles at the same θ value. Hence, AAC and RCB had lower thermal conductivity than RC.
Figure 6 shows the heat capacity (HC) of the tested samples as a function of θ. The HC values of all tested samples increased linearly with the increase in the θ values. In addition, it can be seen that the materials with a higher water holding capacity usually have a higher heat capacity in saturation conditions. This may be because water has a very high volumetric heat capacity (4.18 MJ m−3 K−1 [38]).
Thermal conductivity and heat capacity in air-dried conditions (λdry and HCdry) of the tested samples are shown in Figure 7. The predictive models from previous studies for λdry and HCdry were also plotted. λdry and HCdry depend on a variety of factors such as particle shape, dry density, total porosity, and volumetric solid content [38,39,41,42,47]. Both λdry and HCdry tended to increase as the volumetric solid content (σ) increased, similar to the trend of previous studies. However, the measured data were not expressed well by the previous predictive models. The measured data were fitted by using Equation (24) with a1 = 0.35 and b1 = 0.025. The regression line for HCdry–σ relationship is shown in Figure 7b.
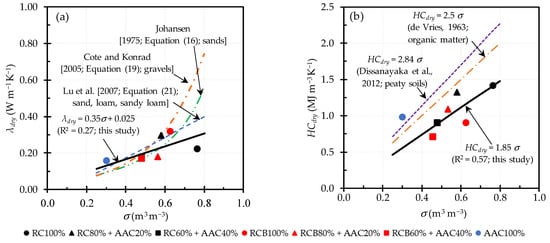
Figure 7.
Measured λdry and HCdry of tested samples as a function of volumetric solid content, σ.
Figure 8 showed the λ and HC values of the tested samples as linear functions of (θ − θr). The proposed linear model for λ based on Equation (25) gave good regressions (R2 > 0.81) for the tested samples, except for the RC80% + AAC20% sample (R2 = 0.71). The regression lines for HC values correlated with (θ − θr) of the tested samples are shown in the figure with relatively high values of R2 (≥0.71).
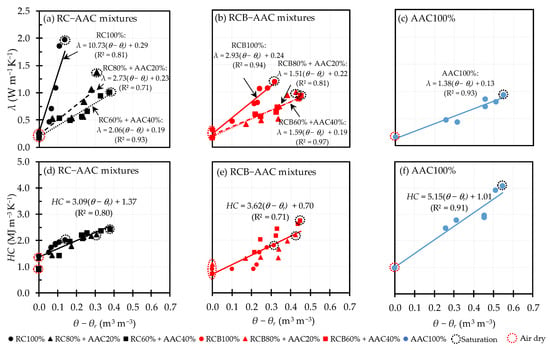
Figure 8.
Measured λ and HC as a function of (θ − θr).
Figure 9 shows the relationships between λe and Se for the tested samples, sands [48], silt loam, and silty clay loam [42]. It is clearly seen that the new λe model performed very well not only in data measured in this study but also in data sets from previous studies. The R2 values for the λe–Se relationship based on Equation (26) for each data set ranged from 0.91 to 0.97.
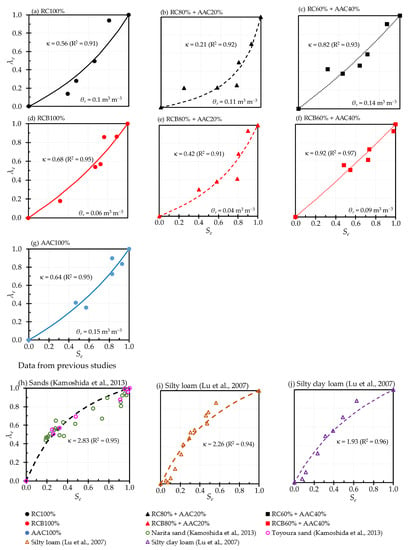
Figure 9.
Normalized thermal conductivity, λe, as a function of effective saturation, Se.
Figure 10 indicates the effects of material type, particle size, and gradation on κ values. In Figure 10a, κ values are plotted as a function of median diameter (D50). The κ values of the tested samples using recycled materials in this study were less than 1, while those of natural materials (i.e., sands, silty loam, and silty clay loam) were more than 1. This means that λe values of recycled materials increase less rapidly than those of natural materials with increasing Se. This may be because recycled materials had higher water absorption capacity than natural materials, which caused water films between particles of recycled materials to form at a higher water content than natural materials. κ values tended to increase with increasing D50 for natural materials, while κ values of recycled materials fluctuated with the increasing D50. Turning to the effect of gradation, the relationship between κ values and the coefficient of uniformity (Cu; Cu = D60/D10; where D60 and D10 (mm) are particle diameters at which 60% and 10% of particles, respectively are smaller) are shown in Figure 10b. The κ values of samples decreased with increasing Cu, and the regression line was fitted: κ = 0.73[log(Cu)]−0.67 (R2 = 0.75).
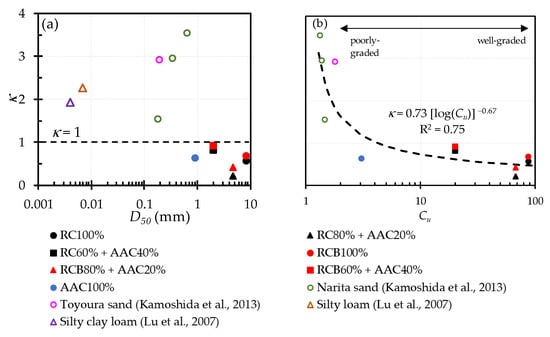
Figure 10.
κ as a function of (a) D50 and (b) Cu.
4.2. Performance of the Predictive Models for Thermal Conductivity
Figure 11 shows scatter plot comparisons of predicted and measured λ for the new models in this study and the previous models. The statistical indexes (RMSE, bias, AIC) of the models are listed in Table 5. Looking at Figure 11, most of the previous models showed worse model performance except for the Woodside and Messmer model [31] for RCB-AAC mixtures and AAC100% samples. In contrast, the new models in this study performed well; most of the predicted values were correlated with the measured values ranging from 1:4/3 to 4/3:1 for all tested samples except for the J-CK-GM model for RC100% and RC80% + AAC20% samples. The RMSE and AIC values of the new models were significantly lower than those of the previous models (see Table 5), in which the J-CK-L model had the lowest RMSE and AIC. Therefore, it can be concluded that the new models are more suitable to describe the thermal conductivity of recycled aggregates and mixtures than previous models.
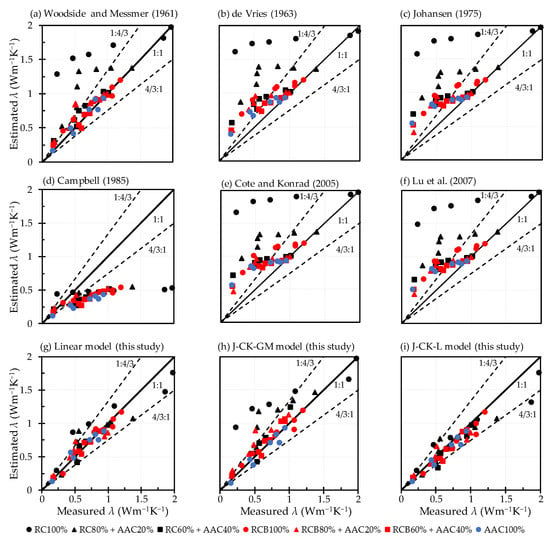
Figure 11.
Scatterplot comparison of estimated and measured λ values of tested samples.

Table 5.
Test of predictive thermal conductivity (λ) models against measured data.
5. Conclusions
The measurement of thermal conductivity and heat capacity of recycled aggregates from concrete, clay brick, and their mixtures with autoclaved aerated concrete grains was carried out in the laboratory during the drying process from saturation to air-dried conditions. The results showed that, when compacted as described in this study, both λ and HC of recycled aggregates increased linearly with the increase in volumetric water content. The existing predictive models for thermal conductivity indicated a need for improvement. Two simple closed-form models (labelled J-CK-GM and J-CK-L) were newly refined based on the relationship between normalized thermal conductivity (λe) and effective saturation (Se). The refined models estimated sufficiently well the measured data of tested samples, and the J-CK-L model especially had the best performance among tested thermal conductivity models. Because the J-CK-L model with a single variable of κ adopted measured data from different mixed proportions of recycled concrete and clay brick aggregate and their mixtures with AAC grains, the model would be useful for quick assessment of the thermal conductivity of roadbed materials and for evaluating the heat balance to mitigate urban heat islands.
Author Contributions
Conceptualization, H.N.T., K.K. and H.G.N.; methodology, H.N.T. and K.K.; software, H.N.T. and H.G.N.; validation, K.K.; formal analysis, H.N.T. and K.K.; investigation, resources, and data curation, H.N.T. and K.K.; writing—original draft preparation, H.N.T.; writing—review and editing, T.K., T.S., P.M., H.G.N. and K.K.; visualization, H.N.T.; supervision, T.K., T.S., P.M., and K.K.; project administration, H.G.N. and K.K.; funding acquisition, K.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the project of Japan Science and Technology Agency (JST), Japan International Cooperation Agency (JICA) on Science, and Technology Research Partnership for Sustainable Development (SATREPS) (no. JPMJSA1701).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We thank Akira Kato, a former Researcher at Saitama University, and Van Nam Pham, a student at Saitama University, for their help in the process of sample preparation and measurement in the laboratory.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations and Symbols
| AAC | Autoclaved aerated concrete |
| AIC | Akaike’s information criterion |
| CDW | Construction and demolition waste |
| LA | Los Angeles abrasion |
| RC | Recycled concrete |
| RCB | Recycled clay brick |
| RMSE | Root mean square error |
| WRCs | Water retention curves |
| A, B, C, D, E | Parameters dependent on physical properties of the soil (Equation (18)) (-) |
| a1, b1 | Empirical parameters in the linear model used for estimating λdry (Equation (24)) (-) |
| a2 | Parameter in linear model (Equation (25)) (-) |
| C* | Specific moisture capacity (-) |
| Cu | Coefficient of uniformity (-) |
| D50 | Mean particle size (mm) |
| F | Soil texture dependent parameter in Equation (21) (-) |
| f | Proportion of aggregate in the mixtures |
| G, H | Coefficients in Equation (22) (-) |
| ga, gb, gc | Depolarization factor of the ellipsoid in different directions (-) |
| HC | Heat capacity (MJ m−3 K−1) |
| HCdry | Heat capacity at air dried (MJ m−3 K−1) |
| k | Number of model parameters (-) |
| ka | Weighting factors for the air phase (-) |
| ks | Weighting factors for the solid phase (-) |
| mc | Clay mass fraction of the soil (kg) |
| r | Equivalent pore radius (μm) |
| Se | Effective saturation (-) |
| Sr | Degree of saturation (%) |
| wabs | Water absorption capacity (%) |
| wAD | Water content in air-dried condition (%) |
| α, n, m | Parameters of van Genuchten WRC (Equation (1)) |
| αi, wi, ni, mi | Parameters of Durner WRC (Equation (2)) (-) |
| χ | Coefficient accounting for soil type (-) |
| ε | Air-filled porosity (m3 m−3) |
| ϕ | Total porosity (m3 m−3) |
| η | Coefficient accounting for grain shape (-) |
| κ | Material dependent parameter (-) |
| λ | Thermal conductivity (W m−1 K−1) |
| λa | Thermal conductivity of air (W m−1 K−1) |
| λapp | Apparent thermal conductivity of the air-filled pore space (W m−1 K−1) |
| λdry | Thermal conductivities at air dry (W m−1 K−1) |
| λe | Normalized thermal conductivity (-) |
| λs | Thermal conductivity of solid phase (W m−1 K−1) |
| λsat | Thermal conductivity at water saturation (W m−1 K−1) |
| λw | Thermal conductivity of water (W m−1 K−1) |
| λv | Apparent thermal conductivity of vapor movement (W m−1 K−1) |
| θ | Volumetric water content (m3 m−3) |
| θr | Residual volumetric water content (m3 m−3) |
| θs | Saturated volumetric water content (m3 m−3) |
| ρd | Dry density (kg m−3) |
| ρs | Density of solid phase (kg m−3) |
| σ | Volumetric solid content (m3 m−3) |
| |ψ| | Water potential (kPa) |
Appendix A


Figure A1.
Tested samples.
Figure A2 compares the thermal conductivity between the tested samples and other materials such as lightweight concrete [49,50], pervious concrete [51], and concrete [52] in air-dried (Figure A2a) and saturated conditions (Figure A2b). The λdry values of most tested samples were lower than those of concrete and lightweight concrete and higher than those of pervious concrete at the same dry density value except for λdry value of RC100% sample. In the saturated conditions, λsat values of tested samples were higher than those of pervious concrete.
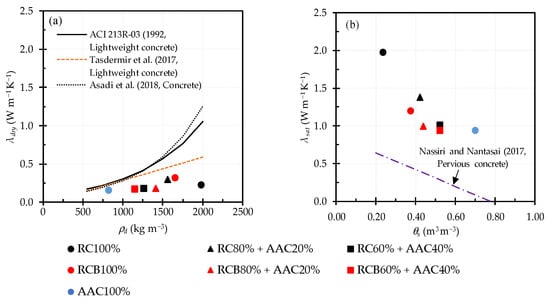
Figure A2.
Comparison of measured thermal conductivities of tested samples in this study with those for (a) lightweight and normal concrete in air dried condition and (b) pervious concrete in saturated condition.
References
- Nguyen, H.G.; Nguyen, T.D.; Nghiem, H.T.; Tran, V.C.; Kato, A.; Matsuno, A.; Isobe, Y.; Kawasaki, M.; Kawamoto, K. Current management condition and waste composition characteristics of construction and demolition waste landfills in hanoi of vietnam. Sustainability 2021, 13, 10148. [Google Scholar] [CrossRef]
- Hoang, N.H.; Ishigaki, T.; Kubota, R.; Yamada, M.; Kawamoto, K. A review of construction and demolition waste management in Southeast Asia. J. Mater. Cycles Waste Manag. 2020, 22, 315–325. [Google Scholar] [CrossRef]
- Hoang, T.; Nguyen, V.P.; Thai, H.N. Use of coal ash of thermal power plant for highway embankment construction. In CIGOS 2019, Innovation for Sustainable Infrastructure. Lecture Notes in Civil Engineering; Ha-Minh, C., Dao, D., Benboudjema, F., Derible, S., Huynh, D., Tang, A., Eds.; Springer: Singapore, 2020; Volume 54, pp. 433–439. [Google Scholar] [CrossRef]
- Deloitte. Resource Efficient Use of Mixed Wastes Improving Management of Construction and Demolition Waste. Available online: https://op.europa.eu/en/publication-detail/-/publication/78e42e6c-d8a6-11e7-a506-01aa75ed71a1/language-en (accessed on 15 January 2022).
- Ministry of Natural Resources and Environment (MONRE). Report on National Environment: Solid Waste; Ministry of Natural Resources and Environment: Hanoi, Vietnam, 2011. (In Vietnamese)
- Nguyen, V.T.; Tong, T.K.; Dang, T.T.H.; Tran, T.V.N.; Nguyen, H.G.; Nguyen, T.D.; Isobe, Y.; Ishigaki, T.; Kawamoto, K. Current status of construction and demolition waste management in Vietnam: Challenges and opportunities. Int. J. GEOMATE 2018, 15, 23–29. [Google Scholar] [CrossRef]
- Farouki, O.T. Thermal Properties of Soils; Defense Tactical Information Center: Hanover, NH, USA, 1981. [Google Scholar]
- Chen, S.X. Thermal conductivity of sands. Heat Mass Transf. 2008, 44, 1241–1246. [Google Scholar] [CrossRef]
- Deng, H.; Deng, D.; Du, Y.; Lu, X. Using lightweight materials to enhance thermal resistance of asphalt mixture for cooling asphalt pavement. Adv. Civ. Eng. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Huang, Q.; Qian, Z.; Hu, J.; Zheng, D. Evaluation of stone mastic asphalt containing ceramic waste aggregate for cooling asphalt pavement. Materials 2020, 13, 2964. [Google Scholar] [CrossRef] [PubMed]
- Pham, V.N.; Kato, A.; Nguyen, H.G.; Nguyen, V.T.; Phan, Q.M.; Kawamoto, K. Gas transport parameters of recycled concrete and clay brick aggregate blended with autoclaved aerated concrete grains. Int. J. GEOMATE 2021, 20, 93–100. [Google Scholar] [CrossRef]
- Poon, C.S.; Chan, D. Feasible use of recycled concrete aggregates and crushed clay brick as unbound road sub-base. Constr. Build. Mater. 2006, 20, 578–585. [Google Scholar] [CrossRef]
- Thai, H.N.; Kato, A.; Nguyen, H.G.; Nguyen, T.D.; Tong, T.K.; Nguyen, V.T.; Uchimura, T.; Maki, T.; Kawamoto, K. Effects of particle size and type of aggregate on mechanical properties and environmental safety of unbound road base and subbase materials: A Literature Review. Int. J. GEOMATE 2021, 20, 148–157. [Google Scholar] [CrossRef]
- Thai, H.N.; Nguyen, T.D.; Nguyen, V.T.; Nguyen, H.G.; Kawamoto, K. Characterization of compaction and CBR properties of recycled concrete aggregates for unbound road base and subbase materials in Vietnam. J. Mater. Cycles Waste Manag. 2022, 24, 34–48. [Google Scholar] [CrossRef]
- TCVN 8859:2011. Aggregate Bases and Subbases of Pavement Structure—Material, Construction, and Acceptance. Vietnam, 2011. Available online: https://thuvienphapluat.vn/TCVN/Xay-dung/Tieu-chuan-Viet-Nam-TCVN-8859-2011-lop-mong-cap-phoi-da-dam-trong-ket-cau-ao-904056.aspx (accessed on 15 January 2022). (In Vietnamese).
- TCVN 8857:2011. Natural Aggregate for Road Pavement Layers Specification for Material, Construction and Acceptance. Vietnam, 2011. Available online: https://thuvienphapluat.vn/TCVN/Giao-thong/TCVN-8857-2011-Lop-ket-cau-ao-duong-o-to-bang-cap-phoi-thien-nhien-904969.aspx (accessed on 15 January 2022). (In Vietnamese).
- TCVN 12790:2020. Soils, Aggregates for Transport Infrastructure—Proctor Compaction Test. Vietnam, 2020. Available online: https://thuvienphapluat.vn/TCVN/Giao-thong/TCVN-12790-2020-Dat-da-dam-dung-trong-cong-trinh-giao-thong-Dam-nen-Proctor-918809.aspx (accessed on 15 January 2022). (In Vietnamese).
- ASTM D1557-12; ASTM D1557 Standard Test Methods for Laboratory Compaction Characteristics of Soil Using Modified Effort (56,000 ft-lbf/ft3 (2,700 kN-m/m3)). ASTM International: West Conshohocken, PA, USA, 2012. [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Durner, W. Hydraulic conductivity estimation for soils with heterogeneous pore structure. Water Resour. Res. 1994, 30, 211–223. [Google Scholar] [CrossRef]
- Seki, K. SWRC fit—A nonlinear fitting program with a water retention curve for soils having unimodal and bimodal pore structure. Hydrol. Earth Syst. Sci. Discuss. 2007, 4, 407–437. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W. Probability laws for pore size distribution. Soil Sci. 1966, 101, 85–92. [Google Scholar] [CrossRef]
- Schober, G. Porosity in autoclaved aerated concrete (AAC): A review on pore structure, types of porosity, measurement methods and effects of porosity on properties. Cem. Wapno Bet. 2011, 39–43. [Google Scholar]
- Chen, G.; Li, F.; Jing, P.; Geng, J.; Si, Z. Effect of pore structure on thermal conductivity and mechanical properties of autoclaved aerated concrete. Materials. 2021, 14, 339. [Google Scholar] [CrossRef]
- Nagihara, S.; Hedlund, M.; Zacny, K.; Taylor, P.T. Improved data reduction algorithm for the needle probe method applied to in-situ thermal conductivity measurements of lunar and planetary regoliths. Planet. Space Sci. 2014, 92, 49–56. [Google Scholar] [CrossRef]
- Yuksel, N. The Review of Some Commonly Used Methods and Techniques to Measure the Thermal Conductivity of Insulation Materials. In Insulation Materials in Context of Sustainability; Almusaed, A., Almssad, A., Eds.; IntechOpen: London, UK, 2016; pp. 113–140. [Google Scholar] [CrossRef]
- Tavman, I.H. Effective thermal conductivity of granular porous materials. Int. Commun. Heat Mass Transf. 1996, 23, 169–176. [Google Scholar] [CrossRef]
- Hermansson, Å.; Charlier, R.; Collin, F.; Erlingsson, S.; Laloui, L.; SršenSr, M. Heat transfer in soils. In Water in Road Structures, Geotechnical, Geological and Earthquake Engineering; A. Dawson, Ed.; Springer: Dordrecht, The Netherlands, 2009; Volume 5, pp. 69–79. [Google Scholar] [CrossRef]
- Jury, W.A.; Horton, R. Soil Physics, 6th ed.; John Wiley and Sons Inc.: New York, NY, USA, 2004. [Google Scholar]
- Woodside, W. Calculation of the thermal conductivity of porous media. Canada J. Phys. 1958, 36, 815–823. [Google Scholar] [CrossRef] [Green Version]
- Woodside, W.; Messmer, J.H. Thermal conductivity of porous media. I. Unconsolidated sands. J. Appl. Phys. 1961, 32, 1688–1699. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory; Petrov, B.N., Csaki, F., Eds.; Akademiai Kiado: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Carrera, J.; Neuman, S.P. Estimation of aquifer parameters under transient and steady state conditions: 1. Maximum likelihood method incorporating prior information. Water Resour. Res. 1986, 22, 199–210. [Google Scholar] [CrossRef]
- Minasny, B.; Mcbratney, A.B.; Bristow, K.L. Comparison of different approaches to the development of pedotransfer functions for water-retention curves. Geoderma 1999, 93, 225–253. [Google Scholar] [CrossRef]
- Lichteneker, K. The electrical conductivity of periodic and random aggregates. Phys. Zeitschrift 1926, 27, 115. [Google Scholar]
- Beziat, A.; Dardaine, M.; Mouche, E. Measurements of the thermal conductivity of clay-sand and clay-graphite mixtures used as engineered barriers for high-level radioactive waste disposal. Appl. Clay Sci. 1992, 6, 245–263. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, Z. Review of soil thermal conductivity and predictive models. Int. J. Therm. Sci. 2017, 117, 172–183. [Google Scholar] [CrossRef]
- de Vries, D.A. Thermal properties of soils. In Physics of the Plant Environment; van Wijk, W.R., Ed.; John Wiley & Sons: New York, NY, USA, 1963; pp. 210–235. [Google Scholar]
- Johansen, O. Thermal Conductivity of Soils. Ph.D. Thesis, University of Trondheim, Trondheim, Norway, 1977. [Google Scholar]
- Campbell, G.S. Soil physics with BASIC. Transport Models for Soil-Plant Systems; Elsevier Science B. V.: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Côté, J.; Konrad, J.M. Thermal conductivity of base-course materials. Can. Geotech. J. 2005, 42, 61–78. [Google Scholar] [CrossRef]
- Lu, S.; Ren, T.; Gong, Y.; Horton, R. An improved model for predicting soil thermal conductivity from water content at room temperature. Soil Sci. Soc. Am. J. 2007, 71, 8–14. [Google Scholar] [CrossRef]
- Sepaskhah, A.R.; Boersma, L. Thermal conductivity of soils as a function of temperature and water content. Soil Sci. Soc. Am. J. 1979, 43, 439–444. [Google Scholar] [CrossRef]
- Becker, B.R.; Misra, A.; Fricke, B.A. Development of correlations for soil thermal conductivity. Int. Commun. Heat mass Transf. 1992, 19, 59–68. [Google Scholar] [CrossRef] [Green Version]
- Hamamoto, S.; Moldrup, P.; Kawamoto, K.; Komatsu, T. Excluded-volume expansion of Archie’s law for gas and solute diffusivities and electrical and thermal conductivities in variably saturated porous media. Water Resour. Res. 2010, 46, 1–14. [Google Scholar] [CrossRef]
- Dong, Y.; McCartney, J.S.; Lu, N. Critical review of thermal conductivity models for unsaturated soils. Geotech. Geol. Eng. 2015, 33, 207–221. [Google Scholar] [CrossRef]
- Dissanayaka, S.H.; Hamamoto, S.; Kawamoto, K.; Komatsu, T.; Moldrup, P. Thermal properties of peaty soils: Effects of liquid-phase impedance factor and shrinkage. Vadose Zo. J. 2012, 11, vzj2011.0092. [Google Scholar] [CrossRef]
- Kamoshida, T.; Hamamoto, S.; Kawamoto, K.; Sakaki, T.; Komatsu, T. Thermal properties of sands at variably-saturated condition: Effectsof particle size and shape, and quartz content. J. Jpn. Soc. Soil Phys. 2013, 16, 11–16. (In Japanese) [Google Scholar] [CrossRef]
- ACI Committee 213R-03. Guide for Structural Lightweight-Aggregate Concrete; American Concrete Institute: Farmington Hills, MI, USA, 1992. [Google Scholar]
- Tasdemir, C.; Sengul, O.; Tasdemir, M.A. A comparative study on the thermal conductivities and mechanical properties of lightweight concretes. Energy Build. 2017, 151, 469–475. [Google Scholar] [CrossRef]
- Nassiri, S.; Nantasai, B. Thermal conductivity of pervious concrete for various porosities. ACI Mater. J. 2017, 114, 265–271. [Google Scholar] [CrossRef]
- Asadi, I.; Shafigh, P.; Bin Abu Hassan, Z.F.; Mahyuddin, N.B. Thermal conductivity of concrete—A review. J. Build. Eng. 2018, 20, 81–93. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).