Application of Physics-Informed Machine Learning Techniques for Power Grid Parameter Estimation
Abstract
:1. Introduction
- We develop the SINDy algorithm for estimating the inertia and damping coefficients for a nonlinear power grid model. We extend the algorithm to the case when the operator does not have accurate knowledge of the model (system identification) describing the system.
- We show that the proposed SINDy algorithm can be implemented in a decentralized manner that only requires exchanging the observed phase angle data between the neighbouring nodes of a power grid. Thus, the estimation can be performed locally (e.g., at phasor data concentrator level).
- We conduct extensive simulations using IEEE bus systems to evaluate and compare the performance of these algorithms.
2. Preliminaries
2.1. System Model
2.2. Power Grid Parameter Estimation Problem
3. Physics-Informed Machine Learning Techniques for Power Grid Parameter Estimation
3.1. Parameter Estimation Using the SINDy Algorithm
| Algorithm 1. SINDy Algorithm. |
Input: Phase angle data and frequency data Output: and
|
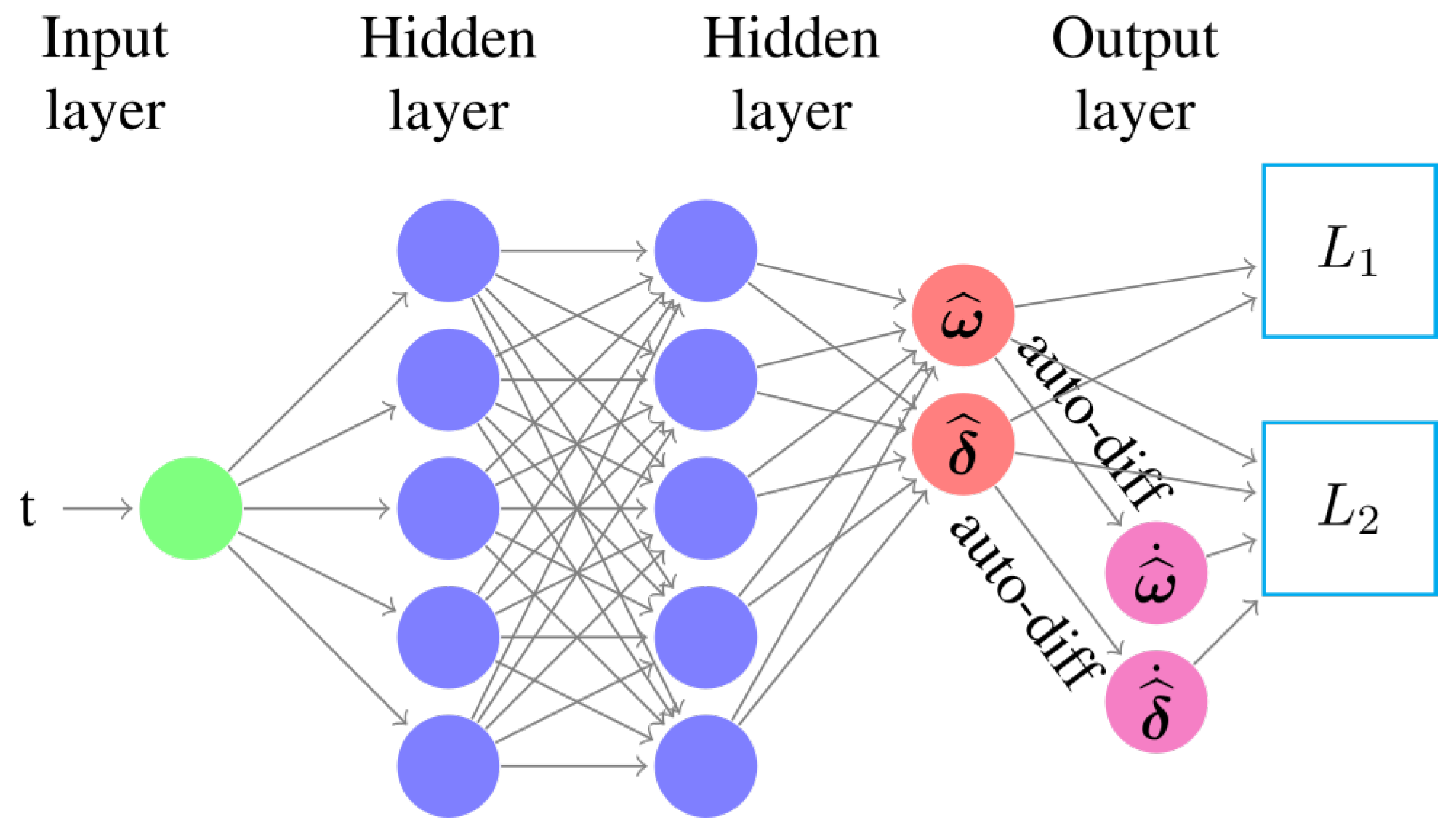
3.2. Parameter Estimation Based on Physics-Informed Neural Networks
3.2.1. Mean Squared Loss
3.2.2. Physics-Based Loss
4. Practical Implementation Aspects
4.1. Unknown System Model
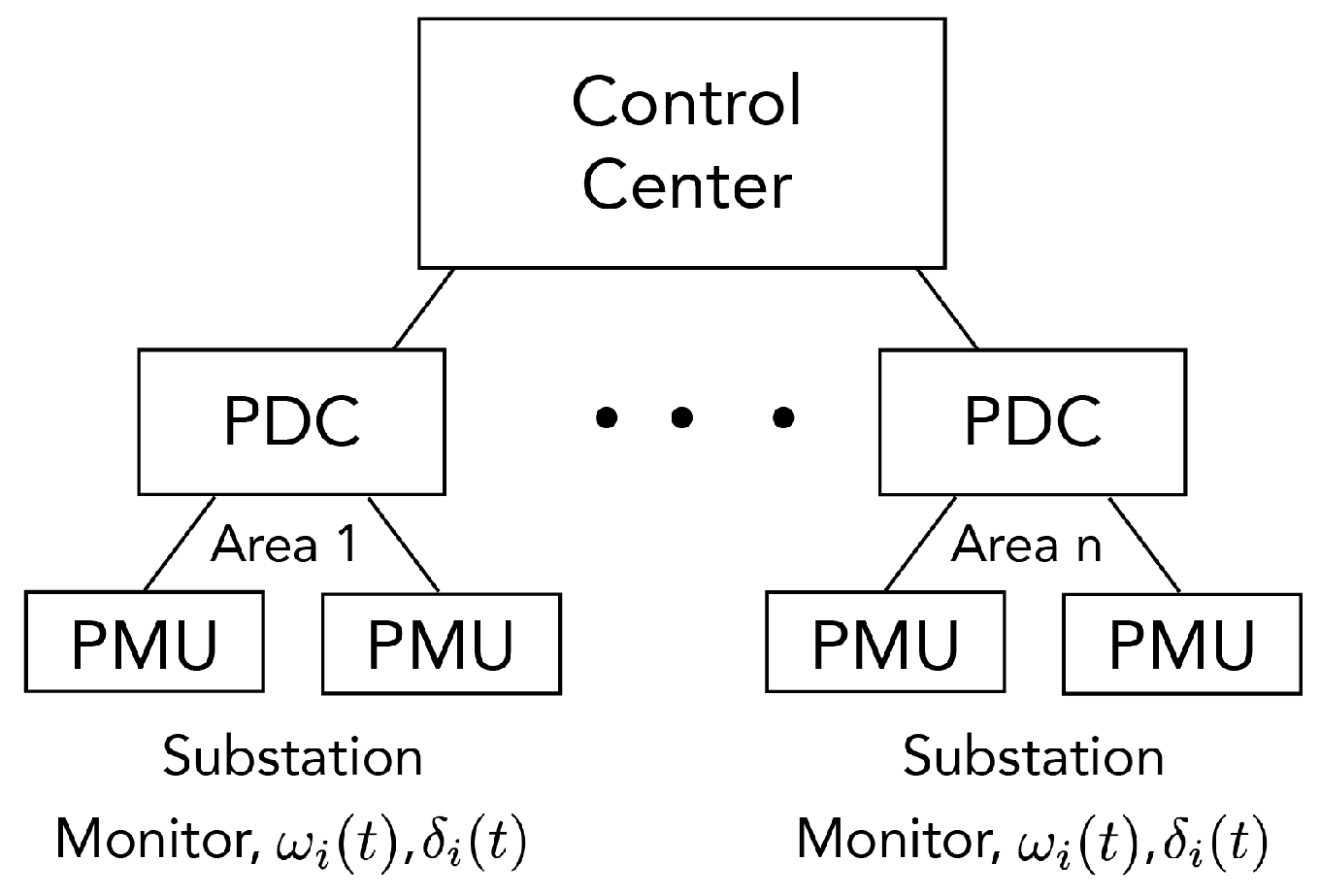
4.2. Decentralised Implementation
4.3. Knowledge of System Parameters
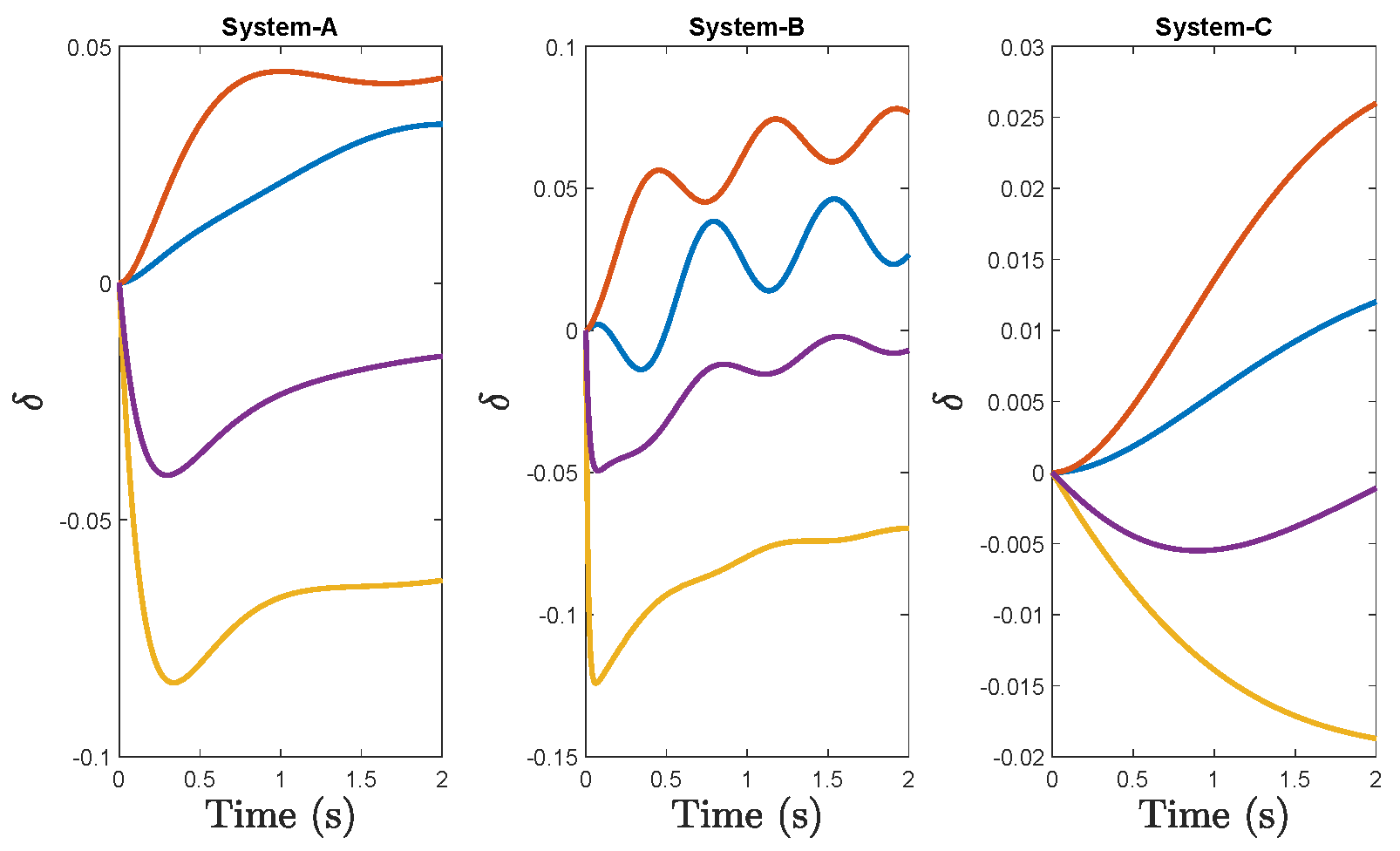
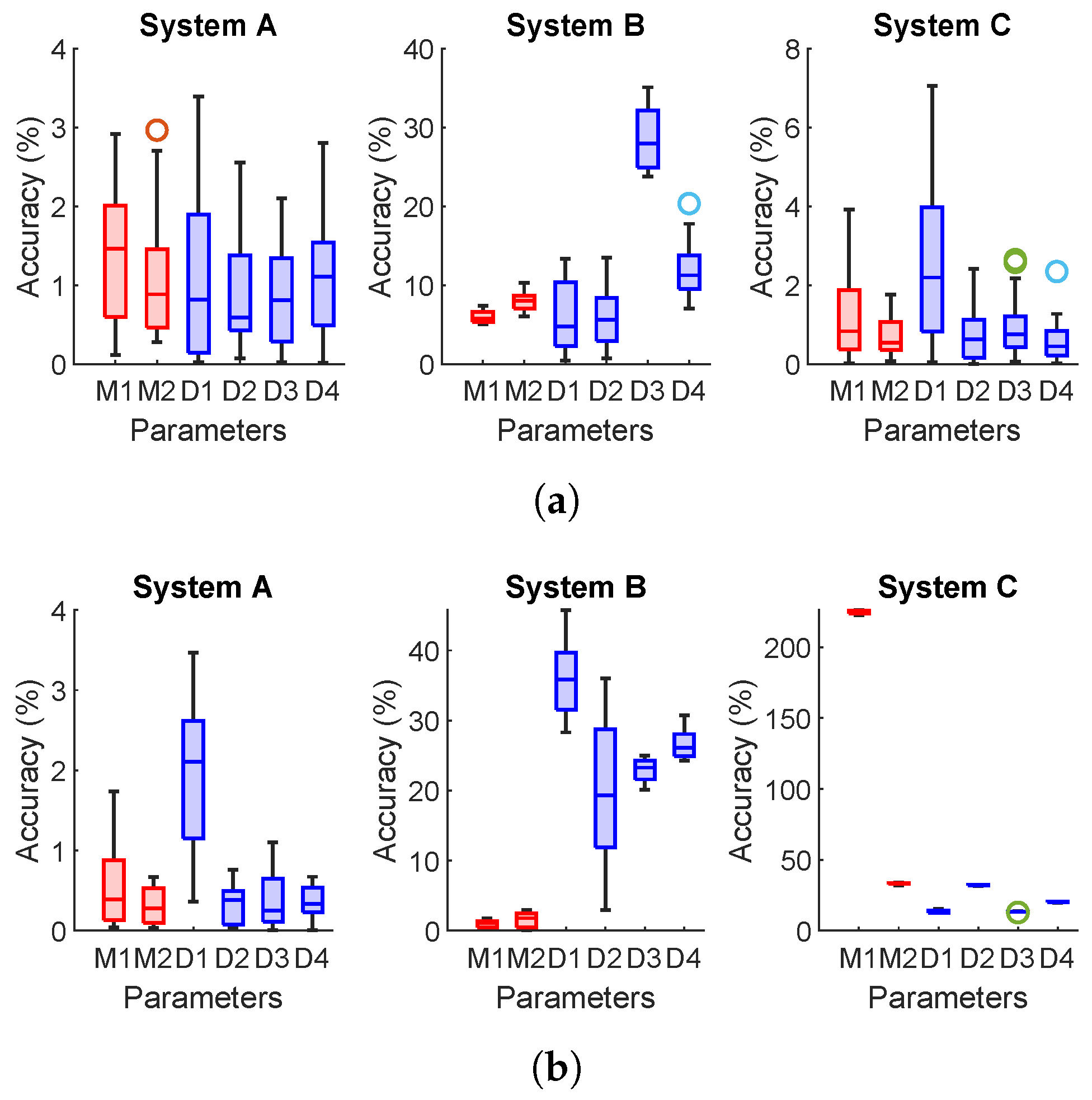
5. Simulation Results
5.1. Dependence on the Observation Time Window
5.2. Simulations with Larger Bus Systems
5.3. Simulations with Unknown System Model
5.4. Simulations with Non-Gaussian Noise
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A. Simulation Parameters
Appendix A.1. 4-Bus System
Appendix A.2. IEEE 6-Bus System
Appendix A.3. IEEE 39-Bus System
References
- Kosterev, D.; Taylor, C.; Mittelstadt, W. Model validation for the August 10, 1996 WSCC system outage. IEEE Trans. Power Syst. 1999, 14, 967–979. [Google Scholar] [CrossRef] [Green Version]
- Schweppe, F.C.; Wildes, J. Power System Static-State Estimation, Part I: Exact Model. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 120–125. [Google Scholar] [CrossRef] [Green Version]
- Schweppe, F.C.; Rom, D.B. Power System Static-State Estimation, Part II: Approximate Model. IEEE Trans. Power Appar. Syst. 1970, PAS-89, 125–130. [Google Scholar] [CrossRef]
- Li, X.; Poor, H.V.; Scaglione, A. Blind topology identification for power systems. In Proceedings of the IEEE International Conference on SmartGrid Communications (SmartGridComm), Vancouver, BC, Canada, 21–24 October 2013; pp. 91–96. [Google Scholar]
- Grotas, S.; Yakoby, Y.; Gera, I.; Routtenberg, T. Power Systems Topology and State Estimation by Graph Blind Source Separation. IEEE Trans. Signal Process. 2019, 67, 2036–2051. [Google Scholar] [CrossRef] [Green Version]
- Weng, Y.; Liao, Y.; Rajagopal, R. Distributed Energy Resources Topology Identification via Graphical Modeling. IEEE Trans. Power Syst. 2017, 32, 2682–2694. [Google Scholar] [CrossRef]
- Deka, D.; Backhaus, S.; Chertkov, M. Structure Learning in Power Distribution Networks. IEEE Trans. Control Netw. Syst. 2018, 5, 1061–1074. [Google Scholar] [CrossRef]
- Tate, J.E.; Overbye, T.J. Line Outage Detection Using Phasor Angle Measurements. IEEE Trans. Power Syst. 2008, 23, 1644–1652. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J.; Poor, H.V. A Learning-to-Infer Method for Real-Time Power Grid Multi-Line Outage Identification. IEEE Trans. Smart Grid 2020, 11, 555–564. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.; Chin, W. Blind False Data Injection Attack Using PCA Approximation Method in Smart Grid. IEEE Trans. Smart Grid 2015, 6, 1219–1226. [Google Scholar] [CrossRef]
- Lakshminarayana, S.; Kammoun, A.; Debbah, M.; Poor, H.V. Data-Driven False Data Injection Attacks Against Power Grids: A Random Matrix Approach. IEEE Trans. Smart Grid 2021, 12, 635–646. [Google Scholar] [CrossRef]
- Ariff, M.A.M.; Pal, B.C.; Singh, A.K. Estimating Dynamic Model Parameters for Adaptive Protection and Control in Power System. IEEE Trans. Power Syst. 2015, 30, 829–839. [Google Scholar] [CrossRef] [Green Version]
- Valverde, G.; Kyriakides, E.; Heydt, G.T.; Terzija, V. Nonlinear Estimation of Synchronous Machine Parameters Using Operating Data. IEEE Trans. Energy Convers. 2011, 26, 831–839. [Google Scholar] [CrossRef]
- Rouhani, A.; Abur, A. Constrained Iterated Unscented Kalman Filter for Dynamic State and Parameter Estimation. IEEE Trans. Power Syst. 2018, 33, 2404–2414. [Google Scholar] [CrossRef]
- Huang, R.; Diao, R.; Li, Y.; Sanchez-Gasca, J.; Huang, Z.; Thomas, B.; Etingov, P.; Kincic, S.; Wang, S.; Fan, R.; et al. Calibrating Parameters of Power System Stability Models Using Advanced Ensemble Kalman Filter. IEEE Trans. Power Syst. 2018, 33, 2895–2905. [Google Scholar] [CrossRef]
- Stiasny, J.; Misyris, G.S.; Chatzivasileiadis, S. Physics-Informed Neural Networks for Non-Linear System Identification Applied to Power System Dynamics. 2020. Available online: https://arxiv.org/abs/2004.04026 (accessed on 28 December 2021).
- Zhao, J.; Gómez-Expósito, A.; Netto, M.; Mili, L.; Abur, A.; Terzija, V.; Kamwa, I.; Pal, B.; Singh, A.K.; Qi, J.; et al. Power System Dynamic State Estimation: Motivations, Definitions, Methodologies, and Future Work. IEEE Trans. Power Syst. 2019, 34, 3188–3198. [Google Scholar] [CrossRef]
- Qi, J.; Sun, K.; Kang, W. Optimal PMU Placement for Power System Dynamic State Estimation by Using Empirical Observability Gramian. IEEE Trans. Power Syst. 2015, 30, 2041–2054. [Google Scholar] [CrossRef] [Green Version]
- Rouhani, A.; Abur, A. Observability Analysis for Dynamic State Estimation of Synchronous Machines. IEEE Trans. Power Syst. 2017, 32, 3168–3175. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [Green Version]
- IEEE/IEC International Standard—Measuring Relays and Protection Equipment—Part 118-1: Synchrophasor for Power Systems—Measurements; IEC/IEEE 60255-118-1:2018; IEEE: Manhattan, NY, USA, 2018; pp. 1–78.
- Kundur, P.; Balu, N.; Lauby, M. Power System Stability and Control; McGraw-Hill Education: New York, NY, USA, 1994. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G. Physics-Informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Likas, A.; Fotiadis, D.I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef] [Green Version]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Netto, M.; Susuki, Y.; Krishnan, V.; Zhang, Y. On Analytical Construction of Observable Functions in Extended Dynamic Mode Decomposition for Nonlinear Estimation and Prediction. IEEE Control Syst. Lett. 2021, 5, 1868–1873. [Google Scholar] [CrossRef]
- Stiasny, J.; Misyris, G.S.; Chatzivasileiadis, S. 2020. Available online: https://github.com/jbesty/PINN_system_identification (accessed on 28 December 2021).
- Brown, M.; Biswal, M.; Brahma, S.; Ranade, S.J.; Cao, H. Characterizing and quantifying noise in PMU data. In Proceedings of the IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, J.; Huang, Z.; Diao, R. Assessing Gaussian Assumption of PMU Measurement Error Using Field Data. IEEE Trans. Power Deliv. 2018, 33, 3233–3236. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Tu, J.H.; Kutz, J.N. Compressed sensing and dynamic mode decomposition. J. Comput. Dyn. 2015, 2, 165–191. [Google Scholar] [CrossRef]
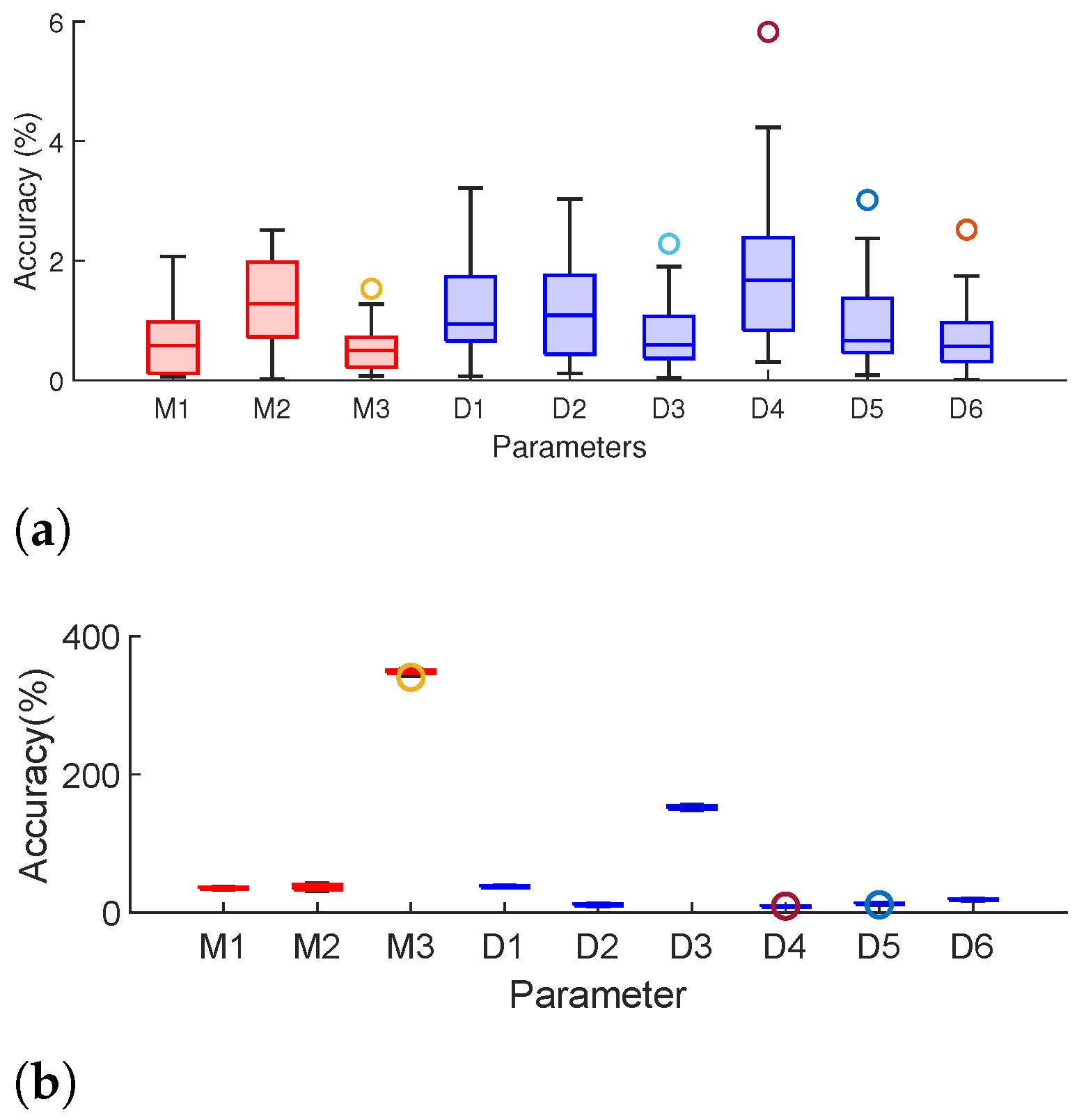
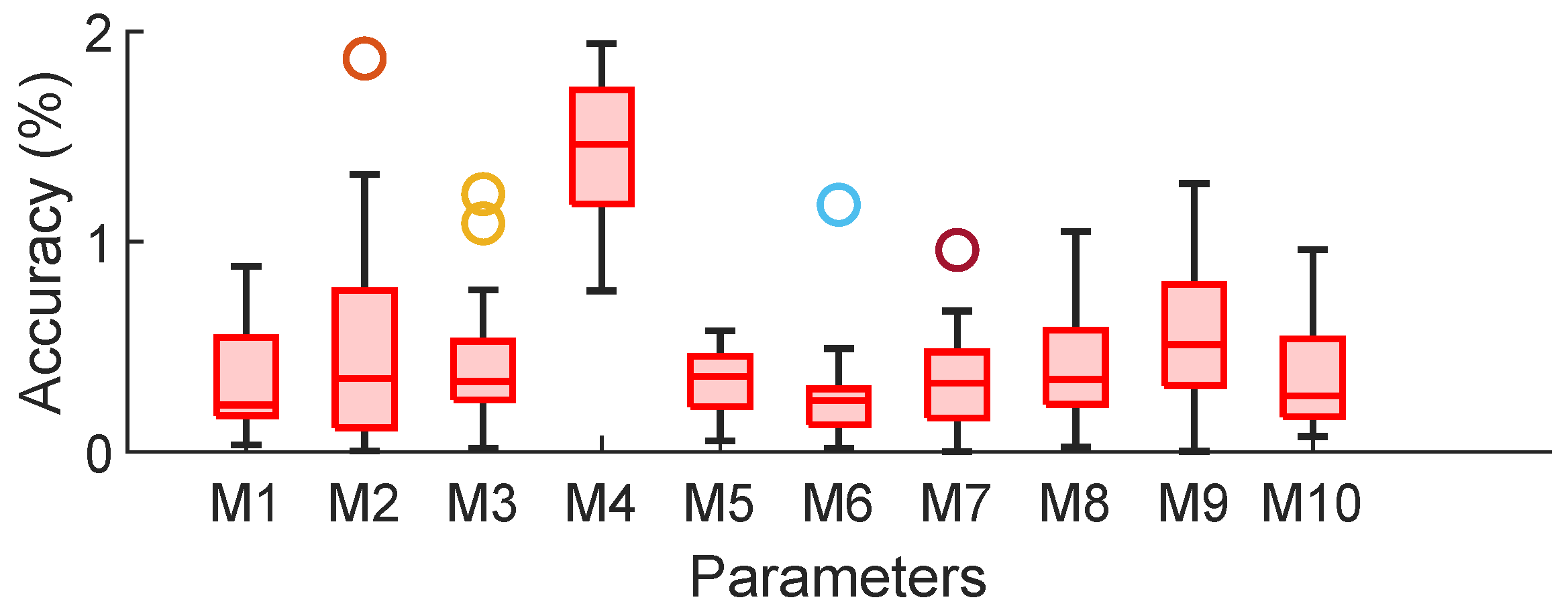
| Algorithm (Number of Buses) | Execution Time (s) |
|---|---|
| PINN (4 bus) | 90 s (from [16]) |
| SINDy (4 bus) | ms |
| SINDy (IEEE 6-bus) | ms |
| SINDy (IEEE 39-bus) | ms |
| Time Window (s) | ||
|---|---|---|
| s | ||
| 1 s | ||
| 2 s | ||
| 5 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lakshminarayana, S.; Sthapit, S.; Maple, C. Application of Physics-Informed Machine Learning Techniques for Power Grid Parameter Estimation. Sustainability 2022, 14, 2051. https://doi.org/10.3390/su14042051
Lakshminarayana S, Sthapit S, Maple C. Application of Physics-Informed Machine Learning Techniques for Power Grid Parameter Estimation. Sustainability. 2022; 14(4):2051. https://doi.org/10.3390/su14042051
Chicago/Turabian StyleLakshminarayana, Subhash, Saurav Sthapit, and Carsten Maple. 2022. "Application of Physics-Informed Machine Learning Techniques for Power Grid Parameter Estimation" Sustainability 14, no. 4: 2051. https://doi.org/10.3390/su14042051
APA StyleLakshminarayana, S., Sthapit, S., & Maple, C. (2022). Application of Physics-Informed Machine Learning Techniques for Power Grid Parameter Estimation. Sustainability, 14(4), 2051. https://doi.org/10.3390/su14042051








