An EOQ Model with Carbon Emissions and Inflation for Deteriorating Imperfect Quality Items under Learning Effect
Abstract
:1. Introduction
2. Literature Review
2.1. Literature Review with Regard to Carbon Emissions and Inspection
2.2. Literature Review with Regard to Defective Items, Inflation and Inspection
2.3. Literature Review with Regard to Defective Items, Inspection, and Learning Effect
2.4. Research Gap
2.5. Contribution Concern with Proposed Model
3. Assumptions
- (i)
- CO2 is directly emitted from electricity and fuels consumption in product storage Daryanto et al. [14].
- (ii)
- Waste due to the deterioration process which is dangerous for the climate is properly arranged by investing in the waste management process.
- (iii)
- The continuity of replacement is allowed.
- (iv)
- Shortages and lead time are not involved in this model.
- (v)
- The screening rate is greater than the demand rate [8].
- (vi)
- The time horizon plane has been taken as finite.
- (vii)
- Lots have some defective items as per consideration by [7].
- (viii)
- Defective quality items follow the S-shaped learning curve suggested by Jaber and Goyal [25].
- (ix)
- Imperfect items are sold at rebate prices.
- (x)
- Lots have a constant deterioration rate in the whole cycle length.
- (xi)
- The inflation rate is constant.
- (xii)
- A carbon tax is allowed.
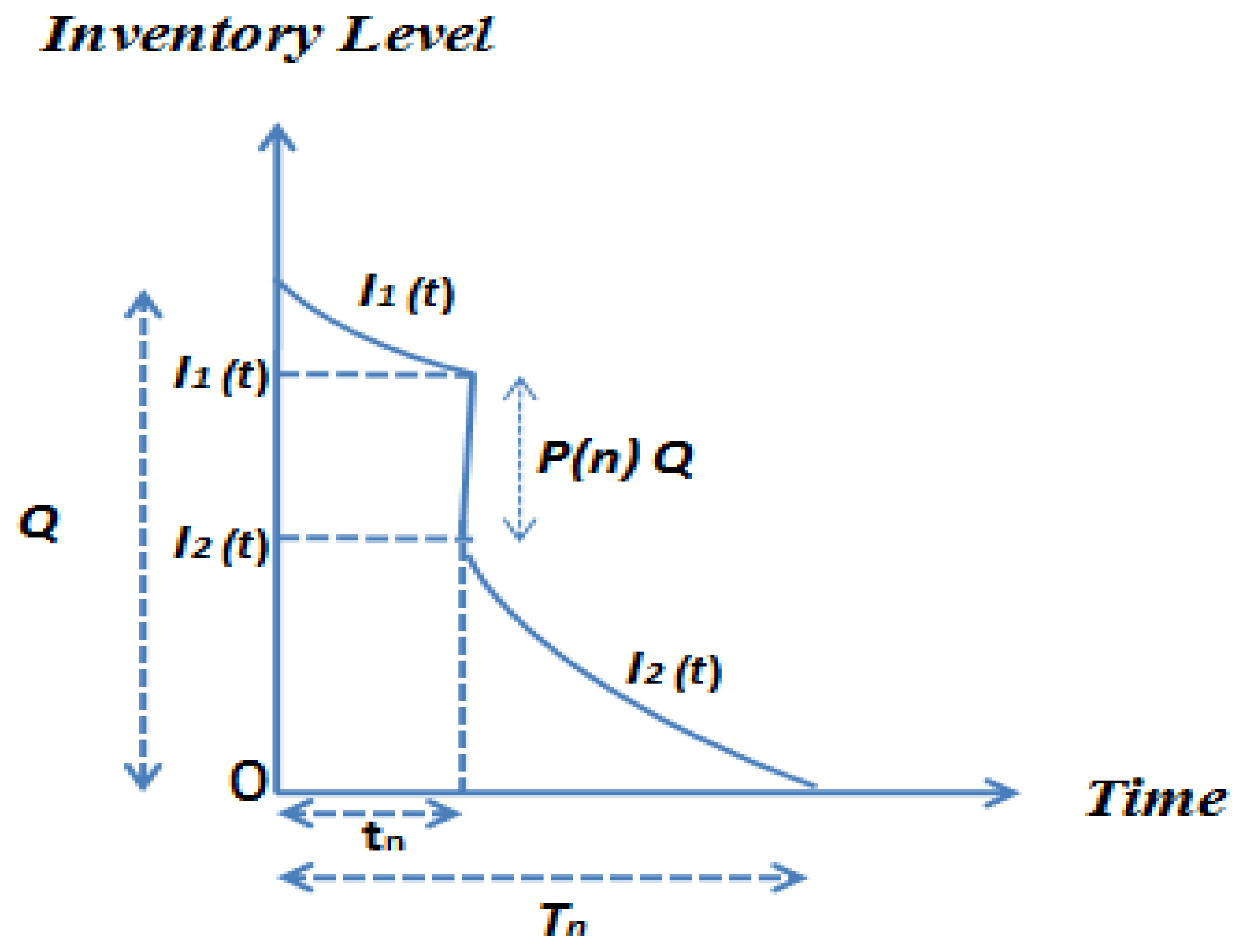
4. Mathematical Model
5. Solution Method
Numerical Example
6. Sensitivity Analysis
6.1. Observations and Managerial Insights
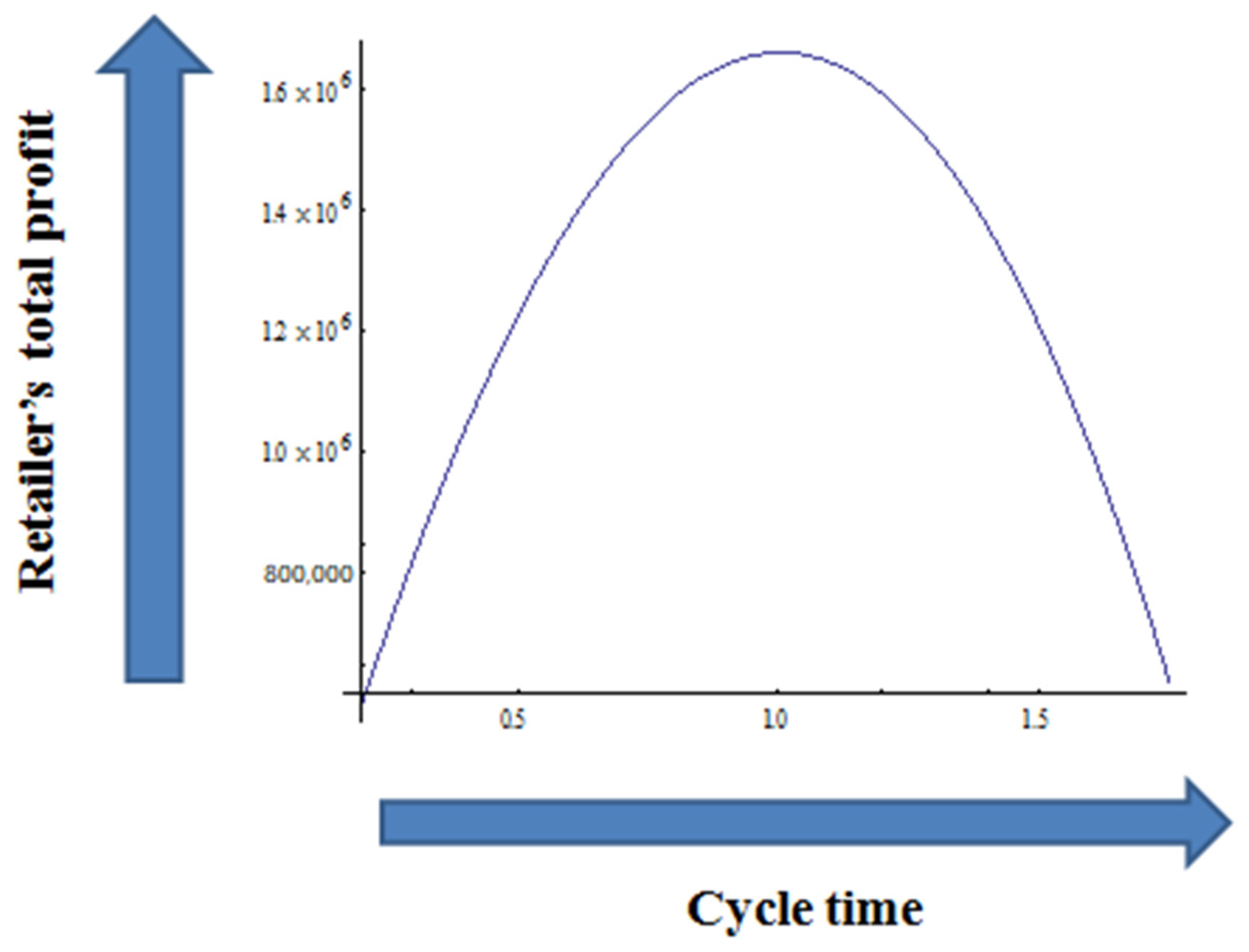
- From Table 4, it is seen that if the number of shipments and learning rate increase from top to bottom, then cycle length, lot size, and retailer’s total profit rapidly increase up to the 10th shipment level with different learning rates. After the 10th shipment, cycle length, lot size, and retailer’s total profit increase very slowly and approach the maturity phase up to the 16th, and this phase is called the learning phase. Finally, order size, cycle length, and buyer’s total profit remain constant on 17th shipments and reach maturity phase. It means that retailers obtain the optimal length of cycle, maximum lot size, and maximum profit when the shipment is the 17th one and the learning rate is 1.4. Hence, the retailer obtains more profit due to decreased carbon emissions. It suggests that retailers should be aware of new strategies in the form of learning to obtain more profit.
- From Table 5, we analyzed that if the deterioration rate increases, then lot size, length of cycle, and buyer’s profit reduce due to deterioration. Deterioration affects the cycle time and order quantity, as well as buyer’s total profit. It reflects that the retailer should be aware during the transaction of business when products are deteriorating items. When this order quantity decreases, then carbon emissions increase due to deterioration. Hence, the retailer obtains less profit due to increased carbon emissions.
- From Table 6, we studied that if the rate of inflation increases, then the length of cycle, lot size, and retailer’s profit decrease. Inflationary situations affect the lot size, cycle length, and buyer’s total profit. It reflects that retailers should be aware during the transaction of business when products are deteriorating items. When this order quantity decreases, then the carbon emissions increase. Hence, retailers obtain less profit due to decreases in cycle time and order quantity and increase in carbon emission.
6.2. Discussion with Observations
7. Concluding Remarks and Future Extension
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notations
| Order quantity has been taken as decision variable (units). | |
| Rate of demand (units/year). | |
| Holding cost (USD/unit). | |
| The imposed unit tax for emissions (USD/ton). | |
| The carbon emission factor for fuels (tones/gallon). | |
| The carbon emission factor for electricity (tones/kWh). | |
| Unit purchasing cost (USD/unit). | |
| Unit selling cost for perfect items (USD/units). | |
| Percentage defective items are presents in . | |
| Imperfect quality items are following the S-shaped learning curve. | |
| Unit selling price for imperfect items, (USD/unit). | |
| Screening cost (USD/units). | |
| Deterioration rate (per year). | |
| The variable amount of electricity utilized to store one unit of goods per time unit (KWh/year). | |
| Holding cost due carbon emission from variable electricity (USD/unit/year). | |
| Holding cost due carbon emission from generator fuels (USD/unit/year). | |
| Deterioration cost (USD/unit). | |
| Cost of waste management due to deterioration (USD/unit). | |
| Screening rate, (USD/unit/year). | |
| Inspection time (year). | |
| Cycle length (year). | |
| Inventory at . | |
| Inventory at . | |
| Total sales revenue (USD). | |
| Total buyer’s cost (USD). | |
| Total buyer’s whole profit (USD). | |
| Discount rate at inflation rate. | |
| , Inflation due to discount rate. |
Appendix A
References
- Whitin, T.M. Theory of Inventory Management; Princeton University Press: Princeton, NJ, USA, 1957; pp. 62–72. [Google Scholar]
- Ghare, P.M.; Schrader, G.P. A model for exponentially decaying inventory models. J. Ind. Eng. 1963, 14, 238–243. [Google Scholar]
- Gupta, S.; Tirpak, D.A.; Burger, N.; Gupta, J.; Höhne, N.; Boncheva, A.I.; Kanoan, G.M. 13.2.1.2 Taxes and charges. In Policies, Instruments and Co-operative Arrangements; Cambridge University Press: Cambridge, UK, 2007; pp. 755–756. Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/ar4-wg3-chapter13-2.pdf (accessed on 15 November 2021).
- Hammami, R.; Nouira, I.; Frein, Y. Effects of customers’ environmental awareness and environmental regulations on the emissionintensity and price of a product. Decis. Sci. 2018, 49, 1116–1155. [Google Scholar] [CrossRef]
- Buzacott, J.A. Economic order quantities with inflation. J. Oper. Res. Soc. 1875, 26, 553–558. [Google Scholar] [CrossRef]
- Misra, R.B. A study of inflationary effects on inventory systems. Logist. Spectr. 1975, 9, 51–55. [Google Scholar]
- Salameh, M.K.; Jaber, M.Y. Economic production quantity model for items with imperfect quality. Int. J. Prod. Econ. 2000, 64, 59–64. [Google Scholar] [CrossRef]
- Jaggi, C.K.; Goel, S.K.; Mittal, M. Credit financing in economic ordering policies for defective items with allowable shortages. Appl. Math. Comput. 2013, 219, 5268–5282. [Google Scholar] [CrossRef]
- Wright, T.P. Factors affecting the cost of airplanes. J. Aeronaut. Sci. 1936, 3, 122–128. [Google Scholar] [CrossRef]
- Xia, L.; He, L. Game theoretic analysis of carbon emission reduction and sales promotion in dyadic supply chain in presence of consumers’ low-carbon awareness. Discret. Dyn. Nat. Soc. 2014. [Google Scholar] [CrossRef] [Green Version]
- Absi, N.; Dauzère-Pérès, S.; Kedad-Sidhoum, S.; Penz, B.; Rapine, C. Lot sizing with carbon emission constraints. Eur. J. Oper. Res. 2013, 227, 55–61. [Google Scholar] [CrossRef]
- Hu, H.; Zhou, W. A decision support system for joint emission reduction investment and pricing decisions with carbon emission trade. Int. J. Multimed. Ubiquitous Eng. 2014, 9, 371–380. [Google Scholar] [CrossRef]
- Datta, T.K.; Pal, A.K. Effects of inflation and time-value of money on an inventory model with linear time-dependent demand rate and shortages. Eur. J. Oper. Res. 1991, 52, 326–333. [Google Scholar] [CrossRef]
- Daryanto, Y.; Wee, H.M.; Astanti, R.D. Three-echelon supply chain model considering carbon emission and item deterioration. Transp. Res. Part E Logist. Transp. Rev. 2019, 122, 368–383. [Google Scholar] [CrossRef]
- Lee, J.Y. Investing in carbon emission reduction in the EOQ model. J. Oper. Res. Soc. 2020, 71, 1289–1300. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Soleymanfar, V.R.; Govindan, K. Sustainable economic production quantity models for inventory systems with shortage. J. Clean. Prod. 2018, 174, 1011–1020. [Google Scholar] [CrossRef]
- Hovelaque, V.; Bironneau, L. The carbon-constrained EOQ model with carbon emission dependent demand. Int. J. Prod. Econ. 2015, 164, 285–291. [Google Scholar] [CrossRef]
- Battini, D.; Persona, A.; Sgarbossa, F. A sustainable EOQ model: Theoretical formulation and applications. Int. J. Prod. Econ. 2014, 149, 145–153. [Google Scholar] [CrossRef]
- Chen, X.; Benjaafar, S.; Elomri, A. The carbon-constrained EOQ. Oper. Res. Lett. 2013, 41, 172–179. [Google Scholar] [CrossRef]
- Sarker, B.R.; Pan, H. Effects of inflation and the time value of money on order quantity and allowable shortage. Int. J. Prod. Econ. 1994, 34, 65–72. [Google Scholar] [CrossRef]
- Hariga, M. An EOQ model for deteriorating items with shortages and time-varying demand. J. Oper. Res. Soc. 1995, 46, 398–404. [Google Scholar] [CrossRef]
- Hariga, M.A.; Ben-Daya, M. Optimal time varying lot-sizing models under inflationary conditions. Eur. J. Oper. Res. 1996, 89, 313–325. [Google Scholar] [CrossRef]
- Jaggi, C.K.; Khanna, A.; Mittal, M. Credit financing for deteriorating imperfect-quality items under inflationary conditions. Int. J. Serv. Oper. Inform. 2011, 6, 292–309. [Google Scholar] [CrossRef]
- Manna, S.K.; Chaudhuri, K.S. An EOQ model for a deteriorating item with non-linear demand under inflation and a trade credit policy. Yugosl. J. Oper. Res. 2005, 15, 209–220. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Goyal, S.K.; Imran, M. Economic production quantity model for items with imperfect quality subject to learning effects. Int. J. Prod. Econ. 2008, 115, 143–150. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Bonney, M. Lot sizing with learning and forgetting in set-ups and in product quality. Int. J. Prod. Econ. 2003, 8, 95–111. [Google Scholar] [CrossRef]
- Khan, M.; Jaber, M.Y.; Wahab, M.I.M. Economic order quantity model for items with imperfect quality with learning in inspection. Int. J. Prod. Econ. 2010, 124, 87–96. [Google Scholar] [CrossRef]
- Konstantaras, I.; Skouri, K.; Jaber, M.Y. Inventory models for imperfect quality items with shortages and learning in inspection. Appl. Math. Model. 2012, 36, 5334–5343. [Google Scholar] [CrossRef]
- Tiwari, S.; Jaggi, C.K.; Bhunia, A.K.; Shaikh, A.A.; Goh, M. Two-warehouse inventory model for non-instantaneous deteriorating items with stock-dependent demand and inflation using particle swarm optimization. Ann. Oper. Res. 2017, 254, 401–423. [Google Scholar] [CrossRef]
- Agarwal, A.; Sangal, I.; Singh, S.R. Optimal policy for non-Instantaneous decaying inventory model with learning effect and partial shortages. Int. J. Comput. Appl. 2017, 161, 13–18. [Google Scholar] [CrossRef]
- Nobil, A.H.; Afshar Sedigh, A.H.; Tiwari, S.; Wee, H.M. An imperfect multi-item single machine production system with shortage, rework, and scrapping considering inspection, dissimilar deficiency levels and non-zero setup times. Sci. Iran. 2019, 26, 557–570. [Google Scholar]
- Jayaswal, M.; Sangal, I.; Mittal, M. Learning effects on stock policies with imperfect quality and deteriorating items under trade credit. Amity Int. Conf. Artif. Intell. (AICAI) 2019, 499–506. [Google Scholar] [CrossRef]
- Jayaswal, M.K.; Mittal, M.; Sangal, I. Ordering policies for deteriorating imperfect quality items with trade-credit financing under learning effect. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 112–125. [Google Scholar] [CrossRef]
- Jayaswal, M.K.; Sangal, I.; Mittal, M.; Tripathi, J. Fuzzy based EOQ Model with Credit Financing and Backorders under Human Learning. Int. J. Fuzzy Syst. Appl. 2021, 10, 14–36. [Google Scholar] [CrossRef]
- Yadav, R.; Pareek, S.; Mittal, M. Supply chain models with imperfect quality items when end demand is sensitive to price and marketing expenditure. RAIRO-Oper. Res. 2018, 52, 725–742. [Google Scholar] [CrossRef] [Green Version]
- Kumar, V.; Sarkar, B.; Sharma, A.N.; Mittal, M. New product launching with pricing, free replacement, rework, and warranty policies via genetic algorithmic approach. Int. J. Compu. Intell. Syst. 2019, 12, 519–529. [Google Scholar] [CrossRef] [Green Version]
- Jaggi, C.K.; Khanna, A. Supply chain model for deteriorating items with stock-dependent consumption rate and shortages under inflation and permissible delay in payment. Int. J. Math. Oper. Res. 2010, 2, 491–514. [Google Scholar] [CrossRef]
- Jaggi, C.K.; Tiwari, S.; Goel, S.K. Credit financing in economic ordering policies for non-instantaneous deteriorating items with price dependent demand and two storage facilities. Ann. Oper. Res. 2017, 248, 253–280. [Google Scholar] [CrossRef]
- Patro, R.; Acharya, M.; Nayak, M.M.; Patnaik, S. A fuzzy EOQ model for deteriorating items with imperfect quality using proportionate discount under learning effects. Int. J. Manag. Decis. Mak. 2018, 17, 171–198. [Google Scholar] [CrossRef]
- Liao, H.C.; Tsai, C.H.; Su, C.T. An inventory model with deteriorating items under inflation when a delay in payment is permissible. Int. J. Prod. Econ. 2000, 63, 207–214. [Google Scholar] [CrossRef]
- Daryanto, Y.; Christata, B. Optimal order quantity considering carbon emission costs, defective items, and partial backorder. Uncertain Supply Chain. Manag. 2021, 9, 307–316. [Google Scholar] [CrossRef]
- Barman, H.; Pervin, M.; Roy, S.K.; Weber, G.W. Back-ordered inventory model with inflation in a cloudy-fuzzy environment. J. Ind. Manag. Optim. 2021, 17, 1913. [Google Scholar] [CrossRef] [Green Version]
- Jayaswal, M.K.; Mittal, M.; Sangal, I.; Yadav, R. EPQ model with learning effect for imperfect quality items under trade-credit financing. Yugosl. J. Oper. Res. 2021, 31, 235–247. [Google Scholar] [CrossRef]
- Mashud, A.H.M.; Roy, D.; Daryanto, Y.; Chakrabortty, R.K.; Tseng, M.L. A sustainable inventory model with controllable carbon emissions, deterioration and advance payments. J. Clean. Prod. 2021, 296, 126608. [Google Scholar] [CrossRef]
- Jayaswal, M.; Sangal, I.; Mittal, M.; Malik, S. Effects of learning on retailer ordering policy for imperfect quality items with trade credit financing. Uncertain Supply Chain. Manag. 2019, 7, 49–62. [Google Scholar] [CrossRef]
- Datta, T.K. Effect of green technology investment on a production-inventory system with carbon tax. Adv. Oper. Res. 2017, 2017, 4834839. [Google Scholar] [CrossRef]
| Author(s) | Impact of Learning | Inspection | Carbon Emissions | Deterioration | Defective Items | Inflation |
|---|---|---|---|---|---|---|
| Wright [9] | ✔ | |||||
| Salameh and Jaber [7] | ✔ | ✔ | ||||
| Jaber et al. [25] | ✔ | ✔ | ✔ | |||
| Khan et al. [27] | ✔ | ✔ | ✔ | |||
| Jaggi and Khanna [37] | ✔ | ✔ | ✔ | ✔ | ||
| Jaggi et al. [23] | ✔ | ✔ | ✔ | ✔ | ||
| Jaggi et al. [8] | ✔ | ✔ | ||||
| Jaggi et al. [38] | ✔ | ✔ | ✔ | ✔ | ||
| Patro et al. [39] | ✔ | ✔ | ✔ | ✔ | ||
| Daryanto et al. [14] | ✔ | ✔ | ✔ | ✔ | ||
| Liao et al. [40] | ✔ | ✔ | ||||
| Daryanto and Christata [41] | ✔ | ✔ | ✔ | |||
| Barman et al. [42] | ✔ | ✔ | ||||
| Jayaswal et al. [32] | ✔ | ✔ | ||||
| Jayaswal et al. [43] | ✔ | ✔ | ✔ | ✔ | ||
| Mashud et al. [44] | ✔ | ✔ | ✔ | |||
| This paper | ✔ | ✔ | ✔ | ✔ | ✔ |
| Model with No Learning Effect | Model with Learning Effect | ||||
|---|---|---|---|---|---|
| Cycle Length (Year) | Lot Size (Units) | Buyer’s Total Profit (Dollars) | Cycle Length (Year) | Lot Size (Units) | Buyer’s Total Profit (Dollars) |
| 0.9032 | 46,694 | 1,472,210 | 1.0049 | 48,225 | 1,662,440 |
| Number of Shipment | Rate of Learning | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Cycle Time | Lot Size | Retailer’s Profit | Cycle Time | Lot Size | Retailer’s Profit | Cycle Length | Lot Size | Retailer’s Profit | |
| 1 | 0.9034 | 46,669 | 1,472,500 | 0.9034 | 46,697 | 1,472,600 | 0.9035 | 46,698 | 1,472,720 |
| 2 | 0.9038 | 46,706 | 1,473,230 | 0.9040 | 46,709 | 1,473,750 | 0.9044 | 46,713 | 1,474,510 |
| 3 | 0.9047 | 46,720 | 1,475,010 | 0.9059 | 46,742 | 1,477,140 | 0.9078 | 46,755 | 1,480,720 |
| 4 | 0.9087 | 46,850 | 1,482,380 | 0.9109 | 46,824 | 1,486,610 | 0.9181 | 46,924 | 1,500,070 |
| 5 | 0.9124 | 46,852 | 1,489,280 | 0.9234 | 47,031 | 1,510,020 | 0.9422 | 47,331 | 1,545,150 |
| 6 | 0.9234 | 47,031 | 1,510,020 | 0.9467 | 47,400 | 1,553,570 | 0.9736 | 47,799 | 1,603,860 |
| 7 | 0.9422 | 47,331 | 1,545,150 | 0.9583 | 47,575 | 1,575,280 | 0.9937 | 48,075 | 1,641,570 |
| 8 | 0.9652 | 47,680 | 1,588,050 | 0.9918 | 48,052 | 1,637,910 | 1.0015 | 48,182 | 1,656,160 |
| 9 | 0.9841 | 47,954 | 1,623,590 | 1.0014 | 48,163 | 1,653,510 | 1.0036 | 48,195 | 1,660,660 |
| 10 | 0.9954 | 48,098 | 1,644,740 | 1.0032 | 48,204 | 1,659,370 | 1.0046 | 48,222 | 1,661,940 |
| 11 | 1.0091 | 48,586 | 1,654,940 | 1.0043 | 48,218 | 1,661,410 | 1.0048 | 48,222 | 1,662,300 |
| 12 | 1.0032 | 48,204 | 1,659,370 | 1.0047 | 48,223 | 1,662,100 | 1.0048 | 48,225 | 1,662,400 |
| 13 | 1.0042 | 48,217 | 1,661,200 | 1.0048 | 48,225 | 1,662,330 | 1.0049 | 48,225 | 1,662,430 |
| 14 | 1.0046 | 48,222 | 1,661,940 | 1.0048 | 48,223 | 1,662,400 | 1.0049 | 48,225 | 1,662,440 |
| 15 | 1.0048 | 48,224 | 1,662,240 | 1.0049 | 48,225 | 1,662,430 | 1.0049 | 48,225 | 1,662,440 |
| 16 | 1.0048 | 48,224 | 1,662,360 | 1.0049 | 48,225 | 1,662,420 | 1.0049 | 48,225 | 1,662,440 |
| 17 | 1.00491 | 48,225 | 1,662,440 | 1.00491 | 48,225 | 1,662,440 | 1.00491 | 48,225 | 1,662,440 |
| 18 | 1.00491 | 48,225 | 1,662,440 | 1.00491 | 48,225 | 1,662,440 | 1.00491 | 48,225 | 1,662,440 |
| Deterioration Rate | Cycle Length (Year) | Lot Size (Units) | Buyer’s Total Profit (USD) |
|---|---|---|---|
| 0.10 | 1.00491 | 48,225 | 1,662,440 |
| 0.15 | 0.6998 | 33,653 | 1,148,080 |
| 0.20 | 0.5365 | 25,828 | 876,186 |
| 0.25 | 0.4349 | 20,951 | 708,152 |
| Inflation Rate | Cycle Length (Year) | Lot Size (Units) | Buyer’s Total Profit (USD) |
|---|---|---|---|
| 0.02 | 1.0349 | 49,735 | 1,710,570 |
| 0.04 | 1.0195 | 48,959 | 1,685,940 |
| 0.06 | 1.0049 | 48,225 | 1,662,440 |
| 0.08 | 0.9910 | 47,531 | 1,639,990 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alamri, O.A.; Jayaswal, M.K.; Khan, F.A.; Mittal, M. An EOQ Model with Carbon Emissions and Inflation for Deteriorating Imperfect Quality Items under Learning Effect. Sustainability 2022, 14, 1365. https://doi.org/10.3390/su14031365
Alamri OA, Jayaswal MK, Khan FA, Mittal M. An EOQ Model with Carbon Emissions and Inflation for Deteriorating Imperfect Quality Items under Learning Effect. Sustainability. 2022; 14(3):1365. https://doi.org/10.3390/su14031365
Chicago/Turabian StyleAlamri, Osama Abdulaziz, Mahesh Kumar Jayaswal, Faizan Ahmad Khan, and Mandeep Mittal. 2022. "An EOQ Model with Carbon Emissions and Inflation for Deteriorating Imperfect Quality Items under Learning Effect" Sustainability 14, no. 3: 1365. https://doi.org/10.3390/su14031365
APA StyleAlamri, O. A., Jayaswal, M. K., Khan, F. A., & Mittal, M. (2022). An EOQ Model with Carbon Emissions and Inflation for Deteriorating Imperfect Quality Items under Learning Effect. Sustainability, 14(3), 1365. https://doi.org/10.3390/su14031365






