Assessment of the Uncertainty Associated with Statistical Modeling of Precipitation Extremes for Hydrologic Engineering Applications in Amman, Jordan
Abstract
1. Introduction
2. Data and Methodology
2.1. Study Site and Data Sets
2.2. The Modified Mann–Kendall Trend Test
2.3. Extreme Precipitation Probability Distributions
2.4. L-Moment Method for Parameter Estimation
2.5. Kolmogorov–Smirnov (KS) Goodness-of-Fit Test
2.6. Bootstrap Approach
- (1)
- For each selected weather station, 10,000 bootstrap samples of sizes n were extracted from the AM extreme precipitation data series.
- (2)
- For each bootstrap sample, the extreme precipitation quantile (XT) at a chosen return period of T years was extracted using the best-fit probability distribution to represent that station using the L-moment method for parameters estimation.
- (3)
- The 10,000 XT values for a chosen return period of T years (obtained in step (2)) in ascending order were ranked.
- (4)
- The two-sided confidence intervals for the ranked XT at α = 5% (i.e., 95% confidence interval) were obtained. For the 10,000 resampling times used in this study, the upper and lower values of the two-sided confidence interval for XT correspond to the 9750th (i.e., 97.5th percentile) and 250th (i.e., 2.5th percentile) of the ranked XT values.
- (5)
- The bootstrap sampling distributions for the extreme precipitation quantile (XT) from 10,000 XT values were obtained for a chosen return period of T years (obtained in step (2)).
- (6)
- The expected value of the sampling distribution of the extreme precipitation quantile (XT) (obtained in step (5)) was obtained.
- (7)
- Steps (2) to (6) were repeated for each of the selected weather stations for a different return period of T years.
3. Results and Discussion
3.1. Trend Analysis of Extreme Precipitation
3.2. The Best-Fit Probability Distribution for Extreme Precipitation
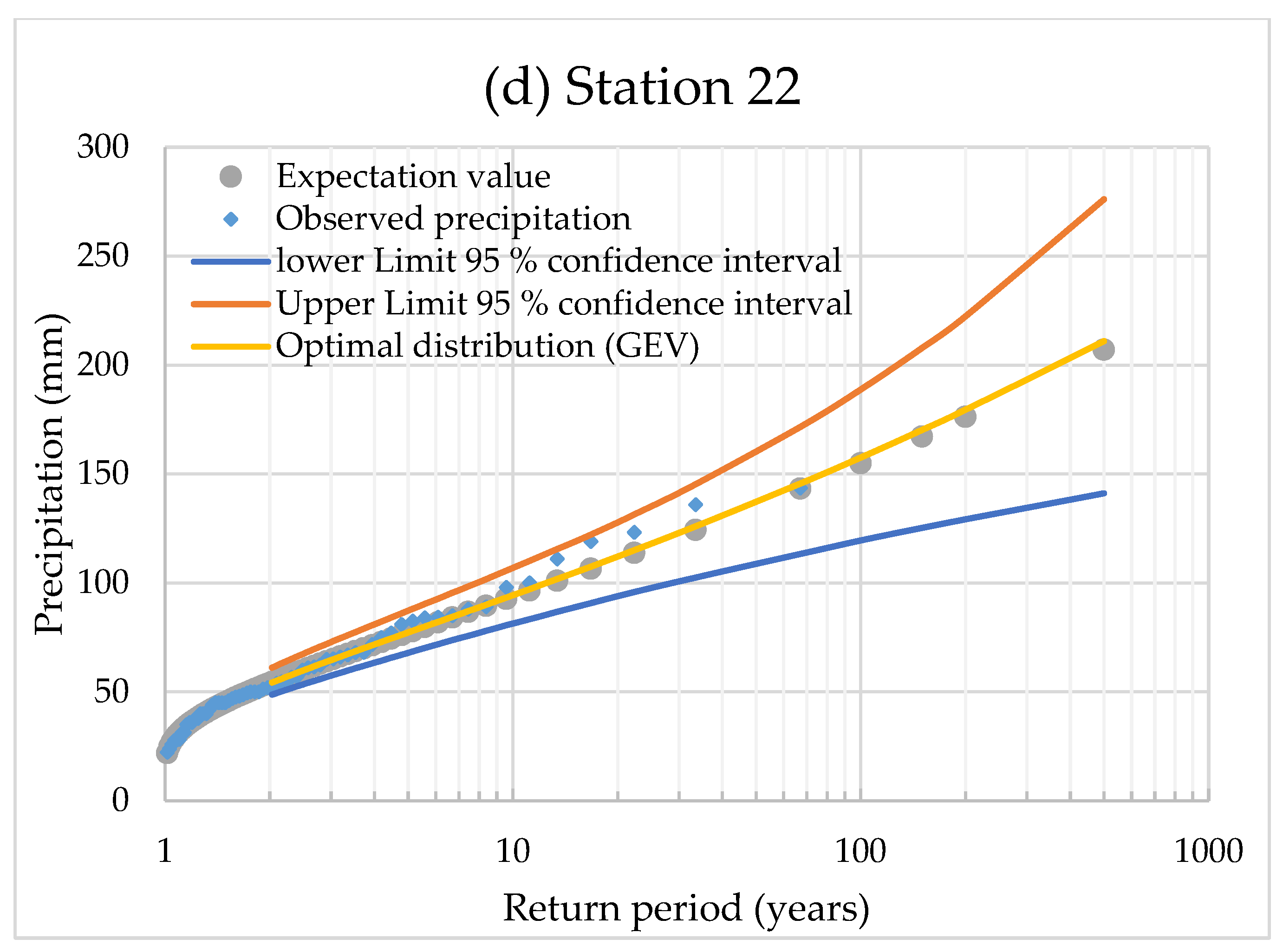
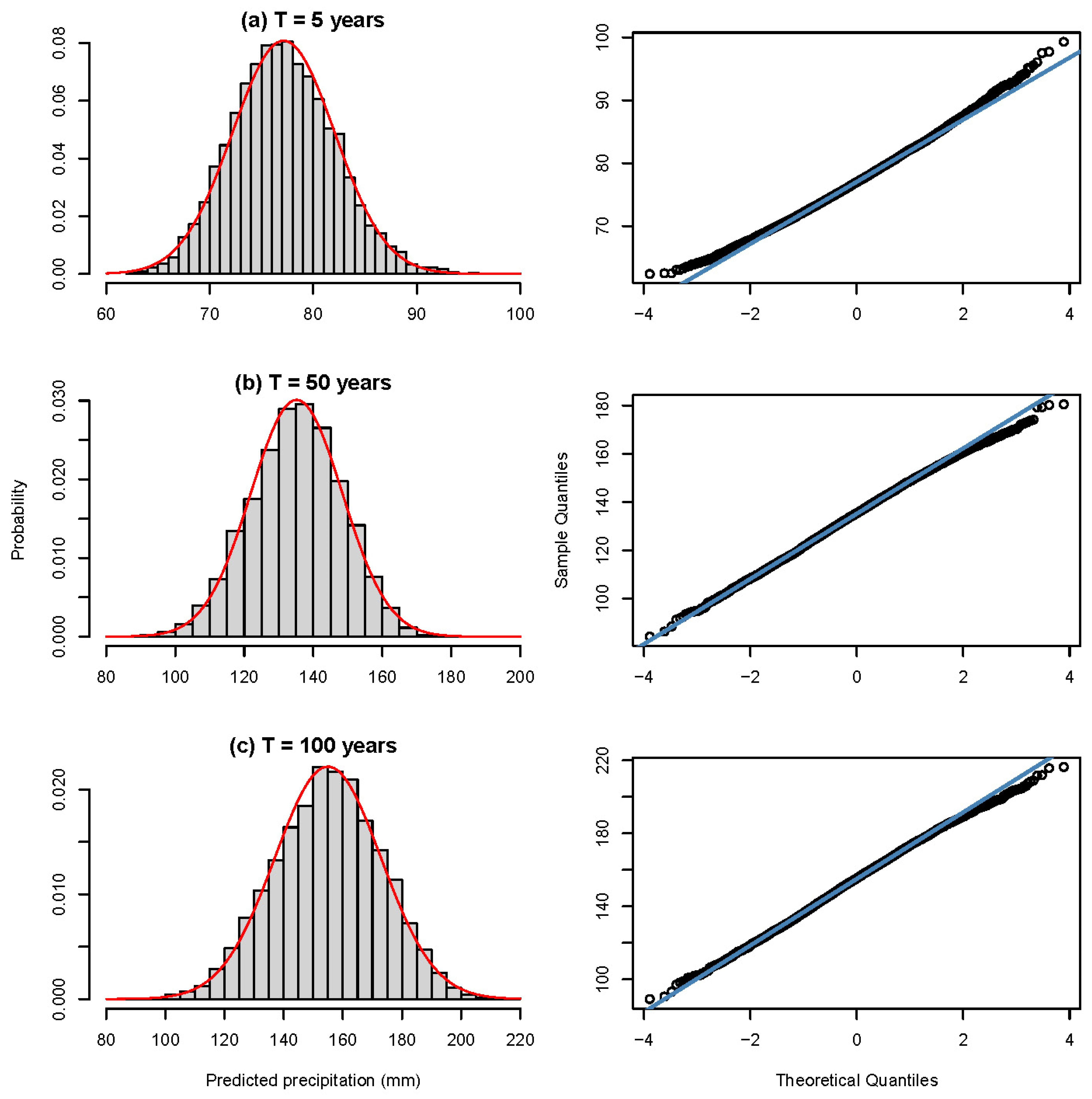
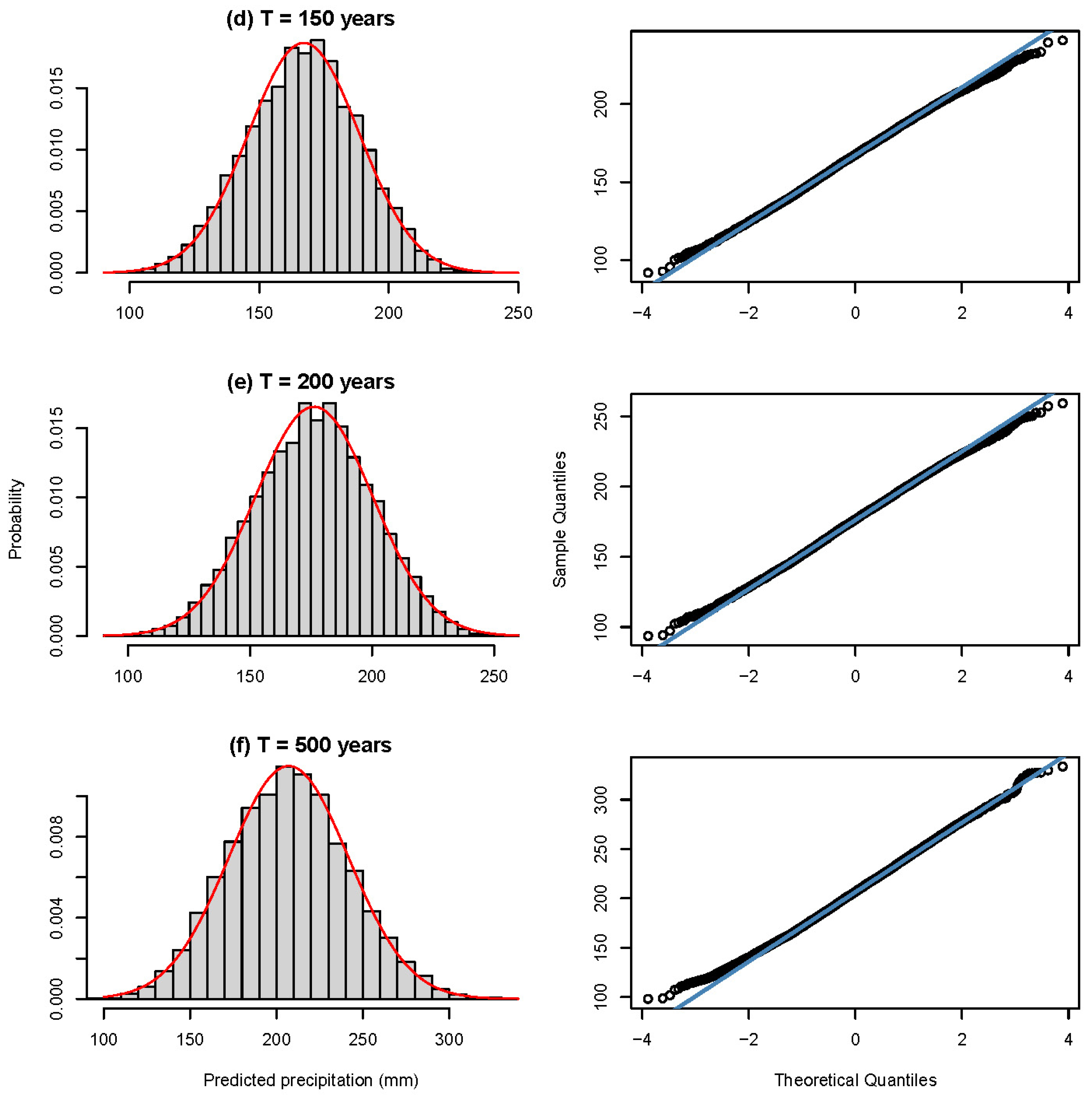
3.3. Quantile Estimations and Uncertainty Bounds
3.4. Effects of Data Resolution from which the AMS Was Extracted
4. Conclusions
- The trend analysis indicated that the observed AM series could be considered stationary, independent, and identically distributed. Therefore, the stationarity and serial independence stationarity assumptions were valid for the frequency analysis;
- Different types of probability distributions fit the extreme precipitation data series of the various weather stations, indicating that a careful selection of distributions is essential. Therefore, it is emphasized that an uncertainty analysis should be conducted using the best-fit probability distribution for extreme precipitation data series rather than a predefined single probability distribution for all stations based on modern extreme value theory;
- The sampling distribution of the precipitation quantile at a particular nonexceedance probability (i.e., particular return period) was obtained using a bootstrap resample simulation framework. This bootstrap sampling distribution allowed not only for the point estimation of the precipitation quantile as the expected value of the sampling distribution (i.e., sampling distribution precipitation quantile estimates) but also for quantifying the behavior of the precipitation quantile, such as the confidence interval, standard error, and skewness;
- The uncertainty associated with the used data (i.e., the sampling uncertainty) in a precipitation frequency analysis was evaluated in terms of the 95% confidence intervals based on the bootstrap resample simulation framework. It is concluded that the precipitation quantiles were subject to significant uncertainty and the band of uncertainty intervals increased as the return period increased. These confidence intervals for several return periods are beneficial for water sector policymakers to take appropriate actions to design and manage various water-related infrastructure;
- The extreme precipitation quantile (XT) obtained by the two methods (the conventional method, typically employed in the literature, and the sampling distribution methods) was comparable;
- The bootstrap resampling for the evaluation of how the record length of the data set alters the results of its summary statistics characteristics showed that a longer record length is desirable to decrease the sampling uncertainty and, therefore, decrease the error in the predicted quantile values, since the predicted quantile values are highly influenced by these summary statistics characteristics (specially the skewness and kurtosis values).
- The study showed that the distribution parameters estimates as well as the precipitation quantile estimates (specially at the higher return periods) were greatly affected by the data record length;
- The results suggest that a series of at least 40 years data records is needed to obtain reasonably accurate estimates of the precipitation quantiles for 100 year return periods and higher. Using only 20 to 25 years of data to obtain reasonably accurate estimates of the higher return periods quantile is risky, since it creates high sampling variability relative to the full data length.
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beskow, S.; Caldeira, T.L.; Rogério, C.; Mello, D.; Faria, L.C.; Alexandre, H.; Guedes, S. Multiparameter probability distributions for heavy rainfall modeling in extreme southern Brazil. J. Hydrol. Reg. Stud. 2015, 4, 123–133. [Google Scholar] [CrossRef]
- Gocic, M.; Velimirovic, L.; Stankovic, M.; Trajkovic, S. Determining the best fitting distribution of annual precipitation data in Serbia using L-moments method. Earth Sci. Inform. 2020, 14, 633–644. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J.; Yan, D.; Wang, Y. Extreme precipitation events identified using detrended fluctuation analysis (DFA) in Anhui, China. Theor. Appl. Climatol. 2014, 117, 169–174. [Google Scholar] [CrossRef]
- Ahmad, I.; Tang, D.; Wang, T.; Wang, M.; Wagan, B. Precipitation Trends over Time Using Mann-Kendall and Spearman’s rho Tests in Swat River Basin, Pakistan. Adv. Meteorol. 2015, 2015, 431860. [Google Scholar] [CrossRef]
- Zin, W.Z.W.; Jemain, A.A. Statistical distributions of extreme dry spell in Peninsular Malaysia. Theor. Appl. Climatol. 2010, 102, 253–264. [Google Scholar] [CrossRef]
- Ibrahim, M.N. Generalized distributions for modeling precipitation extremes based on the L moment approach for the Amman Zara Basin, Jordan. Theor. Appl. Climatol. 2019, 138, 1075–1093. [Google Scholar] [CrossRef]
- Jahanbaksh Asl, S.; Khorshiddoust, A.M.; Dinpashoh, Y.; Sarafrouzeh, F. Frequency analysis of climate extreme events in Zanjan, Iran. Stoch. Environ. Res. Risk Assess. 2013, 27, 1637–1650. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships Demetris. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Tfwala, C.M.; van Rensburg, L.D.; Schall, R.; Mosia, S.M.; Dlamini, P. Precipitation intensity-duration-frequency curves and their uncertainties for Ghaap plateau. Clim. Risk Manag. 2017, 16, 1–9. [Google Scholar] [CrossRef]
- Bartolini, G.; Morabito, M.; Crisci, A.; Grifoni, D.; Torrigiani, T.; Petralli, M.; Maracchi, G.; Orlandini, S. Recent trends in Tuscany (Italy) summer temperature and indices of extremes. Int. J. Climatol. 2008, 28, 1751–1760. [Google Scholar] [CrossRef]
- Ibrahim, M.N. Four-parameter kappa distribution for modeling precipitation extremes: A practical simplified method for parameter estimation in light of the L-moment. Theor. Appl. Climatol. 2022, 150, 567–591. [Google Scholar] [CrossRef]
- REUTERS. Jordan Flash Floods Kill 21 People, Many of Them School Children on Bus. Available online: https://www.reuters.com/article/us-jordan-floods-idUSKCN1MZ2GI (accessed on 9 August 2022).
- Roya News. Jordanians Remember Victims of Dead Sea Tragedy. Available online: https://en.royanews.tv/news/23012/2020-10-25 (accessed on 9 August 2022).
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Singh, V.P. Frequency Distribution. In Handbook of Applied Hydrology; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Oztekin, T. Wakeby distribution for representing annual extreme and partial duration rainfall series. Meteorol. Appl. 2007, 387, 381–387. [Google Scholar] [CrossRef]
- Hinge, G.; Hamouda, M.A.; Long, D.; Mohamed, M.M. Hydrologic utility of satellite precipitation products in flood prediction: A meta-data analysis and lessons learnt. J. Hydrol. 2022, 612, 128103. [Google Scholar] [CrossRef]
- Abebe, W.F.; Ayalew, M.S.; Berhanu, K.B. Detecting Hydrological Variability in Precipitation Extremes: Application of Reanalysis Climate Product in Data-Scarce Wabi Shebele Basin of Ethiopia. J. Hydrol. Eng. 2022, 27, 5021035. [Google Scholar] [CrossRef]
- Hinge, G.; Mazumdar, M.; Deb, S.; Kalita, M.K. District-level assessment of changes in extreme rainfall indices in Barak and other basins in Indian Himalayan states: Risks and opportunities. Model. Earth Syst. Environ. 2022, 8, 1145–1155. [Google Scholar] [CrossRef]
- Ouali, D.; Cannon, A.J. Estimation of rainfall intensity–duration–frequency curves at ungauged locations using quantile regression methods. Stoch. Environ. Res. Risk Assess. 2018, 32, 2821–2836. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Potter, K.W. Testing Flood Frequency Estimation Methods Using a Regional Flood Generation Model. Water Resour. Res. 1985, 21, 1903–1914. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R.; Wood, E.F. An appraisal of the regional flood frequency procedure in the UK Flood Studies Report. Hydrol. Sci. J. 1985, 30, 85–109. [Google Scholar] [CrossRef]
- Lettenmaier, D.P.; Wallis, J.R.; Wood, E.F. Effect of regional heterogeneity on flood frequency estimation. Water Resour. Res. 1987, 23, 313–323. [Google Scholar] [CrossRef]
- Du, H.; Xia, J.; Zeng, S.; She, D.; Liu, J. Variations and statistical probability characteristic analysis of extreme precipitation events under climate change in Haihe River Basin, China. Hydrol. Process. 2014, 28, 913–925. [Google Scholar] [CrossRef]
- Yilmaz, A.G.; Perera, B.J.C. Extreme Rainfall Nonstationarity Investigation and Intensity–Frequency–Duration Relationship. J. Hydrol. Eng. 2014, 19, 1160–1172. [Google Scholar] [CrossRef]
- Yang, T.; Xu, C.-Y.; Shao, Q.-X.; Chen, X. Regional flood frequency and spatial patterns analysis in the Pearl River Delta region using L-moments approach. Stoch Env. Res Risk Assess 2010, 24, 165–182. [Google Scholar] [CrossRef]
- Sen Roy, S.; Balling Jr, R.C. Trends in extreme daily precipitation indices in India. Int. J. Climatol. 2004, 24, 457–466. [Google Scholar] [CrossRef]
- Liu, B.; Chen, X.; Chen, J.; Chen, X. Impacts of different threshold definition methods on analyzing temporal-spatial features of extreme precipitation in the Pearl River Basin. Stoch. Environ. Res. Risk Assess. 2017, 31, 1241–1252. [Google Scholar] [CrossRef]
- Liu, B.; Chen, J.; Chen, X.; Lian, Y.; Wu, L. Uncertainty in determining extreme precipitation thresholds. J. Hydrol. 2013, 503, 233–245. [Google Scholar] [CrossRef]
- Xia, J.; She, D.; Zhang, Y.; Du, H. Spatio-temporal trend and statistical distribution of extreme precipitation events in Huaihe River Basin during 1960–2009. J. Geogr. Sci. 2012, 22, 195–208. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Abolverdi, J.; Khalili, D. Development of Regional Rainfall Annual Maxima for Southwestern Iran by L-Moments. Water Resour. Manag. 2010, 24, 2501–2526. [Google Scholar] [CrossRef]
- Deni, S.M.; Suhaila, J.; Wan Zin, W.Z.; Jemain, A.A. Spatial trends of dry spells over Peninsular Malaysia during monsoon seasons. Theor. Appl. Climatol. 2010, 99, 357–371. [Google Scholar] [CrossRef]
- She, D.; Xia, J.; Song, J.; Du, H. Spatio-temporal variation and statistical characteristic of extreme dry spell in Yellow River Basin, China. Theor. Appl. Clim. 2013, 112, 201–213. [Google Scholar] [CrossRef]
- Zakaria, Z.A.; Shabri, A.; Ahmad, U.N. Regional Frequency Analysis of Extreme Rainfalls in the West Coast of Peninsular Malaysia using Partial L-Moments. Water Resour. Manag. 2012, 26, 4417–4433. [Google Scholar] [CrossRef]
- Saf, B. Regional Flood Frequency Analysis Using L-Moments for the West Mediterranean Region of Turkey. Water Resour. Manag. 2009, 23, 531–551. [Google Scholar] [CrossRef]
- Adamowski, K. Regional analysis of annual maximum and partial duration flood data by nonparametric and L-moment methods. J. Hydrol. 2000, 229, 219–231. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. B 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Pandey, M.D.; Van Gelder, P.H.A.J.M.; Vrijling, J.K. The estimation of extreme quantiles of wind velocity using L-moments in the peaks-over-threshold approach. Struct. Saf. 2001, 23, 179–192. [Google Scholar] [CrossRef]
- Asquith, W.H. L-moments and TL-moments of the generalized lambda distribution. Comput. Stat. Data Anal. 2007, 51, 4484–4496. [Google Scholar] [CrossRef]
- Vogel, R.M.; Fennessey, N.M. L moment diagrams should replace product moment diagrams. Water Resour. Res. 1993, 29, 1745–1752. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Srinivasan, K. Investigation and comparison of sampling properties of L-moments and conventional moments. J. Hydrol. 1999, 218, 13–34. [Google Scholar] [CrossRef]
- Ateeq, K.; Qasim, T.B.; Alvi, A.R. An extension of Rayleigh distribution and applications. Cogent Math. Stat. 2019, 6, 1622191. [Google Scholar] [CrossRef]
- Burn, D.H. The use of resampling for estimating confidence intervals for single site and pooled frequency analysis. Hydrol. Sci. J. 2003, 48, 25–38. [Google Scholar] [CrossRef][Green Version]
- Tung, Y.; Wong, C. Assessment of design rainfall uncertainty for hydrologic engineering applications in Hong Kong. Stoch. Environ. Res. Risk Assess. 2014, 28, 583–592. [Google Scholar] [CrossRef]
- Schendel, T.; Thongwichian, R. Confidence intervals for return levels for the peaks-over-threshold approach. Adv. Water Resour. 2017, 99, 53–59. [Google Scholar] [CrossRef]
- Coles, S.; Pericchi, L.R.; Sisson, S. A fully probabilistic approach to extreme rainfall modeling. J. Hydrol. 2003, 273, 35–50. [Google Scholar] [CrossRef]
- Overeem, A.; Buishand, A.; Holleman, I. Rainfall depth-duration-frequency curves and their uncertainties. J. Hydrol. 2008, 348, 124–134. [Google Scholar] [CrossRef]
- Muller, A.; Arnaud, P.; Lang, M.; Lavabre, J. Uncertainties of extreme rainfall quantiles estimated by a stochastic rainfall model and by a generalized Pareto distribution. Hydrol. Sci. J. 2009, 54, 417–429. [Google Scholar] [CrossRef]
- Huang, Y.F.; Mirzaei, M.; Amin, M.Z.M. Uncertainty Quantification in Rainfall Intensity Duration Frequency Curves Based on Historical Extreme Precipitation Quantiles. Procedia Eng. 2016, 154, 426–432. [Google Scholar] [CrossRef]
- Dupuis, D.J.; Field, C.A. A Comparison of confidence intervals for generalized extreme-value distributions. J. Stat. Comput. Simul. 1998, 61, 341–360. [Google Scholar] [CrossRef]
- Wei, T.; Song, S. Confidence Interval Estimation for Precipitation Quantiles Based on Principle of Maximum Entropy. Entropy 2019, 21, 315. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Vogel, R.M.; Foufoula-Georgiou, E. Frequency Analysis of Extreme Events. In Handbook of Hydrology; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Tiwari, M.K.; Chatterjee, C. Development of an accurate and reliable hourly flood forecasting model using wavelet–bootstrap–ANN (WBANN) hybrid approach. J. Hydrol. 2010, 394, 458–470. [Google Scholar] [CrossRef]
- Skrobek, D.; Krzywanski, J.; Sosnowski, M.; Kulakowska, A.; Zylka, A.; Grabowska, K.; Ciesielska, K.; Nowak, W. Implementation of Deep Learning Methods in Prediction of Adsorption Processes. Adv. Eng. Softw. 2022, 173, 103190. [Google Scholar] [CrossRef]
- Tung, Y.-K.; Yen, B.-C. Hydrosystems Engineering Uncertainty Analysis; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Mamoon, A.A.; Rahman, A. Chapter 4—Uncertainty analysis in design rainfall estimation due to limited data length: A case study in Qatar. In Extreme Hydrology and Climate Variability; Melesse, A.M., Abtew, W., Senay, G., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 37–45. [Google Scholar]
- Department of Statistics. Jordan in Figures; Department of Statistics: Amman, Jordan, 2020. [Google Scholar]
- Ghanem, A.A. Climatology of the areal precipitation in Amman/Jordan. Int. J. Climatol. 2011, 31, 1328–1333. [Google Scholar] [CrossRef]
- Hamed, K.H.; Ramachandra Rao, A. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann-Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability weighted moments: Definition and relation to parameters of several distributions expressable in inverse form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef]
- Dodge, Y. The Concise Encyclopedia of Statistics; Springer: New York, NY, USA, 2009; Volume 23. [Google Scholar]
- Naghettini, M. Fundamentals of Statistical Hydrology; Naghettini, M., Ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 1993. [Google Scholar]
- Li, Z.; Shao, Q.; Xu, Z.; Cai, X. Analysis of parameter uncertainty in semi-distributed hydrological models using bootstrap method: A case study of SWAT model applied to Yingluoxia watershed in northwest China. J. Hydrol. 2010, 385, 76–83. [Google Scholar] [CrossRef]
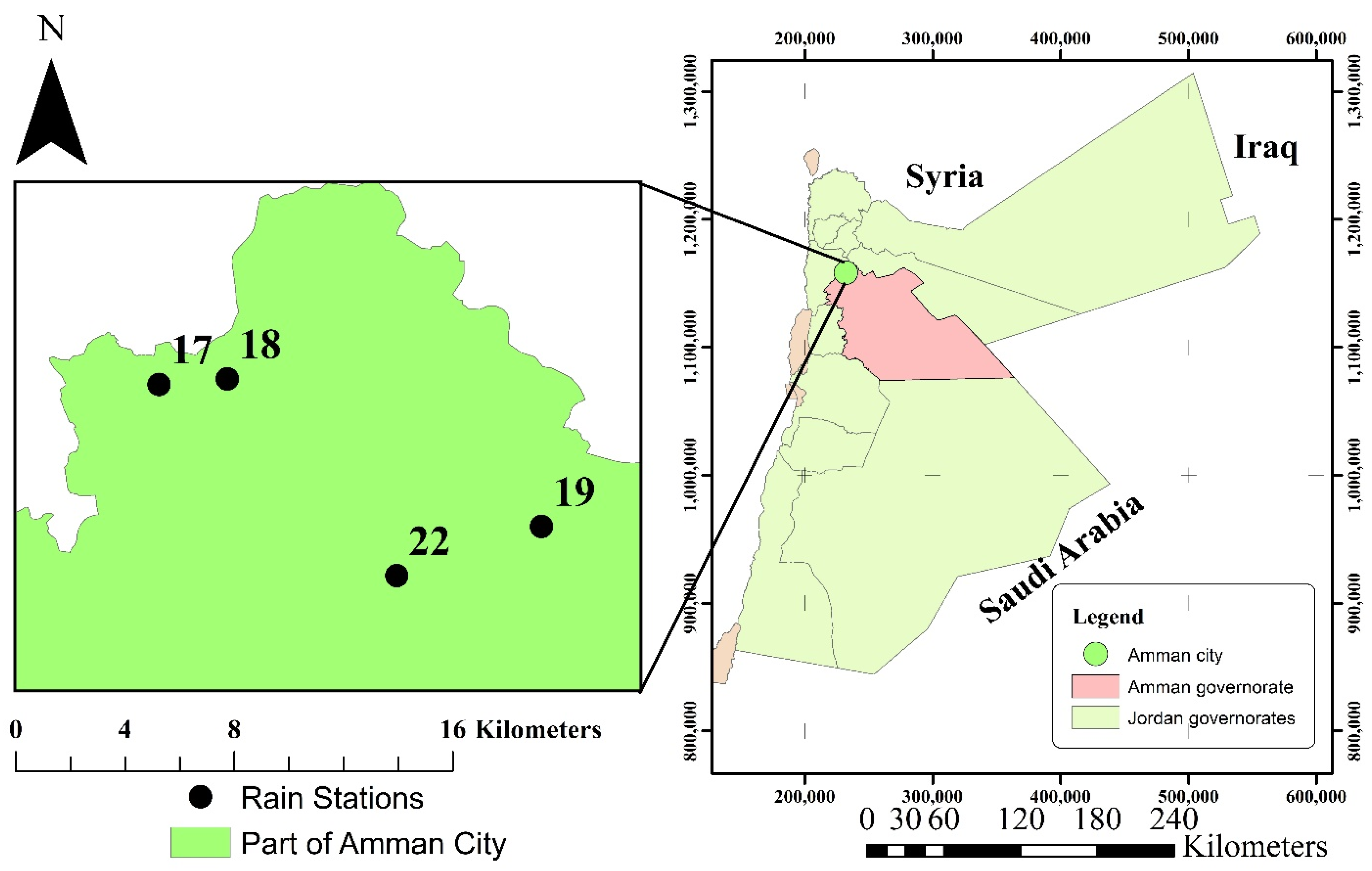
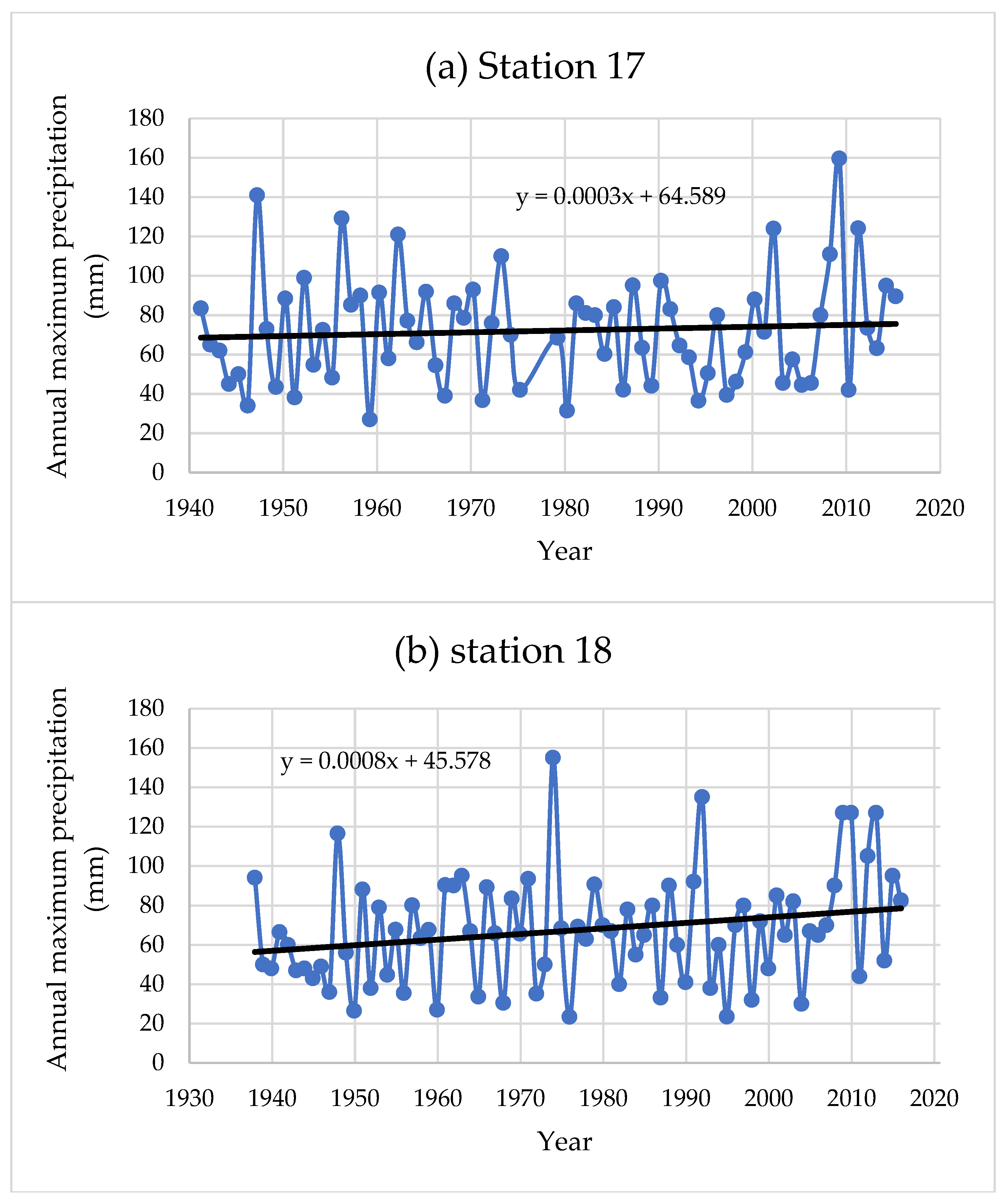

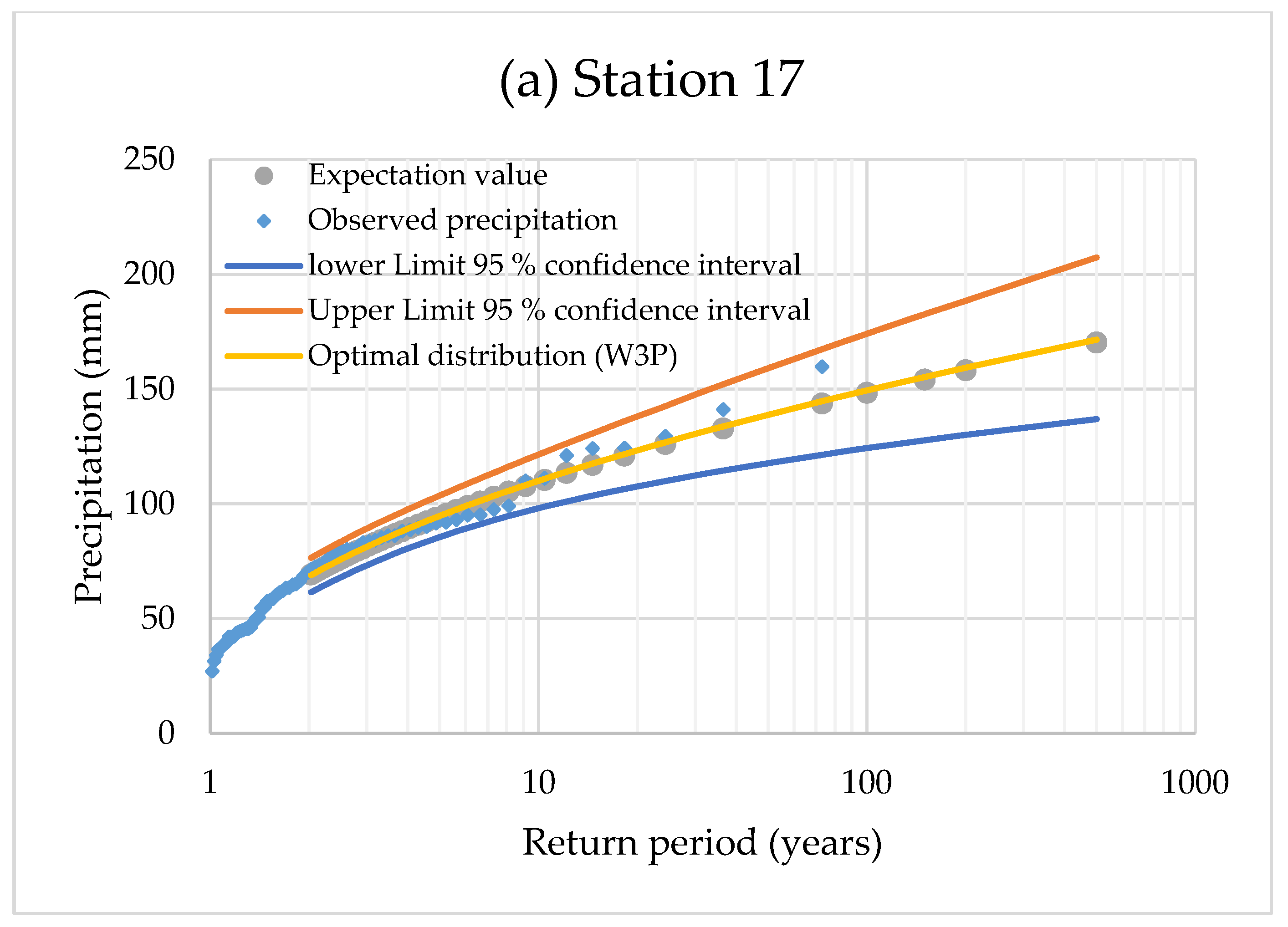
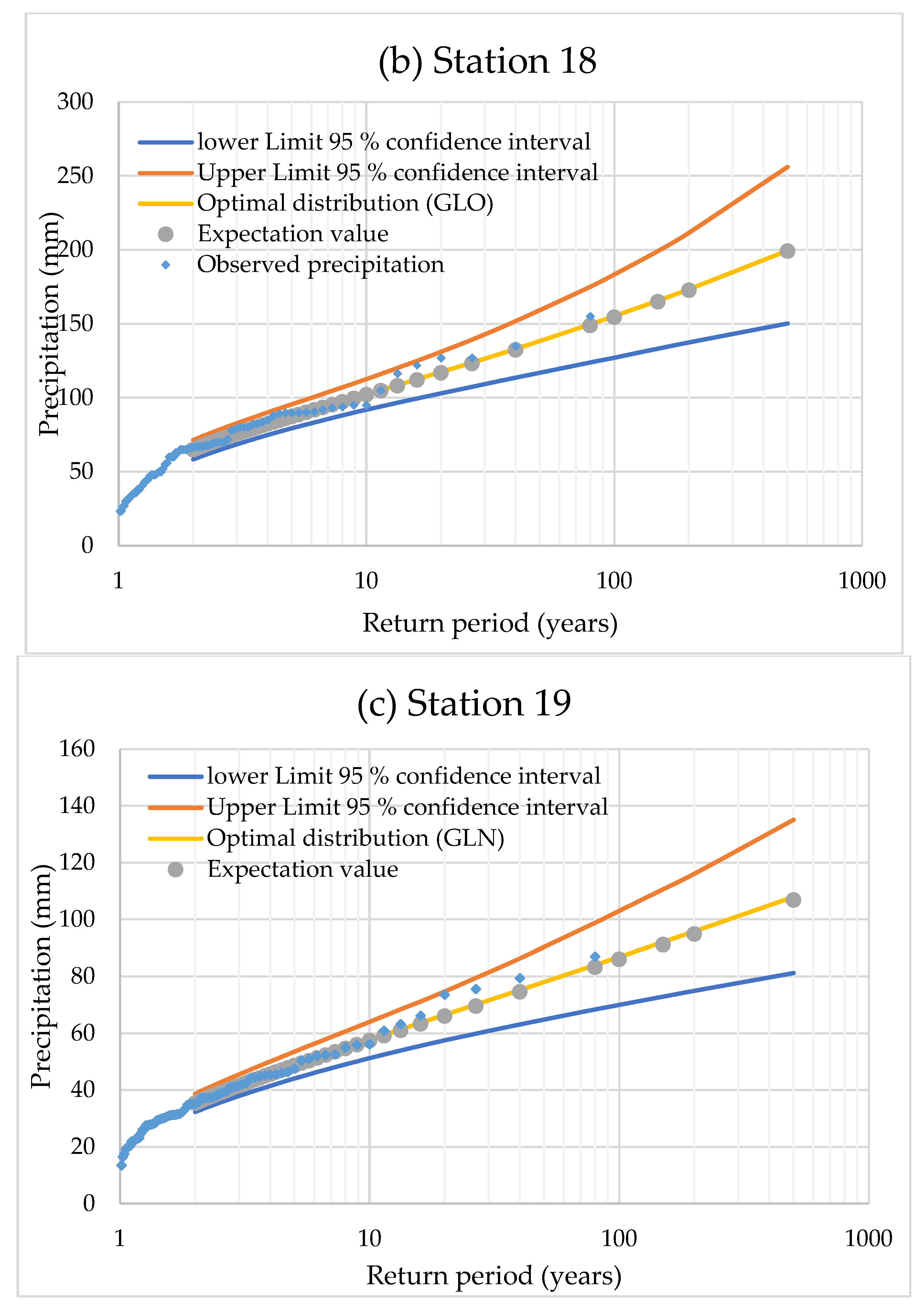
| No. | Station | Station Name | Coordinates a | Elevation | Data | Record Length (years) | Annual Precipitation (mm) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | Latitude | Longitude | Period | Mean | SD | Skewness | Kurt | CV | ||||
| 1 | 17 | SWEILIH | 1,159,000 | 229,500 | 1000 | 1942–2016 | 71 | 488.85 | 180.11 | 0.95 | 0.89 | 36.8 |
| 2 | 18 | JUBEIHA | 1,159,200 | 232,000 | 980 | 1936–2016 | 79 | 463.18 | 165.61 | 0.38 | 0.41 | 35.8 |
| 3 | 19 | AMMAN AIRPORT | 1,153,800 | 243,500 | 790 | 1937–2016 | 79 | 262.55 | 92.63 | 0.42 | −0.44 | 35.3 |
| 4 | 22 | AMMAN HUSSEIN COLLEGE | 1,152,000 | 238,200 | 834 | 1950–2016 | 66 | 373.00 | 137.82 | 0.65 | 0.06 | 36.9 |
| Distributions | CDF | L-Moment Parameters Estimators | Predicted Rainfall Amount Associated with Return Period T Years (Quantiles) |
|---|---|---|---|
| GUM | , | ||
| GAM | If 0 < < then z = π , If ≤ < 1 then z = 1 − τ2, , | The quantile of GAM has no explicit analytical form | |
| PE3 | If 0 < < then z = 3π , If ≤ < 1 then z = 1 − , , | The quantile of GAM has no explicit analytical form | |
| W3P | First, the shape parameter is found by iteratively solving equation , here τ3 is replaced by its sample estimate. , | ||
| GEV | , , | ||
| GP | , | ||
| GLO | , , | ||
| GLN | , | The quantile of GLN has no explicit analytical form |
| Station | MMK Trend Test | KS Goodness-of-Fit Test Dmax Value | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ID | Z Value | GEV | GP | GLO | PE3D | W3P | GLN | GAM | GUM | Best Distribution |
| 17 | 0.46 | 0.078 | 0.083 | 0.091 | 0.074 | 0.064 | 0.077 | 0.074 | 0.082 | W3P |
| 18 | 1.93 | 0.069 | 0.101 | 0.066 | 0.069 | 0.074 | 0.067 | 0.076 | 0.090 | GLO |
| 19 | −0.73 | 0.044 | 0.083 | 0.060 | 0.052 | 0.061 | 0.043 | 0.060 | 0.050 | GLN |
| 22 | 1.68 | 0.043 | 0.082 | 0.055 | 0.062 | 0.068 | 0.050 | 0.077 | 0.068 | GEV |
| Station: 17 | |||||||||
| Return period, T (years) | 2 | 5 | 10 | 20 | 50 | 100 | 150 | 200 | 500 |
| Predicted precipitation quantiles (mm) | 68.42 | 94.78 | 110.10 | 123.37 | 138.86 | 149.47 | 155.33 | 159.35 | 171.53 |
| Upper Limit 95% confidence interval (ULC) (mm) | 75.97 | 103.63 | 121.48 | 138.29 | 159.18 | 174.12 | 182.70 | 188.53 | 207.42 |
| Lower Limit 95% confidence interval (LLC) (mm) | 61.09 | 85.54 | 98.10 | 107.65 | 117.87 | 124.30 | 127.70 | 130.10 | 136.89 |
| ULC relative differences from the predicted (%) | 11.04 | 9.34 | 10.33 | 12.09 | 14.63 | 16.50 | 17.62 | 18.31 | 20.92 |
| LLC relative differences from the predicted (%) | −10.70 | −9.75 | −10.90 | −12.74 | −15.11 | −16.84 | −17.78 | −18.36 | −20.20 |
| Expectation value (mm) | 68.59 | 94.42 | 109.45 | 122.49 | 137.75 | 148.24 | 154.04 | 158.03 | 170.13 |
| Station: 18 | |||||||||
| Return period, T (years) | 2 | 5 | 10 | 20 | 50 | 100 | 150 | 200 | 500 |
| Predicted precipitation quantiles (mm) | 64.76 | 87.47 | 102.43 | 117.44 | 138.31 | 155.25 | 165.72 | 173.41 | 199.52 |
| Upper Limit 95% confidence interval (ULC) (mm) | 71.42 | 95.61 | 112.68 | 131.10 | 159.04 | 183.39 | 199.23 | 211.64 | 256.16 |
| Lower Limit 95% confidence interval (LLC) (mm) | 58.37 | 79.46 | 91.97 | 102.98 | 116.95 | 127.13 | 133.24 | 137.47 | 150.21 |
| ULC relative differences from the predicted (%) | 10.28 | 9.31 | 10.00 | 11.64 | 14.99 | 18.13 | 20.22 | 22.04 | 28.38 |
| LLC relative differences from the predicted (%) | −9.87 | −9.15 | −10.21 | −12.31 | −15.44 | −18.12 | −19.60 | −20.73 | −24.71 |
| Expectation value (mm) | 64.87 | 87.25 | 102.01 | 116.84 | 137.55 | 154.46 | 164.96 | 172.69 | 199.13 |
| Station: 19 | |||||||||
| Return period, T (years) | 2 | 5 | 10 | 20 | 50 | 100 | 150 | 200 | 500 |
| Predicted precipitation quantiles (mm) | 35.26 | 48.70 | 57.75 | 66.53 | 78.06 | 86.88 | 92.10 | 95.83 | 107.96 |
| Upper Limit 95% confidence interval (ULC) (mm) | 38.71 | 53.57 | 64.07 | 74.75 | 90.26 | 103.03 | 110.66 | 116.08 | 135.13 |
| Lower Limit 95% confidence interval (LLC) (mm) | 32.31 | 44.11 | 51.28 | 57.54 | 64.82 | 70.03 | 72.94 | 74.98 | 81.24 |
| ULC relative differences from the predicted (%) | 9.80 | 10.00 | 10.95 | 12.36 | 15.62 | 18.59 | 20.16 | 21.13 | 25.16 |
| LLC relative differences from the predicted (%) | −8.35 | −9.41 | −11.19 | −13.50 | −16.97 | −19.39 | −20.80 | −21.76 | −24.75 |
| Expectation value (mm) | 35.39 | 48.60 | 57.46 | 66.06 | 77.37 | 86.03 | 91.17 | 94.86 | 106.85 |
| Station: 22 | |||||||||
| Return period, T (years) | 2 | 5 | 10 | 20 | 50 | 100 | 150 | 200 | 500 |
| Predicted precipitation quantiles (mm) | 53.88 | 77.31 | 94.43 | 112.16 | 137.19 | 157.61 | 170.23 | 179.50 | 210.93 |
| Upper Limit 95% confidence interval (ULC) (mm) | 60.64 | 87.29 | 106.97 | 127.85 | 160.07 | 188.80 | 207.88 | 222.39 | 276.12 |
| Lower Limit 95% confidence interval (LLC) (mm) | 48.35 | 67.93 | 81.42 | 93.98 | 108.88 | 119.51 | 125.28 | 129.22 | 141.12 |
| ULC relative differences from the predicted (%) | 12.56 | 12.91 | 13.28 | 13.99 | 16.68 | 19.79 | 22.12 | 23.89 | 30.91 |
| LLC relative differences from the predicted (%) | −10.26 | −12.13 | −13.77 | −16.21 | −20.63 | −24.18 | −26.41 | −28.01 | −33.10 |
| Expectation value (mm) | 54.12 | 77.13 | 93.78 | 110.96 | 135.16 | 154.95 | 167.20 | 176.24 | 207.04 |
| Record Length | Average | Standard Deviation (SD) | Coefficient of Variation (CV) | Skewness | Kurtosis | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Average | SD | Average | SD | Average | SD | Average | SD | Average | SD | |
| 10 | 67.692 | 8.852 | 26.711 | 7.014 | 0.395 | 0.093 | 0.334 | 0.599 | 2.548 | 1.028 |
| 15 | 67.653 | 7.199 | 27.030 | 5.727 | 0.400 | 0.076 | 0.440 | 0.545 | 2.818 | 1.024 |
| 20 | 67.576 | 6.173 | 27.170 | 4.939 | 0.402 | 0.066 | 0.498 | 0.485 | 2.964 | 1.021 |
| 30 | 67.570 | 5.047 | 27.345 | 3.994 | 0.405 | 0.053 | 0.571 | 0.398 | 3.151 | 0.953 |
| 40 | 67.556 | 4.356 | 27.384 | 3.452 | 0.406 | 0.046 | 0.603 | 0.340 | 3.232 | 0.853 |
| 50 | 67.531 | 3.888 | 27.457 | 3.102 | 0.407 | 0.041 | 0.626 | 0.303 | 3.287 | 0.770 |
| 75 | 67.555 | 3.186 | 27.539 | 2.507 | 0.408 | 0.033 | 0.652 | 0.239 | 3.350 | 0.618 |
| 80 | 67.555 | 3.109 | 27.540 | 2.437 | 0.408 | 0.032 | 0.655 | 0.234 | 3.356 | 0.605 |
| 90 | 67.549 | 2.910 | 27.553 | 2.277 | 0.408 | 0.030 | 0.661 | 0.217 | 3.370 | 0.565 |
| 100 | 67.542 | 2.745 | 27.554 | 2.183 | 0.408 | 0.029 | 0.664 | 0.208 | 3.376 | 0.534 |
| 150 | 67.536 | 2.237 | 27.557 | 1.782 | 0.408 | 0.024 | 0.674 | 0.167 | 3.407 | 0.436 |
| 200 | 67.540 | 1.943 | 27.565 | 1.531 | 0.408 | 0.021 | 0.680 | 0.143 | 3.420 | 0.375 |
| 500 | 67.520 | 1.229 | 27.589 | 0.972 | 0.409 | 0.013 | 0.689 | 0.090 | 3.439 | 0.234 |
| Max. | 67.692 | 8.852 | 27.589 | 7.014 | 0.409 | 0.093 | 0.689 | 0.599 | 3.439 | 1.028 |
| Min. | 67.520 | 1.229 | 26.711 | 0.972 | 0.395 | 0.013 | 0.334 | 0.090 | 2.548 | 0.234 |
| Percent change | 0.255 | 620.312 | 3.288 | 621.234 | 3.348 | 613.520 | 106.179 | 569.526 | 34.982 | 338.975 |
| Partition Scenarios | Record Length | GLO Probability Distribution Parameters | Return Periods (T) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Location Parameter (ξ) | Scale Parameter (α) | Shape Parameter (k) | 2 | 5 | 10 | 20 | 50 | 100 | 150 | 200 | 500 | ||
| 12.5% | 9 | 54.168 | 14.398 | −268.665 | 54.168 | 38.435 | 28.112 | 18.635 | 7.088 | 0.992 | 5.470 | 8.539 | 17.726 |
| 10 | 24.552 | 58.928 | −281.295 | 24.552 | 30.783 | 30.460 | 27.766 | 20.898 | 13.027 | 7.221 | 2.509 | 16.234 | |
| 10 | 7.421 | 7.463 | −10.147 | 7.421 | 3.337 | 1.445 | 0.090 | 1.828 | 3.007 | 3.658 | 4.106 | 5.470 | |
| 10 | 13.754 | 18.146 | −301.727 | 13.754 | 1.194 | 6.945 | 14.338 | 23.242 | 29.403 | 32.793 | 35.106 | 41.979 | |
| 10 | 8.452 | 28.300 | −118.273 | 8.452 | 4.330 | 12.725 | 21.175 | 33.010 | 42.706 | 48.733 | 53.185 | 68.424 | |
| 10 | 2.341 | 33.279 | −213.760 | 2.341 | 9.483 | 16.282 | 22.293 | 29.475 | 34.461 | 37.221 | 39.114 | 44.794 | |
| 10 | 0.582 | 21.118 | −13.651 | 0.582 | 6.247 | 8.899 | 11.064 | 13.537 | 15.226 | 16.164 | 16.811 | 18.793 | |
| 10 | 0.710 | 33.018 | −289.330 | 0.710 | 11.423 | 18.793 | 25.360 | 33.177 | 38.550 | 41.498 | 43.506 | 49.468 | |
| 25% | 19 | 16.297 | 13.858 | −41.706 | 16.297 | 14.730 | 13.299 | 11.765 | 9.605 | 7.889 | 6.857 | 6.114 | 3.698 |
| 20 | 16.952 | 23.512 | −120.323 | 16.952 | 16.687 | 14.709 | 11.904 | 7.103 | 2.670 | 0.247 | 2.463 | 10.363 | |
| 20 | 2.219 | 11.070 | −35.018 | 2.219 | 3.749 | 3.744 | 3.353 | 2.465 | 1.591 | 1.016 | 0.584 | 0.911 | |
| 20 | 0.468 | 6.807 | −41.162 | 0.468 | 2.175 | 3.905 | 5.574 | 7.761 | 9.421 | 10.395 | 11.088 | 13.303 | |
| 50% | 39 | 7.247 | 2.603 | −19.858 | 7.247 | 5.636 | 4.622 | 3.654 | 2.390 | 1.430 | 0.865 | 0.462 | 0.830 |
| 40 | 7.209 | 3.516 | −24.548 | 7.209 | 5.769 | 4.746 | 3.709 | 2.283 | 1.151 | 0.466 | 0.031 | 1.670 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, M.N. Assessment of the Uncertainty Associated with Statistical Modeling of Precipitation Extremes for Hydrologic Engineering Applications in Amman, Jordan. Sustainability 2022, 14, 17052. https://doi.org/10.3390/su142417052
Ibrahim MN. Assessment of the Uncertainty Associated with Statistical Modeling of Precipitation Extremes for Hydrologic Engineering Applications in Amman, Jordan. Sustainability. 2022; 14(24):17052. https://doi.org/10.3390/su142417052
Chicago/Turabian StyleIbrahim, Mohamad Najib. 2022. "Assessment of the Uncertainty Associated with Statistical Modeling of Precipitation Extremes for Hydrologic Engineering Applications in Amman, Jordan" Sustainability 14, no. 24: 17052. https://doi.org/10.3390/su142417052
APA StyleIbrahim, M. N. (2022). Assessment of the Uncertainty Associated with Statistical Modeling of Precipitation Extremes for Hydrologic Engineering Applications in Amman, Jordan. Sustainability, 14(24), 17052. https://doi.org/10.3390/su142417052







