Modal Identification of Low-Frequency Oscillations in Power Systems Based on Improved Variational Modal Decomposition and Sparse Time-Domain Method
Abstract
:1. Introduction
- (1)
- We propose a method for the modal feature identification of low-frequency oscillations of a unit by combining the improved variational modal decomposition with the sparse time-domain method. The method improves the accuracy and anti-interference in the modal discrimination of low-frequency oscillation signals in power systems.
- (2)
- We use the grey wolf optimization algorithm (GWO) to find the optimal number of eigenmodes and penalty factors for the VMD. The noise in the signal is also filtered out using the improved variational modal decomposition (GWVMD).
- (3)
- We use the sparse time-domain method to accurately identify the modal parameters in the noise-reduced low-frequency oscillation signal and solve the multi-channel identification performance of the low-frequency oscillation identification method.
- (4)
- Through the signal identification experiments in the Hengshan power plant, it can be concluded that the GWVMD-STD method has an overall reduction of 34, 44, and 21% in the frequency error and 37, 41, and 18% in the damping error compared to the EFEMD-HT, RDT-ERA, and TLS-ESPRIT methods.
2. Variational Modal Decomposition
3. Sparse Time-Domain Method
4. Low-Frequency Oscillation Mode Identification Based on Improved VMD and STD
4.1. Improvement in Variational Modal Decomposition
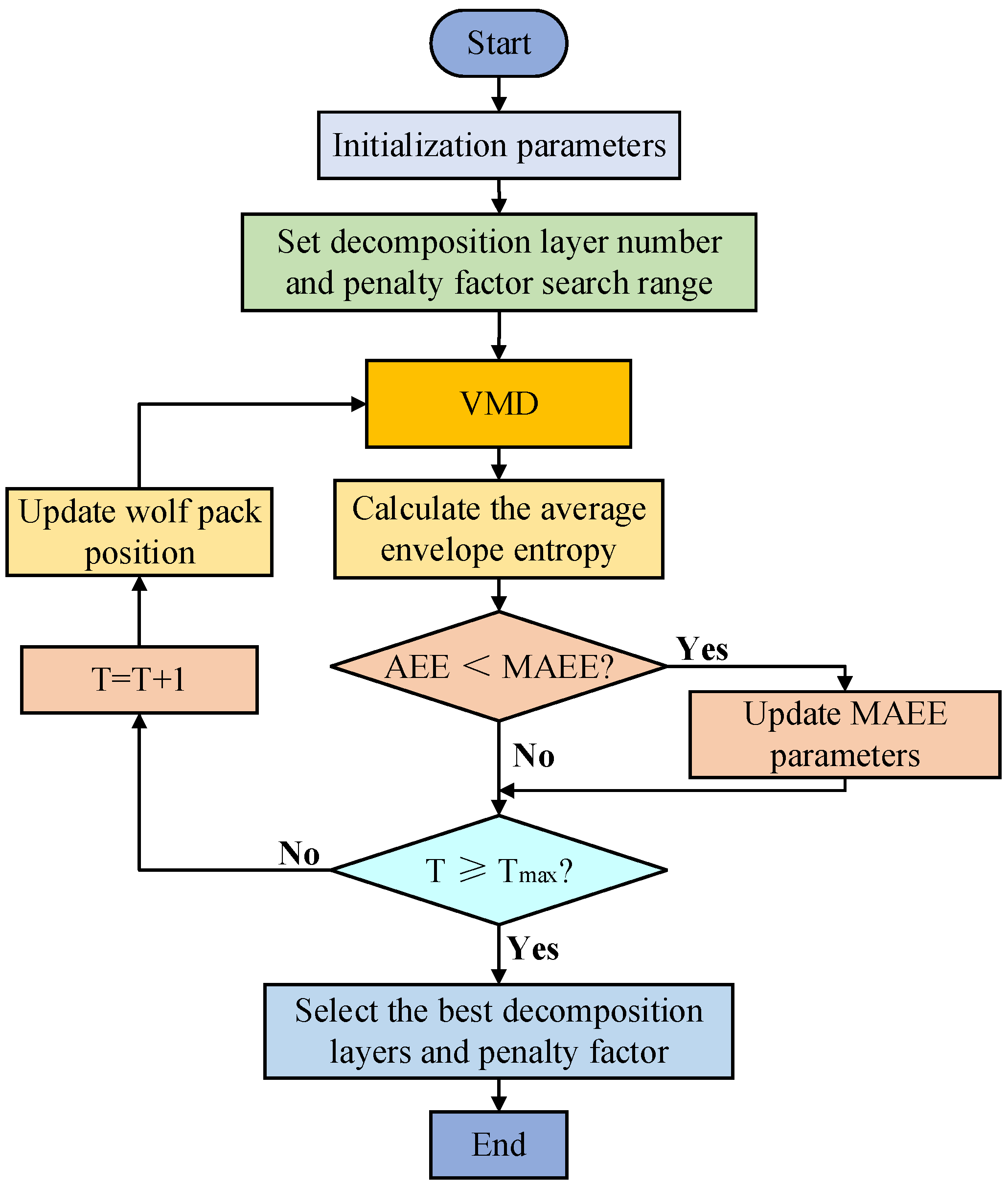
4.2. Overall Process Steps of the Model
4.3. Evaluation Indexes
4.3.1. Signal-to-Noise Ratio
4.3.2. Correlation Coefficient
4.3.3. Mean Squared Error
5. Modal Identification Comparison Experiment
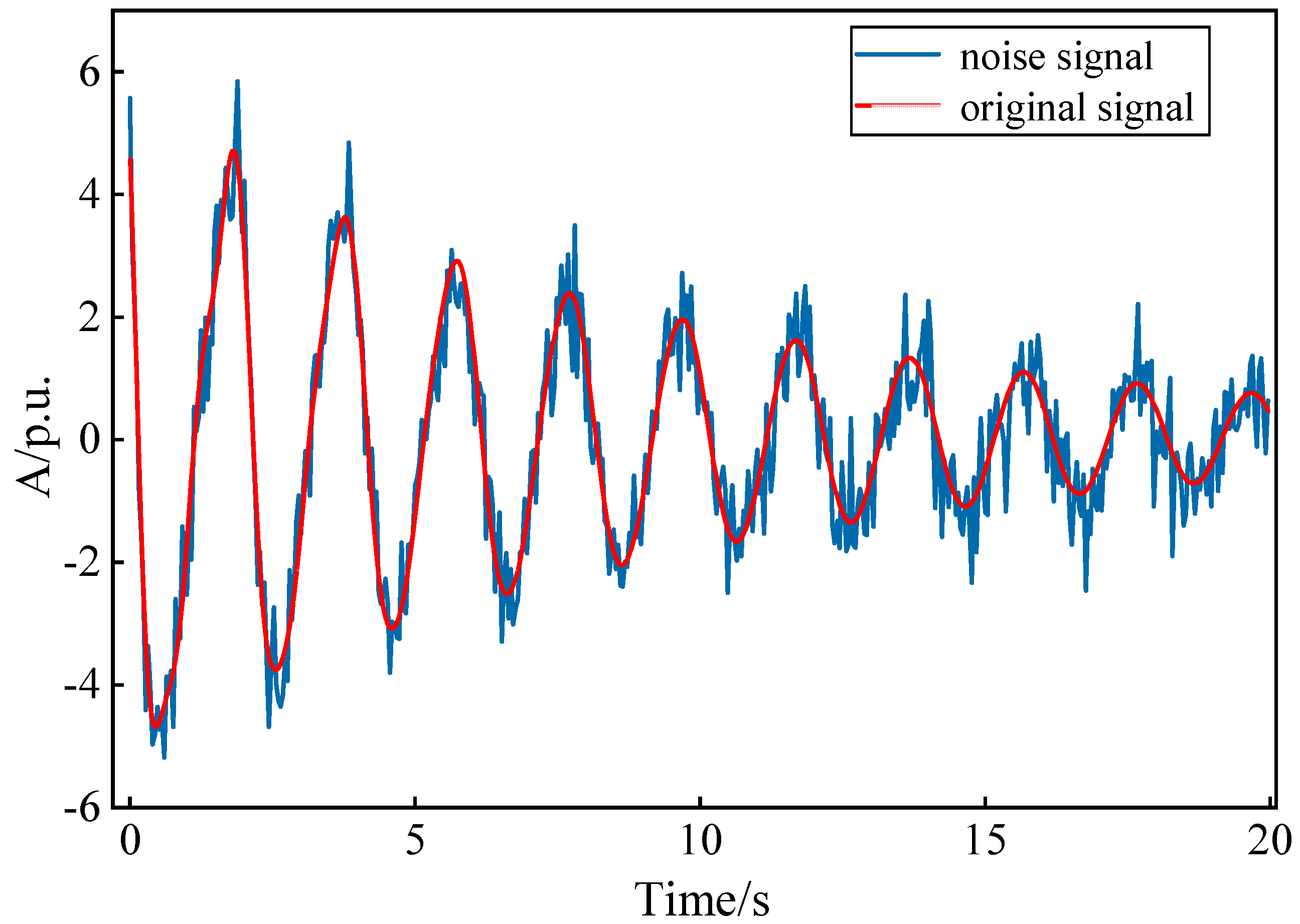
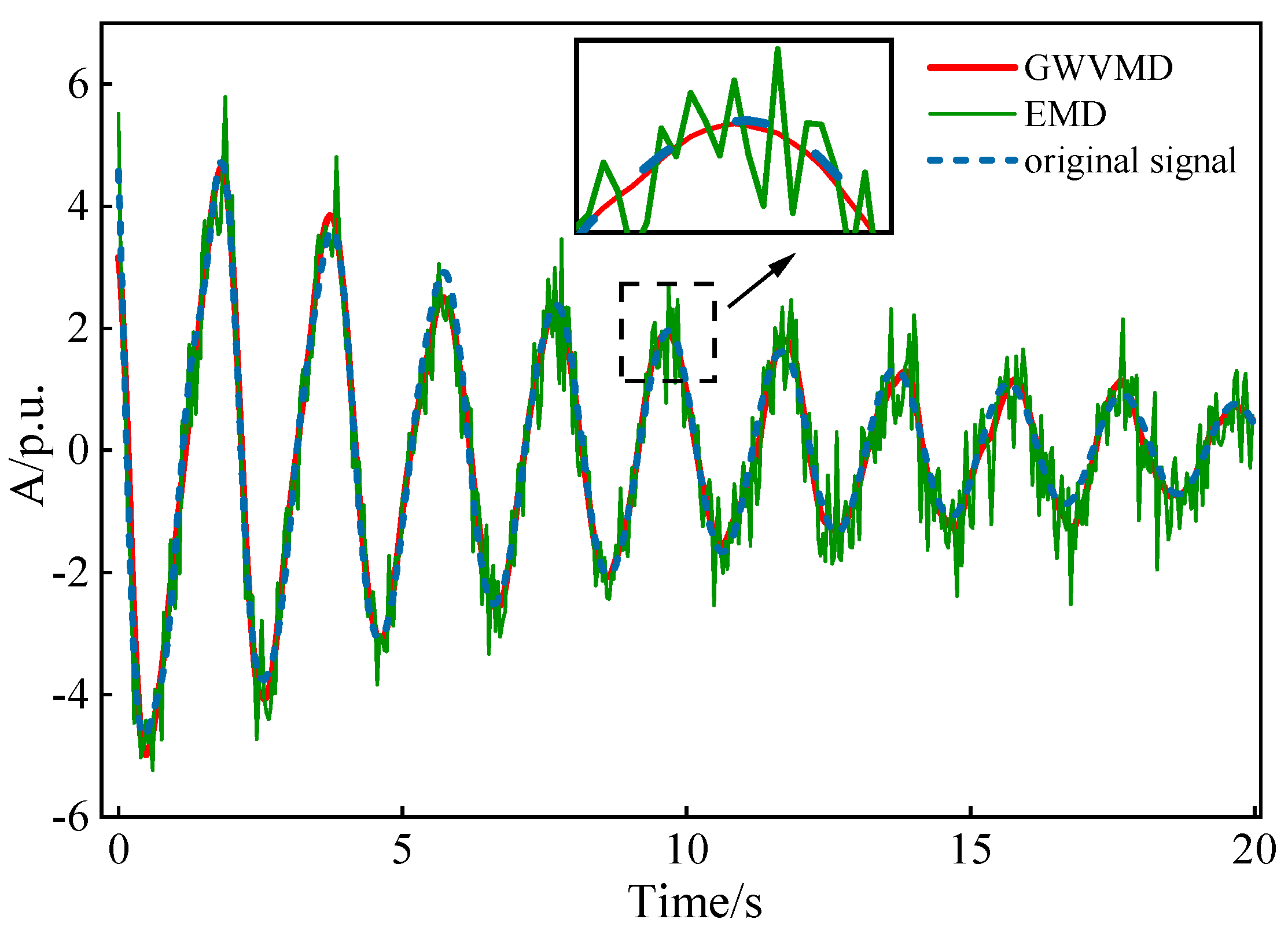
5.1. Numerical Signal Experiment
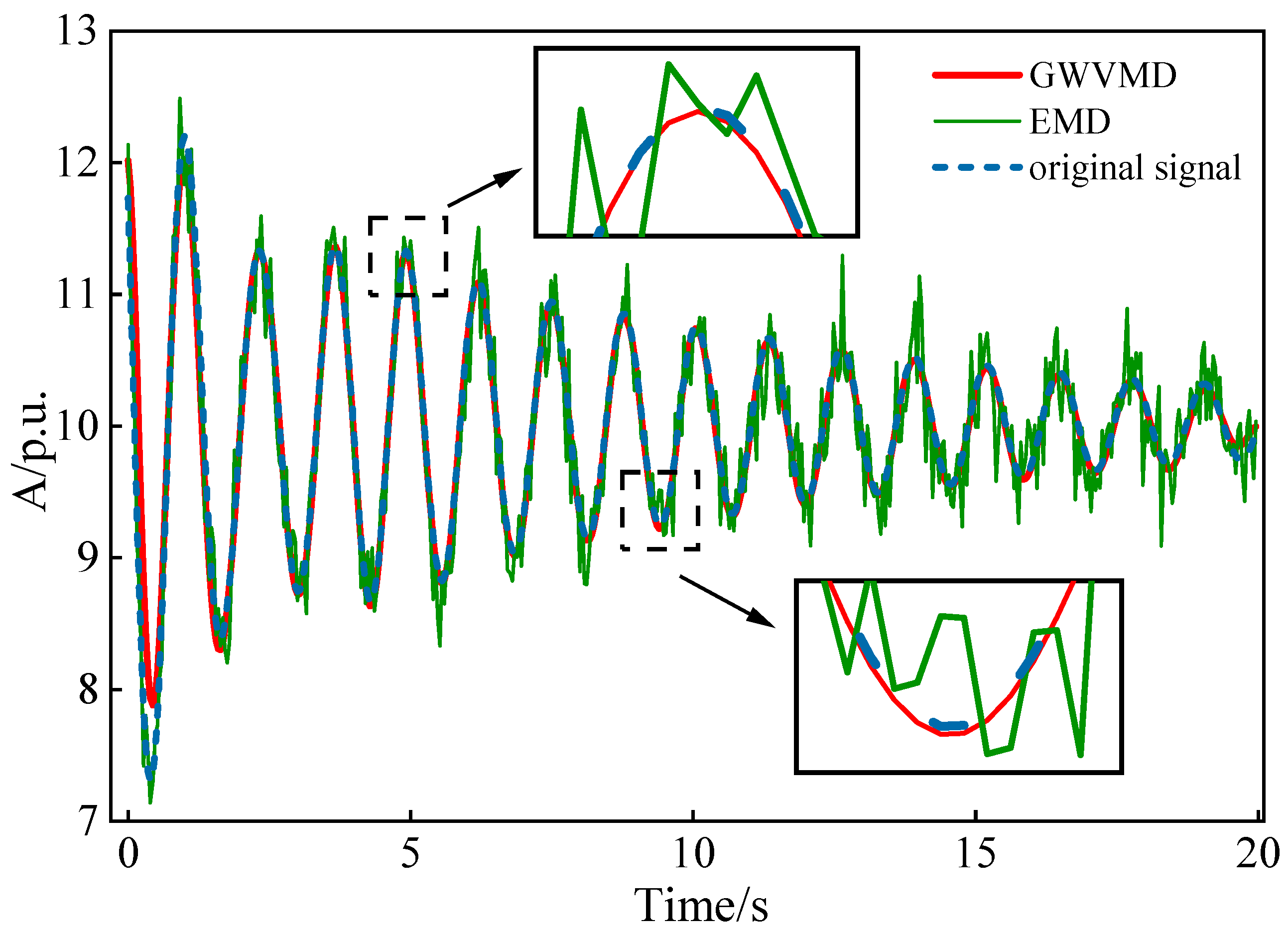
5.2. Hengshan Power Plant Unit Experiment
5.3. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, J.; Jie, H.; Zhou, Y.; Shao, H.; Zhao, S.; Du, Y.; Wang, J.; Sun, S.; Huang, Y.; Shen, Y. A low frequency oscillation suppression method for grid-connected DFIG with virtual inertia. Int. J. Electr. Power Energy Syst. 2023, 144, 108531. [Google Scholar] [CrossRef]
- Zou, X.; Du, X.; Tai, H. Stability analysis fo and direct-drive permanent magnet synchronous generator based wind farm integration system considering wind speed. IET Renew. Power Gener. 2020, 14, 1894–1903. [Google Scholar] [CrossRef]
- Shao, B.; Miao, Z.; Wang, L.; Meng, X.; Chen, Z. Low frequency oscillation analysis of two-stage photovoltaic grid-connected system. Energy Rep. 2022, 8, 241–248. [Google Scholar] [CrossRef]
- Chen, A.; Ba, Y.; Luo, X.; Huang, H.; Meng, L.; Shi, J. Strategy for grid low frequency oscillation suppression via VSC-HVDC linked wind farms. Energy Rep. 2022, 8, 1287–1295. [Google Scholar] [CrossRef]
- Chen, G.; Liu, C.; Fan, C.; Han, X.; Shi, H.; Wang, G.; Ai, D. Research on damping control index of ultra-low frequency oscillation in hydro-dominant power systems. Sustainability 2020, 12, 7316. [Google Scholar] [CrossRef]
- Rudnik, V.; Ufa, R.; Malkova, Y. Analysis of low frequency oscillation in power system with renewable energy sources. Energy Rep. 2022, 8, 394–405. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, L.; Guo, K.; Liu, Q. A review of research on low frequency oscillation damping control of power systems containing new energy generation access. Chin. J. Electr. Eng. 2017, 37, 6278–6290. [Google Scholar]
- Pourbeik, P.; Gibbard, M. Damping and synchronizing torques induced on generators by FACTS stabilizers in multimachine power systems. IEEE Trans. Power Syst. 1996, 11, 1920–1925. [Google Scholar] [CrossRef]
- Kundur, P.; Rogers, G.J.; Wong, D.Y.; Wang, L.; Lauby, M.G. A comprehensive computer program package for small signal stability analysis of power systems. IEEE Trans. Power Syst. 1990, 5, 1076–1083. [Google Scholar] [CrossRef]
- Li, S.; Ye, C.; Zhang, H.; Chen, D.; Zhu, Z. Overview of power system low frequency oscillation suppression based on DFIG power oscillation damper. Power Constr. 2022, 43, 25–33. [Google Scholar]
- Chai, H. Research on the Control Strategy of Suppressing Electromechanical Oscillation of Power Grid by Photovoltaic. Master’s Thesis, Shanxi University, Taiyuan, China, 2021. [Google Scholar]
- Chen, Q.; Fan, D.; Wang, C.; Liu, W.; Yuan, X.; Yuan, X. Small signal model of AC/DC distribution network and analysis of DC side low frequency oscillation. Power Eng. Technol. 2022, 41, 117–125. [Google Scholar]
- Dang, J.; Liu, D.; Zeng, C. Analysis of power system low frequency oscillation based on normal form theory of vector field. Power Sci. Eng. 2012, 28, 26–31. [Google Scholar]
- Mu, X.; Jiang, P.; Xu, M.; Cui, J.; Guan, W.; Liu, Z. Parameter identification of excitation system of a 600 MW unit in Heilongjiang based on time domain analysis. Heilongjiang Electr. Power 2019, 41, 495–498. [Google Scholar]
- Rai, S.; Lalani, D.; Nayak, S.K.; Jacob, T.; Tripathy, P. Estimation of low frequency modes in power system using robust modified Prony. IET Gener. Transm. Distrib. 2016, 10, 1401–1409. [Google Scholar] [CrossRef]
- Netto, M.; Mili, L. A Robust Prony Method for Power System Electromechanical Modes Identification. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Zhu, W.; Ma, J.; Zeng, Z.; Zhou, Y. Low frequency oscillation pattern recognition method based on segmented Fourier neural network. Power Syst. Prot. Control. 2012, 40, 40–45. [Google Scholar]
- Ge, W.; Yin, X.; Ge, Y.; Qu, C.; Huang, X.; Wang, C. Study on Pattern Recognition Method of Power System Low Frequency Oscillation Based on MEMD and HHT. Power Syst. Prot. Control 2020, 48, 124–135. [Google Scholar]
- Su, A.; Sun, Z.; He, X.; Zhang, Y.; Wang, C. Power System Low Frequency Oscillation Mode Identification Based on Multivariate Empirical Mode Decomposition. Power Syst. Prot. Control 2019, 47, 113–125. [Google Scholar]
- Wang, Y. Power System Low Frequency Oscillation Pattern Recognition Based on Deep Learning Algorithm. Master’s Thesis, South China University of Technology, Guangzhou, China, 2017. [Google Scholar]
- Wang, X. Research on Low Frequency Oscillation Mode Identification of Power System Based on Intelligent Computing. Master’s Thesis, South China University of Technology, Guangzhou, China, 2017. [Google Scholar]
- Ma, N.; Xie, X.; He, J.; Wang, H. Overview of research on broadband oscillation of power system with high proportion of new energy and power electronic equipment. Chin. J. Electr. Eng. 2020, 40, 4720–4732. [Google Scholar]
- He, P.; Chen, J.; Geng, S.; Shen, R.; Qi, P. Analysis of Low Frequency Oscillation Characteristics of Interconnected Systems with Wind Power by FACTS Devices. Power Syst. Prot. Control 2020, 48, 86–95. [Google Scholar]
- Wang, M.; Wu, Y. Simulation research on modal analysis of vibration system based on random decrement method. Electromechanical Technol. 2017, 5, 56–64. [Google Scholar]
- Li, Z.; Xiang, J.; Sheng, T.; Xiao, B. Time domain weighted sparse constraint space-time adaptive processing algorithm. J. Air Force Univ. Eng. (Nat. Sci. Ed.) 2020, 21, 87–92. [Google Scholar]
- Han, R.; Teng, Y.; Xie, J.; Wang, X.; Che, Y. Low frequency oscillation identification of power system based on improved STD method. Power Autom. Equip. 2019, 39, 58–63. [Google Scholar]
- Shen, Z.; Ding, R. A Novel Neural Network Approach for Power System Low Frequency Oscillation Mode Identification. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Yan, H.; Hwang, J.; Gao, Y. Power system low frequency oscillation modal parameter identification based on noise like data. Power Gener. Technol. 2022, 43, 19–31. [Google Scholar]
- Si, W.; Li, S.; Xiao, H.; Li, Q. PD characteristics and development degree assessment of oil-pressboard insulation with ball-plate model under 1:1 combined AC-DC voltage. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3677–3686. [Google Scholar] [CrossRef]
- Song, Y.; Liu, G.; Zhu, L.; Wang, J. Application of Improved Grey Wolf Optimization Algorithm in SVM Parameter Optimization. Sens. Microsyst. 2022, 41, 151–155. [Google Scholar]
- Wu, T.; Sun, K.; Shi, W. Research on cable partial discharge noise reduction based on AVMD adaptive wavelet packet method. Power Syst. Prot. Control. 2020, 48, 95–103. [Google Scholar]
- Wu, H.; Zhu, C.; Zhang, Y.; Long, Y. An adaptive typical day selection method based on improved fuzzy clustering algorithm. Smart Power 2022, 50, 60–67. [Google Scholar]
- Yong, T. Study on Power System Oscillation of Hydroelectric Units Containing High Permeability. Master’s Thesis, Northeastern Electric Power University, Jilin, China, 2020. [Google Scholar]
- Cheng, Y.; Ping, H.; Zhu, Y. Research on low-frequency oscillation of power system based on optimized VMD-HT algorithm. J. Jiangxi Electr. Power Vocat. Tech. Coll. 2022, 35, 7–10. [Google Scholar]
- Ouyang, Z. Research on the Analysis Method of Power System Pan-Band Oscillation Based on the Measured Signal. Master’s Thesis, Hunan University, Changsha, China, 2020. [Google Scholar]
- Zhang, C.; Qiu, B.; Liu, J. Low-frequency oscillation mode identification of power system based on EFEMD-HT energy method. South. Power Grid Technol. 2022, 16, 48–57. [Google Scholar]
- Zeng, X.; Xiao, H.; Wang, H.; Liu, J. Low-frequency oscillation mode parameter identification based on RDT and ERA algorithm. J. Electr. Power 2018, 33, 471–477. [Google Scholar]
- Zhu, J. Low-frequency oscillation mode identification of power system based on improved TLS-ESPRIT. Electr. Switch 2021, 59, 64–67. [Google Scholar]




| Parameter | Numerical Simulation | Hengshan Power Plant Signal |
|---|---|---|
| Number of wolves | 60 | 80 |
| Number of iterations | 100 | 150 |
| Dimensionality | 2 | 2 |
| Upper boundary of k | 5000 | 6000 |
| Lower boundary of k | 200 | 200 |
| Upper boundary of α | 10 | 12 |
| Lower boundary of α | 2 | 2 |
| Method | Component Number | SNR | Coef | MSE |
|---|---|---|---|---|
| EMD | 7 | 10.1724 | 0.9312 | 1.3145 |
| GWVMD | 5 | 21.3372 | 0.9971 | 0.7932 |
| Method | Type | Frequency | Damping Ratio | Frequency Error | Damping Ratio Error |
|---|---|---|---|---|---|
| Prony | Modal 1 | 0.5034 | 0.0351 | 0.0034 | 0.0033 |
| Modal 2 | 1.0177 | 0.0550 | 0.0177 | 0.0073 | |
| Modal 3 | 1.5401 | 0.0579 | 0.0401 | 0.0049 | |
| ITD | Modal 1 | 0.4973 | 0.0609 | 0.0027 | 0.0027 |
| Modal 2 | 0.9927 | 0.0283 | 0.0073 | 0.0194 | |
| Modal 3 | 1.4807 | 0.0489 | 0.0193 | 0.0041 | |
| HHT | Modal 1 | 0.5031 | 0.0425 | 0.0031 | 0.0107 |
| Modal 2 | 1.0086 | 0.0615 | 0.0086 | 0.0138 | |
| Modal 3 | 1.5162 | 0.0591 | 0.0162 | 0.0061 | |
| STD | Modal 1 | 0.5009 | 0.0541 | 0.0009 | 0.0011 |
| Modal 2 | 1.0034 | 0.0490 | 0.0034 | 0.0013 | |
| Modal 3 | 1.5087 | 0.0539 | 0.0087 | 0.0009 |
| Method | Component Number | SNR | Coef | MSE |
|---|---|---|---|---|
| EMD | 6 | 16.6903 | 0.8923 | 1.9223 |
| GWVMD | 4 | 21.9122 | 0.9773 | 1.0817 |
| Method | Component Number | SNR | Coef | MSE |
|---|---|---|---|---|
| EMVMD | 5 | 18.9127 | 0.9012 | 1.9223 |
| PSOVMD | 5 | 19.1947 | 0.9153 | 1.7037 |
| SVDVMD | 4 | 20.0011 | 0.9371 | 1.6939 |
| GWVMD | 4 | 21.9122 | 0.9773 | 1.0817 |
| Method | Type | Frequency | Damping Ratio | Frequency Error | Damping Ratio Error |
|---|---|---|---|---|---|
| Prony | Modal 1 | 0.7898 | 0.0313 | 0.0113 | 0.0191 |
| Modal 2 | 0.9946 | 0.0647 | 0.0134 | 0.0203 | |
| ITD | Modal 1 | 0.7906 | 0.0290 | 0.0121 | 0.0168 |
| Modal 2 | 0.9942 | 0.0636 | 0.0130 | 0.0192 | |
| HHT | Modal 1 | 0.7878 | 0.0339 | 0.0093 | 0.0217 |
| Modal 2 | 0.9954 | 0.0673 | 0.0142 | 0.0229 | |
| STD | Modal 1 | 0.7846 | 0.0246 | 0.0061 | 0.0124 |
| Modal 2 | 0.9893 | 0.0591 | 0.0081 | 0.0147 |
| Method | Type | Frequency | Damping Ratio | Frequency Error | Damping Ratio Error |
|---|---|---|---|---|---|
| EFEMD-HT | Modal 1 | 0.7868 | 0.0300 | 0.0083 | 0.0178 |
| Modal 2 | 0.9919 | 0.0636 | 0.0107 | 0.0192 | |
| RDT-ERA | Modal 1 | 0.7876 | 0.0305 | 0.0091 | 0.0183 |
| Modal 2 | 0.9925 | 0.0641 | 0.0113 | 0.0197 | |
| TLS-ESPRIT | Modal 1 | 0.7859 | 0.0280 | 0.0074 | 0.0158 |
| Modal 2 | 0.9911 | 0.0605 | 0.0099 | 0.0161 | |
| GWVMD-STD | Modal 1 | 0.7846 | 0.0246 | 0.0061 | 0.0124 |
| Modal 2 | 0.9893 | 0.0591 | 0.0081 | 0.0147 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Wu, Z.; Dong, Z.; Yang, S. Modal Identification of Low-Frequency Oscillations in Power Systems Based on Improved Variational Modal Decomposition and Sparse Time-Domain Method. Sustainability 2022, 14, 16867. https://doi.org/10.3390/su142416867
Liu L, Wu Z, Dong Z, Yang S. Modal Identification of Low-Frequency Oscillations in Power Systems Based on Improved Variational Modal Decomposition and Sparse Time-Domain Method. Sustainability. 2022; 14(24):16867. https://doi.org/10.3390/su142416867
Chicago/Turabian StyleLiu, Lei, Zheng Wu, Ze Dong, and Shaojie Yang. 2022. "Modal Identification of Low-Frequency Oscillations in Power Systems Based on Improved Variational Modal Decomposition and Sparse Time-Domain Method" Sustainability 14, no. 24: 16867. https://doi.org/10.3390/su142416867
APA StyleLiu, L., Wu, Z., Dong, Z., & Yang, S. (2022). Modal Identification of Low-Frequency Oscillations in Power Systems Based on Improved Variational Modal Decomposition and Sparse Time-Domain Method. Sustainability, 14(24), 16867. https://doi.org/10.3390/su142416867






