Optimization of Resource Allocation in Automated Container Terminals
Abstract
1. Introduction
2. Literature Review
3. Modeling the Handling Operations in Container Terminals
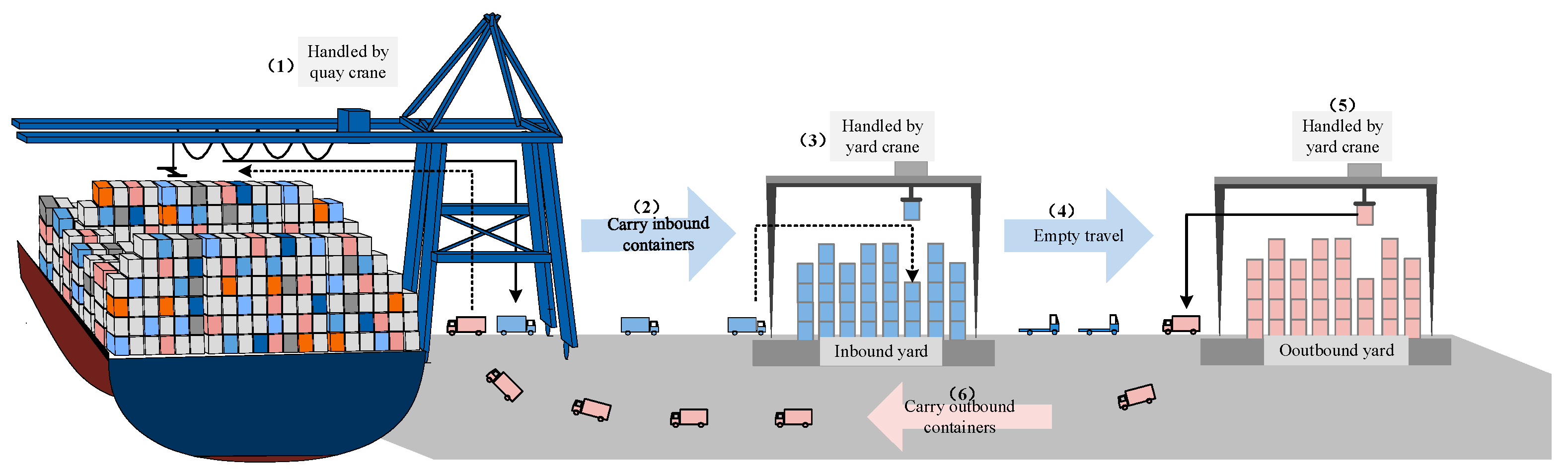
3.1. Problem Description
- Specific information of the vessels and task assignments is not considered, because this paper provides an estimation of the system performance from the long-time run;
- The service times at all stations are assumed to follow exponential distributions. Exponential distribution is used, and we ignore the impact of it on the results because we mainly focus on the analysis of double cycling. The results of Koenigsberg and Lam [21] show there is small difference between the exponential and normal distributions;
- All servers have an FCFS (first come first service) policy;
- The buffer size of each queue is unlimited;
- All the AGVs complete an import and export container in a cycle;
- Road congestion is not considered in this paper.
3.2. Product Form Equilibrium
3.3. Performance Analysis
4. Resource Allocation Optimization
4.1. Resource Allocation Model
4.2. Performance Calculation
5. Numerical Experiments
5.1. Convex Behavior of the Objective Function
5.2. Validity of the Proposed Model
5.2.1. Operation Time
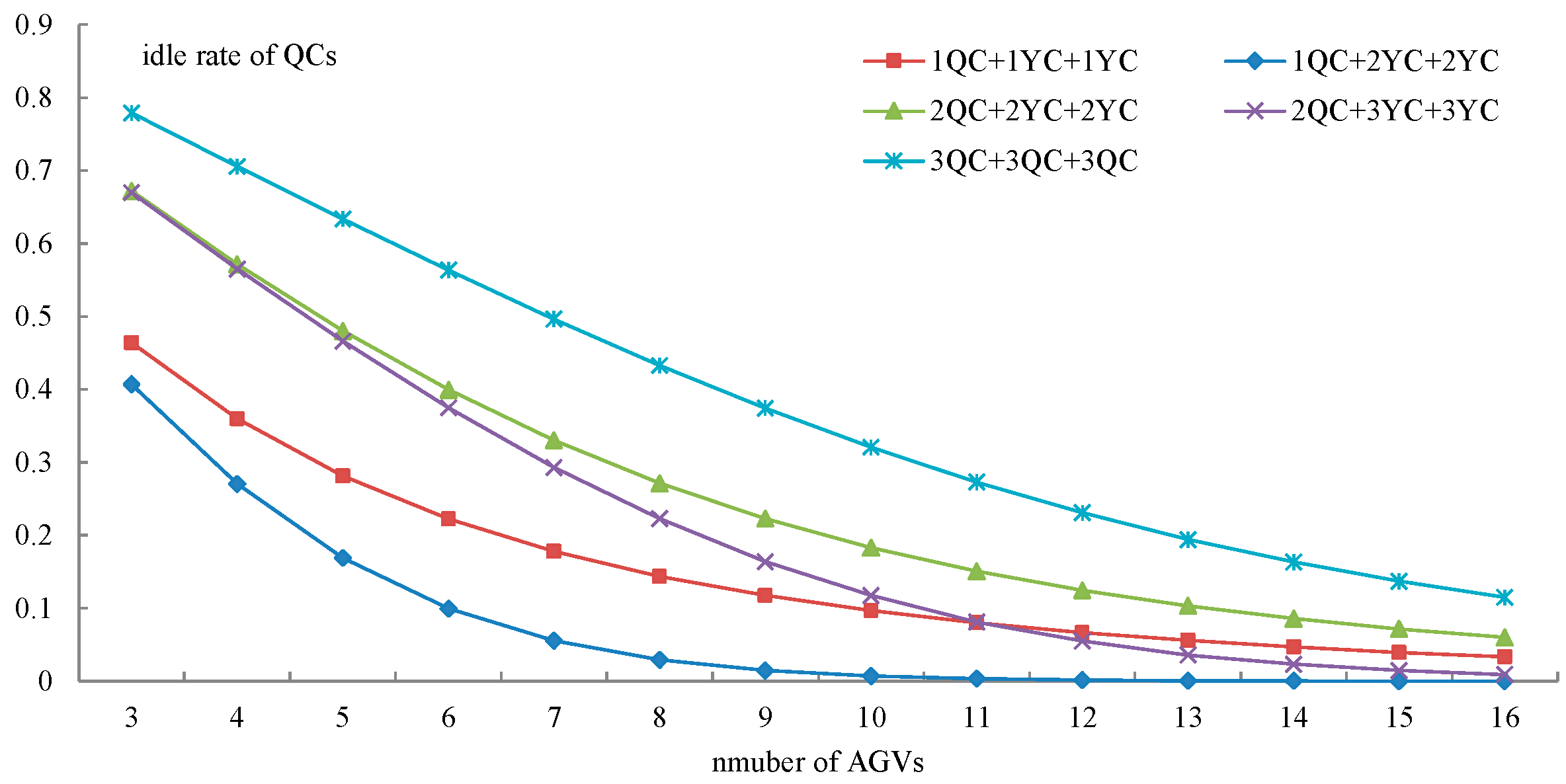
5.2.2. Idle Rate of QCs and YCs
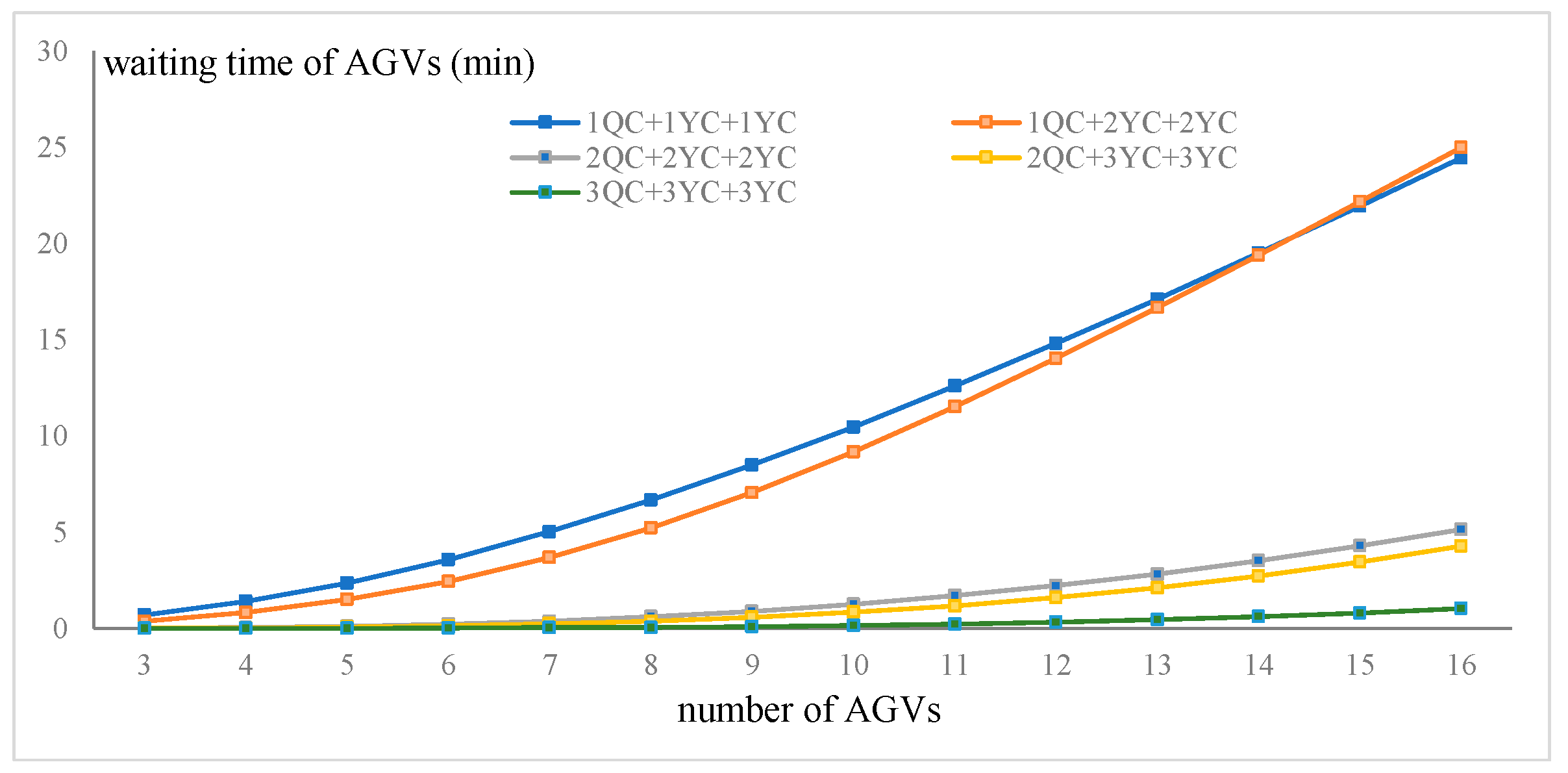
5.2.3. Waiting Time of AGVs
5.3. Sensitive Analysis
5.4. Resource Allocation Insights
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Goodchild, A.V.; Daganzo, C.F. Double-cycling strategies for container ships and their effect on ship loading and unloading operations. Transp. Sci. 2006, 40, 473–483. [Google Scholar] [CrossRef]
- Goodchild, A.V.; Daganzo, C.F. Crane double cycling in container ports: Planning methods and evaluation. Transp. Res. Part B Methodol. 2007, 41, 875–891. [Google Scholar] [CrossRef]
- Zhang, R.; Jin, Z.; Ma, Y.; Luan, W. Optimization for two-stage double-cycle operations in container terminals. Comput. Ind. Eng. 2015, 83, 316–326. [Google Scholar] [CrossRef]
- Lee, C.Y.; Liu, M.; Chu, C. Optimal Algorithm for the General Quay Crane Double-Cycling Problem. Transp. Sci. 2015, 49, 957–967. [Google Scholar] [CrossRef]
- Speer, U.; Fischer, K. Scheduling of Different Automated Yard Crane Systems at Container Terminals. Transp. Sci. 2016, 51, 305–324. [Google Scholar] [CrossRef]
- Vis, I.F.A.; de Koster, R.M.B.M.; Savelsbergh, M.W.P. Minimum vehicle fleet size under time-window constraints at a container terminal. Transp. Sci. 2015, 39, 249–260. [Google Scholar] [CrossRef]
- Liu, C.-I.; Jula, H.; Vukadinovic, K.; Ioannou, P. Automated guided vehicle system for two container yard layouts. Transp. Res. Part C Emerg. Technol. 2004, 12, 349–368. [Google Scholar] [CrossRef]
- Petering, M. Effect of block width and storage yard layout on marine container terminal performance. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 591–610. [Google Scholar] [CrossRef]
- Petering, M. Development and simulation analysis of real-time, dual-load yard truck control systems for seaport container transshipment terminals. OR Spectrum 2010, 32, 633–661. [Google Scholar] [CrossRef]
- Sauri, S.; Morales-Fusco, P.; Enrique, M.; Benítezm, P. Comparing Manned and Automated Horizontal Handling Equipment at Container Terminals. Transp. Res. Rec. 2014, 2409, 2014. [Google Scholar] [CrossRef]
- Kang, S.; Medina, J.C.; Ouyang, Y. Optimal operations of transportation fleet for unloading activities at container ports. Transp. Res. Part B Methodol. 2008, 42, 970–984. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, Q.; Sheu, J.-B. Modeling the productivity and stability of a terminal operation system with quay crane double cycling. Transp. Res. Part E Logist. Transp. Rev. 2019, 122, 181–197. [Google Scholar] [CrossRef]
- Roy, D.; Nigam, S.; de Koster, R.; Adan, I.; Resing, J. Robot-storage zone assignment strategies in mobile fulfillment systems. Transp. Res. Part E Logist. Transp. Rev. 2019, 122, 119–142. [Google Scholar] [CrossRef]
- George, D.K.; Xia, C.H. Fleet-sizing and service availability for a vehicle rental system via closed queuing networks. Eur. J. Oper. Res. 2011, 211, 198–207. [Google Scholar] [CrossRef]
- Hu, L.; Liu, Y. Joint design of parking capacities and fleet size for one-way station-based carsharing systems with road congestion constraints. Transp. Res. Part B Methodol. 2016, 93, 268–299. [Google Scholar] [CrossRef]
- Mishra, N.; Roy, D.; Ommeren, J.K.V. A Stochastic Model for Interterminal Container Transportation. Transp. Sci. 2017, 51, 61–87. [Google Scholar] [CrossRef]
- Roy, D.; De Koster, R.; Bekker, R. Modeling and Design of Container Terminal Operations. Oper. Res. 2020, 68, 686–715. [Google Scholar] [CrossRef]
- Roy, D.; de Koster, R. Stochastic modeling of unloading and loading operations at a container terminal using automated lifting vehicles. Eur. J. Oper. Res. 2015, 266, 895–910. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C. Modeling and analysis for an automated container terminal considering battery management. Comput. Ind. Eng. 2021, 156, 107258. [Google Scholar] [CrossRef]
- Alessandri, A.; Sacone, S.; Siri, S. Modelling and optimal receding-horizon control of maritime container terminals. J. Math. Model. Algorithm 2007, 6, 109–133. [Google Scholar] [CrossRef]
- Koenigsberg, E.; Lam, R.C. Cyclic queue models of fleet operations. Oper. Res. 1976, 24, 516–529. [Google Scholar] [CrossRef]
- Gordon, W.J.; Newell, G.F. Closed queuing systems with exponential servers. Oper. Res. 1967, 15, 254–265. [Google Scholar] [CrossRef]
- Shanthikumar, J.G.; Yao, D.D. Second-order properties of the throughput of a closed queuing network. Math. Oper. Res. 1988, 13, 524–534. [Google Scholar] [CrossRef]
- Buzen, J.P. Computational algorithms for closed queuing networks with exponential servers. Commun. ACM 1973, 16, 527–531. [Google Scholar] [CrossRef]
- Ruscheweyh, S.; Sheil-Small, T. Hadamard products of Schlicht functions and the Pólya-Schoenberg conjecture. Comment. Math. Helv. 1973, 48, 119–135. [Google Scholar] [CrossRef]




| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Expected service rate of QCs (moves per minute) | 0.35 | Expected travel time from inbound yard blocks to outbound yard blocks (min) | 5 |
| Expected travel time from quayside to inbound yard blocks (min) | 3.57 | Expected service rate of YCs at outbound yard blocks (moves per minute) | 0.49 |
| Expected service rate of YCs at inbound yard blocks (moves per minute) | 0.41 | Expected travel time from quayside to outbound yard blocks (min) | 3.45 |
| Total containers (TEU) | 4000 | Cost of QCs per unit time | 4.5 |
| Cost of YCs per unit time | 1.75 | Cost of AGVs per unit time | 1 |
| Resource Allocation Schedules | Number of AGVs | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 1QC + 1YC + 1YC | 3520 | 3149 | 3015 | 3000 | 3050 | 3141 | 3256 | 3389 | 3534 | 3688 | 3848 | 4014 | 4183 | 4355 |
| 1QC + 2YC + 2YC | 4473 | 3852 | 3602 | 3546 | 3600 | 3718 | 3872 | 4044 | 4226 | 4413 | 4602 | 4792 | 4982 | 5173 |
| 2QC + 2YC + 2YC | 5484 | 4368 | 3730 | 3341 | 3098 | 2950 | 2866 | 2827 | 2820 | 2837 | 2871 | 2918 | 2974 | 3038 |
| 2QC + 3YC + 3YC | 6503 | 5119 | 4313 | 3806 | 3479 | 3270 | 3145 | 3082 | 3066 | 3084 | 3128 | 3189 | 3262 | 3344 |
| 3QC + 3YC + 3YC | 7773 | 6046 | 5015 | 4335 | 3861 | 3519 | 3268 | 3084 | 2951 | 2857 | 2794 | 2756 | 2738 | 2736 |
| Resource Allocation Schedules | Number of AGVs | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 1QC + 1YC + 1YC | 317 | 260 | 230 | 213 | 202 | 195 | 190 | 187 | 185 | 183 | 182 | 182 | 181 | 180 |
| 1QC + 2YC + 2YC | 304 | 245 | 216 | 200 | 193 | 189 | 187 | 186 | 186 | 186 | 186 | 186 | 187 | 187 |
| 2QC + 2YC + 2YC | 286 | 216 | 176 | 150 | 134 | 122 | 114 | 108 | 104 | 101 | 98 | 97 | 95 | 94 |
| 2QC + 3YC + 3YC | 285 | 215 | 174 | 148 | 130 | 118 | 109 | 103 | 100 | 97 | 95 | 94 | 94 | 93 |
| 3QC + 3YC + 3YC | 285 | 214 | 171 | 143 | 123 | 109 | 98 | 90 | 84 | 79 | 75 | 72 | 70 | 67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, H.; Wu, M. Optimization of Resource Allocation in Automated Container Terminals. Sustainability 2022, 14, 16869. https://doi.org/10.3390/su142416869
Zhang X, Li H, Wu M. Optimization of Resource Allocation in Automated Container Terminals. Sustainability. 2022; 14(24):16869. https://doi.org/10.3390/su142416869
Chicago/Turabian StyleZhang, Xiaoju, Huijuan Li, and Meng Wu. 2022. "Optimization of Resource Allocation in Automated Container Terminals" Sustainability 14, no. 24: 16869. https://doi.org/10.3390/su142416869
APA StyleZhang, X., Li, H., & Wu, M. (2022). Optimization of Resource Allocation in Automated Container Terminals. Sustainability, 14(24), 16869. https://doi.org/10.3390/su142416869






