Modelling of a Wave Energy Converter Impact on Coastal Erosion, a Case Study for Palm Beach-Azur, Algeria
Abstract
1. Introduction
2. Materials and Methods
2.1. SWAN Mathematical Model
2.2. Wave Refraction Calculation
- The energy attenuation when Ks < 1 (wave divergence);
- The conservation of energy when Ks = 1 (rectilinear wave propagation);
- The concentration of energy when Ks > 1 (convergence of waves).
Application of the Model
- Refraction on the bottoms and around the structures;
- Friction on the bottom;
- Surge.
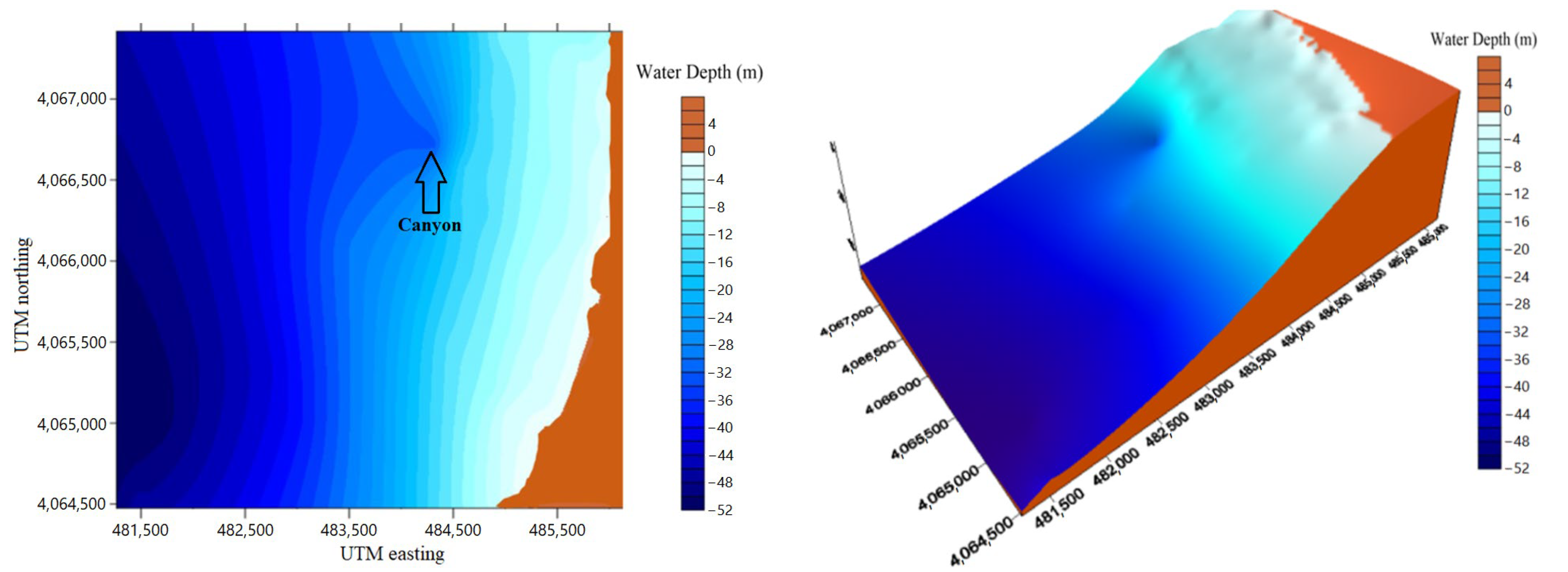
2.3. Bathymetry Data
2.4. Offshore Swell Data
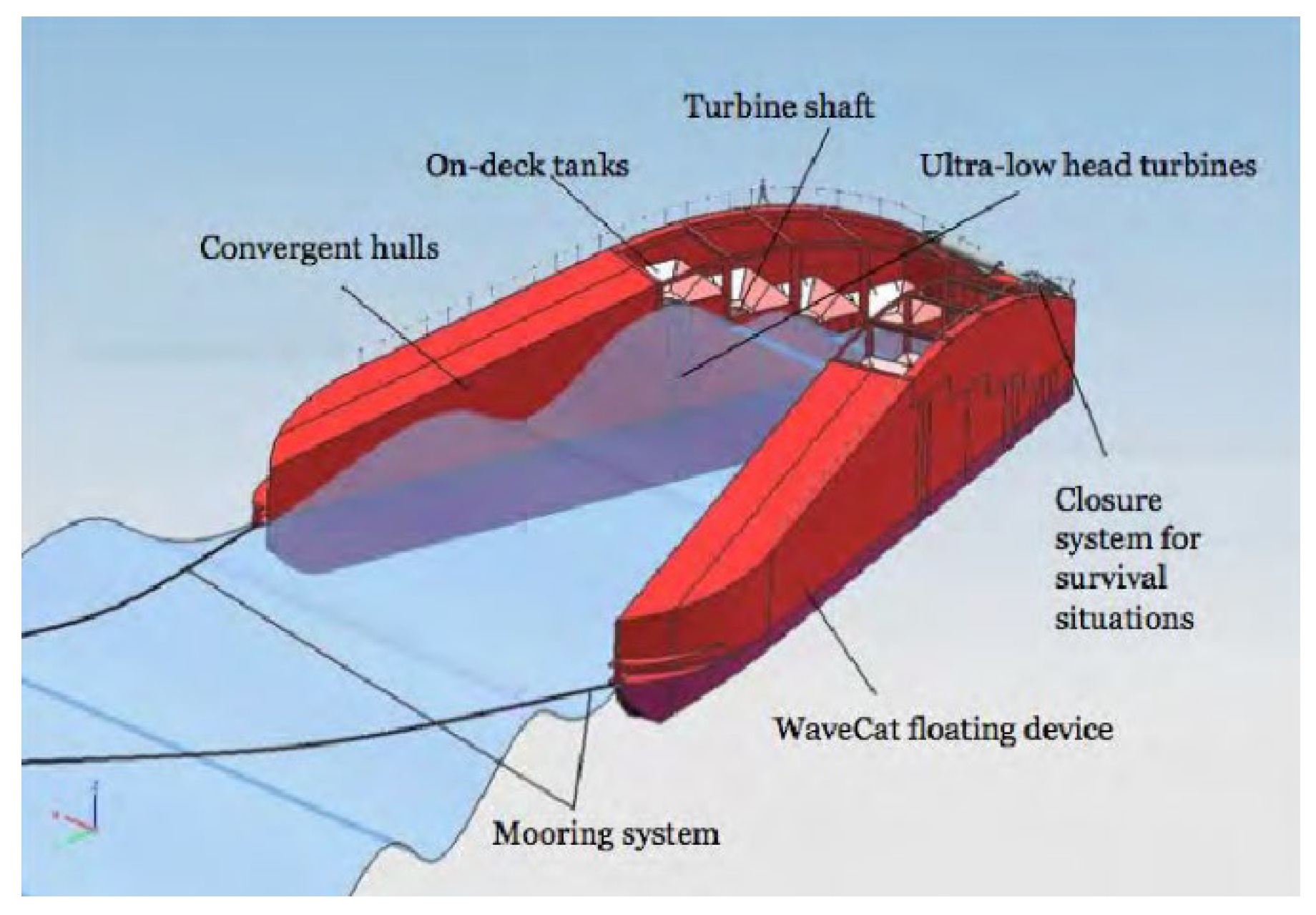
2.5. WEC Type and Integration Data
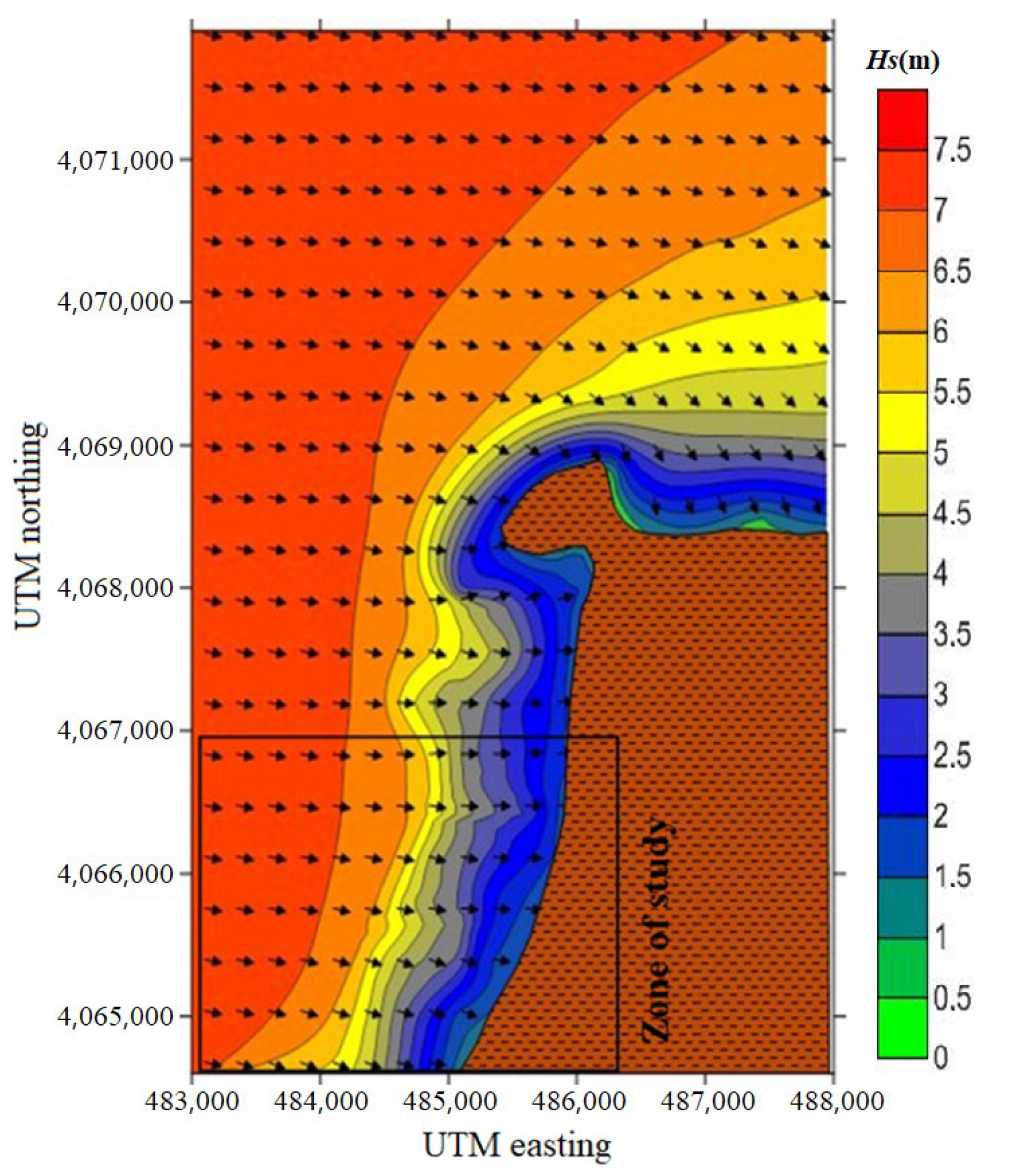
3. Zone of Study
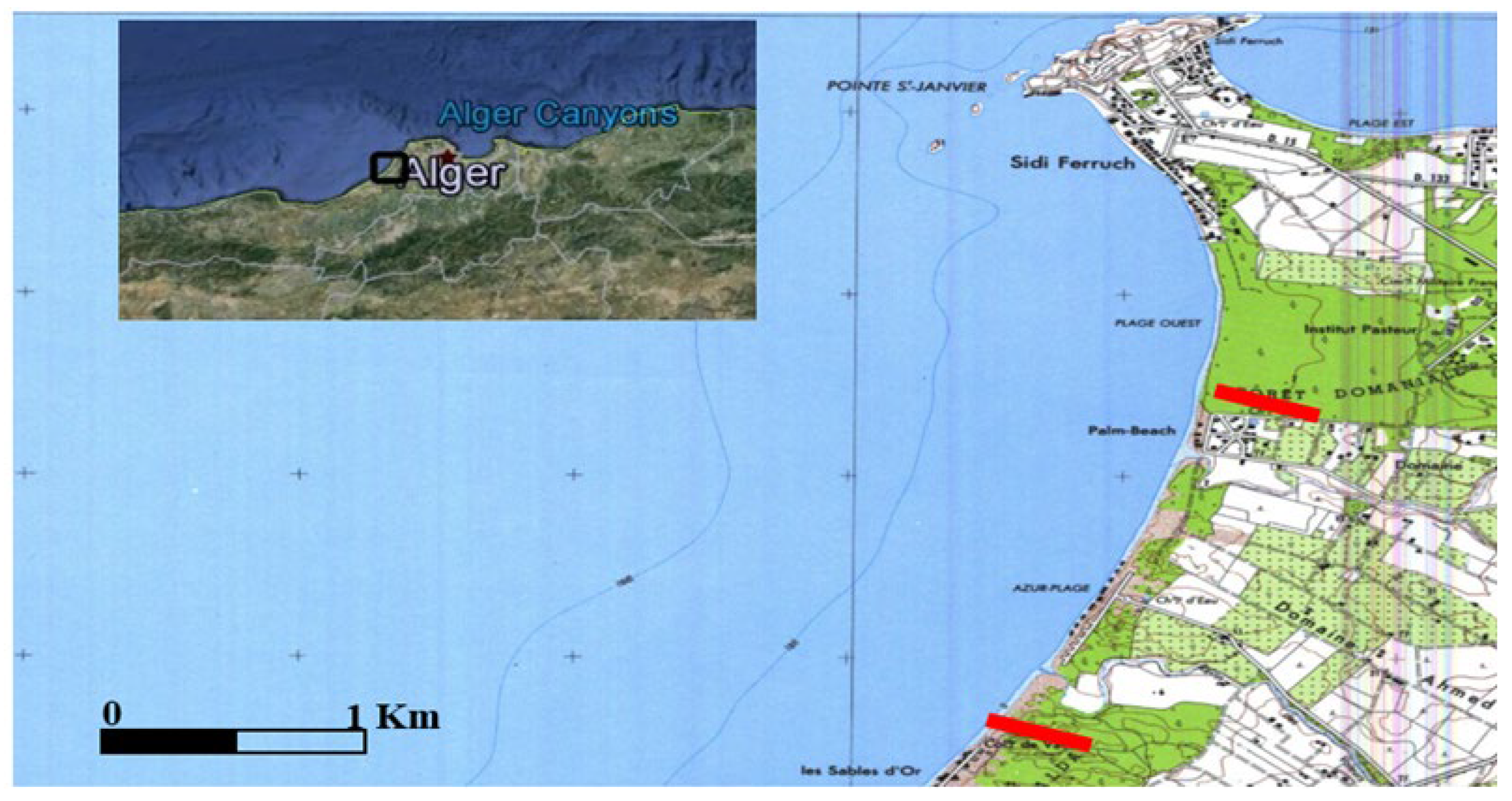
3.1. Geographical Location
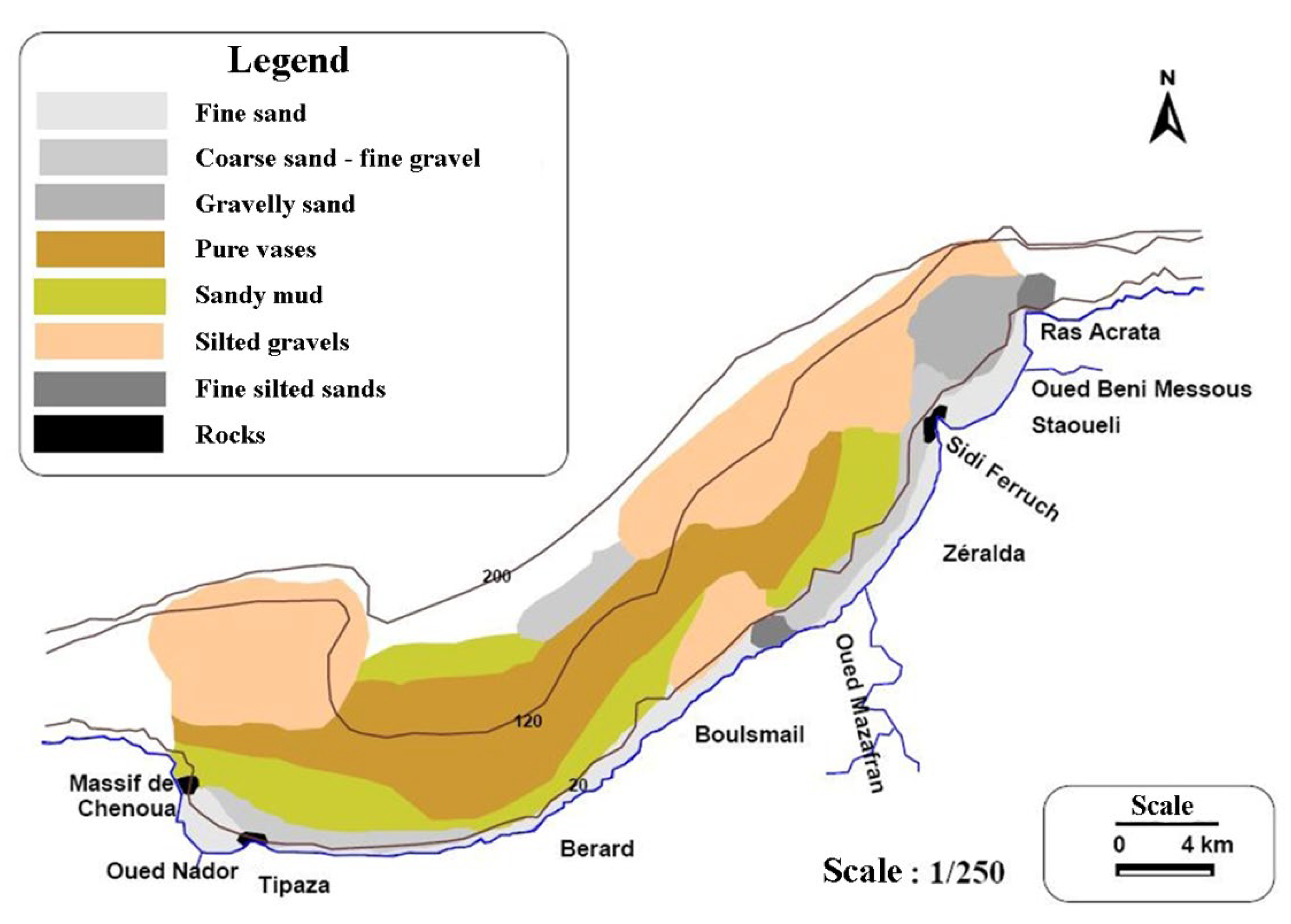
3.2. Sedimentology of The Zone of Study
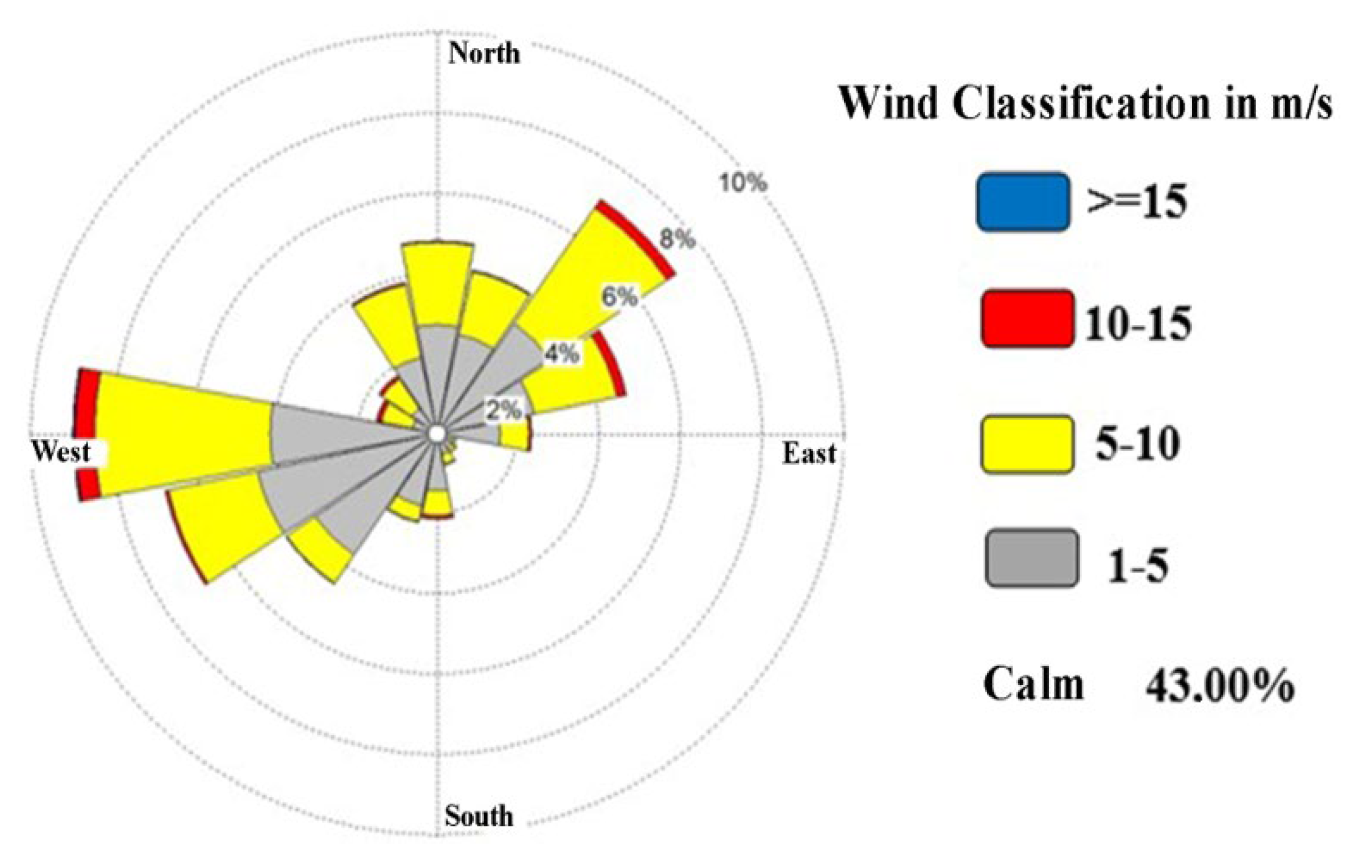
3.3. Climate and Wind Data
- I.
- A winter period (October-March), with prevailing winds from the west, with a frequency ranging from 60 to 80%;
- II.
- During summer (April-September), the prevailing winds are from the east and the northeast, with 45 to 75% frequencies for the northeast direction.
3.4. The Sea Swells
- The highest appearance frequencies are related to those swells from the west, east, and northeast. The weakest ones are recorded for swells in the north and north-west directions;
- The frequencies of observations over the year of the easterly and westerly swells are roughly identical. However, a slight predominance of the eastern sector exists.
- I.
- In winter: western swells dominate with the majority of amplitudes of 1 and 3 m and can reach up to 4 m;
- II.
- In summer: The most dominant swells come from the northeast sector with smaller amplitudes, and the swells from the west are quite significant.
4. Results
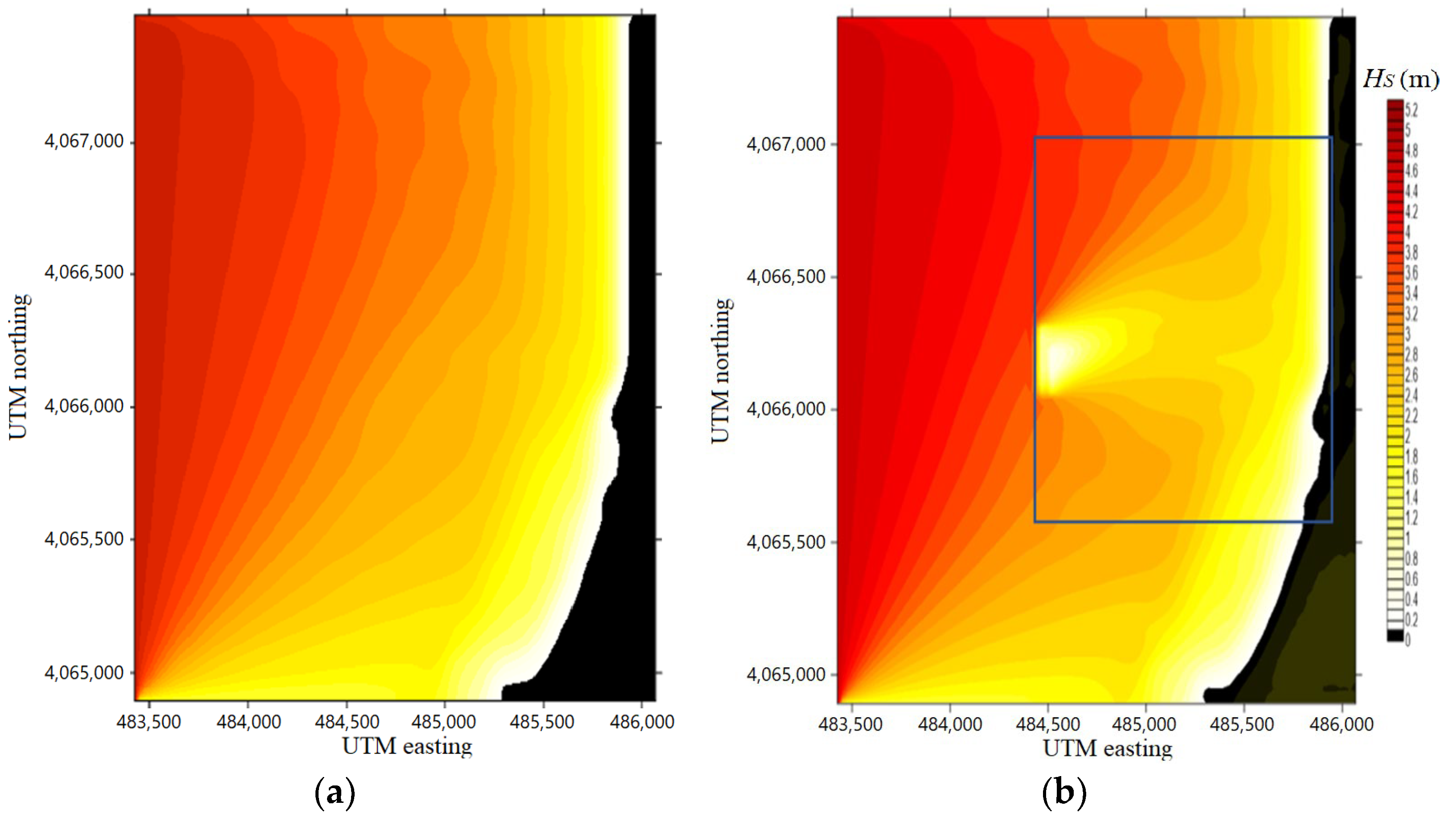
4.1. Wave Modelling
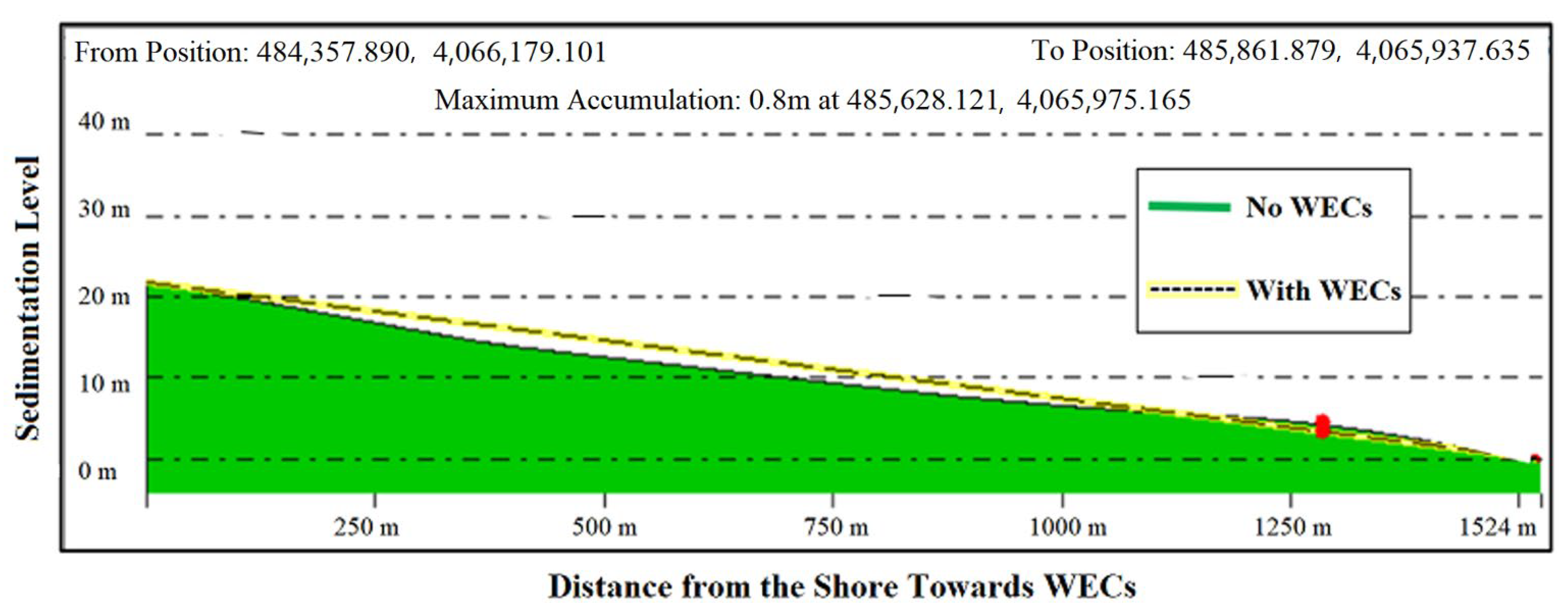
4.2. Sedimentation Pattern near Wave Energy Converters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef]
- Antonio, F.D.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- McCormick, M.E. Ocean Wave Energy Conversion; Dover Publications: Mineola, NY, USA, 2007; p. 233. [Google Scholar]
- Thorpe, T.W. A brief review of wave energy. In Harwell Laboratory, Energy Technology Support Unit; AEA Technology: UK, 1999. [Google Scholar]
- Atan, R.; Finnegan, W.; Nash, S.; Goggins, J. The effect of arrays of wave energy converters on the nearshore wave climate. Ocean Eng. 2019, 172, 373–384. [Google Scholar] [CrossRef]
- Chang, G.; Ruehl, K.; Jones, C.A.; Roberts, J.; Chartrand, C. Numerical modeling of the effects of wave energy converter characteristics on nearshore wave conditions. Renew. Energy 2016, 89, 636–648. [Google Scholar] [CrossRef]
- Greaves, D.; Iglesias, G. Wave and tidal energy. In Wave and Tidal Energy; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Contardo, S.; Hoeke, R.; Hemer, M.; Symonds, G.; McInnes, K.; O’Grady, J. In situ observations and simulations of coastal wave field transformation by wave energy converters. Coast. Eng. 2018, 140, 175–188. [Google Scholar] [CrossRef]
- Gonçalves, M.; Martinho, P.; Guedes Soares, C. Wave energy conditions in the western French coast. Renew. Energy 2014, 62, 155–163. [Google Scholar] [CrossRef]
- Guillou, N.; Chapalain, G. Numerical modelling of nearshore wave energy resource in the Sea of Iroise. Renew. Energy 2015, 83, 942–953. [Google Scholar] [CrossRef]
- Iglesias, G.; López, M.; Carballo, R.; Castro, A.; Fraguela, J.A.; Frigaard, P. Wave energy potential in Galicia (NW Spain). Renew. Energy 2009, 34, 2323–2333. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave energy potential along the Death Coast (Spain). Energy 2009, 34, 1963–1975. [Google Scholar] [CrossRef]
- Mendes, R.P.G.; Calado, M.R.A.; Mariano, S.J.P.S. Wave energy potential in Portugal–Assessment based on probabilistic description of ocean waves parameters. Renew. Energy 2012, 47, 1–8. [Google Scholar] [CrossRef]
- Appendini, C.M.; Urbano-Latorre, C.P.; Figueroa, B.; Dagua-Paz, C.J.; Torres-Freyermuth, A.; Salles, P. Wave energy potential assessment in the Caribbean Low Level Jet using wave hindcast information. Appl. Energy 2015, 137, 375–384. [Google Scholar] [CrossRef]
- Garcia, C.; Canals, M. Wave energy resource assessment and recoverable wave energy in Puerto Rico and the US Virgin Islands. In Proceedings of the MTS/IEEE OCEANS 2015—Genova: Discovering Sustainable Ocean Energy for a New World, Genova, Italy, 18–21 May 2015. [Google Scholar]
- Sierra, J.P.; Martín, C.; Mösso, C.; Mestres, M.; Jebbad, R. Wave energy potential along the Atlantic coast of Morocco. Renew. Energy 2016, 96, 20–32. [Google Scholar] [CrossRef]
- Khan, A.; Xie, W.; Zhang, B.; Liu, L.W. A survey of interval observers design methods and implementation for uncertain systems. J. Frankl. Inst. 2021, 358, 3077–3126. [Google Scholar] [CrossRef]
- Khan, A.; Xie, W.; Liu, L.W. Set-membership interval state estimator design using observability matrix for discrete-time switched linear systems. IEEE Sens. J. 2020, 20, 6121–6129. [Google Scholar] [CrossRef]
- Choupin, O.; Andutta, F.P.; Etemad-Shahidi, A.; Tomlinson, R. A decision-making process for wave energy converter and location pairing. Renew. Sustain. Energy Rev. 2021, 147, 111225. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- SWAN Team—SWAN User Manual, Delft University of Technology. 2022. Available online: https://swanmodel.sourceforge.io/ (accessed on 11 October 2022).
- Carballo, R.; Iglesias, G. Wave farm impact based on realistic wave-WEC interaction. Energy 2013, 51, 216–229. [Google Scholar] [CrossRef]
- GEBCO. (n.d.). GEBCO—The General Bathymetric Chart of the Oceans. Available online: https://www.gebco.net/ (accessed on 6 January 2022).
- SSMO. Summary of Synoptic Meteologic Observations: Mediteranean Marine Areas; U.S Naval weather service Command: Kiln, MS, USA, 1970; Volume 2, 632p. [Google Scholar]
- Fernandez, H.; Iglesias, G.; Carballo, R.; Castro, A.; Fraguela, J.A.; Taveira-Pinto, F.; Sanchez, M. The new wave energy converter WaveCat: Concept and laboratory tests. Mar. Struct. 2012, 29, 58–70. [Google Scholar] [CrossRef]
- Belkacem, Y. Intégration des Mesures in situ et des Données Satellitaires dans un Système D’information Géographique pour Caractériser les eaux Côtières. Ph.D. Thesis, University of sciences and technology Hourai-Boumedien, Algiers, Algeria, 2010. [Google Scholar]
- LEM (Laboratoire des Études Maritimes). Etude de Délimitation d’une Zone d’extraction de Sable sur la Baie d’Alger; Maritime Studies Laboratory of Algeria: Algiers, Algeria, 1998. [Google Scholar]
- National Office of Meteorology. Available online: https://www.aps.dz (accessed on 10 January 2021).
- Zemenzer, S. Ensablement du port par transport sédimentaire simulation et application du modèle de Gao et Collins (1994) au port de Sidi Fredj; Mémoire d’ingéniorat, Institut de Sciences de la Mer et de l’Aménagement du Littoral: Dély Ibrahim, Alger, 2004. [Google Scholar]


| Offshore Swell Direction | Peak Period (S) | Significant Height Offshore (m) |
|---|---|---|
| N 340° | 8 | 6.8 |
| N 30° | 9 | 7 |
| N 280° | 10 | 8 |
| Parameters | No WECs | With WECs |
|---|---|---|
| Average of Hs (m) | 2.56 | 2.26 |
| Average ΔHs (m) | 0.3 | |
| Average ΔHs (%) | 30% | |
| Shoaling Coefficient Ks | 0.512 | 0.452 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradi, M.; Chertouk, N.; Ilinca, A. Modelling of a Wave Energy Converter Impact on Coastal Erosion, a Case Study for Palm Beach-Azur, Algeria. Sustainability 2022, 14, 16595. https://doi.org/10.3390/su142416595
Moradi M, Chertouk N, Ilinca A. Modelling of a Wave Energy Converter Impact on Coastal Erosion, a Case Study for Palm Beach-Azur, Algeria. Sustainability. 2022; 14(24):16595. https://doi.org/10.3390/su142416595
Chicago/Turabian StyleMoradi, Mehrdad, Narimene Chertouk, and Adrian Ilinca. 2022. "Modelling of a Wave Energy Converter Impact on Coastal Erosion, a Case Study for Palm Beach-Azur, Algeria" Sustainability 14, no. 24: 16595. https://doi.org/10.3390/su142416595
APA StyleMoradi, M., Chertouk, N., & Ilinca, A. (2022). Modelling of a Wave Energy Converter Impact on Coastal Erosion, a Case Study for Palm Beach-Azur, Algeria. Sustainability, 14(24), 16595. https://doi.org/10.3390/su142416595








