Abstract
A traditional logistics decision model mainly studies the location decision of logistics distribution centers, storage inventory management, vehicle scheduling, and transportation routes. The logistics location-inventory-routing problem (LIRP) is an integrated optimization of the three problems—a comprehensive optimization problem for the whole logistics system. This review paper uses the PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analysis) method to review the literature on LIRP systematically. A total of 112 LIRP-related studies published between 2010 and 2021 are reviewed and classified based on 10 abstract and citation databases. The classification includes four aspects: problem characteristics, demand data types, model-based solutions, and application fields. From this systematic review, a few observations are recorded. First, the most popular problems among researchers are the multi-period multi-product problem, the multi-echelon single-link problem, and the multi-depot multi-retailer problem. Based on the objective function, the minimization of total supply chain cost is the primary concern of the LIRP literature. Researchers also favor other problem characteristics such as multi-objective programming, inventory control replenishment policy, and a homogeneous fleet of vehicles. We found that stochastic data are a common factor in an uncertain environment and have broad coverage. When dealing with the LIRP, heuristic and metaheuristic algorithms are the most widely used solution methodologies in the literature. In the application field of LIRP, the perishable products logistics network is mentioned in most applications. Finally, we discuss and emphasize the challenges of and recommendations for future work. This paper provides a systematic review of the literature on LIRP based on the PRISMA method, which contributes vital support and valuable information for researchers interested in LIRP.
1. Introduction
There has been significant development of networks and logistics, which has seen logistics distribution receiving increasing attention and development. For a long time, logistics management mainly focused on the location selection of distribution centers (DCs), inventory control, and vehicle routing arrangements. These three factors are classified according to the strategic, tactical, and operational levels of a logistics system. Therefore, modern logistics enterprises need to make decisions: firstly, the location of the DCs; secondly, the optimal inventory of these DCs; and finally, on the route through which vehicles carry the goods to the customers. A standard network structure is shown in Figure 1.
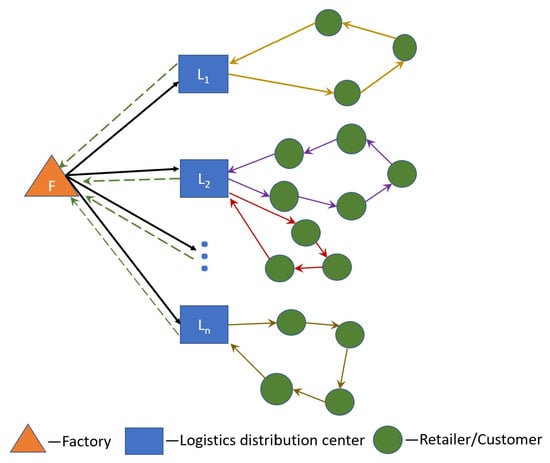
Figure 1.
Schematic diagram of secondary distribution network.
The logistics of DCs play an increasingly important role in enterprise circulation, where an enterprise’s success directly depends on its ability to connect various resources. As a result, solving the logistics distribution center location problem leads to positive impact in terms of improving inventory turnover, accelerating commodity circulation, and reducing costs. On the other hand, the inventory control system belongs to the ordering system of the DC. Its primary purpose is to control the inventory of the DC. This includes efforts to determine the best inventory and order point for proper storage, reduced costs and unnecessary transportation links, and shortened circulation cycles of materials. Vehicle routing controls the distribution of the goods to the customers. For example, the demand for goods and delivery, delivery time, vehicle capacity constraints, mileage, and the time limit are constrained in order to achieve specific goals (such as the shortest vehicle mileage, the lowest total cost of transportation, the shortest time for a vehicle to reach a particular place, the minimum number of vehicles utilized, etc.). One does note that the more warehouses are used, the shorter shipping routes are achieved and the satisfaction of service customers is higher, but this increases operating costs. The location-inventory-routing problem (LIRP) of a logistics system is essentially a trade-off between benefits and costs. For the system to function optimally, a balance must be struck. As a result, the LIRP needs to be studied from a systems perspective.
Many industries have acknowledged that global supply chain optimization can significantly reduce costs [1]. Factory location, inventory control, and vehicle routing play vital roles in the global optimization of a supply chain network. In addition, these three issues are interdependent. The authors of [2] pointed out that location decisions often lead to suboptimal solutions when routing decisions are ignored. In addition, ignoring the facility location problem of inventory control will lead to a wrong system cost estimation [3]. Moreover, the authors of [4] showed that when they considered “combining these three decisions in one model”, significant savings could be realized. Therefore, it is essential to conduct a study on the combination of location, inventory, and routing.
Logistics service networks are designed to achieve different goals, ranging from low total supply chain cost (TSCC) to high responsiveness. In order to enhance their total profitability and competitiveness, the logistics service network plays an important role in supply chain management [5]. Comprehensive optimization and supply chain activity management ought to be based on this relationship. In addition to the DC location problem, integration problems such as the location-routing problem (LRP), inventory-routing problem (IRP), location-inventory problem (LIP), and LIRP are also studied [6].
There have been in-depth and fruitful studies on LIP, LRP, and IRP. Though one can find related work on LIRP [7,8,9,10,11], these problems are not LIRP in the strictest sense. Regarding transportation decisions, these studies mainly considered the mode of transportation rather than the vehicle routing arrangement under the direct distribution mode. It is generally believed that [12], published in 2003, is the first known result on LIRP. The authors established a mathematical model of the location path problem for inventory control decision-making and presented a two-stage heuristic algorithm. In 2005, Ref. [13] proposed a globally optimal heuristic algorithm to solve LIRP based on the algorithms by [12].
The systematic review presented here mainly studies the supply chain logistics of the LIRP literature from 1 January 2010 to 31 December 2021. The main contribution of this systematic review is the application of the LIRP-oriented PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analysis) method based on the problem characteristics, demand data types, model-based solutions, and application fields. Most of the existing review papers only focus on the combined optimization problems of LIP, LRP, and IRP, but in this study, we extend the review to three integrated optimization problems of location, inventory, and routing. To the best of our knowledge, previous literature reviews of LIRP have only reviewed a small number of works, and there has been no systematic review of LIRP that considered the PRISMA method.
This paper is organized as follows. Section 2 looks at previous review papers on the pairwise association of location, inventory, and routing. Section 3 introduces a method based on PRISMA’s systematic review process. In Section 4, various LIRPs are reviewed according to the suggested classifications for problem characteristics, demand data types, and model-based solutions. Section 5 provides an overview of current trends, eight types of application areas, and quantitative analysis of the observations. In Section 6, future challenges and recommendations for LIRP are presented, such as multi-levels, green, multi-links, shortages, time windows, supply chain disruption risk, low carbon environmental protection, and the uncertain demand of the LIRP. Finally, Section 7 draws conclusions related to LIRP for systematic reviews.
2. Previous Review Papers
Most of the existing review papers focus on the integration of LRP, IRP, and LIP. The authors of [14] discussed the development of the LIP modeling literature and provide a table summarizing the characteristics of published papers. They also include objective functions, cost components, and key modeling properties. The authors reviewed the LIP literature from 1976 to 2013 and noted that most of the actual case studies are published only a few years before their paper. The paper shows that industry practitioners and researchers are increasingly interested in the topic and are concerned about practical applications of the models developed in the study.
As for the review of LRP, Ref. [15] defined the standard LRP as a deterministic, static, discrete, single-echelon, and single-objective problem in which each customer (vertex) must be visited once for the delivery of a good from a facility, and there is also no correlation with inventory decisions. A review of the LRP literature from 2006 to 2014 is presented following the classification of variations on this problem, providing readers with concise excerpts of papers to convey the central ideas of each work and discussing the latest developments in the field. In addition, Ref. [16] conducted a review study, and the selected LRP articles are divided into five main categories: (a) research type, (b) deployed solutions, (c) problem scenario characteristics, (d) problem physical characteristics, and (e) the objective functions considered in the model. Each item had subcategories, among which the subcategories of (d) and (e) followed the classification of [15]. Some of these specifications are reviewed in this paper.
Furthermore, for the review of IRP, Ref. [17] mentioned the “basic version” that most IRP research focuses on, as well as the “extension of basic version” in more detail. The literature is classified and reviewed based on seven criteria: time frame, structure, route, inventory strategy, inventory decision, fleet form, and fleet capacity. However, the specific databases and techniques utilized in selecting papers are not mentioned. In some categories of practical application problems, Ref. [17] only discussed the benchmark examples. Similarly, Refs. [18,19,20,21,22,23,24] are reviews of IRP models and classification of solutions; Refs. [21,22] both proposed the concept of sustainable logistics management. However, Ref. [25] only studied the literature review of IRP for suppliers to determine the quantity allocated to retailers. We identified and discussed two kinds of problem classifications for this review paper: (a) benchmark examples and (b) practical applications.
In summary, the current literature only reviews the two integration optimization problems with minimal mention of the three integrated LIRP works of literature. Although Ref. [26] reviewed a small number of articles on LIRP (11 papers), it does not explicitly propose the authors’ review methods. Table 1 presents their research focus and is grouped according to the time horizon of the reviewed papers and the number of papers reviewed.

Table 1.
Previous review papers.
3. Research Methodology
In this study, the PRISMA method is used to provide a systematic review on the literature related to LIRP. PRISMA’s preferred reporting project is a 27-item checklist that is used to improve the transparency of systematic reviews [27]. It synthesizes studies, provides a high level of perspective on evidence, and is less subject to subjective factor bias. These items cover all aspects of the papers, including title, abstract, introduction, method, results, discussion, funding, etc. This technique is the smallest set of evidence-based items in systems evaluation and meta-analysis reports [28]. It is designed to help reviewers explain the purpose of the review and the methodologies employed and to report the findings of the work [28]. Scholars have extensively applied the PRISMA method in many scientific fields [29]. This is particularly true in medicine, where clinical practice guidelines and protocols are developed. PRISMA is also used in the field of transmission area [30].
3.1. Data Collection Methods
In this subsection, the research questions, inclusion criteria, exclusion criteria, and PRISMA four-phase flow diagram are discussed. This paper systematically combs the literature, mainly aiming at the following research questions:
- What is the classification of LIRP based on the type of problem and the characteristics of variables?
- What are the model-based solutions for LIRP?
- What are the current trends of LIRP?
- What are the challenges and future work directions of LIRP in real-world applications?
In PRISMA, research objectives and problems, keywords, and a set of inclusion and exclusion criteria are developed. In this paper, we evaluate these criteria based on the problem characteristics, data types in demand, model-based solutions, and application fields of LIRP. In addition, location, inventory, and routing are treated as equally important. This results in the selection of “location-inventory-routing problem” OR “location inventory routing problem” OR “inventory location routing problem” OR “location routing inventory problem” OR “LIRP” OR “ILRP” OR “LRIP” as the search keywords. We use search terms (such as “location” AND “inventory” AND “routing”) in database searches to make sure the search focused on the literature related to mathematics and computer science, particularly pattern formulation, rather than social-science-related research in supply chain logistics.
Based on the PRISMA guidelines, 10 abstract and citation databases (AIMS, NSTL, IEEE Xplore, Web of Science, Google Scholar, ScienceDirect, Scopus, Springer Link, Taylor & Francis Online, and Wiley Online Library) are searched by title, abstract, and content of the paper. The search is conducted in March 2022 and is limited to works published between 1 January 2010, and 31 December 2021.
As shown in Figure 2, the retrieval results are shown as a flow diagram. First, there are 1456 records in the search results. After removing non-English books, chapters, editorials, reports, and articles, the number of searches is reduced to 927. After a corresponding assessment of titles and abstracts related to inclusion and exclusion criteria, the total number of papers is further reduced to 339. The following studies are eligible for inclusion:
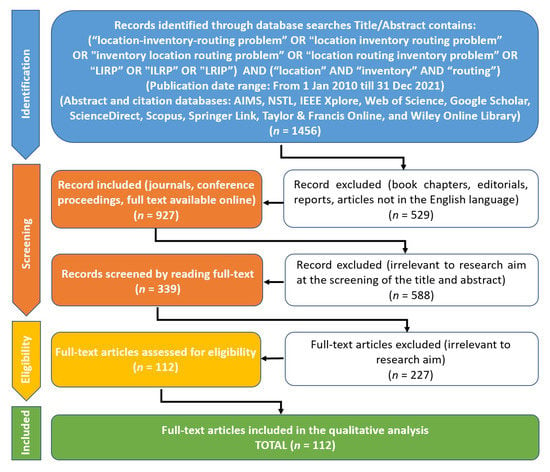
Figure 2.
PRISMA four-phase flow diagram.
- Papers retrieved must be published in proceedings of peer-reviewed international journals or international conferences in the English language.
- The topic must include (but is not limited to) at least one paper on location inventory path, covering logistics location, inventory decision, and route optimization decision.
- The article must have at least one essential attribute related to the title, keywords, abstract, and body content mentioned previously.
As a result, 227 articles are found irrelevant to the study and are deleted, leaving 112 articles. Articles on software or system development, economy-related analysis, and user balance issues regarding LIRP research, such as in [31], are excluded from this systematic review.
3.2. Descriptive Statistics
After collecting the papers, inductive statistics are carried out as below. The descriptive analysis of the 112 selected papers based on the year of publication shows increasing interest in the topic of LIRP for over a decade since 2010, as shown in Figure 3.
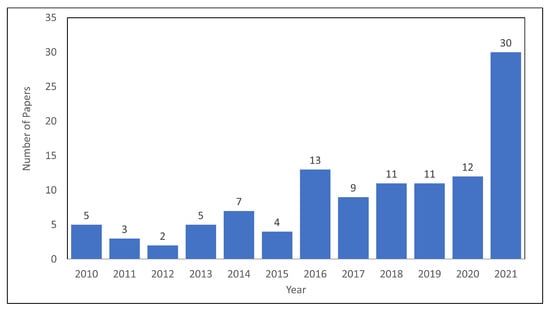
Figure 3.
Publication trend from 2010 to 2021.
As shown in Table 2, the distribution of papers over the years is according to the type of papers published, i.e., journal or conference papers. From Table 3, the number of papers published in international journals is increasing yearly. Table 3 shows that most of the papers on LIRP are published by Elsevier, which is a well-known high-grade academic journal. As a whole, publication in such academic journals indicates that the level of LIRP papers has increased, and the trend in this table shows that LIRP has attracted more and more attention from researchers in the past decade.

Table 2.
Distribution of papers based on type of publication over the years.

Table 3.
Publisher overview of LIRP publications.
Table 4 shows the real-world data set used in the selected literature. It can be summarized that 44 out of 112 articles tested their algorithms using real-world data sets.

Table 4.
Distribution of the literature that used real-world data (based on year).
3.3. Category Classification
In this subsection, the selected literature is grouped and classified. Table 5 gives the classification of the LIRP. This classification is divided into four different categories. The first category is problem characteristics, which is further divided into three subcategories according to inventory, route, and logistics of DCs. First, based on inventory characteristics, Refs. [32,33] proposed a classification of the number of periods and products (P-P). For this variant, there are four different subcategories representing single-period single-product (Single-Single), single-period multi-product (Single-Multi), multi-period single-product (Multi-Single), and multi-period multi-product (Multi-Multi). Secondly, Ref. [34] focuses on the echelons of supply chain management and the quantity classification of links between customers, which can also be divided into three subcategories. They are single-echelon single-link (Single-Single), multi-echelon single-link (Multi-Single), and multi-echelon multi-link (Multi-Multi). Thirdly, Ref. [34] also studied the number of depots (or DCs) and the quantity classification of retailers (or customers) in supply chain management. This can be divided into two subcategories: single-depot multi-retailer (Single-Multi) and multi-depot multi-retailer (Multi-Multi).

Table 5.
Classification of the LIRP.
The second category is classified according to the characteristics of the demand data [35]. The demand data types studied in this systematic review are classified as deterministic, variable, stochastic, and fuzzy. The third category is based on the models and solutions to the problem, which is used in [33] to review the literature. The models include mixed integer programming (MIP), mixed integer linear programming (MILP), and mixed integer nonlinear programming (MINLP), where MIP includes both linear (MILP) and nonlinear (MINLP) models. In addition, the solutions include exact algorithm, heuristic and metaheuristic, mixed exact and heuristic and metaheuristic, and other approaches. The fourth and final category is based on application areas, which include E-commerce logistics system (ECLS), hazmat supply chain (HSC), perishable products logistics network (PPLN), cold-chain logistics network (CCLN), environmentally sustainable supply chain (ESSC), humanitarian supply chain (HUSC), healthcare logistics (HEL), and other logistics supply chain management.
4. Review of Literature
This section reviews 112 selected papers from the past decade in detail and systematically based on the suggested classifications shown in Table 5. In each subsection below, we discuss a variety of works, including variations, approaches to the problem, proposed solutions, and challenges the authors solved. The first and second research questions mentioned in Section 3.1 are addressed in this section.
4.1. Classification based on Problem Characteristics
4.1.1. LIRP Classification Based on Inventory Periodicity and Quantity of Productions
Single-Period Single-Product Problem (SPSPP)
The researchers in [36] proposed research on integrated LRIP based on the time window (TW) of a stochastic demand single-level logistics distribution network with SPSPP. From the perspective of logistics integration, the integrated LRIP model of logistics integration is established under the condition of random demand, and a particle swarm optimization (PSO) algorithm is designed to solve the problem. A real example is considered where a beverage company plans to redesign its distribution network in the central and northern Jiangsu region of China.
Next, Ref. [37] considered that the distribution of a single product from a business firm’s retailer through a series of warehouses could be located on different booking sites, but these requirements may vary from one period to the next. The assumption that the product is perishable in their model means that it has a specific shelf life. This particular shelf life is measured by the number of time periods, so the model takes the form of a single period. It is also assumed that there will never be a shortage. A retailer’s inventory level is limited by two constraints: the actual capacity of the retail store and the product warranty period. Therefore, MIP is established, and the general algebraic modeling system (GAMS) is used to solve small problem instances.
Interestingly, Ref. [38] presented three key problems of logistics center location, inventory strategy, and vehicle routing selection for SPSPP in ECLS design based on the MIP model. A pseudo parallel genetic algorithm (PPGA) combined with simulated annealing (SA) is proposed, and benchmark data experiments verify the model’s validity.
Single-Period Multi-Product Problem (SPMPP)
In the global supply chain cost and environmental impact minimization problem, it is common to consider the multi-product supply chain location, inventory, production, distribution, transportation mode selection, and other functions of the mathematical model within a single period to achieve the overall optimization.
The authors of [39] proposed that the numerical values obtained from actual companies can be applied to the LIRP of SPMPP transportation, which not only determines optimal transport routes, inventory levels, volumes and modes of transport, but also considers supply chain networks with environmental responsibility issues such as CO emissions. The research result of the literature provides a new allocation for the global supply chain development of real firms such as the European Union while minimizing both economic and environmental impacts. In addition, Ref. [40] put forward the concept of period, that is, “the mobile facility performs its closed tour in a time interval”. In the case of a single period, numerical results are given for setting the average cost of the supply chain for different product quantities.
Multi-Period Single-Product Problem (MPSPP)
It is also common to consider an MPSPP supply chain design, usually based on an inventory management strategy. The work of [41] proposed the LIRP as a supply chain design method that considers inventory management and routing costs, overcoming the need to decompose decisions as in conventional methods, which leads to suboptimal solutions. The decisions made in the paper include the (1) location of the warehouse, (2) inventory of two levels of the supply chain, (3) distribution from the retailer to the warehouse, and (4) multi-period route. A variety of products are considered as one unit without considering different strategies for different products. A hybrid algorithm for supply-chain optimization is proposed using exact methods to estimate distribution costs while the rest of the path decision is calculated by a heuristic program. By switching between decision space and information sharing, the hybrid optimization algorithm could optimize all parts of the problem globally without oversimplifying the problem. The results of the randomly generated examples show that the sequential heuristic that simulates the traditional sequential approach saves a lot of cost and is computationally efficient compared to the commercial solver.
In [42], the authors argued that each customer has different needs for a single product in different periods and is served by different fleet types. A MIP model is used to describe the problem. Since business solutions cannot solve this complex problem, a heuristic algorithm derived from a generalized variable neighborhood search (GVNS) is proposed to solve the MIP model of LIRP. For [43], the LIRP of an MPSPP closed-loop supply chain (CLSC) with single product, multiple suppliers, manufacturers, DCs, customers, and recycling centers is studied. The problem is transformed into a two-objective MINLP model. Two metaheuristic algorithms—a non-dominated sorting genetic algorithm II (NSGA-II) and a multi-objective particle swarm optimization (MOPSO)—are used to solve the problem. In [44], by taking the perishable products logistics network (PPLN) as the research object, the paper studied the multi-period LIRP of perishable products in the case of path disruption within a certain period. In this model, the retailer’s price is a decreasing function of time and product life. The MINLP model aims to maximize the total profit (TP) of a logistics network system. An efficient genetic algorithm (GA) is developed to solve the actual large-scale data type problem better.
The work in [45] presented a novel multi-period LIRP for the red meat supply chain in an emerging economy with a heterogeneous fleet of vehicles (HEFV) and logistics decisions. A MILP model is established and verified by available GAMS software, and a case study of Iran is given. In [46], a multi-period LIRP with TW and fuel consumption under the condition that a single product meets the needs of retailers is proposed. The author incorporated fuel consumption into the variable transportation cost, which better reflects real-life situations. This problem simultaneously optimizes the location, routing, and inventory decisions of DCs and customers in multi-level supply chains and is expressed by an MINLP model. Then, a two-stage hybrid metaheuristic algorithm is proposed to solve the problem. In the first stage, a custom GA is proposed. In the second stage, the gradient descent algorithm is used to improve the inventory decision to further reduce the total cost [46].
Multi-Period Multi-Product Problem (MPMPP)
The MPMPP is more suitable for an actual logistics supply chain situation; hence, more research is related to this aspect. In [47], LRIP of the MPMPP optimization model with random customer demand is proposed, and hybrid GA is proposed to solve the model. The work in [48] studied the multi-objective integration model of LIRP in the MPMPP supply chain system. In addition, the model also takes into account the probabilistic travel time between retailers. Considering these complexities, the model is closer to the problems in real life. In a practical scenario, multiple industries in the MPMPP system make location-routing-inventory decisions and interactions simultaneously. A multi-objective imperialist competitive algorithm was also proposed to solve the bi-objective LIRP of the MPMPP distribution system in [48]. The authors in [49] studied the LIRP decision of the MPMPP in a three-level supply chain, including suppliers, warehouses, and customers. The products are delivered from the warehouse to the customer by the homogeneous fleet of vehicles (HOFV). A hybrid integer programming formula is proposed to describe the problem, and a new hybrid heuristic algorithm is designed to solve the model based on SA and an imperialist competition algorithm.
Next, Ref. [50] studied a new multi-period, multi-echelon, and multi-product fuel supply chain integration model and obtained its global optimal solution. Its main features are the design of an integrated supply chain model that considers both pipeline routes and facility installation and expansion, optimizing location allocation of facilities and routes, capacity expansion, inventory, production, import and export, as well as routes and modes of transportation in a wide geographical area. In order to achieve this goal, a deterministic MILP based on the information of the Iranian fuel chain is proposed and applied to a practical problem. A number of scenario and sensitivity analyses are proposed for different cases to deepen the model further.
The work of [51] proposed a new bi-objective LIRP, which considered the MPMPP with HEFV in two-stage distribution networks. One paper [52] established an MPMPP sustainable CLSC model under mixed uncertainty. The model combined the routing decision, inventory decision, and location allocation decision. The authors of [32] established a comprehensive and reliable supply chain distribution network; integrated location selection, inventory, and route decision into an MPMPP model; and proposed a new bi-objective MINLP method. Moreover, in order to minimize the total cost of inventory, which includes the cost of ordering, holding and shortage, as well as the cost of route transportation, this model also minimizes the total cost of failures associated with disruptions at of distribution centers, thus ensuring the reliability of the supply chain network. A metaheuristic method is proposed to solve the model.
In addition, Ref. [53] studied a three-echelon LIRP with MPMPP and established a comprehensive PPLN model within a limited time range. Then, the optimal solution of this MINLP is solved by a Lagrangian relaxation algorithm, and the feasibility analysis is performed by a heuristic algorithm. The authors of [33] analyzed the integrated fuzzy model with minimum delay in the LIRP of PPLN with multiple products considering environmental constraints. A multi-period model with three main objective functions is designed to minimize the TSCC, network time, and the amount of pollution caused by supply chain activities. The NSGA-II and the Pareto-based selection algorithm (PESA)-II are used to solve the model. Note that [54] extended a new MILP model of MPMPP to establish pharmacies and hospitals regarding the environmental impact of the entire green HEL and green effects related to CO emissions from transport vehicles.
4.1.2. LIRP Classification Based on Echelons and Links
Single-Echelon Single-Link Problem (SESLP)
Among the literature that studied the SESLP are [36,41,55,56]. The research of [55] gives a solution to finding an optimal or approximately optimal solution in a reasonable time, which requires a powerful heuristic algorithm to compute. This is done by integrating with inventory and routing to develop a custom heuristic technique to address the proposed model [55]. In [56], the authors established a MILP model of LIRP for a polluting environmental supply chain and used a CPLEX solver in MATLAB to solve the problem.
Multi-Echelon Single-Link Problem (MESLP)
Multi-echelon is a common situation in a logistics system, and the distance between two sites is also directly observed when the path is generally considered (a single link). The multi-echelon batch problem with setup time has received much attention in the previous operational and optimization literature. For example, [57] proposed several MIP formulas with a setup time for the MPMPP and MESLP models. The work in [58] studied the configuration of a three-echelon dual-sales channel supply chain network consisting of one supplier, one DC, and two types of customers.
Moreover, Refs. [48,49,59,60,61,62,63] also put forward the LIRP to describe a MESLP logistics distribution system. The work in [59] studied a class of two-echelon inventory decision problems with one depot and multiple retailers. Piecewise linearization is used to convert the resulting MINLP into a MIP, and CPLEX is used to solve it. Then, Ref. [60] established an MINLP model with four levels of supply, production, distribution, and demand under the condition of uncertain demand. The authors designed 10 large-scale sample problems that GAMS could not solve. Instead, the proposed GA obtained the approximate solution in a reasonable time.
The authors of [61] proposed a new LIR model for CCLN and used NSGA-II to solve the MINLP model. The image of the CCLN system is shown in Figure 4; it is a two-echelon single-link problem. The work in [62] described a MESLP supply chain that includes suppliers, business firms, DCs, and customers. Modeled after MINLP, their strategy is to use a network data envelopment analysis (NDEA) to calculate the association efficiency so that the GA would have a better selection performance. Next, Ref. [63] considered a system consisting of MESLP and used historical data to approximate the needs of each customer. A practical case is taken as an example to build a MILP model, and subsequently, the general GAMS software is used to solve the data set of actual cases. The work of [64] analyzed the influence of service time on TSCC of a two-echelon CCLN, and the improved multi-objective ant colony optimization (MACO) algorithm is used to give the solution of the multi-objective programming (MOP) of the LIRP.
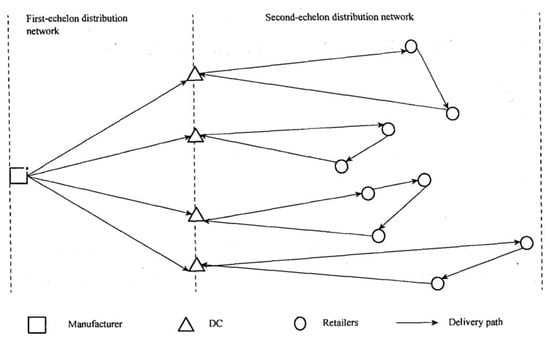
Figure 4.
LIRP in cold-chain logistics system (two-echelon single-link) (source: [61]).
Multi-Echelon Multi-Link Problem (MEMLP)
The authors of [34] applied the heuristic LIRP model method to the city of Jakarta in Indonesia. Two links are considered in the paper, where Link 1 (blue) is the longer distance and Link 2 (green) is the shorter distance. The diagram of the system studied is shown in Figure 5, which includes two supplier provinces, two UCCs (Urban Consolidation Centers), four traditional markets (TMs), and two links. The results obtained in the literature indicate that vehicles on longer routes (blue) have a higher capacity than vehicles on urban (shorter) (green) routes [34]. Note that [65] designed three types of vehicle links simultaneously when optimizing the explosive waste network: direct route, sightseeing route, and round-trip route.
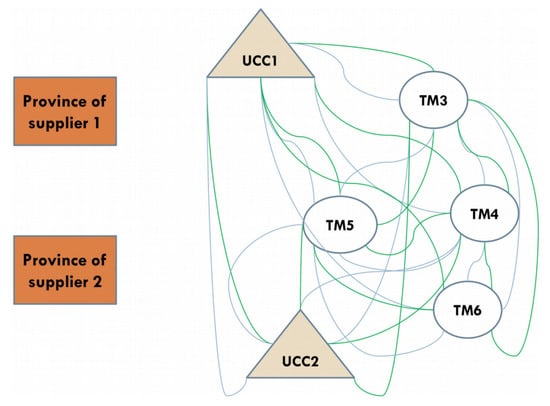
Figure 5.
LIRP in cold-chain logistics system (source: [34]).
4.1.3. LIRP Classification Based on Number of Depots and Retailers
Single-Depot Multi-Retailer Problem (SDMRP)
The work in [59] discussed the SDMRP model and included a DC system and a single depot responsible for providing one product to retailers. The model’s goals are to determine the time and quantity of delivery by retailers as well as complementary strategies in the warehouse to minimize the TSCC. Next, Ref. [66] discussed the integrated LIRP of a decentralized logistics system in which a single supplier operates a product. Their model did not consider the backorder cost but did consider the service level constraint, and it is a single objective function that minimizes the total cost including ordering cost, warehouse setup cost, inventory holding cost, and vehicle transportation cost. Finally, a two-stage coordinated iterative solution is proposed to solve the model. From this, it followed that the SDMRP is an IRP after selecting one depot.
Multi-Depot Multi-Retailer Problem (MDMRP)
MDMRP includes the selection of multi-depot among multiple alternate addresses and the distribution of inventory from multi-depot to multi-retailer, which is more in line with real-life supply chain logistics. As a result, there have been many studies on MDMRP. The authors of [40] studied the inventory management decision of MDMRP systems with storage capacity in the discrete-time planning scope and presented a MILP model that gives the understanding boundary. They then used a mixed method to embed the exact algorithm into the heuristic scheme to obtain the results. The model presented in [58] combined LRP and LIP. By generating distribution network logistics problems for several physical retailers and online e-retailers of different sizes, the proposed GA can be applied to diverse performance standards. The researchers in [67] pointed out that the solution in LIRP means that established warehouses, vehicles assigned to customers, and vehicle scheduling must be determined. Then, Ref. [68] studied the LIRP of a distribution system that consisted of one central warehouse, multiple potential DCs, and a multi-retailer. An MINLP model is introduced and solved by a nested Lagrange relaxation algorithm.
Next, Ref. [69] established the integrated LRIP model for an MDMRP two-stage logistics distribution network that considers the characteristics of deteriorated goods and introduces the idea of just-in-time (JIT), and an improved particle swarm optimization (PSO) algorithm is designed to solve this model. In [70], the MOP model of LIRP considering customer time satisfaction of MDMRP is studied, and an improved GA is introduced to solve the model. The work in [71] considered a supply chain network with multi-depot and geographically dispersed customers, constructed a MIP, and then proposed a mixed metaheuristic algorithm to solve the problem. For [72], the work examined a class of two-echelon networks consisting of a single factory, a set of potential depots (similar to DCs), and a set of customers (such as retailers). It is a batch routing problem with deterministic requirements for multi-period site selection, where the problem is solved by combining a GA with a local search process.
Moreover, Ref. [73] proposed a LIRP model to calculate and determine the optimal TSCC for each period, including the warehouses used, the number of customers and shipments, as well as the scheduling and routing of vehicles. An improved GA (IGA) is used to solve the mathematical model. The work of [74] proposed a heuristic algorithm to solve the LIRP of an MDMRP in a three-echelon with one supplier. An MINLP model is proposed and used in the food logistics system of the DKI company in Jakarta by using a heuristic method.
Furthermore, Ref. [75] studied the cyclic supplier selection and order assignment problem based on the multi-depot multi-capacity green routing issue with HEFV in an MPMPP of CLSC. In the paper, a MILP of the MOP model is established by using new methods such as a fuzzy best–worst method and combining it with other decision-making methods [75]. Next, Ref. [76] researched a type of third-party logistics in which suppliers are responsible for providing supply chain distribution to a factory that manufactures a product, delivering the product from the factory to multi-depots, keeping it in warehouses (when needed), and then transporting it to retailers at a fixed rate of demand. The authors proposed a novel method to optimize LIRP as well as an improved tabu search (TS) algorithm to solve it.
The work in [77] gave the locations of possible depots and retailers and determined the needs of each customer for vehicle services in advance. The problem is designed to minimize the TSCC, which includes the cost of building multi-depots, production, inventory, and transporting vehicles to a multi-retailer. An improved harmony search (MHS) algorithm with dynamic parameter settings and a multi-local neighborhood search are proposed to solve this LIRP [77].
4.2. Classification Based on Demand Data Types
Retailers’ demand for information is constantly misinterpreted and amplified as it travels up the transmission channel along the supply chain. Changes in the demand of end sellers and consumers significantly increases the instability of enterprise product production, supply, inventory management, and marketing. Therefore, different demand data types directly affect the results of the LIRP. The work of [20] proposed that the characteristics of customer demand can be divided into certainty and uncertainty, where certainty demand is deterministic, and uncertainty includes variable, stochastic, and fuzzy. On the one hand, the economic order quantity and its variation are used to solve the replenishment time and quantity problem under the condition of demand, and all parameters are determined. On the other hand, when uncertainties are significant, the uncertain demand must be considered in the model, so the modeling scheme needs to include a one-time decision model, a continuous decision model, and a periodic decision model [20].
Deterministic demand assumes that the specific demand of customers (such as retailers) at a certain location and in a certain period is given and known in the model hypothesis. According to this demand, relevant inventory and transportation costs are obtained, making the model easier to establish and solve. Among the literature reviewed, there are 37 papers concerning deterministic needs [5,37,39,41,43,44,45,46,49,50,59,63,65,69,70,71,72,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95].
Uncertain demands including variable form, random form (given a random process or probability), fuzzy form, and so forth appear in the paper. Demand is a variable form, which mainly assumes that customer demand has a coefficient of change or is a hypothetical consumer demand function or that these needs may differ from time to time. There are 21 papers that covered this issue [42,55,56,57,73,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111].
Demand is stochastic in form and mainly follows normal distribution or Poisson distribution. In practice, changes in customer requirements affect LIRP’s outcome decisions. In the demand-driven market, distributed network design is a complex system engineering problem. If customer demand is stochastic, then the objective is to minimize TSCC while preserving a certain quantity of safety stock in each DC to achieve a definite level of service to the customers served. A total of 46 papers addressed this issue [4,6,32,34,35,36,38,40,47,48,52,53,58,60,61,62,66,67,68,74,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136].
The authors of [137] mentioned that in a Vendor Management Inventory (VMI) environment, orders and production cycles from suppliers to enterprises tend to be long. As a result, market conditions may change. For example, requirements may increase, be similar, or decrease compared to projected requirements. Managers’ experience can give the demands of various market environments, and historical data statistics can be used to obtain the probability distribution. It is appropriate to use a Fuzzy Random Variable (FRV) to describe customer demand. The fuzzy formal literature uses the uncertain programming theory proposed by [12] and the fuzzy programming theory proposed by [138]. There are eight papers that discussed this issue [33,52,54,75,137,139,140,141].
4.3. Classification Based on Models and Solutions
LIRP modeling can be divided into three formulations: MIP, MILP, and MINLP. There are four types of methods for solving the LIRP models: (a) exact, (b) heuristic and metaheuristic, (c) mixed exact and heuristic and metaheuristic, and (d) other approaches. Nevertheless, exact methods can yield optimal solutions, but the elapsed time costs involved increase exponentially. Consequently, in solving large-size data instances or when time-efficiency is restricted and optimality is not a priority, then heuristic and/or metaheuristic algorithms are mostly preferred [16]. The remainder of this subsection discusses solution methods based on the three mathematical formulations.
- Solution Methods of MIP Model
There are 34 MIP models of LIRP in the literature, among which 22 are single-objective functions and 12 are multi-objective functions. Four of them are solved using exact algorithms. The authors of [80] proposed column generation between hybrids of Lagrange relaxation and local search and proposed a heuristic program to solve a single-objective MIP model. In [124], an exact algorithm based on the generalized bending decomposition (GBD) method is proposed to solve the integrated LIRP model. Moreover, Ref. [112] proposed an exact algorithm, namely the P-center method, for solving a single-objective MIP model. In addition, Ref. [130] innovatively used the YALMIP toolbox algorithm, a free MATLAB toolbox developed by [142] in 2004, to solve the MIP model.
In this review paper, 27 papers used heuristic and metaheuristic algorithms to solve the MIP model. These algorithms include hybridization of TS, GVNS, pseudo-parallel genetic algorithm integrating performance (PPGASA), genetic algorithm and simulated sampling (GASA), imperialist competitive–simulated sampling (IC-SA) algorithm, improved GA and SA algorithm, NSGA-II, NSGA-III, general variable neighborhood search (GVNS), simulated Taguchi method, multi-objective parallel sampling, multi-objective PSO, and multi-objective evolutionary algorithm [131].
Two works in the literature use mixed exact and heuristic and metaheuristic to solve MIP. The method proposed in [81] for solving ILRP combined non-traditional column generation methods with Lagrangian relaxation methods within a framework called relaxation and price. In addition, a two-phase heuristic algorithm is adopted to solve the shortest path of ILRP with clustering profits. According to the complexity of research problems, Ref. [103] proposed a hybrid heuristic algorithm for solving large-size calculating examples. The algorithm combined a K-means clustering algorithm with GA and compared the results of a CPLEX algorithm on small- and medium-scale problems. Experimental results showed that this algorithm could gain a better solution of LIRP in a reasonable time.
One paper used other approaches to solve the analysis results [133]. The authors built a robust two-stage stochastic LIRP for PPLN. The problem is solved using the sample average approximation method and analyzed using two variability criteria, i.e., partial low deviation from the mean (PLDM) and partial low deviation from the target (PLDT).
- Solution Methods of MILP Model
There are 40 MILP models of LIRP in the literature, among which 22 are single objective function and 18 are multi-objective functions. From the literature, 18 papers use an exact algorithm to solve the MILP model. The authors of [39] presented a MILP of LIRP on the environmental impact of CO emissions, and the optimization results are obtained by the traffic mode analysis experiment. In addition, Ref. [90] established a LIRP that considered MILP of food waste and fuel consumption and successfully obtained the optimal solution for the case by using LINGO11. In [97], a MILP model is reconstructed into a set-packaging model, and an efficient branch-price algorithm is used to solve the large problem cases. Moreover, Ref. [115] studied LIRP with transshipment where a P-center algorithm is used to select transshipment points from existing customers and presented sensitivity analysis according to actual distribution center number and truck size data.
GAMS/CPLEX, operational planning analysis software that solves the MILP model of MOP, is used in 13 of the reviewed papers. In [51], the authors proposed that fuzzy MILP is established under the condition of satisfying customers’ uncertain demands for each product assigned to them from the factory. The CPLEX solver in GAMS 24.1.2 software is used to obtain the results. An example is given to prove the validity of the LIRP model, and sensitivity analysis based on demand reduction is also performed. The work in [56] proposed a MILP model and used a CPLEX solver to solve small-problem examples. However, for large- and medium-sized cases, the metaheuristic algorithm of GVNS is used to solve them because of the large amount of computation. It is a mixture of exact and heuristic and metaheuristic algorithms for solving the model. The authors of [57] applied the relax-and-fix approach, which is a heuristic algorithm to solve the model, while CPLEX tests a precise method to illustrate the efficiency of each formulation. Moreover, Ref. [65] proposed a MILP model for solving real case research of the EWM corporation in the city of Nanchuan. CPLEX is used to gain the result of the problem, and sensitivity analysis is conducted.
In [83], the author formulated the problem as an accurate MILP model of dual-objective LIRP, which can optimize the operation cost, risk, and carbon emission cost of the hazardous goods supply chain. In order to solve the MOP, the dictionary weighting method is adopted, and CPLEX is used to obtain the results. In addition, Ref. [93] proposed a novel design approach for a two-echelon logistics network for comprehensive cooperation. The authors introduced two MILP models and an assessment of cooperation’s economy, environmental, and social benefits in comprehensive decision planning. The two models are then solved using IBM ILOG CPLEX Optimization Studio 12.9, and three sustainability metrics are evaluated.
Furthermore, Ref. [108] established a bi-objective MILP to design green supply chain management (GSCM) that considered forward and reverse flows. This LIRP model also considered simultaneous pickup and delivery, vehicle routing problem (VRP), and TW. The paper reported that the optimal value of decision variables could be obtained using the CPLEX solver in GAMS. The authors of [121] proposed LRIP with bi-objective, MPMPP, capable facility, and ATM-supplemented incentive with TW under uncertain demand. The uncertain parameters are processed by chance-constrained fuzzy programming, and the synthetic model is transformed into a concise MILP. In order to encode the mathematical model, GAMS 24.1 is used to solve the problem. The work in [127] proposed a bi-objective MILP model considering LIRP with uncertainty in demand for HEL. The model was run on real-world data using GAMS software. The model in [130] adopted a MILP model and a robust optimization method to optimize the problem under uncertainty conditions. In order to solve the model and demonstrate its feasibility, GAMS software was used, and the results from MATLAB software were compared.
In [139], a bi-objective MILP model is established and designed as a GSCM. GAMS 24.1/CPLEX is used to solve the MILP model. The results of implementing the model on Iran’s automotive parts production chain show that the model is accurate and efficient. The work in [140] used a MILP model of MOP to design an MPMPP of CLSC that considered vehicle scheduling and quantity discounts. The model is solved using case-study data from GAMS. Moreover, Ref. [50] proposed a MILP model that uses another optimization solver, ILOG OPL Studio 3.6, to obtain optimal values and was implemented in a real instance on part of Iran’s petroleum supply chain network.
In addition, 18 papers considered in this review used heuristic and metaheuristic algorithms to solve the target MILP. These heuristic algorithms include a GA combined with a local search procedure, gene-simulated sampling algorithm (GSAA), improved ant colony optimization (ACO), improved tabu search algorithm, two-phase heuristic SA, multi-objective ACO, multi-objective PSO, modified harmony search (MHS) algorithm, multi-objective black widow optimization (MOBWO) algorithm, NSGA-II and PESA-II, hybrid firefly algorithm and simulated annealing (HFFA-SA), novel intelligent SA, and fuzzy decision-making trial and evaluation laboratory (FDEMATEL).
Finally, another analysis method is used to solve the LIRP model of MILP. In [75], Fuzzy Analysis Network Process (FANP), Fuzzy Decision Test and Evaluation Laboratory (FDEMATEL), and HEFV are adopted to solve the GSCM of MDMRP in the multi-product CLSC.
- Solution Methods of MINLP Model
There are 38 LIRPs of the MINLP models, among which 20 are single objective function and 18 are multi-objective functions. Four papers employed the exact algorithm-solving model. In [59], LIRP is expressed as an MINLP, and the solution obtained by solving the novel model with CPLEX is compared with two previously proposed heuristic algorithms for solving the original MINLP based on the Lagrange relaxation method. The authors of [68] established a nonlinear hybrid integration programming model and proposed a nested solution algorithm based on Lagrange relaxation. The authors of [114] established an MINLP model for the LIRP under uncertain conditions, which is solved by GAMS 24.1.2 software. In [136], a bi-objective stochastic MINLP with uncertain demand is built, and the compiler program of Lingo software solved the result of this LIRP model.
There are five papers on solving MINLP using mixed exact and heuristic and metaheuristic algorithms. For example, Ref. [35] proposed a bi-objective MINLP model with subjective cost utility under the consideration of product users’ supply interruption risk preference and solved the model by using the Lagrange relaxation method and an improved GA. In [53], a PPLN is delivered to the customer in a limited time range, the MINLP of LIRP is given, and the Lagrange relaxation method is used to solve the obtained model to determine the lower limit. A heuristic algorithm is presented to obtain the Lagrange relaxation algorithm’s feasible results and to determine the upper bound [53].
In addition, 27 papers applied heuristic and metaheuristic algorithms to solve the MINLP. The heuristic algorithms used include an improved GA, SA, hybrid ACO algorithm, TS, firefly algorithm (FA), PSO, bi-objective adaptive large neighborhood search algorithm (BOALNS), multi-objective gray wolf optimization algorithms (MOGWO), NSGA-II, PESA-II, multi-objective PSO, and NSGA-III algorithm.
Two papers used other algorithms to solve the LIRP. The authors of [87] obtained the comprehensive LIRP of MINLP considering deterministic demand and MPSPP, applied it to the HSC, and solved the problem by a simulation method. The authors of [107] proposed an MINLP model of MOP for sustainable municipal solid waste management systems. The model is implemented in a case study in southeastern Tehran and solved using Lexicographic and AUGMECON2 methods [107].
4.4. Classification Based on Applications
In the field of applications, most of the recent works that introduced the application of the LIRP model are classified as follows: ECLS, HSC, PPLN, CCLN, ESSC, HUSC, HEL, and others. In the 21st century, with increasing access to information and the Internet’s popularity, E-commerce flourished globally. The ECLS, as an essential part of E-commerce, should be constantly improved to keep pace with the times [5]. With its success, the returns are becoming more and more frequent, and there are data showing that it can help companies get better customer repurchase rates [111]. The authors of [5] established a LIRP model for returning goods without quality defects given the problems in ECLS. In [111], for the design of the CLSC network in ECLS, an MINLP model combining the two objectives of TP optimization and CS is proposed. Furthermore, Ref. [137] proposed a fuzzy stochastic MIP model combining LIRP for ECLS, which consists of a single supplier and MDMRP.
The solutions to an efficient supply chain have become challenging due to environmental regulatory requirements, especially for HSC. Hazardous goods here include industrial/non-industrial hazardous materials and waste pollutants. Companies must make decisions of LIRP while considering the CEEI. The authors of [84] considered a comprehensive LIRP, which included minimized operational costs, risks, and carbon emissions associated with the HSC. Moreover, Ref. [106] developed a mathematical model for the LIRP for a two-level HSC and considered HEFV seeking to mitigate supply chain risks, minimize TSCC, and reduce the CEEI.
Another application of the LIRP model is in PPLN, where perishables are defined as any product that declines in quality over time due to environmental conditions, such as meat and meat byproducts, fish and seafood, dairy products, foods, fruits, vegetables, and flowers. Many researchers have studied the concept of PPLN [133]. The authors of [55] applied the economic order quantity strategy in the PPLN and discussed a perishable product LIRP model. Given the importance of supply chains and perishable goods, some researchers have considered the integrity of supply chains and perishable goods. The authors of [91] researched a MIP model for LIRP of perishable food produced with TW and used an improved ACO algorithm to solve it. They studied the model and algorithm by taking Dalian, China, as an example.
With the increasing demand for fresh, refrigerated, and frozen foods, research on CCLN has significantly increased. CCLN refers to organizations working together in different processes and activities to bring products and services to market. CCLN differs from other supply chains in the importance of factors such as food quality and safety, weather-related variability, and limited shelf life. Hence, there are complexities and challenges in its management when compared to alternative supply chains. It is imperative to build an integrated model to effectively optimize the cost of CCLN [61]. With the development of modern logistics towards informatization, globalization, and integration, distribution plays an essential role in the whole logistics system. Since the energy consumption and CO emissions of CCLN are usually much higher than those of traditional room-temperature logistics, the location of distribution points and optimization of transportation routes strongly correlate with energy consumption and CO emissions. Therefore, location optimization of cold-chain green logistics distribution paths has become an important research topic [109].
ESSC includes GSCM and sustainable CLSC, which takes into account the development of supply chain networks for supplier selection and order allocation, as well as low CO emissions that reduce harmful impacts on the environment while reducing economic costs [141]. Sustainable or GSCM refers to integrating sustainable environmental processes into traditional supply chains. GSCM is not about mitigating the harmful effects of business and supply chain operations but about adding value and/or creating value through the operation of the entire chain. Undeniably, reducing air, water, and waste pollution is the primary goal of the green supply chain. In particular, green operations can also improve a company’s asset efficiency as well as its positive image by reducing waste generation, product reuse and recycling, reducing manufacturing costs, and improving customer satisfaction [108]. A sustainable CLSC aims to reduce waste by recycling previously discarded products (repairing, reselling, or dismantling parts) into the value chain [140].
At present, disasters, regardless of their origin (whether natural or man-made), are difficult to predict. One does not know where, when, and on what scale they will occur; this is combined with uncertainties regarding demographic characteristics, the condition of existing infrastructure, and the needs required to respond to emergencies. Therefore, proper management of HUSC has become a fundamental global challenge because it is responsible for estimating, providing, storing, transporting, and allocating personnel, resources, and services needed for/to affected areas. Through a series of activities carried out at different times, the aim is to help survivors of disasters, reduce the impact of disasters, and maintain social stability. Therefore, developing a LIRP model provides the person in charge of the logistics network with enough information so that he/she can make the best decisions about location, distribution, and inventory management. This ultimately ensures timely delivery of goods (products or services) to stakeholders (affected areas) to minimize the negative economic and social impact caused by the occurrence of adverse events [110].
HEL includes pharmaceutical supply chains and blood distribution system design in the literature reviewed. The medicine supply chain is a way of distributing medical products of appropriate quality at the appropriate place and time between the recipient or consumer [54]. The blood distribution system means designing an effective supply chain network to meet the needs of hospitals in a specific area [126]. Pharmacies and hospitals are major pharmaceutical industry customers, and their demand fluctuates. This uncertainty in demand has led to problems in the industry. For example, a shortage of certain medicines may have severe consequences for patients, while buying products in large quantities may lead to the perishability of products, thus increasing network costs. Despite advances in product production, storage, and distribution (those that rely on commercial methods and technologies), many pharmaceutical companies still face severe problems in satisfying customer demand and satisfaction, indicating the need to develop models and optimization techniques [127].
Finally, five pieces of the literature are classified as other types of applications. The authors of [36] apply logistics management to beverage factory logistics distribution. In contrast, Ref. [70] applies the LIRP model to a household appliance enterprise. The authors of [85] design a LIRP model according to the practical application of water trucks regularly spraying water for dust suppression purposes of the transport road in an open-pit mine. The purpose is to propose and compare two methods of setting reservoirs along the road network to minimize the penalty cost and path cost of the roads’ humidity deficiency. The authors of [121] aimed to model and solve an integrated LIRP in the cash-in-transit sector, and the model’s capabilities provided a helpful reference for security operators in real-world situations. In [124], an integrated LIRP model of joint optimization decision in supply chain network design is proposed by taking the data of a Chinese passenger car enterprise as an example.
5. Current Trends
5.1. Descriptive Analysis
This section addresses the third research question raised in Section 3.1. Figure 6 shows a graph of the number of papers by model type. Among the 112 selected papers, since the review is all about the integrated LIRP, there are cross-multiple patterns in these categories of papers. A total of 85 papers are classified as MDMRP, which is the largest number in this review. This is followed by MPMPP (51), MESLP (46), MPSPP (24), SPSPP (8), MEMLP (6), SESLP (4), SDMRP (4), and SPMPP (3). Table 6 shows the overlapping number of MDMRP, MPMPP, and MESLP problems. The combination of all three problems gives the largest number, with 23, followed by the combination of MPMPP and MDMRP, with 13.
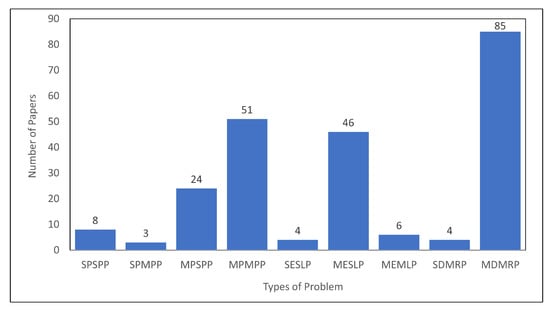
Figure 6.
Distribution based on the problem characteristics of LIRP.

Table 6.
Number of papers with overlapping of MPMPP, MESLP, and MDMRP.
Table S1 (see Supplementary Documentation) has three different LIRP categories based on problem characteristics. The first category has four subcategories based on inventory periodicity and the quantity of products shipped. These are SPSPP, SPMPP, MPSPP, and MPMPP, which stand for single-single, single-multi, multi-single, and multi-multi, respectively. The second type of problem variable is related to the inventory echelon and the number of path links (E-L), which can be divided into three subcategories: SESLP, MESLP, and MEMLP. The third type of problem variable is based on the number of depots (DCs) and retailers (D-R), which has two subcategories: SDMRP and MDMRP. They represent single-multi and multi-multi, respectively.
In Figure 6, of the 86 papers reviewed based on P-P, 51 papers are classified under MPMPP, second came MPSPP with 24 papers, followed by SPSPP with eight papers, and finally SPMPP with three papers. Of the 55 papers reviewed based on E-L numbers, 46 are classified as MESLP, 5 as MEMLP, and 4 as SESLP. Of the 89 papers reviewed based on the number of D-R, 85 are classified under MDMRP, and only 4 are SDMRP.
Table S2 (see Supplementary Documentation) shows the problem characteristics, demand data types, and model categories based on the LIRP abstract. The problem features are MOP, CLSC, Reverse Logistics (RL), Multi-stages (MS), TW, GSCM, HOFV, HEFV, Capacity Planning (CP), Inventory Control Replenishment Policy (ICRP), and Transshipment (TR). These features are described as follows.
MOP involves two or more optimization objectives in the study. There are 48 MOP articles, accounting for 42.85% of the literature. Table 7, Table 8 and Table 9 show the number of single-objective programming and MOP in each problem type, programming model, and data type. As one can see from Table 7, MDMRP is the most popular type of problem among the MOP models, which amounted to 39 articles in this review. Table 8 shows that MOP is used in 18 works of the literature reviewed in MINLP. Table 9 shows that MOP is used in 20 pieces of the literature for which the stochastic demand data type is applied.

Table 7.
Types of objective function based on types of problem.

Table 8.
Types of objective function based on model type.

Table 9.
Types of objective function based on demand data types.
CLSC means that in the context of global competition and environmental sensitivity, enterprises have the responsibility to recover discarded products and recycle or destroy them so as to maintain the environment and make profits from the discarded products. After customers consume the recyclable products, the business will recover the products and recycle or dispose them. The concept of CLSC has gained attention for its identification of seamlessly managed forward logistics (FL) and reverse logistics (RL) [43]. Some literature only considers RL, such as [65,79,92,123].
Previous research has shown that the dairy supply chain of LIRP is considered to be MS to ensure that the problem is closer to real situations and obtain better results [45]. The model of [45] presented problem planning in MS, in which the first stage included suppliers and facilities and the second stage looked at packaging facilities, cold storage inventory, and customers. The LIRP problem is not only multi-period, multi-product, multi-echelon, multi-link, multi-depot, and multi-retailer, but it also has MS for a supply chain model.
TW is a time limit and comes in two types. One is under a hard TW, where the customer’s needs can only be met at predetermined intervals. Another is that the delivery time can occur before or after a predefined interval in the soft TW [120]. GSCM combines the economic and environmental aspects of the supply chain to manage the system’s environmental impact while maximizing the performance of the entire supply chain [122]. The characteristics of both TW and GSCM are considered in the study of supply chain management.
On the other hand, fleet type plays a crucial role in transporting different goods, and it is divided into HOFV and HEFV. While a HOFV is a fleet of vehicles of the same size and capacity, which is rare in the industry, a HEFV is a fleet of vehicles of different sizes, which is generally more flexible and cost-effective for changing requirements.
CP is the process of determining the production capacity an organization needs to meet the changing demands for its products. There are two types of CP decisions to be made. One type is strategic decisions to locate DCs with different CP levels and to assign customers to DCs with different task levels that are related to the availability of DCs due to outages. The other is business decisions, i.e., decisions on the route of vehicles and the replenishment of CP stocks due to shortages in various transportation centers [32].
ICRP stands for inventory control replenishment policy, which is the process of moving inventory items along the supply chain to ensure that inventory levels are sufficient to meet demand. The importance of selecting appropriate complementary policies in LIRP of GSCM issues has been highlighted in some previous studies [109].
TR is interested in the supply chain because it allows goods to move from one warehouse to another or from one overstocked customer to another. This is profitable for suppliers because they can save on transportation costs in transporting goods to their respective customers, while customers can also save on costs for storage space and access to obsolete inventory. Some studies have implemented TR and demonstrated that it is effective compared to LRIP without TR [115].
Figure 7 shows the distribution of other problem characteristics mentioned previously. The most-studied feature is the MOP problem, which was mentioned in 48 papers. ICRP has the second highest coverage with 38 articles. In summary, MOP and ICRP are this review’s commonly used problem features for LIRP. In addition, TR is the least-studied among the problem feature types, with only six papers.
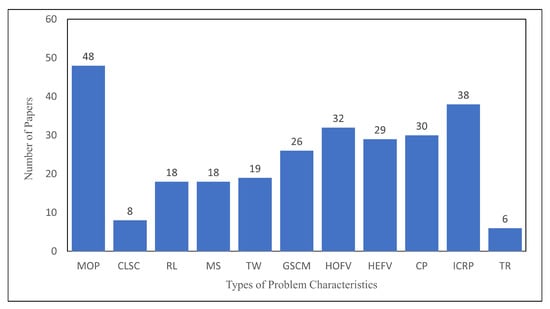
Figure 7.
Distribution of other characteristics of the problem.
A similar pattern can be observed for the distribution of papers for MPMPP, MESLP, and MDMRP, which account for a large proportion of the problem classification. These observations are clearly shown in Figure 8, Figure 9 and Figure 10. In MPMPP, MOP accounted for 45.1%, CP for 39.2%, HEFV for 37.3%, and GSCM for 27.5%. In MELSP, MOP accounted for 54.3%, HEFV, CP and ICRP for 34.8%, HOFV for 30.4%, and GSCM for 28.2%. In MDMRP, MOP accounted for 45.9%, ICRP for 40.0%, CP for 30.6%, HOFV for 29.4%, and GSCM for 25.9%. Proportionally, MOP ranks the highest, followed by ICRP, HEFV, HOFV, and GSCM.
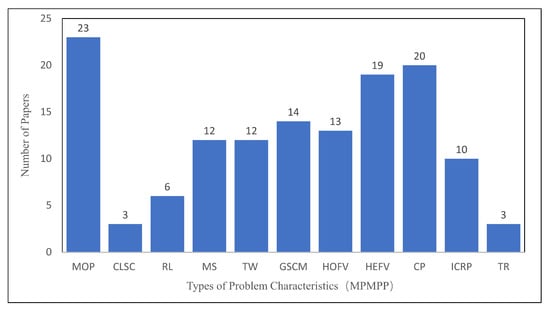
Figure 8.
Distribution of papers based on MPMPP.
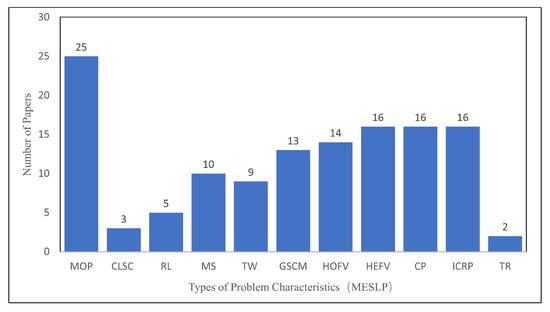
Figure 9.
Distribution of papers based on MESLP.
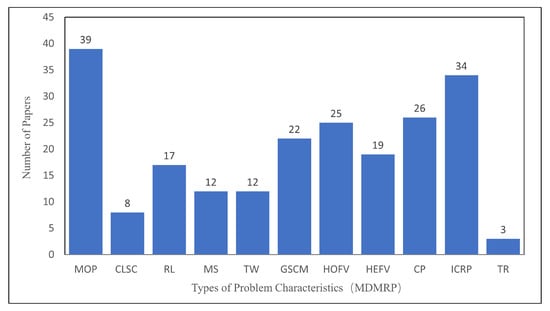
Figure 10.
Distribution of papers based on MDMRP.
Table 10 shows the different demand data types studied in LIRP over the years. We found that 37 papers studied the deterministic demand and 46 papers studied stochastic demand, which are the most popular topics among researchers. In addition, variable demand accounts for 21 papers, and fuzzy demand is the least-studied in this study, accounting for only 8 papers that have been paid attention to in the past two years.

Table 10.
Distribution of papers based on demand data types over the years.
In Table 11, we can see that compared with models based on the demand data types, researchers focused mostly on the use of stochastic MINLP, followed by the stochastic MIP. Fuzzy demand received the least attention from the researchers, where no research has been conducted on fuzzy MINLP.

Table 11.
Distribution of models based on demand data types.
As shown in Table 12, 41.2% of the literature using stochastic demand data type is found in MPMPP, 41.3% in MESLP, and 41.2% in MDMRP. It can be seen that the random demand is considered the most in its problem classification. Only three papers considered the SPMPP problem, and none were concerned with variable problems. In the literature review, only eight papers used the fuzzy demand, and these eight are all MDMRP, among which six are MPMPP, five are MESLP, and one overlaps SPSPP and SPMPP.

Table 12.
Distribution of types of problem based on the demand data types.
As can be seen from Table 13, almost half of the literature on MPMPP and MESLP uses the MILP model, while the MINLP model is most-used in MDMRP.

Table 13.
Distribution of types of problem based on the model types.
Table S3 (see Supplementary Documentation) gives a record of the paper in accordance with the nine unique optimization objectives of LIRP. In the single-objective optimization problem, only one objective function is concerned in the study, which is usually about minimizing TSCC or maximizing TP. Among the literature reviewed here, there are 63 articles that covered single-objective functions. There are 60 papers on TSCC and 3 papers on TP. On the other hand, the following objective functions are considered in MOP: TSCC, Transportation Costs (TC), Total Traversed Distance (TTD), PM, Customer Satisfaction (CS), CO Emission and Environmental Impacts (CEEI), Positive Social Impacts (PSI), Supply Chain Risks (SCR), and Shortage Cost (SC).
In the 48 MOP papers in this review, in addition to minimizing TSCC and maximizing TP used in single-objective programming, the literature reviewed also used minimizing TC in reverse logistics, minimizing TTD, maximizing CS, minimizing CEEI, maximizing PSI, minimizing SCR, and minimizing SC as other objective functions. TSCC includes the cost function of location cost, inventory cost, and routing cost in the supply chain, while TP maximizes the difference between the benefit of transporting goods to customers and the TSCC function of the supply chain [50].
In the case of RL, TC calculates the transportation cost in reverse flow [79]. TTD is the total traversed distance in LIRP [102]. CS includes the time of delivery of goods from the DCs to the customer, where punctuality, stability, and satisfaction are usually used as evaluation methods. TSCC and CS are usually regarded as two separate objective functions, and some have weighted them as a single objective function, such as in [39,59,87].
CEEI is the impact of CO emissions on the environment and consists of: (a) facility carbon emissions, (b) path carbon emissions, (c) inventory carbon emission, which primarily refers to the emission of energy consumption and goods emissions in the inventory process, and (d) other carbon emissions, including procurement, production and recycling [96]. TSCC and CEEI are divided into two objectives but are sometimes combined as one objective function, such as in [42,75,84,128]. PSI considers the maximization of social benefit impacts, such as the maximization of job creation relative to the unemployment rate and the maximum balance of economic development [52]. Generally, economic, environmental, and social impacts are considered simultaneously in LIRP to adapt to the strategy of sustainable development [140].
SCR includes the risk of lost sales, the risk of facility disruption, the risk of total inventory of the site selection center, the risk of transportation accidents during travel, the risk of transfer from the collection center to the recycling center, and the risk of default fees [65]. Facility outage risk is when, from a traditional point of view, established facilities that are always considered available are, in practice, not always available due to the risk of disruption. These operations may be disrupted for specific reasons, such as natural disasters, strikes, economic downturns, acts of terrorism, maintenance disruptions, power outages, etc. These risks can result in negative financial impacts and operating results, including high shipping costs, order delays, inventory shortages, etc. Interruption of the supply chain affects the performance of the organization to a great extent. Therefore, appropriate and effective strategies must be adopted to design a supply chain with minimal cost and risk. In order to minimize the risk of interruption and failure costs, logistics system providers should design a reliable network [32].
SC is the penalty cost considering the customer’s product shortage. The goal is to minimize the total amount of negative inventories (i.e., customer product shortages) for each product in a warehouse for each customer [51]. TSCC and SC are also discussed as a single objective function, as mentioned in [117].
Figure 11 shows the distribution of LIRP’s nine objective functions. The most widely covered is TSCC, the ultimate logistics system management goal, with 47 papers. CEEI minimization, CS minimization, and SCR minimization followed, with 18, 16, and 15 papers, respectively. On the other hand, TC minimization, TP maximization, and TTD minimization are least studied in LIRP, with only two, two, and one paper, respectively.
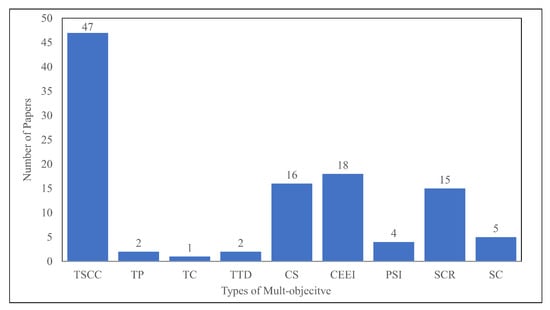
Figure 11.
Distribution of papers based on types of MOP.
According to Figure 12, minimizing TSCC covers the maximum percentage of papers considering MPMPP (47 papers). Next comes the minimization of CEEI, the minimization of SCR, and the maximization of CS, covering 12, 10, and 9, respectively. It is important to note that the MPMPP classification paper does not mention TC minimization.
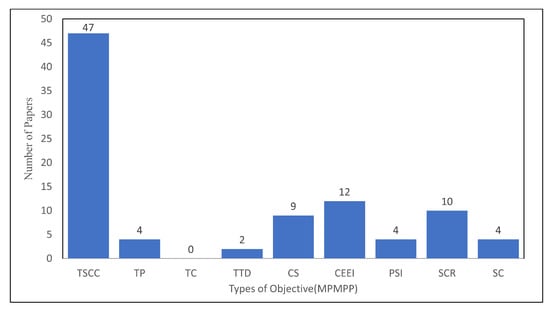
Figure 12.
Distribution of papers based on types of objective of MPMPP.
In Figure 13, the minimization of TSCC covers the largest portion of MESLP (43 papers), followed by SCR minimization with 9 papers. Among the selected papers, SCR minimization ranked third among the other objectives.
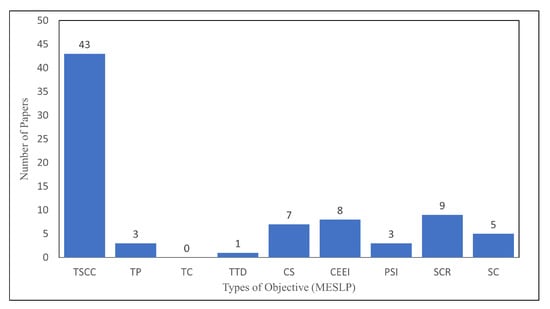
Figure 13.
Distribution of papers based on types of objective of MESLP.
In Figure 14, TSCC minimization covers 81 papers, the largest portion covered by MDMRP optimization goals. The minimization of CEEI and the maximization of CS are the second (18 papers) and third (14 papers) largest, respectively. TC coverage is limited to one paper, while TTD has none.
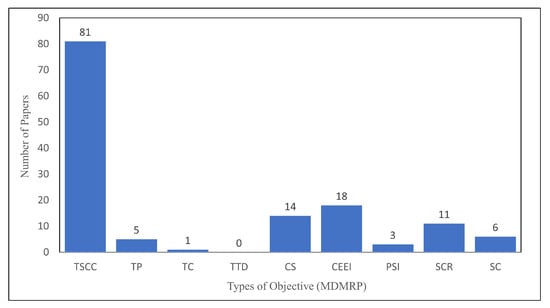
Figure 14.
Distribution of papers based on types of objective of MDMRP.
Table S4 (see Supplementary Documentation) lists the specific paper summaries of the eight ICRPs selected based on the second-best problem characteristics. The ICRP mentioned in this review includes , , FRP, JITD, , POT, , and inventory policies.
The in the column of “Inventory Policy” refers to continuous review inventory control policy [124]; that is, when the inventory level of the distribution center drops to or is below the reorder point R, a fixed quantity Q is ordered from the supplier [48]. refers to periodic review inventory control policy, in which T is the defined interval and S is the maximum inventory level [124]. It can be seen that the inventory control strategy is to reorder a quantity (variable) at a fixed interval T to bring the available inventory back to the preset maximum inventory level S.
For FRP, the goal is not to determine the frequency or size of replenishment service but rather to construct a long-term replenishment strategy (i.e., inventory rules and routing patterns) over a limited planning period [71]. All customers must be accessed and served. JITD means just-in-time distribution, and it is a mode of distribution in terms of demand–pull replenishment [69]. This replenishment strategy is a popular inventory management strategy based on lean management concepts and improving customer satisfaction [42]. This policy plays a positive influence on the sustainable achievement of the enterprise.
The “order-up to level” policy is periodically reviewed when stock levels are reviewed, and an item amount is ordered to return stock levels to the target level. It is a strategy in inventory management that involves ordering up to the optimal inventory level [41]. Moreover, the power-of-two (POT) policy assumes that the ratio of the cycle times is a power-of-two number [59]. The continuous-review policy means that the inventory levels are constantly tracked, and replenishment can be ordered at any time [67]. Furthermore, the inventory strategy requires replenishment orders to be placed after the size of each demand equals the size of the demand [116]. In this strategy, once a demand request is received and a response is received, the inventory level is reduced by one unit and a replacement order is sent by reducing the inventory of each unit [117]. As shown in Figure 15, the policy covers 18 papers, which is the largest part of ICRP. is the second, with five papers. POT inventory policy only has one paper.
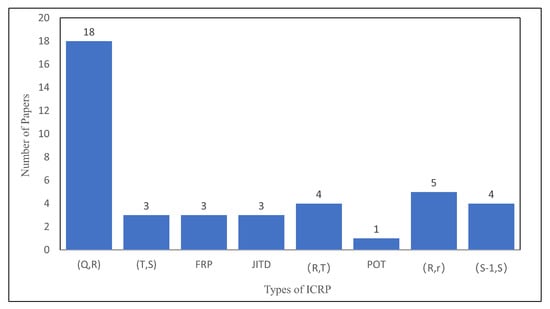
Figure 15.
Distribution of papers based on the ICRP.
Table S5 (see Supplementary Documentation) lists the detailed approaches for solving LIRP in the selected literature. In addition, Table S6 (see Supplementary Documentation) summarizes the types of model-type-based solution methods used to solve LIRP in this paper. The distribution of 112 papers based on solutions used by LIRP over the past decade is shown in Table 14 below.

Table 14.
Distribution of papers based on solution approaches over the years.
These algorithm classifications fall into four distinct categories: (a) exact only, (b) heuristic and metaheuristic, (c) exact, heuristic and metaheuristic, and (d) other approaches. The papers in category (a) only take the exact algorithm as the solution of LIRP. Category (b) includes selected papers that use heuristic and metaheuristic algorithms to plug in the relevant data to solve LIRP. Then, category (c) proposes a new mixture of exact and heuristic and metaheuristic algorithm to solve the LIRP. Research papers that used GAMS/CPLEX or other exact methods to compare to another newly proposed heuristic and metaheuristic algorithm (as a benchmark for small instances) are placed in category (b) rather than category (c). Finally, papers using simulation and other methods are classified into the fourth category.
As shown in Table 15, heuristic and metaheuristic algorithms are the most popular approaches to LIRP, especially for MPMPP, MESLP, and MDMRP. It should be noted that no other approaches have been used to study SPSPP, SESLP, MESLP, MEMLP, and SDMRP. Of the three papers related to SPMPP, one uses exact, one uses heuristic and metaheuristic algorithms, and one focuses on other approaches. Meanwhile, one of the four papers on SESLP uses mixed exact and heuristics and metaheuristics, while the rest use heuristic and metaheuristic algorithms. One of the four papers on SDMRP uses an exact algorithm, while the rest use heuristic and metaheuristic algorithms.

Table 15.
Distribution of solution approaches based on the types of problem.
Table 16 shows that heuristic and metaheuristic algorithms are the most commonly used methods to obtain the optimal solution for the LIRP model, especially for MILP and MINLP. Only one paper used other methods to solve MIP.

Table 16.
Distribution of LIRP models based on the solution approaches.
Table S7 (see Supplementary Documentation) lists the classification of applications for LIRP in the selected literature. As can be seen from Figure 16, PPLN is the most applied field with 21 papers, HSC ranks second with 15 papers, and ESSC ranks third with 13 papers. HUSC is the least applied domain, with only three papers.
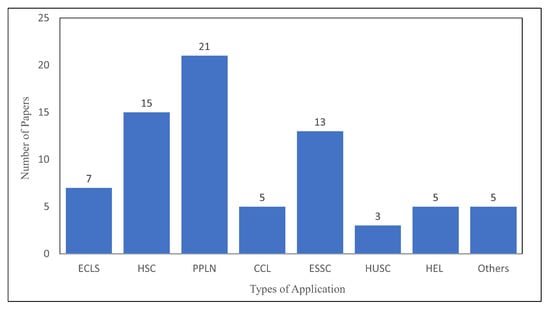
Figure 16.
Distribution of papers based on the types of application.
Table 17 shows that from 2010 to 2012 and from 2014 to 2015, only one paper applied these models; in 2013, there were three. With the progression of time, the application trend of LIRP has attracted increasing attention since 2016. PPLN has a maximum of 10 articles in 2021.

Table 17.
Distribution of papers based on the types of application over the years.
5.2. Overall Observations
In the variation of the problem, as seen in Figure 6, the periodicity of many-to-many consideration, products, echelons, and depot selection are researched heavily in the literature. For simplicity, we sort the problems from low-to-high complexity: SPSPP, SESLP, SPMPP, SDMRP, MPSPP, MESLP, MDMRP, MPMPP, and MEMLP. Among all the problems, SPSPP is the simplest because it involves a single-period (this period is long-term invariable) single-product logistics supply chain network design. However, it is not suitable for real-life situations. MPMPP reflects that LIRP is periodic and logistics products are diversified. MDMRP has the widest coverage in the review due to its practicality, while MEMLP can bring logistics management systems closer to the multi-link destination situation, which reflects the real-life situation.
The characteristics of demand data affect the planning results of the LIRP model. Currently, most LIRP studies assume that the input data are deterministic; in other words, all data are given in advance as known quantities. However, the assumption that the demand data are known in advance is unrealistic, so some studies address this problem by considering random or fuzzy demand data [16]. Stochastic LIRP deals with many works with input data as a probability distribution. Table 10 shows that many works have adopted this method. However, the prerequisite for using probability distributions to describe uncertainty is to obtain accurate historical statistical data. Otherwise, the probability distribution of the customer demand uncertainty cannot be obtained. As the production and operation process becomes more complex and the product life-cycle shorter, obtaining accurate historical statistics data is not easy. As a result, a growing number of researchers are using fuzzy mathematics to express uncertainty in inventory management.
As seen from Figure 7, MOP and ICRP have extensive coverage, with their popularity and innovation utilized to establish a MOP model, which is considered ICRP. Maximizing CS and minimizing SCR in MOP have attracted the attention of many scholars, and this is considered standard practice when customers choose merchants in today’s society. CLSC, MS, TW, and TR are the parts that are not considered in the literature and need to be further studied and discussed.
In Table 14, the heuristic and metaheuristic algorithms have the highest coverage because they can compute large case results reasonably. However, optimality is not guaranteed. For this reason, precise solutions are needed as benchmarks to compare with the solutions obtained by heuristic and metaheuristic algorithms. A certain number of research papers falling into the third category (exact, heuristic and metaheuristic) are shown in Table 14. Note that the two-stage heuristic and metaheuristic algorithm combining exact algorithms is a developing trend of the LIRP problem.
Regarding problem application classification and the literature on pairwise sets, Ref. [21] proposed two IRP classifications: PPLN and ESSC. The work of [16] focused on ESSC and HEL classification of LRP. Increasing awareness of the damaging environmental impact of logistics supply chains is paving the way for more environmentally friendly use of science and technology, which is conducive to environmental protection policies. Although the presence of ESSC in logistics supply chain systems (see Figure 16) is small, it will soon become an unavoidable standard when studying the integration of the LIRP. This will stimulate interest among researchers to conduct studies on this aspect.
6. Challenges and Future Work
In this section, we discuss the fourth and final research question: the challenges and future work. Today, market globalization can quickly and accurately meet the needs of customers. It has become the key to the success of enterprises. Now the competition between enterprises is not only a competition for efficiency but also a competition for supply chains. Hence, the overall optimization of LIRP has become a hot issue in business and academic circles. With the continuous expansion and development of logistics systems, the three core problems in optimizing logistics systems that call for attention are facility location, inventory control, and vehicle routing arrangement. As the number of facilities in the logistics system increases, the inventory and the resulting inventory cost tend to increase.
As the number of facilities such as DCs increases, the transportation distance and cost can be reduced. Given the number of these facilities increasing over time and with smaller order quantities, the high frequency of small batches can reduce the inventory cost of transportation, improving transportation cost. The facility location, transportation, and inventory decisions influence each other. Thus, to control the total logistics cost, one must carry on the overall analysis from the system perspective. The logistics-combined LRIP is fully considered in the study of systematic optimization. Various goods are considered to minimize the entire system cost (leading to a more realistic system in terms of application). Further, a series of facility locations are selected, and from each selected facility, each customer’s tour route is identified. In addition, multiple periods are determined based on the customer’s inventory strategy adopted by the optimal order quantity.
The CO emissions generated by the system inevitably have more impact on the environment. How to better solve this problem has become a topic for contemporary scholars. Since 2020, the COVID-19 pandemic has significantly compromised supply chain management by affecting the production and transportation of products. Hence, it is worth considering how to reduce the economic loss due to risk from the perspective of an integrated LIRP. On the other hand, the current research on the LIRP problem mainly focuses on a single product with a few multi-stage studies. The LIRP is an NP-hard problem, so one-step heuristic and metaheuristic algorithms are notorious for trapping the local optimum. Currently, many scholars use two-stage heuristic and metaheuristic algorithms to avoid this problem. However, in essence, the LIRP is broken down into two problems: returning to the process of separate optimization or partial integration optimization without reflecting on “integration optimization”. There is still much room for optimization of the solving algorithm of the LIRP problem, and subsequent research can be carried out from these aspects.
6.1. LIRP with Multi-Period and Multi-Stage
While a plant location decision is a strategic decision that requires work for many years and significant investment by the company, in the LIRP, the inventory decision is an operational one that can change daily. In addition, some problem characteristics of the LIRP are different, such as product or vehicle type. Therefore, it is necessary to conduct multi-stage modeling of the problem to obtain more realistic results. For example, Ref. [45] adopted the two-stage model according to the two different types of products transported in the red meat supply chain. In the first phase, carcasses are prepared and distributed between packaging facilities followed by red meat production operations. In the second stage, packaged meat is distributed to retailers, and, if necessary, cold-storage facilities are used [45]. In addition to an agricultural supply chain, other logistics supply chains are also used, such as the two-stage model in HUSC. As mentioned in [99] concerning HUSC, the first stage of the model is to deal with the location of inventory and DCs. The second stage is to decide the time of vehicle routes and supplies to the disaster areas.
These two scenario features allow decision makers to make more robust decisions about facility location by considering potential changes in planning routes with shorter cycles. We reviewed the recent studies on LIRP and found that 67.0% of the studies solved the multi-period LIRP, while 15.2% of the papers involved multi-stage LIRP (e.g., [45,91,99,133]), but not many considered multi-period and multi-stage simultaneously. The arrangement of input resources, position, and quantity between nodes in a multi-cycle and multi-stage state can be manually adjusted and controlled. Apart from reducing the uncertainty risk of the system, this practice also optimizes the investment of workforce and resources in the operation process. In summary, the number of works on multi-period and multi-stage LIRP is expected to grow, along with considerations of actual applications of the model.
6.2. LIRP with Multi-Echelon Multi-Link
Urban areas have multiple road networks that connect places. To apply the LIRP model in urban areas, multiple links must be considered to represent road networks [34]. The results from [34] show that the optimal link is not always the shortest. This is because the congestion cost factor determines the vehicle route. In a city, distance is not the only consideration in determining the route of access [143]. Based on the current systematic review, it can be seen that the LIRP model of MEMLP is rarely considered, as shown in Figure 6. Hence, there is still room for research on this issue.
6.3. LIRP with Green Closed-Loop Supply Chain
With the development of human social activities, especially in the face of resource shortage and environmental pollution in recent years, experts and scholars have studied CLSC [111]. Due to the short starting time, complex research, and high technical requirements, the current research trends are mainly divided into the following categories: (a) network research of CLSC, (b) inventory control, (c) pricing, and (d) coordination mechanisms. In actual production, although the design concept of CLSC has been widely used in all links of enterprise operations, enterprises are paying more attention to the construction of reverse logistics (RL) and gradually realizing the importance of RL for enterprises. However, the attention is still not as high compared with the forward supply chain [108]. The lack of practical experience in the design, operation, and maintenance of CLSC and the backwardness of technology management also seriously hinder its development. Due to the large variety of products and small order quantities for service spare parts, it is impossible to form economies of scale under economic laws. Thus, the technical means required in the CLSC are more stringent, and the difficulty is significantly increased.
6.4. LIRP with Time Window and Shortage Allowance
Logistics TW refers to the limited time horizon over which customers schedule within a cycle in the logistics activity process. In the delivery phase, customers always expect to be served within their intended time frame. Therefore, considering that customer demand in LIRP has the constraint of TW, customer satisfaction with delivery time as an objective function has become a hot topic. Moreover, customer requirements for vehicle service time are not completely rigid, and both early and late delivery affect customer satisfaction [120].
Due to the lack of predictability in the supply chain and the lack of forwarding insight into supplier supply capacity and uncertainty, suppliers often face inventory shortages caused by various uncertain factors. At the same time, there is also a lack of real-time tracking and monitoring of suppliers’ supply, which often leads to uncontrollable situations where the products are out of stock. The vast literature does not fully consider strategies that simultaneously satisfy customer demand and allow for out-of-stock inventory. However, these are essential factors that affect the TSCC. As a result, it is of practical significance to minimize TSCC, maximize CS, and minimize SC as the objective functions of a multi-objective LIRP.
6.5. LIRP with Out of Stock Inventory and Transport Disruption during COVID-19
The global COVID-19 pandemic is holding back development in many countries. The fourth wave of the 2021 Delta mutation has created new obstacles to the recovery of the global supply chain by creating backorders and shipping delays in many regions. In addition, sudden events such as natural disasters in China and Germany in 2021 and cyber attacks on major ports in South Africa lead to more severe supply chain disruptions and drive the global supply chain to collapse [35].
During the pandemic, international trade reached a further standstill, and disruptions to global supply chains have led to short-term business losses and lower corporate profits [55]. Therefore, considering the risk of transportation disruption, minimizing supply chain risk (SCR) as a goal of optimizing multiple objectives will provide enterprises with better transportation strategies and improve corporate profits.
6.6. LIRP in an Uncertain Environment
Decisions in real life are usually made under uncertain conditions, such as randomness and fuzziness. At present, FRV is a measurable function from probability space to a fuzzy variable set, which is essentially a random variable with fuzzy value, and has been further studied in supply chain management [144]. It can be seen from Table 11 that eight works of literature reviewed in this paper used FRV to study LIRP. The authors of [145] first proposed the concept of FRV and then gave different definitions according to the different testability of FRV, using the definition of [137]. The work of [146] provides an independent, comprehensive, and up-to-date introduction to uncertainty planning theory, including numerous modeling ideas, hybrid intelligence algorithms, and applications to system reliability design, project scheduling problems, VRP, facility location problems, and machine scheduling problems. The opportunity constraint programming proposed by the author is applied to the LIRP of integration optimization, which previous researchers did not use.
6.7. LIRP with Modern Heuristic Algorithms
In terms of algorithm implementation, exact, heuristic, and metaheuristic algorithms are widely used to solve MIP, MILP, and MINLP models of the LIRP. Exact algorithms can obtain optimality, while heuristic and metaheuristic algorithms can be used to improve problem-solving efficiency. Increasing numbers of new exact algorithms, such as modern column generation, relaxation, and decomposition methods, have been developed for solving large instances and could be an attractive area for future research. The decomposition algorithms widely used in the LIRP-related studies include Lagrangian decomposition, Benders decomposition, and extended variants of other decomposition methods.
These exact algorithms are used to develop tighter lower bounds of the feasible region so that developed heuristics can be benchmarked against optimal solutions for large problem instances. GAMS/CPLEX and LINGO are the most commonly used methods to solve the optimal solution of small instances. However, in the face of large instance problems, it is necessary to decompose the problem into less-complex subproblems and get the optimal solution in a reasonable time [28].
Here, we summarize the main research articles in recent years and find that 63.4% of the literature considers heuristic and metaheuristic algorithms to solve the LIRP. The LIRP is often challenging to solve due to the complexity of the model, so heuristic algorithms are developed and are gradually changed from simple interchange methods to more complex heuristic and metaheuristic algorithms. Accurate decomposition and cutting algorithms have been applied to small examples. In recent years, more scholars have abandoned the deterministic and static versions of LIRP and have proposed models and algorithms that can deal with the stochastic and fuzzy versions of the LIRP in order to deal with uncertainty.
6.8. LIRP in Healthcare Logistics
HEL is considered to be a global imperative, given its impact on the human living environment. Any problems with the access to medicines during mass distribution and manufacturing can endanger people’s lives [54]. Shortages of certain perishable medicines can have severe consequences for patients, while large purchases of products can lead to perishability [127]. The work of [89] recommended localization of blood banks to improve efficiency and to benefit from the advantages of risk concentration. Under the proposed distribution network, some hospitals are selected as local blood banks to monitor and service nearby hospitals. Transport and storage of medical supplies requires higher temperatures, and cold-chain transport and cryogenic storage also contribute to increased CO emissions. Methods on how to select the location of the regional medical logistics center under the constraint of CO emissions and to complete the transportation and distribution of medical products through road, rail, and air transportation are of great significance to the planning and construction of a medical logistics network [135].
The LIRP model can be used to plan many medical logistics scenarios. However, this review found that, as seen from Table 17, only five studies in recent years were on the LIRP model for optimizing HEL. Given the importance of optimizing medical logistics systems, it is hoped that in the future additional LIRP research will be used to study this issue and LIRP-related cases of HEL will be designed.
7. Conclusions
This paper systematically reviewed the research progress of the LIRP, proposed a new classification method, and classified 112 works from the literature published from 2010 to 2021 according to different criteria. The PRISMA method systematically reviewed LIRP from four aspects: problem characteristics, demand data types, model-based solutions, and application fields. The selected literature showed that the LIRP is on the rise, and it is predicted that works on it will continue to increase in the coming decades. The following work is done in this paper.
First, the problem features are classified into SPSPP, SPMPP, MPSPP, MPMPP, SESLP, MESLP, MEMLP, SDMRP, and MDMRP. In addition, MOP, CLSC, RL, MS, TW, GSCM, HOFV, HEFV, CP, ICRP, and TR are further classified under each problem feature. Some of the problem features are emerging and receiving more consideration from the LIRP research field. In the study of MPMPP, MESLP, and MDMRP, MOP is the most studied, followed by ICRP, HEFV, HOFV, and GSCM. It is found from the analysis that many papers considered MOP in the LIRP models, most of which combined classic TSCC with other standards from different aspects, such as CEEI, CS, and SC problems. At the same time, ICRP is also analyzed, where (Q,R) is the most commonly used ICRP in the literature.
Secondly, the characteristics of demand data are analyzed, which are classified into four categories: deterministic, variable, stochastic, and fuzzy. Compared with other types of demand data, the LIRP of stochastic requirements is the most-researched problem. However, fuzzy data are considered less, and there is a gap in research and development.
Thirdly, in terms of solving methods, three different mathematical programming models, namely MIP, MILP, and MINLP, are analyzed and solved. We find heuristic and metaheuristic algorithms to be the most prominent method and identified various algorithms implemented to solve the LIRP variables. However, to the best of our knowledge, there are abundant research methods for separating location, inventory, and routing problems, such as machine learning methods, statistical methods, artificial neural networks, and support vector machine. These methods have been applied to the solutions of the VRP in the literature, and researchers can also apply these methods to the LIRP.
Finally, in the actual environment, the model’s applicability and practicability are becoming an increasingly significant factor, and the analysis of LIRP is becoming more specific. In this paper, LIRP applications are subdivided into ECLS, HSC, PPLN, CCL, ESSC, HUSC, HEL, and others; among which, PPLN, HSC, and ESSC are more widely used. Despite the proliferation of the literature on LIRP, the research on the LIRP is far from exhaustive, and many novel challenges and promising applications are naturally emerging. Consequently, this creates a more exciting environment for LIRP research.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su142315853/s1. Refs. [4,5,6,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,139,140,141] are citied in supplementary materials.
Author Contributions
Conceptualization, L.L., L.S.L. and C.Y.C.; methodology, L.L., L.S.L. and C.Y.C.; validation, L.L. and L.S.L.; formal analysis, L.L., L.S.L. and H.-V.S.; investigation, L.L. and L.S.L.; resources, L.L.; data curation, L.L. and L.S.L.; writing—original draft preparation, L.L., L.S.L., H.-V.S. and C.Y.C.; writing—review and editing, L.L., L.S.L., H.-V.S. and C.Y.C.; visualization, L.L.; supervision, L.S.L. and C.Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ministry of Higher Education Malaysia through the Fundamental Research Grant Scheme with reference code FRGS/1/2019/STG06/UPM/02/1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IRP | Inventory-routing problem |
| LIP | Location-inventory problem |
| LRP | Location-routing problem |
| LIRP | Location-inventory-routing problem |
| MIP | Mixed integer programming |
| MILP | Mixed integer linear programming |
| MINLP | Mixed integer nonlinear programming |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analysis |
| CLSC | Closed-loop supply chain |
| GSCM | Green supply-chain management |
| TSCC | Total supply-chain cost |
| ECLS | E-commerce logistics system |
| HSC | Hazmat supply chain |
| PPLN | Perishable-products logistics network |
| CCLN | Cold-chain logistics network |
| ESSC | Environmentally sustainable supply chain |
| HUSC | Humanitarian supply chain |
| HEL | Healthcare logistics |
| MOP | Multi-objective programming |
| CP | Capacity planning |
| CS | Customer satisfaction |
| DC | Distribution center |
| RL | Reverse logistics |
| MS | Multi-stages |
| SC | Shortage cost |
| TC | Transportation cost |
| TP | Total profit |
| TW | Time window |
| CEEI | CO2 emission and environmental impacts |
| HOFV | Homogeneous fleet of vehicles |
| HEFV | Heterogeneous fleet of vehicles |
| ICRP | Inventory control replenishment policy |
| PSI | Positive social impacts |
| SCR | Supply-chain risks |
| TTD | Total traversed distance |
| SPSPP | Single-period single-product problem |
| SPMPP | Single-period multi-product problem |
| MPSPP | Multi-period single-product problem |
| MPMPP | Multi-period multi-product problem |
| SESLP | Single-echelon single-link problem |
| MESLP | Multi-echelon single-link problem |
| MEMLP | Multi-echelon multi-link problem |
| SDMRP | Single-depot multi-retailer problem |
| MDMRP | Multi-depot multi-retailer problem |
References
- Archetti, C.; Bertazzi, L.; Laporte, G.; Speranza, M.G. A branch-and-cut algorithm for a vendor-managed inventory-routing problem. Transp. Sci. 2007, 41, 382–391. [Google Scholar] [CrossRef]
- Salhi, S.; Rand, G.K. The effect of ignoring routes when locating depots. Eur. J. Oper. Res. 1989, 39, 150–156. [Google Scholar] [CrossRef]
- Chen, Q.; Li, X.; Ouyang, Y. Joint inventory–location problem under the risk of probabilistic facility disruptions. Transp. Res. Part Methodol. 2011, 45, 991–1003. [Google Scholar] [CrossRef]
- Ahmadi Javid, A.; Azad, N. Incorporating location, routing and inventory decisions in supply chain network design. Transp. Res. Part Logist. Transp. Rev. 2010, 46, 582–597. [Google Scholar] [CrossRef]
- Li, Y.; Guo, H.; Wang, L.; Fu, J. A hybrid genetic-simulated annealing algorithm for the location-inventory-routing problem considering returns under e-supply chain environment. Sci. World J. 2013, 2013, 125893. [Google Scholar] [CrossRef] [PubMed]
- Yuchi, Q.; Wang, N.; He, Z.; Chen, H. Hybrid heuristic for the location-inventory-routing problem in closed-loop supply chain. Int. Trans. Oper. Res. 2021, 28, 1265–1295. [Google Scholar] [CrossRef]
- Perl, J.; Sirisoponsilp, S. Distribution networks: Facility location, transportation and inventory. Int. J. Phys. Distrib. Logist. Manag. 1988, 18, 18–26. [Google Scholar] [CrossRef]
- Jayaraman, V. Transportation, facility location and inventory issues in distribution network design. Int. J. Oper. Prod. Manag. 1998, 18, 471–494. [Google Scholar] [CrossRef]
- Nozick, L.K.; Turnquist, M.A. Integrating inventory impacts into a fixed-charge model for locating distribution centers. Transp. Res. Part E Logist. Transp. Rev. 1998, 34, 173–186. [Google Scholar] [CrossRef]
- Nozick, L.K.; Turnquist, M.A. Inventory, transportation, service quality and the location of distribution centers. Eur. J. Oper. Res. 2001, 129, 362–371. [Google Scholar] [CrossRef]
- Ambrosino, D.; Scutellà, M. Distribution network design: New problems and related models. Eur. J. Oper. Res. 2005, 165, 610–624. [Google Scholar] [CrossRef]
- Liu, S.-C.; Lee, S.B. A two-phase heuristic method for the multi-depot location routing problem taking inventory control decisions into consideration. Int. J. Adv. Manuf. Technol. 2003, 22, 941–950. [Google Scholar] [CrossRef]
- Liu, S.-C.; Lin, C.C. A heuristic method for the combined location routing and inventory problem. Int. J. Adv. Manuf. Technol. 2005, 26, 372–381. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Rashidi Bajgan, H.; Fahimnia, B.; Kaviani, M. Location-inventory problem in supply chains: A modelling review. Int. J. Prod. Res. 2014, 53, 3769–3788. [Google Scholar] [CrossRef]
- Drexl, M.; Schneider, M. A survey of variants and extensions of the location-routing problem. Eur. J. Oper. Res. 2014, 241, 283–308. [Google Scholar] [CrossRef]
- Mara, S.T.W.; Kuo, R.J.; Asih, A.M.S. Location-routing problem: A classification of recent research. Int. Trans. Oper. Res. 2021, 28, 2941–2983. [Google Scholar] [CrossRef]
- Coelho, L.C.; Cordeau, J.-F.; Laporte, G. Thirty years of inventory routing. Transp. Sci. 2013, 48, 472. [Google Scholar] [CrossRef]
- Roldán, R. Inventory routing problem with stochastic demand and lead time: State of the art. In Proceedings of the Joint Conference SOCO’14-CISIS’14, Advances in Intelligent Systems and Computing, Bilbao, Spain, 25–27 June 2014; Springer: Cham, Switzerland, 2014; pp. 1–10. [Google Scholar]
- Feshari, M.; Nazemi, A.; Sheikhtajian, S. A Library review study: Conceptual model for maritime inventory-routing problem. Int. J. Supply Oper. Manag. 2017, 4, 341–358. [Google Scholar]
- Roldán, R.F.; Basagoiti, R.; Coelho, L.C. A survey on the inventory-routing problem with stochastic lead times and demands. J. Appl. Log. 2017, 24, 15–24. [Google Scholar] [CrossRef]
- Malladi, K.T.; Sowlati, T. Sustainability aspects in inventory routing problem: A review of new trends in the literature. J. Clean. Prod. 2018, 197, 804–814. [Google Scholar] [CrossRef]
- Soysal, M.; Çimen, M.; Belbağ, S.; Toğrul, E. A review on sustainable inventory routing. Comput. Ind. Eng. 2019, 132, 395–411. [Google Scholar] [CrossRef]
- Cao, J. The inventory routing problem: A review. In Proceedings of the 20th COTA International Conference of Transportation Professionals, Xi’an, China, 14–16 August 2020; pp. 4488–4499. [Google Scholar]
- Thinakaran, N.; Jayaprakash, J.; Elanchezhian, C. Greedy algorithm for inventory routing problem in a supply chain—A review. Mater. Today Proc. 2019, 16, 1055–1060. [Google Scholar] [CrossRef]
- Harahap, A.Z.M.K. Deterministic inventory routing problem (DIRP): A literature review. Int. J. Supply Chain. Manag. 2017, 6, 284–288. [Google Scholar]
- Saragih, N.I.; Bahagia, S.N.; Syabri, I. A survey on location-routing-inventory problem. J. Adv. Res. Dyn. Control Syst. 2019, 11, 401–404. [Google Scholar]
- Page, M.J. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. Syst. Rev. 2021, 10, 89. [Google Scholar] [CrossRef] [PubMed]
- Ting, K.H.; Lee, L.S.; Pickl, S.; Seow, H.-V. Shared Mobility Problems: A Systematic Review on Types, Variants, Characteristics, and Solution Approaches. Appl. Sci. 2021, 11, 7996. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; The, P.G. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. PLoS Med. 2009, 6, 339. [Google Scholar] [CrossRef] [PubMed]
- Neilson, A.; Indratmo Daniel, B.; Tjandra, S. Systematic review of the literature on big data in the transportation domain: Concepts and applications. Big Data Res. 2019, 17, 35–44. [Google Scholar] [CrossRef]
- De Armas, J.; Rodríguez-Pereira, J.; Vieira, B.; Ramalhinho, H. Optimizing assistive technology operations for aging populations. Sustainability 2021, 13, 6925. [Google Scholar] [CrossRef]
- Rayat, F.; Musavi, M.; Bozorgi-Amiri, A. Bi-objective reliable location-inventory-routing problem with partial backordering under disruption risks: A modified AMOSA approach. Appl. Soft Comput. 2017, 59, 622–643. [Google Scholar] [CrossRef]
- Daroudi, S.; Kazemipoor, H.; Najafi, E.; Fallah, M. The minimum latency in location routing fuzzy inventory problem for perishable multi-product materials. Appl. Soft Comput. 2021, 110, 107543. [Google Scholar] [CrossRef]
- Saragih, N.; Bahagia, S.; Suprayogi, S.; Syabri, I. Location-inventory-routing model with considering urban road networks. J. Ind. Eng. Manag. 2021, 14, 3557. [Google Scholar] [CrossRef]
- Song, Y.; Liu, Y.Q.; Sun, Q.; Chen, M.F.; Xu, H.T. A joint optimization model considering the product user’s risk preference for supply system disruption. Math. Probl. Eng. 2021, 2021, 5081753. [Google Scholar] [CrossRef]
- Ma, H.; Yang, X.; Zhang, D. The research into ILRIP for single-stage logistics distribution network under stochastic demand based on JITD. In Proceedings of the 7th International Conference on Service Systems and Service Management, ICSSSM’ 10, Tokyo, Japan, 28–30 June 2010; pp. 639–644. [Google Scholar]
- Hiassat, A.; Diabat, A. A location-inventory-routing-problem with perishable products. In Proceedings of the 41st International Conference on Computers and Industrial Engineering, Los Angeles, CA, USA, 23–25 October 2011; pp. 130–135. [Google Scholar]
- Liu, B.; Chen, H.; Li, Y.; Liu, X. A pseudo-parallel genetic algorithm integrating simulated annealing for stochastic location-inventory-routing problem with consideration of returns in e-commerce. Discret. Dyn. Nat. Soc. 2015, 2015, 586581. [Google Scholar] [CrossRef]
- Thi Phuong Nha, L.; Lee, T.-R. Model selection with considering the CO2 emission alone the global supply chain. J. Intell. Manuf. 2013, 24, 653–672. [Google Scholar]
- Sajjadi, S.R.; Cheraghi, S.H. Multi-products location routing problem integrated with inventory under stochastic demand. Int. J. Ind. Syst. Eng. 2011, 7, 454–476. [Google Scholar] [CrossRef]
- Guerrero, W.J.; Prodhon, C.; Velasco, N.; Amaya, C.A. Hybrid heuristic for the inventory location-routing problem with deterministic demand. Int. J. Prod. Econ. 2013, 146, 359–370. [Google Scholar] [CrossRef]
- Karakostas, P.; Sifaleras, A.; Georgiadis, M.C. Adaptive variable neighborhood search solution methods for the fleet size and mix pollution location-inventory-routing problem. Expert Syst. Appl. 2020, 153, 113444. [Google Scholar] [CrossRef]
- Forouzanfar, F.; Tavakkoli-Moghaddam, R.; Bashiri, M.; Baboli, A.; Hadji Molana, S.M. New mathematical modeling for a location–routing–inventory problem in a multi-period closed-loop supply chain in a car industry. J. Ind. Eng. Int. 2017, 14, 537–553. [Google Scholar] [CrossRef]
- Yavari, M.; Enjavi, H.; Geraeli, M. Demand management to cope with routes disruptions in location-inventory-routing problem for perishable products. Res. Transp. Bus. Manag. 2020, 37, 100552. [Google Scholar] [CrossRef]
- Rahbari, M.; Razavi Hajiagha, S.H.; Amoozad Mahdiraji, H.; Riahi Dorcheh, F.; Garza-Reyes, J.A. A novel location-inventory-routing problem in a two-stage red meat supply chain with logistic decisions: Evidence from an emerging economy. Kybernetes 2021, 51, 1498–1531. [Google Scholar] [CrossRef]
- Wu, W.; Zhou, W.; Lin, Y.; Xie, Y.; Jin, W. A hybrid metaheuristic algorithm for location inventory routing problem with time windows and fuel consumption. Expert Syst. Appl. 2021, 166, 114034. [Google Scholar] [CrossRef]
- Ma, Z.; Dai, Y. Logistics for sustained economic development-infrastructure, information, integration. In Proceedings of the 2010 International Conference of Logistics Engineering and Management, Chengdu, China, 8–10 October 2010; pp. 2562–2568. [Google Scholar]
- Nekooghadirli, N.; Tavakkoli-Moghaddam, R.; Ghezavati, V.R.; Javanmard, S. Solving a new bi-objective location-routing-inventory problem in a distribution network by meta-heuristics. Comput. Ind. Eng. 2014, 76, 204–221. [Google Scholar] [CrossRef]
- Ghorbani, A.; Akbari Jokar, M.R. A hybrid imperialist competitive-simulated annealing algorithm for a multisource multi-product location-routing-inventory problem. Comput. Ind. Eng. 2016, 101, 116–127. [Google Scholar] [CrossRef]
- Moradi Nasab, N.; Amin-Naseri, M.R. Designing an integrated model for a multi-period, multi-echelon and multi-product petroleum supply chain. Energy 2016, 114, 708–733. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Raziei, Z. A new bi-objective location-routing-inventory problem with fuzzy demands. IFAC-PapersOnLine 2016, 49, 1116–1121. [Google Scholar] [CrossRef]
- Zhalechian, M.; Tavakkoli-Moghaddam, R.; Zahiri, B.; Mohammadi, M. Sustainable design of a closed-loop location-routing-inventory supply chain network under mixed uncertainty. Transp. Res. Part Logist. Transp. Rev. 2016, 89, 182–214. [Google Scholar] [CrossRef]
- Rafie-Majd, Z.; Pasideh, S.H.R.; Naderi, B. Modelling and solving the integrated inventory-location-routing problem in a multi-period and multi-perishable product supply chain with uncertainty: Lagrangian relaxation algorithm. Comput. Chem. Eng. 2018, 109, 9–22. [Google Scholar] [CrossRef]
- Goodarzian, F.; Wamba, S.F.; Mathiyazhagan, K.; Taghipour, A. A new bi-objective green medicine supply chain network design under fuzzy environment: Hybrid metaheuristic algorithms. Comput. Ind. Eng. 2021, 160, 107535. [Google Scholar] [CrossRef]
- Hiassat, A.; Diabat, A.; Rahwan, I. A genetic algorithm approach for location-inventory-routing problem with perishable products. J. Manuf. Syst. 2017, 42, 93–103. [Google Scholar] [CrossRef]
- Karakostas, P.; Sifaleras, A.; Georgiadis, M.C. Variable neighborhood search-based solution methods for the pollution location-inventory-routing problem. Optim. Lett. 2022, 16, 211–235. [Google Scholar] [CrossRef]
- Wu, T.; Shi, L.; Geunes, J.; Akartunali, K. On the equivalence of strong formulations for capacitated multi-level lot sizing problems with setup times. J. Glob. Optim. 2012, 53, 615–639. [Google Scholar] [CrossRef][Green Version]
- Hsieh, C.L.; Liao, S.H.; Ho, W.C. Incorporating location, routing and inventory decisions in dual sales channel—A hybrid genetic approach. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Bangkok, Thailand, 10–13 December 2013; pp. 452–456. [Google Scholar]
- Diabat, A.; Theodorou, E. A location–inventory supply chain problem: Reformulation and piecewise linearization. Comput. Ind. Eng. 2015, 90, 381–389. [Google Scholar] [CrossRef]
- Nakhjirkan, S.; Mokhatab Rafiei, F. An integrated multi-echelon supply chain network design considering stochastic demand: A genetic algorithm based solution. Promet. Traffic Traffico 2017, 29, 391–400. [Google Scholar] [CrossRef]
- Zheng, J.; Li, K.; Wu, D. Models for location inventory routing problem of cold chain logistics with NSGA-II algorithm. J. Donghua Univ. 2017, 34, 533–539. [Google Scholar]
- Nakhjirkan, S.; Rafiei, F.M.; Kashan, A.H. Developing an integrated decision making model in supply chain under demand uncertainty using genetic algorithm and network data envelopment analysis. Int. J. Math. Oper. Res. 2019, 14, 53–81. [Google Scholar] [CrossRef]
- Rahbari, M.; Razavi Hajiagha, S.H.; Raeei Dehaghi, M.; Moallem, M.; Riahi Dorcheh, F. Modeling and solving a five-echelon location–inventory–routing problem for red meat supply chain. Kybernetes 2020, 50, 66–99. [Google Scholar] [CrossRef]
- Li, K.; Li, D.; Wu, D. Multi-objective optimization for location-routing-inventory problem in cold chain logistics network with soft time window constraint. J. Eur. Des Syst. Autom. 2020, 53, 803–809. [Google Scholar] [CrossRef]
- Zhao, J.; Ke, G.Y. Incorporating inventory risks in location-routing models for explosive waste management. Int. J. Prod. Econ. 2017, 193, 123–136. [Google Scholar] [CrossRef]
- Jha, J.K.; Shanker, K. An integrated inventory problem with transportation in a divergent supply chain under service level constraint. J. Manuf. Syst. 2014, 33, 462–475. [Google Scholar] [CrossRef]
- Aghighi, A.; Malmir, B. Designing distribution networks of perishable products under stochastic demands and routs. In Proceedings of the 2016 International Conference on Industrial Engineering and Operations Management, Detroit, MI, USA, 23–25 September 2016; pp. 1008–1019. [Google Scholar]
- Wang, X. An integrated multi-depot location- inventory-routing problem for logistics distribution system planning of a chain enterprise. In Proceedings of the 2010 International Conference on Logistics Systems and Intelligent Management, Harbin, China, 9–10 January 2010; pp. 1427–1431. [Google Scholar]
- Yang, X.; Ma, H.; Zhang, D. Research into ILRIP for logistics distribution network of deteriorating item based on JITD. In Proceedings of the Communications in Computer and Information Science, Kaminoyama, Japan, 18–20 August 2010; pp. 152–160. [Google Scholar]
- Shuai, D.; Yanhui, L.; Lan, Y. Combine cost and time satisfaction into a multi-objective programming for integrated logistics system. In Proceedings of the 2011 International Conference on Computer Science and Service System (CSSS), Nanjing, China, 27–29 June 2011; pp. 283–287. [Google Scholar]
- Zhang, Y.; Qi, M.; Miao, L.; Liu, E. Hybrid metaheuristic solutions to inventory location routing problem. Transp. Res. Part E Logist. Transp. Rev. 2014, 70, 305–323. [Google Scholar] [CrossRef]
- Kechmane, L.; Nsiri, B.; Baalal, A. Optimization of a two-echelon location lot-sizing routing problem with deterministic demand. Math. Probl. Eng. 2018, 2018, 2745437. [Google Scholar] [CrossRef]
- Saif-Eddine, A.S.; El-Beheiry, M.M.; El-Kharbotly, A.K. An improved genetic algorithm for optimizing total supply chain cost in inventory location routing problem. Ain Shams Eng. J. 2019, 10, 63–76. [Google Scholar] [CrossRef]
- Saragih, N.I.; Bahagia, S.N.; Suprayogi Syabri, I. A heuristic method for location-inventory-routing problem in a three-echelon supply chain system. Comput. Ind. Eng. 2019, 127, 875–886. [Google Scholar] [CrossRef]
- Govindan, K.; Mina, H.; Esmaeili, A.; Gholami-Zanjani, S.M. An integrated hybrid approach for circular supplier selection and closed loop supply chain network design under uncertainty. J. Clean. Prod. 2020, 242, 118317. [Google Scholar] [CrossRef]
- Li, T.; Yang, W. Supply chain planning problem considering customer inventory holding cost based on an improved tabu search algorithm. Appl. Math. Nonlinear Sci. 2020, 5, 557–564. [Google Scholar] [CrossRef]
- Misni, F.; Lee, L.S. Modified harmony search algorithm for location-inventory-routing problem in supply chain network design with product returns. Malays. J. Math. Sci. 2021, 15, 1–20. [Google Scholar]
- Ahmadi-Javid, A.; Seddighi, A.H. A location-routing-inventory model for designing multisource distribution networks. Eng. Optim. 2012, 44, 637–656. [Google Scholar] [CrossRef]
- Deng, S.; Li, Y.; Zhou, T.; Cao, Y. Study on recyclable reserve logistics network optimization based on e-commerce. In Proceedings of the 2014 International Conference on Management of e-Commerce and e-Government, Shanghai, China, 31 October–2 November 2014; pp. 337–340. [Google Scholar]
- Guo, H.; Li, Y. Multiobjective location-inventory-routing problem taking returns into consideration. In Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2014; pp. 19–26. [Google Scholar]
- Guerrero, W.J.; Prodhon, C.; Velasco, N.; Amaya, C.A. A relax-and-price heuristic for the inventory-location-routing problem. Int. Trans. Oper. Res. 2015, 22, 129–148. [Google Scholar] [CrossRef]
- Deng, S.; Li, Y.; Guo, H.; Liu, B. Solving a closed-loop location-inventory-routing problem with mixed quality defects returns in e-commerce by hybrid ant colony optimization algorithm. Discret. Dyn. Nat. Soc. 2016, 2016, 6467812. [Google Scholar] [CrossRef]
- Fan, J.; Tian, X.F.; Deng, S.; Guo, H.; Zhang, Z.L. Multi-objective location-inventory-routing problem based on time-satisfaction degree. In Proceedings of the 6th International Conference on Logistics and Supply Chain Management, Changsha, China, 1–3 December 2016; pp. 295–303. [Google Scholar]
- Lerhlaly, S.; Lebbar, M.; Allaoui, H.; Ouazar, D.; Afifi, S. An integrated inventory location routing: Problem considering CO2 emissions. Contemp. Eng. Sci. 2016, 9, 303–314. [Google Scholar] [CrossRef]
- Riquelme-Rodríguez, J.-P.; Gamache, M.; Langevin, A. Location arc routing problem with inventory constraints. Comput. Oper. Res. 2016, 76, 84–94. [Google Scholar] [CrossRef]
- Yuchi, Q.; He, Z.; Yang, Z.; Wang, N. A location-inventory-routing problem in forward and reverse logistics network design. Discret. Dyn. Nat. Soc. 2016, 2016, 3475369. [Google Scholar] [CrossRef]
- Abou El Madj, B. An inventory location routing model with environmental considerations. In Proceedings of the MATEC Web of Conferences, Tianjin, China, 6–9 July 2017; p. 00002. [Google Scholar]
- Guo, H.; Li, C.; Zhang, Y.; Zhang, C.; Wang, Y. A nonlinear integer programming model for integrated location, inventory, and routing decisions in a closed-loop supply chain. Complexity 2018, 2018, 2726070. [Google Scholar] [CrossRef]
- Kaya, O.; Ozkok, D. A network design problem with location, inventory and routing decisions. In Proceedings of the GECCO 2018 Companion—Proceedings of the 2018 Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018; Association for Computing Machinery, Inc.: New York, NY, USA, 2018; pp. 139–140. [Google Scholar]
- Sun, Q.; Chien, S.; Hu, D.W.; Ma, B.S. Optimizing the location-inventory-routing problem for perishable products considering food waste and fuel consumption. In Proceedings of the CICTP 2018: Intelligence, Connectivity, and Mobility—Proceedings of the 18th COTA International Conference of Transportation Professionals, Beijing, China, 5–8 July 2018; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2018; pp. 482–491. [Google Scholar]
- Chen, C.; Tian, Z.; Yao, B. Optimization of two-stage location-routing-inventory problem with time-windows in food distribution network. Ann. Oper. Res. 2019, 273, 111–134. [Google Scholar]
- Misni, F.; Lee, L.S.; Seow, H.-V. Hybrid harmony search-simulated annealing algorithm for location-inventory-routing problem in supply chain network design with defect and non-defect items. Appl. Sci. 2020, 10, 6625. [Google Scholar] [CrossRef]
- Aloui, A.; Mrabti, N.; Hamani, N.; Delahoche, L. Towards a collaborative and integrated optimization approach in sustainable freight transportation. IFAC PapersOnLine 2021, 54, 671–676. [Google Scholar] [CrossRef]
- Nasr, N.; Niaki, S.T.A.; Hussenzadek Kashan, A.; Seifbarghy, M. An efficient solution method for an agri-fresh food supply chain: Hybridization of lagrangian relaxation and genetic algorithm. Environ. Sci. Pollut. Res. 2021 online ahead of print.
- Misni, F.; Lee, L.S.; Jaini, N.I. Multi-objective hybrid harmony search-simulated annealing for location-inventory-routing problem in supply chain network design of reverse logistics with CO2 emission. J. Physics: Conf. Ser. 2021, 1988, 012054. [Google Scholar] [CrossRef]
- Tang, J.; Ji, S.; Jiang, L. The design of a sustainable location-routing-inventory model considering consumer environmental behavior. Sustainability 2016, 8, 211. [Google Scholar] [CrossRef]
- Ahmadi-Javid, A.; Amiri, E.; Meskar, M. A profit-maximization location-routing-Pricing Problem: A Branch-and-Price Algorithm. Eur. J. Oper. Res. 2018, 271, 866–881. [Google Scholar] [CrossRef]
- Tavana, M.; Abtahi, A.-R.; Di Caprio, D.; Hashemi, R.; Yousefi-Zenouz, R. An integrated location-inventory-routing humanitarian supply chain network with pre- and post-disaster management considerations. Socio-Econ. Plan. Sci. 2018, 64, 21–37. [Google Scholar] [CrossRef]
- Vahdani, B.; Veysmoradi, D.; Noori, F.; Mansour, F. Two-stage multi-objective location-routing-inventory model for humanitarian logistics network design under uncertainty. Int. J. Disaster Risk Reduct. 2018, 27, 290–306. [Google Scholar] [CrossRef]
- Fatemi Ghomi, S.M.T.; Asgarian, B. Development of metaheuristics to solve a transportation inventory location routing problem considering lost sale for perishable goods. J. Model. Manag. 2019, 14, 175–198. [Google Scholar] [CrossRef]
- Karakostas, P.; Sifaleras, A.; Georgiadis, M.C. A general variable neighborhood search-based solution approach for the location-inventory-routing problem with distribution outsourcing. Comput. Chem. Eng. 2019, 126, 263–279. [Google Scholar] [CrossRef]
- Pourhejazy, P.; Kwon, O.K.; Lim, H. Integrating sustainability into the optimization of fuel logistics networks. KSCE J. Civ. Eng. 2019, 23, 1369–1383. [Google Scholar] [CrossRef]
- Aloui, A.; Hamani, N.; Delahoche, L. An integrated optimization approach using a collaborative strategy for sustainable cities freight transportation: A Case study. Sustain. Cities Soc. 2021, 75, 103331. [Google Scholar] [CrossRef]
- Aydemir-Karadag, A. Bi-objective adaptive large neighborhood search algorithm for the healthcare waste periodic location inventory routing problem. Arab. J. Sci. Eng. 2022, 47, 3861–3876. [Google Scholar] [CrossRef] [PubMed]
- Morales Chavez, M.M.; Costa, Y.; Sarache, W. A three-objective stochastic location-inventory-routing model for agricultural waste-based biofuel supply chain. Comput. Ind. Eng. 2021, 162, 107759. [Google Scholar] [CrossRef]
- Rahbari, M.; Arshadi Khamseh, A.; Sadati-Keneti, Y.; Jafari, M.J. A risk-based green location-inventory-routing problem for hazardous materials: NSGA II, MOSA, and multi-objective black widow optimization. Environ. Dev. Sustain. 2022, 24, 2804–2840. [Google Scholar] [CrossRef]
- Rabbani, M.; Mokarrari, K.R.; Akbarian-saravi, N. A multi-objective location inventory routing problem with pricing decisions in a sustainable waste management system. Sustain. Cities Soc. 2021, 75, 103319. [Google Scholar] [CrossRef]
- Zarrat Dakhely Parast, Z.; Haleh, H.; Avakh Darestani, S.; Amin-Tahmasbi, H. Green reverse supply chain network design considering location-routing-inventory decisions with simultaneous pickup and delivery. Sustain. Supply Chain. Netw. Des. 2021. [Google Scholar] [CrossRef] [PubMed]
- Zhu, A.; Wen, Y.; Kaplan, M. Green logistics location-routing optimization solution based on improved GA a1gorithm considering low-carbon and environmental protection. J. Math. 2021, 2021, 6101194. [Google Scholar] [CrossRef]
- Monroy, A.G.A.; Díaz, H.L. A parallel programming approach to the solution of the location-inventory and multi-echelon routing problem in the humanitarian supply chain. Transp. Res. Procedia 2021, 58, 495–502. [Google Scholar] [CrossRef]
- Shafiee Moghadam, S.; Aghsami, A.; Rabbani, M. A hybrid NSGA-II algorithm for the closed-loop supply chain network design in e-commerce. RAIRO—Oper. Res. 2021, 55, 1643–1674. [Google Scholar] [CrossRef]
- Seyedhosseini, S.M.; Bozorgi-Amiri, A.; Daraei, S. An integrated location-routing-inventory problem by considering supply disruption. iBusiness 2014, 06, 29–37. [Google Scholar] [CrossRef][Green Version]
- Ghani, N.E.A.; Shariff, S.S.R.; Zahari, S.M. Optimization of location routing inventory problem with transshipment. In AIP Conference Proceedings; American Institute of Physics Inc.: College Park, MA, USA, 2015; p. 050043. [Google Scholar]
- Angazi, H. An integrated location inventory routing model in supply chain network designing under uncertainty. Decis. Sci. Lett. 2016, 5, 551–568. [Google Scholar] [CrossRef]
- Shariff, S.S.R.; Kamal, N.S.; Omar, M.; Moin, N.H. Location routing inventory problem with transshipment points using p-center. J. Ind. Eng. Manag. Sci. 2016, 1, 59–72. [Google Scholar]
- Gholamian, M.R.; Heydari, M. An inventory model with METRIC approach in location-routing-inventory problem. Adv. Prod. Eng. Manag. 2017, 12, 115–126. [Google Scholar] [CrossRef][Green Version]
- Habibi, F.; Asadi, E.; Sadjadi, S.J. Developing a location-inventory-routing model using METRIC approach in inventory policy. Uncertain Supply Chain. Manag. 2017, 5, 337–358. [Google Scholar] [CrossRef]
- Asadi, E.; Habibi, F.; Nickel, S.; Sahebi, H. A bi-objective stochastic location-inventory-routing model for microalgae-based biofuel supply chain. Appl. Energy 2018, 228, 2235–2261. [Google Scholar] [CrossRef]
- Habibi, F.; Asadi, E.; Sadjadi, S.J. A location-inventory-routing optimization model for cost effective design of microalgae biofuel distribution system: A case study in Iran. Energy Strategy Rev. 2018, 22, 82–93. [Google Scholar] [CrossRef]
- Momenikiyai, M.; Ebrahimnejad, S.; Vahdani, B. A bi-objective mathematical model for inventory-distribution-routing problem under risk pooling effect: Robust meta-heuristic approach. Econ. Comput. Econ. Cybern. Stud. Res. 2018, 52, 257–274. [Google Scholar]
- Fallah-Tafti, A.; Vahdatzad, M.A.; Sadegheiyeh, A. A comprehensive mathematical model for a location-routing-inventory problem under uncertain demand: A numerical illustration in cash-in-transit sector. Int. J. Eng. Trans. B Appl. 2019, 32, 1634–1642. [Google Scholar]
- Manavizadeh, N.; Shaabani, M.; Aghamohamadi, S. Designing a green location routing inventory problem considering transportation risks and time window: A case study. J. Ind. Syst. Eng. 2019, 12, 27–56. [Google Scholar]
- Rabbani, M.; Heidari, R.; Yazdanparast, R. A stochastic multi-period industrial hazardous waste location-routing problem: Integrating NSGA-II and monte carlo simulation. Eur. J. Oper. Res. 2019, 272, 945–961. [Google Scholar] [CrossRef]
- Zheng, X.; Yin, M.; Zhang, Y. Integrated optimization of location, inventory and routing in supply chain network design. Transp. Res. Part B Methodol. 2019, 121, 1–20. [Google Scholar] [CrossRef]
- Biuki, M.; Kazemi, A.; Alinezhad, A. An integrated location-routing-inventory model for sustainable design of a perishable products supply chain network. J. Clean. Prod. 2020, 260. [Google Scholar] [CrossRef]
- Kaya, O.; Ozkok, D. A blood bank network design problem with integrated facility location, inventory and routing decisions. Netw. Spat. Econ. 2020, 20, 757–783. [Google Scholar] [CrossRef]
- Karimkhani, S.Z.; Mina, H.; Biuki, M.; Govindan, K. A chance constrained fuzzy goal programming approach for perishable pharmaceutical supply chain network design. Ann. Oper. Res. 2020, 295, 425–452. [Google Scholar] [CrossRef]
- Aghighi, A.; Goli, A.; Malmir, B.; Tirkolaee, E.B. The stochastic location-routing-inventory problem of perishable products with reneging and balking. J. Ambient. Intell. Humaniz. Comput. 2021, 1–20. [Google Scholar] [CrossRef]
- Ji, S.; Tang, J.; Sun, M.; Luo, R. Multi-objective optimization for a combined location-path-inventory system considering carbon-capped differences. J. Ind. Manag. Optim. 2022, 18, 1949–1977. [Google Scholar] [CrossRef]
- Josiah, T.; Suhada, A.; Chetthamrongchai, P.; Purbasari, H. Optimization of the location, inventory and routing of capacity vehicles with interval uncertainty. Ind. Eng. Manag. Syst. 2021, 20, 654–661. [Google Scholar] [CrossRef]
- Liu, A.; Zhu, Q.; Xu, L.; Lu, Q.; Fan, Y. Sustainable supply chain management for perishable products in emerging markets: An integrated location-inventory-routing model. Transp. Res. Part E Logist. Transp. Rev. 2021, 150, 102319. [Google Scholar] [CrossRef]
- Mahjoob, M.; Fazeli, S.S. Green supply chain network design with emphasis on inventory decisions. Sustain. Oper. Comput. 2021, 2, 214–229. [Google Scholar] [CrossRef]
- Harati, S.; Roghanian, E.; Hafezalkotob, A.; Shojaie, A.A. A robust two-stage stochastic location-routing-inventory model for perishable items. Teh. Vjesn. Tech. Gaz. 2021, 28, 1989–1995. [Google Scholar]
- Shu, B.; Pei, F.; Zheng, K.; Yu, M. LIRP optimization of cold chain logistics in satellite warehouse mode of supermarket chains. J. Intell. Fuzzy Syst. 2021, 41, 4825–4839. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Sun, W.; Pu, Y. Research on NSGA-III in location-routing-inventory problem of pharmaceutical logistics intermodal network. J. Intell. Fuzzy Syst. 2021, 41, 699–713. [Google Scholar] [CrossRef]
- Tavakkoli-Moghaddam, R.; Forouzanfar, F.; Ebrahimnejad, S. Incorporating location, routing, and inventory decisions in a bi-objective supply chain design problem with risk-pooling. J. Ind. Eng. Int. 2013, 9, 19. [Google Scholar] [CrossRef][Green Version]
- Chen, D.; Chen, D.; Sun, G.; Liu, G. Combined location routing and inventory problem of e-commerce distribution system with fuzzy random demand. Int. J. Hybrid Inf. Technol. 2014, 7, 429–442. [Google Scholar] [CrossRef]
- Lin, R.-H. An integrated model for supplier selection under a fuzzy situation. Int. J. Prod. Econ. 2012, 138, 55–61. [Google Scholar] [CrossRef]
- Gholipour, S.; Ashoftehfard, A.; Mina, H. Green supply chain network design considering inventory-location-routing problem: A fuzzy solution approach. Int. J. Logist. Syst. Manag. 2020, 35, 436–452. [Google Scholar] [CrossRef]
- Khalili Nasr, A.; Tavana, M.; Alavi, B.; Mina, H. A novel fuzzy multi-objective circular supplier selection and order allocation model for sustainable closed-loop supply chains. J. Clean. Prod. 2021, 287, 124994. [Google Scholar] [CrossRef]
- Tavana, M.; Tohidi, H.; Alimohammadi, M.; Lesansalmasi, R. A location-inventory-routing model for green supply chains with low-carbon emissions under uncertainty. Environ. Sci. Pollut. Res. 2021, 28, 50636–50648. [Google Scholar] [CrossRef]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Prodhon, C.; Prins, C. A survey of recent research on location-routing problems. Eur. J. Oper. Res. 2014, 238, 1–17. [Google Scholar] [CrossRef]
- Liu, Y.-K.; Liu, B. Fuzzy random variables: A scalar expected value operator. Fuzzy Optim. Decis. Mak. 2003, 2, 143–160. [Google Scholar] [CrossRef]
- Kwakernaak, H. Fuzzy random variables—I. definitions and theorems. Inf. Sci. 1978, 15, 1–29. [Google Scholar] [CrossRef]
- Liu, B. Theory and Practice of Uncertain Programming. Stud. Fuzziness Soft Comput. 2009, 239, 1–205. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).