Joint Optimization of Allocations and Relocations in One-Way Carsharing Systems with Two Operators
Abstract
1. Introduction
- In a two-operator carsharing system, the allocations and relocations are jointly optimized. The users’ preferences between operators are considered. The number of shared cars at the departing station, the number of parking spaces at the destination, and the travel cost simultaneously impact the users’ preferences.
- A nonlinear mixed-integer bilevel programming model is set to determine the optimal allocations, relocations, and how users choose between operators. The results show that the allocations impact the operators mutually in a two-operator carsharing system. The users’ preferences also play a vital role in improving the performance of the system.
2. Literature Review
2.1. Single-Operator Carsharing Systems
2.2. Multiple-Operator Carsharing Systems
2.3. Interactions among Multiple Parities
3. Model Formulation
3.1. Problem Description
- Types of cars used by both operators are the same;
- Locations of the potential carsharing stations are pre-known, and there is an upper limit on the total number of parking spaces at each location;
- Operators pay for gas consumption during the trip;
- All trips start and end at carsharing stations.
3.2. Mutal Impact between Operators
3.2.1. Notations
3.2.2. Interactions between Operators
- (1)
- Parking spaces
- (2)
- Users
- (i)
- With users’ preferences
- (ii)
- Without users’ preferences
3.3. Bilevel Programming Model
3.3.1. Upper-Level Model
- (1)
- Objective function
- (2)
- Constraints
- Allocation of parking spaces
- Allocation of shared cars
- Users choose the leader
- Decision variables for the leader
3.3.2. Lower-Level Model
- (1)
- Objective function
- (2)
- Constraints
- Allocation of parking spaces
- Allocation of shared cars
- Users choosing the follower
- Decision variables for the follower
3.4. Solution Algorithm
- Define the chromosome
- Population initialization
- Fitness function
- Selection of the chromosome
- Piece-wised adaptive function
- (1)
- Crossover
- (2)
- Mutation
4. Case Studies
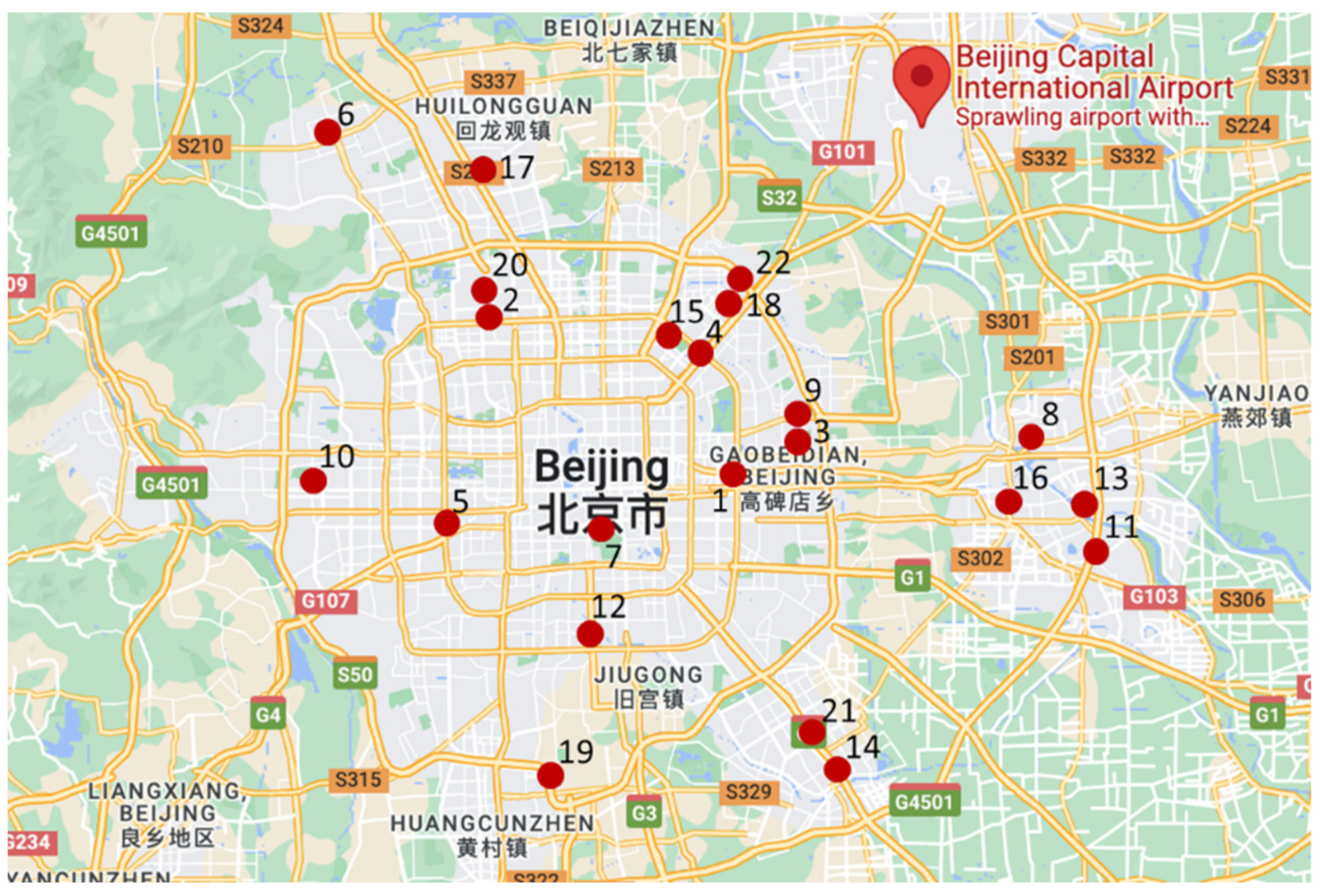
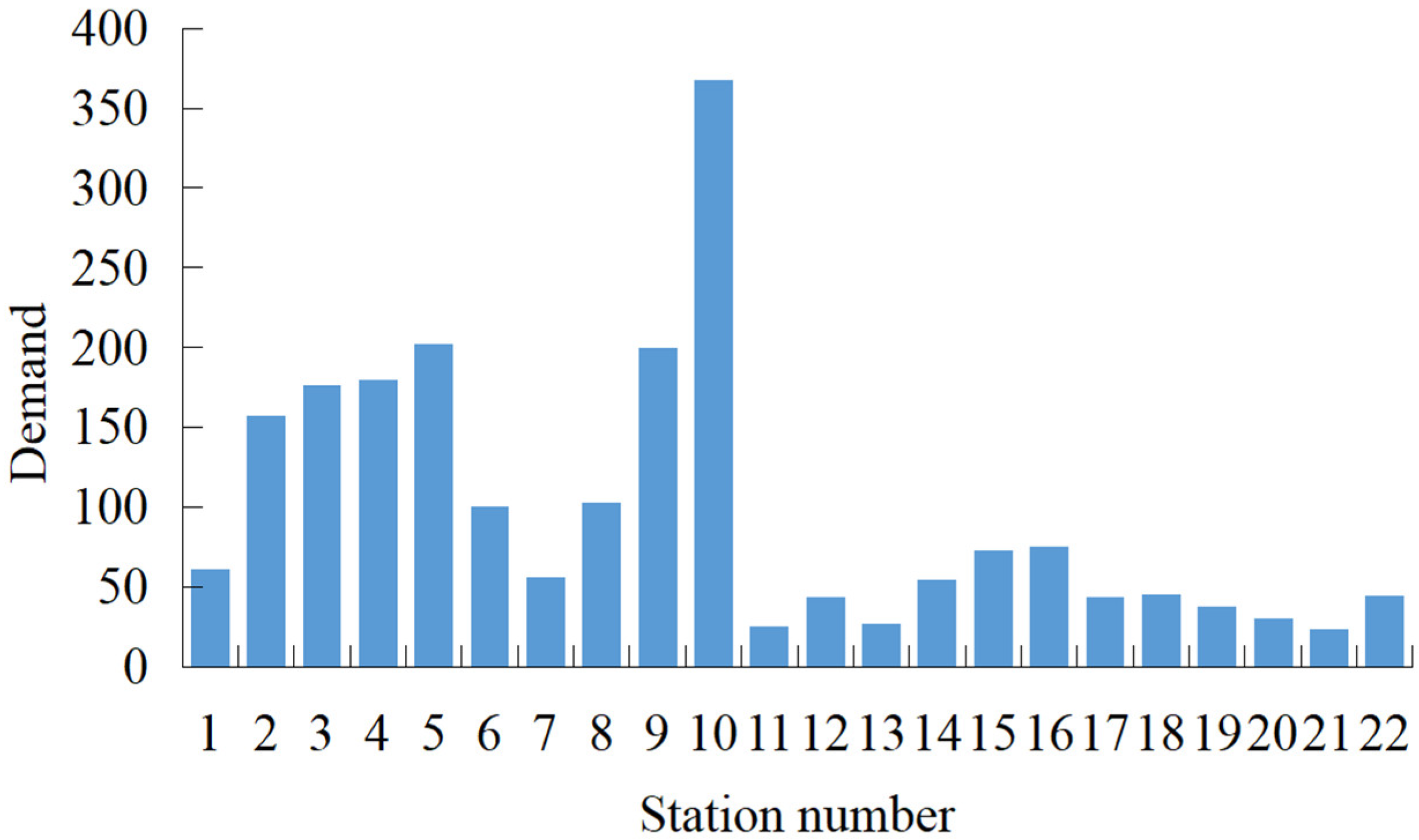
4.1. Description about the Carsharing System
- (1)
- Single-operator carsharing systems
- (2)
- Two-operator carsharing systems
- (i)
- Without considering users’ preferences
- (ii)
- Considering users’ preferences
4.2. Performance of the Two-Operator Carsharing System
- (1)
- Revenue and costs
- (2)
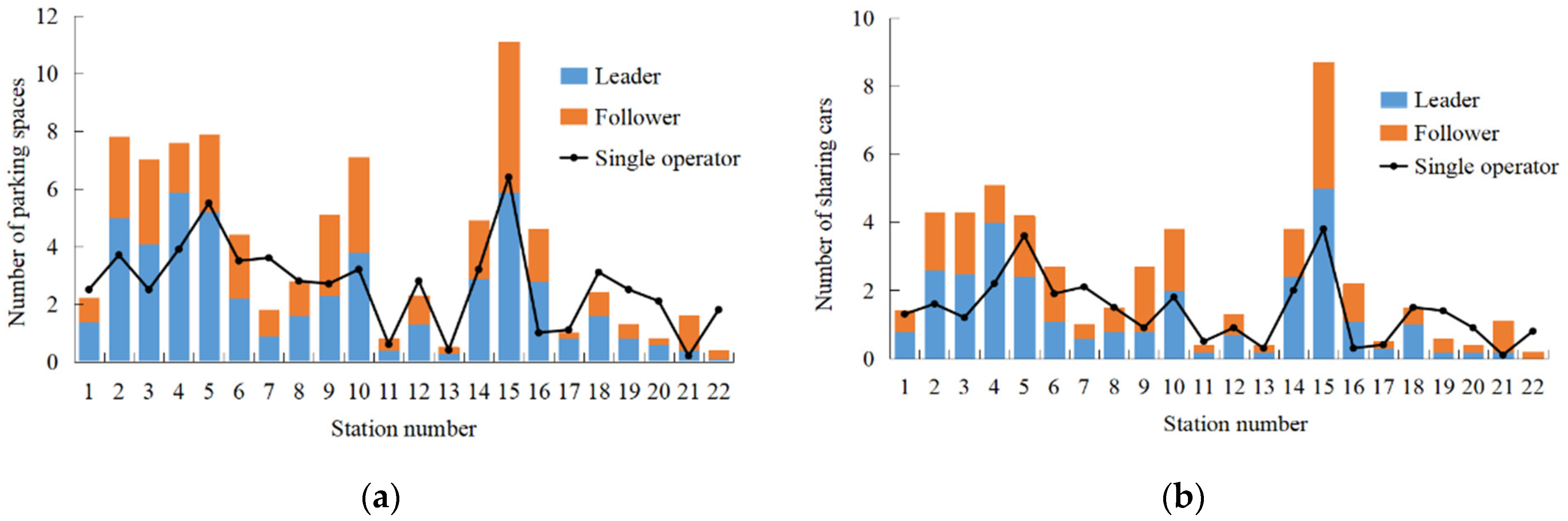
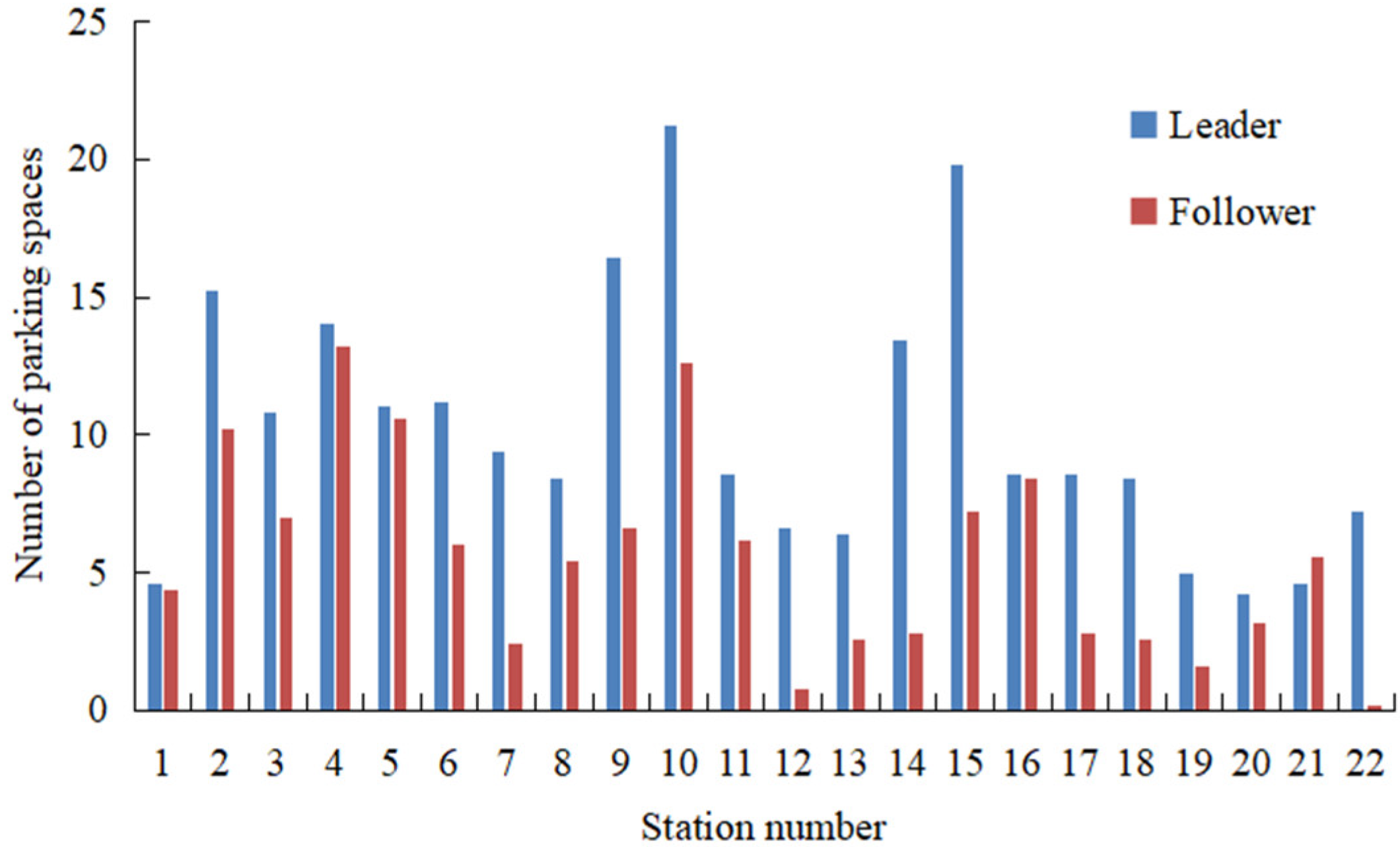
- Allocations
- (3)
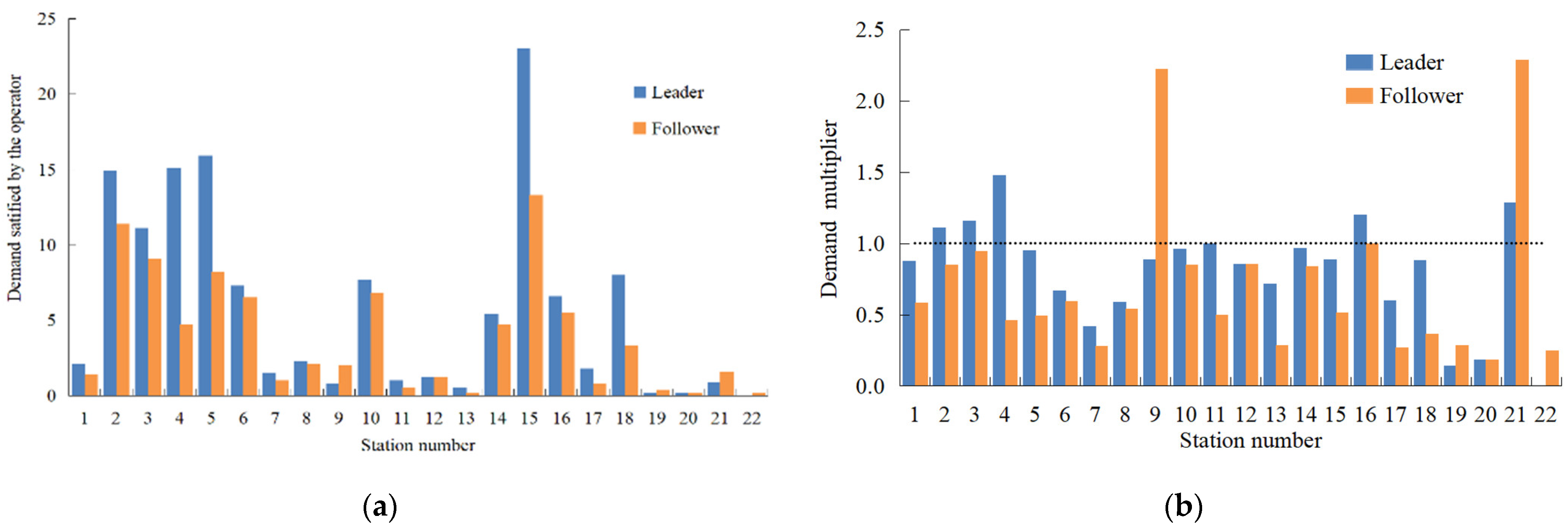
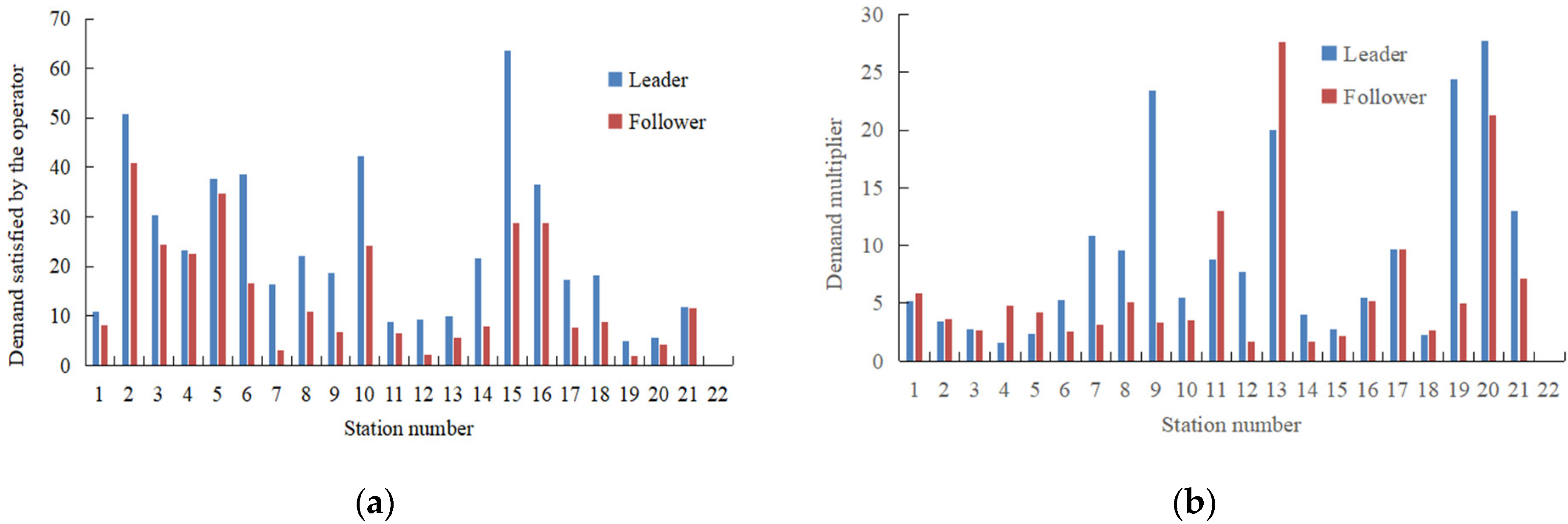
- Demand satisfaction
4.3. Impact of Considering Users’ Preferences
- (1)
- Revenue and costs
- (2)
- Allocations
- (3)
- Demand satisfaction
5. Conclusions
- (1)
- It is necessary to study the interactions between the operators.
- (2)
- Users’ preferences have a major impact on the performance of each operator.
Funding
Conflicts of Interest
References
- Li, M.; Zeng, Z.; Wang, Y. An innovative car sharing technological paradigm towards sustainable mobility. J. Clean. Prod. 2021, 288, 125626. [Google Scholar] [CrossRef]
- Lu, R.; Zhao, X.; Wang, Y. A Tailored Pricing Strategy for Different Types of Users in Hybrid Carsharing Systems. Algorithms 2022, 15, 172. [Google Scholar] [CrossRef]
- Martin, L.; Minner, S.; Pocas, D.; Schulz, A.S. The Competitive Pickup and Delivery Orienteering Problem for Balancing Car-Sharing Systems. Transp. Sci. 2021, 55, 1232–1259. [Google Scholar] [CrossRef]
- Cheng, Y.; Chen, X.; Ding, X.; Zeng, L. Optimizing location of car-sharing stations based on potential travel demand and present operation characteristics: The case of Chengdu. J. Adv. Transp. 2019, 2019, 7546303. [Google Scholar] [CrossRef]
- Li, W.; Li, Y.; Fan, J.; Deng, H. Siting of Carsharing Stations Based on Spatial Multi-Criteria Evaluation: A Case Study of Shanghai EVCARD. Sustainability 2017, 9, 152. [Google Scholar] [CrossRef]
- Becker, H.; Ciari, F.; Axhausen, K.W. Comparing car-sharing schemes in Switzerland: User groups and usage patterns. Transp. Res. Part A Policy Pract. 2017, 97, 17–29. [Google Scholar] [CrossRef]
- Balac, M.; Becker, H.; Ciari, F.; Axhausen, K.W. Modeling competing free-floating carsharing operators—A case study for Zurich, Switzerland. Transp. Res. Part C Emerg. Technol. 2019, 98, 101–117. [Google Scholar] [CrossRef]
- Hu, L.; Liu, Y. Joint design of parking capacities and fleet size for one-way station-based carsharing systems with road congestion constraints. Transp. Res. B-Methodol. 2016, 93, 268–299. [Google Scholar] [CrossRef]
- Sai, Q.; Bi, J.; Chai, J. Optimal model for carsharing station location based on multi-factor constraints. Algorithms 2020, 13, 43. [Google Scholar] [CrossRef]
- Guo, H.; Chen, Y.; Liu, Y. Shared autonomous vehicle management considering competition with human-driven private vehicles. Transp. Res. Part C Emerg. Technol. 2022, 136, 103547. [Google Scholar] [CrossRef]
- Huang, K.; Correia, G.H.D.A.; An, K. Solving the station-based one-way carsharing network planning problem with relocations and non-linear demand. Transp. Res. C Emerg. Technol. 2018, 90, 1–17. [Google Scholar] [CrossRef]
- Deza, A.; Huang, K.; Metel, M.R. Charging station optimization for balanced electric car sharing. Discret. Appl. Math. 2020, 308, 187–197. [Google Scholar] [CrossRef]
- Xu, M.; Meng, Q.; Liu, Z. Electric vehicle fleet size and trip pricing for one-way carsharing services considering vehicle relocation and personnel assignment. Transp. Res. B-Meth. 2018, 111, 60–82. [Google Scholar] [CrossRef]
- Huang, K.; An, K.; Correia, G.H.D.A. Planning station capacity and fleet size of one-way electric carsharing systems with continuous state of charge functions. Eur. J. Oper. Res. 2020, 287, 1075–1091. [Google Scholar] [CrossRef]
- Nourinejad, M.; Roorda, M.J. A dynamic carsharing decision support system. Transp. Res. E-Log. 2014, 66, 36–50. [Google Scholar] [CrossRef]
- Yang, S.; Wu, J.; Sun, H.; Qu, Y.; Wang, D.Z.W. Integrated optimization of pricing and relocation in the competitive carsharing market: A multi-leader-follower game model. Transp. Res. Part C Emerg. Technol. 2022, 138, 103613. [Google Scholar] [CrossRef]
- Fernández, J.; Boglárka, G.; Redondo, J.L.; Ortigosa, P.M.; Arrondo, A.G. A planar single-facility competitive location and design problem under the multi-deterministic choice rule. Comput. Oper. Res. 2017, 78, 305–315. [Google Scholar] [CrossRef]
- Ma, H.; Guan, X.; Wang, L. A single-facility competitive location problem in the plane based on customer choice rules. J. Data Inf. Manag. 2020, 2, 323–336. [Google Scholar] [CrossRef]
- Beresnev, V. Branch-and-bound algorithm for a competitive facility location problem. Comput. Oper. Res. 2013, 40, 2062–2070. [Google Scholar] [CrossRef]
- Beresnev, V.L. On the competitive facility location problem with a free choice of suppliers. Autom. Remote Control 2014, 75, 668–676. [Google Scholar] [CrossRef]
- Beresnev, V.; Melnikov, A. Exact method for the capacitated competitive facility location problem. Comput. Oper. Res. 2018, 95, 73–82. [Google Scholar] [CrossRef]
- Nasiri, M.M.; Mahmoodian, V.; Rahbari, A.; Farahmand, S. A modified genetic algorithm for the capacitated competitive facility location problem with the partial demand satisfaction. Comput. Ind. Eng. 2018, 124, 435–448. [Google Scholar] [CrossRef]
- Lin, Y.H.; Tian, Q. Generalized Benders decomposition for competitive facility location with concave demand and zone-specialized variable attractiveness. Comput. Oper. Res. 2021, 130, 105236. [Google Scholar] [CrossRef]
- Kress, D.; Pesch, E. Competitive location and pricing on networks with random utilities. Netw. Spat. Econ. 2016, 16, 837–863. [Google Scholar] [CrossRef]
- Jakobović, D.; Golub, M. Adaptive genetic algorithm. J. Comput. Inf. Technol. 1999, 7, 229–235. [Google Scholar]

| Reference | Number of Operators | Mutual Impacts of Operators | Users’ Preference | Joint Optimization of Allocation and Relocations |
|---|---|---|---|---|
| [8,9] | 1 | - | - | No |
| [11,12,13,14,15,16] | 1 | - | - | Yes |
| [4] | 2 | No | No | No |
| [23] | 2 | Yes | No | Yes |
| [5] | Multiple | No | No | No |
| [24] | Multiple | No | No | Yes |
| Set | |
| Set of locations of potential carsharing stations, are commonly used indices | |
| Set of time steps | |
| Set of time-space nodes, and means the status of station at time step | |
| Set of arcs representing that users travel from station at time step and arrive at station at time step , . is the time steps needed during the trip and it I s pre-given. It is calculated based on travel distances between stations. The equation is , is the travel speed at time step | |
| Set of carsharing operators. The leader is denoted as ; the follower labeled as | |
| Parameters | |
| Depreciation cost per day per sharing car, CNY/day | |
| Gas consumption per time step, CNY/time step | |
| Relocation cost per time step, CNY/time step | |
| Maintenance cost per parking space per day, CNY/day | |
| Travel demand between stations at different time steps, | |
| Upper limit of the number of parking spaces operators can allocate at station , | |
| Cost charged by operator per kilometer, CNY/kilometer, | |
| Cost charged by operator per time step, CNY/time step, | |
| Decision variables for the leader | |
| Number of parking spaces the leader sets at station , | |
| Number of sharing cars the leader allocates at station at the beginning of the operational period, | |
| Number of relocations performed by the leader between stations (departing at time step ) and (arriving at time step ), | |
| Decision variables for the follower | |
| Number of parking spaces the follower sets at station , | |
| Number of sharing cars the follower allocates at station at the beginning of the operational period, | |
| Number of relocations performed by the follower between stations (departing at time step ) and (arriving at time step ), | |
| Auxiliary variables | |
| Travel utility when users choose operator between stations and , | |
| Probability that users choose operator when they travel from station to , | |
| Number of users choosing operator from station to | |
| Number of available sharing cars operator allocates at station at time step , | |
| Stage Number | Crossover Rate | Mutation Rate | ||
|---|---|---|---|---|
| 1 | 0.9 | 0.8 | 0.04 | 0.02 |
| 2 | 0.7 | 0.6 | 0.06 | 0.04 |
| 3 | 0.5 | 0.4 | 0.08 | 0.06 |
| Upper-level model do |
| Step 1: Initialization . by steps in Figure 1 |
| Step 2: Fitness evaluation is taken as the fitness function for the CAGA of the upper-level model. The bigger the fitness function , the better quality of the corresponding chromosome owned. |
| Step 3: Crossover , then . It is evaluated by the fitness function. |
| Step 4: Mutation to perform multiple—point mutations, the the new fearible solutin , the fitness value is also evaluated. |
| Step 5: Update the new population for next generation , keeping n popultions with the highest fitness value . |
| Step 6: Output current optimal solution , the corresponding chromosome is currently optimal. Output the . |
| Lower-level model |
| do |
| Step 7: Initialization |
| Step 8: Fitness evaluation , the fitness of all chromosomes can be obtained . |
| Step 9: Crossover , is generated with a and evaluated by the fitness function. |
| Step 10: Mutation to perform multiple-point mutation, and the new population , the fitness value is also evaluated. |
| Step 11: Update new population for next generation for the next generation. |
| ; |
| Step 12: End do (For g do) Repeat steps 8–11 until the CAGA for the lower-level model reaches one of the ending criteria. ), the difference between the maximal fitness obtained from two adjacent iterations is below an exceptionally small value (taken as 0.001). , outuput the . |
| Step 13: Generate new feasible solutions for the upper-level model Given solutions obtained in Step 12, repeating steps 1–12 until reaching one of the ending criteria of the upper-level model |
| do) When the CAGA for the upper-level model reaches one of the ending criteria, the algorithm terminates, and the optimal solution is output. There are also two ending criteria for the upper-level model. 2. Difference between the maximal fitness obtained from two adjacent iterations is below an exceptionally small value (taken as 0.001). |
| Indicators | Single Operator | Two Operators | |
|---|---|---|---|
| The Leader (Growth Rate %) | The Follower (Growth Rate %) | ||
| Revenue (CNY) | 4714 | 4117.8 (−12.65) | 2769.5 (−41.25) |
| Profit (CNY) | 3316.7 | 2833.0 (−14.58) | 1730.5 (−47.82) |
| Relocation cost (CNY) | 161.1 | 186.6 (15.79) | 226.8 (40.79) |
| Depreciation cost of sharing cars (CNY) | 527.0 | 494.7 (−6.13) | 421.2 (25.81) |
| Maintenance cost of parking spaces (CNY) | 709.2 | 603.6 (−14.89) | 409.2 (−40.61) |
| Satisfied demands | 135.8 | 127.5 (−6.11) | 85.1 (−37.33) |
| Number of sharing cars | 31.0 | 29.1 (−6.13) | 23 (−25.81) |
| Number of parking spaces | 59.1 | 50.3 (−14.89) | 35.1 (−40.61) |
| Number of relocations | 3.9 | 4.3 (10.26) | 4.9 (25.64) |
| Average demand per car satisfies | 4.4 | 4.4 (0.00) | 3.7 (−15.54) |
| Average time steps per user takes | 2.33 | 2.21 (−4.98) | 2.28 (−2.08) |
| Average profit per car makes | 106.99 | 97.31 (−9.01) | 75.24 (−29.68) |
| Average profit per parking space brings | 56.12 | 56.32 (0.36) | 49.3 (−12.15) |
| Indicators | Leader | Follower | ||
|---|---|---|---|---|
| Value | Growth Rate (%) | Value | Growth Rate (%) | |
| Revenue (CNY) | 15,202.8 | 222.50 | 7890.0 | 67.37 |
| Profit (CNY) | 9112.7 | 174.76 | 4520.6 | 36.30 |
| Relocation cost (CNY) | 0 | −100.00 | 0 | −100.00 |
| Depreciation cost of sharing cars (CNY) | 3406.8 | 546.45 | 1900.6 | 260.65 |
| Maintenance cost of parking spaces (CNY) | 2683.2 | 278.34 | 1468.8 | 107.11 |
| Demand satisfied by the operator | 498.2 | 266.84 | 305.5 | 124.98 |
| Number of sharing cars | 200.4 | 546.45 | 111.8 | 260.65 |
| Number of parking spaces | 223.6 | 278.34 | 122.4 | 107.11 |
| Number of relocations | 0 | −100.00 | 0 | −100.00 |
| Average demand per car satisfies | 2.49 | −43.25 | 2.73 | −37.62 |
| Average time steps per user takes | 2.24 | −3.63 | 2.07 | −11.05 |
| Average profit per car makes | 45.47 | −57.50 | 40.43 | −62.21 |
| Average profit per parking space brings | 40.75 | −27.38 | 36.93 | −34.19 |
| Indicators | Leader | Follower |
|---|---|---|
| Revenue (CNY) | 269.19 | 184.89 |
| Profit (CNY) | 221.67 | 161.23 |
| Number of relocations | −100 | −100 |
| Number of sharing cars | 588.66 | 386.09 |
| Number of parking spaces | 344.53 | 248.72 |
| Demand satisfied by the operator | 290.72 | 259.02 |
| Average demand per car satisfies | −43.26 | −26.14 |
| Average time steps per user takes | 1.42 | −9.16 |
| Average profit per car makes | −53.29 | −46.26 |
| Average profit per parking space brings | −27.64 | −25.09 |
| Indicators | Single Operator | Without Users’ Preferences | With Users’ Preferences | ||
|---|---|---|---|---|---|
| Leader | Follower | Leader | Follower | ||
| Profit | 70.36 | 68.80 | 62.48 | 59.94 | 57.30 |
| Relocation cost | 3.42 | 4.53 | 8.19 | 0.00 | 0.00 |
| Depreciation cost of sharing cars | 11.18 | 12.01 | 14.12 | 22.41 | 24.09 |
| Maintenance cost of parking spaces | 15.04 | 14.66 | 15.21 | 17.65 | 18.62 |
| Profit ratio to cost | 188.54 | 220.49 | 166.55 | 149.63 | 134.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, R. Joint Optimization of Allocations and Relocations in One-Way Carsharing Systems with Two Operators. Sustainability 2022, 14, 15308. https://doi.org/10.3390/su142215308
Lu R. Joint Optimization of Allocations and Relocations in One-Way Carsharing Systems with Two Operators. Sustainability. 2022; 14(22):15308. https://doi.org/10.3390/su142215308
Chicago/Turabian StyleLu, Rongqin. 2022. "Joint Optimization of Allocations and Relocations in One-Way Carsharing Systems with Two Operators" Sustainability 14, no. 22: 15308. https://doi.org/10.3390/su142215308
APA StyleLu, R. (2022). Joint Optimization of Allocations and Relocations in One-Way Carsharing Systems with Two Operators. Sustainability, 14(22), 15308. https://doi.org/10.3390/su142215308






