A Q-Learning-Based Approximate Solving Algorithm for Vehicular Route Game
Abstract
1. Introduction
- To adapt to the real-time of smart traffic, the Nash equilibrium coefficient of route games is proposed in this paper, which means the proportion of vehicles whose current route strategies are optimal;
- A Q-learning-based approximate solving algorithm is designed to generate the coordinated route schemes for the classic route game. This approximate Nash equilibrium-based method is more suitable for the dynamic traffic compared with the hard-solved precise solving algorithm;
- A decentralized route coordination framework (that can be applied to large road networks based on the assumption of IoVs) is built to alleviating Braess’ paradox in VRG.
2. Basic Assumptions and Formalizations
2.1. Concepts of the Art
- Braess’ paradox: with the proliferation of selfish VRG systems, the road efficiency is reduced since numerous vehicles obey the same guidance from the selfish VRG systems [15];
- Rout games: In a route game, the vehicles and their requirements are set as players and payoffs, respectively. The Nash equilibrium represents the final coordination routes. The route game can generate the route strategies systematically for a group of vehicles based on agents’ interaction relationship [17];
- Pure/mixed strategy: Pure strategy denotes a certain action chosen by each player in a game theory. Mixed strategy denotes a random action distribution with certain probability [33];
- Symmetrical games: All agents are non-personalized, which leads to the symmetry of the payoff matrix in the game. The symmetry makes the symmetrical games have some special mathematical properties [20].
2.2. Formalization of the Route Game
2.2.1. Description of the Traffic Scenario
2.2.2. Establishment of the Classic Route Game
- Step 1. The game information (such as the strategies and payoff functions) is obtained by vehicles based on the IoVs technology;
- Step 2. Based on the built route game , the on-board computer of each vehicle predicts the route strategies of others;
- Step 3. Based on the prediction result of other vehicles’ route strategies, all vehicles simultaneously calculate their own optimal route strategies θ and receive the payoff π.
3. Contributions to Solving Algorithms
3.1. Potential Function-Based Precise Algorithm
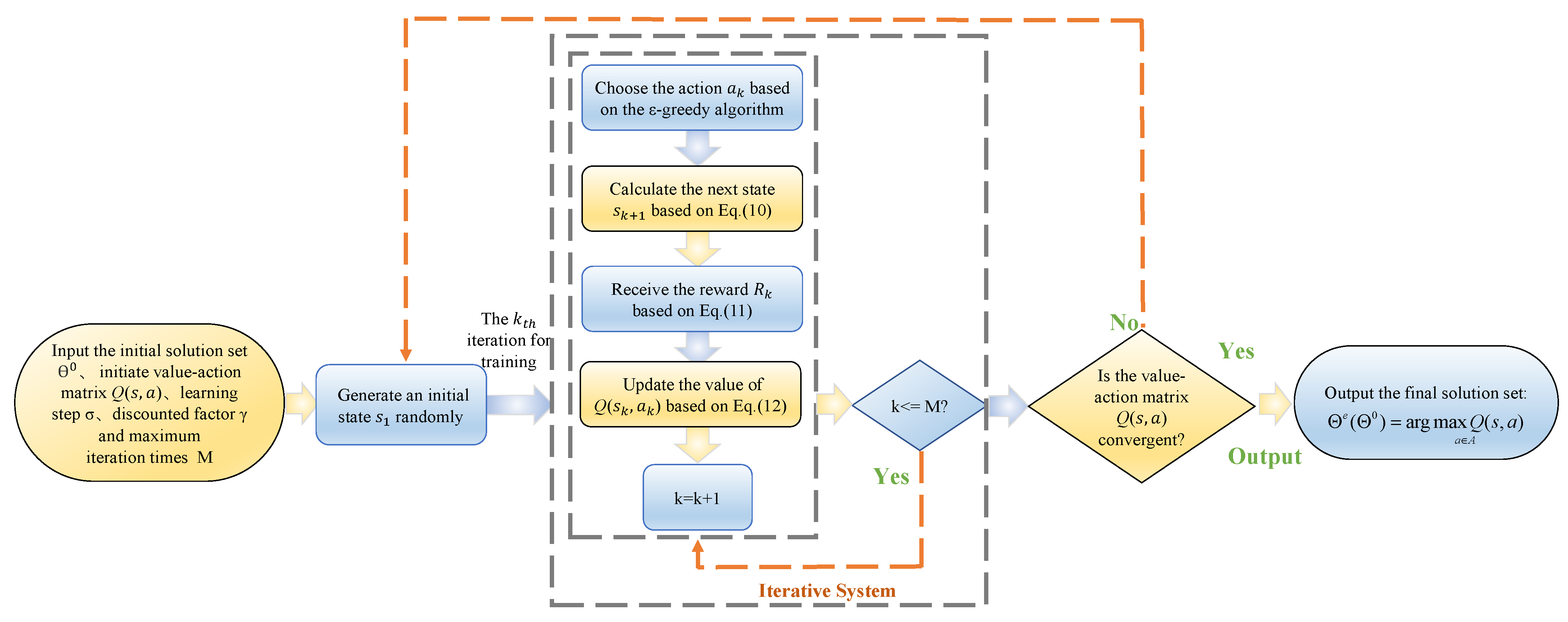
3.2. Q-Learning-Based Approximate Solving Algorithm
3.2.1. Definition of Approximate Nash Equilibrium
3.2.2. Q-Learning Matched with the Route Game
3.3. Discussion
4. Numerical Experiments
4.1. Preparation
4.2. Effectiveness of the Precise Algorithm (Control Group)
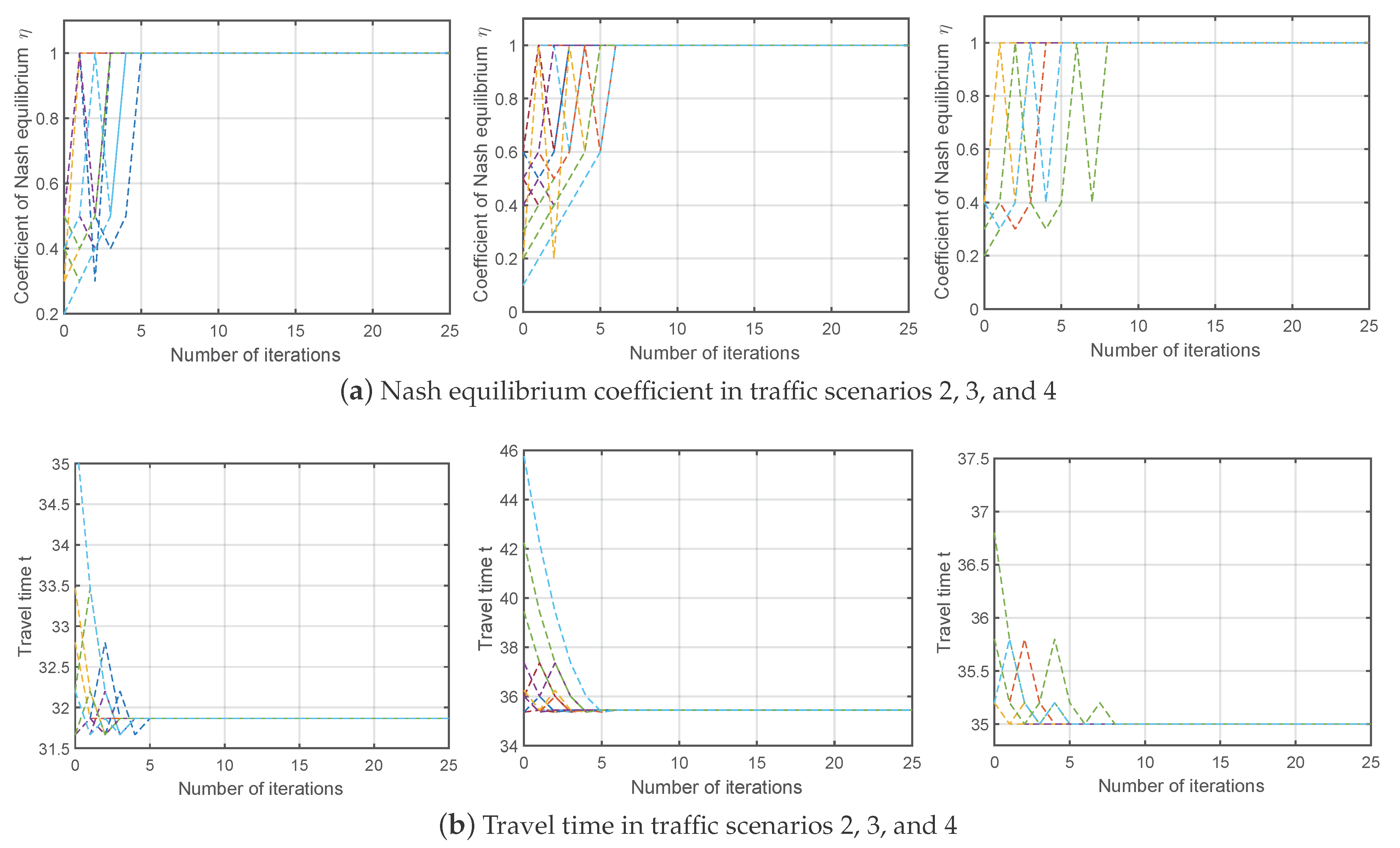
4.3. Availability of the Q-Learning-Based Approximate Solving Algorithm
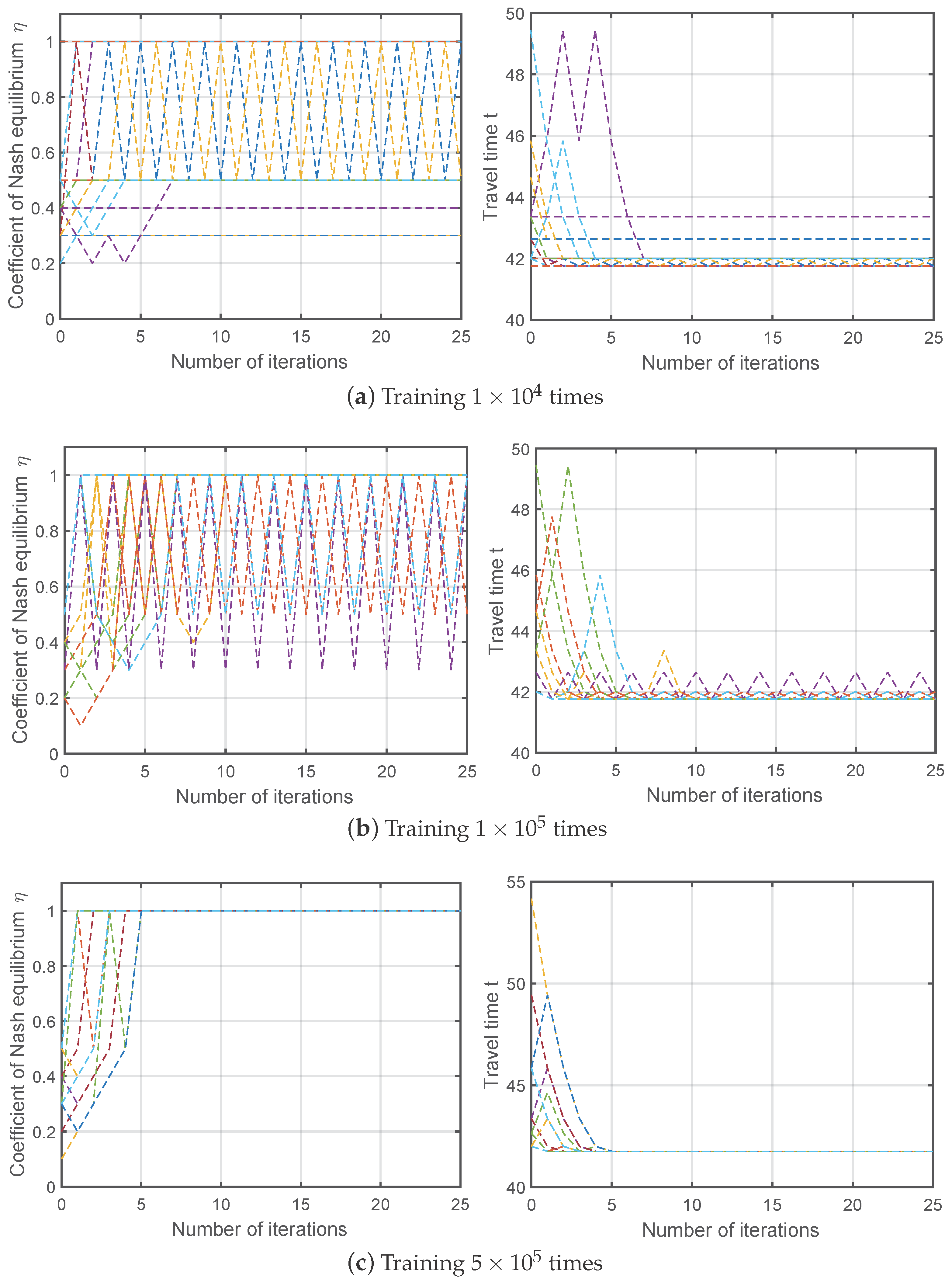
4.4. Robustness of the Q-Learning-Based Approximate Solving Algorithm
4.5. Discussion
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saberi, M.; Hamedmoghadam, H.; Ashfaq, M.; Hosseini, S.A.; Gu, Z.; Shafiei, S.; Nair, D.J.; Dixit, V.; Gardner, L.; Waller, S.T.; et al. A simple contagion process describes spreading of traffic jams in urban networks. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Tang, Z.; Guo, J. Could a smart city ameliorate urban traffic congestion? A quasi-natural experiment based on a smart city pilot program in China. Sustainability 2020, 12, 2291. [Google Scholar] [CrossRef]
- Afrin, T.; Yodo, N. A survey of road traffic congestion measures towards a sustainable and resilient transportation system. Sustainability 2020, 12, 4660. [Google Scholar] [CrossRef]
- Tang, C.; Hu, W.; Hu, S.; Stettler, M.E.J. Urban Traffic Route Guidance Method with High Adaptive Learning Ability under Diverse Traffic Scenarios. IEEE Trans. Intell. Transp. Syst. 2020, 22, 2956–2968. [Google Scholar] [CrossRef]
- Zhang, L.; Khalgui, M.; Li, Z. Predictive intelligent transportation: Alleviating traffic congestion in the internet of vehicles. Sensors 2021, 21, 7330. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Yu, X.; Liu, Y. PCNN: Deep convolutional networks for short-term traffic congestion prediction. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3550–3559. [Google Scholar] [CrossRef]
- Sun, J.; Kim, J. Joint prediction of next location and travel time from urban vehicle trajectories using long short-term memory neural networks. Transp. Res. C-Emerg. Technol. 2021, 128, 103114. [Google Scholar] [CrossRef]
- Li, J.; Ma, Y.; Gao, R.; Cao, Z.; Lim, A.; Song, W.; Zhang, J. Deep Reinforcement Learning for Solving the Heterogeneous Capacitated Vehicle Routing Problem. IEEE Trans. Cybern. 2021; in press. [Google Scholar]
- Zhang, L.; Khalgui, M.; Li, Z.; Zhang, Y. Fairness concern-based coordinated vehicle route guidance using an asymmetrical congestion game. IET Intell. Transp. Syst. 2022; in press. [Google Scholar]
- Yang, S.B.; Guo, C.; Yang, B. Context-aware path ranking in road networks. IEEE Trans. Knowl. Data Eng. 2022, 34, 3153–3168. [Google Scholar] [CrossRef]
- Braess, D.; Nagurney, A.; Wakolbinger, T. On a paradox of traffic planning. Transp. Sci. 2005, 39, 446–450. [Google Scholar] [CrossRef]
- Scarsini, M.; Schröder, M.; Tomala, T. Dynamic atomic congestion games with seasonal flows. Oper. Res. 2018, 66, 327–339. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, B.; Chen, X.; Wang, C. Atomic dynamic flow games: Adaptive vs. nonadaptive agents. Oper. Res. 2021, 69, 1680–1695. [Google Scholar] [CrossRef]
- Lee, J. Multilateral bargaining in networks: On the prevalence of inefficiencies. Oper. Res. 2018, 66, 1204–1217. [Google Scholar] [CrossRef]
- Acemoglu, D.; Makhdoumi, A.; Malekian, A.; Ozdaglar, A. Informational Braess’ paradox: The effect of information on traffic congestion. Oper. Res. 2018, 66, 893–917. [Google Scholar] [CrossRef]
- Lin, K.; Li, C.; Fortino, G.; Rodrigues, J.J. Vehicle route selection based on game evolution in social internet of vehicles. IEEE Internet Things J. 2018, 5, 2423–2430. [Google Scholar] [CrossRef]
- Mostafizi, A.; Koll, C.; Wang, H. A Decentralized and Coordinated Routing Algorithm for Connected and Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11505–11517. [Google Scholar] [CrossRef]
- Du, L.; Chen, S.; Han, L. Coordinated online in-vehicle navigation guidance based on routing game theory. Transp. Sci. Rec. 2015, 2497, 106–116. [Google Scholar] [CrossRef]
- Du, L.; Han, L.; Li, X.Y. Distributed coordinated in-vehicle online routing using mixed-strategy congestion game. Transp. Res. B-Meth. 2014, 67, 1–17. [Google Scholar] [CrossRef]
- Du, L.; Han, L.; Chen, S. Coordinated online in-vehicle routing balancing user optimality and system optimality through information perturbation. Transp. Res. B-Meth. 2015, 79, 121–133. [Google Scholar] [CrossRef]
- Spana, S.; Du, L.; Yin, Y. Strategic Information Perturbation for an Online In-Vehicle Coordinated Routing Mechanism for Connected Vehicles Under Mixed-Strategy Congestion Game. IEEE Trans. Intell. Transp. Syst. 2021, 23, 4541–4555. [Google Scholar] [CrossRef]
- Monderer, D.; Shapley, L.S. Potential games. Games Econom. Behav. 1996, 14, 124–143. [Google Scholar] [CrossRef]
- Milchtaich, I. Congestion games with player-specific payoff functions. Games Econom. Behav. 1996, 13, 111–124. [Google Scholar] [CrossRef]
- Harks, T.; Klimm, M.; Möhring, R.H. Characterizing the existence of potential functions in weighted congestion games. Theory Comput. Syst. 2011, 49, 46–70. [Google Scholar] [CrossRef]
- Harks, T.; Klimm, M. On the existence of pure Nash equilibria in weighted congestion games. Math. Oper. Res. 2012, 37, 419–436. [Google Scholar] [CrossRef]
- Lin, H.H.; Hsu, I.C.; Lin, T.Y.; Tung, L.M.; Ling, Y. After the Epidemic, Is the Smart Traffic Management System a Key Factor in Creating a Green Leisure and Tourism Environment in the Move towards Sustainable Urban Development? Sustainability 2022, 14, 3762. [Google Scholar] [CrossRef]
- Ali, M.S.; Coucheney, P.; Coupechoux, M. Distributed Learning in Noisy-Potential Games for Resource Allocation in D2D Networks. IEEE Trans. Mob. Comput. 2019, 19, 2761–2773. [Google Scholar] [CrossRef]
- Ganzfried, S. Algorithm for Computing Approximate Nash Equilibrium in Continuous Games with Application to Continuous Blotto. Games 2021, 12, 47. [Google Scholar] [CrossRef]
- Kamalapurkar, R.; Klotz, J.R.; Dixon, W.E. Concurrent learning-based approximate feedback-Nash equilibrium solution of N-player nonzero-sum differential games. IEEE/CAA J. Autom. Sin. 2014, 1, 239–247. [Google Scholar]
- Xu, Q.; Su, Z.; Lu, R. Game Theory and Reinforcement Learning Based Secure Edge Caching in Mobile Social Networks. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3415–3429. [Google Scholar] [CrossRef]
- Zhao, C.; Guo, D. Particle Swarm Optimization Algorithm With Self-Organizing Mapping for Nash Equilibrium Strategy in Application of Multiobjective Optimization. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 5179–5193. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Wu, S.; Luo, M.; Zhang, J.; Zhang, D.; Zhang, L. Pharmaceutical Supply Chain in China: Pricing and Production Decisions with Price-Sensitive and Uncertain Demand. Sustainability 2022, 14, 7551. [Google Scholar] [CrossRef]
- Lazar, D.; Coogan, S.; Pedarsani, R. Routing for traffic networks with mixed autonomy. IEEE Trans. Automat. Control 2020, 66, 2664–2676. [Google Scholar] [CrossRef]
- Ullah, I.; Khan, M.A.; Alsharif, M.H.; Nordin, R. An anonymous certificateless signcryption scheme for secure and efficient deployment of Internet of vehicles. Sustainability 2021, 13, 10891. [Google Scholar] [CrossRef]
- Zhou, B.; Song, Q.; Zhao, Z.; Liu, T. A reinforcement learning scheme for the equilibrium of the in-vehicle route choice problem based on congestion game. Appl. Math. Comput. 2020, 371, 124895. [Google Scholar] [CrossRef]
- Nash, J.F., Jr. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef]
- Rosenthal, R.W. A class of games possessing pure-strategy Nash equilibria. Internat. J. Game Theory 1973, 2, 65–67. [Google Scholar] [CrossRef]
- Umair, M.; Cheema, M.A.; Cheema, O.; Li, H.; Lu, H. Impact of COVID-19 on IoT adoption in healthcare, smart homes, smart buildings, smart cities, transportation and industrial IoT. Sensors 2021, 21, 3838. [Google Scholar] [CrossRef]
- Tan, T.; Bao, F.; Deng, Y.; Jin, A.; Dai, Q.; Wang, J. Cooperative Deep Reinforcement Learning for Large-Scale Traffic Grid Signal Control. IEEE Trans. Cybern. 2020, 50, 2687–2700. [Google Scholar] [CrossRef]
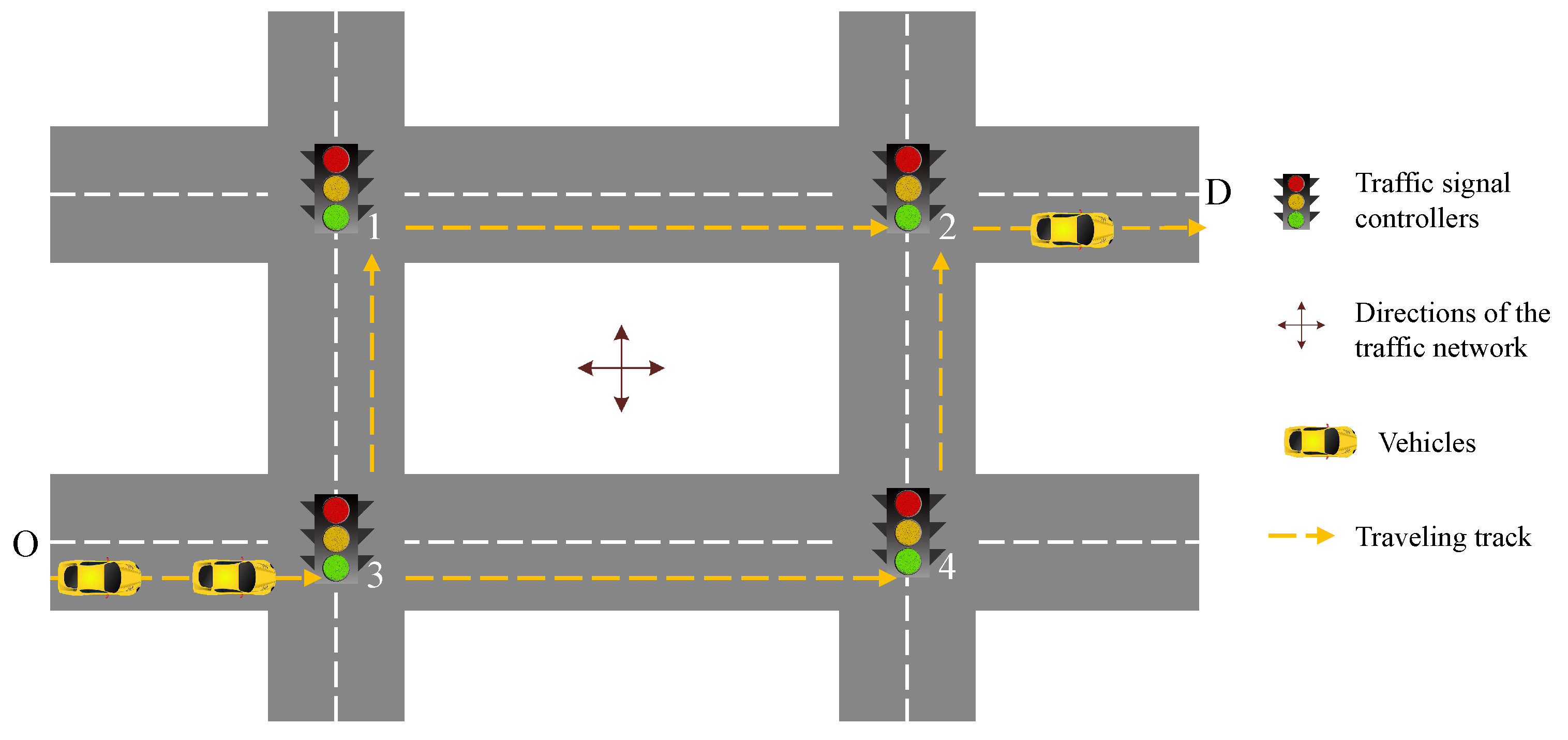
| Traffic Scenario | n | m | ||||
|---|---|---|---|---|---|---|
| Scenario 1 | 10 | 2 | 10 | 10 | 30 | 26 |
| Scenario 2 | 10 | 2 | 15 | 10 | 25 | 20 |
| Scenario 3 | 10 | 2 | 10 | 15 | 30 | 24 |
| Scenario 4 | 10 | 2 | 30 | 30 | 30 | 30 |
| Method 1 | Method 2 | Method 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | – | 0.99:1.00 | 43.47 | – | 0:1 | 52.00 | 1.00 | 2:3 | 41.76 |
| Scenario 2 | – | 0.98:1.00 | 32.56 | – | 0:1 | 40.00 | 1.00 | 2:3 | 31.86 |
| Scenario 3 | – | 1.01:1.00 | 36.97 | – | 0:1 | 40.00 | 1.00 | 3:7 | 35.44 |
| Scenario 4 | – | 1.00:1.00 | 35.00 | – | 1:0 | 40.00 | 1.00 | 1:1 | 35.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Lyu, L.; Zheng, S.; Ding, L.; Xu, L. A Q-Learning-Based Approximate Solving Algorithm for Vehicular Route Game. Sustainability 2022, 14, 12033. https://doi.org/10.3390/su141912033
Zhang L, Lyu L, Zheng S, Ding L, Xu L. A Q-Learning-Based Approximate Solving Algorithm for Vehicular Route Game. Sustainability. 2022; 14(19):12033. https://doi.org/10.3390/su141912033
Chicago/Turabian StyleZhang, Le, Lijing Lyu, Shanshui Zheng, Li Ding, and Lang Xu. 2022. "A Q-Learning-Based Approximate Solving Algorithm for Vehicular Route Game" Sustainability 14, no. 19: 12033. https://doi.org/10.3390/su141912033
APA StyleZhang, L., Lyu, L., Zheng, S., Ding, L., & Xu, L. (2022). A Q-Learning-Based Approximate Solving Algorithm for Vehicular Route Game. Sustainability, 14(19), 12033. https://doi.org/10.3390/su141912033







