To Be or Not to Be? Strategic Analysis of Carbon Tax Guiding Manufacturers to Choose Low-Carbon Technology

Abstract

This paper analyzes the environmental tax’s effect on manufacturers’ choice of low-carbon technology in competitive supply chains. The existing studies only consider a single oligopoly enterprise and ignore the competition between supply chains. Few papers study the manufacturer’s technology choice under the carbon tax policy in the competitive supply chains, especially investigating the factors influencing the technology choice, including the market volume, and technology carbon emission reduction efficiency because different industry sectors have their distinctive carbon emissions reduction efficiencies and facing the different market volume. The study adopts a game theoretical approach, including the three-level supply chain consisting of the regulator, the manufacturers, and the retailers. A high carbon tax does not always help firms choose low-carbon technology. However, the monotonous effect of the carbon tax on manufacturer technology selection is no longer valid if the market volume and the carbon-reducing efficiency are considered. When the market volume is large, the regulator can set a high carbon tax to induce the manufacturers to choose low-carbon technology. We identify cases where the manufacturers are caught in a prisoner’s dilemma. When the market volume is small, and the carbon-reducing efficiency is high, the competitive manufacturers adopt the common technology. However, if the regulator increases the carbon tax, the manufacturers acquire the differential technology strategic choice, which is the Pareto optimal. We also extend the base model to the imperfect substitutable Cournot model and the Bertrand model to check the robustness and find our main results still hold in these extensions.

1. Introduction

Climate change and environmental protection have made some countries consider environmental policy urgent. The International Energy Agency (IEA) reported that “global energy-related carbon dioxide emissions rose to a record 36.3 billion tons in 2021, their highest ever level, of which the manufacturing industry accounts for nearly a quarter.” [1]. Regulators must use the available tools to induce enterprises to choose low-carbon/green technology. Such tools include environmental tax, fines, subsidies, consumer rebates, carbon cap-and-trade, and other mechanisms. The carbon tax approach recently gained significant traction among regulators and the business media, primarily because it directly measures the firm’s emission price. A carbon tax is generally considered one of the most effective market-based mechanisms and is widely accepted around the world. Currently, more than 20 countries, including Canada, Australia, the United Kingdom (UK), and the United States, have implemented carbon tax policies [2]. The regulator levies a carbon tax on the manufacturer’s carbon emissions. To lower the carbon emission, the manufacturer must decide whether to adopt pollution abatement technology, which can be a lower-emission production method/process or an energy-efficient manufacturing equipment/facility [3,4]. In the semiconductor industry, manufacturers use perfluorocarbons (PFCs) in their wafer-cleaning processes and emit undecomposed ones into the air (EPA, 2016). This has called for the need to reduce PFCs emissions in the industry since PFCs are greenhouse gases whose global warming potential is at least 1000 times higher than CO₂ [5]. There have been growing concerns about pollutants emitted from manufacturers’ production processes. If the manufacturer chooses to use low-carbon technology, the production cost will increase. Because the manufacturer’s choice of low-carbon technology often leads to increased production cost. There are trade-offs between carbon emission cost and production cost involved in the manufacturer’s decision. If the regulatory policies are not organized appropriately, they may cause inefficiencies in environmental or economic terms [6].

A carbon tax can guide manufacturers’ green technology choices, but it can raise opposition because it may simultaneously lower demand for the high cost of green technology production [7,8]. So, if the regulator doesn’t carefully consider the market condition and the technology character, the political aim will not be achieved. Our approach provides a practical and innovative approach to optimal carbon tax. Different industry sectors (e.g., steel, construction, telecommunication, energy, cement, chemical, and many others) have their distinctive efficiencies for carbon emission reduction [9]. The goal of this current study is to explore the possibilities and limitations of the carbon tax policy in guiding firms’ low-carbon technology choices. The question we ask is: (1) Does a high carbon tax help firms choose low-carbon technology? (2) How do exogenous parameters, such as the market volume and the carbon-reducing efficiency, influence a firm’s decision? (3) Under what conditions should the carbon tax be implemented in the competitive circumstance? This study also provides managerial implications and policy insights by addressing these questions in a game theoretical model.

To analyze the effects of carbon tax policy, we develop and study three modes of the leader-follower Stackelberg game between two key players: two competitive supply chains (the follower) and the regulator (the leader). Each supply chain has one manufacturer and one retailer. Each manufacturer produces the production by choosing the common or low-carbon technology, then wholesale production to their retailer. Here, the channel cross will not be considered. Instead, we assume that the firm has a choice between a finite number of alternatives, each characterized by one unit producing cost and the carbon emission tax cost. In the technology choice framework, we also assume that a continuum of technologies is available, and a single technology is selected from those infinite numbers of options. We study the basic Cournot duopoly model with two competitive supply chains and then extend to the imperfect substitution Cournot duopoly model and the Bertrand duopoly price model. We analyze how firms’ decision to acquire low-carbon technology is affected by the carbon tax that the regulator sets.

A high carbon tax does not always help firms choose low-carbon technology. The manufacturers’ technology choice depends on the market volume and the carbon-reducing efficiency of the low-carbon technology. Particularly, we identify cases where the prisoner’s dilemma catches the manufacturers. When the carbon tax is low, and the market volume is small, the competitive manufacturers adopt the common technology. However, suppose the regulator increases the carbon tax. In that case, the manufacturers acquire the differential technology strategic choice, which is the Pareto optimal, because there are some equilibrium outcomes of the game that would be better for both firms. The findings are consistent in the extension models, whereby the regulator chooses the carbon tax. The regulator cannot induce both manufacturers’ low-carbon technology choices when the market volume is small.

In contrast, the regulator can set a high carbon tax to induce manufacturers to choose low-carbon technology when the market volume is large. Therefore, the regulator should be especially aware of the present market condition and the reduced efficiency of low-carbon technology. However, if the regulator ignores the factors above-mentioned, he will not generate good outcomes. We also shed light on the non-monotonous effect of the carbon tax policy on the manufacturers’ technology selection. Krass et al. showed that the firm’s reaction to an increase in tax might be non-monotone: while an initial tax increase may motivate the switch to green technology, a further tax increase may motivate the reverse switch [10]. We demonstrate that the non-monotonous effect of the carbon tax on the manufacturer technology selection is no longer valid if the market volume and the carbon-reducing efficiency are considered, which is our key contribution.

The rest of this paper is organized as follows: Section 2 reviews the relevant literature and identifies the literature positioning of this paper. Section 3 describes the model and the structure of the game; Section 4 examines the Nash equilibrium and the mixed strategy Nash equilibrium of the game, and Section 5 extends the model from the two aspects, including the imperfect substitute and price game, to discuss our results’ robustness; Section 6 is the conclusion and future research.

2. Literature Review

Also increasing the political and societal concerns about carbon emissions, low-carbon technology has become an important topic, defined as the efficient use of energy or resources during the manufacturing process [11,12]. The literature review primarily relates to two streams of the research: one is the effect of environmental regulation policy on manufacturers’ decisions, and the other is the impact of the carbon tax policy on firms’ technology choices.

There are several types of regulations already being practiced by the governments, such as carbon/emission tax [2,13,14,15,16], tax subsidy [17,18,19,20], carbon cap-and-trade [21,22,23,24,25], and subsidy [8,19]. Nault and Barrie are early pioneering studies that compare subsidies with taxes and show that their effects are equivalent [26]. Letmathe and Balakrishnan developed a linear mixed integer programming model that calculates the optimal production quantities under different environmental constraints, including the emissions tax [27]. Choi explores the effects of the carbon footprint taxation scheme on the optimal sourcing decision choice and reveals that a properly designed carbon taxation scheme can mitigate risk for the fashion retailer [28]. However, Drake et al. explore the impact of taxation and cap-and-trade on a firm’s technology choices decisions and find that the cap-and-trade policy results in greater expected profits than the emissions tax [29]. Chen and Wang study the ordering and transportation model selection problem under the cap-and-trade models [3]. Chan et al. analyze the effects of environmental taxes on the performance of newsvendor supply chains when the retailer is risk-averse [30]. Chen et al. discusses the optimal carbon tax design concerning different power structures and green technology investment efficiencies [7]. Their findings show that the carbon tax should be differentiated across industry sectors whether customers are sensitive to carbon emissions. Those factors should be considered. However, most of the above research considers a carbon tax as the constraint or factor and concentrates on optimizing enterprise decisions. Few researchers have studied the limitation considering the market volume and the carbon-reducing efficiency through modeling supply chain enterprises’ behaviors.

In order to reduce carbon emissions, it is essential to encourage organizations to invest in green and cleaner technologies [22,23,31]. In the sustainable operations management literature, several studies investigate technology choices under emissions regulation [14,32,33,34,35,36,37]. Specifically, several studies show that environmental policy can stimulate the adoption of new technology, which reduces pollution emissions [38,39,40,41]. Such as Requate and Perino have analyzed the optimal environmental policy scheme that generates the most incentives to acquire a new abatement technology [41]. Bi et al. model a Stackelberg game which shows that the green technology level, environmental improvement coefficient, and unit cost increase coefficient play important roles in the government subsidy strategy [42]. Drake suggests that carbon tariffs improve the efficiency of emissions regulation, enabling it to reduce global emissions in many settings [29]. Han et al. build a mixed-integer linear programming model for a real-world firm to explore how to select the reduction technology and design a green supply chain network under carbon emissions restrictions [43]. Wang X et al. find that more aggressive regulation encourages more firms to adopt green technology once it becomes available but may discourage a firm from developing it in the first place when facing intense competition [44]. Therefore, for an industry with intense competition, a government agency should remain cautious about being too aggressive with regulation, which could potentially stifle innovation.

Similarly, our paper examines how an appropriate carbon tax induces firms to adopt low-carbon technology. However, unlike the previous literature, our work differs from the above in several dimensions; most importantly, the questions we address are: Can the high carbon tax induce the manufacturer to adopt green technology? Under what conditions can certain technology choices be induced? At the same time, our model is such as the above in that we also study the validation of the carbon tax policy in the operational framework.

Our article models a Stackelberg game wherein the regulator sets the carbon emission tax, and the monopolist firm decides whether a switch to low-carbon technology. However, to our knowledge, several studies examine the environmental regulation on the firms’ incentives to invest the green technologies in operations management literature. At the same time, few papers address the issue of a firm’s strategic technology options, especially under competing circumstances. Overall, existing research assumes either the monopolistic or the horizontal market, while our research concentrates on the competitive market.

This paper examines the manufacturers’ choice of adopting low-carbon technology under certain carbon tax conditions in a competitive circumstance. We aim to answer the following research questions: First, under what conditions will the strategy of adopting the low-carbon technology be better than the common technology for the manufacturers? Second, how do the market volume and the carbon reduction efficiency of the low-carbon technology impact the manufacturers’ decisions and the equilibrium solutions? Finally, what influences the other competitive manufacturer and the retailer if the manufacturer considers adopting low-carbon technology?

3. The Basic Model

We consider two competitive supply chains ($i=1,2$), where each supply chain consists of one manufacturer and one retailer. A manufacturer $i$ ($M_i$) produces certain products and distributes them through her exclusive retailer $i$ ($R_i$) at a wholesale price $w_i$. The manufacturers produce homogeneous goods. Then, the retailer serves the end market consumers at constant unit sale costs, normalized to zero.

3.1. Producing Technology and Cost

There is one “baseline” production system that allows the manufacturers to produce units of production, where is the fixed cost normalized to be zero and c represents the variable cost. As a “by-product” of such a production system, the manufacturers produce units of carbon emissions per unit. The number of carbon emissions can be reduced by employing low-carbon technology. To distinguish the emission-reducing technology from the technology in the “baseline” production system, we call them the low-carbon technology (L) and common technology (C) separately, and the two different types of technology are available for both manufacturers. This assumption enables us to focus on the issues of the manufacturers’ strategic technology choices. For example, Fuji Film improves the usage efficiency and product life of its toners to lower carbon emissions. AU Optronics curbs the carbon emissions of its products by 30% by developing thin film transistor (TFT) display technology [2]. Following previous literature, we assume that two manufacturers compete directly on the marginal customers; thus, this model fully covers the market.

To analyze the impact of the carbon tax on the manufacturer’s technology choice, we assume the enterprise adopts different technology can only lower carbon emissions and will not influence the product’s properties. The manufacturers have two strategies in our model setup: they can choose low-carbon or common technology. The manufacturer can choose either technology but not both for a certain period. Compared to the common technology, the production cost of the low-carbon technology is high, but its carbon emission is low. Therefore, let $\xi$ denote the unit-producing cost when the low-carbon technology is adopted. Similarly, we don’t consider the fixed production cost when the manufacturers adopt low-carbon technology. Thus, we can rewrite the producing cost of the common technology as $\delta \xi$ ($0<\delta <1$), which $\left(1-\delta \right)\xi$ is the cost saving of the common technology.

At the same time, we can use $s$ to denote the carbon emission of the common technology. In addition, we use $t$ to denote the carbon tax charged by the regulator per unit of carbon emission. Without loss of generality, we assume the reducing efficiency of the low-carbon technology is higher than the common technology. Similarly, we use $\beta s$ to denote the production’s carbon emission cost when the low-carbon technology is adopted, where $1-\beta$ ($0<\beta <1$) is the reducing efficiency of the low-carbon technology. Thus, the unit cost of production for each manufacturer consists of two parts: the sum of production costs and the carbon tax cost. When the manufacturer adopts the common technology, the cost is

$$c_c\left(q,t\right)=\left(\delta \xi +ts\right)q,$$

(1)

when the manufacturer adopts low-carbon technology, the cost is

$$c_L\left(q,t\right)=\left(\xi +\beta st\right)q.$$

(2)

3.2. Demand Function

We assume that there is no effect of carbon emission on demand, meaning that consumers are unwilling to pay a higher price for low-carbon production. Since the manufacturers’ technology decision does not impact the demand forms, we adopt a well-known basic Cournot model that is a perfect substitutable inverse demand function to describe the market

$$p=a-q_i-q_{3-i},$$

(3)

In the function, $a$ is market volume, $p$ is market clearing price, and $q_i$ is order quantities of the retailer $i$. Such inverse demand function is widely adopted in operations management literature. The demand function indicates that the productions produced by the two manufacturers are perfectly substitutable. Section 5 extends the demand model into the case with imperfect substitutable productions. In addition, we also address the case where two retailers are involved in Bertrand (price) game.

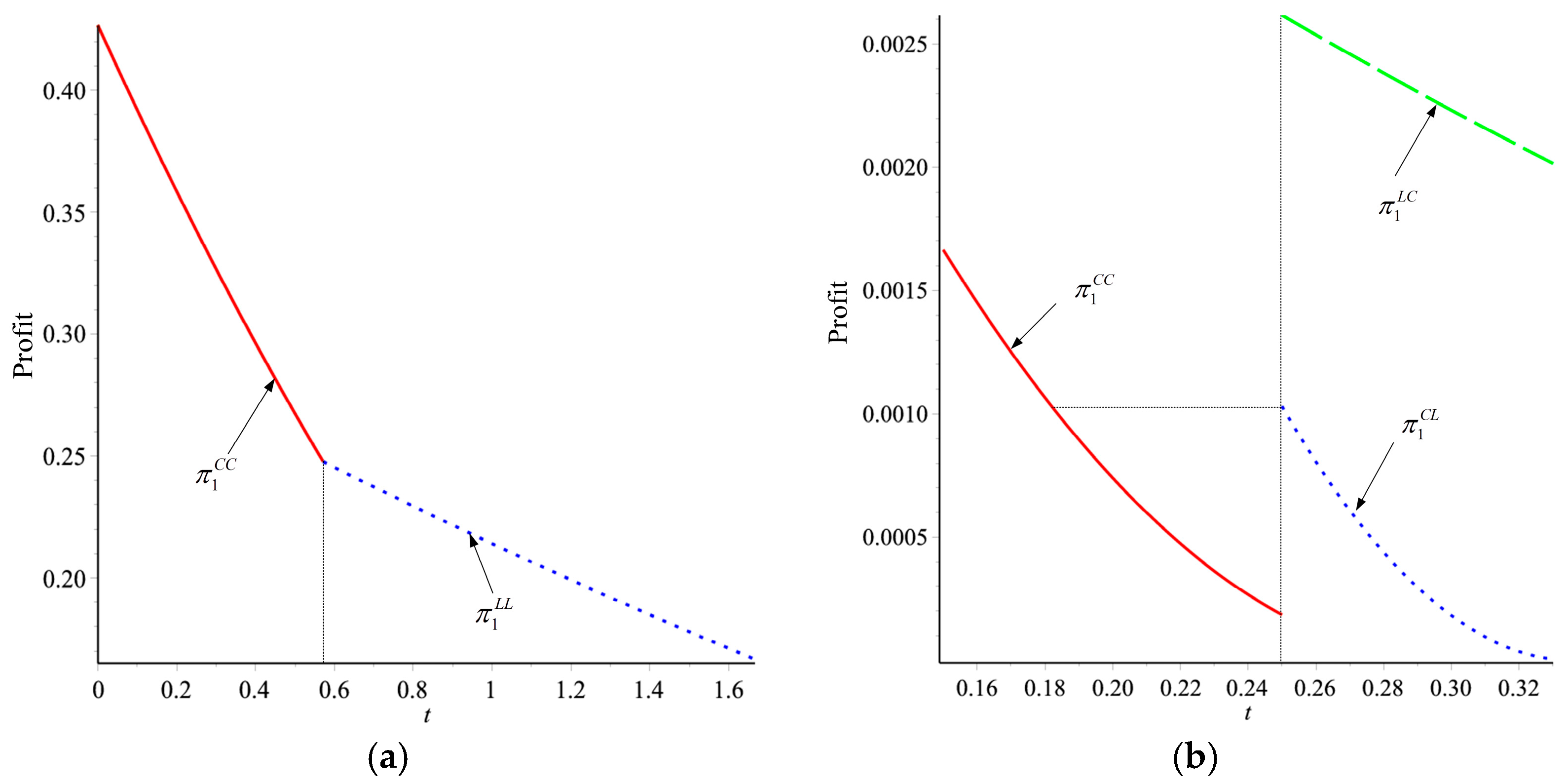
3.3. Event Sequences and Profit Functions

The event sequences are in the following. First, the government announces the carbon tax rate $t$. Then, the manufacturers receive the tax rate and choose production technology to produce, and each manufacturer sets its wholesale price $w_i$. Next, each retailer determines the order quantity $q_i$ upon receiving the wholesale price. Last, the manufacturer $i$ supplies $q_i$ to her exclusive retailer. Finally, consumers purchase product and all firms receive their profits. According to the timeline of the event sequences, Figure 1 is illustrated.

In our model, all players make decisions responding to the received information. Our model also assumes that two manufacturers set their wholesale prices simultaneously so that no manufacturer holds any advantage in action. We adopt the backward induction to solve the game for obtaining the equilibrium order quantities, which helps us to obtain the equilibrium profits under different cases. We then use the equilibrium profits to obtain the equilibrium technology choice. The retailer chooses the output $q_{Ri}$ to maximize its profit from retail sales, taking the unit wholesale price $w_i$ as given. The retailer’s problem is

$${\pi }_{R_i}=\left(a-{\displaystyle \sum _{i=1}^2{q}_i}-w_i-c\right)q_i,$$

(4)

Performing the optimization in Equation (4) provides $q_i$, the retailer’s output in the setting given unit wholesale price $w_i$ is

$$q_i=\frac{a-2w_i+w_{3-i}}{3},$$

(5)

Anticipating the retailer’s response to the wholesale price it sets, the manufacturer chooses $w_i$ to maximize its profit.

Given the two optional strategies for both firms, combining the four strategies is possible: (i). Both the manufacturers choose the common technology, denoted as case $\left(C,C\right)$; (ii). The manufacturer1 adopts the common technology, but manufacturer2 adopts low-carbon technology, denoted as case $\left(C,L\right)$; (iii). The manufacturer1 adopts the low-carbon technology, but the manufacturer2 adopts the common technology, denoted as case $\left(L,C\right)$; (iv). Both manufacturers choose the low-carbon technology, denoted as a case $\left(L,L\right)$. Since cases (ii) and (iii) are symmetric, we combine them and analyze them. Technical strategy choice of competitive manufacturers will be indicated by the superscript. We will discuss the strategic technology choices of the manufacturers below.

First, analyze the case $\left(C,C\right)$, so the manufacture1′s profit function is

$${\pi }_{M_1}^{CC}=\left(w_1-\delta \xi -ts\right)q_1^{},$$

(6)

And the manufacture2′ profit function is

$${\pi }_{M_2}^{CC}=\left(w_2-\delta \xi -ts\right)q_2^{}.$$

(7)

The same can be expressed in the setting of the $\left(C,L\right)$, $\left(L,C\right)$, and $\left(L,L\right)$. For a given carbon tax $t$, the profit functions are summarized in

Table 1. The Profit Functions of the Retailers and Manufacturers.

Profit Functions of the Retailers and Manufacturers		Retailer2/Manufacturer2
		$\mathbf{Common}\mathbf{Technology}\mathit{C}$	Low-Carbon Technology L
Retailer1 /Manufacturer1	Common technology C	$\begin{array}{c}{\pi }_{R_i}^{CC}=\left(p-w_i\right)q_i\\ {\pi }_{M_i}^{CC}=\left(w_i-\delta \xi -st\right)q_i\end{array}$	$\begin{array}{c}{\pi }_{R_i}^{CL}=\left(p-w_i\right)q_i\\ {\pi }_{M_1}^{CL}=\left(w_1-\delta \xi -st\right)q_1\\ {\pi }_{M_2}^{CL}=\left(w_2-\xi -\beta st\right)q_2\end{array}$
	Low-carbon technology L	$\begin{array}{c}{\pi }_{R_i}^{LC}=\left(p-w_i\right)q_i\\ {\pi }_{M_1}^{LC}=\left(w_1-\xi -\beta st\right)q_1\\ {\pi }_{M_2}^{LC}=\left(w_2-\delta \xi -st\right)q_2\end{array}$	$\begin{array}{c}{\pi }_{R_i}^{LL}=\left(p-w_i\right)q_i\\ {\pi }_{M_i}^{LL}=\left(w_i-\xi -\beta st\right)q_i\end{array}$

Note: ${\pi }_{R_i}$ and ${\pi }_{M_i}$ denote the profit functions of the retailer $i$ and manufacturer $i$.

.

Performing the maximization in Equation (7) yields $w_i$ is the product’s wholesale price in the $\left(C,C\right)$ setting. Substituting $w_i$ into Equation (5) yields the equilibrium retail output $q_i^{CC}$, and the optimal results under the four cases of the basic model are listed in Supplementary Tables S1.

4. Analysis

To analyze the game between the two supply chains in the basic model, where the productions produced by the two manufacturers are perfectly substitutable, we first obtain and summarize the Nash equilibrium and then analyze the mixed equilibrium.

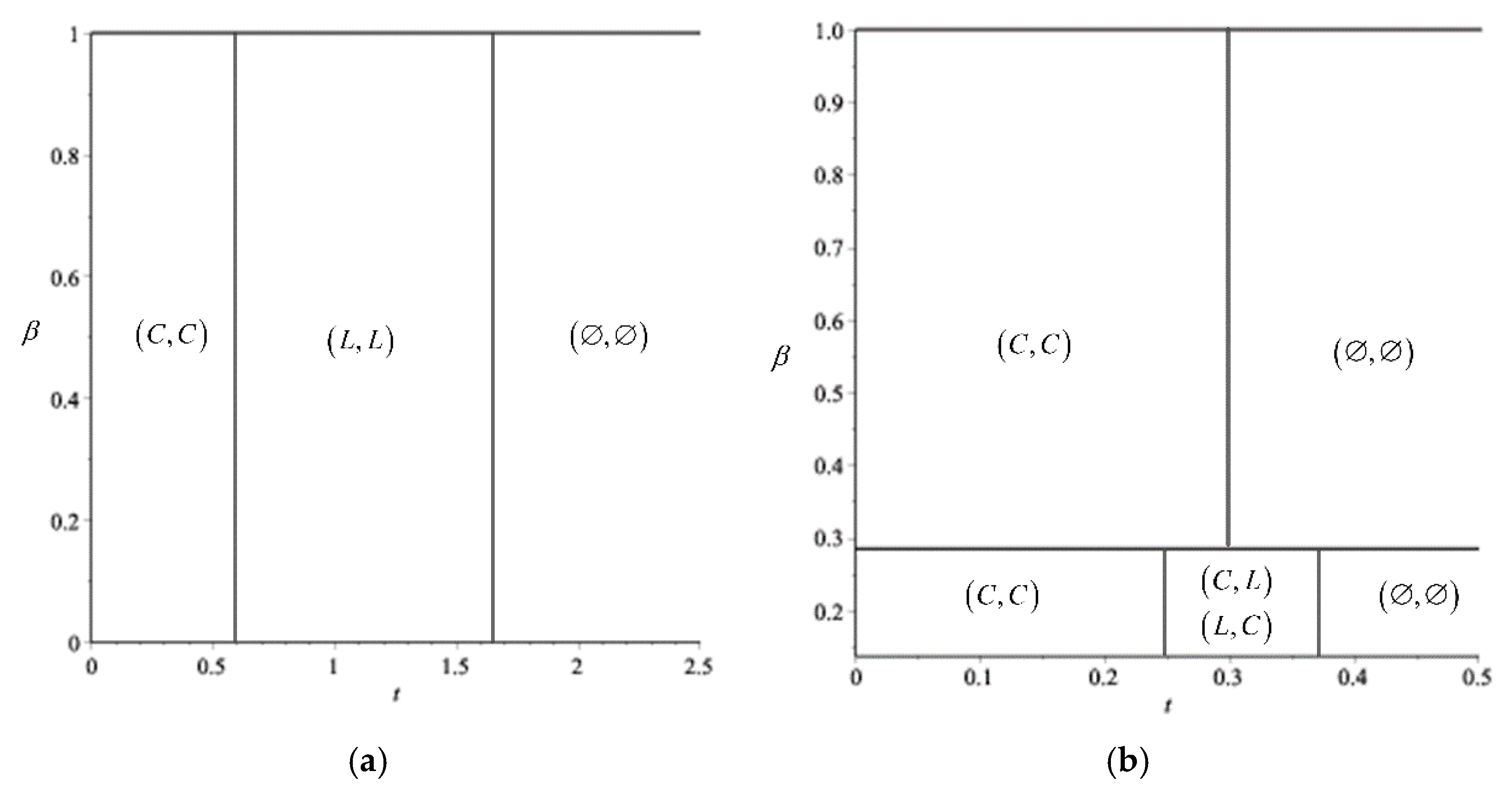
4.1. Nash Equilibrium

The manufacturers’ low-carbon technology decision depends on reducing efficiency and production cost. We solve the Nash equilibrium solution between the manufacturers’ strategy selection. If manufacturer1 adopts the “common technology” strategy, we compare manufacture2′s profit under the different strategies to conclude that manufacture2′s the strategy of the technology choice.

Let $\Delta {\pi }_{M_2}^{CC-CL}$ be the difference in the optimal profits of the manufacture2′s technology choice, so $\Delta {\pi }_{M_2}^{CC-CL}={\pi }_{M_2}^{CC}-{\pi }_{M_2}^{CL}$, then we can get

$$\Delta {\pi }_{M_2}^{CC-CL}=14\left(st-st\beta +\delta \xi -\xi \right)\left(7st\beta +3st+3\delta \xi -10a+10c+7\xi \right)/675,$$

(8)

Compare the profit under the different carbon tax intervals to determine manufacture2′s technology strategy choice. Similarly, if manufacturer1 adopts the low-carbon technology strategy, we compare manufacture2′s profit under the different strategies.

Let $\Delta {\pi }_{M_2}^{LC-LL}={\pi }_{M_2}^{LC}-{\pi }_{M_2}^{LL}$ be the difference between manufacturer2′s optimal profits. Then we can get

$$\Delta {\pi }_{M_2}^{LC-LL}=14\left(\beta st-st-\delta \xi +\xi \right)\left(10a-10c-3\xi -7\delta \xi -3\beta st-7st\right)/675,$$

(9)

Now, compare the profit under the different carbon tax intervals to determine the manufacture2′s technology choice. Owing to the symmetry, manufacturer1′s technology choice results are such as that of manufacturer2. Therefore, we can characterize the equilibrium technology strategies for the two manufacturers, summarized in Proposition 1.

Proposition 1.

The equilibria technology strategies of the two competitive manufacturers under the perfect substitutable production are below:

(i)

When the market volume is large ($a>{\overline{a}}^{PS}$), if the carbon tax $t\in \left[0,t_{11}\right]$, then the equilibrium is $\left(C,C\right)$; if the carbon tax $t\in \left(t_{11},t_{12}\right]$, then the equilibrium is $\left(L,L\right)$; if the carbon tax $t\in \left(t_{12},\infty \right)$, then the equilibrium is $\left(\varnothing ,\varnothing \right)$.

(ii)

When the market volume is small, and the efficiency of the low-carbon technology is high, that is $0\le a\le {\overline{a}}^{PS}$ and $0<\beta \le 2/7$, if the carbon tax $t\in \left[0,t_{13}\right]$, then the equilibrium is $\left(C,C\right)$; if the carbon tax $t\in \left(t_{13},t_{14}\right]$, then the equilibrium are $\left(C,L\right)$ or $\left(L,C\right)$; if the carbon tax $t\in \left(t_{14},\infty \right)$, then the equilibrium is $\left(\varnothing ,\varnothing \right)$.

(iii)

When the market volume is small, and the efficiency of the low-carbon technology is low, that is $0\le a\le {\overline{a}}^{PS}$ and $2/7<\beta \le 1$, if the carbon tax $t\in \left[0,t_{15}\right]$, then the equilibrium is $\left(C,C\right)$; if the carbon tax $t\in \left(t_{15},\infty \right)$, then the equilibrium is $\left(\varnothing ,\varnothing \right)$.

The equilibrium strategies for the competitive manufacturers are shown in

Table 2. The Equilibrium Strategies in the Perfect Substitutable Production Model.

Cases	$a$	$0\le a\le {\overline{a}}^{PS}$					$a>{\overline{a}}^{PS}$
	$\beta$	$0<\beta \le 2/7$			$2/7<\beta <1$		$0<\beta <1$
	$t$	$\left[0,t_{13}\right]$	$\left(t_{13},t_{14}\right]$	$\left(t_{14},\infty \right)$	$\left[0,t_{15}\right]$	$\left(t_{15},\infty \right)$	$\left[0,t_{11}\right]$	$\left(t_{11},t_{12}\right]$	$\left(t_{12},\infty \right)$
Equilibrium		$\left(C,C\right)$	$\left(C,L\right)$$\mathrm{or}\left(L,C\right)$	$\left(\varnothing ,\varnothing \right)$	$\left(C,C\right)$	$\left(\varnothing ,\varnothing \right)$	$\left(C,C\right)$	$\left(L,L\right)$	$\left(\varnothing ,\varnothing \right)$

Note: $\varnothing$ denotes one manufacturer doesn’t choose any technology. ${\overline{a}}^{PS}=\frac{\xi \left(1-\beta \delta \right)}{1-\beta }$, $t_{11}=\frac{\xi \left(1-\delta \right)}{s\left(1-\beta \right)}$, $t_{12}=\frac{a-\xi }{\beta s}$, $t_{13}=\frac{10a-\xi \left(7+3\delta \right)}{s\left(7\beta +3\right)}$, $t_{14}=\frac{5a-\xi \left(7\delta -2\right)}{s\left(7-2\beta \right)}$, $t_{15}=\frac{a-\delta \xi }{s}$.

.

The conventional wisdom suggests manufacturers are inclined to adopt low-carbon technologies once the regulator charges a high carbon tax. However, our research shows that it may not always be the case. For example, proposition1 reveals that both manufacturers may adopt low-carbon technology to compete for consumers when the market volume exceeds a threshold value ($a>\overline{a}$) under the carbon tax interval $\left(t_{11},t_{12}\right]$. Otherwise, once the market volume is lower than the threshold value ($a<{\overline{a}}^{PS}$), it is not an equilibrium for both manufacturers to adopt low-carbon technology. One is inclined to adopt the low-carbon technology only if the carbon tax is in the interval $\left(t_{13},t_{14}\right]$.

In addition, from Proposition 1, we know the value of market volume deeply determines the profits of two manufacturers. Furthermore, when the market is small, and the carbon-reducing efficiency is low, no carbon tax policy can guide the manufacturer to adopt the low-carbon technology. In addition, we also notice from Proposition 1 that manufacturers always adopt common technology to save production costs when the carbon tax is sufficiently low. However, when the carbon tax exceeds a limited value, they withdraw from the market rather than adopt low-carbon technology. There is also ongoing debate in the literature about whether a carbon tax should be differentiated across industry sectors. Each section also exhibits different levels of efficiency in reducing carbon emissions. Industrial sectors are often operating in different market, and their efficiency in carbon-reducing are often different. For instance, the heavy machinery sector may be more effective than the other sector. So, these characteristics should be taken into consideration when designing a new carbon tax [9].

Then we examine the preferences of retailers on the two production technologies. Recall that we find from Table 2 that retailers always share the same benefits with their respective manufacturers. Consequently, the retailer’s profit in each case always equals two-thirds that of the manufacturer. In the following, we examine the impacts of the carbon tax on manufacturers’ profits. As revealed, manufacturers’ profits decrease as the carbon tax increases when one manufacturer faces competition from the other. Due to the mathematics complexity, a numerical study is adopted to demonstrate the impacts of a carbon tax on the manufacturers’ profits. Without loss of generality, we take manufacturer1 as an example to demonstrate owing to the symmetry. Therefore, we also divide two cases to study the impacts of the market volume. When the market volume is large, let $a=3$, $\beta =0.3$, $c=0$, $\xi =1$, $s=1$, $\delta =0.6$, and our result is plotted in Figure 2a. From Figure 2a, we notice that manufacturer1′s profit always decreases as carbon tax increases when the market volume is sufficiently large. In this case, two manufacturers would be involved in the “prisoner’s dilemma” that any manufacturer doesn’t adopt differentiated production technology, which hurts their benefits. However, the dilemma might be overcome when the market volume is small. When market volume is small, let $a=0.9$, $\beta =0.08$, $c=0$, $\xi =1$, $s=1$, $\delta =0.6$, and our result is depicted in Figure 2b. We can see from Figure 2b the manufacturer1′s profit is decreasing with the increasing carbon tax from Figure 2b, and who can benefit from the changes in her production technology? This is because any manufacturer has the incentive to adopt differentiated production technology to avoid intense competition when the market volume is small. In addition, we also find that manufacturer can gain more profit once she first changes from the common technology to the low-carbon technology. Because once the manufacturer adopts the low-carbon technology, the other manufacturer might abandon the low-carbon technology to avoid intense competition.

Similar to the impacts of the carbon tax on the manufacturers’ profit, Figure 3 means the strategic technology choice of the manufacturers. Figure 3a illustrates the effects of the carbon tax and the carbon-reducing efficiency on the manufacturers’ strategic technology choice when the market volume is large. The manufacturers’ strategic technology choice is only affected by the carbon tax, and the carbon-reducing efficiency has no effect on the technology choice. If the carbon tax is low, the manufacturers’ equilibrium is common technology, but with the carbon tax increases, the manufacturers’ equilibrium is low-carbon technology, which means the impact of a carbon tax on the low-carbon technology choice is monotonous. Figure 3b shows the effects of the carbon tax and the carbon-reducing efficiency on the manufacturers’ strategic technology choice when the market volume is small. Notably, which is determined by two thresholds, the carbon and carbon-reducing efficiency, which is different from Figure 3a. No matter what kind of carbon tax policy, it cannot guide both manufacturers to choose the low-carbon technology when the market volume is small. Only when the carbon-reducing efficiency is high the strategy can obtain differentiated equilibrium.

Proposition 2.

If the market volume is small ($0\le a\le {\overline{a}}^{PS}$) and the reducing efficiency of the low-carbon technology is high ($0<\beta \le 2/7$), two competitive manufacturers would be involved in the “prisoner’s dilemma” under the carbon tax policy.

Proposition 2 shows two competitive manufacturers would be involved in the “prisoner’s dilemma” under the carbon tax policy. However, the dilemma might be overcome when the market volume is small and the reducing efficiency of the low-carbon technology is high. When the carbon tax is low, manufacturers in the two competitive supply chains choose the common technology, and profits decline with the increase in the carbon tax; But when the carbon tax is increased, this dilemma will be overcome. Manufacturers in the two competitive supply chains adopt differentiated technology strategies, and their profits will increase relative to the use of ordinary technology. This proposition shows that strict regulation will improve the “prisoner’s dilemma,” and encourage enterprises to adopt differentiated technology strategies, and thus improve profits.

Proposition 3.

When the market volume is large, the size of the carbon tax interval$\left(t_{11},t_{12}\right]$for the Nash equilibrium’s strategy$\left(L,L\right)$increases$\beta$and decreases$\delta$.

This proposition elaborates on the impact of the low-carbon technology cost and the reduced efficiency on the size of the carbon tax interval when the market volume is large. During this interval, the regulator can guide the manufacturers to choose low-carbon technology. It can be seen when the market volume is large, the better the carbon emission reduction efficiency, or the less production cost, the more maneuverable space for the regulator to guide the manufacturers to choose the low-carbon technology through the carbon tax so if the low-carbon technology can be developed efficiently, which can greatly help the regulator guide manufacturers to choose the low-carbon technology and achieve the policy goal of reducing carbon emissions.

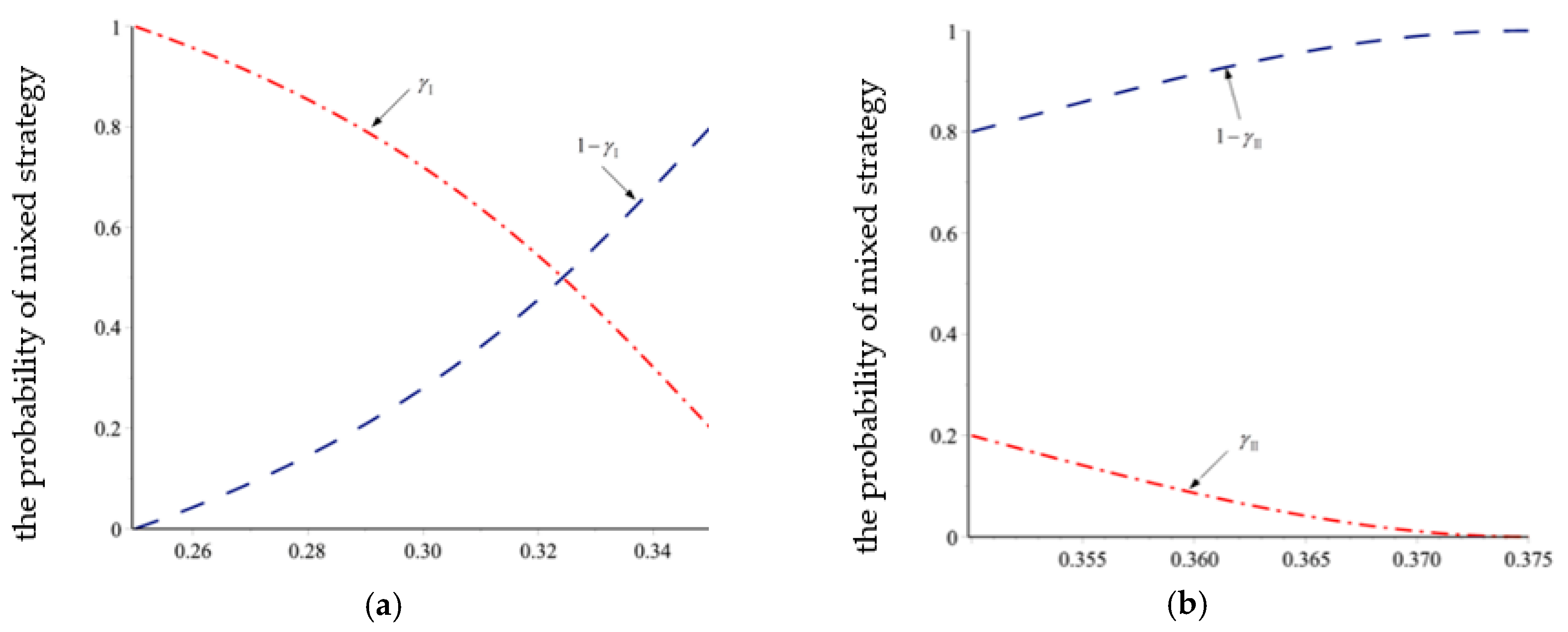
4.2. Mixed Strategy Nash Equilibrium

From Proposition 1, when the market volume is larger, there are two pure strategies Nash equilibria in the carbon tax interval $\left(t_{13},t_{14}\right]$. We can see the Nash equilibrium technology strategy is $\left(C,L\right)$ or $\left(L,C\right)$, so the mixed strategy Nash equilibrium exists according to the Nash Theorem.

Assuming the manufacturer selects the common technology strategy’s probability is $r$ and who chooses the low-carbon technology strategy’s probability is $1-r$, expect a profit of the manufacturer1 adopting the common technology strategy is $r{\pi }_{M_1}^{CC}+\left(1-r\right){\pi }_{M_1}^{CL}$, and expect a profit of the manufacturer2 adopting the low-carbon strategy technology strategy is $r{\pi }_{M_1}^{LC}+\left(1-r\right){\pi }_{M_1}^{LL}$. A mixed strategy will promote that the manufacturers expect profit between selecting the common technology and the low-carbon technology are equal, particularly,

$$r{\pi }_{M_1}^{CC}+\left(1-r\right){\pi }_{M_1}^{CL}=r{\pi }_{M_1}^{LC}+\left(1-r\right){\pi }_{M_1}^{LL}.$$

(10)

Suppose the carbon tax is in the interval $\left(t_{13},t_{14}\right]$ when the market volume is small ($a\le \overline{a}$)and the reducing efficiency is high ($0<\beta \le 2/7$). In that case, we can obtain the probability of the manufacturer’s common technology choice. Owing to the symmetry, the manufacturers select the common or low-carbon technology at the same probability. The manufacturer’s probability of adopting the common technology is $r_1$ at the carbon tax interval $\left(t_{13},t_{15}\right]$, while the probability is $r_{11}$ at the carbon tax interval $\left(t_{15},t_{14}\right]$. We can get

$$r_1=\frac{{\left(5a+2\xi -7\delta \xi -7\beta st+2st\right)}^2}{{\left(5a-7\xi +2\delta \xi -7\beta st+2st\right)}^2-4\left(\delta \xi -\xi -\beta st+st\right)\left(5a+\xi -6\delta \xi +\beta st-6st\right)},$$

(11)

$$r_{11}=\frac{{\left(5a+2\xi -7\delta \xi -7st+2\beta st\right)}^2}{{\left(5a-7\delta \xi +2\xi +2\beta st-7st\right)}^2+{\left(5a-7\xi +2\delta \xi +2st-7st\beta \right)}^2}.$$

(12)

Proposition 4.

When the market volume ($a\le \overline{a}$) is small, and the reducing efficiency of low-carbon technology ($0<\beta \le 2/7$) is high under the carbon tax interval$\left(t_{13},t_{14}\right]$, the mixed strategy Nash equilibrium exists. As a result, the manufacturer’s probability of adopting the common technology is$\left(r_1,1-r_1\right)$at the carbon tax interval$\left(t_{13},t_{15}\right]$while the probability is$\left(r_{11},1-r_{11}\right)$at the carbon tax interval$\left(t_{15},t_{14}\right]$.

This proposition illustrates the impact of the carbon tax on the probability of the mixed strategy. When the market volume is small and the carbon-reducing efficiency is high, the probability of the manufacturer adopting the common technology is different in the different carbon tax intervals.

Because the mixed strategy probability expression (11) is complicated, we let $a=0.9,\beta =0.08,c=0,\xi =1,s=1,\delta =0.6$ and simulate, then can obtain Figure 4. We see from Figure 4a that: When the carbon tax is low, the probability of common technology over low-carbon technology is higher, and the probability of choosing common technology decreases, but choosing low-carbon technology increases; When the carbon tax increases to the critical value, the probability of manufacturers choosing the two strategies are equal; When the carbon tax continues to increase, the probability of manufacturers choosing common technology decreases, but the probability of choosing low-carbon technology increases. Through the simulation from Figure 4b, we can see with the increase in a carbon tax, the probability of manufacturers choosing common technology decreases, the probability of choosing low-carbon technology increases, and the probability of manufacturers choosing low-carbon technology is always higher than the common technology, and this shows manufacturers prefer the low-carbon technology.

5. Extensions

The previous section has analyzed the case with the perfect substitutive quantity game. In this section, we extend the preceding model into the imperfect substitutive Cournot (quality) game and the Bertrand (price) game to demonstrate the robustness of the basic model.

5.1. Imperfect Substitute

Toyota forecasted demand for fuel-efficient cars would be high and released the first mass-produced hybrid vehicle in 1997. By contrast, GM still insisted on producing fuel vehicles and claimed that hybrid cars did not make sense even in 2004 [44]. Toyota has attracted a large number of customers who are concerned about fuel efficiency and carbon emissions. A hybrid vehicle is the imperfect substitution of the fuel vehicle. In order to characterize the difference between two productions, the inverse demand functions for the retailer $i$ are assumed to be

$$p_i=a-q_i-b{q}_{3-i},$$

(13)

where $q_i$ and $q_{3-i}$ represent order quantity of retailers, $p_i$ is the retail price of the retailer $i$. The parameter $b$ measures the substitutive degree of retailers’ two products. If $b=0$ the demands of two products are independent, and if $b=1$ they become perfect substitutes as in the basic model. Other parameters and assumptions are the same as in Section 3, except that the unit retail cost of each retailer is assumed to be zero to avoid complex mathematics.

Backward induction is again employed to characterize the equilibria of four cases. To keep clean of the main body, the equilibria and payoffs of all players in supply chains are listed in Supplement Table S2, which can be found in Supplement. Based on the results in Supplement Table S2, the following Proposition 5 can be obtained.

Proposition 5.

The equilibria technology strategy of the two manufacturers under the imperfect substitute production is below:

(i)

When the market volume is large ($a>{\overline{a}}^{IS}$), if the tax $t\in \left[0,t_{21}\right]$, then the equilibrium is $\left(C,C\right)$; if the tax $t\in \left(t_{21},t_{22}\right]$, then the equilibrium is $\left(L,L\right)$; if the tax $t\in \left(t_{22},\infty \right)$, then the equilibrium is $\left(\varnothing ,\varnothing \right)$.

(ii)

When the market volume is small ($0\le a\le {\overline{a}}^{IS}$), and the efficiency of the low-carbon technology is high ($0<\beta \le 2b/\left(8-b^2\right)$), if the tax $t\in \left[0,t_{23}\right]$, then the equilibrium is $\left(C,C\right)$; if the tax $t\in \left(t_{23},t_{24}\right]$, then the equilibrium is $\left(C,L\right)$ or $\left(L,C\right)$; if the tax $t\in \left(t_{24},\infty \right)$, then the equilibrium is $\left(\varnothing ,\varnothing \right)$.

(iii)

When the market volume is small ($0\le a\le {\overline{a}}^{IS}$), and the efficiency of the low-carbon technology is low ($2b/\left(8-b^2\right)<\beta \le 1$), if the tax $t\in \left[0,t_{25}\right]$, then the equilibrium is $\left(C,C\right)$; if the tax $t\in \left(t_{25},\infty \right)$, then the equilibrium is $\left(\varnothing ,\varnothing \right)$.

With imperfect substitutes, the equilibria technology choices of the manufacturers are shown in

Table 3. The Equilibria of Technology Strategy in the Case of the Imperfect Substitutes.

Cases	$a$	$0<a\le {\overline{a}}^{IS}$					${\overline{a}}^{IS}<a\le 1$
	$\beta$	$0<\beta \le 2b/\left(8-b^2\right)$			$2b/\left(8-b^2\right)<\beta <1$		$0<\beta <1$
	$t$	$\left[0,t_{23}\right]$	$\left(t_{23},t_{24}\right]$	$\left(t_{24},\infty \right)$	$\left[0,t_{25}\right]$	$\left(t_{25},\infty \right)$	$\left[0,t_{21}\right]$	$\left(t_{21},t_{22}\right]$	$\left(t_{22},\infty \right)$
Equilibria		$\left(C,C\right)$	$\left(C,L\right)$$\mathrm{or}\left(L,C\right)$	$\left(\varnothing ,\varnothing \right)$	$\left(C,C\right)$	$\left(\varnothing ,\varnothing \right)$	$\left(C,C\right)$	$\left(L,L\right)$	$\left(\varnothing ,\varnothing \right)$

Note: $\varnothing$ denotes one manufacturer doesn’t choose any technology. $\overline{a}=\frac{\xi \left(1-\beta \delta \right)}{1-\beta }$, $t_{21}=\frac{\xi \left(1-\delta \right)}{s\left(1-\beta \right)}=t_{11}$, $t_{22}=t_{12}=\frac{a-\xi }{\beta s}$, $t_{25}=\frac{a-\delta \xi }{s}$, $t_{23}=\frac{\left(8-b^2\right)\left(1+\delta \right)\xi -4b\delta \xi +2a\left(b^2+2b-8\right)}{s\left(\beta b^2+b^2+4b-8\beta -8\right)}$, $t_{24}=\frac{\xi \left(8\delta -b^2\delta -2b\right)+a\left(b^2+2b-8\right)}{s\left(b^2+2b\beta -8\right)}$.

.

5.2. Price Game

The carbon emission attribute of production has become an important factor influencing purchasing decisions and product demands. At least the emission sensitivity demand should be considered when making product pricing and emission reduction decisions. In this section, we suppose that the retailers are involved in the price game rather than the quantity game. Linear demand functions have been extensively adopted in the operation management literature [45,46]. The demand functions of the two retailers are given by

$$q_i=a-p_i+d{p}_{3-i},$$

(14)

The parameter $0<d<1$ represents price competition intensity, and the larger $d$ indicates more intense competition. The retailer chooses production price $p_i^{}$ to maximize its profit from retail sales, taking the unit wholesale price $w_i$ as given. The retailer’s problem is:

$${\pi }_{R_i}=\left(a-p_i+d{p}_j\right)\left(p_i-w_i\right),$$

(15)

To simplify the computation, we let the retailer’s cost be zero. If not, which will not change the results. Deviate the Equation (15) concerning the $p_i$, and we can obtain the retailer price

$$p_i=\frac{a\left(d+2\right)+d{w}_{3-i}+2w_i}{4-d^2}.$$

(16)

Similarly, we can obtain manufacturers’ profit function under the case $\left(C,C\right)$

$${\pi }_{M_1}^{CC}=\left(w_1-\delta \xi -ts\right)\left(a-p_1+d{p}_2\right),$$

(17)

$${\pi }_{M_2}^{CC}=\left(w_2-\delta \xi -ts\right)\left(a-p_2+d{p}_1\right).$$

(18)

Then we obtain the results of $\left(p_1^{CC},p_2^{CC}\right)$, $\left(w_1^{CC},w_2^{CC}\right)$ and $\left({\pi }_{M_1}^{CC},{\pi }_{M_2}^{CC}\right)$. Similarly, we can obtain the result of the case $\left(L,C\right)$ $\left(C,L\right)$ and $\left(L,L\right)$. Finally, the equilibrium payoffs of all players in supply chains are listed in Table S3. From this, we can obtain the following Proposition 6.

Proposition 6.

With the price game, the equilibrium technology choices of the manufacturers are shown in

Table 4. The Equilibria of Production Technology in the Case of Price Game.

Cases	$a$	$0<a\le \overline{a}$					$a>\overline{a}$
	$\beta$	$0<\beta \le 2/7$			$2/7<\beta <1$		$0<\beta <1$
	$t$	$\left[0,t_{33}\right]$	$\left(t_{33},t_{34}\right]$	$\left(t_{34},\infty \right)$	$\left[0,t_{35}\right]$	$\left(t_{35},\infty \right)$	$\left[0,t_{31}\right]$	$\left(t_{31},t_{32}\right]$	$\left(t_{32},\infty \right)$
Equilibria		$\left(C,C\right)$	$\left(C,L\right)$$\mathrm{or}\left(L,C\right)$	$\left(\varnothing ,\varnothing \right)$	$\left(C,C\right)$	$\left(\varnothing ,\varnothing \right)$	$\left(C,C\right)$	$\left(L,L\right)$	$\left(\varnothing ,\varnothing \right)$

Note: $\varnothing$ denotes one manufacturer doesn’t choose any technology. $\overline{a}=\frac{\xi \left(1-d\right)\left(1-\delta \beta \right)}{1-\beta }$, $t_{31}=\frac{\xi \left(1-\delta \right)}{s\left(1-\beta \right)}$, $t_{32}=\frac{a-\xi }{\beta s}$, $t_{33}=\frac{2a\left(d^2+2d-8\right)-\xi \left(d^2-8\right)-\left(d^2+4d-8\right)\delta \xi }{s\left(\beta d^2-8\beta +d^2+4d-8\right)}$, $\begin{array}{l}{t}_{34}=\frac{8a-\left(2d^4-9d^2+8\right)\delta \xi -ad\left(2d^2+3d-6\right)+d\xi \left(2-d^2\right)}{\left(2d^4-9d^2+8\right)s-d\beta s\left(2-d^2\right)}\\ \end{array}$, $t_{35}=\frac{a-\delta \xi \left(1-d\right)}{s\left(1-d\right)}$.

.

6. Conclusions and Future Research

There is an important growing awareness about carbon emission reduction. One important strategic response from the manufacturing sector is adopting low-carbon technology. We analyze the duopoly firms’ strategic technology choices under the carbon tax policy. We consider the three-level supply chain consisting of the regulator and two competitive supply chains with their manufacturer and retailer. In our model, firms can adopt the common technology, which produces a cost advantage. At the same time, the carbon emission is high, or it can adopt the low-carbon technology, which has the carbon emission advantage while the production cost is high. This research makes several important contributions. We complement the existing literature on the carbon tax by analyzing the technology choice of the competitive manufacturers in the supply chain. This study provides a practical and innovative insight into examining the efficiency of government policies. Furthermore, different industry sectors have their distinctive market volume and carbon-reducing efficiency. By considering the market and carbon-reducing efficiency of the technology choice, we also contribute to the green technology investment literature in sustainable supply chain management. Practically, we help manufacturers make optimal operational and technology choice decisions to improve their economic and environmental performances.

Our results generate some interesting findings. We prove that a high carbon tax does not always help firms choose low-carbon technology. Whether or not the manufacturers select the low-carbon technology largely depends on the market volume and the carbon-reducing efficiency besides the high carbon tax. Therefore, in designing the carbon tax, it is critical to consider the market and the carbon-reducing efficiency of the different industry sections. Furthermore, our results also reveal that the manufacturer’s profit always decreases with the carbon tax increase when the market is large, but it is not always the truth when the market is small. This finding complements previous studies, especially if the market is small and the carbon-reducing efficiency of the low-carbon technology is high. Interestingly, the manufacturers are caught in the “prisoner dilemma.” The manufacturers adopt differentiated strategies at high carbon tax intervals, which makes the competitive manufacturers achieve the Pareto optimality. We also show that if the manufacturers adopt the same common technology, they might be in a prisoner’s dilemma. Although adopting common technology is an equilibrium strategy, the manufacturers would not be better off. So, the proper carbon tax should encourage the manufacturers to adopt the low-carbon technology and obtain more profit at the same time when the regulators design the carbon tax mechanism for carbon emission reduction. The optimal carbon tax should be designed not only for environmental performance but for economic performance. Finally, our findings indicate that firm’s optimal decision on low-carbon technology is mainly influenced by the balance between the producing cost saving of the common technology and the carbon tax cost levied by the regulator. Fundamentally, we need to invest in green technologies to improve carbon-reducing efficiency. Our findings will support policymakers in implementing a carbon tax to support their long-term sustainable development.

We also examine the manufacturers’ technology choices when the production is substitutable, and the competitive product price is. The result coincides with the basic model, so the carbon tax guiding the manufacturers to select the low-carbon technology has robustness, which has great instructiveness to the regulator. Furthermore, our results suggest that they would have good outcomes if the regulator could gather accurate information about the market volume and the carbon-reducing efficiency. Our paper is especially useful in many countries where policymakers seek to balance environmental protection and economic development. In those contexts, the design of proactive regulation could have significant effects on firms’ decisions.

This study also has limitations. First, our model studies the technology choice of the manufacturers in the static time situation under the carbon tax. However, in reality, the impact of the carbon tax on the technology choice is often dynamic change. Second, this research is studied under the carbon tax policy without considering the impact of other carbon emission reduction policies, such as carbon trading and emission reduction subsidies, on the enterprise’s technology selection. In reality, most carbon taxes do not exist alone, and many governments use a portfolio of policies such as clean energy standards and cap-and-trade policies, or other environmental policies are in place that will impact carbon emission. Finally, the research is mainly limited to the theoretical level, and there is no actual data collected.

There are several possible extensions for future investigation. One possible direction for future research is to examine the dynamic carbon tax impact on the manufacturer’s technology choice. Intuitively, the dynamic carbon tax is complicated, which will cause the demand function and computation process to change. Another possible direction can be extended to the design of other carbon emissions control policies, such as carbon reduction subsidies and carbon cap-and-trade measures. Finally, collecting the data about carbon emission and carbon tax, the empirical analysis model can be constructed by analyzing the impact of the carbon tax on carbon emission reduction, which may be very interesting.