Using Industry 4.0’s Big Data and IoT to Perform Feature-Based and Past Data-Based Energy Consumption Predictions
Abstract
1. Introduction
2. Literature Review
2.1. Smart Meters
2.2. Energy Consumption Forecasting Methods
3. Materials and Methods
3.1. Business Understanding
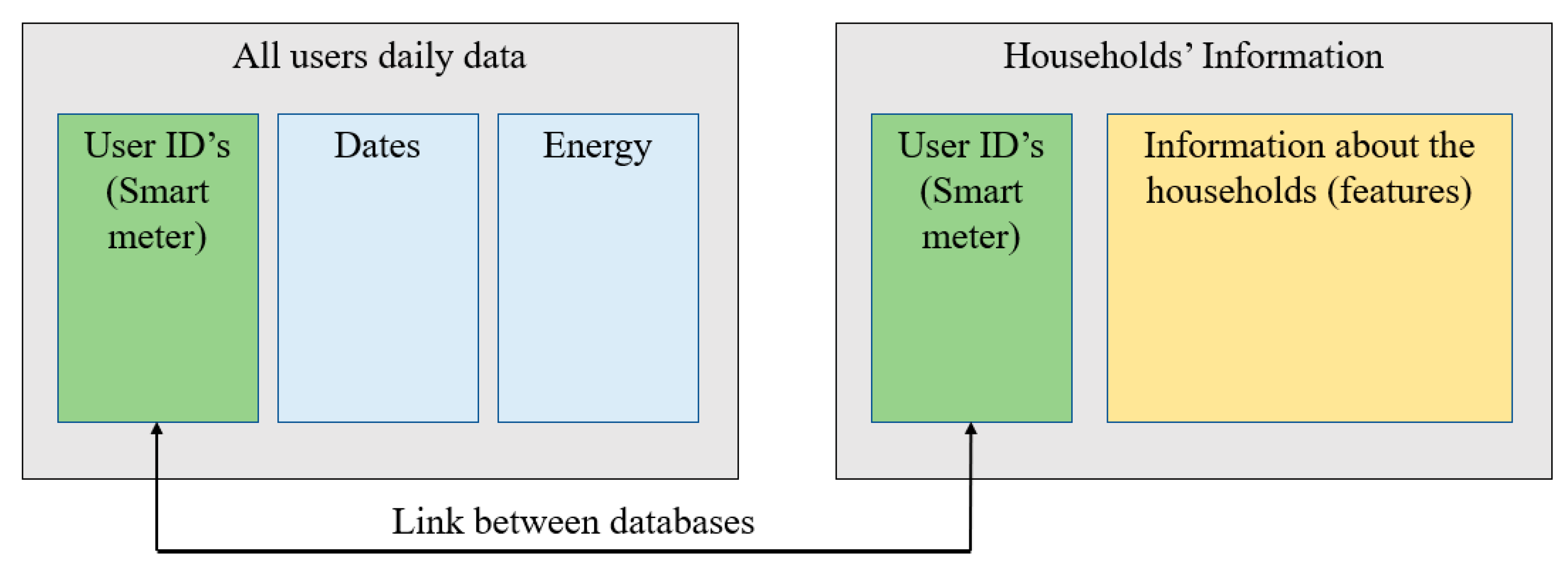
3.2. Data Understanding
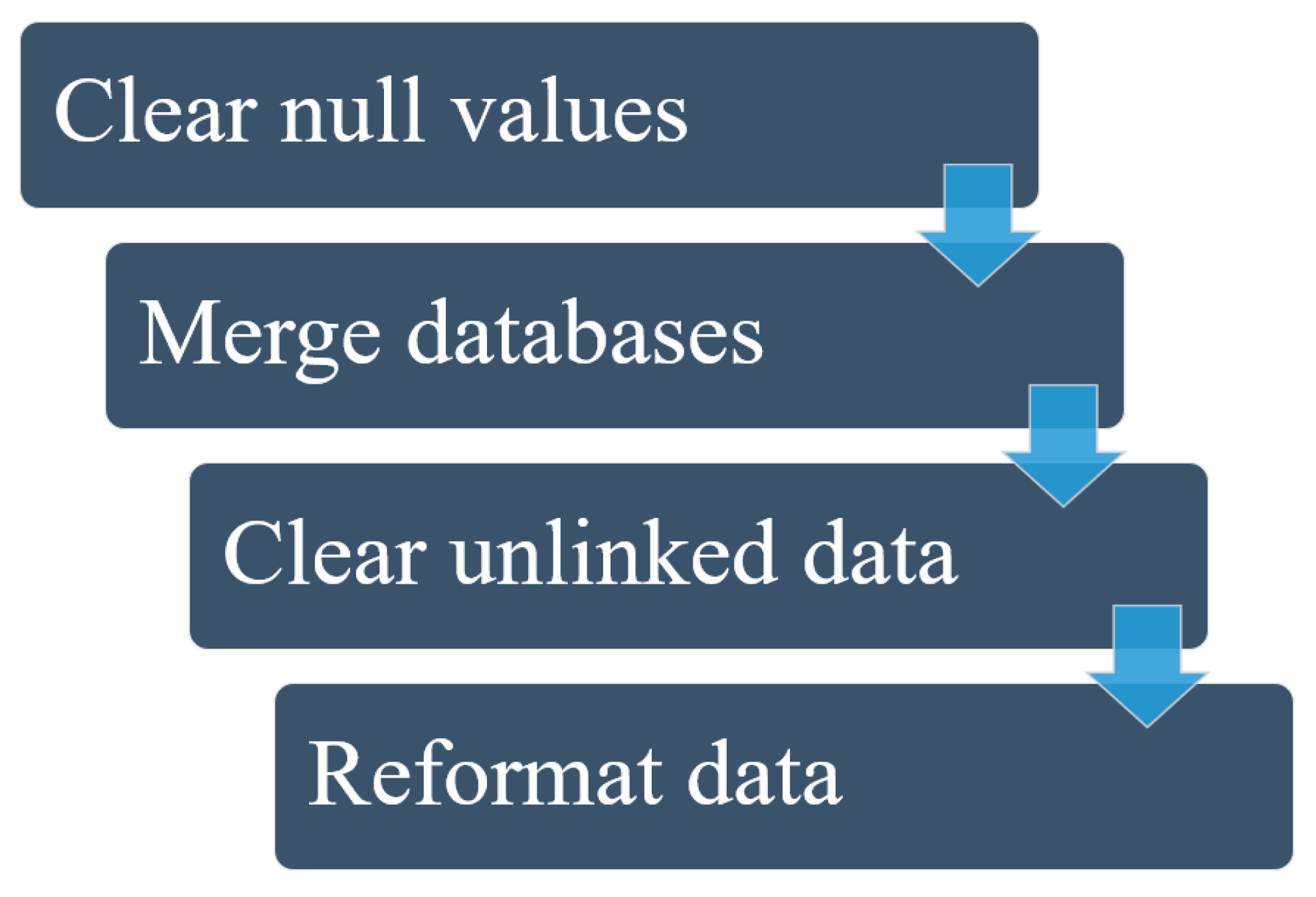
3.3. Data Preparation
3.4. Modeling
3.4.1. Feature-Based Prediction
3.4.2. Past Data-Based Prediction
3.5. Evaluation
4. Results
4.1. Feature-Based Prediction
4.2. Past Data-Based Prediction
5. Discussion
5.1. Feature-Based Prediction
5.2. Past Data-Based Prediction
5.3. Data Gathering and Privacy Concerns
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Featured-Based Prediction Algorithm
- (Text version of the Python® Jupyter Notebooks archive)
- #Initial Imports
- import numpy as np
- import pandas as pd
- import matplotlib.pyplot as plt
- from sklearn.metrics import mean_squared_error as rmse
- #load first database
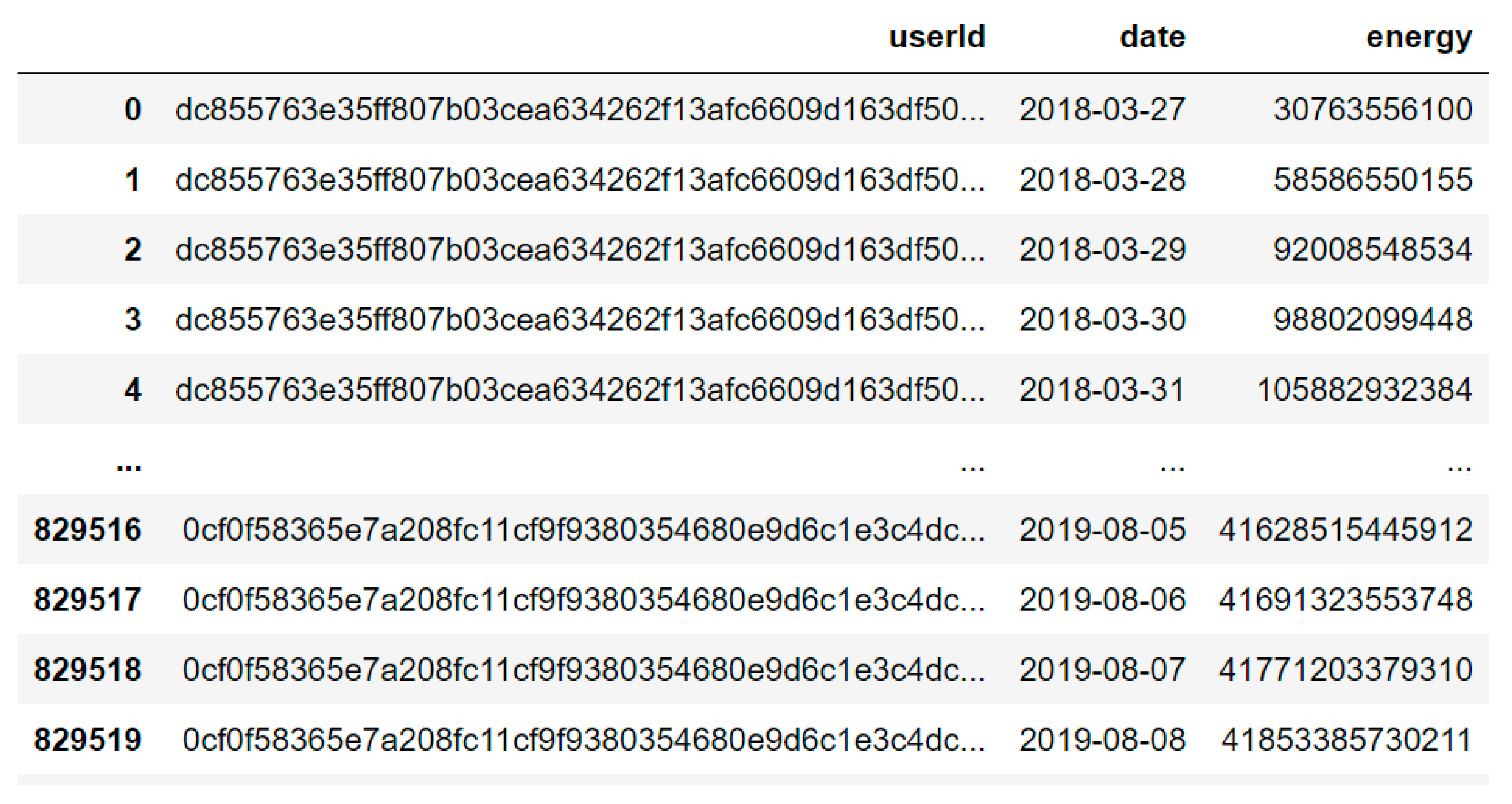
- dataMain = pd.read_csv(‘all-users-daily-data-GEM-House.csv’)
- print(dataMain.shape)
- dataMain.head()
- dataMain
- #checking some details about the database
- df1 = pd.DataFrame(dataMain)
- print (df1.dtypes)
- print (dataMain[‘userId’].nunique())
- print (dataMain.describe())
- earliest = min(dataMain[‘date’])
- print (earliest)
- latest = max(dataMain[‘date’])
- print (latest)
- #looking for null values and duplicates
- print (dataMain.isnull().sum().sum())
- dataMainDup = dataMain.duplicated()
- truesDataMainDup = dataMainDup.sum()
- print (truesDataMainDup)
- #create ‘dates’ column as a time series object
- dataMain[‘dates’] = pd.to_datetime(dataMain[‘date’], format = ‘%Y/%m/%d’)
- #check how the date values are distributed among smart meters
- dataMain[‘date’].value_counts()
- #load second database
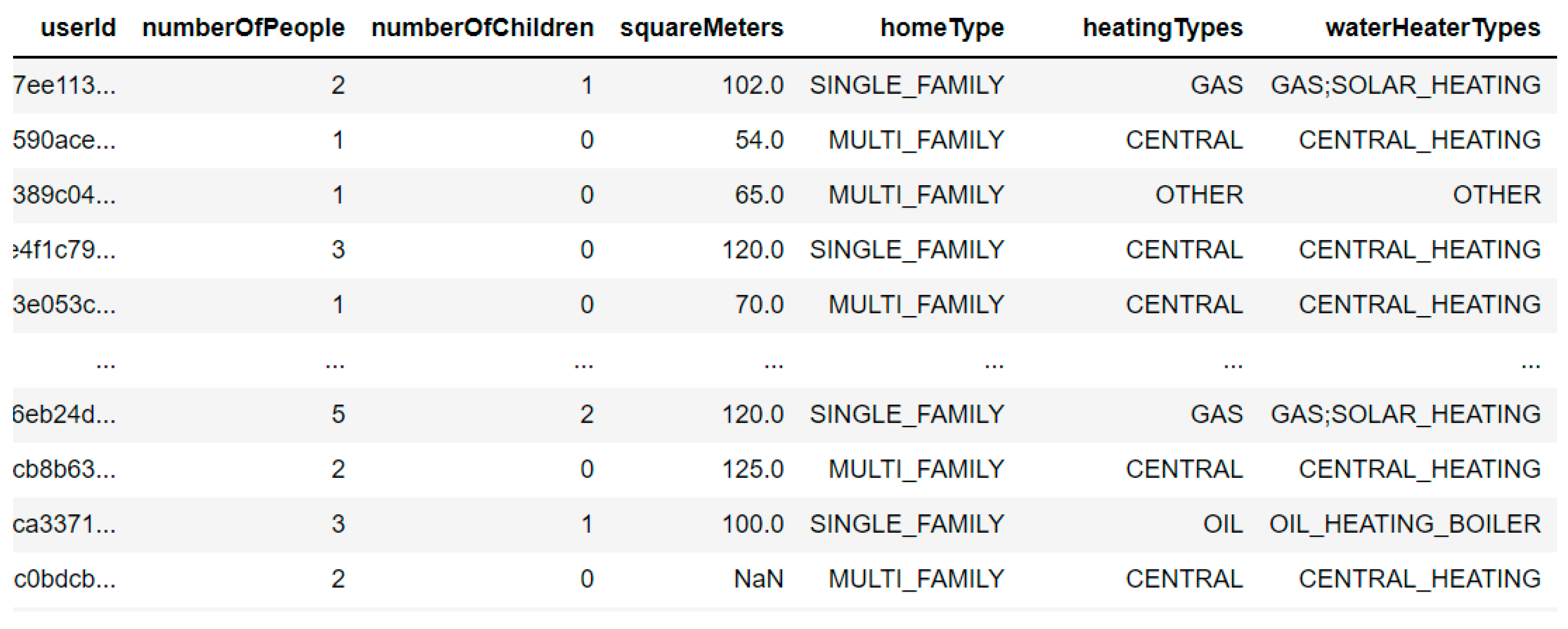
- households = pd.read_csv(‘household-information.csv’)
- print(households.shape)
- households.head()
- households
- #checking details about the second database
- df = pd.DataFrame(households)
- print (df.dtypes)
- print (households[‘userId’].nunique())
- print (households[‘numberOfPeople’].nunique())
- print (households[‘numberOfChildren’].nunique())
- print (households[‘homeType’].nunique())
- print (households[‘heatingTypes’].nunique())
- print (households[‘coolingType’].nunique())
- print (households[‘heatingTypeOther’].nunique())
- print (households[‘waterHeaterTypeOther’].nunique())
- households.describe()
- #Checking null values and duplicates(1)
- households.isnull().sum().sum()
- #Checking null values and duplicates(2)
- householdsDup = households.duplicated()
- truesHouseholdsDup = householdsDup.sum()
- truesHouseholdsDup
- #Checking null values and duplicates(3)
- households.columns[households.isna().any()].tolist()
- #Checking null values and duplicates(4)
- print (households[‘numberOfPeople’].isnull().sum().sum())
- print (households[‘numberOfChildren’].isnull().sum().sum())
- print (households[‘squareMeters’].isnull().sum().sum())
- print (households[‘homeType’].isnull().sum().sum())
- print (households[‘heatingTypes’].isnull().sum().sum())
- print (households[‘waterHeaterTypes’].isnull().sum().sum())
- print (households[‘coolingType’].isnull().sum().sum())
- print (households[‘heatingTypeOther’].isnull().sum().sum())
- print (households[‘waterHeaterTypeOther’].isnull().sum().sum())
- households = households.drop(columns = [‘heatingTypeOther’, ‘waterHeaterTypeOther’])
- #Droping lines with null values
- householdsClean = households.dropna()
- householdsClean
- #checking the number of different smart meters
- householdsClean[‘userId’].nunique()
- #list of features of the second database
- features1 = list(householdsClean.columns.values.tolist())
- features1
- #Merging databases
- GEM = dataMain
- GEM = GEM.merge(householdsClean, how = ‘left’, on = ‘userId’)
- #Dropping rows that do not have features corresponding to that smart meter.
- GEM = GEM.dropna()
- GEM
- #Rechecking null values
- GEM.isnull().sum().sum()
- #checking the number of different smart meters
- GEM[‘userId’].nunique()
- #Checking data types.
- df4 = pd.DataFrame(GEM)
- print (df4.dtypes)
- #It is needed to change categorical variables into dummy variables. It is also needed to split columns with more than one
- #response in the same cell, then we have only one information per cell.
- GEM[‘heatingTypes’].value_counts()
- GEM[‘waterHeaterTypes’].value_counts()
- GEM[[‘waterHeaterTypesA’, ‘waterHeaterTypesB’, ‘waterHeaterTypesC’]] = GEM[‘waterHeaterTypes’].str.split(‘;’, −1, expand = True)
- GEM
- #Spliting the information about heating types
- GEM[[‘heatingTypesA’, ‘heatingTypesB’, ‘heatingTypesC’, ‘heatingTypesD’,‘heatingTypesE’]] = GEM[‘heatingTypes’].str.split(‘;’, −1, expand = True)
- #Getting dummies to every heating type column
- GEM[‘heatingTypesE’].value_counts()
- GEM[‘heatingTypesEEletric’] = pd.get_dummies(GEM[‘heatingTypesE’])
- GEM.rename(columns = {‘heatingTypesEEletric’:‘htElectric5’}, inplace = True)
- pd.get_dummies(GEM[‘heatingTypesD’])
- GEM[[‘htElectric4’,‘htGas4’]] = pd.get_dummies(GEM[‘heatingTypesD’])
- pd.get_dummies(GEM[‘heatingTypesC’])
- GEM[[‘htCentral3’,‘htGas3’,‘htPellet3’]] = pd.get_dummies(GEM[‘heatingTypesC’])
- pd.get_dummies(GEM[‘heatingTypesB’])
- GEM[[‘htCentral2’,‘htElectric2’,‘htGas2’,‘htHeat_Pump2’, ‘htOil2’, ‘htPellet2’, ‘htPortable_Electric2’, ‘htWood2’]] = pd.get_dummies(GEM[‘heatingTypesB’])
- pd.get_dummies(GEM[‘heatingTypesA’])
- GEM[[‘htCentral1’,‘htElectric1’,‘htGas1’,‘htHeat_Pump1’, ‘htOil1’, ‘htOther1’, ‘htPellet1’, ‘htPortable_Electric1’, ‘htWood1’]] = pd.get_dummies(GEM[‘heatingTypesA’])
- #Getting one column to each heating type
- GEM[‘heatingTypeCentral’] = GEM[‘htCentral3’] + GEM[‘htCentral2’] + GEM[‘htCentral1’]
- GEM[‘heatingTypeElectric’] = GEM[‘htElectric5’] + GEM[‘htElectric4’] + GEM[‘htElectric2’] + GEM[‘htElectric1’]
- GEM[‘heatingTypeGas’] = GEM[‘htGas4’] + GEM[‘htGas3’] + GEM[‘htGas2’] + GEM[‘htGas1’]
- GEM[‘heatingTypeHeat_Pump’] = GEM[‘htHeat_Pump2’] + GEM[‘htHeat_Pump1’]
- GEM[‘heatingTypeOil’] = GEM[‘htOil2’] + GEM[‘htOil1’]
- GEM[‘heatingTypeOther’] = GEM[‘htOther1’]
- GEM[‘heatingTypePellet’] = GEM[‘htPellet3’] + GEM[‘htPellet2’] + GEM[‘htPellet1’]
- GEM[‘heatingTypePortable_Electric’] = GEM[‘htPortable_Electric2’] + GEM[‘htPortable_Electric1’]
- GEM[‘heatingTypeWood’] = GEM[‘htWood2’] + GEM[‘htWood1’]
- GEM
- #Dropping the columns created to allocate data in the middle of the process
- GEM = GEM.drop([‘heatingTypesA’,
- ‘heatingTypesB’, ‘heatingTypesC’, ‘heatingTypesD’, ‘heatingTypesE’, ‘htElectric5’, ‘htElectric4’, ‘htGas4’, ‘htCentral3’, ‘htGas3’, ‘htPellet3’, ‘htCentral2’, ‘htElectric2’, ‘htGas2’, ‘htHeat_Pump2’, ‘htOil2’, ‘htPellet2’, ‘htPortable_Electric2’, ‘htWood2’, ‘htCentral1’, ‘htElectric1’, ‘htGas1’, ‘htHeat_Pump1’, ‘htOil1’, ‘htOther1’, ‘htPellet1’, ‘htPortable_Electric1’, ‘htWood1’], axis = 1)
- list(GEM.columns.values.tolist())
- #Spliting and getting dummy variables for water heating types
- GEM[‘waterHeaterTypes’].value_counts()
- GEM[[‘waterHeaterTypesA’, ‘waterHeaterTypesB’, ‘waterHeaterTypesC’]] = GEM[‘waterHeaterTypes’].str.split(‘;’, −1, expand = True)
- #Checking the categories
- pd.get_dummies(GEM[‘waterHeaterTypesA’])
- pd.get_dummies(GEM[‘waterHeaterTypesB’])
- pd.get_dummies(GEM[‘waterHeaterTypesC’])
- #Getting dummies
- GEM[[‘wtCentralHeating1’,‘wtFlowWaterHeating1’,‘wtGas1’,‘wtOilHeatingBoiler1’, ‘wtOther1’,
- ‘wtSolarHeating1’]] = pd.get_dummies(GEM[‘waterHeaterTypesA’])
- GEM[[‘wtCentralHeating2’,‘wtFlowWaterHeating2’,‘wtGas2’,‘wtOilHeatingBoiler2’, ‘wtSolarHeating2’]] = pd.get_dummies(GEM[‘waterHeaterTypesB’])
- GEM[[‘wtFlowWaterHeating3’,‘wtSolarHeating3’]] = pd.get_dummies(GEM[‘waterHeaterTypesC’])
- #Summing the commom categories into one column
- GEM[‘waterHeatingTypeCentralHeating’] = GEM[‘wtCentralHeating1’] + GEM[‘wtCentralHeating2’]
- GEM[‘waterHeatingTypeFlowWaterHeating’] = GEM[‘wtFlowWaterHeating1’] + GEM[‘wtFlowWaterHeating2’] + GEM[‘wtFlowWaterHeating3’]
- GEM[‘waterHeatingTypeGas’] = GEM[‘wtGas1’] + GEM[‘wtGas2’]
- GEM[‘waterHeatingTypeOilHeatingBoiler’] = GEM[‘wtOilHeatingBoiler1’] + GEM[‘wtOilHeatingBoiler2’]
- GEM[‘waterHeatingTypeOther’] = GEM[‘wtOther1’]
- GEM[‘waterHeatingTypeSolarHeating’] = GEM[‘wtSolarHeating1’] + GEM[‘wtSolarHeating2’] + GEM[‘wtSolarHeating3’]
- #Dropping intermediate columns
- GEM = GEM.drop([‘waterHeaterTypesA’, ‘waterHeaterTypesB’, ‘waterHeaterTypesC’,‘wtCentralHeating1’, ‘wtFlowWaterHeating1’, ‘wtGas1’, ‘wtOilHeatingBoiler1’, ‘wtOther1’, ‘wtSolarHeating1’, ‘wtCentralHeating2’, ‘wtFlowWaterHeating2’, ‘wtGas2’, ‘wtOilHeatingBoiler2’, ‘wtSolarHeating2’, ‘wtFlowWaterHeating3’, ‘wtSolarHeating3’],axis = 1)
- GEM
- #Dropping the two original categorical columns
- GEM = GEM.drop([‘heatingTypes’, ‘waterHeaterTypes’],axis = 1)
- GEM
- #The next variables do not have more than one info per cell
- #Getting dummies for home type
- pd.get_dummies(GEM[‘homeType’])
- GEM[[‘homeTypeMultiFamily’,‘homeTypeSingleFamily’]] = pd.get_dummies(GEM[‘homeType’])
- #Getting dummies for cooling type
- pd.get_dummies(GEM[‘coolingType’])
- GEM[[‘coolingTypeCentralAirConditioner’,‘coolingTypeGeothermal’, ‘coolingTypeNone’,‘coolingTypePortableAirConditioner’]] = pd.get_dummies(GEM[‘coolingType’])
- #Dropping the original columns
- GEM = GEM.drop([‘homeType’, ‘coolingType’],axis = 1)
- #Sorting rows by user id and date
- GEM = GEM.sort_values([‘userId’, ‘date’])
- #Creating a new variable, subtracting the energy value from the previous column, so we have the energy consumed, instead of the
- #energy accumulated
- GEM[‘energyUsage’] = GEM[‘energy’].diff()
- GEM
- GEM.isnull().sum().sum()
- #We need to delete the first row of every smart meter, because we do not have the previous value to subtract
- GEM[‘num_in_group’] = GEM.groupby(‘userId’).cumcount()
- GEM = GEM[GEM[‘num_in_group’] > 0]
- GEM
- GEM[‘numberOfPeople’].value_counts()
- GEM[‘numberOfChildren’].value_counts()
- #We need to transform ‘number of people’ and ‘number of children’ into integers.
- #First we deal with the ‘8 + ’ and ‘7 + ’ issue.
- GEM[‘nPeople’] = [8 if a == ‘8 + ’ else a for a in GEM[‘numberOfPeople’]]
- GEM[‘nChildren’] = [7 if a == ‘7 + ’ else a for a in GEM[‘numberOfChildren’]]
- #Then we change the data type
- GEM[‘nPeople’] = GEM[‘nPeople’].astype(int)
- GEM[‘nChildren’] = GEM[‘nChildren’].astype(int)
- #Finally we delete the original columns, including the original energy column
- GEM = GEM.drop([‘energy’,
- ‘numberOfPeople’,
- ‘numberOfChildren’,‘num_in_group’],axis = 1)
- GEM
- #Shifting the columns’ order to have the energy as the last column
- cols = GEM.columns.tolist()
- cols
- cols = [‘userId’, ‘date’, ‘dates’, ‘squareMeters’, ‘nPeople’, ‘nChildren’, ELECTRIC_VEHICLE’, ‘TV’, ‘DISH_WASHER’, ‘ELECTRIC_HEATING’, ‘SAUNA’, ‘HEAT_PUMP’, ‘CABLE_BOX’, ‘FRIDGE_COMBO’, ‘COFFEE_MACHINE’, ‘TUMBLE_DRYER’, ‘FREEZER’, ‘POOL_PUMP’, ‘HOB’, ‘WASHING_MACHINE’, ‘GAME_CONSOLE’, ‘REFRIGERATOR’, ‘FLOW_WATER_HEATER’, ‘TOASTER’, ‘HOME_BATTERY’, ‘MICROWAVE’, ‘IRON’, ‘TABLET’, ‘HEATING_FAN’, ‘GRILL’, ‘DVD’, ‘COMPUTER’, ‘OVEN’, ‘ELECTRIC_SHOWER’, ‘KETTLE’, ‘OTHERS’, ‘heatingTypeCentral’, ‘heatingTypeElectric’, ‘heatingTypeGas’, ‘heatingTypeHeat_Pump’, ‘heatingTypeOil’, ‘heatingTypeOther’, ‘heatingTypePellet’, ‘heatingTypePortable_Electric’, ‘heatingTypeWood’, ‘waterHeatingTypeCentralHeating’, ‘waterHeatingTypeFlowWaterHeating’, ‘waterHeatingTypeGas’, ‘waterHeatingTypeOilHeatingBoiler’, ‘waterHeatingTypeOther’, ‘waterHeatingTypeSolarHeating’, ‘homeTypeMultiFamily’, ‘homeTypeSingleFamily’, ‘coolingTypeCentralAirConditioner’, ‘coolingTypeGeothermal’, ‘coolingTypeNone’, ‘coolingTypePortableAirConditioner’, ‘energyUsage’]
- GEM = GEM[cols]
- GEM
- #Now all the data types are correct
- #pd.set_option(‘display.max_rows’, None)
- df1 = pd.DataFrame(GEM)
- print (df1.dtypes)
- # Define the function to calculate the sMAPE
- #import numpy as np
- def smape(a, f):
- return 1/len(a) * np.sum(200 * np.abs(f-a) / (np.abs(a) + np.abs(f)))
- #Sorting the rows by date, to set the dates as index
- GEM = GEM.sort_values(by = [‘dates’, ‘userId’])
- #indexing
- GEM = GEM.set_index(GEM[‘dates’])
- GEM = GEM.sort_index()
- GEM
- #Checking how many rows we have for each smart meter
- pd.set_option(‘display.max_rows’, 10)
- GEM[‘userId’].value_counts(sort = False)
- #Creating a new database, dropping smart meters with less than 400 rows
- GEM2 = GEM[GEM.groupby(‘userId’).userId.transform(‘count’) > 399].copy()
- GEM2[‘userId’].value_counts(sort = False)
- #We now have 467 smart meters
- #Creating the Features Matrix and separating it from the energy consumption
- GEM_Features = GEM2
- GEM_Features = GEM_Features.drop([‘date’, ‘dates’,‘energyUsage’ ], axis = 1)
- GEM_Features = GEM_Features.groupby(‘userId’).first().reset_index()
- GEM_Features
- #Creating the energy consumption matrix and summing by month
- GEM_Energy = GEM2
- GEM_Energy = GEM_Energy.drop([ ‘date’, ‘squareMeters’, ‘nPeople’, ‘nChildren’, ‘ELECTRIC_VEHICLE’, ‘TV’, ‘DISH_WASHER’,
- ‘ELECTRIC_HEATING’, ‘SAUNA’, ‘HEAT_PUMP’, ‘CABLE_BOX’, ‘FRIDGE_COMBO’, ‘COFFEE_MACHINE’,
- ‘TUMBLE_DRYER’, ‘FREEZER’, ‘POOL_PUMP’, ‘HOB’, ‘WASHING_MACHINE’, ‘GAME_CONSOLE’, ‘REFRIGERATOR’,
- ‘FLOW_WATER_HEATER’, ‘TOASTER’, ‘HOME_BATTERY’, ‘MICROWAVE’, ‘IRON’, ‘TABLET’, ‘HEATING_FAN’,
- ‘GRILL’, ‘DVD’, ‘COMPUTER’, ‘OVEN’, ‘ELECTRIC_SHOWER’, ‘KETTLE’, ‘OTHERS’, ‘heatingTypeCentral’,
- ‘heatingTypeElectric’, ‘heatingTypeGas’, ‘heatingTypeHeat_Pump’, ‘heatingTypeOil’,
- ‘heatingTypeOther’, ‘heatingTypePellet’, ‘heatingTypePortable_Electric’, ‘heatingTypeWood’,
- ‘waterHeatingTypeCentralHeating’, ‘waterHeatingTypeFlowWaterHeating’, ‘waterHeatingTypeGas’,
- ‘waterHeatingTypeOilHeatingBoiler’, ‘waterHeatingTypeOther’, ‘waterHeatingTypeSolarHeating’,
- ‘homeTypeMultiFamily’, ‘homeTypeSingleFamily’, ‘coolingTypeCentralAirConditioner’,
- ‘coolingTypeGeothermal’, ‘coolingTypeNone’, ‘coolingTypePortableAirConditioner’], axis = 1)
- GEM_Energy = GEM_Energy.groupby([‘userId’, GEM_Energy[‘dates’].dt.to_period(‘M’)]).sum()
- GEM_Energy = GEM_Energy.reset_index(level = ‘userId’)
- GEM_Energy = GEM_Energy.reset_index()
- GEM_Energy
- #Merging GEM_Energy and GEM_Features, setting energyUsage as last column
- GEM_C = GEM_Energy
- GEM_C = GEM_C.merge(GEM_Features, how = ‘left’, on = ‘userId’)
- GEM_C
- cols = [‘userId’, ‘dates’, ‘squareMeters’, ‘nPeople’, ‘nChildren’, ELECTRIC_VEHICLE’, ‘TV’, ‘DISH_WASHER’, ‘ELECTRIC_HEATING’, ‘SAUNA’, ‘HEAT_PUMP’, ‘CABLE_BOX’, ‘FRIDGE_COMBO’, ‘COFFEE_MACHINE’, ‘TUMBLE_DRYER’, ‘FREEZER’, ‘POOL_PUMP’, ‘HOB’, ‘WASHING_MACHINE’, ‘GAME_CONSOLE’, ‘REFRIGERATOR’, ‘FLOW_WATER_HEATER’, ‘TOASTER’, ‘HOME_BATTERY’, ‘MICROWAVE’, ‘IRON’, ‘TABLET’, ‘HEATING_FAN’, ‘GRILL’, ‘DVD’, ‘COMPUTER’, ‘OVEN’, ‘ELECTRIC_SHOWER’, ‘KETTLE’, ‘OTHERS’, ‘heatingTypeCentral’, ‘heatingTypeElectric’, ‘heatingTypeGas’, ‘heatingTypeHeat_Pump’, ‘heatingTypeOil’, ‘heatingTypeOther’, ‘heatingTypePellet’, ‘heatingTypePortable_Electric’, ‘heatingTypeWood’, ‘waterHeatingTypeCentralHeating’, ‘waterHeatingTypeFlowWaterHeating’, ‘waterHeatingTypeGas’, ‘waterHeatingTypeOilHeatingBoiler’, ‘waterHeatingTypeOther’, ‘waterHeatingTypeSolarHeating’, ‘homeTypeMultiFamily’, ‘homeTypeSingleFamily’, ‘coolingTypeCentralAirConditioner’, ‘coolingTypeGeothermal’, ‘coolingTypeNone’, ‘coolingTypePortableAirConditioner’, ‘energyUsage’]
- GEM_C = GEM_C[cols]
- GEM_C
- #Drop ID’s and dates
- GEM_C = GEM_C.drop([‘userId’, ‘dates’ ], axis = 1)
- GEM_C
- #Imports for classification
- import os
- import random
- import itertools
- import numpy as np
- import pandas as pd
- import matplotlib.pyplot as plt
- from sklearn.manifold import TSNE
- from sklearn.preprocessing import StandardScaler
- from sklearn.model_selection import train_test_split
- from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
- #Train-Test Split
- y = GEM_C[‘energyUsage’]
- X_train, X_test, y_train, y_test = train_test_split(GEM_C, y, random_state = 1, test_size = 0.2)
- y_train.shape
- X_train.shape
- X_train
- X_train = X_train.drop([‘energyUsage’], axis = 1)
- X_test = X_test.drop([‘energyUsage’], axis = 1)
- X_test
- y_test.shape
- X_test.shape
- #Random Forest Regressor
- from sklearn.ensemble import RandomForestRegressor
- forest = RandomForestRegressor(1000)
- forest.fit(X_train, y_train)
- #xfit = np.linspace(0, 10, 1000)
- #y_pred = forest.predict(X_test)
- # Use the forest’s predict method on the test data
- predictions = forest.predict(X_test)
- # Calculate the absolute errors
- error = smape(y_test, predictions)
- error2 = rmse(y_test, predictions, squared = False)
- # Print out the errors
- print(‘Smape:’, round(np.mean(error), 2), ‘.’)
- print(‘RMSE:’, round(np.mean(error2), 2), ‘.’)
- SummaryTable = pd.DataFrame(columns = [‘Method’, ‘sMAPE’, ‘RMSE’])
- SummaryTable = SummaryTable.append({‘Method’: ‘Random Forest’, ‘sMAPE’: error, ‘RMSE’: error2},ignore_index = True)
- print(SummaryTable)
- #Support Vector Machines Regression (without Standard Scaling)
- from sklearn.svm import SVR
- SVMregressor = SVR(kernel = ‘rbf’)
- SVMregressor.fit(X_train, y_train)
- y_pred = SVMregressor.predict(X_test)
- errorSVM = smape(y_test, y_pred)
- error2SVM = rmse(y_test, y_pred, squared = False)
- print(‘Smape:’, round(np.mean(errorSVM), 2), ‘.’)
- print(‘RMSE:’, round(np.mean(error2SVM), 2), ‘.’)
- SummaryTable = SummaryTable.append({‘Method’: ‘SVM w/o Scaling’, ‘sMAPE’: errorSVM, ‘RMSE’: error2SVM},ignore_index = True)
- print(SummaryTable)
- #Support Vector Machines Regression (with Standard Scaling)
- from sklearn.preprocessing import StandardScaler
- sc_X = StandardScaler()
- sc_y = StandardScaler()
- X = sc_X.fit_transform(X_train)
- y_train2 = y_train.array.reshape(−1, 1)
- y = sc_y.fit_transform(y_train2)
- X2 = sc_X.fit_transform(X_test)
- regressor = SVR(kernel = ‘rbf’)
- regressor.fit(X, y)
- y_pred = regressor.predict(X2)
- y_pred = sc_y.inverse_transform(y_pred)
- errorSVM = smape(y_test, y_pred)
- error2SVM = rmse(y_test, y_pred, squared = False)
- print(‘Smape:’, round(np.mean(errorSVM), 2), ‘.’)
- print(‘RMSE:’, round(np.mean(error2SVM), 2), ‘.’)
- SummaryTable = SummaryTable.append({‘Method’: ‘SVM with Scaling’, ‘sMAPE’: errorSVM, ‘RMSE’: error2SVM},ignore_index = True)
- print(SummaryTable)
- #Linear Regression (Baseline)
- from sklearn import linear_model, metrics
- reg = linear_model.LinearRegression()
- reg.fit(X_train, y_train)
- y_pred2 = reg.predict(X_test)
- errorSVM = smape(y_test, y_pred2)
- error2SVM = rmse(y_test, y_pred2, squared = False)
- print(‘Smape:’, round(np.mean(errorSVM), 2), ‘.’)
- print(‘RMSE:’, round(np.mean(error2SVM), 2), ‘.’)
- SummaryTable = SummaryTable.append({‘Method’: ‘Linear Regression’, ‘sMAPE’: errorSVM, ‘RMSE’: error2SVM},ignore_index = True)
- print(SummaryTable)
- #Bayesian Ridge Linear Regression
- from sklearn.linear_model import BayesianRidge
- BaRi = BayesianRidge()
- BaRi.fit(X_train, y_train)
- y_pred3 = BaRi.predict(X_test)
- errorSVM = smape(y_test, y_pred3)
- error2SVM = rmse(y_test, y_pred3, squared = False)
- print(‘Smape:’, round(np.mean(errorSVM), 2), ‘.’)
- print(‘RMSE:’, round(np.mean(error2SVM), 2), ‘.’)
- SummaryTable = SummaryTable.append({‘Method’: ‘Bayesian Ridge’, ‘sMAPE’: errorSVM, ‘RMSE’: error2SVM},ignore_index = True)
- print(SummaryTable)
- #Ridge Linear Regression
- from sklearn.linear_model import Ridge
- Ridgemodel = Ridge(alpha = 225)
- Ridgemodel.fit(X_train, y_train)
- y_pred4= Ridgemodel.predict(X_test)
- errorSVM = smape(y_test, y_pred4)
- error2SVM = rmse(y_test, y_pred4, squared = False)
- print(‘Smape:’, round(np.mean(errorSVM), 2), ‘.’)
- print(‘RMSE:’, round(np.mean(error2SVM), 2), ‘.’)
- SummaryTable = SummaryTable.append({‘Method’: ‘Ridge Linear Regression’, ‘sMAPE’: errorSVM, ‘RMSE’: error2SVM},ignore_index = True)
- print(SummaryTable)
Appendix B. Past Data-Based Prediction Algorithm
- (Text version of the Python® Jupyter Notebooks archive)
- #Initial Imports
- import numpy as np
- import pandas as pd
- import matplotlib.pyplot as plt
- fifrom sklearn.metrics import mean_squared_error as rmse
- #load first database
- dataMain = pd.read_csv(‘all-users-daily-data-GEM-House.csv’)
- print(dataMain.shape)
- dataMain.head()
- dataMain
- #checking some details about the database
- df1 = pd.DataFrame(dataMain)
- print (df1.dtypes)
- print (dataMain[‘userId’].nunique())
- print (dataMain.describe())
- earliest = min(dataMain[‘date’])
- print (earliest)
- latest = max(dataMain[‘date’])
- print (latest)
- #looking for null values and duplicates
- print (dataMain.isnull().sum().sum())
- dataMainDup = dataMain.duplicated()
- truesDataMainDup = dataMainDup.sum()
- print (truesDataMainDup)
- #create ‘dates’ column as a time series object
- dataMain[‘dates’] = pd.to_datetime(dataMain[‘date’], format = ‘%Y/%m/%d’)
- #check how the date values are distributed among smart meters
- dataMain[‘date’].value_counts()
- #load second database
- households = pd.read_csv(‘household-information.csv’)
- print(households.shape)
- households.head()
- households
- #checking detais about the second database
- df = pd.DataFrame(households)
- print (df.dtypes)
- print (households[‘userId’].nunique())
- print (households[‘numberOfPeople’].nunique())
- print (households[‘numberOfChildren’].nunique())
- print (households[‘homeType’].nunique())
- print (households[‘heatingTypes’].nunique())
- print (households[‘coolingType’].nunique())
- print (households[‘heatingTypeOther’].nunique())
- print (households[‘waterHeaterTypeOther’].nunique())
- households.describe()
- #Checking null values and duplicates(1)
- households.isnull().sum().sum()
- #Checking null values and duplicates(2)
- householdsDup = households.duplicated()
- truesHouseholdsDup = householdsDup.sum()
- truesHouseholdsDup
- #Checking null values and duplicates(3)
- households.columns[households.isna().any()].tolist()
- #Checking null values and duplicates(4)
- print (households[‘numberOfPeople’].isnull().sum().sum())
- print (households[‘numberOfChildren’].isnull().sum().sum())
- print (households[‘squareMeters’].isnull().sum().sum())
- print (households[‘homeType’].isnull().sum().sum())
- print (households[‘heatingTypes’].isnull().sum().sum())
- print (households[‘waterHeaterTypes’].isnull().sum().sum())
- print (households[‘coolingType’].isnull().sum().sum())
- print (households[‘heatingTypeOther’].isnull().sum().sum())
- print (households[‘waterHeaterTypeOther’].isnull().sum().sum())
- households = households.drop(columns = [‘heatingTypeOther’, ‘waterHeaterTypeOther’])
- #Droping lines with null values
- householdsClean = households.dropna()
- householdsClean
- #checking the number of different smart meters
- householdsClean[‘userId’].nunique()
- #list of features of the second database
- features1 = list(householdsClean.columns.values.tolist())
- features1
- #Merging databases
- GEM = dataMain
- GEM = GEM.merge(householdsClean, how = ‘left’, on = ‘userId’)
- #Dropping rows that do not have features corresponding to that smart meter.
- GEM = GEM.dropna()
- GEM
- #Rechecking null values
- GEM.isnull().sum().sum()
- #checking the number of different smart meters
- GEM[‘userId’].nunique()
- #Checking data types.
- df4 = pd.DataFrame(GEM)
- print (df4.dtypes)
- #It is needed to change categorical variables into dummy variables. It is also needed to split columns with more than one
- #response in the same cell, then we have only one information per cell.
- GEM[‘heatingTypes’].value_counts()
- GEM[‘waterHeaterTypes’].value_counts()
- GEM[[‘waterHeaterTypesA’, ‘waterHeaterTypesB’, ‘waterHeaterTypesC’]] = GEM[‘waterHeaterTypes’].str.split(‘;’, −1, expand = True)
- GEM
- #Spliting the information about heating types
- GEM[[‘heatingTypesA’, ‘heatingTypesB’, ‘heatingTypesC’, ‘heatingTypesD’,‘heatingTypesE’]] = GEM[‘heatingTypes’].str.split(‘;’, −1, expand = True)
- #Getting dummies to every heating type column
- GEM[‘heatingTypesE’].value_counts()
- GEM[‘heatingTypesEEletric’] = pd.get_dummies(GEM[‘heatingTypesE’])
- GEM.rename(columns = {‘heatingTypesEEletric’:‘htElectric5’}, inplace = True)
- pd.get_dummies(GEM[‘heatingTypesD’])
- GEM[[‘htElectric4’,‘htGas4’]] = pd.get_dummies(GEM[‘heatingTypesD’])
- pd.get_dummies(GEM[‘heatingTypesC’])
- GEM[[‘htCentral3’,‘htGas3’,‘htPellet3’]] = pd.get_dummies(GEM[‘heatingTypesC’])
- pd.get_dummies(GEM[‘heatingTypesB’])
- GEM[[‘htCentral2’,‘htElectric2’,‘htGas2’,‘htHeat_Pump2’, ‘htOil2’, ‘htPellet2’, ‘htPortable_Electric2’, ‘htWood2’]] = pd.get_dummies(GEM[‘heatingTypesB’])
- pd.get_dummies(GEM[‘heatingTypesA’])
- GEM[[‘htCentral1’,‘htElectric1’,‘htGas1’,‘htHeat_Pump1’, ‘htOil1’, ‘htOther1’, ‘htPellet1’, ‘htPortable_Electric1’, ‘htWood1’]] = pd.get_dummies(GEM[‘heatingTypesA’])
- #Getting one column to each heating type
- GEM[‘heatingTypeCentral’] = GEM[‘htCentral3’] + GEM[‘htCentral2’] + GEM[‘htCentral1’]
- GEM[‘heatingTypeElectric’] = GEM[‘htElectric5’] + GEM[‘htElectric4’] + GEM[‘htElectric2’] + GEM[‘htElectric1’]
- GEM[‘heatingTypeGas’] = GEM[‘htGas4’] + GEM[‘htGas3’] + GEM[‘htGas2’] + GEM[‘htGas1’]
- GEM[‘heatingTypeHeat_Pump’] = GEM[‘htHeat_Pump2’] + GEM[‘htHeat_Pump1’]
- GEM[‘heatingTypeOil’] = GEM[‘htOil2’] + GEM[‘htOil1’]
- GEM[‘heatingTypeOther’] = GEM[‘htOther1’]
- GEM[‘heatingTypePellet’] = GEM[‘htPellet3’] + GEM[‘htPellet2’] + GEM[‘htPellet1’]
- GEM[‘heatingTypePortable_Electric’] = GEM[‘htPortable_Electric2’] + GEM[‘htPortable_Electric1’]
- GEM[‘heatingTypeWood’] = GEM[‘htWood2’] + GEM[‘htWood1’]
- GEM
- #Dropping the columns created to allocate data in the middle of the process
- GEM = GEM.drop([‘heatingTypesA’,
- ‘heatingTypesB’, ‘heatingTypesC’, ‘heatingTypesD’, ‘heatingTypesE’, ‘htElectric5’, ‘htElectric4’, ‘htGas4’, ‘htCentral3’, ‘htGas3’, ‘htPellet3’, ‘htCentral2’, ‘htElectric2’, ‘htGas2’, ‘htHeat_Pump2’, ‘htOil2’, ‘htPellet2’, ‘htPortable_Electric2’, ‘htWood2’, ‘htCentral1’, ‘htElectric1’, ‘htGas1’, ‘htHeat_Pump1’, ‘htOil1’, ‘htOther1’, ‘htPellet1’, ‘htPortable_Electric1’, ‘htWood1’],axis = 1)
- list(GEM.columns.values.tolist())
- #Spliting and getting dummy variables for water heating types
- GEM[‘waterHeaterTypes’].value_counts()
- GEM[[‘waterHeaterTypesA’, ‘waterHeaterTypesB’, ‘waterHeaterTypesC’]] = GEM[‘waterHeaterTypes’].str.split(‘;’, −1, expand = True)
- #Checking the categories
- pd.get_dummies(GEM[‘waterHeaterTypesA’])
- pd.get_dummies(GEM[‘waterHeaterTypesB’])
- pd.get_dummies(GEM[‘waterHeaterTypesC’])
- #Getting dummies
- GEM[[‘wtCentralHeating1’,‘wtFlowWaterHeating1’,‘wtGas1’,‘wtOilHeatingBoiler1’, ‘wtOther1’,
- ‘wtSolarHeating1’]] = pd.get_dummies(GEM[‘waterHeaterTypesA’])
- GEM[[‘wtCentralHeating2’,‘wtFlowWaterHeating2’,‘wtGas2’,‘wtOilHeatingBoiler2’, ‘wtSolarHeating2’]] = pd.get_dummies(GEM[‘waterHeaterTypesB’])
- GEM[[‘wtFlowWaterHeating3’,‘wtSolarHeating3’]] = pd.get_dummies(GEM[‘waterHeaterTypesC’])
- #Summing the commom categories into one column
- GEM[‘waterHeatingTypeCentralHeating’] = GEM[‘wtCentralHeating1’] + GEM[‘wtCentralHeating2’]
- GEM[‘waterHeatingTypeFlowWaterHeating’] = GEM[‘wtFlowWaterHeating1’] + GEM[‘wtFlowWaterHeating2’] + GEM[‘wtFlowWaterHeating3’]
- GEM[‘waterHeatingTypeGas’] = GEM[‘wtGas1’] + GEM[‘wtGas2’]
- GEM[‘waterHeatingTypeOilHeatingBoiler’] = GEM[‘wtOilHeatingBoiler1’] + GEM[‘wtOilHeatingBoiler2’]
- GEM[‘waterHeatingTypeOther’] = GEM[‘wtOther1’]
- GEM[‘waterHeatingTypeSolarHeating’] = GEM[‘wtSolarHeating1’] + GEM[‘wtSolarHeating2’] + GEM[‘wtSolarHeating3’]
- #Dropping intermediate columns
- GEM = GEM.drop([‘waterHeaterTypesA’, ‘waterHeaterTypesB’, ‘waterHeaterTypesC’,‘wtCentralHeating1’, ‘wtFlowWaterHeating1’, ‘wtGas1’, ‘wtOilHeatingBoiler1’, ‘wtOther1’, ‘wtSolarHeating1’, ‘wtCentralHeating2’, ‘wtFlowWaterHeating2’, ‘wtGas2’, ‘wtOilHeatingBoiler2’, ‘wtSolarHeating2’, ‘wtFlowWaterHeating3’, ‘wtSolarHeating3’],axis = 1)
- GEM
- #Dropping the two original categorical columns
- GEM = GEM.drop([‘heatingTypes’, ‘waterHeaterTypes’],axis = 1)
- GEM
- #The next variables do not have more than one info per cell
- #Getting dummies for home type
- pd.get_dummies(GEM[‘homeType’])
- GEM[[‘homeTypeMultiFamily’,‘homeTypeSingleFamily’]] = pd.get_dummies(GEM[‘homeType’])
- #Getting dummies for cooling type
- pd.get_dummies(GEM[‘coolingType’])
- GEM[[‘coolingTypeCentralAirConditioner’,‘coolingTypeGeothermal’, ‘coolingTypeNone’,‘coolingTypePortableAirConditioner’]] = pd.get_dummies(GEM[‘coolingType’])
- #Dropping the original columns
- GEM = GEM.drop([‘homeType’, ‘coolingType’],axis = 1)
- #Sorting rows by user id and date
- GEM = GEM.sort_values([‘userId’, ‘date’])
- #Creating a new variable, subtracting the energy value from the previous column, so we have the energy consumed, instead of the
- #energy accumulated
- GEM[‘energyUsage’] = GEM[‘energy’].diff()
- GEM
- GEM.isnull().sum().sum()
- #We need to delete the first row of every smart meter, because we do not have the previous value to subtract
- GEM[‘num_in_group’] = GEM.groupby(‘userId’).cumcount()
- GEM = GEM[GEM[‘num_in_group’] > 0]
- GEM
- GEM[‘numberOfPeople’].value_counts()
- GEM[‘numberOfChildren’].value_counts()
- #We need to transform ‘number of people’ and ‘number of children’ into integers.
- #First we deal with the ‘8 + ’ and ‘7 + ’ issue.
- GEM[‘nPeople’] = [8 if a == ‘8 + ’ else a for a in GEM[‘numberOfPeople’]]
- GEM[‘nChildren’] = [7 if a == ‘7 + ’ else a for a in GEM[‘numberOfChildren’]]
- #Then we change the data type
- GEM[‘nPeople’] = GEM[‘nPeople’].astype(int)
- GEM[‘nChildren’] = GEM[‘nChildren’].astype(int)
- #Finally we delete the original columns, including the original energy column
- GEM = GEM.drop([‘energy’,
- ‘numberOfPeople’,
- ‘numberOfChildren’,‘num_in_group’],axis = 1)
- GEM
- #Shifting the columns’ order to have the energy as the last column
- cols = GEM.columns.tolist()
- cols
- cols = [‘userId’, ‘date’, ‘dates’, ‘squareMeters’, ‘nPeople’, ‘nChildren’, ELECTRIC_VEHICLE’, ‘TV’, ‘DISH_WASHER’, ‘ELECTRIC_HEATING’, ‘SAUNA’, ‘HEAT_PUMP’, ‘CABLE_BOX’, ‘FRIDGE_COMBO’, ‘COFFEE_MACHINE’, ‘TUMBLE_DRYER’, ‘FREEZER’, ‘POOL_PUMP’, ‘HOB’, ‘WASHING_MACHINE’, ‘GAME_CONSOLE’, ‘REFRIGERATOR’, ‘FLOW_WATER_HEATER’, ‘TOASTER’, ‘HOME_BATTERY’, ‘MICROWAVE’, ‘IRON’, ‘TABLET’, ‘HEATING_FAN’, ‘GRILL’, ‘DVD’, ‘COMPUTER’, ‘OVEN’, ‘ELECTRIC_SHOWER’, ‘KETTLE’, ‘OTHERS’, ‘heatingTypeCentral’, ‘heatingTypeElectric’, ‘heatingTypeGas’, ‘heatingTypeHeat_Pump’, ‘heatingTypeOil’, ‘heatingTypeOther’, ‘heatingTypePellet’, ‘heatingTypePortable_Electric’, ‘heatingTypeWood’, ‘waterHeatingTypeCentralHeating’, ‘waterHeatingTypeFlowWaterHeating’, ‘waterHeatingTypeGas’, ‘waterHeatingTypeOilHeatingBoiler’, ‘waterHeatingTypeOther’, ‘waterHeatingTypeSolarHeating’, ‘homeTypeMultiFamily’, ‘homeTypeSingleFamily’, ‘coolingTypeCentralAirConditioner’, ‘coolingTypeGeothermal’, ‘coolingTypeNone’, ‘coolingTypePortableAirConditioner’, ‘energyUsage’]
- GEM = GEM[cols]
- GEM
- #Now all the data types are correct
- #pd.set_option(‘display.max_rows’, None)
- df1 = pd.DataFrame(GEM)
- print (df1.dtypes)
- # Define the function to calculate the sMAPE
- #import numpy as np
- def smape(a, f):
- return 1/len(a) * np.sum(200 * np.abs(f-a) / (np.abs(a) + np.abs(f)))
- #importing tools to forecast
- import os
- import statsmodels as sm
- from statsmodels.tsa.api import ExponentialSmoothing, SimpleExpSmoothing, Holt
- from statsmodels.tsa.arima.model import ARIMA
- %matplotlib inline
- #Sorting the rows by date, to set the dates as index
- GEM = GEM.sort_values(by = [‘dates’, ‘userId’])
- #indexing
- GEM = GEM.set_index(GEM[‘dates’])
- GEM = GEM.sort_index()
- GEM
- #Checking how many rows we have for each smart meter
- pd.set_option(‘display.max_rows’, 10)
- GEM[‘userId’].value_counts(sort = False)
- #Creating a new database, dropping smart meters with less than 900 rows
- GEM2 = GEM[GEM.groupby(‘userId’).userId.transform(‘count’) > 900].copy()
- GEM2[‘userId’].value_counts(sort = False)
- #We now have 277 smart meters
- #Splitting the dataset into two slices (test and train) to feed in the forecast models
- GEM_test2 = GEM2[‘2020–05−01’:‘2020–10−31’]
- GEM_train2 = GEM2[‘2017–11−02’:‘2020–04−30’]
- #Checking if the two slices have the same number of unique smart meters
- GEM_test2[‘userId’].nunique()
- GEM_train2[‘userId’].nunique()
- #Creating a smart meters’ list to be used in forecast loops
- uniqueIds = list(set(GEM_train2[‘userId’]))
- nIds = len(uniqueIds)
- nIds
- #Naive forecasts (baseline)
- #creating the error’s recording table
- smapesNaiveTable = pd.DataFrame(columns = [‘Id’, ‘sMAPE_nf’])
- RMSENaiveTable = pd.DataFrame(columns = [‘Id’, ‘RMSE_nf’])
- #Setting loop
- for x in uniqueIds:
- #filtering for every smart meter
- GEM_train2x = GEM_train2.loc[GEM_train2[‘userId’] == x]
- GEM_test2x = GEM_test2.loc[GEM_test2[‘userId’] == x]
- #setting the number of forecasts
- n_train = len(GEM_train2x)
- n_test = len(GEM_test2x)
- #Setting the frequency of the data
- GEM_train2x.index = pd.DatetimeIndex(GEM_train2x.index.values,
- freq = GEM_train2x.index.inferred_freq)
- #applying the forecast model
- y_hat_naive = GEM_test2x.copy()
- y_hat_naive[‘naive_forecast’] = GEM_train2x[‘energyUsage’][n_train−1]
- #getting the error value
- sMAPE_nf= smape(GEM_test2x[‘energyUsage’].values,y_hat_naive[‘naive_forecast’].values)
- RMSE_nf= rmse(GEM_test2x[‘energyUsage’].values,y_hat_naive[‘naive_forecast’].values, squared = False)
- #recording the error value
- smapesNaiveTable = smapesNaiveTable.append({‘Id’: x, ‘sMAPE_nf’: sMAPE_nf},ignore_index = True)
- RMSENaiveTable = RMSENaiveTable.append({‘Id’: x, ‘RMSE_nf’: RMSE_nf},ignore_index = True)
- print(smapesNaiveTable)
- #IdMean = GEMx[‘energyUsage’].mean()
- smapesNaiveTable.describe()
- RMSENaiveTable.describe()
- RMSENaiveTable
- #Moving Average forecasts
- #creating the error’s recording table
- smapesTable = pd.DataFrame(columns = [‘Id’, ‘sMAPE_ma’])
- RMSETable = pd.DataFrame(columns = [‘Id’, ‘RMSE_ma’])
- #Setting loop
- for x in uniqueIds:
- #filtering for every smart meter
- GEM_train2x = GEM_train2.loc[GEM_train2[‘userId’] == x]
- GEM_test2x = GEM_test2.loc[GEM_test2[‘userId’] == x]
- #setting the number of forecasts
- n_train = len(GEM_train2x)
- n_test = len(GEM_test2x)
- #Setting the frequency of the data
- GEM_train2x.index = pd.DatetimeIndex(GEM_train2x.index.values,
- freq = GEM_train2x.index.inferred_freq)
- #applying the forecast model
- y_hat_ma = GEM_test2x.copy()
- model = ARIMA(GEM_train2x[‘energyUsage’], order = (1, 0, 0))
- model_fit = model.fit()
- y_hat_ma = model_fit.forecast(n_test)
- #getting the error value
- sMAPE_ma= smape(GEM_test2x[‘energyUsage’].values,y_hat_ma.values)
- RMSE_ma = rmse(GEM_test2x[‘energyUsage’].values,y_hat_ma.values, squared = False)
- #recording the error value
- smapesTable = smapesTable.append({‘Id’: x, ‘sMAPE_ma’: sMAPE_ma},ignore_index = True)
- RMSETable = RMSETable.append({‘Id’: x, ‘RMSE_ma’: RMSE_ma},ignore_index = True)
- print(smapesTable)
- #IdMean = GEMx[‘energyUsage’].mean()
- #Getting the mean error value
- MeanSmapeMA = smapesTable[‘sMAPE_ma’].mean()
- MeanSmapeMA
- MeanRMSEMA= RMSETable[‘RMSE_ma’].mean()
- MeanRMSEMA
- RMSETable.describe()
- #Arima forecasts
- #creating the error’s recording table
- smapesTable1 = pd.DataFrame(columns = [‘Id’, ‘sMAPE_arima’])
- RMSETable1 = pd.DataFrame(columns = [‘Id’, ‘RMSE_arima’])
- #Setting loop
- for x in uniqueIds:
- #filtering for every smart meter
- GEM_train2x = GEM_train2.loc[GEM_train2[‘userId’] == x]
- GEM_test2x = GEM_test2.loc[GEM_test2[‘userId’] == x]
- #setting the number of forecasts
- n_train = len(GEM_train2x)
- n_test = len(GEM_test2x)
- #Setting the frequency of the data
- GEM_train2x.index = pd.DatetimeIndex(GEM_train2x.index.values,
- freq = GEM_train2x.index.inferred_freq)
- #applying the forecast model
- model = ARIMA(GEM_train2x[‘energyUsage’], order = (1,1,1))
- model_fit = model.fit()
- y_hat_arima = model_fit.forecast(n_test)
- #getting the error value
- sMAPE_arima= smape(GEM_test2x[‘energyUsage’].values,y_hat_arima.values)
- RMSE_arima= rmse(GEM_test2x[‘energyUsage’].values,y_hat_arima.values, squared = False)
- #recording the error value
- smapesTable1 = smapesTable1.append({‘Id’: x, ‘sMAPE_arima’: sMAPE_arima},ignore_index = True)
- RMSETable1 = RMSETable1.append({‘Id’: x, ‘RMSE_arima’: RMSE_arima},ignore_index = True)
- print(smapesTable1)
- #Getting the mean error value
- MeanSmapeARIMA = smapesTable1[‘sMAPE_arima’].mean()
- MeanSmapeARIMA
- RMSETable1.describe()
- #Exponential Smoothing Forecasts -> Auto parameter optimization
- #creating the error’s recording table
- smapesTable2 = pd.DataFrame(columns = [‘Id’, ‘sMAPE_ES’])
- RMSETable2 = pd.DataFrame(columns = [‘Id’, ‘RMSE_ES’])
- #Setting loop
- for x in uniqueIds:
- #filtering for every smart meter
- GEM_train2x = GEM_train2.loc[GEM_train2[‘userId’] == x]
- GEM_test2x = GEM_test2.loc[GEM_test2[‘userId’] == x]
- #setting the number of forecasts
- n_train = len(GEM_train2x)
- n_test = len(GEM_test2x)
- #Setting the frequency of the data
- GEM_train2x.index = pd.DatetimeIndex(GEM_train2x.index.values,
- freq = GEM_train2x.index.inferred_freq)
- #applying the forecast model
- fit3 = SimpleExpSmoothing(GEM_train2x[‘energyUsage’], initialization_method = “estimated”).fit()
- fcast3 = fit3.forecast(n_test).rename(r”$\alpha = %s$” % fit3.model.params[“smoothing_level”])
- #getting the error value
- sMAPE_es= smape(GEM_test2x[‘energyUsage’].values,fcast3.values)
- RMSE_es= rmse(GEM_test2x[‘energyUsage’].values,fcast3.values, squared = False)
- #recording the error value
- smapesTable2 = smapesTable2.append({‘Id’: x, ‘sMAPE_ES’: sMAPE_es},ignore_index = True)
- RMSETable2 = RMSETable2.append({‘Id’: x, ‘RMSE_ES’: RMSE_es},ignore_index = True)
- print(smapesTable2)
- #Getting the mean error value
- MeanSmapeSES = smapesTable2[‘sMAPE_ES’].mean()
- MeanSmapeSES
- #Import tools for Neural Network forecasts
- import tensorflow as tf
- from tensorflow.keras.models import Sequential
- from tensorflow.keras.layers import Dense
- from tensorflow.keras.layers import LSTM
- from sklearn.preprocessing import MinMaxScaler
- from sklearn.metrics import mean_squared_error
- #Neural Network with LSTM Recurrent Neural Networks forecasts
- #creating the error’s recording table
- smapesTable3 = pd.DataFrame(columns = [‘Id’, ‘sMAPE_NN’])
- RMSETable3 = pd.DataFrame(columns = [‘Id’, ‘RMSE_NN’])
- #Setting a specific database to this forecast
- GEMNN= pd.DataFrame()
- GEMNN[[‘userId’, ‘Energy’]] = GEM2[[‘userId’, ‘energyUsage’]]
- scaler = MinMaxScaler(feature_range = (0, 1))
- #GEMNN = scaler.fit_transform(GEMNN)
- sm = 1
- #Setting loop
- for x in uniqueIds:
- #filtering for every smart meter
- GEMNNx = GEMNN.loc[GEMNN[‘userId’] == x]
- GEMNNx = GEMNNx.drop([‘userId’],axis = 1)
- GEMNNx = GEMNNx.reset_index(drop = True)
- GEMNNx = scaler.fit_transform(GEMNNx)
- #setting the number of forecasts
- train_size = int(len(GEMNNx) * 0.80)
- test_size = len(GEMNNx) - train_size
- train, test = GEMNNx [0:train_size], GEMNNx[train_size:len(GEMNNx)]
- #print(len(train), len(test))
- #print(train [1:2], test [1:2])
- #Building the datasets that will feed the model
- dataX, dataY = [], []
- for i in range(len(train)−2):
- a = train[i:i + 1]
- b = train[i + 1:i + 2]
- dataX.append(a)
- dataY.append(b)
- trainX, trainY = np.array(dataX), np.array(dataY)
- trainY3d = np.vstack(trainY)
- trainY2d = np.ravel(trainY3d)
- #print(trainY2d)
- dataU, dataV = [], []
- for i in range(len(test)−2):
- c = test[i:i + 1]
- d = test[i + 1:i + 2]
- dataU.append(c)
- dataV.append(d)
- testX, testY = np.array(dataU), np.array(dataV)
- testY3d = np.vstack(testY)
- testY2d = np.ravel(testY3d)
- #print(testY2d)
- #Reshape the datasets to feed the model
- trainX = np.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))
- testX = np.reshape(testX, (testX.shape[0], 1, testX.shape[1]))
- #applying the forecast model
- look_back = 1
- model = Sequential()
- model.add(LSTM(4, input_shape = (1, look_back)))
- model.add(Dense(1))
- model.compile(loss = ‘mean_squared_error’, optimizer = ‘adam’)
- model.fit(trainX, trainY, epochs = 150, batch_size = 1, verbose = 2)#epochs = 100 is the real deal
- # make predictions
- trainPredict = model.predict(trainX)
- testPredict = model.predict(testX)
- # invert predictions
- trainPredict = scaler.inverse_transform(trainPredict)
- trainY2d = scaler.inverse_transform([trainY2d]) #have to fix it, originally it was trainY, but the array dimension was wrong
- testPredict = scaler.inverse_transform(testPredict)
- testY2d = scaler.inverse_transform([testY2d]) #have to fix it, originally it was testY, but the array dimension was wrong
- # calculate root mean squared error
- #trainScore = np.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
- #print(‘Train Score: %.2f RMSE’ % (trainScore))
- #testScore = np.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
- #print(‘Test Score: %.2f RMSE’ % (testScore))
- #getting the error value
- sMAPE_nn= smape(testY2d[0], testPredict[:,0])
- RMSE_nn= rmse(testY2d[0], testPredict[:,0], squared = False)
- #recording the error value
- smapesTable3 = smapesTable3.append({‘Id’: x, ‘sMAPE_NN’: sMAPE_nn},ignore_index = True)
- RMSETable3 = RMSETable3.append({‘Id’: x, ‘RMSE_NN’: RMSE_nn},ignore_index = True)
- print(‘Smart Meter number:’, sm)
- sm = sm + 1
- print(smapesTable3)
- #Getting the mean error value
- MeanSmapeNN = smapesTable3[‘sMAPE_NN’].mean()
- print(MeanSmapeNN)
- print(smapesTable3)
- #Getting the mean error value
- MeanSmapeNN = smapesTable3[‘sMAPE_NN’].mean()
- MeanSmapeNN
- #Random Forest Imports and function definitions
- from numpy import asarray
- from pandas import DataFrame
- from pandas import concat
- from sklearn.metrics import mean_absolute_error
- from sklearn.ensemble import RandomForestRegressor
- # transform a time series dataset into a supervised learning dataset
- def series_to_supervised(data, n_in = 1, n_out = 1, dropnan = True):
- n_vars = 1 if type(data) is list else data.shape[1]
- df = DataFrame(data)
- cols = list()
- # input sequence (t-n, ... t−1)
- for i in range(n_in, 0, −1):
- cols.append(df.shift(i))
- # forecast sequence (t, t + 1, ... t + n)
- for i in range(0, n_out):
- cols.append(df.shift(-i))
- # put it all together
- agg = concat(cols, axis = 1)
- # drop rows with NaN values
- if dropnan:
- agg.dropna(inplace = True)
- return agg.values
- # split a univariate dataset into train/test sets
- def train_test_split(data, n_test):
- return data[:-n_test, :], data[-n_test:, :]
- # fit an random forest model and make a one step prediction
- def random_forest_forecast(train, testX):
- # transform list into array
- train = asarray(train)
- # split into input and output columns
- trainX, trainy = train[:, :−1], train[:, −1]
- # fit model
- model = RandomForestRegressor(n_estimators = 1000)
- model.fit(trainX, trainy)
- # make a one-step prediction
- yhat = model.predict([testX])
- return yhat[0]
- # walk-forward validation for univariate data
- def walk_forward_validation(data, n_test):
- predictions = list()
- # split dataset
- train, test = train_test_split(data, n_test)
- # seed history with training dataset
- history = [x for x in train]
- # step over each time-step in the test set
- for i in range(len(test)):
- # split test row into input and output columns
- testX, testy = test[i, :−1], test[i, −1]
- # fit model on history and make a prediction
- yhat = random_forest_forecast(history, testX)
- # store forecast in list of predictions
- predictions.append(yhat)
- # add actual observation to history for the next loop
- history.append(test[i])
- # summarize progress
- #print(‘ > expected = %.1f, predicted = %.1f’ % (testy, yhat))
- # estimate prediction error
- error = smape(test[:, −1], predictions)
- error2 = rmse(test[:, −1], predictions, squared = False)
- return error, error2, test[:, −1], predictions
- #Random Forest forecasts
- #creating the error’s recording table
- smapesTable4 = pd.DataFrame(columns = [‘Id’, ‘sMAPE_RF’])
- RMSETable4 = pd.DataFrame(columns = [‘Id’, ‘RMSE_RF’])
- #Setting a specific database to this forecast
- GEMRF= pd.DataFrame()
- GEMRF[[‘userId’, ‘Energy’]] = GEM2[[‘userId’, ‘energyUsage’]]
- sm = 1
- #Setting loop
- for x in uniqueIds:
- #filtering for every smart meter
- GEMRFx = GEMRF.loc[GEMRF[‘userId’] == x]
- GEMRFx = GEMRFx.drop([‘userId’],axis = 1)
- GEMRFx = GEMRFx.reset_index(drop = True)
- values =GEMRFx.values
- # transform the time series data into supervised learning
- data = series_to_supervised(values, n_in = 10)#n_in = 6 originally
- # evaluate and getting the error value
- smape_rf,rmse_rf, y, yhat = walk_forward_validation(data, 12)
- #recording the error value
- smapesTable4 = smapesTable4.append({‘Id’: x, ‘sMAPE_RF’: smape_rf},ignore_index = True)
- RMSETable4 = RMSETable4.append({‘Id’: x, ‘RMSE_RF’: rmse_rf},ignore_index = True)
- print(‘Smart Meter number:’, sm)
- sm = sm + 1
- print(smapesTable4)
- #Getting the mean error value
- MeanSmapeRF = smapesTable4[‘sMAPE_RF’].mean()
- MeanSmapeRF
- RMSETable4.describe()
- #Naive forecast to be a baseline and compare with the other methods.
- smapesTable = smapesTable.merge(smapesTable1, how = ‘left’, on = ‘Id’)
- smapesTable = smapesTable.merge(smapesTable2, how = ‘left’, on = ‘Id’)
- smapesTable = smapesTable.merge(smapesTable3, how = ‘left’, on = ‘Id’)
- smapesTable = smapesTable.merge(smapesTable4, how = ‘left’, on = ‘Id’)
- smapesTable = smapesTable.merge(smapesNaiveTable, how = ‘left’, on = ‘Id’)
- smapesTable
- smapesTable.describe()
- RMSETable = RMSETable.merge(RMSETable1, how = ‘left’, on = ‘Id’)
- RMSETable = RMSETable.merge(RMSETable2, how = ‘left’, on = ‘Id’)
- RMSETable = RMSETable.merge(RMSETable3, how = ‘left’, on = ‘Id’)
- RMSETable = RMSETable.merge(RMSETable4, how = ‘left’, on = ‘Id’)
- RMSETable = RMSETable.merge(RMSENaiveTable, how = ‘left’, on = ‘Id’)
- RMSETable
- RMSETable.describe()
References
- Kagermann, H.; Helbig, J.; Hellinger, A.; Wahlster, W. Recommendations for Implementing the Strategic Initiative INDUSTRIE 4.0: Securing the Future of German Manufacturing Industry; Final Report of the Industrie 4.0 Working Group: Berlin, Germany, 2013. [Google Scholar]
- Schwab, K. The Fourth Industrial Revolution; Currency: New York, NY, USA, 2017. [Google Scholar]
- Fettermann, D.C.; Cavalcante, C.G.S.; de Almeida, T.D.; Tortorella, G.L. How Does Industry 4.0 Contribute to Operations Management? J. Ind. Prod. Eng. 2018, 35, 255–268. [Google Scholar] [CrossRef]
- Li, L. China’s Manufacturing Locus in 2025: With a Comparison of “Made-in-China 2025” and “Industry 4.0”. Technol. Forecast. Soc. Chang. 2018, 135, 66–74. [Google Scholar] [CrossRef]
- Lee, J.; Bagheri, B.; Kao, H.-A. A Cyber-Physical Systems Architecture for Industry 4.0-Based Manufacturing Systems. Manuf. Lett. 2015, 3, 18–23. [Google Scholar] [CrossRef]
- Demir, K.A.; Döven, G.; Sezen, B. Industry 5.0 and Human-Robot Co-Working. Procedia. Comput. Sci. 2019, 158, 688–695. [Google Scholar] [CrossRef]
- Leusin, M.; Frazzon, E.; Uriona Maldonado, M.; Kück, M.; Freitag, M. Solving the Job-Shop Scheduling Problem in the Industry 4.0 Era. Technologies 2018, 6, 107. [Google Scholar] [CrossRef]
- Frazzon, E.M.; Kück, M.; Freitag, M. Data-Driven Production Control for Complex and Dynamic Manufacturing Systems. CIRP Annals 2018, 67, 515–518. [Google Scholar] [CrossRef]
- Davis, J.; Edgar, T.; Porter, J.; Bernaden, J.; Sarli, M. Smart Manufacturing, Manufacturing Intelligence and Demand-Dynamic Performance. Comput. Chem. Eng. 2012, 47, 145–156. [Google Scholar] [CrossRef]
- Shrouf, F.; Miragliotta, G. Energy Management Based on Internet of Things: Practices and Framework for Adoption in Production Management. J. Clean. Prod. 2015, 100, 235–246. [Google Scholar] [CrossRef]
- Ren, A.; Wu, D.; Zhang, W.; Terpenny, J.; Liu, P. Cyber Security in Smart Manufacturing: Survey and Challenges. In Proceedings of the InIIE Annual Conference, Pittsburgh, PA, USA, 20–23 May 2017; pp. 716–721. [Google Scholar]
- Dou, R.; Nan, G. Optimizing Sensor Network Coverage and Regional Connectivity in Industrial IoT Systems. IEEE Syst. J. 2017, 11, 1351–1360. [Google Scholar] [CrossRef]
- Chang, S.-I.; Chang, I.-C.; Li, H.-J.; He, T.-H. The Study of Intelligent Manufacturing Internal Control Mechanism by Using a Perspective of the Production Cycle. J. Ind. Prod. Eng. 2014, 31, 119–127. [Google Scholar] [CrossRef]
- Jha, A.; Pratihar, D.K.; Tiwari, M.K. Many-Objective Energy Efficient Scheduling with Load Management in Intelligent Manufacturing Systems. In Proceedings of the InIIE Annual Conference, Pittsburgh, PA, USA, 20–23 May 2017; pp. 151–156. [Google Scholar]
- Evans, P.C.; Annunziata, M. Industrial Internet. Push. Boundaries Minds Mach. 2012, 26. Available online: http://energyoutlook2013.naseo.org/presentations/Evans.pdf (accessed on 7 October 2022).
- Lăzăroiu, G.; Ionescu, L.; Andronie, M.; Dijmărescu, I. Sustainability Management and Performance in the Urban Corporate Economy: A Systematic Literature Review. Sustainability 2020, 12, 7705. [Google Scholar] [CrossRef]
- European Commission, Directorate-General for Communication. European Commission Digital Agenda for Europe: Rebooting Europe’s Economy; Publications Office: Luxembourg, 2014. [Google Scholar]
- Pathik, N.; Gupta, R.K.; Sahu, Y.; Sharma, A.; Masud, M.; Baz, M. AI Enabled Accident Detection and Alert System Using IoT and Deep Learning for Smart Cities. Sustainability 2022, 14, 7701. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, J.-Y. How Should the Structure of Smart Cities Change to Predict and Overcome a Pandemic? Sustainability 2022, 14, 2981. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, D.; Liu, Z.; Osmani, M.; Demian, P. Construction 4.0, Industry 4.0, and Building Information Modeling (BIM) for Sustainable Building Development within the Smart City. Sustainability 2022, 14, 10028. [Google Scholar] [CrossRef]
- Nascimento, D.R.; Tortorella, G.L.; Fettermann, D. Association between the Benefits and Barriers Perceived by the Users in Smart Home Services Implementation. Kybernetes 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Arif, A.; Alghamdi, T.A.; Khan, Z.A.; Javaid, N. Towards Efficient Energy Utilization Using Big Data Analytics in Smart Cities for Electricity Theft Detection. Big Data Res. 2022, 27, 100285. [Google Scholar] [CrossRef]
- Cortese, T.T.P.; de Almeida, J.F.S.; Batista, G.Q.; Storopoli, J.E.; Liu, A.; Yigitcanlar, T. Understanding Sustainable Energy in the Context of Smart Cities: A PRISMA Review. Energies 2022, 15, 2382. [Google Scholar] [CrossRef]
- Shokry, M.; Awad, A.I.; Abd-Ellah, M.K.; Khalaf, A.A.M. Systematic Survey of Advanced Metering Infrastructure Security: Vulnerabilities, Attacks, Countermeasures, and Future Vision. Future Gener. Comput. Syst. 2022, 136, 358–377. [Google Scholar] [CrossRef]
- Yang, B.; Liu, S.; Gaterell, M.; Wang, Y. Smart Metering and Systems for Low-Energy Households: Challenges, Issues and Benefits. Adv. Build. Energy Res. 2019, 13, 80–100. [Google Scholar] [CrossRef]
- Quilumba, F.L.; Lee, W.-J.; Huang, H.; Wang, D.Y.; Szabados, R.L. Using Smart Meter Data to Improve the Accuracy of Intraday Load Forecasting Considering Customer Behavior Similarities. IEEE Trans. Smart Grid 2015, 6, 911–918. [Google Scholar] [CrossRef]
- Arora, S.; Taylor, J.W. Forecasting Electricity Smart Meter Data Using Conditional Kernel Density Estimation. Omega 2016, 59, 47–59. [Google Scholar] [CrossRef]
- Fekri, M.N.; Patel, H.; Grolinger, K.; Sharma, V. Deep Learning for Load Forecasting with Smart Meter Data: Online Adaptive Recurrent Neural Network. Appl. Energy 2021, 282, 116177. [Google Scholar] [CrossRef]
- ben Taieb, S.; Taylor, J.W.; Hyndman, R.J. Hierarchical Probabilistic Forecasting of Electricity Demand With Smart Meter Data. J. Am. Stat. Assoc. 2021, 116, 27–43. [Google Scholar] [CrossRef]
- Haq, E.U.; Huang, J.; Xu, H.; Li, K.; Ahmad, F. A Hybrid Approach Based on Deep Learning and Support Vector Machine for the Detection of Electricity Theft in Power Grids. Energy Rep. 2021, 7, 349–356. [Google Scholar] [CrossRef]
- Avancini, D.B.; Rodrigues, J.J.P.C.; Martins, S.G.B.; Rabêlo, R.A.L.; Al-Muhtadi, J.; Solic, P. Energy Meters Evolution in Smart Grids: A Review. J. Clean. Prod. 2019, 217, 702–715. [Google Scholar] [CrossRef]
- Gumz, J.; Fettermann, D.C.; Sant’Anna, Â.M.O.; Tortorella, G.L. Social Influence as a Major Factor in Smart Meters’ Acceptance: Findings from Brazil. Results Eng. 2022, 15, 100510. [Google Scholar] [CrossRef]
- Andronie, M.; Lăzăroiu, G.; Ștefănescu, R.; Uță, C.; Dijmărescu, I. Sustainable, Smart, and Sensing Technologies for Cyber-Physical Manufacturing Systems: A Systematic Literature Review. Sustainability 2021, 13, 5495. [Google Scholar] [CrossRef]
- Porter, M.E.; Heppelmann, J.E. How Smart, Connected Products Are Transforming Competition. Harv. Bus. Rev. 2014, 92, 64–88. [Google Scholar]
- Kaur, M.; Mathew, L.; Alokdeep, A.; Kumar, A. Implementation of Smart Metering Based on Internet of Things. In IOP Conference Series: Materials Science and Engineering, Proceedings of the 3rd International Conference on Communication Systems (ICCS-2017); Rajasthan, India, 14–16 October 2017, Institute of Physics Publishing: Bristol, UK, 2018; Volume 331. [Google Scholar]
- Lloret, J.; Tomas, J.; Canovas, A.; Parra, L. An Integrated IoT Architecture for Smart Metering. IEEE Commun. Mag. 2016, 54, 50–57. [Google Scholar] [CrossRef]
- March, H.; Morote, Á.-F.; Rico, A.-M.; Saurí, D. Household Smart Water Metering in Spain: Insights from the Experience of Remote Meter Reading in Alicante. Sustainability 2017, 9, 582. [Google Scholar] [CrossRef]
- Boyle, T.; Giurco, D.; Mukheibir, P.; Liu, A.; Moy, C.; White, S.; Stewart, R. Intelligent Metering for Urban Water: A Review. Water 2013, 5, 1052–1081. [Google Scholar] [CrossRef]
- Michaels, L.; Parag, Y. Motivations and Barriers to Integrating ‘Prosuming’ Services into the Future Decentralized Electricity Grid: Findings from Israel. Energy Res. Soc. Sci. 2016, 21, 70–83. [Google Scholar] [CrossRef]
- Silvast, A.; Williams, R.; Hyysalo, S.; Rommetveit, K.; Raab, C. Who “uses” Smart Grids? The Evolving Nature of User Representations in Layered Infrastructures. Sustainability 2018, 10, 3738. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pörtner, H.-O.; Roberts, D.; Skea, J.; Shukla, P.R.; Pirani, A.; Moufouma-Okia, W.; Péan, C.; Pidcock, R.; et al. (Eds.) IPCC Summary for Policymakers. In Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change; World Meteorological Organization: Geneva, Switzerland, 2018; pp. 3–35. [Google Scholar]
- Moser, C. The Role of Perceived Control over Appliances in the Acceptance of Electricity Load-Shifting Programmes. Energy Effic. 2017, 10, 1115–1127. [Google Scholar] [CrossRef]
- Faruqui, A.; Harris, D.; Hledik, R. Unlocking the €53 Billion Savings from Smart Meters in the EU: How Increasing the Adoption of Dynamic Tariffs Could Make or Break the EU’s Smart Grid Investment. Energy Policy 2010, 38, 6222–6231. [Google Scholar] [CrossRef]
- Weron, R. Electricity Price Forecasting: A Review of the State-of-the-Art with a Look into the Future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Aggarwal, S.K.; Saini, L.M.; Kumar, A. Electricity Price Forecasting in Deregulated Markets: A Review and Evaluation. Int. J. Electr. Power Energy Syst. 2009, 31, 13–22. [Google Scholar] [CrossRef]
- Peng, Y.; Dong, M.; Zuo, M.J. Current Status of Machine Prognostics in Condition-Based Maintenance: A Review. Int. J. Adv. Manuf. Technol. 2010, 50, 297–313. [Google Scholar] [CrossRef]
- Gao, R.; Wang, L.; Teti, R.; Dornfeld, D.; Kumara, S.; Mori, M.; Helu, M. Cloud-Enabled Prognosis for Manufacturing. CIRP Ann. 2015, 64, 749–772. [Google Scholar] [CrossRef]
- Syntetos, A.A.; Babai, Z.; Boylan, J.E.; Kolassa, S.; Nikolopoulos, K. Supply Chain Forecasting: Theory, Practice, Their Gap and the Future. Eur. J. Oper. Res. 2016, 252, 1–26. [Google Scholar] [CrossRef]
- Kück, M.; Freitag, M. Forecasting of Customer Demands for Production Planning by Local K-Nearest Neighbor Models. Int. J. Prod. Econ. 2021, 231, 107837. [Google Scholar] [CrossRef]
- Khan, A.R.; Mahmood, A.; Safdar, A.; Khan, Z.A.; Khan, N.A. Load Forecasting, Dynamic Pricing and DSM in Smart Grid: A Review. Renew. Sustain. Energy Rev. 2016, 54, 1311–1322. [Google Scholar] [CrossRef]
- Hong, T.; Fan, S. Probabilistic Electric Load Forecasting: A Tutorial Review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Tajeuna, E.G.; Bouguessa, M.; Wang, S. A Network-Based Approach to Enhance Electricity Load Forecasting. In Proceedings of the 2018 IEEE International Conference on Data Mining Workshops (ICDMW), Singapore, 17 November 2018; pp. 266–275. [Google Scholar]
- Du, D.; Xie, J.; Fu, Z. Short-Term Power Load Forecasting Based on Spark Platform and Improved Parallel Ridge Regression Algorithm. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 8951–8956. [Google Scholar]
- Chen, W.; Xiao, Y.; Deng, J.; Li, F.; Guo, B.; Zhang, F.; Xu, L. Improved Bayesian Ridge Regression Based Data Missing Reconstruction of Smart Meters. In Proceedings of the 2nd International Conference on Internet of Things and Smart City (IoTSC 2022), Xiamen, China, 18–20 February 2022; Ye, X., Falcone, F., Cui, H., Eds.; SPIE: Bellingham, WA, USA, 2022; p. 57. [Google Scholar]
- Kallitsis, M.G.; Michailidis, G.; Tout, S. Correlative Monitoring for Detection of False Data Injection Attacks in Smart Grids. In Proceedings of the 2015 IEEE International Conference on Smart Grid Communications (SmartGridComm), Miami, FL, USA, 2–5 November 2015; pp. 386–391. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. Adv. Neural Inf. Process. Syst. 1996, 9, 155–161. [Google Scholar]
- Rafati, A.; Joorabian, M.; Mashhour, E.; Shaker, H.R. Machine Learning-Based Very Short-Term Load Forecasting in Microgrid Environment: Evaluating the Impact of High Penetration of PV Systems. Electr. Eng. 2022, 104, 2667–2677. [Google Scholar] [CrossRef]
- Čurčić, T.; Kalloe, R.R.; Kreszner, M.A.; van Luijk, O.; Puertas Puchol, S.; Caba Batuecas, E.; Salcedo Rahola, T.B. Gaining Insights into Dwelling Characteristics Using Machine Learning for Policy Making on Nearly Zero-Energy Buildings with the Use of Smart Meter and Weather Data. J. Sustain. Dev. Energy Water Environ. Syst. 2022, 10, 1–13. [Google Scholar] [CrossRef]
- Ho, T.K. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Mai, T.T.; Nguyen, P.H.; Haque, N.A.N.M.M.; Pemen, G.A.J.M. Exploring Regression Models to Enable Monitoring Capability of Local Energy Communities for Self-management in Low-voltage Distribution Networks. IET Smart Grid 2022, 5, 25–41. [Google Scholar] [CrossRef]
- Konstantopoulos, C.; Sioutas, S.; Tsichlas, K. Machine Learning Techniques for Regression in Energy Disaggregation. In Artificial Intelligence Applications and Innovations, Proceedings of the 18th IFIP WG 12.5 International Conference, AIAI 2022, Hersonissos, Greece, 17–20 June 2022; Springer: Cham, Switzerland, 2022; Volume 646, pp. 356–366. [Google Scholar] [CrossRef]
- Makridakis, S. A Survey of Time Series. Int. Stat. Rev. 1976, 44, 29. [Google Scholar] [CrossRef]
- Pooniwala, N.; Sutar, R. Forecasting Short-Term Electric Load with a Hybrid of ARIMA Model and LSTM Network. In Proceedings of the 2021 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 27–29 January 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Shaukat, M.A.; Shaukat, H.R.; Qadir, Z.; Munawar, H.S.; Kouzani, A.Z.; Mahmud, M.A.P. Cluster Analysis and Model Comparison Using Smart Meter Data. Sensors 2021, 21, 3157. [Google Scholar] [CrossRef]
- Muneer, A.; Ali, R.F.; Almaghthawi, A.; Taib, S.M.; Alghamdi, A.; Abdullah Ghaleb, E.A. Short Term Residential Load Forecasting Using Long Short-Term Memory Recurrent Neural Network. Int. J. Electr. Comput. Eng. (IJECE) 2022, 12, 5589. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Prentice Hall: Bergen County, NJ, USA, 2009; ISBN 9780131471399. [Google Scholar]
- Luo, X.; Zhang, D. An Adaptive Deep Learning Framework for Day-Ahead Forecasting of Photovoltaic Power Generation. Sustain. Energy Technol. Assess. 2022, 52, 102326. [Google Scholar] [CrossRef]
- Haque, A.; Rahman, S. Short-Term Electrical Load Forecasting through Heuristic Configuration of Regularized Deep Neural Network. Appl. Soft. Comput. 2022, 122, 108877. [Google Scholar] [CrossRef]
- Zhang, T.; Siebers, P.O.; Aickelin, U. Simulating User Learning in Authoritative Technology Adoption: An Agent Based Model for Council-Led Smart Meter Deployment Planning in the UK. Technol. Forecast. Soc. Chang. 2016, 106, 74–84. [Google Scholar] [CrossRef]
- Geetha, R.; Ramyadevi, K.; Balasubramanian, M. Prediction of Domestic Power Peak Demand and Consumption Using Supervised Machine Learning with Smart Meter Dataset. Multimed. Tools Appl. 2021, 80, 19675–19693. [Google Scholar] [CrossRef]
- Jincheng, Y.; Zelin, G.; Tiejiang, Y.; Shangmin, Q.; Ning, L. Fault Prediction of Intelligent Electricity Meter Based on Multi-Classification Machine Learning Model. In Proceedings of the 2021 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 28–30 June 2021; pp. 293–297. [Google Scholar]
- Shearer, C. The CRISP-DM Model: The New Blueprint for Data Mining. J. Data Warehous. 2000, 5, 13–22. [Google Scholar]
- Schafer, F.; Zeiselmair, C.; Becker, J.; Otten, H. Synthesizing CRISP-DM and Quality Management: A Data Mining Approach for Production Processes. In Proceedings of the 2018 IEEE International Conference on Technology Management, Operations and Decisions (ICTMOD), Marrakech, Morocco, 21–23 November 2018; pp. 190–195. [Google Scholar]
- Schröer, C.; Kruse, F.; Gómez, J.M. A Systematic Literature Review on Applying CRISP-DM Process Model. Procedia. Comput. Sci. 2021, 181, 526–534. [Google Scholar] [CrossRef]
- Martinez-Plumed, F.; Contreras-Ochando, L.; Ferri, C.; Hernandez-Orallo, J.; Kull, M.; Lachiche, N.; Ramirez-Quintana, M.J.; Flach, P. CRISP-DM Twenty Years Later: From Data Mining Processes to Data Science Trajectories. IEEE Trans. Knowl. Data Eng. 2021, 33, 3048–3061. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H. Smart Grid Customers’ Acceptance and Engagement: An Overview. Renew. Sustain. Energy Rev. 2016, 65, 1285–1298. [Google Scholar] [CrossRef]
- Darby, S. Smart Metering: What Potential for Householder Engagement? Build. Res. Inf. 2010, 38, 442–457. [Google Scholar] [CrossRef]
- Rajamoorthy, R.; Saraswathi, H.V.; Devaraj, J.; Kasinathan, P.; Elavarasan, R.M.; Arunachalam, G.; Mostafa, T.M.; Mihet-Popa, L. A Hybrid Sailfish Whale Optimization and Deep Long Short-Term Memory (SWO-DLSTM) Model for Energy Efficient Autonomy in India by 2048. Sustainability 2022, 14, 1355. [Google Scholar] [CrossRef]
- Milojkovic, F. GEM House Opendata: German Electricity Consumption in Many Households over Three Years 2018–2020 (Fresh Energy). Available online: https://ieee-dataport.org/open-access/gem-house-opendata-german-electricity-consumption-many-households-over-three-years−2018 (accessed on 11 May 2022).
- Campillo, J.; Dahlquist, E.; Wallin, F.; Vassileva, I. Is Real-Time Electricity Pricing Suitable for Residential Users without Demand-Side Management? Energy 2016, 109, 310–325. [Google Scholar] [CrossRef]
- Wemyss, D.; Castri, R.; Cellina, F.; de Luca, V.; Lobsiger-Kägi, E.; Carabias, V. Examining Community-Level Collaborative vs. Competitive Approaches to Enhance Household Electricity-Saving Behavior. Energy Effic. 2018, 11, 2057–2075. [Google Scholar] [CrossRef]
- Ponnusamy, V.K.; Kasinathan, P.; Madurai Elavarasan, R.; Ramanathan, V.; Anandan, R.K.; Subramaniam, U.; Ghosh, A.; Hossain, E. A Comprehensive Review on Sustainable Aspects of Big Data Analytics for the Smart Grid. Sustainability 2021, 13, 13322. [Google Scholar] [CrossRef]
- Poongavanam, E.; Kasinathan, P.; Kanagasabai, K. Optimal Energy Forecasting Using Hybrid Recurrent Neural Networks. Intell. Autom. Soft Comput. 2023, 36, 249–265. [Google Scholar] [CrossRef]
- Gumz, J.; Fettermann, D.C. What Improves Smart Meters’ Implementation? A Statistical Meta-Analysis on Smart Meters’ Acceptance. Smart Sustain. Built Environ. 2021, forthcoming. [Google Scholar] [CrossRef]
- Buryk, S.; Mead, D.; Mourato, S.; Torriti, J. Investigating Preferences for Dynamic Electricity Tariffs: The Effect of Environmental and System Benefit Disclosure. Energy Policy 2015, 80, 190–195. [Google Scholar] [CrossRef]
- Pop, R.-A.; Dabija, D.-C.; Pelău, C.; Dinu, V. Usage Intentions, Attitudes, and Behaviors Towards Energy-Efficient Applications During the COVID−19 Pandemic. J. Bus. Econ. Manag. 2022, 23, 668–689. [Google Scholar] [CrossRef]
- Chen, C.; Xu, X.; Arpan, L. Between the Technology Acceptance Model and Sustainable Energy Technology Acceptance Model: Investigating Smart Meter Acceptance in the United States. Energy Res. Soc. Sci. 2017, 25, 93–104. [Google Scholar] [CrossRef]
- Boudet, H.S. Public Perceptions of and Responses to New Energy Technologies. Nat. Energy 2019, 4, 446–455. [Google Scholar] [CrossRef]
- Bugden, D.; Stedman, R. A Synthetic View of Acceptance and Engagement with Smart Meters in the United States. Energy Res. Soc. Sci. 2019, 47, 137–145. [Google Scholar] [CrossRef]
- Zhou, S.; Noonan, D.S. Justice Implications of Clean Energy Policies and Programs in the United States: A Theoretical and Empirical Exploration. Sustainability 2019, 11, 807. [Google Scholar] [CrossRef]
- Wang, S.; Cui, L.; Que, J.; Choi, D.-H.; Jiang, X.; Cheng, S.; Xie, L. A Randomized Response Model for Privacy Preserving Smart Metering. IEEE Trans. Smart Grid 2012, 3, 1317–1324. [Google Scholar] [CrossRef] [PubMed]
- King, N.J.; Jessen, P.W. Smart Metering Systems and Data Sharing: Why Getting a Smart Meter Should Also Mean Getting Strong Information Privacy Controls to Manage Data Sharing. Int. J. Law Inf. Technol. 2014, 22, 215–253. [Google Scholar] [CrossRef]
- Buchanan, K.; Banks, N.; Preston, I.; Russo, R. The British Public’s Perception of the UK Smart Metering Initiative: Threats and Opportunities. Energy Policy 2016, 91, 87–97. [Google Scholar] [CrossRef]
- Khatua, P.K.; Ramachandaramurthy, V.K.; Kasinathan, P.; Yong, J.Y.; Pasupuleti, J.; Rajagopalan, A. Application and Assessment of Internet of Things toward the Sustainability of Energy Systems: Challenges and Issues. Sustain. Cities Soc. 2020, 53, 101957. [Google Scholar] [CrossRef]
| Method | sMAPE (%) | RMSE (×1011) |
|---|---|---|
| Random Forest | 17.92 | 7.656 |
| Support Vector Machines | 19.98 | 8.153 |
| Support Vector Machines (unscaled) | 43.74 | 15.729 |
| Linear Regression | 30.01 | 11.314 |
| Bayesian Ridge | 43.96 | 15.540 |
| Ridge Linear Regression | 29.79 | 11.323 |
| Method | Naïve Forecasting | Moving-Average | Arima | Expon. Smoothing | Random Forest | Neural Networks | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Measures | sMAPE (%) | RMSE (×1010) | sMAPE (%) | RMSE (×1010) | sMAPE (%) | RMSE (×1010) | sMAPE (%) | RMSE (×1010) | sMAPE (%) | RMSE (×1010) | sMAPE (%) | RMSE (×1010) |
| Mean | 31.53 | 3.748 | 29.43 | 3.370 | 28.47 | 3.339 | 28.58 | 3.372 | 25.63 | 3.248 | 23.67 | 2.812 |
| Std Dev | 16.24 | 2.837 | 15.72 | 3.339 | 14.37 | 2.508 | 14.09 | 2.601 | 12.06 | 2.431 | 9.95 | 1.949 |
| Min | 0.02 | 0.025 | 7.595 | 0.742 | 0.047 | 0.026 | 0.038 | 0.025 | 0.349 | 0.008 | 4.699 | 0.379 |
| 25% (Q1) | 21.24 | 2.122 | 19.94 | 1.955 | 19.95 | 1.862 | 20.14 | 1.896 | 18.22 | 1.889 | 17.57 | 1.724 |
| 50% (Q2) | 27.92 | 2.001 | 24.89 | 2.757 | 24.91 | 2.740 | 25.31 | 2.754 | 23.70 | 2.704 | 21.96 | 2.360 |
| 75% (Q3) | 37.22 | 2.325 | 34.40 | 3.950 | 33.56 | 3.981 | 34.6 | 3.946 | 30.68 | 3.972 | 26.97 | 3.176 |
| Max | 122.80 | 22.042 | 148.47 | 18.374 | 127.20 | 20.424 | 123.57 | 24.165 | 80.88 | 2.291 | 78.16 | 17.996 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gumz, J.; Fettermann, D.C.; Frazzon, E.M.; Kück, M. Using Industry 4.0’s Big Data and IoT to Perform Feature-Based and Past Data-Based Energy Consumption Predictions. Sustainability 2022, 14, 13642. https://doi.org/10.3390/su142013642
Gumz J, Fettermann DC, Frazzon EM, Kück M. Using Industry 4.0’s Big Data and IoT to Perform Feature-Based and Past Data-Based Energy Consumption Predictions. Sustainability. 2022; 14(20):13642. https://doi.org/10.3390/su142013642
Chicago/Turabian StyleGumz, Jonathan, Diego Castro Fettermann, Enzo Morosini Frazzon, and Mirko Kück. 2022. "Using Industry 4.0’s Big Data and IoT to Perform Feature-Based and Past Data-Based Energy Consumption Predictions" Sustainability 14, no. 20: 13642. https://doi.org/10.3390/su142013642
APA StyleGumz, J., Fettermann, D. C., Frazzon, E. M., & Kück, M. (2022). Using Industry 4.0’s Big Data and IoT to Perform Feature-Based and Past Data-Based Energy Consumption Predictions. Sustainability, 14(20), 13642. https://doi.org/10.3390/su142013642











