Calculation Method for Investigating the Behavior of Ground Surface Settlement of Underpass Buildings in TBM Double-Line Tunnels
Abstract
1. Introduction
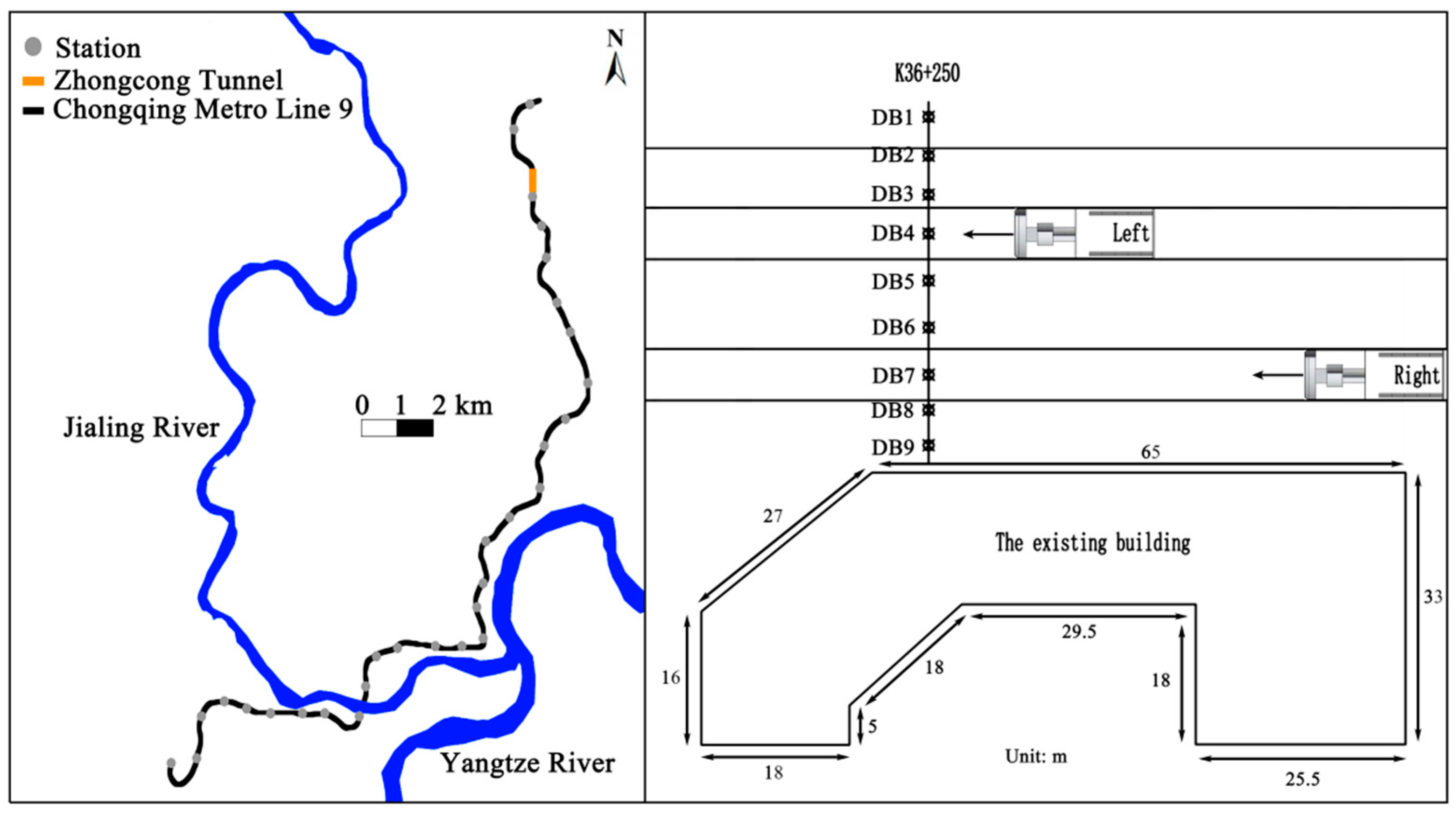
2. Project Description
3. Numerical Simulation
3.1. TBM Tunneling Parameters
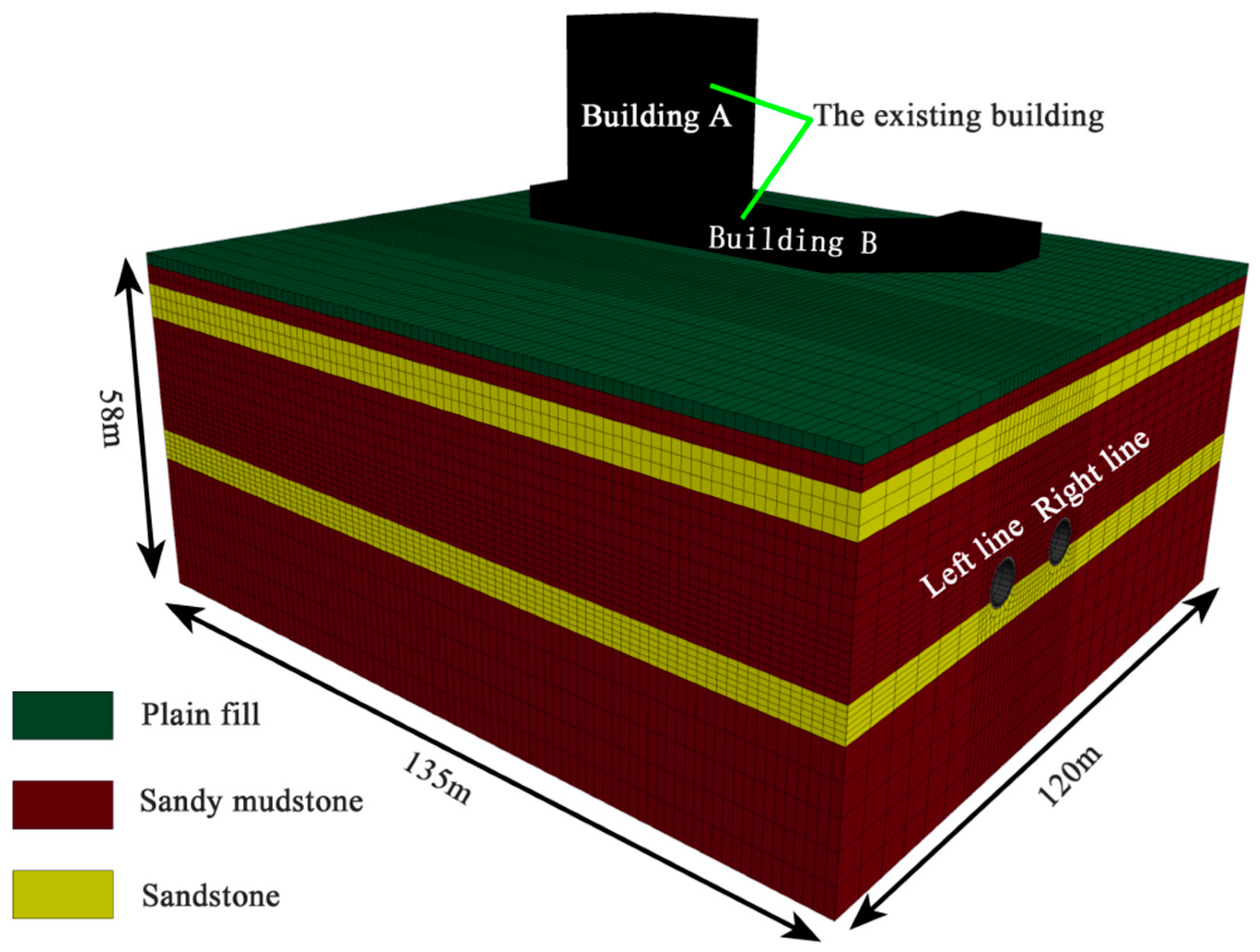
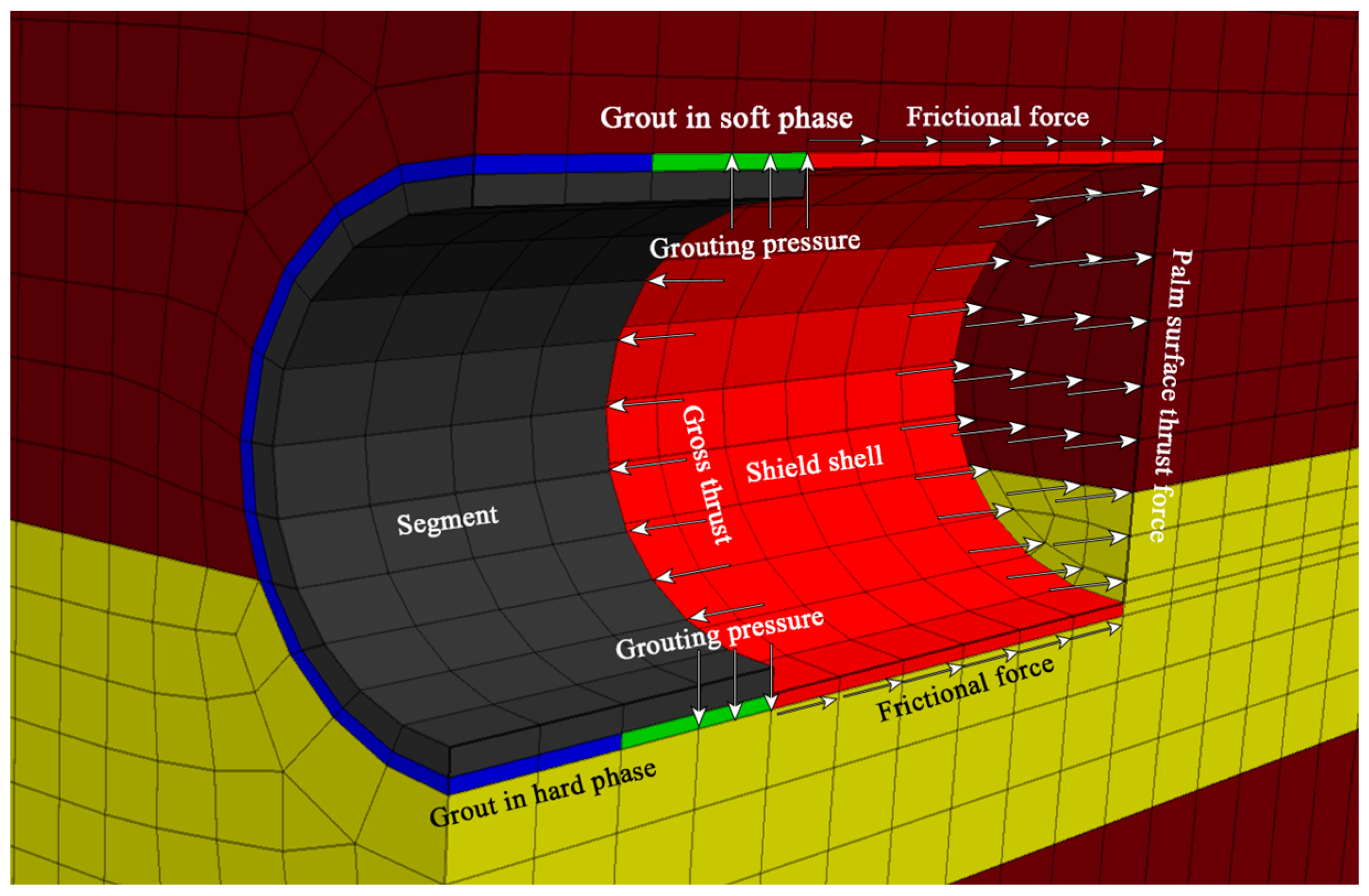
3.2. Calculation Models
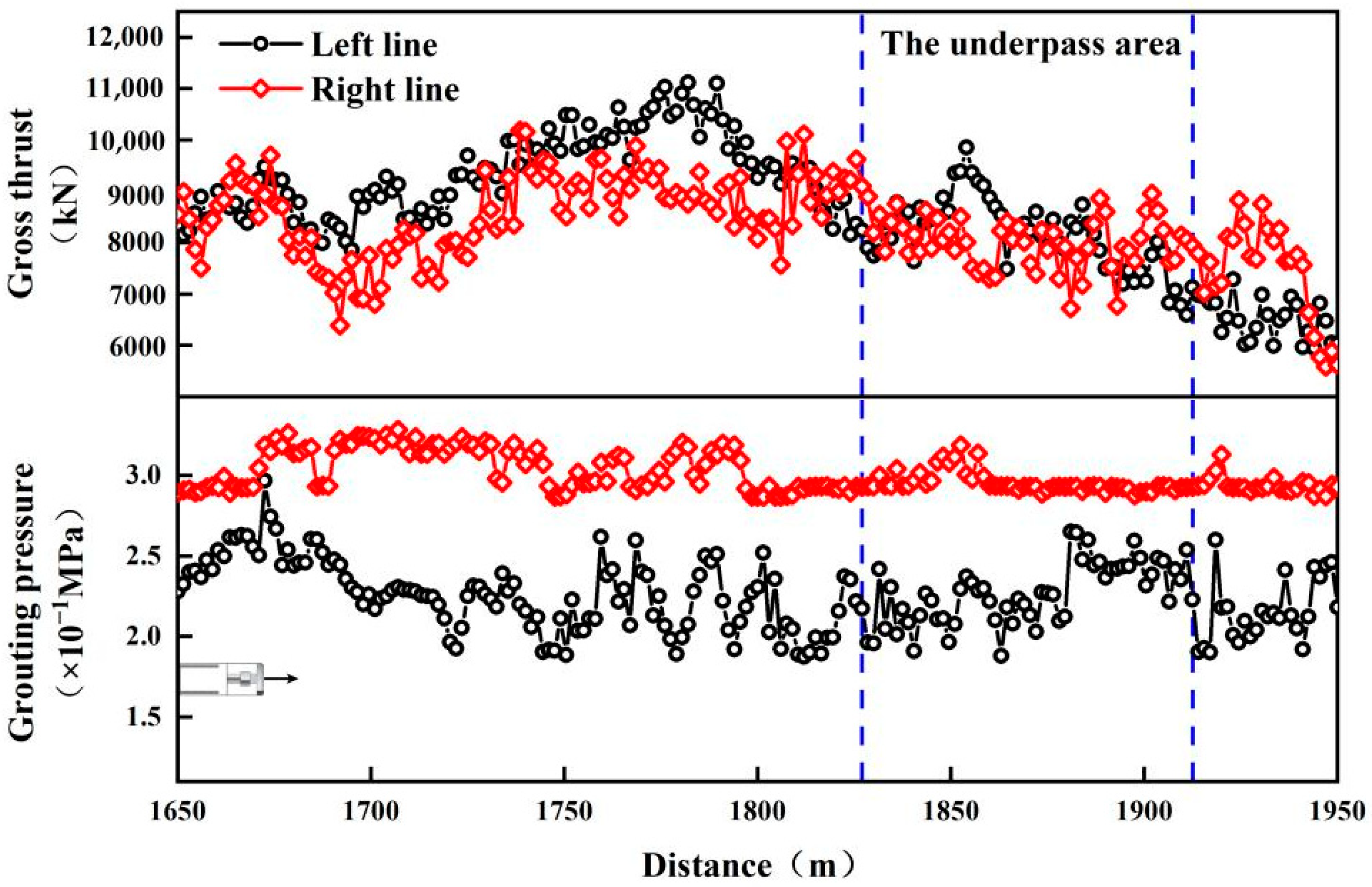
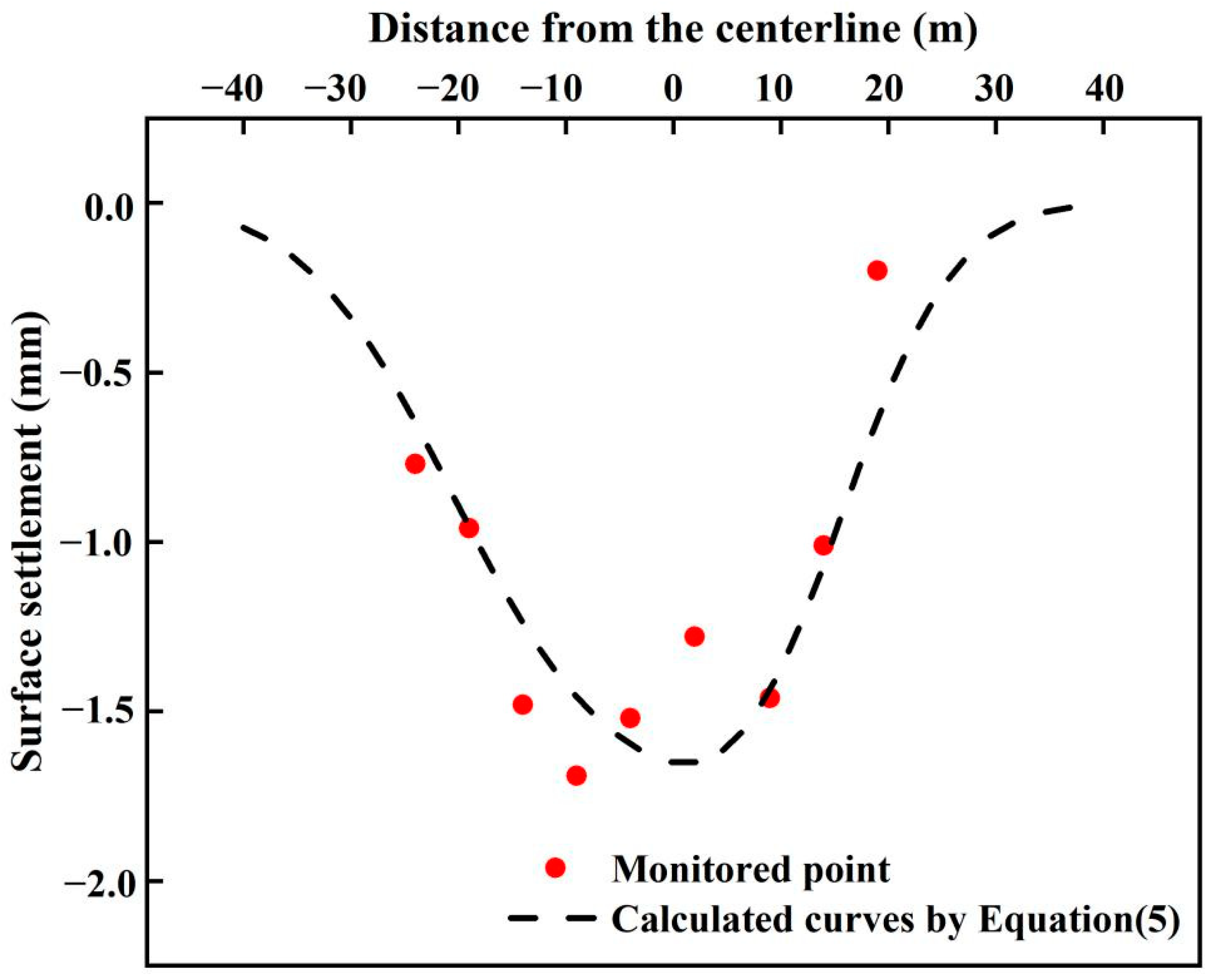
3.3. Model Validation
4. Orthogonal Test
4.1. Orthogonal Experimental Design
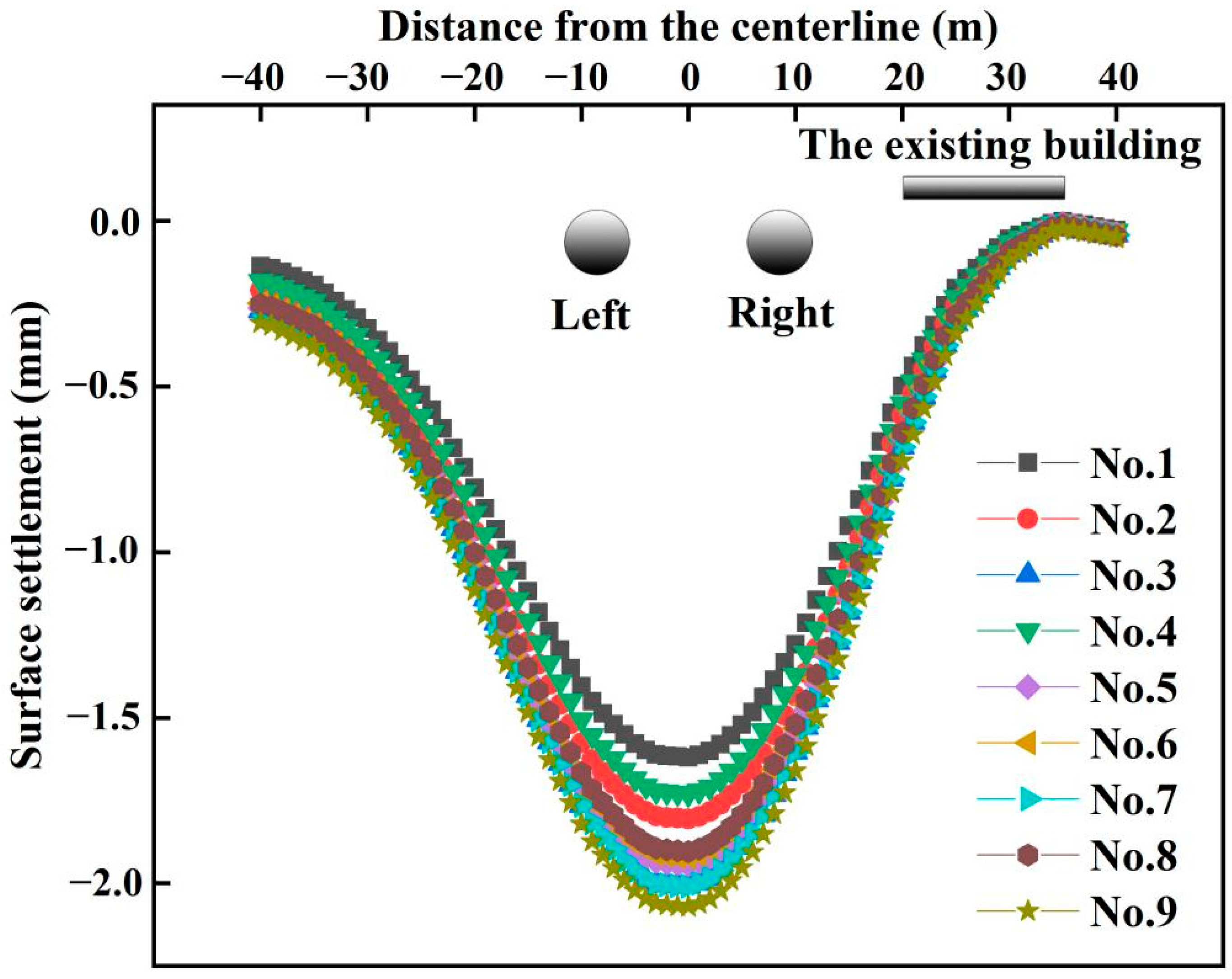
4.2. Analysis of Experimental Results
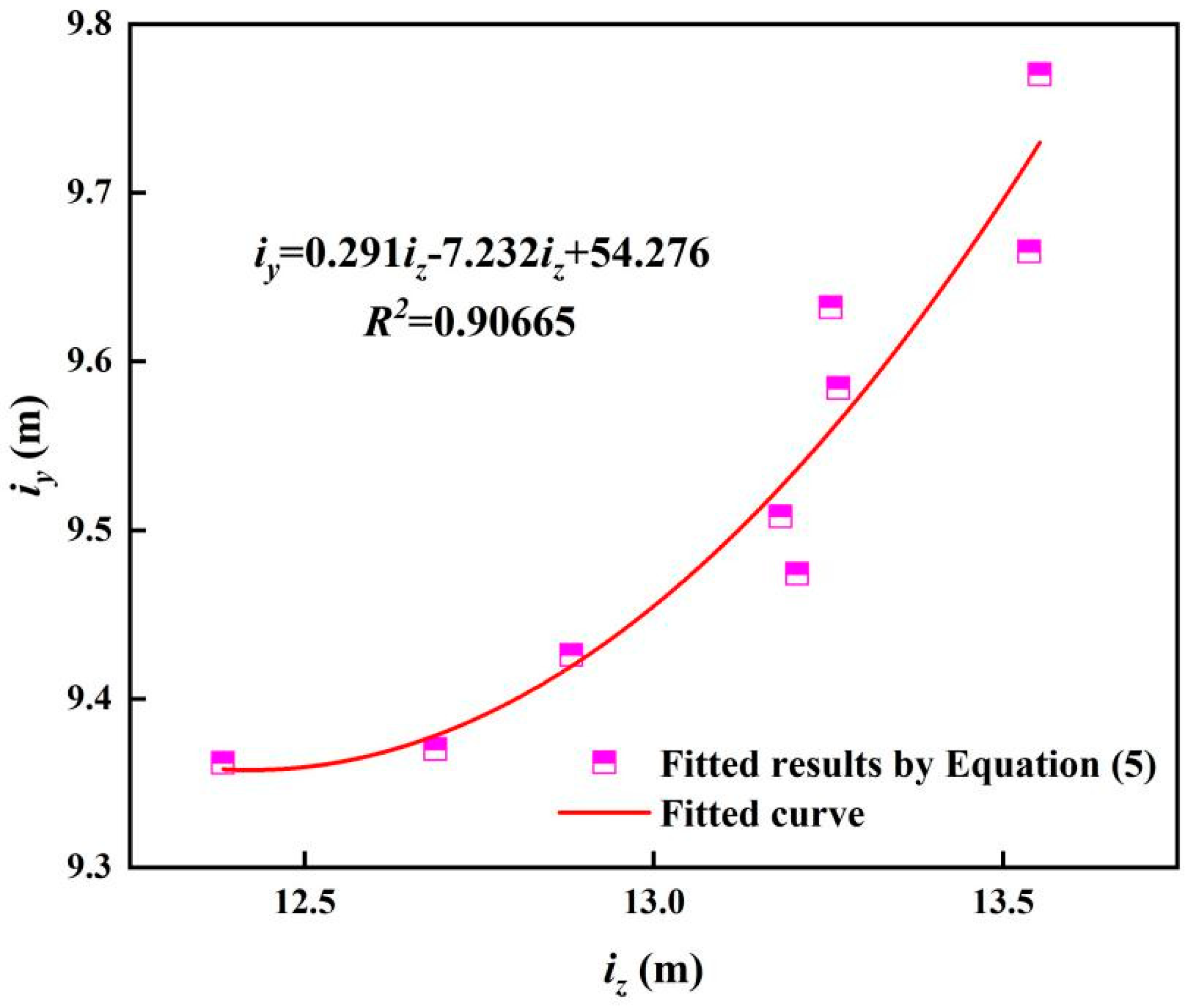
5. Improved Ground Surface Settlement Equations
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Comodromos, E.M.; Papadopoulou, M.C.; Konstantinidis, G.K. Numerical Assessment of Subsidence and Adjacent Building Movements Induced by TBM-EPB Tunneling. J. Geotech. Geoenviron. Eng. 2014, 140, 04014061. [Google Scholar] [CrossRef]
- Fu, J.; Yang, J.; Zhang, X.; Klapperich, H.; Abbas, S.M. Response of the ground andadjacent buildings due to tunnelling in completely weathered graniticsoil. Tunn. Undergr. Space Technol. 2014, 43, 377–388. [Google Scholar] [CrossRef]
- Peck, R. Deep excavations and tunnelling in soft ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 29 August 1969; pp. 226–290. [Google Scholar]
- Gioda, G.; Swoboda, G. Developments and applications of the numerical analysis of tunnels in continuous media. Int. J. Numer. Anal. Methods Geomech. 1999, 23, 1393–1405. [Google Scholar] [CrossRef]
- Liang, J.; Tang, X.; Wang, T.; Lin, W.; Yan, J.; Fu, C. Analysis for Ground Deformation Induced by Undercrossed Shield Tunnels at a Small Proximity Based on Equivalent Layer Method. Sustainability 2022, 14, 9972. [Google Scholar] [CrossRef]
- Xu, Y.F. Analysis of ground surface settlement induced by shield construction. Undergr. Eng. Tunn. 2000, 10, 21–25. [Google Scholar] [CrossRef]
- Yu, X.; Ren, H.; Hu, X. Analysis of the disturbance to surrounding soils during shield driving for the hangzhou metro line 1 project. Mod. Tunn. Technol. 2014, 51, 166–173. [Google Scholar] [CrossRef]
- Liu, B.; Tao, L.G.; Ding, C.G. Prediction for ground subsidence induced by subway double tube tunneling. J. China Univ. Min. Technol. 2006, 35, 356–361. [Google Scholar] [CrossRef]
- Han, X.; Li, N. Comparative analysis of strata prediction models for ground movement induced by tunnel construction. Chin. J. Rock Mech. Eng. 2007, 26, 594–600. [Google Scholar] [CrossRef]
- Wei, G. Study on calculation for width parameter of surface settlement trough induced by shield tunnel. Ind. Constr. 2009, 39, 74–79. [Google Scholar] [CrossRef]
- Li, X.; Du, S.; Zhang, D. Numerical simulation of the interaction between two parallel shield tunnels. In Proceedings of the CPTT 2012: Better Pipeline Infrastructure for a Better Life, Wuhan, China, 19–22 October 2012; pp. 1521–1533. [Google Scholar] [CrossRef]
- Wang, F.; Miao, L.; Li, C. Numerical analysis of shield tunnel settlement considering construction process. Chin. J. Rock Mech. Eng. 2013, 32, 2907–2914. [Google Scholar] [CrossRef]
- Feng, H.; Yu, R. Numerical analysis of influence of double—Line tunnel shield tunneling on ground surface settlement. J. Railw. Eng. Soc. 2019, 36, 78–83. [Google Scholar] [CrossRef]
- Faherty, R.; Acikgoz, S.; Wong, E.K.; Hewitt, P.; Viggiani, G.M. Tunnel-soil-structure interaction mechanisms in a metallic arch bridge. Tunn. Undergr. Space Technol. 2022, 123, 104429. [Google Scholar] [CrossRef]
- Franza, A.; Miraei, S.; Boldini, D.; Losacco, N. An equivalent beam approach for assessing tunnelling-induced distortions of frames with infills. Tunn. Undergr. Space Technol. 2022, 129, 104686. [Google Scholar] [CrossRef]
- Klar, A. A Fourier-based elastic continuum solution for jointed pipeline response to tunneling. Tunn. Undergr. Space Technol. 2022, 119, 104237. [Google Scholar] [CrossRef]
- Pirastehfar, K.; Shivaei, S.; Sadaghiani, M.H.; Nikooee, E. 3D numerical investigation of the effects of driving of the new mechanized tunnel on existing segmental linings and ground surface settlements-a case study: Shiraz metro line 2. Int. J. Geotech. Eng. 2022, 16, 878–889. [Google Scholar] [CrossRef]
- Liu, W.; Wu, X.; Zhang, L.; Zheng, J.; Teng, J. Global sensitivity analysis of tunnel-induced building movements by a precise metamodel. J. Comput. Civ. Eng. 2017, 31, 04017037. [Google Scholar] [CrossRef]
- Dalgic, K.D.; Hendriks, M.A.N.; Ilki, A. Building response to tunnelling-and excavation-induced ground movements: Using transfer functions to review the limiting tensile strain method. Struct. Infrastruct. Eng. 2018, 14, 766–779. [Google Scholar] [CrossRef]
- Lai, H.; Zheng, H.; Chen, R.; Kang, Z.; Liu, Y. Settlement behaviors of existing tunnel caused by obliquely under-crossing shield tunneling in close proximity with small intersection angle. Tunn. Undergr. Space Technol. 2020, 97, 103258. [Google Scholar] [CrossRef]
- Xu, J.; Franza, A.; Marshall, A.M.; Losacco, N.; Boldini, D. Tunnel–framed building interaction: Comparison between raft and separate footing foundations. Géotechnique 2021, 71, 631–644. [Google Scholar] [CrossRef]
- Guan, H. Study on the Calculating Models of Key Parameters & Mechanical Behavior of the EPB Shield Machine. Ph.D. Thesis, Southwest Jiaotong University, Sichuan, China, 2008. [Google Scholar]
- Shi, C.; Peng, L.; Lei, M. Study of time-space united calculating method of stratum deformation caused by shield tunnel excavation. Rock Soil Mech. 2009, 30, 2379–2384. [Google Scholar] [CrossRef]
- He, M.D.; Liu, J.; Le, G.P.; Wang, M.; Zhang, D. Study of impact of shield tunneling side-crossing on adjacent high buildings. Chin. J. Rock Mech. Eng. 2010, 29, 603–608. [Google Scholar]
- Lin, Z.J. Study on Effect of Construction of Undercrossing Shield Tunnel on Existing High-Speed Railway Tunnel and Its Control Technology; Central South University: Changsha, China, 2013. [Google Scholar]
- Ren, L.Q. Optimum Design and Analysis of Experiments; Higher Education Press: Beijing, China, 2003; pp. 23–24. [Google Scholar]
- Lai, H.P.; Wang, T.T.; Zhang, L.J.; Yuan, Y.; Luo, W. Construction control of shield tunneling underneath existing metro tunnel considering friction between shield shell and soil. Tunn. Constr. 2021, 41, 729. [Google Scholar] [CrossRef]
- Wei, G. Evaluation and Control of Environmental Effects of Double-Line Shield Tunnel Construction; Architecture and Building Press: Beijing, China, 2018; pp. 56–60. [Google Scholar]

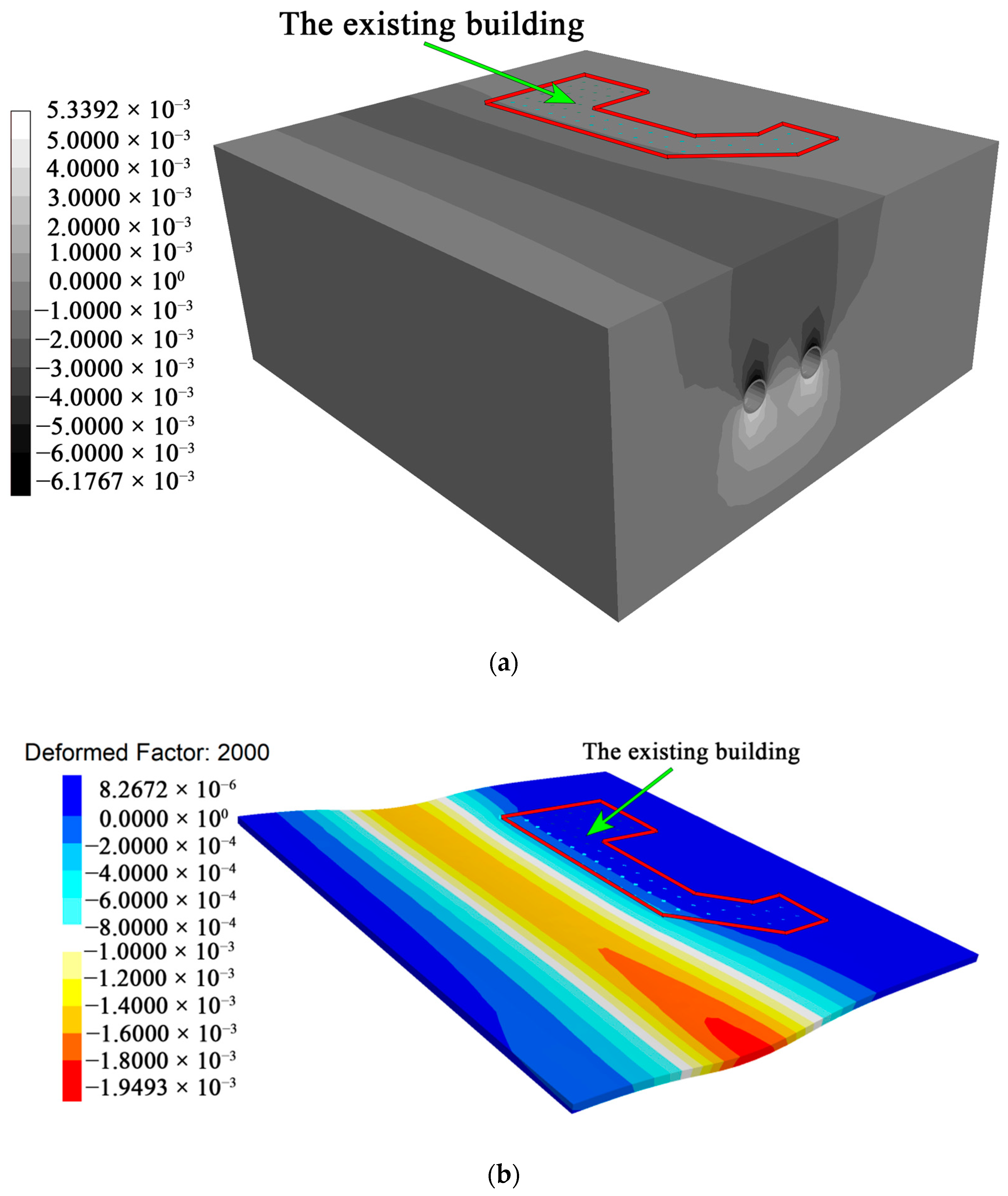

| Properties | Plain Fill | Sandy Mudstone | Sandstone | Segment | Pile | Shield Shell | Grout in Soft Phase | Grout in Hard Phase |
|---|---|---|---|---|---|---|---|---|
| Volumetric weight γ (kN·m−3) | 18 | 27.8 | 27.2 | 25 | 24 | 75.83 | 18 | 18 |
| Elastic modulus E (MPa) | 4.2 | 1620 | 4100 | 27,600 | 31,000 | 210,000 | 200 | 1800 |
| Poisson’s ratio υ | 0.38 | 0.32 | 0.22 | 0.2 | 0.2 | 0.26 | 0.25 | 0.2 |
| Cohesion c (kPa) | 11 | 1720 | 7560 | |||||
| Internal friction angle φ (°) | 11 | 35 | 43.8 |
| Level | Grouting Pressure | Frictional Force | Palm Surface Thrust Force |
|---|---|---|---|
| 1 | 1Fz | = 0.1 | 1Ft |
| 2 | 0.75Fz | = 0.15 | 1.25Ft |
| 3 | 0.5Fz | = 0.2 | 1.5Ft |
| Number | Grouting Pressure | Frictional Force | Palm Surface Thrust Force |
|---|---|---|---|
| 1 | 1Fz | = 0.1 | 1Ft |
| 2 | 1Fz | = 0.15 | 1.25Ft |
| 3 | 1Fz | = 0.2 | 1.5Ft |
| 4 | 0.75Fz | = 0.1 | 1.25Ft |
| 5 | 0.75Fz | = 0.15 | 1.5Ft |
| 6 | 0.75Fz | = 0.2 | 1Ft |
| 7 | 0.5Fz | = 0.1 | 1.5Ft |
| 8 | 0.5Fz | = 0.15 | 1Ft |
| 9 | 0.5Fz | = 0.2 | 1.25Ft |
| Number | Sz (mm) | Sl (mm) | Sy (mm) |
|---|---|---|---|
| 1 | −1.450 | −1.620 | −1.522 |
| 2 | −1.626 | −1.806 | −1.698 |
| 3 | −1.817 | −2.009 | −1.891 |
| 4 | −1.553 | −1.730 | −1.627 |
| 5 | −1.755 | −1.943 | −1.829 |
| 6 | −1.732 | −1.920 | −1.809 |
| 7 | −1.817 | −2.009 | −1.891 |
| 8 | −1.716 | −1.904 | −1.794 |
| 9 | −1.873 | −2.070 | −1.953 |
| Level | Sz (mm) | Sl (mm) | Sy (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | −1.631 | −1.607 | −1.633 | −1.812 | −1.786 | −1.815 | −1.704 | −1.680 | −1.708 |
| 2 | −1.680 | −1.699 | −1.684 | −1.864 | −1.884 | −1.869 | −1.755 | −1.774 | −1.759 |
| 3 | −1.802 | −1.807 | −1.796 | −1.994 | −2.000 | −1.987 | −1.879 | −1.884 | −1.870 |
| R | 0.171 | 0.200 | 0.163 | 0.182 | 0.232 | 0.172 | 0.175 | 0.204 | 0.162 |
| Number | Smax z (mm) | Smax z (mm) | Equation (4) | Equation (5) | |||||
|---|---|---|---|---|---|---|---|---|---|
| iz (m) | iy (m) | R2 | iz (m) | iy (m) | TR | R2 | |||
| 1 | −1.106 | −0.908 | 13.119 | 10.638 | 0.98664 | 12.384 | 9.362 | 1.151 | 0.99679 |
| 2 | −1.216 | −1.015 | 13.671 | 10.859 | 0.98208 | 12.883 | 9.426 | 1.161 | 0.99383 |
| 3 | −1.344 | −1.127 | 14.047 | 11.081 | 0.97981 | 13.265 | 9.584 | 1.160 | 0.99165 |
| 4 | −1.168 | −0.975 | 13.466 | 10.758 | 0.98351 | 12.688 | 9.370 | 1.160 | 0.99500 |
| 5 | −1.296 | −1.095 | 14.020 | 11.014 | 0.97848 | 13.206 | 9.474 | 1.167 | 0.99132 |
| 6 | −1.287 | −1.063 | 14.025 | 11.104 | 0.98169 | 13.254 | 9.632 | 1.157 | 0.99314 |
| 7 | −1.255 | −1.069 | 14.674 | 12.102 | 0.96924 | 13.553 | 9.770 | 1.243 | 0.99416 |
| 8 | −1.266 | −1.073 | 13.994 | 11.039 | 0.97913 | 13.182 | 9.508 | 1.167 | 0.99185 |
| 9 | −1.369 | −1.165 | 14.339 | 11.247 | 0.97688 | 13.538 | 9.665 | 1.165 | 0.98949 |
| Smax z (mm) | Smax y (mm) | TR | iz (m) | iy (m) |
|---|---|---|---|---|
| −1.106 | −0.908 | 1.17 | 13.112 | 9.480 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, T.; Zhang, H.; Guo, Y.; Tang, Y.; Li, Q.; Okubo, S. Calculation Method for Investigating the Behavior of Ground Surface Settlement of Underpass Buildings in TBM Double-Line Tunnels. Sustainability 2022, 14, 13410. https://doi.org/10.3390/su142013410
Ren T, Zhang H, Guo Y, Tang Y, Li Q, Okubo S. Calculation Method for Investigating the Behavior of Ground Surface Settlement of Underpass Buildings in TBM Double-Line Tunnels. Sustainability. 2022; 14(20):13410. https://doi.org/10.3390/su142013410
Chicago/Turabian StyleRen, Ting, Hailong Zhang, Yuancheng Guo, Yang Tang, Qinglin Li, and Seisuke Okubo. 2022. "Calculation Method for Investigating the Behavior of Ground Surface Settlement of Underpass Buildings in TBM Double-Line Tunnels" Sustainability 14, no. 20: 13410. https://doi.org/10.3390/su142013410
APA StyleRen, T., Zhang, H., Guo, Y., Tang, Y., Li, Q., & Okubo, S. (2022). Calculation Method for Investigating the Behavior of Ground Surface Settlement of Underpass Buildings in TBM Double-Line Tunnels. Sustainability, 14(20), 13410. https://doi.org/10.3390/su142013410










