Feasibility of Applying Mel-Frequency Cepstral Coefficients in a Drive-by Damage Detection Methodology for High-Speed Railway Bridges

Abstract

In this paper, a drive-by damage detection methodology for high-speed railway (HSR) bridges is addressed, to appraise the application of Mel-frequency cepstral coefficients (MFCC) to extract the Damage Index (DI). A finite element (FEM) 2D VTBI model that incorporates the train, ballasted track and bridge behavior is presented. The formulation includes track irregularities and a damaged condition induced in a specified structure region. The feasibility of applying cepstrum analysis components to the indirect damage detection in HSR by on-board sensors is evaluated by numerical simulations, in which dynamic analyses are performed through a code implemented in MATLAB. Different damage scenarios are simulated, as well as external excitations such as measurement noises and different levels of track irregularities. The results show that MFCC-based DI are highly sensitive regarding damage detection, and robust to the noise. Bridge stiffness can be recognized satisfactorily at high speeds and under different levels of track irregularities. Moreover, the magnitude of DI extracted from MFCC is related to the relative severity of the damage. The results presented in this study should be seen as a first attempt to link cepstrum-based features in an HSR drive-by damage detection approach.

1. Introduction

With the continuous development of new HSR lines around the globe, bridges account for a large proportion of these infrastructures and, as a result, the demand for condition assessment of such a great number of bridges is steadily increasing [1,2,3]. In recent decades, vibration-based Structural Health Monitoring (SHM) has been extensively explored as one of the most common assessment methodologies. Indeed, SHM has been an active field of research for over three decades. In conventional approaches (direct SHM), the dynamic responses of structures are typically evaluated using sensors installed directly on the bridge. However, these types of monitoring are time-consuming and laborious in deploying sensors and equipment, which are often planned on a one-system-per-bridge basis [4,5].

For this reason, indirect approaches for SHM of bridges have garnered increased interest, particularly as an efficient and comprehensive method of inspecting many railway bridges with a single run. The main approach used consists in the drive-by estimation of passing railway bridges based on the on-board measured data of an in-service train traveling on the specific routes [6,7]. Based on VBI, these approaches analyze the vibration signals of a moving vehicle, using embedded sensors. The idea of these systems is that a moving vehicle crossing a bridge can function as a mobile exciter and sensor. Because of the dynamic interaction between the passing vehicle and the vibrating bridge, the vehicle’s response contains bridge-related information and can be used for bridge health evaluation. Not only do indirect SHM frameworks require no instrumentation on the bridge, but they also give a greater spatial resolution monitoring system, as the response of the passing vehicle and the bridge is measured at multiple contact points along the bridge [8].

Drive-by bridge evaluation has been proposed for cost-effective SHM, and numerous research on bridge performance evaluation and damage detection using this method have been conducted in the highway field. However, there are not enough studies on procedures for drive-by bridge inspection on HSR [9]. The feasibility of estimating bridge conditions by extracting their natural frequencies using moving vehicles was introduced and described theoretically and experimentally by [10,11]. Afterward, the parameters that influence the drive-by evaluation of bridges were discussed [12], and a filtering approach was proposed for this drive-by extraction method [13]. In addition to these pioneering efforts, the estimation of bridge vibration using the drive-by system has been researched worldwide, with a focus on scaled-down model experiments [14,15,16,17]. Moreover, further investigations on drive-by bridge evaluation (referred to as vehicle scanning) and its applications to highway bridges and railway tracks have recently been conducted [18].

In recent years, a variety of drive-by bridge inspection methods have been proposed, such as those employing particle filters [19], data-driven neural networks [20], frequency-independent underdamped pinning stochastic resonance [21], the bridge displacement profile [22], the bridge frequency with two vehicles [23] and a data-driven approach [8]. In most of these investigations in SHM, the fundamental frequency of the bridge was discovered indirectly via a frequency domain analysis of the mixed bridge responses of vehicles, which has been limited to relatively slow-moving vehicles that remain on the bridges for an extended period, due to limited frequency resolution and bridge–vehicle interactions [24]. At high vehicle speeds, the frequency resolution of the on-vehicle measured data and the transmission of the bridge reaction to the car via bridge–vehicle interactions are significantly undermined [6]. In like manner, to identifying bridge frequencies, other parameters of the bridge such as bridge modal shapes, bridge damping [25,26,27,28], and bridge damage can also be identified from vehicle responses. A comprehensive analysis of the most recent development of the drive-by bridge assessment is presented in [29], with its applications categorized according to the following aspects: modal identification, damage detection, pavement roughness detection, attempts by or including modern devices, identification of vehicle properties and railway track detection.

Regarding bridge damage detection as a relevant application of the drive-by bridge inspection method [30,31,32,33], based on the identified modal parameters, the structural damage of the bridge under different conditions can be detected [6,34,35,36,37]. For damage detection of railway tracks, a theoretical framework for a two-axle test vehicle traveling over train lines was proposed by [38]. The driving component of the contact-point response was processed by the Hilbert transform to take the instantaneous amplitude squared (IAS), which was identified as a good damage indicator, yet the damaged region cannot be excited appropriately at higher vehicle speeds.

An overview of recent progress in vibration-based damage identification methods and theoretical development of damage detection strategies for bridge structures is provided by [39], including intelligent algorithms, the Bayesian theory, and time-domain signal processing–based methodologies. Structural damage detection and SHM methods can be categorized as modal-based [40] or signal-based [41]. Modal-based approaches employ alterations in measured modal parameters or their derivatives, to determine structural deterioration. Signal-based approaches rely on vibration measurements, which are indicative of structural damage. These methods use adequate signal processing techniques to detect damage by tracking alterations in the features generated directly from the recorded dynamic responses or their associated spectra. Principal vibration signal processing techniques are based on time and frequency analysis, time-frequency analysis, and cepstral analysis [41,42]. Indirect damage detection was also studied, by utilizing mature technologies to process the vehicle responses, such as wavelet transform [30], frequency response function [43], and machine learning approach [44,45,46,47,48], among others. Deep learning algorithms have also been applied to the prediction of time-history responses of the bridge under vehicular loads with few and measurable input features extracted from VBI systems and vehicle responses to produce reliable training data [49].

Recent research has focused on the novel idea of cepstrum-based operational modal analysis [42,50,51,52,53,54]. Cepstrum analysis provides information from the vibration signal as a function of quefrency, and appears to be effective for identifying subtle spectrum changes. Initial studies of cepstrum-based analysis have demonstrated the method’s great potential for SHM applications [55]. Nevertheless, in this field, there are few recent research papers on employing cepstrum for damage detection, and they all involve non-destructive evaluation or direct SHM. Cepstral distance has been used to extract features for damage detection in layered carbon fiber reinforced polymer [56] and to generate frequency response functions using response-only measurements, where the difference between baseline and damaged frequency response functions was then used to compress the data and to train neural networks for damage-detection [52].

Mel-frequency cepstrum (MFC) is a type of cepstrum analysis that has also drawn the attention of SHM researchers. In contrast with the performance of conventional delamination detection methods, which are easily impacted by environmental noise and the subjectivity of the inspector, independent component analysis and MFCC were associated with a radial basis function network for delamination detection, and experiments and field tests have demonstrated the robustness of the technique to noise, even with insufficient training data [57]. Damage identification based on auto-regressive coefficients was also undertaken as a point of comparison with adapting MFCC, and their Mahalanobis distance used as damage features in a computational 10 degrees of freedom (DOFs) and on a nonlinearly behaving laboratory structure. The method based on MFCC presented better results than the one based on auto-regressive coefficients [58]. MFCC were also adopted as features in a vibration-based SHM methodology proposed to assess the health conditions of monitored civil structures by drawing knowledge from rich classification models trained on large datasets, such as audio sets (the source domain) commonly used for speech and speaker recognition purposes [59,60,61].

Despite being a research subject that has recently aroused interest in the SHM area, there are still only a small number of works applying MFCC to indirect health monitoring for damage detection. Indeed, to the best of the authors’ knowledge, only two studies have addressed this topic. Firstly, a novel damage feature extracted from adapted MFCC was proposed for damage detection of bridges using drive-by data, focusing on the highway SHM field and the concept of using mobile sensor network [62]. The numerical analysis and laboratory experiment results showed that the approach could identify the existence of damage and provide useful information about its severity. Subsequently, the aforementioned adapted MFCC was applied to a drive-by damage detection framework [63]. The method’s feasibility was verified numerically with a single DOFs sprung mass model and by a laboratory experiment.

In this paper, a drive-by damage detection methodology for HSR bridges is addressed to appraise the application of MFCC to extract features that are related to bridge damage. The organization of the article is as follows: firstly, a 2D VTBI model that incorporates the train, ballasted track and bridge behavior is presented, in which the train cars consist of four-axle vehicles, the track is modeled as a beam resting on uniformly distributed spring-mass systems, and the bridge deck of the HSR is modeled as a simply supported Bernoulli-Euler beam. The formulation includes track irregularities and damage conditions induced in a specified structure region. Secondly, the proposed drive-by damage detection strategy is demonstrated, and the premises of the damage index extraction from the MFCC approach are discussed. Afterward, the feasibility of applying cepstrum analysis components to the indirect damage detection in HSR by on-board sensors is evaluated by numerical simulations, in which dynamic analyses are performed through a code implemented in MATLAB^® [64]. Different damage scenarios are simulated, as well as external excitations such as measurement noises and different levels of track irregularities. Finally, the key results are summarized in the last section, and some prospects are highlighted. The results presented in this study should be seen as a first attempt to link cepstrum-based features in an HSR drive-by damage detection approach.

2. Methodology

2.1. Vehicle-Track-Bridge Dynamic Interaction System

The passing trains induce severe vibrations in the substructures, which may affect the proper operation of the track and bridge structures. In turn, the track and bridge’s sharply dynamic behaviors can influence the trains’ dynamic performance. In order to evaluate the dynamic performance and service life of the train–track–bridge system, it is necessary to take the train, the track, and the bridge as a coupled system into account and analyze them simultaneously [65].

In general, in train–bridge dynamic interaction models, the bridge subsystem is usually modeled on the finite element method (FEM) or continuous beam theories, whereas the theory of multi-body system dynamics is adopted to establish the moving vehicle subsystem, which implies that most of the vehicle degrees of freedom, or equations of motion, are assigned to the motions of the vehicle bodies [66,67]. A comprehensive literature review of railway vehicle modeling is provided in [67], and a substantial state-of-the-art review of train–track–bridge dynamic interaction is presented in [65].

This section describes the 2-dimensional VTBI model used in the present study to numerically simulate a high-speed train response to a bridge-crossing event. Plane VBI systems can satisfactorily predict vertical dynamic response [68,69]. As to ballasted railways tracks consisting of rails, pads, sleepers, ballast, and sub-ballast, it is possible to depict the track with varying degrees of complexity, which may be roughly categorized by the number of sprung layers taken into account [70].

2.1.1. Vehicle Model

The multi-rigid-body vehicle model considered is schematically depicted in Figure 1a. It is assumed that the train is composed of $N_c$ independent vehicles and crosses the bridge at a constant speed $v$. Each vehicle has one carbody, two bogies, and four wheelsets. The carbody frame has been modeled as a rigid body with a concentrated mass $m_c$ and rotary inertia $J_c$. Similarly, each bogie frame has also been modeled as a rigid body and has a concentrated mass $m_b$ and a rotary inertia $J_b$. The carbody and bogie frame rotary inertias are about the transverse horizontal axis through its center of gravity. The wheelsets are represented as lumped masses $m_w$ that are connected to the bogie frames by means of spring-dashpot sets representing the primary suspension with spring stiffness $k_{1y}$ and damping coefficient $c_{1y}$. Bogie frames are coupled to the carbody by spring-dashpot sets with spring stiffness $k_{2y}$ and damping coefficient $c_{2y}$, representing the secondary suspension system.

In total, the vehicle model has ten independent DOFs that correspond to seven vertical displacements for the masses ($y_c, y_{b1}, y_{b2}, y_{w1}, y_{w2}, y_{w3}$, and $y_{w4}$), and three rotations of the rigid bars (${\theta }_c, {\theta }_{b1},$ and ${\theta }_{b2}$). This model has been extensively discussed in the literature, and its equations of motion may be found in a variety of sources [70,71].

2.1.2. Track Model

As depicted in Figure 1b, the track is modeled as a beam resting on uniformly distributed spring-mass systems. The rail is modeled specifically as an Euler–Bernoulli beam using FEM discretization, whose behavior is characterized by four parameters: Young’s modulus $E_r$, sectional area $A_r$, moment of inertia $I_r$, and mass per unit length a mass per unit length of ${\overline{m}}_r$. The sleepers are represented as masses $M_s$ separated by a regular spacing $L_s$ and coupled to the rail by a spring-dashpot system with stiffness $K_p$ and viscous damping $C_p$ representing the pad. The ballast is depicted as a lumped mass $M_{ba}$ that interacts with the sleeper via a spring-dashpot layer with stiffness $K_{ba}$ and a damping coefficient $C_{ba}$. The third layer represents the dynamic qualities of the sub-ballast, using an additional spring-dashpot system in parallel with stiffness $K_{sb}$ and viscous damping $C_{sb}$, respectively. The rail irregularities $r\left(x\right)$ at the $x$-coordinate are taken into account by introducing random irregularity profile functions on the rail surface, which describe the deviation from a perfectly smooth track. The track irregularities are measured relative to the beam’s vertical static equilibrium locations (mean horizontal axle).

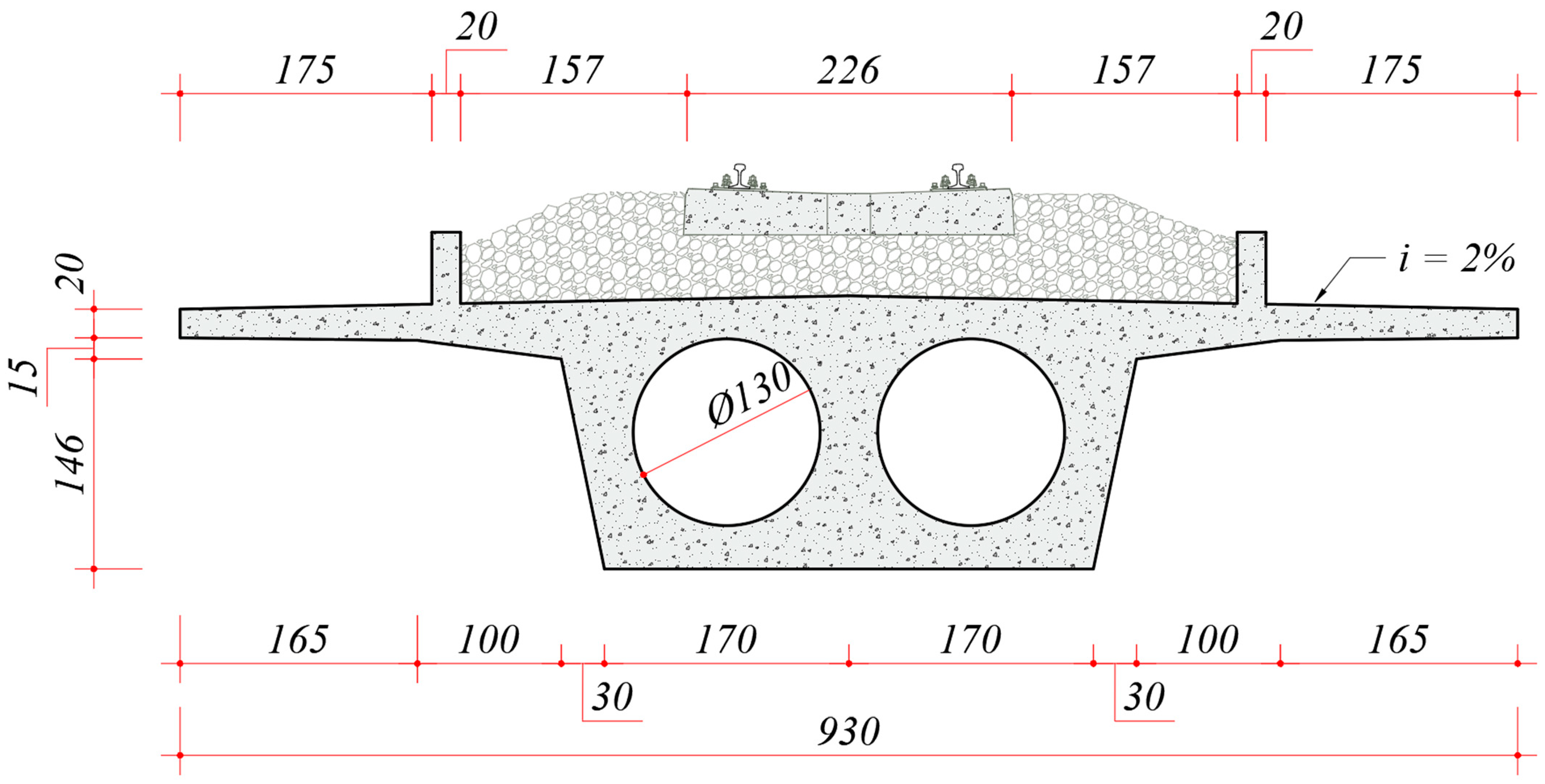
2.1.3. Bridge Model

The bridge deck of the HSR is modeled as a simply supported Bernoulli-Euler beam (Figure 1c) with a mass per unit length of $\overline{m}$, Young’s modulus $E_b$, sectional area $A_b$, moment of inertia $I_b$ and equivalent damping coefficient $c$. The bridge is implemented utilizing FEM formulation with beam elements. Numerous papers have detailed the elemental matrices [70,72], and the assembly of these matrices into global form yields the set of motion equations that characterize the dynamic behavior of the bridge. In order to simulate the structure damage being identified and localized indirectly by the passing vehicle, a beam region has its bending stiffness affected by a coefficient $f_{sr}$ (reduction stiffness ratio).

2.1.4. Equations of Motion for the VTBI System

All the above-mentioned subsystems are incorporated into a single VTBI model. The train convoy is composed of $c=1, 2,\dots ,N_c$ independent cars traveling in succession. The vehicles travel on a rail supported by three layers of spring-dashpot systems representing the pad, ballast, and sub-ballast. The track is then supported by either the bridge or a rigid foundation (Figure 1b). The length of the track is adequate to prevent the vehicle from reaching the bridge until it has reached dynamic equilibrium. It is also sufficiently long for the vehicle to completely exit the bridge [70].

A set of motion equations specifies each subsystem. These second-order differential equations can be expressed in a general matrix form, using the mass, damping, and stiffness time-dependent global matrices—$M$, $C,$ and $K,$ respectively—together with the vector of external forces $F$ and solved for the vector $X$ of the global displacements (DOFs). The coupled equations of motion of the model as a whole can be represented in a sub-matrices form as

$$\left[\begin{array}{ccc}{\mathbf{M}}_{\mathrm{V}}& 0& 0\\ 0& {\mathbf{M}}_{\mathrm{T}}& 0\\ 0& 0& {\mathbf{M}}_{\mathrm{B}}\end{array}\right]\left\{\begin{array}{c}{\ddot{\mathbf{X}}}_{\mathrm{V}}\\ {\ddot{\mathbf{X}}}_{\mathrm{T}}\\ {\ddot{\mathbf{X}}}_{\mathrm{B}}\end{array}\right\}+\left[\begin{array}{ccc}{\mathbf{C}}_{\mathrm{V}}& {\mathbf{C}}_{\mathrm{VT}}& 0\\ {\mathbf{C}}_{\mathrm{TV}}& {\mathbf{C}}_{\mathrm{T}}& {\mathbf{C}}_{\mathrm{TB}}\\ 0& {\mathbf{C}}_{\mathrm{BT}}& {\mathbf{C}}_{\mathrm{B}}\end{array}\right]\left\{\begin{array}{c}{\dot{\mathbf{X}}}_{\mathrm{V}}\hfill \\ {\dot{\mathbf{X}}}_{\mathrm{T}}\hfill \\ {\dot{\mathbf{X}}}_{\mathrm{B}}\hfill \end{array}\right\}+\left[\begin{array}{ccc}{\mathbf{K}}_{\mathrm{V}}& {\mathbf{K}}_{\mathrm{VT}}& 0\\ {\mathbf{K}}_{\mathrm{TV}}& {\mathbf{K}}_{\mathrm{T}}& {\mathbf{K}}_{\mathrm{TB}}\\ 0& {\mathbf{K}}_{\mathrm{BT}}& {\mathbf{K}}_{\mathrm{B}}\end{array}\right]\left\{\begin{array}{c}{\mathbf{X}}_{\mathrm{V}}\hfill \\ {\mathbf{X}}_{\mathrm{T}}\hfill \\ {\mathbf{X}}_{\mathrm{B}}\hfill \end{array}\right\}=\left\{\begin{array}{c}{\mathbf{F}}_{\mathrm{V}}\\ {\mathbf{F}}_{\mathrm{T}}\\ {\mathbf{F}}_{\mathrm{B}}\end{array}\right\}$$

(1)

where the subscripts $\mathrm{V}$, $\mathrm{T}$, and $\mathrm{B}$ the vehicle, track, and bridge subsystems, respectively. In Equation (1), the coupling of the subsystems is mathematically described with additional off-diagonal block matrices. These coupling terms are determined by the beam element’s shape function and the mechanical parameters of the system. A complete derivation of these mathematical expressions is presented by [73] in greater detail.

The coupling terms between the vehicle and the track depend on the vehicle’s position; hence, they are time-dependent and must be computed at each time step. Conversely, the coupling terms between the track and bridge stay unchanged, since their configuration does not vary within a single simulation. It should be noted that when the vehicle and track are connected, some of the vehicle’s DOFs are combined with those of the track. Consequently, the mass matrix of the track $M_T$ must be modified at each time step, to account for the increased masses of the wheels [70,71,72,73].

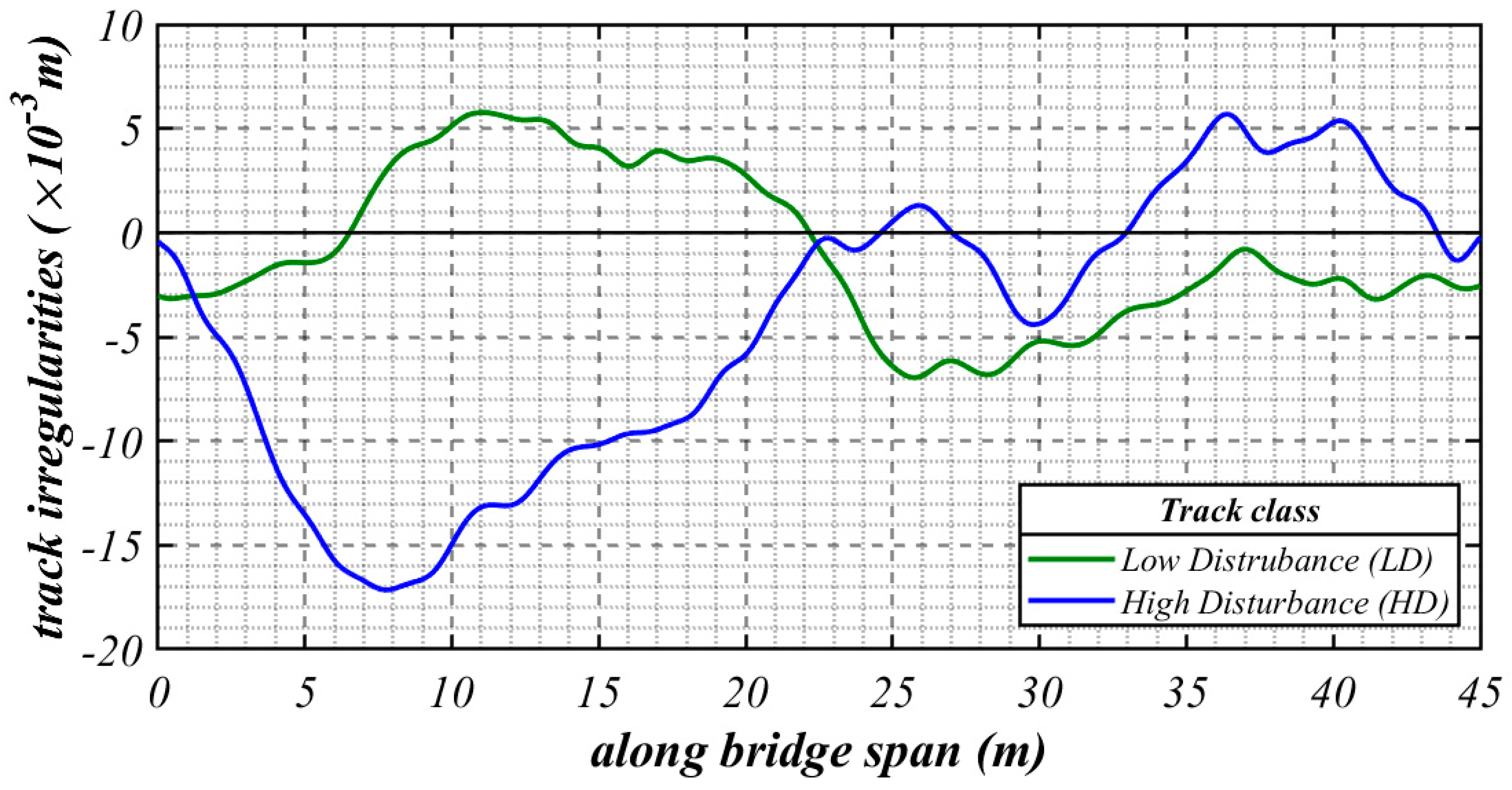
2.2. Irregularity of Track Vertical Profile

In general, with the exception of areas with turnouts, road crossings, and deteriorating rail lines, the irregularities of the track’s vertical profile can be viewed as stationary ergodic Gaussian random processes in a space domain along the track’s length, which is characterized by a superposition of random harmonic waves with varying wavelengths, phases, and amplitudes [74]. Power spectral density (PSD) is the most significant and widely employed statistical function for simulating random track irregularities. PSD of track irregularities are curves of constant variation, in which spectral density is the ordinate and either frequency or wavelength is the abscissa, in which the relationship between irregularity amplitude and frequency is clearly evidenced [72].

For the numerical simulations presented in Section 3, two vertical track profiles with random vertical irregularities were generated using a random function $r\left(x\right)$ of zero expectance and constant variance presented by [75], and expressed by a trigonometry series as

$$r(x)=2{\displaystyle \sum _{j=1}^N\sqrt{S\left({\Omega }_j\right)\Delta \Omega }\mathit{cos}\left({\Omega }_{j}x+{\varphi }_j\right)},$$

(2)

where ${\varphi }_j$ is a random phase with uniformity distribution in $\left[0, 2\pi rad\right]$, $S\left({\mathsf{\Omega }}_j\right)$ is the PSD function evaluated in the $j$th spatial frequency ${\mathsf{\Omega }}_j\left(\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{m}\right)$ of the discrete domain ${\mathsf{\Omega }}_j={\mathsf{\Omega }}_l+\left(j-1/2\right){\mathsf{\Delta }}_{\mathsf{\Omega }}$, with $j=1,2,\dots ,N$, and whose frequency band ${\mathsf{\Delta }}_{\mathsf{\Omega }}=\left({\mathsf{\Omega }}_c-{\mathsf{\Omega }}_r\right)/N$ is defined by the lower and upper limit’s spatial frequencies, respectively ${\mathsf{\Omega }}_l=2\pi /L_{r,max}$ and ${\mathsf{\Omega }}_u=2\pi /L_{r,min}$, and by the wavelength range $\left[L_{r,min}, L_{r,max}\right]$ in which the PSD function is included.

For Equation (2), the following were assumed: $N=3540$ (number of spatial frequencies), $L_{r,min}=1.524 \mathrm{m}$, $L_{r,max}=304.8 \mathrm{m}$, and the German PSD function has been used, which is written by

$$S_V\left(\Omega \right)=\frac{A_V{\Omega }_c{}^2}{\left({\Omega }^2+{\Omega }_r{}^2\right)\left({\Omega }^2+{\Omega }_c{}^2\right)}\begin{array}{c}\end{array}\left[\frac{{\mathrm{m}}^2}{\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{m}}\right],$$

(3)

where ${\mathsf{\Omega }}_c$ and ${\mathsf{\Omega }}_r$ are the cut-off frequencies and $A_V$ is the roughness constant, whose values are presented in

Table 1. Roughness coefficients and cut-off frequencies for German track irregularity PSDs [72].

Track Class	${\mathbf{\Omega }}_{\mathit{c}} (\mathbf{rad}/\mathbf{m})$	${\mathbf{\Omega }}_{\mathit{r}} (\mathbf{rad}/\mathbf{m})$	${\mathit{A}}_{\mathit{V}}$$({\mathbf{m}}^2\times \mathbf{rad}/\mathbf{m})$
Low disturbance	0.8246	0.0206	4.032 × 10−7
High disturbance	0.8246	0.0206	1.080 × 10−6

. Figure 2 shows the irregularity profiles used in the numerical simulations.

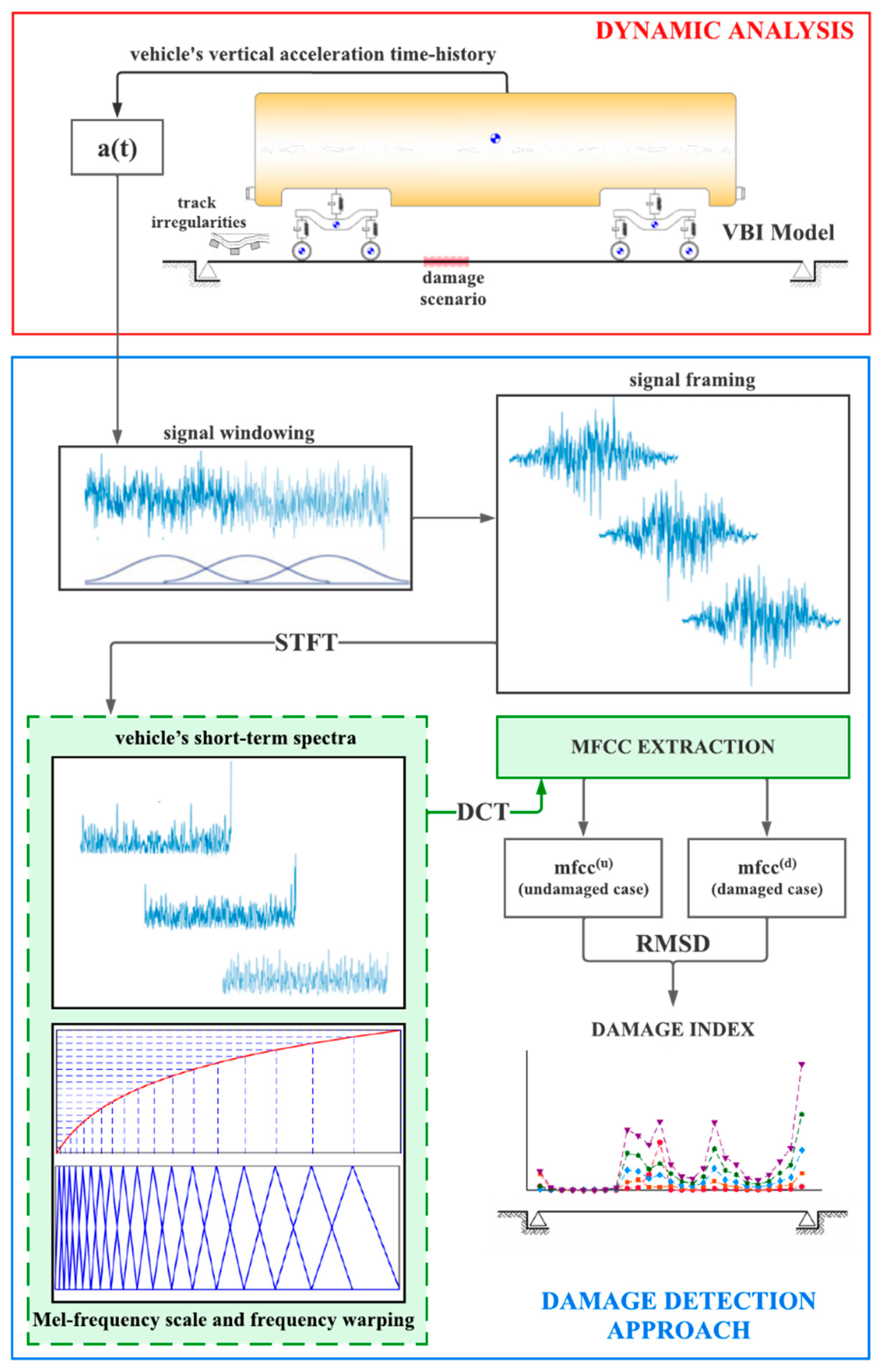
2.3. Drive-by Damage Detection Using MFCC

The main goal of feature extraction is to turn the unprocessed input signal into a representation with minimal variables, which contains the most discriminating information and which can adequately reduce the input’s dimensionality and eliminate redundant or irrelevant information, in order to produce the series of feature vectors. With this intention, cepstral analysis is frequently used to derive MFCC features from raw data [42]. The MFCC represents a signal’s short-term power spectrum, using a linear cosine transform of a log power spectrum on a nonlinear Mel frequency scale [76].

Cepstrum analysis scans and extracts information for a range of frequencies instead of merely looking for peaks, and assigns equal weights to different frequency ranges. In contrast, MFC analysis assigns more weights to lower frequency, which is crucial for bridge monitoring. MFC is originally designed to mimic how human beings respond with their auditory system, for which the conceptual distance between 100 Hz and 200 Hz is substantially more meaningful than the same linear distance between 10,000 Hz and 10,100 Hz. The scenario is comparable to the bridge’s frequency domain, where the lower frequency range containing the most significant modes is usually more meaningful than the higher frequency ranges [62].

The framework proposed in this paper for drive-by damage detection of HSR bridges using MFCC for feature extraction is discussed in this section, and can be summarized by the flow chart depicted in Figure 3.

2.3.1. Vehicle’s Acceleration Segmentation Short-Term Spectra

The Short-time Fourier Transform (STFT) is used to analyze how the frequency content of the vehicle’s acceleration signal changes over time. Thus, the vehicle’s vertical acceleration time history responses for both the healthy (undamaged) scenario and a damaged one, respectively ${\mathit{a}}^{\mathit{u}}\left(\mathit{t}\right)$ and ${\mathit{a}}^{\mathit{d}}\left(\mathit{t}\right)$, are discretized into $\mathit{j}$ segments, by sliding a window function over them. This function hops through the original signals at intervals of a pre-established number of samples. After segmentation and windowing, the vehicle’s short-term spectra of each frame of both cases, $X_j^u\left(f\right)$ and $X_j^d\left(f\right)$, are obtained by the STFT by taking the discrete fourier transform (DFT) of all the segments.

This work used the Hanning window function in the signal time discretization. When dealing with non-stationary signals, as is the case for a variety of structural response time-histories, the framing and windowing techniques are particularly advantageous. In fact, when the monitored system is excited by a very non-stationary input, such as high-speed train excitation in a bridge, the response exhibits non-stationarity features in its transient part, which is frequently the only time history recorded for short-term SHM applications [58].

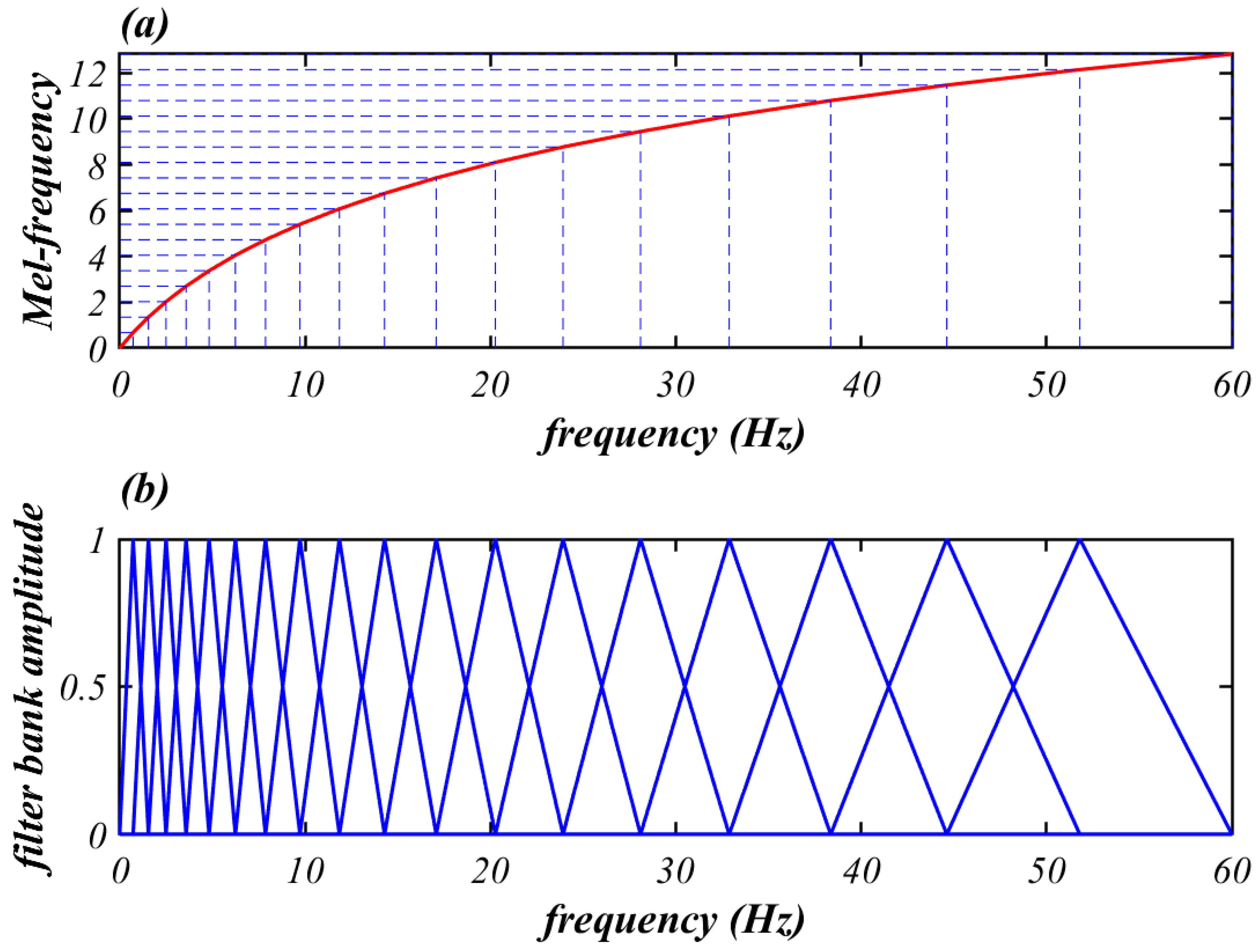
2.3.2. Adapted Mel-Frequency Scale and Frequency Warping

After the STFT has been evaluated, the frequency spectrum of each frame, in a procedure known as frequency warping, is undertaken to emphasize the signal’s Mel-frequency characteristics.

Although MFC is used for numerous applications, there is no single formula for the correspondence between Hertz and Mel frequency scales. The most widely used is given by

$$m=1127\mathit{ln}\left(1+f/700\right),$$

(4)

where $m$ is the Mel-scale frequency, and $f$ is the Hertz-scale frequency. Considering that lower frequency of bridges is always more important, an adapted formula for the transformation, to mimic the trending of Mel-scale in Equation (4) was proposed by [62] and is as follows

$$m=5\mathit{ln}\left(1+f/5\right),$$

(5)

where $m$ is the Mel-scale frequency, and $f$ is the Hertz-scale frequency.

Frequency warping is accomplished by applying a set of $N$ triangular filters, called filter bank, to weigh the DFT values. The filter bank points are uniformly spaced on the Mel-frequency scale, and their centers are symmetric with respect to one another [61]. This procedure reduces distorted information in the spectrum (or Mel-spectra, or cepstrum) of the vehicle responses at high frequencies, higher than the significant ones from the bridge. For exemplification purposes, Figure 4 shows a frequency warping for a filter bank composed of twenty filters whose Hertz-scale frequency range from 0 to 60 Hz.

2.3.3. Mel-Frequency Cepstral Coefficients (MFCC)

The next step is obtaining the list of MFCC associated with the short-term spectra. The inverse discrete cosine transform (DCT) is employed, and then the $mfc{c}_j$ discrete vector related to $j$th short-term cepstrum $X_j\left(f\right)$ becomes

$$mfc{c}_j={\left\{mfc{c}_k^j\right\}}^T, k=1,2,\dots ,N_f-2,$$

(6)

with the $k$th component $mfc{c}_k^j$ given by

$$mfc{c}_k^j={\displaystyle \sum _{n=2}^{N_f-1}Log{X}_n\mathit{cos}\left(\frac{\pi }{N-2}\left(n-\frac{3}{2}\right)k\right)}$$

(7)

In Equations (6) and (7), $N_f$ is the number of filters in the filter bank, and $Log{X}_n$ denotes the $n$th filter log-energy output, which can be written as

$$Log{X}_n=\mathit{log}\left({\displaystyle \sum _{l=1}^{L}T{F}_n\left(f\right)\times {\left|X_j\left(f\right)\right|}^2}\right),$$

(8)

in which $T{F}_n$ is the $n$th triangular filter that is applied over the $j$th short-term power spectrum ${\left|X_j\left(f\right)\right|}^2$, in its $l=1,2,\dots ,L$ samples.

2.3.4. Damage Index

In the last stage of the procedure, MFCC are used to calculate the damage indices (DI), from which the HSR bridge damage prognosis is performed by comparing the aforementioned $mfc{c}_j^u$ vectors extracted from the recorded vehicle’s responses when it crosses the undamaged bridge, with the $mfc{c}_j^d$ ones provided by the vehicle passing over the bridge under the presence of damage. The along bridge span DI are taken by the Root Mean Square Deviation described as

$$D{I}_j=\sqrt{\frac{{\displaystyle \sum _{k=1}^{N-2}{\left(mfc{c}_k^{j\left(u\right)}-mfc{c}_k^{j\left(d\right)}\right)}^2}}{{\displaystyle \sum _{k=1}^{N-2}{\left(mfc{c}_k^{j\left(u\right)}\right)}^2}}}.$$

(9)

3. Numerical Simulations: Results and Discussion

The previously discussed VBI model and the drive-by damage detection procedure were implemented in MATLAB^® [64], and the feasibility of using damage features extracted from MFCC in indirect SHM of HSR infrastructure is numerically evaluated in this section for two different levels of track conditions: low disturbance (LD) and high disturbance (HD) (as described in Section 2.2), in addition to the case where no irregularity is considered (NC), for train speeds of $144 \mathrm{k}\mathrm{m}/\mathrm{h}$ and $288 \mathrm{k}\mathrm{m}/\mathrm{h}$. To analyze the sensitivity of the method regarding the intensity of the damage, five damage scenarios were simulated on the bridge, assuming bending stiffness reductions of $f_{sr}=5\%, 10\%, 15\%, 20\%$ and 25% in a region of the Euler-Bernoulli beam with $1.2 \mathrm{m}$ length (The bridge span is $L=45 \mathrm{m}$). On the other hand, to verify the sensitivity of MFFC-based DI as to the damage location, these damage scenarios were considered for different cases, in which these regions were located around the cross-section situated at the midspan and at 1/4 of the span from the left support.

The bridge parameters are summarized in

Table 2. Properties of the bridge model.

Properties		Notation	Value	Unit
Deck	Reinforced concrete density	${\rho }_c$	2500	kg/m3
	Reinforced concrete area	$A_c$	6.0191	m2
Ballast [72]	Ballast density	${\rho }_b$	1750	kg/m3
	Ballast area	$A_b$	3.6315	m2
Sleeper [72]	Sleeper mass (half)	$m_s$	170	kg
	Sleeper spacing (half)	$l_s$	0.60	m
Rail [72]	Rail mass per unit length (per rail seat)	${\overline{m}}_r$	60.64	kg/m
Euler-Bernoulli beam:
Mass per unit length		$\overline{m}$	13,350	kg/m
Modulus of elasticity		$E$	39	GPa
Cross-section moment of inertia		$I$	2.60	m4
Span length		$L$	45	m

and were determined from an idealized cross-section with a reinforced concrete deck and ballasted track (Figure 5). The rail profile was assumed to be smooth, and a track length of 40 m was considered before the bridge. The VTBI model was discretized with a bridge mesh size of 0.6 m, a rail mesh size of 0.2 m. At the first and second bridge modes, the Rayleigh damping coefficients were set to achieve a damping ratio of 0.5%. Vehicle properties were assumed for the Siemens ICE3 Velaro High-Speed Train [69] and are listed in

Table 3. Mechanical, geometrical, and suspension properties of the 2D vehicle model (ICE3 Velaro) [69].

Properties		Notation	Value	Unit
Concentrated masses	Carbody	$m_c$	47,800	kg
	Bogies	$m_b$	3500	kg
	Wheelsets	$m_w$	1800	kg
Rotary inertia	Carbody	$J_c$	1.96 × 106	kg·m2
	Bogies	$J_b$	1715	kg·m2
Stiffness coefficient (*)	Primary suspension	$k_{1y}$	2.40 × 106	N/m
	Secondary suspension	$c_{1y}$	2.00 × 104	N·s/m
Damping coefficient (*)	Primary suspension	$k_{2y}$	7.00 × 105	N/m
	Secondary suspension	$c_{2y}$	4.00 × 104	N·s/m
Distances
Distance between bogie centers in one car		$L_c$	17.375	m
Distance between wheelset axles in one bogie		$L_b$	2.50	m
Distance between bogie centers from adjacent cars		$L_{ac}$	7.40	m

⁽*⁾ For the 2-D model, the stiffness and damping coefficients of each spring-damper set in the suspension systems correspond to the equivalent constants of a parallel arrangement of the axle boxes at both sides of each axle. Thus, the assumed values were taken from the reference values (given per axle box) multiplied by two for these properties.

.

3.1. Dynamic Analysis

In the dynamic analyses, a train composed of three cars was considered for all the numerical simulations. VTBI’s equations of motion system—Equation (1)—were solved by Newmark-$\beta$ method algorithm, considering a constant time step $\mathsf{\Delta }t$ equal to $0.0005$s.

In the assembly of the global VTBI matrices of Equation (4), on the bridge level, the structural damping was computed assuming Rayleigh proportional damping, defined by setting a damping ratio of $\nu =2.5\%$ for the bridge’s first and second vertical mode.

Table 4. Bridge’s natural vibration frequencies.

Vertical bending mode	1st	2nd	3rd	4th	5th	6th	7th	8th
Frequency (Hz)	2.14	8.55	19.24	34.21	53.45	76.96	104.75	136.82

presents the first eight natural frequency values of the bridge. The obtained vehicle’s natural frequency values and their corresponding mode shapes are enumerated in

Table 5. Vehicle’s natural vibration frequencies.

Mode	Frequency (Hz)
	Carbody	Front Bogie	Rear Bogie
Vertical (bouncing)	0.804	6.317	6.323
Pitching	1.089	10.525	10.525

.

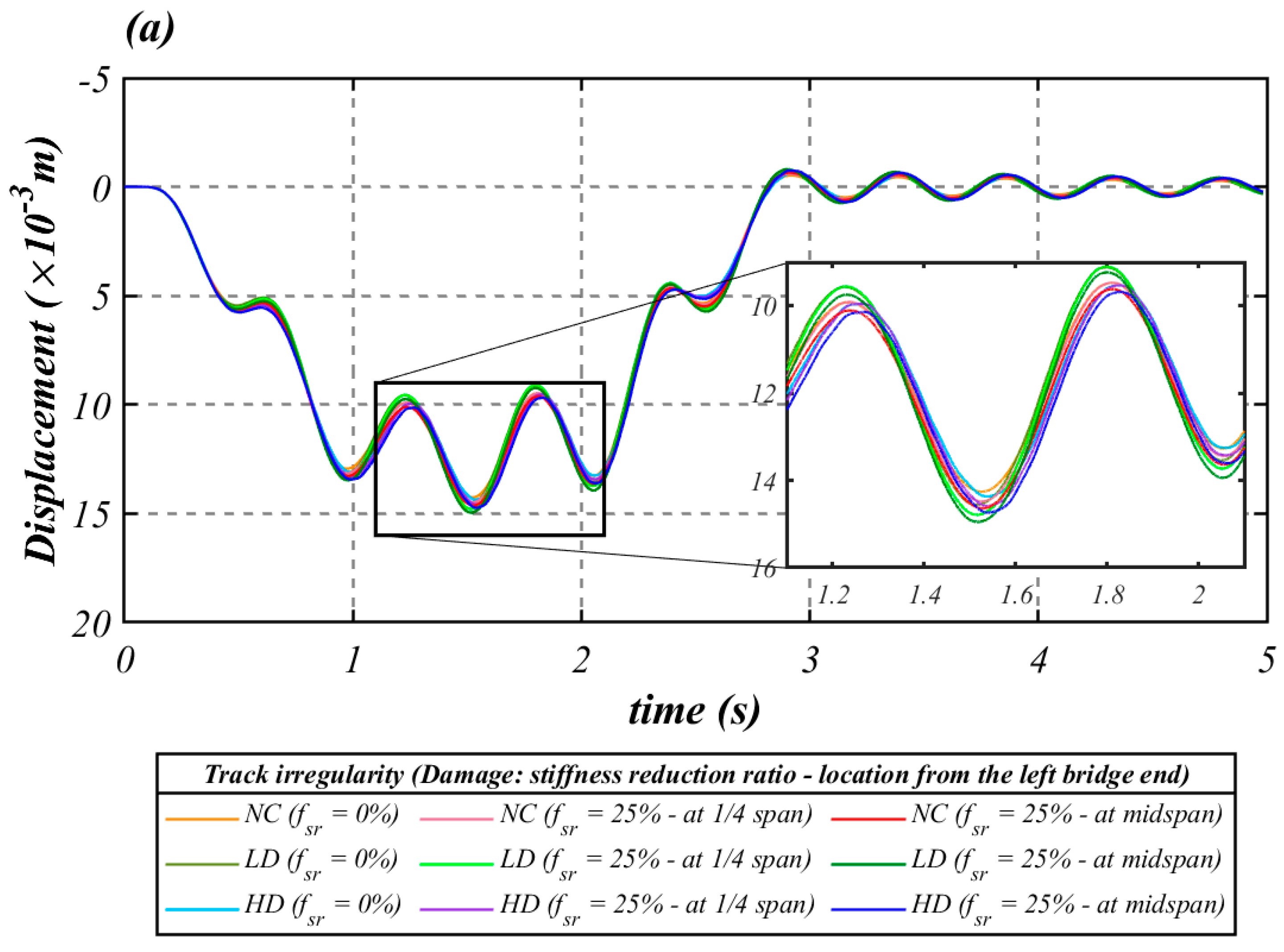
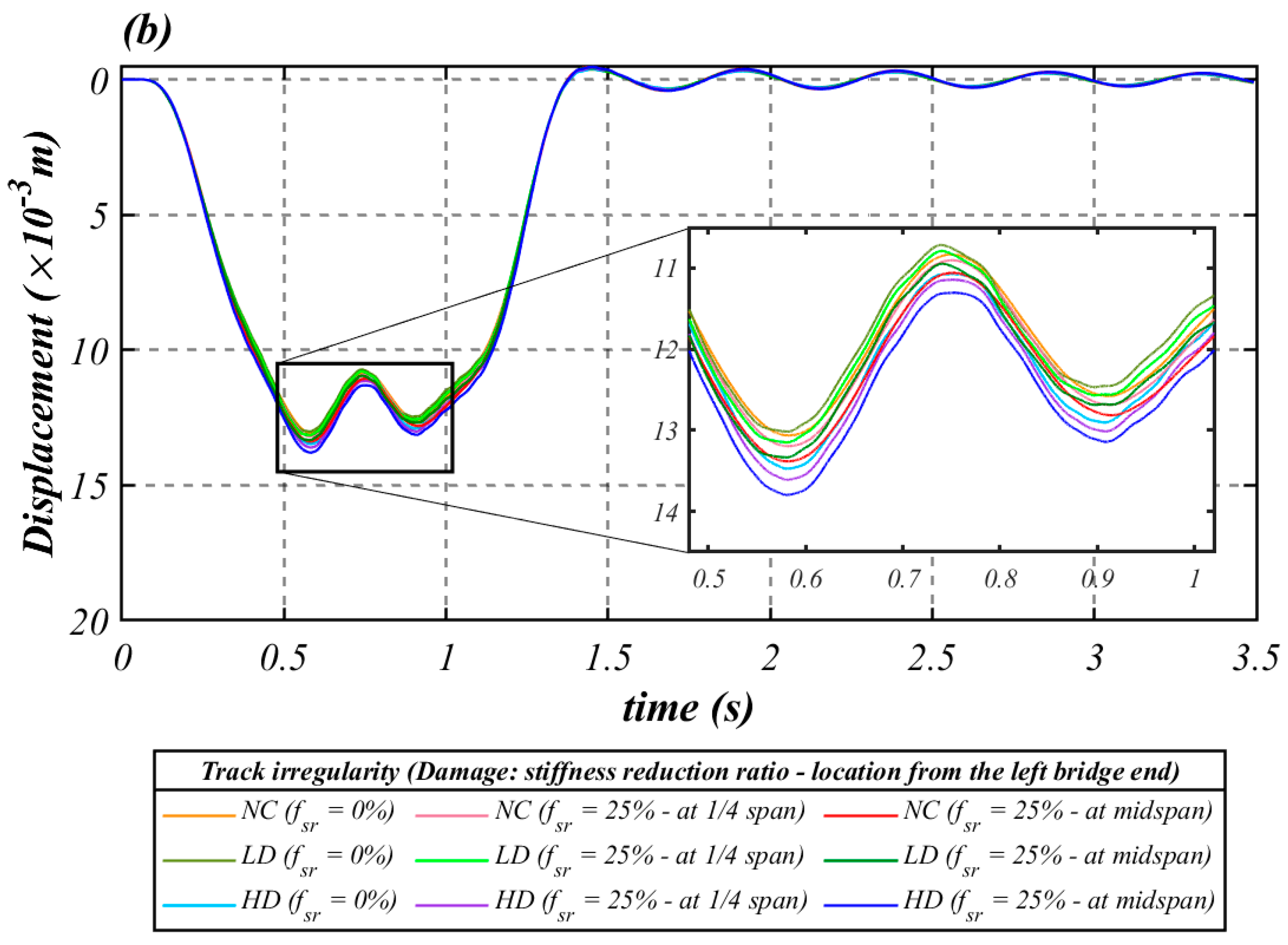
3.1.1. Bridge Response

In order to analyze the impact of track irregularities and damage conditions on the bridge response, the displacements (Figure 6) and accelerations (Figure 7) at midspan were compared for the two operating speeds mentioned above, with respect to the three track irregularity levels and to two damage conditions, where $f_{sr}=0$ (undamaged case) and $f_{sr}=25\%$ (the most extreme condition) were located at the midspan and 1/4 of the span from the left support, respectively.

Regarding the influence of the track conditions, it can be observed that the irregularities do not considerably impact the vertical displacement response of the structure (the maximum variation between results was limited to the order of 1 mm). However, in contrast, some influence is observed on the vertical acceleration response. The same considerations can be observed regarding the influence of the simulated damage conditions on the dynamic behavior of the bridge, but with the exception that, with increasing speed, the influence of the damage condition for the same level of track irregularity reduces significantly.

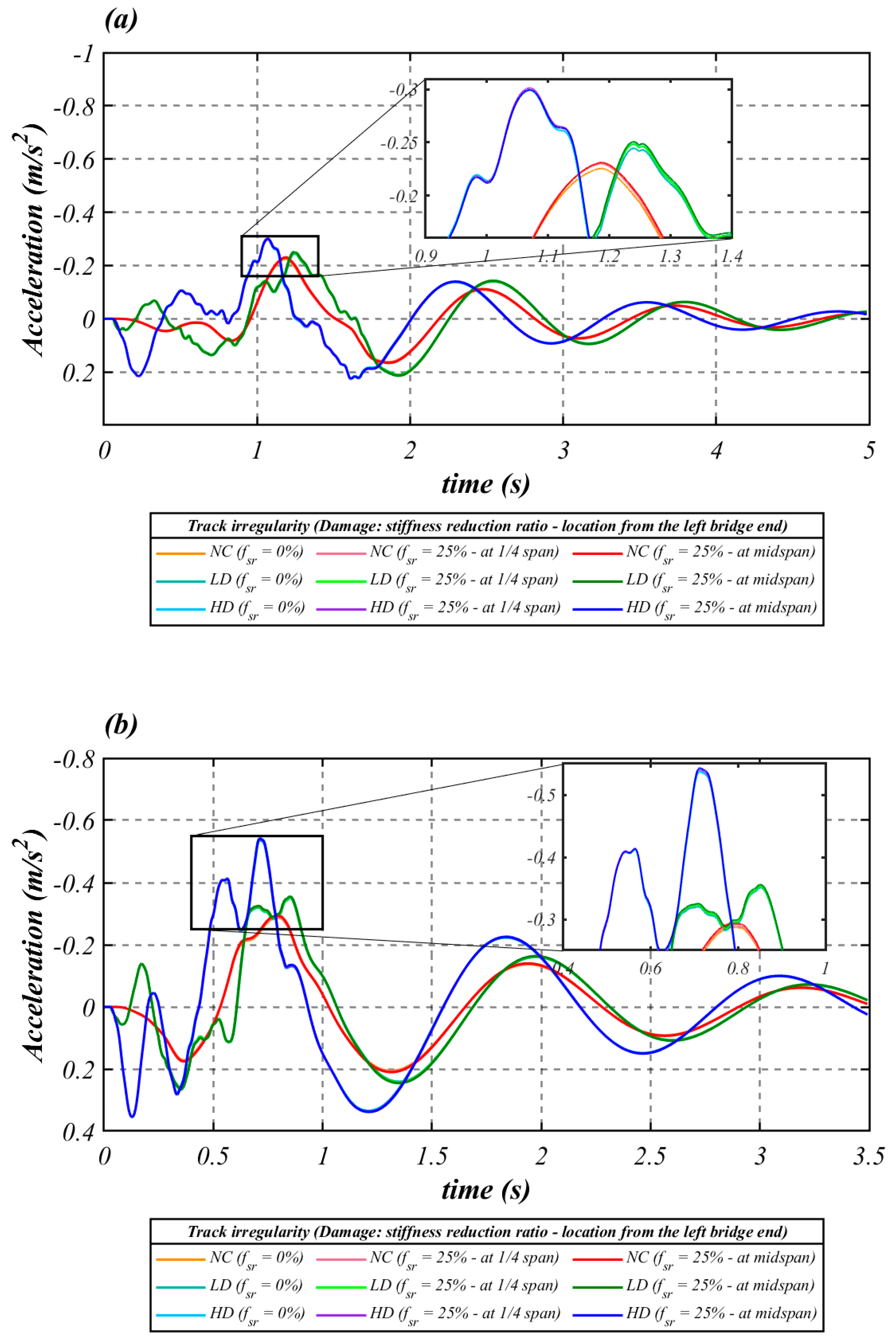
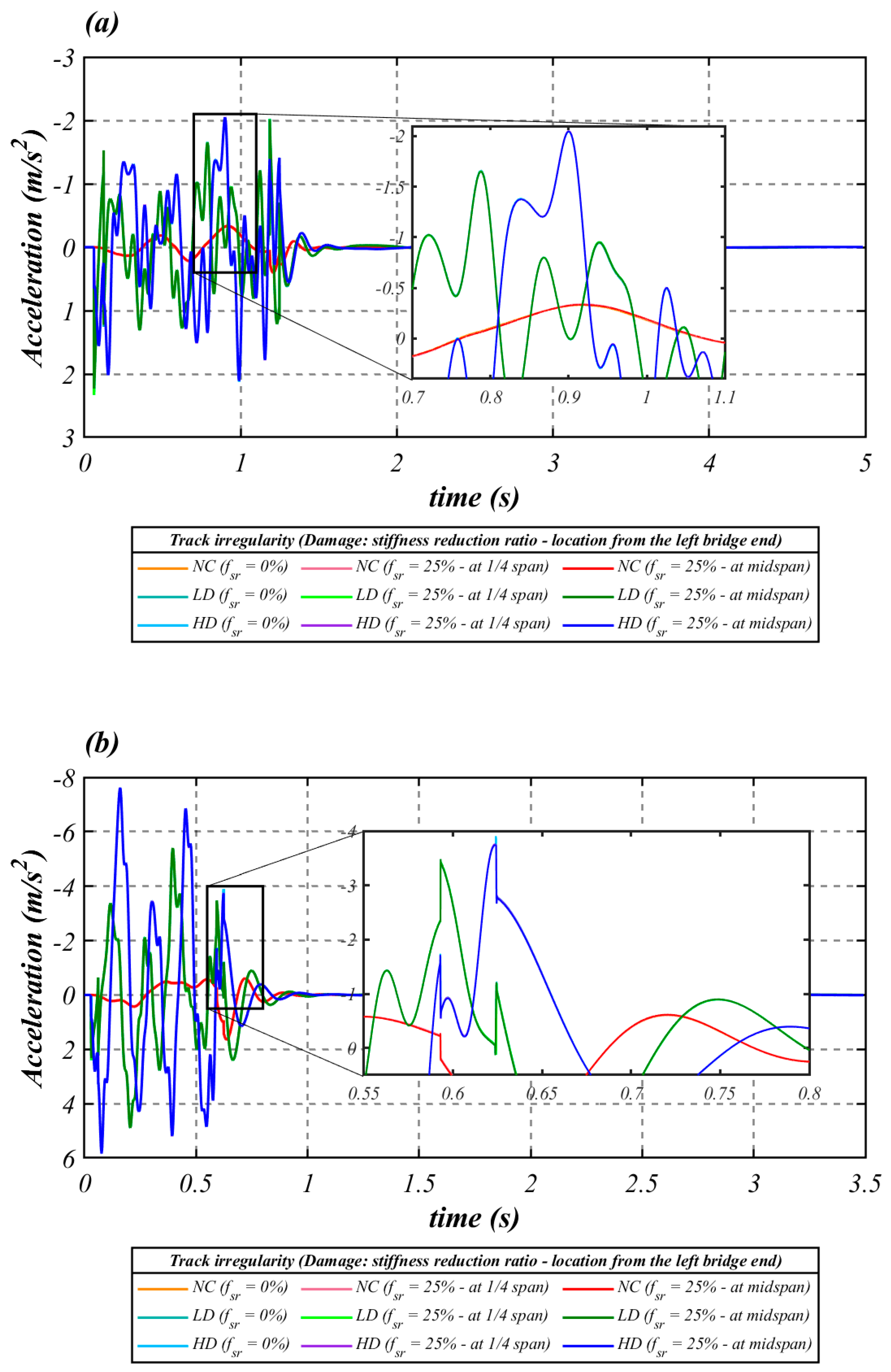
3.1.2. Vehicle Response

In order to evaluate the influence of track and damage conditions on the responses of the vehicle components, the time-histories of the vertical acceleration of the carbody and the front bogie are depicted in Figure 8 and Figure 9, respectively, for the same scenarios used for the previous discussion on the bridge response.

In contrast to what was observed for the bridge, the degree of track irregularity significantly influences the dynamic responses of both vehicle components. As for the effect of structural damage on vehicle responses, the following observations are worth noting:

• As shown in Figure 9, different damage conditions are not visibly distinguished by the bogie responses. However, due to the reduction provided by the secondary suspension system in both the frequencies and the amplitude of the carbody’s responses relative to those of the bogie, different damage conditions were picked up by the car body’s vertical accelerations, albeit subtly. For this reason, the methodology proposed in this paper was applied, concerning the carbody accelerations.
• Figure 8a,b shows that the differences between the responses to damage severity become less apparent with increasing speed. This aspect represents the main challenge to be overcome in developing vibration-based drive-by damage detection methodologies for indirect SHM of HSR bridges.

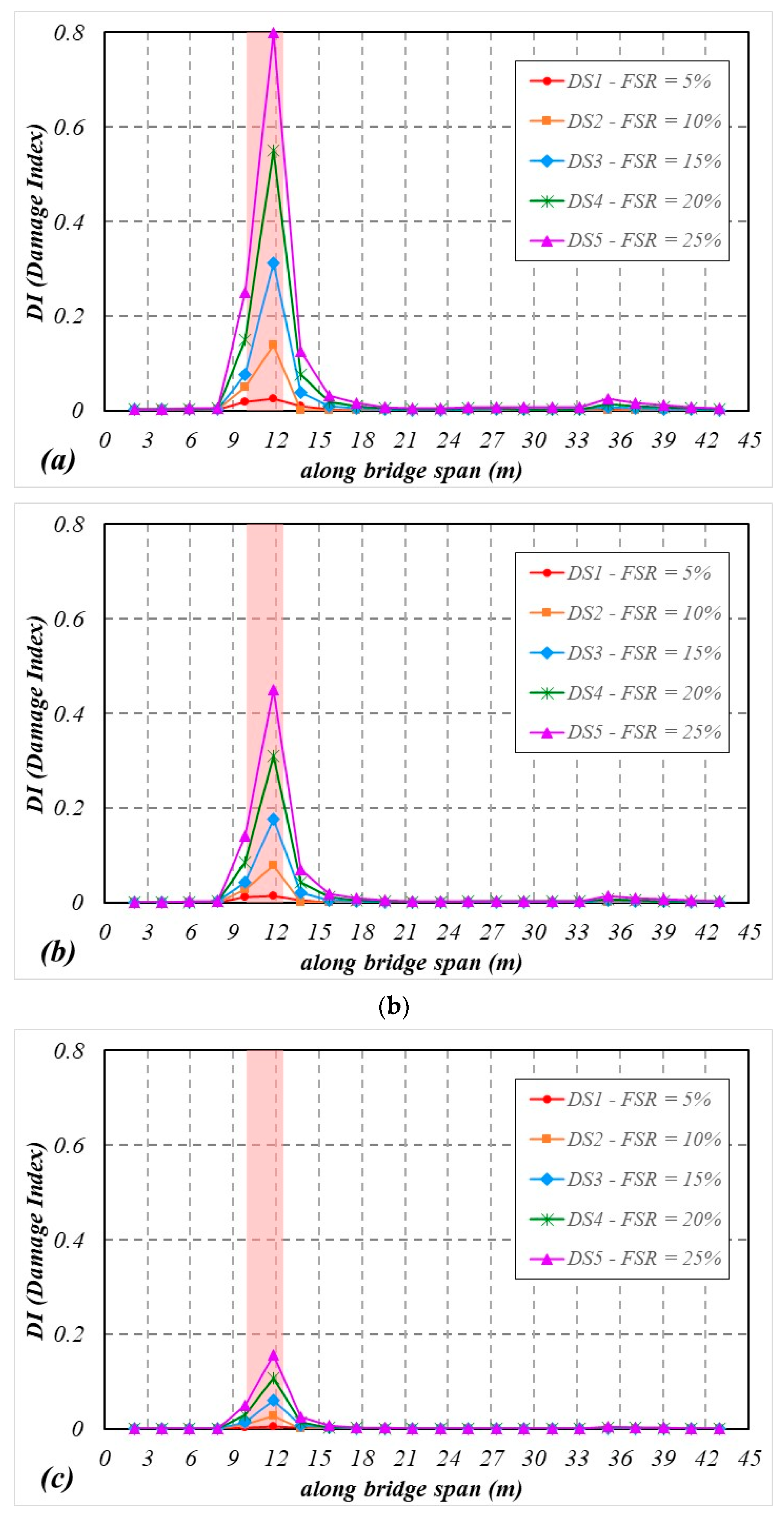
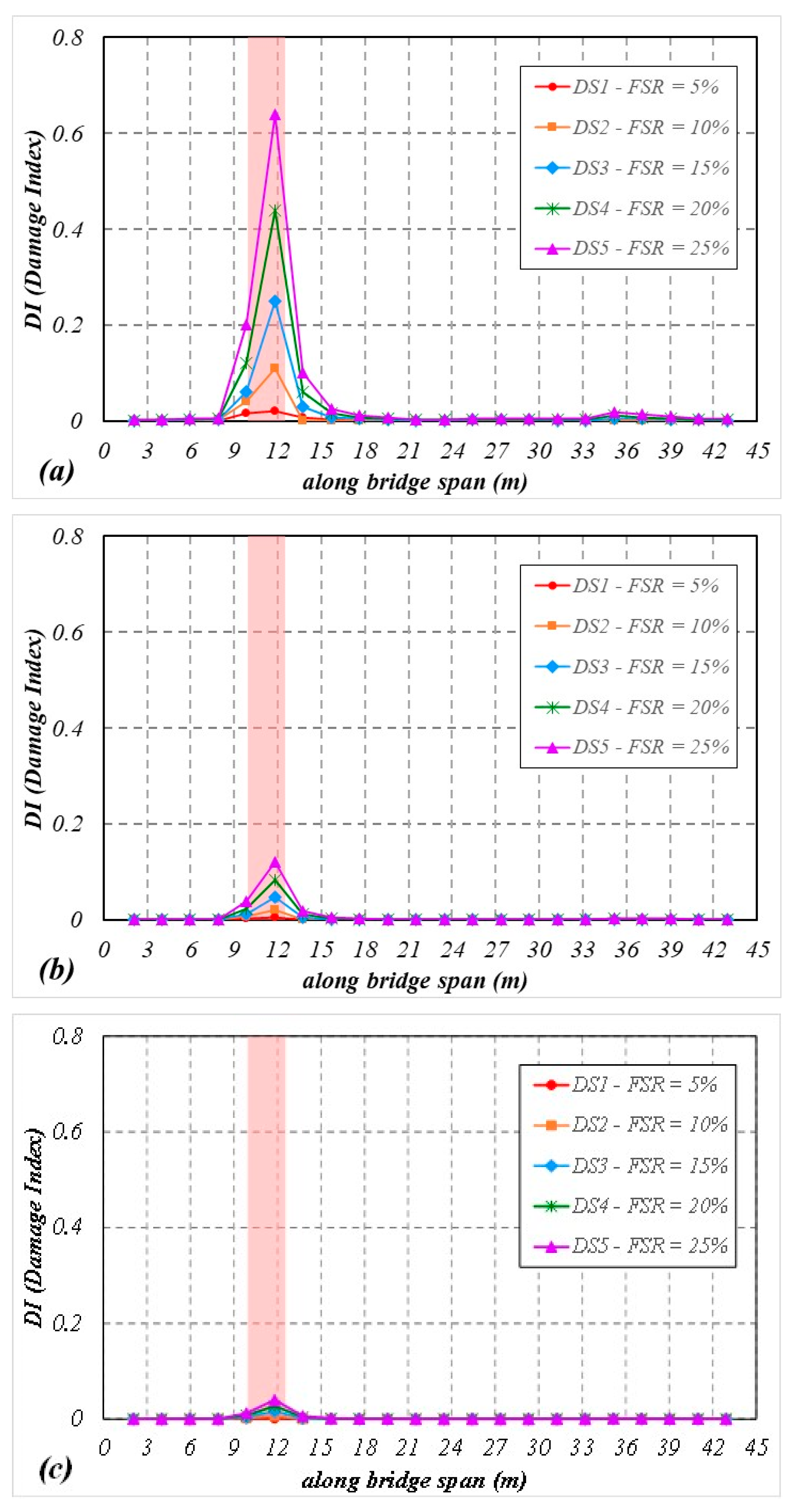
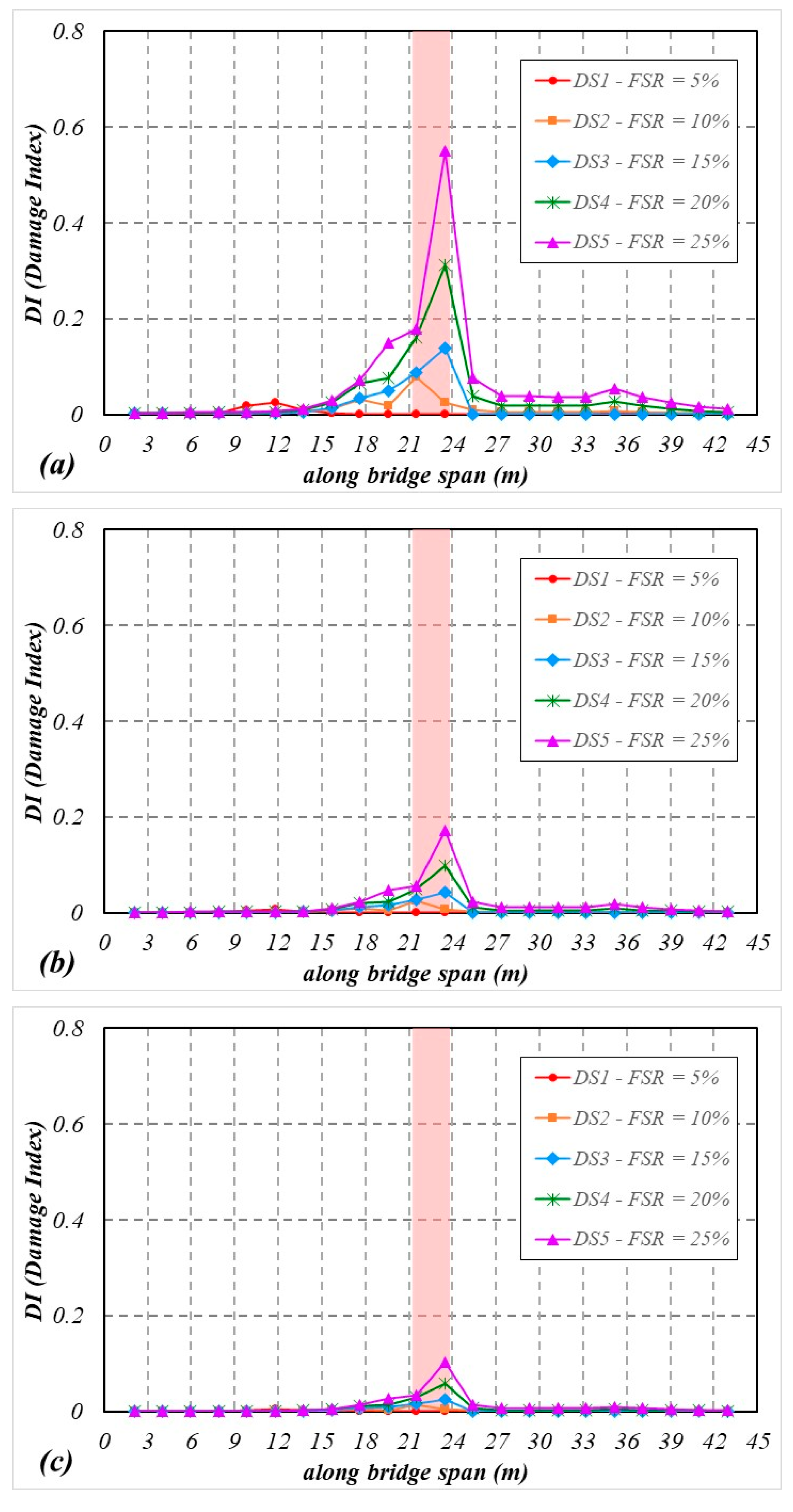
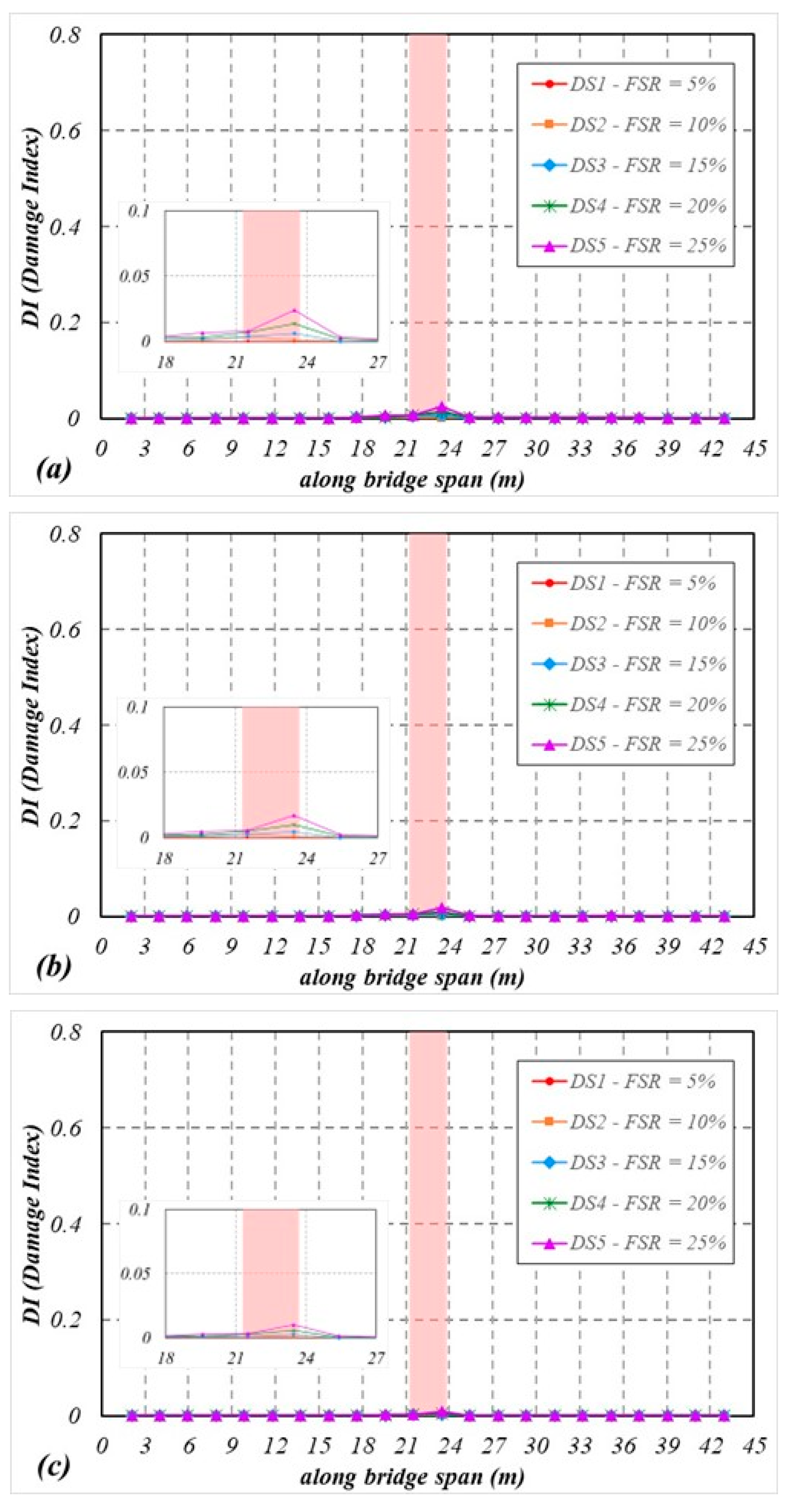
3.2. Performance of the Proposed Drive-by Damage Detection Using MFCC

To analyze the performance of the proposed damage detection procedure, all the scenarios described at the beginning of this section were used to obtain the results discussed below. The post-processing of the output data from the dynamic analyses for extracting the MFCC and obtaining the short-term DI were carried out according to the following considerations:

• The output dataset corresponding to the time-histories of the carbody’s vertical acceleration recorded at each case were corrupted by 5% white noise, to simulate the effect of measurement disturbances.
• No bandpass filters were used in the signal processing, since this procedure is already covered in the frequency warping stage, with the filter bank application.
• The filter bank was configured with 50 triangular filters, whose corresponding 50 frequency values in Hertz, equally spaced on a Mel-frequency scale, had a cut-off frequency of 60 Hz.
• For the segmentation/windowing of the carbody’s signal recorded, the STFT was set up with a window function length of $2^{11}$ samples (22 frames) to guarantee enough segments for damage identification on the bridge. Moreover, as the window functions taper off at the edges to avoid spectral ringing, the corresponding overlapping used was 34/64 of the windowing length.

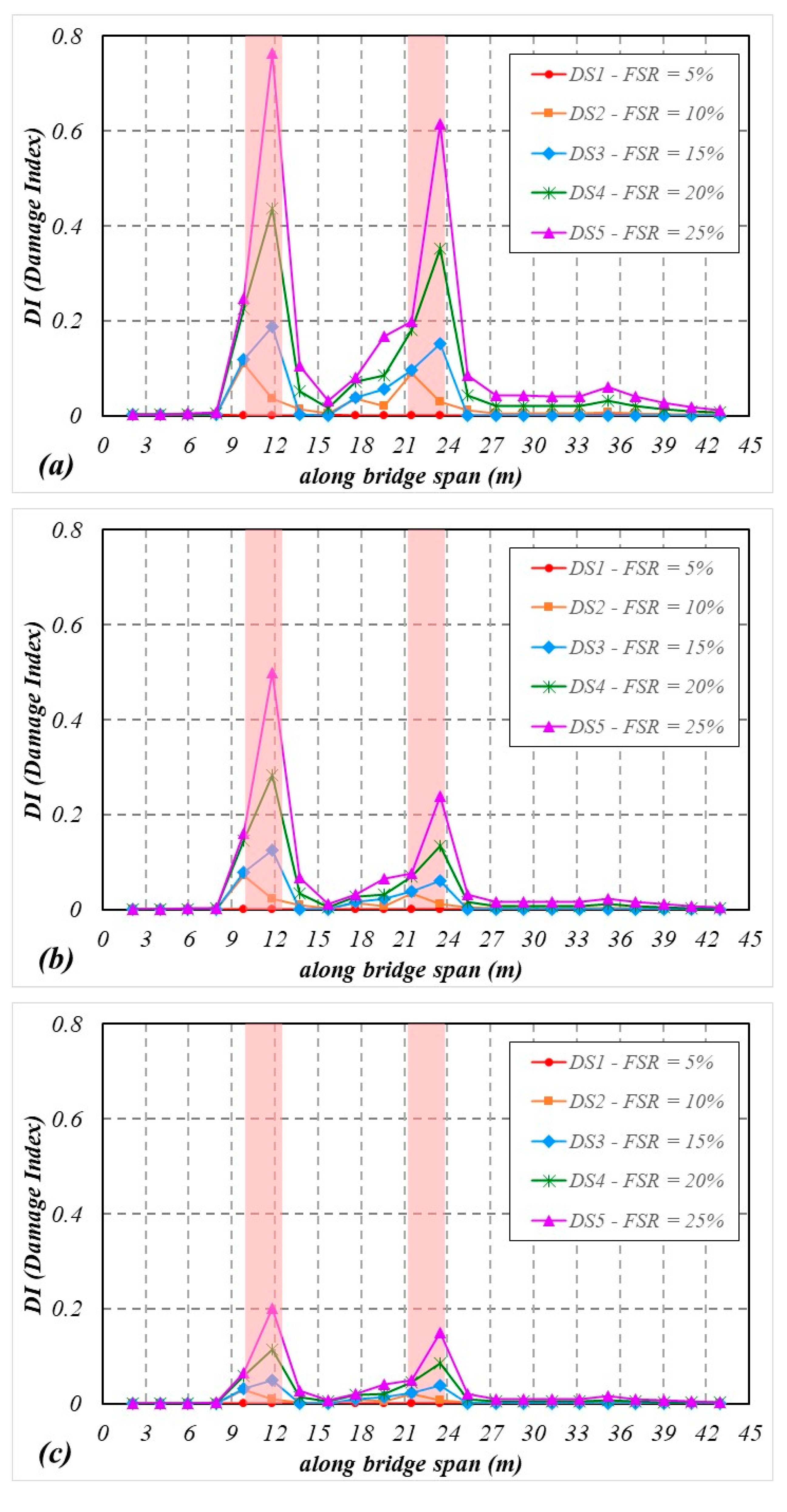
Damage Detection Performance

The performance of MFCC in providing DI that can determine whether the system is under a structural damaged condition is now being discussed. Figure 10 and Figure 11 display, for the train running speeds of $v=144 \mathrm{k}\mathrm{m}/\mathrm{h}$ and $v=288 \mathrm{k}\mathrm{m}/\mathrm{h}$, respectively, the DI values obtained for the cases where different damage scenarios were applied in the section at 1/4 of the span, under the three levels of track irregularities mentioned earlier. Analogously, Figure 12 and Figure 13 show the DI values obtained for the same conditions, but with the damage located at mid-span.

By looking at these graphics (Figure 10, Figure 11, Figure 12 and Figure 13), one can immediately see that the DI values obtained from MFCC provided robust features regarding the location of the damage. The DI values were able to indicate accurately the damage location and severity in all cases.

It can also be seen that, although the sensitivity of the proposed DI to the degree of damage and its location is unaffected, the magnitude of the feature correlates with both the speed at which the vehicle passes over the bridge and the degree of track irregularities. In this last aspect, the detectability of the technique corroborates the fact that abnormal excitations induced by roadway irregularities are more expressive than damage (especially for slight damage).

Figure 14 shows that for a multiple damage scenario, it is observed that the DI values are approximately the same as those observed for singular damage scenarios.

The different patterns of distribution of its values, in response to different damage conditions and sources of excitation, together with the potential to detect the presence and severity of the damage, suggest its feasibility and the merits of investigating its application in a drive-by methodology for damage detection of HSR bridges in a pattern recognition approach. Once these cepstrum-based features become available, they can be statistically analyzed to recognize their pattern and correlate it to a damage location.

4. Conclusions and Prospects

This research assesses the applicability of MFCC to a drive-by damage detection approach for HSR bridges. The proposed framework was implemented in MATLAB, and, using numerical simulations, damage indices (DI) were extracted from the root mean square deviation of the MFCC. They were calculated using the recorded vehicle responses when it crossed an undamaged bridge and those obtained when it passed over the structure, under induced damage scenarios in which a region of the bridge had a bending stiffness reduction in a delimited extension of its length. The dynamic analyses were performed using a finite element (FEM) 2D VTBI model that incorporates the train, ballasted track and bridge behavior. The influence of external excitations such as measurement noises and different levels of track irregularities in the methodology effectiveness were explored. Finally, the key results were summarized in the last section, and some prospects were highlighted. The results presented in this study should be seen as a first attempt to link cepstrum-based features in an HSR drive-by damage detection approach. The following major conclusions are obtained from our analysis:

• The DI values acquired from MFCC offer robust information regarding the location of the damage. In all circumstances, the DI values reliably reflect the location and severity of the damage.
• The amplitude of the feature extracted from MFCC correlates with the vehicle’s speed over the bridge and the degree of track irregularities. The DI values are more sensitive to excitation sources caused by track irregularities than those induced by damage.
• The results indicate that the distribution patterns of DI differ concerning different damage locations, with a tendency to exhibit peaks near these damaged zones.
• In this paper, no attempt has been made to apply any dimensionality reduction techniques to the extracted features, such as principal component analysis, in which a linear mapping of the MFCC can be performed to extract the components more likely to be influenced by structural properties than by other excitation sources. Neither have more sophisticated techniques such as deep learning or time series analysis been applied, to compare the statistical distributions of the MFCC and extract damage location from them. These prospects will be investigated in the future.