Experimental Validation of a Double-Deck Track-Bridge System under Railway Traffic
Abstract
:1. Introduction
- -
- Development of an advanced methodology capable of characterizing the degradation of the continuous ballast layer over bridges, particularly in the longitudinal joints between adjacent decks of double-deck bridges. In these specific zones, the ballast is subjected to cyclic movements induced by rail traffic, which can significantly reduce the interaction effect between adjacent decks. The two-step proposed methodology consists, first, of a model updating strategy based on experimental modal parameters and using a genetic algorithm, and second, of a validation strategy to evaluate the robustness of the calibrated model in adequately simulating the dynamic response of the bridge for the train passages. An important contribution of this work is the validation of the dynamic responses on the deck carrying the passing train, as well as on the neighbourhood half-deck, which represents a challenge in terms of the model accuracy and efficiency.
- -
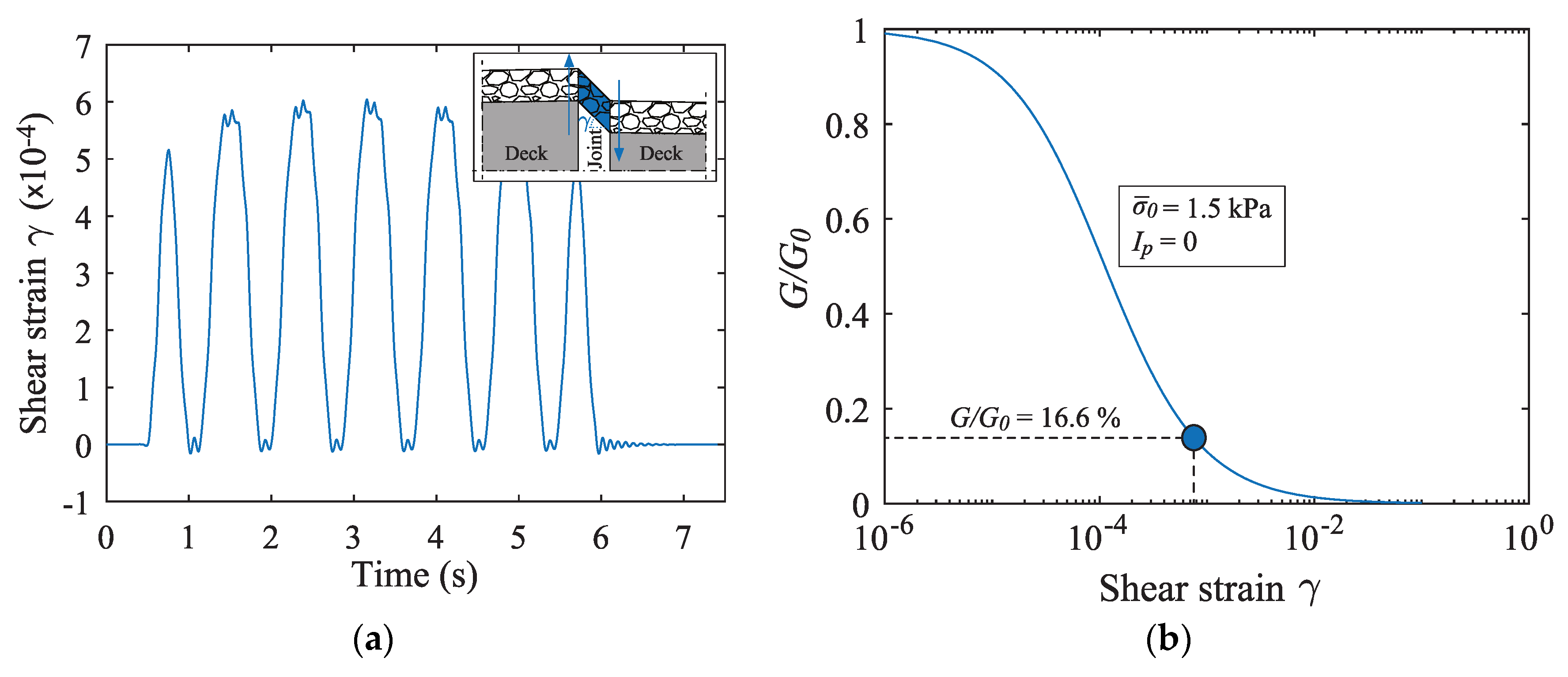
- The accurate characterization of the level of degradation of the ballast over the joint between half-decks, due to the cyclic shear strain induced by traffic loads, involves the use of a dedicated shear modulus degradation curve, proposed by Ishibashi et al. [30]. This curve can realistically estimate the ballast shear modulus reduction under the high amplitude dynamic displacements that occur during the trains’ passage.
- -
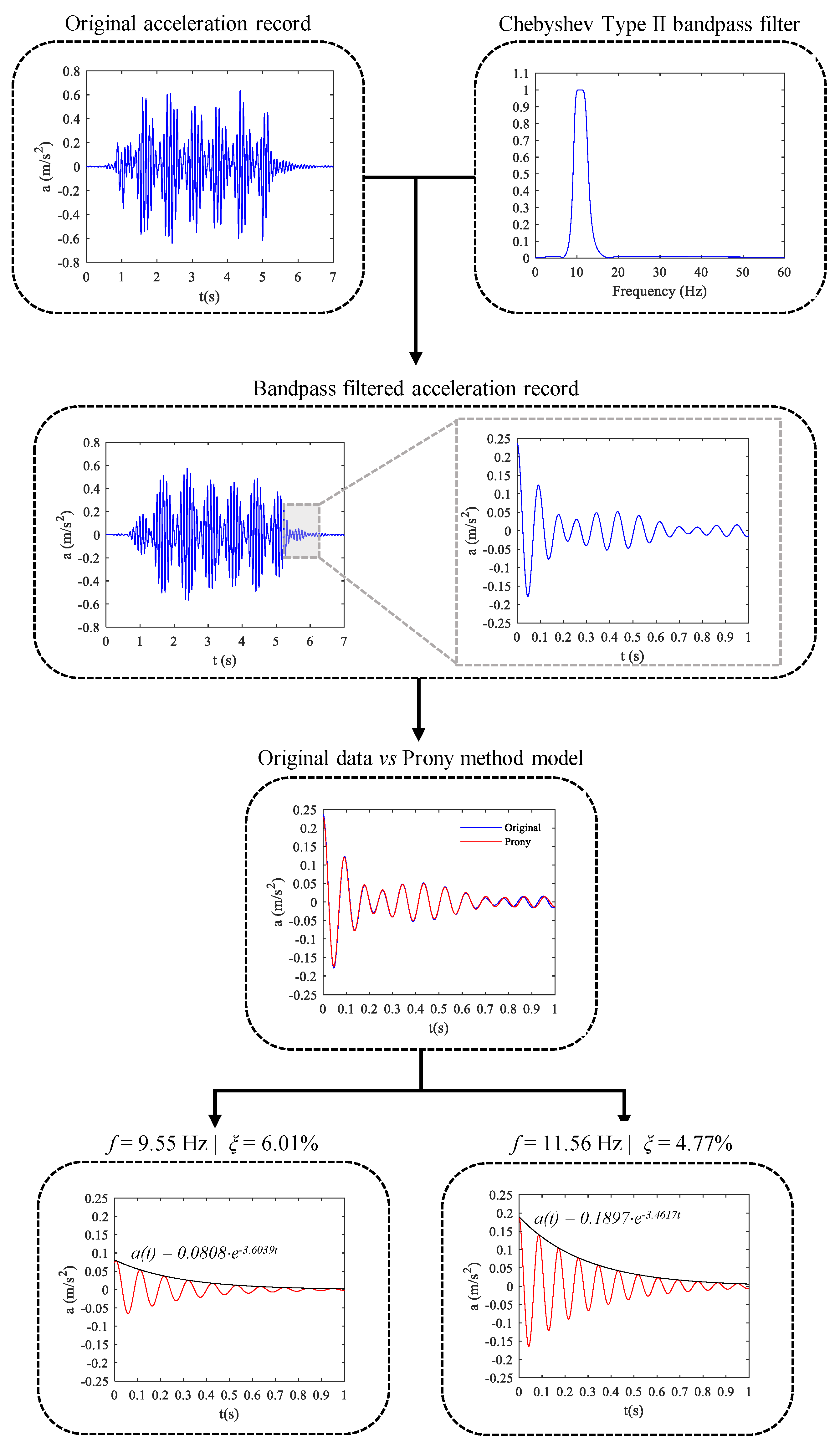
- The application of the Prony method is used for the estimation of the modal damping coefficients [31]. Comparatively to the classical Logarithm Decrement (LD) method, this method is also based on the free vibration period after the train crossing of the bridge; however, it is more efficient in situations where coupled modes of vibration are present (i.e., modes of vibration with close or very close frequencies). The existence of coupled modes is quite common in short-medium span railway bridges where the natural frequencies of the fundamental torsion and bending modes are close or even merged. The accurate modal damping estimation is decisive for the characterization of the dynamic response of the bridge, particularly in resonances or near resonances scenarios.
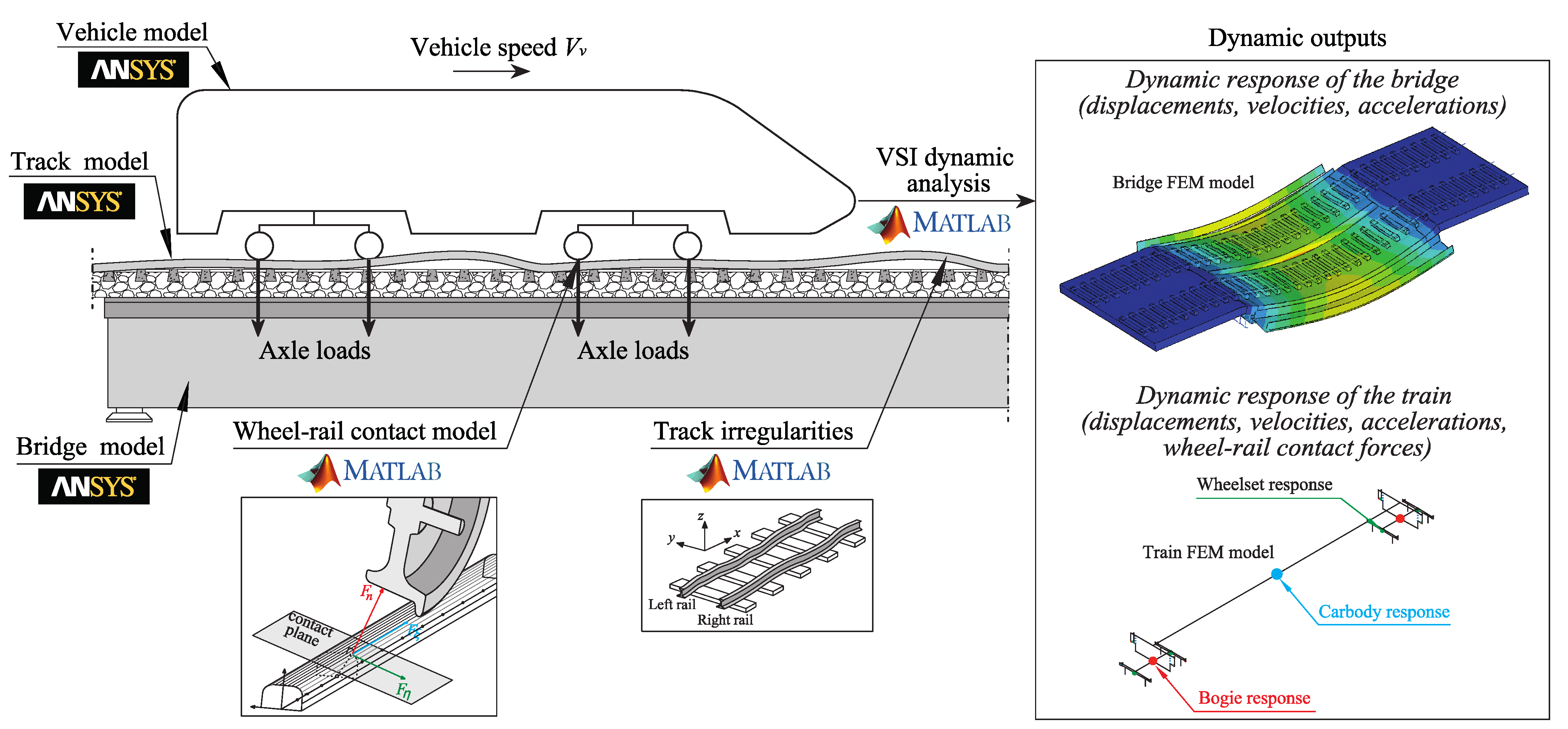
2. Numerical Modelling
2.1. Bridge Numerical Model
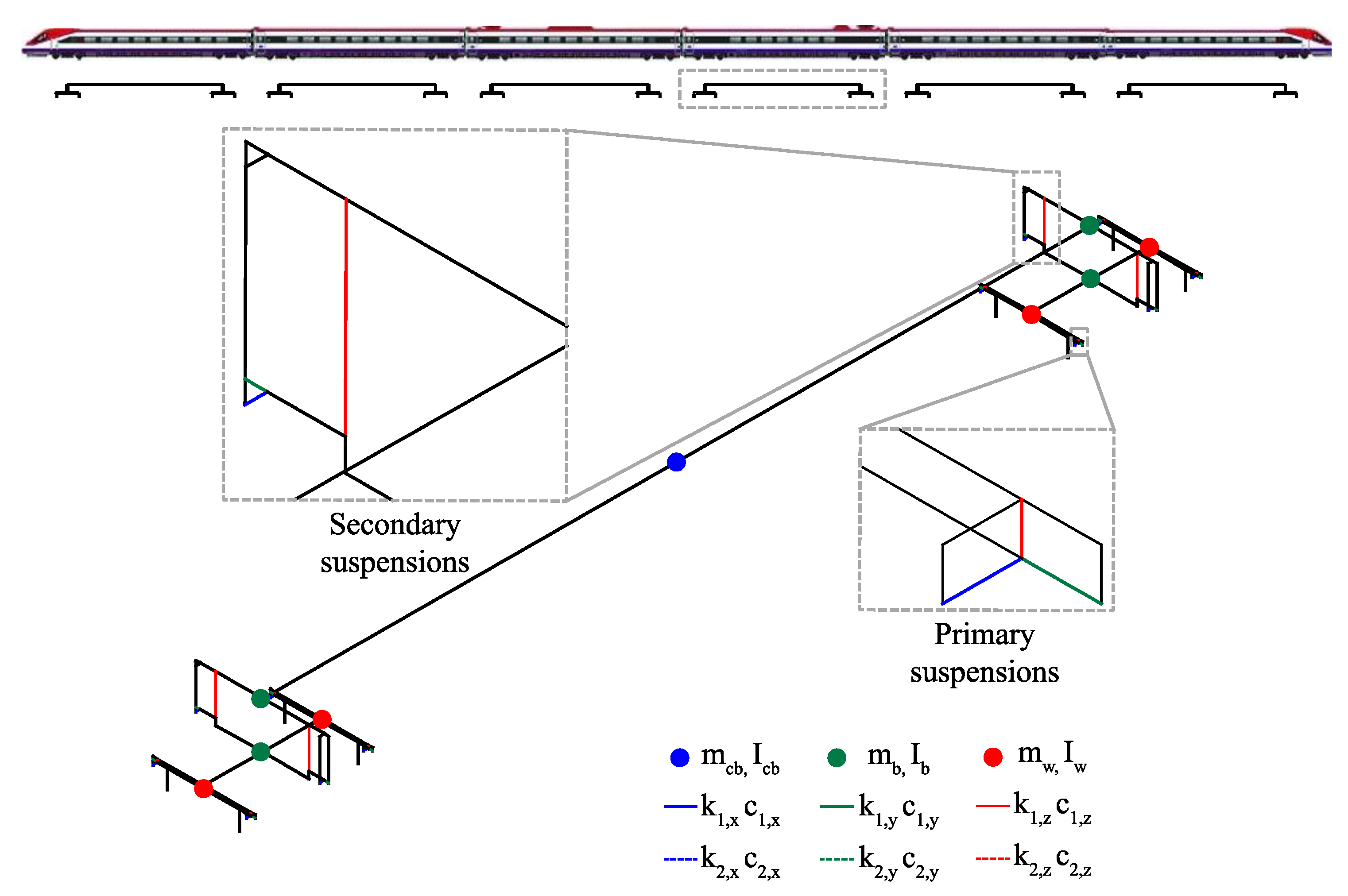
2.2. Train Numerical Model
2.3. Methodology of the Train-Bridge Dynamic Interaction
2.3.1. Wheel-Rail Contact Formulation
2.3.2. Dynamic Equations of the Train-Bridge Coupling
3. Dynamic Tests
3.1. Ambient Vibration Test
3.2. Test under Railway Traffic
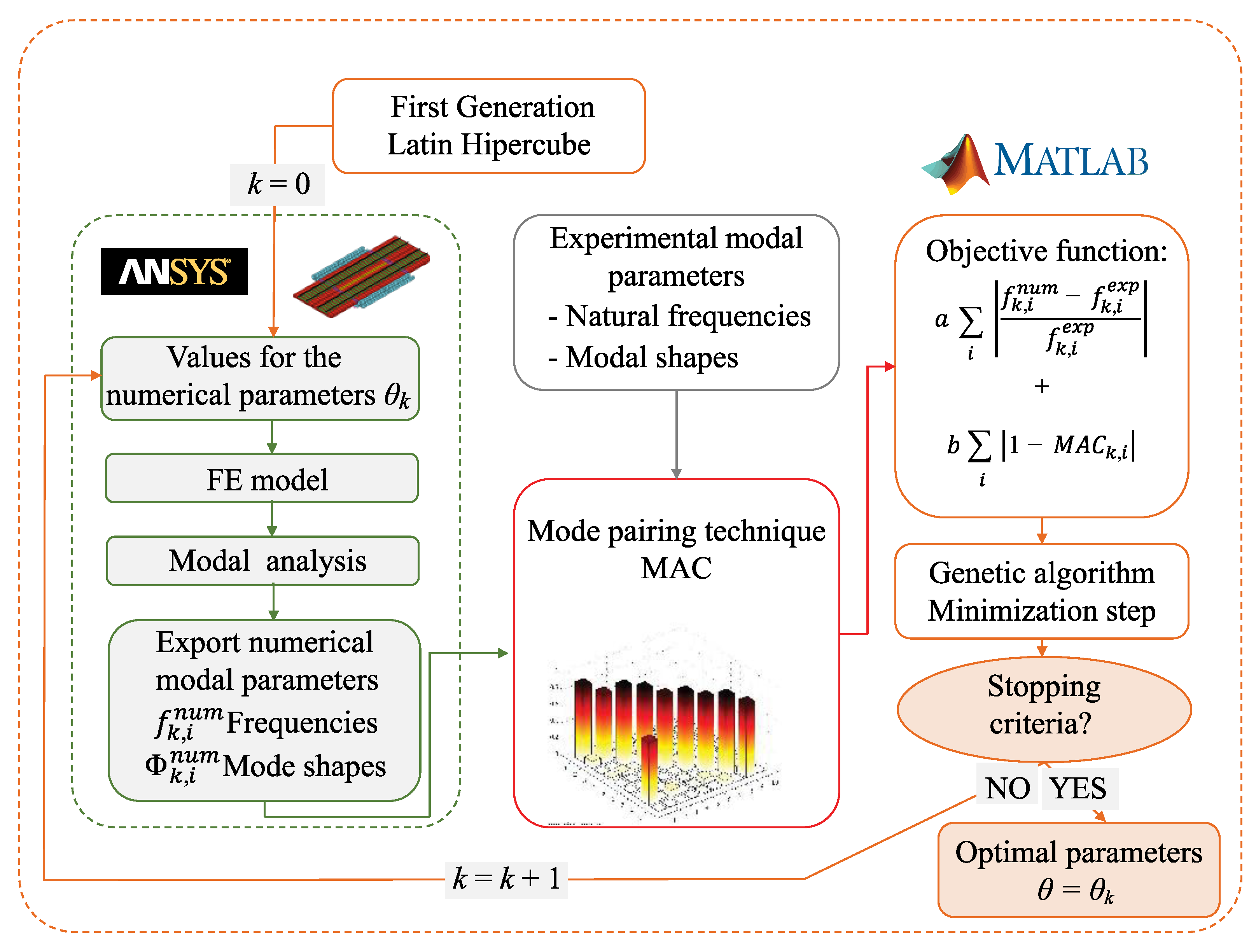
4. Model Updating
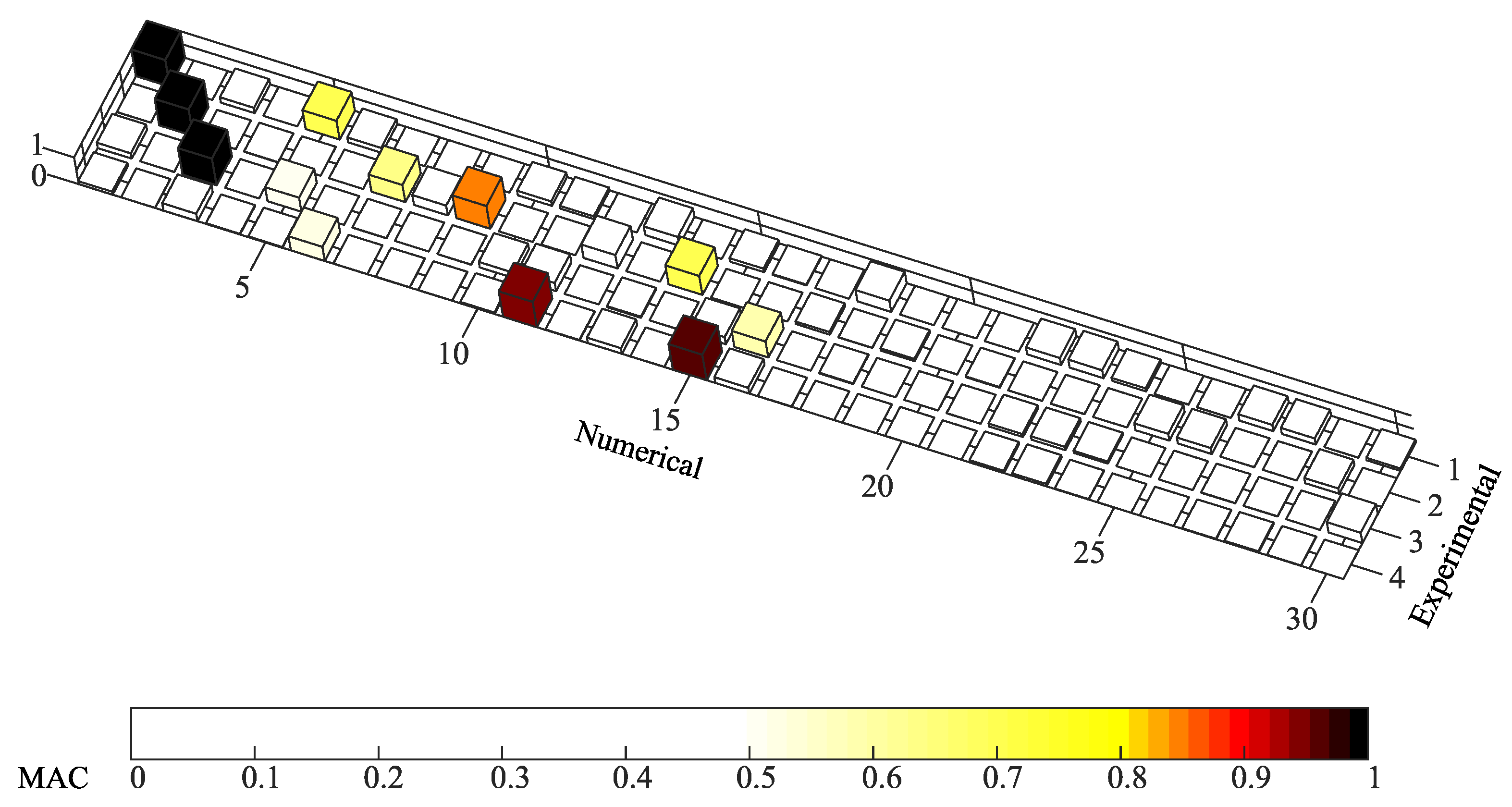
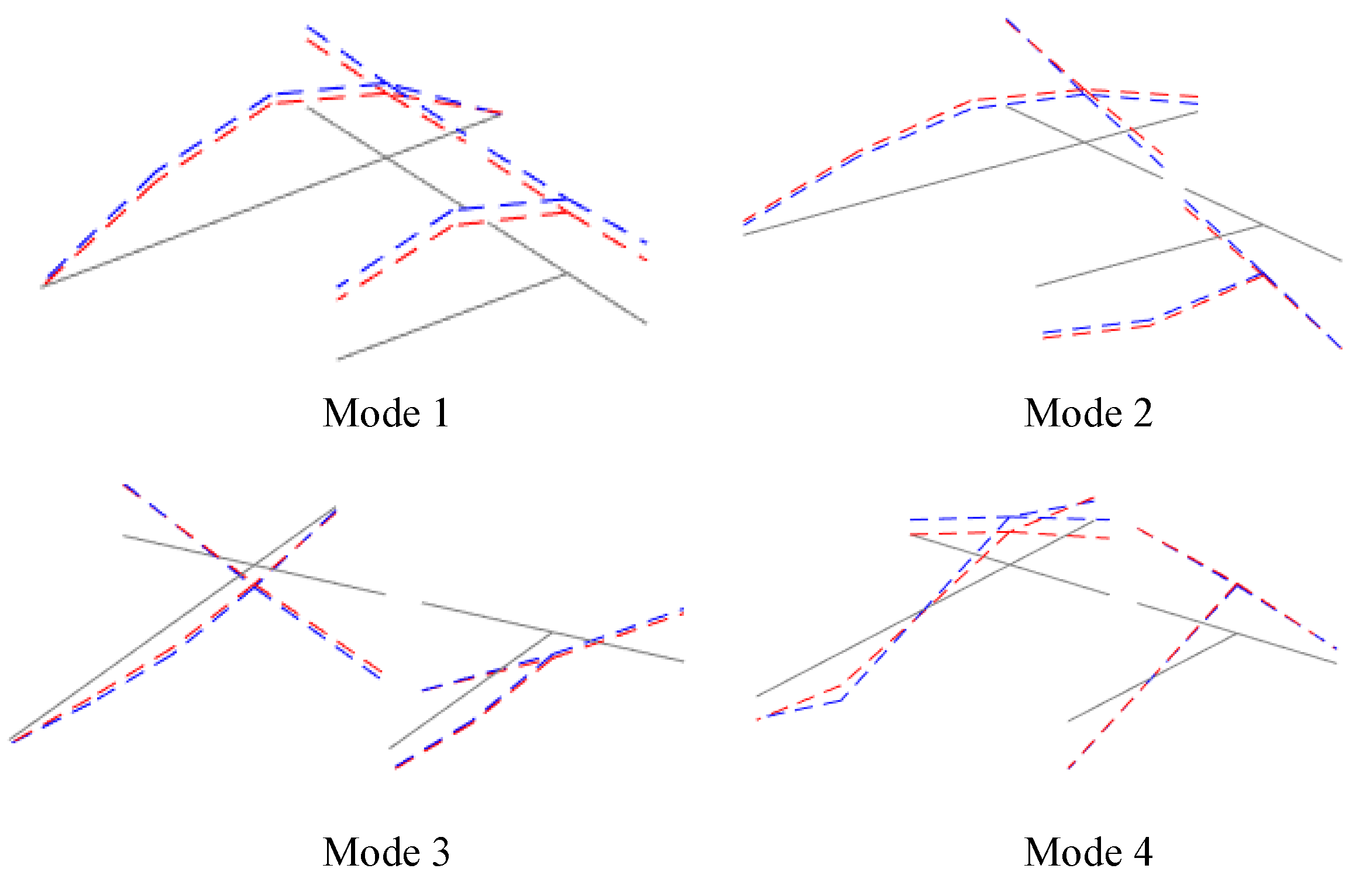
4.1. Mode Pairing
4.2. Sensitivity Analysis
4.3. Optimization
5. Model Validation
5.1. Initial Considerations
5.2. Comparison between Numerical and Experimental Bridge Response before and after the Updating Process
5.3. Influence of the Vertical Stiffness of the Bearing Supports
5.4. Influence of the Degradation of the Longitudinal Joint
6. Conclusions
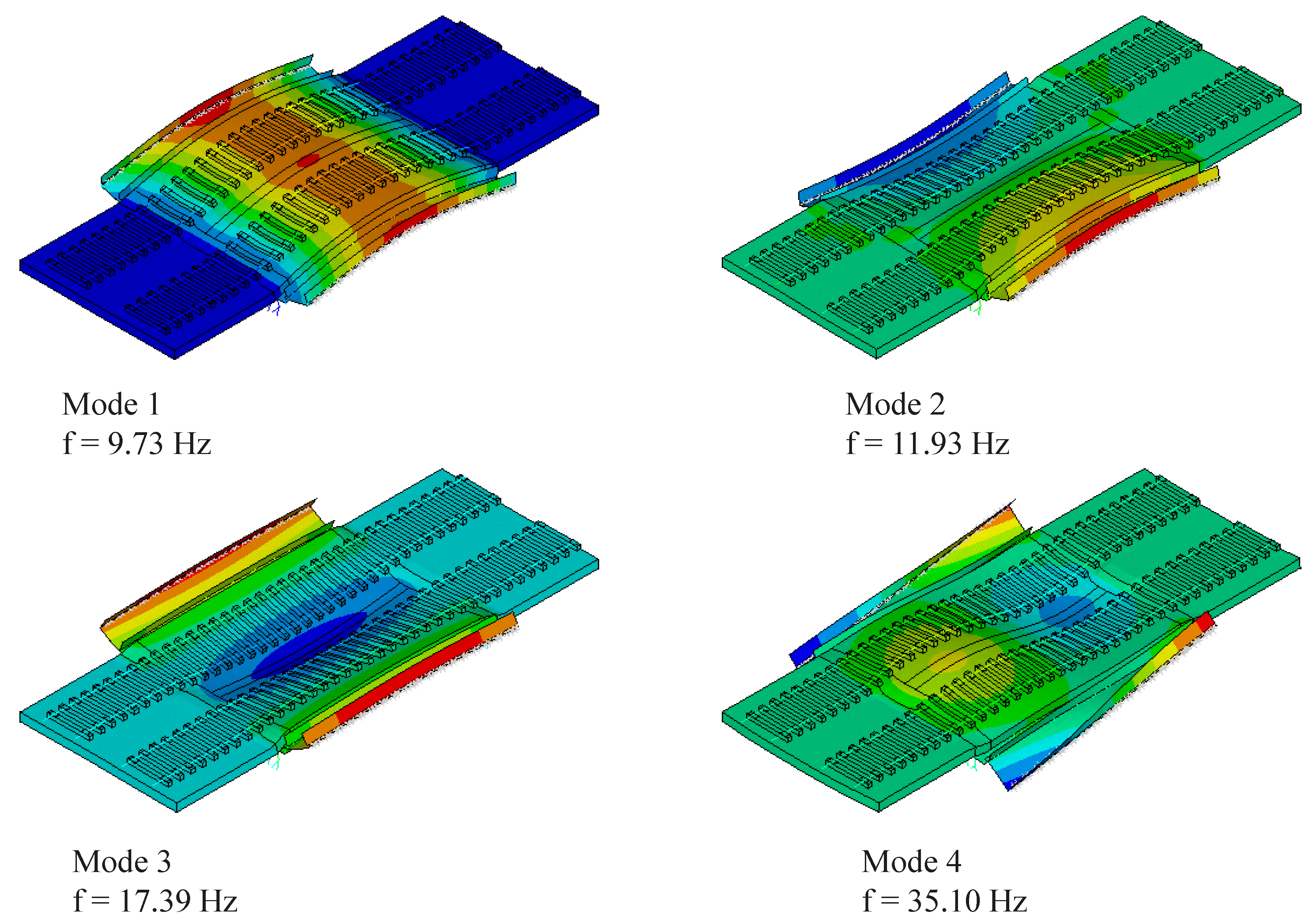
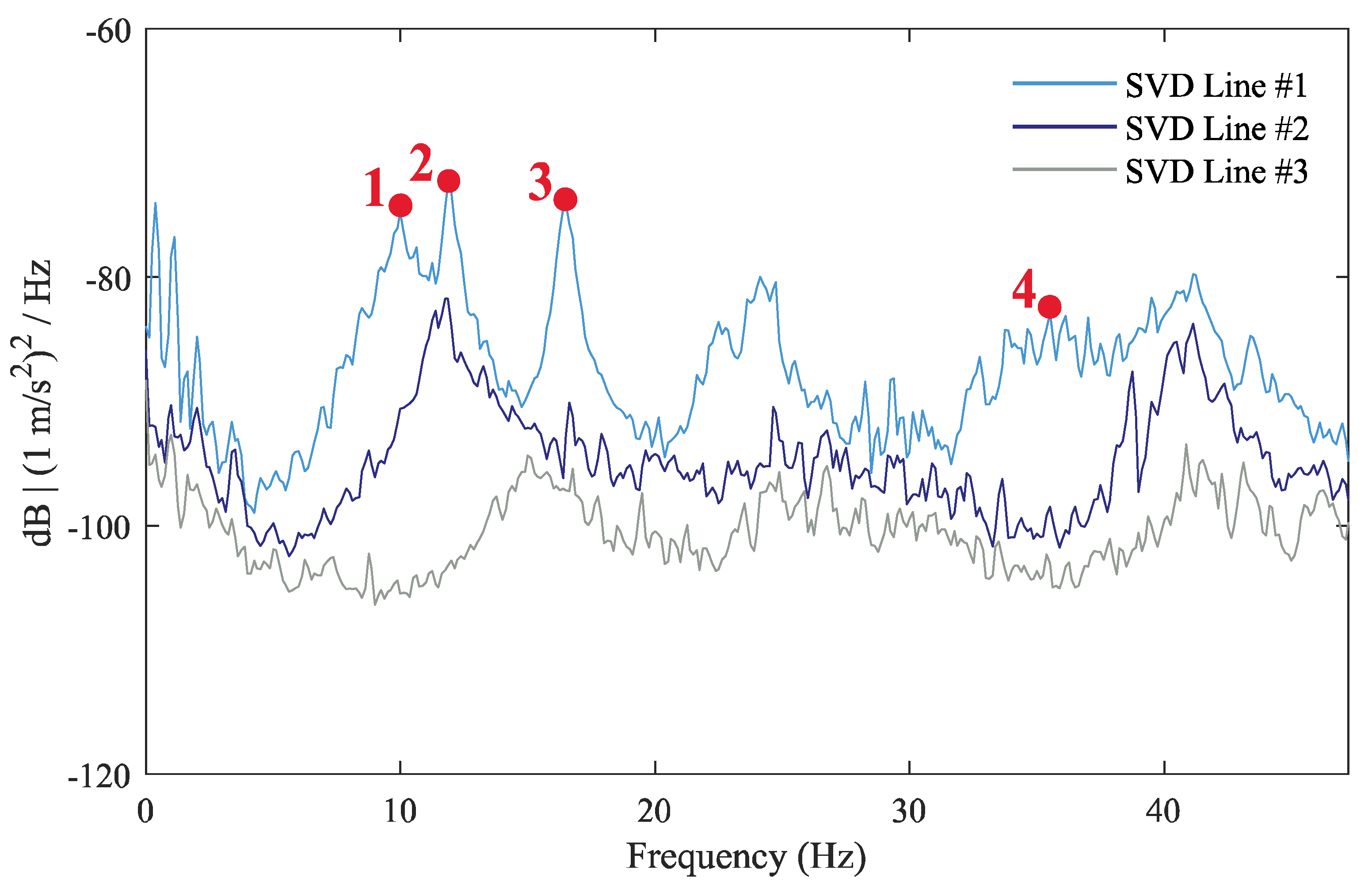
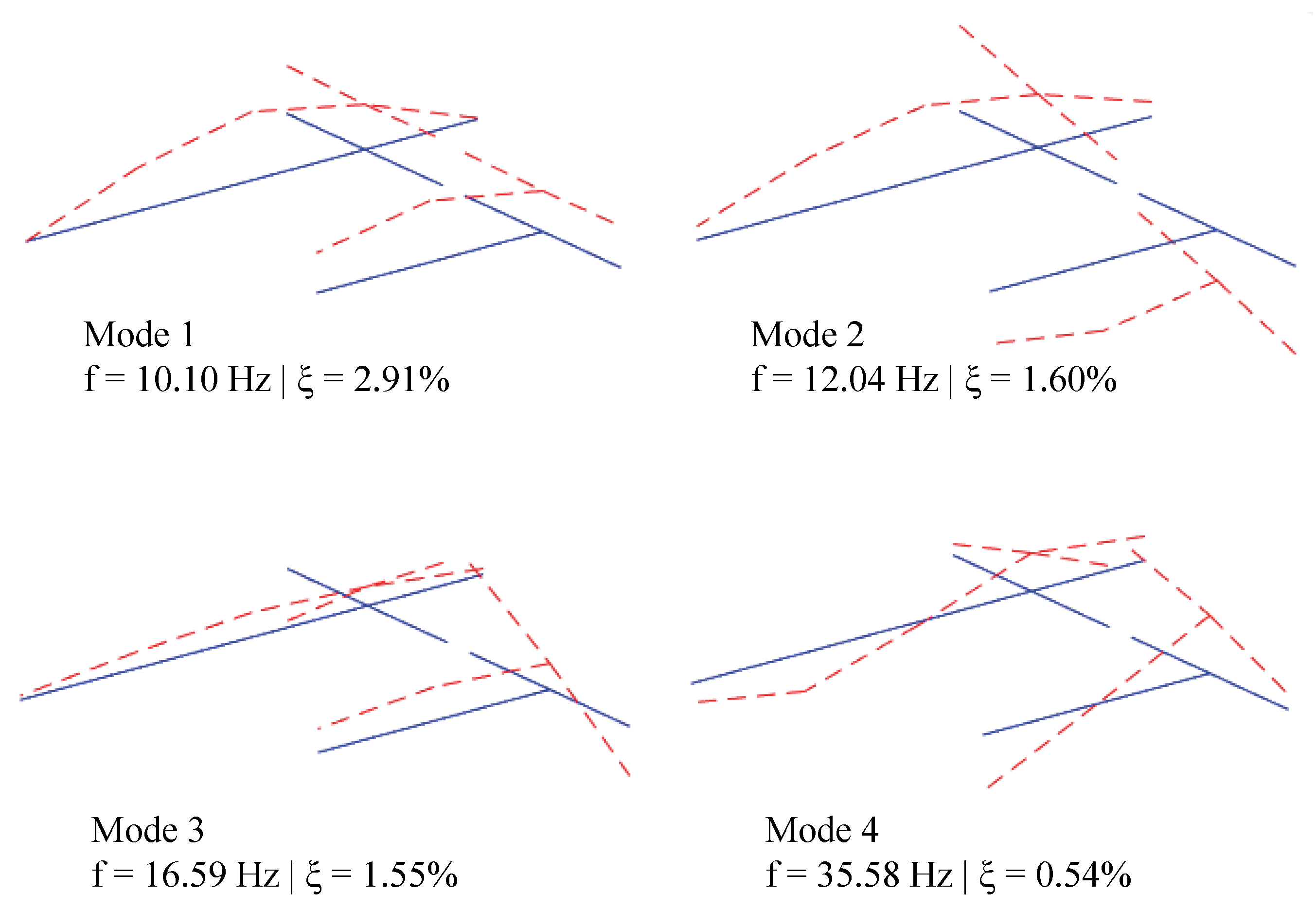
- The ambient vibration test allowed the identification of four global modes, namely the first and second vertical bending modes and two torsion modes. These modes were also identified in the initial numerical model, although still with considerable differences in terms of frequency value (errors up to almost 5%).
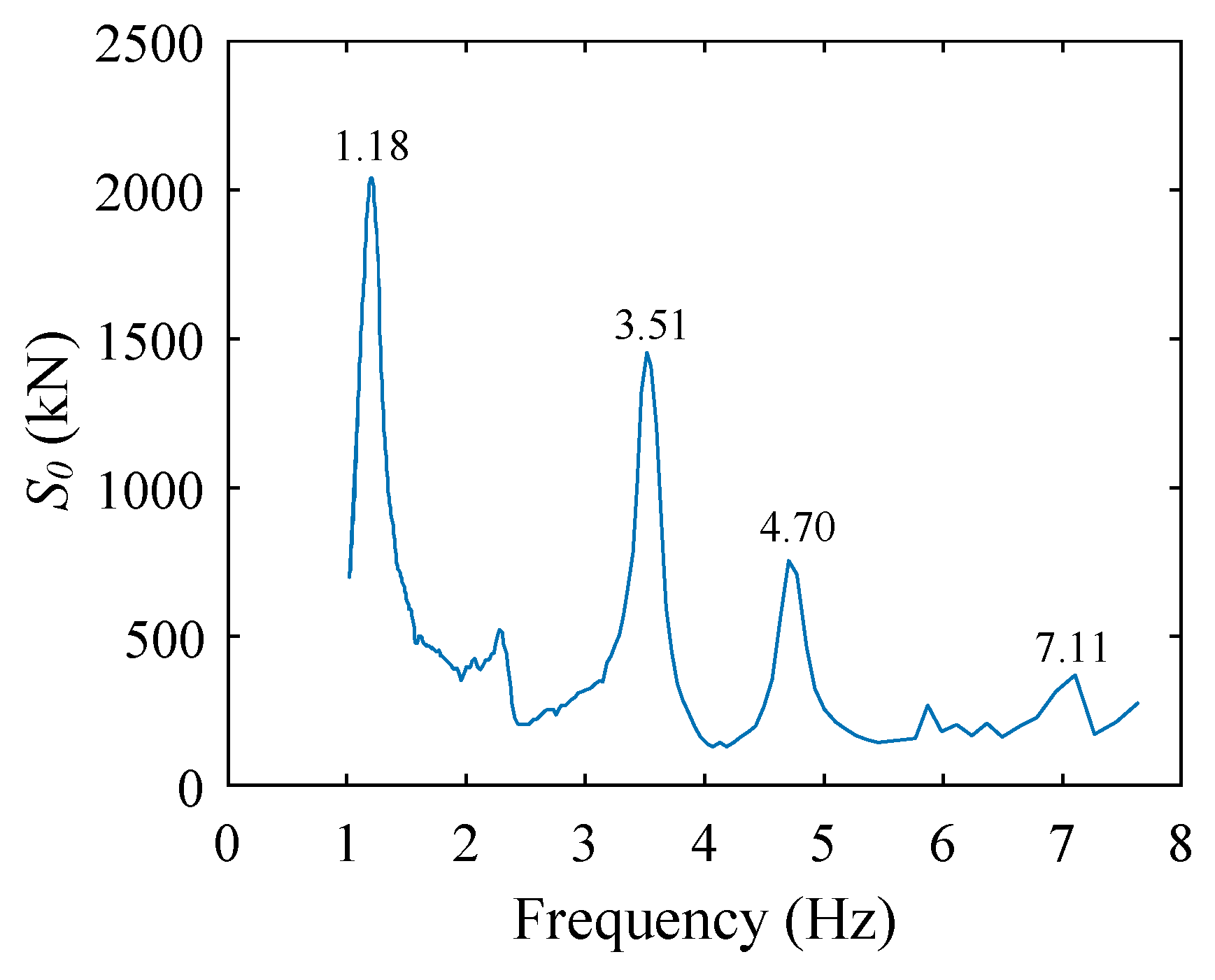
- Experimental modal damping was identified using the free vibration records obtained in the tests under railway traffic. Given the difficulty in separating the contribution of the first bending and torsional modes for the free vibration (frequencies close to each other), the Prony method was used. By adopting this methodology to the records obtained during the tests under railway traffic, mean damping ratios of 6.69% and 4.72% were estimated for the first bending and torsional modes, respectively.
- Before performing the automatic optimization process, a sensitivity analysis was carried out, showing that 5 out of the 13 analysed parameters had a significant influence in the modal response, namely the modulus of elasticity of the concrete and ballast in the longitudinal joint, the density of concrete and ballast and the vertical stiffness of the bearing supports. Based on this outcome, an updating procedure based on a genetic algorithm was carried out to calibrate the numerical model. A significant reduction in the differences between numerical and experimental natural frequencies was achieved; more precisely, the average error of the frequencies decreased from 2.65% before updating, to 0.69% after updating. Regarding the MAC coefficients, they suffer an overall increase, reaching values close to 1.0 (between 0.968 and 0.997).
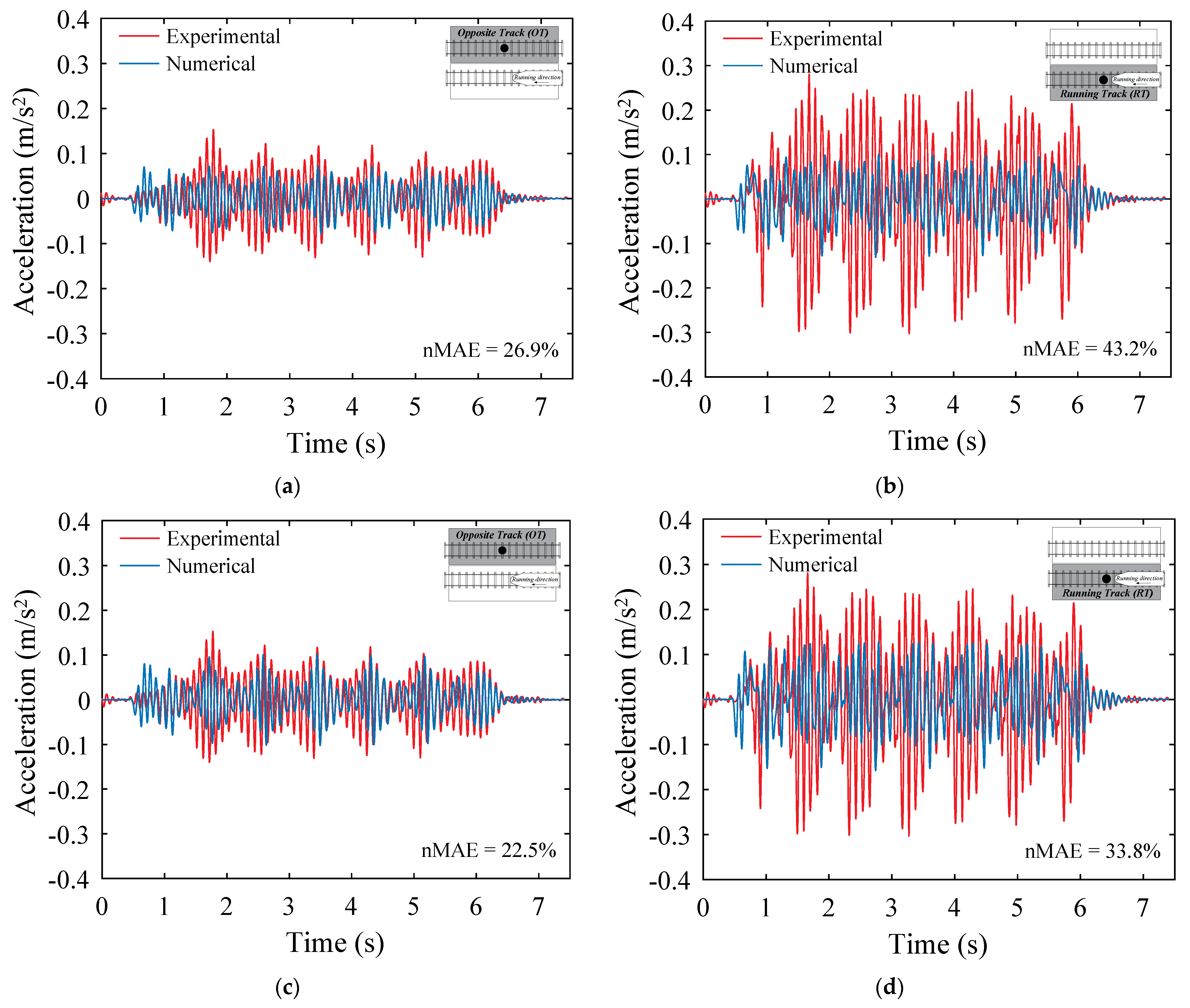
- Regarding the validation of the model, a good agreement between experimental and numerical results was observed, in particular with the model obtained after the updating. The improvement in the results was confirmed through the nMAE indicator, which reduced from 26.9% to 22.5% and from 43.2% to 33.8% regarding the responses obtained in the OT and RT sides, respectively. However, as confirmed with the results in the frequency domain, the amplitudes of the numerical and experimental responses were still considerably different, especially in the RT side. Therefore, to improve the results, and since the updating process was based on modal data obtained with ambient vibration measurements, two modifications in the FE model of the bridge were carried out with the objective of getting a closer match between experimental and numerical responses of the bridge under railway traffic.
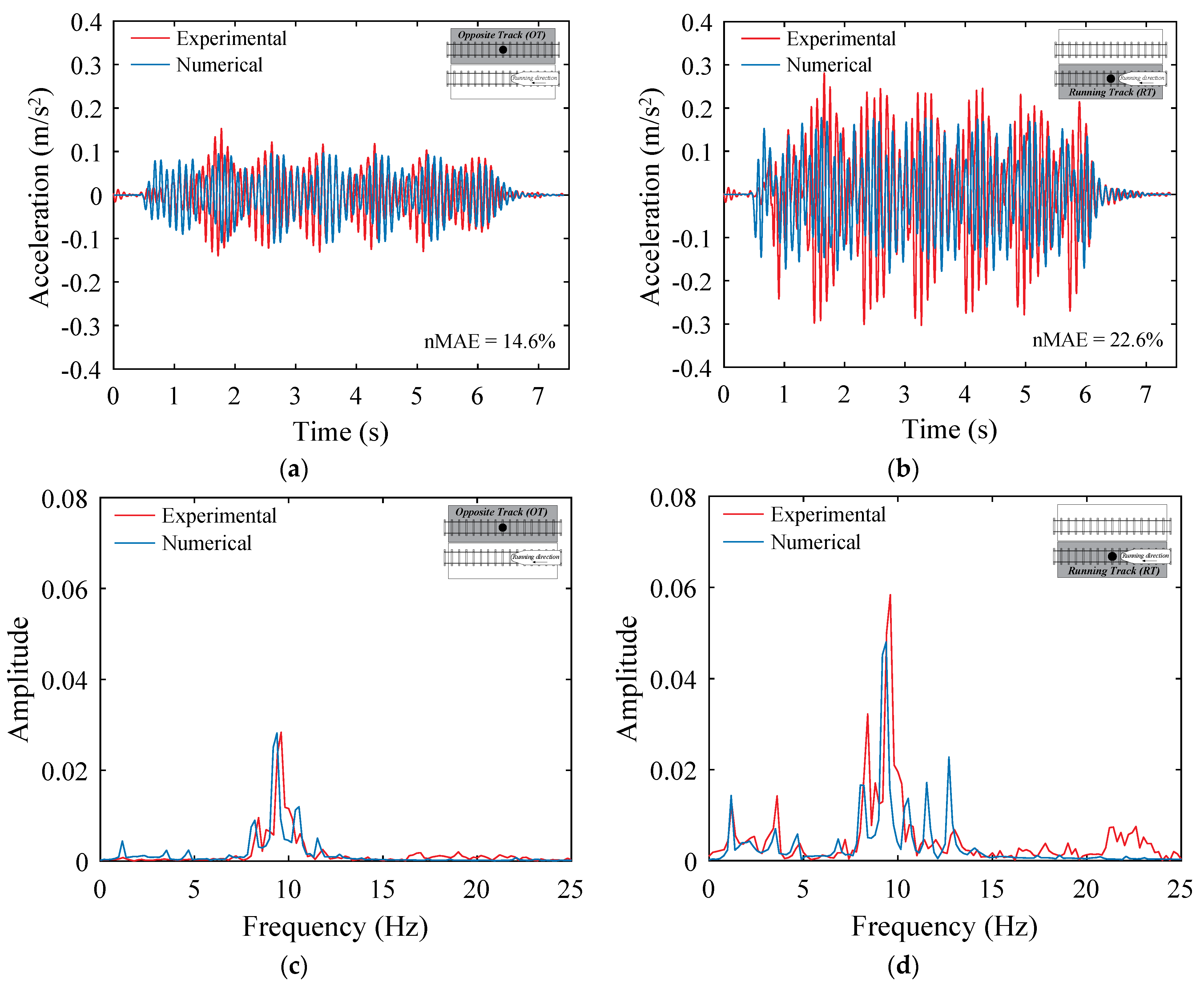
- Since the vertical stiffness of the bearing supports proved to have a significant influence in the model updating process, an evaluation of its influence in the vertical response of the bridge was conducted. After performing successive changes to this parameter, a vertica1 stiffness of 132 MN/m was achieved, which guaranteed a compromise in terms of agreement between the numerical and experimental accelerations on both track sides. By doing so, the numerical time-histories significantly approached the experimental ones and the nMAE indicator suffered a significant reduction to 14.6% and 22.6% relative to the responses obtained in OT and RT sides, respectively. This enhancement was also notable in the frequency domain, since the amplitudes of the main peaks obtained in the numerical analyses increased, showing a better agreement with the measured data.
- Finally, the behaviour of the ballast located over the longitudinal joint was also analysed. The effects of a possible degradation of this material were evaluated based on the shear strain levels that occur in the joint due to the relative cyclic movements between the two adjacent half-decks. After evaluating the maximum plausible degradation of the ballast layer over the joint through a shear modulus degradation curve, a reduction in the modulus of elasticity of the ballast on this location was tested. An optimal value of 36 MPa was obtained, which guaranteed the best compromise in the agreement between numerical and experimental results. By doing so, the numerical results improved in relation to the experimental ones, leading to the lowest levels of the nMAE indicator on both sides, more specifically 13.4% to 21.1% with respect to the OT and RT sides, respectively.
Author Contributions
Funding
Conflicts of Interest
References
- Zhai, W.; Cai, C. Effect of Locomotive Vibrations on Pantograph-Catenary System Dynamics. Veh. Syst. Dyn. 1998, 29, 47–58. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Z.; Liu, Z.; Wang, R. A spatial coupling model to study dynamic performance of pantograph-catenary with vehicle-track excitation. Mech. Syst. Signal Process. 2020, 151, 107336. [Google Scholar] [CrossRef]
- Galvín, P.; Romero, A.; Moliner, E.; De Roeck, G.; Martínez-Rodrigo, M. On the dynamic characterisation of railway bridges through experimental testing. Eng. Struct. 2020, 226, 111261. [Google Scholar] [CrossRef]
- Montenegro, P.; Carvalho, H.; Ribeiro, D.; Calçada, R.; Tokunaga, M.; Tanabe, M.; Zhai, W. Assessment of train running safety on bridges: A literature review. Eng. Struct. 2021, 241, 112425. [Google Scholar] [CrossRef]
- Olmos, J.; Astiz, M. Improvement of the lateral dynamic response of a high pier viaduct under turbulent wind during the high-speed train travel. Eng. Struct. 2018, 165, 368–385. [Google Scholar] [CrossRef]
- Meixedo, A.; Ribeiro, D.; Calçada, R.; Delgado, R. Global and Local Dynamic Effects on a Railway Viaduct with Precast Deck. Engineering 2014, 104, 77. [Google Scholar] [CrossRef]
- Zangeneh, A.; Svedholm, C.; Andersson, A.; Pacoste, C.; Karoumi, R. Identification of soil-structure interaction effect in a portal frame railway bridge through full-scale dynamic testing. Eng. Struct. 2018, 159, 299–309. [Google Scholar] [CrossRef]
- Melo, L.R.T.; Ribeiro, D.; Calçada, R.; Bittencourt, T.N. Validation of a vertical train–track–bridge dynamic interaction model based on limited experimental data. Struct. Infrastruct. Eng. 2019, 16, 181–201. [Google Scholar] [CrossRef]
- Zhai, W.; Han, Z.; Chen, Z.; Ling, L.; Zhu, S. Train-track-bridge dynamic interaction: A state-of-the-art review. Veh. Syst. Dyn. 2019, 57, 984–1027. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Gai, Y.; Wu, T. Simulation of train–bridge interaction under wind loads: A rigid-flexible coupling approach. Int. J. Rail Transp. 2017, 6, 163–182. [Google Scholar] [CrossRef]
- Antolín, P.; Zhang, N.; Goicolea, J.M.; Xia, H.; Astiz, M.; Oliva, J. Consideration of nonlinear wheel–rail contact forces for dynamic vehicle–bridge interaction in high-speed railways. J. Sound Vib. 2013, 332, 1231–1251. [Google Scholar] [CrossRef]
- Zhang, N.; Xia, H. Dynamic analysis of coupled vehicle–bridge system based on inter-system iteration method. Comput. Struct. 2013, 114–115, 26–34. [Google Scholar] [CrossRef]
- Szafrański, M. A dynamic vehicle-bridge model based on the modal identification results of an existing EN57 train and bridge spans with non-ballasted tracks. Mech. Syst. Signal Process. 2020, 146, 107039. [Google Scholar] [CrossRef]
- Ribeiro, D.; Calçada, R.; Delgado, R.; Brehm, M.; Zabel, V. Finite-element model calibration of a railway vehicle based on experimental modal parameters. Veh. Syst. Dyn. 2013, 51, 821–856. [Google Scholar] [CrossRef]
- Tomioka, T.; Takigami, T.; Suzuki, Y. Numerical analysis of three-dimensional flexural vibration of railway vehicle car body. Veh. Syst. Dyn. 2006, 44, 272–285. [Google Scholar] [CrossRef]
- Chellini, G.; Nardini, L.; Salvatore, W. Dynamical identification and modelling of steel–concrete composite high-speed railway bridges. Struct. Infrastruct. Eng. 2011, 7, 823–841. [Google Scholar] [CrossRef]
- Axelsson, E.; Syk, A.; Ülker-Kaustell, M.; Battini, J.-M. Effect of Axle Load Spreading and Support Stiffness on the Dynamic Response of Short Span Railway Bridges. Struct. Eng. Int. 2014, 24, 457–465. [Google Scholar] [CrossRef] [Green Version]
- Museros, P.; Romero, M.; Poy, A.; Alarcón, E. Advances in the analysis of short span railway bridges for high-speed lines. Comput. Struct. 2002, 80, 2121–2132. [Google Scholar] [CrossRef] [Green Version]
- Bornet, L.; Andersson, A.; Zwolski, J.; Battini, J.-M. Influence of the ballasted track on the dynamic properties of a truss railway bridge. Struct. Infrastruct. Eng. 2014, 11, 796–803. [Google Scholar] [CrossRef]
- Melo, L.R.T.; Malveiro, J.; Ribeiro, D.; Calçada, R.; Bittencourt, T. Dynamic analysis of the train-bridge system considering the non-linear behaviour of the track-deck interface. Eng. Struct. 2020, 220, 110980. [Google Scholar] [CrossRef]
- Rauert, T.; Bigelow, H.; Hoffmeister, B.; Feldmann, M. On the prediction of the interaction effect caused by continuous ballast on filler beam railway bridges by experimentally supported numerical studies. Eng. Struct. 2010, 32, 3981–3988. [Google Scholar] [CrossRef]
- Sánchez-Quesada, J.; Moliner, E.; Romero, A.; Galvín, P.; Martínez-Rodrigo, M. Ballasted track interaction effects in railway bridges with simply-supported spans composed by adjacent twin single-track decks. Eng. Struct. 2021, 247, 113062. [Google Scholar] [CrossRef]
- Stollwitzer, A.; Fink, J.; Malik, T. Experimental analysis of damping mechanisms in ballasted track on single-track railway bridges. Eng. Struct. 2020, 220, 110982. [Google Scholar] [CrossRef]
- Battini, J.-M.; Ülker-Kaustell, M. A simple finite element to consider the non-linear influence of the ballast on vibrations of railway bridges. Eng. Struct. 2011, 33, 2597–2602. [Google Scholar] [CrossRef]
- Rebelo, C.; Simoesdasilva, L.; Rigueiro, C.; Pircher, M. Dynamic behaviour of twin single-span ballasted railway viaducts—Field measurements and modal identification. Eng. Struct. 2008, 30, 2460–2469. [Google Scholar] [CrossRef]
- Rigueiro, C.; Rebelo, C.; Simoesdasilva, L. Influence of ballast models in the dynamic response of railway viaducts. J. Sound Vib. 2010, 329, 3030–3040. [Google Scholar] [CrossRef]
- Malveiro, J.; Ribeiro, D.; Sousa, C.; Calçada, R. Model updating of a dynamic model of a composite steel-concrete railway viaduct based on experimental tests. Eng. Struct. 2018, 164, 40–52. [Google Scholar] [CrossRef]
- Brehm, M.; Zabel, V.; Bucher, C. An automatic mode pairing strategy using an enhanced modal assurance criterion based on modal strain energies. J. Sound Vib. 2010, 329, 5375–5392. [Google Scholar] [CrossRef]
- Zhai, W.; Wang, S.; Zhang, N.; Gao, M.; Xia, H.; Cai, C.; Zhao, C. High-speed train–track–bridge dynamic interactions—Part II: Experimental validation and engineering application. Int. J. Rail Transp. 2013, 1, 25–41. [Google Scholar] [CrossRef]
- Ishibashi, I.; Zhang, X. Unified Dynamic Shear Moduli and Damping Ratios of Sand and Clay. Soils Found. 1993, 33, 182–191. [Google Scholar] [CrossRef] [Green Version]
- ERRI. Railway Bridges for Speeds >200 km/h, Recommendations for Calculating Damping in Rail Bridge Decks; European Rail Research Institute: Utrecht, The Netherlands, 1999. [Google Scholar]
- ANSYS®. 2018. Available online: https://www.ansys.com/ (accessed on 28 March 2022).
- Manterola, J. Puentes: Apuntes Para su Diseño, Cálculo y Construcción; Colegio de Ingenieros de Caminos, Canales y Puertos: Madrid, Spain, 2006. [Google Scholar]
- Henriques, A.A.R. Aplicação de Novos Conceitos de Segurança No Dimensionamento do Betão Estrutural; University of Porto: Porto, Portugal, 1998. [Google Scholar]
- Neville, A.M. Properties of Concrete, 4th ed.; John Wiley and Sons: New York, NY, USA, 1996. [Google Scholar]
- Ricci, L.; Nguyen, V.; Sab, K.; Duhamel, D.; Schmitt, L. Dynamic behaviour of ballasted railway tracks: A discrete/continuous approach. Comput. Struct. 2005, 83, 2282–2292. [Google Scholar] [CrossRef]
- Shahu, J.T.; Rao, N.K. Yudhbir Parametric study of resilient response of tracks with a sub-ballast layer. Can. Geotech. J. 1999, 36, 1137–1150. [Google Scholar] [CrossRef]
- Montenegro, P.A. A Methodology for the Assessment of the Train Running Safety on Bridges. Ph.D. Thesis, Faculty of Engineering of the University of Porto, Porto, Portugal, 2015. [Google Scholar]
- Ribeiro, D. Dynamic Effects Induced by Traffic in Railway Bridges: Numerical Modeling, Calibration and Experimental Validation. Ph.D. Thesis, Faculty of Engineering of the University of Porto, Porto, Portugal, 2012. (In Portuguese). [Google Scholar]
- Montenegro, P.A.; Neves, S.; Calçada, R.; Tanabe, M.; Sogabe, M. Wheel–rail contact formulation for analyzing the lateral train–structure dynamic interaction. Comput. Struct. 2015, 152, 200–214. [Google Scholar] [CrossRef] [Green Version]
- Hertz, H. Ueber die Berührung fester elastischer Körper. Mathematik 1882, 1882, 156–171. [Google Scholar] [CrossRef]
- Shabana, A.A.; Zaazaa, K.E.; Sugiyama, H. Railroad Vehicle Dynamics: A computational Approach; CRC Press—Taylor & Francis Group: Boca Raton, FL, USA, 2008. [Google Scholar]
- Kalker, J. Book of tables for the Hertzian creep-force law. In Proceedings of the 2nd Mini Conference on Contact Mechanics and Wear of Wheel/Rail Systems, Budapest, Hungary, 29–31 July 1996. [Google Scholar]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications: New York, NY, USA, 2000. [Google Scholar]
- MATLAB®. 2020. Available online: https://www.mathworks.com/products/matlab.html (accessed on 28 March 2022).
- ARTeMIS. ARTeMIS Extractor Pro—Academic License, User’s Manual, SVS 2009; ARTeMIS: Eindhoven, The Netherlands, 2009. [Google Scholar]
- Marple, S.L. Digital Spectral Analysis: Second Edition; Courier Dover Publications: New York, NY, USA, 2019. [Google Scholar]
- Petsounis, K.; Fassois, S. Parametric Time-Domain Methods for The Identification of Vibrating Structures—A Critical Comparison and Assessment. Mech. Syst. Signal Process. 2001, 15, 1031–1060. [Google Scholar] [CrossRef]
- Allemang, R.J. The modal assurance criterion–twenty years of use and abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamic of Structures, 3rd ed.; McGraw-Hill, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Ribeiro, D.; Calçada, R.; Brehm, M.; Zabel, V. Calibration of the numerical model of a track section over a railway bridge based on dynamic tests. Structures 2021, 34, 4124–4141. [Google Scholar] [CrossRef]
- Sarin, H.; Kokkolaras, M.; Hulbert, G.; Papalambros, P.; Barbat, S.; Yang, R.-J. A Comprehensive Metric for Comparing Time Histories in Validation of Simulation Models with Emphasis on Vehicle Safety Applications. In Proceedings of the 2008 ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference (DETC 2008), New York, NY, USA, 3–6 August 2008; pp. 1275–1286. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Lombaert, G.; De Roeck, G. Dynamic Analysis of Multispan Viaducts with Weak Coupling between Adjacent Spans. J. Bridg. Eng. 2014, 19, 83–90. [Google Scholar] [CrossRef]













| Parameters | Statistical Properties | Limits | Adopted Value | References | |||
|---|---|---|---|---|---|---|---|
| Distribution Type | Mean Value/Standard Deviation | Lower | Upper | ||||
| Ec (GPa) | Modulus of elasticity of concrete | Normal | 37.4/3.74 | 29.9 | 44.9 | 37.4 | [14,34,35] |
| ρc (kg/m3) | Density of concrete | Normal | 2500/250 | 2000 | 3000 | 2500 | |
| υc | Poisson ratio of concrete | - | -/- | 0.16 | 0.24 | 0.20 | |
| Es (GPa) | Modulus of elasticity of steel | Normal | 210/8.4 | 193.2 | 226.8 | 210.0 | [14] |
| ρs (kg/m3) | Density of steel | - | -/- | 7700 | 8000 | 7850 | |
| υs | Poisson ratio of steel | - | -/- | 0.28 | 0.32 | 0.30 | |
| Eb (MPa) | Modulus of elasticity of ballast | Uniform | 169/22.5 | 130 | 208 | 145 | [20,36,37] |
| Ebl (MPa) | Modulus of elasticity of ballast (longitudinal joint) | Uniform | 79.8/37.7 | 14.5 | 145 | 145 | |
| Ebt (MPa) | Modulus of elasticity of ballast (transversal joints) | Uniform | 79.8/37.7 | 14.5 | 145 | 145 | |
| ρb (kg/m3) | Density of ballast | Uniform | 1800/260 | 1350 | 2250 | 1800 | |
| υb | Poisson ratio of ballast | - | -/- | 0.15 | 0.20 | 0.15 | |
| Kv (MN/m) | Vertical stiffness of the support | Uniform | 355.5/111.7 | 162 | 549 | 324 | [33] |
| Kh (kN/m) | Horizontal stiffness of the support | Uniform | 1730/476 | 905 | 2556 | 1809 | |
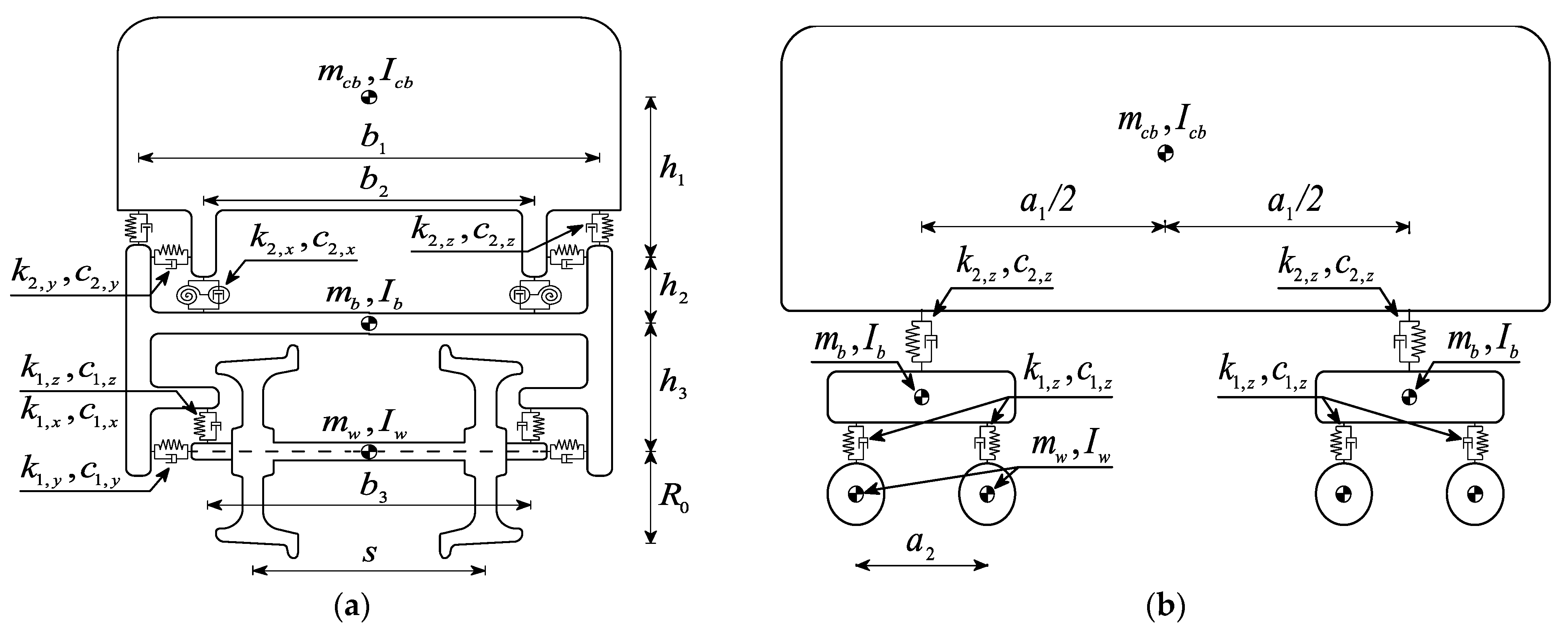
| Parameters | Unit | Value | |
|---|---|---|---|
| Car body | Car body mass | mcb (kg) | 38,445 |
| Car body roll moment of inertia | Icb,x (kg·m2) | 55,120 | |
| Car body pitch moment of inertia | Icb,y (kg·m2) | 1,475,000 | |
| Car body yaw moment of inertia | Icb,z (kg·m2) | 1,477,000 | |
| Bogie | Bogie mass | mb (kg) | 4858 |
| Bogie roll moment of inertia | Ib,x (kg·m2) | 2700 | |
| Bogie pitch moment of inertia | Ib,y (kg·m2) | 1931.5 | |
| Bogie yaw moment of inertia | Ib,z (kg·m2) | 3878.8 | |
| Wheelset | Wheelset mass | mw (kg) | 1711 |
| Wheelset roll moment of inertia | Iw,x (kg·m2) | 733.4 | |
| Wheelset yaw moment of inertia | Iw,z (kg·m2) | 733.4 | |
| Primary suspension | Stiffness of the primary longitudinal suspension | k1,x (N/m) | 4,498,100 |
| Stiffness of the primary transversal suspension, | k1,y (N/m) | 30,948,200 | |
| Stiffness of the primary vertical suspension | k1,z (N/m) | 1,652,820 | |
| Damping of the primary vertical suspension | c1,z (N·s/m) | 16,739 | |
| Secondary suspension | Stiffness of the secondary longitudinal suspension | k2,x (N/m) | 4,905,000 |
| Stiffness of the secondary transversal suspension | k2,y (N/m) | 2,500,000 | |
| Stiffness of the secondary vertical suspension | k2,z (N/m) | 734,832 | |
| Damping of the secondary longitudinal suspension | c2,x (N·s/m) | 400,000 | |
| Damping of the secondary transversal suspension | c2,y (N·s/m) | 17,500 | |
| Damping of the secondary vertical suspension | c2,z (N·s/m) | 35,000 | |
| Longitudinal distance between bogies | a1 (m) | 19 | |
| Longitudinal distance between wheelsets | a2 (m) | 2.7 | |
| Transversal distance between vertical secondary suspensions | b1 (m) | 2.144 | |
| Transversal distance between longitudinal secondary suspensions | b2 (m) | 2.846 | |
| Transversal distance between primary suspensions | b3 (m) | 2.144 | |
| Vertical distance between car body center and secondary suspension | h1 (m) | 0.936 | |
| Vertical distance between bogie center and secondary suspension | h2 (m) | 0.142 | |
| Vertical distance between bogie center and wheelset center | h3 (m) | 0.065 | |
| Nominal rolling radius | R0 (m) | 0.43 | |
| Gauge | S (m) | 1.67 | |
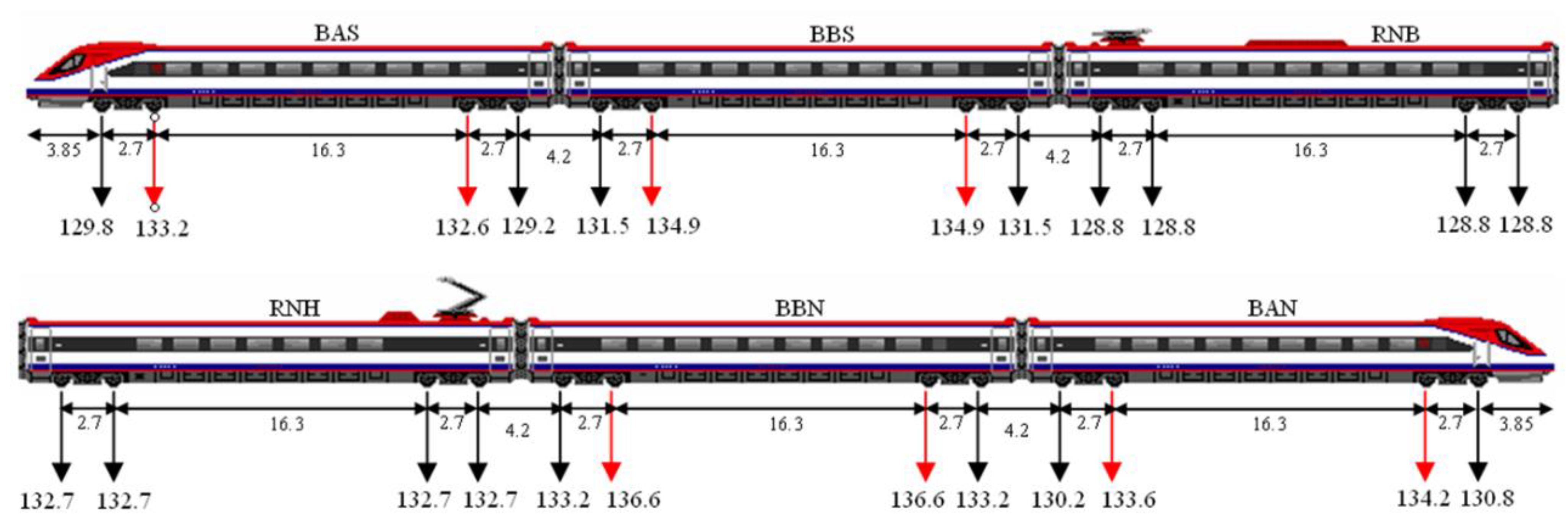
| Vehicle | Car Body (kg) | Bogie [×2] (kg) | Axle Average [×4] (kg) | Total Sum (kg) |
|---|---|---|---|---|
| BAS | 36,936 | 4858 | 1711 | 53,496 |
| BBS | 37,752 | 4858 | 1711 | 54,312 |
| RNB | 35,958 | 5204 | 1538 | 52,518 |
| RNH | 37,548 | 5204 | 1538 | 54,108 |
| BBN | 38,445 | 4858 | 1711 | 55,005 |
| BAN | 37,345 | 4858 | 1711 | 53,905 |
| Train Speed (km/h) | Mode 1 | Mode 2 | ||||
|---|---|---|---|---|---|---|
| f (Hz) | amax (m/s2) | ξ (%) | f (Hz) | amax (m/s2) | ξ (%) | |
| 110 | 9.21 | 0.0774 | 7.86 | 11.93 | 0.0233 | 4.64 |
| 135 | 9.57 | 0.0951 | 6.20 | 11.46 | 0.1803 | 4.76 |
| 140 | 9.55 | 0.0790 | 6.01 | 11.56 | 0.1899 | 4.77 |
| 6.69% | 4.72% | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saramago, G.; Montenegro, P.A.; Ribeiro, D.; Silva, A.; Santos, S.; Calçada, R. Experimental Validation of a Double-Deck Track-Bridge System under Railway Traffic. Sustainability 2022, 14, 5794. https://doi.org/10.3390/su14105794
Saramago G, Montenegro PA, Ribeiro D, Silva A, Santos S, Calçada R. Experimental Validation of a Double-Deck Track-Bridge System under Railway Traffic. Sustainability. 2022; 14(10):5794. https://doi.org/10.3390/su14105794
Chicago/Turabian StyleSaramago, Gabriel, Pedro Aires Montenegro, Diogo Ribeiro, Artur Silva, Sergio Santos, and Rui Calçada. 2022. "Experimental Validation of a Double-Deck Track-Bridge System under Railway Traffic" Sustainability 14, no. 10: 5794. https://doi.org/10.3390/su14105794
APA StyleSaramago, G., Montenegro, P. A., Ribeiro, D., Silva, A., Santos, S., & Calçada, R. (2022). Experimental Validation of a Double-Deck Track-Bridge System under Railway Traffic. Sustainability, 14(10), 5794. https://doi.org/10.3390/su14105794








