Analysis and Control of Chaos in the Boost Converter with ZAD, FPIC, and TDAS
Abstract
:1. Introduction
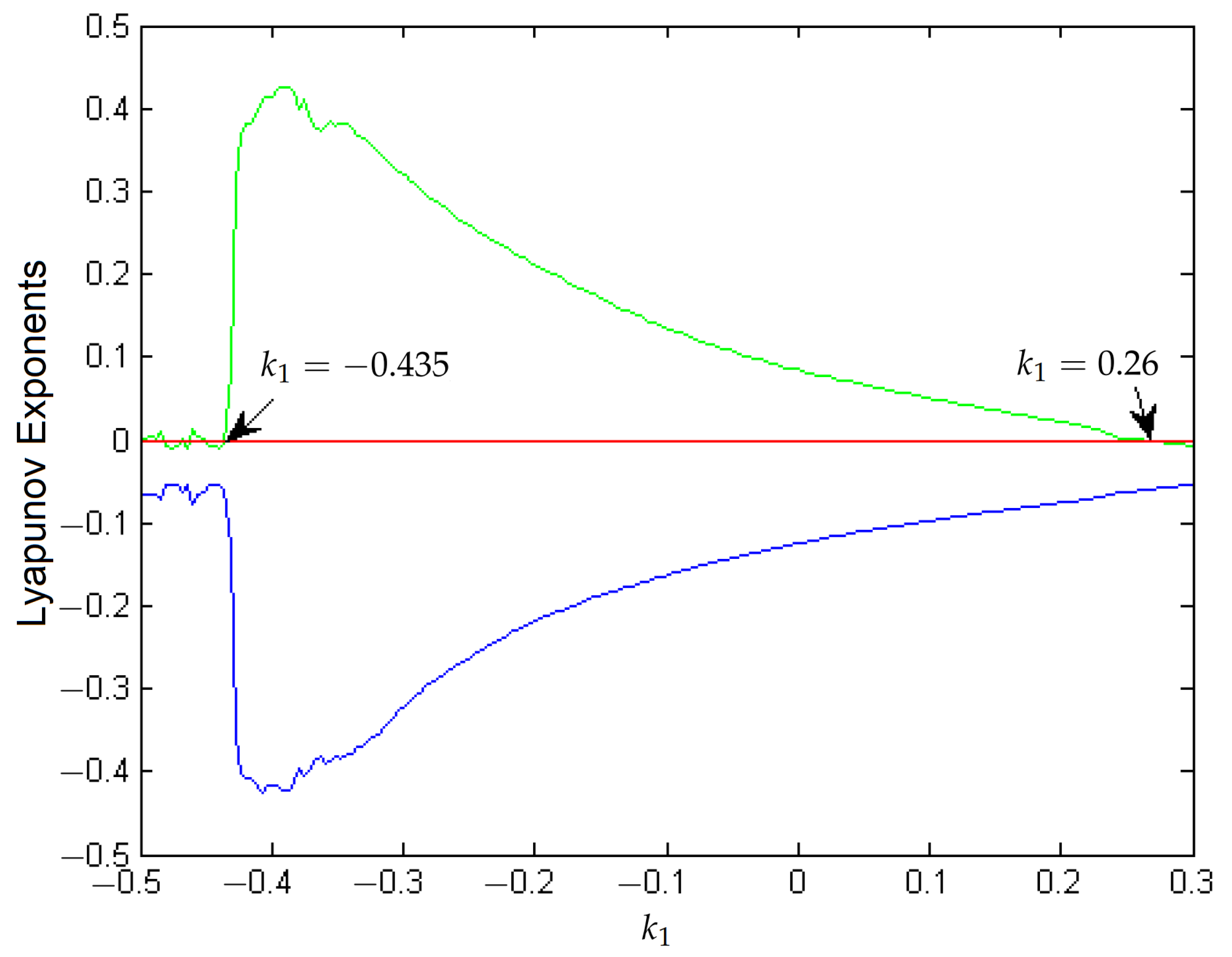
- Existence of chaos is demonstrated numerically for positive Lyapunov exponents.
- Chaos in the boost converter controlled with ZAD and FPIC is minimized, increasing the parameter N of the FPIC.
- FPIC is used to control the system when there is a time delay in the sampling of signals.
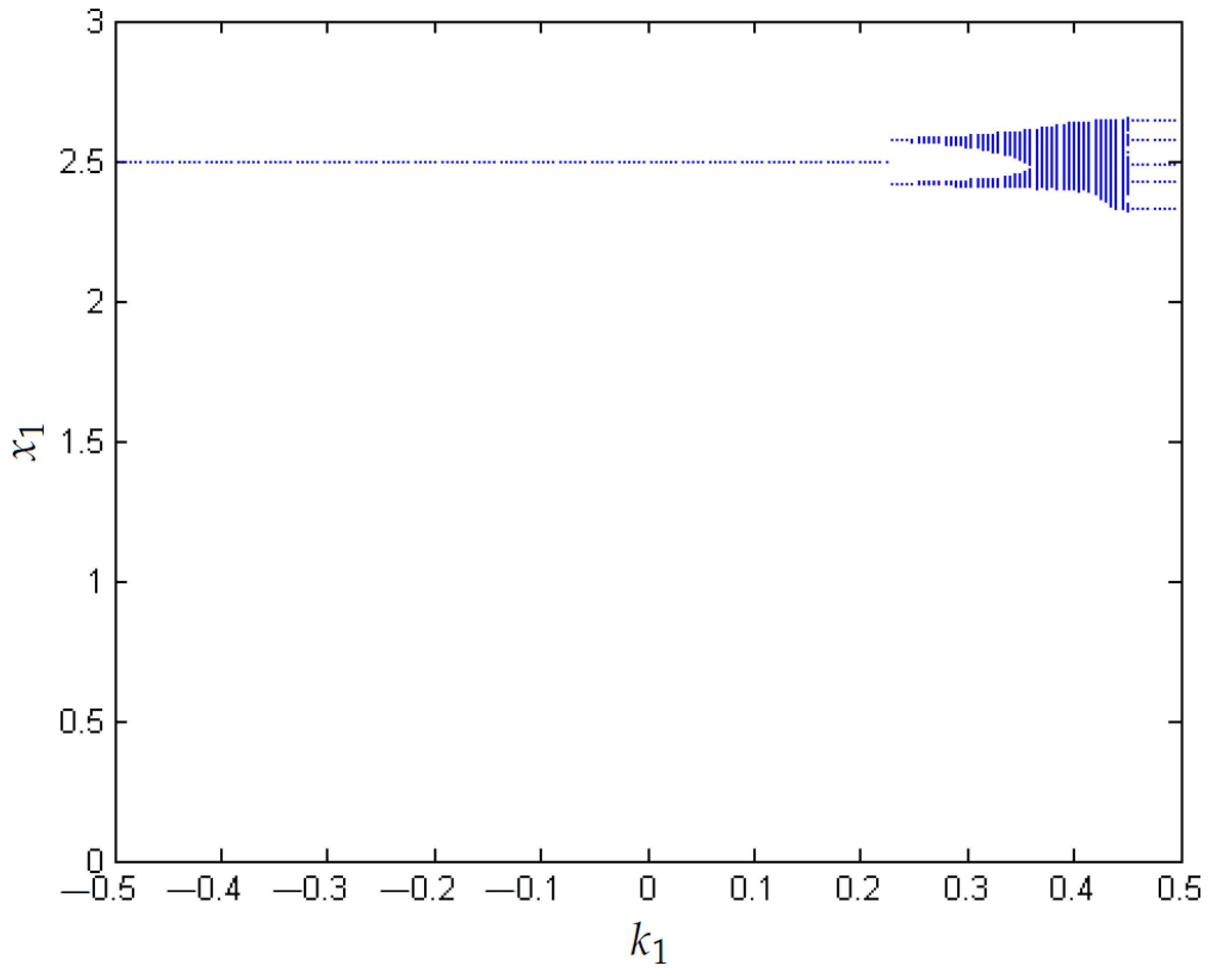
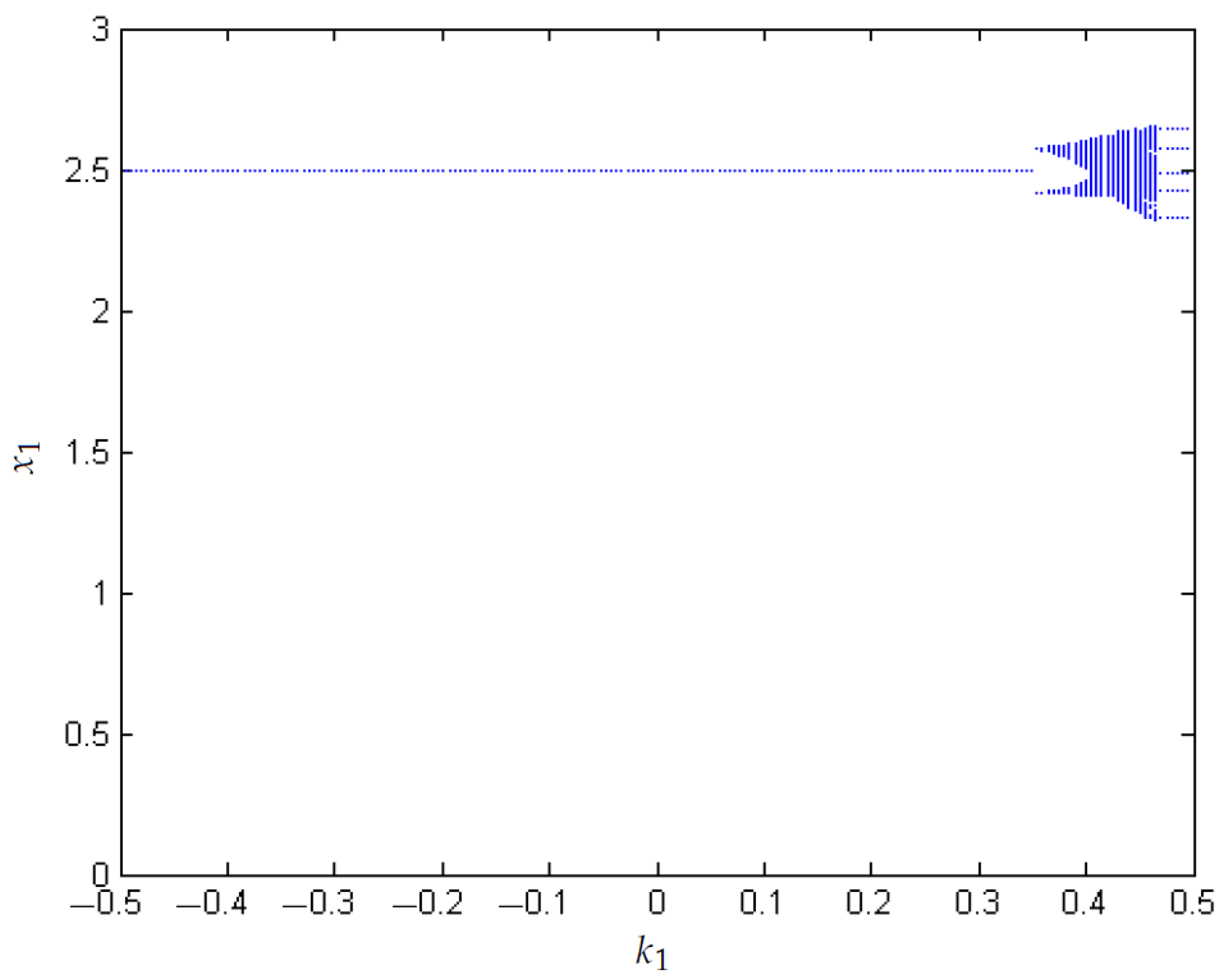
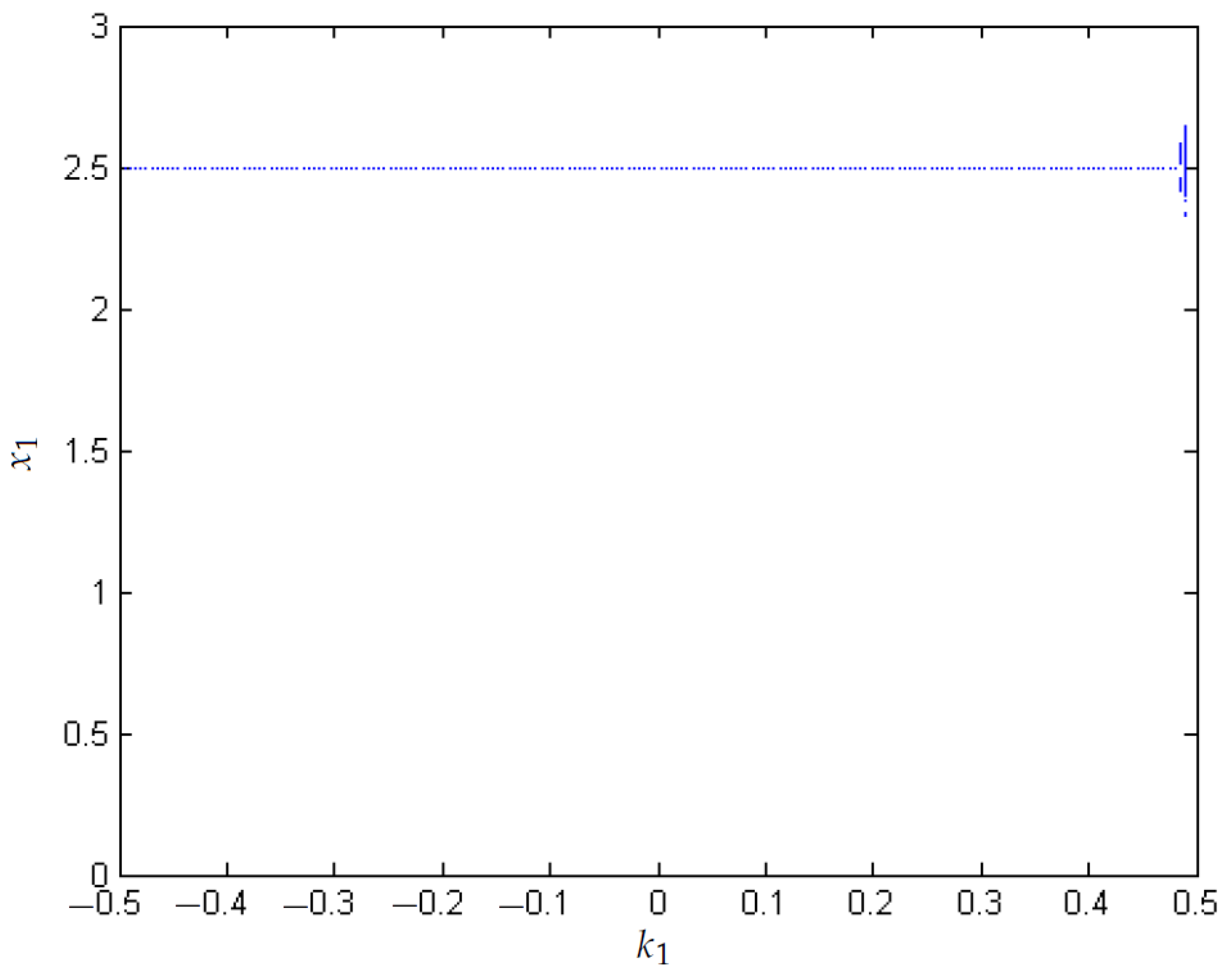
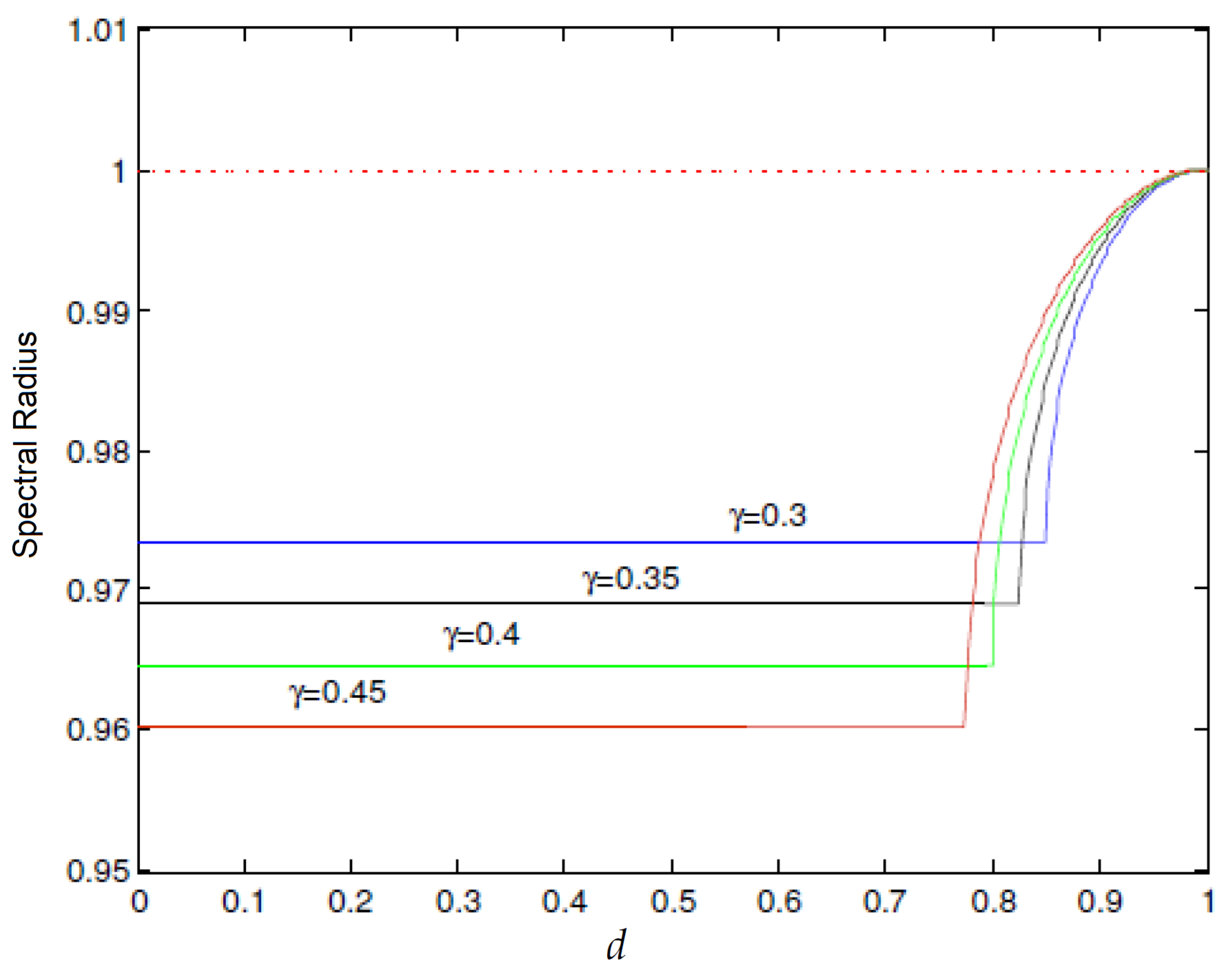
- Bifurcation diagrams are used to visualize the chaos is reduced when the value of N is increased from 0.1 to 0.6.
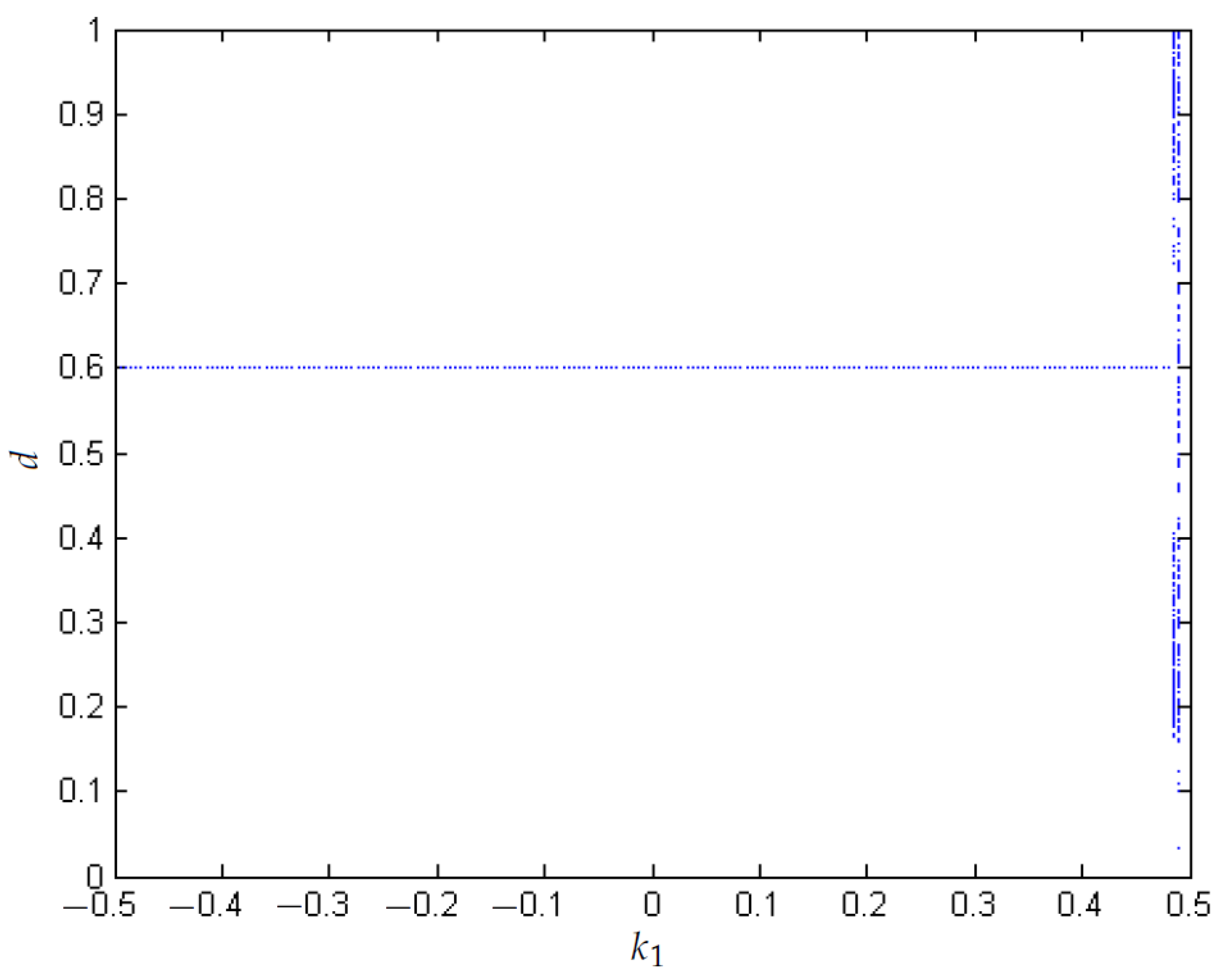
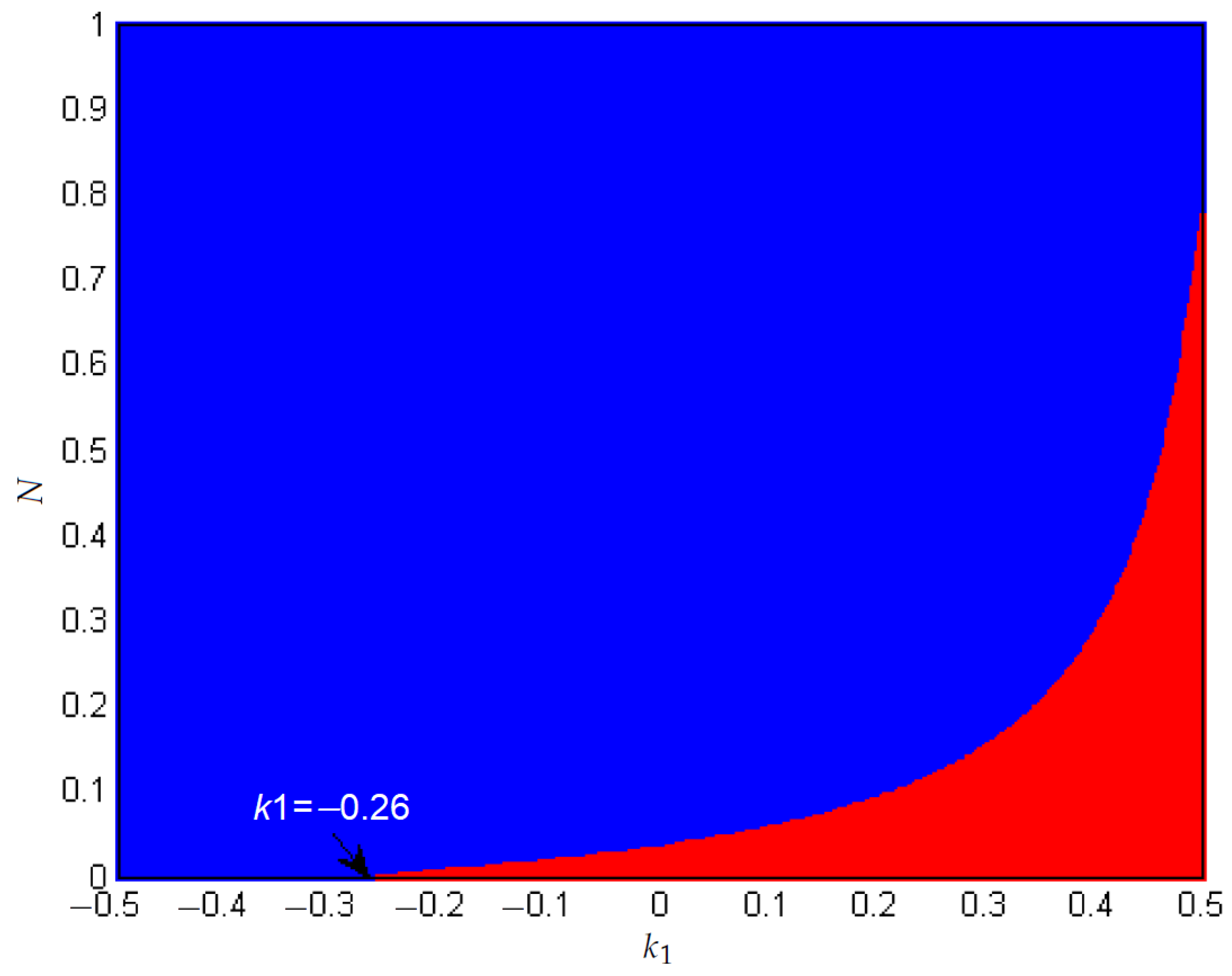
- A biparametric diagram that considers N versus is used to study the boost behavior, showing that for greater values of N, the system is more stable. In addition, when , chaos can be presented for small values of N.
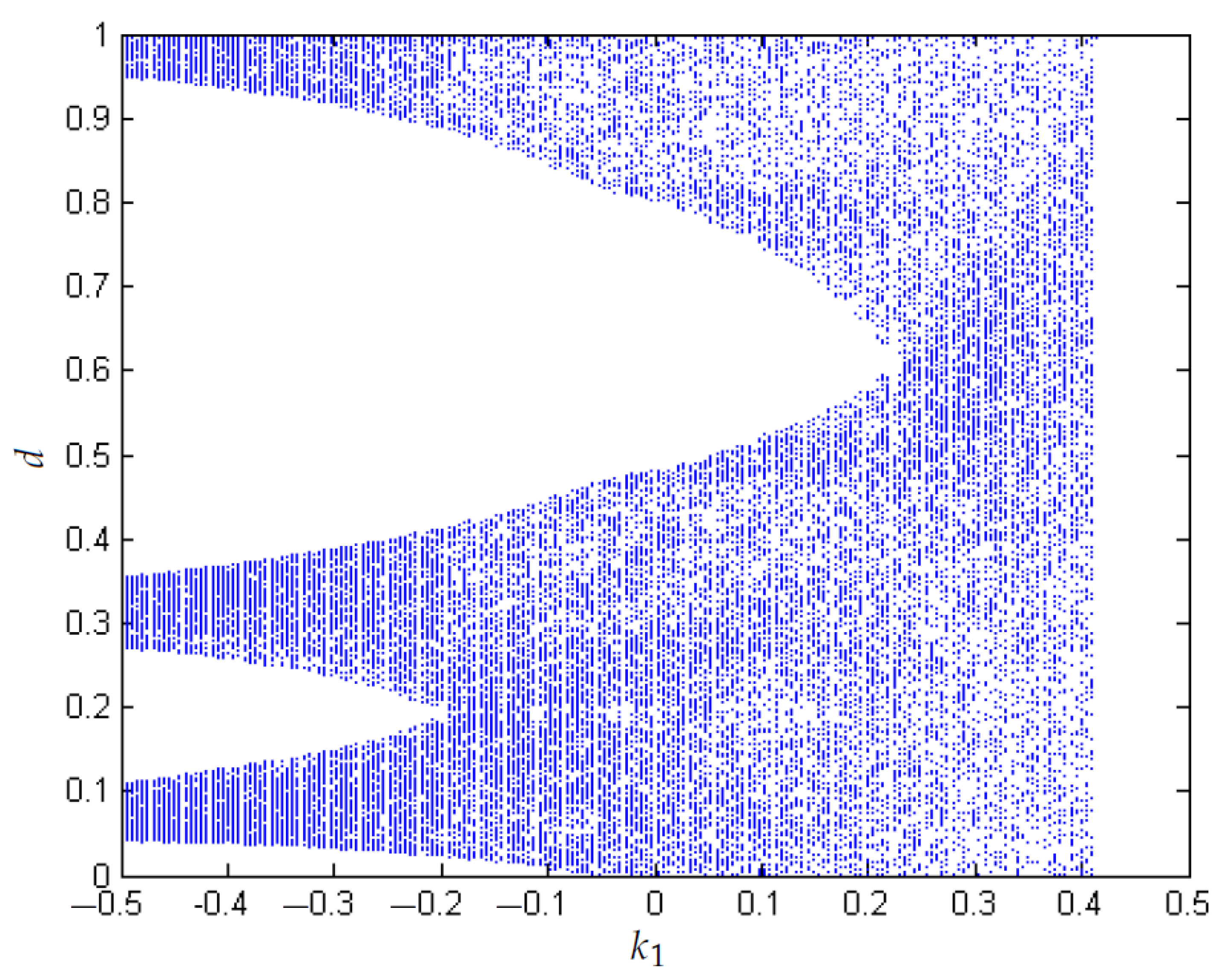
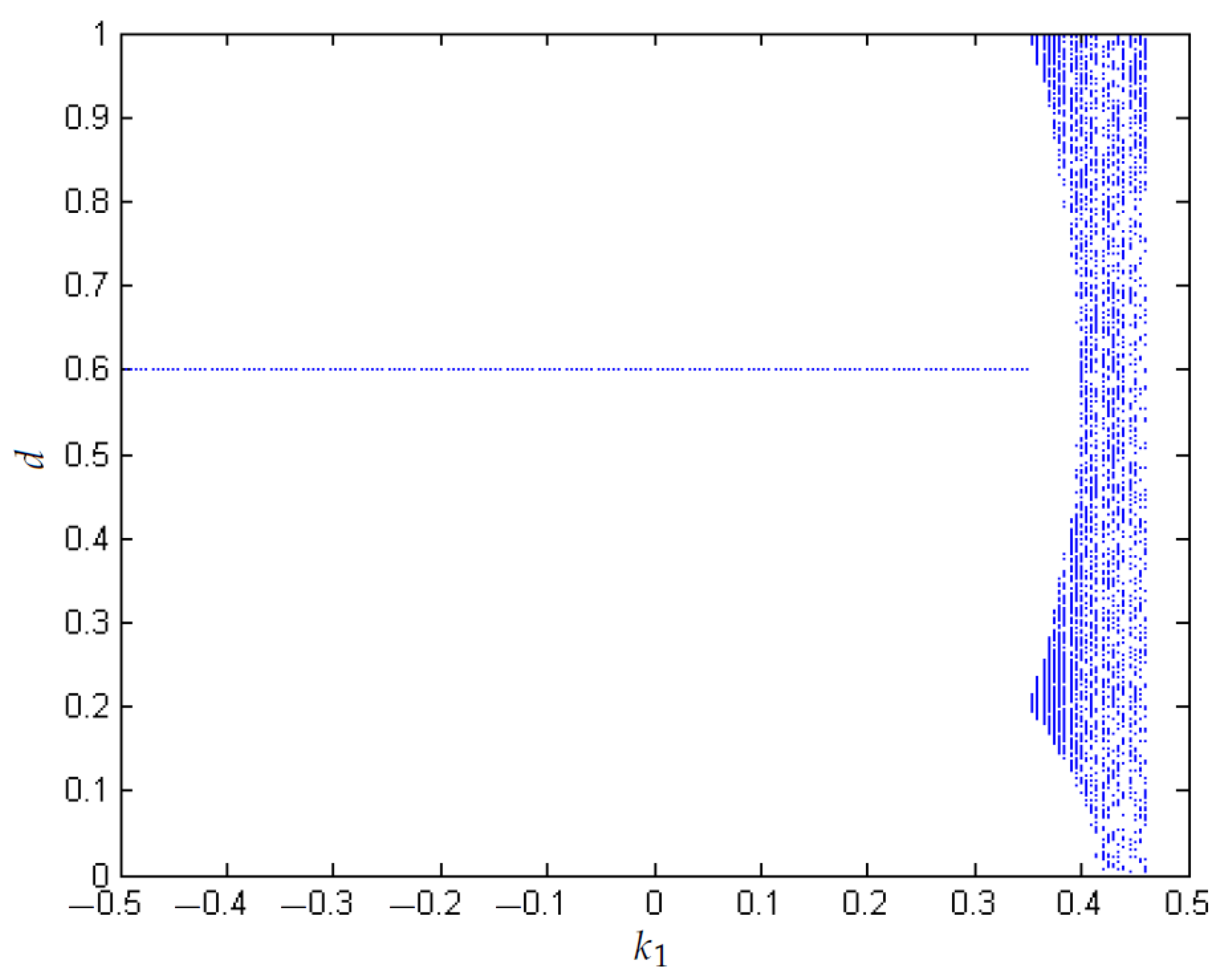
- A biparametric diagram that considers the control constant TDAS versus the control parameter is used to show that for negative values of TDAS (close to −0.2) and small values of (close to 0) the system is stable.
2. Materials and Method
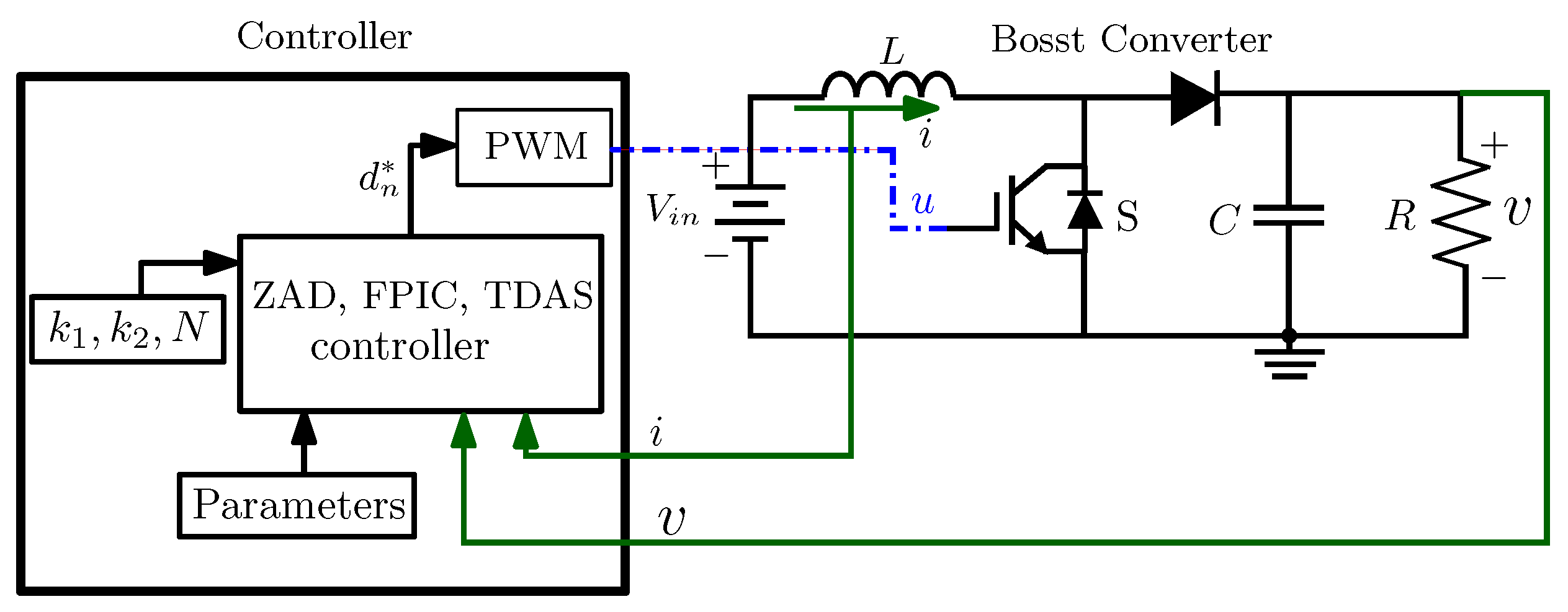
2.1. Boost Converter
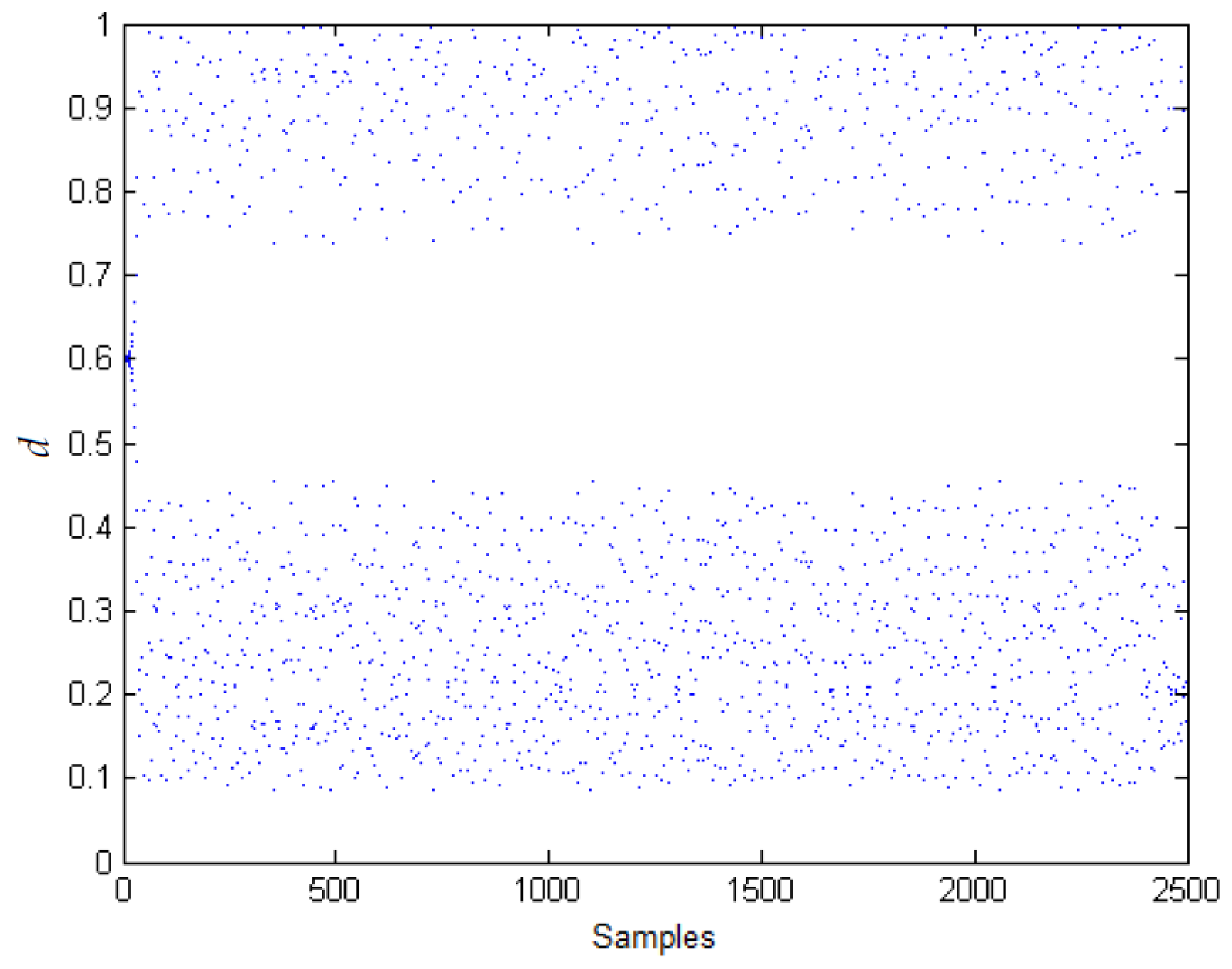
2.2. Duty Cycle
2.3. Definition of Chaos
2.4. Control of Chaos with FPIC
2.5. Control of Chaos with TDAS
3. Results and Analysis
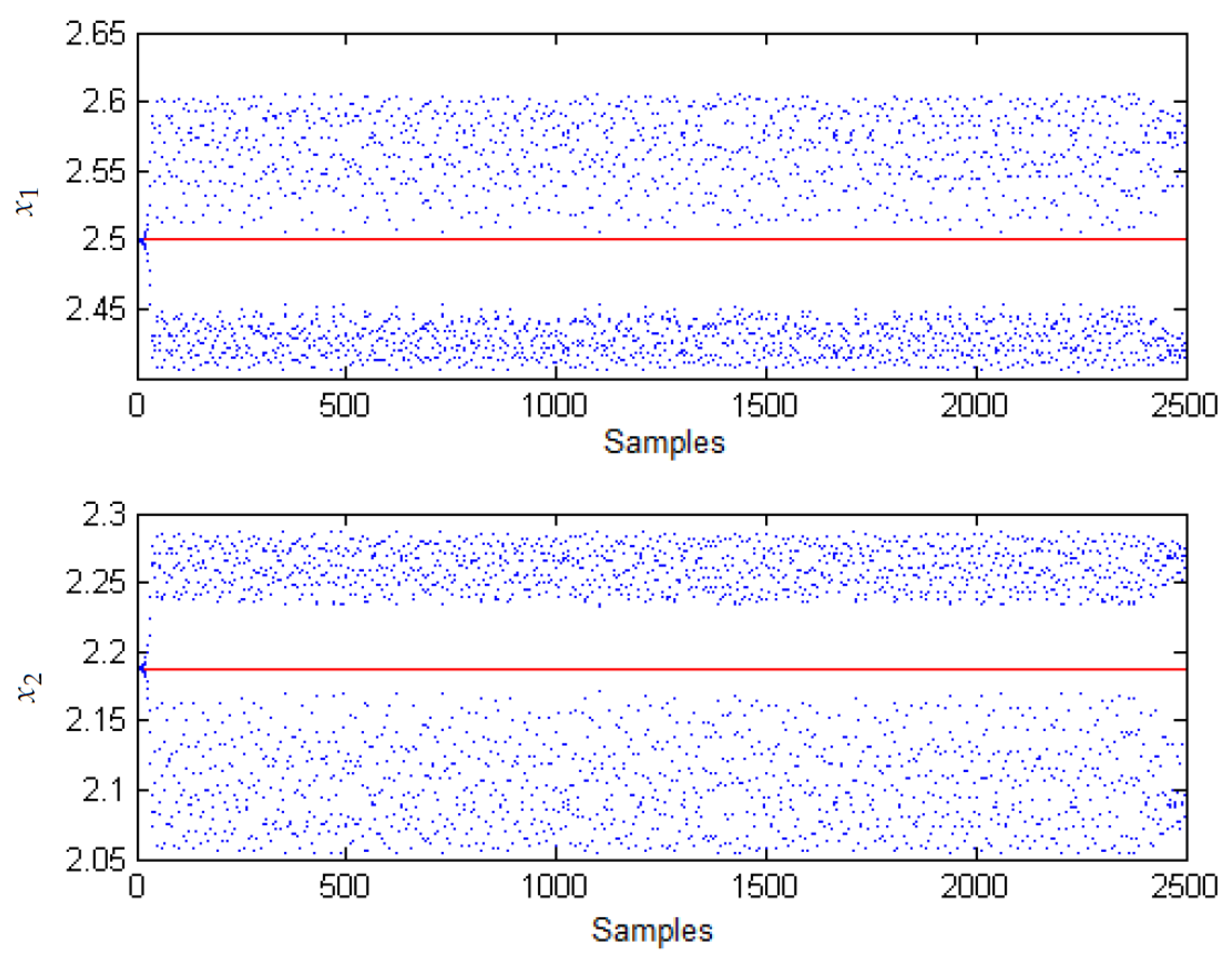
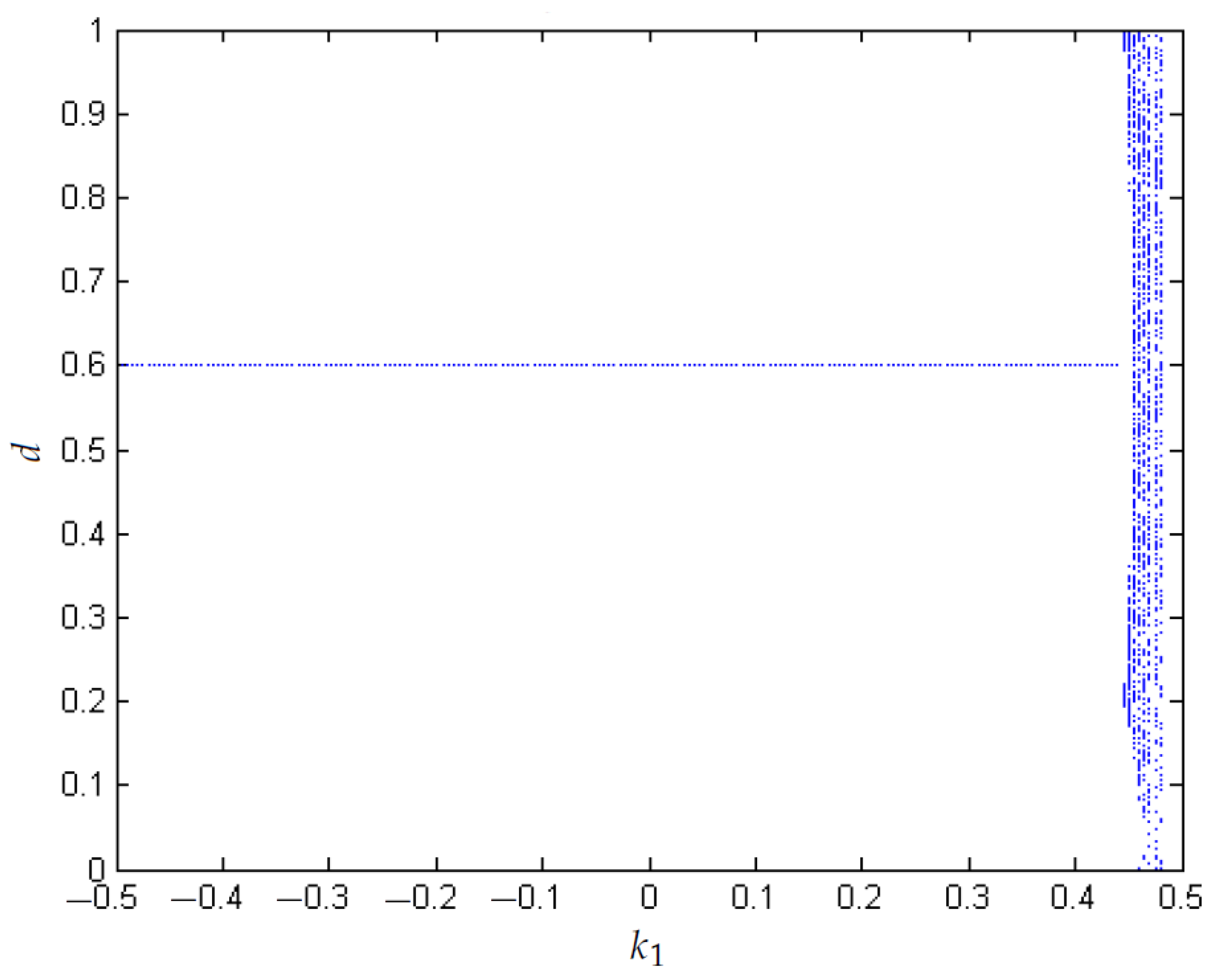
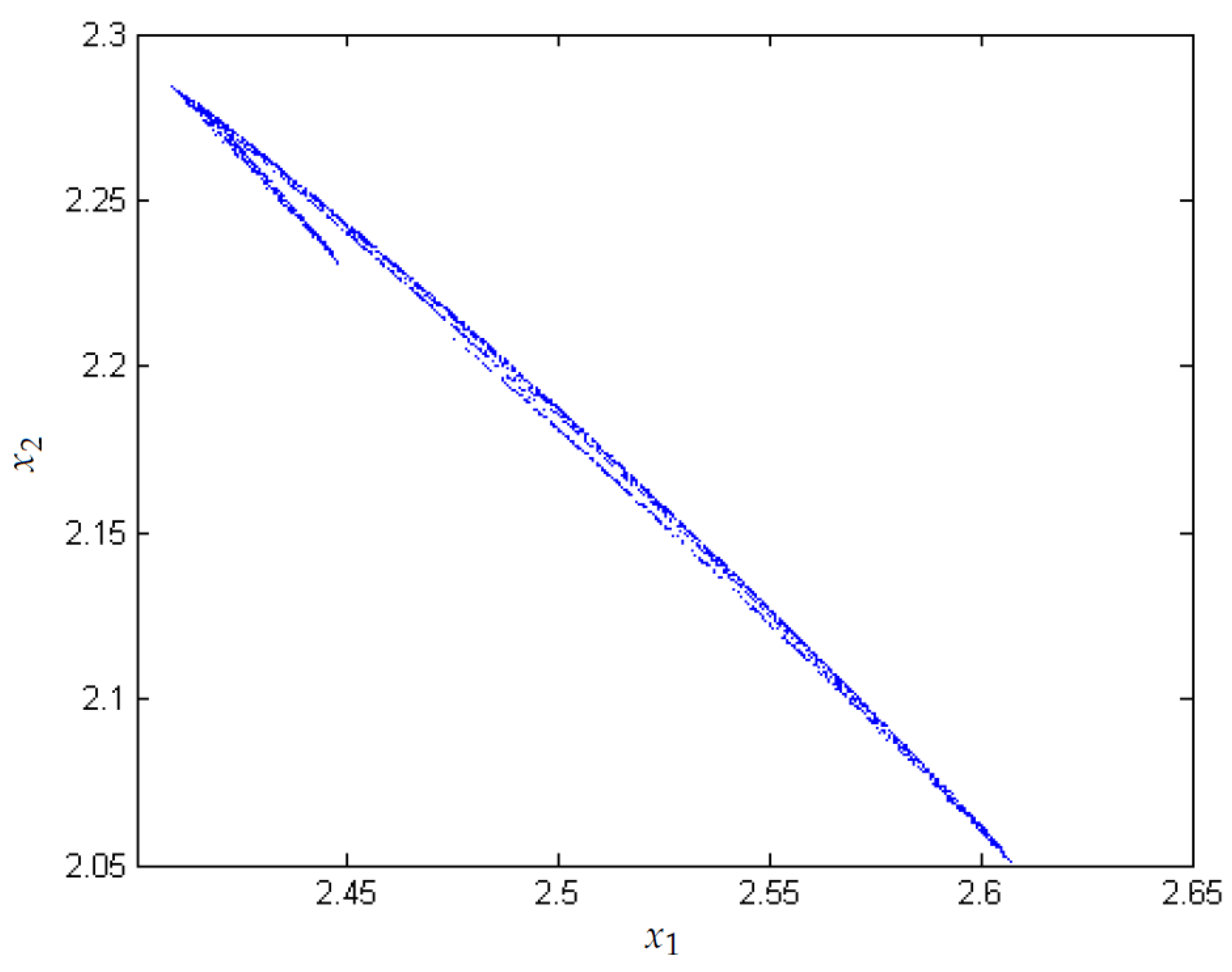
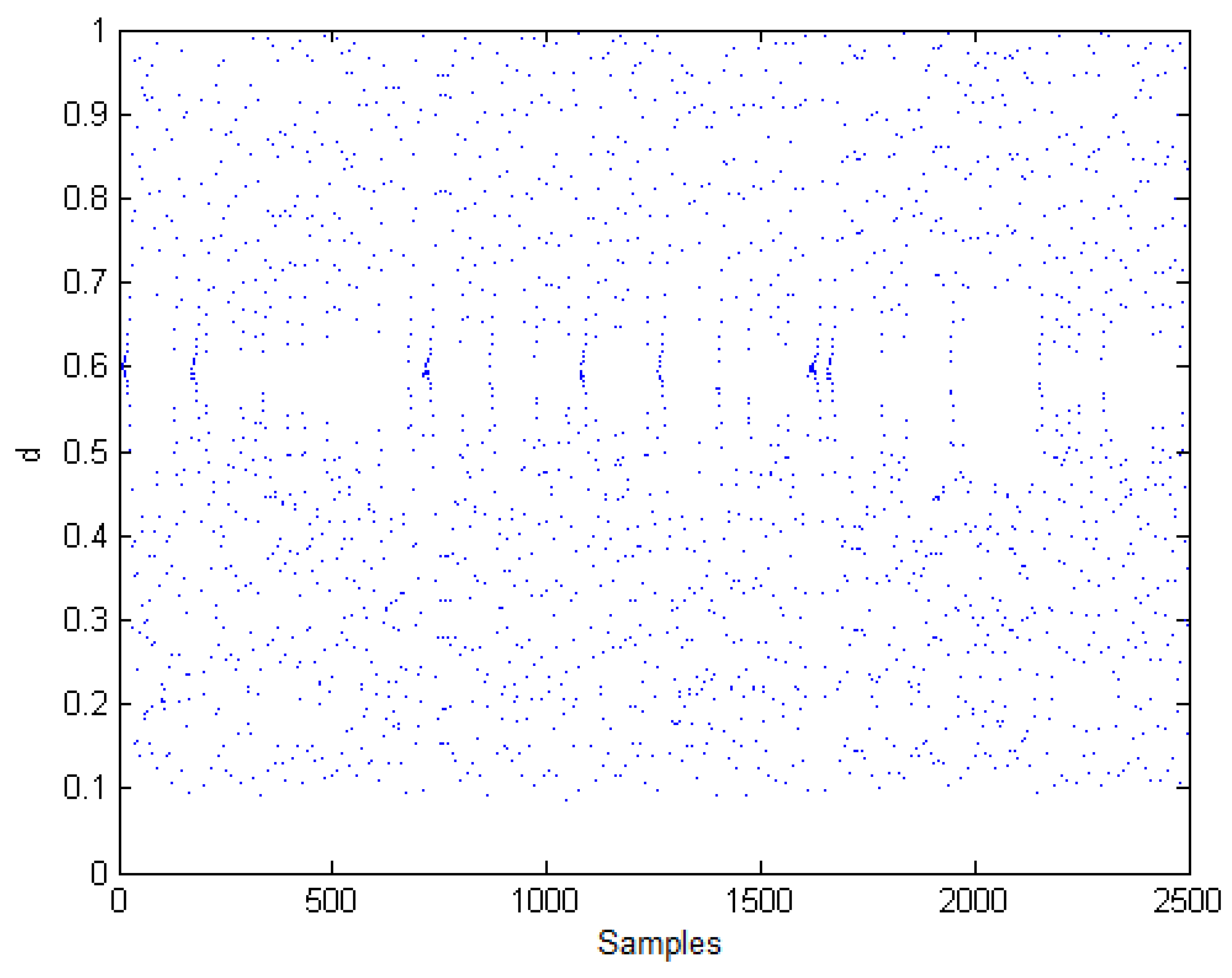
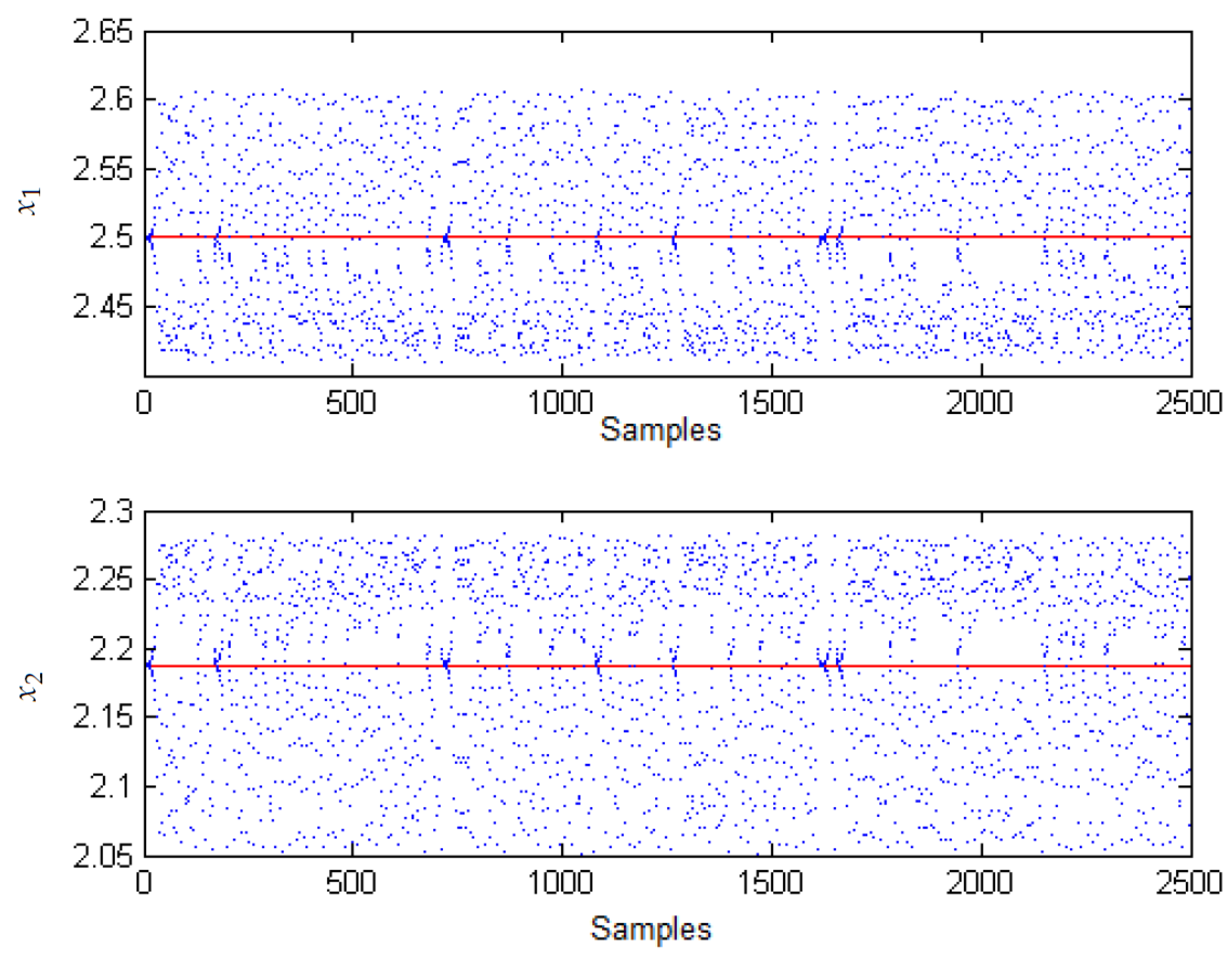
3.1. Chaos in the Boost Converter
3.2. Control of Chaos with FPIC
3.3. FPIC Control with Time Delay
3.4. Control of Chaos
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Forouzesh, M.; Shen, Y.; Yari, K.; Siwakoti, Y.P.; Blaabjerg, F. High-Efficiency High Step-Up DC–DC Converter With Dual Coupled Inductors for Grid-Connected Photovoltaic Systems. IEEE Trans. Power Electron. 2018, 33, 5967–5982. [Google Scholar] [CrossRef]
- Buso, P.M.S. Digital Control in Power Electronics; Morgan & Claypool Publishers: San Rafael, CA, USA, 2015. [Google Scholar]
- Mohan, N. Power Electronics: A First Course; Wiley: Hoboken, NJ, USA, 2011; p. 288. [Google Scholar]
- Mohan, N. Advanced Electric Drives: Analysis, Control, and Modeling using MATLAB/Simulink; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; p. 208. [Google Scholar]
- Revelo-Fuelagán, J.; Candelo-Becerra, J.E.; Hoyos, F.E. Power Factor Correction of Compact Fluorescent and Tubular LED Lamps by Boost Converter with Hysteretic Control. J. Daylighting 2020, 7, 73–83. [Google Scholar] [CrossRef]
- Amador, A.; Casanova, S.; Granada, H.A.; Olivar, G.; Hurtado, J. Codimension-Two Big-Bang Bifurcation in a ZAD-Controlled Boost DC-DC Converter. Int. J. Bifurc. Chaos 2014, 24, 1450150. [Google Scholar] [CrossRef]
- Fossas, E.; Olivar, G. Study of chaos in the buck converter. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1996, 43, 13–25. [Google Scholar] [CrossRef] [Green Version]
- Toribio, E.; El Aroudi, A.; Olivar, G.; Benadero, L. Numerical and experimental study of the region of period-one operation of a PWM boost converter. IEEE Trans. Power Electron. 2000, 15, 1163–1171. [Google Scholar] [CrossRef]
- Poddar, G.; Chakrabarty, K.; Banerjee, S. Experimental control of chaotic behavior of buck converter. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1995, 42, 502–504. [Google Scholar] [CrossRef]
- di Bernardo, M.; Garefalo, F.; Glielmo, L.; Vasca, F. Switchings, bifurcations, and chaos in DC/DC converters. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1998, 45, 133–141. [Google Scholar] [CrossRef]
- Munoz, J.; Osorio, G.; Angulo, F. Boost converter control with ZAD for power factor correction based on FPGA. In Proceedings of the 2013 Workshop on Power Electronics and Power Quality Applications (PEPQA). IEEE, Bogota, Colombia, 6–7 July 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Angulo, F.; Burgos, J.; Olivar, G. Chaos stabilization with TDAS and FPIC in a buck converter controlled by lateral PWM and ZAD. In Proceedings of the 2007 Mediterranean Conference on Control & Automation. IEEE, Athens, Greece, 27–29 June 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Aroudi, A.E.; Debbat, M.; Martinez-Salamero, L. Poincaré maps modeling and local orbital stability analysis of discontinuous piecewise affine periodically driven systems. Nonlinear Dyn. 2007, 50, 431–445. [Google Scholar] [CrossRef]
- Hoyos Velasco, F.E.; García, N.T.; Garcés Gómez, Y.A. Adaptive Control for Buck Power Converter Using Fixed Point Inducting Control and Zero Average Dynamics Strategies. Int. J. Bifurc. Chaos 2015, 25, 1550049. [Google Scholar] [CrossRef]
- Repecho, V.; Biel, D.; Ramos-Lara, R. Robust ZAD Sliding Mode Control for an 8-Phase Step-Down Converter. IEEE Trans. Power Electron. 2020, 35, 2222–2232. [Google Scholar] [CrossRef]
- Vergara Perez, D.D.C.; Trujillo, S.C.; Hoyos Velasco, F.E. Period Addition Phenomenon and Chaos Control in a ZAD Controlled Boost Converter. Int. J. Bifurc. Chaos 2018, 28, 1850157. [Google Scholar] [CrossRef]
- Repecho, V.; Biel, D.; Ramos-Lara, R.; Vega, P.G. Fixed-Switching Frequency Interleaved Sliding Mode Eight-Phase Synchronous Buck Converter. IEEE Trans. Power Electron. 2018, 33, 676–688. [Google Scholar] [CrossRef] [Green Version]
- Perez, D.D.C.V.; Trujillo, S.C.; Velasco, F.E.H. On the dynamic behavior of the current in the condenser of a boost converter controlled with ZAD. TELKOMNIKA (Telecommun. Computi. Electron. Control) 2020, 18, 1678. [Google Scholar] [CrossRef]
- Pierre, T.; Bonhomme, G.; Atipo, A. Controlling the Chaotic Regime of Nonlinear Ionization Waves using the Time-Delay Autosynchronization Method. Phys. Rev. Lett. 1996, 76, 2290–2293. [Google Scholar] [CrossRef]
- Hoyos, F.E.; Candelo-Becerra, J.E.; Hoyos Velasco, C.I. Model-Based Quasi-Sliding Mode Control with Loss Estimation Applied to DC–DC Power Converters. Electronics 2019, 8, 1086. [Google Scholar] [CrossRef] [Green Version]
- Hoyos Velasco, F.E.; Candelo, J.E.; Silva Ortega, J.I. Performance evaluation of a DC-AC inverter controlled with ZAD-FPIC. INGE CUC 2018, 14, 9–18. [Google Scholar] [CrossRef]
- Angulo, F.; Fossas, E.; Ocampo-Martinez, C.; Olivar, G. Stabilization of chaos wiht FPIC: Application to ZAD-strategy buck converters. In Proceedings of the 16th World Congress of the International Federation on Automatic Control; Proceedings of the 16th IFAC World Congress, Prague, Czech Republic, 3–8 July 2005. [Google Scholar]
- Pyragas, K. Continuous control of chaos by self-controlling feedback. Phys. Lett. A 1992, 170, 421–428. [Google Scholar] [CrossRef]
- Pyragas, K. Control of Chaos via an Unstable Delayed Feedback Controller. Phys. Rev. Lett. 2001, 86, 2265–2268. [Google Scholar] [CrossRef] [PubMed]
- Senkerik, R.; Zelinka, I.; Davendra, D.; Oplatkova, Z. Evolutionary Design of Chaos Control in 1D; Springer: Berlin, Germany, 2010; Volume 267, pp. 165–190. [Google Scholar] [CrossRef]
- Iñarrea, M.; Peláez, J. Libration Control of Electrodynamic Tethers Using the Extended Time-Delayed Autosynchronization Method. J. Guidance Control Dyn. 2010, 33, 923–933. [Google Scholar] [CrossRef] [Green Version]
- Rusinek, R.; Mitura, A.; Warminski, J. Time delay Duffing’s systems: Chaos and chatter control. Meccanica 2014, 49, 1869–1877. [Google Scholar] [CrossRef] [Green Version]
- Doering, C.I.; Lopes, A.O. Equacoes Diferenciais Ordinárias; Instituto Nacional de Matemática Pura e Aplicada: Rio de Janeiro, Brazil, 2016; p. 423. [Google Scholar]
- Fossas, E.; Griño, R.; Biel, D. Quasi-sliding control based on pulse width modulation, zero averaged dynamics and the L2 norm. In Proceedings of the Advances in Variable Structure Systems, Gold Coast, Australia, 7–9 December 2000; pp. 335–344. [Google Scholar] [CrossRef]
- Nonlinear Control and Control of Chaos. In Nonlinear Phenomena in Power Electronics; IEEE: Piscataway, NJ, USA, 2009. [CrossRef]
- Banerjee, S.; Verghese, G.C. Basics of Bifurcation and Chaos Theory. In Nonlinear Phenomena in Power Electronics; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Banerjee, S.; Banerjee, S. Nonlinear Phenomena in Other Power Electronic Systems. In Nonlinear Phenomena in Power Electronics; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Banerjee, S.; Verghese, G.C. Nonlinear Phenomena in DC/DC Converters. In Nonlinear Phenomena in Power Electronics; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar] [CrossRef]










| Controller | Advantage | Drawbacks |
|---|---|---|
| ZAD | The technique is useful to obtain a low steady-state error and maintain a fixed switching frequency [20,21,22]. | It is not robust when the system parameters change and for real-time application necessitates a high sampling rate and signal sensing synchronization with a PWM working in centered symmetric mode [20,22]. |
| FPIC | This technique is very useful for stabilizing higher period and order orbits, and also for controlling chaos [20,21,22]. | This technique lacks feedback from the regulated variables and is not robust enough to respond to changes in the system parameters [20,22]. |
| TDAS | It is useful to stabilize unstable periodic orbits and steady states [12,23,24,25]. It allows feedback and does not require rapid switching operations [26]. It is not necessary to have a reference signal according to the orbits [25,26]. | As the control uses the current state and one delay period, when the perturbation is small it presents low-quality stabilization, for example during high periodic orbits [27]. |
| Criteria | Decision | Topology |
|---|---|---|
| 1 | ||
| 2 | ||
| 1 and 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trujillo, S.C.; Candelo-Becerra, J.E.; Hoyos, F.E. Analysis and Control of Chaos in the Boost Converter with ZAD, FPIC, and TDAS. Sustainability 2022, 14, 13170. https://doi.org/10.3390/su142013170
Trujillo SC, Candelo-Becerra JE, Hoyos FE. Analysis and Control of Chaos in the Boost Converter with ZAD, FPIC, and TDAS. Sustainability. 2022; 14(20):13170. https://doi.org/10.3390/su142013170
Chicago/Turabian StyleTrujillo, Simeón Casanova, John E. Candelo-Becerra, and Fredy E. Hoyos. 2022. "Analysis and Control of Chaos in the Boost Converter with ZAD, FPIC, and TDAS" Sustainability 14, no. 20: 13170. https://doi.org/10.3390/su142013170
APA StyleTrujillo, S. C., Candelo-Becerra, J. E., & Hoyos, F. E. (2022). Analysis and Control of Chaos in the Boost Converter with ZAD, FPIC, and TDAS. Sustainability, 14(20), 13170. https://doi.org/10.3390/su142013170








