Evaluation of the Main Control Strategies for Grid-Connected PV Systems
Abstract
:1. Introduction
- Traditional methods: In this branch, the measured values (normally the PV voltage and current) are used to set the control parameter. Within this category, the well-known perturb and observe (P&O) and the incremental conductance (INC) are very popular [17,18]. The gradient descent method has a similar operating principle, where the gradient of the power with respect to voltage is used to set the voltage reference value [19,20].
- Mathematical models: Here, a model is derived based on the characteristics of the PV source. The objective of this model is to allocate the position of the maximum power point (MPP). The fractional open-circuit voltage method, fractional short-circuit current method [21,22], and temperature algorithm [23,24] are examples from this methodology. Temperature or radiation sensor can be utilized in such schemes in addition to the voltage or current measurements [25].
- Methods for partial shading: The partial shading methods are designed to capture the global maximum of the power–voltage (P-V) curve when nonuniform distribution of radiation happens [30]. Heavy smoke, clouds, and shadowing from nearby buildings are the main causes of partial shading [31]. Optimization techniques are employed to hunt the ultimate maximum of the produced power. Particle swarm optimization, genetic algorithm, simulated annealing, bat algorithm, etc. are common for such execution [32,33].
- Investigation of the primary control objectives for the two-stage PV topology.
- Experimental assessment of the performance of the MPPT operation using adaptive step-size.
- Comparative evaluation among the main control algorithms for the inversion-stage, where the VOC, FS-MPC, and DB will be considered for comparison.
- Robustness assessment of all studied methods against system’s parameter variation.
- Estimation of these parameters based on an extended Kalman filter.
- Future scope will also be addressed.
2. Model of the PV System
2.1. PV Source Scheme
2.2. Boost Converter Modeling
2.3. Model of the Inversion Stage with Grid Connection
3. Main Control Strategies for the Two-Stage PV System
3.1. Maximum Power Point Tracking
- The perturb and observe method
- The incremental conductance method
3.2. Active and Reactive Power Control
- The voltage-oriented control
- The finite-set model predictive control
- The dead-beat technique
3.3. Parameter Estimation Based on EKF
- Initialization for the state variables and covariance matrices.
- Projection of state vector
- Prediction of error covariance matrixwhere
- Computation of Kalman constant
- Estimation correction based on measurements
- Update of error covariance matrix
- Repeat from step 2.
4. Experimental Tests and Evaluations
4.1. Lab Setup Description
4.2. Assessment of the MPPT Performance
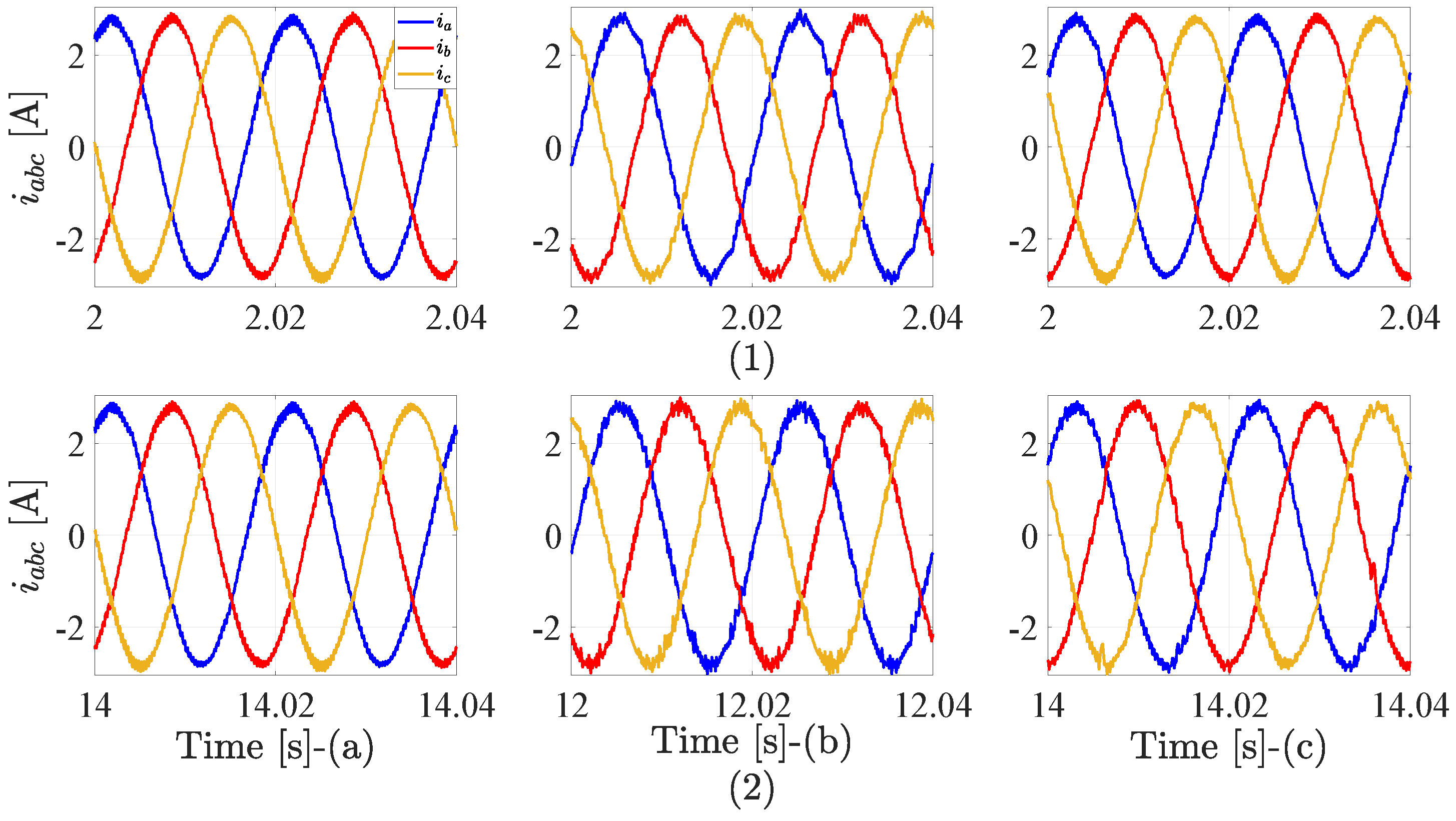
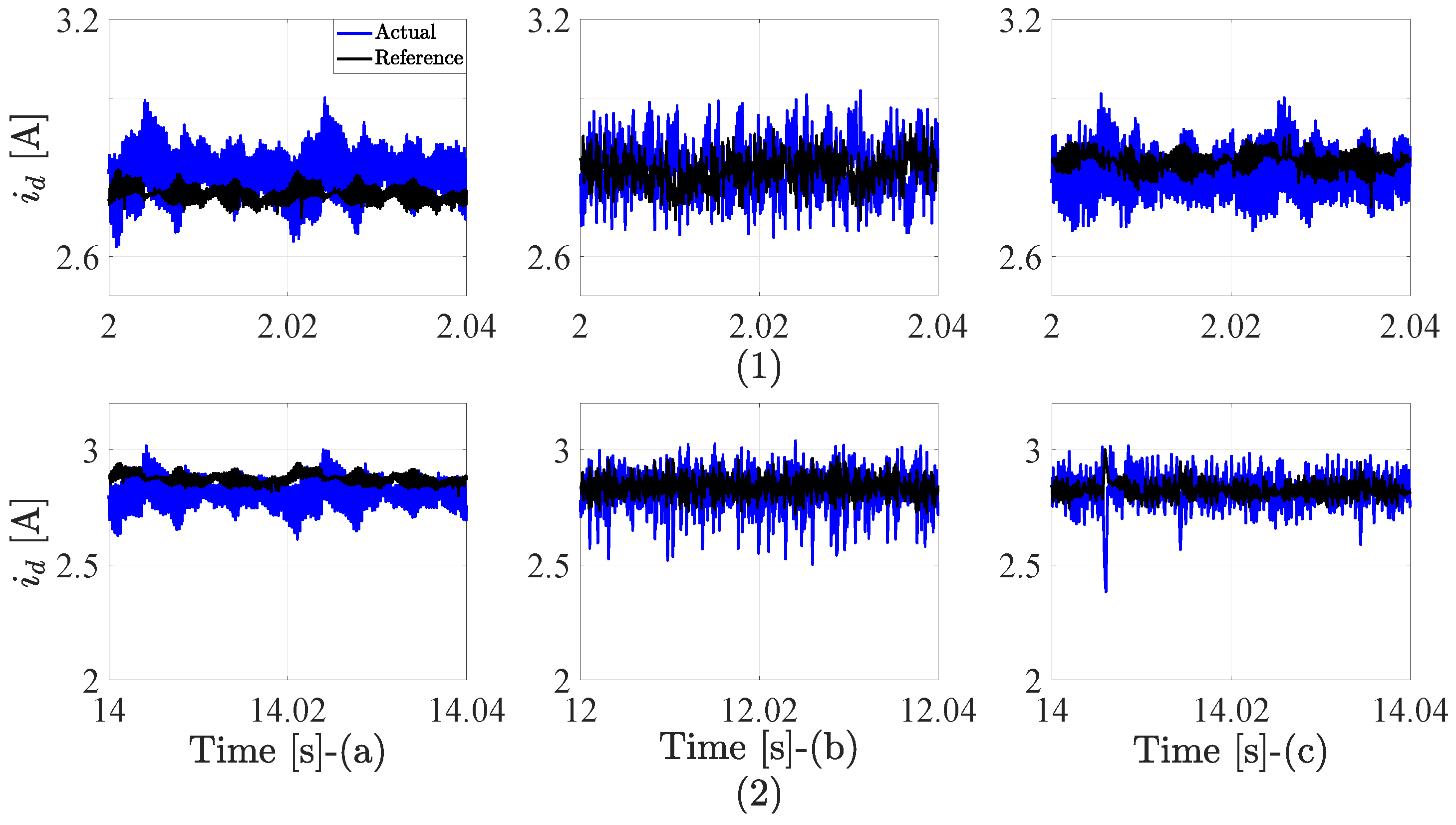
4.3. Inverter Control Results
4.4. EKF Estimation
4.5. Robustness Assessment
5. Future Work
- Implementation of different power control strategies in addition to the MPPT function. The PV system should be able to support the grid [67]. In this matter, different functions are to be included within the MPPT operation. For example, constant power generation is required to protect the grid against overloading at situations of peak power generation [68].
- Simplification and calculation reduction of the FS-MPC techniques, especially when considering multilevel inverters [69].
- Multi-objective realization for the control scheme, where different purposes can be achieved.
- Sensorless control is preferred as a back-up strategy in situations of sensor failure, where the control objective can be fulfilled with a minimum number of sensors. However, this may lead to deterioration of the controller quality [72].
- Low voltage ride through capability and improvement of the PV system [73].
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alshahrani, A.; Omer, S.; Su, Y.; Mohamed, E.; Alotaibi, S. The technical challenges facing the integration of small-scale and large-scale PV systems into the grid: A critical review. Electronics 2019, 8, 1443. [Google Scholar] [CrossRef]
- Aleem, S.A.; Hussain, S.S.; Ustun, T.S. A review of strategies to increase PV penetration level in smart grids. Energies 2020, 13, 636. [Google Scholar] [CrossRef]
- Seyedmahmoudian, M.; Rahmani, R.; Mekhilef, S.; Oo, A.M.T.; Stojcevski, A.; Soon, T.K.; Ghandhari, A.S. Simulation and hardware implementation of new maximum power point tracking technique for partially shaded PV system using hybrid DEPSO method. IEEE Trans. Sustain. Energy 2015, 6, 850–862. [Google Scholar] [CrossRef]
- Liu, G.; Rasul, M.G.; Amanullah, M.T.O.; Khan, M.M.K. Techno-economic simulation and optimization of residential grid-connected PV system for the Queensland climate. Renew. Energy 2012, 45, 146–155. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- Zheng, H.; Li, S.; Challoo, R.; Proano, J. Shading and bypass diode impacts to energy extraction of PV arrays under different converter configurations. Renew. Energy 2014, 68, 58–66. [Google Scholar] [CrossRef]
- Taghvaee, M.H.; Radzi, M.A.M.; Moosavain, S.M.; Hizam, H.; Marhaban, M.H. A current and future study on non-isolated DC–DC converters for photovoltaic applications. Renew. Sustain. Energy Rev. 2013, 17, 216–227. [Google Scholar] [CrossRef]
- Başoğlu, M.E. Comprehensive review on distributed maximum power point tracking: Submodule level and module level MPPT strategies. Sol. Energy 2022, 241, 85–108. [Google Scholar] [CrossRef]
- Ali, K.; Yasir, M.; Liu, H.; Yang, Z.; Yuan, X. A comprehensive review on grid connected photovoltaic inverters, their modulation techniques, and control strategies. Energies 2020, 13, 4185. [Google Scholar]
- Shawky, A.; Ahmed, M.; Orabi, M.; Aroudi, A.E. Classification of three-phase grid-tied microinverters in photovoltaic applications. Energies 2020, 13, 2929. [Google Scholar] [CrossRef]
- Wu, T.-F.; Chang, C.-H.; Lin, L.-C.; Kuo, C.-L. Power loss comparison of single-and two-stage grid-connected photovoltaic systems. IEEE Trans. Energy Convers. 2011, 26, 707–715. [Google Scholar] [CrossRef]
- Lakshmi, M.; Hemamalini, S. Coordinated control of MPPT and voltage regulation using single-stage high gain DC–DC converter in a grid-connected PV system. Electr. Power Syst. Res. 2019, 169, 65–73. [Google Scholar] [CrossRef]
- Kumar, N.; Singh, B.; Panigrahi, B.K. LLMLF-based control approach and LPO MPPT technique for improving performance of a multifunctional three-phase two-stage grid integrated PV system. IEEE Trans. Sustain. Energy 2019, 11, 371–380. [Google Scholar] [CrossRef]
- Ahmed, M.; Abdelrahem, M.; Harbi, I.; Kennel, R. An Adaptive Model-Based MPPT Technique with Drift-Avoidance for Grid-Connected PV Systems. Energies 2020, 13, 6656. [Google Scholar] [CrossRef]
- Karami, N.; Moubayed, N.; Outbib, R. General review and classification of different MPPT Techniques. Renew. Sustain. Energy Rev. 2017, 68, 1–18. [Google Scholar] [CrossRef]
- Motahhir, S.; Hammoumi, A.E.; Ghzizal, A.E. The most used MPPT algorithms: Review and the suitable low-cost embedded board for each algorithm. J. Clean. Prod. 2020, 246, 118983. [Google Scholar] [CrossRef]
- Sera, D.; Mathe, L.; Kerekes, T.; Spataru, S.V.; Teodorescu, R. On the perturb-and-observe and incremental conductance MPPT methods for PV systems. IEEE J. Photovolt. 2013, 3, 1070–1078. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Samanta, S.; Mishra, S. Steady Output and Fast Tracking MPPT (SOFT-MPPT) for P&O and InC Algorithms. IEEE Trans. Sustain. Energy 2020, 12, 293–302. [Google Scholar]
- Pradhan, R.; Subudhi, B. A steepest-descent based maximum power point tracking technique for a photovoltaic power system. In Proceedings of the 2012 2nd International Conference on Power, Control and Embedded Systems, Allahabad, India, 17–19 December 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
- Verma, D.; Nema, S.; Shandilya, A.M.; Dash, S.K. Maximum power point tracking (MPPT) techniques: Recapitulation in solar photovoltaic systems. Renew. Sustain. Energy Rev. 2016, 54, 1018–1034. [Google Scholar] [CrossRef]
- Sher, H.A.; Murtaza, A.F.; Noman, A.; Addoweesh, K.E.; Al-Haddad, K.; Chiaberge, M. A new sensorless hybrid MPPT algorithm based on fractional short-circuit current measurement and P&O MPPT. IEEE Trans. Sustain. Energy 2015, 6, 1426–1434. [Google Scholar]
- Nadeem, A.; Sher, H.A.; Murtaza, A.F. Online fractional open-circuit voltage maximum output power algorithm for photovoltaic modules. IET Renew. Power Gener. 2020, 14, 188–198. [Google Scholar] [CrossRef]
- Coelho, R.F.; Concer, F.M.; Martins, D.C. A MPPT approach based on temperature measurements applied in PV systems. In Proceedings of the 2010 IEEE International Conference on Sustainable Energy Technologies (ICSET), Kandy, Sri Lanka, 6–9 December 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- De Brito, M.A.G.; Galotto, L.; Sampaio, L.P.; Melo, G.d.e.; Canesin, C.A. Evaluation of the main MPPT techniques for photovoltaic applications. IEEE Trans. Ind. Electron. 2012, 60, 1156–1167. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Wen, H.; Xiao, W. Comprehensive studies on operational principles for maximum power point tracking in photovoltaic systems. IEEE Access 2019, 7, 121407–121420. [Google Scholar] [CrossRef]
- Robles Algarín, C.; Giraldo, J.T.; Alvarez, O.R. Fuzzy logic based MPPT controller for a PV system. Energies 2017, 10, 2036. [Google Scholar] [CrossRef]
- Boumaaraf, H.; Talha, A.; Bouhali, O. A three-phase NPC grid-connected inverter for photovoltaic applications using neural network MPPT. Renew. Sustain. Energy Rev. 2015, 49, 1171–1179. [Google Scholar] [CrossRef]
- Messalti, S.; Harrag, A.; Loukriz, A. A new variable step size neural networks MPPT controller: Review, simulation and hardware implementation. Renew. Sustain. Energy Rev. 2017, 68, 221–233. [Google Scholar] [CrossRef]
- Podder, A.K.; Roy, N.K.; Pota, H.R. MPPT methods for solar PV systems: A critical review based on tracking nature. IET Renew. Power Gener. 2019, 13, 1615–1632. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A new MPPT design using grey wolf optimization technique for photovoltaic system under partial shading conditions. IEEE Trans. Sustain. Energy 2015, 7, 181–188. [Google Scholar] [CrossRef]
- Ahmed, M.; Abdelrahem, M.; Kennel, R. Highly efficient and robust grid connected photovoltaic system based model predictive control with kalman filtering capability. Sustainability 2020, 12, 4542. [Google Scholar] [CrossRef]
- Kermadi, M.; Salam, Z.; Eltamaly, A.M.; Ahmed, J.; Mekhilef, S.; Larbes, C.; Berkouk, E.M. Recent developments of MPPT techniques for PV systems under partial shading conditions: A critical review and performance evaluation. IET Renew. Power Gener. 2020, 14, 3401–3417. [Google Scholar] [CrossRef]
- Seyedmahmoudian, M.; Horan, B.; Soon, T.K.; Rahmani, R.; Oo, A.M.T.; Mekhilef, S.; Stojcevski, A. State of the art artificial intelligence-based MPPT techniques for mitigating partial shading effects on PV systems—A review. Renew. Sustain. Energy Rev. 2016, 64, 435–455. [Google Scholar] [CrossRef]
- Safari, A.; Mekhilef, S. Simulation and hardware implementation of incremental conductance MPPT with direct control method using cuk converter. IEEE Trans. Ind. Electron. 2010, 58, 1154–1161. [Google Scholar] [CrossRef]
- Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of perturb and observe MPPT algorithm implementation techniques for PV pumping applications. IEEE Trans. Sustain. Energy 2011, 3, 21–33. [Google Scholar] [CrossRef]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kang, Y. A variable step size INC MPPT method for PV systems. IEEE Trans. Ind. Electron. 2008, 55, 622–2628. [Google Scholar]
- Loukriz, A.; Haddadi, M.; Messalti, S. Simulation and experimental design of a new advanced variable step size Incremental Conductance MPPT algorithm for PV systems. ISA Trans. 2016, 62, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Thanapalan, K.; Procter, A.; Carr, S.; Maddy, J. Adaptive hybrid maximum power point tracking method for a photovoltaic system. IEEE Trans. Energy Convers. 2013, 28, 353–360. [Google Scholar] [CrossRef]
- Zakzouk, N.E.; Elsaharty, M.A.; Abdelsalam, A.K.; Helal, A.A.; Williams, B.W. Improved performance low-cost incremental conductance PV MPPT technique. IET Renew. Power Gener. 2016, 10, 561–574. [Google Scholar] [CrossRef]
- Kadri, R.; Gaubert, J.-P.; Champenois, G. An improved maximum power point tracking for photovoltaic grid-connected inverter based on voltage-oriented control. IEEE Trans. Ind. Electron. 2010, 58, 66–75. [Google Scholar] [CrossRef]
- Noguchi, T.; Tomiki, H.; Kondo, S.; Takahashi, I. Direct power control of PWM converter without power-source voltage sensors. IEEE Trans. Ind. Appl. 1998, 34, 473–479. [Google Scholar] [CrossRef]
- Zhang, N.; Tang, H.; Yao, C. A systematic method for designing a PR controller and active damping of the LCL filter for single-phase grid-connected PV inverters. Energies 2014, 7, 3934–3954. [Google Scholar] [CrossRef]
- Tafti, H.D.; Maswood, A.I.; Ukil, A.; Gabriel, O.H.P.; Ziyou, L. NPC photovoltaic grid-connected inverter using proportional-resonant controller. In Proceedings of the 2014 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Hong Kong, China, 7–10 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Rodriguez, J.; Garcia, C.; Mora, A.; Flores-Bahamonde, F.; Acuna, P.; Novak, M.; Zhang, Y.; Tarisciotti, L.; Davari, S.A.; Zhang, Z.; et al. Latest advances of model predictive control in electrical drives. Part I: Basic concepts and advanced strategies. IEEE Trans. Power Electron. 2021, 37, 3927–3942. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Mei, X.; Rodríguez, J.; Kennel, R. Advanced control strategies of induction machine: Field oriented control, direct torque control and model predictive control. Energies 2018, 11, 120. [Google Scholar] [CrossRef]
- Ahmed, M.; Harbi, I.; Kennel, R.; Abdelrahem, M. Predictive Fixed Switching Maximum Power Point Tracking Algorithm with Dual Adaptive Step-Size for PV Systems. Electronics 2021, 10, 3109. [Google Scholar] [CrossRef]
- Bouafia, A.; Gaubert, J.-P.; Krim, F. Predictive direct power control of three-phase pulsewidth modulation (PWM) rectifier using space-vector modulation (SVM). IEEE Trans. Power Electron. 2009, 25, 228–236. [Google Scholar] [CrossRef]
- Shongwe, S.; Hanif, M. Comparative analysis of different single-diode PV modeling methods. IEEE J. Photovolt. 2015, 5, 938–946. [Google Scholar] [CrossRef]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 40. [Google Scholar]
- Manoharan, P.; Subramaniam, U.; Babu, T.S.; Padmanaban, S.; Holm-Nielsen, J.B.; Mitolo, M.; Ravichandran, S. Improved perturb and observation maximum power point tracking technique for solar photovoltaic power generation systems. IEEE Syst. J. 2020, 15, 3024–3035. [Google Scholar] [CrossRef]
- Abdelsalam, A.K.; Massoud, A.M.; Ahmed, S.; Enjeti, P.N. High-performance adaptive perturb and observe MPPT technique for photovoltaic-based microgrids. IEEE Trans. Power Electron. 2011, 26, 1010–1021. [Google Scholar] [CrossRef]
- Killi, M.; Samanta, S. Modified perturb and observe MPPT algorithm for drift avoidance in photovoltaic systems. IEEE Trans. Ind. Electron. 2015, 62, 5549–5559. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. A review of maximum power point tracking techniques of PV system for uniform insolation and partial shading condition. Renew. Sustain. Energy Rev. 2013, 19, 475–488. [Google Scholar] [CrossRef]
- Soon, T.K.; Mekhilef, S. A fast-converging MPPT technique for photovoltaic system under fast-varying solar irradiation and load resistance. IEEE Trans. Ind. Inform. 2014, 11, 176–186. [Google Scholar] [CrossRef]
- Mei, Q.; Shan, M.; Liu, L.; Guerrero, J.M. A novel improved variable step-size incremental-resistance MPPT method for PV systems. IEEE Trans. Ind. Electron. 2010, 58, 2427–2434. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Blaabjerg, F. Reactive power injection strategies for single-phase photovoltaic systems considering grid requirements. IEEE Trans. Ind. Appl. 2014, 50, 4065–4076. [Google Scholar] [CrossRef]
- Rodríguez, J.; Kennel, R.M.; Espinoza, J.R.; Trincado, M.; Silva, C.A.; Rojas, C.A. High-performance control strategies for electrical drives: An experimental assessment. IEEE Trans. Ind. Electron. 2011, 59, 812–820. [Google Scholar] [CrossRef]
- Xia, C.; Liu, T.; Shi, T.; Song, Z. A simplified finite-control-set model-predictive control for power converters. IEEE Trans. Ind. Inform. 2013, 10, 991–1002. [Google Scholar]
- Young, H.A.; Perez, M.A.; Rodriguez, J. Analysis of finite-control-set model predictive current control with model parameter mismatch in a three-phase inverter. IEEE Trans. Ind. Electron. 2016, 63, 3100–3107. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D.; Peng, Z. Improved finite-control-set model predictive control for active front-end rectifiers with simplified computational approach and on-line parameter identification. ISA Trans. 2017, 69, 51–64. [Google Scholar] [CrossRef]
- Yan, L.; Song, X. Design and implementation of Luenberger model-based predictive torque control of induction machine for robustness improvement. IEEE Trans. Power Electron. 2019, 35, 2257–2262. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Liang, J.; Liu, J.; Zhang, N.; Walker, P.D. Robust deadbeat predictive power control with a discrete-time disturbance observer for PWM rectifiers under unbalanced grid conditions. IEEE Trans. Power Electron. 2018, 34, 287–300. [Google Scholar] [CrossRef]
- Abdelrahem, M.; Hackl, C.M.; Kennel, R.; Rodriguez, J. Efficient direct-model predictive control with discrete-time integral action for PMSGs. IEEE Trans. Energy Convers. 2018, 34, 1063–1072. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A modified P&O maximum power point tracking method with reduced steady-state oscillation and improved tracking efficiency. IEEE Trans. Sustain. Energy 2016, 7, 1506–1515. [Google Scholar]
- Tafti, H.D.; Konstantinou, G.; Townsend, C.D.; Farivar, G.G.; Sangwongwanich, A.; Yang, Y.; Pou, J.; Blaabjerg, F. Extended functionalities of photovoltaic systems with flexible power point tracking: Recent advances. IEEE Trans. Power Electron. 2020, 35, 9342–9356. [Google Scholar] [CrossRef]
- Peng, Q.; Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. Grid-friendly power control for smart photovoltaic systems. Sol. Energy 2020, 210, 115–127. [Google Scholar] [CrossRef]
- Novak, M.; Dragicevic, T. Supervised Imitation Learn. Finite-Set Model Predict. Control Syst. Power Electronics. IEEE Trans. Ind. Electron. 2020, 68, 1717–1723. [Google Scholar] [CrossRef]
- Dragičević, T.; Novak, M. Weighting factor design in model predictive control of power electronic converters: An artificial neural network approach. IEEE Trans. Ind. Electron. 2018, 66, 8870–8880. [Google Scholar] [CrossRef] [Green Version]
- Elmorshedy, M.F.; Xu, W.; Allam, S.M.; Rodriguez, J.; Garcia, C. MTPA-based finite-set model predictive control without weighting factors for linear induction machine. IEEE Trans. Ind. Electron. 2020, 68, 2034–2047. [Google Scholar] [CrossRef]
- Chen, X.; Wu, W.; Gao, N.; Chung, H.S.-H.; Liserre, M.; Blaabjerg, F. Finite control set model predictive control for LCL-filtered grid-tied inverter with minimum sensors. IEEE Trans. Ind. Electron. 2020, 67, 9980–9990. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Sujod, M.Z.; Blaabjerg, F. Low voltage ride-through capability control for single-stage inverter-based grid-connected photovoltaic power plant. Sol. Energy 2018, 159, 665–681. [Google Scholar] [CrossRef] [Green Version]
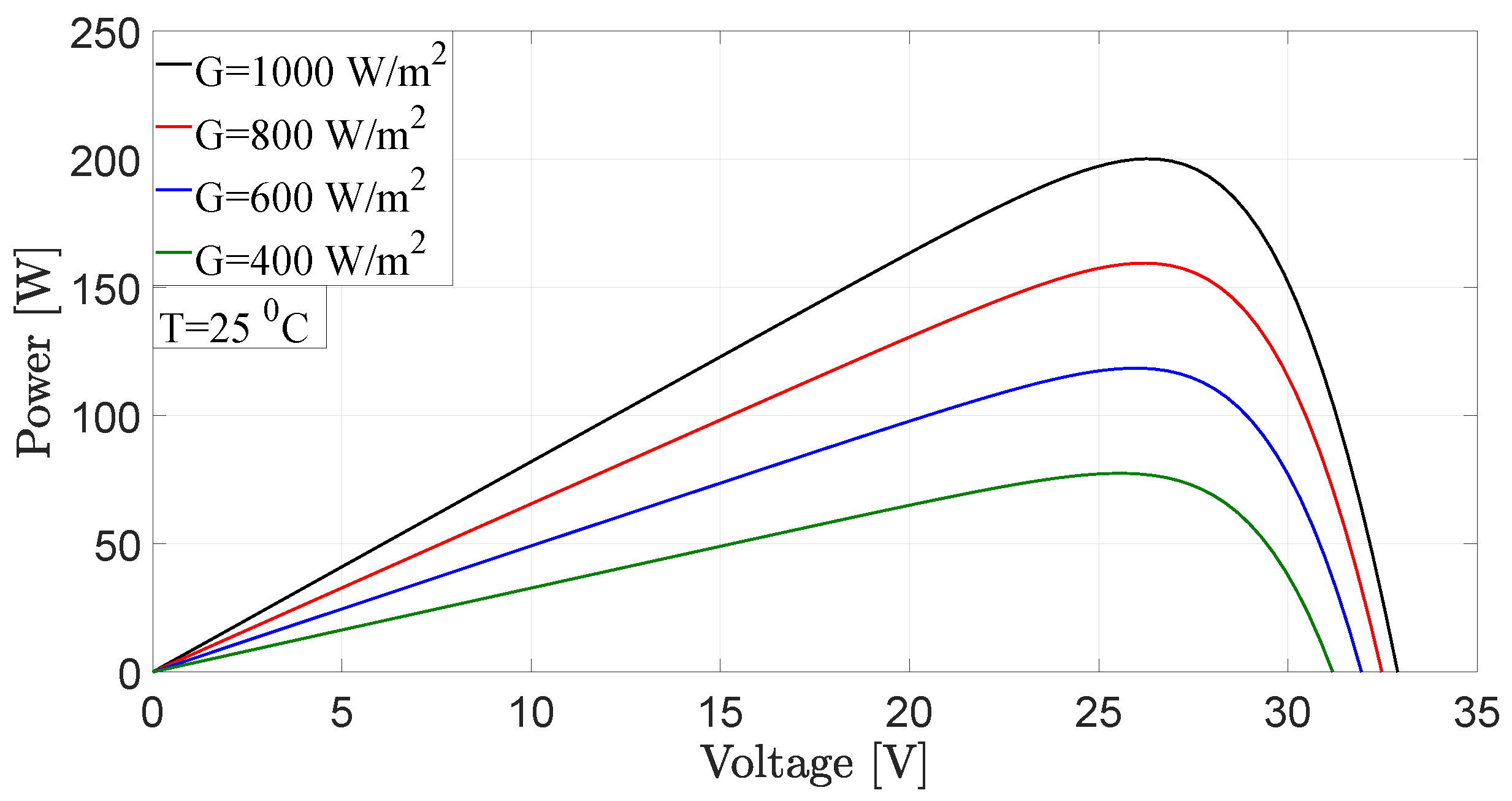
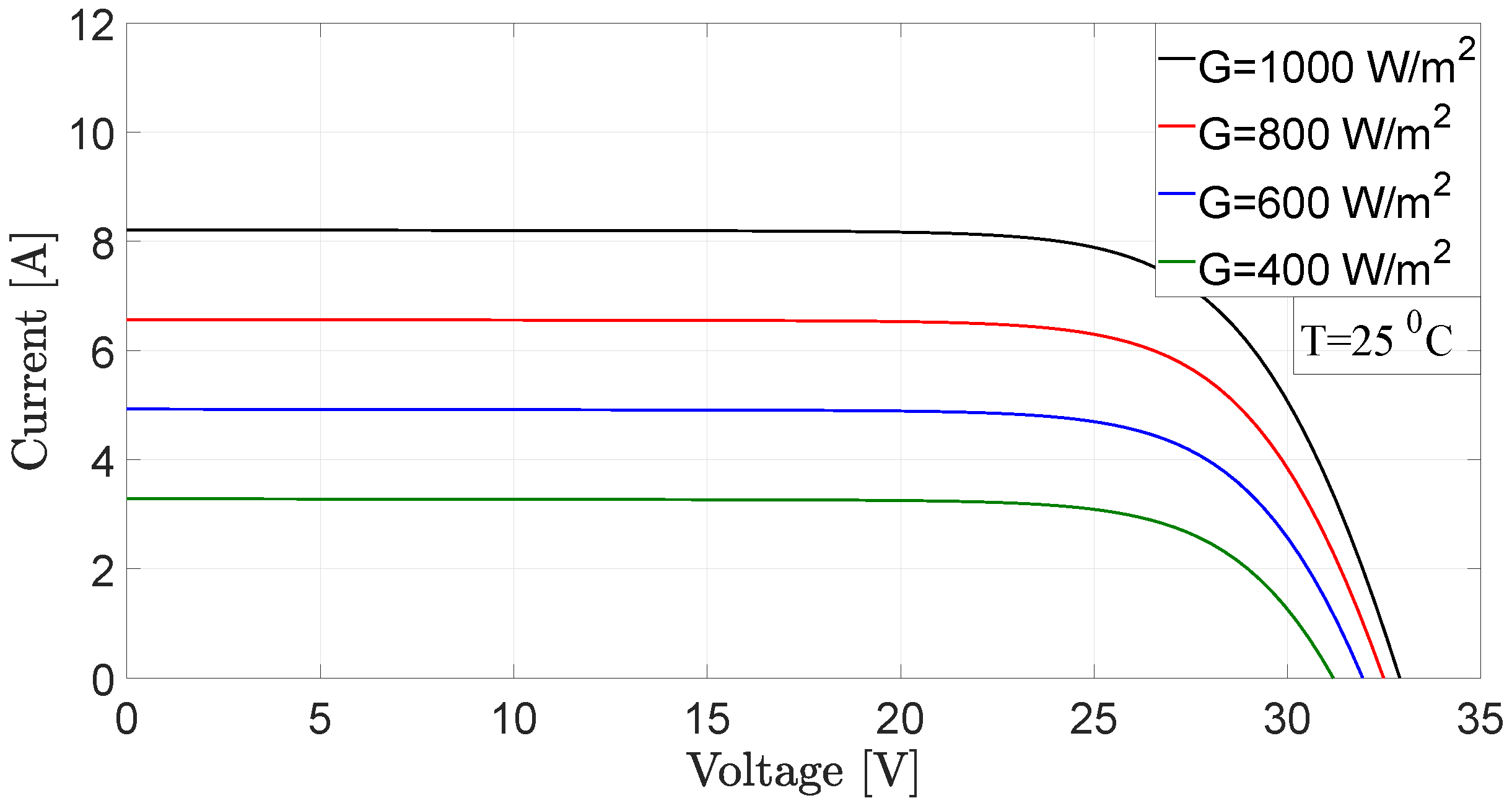
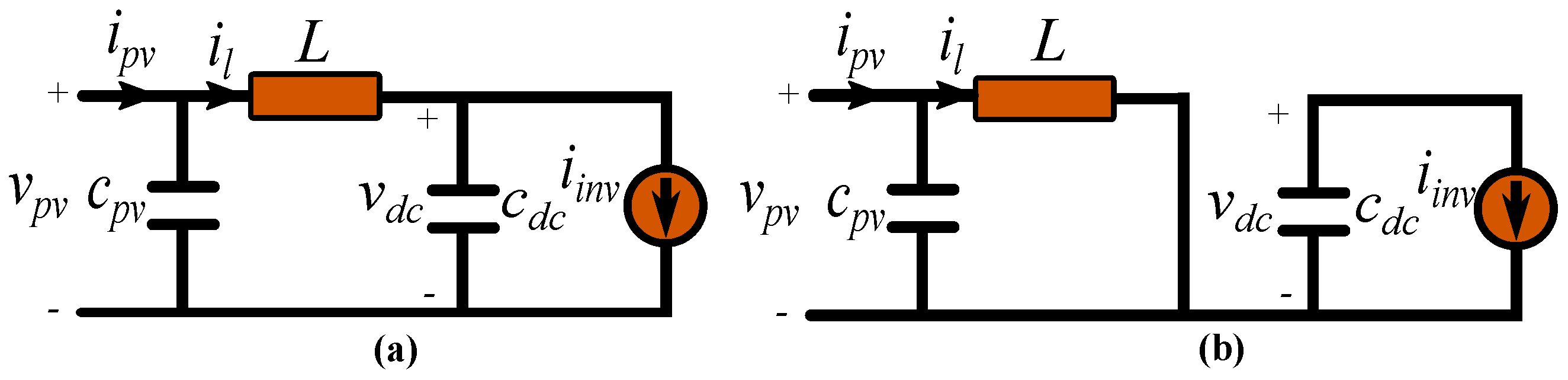


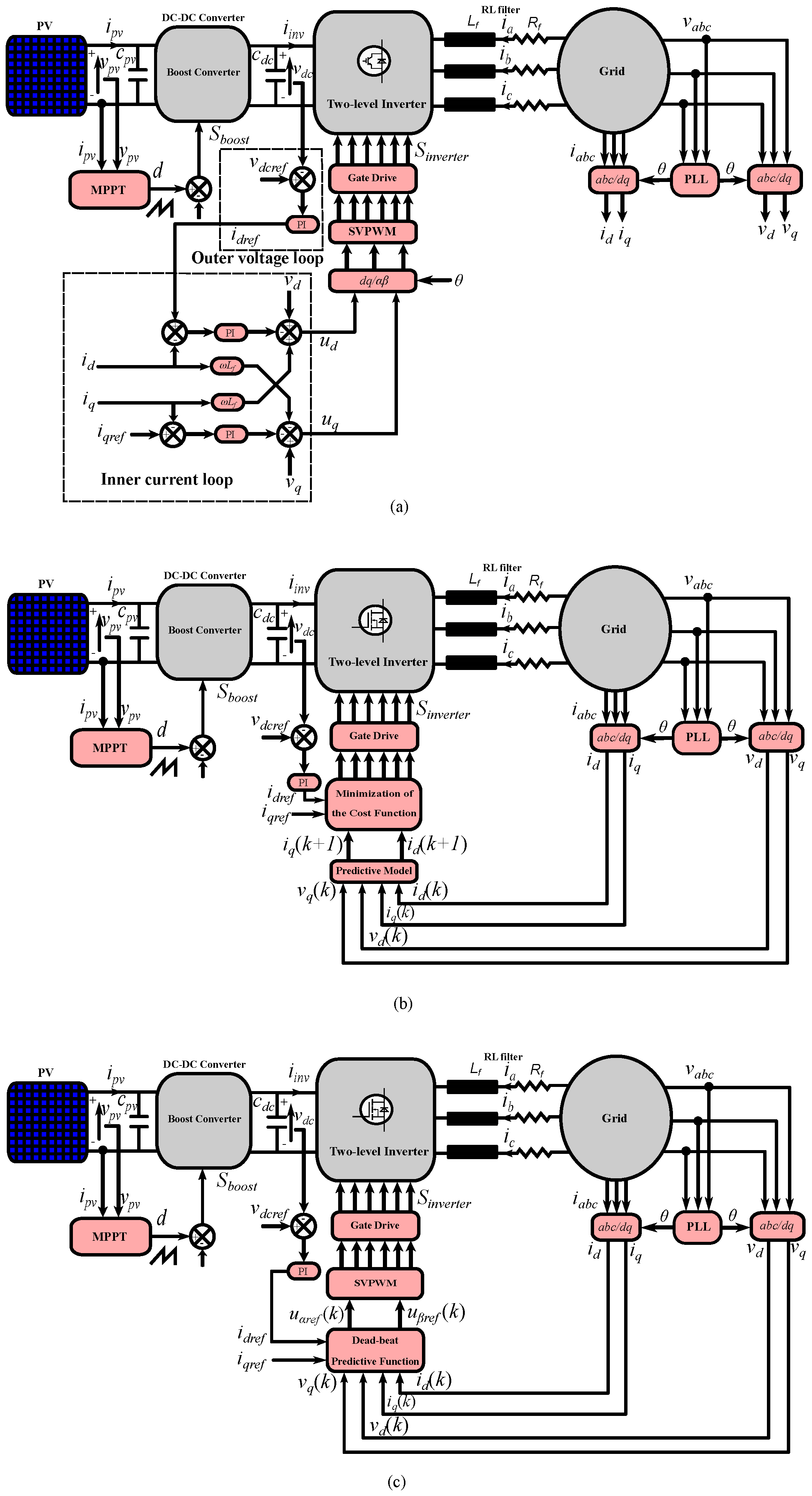

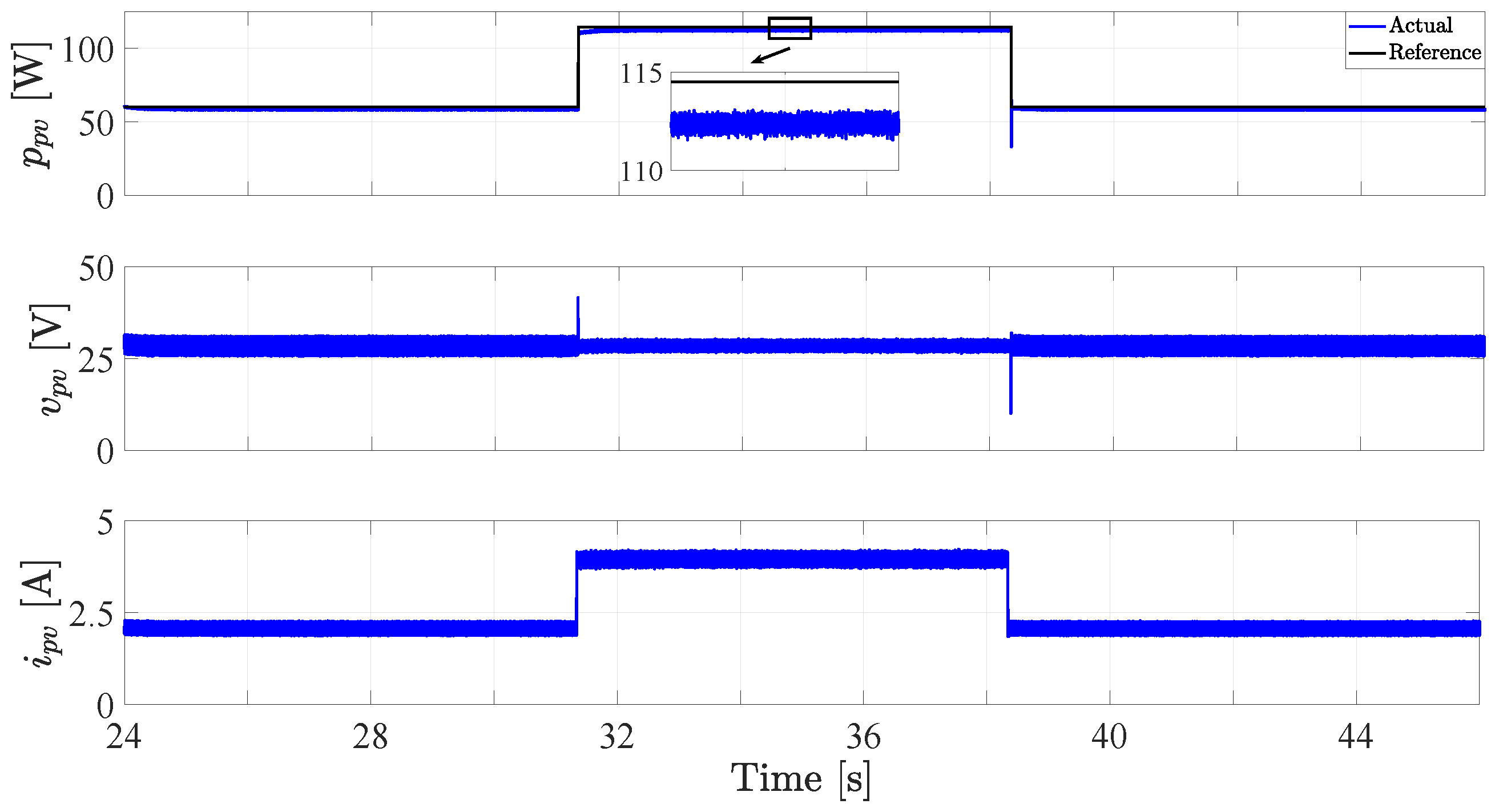
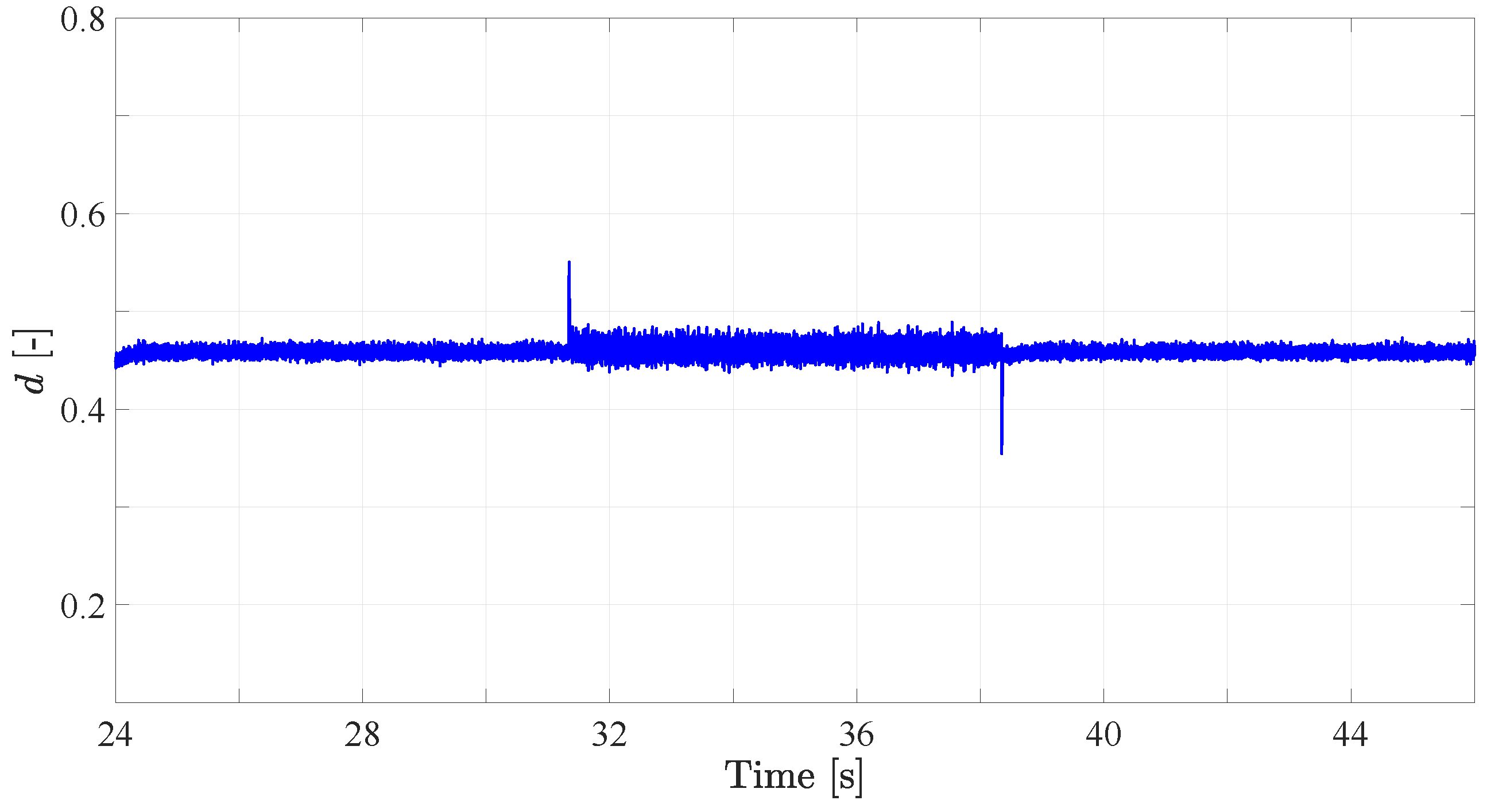

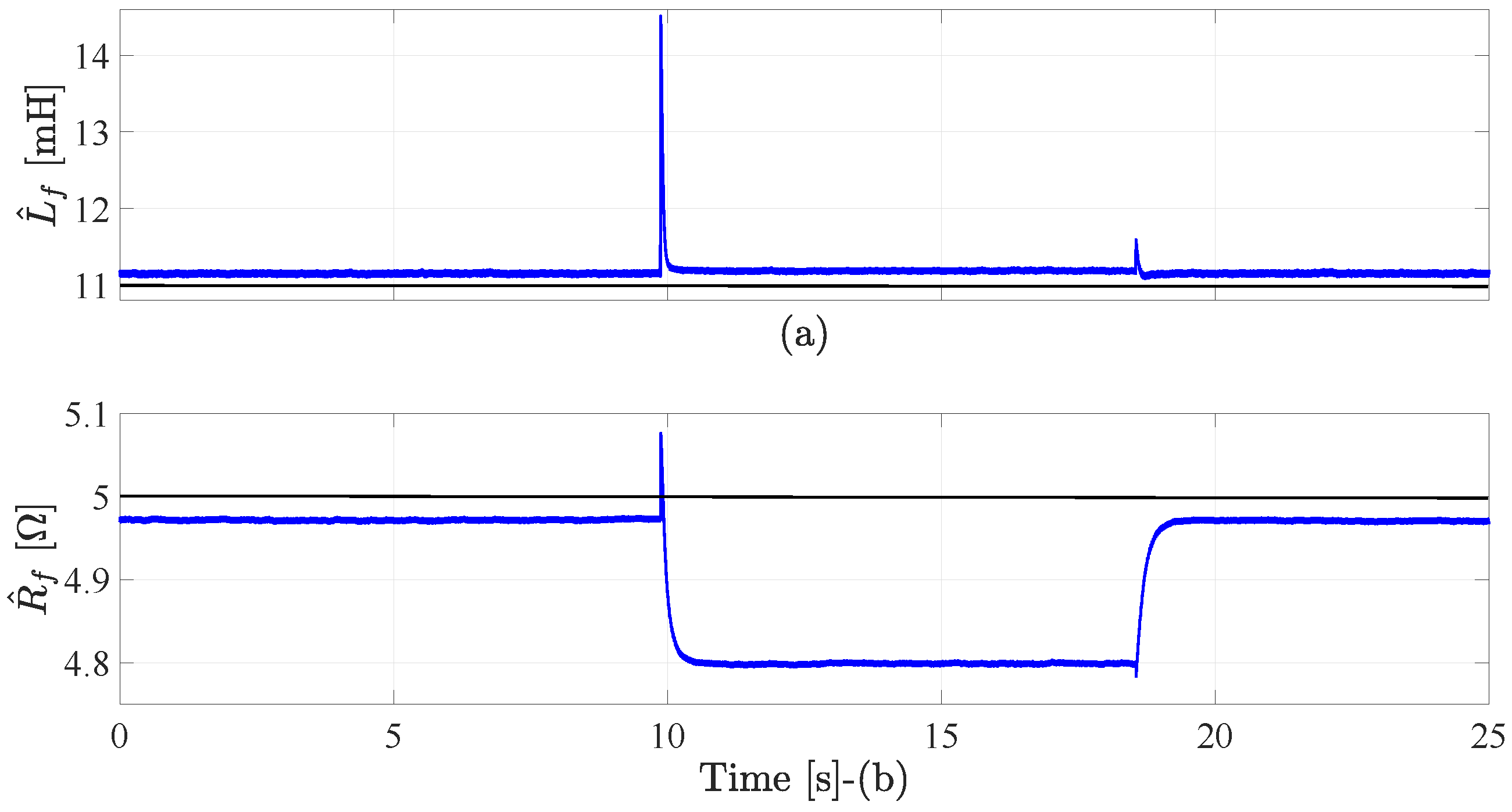
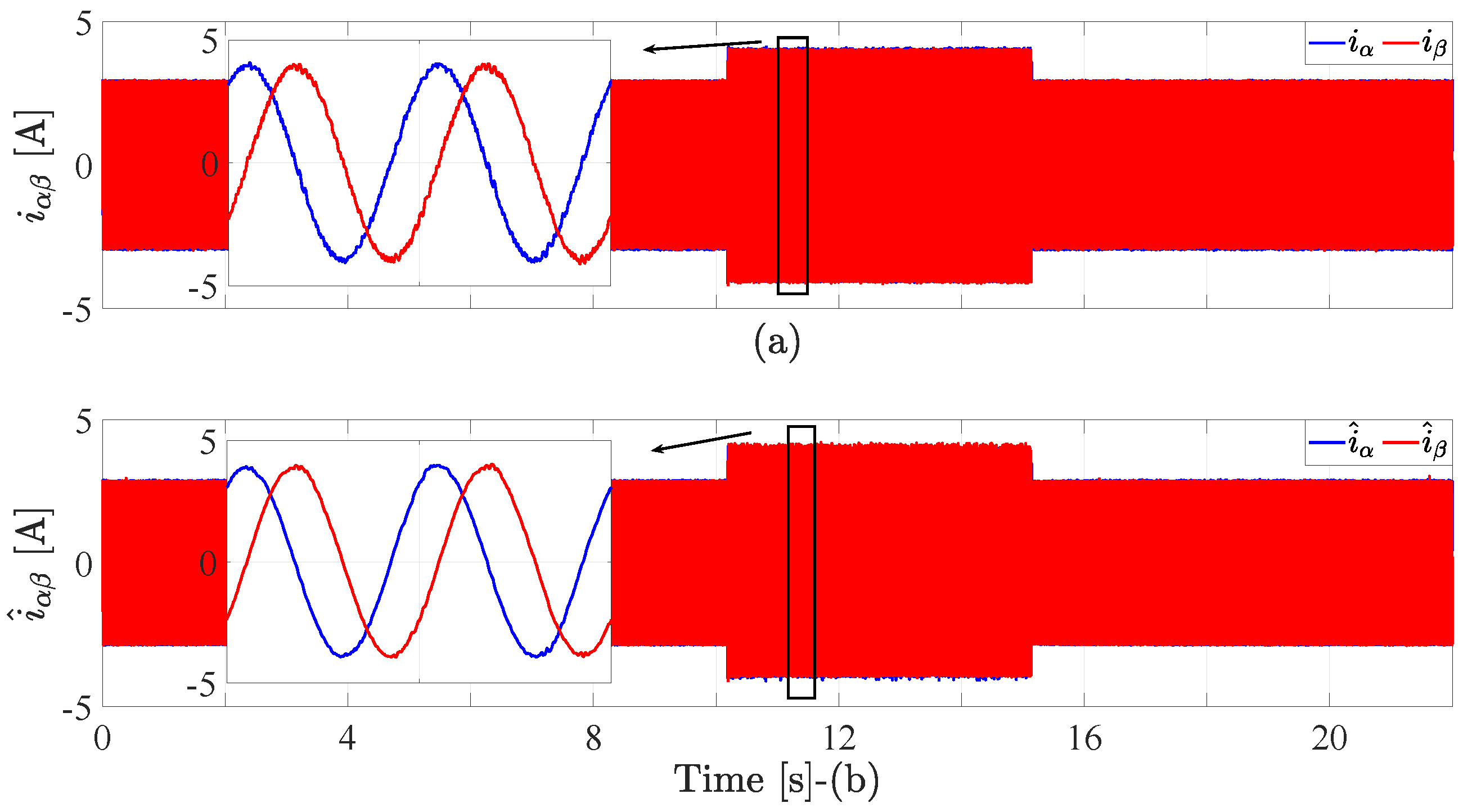
| Variable | Value |
|---|---|
| Boost inductance | mH |
| DC-link capacitor | |
| Power switch | single switch (IGBT-Module FF50R12RT4) |
| Diode | fast recovery diode BYW77PI200 |
| DC-link reference voltage | 50 V |
| Load resistance | |
| Load inductance | 11 mH |
| PV emulator resistors | / |
| Sampling time |
| Method | (%) |
|---|---|
| P&O with adaptive step-size | 97.45 |
| Technique | THD % |
|---|---|
| VOC (low/high power) | 3.59/ 2.48 |
| FS-MPC (low/high power) | 4.52/ 3.41 |
| DB (low/high power) | 3.80/ 3.01 |
| Method | Execution Time (s) |
|---|---|
| VOC | 14.62 |
| FS-MPC | 15.22 |
| DB | 14.51 |
| Case | THD % |
|---|---|
| Actual (low/high power) | 3.81/3.05 |
| Filtered (low/high power) | 1.55/1.97 |
| Method | THD % (7 mH/15 mH) |
|---|---|
| VOC | 3.59/3.61 |
| FS-MPC | 4.42/4.99 |
| DB | 3.61/4.89 |
| Parameter | VOC | FS-MPC | DB |
|---|---|---|---|
| Switching frequency | Fixed | Variable | Fixed |
| PI requirements | 3 | 1 | 1 |
| Computation burden | Low | Moderate | Low |
| Steady-state performance | Excellent | Good | Very good |
| Tuning efforts | High | Low | Low |
| Dependency on parameters | Low | Moderate | High |
| Multi-objective inclusion | Hard | Easy | Hard |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, M.; Harbi, I.; Kennel, R.; Rodríguez, J.; Abdelrahem, M. Evaluation of the Main Control Strategies for Grid-Connected PV Systems. Sustainability 2022, 14, 11142. https://doi.org/10.3390/su141811142
Ahmed M, Harbi I, Kennel R, Rodríguez J, Abdelrahem M. Evaluation of the Main Control Strategies for Grid-Connected PV Systems. Sustainability. 2022; 14(18):11142. https://doi.org/10.3390/su141811142
Chicago/Turabian StyleAhmed, Mostafa, Ibrahim Harbi, Ralph Kennel, José Rodríguez, and Mohamed Abdelrahem. 2022. "Evaluation of the Main Control Strategies for Grid-Connected PV Systems" Sustainability 14, no. 18: 11142. https://doi.org/10.3390/su141811142
APA StyleAhmed, M., Harbi, I., Kennel, R., Rodríguez, J., & Abdelrahem, M. (2022). Evaluation of the Main Control Strategies for Grid-Connected PV Systems. Sustainability, 14(18), 11142. https://doi.org/10.3390/su141811142










