Glare-Free Airport-Based Photovoltaic System via Optimization of Its Azimuth Angle

Abstract

Photovoltaic modules and systems (PVs) play an important role in achieving self-sustainable airports. In particular, airport-based PVs (A-PVs) have access to their full potential because airports are typically located in open spaces. However, the reflection of solar light by A-PVs’ front glass is unavoidable and may cause an accident due to solar glare (SG). In this study, we theoretically calculated the risk of SG from A-PVs depending on their azimuthal installation orientation (θ_PV) and derived a general design rule for minimizing the SG. The simulation reveals that the SG from A-PVs facing the runway and potential flight path causes after-images in pilots and ground workers throughout the year (>800 h/year). On the other hand, modifying their θ_PV, facing opposite runways and flight paths, significantly reduces the SG (<1 h/year) by reflecting the incident light outside the aircraft route. Although the θ_PV is not southward, their annual energy generation with an optimized θ_PV decreases by only 5–7% compared with A-PVs facing southward. This universal design approach is verified at four other airports, confirming the model’s validity. We believe our study will contribute to more solar light harvesting at airports without glare hazards.

1. Introduction

Renewable energy is a sustainable solution to meet the increased energy demand without the emission of greenhouse gases. Incorporating renewable energy sources into existing facilities boosts the energy sufficiency rate. Photovoltaic modules and systems (PVs) have been widely accepted due to their convenience of installation and high efficiency [1,2,3,4]. As a result, airport-based PVs (A-PVs) have increased rapidly [5,6,7], and many projects are in the planning stages. Airports are generally located on flat terrain and have low-rise buildings without shading for safety during aircraft landing and take-off [5].In addition, free space around the runway is mandatory for appropriate pilot vision and airplane safety. Due to these geographical factors, airports are suitable for harvesting solar light using PVs. As the aviation industry emits 3% of total greenhouse gases, A-PVs could facilitate sustainable industry growth and help overcome global warming [6]. Several A-PVs have been successfully installed and generate electricity at the rooftops of terminals and vacant land between runways [7]. In addition, a pioneering study has attempted to expand the potential area of A-PV to the pavement of runways [8].

However, the solar glare (SG) induced by A-PVs is unavoidable because of the refractive index difference between air and the front glass, as shown in Figure 1. The flat front glass of the A-PV reflects approximately 4% of normal incident solar light. Its reflectance increases significantly with a greater incident angle (θ_i) of the oblique incident light, as displayed in Figure 1. Previous studies have reported that the SG from reflected light increases the risk of an accident due to loss of consciousness in workers. [9,10,11]. The SG entering the retina makes it challenging for people to recognize the surrounding area and can sometimes causes temporary loss of sight. When intense light irradiates it from a small solid angle, human vision is hampered, and it is challenging to identify surrounding objects for approximately 4–12 s; this is also called the after-image effect [9,12]. The statistics of ground vehicle accidents show that accident ratios increase under SG [9,10,11,12].

The SG is more critical to pilots and ground staff of the aviation industry. Pilots affected by an after-image might move the plane a longer distance without recognizing the surrounding situation as a ground vehicle does under similar circumstances. [13]. In addition, aviation crashes commonly cause fatal results. The SG can influence pilots and ground workers from A-PVs when a flight is in landing, take-off, and taxiing on a runway [14]. The altitude of an airplane is sufficiently low near airports so that the SG from A-PVs can reach the pilots’ eyes. Until now, the risk of solar glare (R_SG) has been the main hindrance to the widespread use of A-PVs. To reduce their R_SG and maximize power output, anti-glare coating and optical structures have been implemented on A-PVs [15,16]. However, the optical coating and structures are vulnerable to soiling, UV irradiation, acidic rain, humidity, and heat [17,18]. Thus, during the lifetime of PVs (~25 years), A-PVs are not free from R_SG regardless of implementing antireflection layers.

Due to the R_SG of A-PVs, analyzing their SG at the planning stage is mandatory in many countries (e. g. Federal Aviation Administration’s regulations in the United States) [13,19]. For analysis, simulation tools for R_SG have been developed that consider the terrain, year around azimuth, and solar elevation angle [20,21]. Many research groups have investigated the R_SG of A-PVs, and the results have been reflected in their design [22,23,24]. Following the simulation results, the A-PVs were installed only in specific sites and directions, where their R_SG was negligible. Although their research identified R_SG of A-PVs at individual sites, comprehensive design guidelines for A-PVs have seldom been proposed. The lack of a universal design rule for A-PVs causes a loss of time and cost for repeatedly conducted calculations at each site. Establishing a general guideline for mitigating the R_SG of A-PVs will save time and expenses in determining the possible A-PVs for each project.

Furthermore, most of the previously reported R_SG analyses considered only south-facing A-PV cases, resulting in the loss of many possible sites [19,25,26]. Usually, south-facing PVs generate maximum energy; however, the change in their azimuth angle (θ_PV) will not cause significant efficiency sacrifice in the case of PVs installed in open spaces with a fixed elevation angle (φ_PV) [27,28,29]. In addition, the attainable advantage of modifying θ_PV is the reduced R_SG of A-PVs by reflecting the solar light out of the potential landing/take-off paths and taxing routes. Despite reasonable energy generation and reduced R_SG of A-PVs via optimized θ_PV, non-south-facing cases have not been intensively studied, thereby missing many potential sites for A-PVs in previous projects. Some previous studies minimized the glare by rotating θ_PV and φ_PV; however, the lack of systematic analysis makes it difficult to suggest general guidelines.

In this study, we investigate the relationship between R_SG and θ_PV of A-PVs to derive general guidelines for glare-free A-PVs installed in the northern hemisphere. Theoretical calculations of R_SG and θ_PV at specific sites reveals that the R_SG strongly depends on the θ_PV, whereas only a minor change in annual energy generation rate (AER) is observed in non-south facing A-PVs. On the other hand, the A-PV facing opposite the possible flight paths and ground routes tends to dramatically decrease R_SG. Based on individual site results, we proposed a simple yet effective procedure for optimizing θ_PV: (i) considering sites where possible routes are located on only one side, (ii) starting the calculation of A-PV’s R_SG and AER whose θ_PV are 135 (East side of the airport) and 225° (West side of the airport), (iii) rotating A-PV southward and repeating it until R_SG is negligible, and (iv) determining the θ_PV as an optimized point. Four case studies from other airports verify that the suggested method could be a universal approach for reducing R_SG. We believe that the results presented here will be beneficial for designing glare-free A-PVs without significant sacrifice of energy generation.

2. Simulation Methods

To quantify the effect of θ_PV on aviation safety, we theoretically calculated the R_SG of A-PV using the commercially available Solar Glare Hazard Analysis Tool (SGHAT), which has been widely adopted to calculate R_SG for many projects, as summarized in Table S1. Moreover, the aviation safety administrators of many countries (including the Federal Aviation Administrator and the US Department of Defense) have verified the simulation tool [13,30]. The SGHAT interacting with a web-based map service (Google Map) shows potential light reflection from a reflective surface that occurs annually, considering the azimuth and elevation angle of the incident sunlight that varies with season and time [31,32]. The detailed procedure for calculating R_SG and AER is shown in Figure 2. The reflectance and light path from A-PV were monitored using the elevation (φ_sun(t)) and azimuth angle (θ_sun(t)) of incident solar light to the interface of the air (refractive index of n₁) and front glass of the PV module (refractive index of n₂) with φ_PV and θ_PV. Based on this data, the glare reaching pilots and ground workers was evaluated at each point (α) of the potential route and path. As the glare is mainly affected by the subtended source angle (θ_Source) and irradiance intensity of light at the observer’s retina (I_retina), these two values were obtained through the SGHAT. Here, we assumed that incident natural light is randomly polarized, and the reflection of A-PV shown in Figure 1 is an average of p and s wave light. If glare occurred, we set that minute as a risk time and repeated the calculation for the next minute. Depending on the intensity of glare, it could be categorized as a low potential of after-image (LPAI) and potential after-image (PAI). The condition of LPAI and PAI will be discussed in the next section. If glare did not occur at point α at a specific minute, we moved to another path point and repeated the glare analysis. If glare was not detected the entire path, the time was defined as a glare-free time. The annual solar glare time (T_SG) is the sum of glare minutes when the pilot is under PAI and LPAI. Meanwhile, the AER of each installed A-PV was obtained based on φ_sun(t), θ_sun(t), φ_PV, and θ_PV under STC conditions (1000 W/m²). Finally, the R_SG and AER from the A-PVs were compared by varying their θ_PV. However, the tool did not consider obstacles (natural or artificial) surrounding A-PVs, such as clouds, trees, hills, and buildings; the R_SG and AER may be exaggerated compared with their empirically measured values. Under a cloudy day, the intensity of I_retina will decrease, corresponding with the decreased intensity of normal incident light. Thus, the time for LPAI and PAI would decline.

The airport used to analyze R_SG and AER was the Incheon International Airport (ICN) in South Korea, located at 37.46° N, 126.44° E. As shown in Figure 3, there are three runways and two main ground routes in the ICN. Hereafter, we set the θ_PV of the north and south to 0 and 180°, respectively. The angle of one runway is 160°, whereas the other has an azimuth angle of 150°. When the aircraft takes off and lands on the runway, it requires approximately 3.2 km (2 miles) of the flight path (FP) [13]. As the direction of the aircraft’s final approach routes varies depending on the wind direction and speed, two FPs are set on each runway. Thus, the total possible FPs in ICN is six: FP1 to 6 (marked as solid green lines in Figure 3). Moreover, two main routes (R1 and R2, dashed yellow lines) were selected, where the airplane moved on the ground for taxiing. Meanwhile, we assumed that A-PVs were installed at 12 sites in the ICN. Six A-PVs (W1–W6) were located on the leftmost runway, whereas another four (E1–E4) were on the rightmost runway. Two possible sites (C1 and C2) were considered in the center of the airport, located between R1 and R2. Each site had the same size (70,000 m²), suitable for a 7 MW PV power plant. The φ_PV of all A-PVs was fixed at 30°, considering the latitude of the airport. It was assumed that smooth glass without antireflection coating covered the A-PVs. The simulation only considered mono-facial PVs rather than bifacial ones because the light reflection from a rear glass in bifacial PV is randomized due to scattered, rear incident light. We believe the mono-facial case results will be similar to those of bifacial PVs.

3. Results

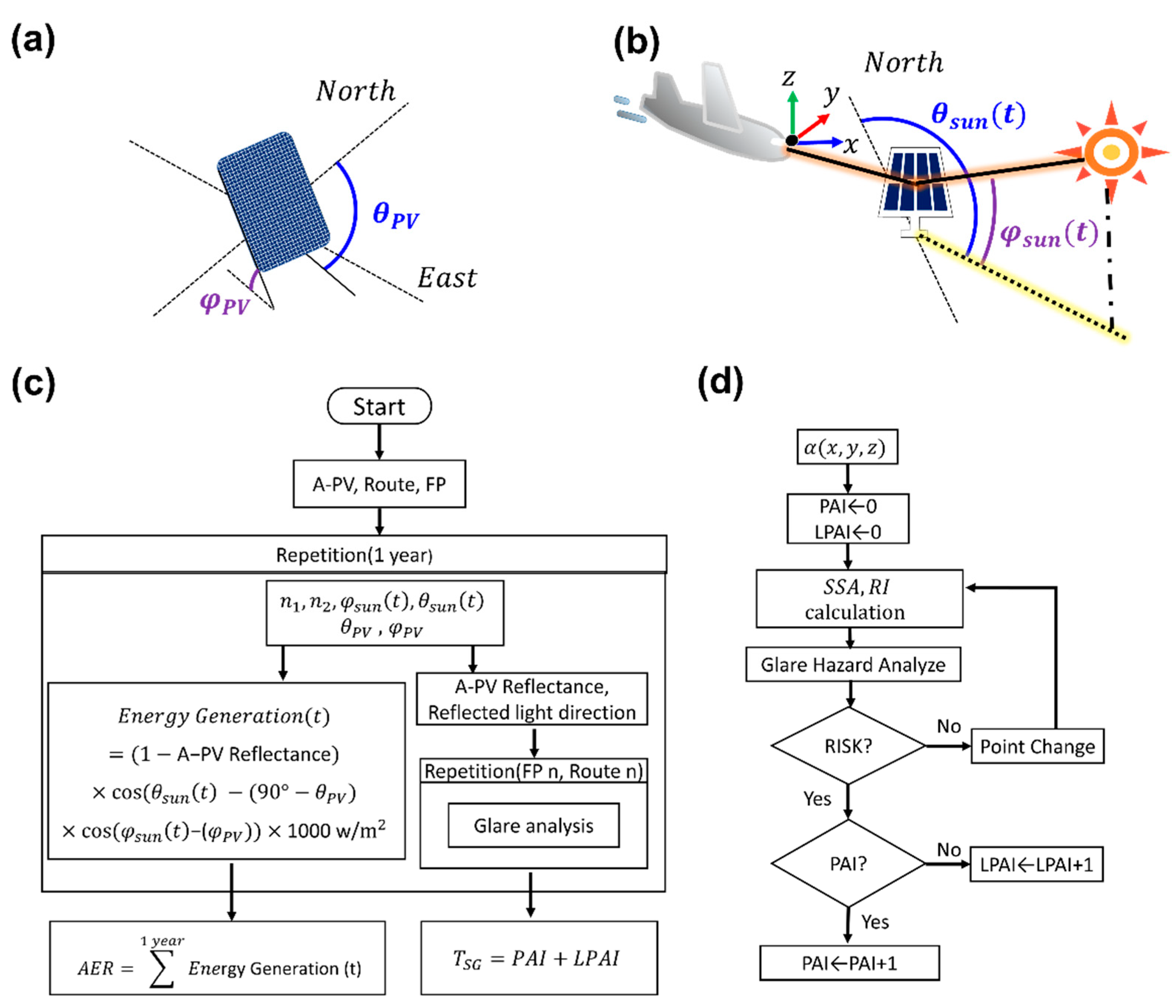
3.1. Glare of A-PVs According to Their Installation Angle at a Single Site

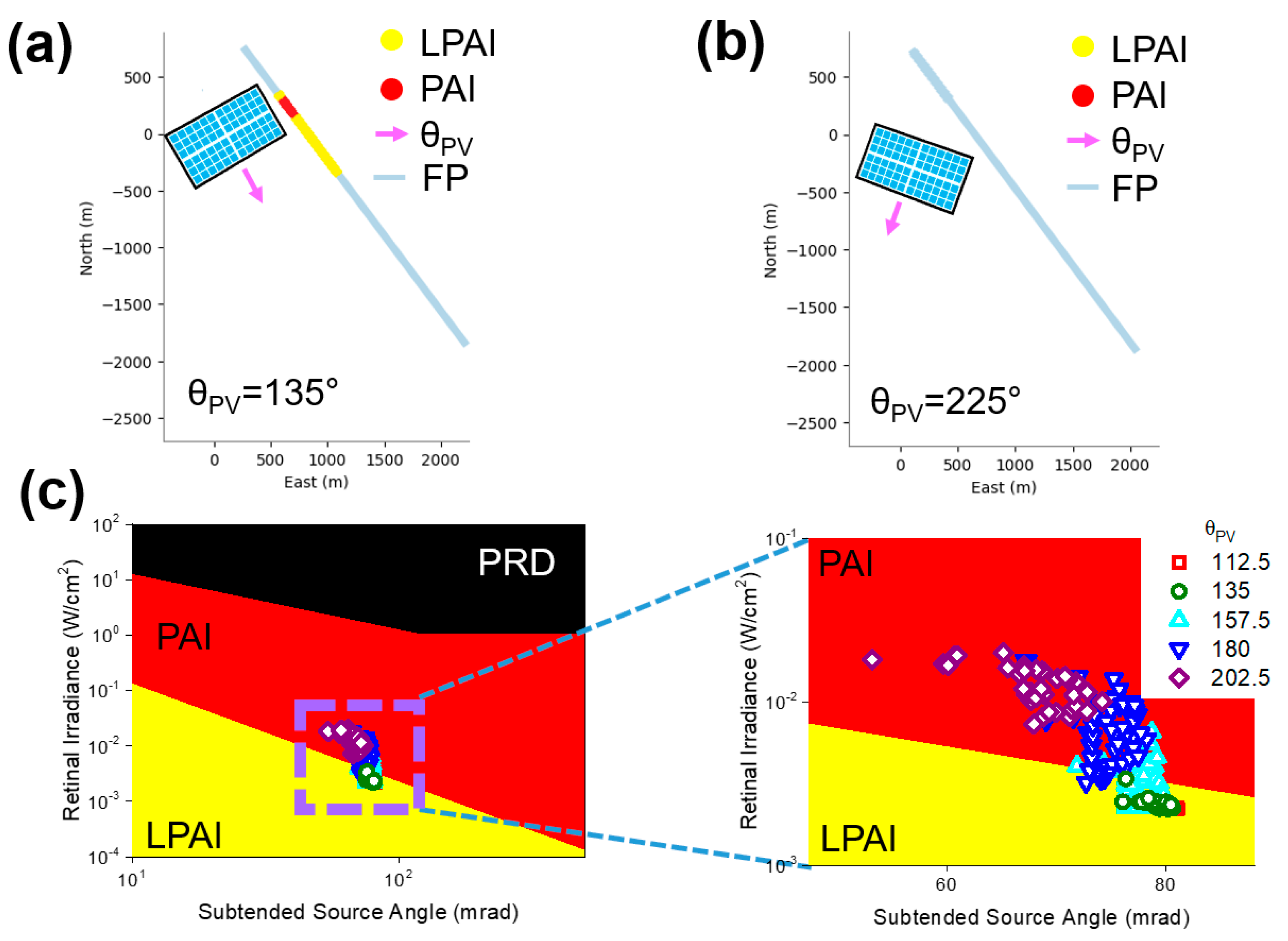
To figure out the general relationship between θ_PV and R_SG, we calculated I_retina and θ_Source of a pilot in the flight path (FP2) caused by a single A-PV (W1) depending on θ_PV, as marked in Figure 4 and Figure 5. According to previous studies, the response of the human eye to incident light can be categorized into four sections depending on the I_retina and θ_Source: (i) no effect, (ii) LPAI, (iii) PAI, and (iv) permanent retina damage (PRD) [9]. Typically, the risk of an accident increases when a person experiences an after-image for a few seconds. Figure 4c displays the ocular impact of light as a function of θ_Source and I_retina. In cases of weak I_retina and large θ_Source, the risk of an after-image from light is reduced, defined as LPAI. At the PAI stage, the possibility of an after-image increases due to increased I_retina and narrow θ_Source. However, discomfort from limited vision is recovered after 4–12 s without PRD. Under extreme I_retina, the retina can irreversibly burn, causing PRD. As PRD typically occurs in light-concentrating systems, it was not expected in A-PVs.

Figure 4a,b show the annual R_SG map in FP2 caused by W1 located on its west. When W1 faces southeast (θ_PV = 135°), W1 bounces off the incident light from the southwest to the pilot in FP2. Remarkably, the reflected light intensity is sufficiently strong to cause LPAI and PAI in pilots. Especially if the pilot is at a low altitude close to W1, they will be exposed to a dangerous situation by a strong reflection of the incident light, marked as LPAI (yellow) and PAI. (red) in Figure 4a. On the other hand, as W1 is rotated to the southwest (θ_PV = 225°), it does not cause any glare, and thus, the pilot’s vision is not disturbed. Although W1 is rotated at the same angle from the south, generating the same energy, R_SG for each case is totally different. As proven by calculated θ_Source and I_retina in Figure 4c, they are strongly governed by the θ_PV of W1. As θ_PV increases from 112.5 to 180°, I_retina increases from 10⁻³ to 10⁻² W/cm². South-facing W1 may reflect light from the west with a large θ_i to FP2 for a longer time, whereas the rear reflector (backsheet) of W1 facing eastward bounces off incident light from the west to the outside airport. As a result, the pilots are more frequently exposed to PAI in the south-facing W1 (θ_PV = 180°) compared with the case of the east-south-east-facing W1 (θ_PV = 112.5°). Moreover, the PAI became more dominant in the south-facing W1. In contrast, as the A-PV turns from south to west (θ_PV = 225–247.5°), I_retina from W1 decreases. When θ_PV is larger than 225°, I_retina is weak enough not to affect the pilot’s vision (not shown in Figure 4c due to decreased intensity). Hence, the angular dependence of I_retina and θ_Source indicates that the control of θ_PV is a solution for lowering R_SG in A-PVs.

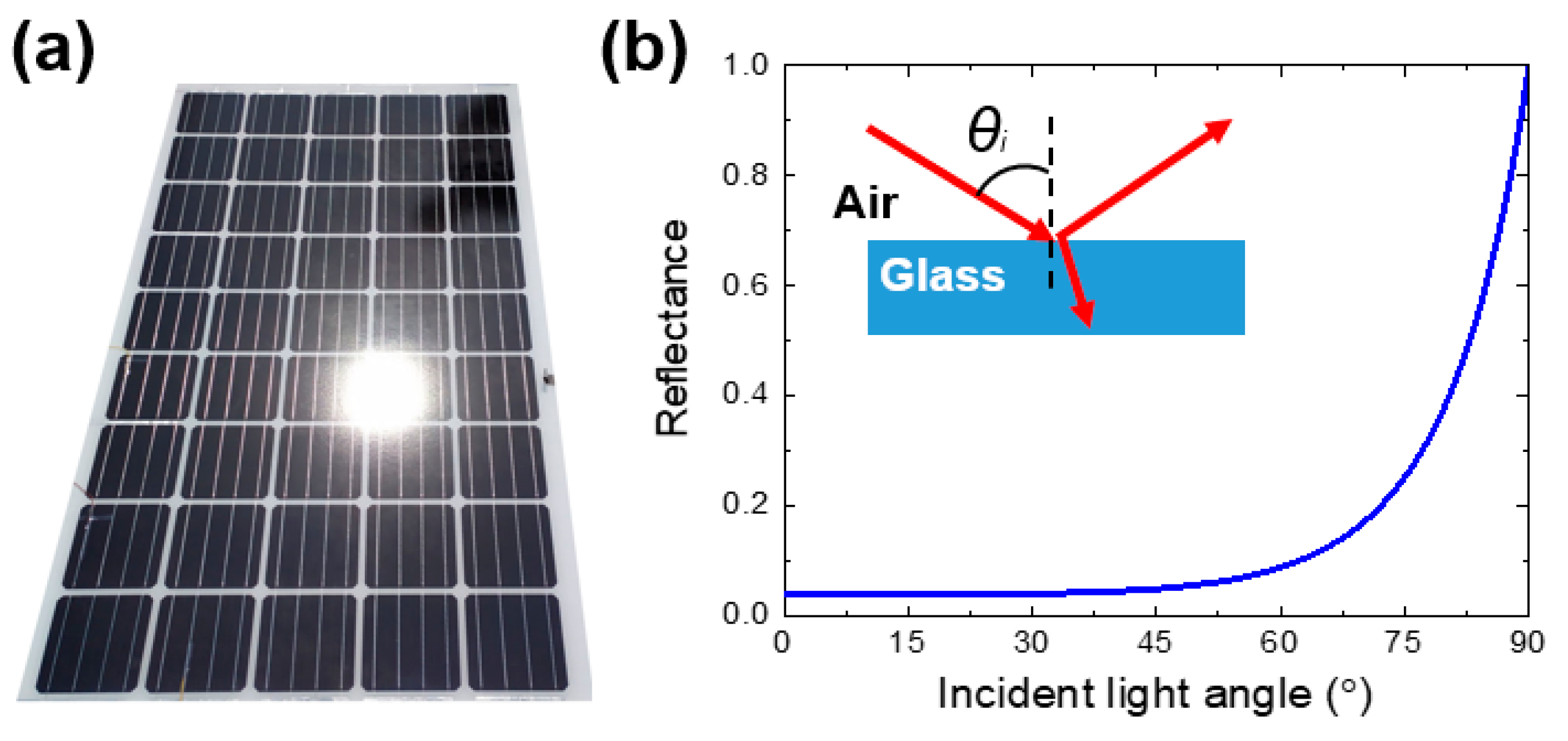
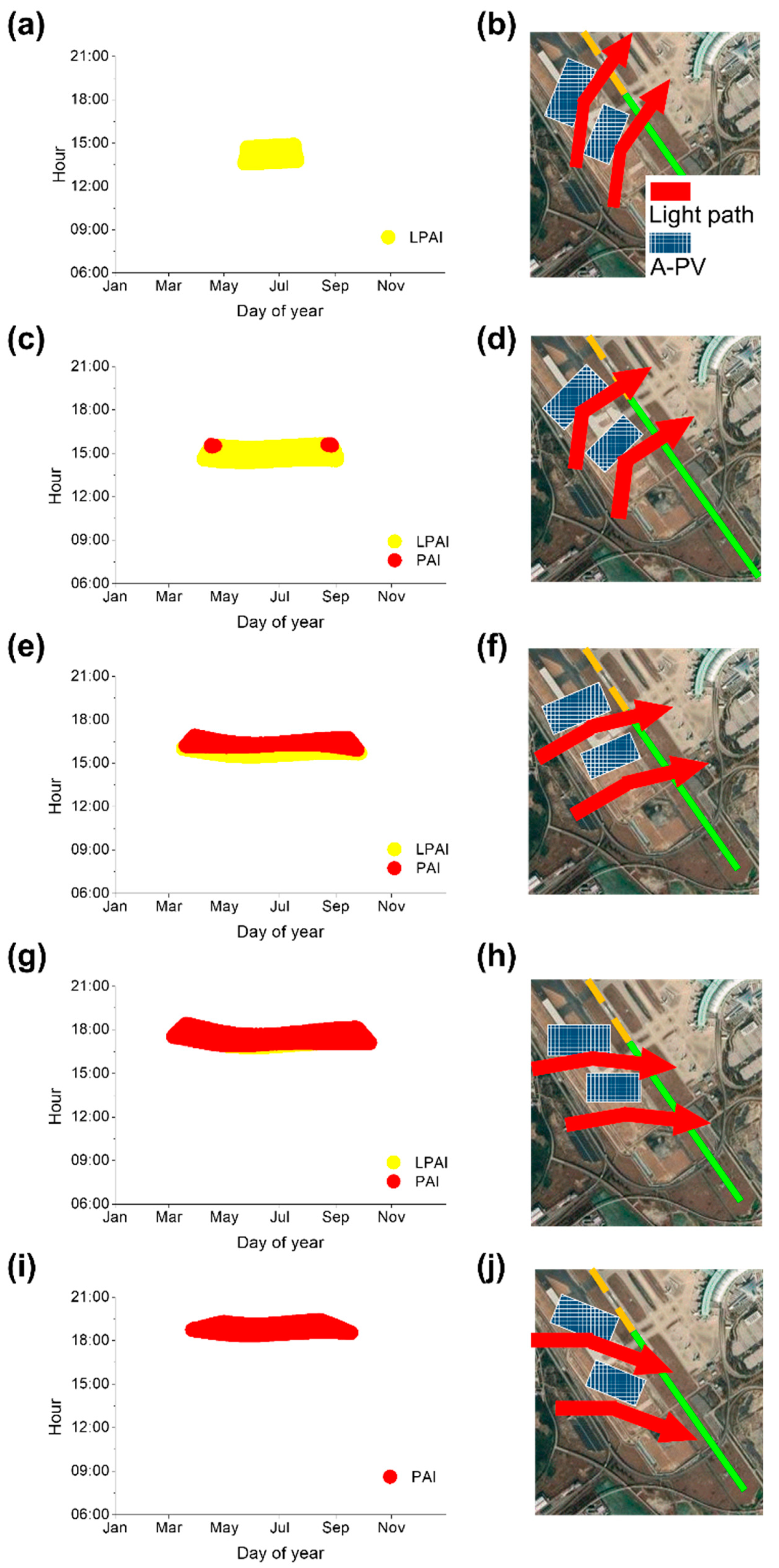
The detailed time and season of PAI and LPAI from W1 are displayed in Figure 5. Typically, the reflectance suddenly increases at the interface between the air and glass when θ_i exceeds 60°, as marked in Figure 1. Here, θ_i is determined by φ_sun(t) and θ_sun(t). Both angles should be lower than 60° to avoid the R_SG. As φ_sun(t) varies less than 90° throughout the year, A-PVs with a fixed φ_PV of 30° are free from the source of SG induced by time-varying φ_sun(t). In contrast, the θ_sun(t) changes by approximately 120° (winter) to 240° (summer) every day, sufficiently large to increase θ_i more than 75° at any time. At the moment, A-PV reflects incident solar light to the opposite side with strong intensity, as marked in Figure 1b. Thus, the pilots and workers opposite the incident light might be under the influence of SG. For the case of W1, when the A-PV faces east-south-east (θ_PV = 112.5°), LPAI occurs in the afternoon (13:00–15:00) from May to August (please see Figure 5a). Solar light from the southwest bounces off to FP2, as shown in Figure 5b. As the φ_sun(t) is more than 60° during glare occurrence (afternoon of summer), the pilots are influenced by the reflected light with a large elevation angle from the bottom of the flight. Thus, the reflected light affects only for a minimal time and limited area. In addition, PAI is not observed in FP2, where the θ_PV of W1 is 112.5°. After 15:00, the solar light irradiates the backsheet of W1 and is reflected outside the airport. In addition, from September to April, no glare occurs because of the low φ_sun(t), owing to the tilt of the Earth’s axis (23.5°). This season, most reflected light passes below the FP2, so the pilots are free from SG.

As W1 rotates southward, the time for SG is shifted to the late afternoon (Figure 5c–h). In the late afternoon, W1 reflects incident light from the west to the pilot moving through FP2, located on its east side. The reflected light interferes with the pilot’s vision near the ground because of the lowered φ_sun(t). Moreover, the azimuth angle between the south-facing W1 and the incident light from the west increases rapidly, resulting in increased intensity of reflected light. As a result, the south-facing W1 obstructs the pilot’s view for a longer time with increased intensity than the east-south-east-facing counterpart. The time corresponding to the impact of the SG is extended from March to October. Due to increased intensity, pilots are under the influence of PAI during sunset. Although pilots under PAI do not immediately cause accidents, airplanes fly with an increased possibility of collision accidents due to the momentary vision loss of pilots and workers. According to the case of ground vehicle studies conducted in Arizona, USA, drivers under the influence of glare have a 5–10% higher accident probability than others [33]. Considering the annual number of airline flights worldwide (~40 million), the increased possibility of SG from A-PV is not negligible.

In W1 installed in the south-south-west direction (θ_PV = 202.5°), the T_SG decreases compared with the south-facing case, as shown in Figure 5i,j. Here, the SG only occurs after 18:00, from April to October. Before 18:00, the W1 with a θ_PV of 202.5° reflects incident light from the west outside the airport. In addition, the reflectance is low due to decreased θ_i, resulting in significantly reduced LPAI and PAI compared with the south-facing case. However, at sunset in the summer, the θ_sun(t) exceeds 270° (westward). Thus, the intense solar light with a θ_sun(t) can be transferred to the pilots moving FP2 and R2 in the early evening from May to August.

If we turn W1 further west, pilots on R2 and FP2 will not be affected by SG (not shown in Figure 5). When W1 faces southwest and west-south-west (θ_PV = 225 and 247.5°), the backsheet of the A-PV scatters the incident light from the east. Due to the diffusive reflection of the backsheet, the incident solar light disperses in random directions with decreased intensity. The result would be similar in the case of bifacial A-PVs because the A-PVs effectively absorb most of the light coming from the east with small θ_i early in the morning. Additionally, the solar light from the south will bounce off to the northwest side of W1 around noon. As no aviation facilities and flight routes are located on the northwest side of W1, the southwest facing W1 does not affect the pilot’s vision. Furthermore, the solar light from the west is not transferred to the airport owing to the reduced θ_i. Consequently, the result shows that the A-PV facing the possible routes and flight paths causes SG, whereas the A-PV facing opposite to the potential route and flight path mitigates R_SG.

3.2. Glare and AER of A-PVs Located at Various Positions

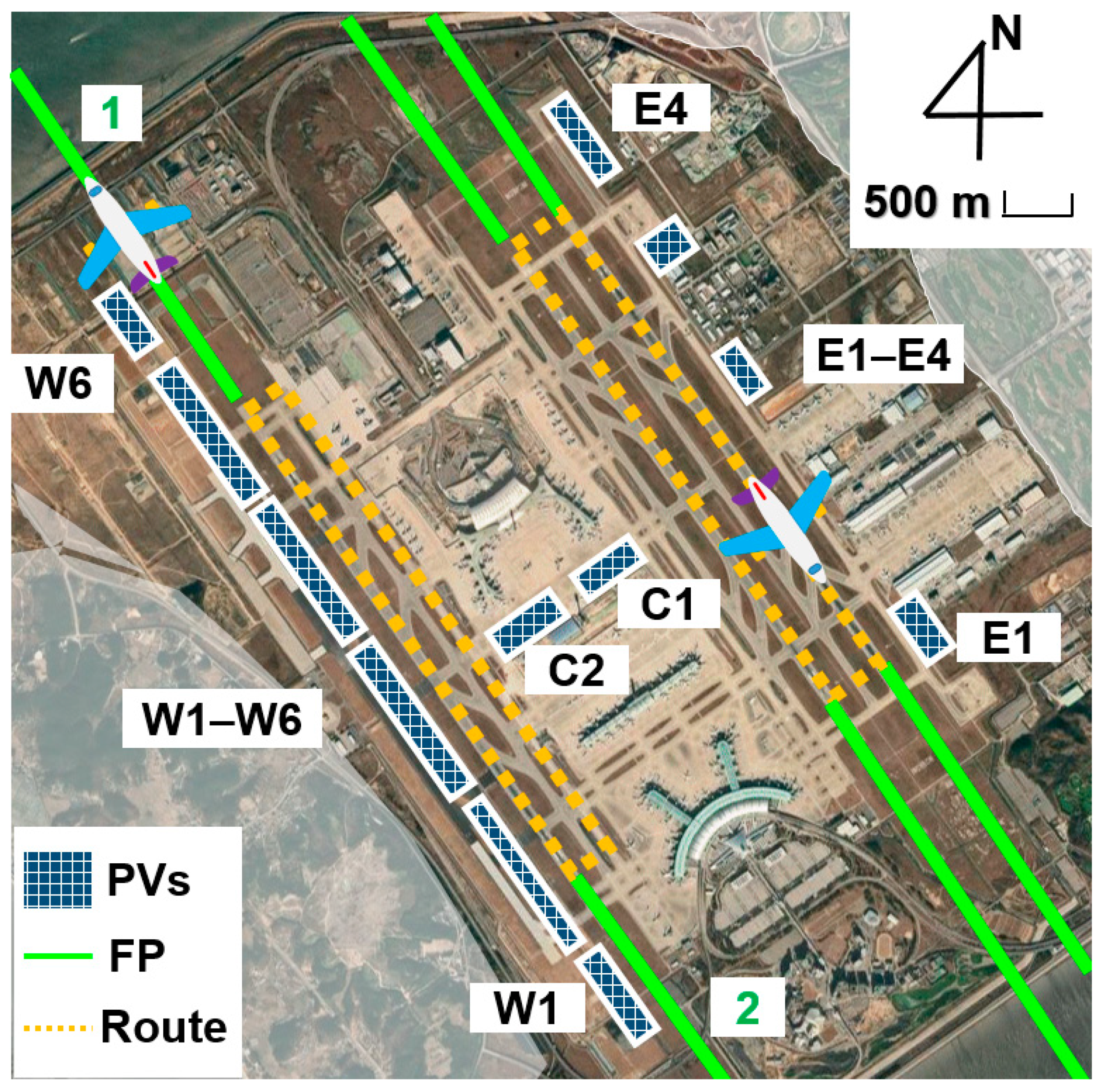
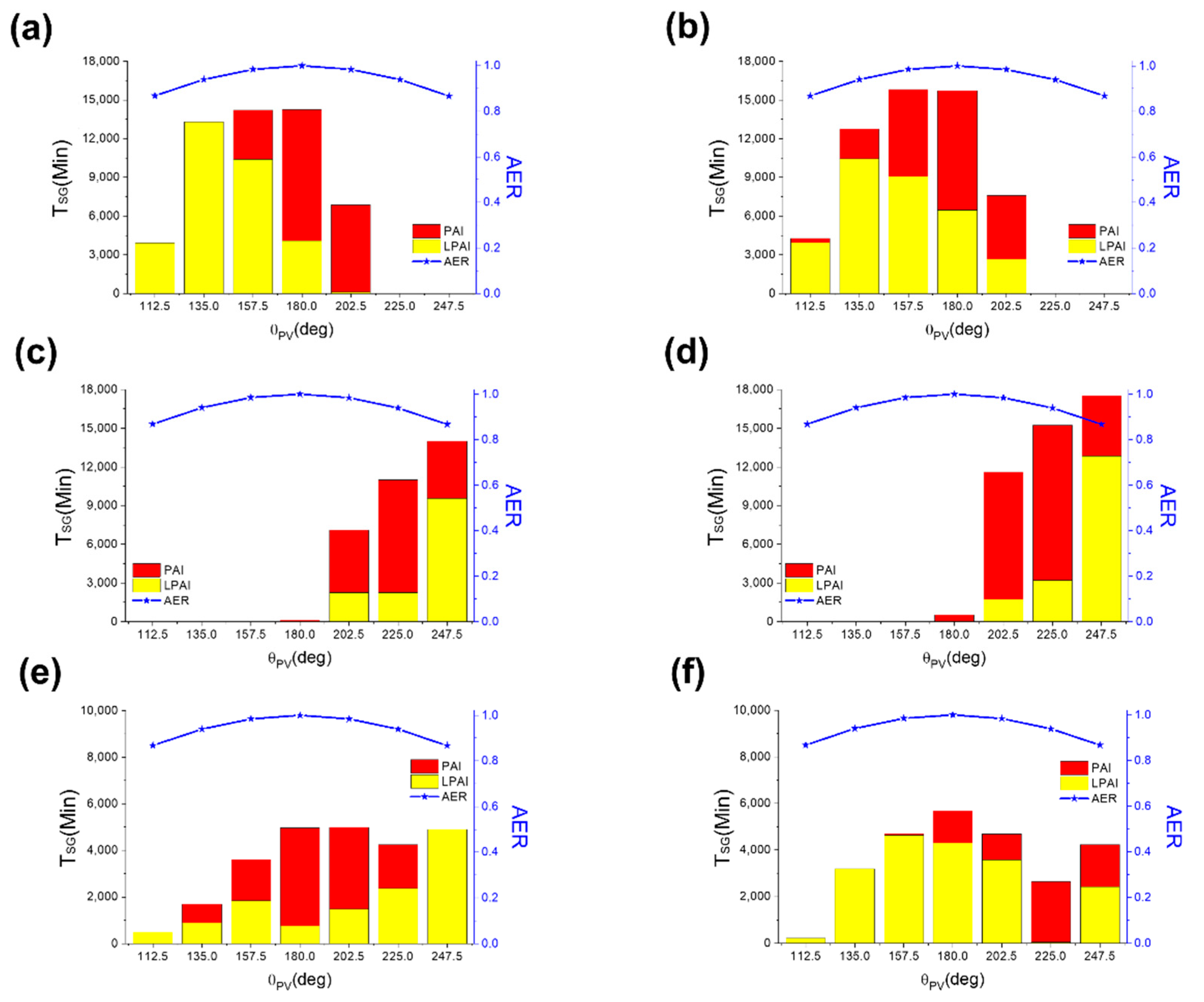
Rotating A-PV in the opposite direction of FPs and routes effectively reduces R_SG and can guarantee pilot safety in the case of W1. To validate this approach at other sites, we calculated the T_SG at all possible paths and ground routes from six A-PVs: (i) two installed on the west side of the west runway (W1, W2), (ii) another two on the east side of the east runway (E3, E4), and (iii) the last two located in the middle of the taxiway (C1, C2). Possible ground paths of airplanes surround the C1 and C2 A-PVs, whereas the planes move only on one side of the A-PV in the other cases. For a quantitative comparison at each site, the T_SG and the sum of LPAI and PAI from them are simulated under various θ_PV (112.5–247.5°). As the A-PV is supposed to generate electricity, its AER is also considered at each θ_PV. Here, AER divides the energy generation of A-PV with a specific angle by that of the south-facing case (θ_PV = 180°) where power generation is maximized.

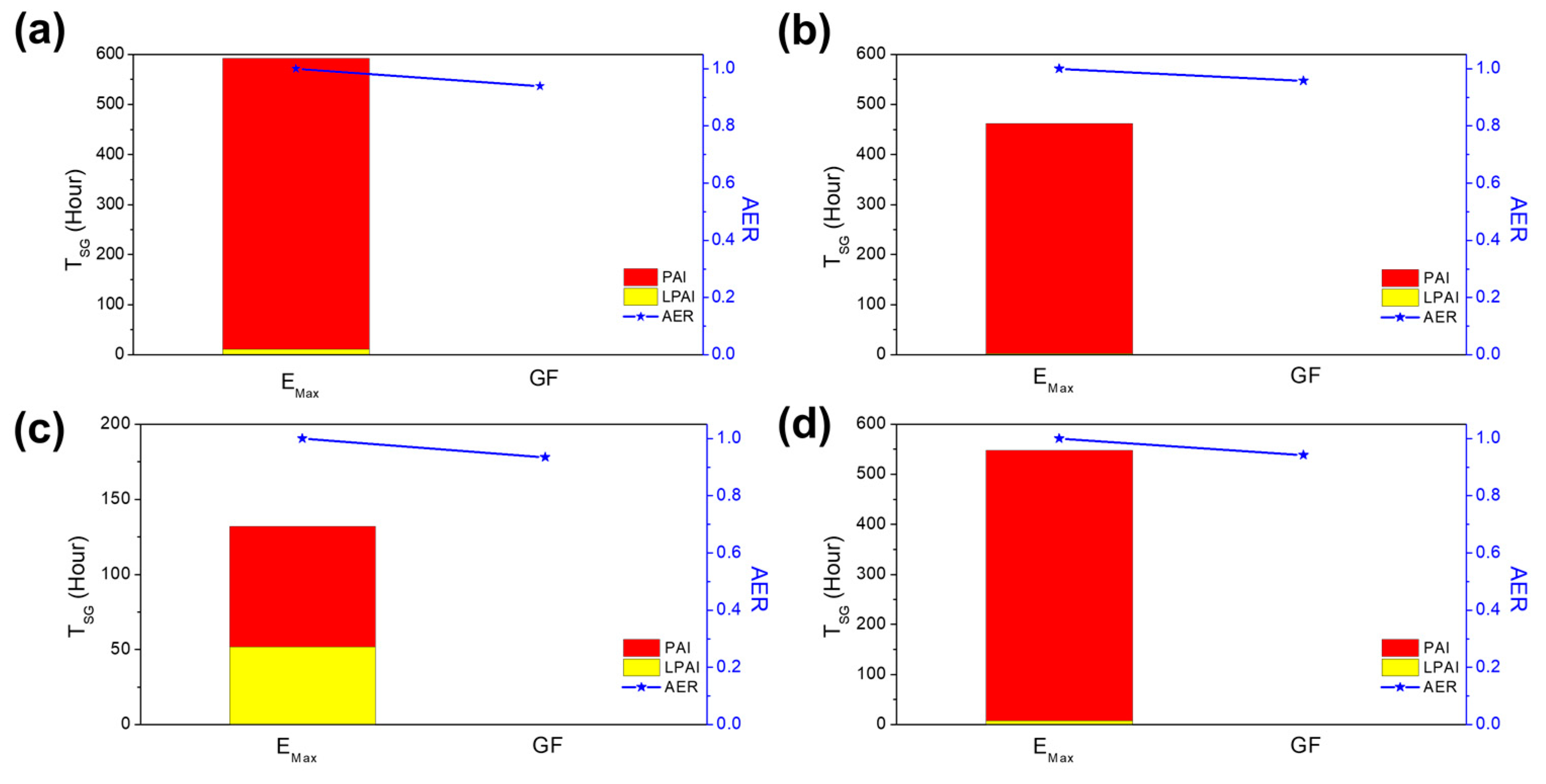
Figure 6 shows the calculated T_SG and AER of A-PVs depending on the θ_PV. The results are summarized in

Table 1. T_SG (minutes) and AER of A-PVs with various θ_PV.

	θPV	112.5°	135°	157.5°	180°	202.5°	225°	247.5°
A-PV
W1	TSG	3899	13,310	14,223	14,232	6860	0	0
	AER	0.87	0.94	0.98	1	0.98	0.94	0.87
W2	TSG	4272	12,767	15,816	15,742	7591	0	0
	AER	0.87	0.94	0.98	1	0.98	0.94	0.87
E3	TSG	0	0	0	123	7098	10,980	13,990
	AER	0.87	0.94	0.98	1	0.98	0.94	0.87
E4	TSG	0	0	0	531	11,611	15,244	17,547
	AER	0.87	0.94	0.98	1	0.98	0.94	0.87
C1	TSG	479	1686	3610	4965	4993	4241	4906
	AER	0.87	0.94	0.98	1	0.98	0.94	0.87
C2	TSG	227	3199	4696	5682	4687	2634	4236
	AER	0.87	0.94	0.98	1	0.98	0.94	0.87

. For the case of W1 and W2, their T_SG is extended as θ_PV increases from 112.5° (facing east-south-east) to 180° (south). Solar light from the east is reflected outside the FPs and routes in the morning, whereas the A-PV sends incident solar light from the south and southwest to the FPs and routes with strong intensity in the afternoon. As a result, T_SG increases, and PAI becomes predominant at the A-PV facing south in the afternoon. For example, when θ_PV of W1 and W2 is 112.5°, the T_SG is approximately 4000 min. It gradually increases as W1 and W2 rotate to the south. Finally, the T_SG is over 10,000 min when they face south (θ_PV = 180°). Furthermore, the annual PAI time increases from 0 (θ_PV = 112.5°) to 10,153 min (θ_PV = 180°), consistent with the results for W1 (please see Figure 6a). Here, the slight difference in T_SG and intensity of glare between the two A-PVs is attributed to the different altitudes of planes at ground routes and FPs. W1 mainly affects pilots in FP2, who are located at a higher altitude than ground routes (R1). On the other hand, the T_SG decreases as W1 and W2 face westward, opposite possible routes. As the southwest-facing W1 and W2 (θ_PV of 225 and 247.5°) mirrors incident light from the south and west to the outside airports, they are glare-free. In the point of AER, increased energy generation of southwest facing W1 and W2 in the afternoon can compensate for their energy loss in the early morning. The AER slightly declines to 0.94 and 0.87 in the cases of θ_PV of 225 and 247.5°, respectively. However, the significantly reduced R_SG of southwest-facing W1 and W2 outweighs the slight energy losses. This result also implies that rearrangement of the A-PV orientation, facing opposite to the possible aircraft routes, leads to reduced R_SG of A-PVs with a small sacrifice of energy generation.

The proposed method is also valid for A-PVs located east of airports. Similar to W1 and W2, E3 and E4, facing opposite routes and FPs, are glare-free (Figure 6c,d). Their glare becomes negligible as the θ_PV of E3 and E4 turns east from the south. Light from the south and southwest with large θ_i is transferred outside the airport at the southeast-facing E3 and E4. Moreover, light from the west is not a source of SG because the backsheet of A-PV scatters incident light. Thus, it is possible to demonstrate glare-free E3 and E4 with a small sacrifice of energy loss (only 2%) when θ_PV is 157.5°. In contrast, the southwest-facing E3 and E4 creates glare for pilots by bouncing off the incident light from the south and southeast to the routes and FPs in the morning. In the worst case, where θ_PV is 247.5°, the T_SG exceeds 15,000 min. Here, the angles of R1 and R2 are slightly different; thus, the trends of A-PV located east (E1, E2) and west (W1, W2) are not exactly symmetric. Despite a minor change in T_SG in E1 and E2, the result indicates that modifying the θ_PV of A-PV to opposite possible aircraft routes is a practical approach to reducing the R_SG in both cases.

Meanwhile, it is recommended not to install A-PVs inside possible taxiways. Regardless of θ_PV, C1 and C2 trigger glare in either direction, as shown in Figure 6e,f. When C1 and C2 face westward, they reflect the incident solar light from east to the R1 in the morning. Conversely, when C1 and C2 face eastward, they also cause SG and affect the pilots moving at FP3, FP4, and R2 located on the east side in the afternoon. This implies that A-PVs installed inside the taxiway reflects incident light in its facing direction and causes SG because it always faces flight paths and routes, independent of its θ_PV. Moreover, installing an A-PV on the roof of a concourse is not recommended because it is usually located in the middle of taxiways.

3.3. Guideline for Designing Glare-Free A-PVs

Throughout these case studies, we found that optimizing θ_PV paves a way to mitigate glare from A-PVs. Based on the results of the previous section, we propose a general method to optimize the θ_PV of A-PVs in the northern hemisphere, as shown in Figure 7. Changing the initial position and rotation angle direction would also be effective for A-PVs installed in the southern hemisphere. The suggested method consists of four steps. First, it is required to check whether possible routes and FPs surround planning sites. If the routes and FPs are located on both sides of the site, they should be excluded for A-PVs, as verified in the case of C1 and C2. Second, if FPs and routes are located on only one side of the A-PV, the calculation of T_SG should start with the specific conditions. In the case of A-PVs located on the east side of FPs and routes, glare calculation should start at a θ_PV of 135°, facing opposite the runways and FPs. In contrast, the recommended starting point of θ_PV is 225° in the case of A-PVs located on the west side of FPs and routes. If the glare is not observed at a specific angle, A-PVs can rotate more southward until T_SG is negligible. In contrast, the A-PV should turn in the opposite direction of FPs and routes once glare has been detected. Repeated calculations with a small rotation angle allow one to find better A-PV conditions. However, calculations with a small rotation angle increases the number of steps for the optimization process. As a result, we set the minimum rotating angle of A-PV as 22.5°, considering the trade-off relationship between simplicity and accuracy. Finally, the most southward point is designated as the optimal θ_PV.

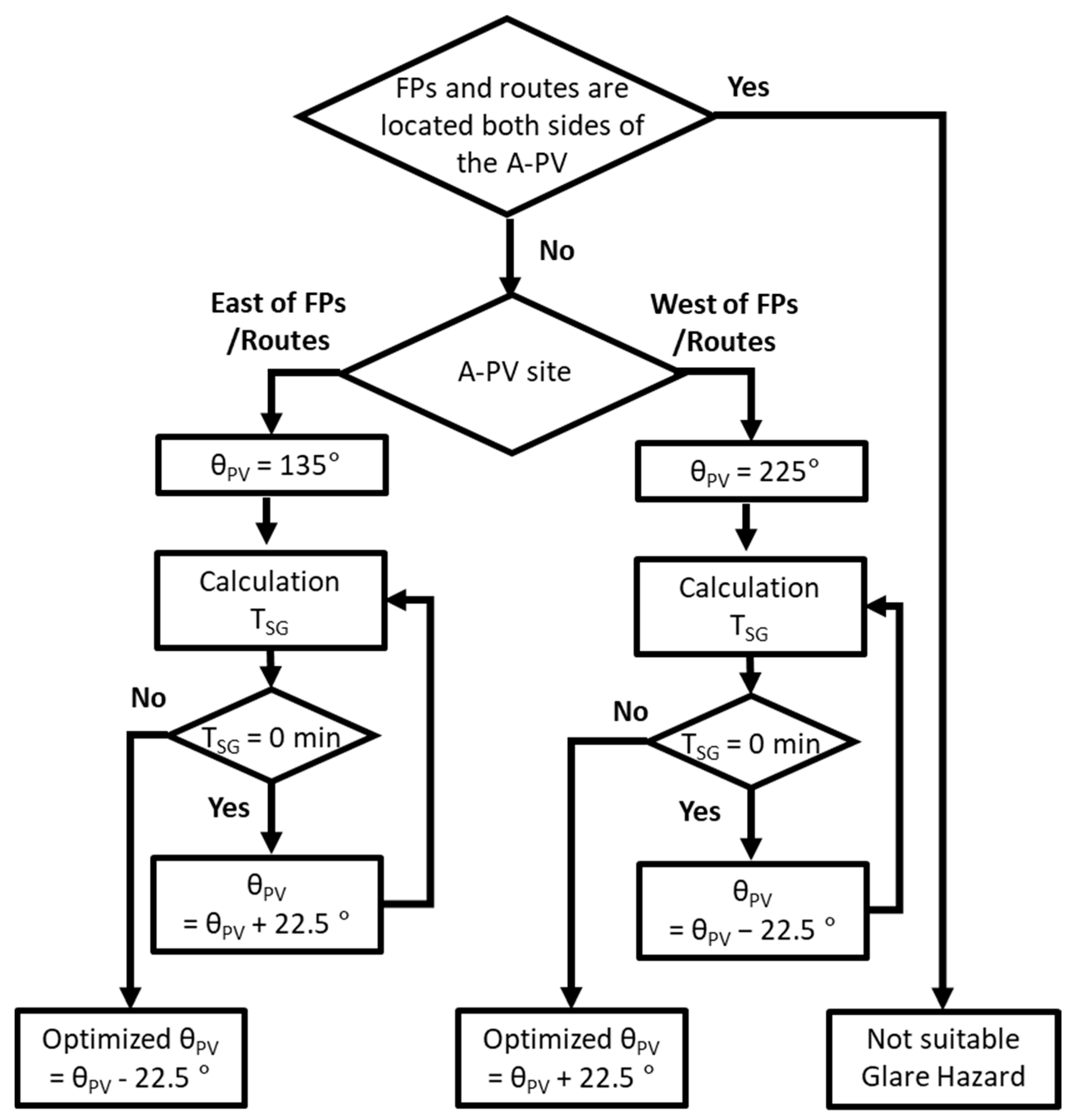
3.4. Glare and AER of A-PVs with Optimized θ_PV in the ICN

All candidate sites studied in Section 3.3 would not be recommended for installation of A-PVs due to the glare when θ_PV is 180° (which maximizes energy generation). However, optimizing θ_PV enables us to increase the number of possible sites for A-PV. According to the proposed method for optimizing the θ_PV, we designed A-PVs for ICN, as shown in Figure 8. Then, we calculated the minimum required steps to optimize θ_PV using our proposed method and for methods starting with A-PVs facing south, respectively. In the cases of W1–W6, located on the west side of FP1,2 and route 1, the optimized θ_PV was 225°. Similarly, all A-PVs located rightmost of the east route (E1–E4) did not cause any SG when their θ_PV were 135–157.5°. A-PVs situated in the middle of the taxiway (C1, C2) were excluded because they experienced SGs regardless of θ_PV. Our suggested procedure for optimizing θ_PV could save time and effort compared with the current method of starting from the south-facing A-PV, as summarized in

Table 2. The number of steps to optimize θ_PV in A-PVs. Here, we assumed that the minimum rotation angle of θ_PV was 22.5 degrees.

	Sites	W1	W2	W3	W4	W5	W6	C1	C2	E1	E2	E3	E4	Sum
Model
Proposed		2	2	2	2	2	2	0	0	2	3	3	3	23
Start from south facing A-PV		3	3	3	3	3	3	7	7	3	2	2	2	41

. For example, in the cases of W1–W6, we only needed to simulate twice (θ_PV of 225 and 202.5°) following the suggested method. On the other hand, an additional calculation (θ_PV of 180, 202.5, and 225°) would be required if someone started the analysis at θ_PV of 180°. Similarly, the proposed model allows us to decrease the steps for deriving the optimized θ_PV in the case of E1, compared with starting the calculation from the south-facing A-PV. Moreover, this method would be more effective in the cases of C1 and C2 by eliminating useless calculations of their T_SG and AER. As a result, it is possible to save steps in optimizing θ_PV from 41 to 23. The effect of the proposed model to reduce the number of steps will become more significant, as more sites are considered for A-PVs.

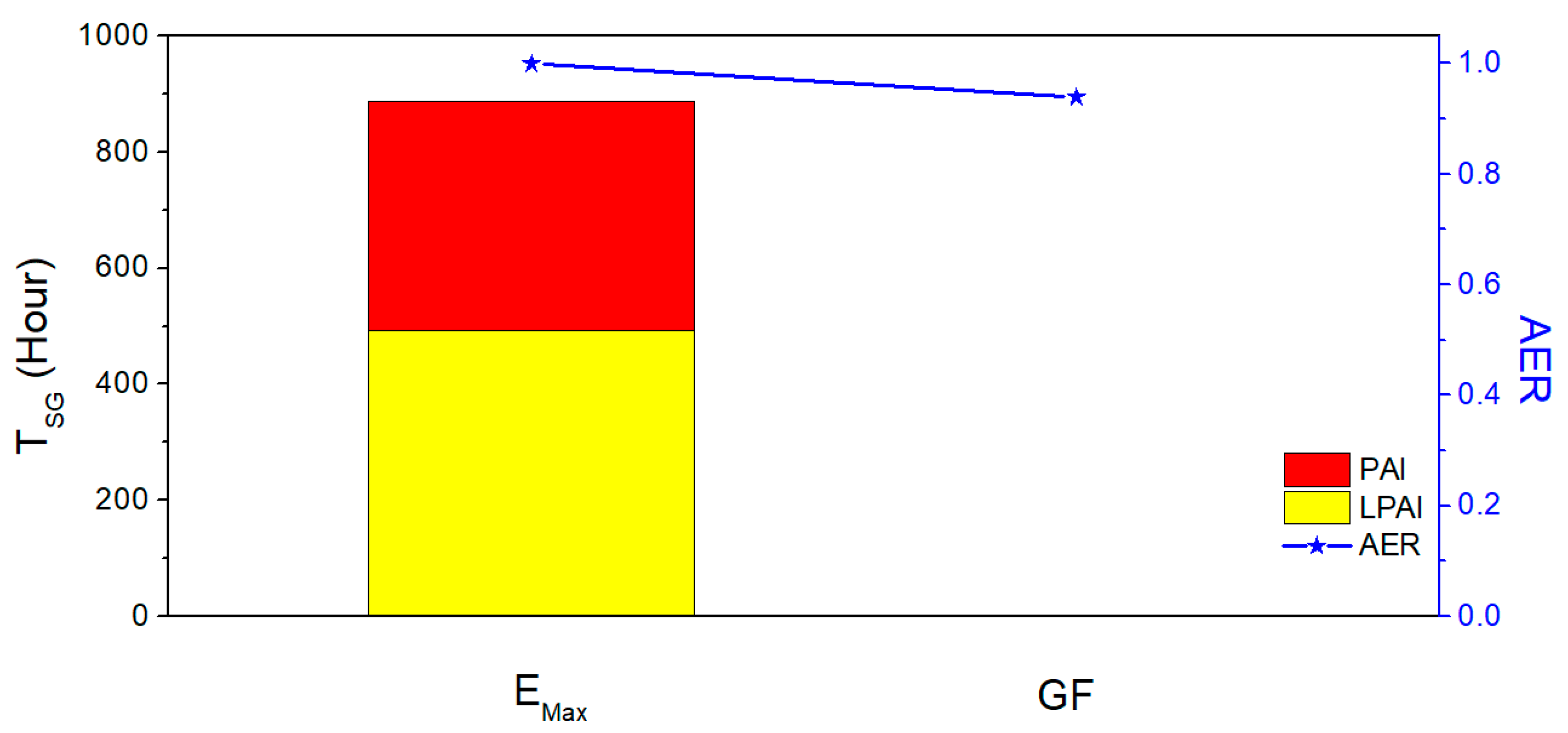
To comprehensively evaluate energy sacrifice for realizing glare-free conditions at ICN, we compared AER and T_SG of possible A-PVs with optimized θ_PV (GF) with south-facing cases for maximizing energy generation (E_Max). As glare from C1 and C2 was unavoidable independent of their angle, they were excluded from AER calculations. With only 4.8% of AER sacrifice, the optimized A-PVs successfully generated electricity (Figure 9). Energy loss was mainly attributed to the decreased energy generation of GF cases at noon when the intensity of the incident light is maximized. However, the safety advantage of optimized A-PVs is huge enough to compensate for their energy loss. T_SG from all A-PVs declined from 886 (E_Max) to 0 h (GF). Despite unavoidable energy losses for the GF, the modification of the θ_PV allows us to utilize solar energy safely in the case of ICN.

3.5. Verification of Proposed A-PV Azimuth Angle Optimization Method

We verified the proposed method for optimizing θ_PV of A-PV at four other airports: Gimpo (GMP, Seoul, Korea), Gwangju (KWJ, Gwangju, Korea), Beijing capital (PEK, Beijing, China), and Narita (NRT, Chiba, Japan). These four airports are situated in the northern hemisphere with a latitude of 35–40 degrees. Figure 10 is a satellite map with optimized A-PV for the four airports. For the simulation, we assumed that A-PVs were deployed in the west and east of their possible flight paths. Here, the simulation conditions for the four cases, including tilt of A-PV, weather, flight speed, and position during landing and take-off, are precisely the same as those of ICN. All sites were not suitable for A-PVs with θ_PV of 180°. Throughout the suggested procedure for optimizing θ_PV, it was possible to extend installation sites for A-PV without glare issues. The AER and T_SG of A-PVs with optimized glare-free conditions (GF) are compared with those of A-PVs facing the true south (E_Max), as shown in Figure 11 and summarized in

Table 3. LPAI, PAI (minute), and AER of A-PVs installed at GMP, KWJ, PEK and NRT.

Site	GMP			KWJ			PEK			NRT
	LPAI	PAI	AER	LPAI	PAI	AER	LPAI	PAI	AER	LPAI	PAI	AER
EMax	651	34,837	1	158	27,542	1	3106	4803	1	489	32,398	1
GF.	0	0	0.94	0	0	0.96	0	0	0.94	0	0	0.94

.

There were seven possible A-PV sites at GMP, with a runway angle of 140°. Two potential locations for A-PVs (GE1 and GE2) were on the runway’s east side, whereas the other five sites, GW1–5, were on its west side. Detailed T_SG induced by A-PVs with various θ_PV is shown in Figure S1. Consistent with the ICN case, E1 and E2 exhibited reduced T_SG when they turned east (θ_PV = 112.5–135°) by absorbing most of the incident sunlight from the east early in the morning. However, if they faced the south and southwest, solar light with a large θ_i would affect pilots on the routes and flight paths. In contrast, GW1–GW5 with θ_PV of 225° did not disturb the pilots’ vision at GMP. Thus, the optimized θ_PV of GW1–GW5 was 225°, whereas that of GE1 and GE2 were 135 and 157.5°, respectively. The differences in optimized θ_PV between GE1 and GE2 originated from different altitudes of flights near GE1 and GE2. Despite reduced R_SG, the attainable energy under GF was 94.6% of A-PVs facing the true south. Moreover, the time for optimizing θ_PV for each site could be reduced by adopting our suggested procedure. To find the optimized point, south-facing GW1–GW5 must be rotated twice by 22.5 degrees; thus, three sets of calculations (at θ_PV of 135, 157.5, and 180°) are required. However, our suggested method only requires a two-step calculation (at θ_PV of 135 and 157.5°).

The proposed method was also valid for the KWJ, whose runways and flight paths are almost symmetrical to the GMP. The runway of KWJ lies at 220°; six different sites were selected for A-PV installation, as shown in Figure 10. KW1–2 was on the west side of the runways, whereas the others were east of the airport (KE1–4). Despite the maximized energy generation in E_Max, the sum of T_SG from each A-PV exceeded 460 h per year. Due to the reduced angular difference between the route and θ_PV of A-PV under E_Max conditions, most of them were PAI. Detailed T_SG induced by south-facing A-PVs is displayed in Figure S2. However, if the A-PVs were rotated to 135° and 202.5° for KE1–2 and KW1–4, respectively, the T_SG decreased to zero. In addition, the AER under GF is 0.96, which is only 4% lower than that of E_Max. Hence, our proposed method is applicable to design A-PVs for several airports with north-south runways.

We could successfully optimize θ_PV of A-PVs using the suggested method at PEK and NRT, whose FPs and routes were 170 and 140°, respectively. Due to the limited open area in PEK, potential sites for A-PVs were close to routes. As a result, the T_SG from A-PVs was smaller than in other cases. Meanwhile, the potential sites for A-PVs were only on the west of FPs and routes due to existing mountains, buildings, and another route in the east of them. For both cases, the optimized angle for A-PV located on the west side of FPs and routes was 225°. The detailed calculations of T_SG and AER are shown in Figure S3. All south-facing A-PVs introduced glare issues to pilots and ground workers at both airports. However, rotating the A-PVs to the southwest made them safe from reflected light. The A-PVs on the east side of the route minimized T_SG and maximized AER when their θ_PV were 135°. The AERs for optimized A-PVs were 0.94 in both cases. This result again indicates that rotating θ_PV following the suggested procedure contributes to a more sustainable airport without any additional risk.

It should be noted that careful consideration is required for A-PVs installed at airports with east-west runways. In east-west runways, the light reflected by the A-PV facing opposite runways may strongly affect the pilots at sunset and sunrise during the summer because the solar light irradiates from the backside of the A-PVs. The azimuth angle of the solar light is less than 90° (sunrise) and exceeds 270° (sunset). In such cases, the reflected light penetrates the A-PVs backward, where the possible flight path and runway are located. However, the A-PV facing opposite them still exhibits a decreased T_SG without significant AER reduction.

4. Conclusions

A-PVs can reduce CO₂ emissions in the airport and aviation industry by harvesting solar light in unused areas near runways. However, their unavoidable SG may affect pilot vision and trigger fatal accidents. Establishing a general guideline for mitigating the R_SG of A-PVs could facilitate in saving time and expenditures when determining potential A-PV sites. Therefore, to propose an available SG-mitigating approach, we systematically analyzed the R_SG of A-PVs to air traffic, depending on their θ_PV. First, we compared the T_SG and AER of A-PVs under various θ_PV at possible PV installation sites near the runway of ICN. The computational simulation indicated that solar light reflected by the A-PVs could be redirected into the flight path and runway and was sufficiently strong to cause an after-image in pilots and ground workers. Pilots and ground workers could be exposed to SG when light with large θ_i irradiated the A-PV facing flight paths or runways. In contrast, R_SG became negligible in A-PVs facing the opposite direction of flight paths and runways. By modifying the A-PV θ_PV, designing a glare hazard-free solar energy harvesting system was possible. This approach was valid for reducing the R_SG of A-PVs at candidate installation sites of ICN and other airports. As an airport is an almost open space without shading, the sacrifice corresponding to the annual energy generation for SG-free conditions is less than 6% in A-PVs. Moreover, the suggested method allows us to save time and efforts in determining optimized θ_PV. Pertaining to glare hazards and annual energy generation, we believe that this study could be used as a guideline for installing A-PVs in airports. In addition, the results shown here allowed us to save time and effort in finding SG-free conditions for A-PVs and installing them. As studies on mitigating SG of A-PVs are conducted further, airports will become energy self-sustainable facilities without emitting greenhouse gases.