Abstract
Although polychlorinated biphenyls (PCBs) have been long banned from use, both they and dioxins are still considered persistent organic pollutants. The reason is twofold: their relative inertness (especially to oxidation) and their ability to accumulate in fat tissue. The current study sheds light on the interactions of PCBs with water, chlorine, and chlorine dioxide. Necessary insight is gained from Atoms in Molecules (AIM) and Non-Covalent Interactions (NCI) index and analyses for the 1:1 complexes of PCBs with water and chlorine (Cl) molecules. Further, Symmetry-Adapted Perturbation Theory (SAPT) calculations reveal the strength and nature of the intermolecular interactions, and the presence of halogen bonding is demonstrated in AIM, NCI, and SAPT studies. The stability of water, chlorine, and chlorine dioxide (ClO) complexes with PCBs is discussed using the supramolecular MP2 approach. Finally, analysis of microsolvation shells of PCBs showed the origins of the hydrophobicity and environmental persistence of these chemicals. Our results are applicable to the sustainability of water treatment strategies providing a description of forces and interactions at the molecular level.
1. Introduction
Persistent organic pollutants (POPs), according to the text of the United Nations Stockholm Convention of 22nd May 2001, are chemicals that possess toxic properties, resist degradation, bioaccumulate, and are transported, through air, water, and migratory species, across international boundaries and are deposited far from their place of release, where they accumulate in terrestrial and aquatic ecosystems [1]. Although the list of POPs is open to additions and amendments, the most widespread classification of the considered chemicals is known as “the dirty dozen”: aldrin, chlordane, DDT, dieldrin, endrin, heptachlor, hexachlorobenzene, mirex, toxaphene, polychlorinated biphenyls, polychlorinated dibenzo-p-dioxins, and polychlorinated dibenzofurans [2]. It is easy to observe that most of these chemicals contain chlorine atoms in their molecular structure. This fact adds to their generally hydrophobic nature, leading to chemical stability, inertness, and bioaccumulation in fatty tissues. The presence of –Cl atom in the structure of the discussed compounds increases the spectrum of possible interactions with the aquatic environment. In addition to intermolecular hydrogen bonds (HBs) and electrostatic interactions, there can also be halogen bonds. The van der Waals forces present in interactions of chlorine-containing compounds with other species are also enhanced by large electron clouds of chlorine atoms. This influences the intermolecular interactions of POPs with the environment, including water. In turn, these interactions are, in the long-term, responsible for the fate of POPs in the environment, including transport and bioaccumulation. The above reasons prompted us to investigate the diversity of non-covalent interactions [3] in a selected group of POPs—polychlorinated biphenyls.
Polychlorinated biphenyls (PCBs), a family of 209 congeneric chemicals, have been used in heat transfer fluids relevant to high-power electric transformers and capacitors, as well as in diverse paints and plastics [4]. Their inertness, low reactivity, and resistance to heat made them ideal in these applications, but their toxicity and bioaccumulation propensities were the reasons for banning PCBs. To this day, however, PCBs persist in the environment as organic pollutants [5]. The potential for further contamination of the environment by PCB is great, as it can be found in many types of obsolete and decommissioned industrial equipment as well as in many devices still operating, e.g., high-power electrical transformers. It is important to emphasize that detectable amounts of PCBs are present in an environment considered pristine by the general public, such as Antarctic fish tissues [6]. Monitoring and neutralizing these pollutants in water, soil, and the biosphere is a major challenge towards achieving a sustainable economy.
Only 12 out of the 209 congeneric PCBs are considered dioxin-like in their toxicity; these congeners can adopt a coplanar conformation, allowing them to bind to the aryl hydrocarbon (Ah) receptor affecting protein synthesis [7]. It is also suspected that non-covalent interactions between selenocysteine residues and PCBs are responsible for the toxicity of PCBs against the thyroid gland [8]. It should be noted, however, that the planarity of many PCBs in the solid state is an environmentally driven effect: in the gas phase, even the parent compound, biphenyl, adopts a twisted conformation with an angle between ring planes close to 40 degrees [9,10]. The dioxin-like PCB congeners are those with no more than one chlorine substituent in the ortho positions of the rings, which ensures a low torsional barrier and the possibility of adopting the coplanar structure [11]. It should be stressed that while chlorinated dioxins are not commercially useful and their occurrence in nature results from side reactions (e.g., during synthesis of herbicides) or oxidation (burning of organic compounds containing chlorine), the PCBs on the other hand, were very attractive due to their properties (stability, resistance to heat and chemicals, large heat conductivity) and, therefore, were introduced into the environment in large amounts [4].
The nomenclature of the PCBs followed in this article was proposed by Ballschmiter and Zell [12] and is not directly related to the substitution pattern; however, the higher the number, the larger is the number of chlorine atoms in a particular PCB. The dioxin-like PCBs described within this study do not possess ortho chlorine substituents. Their numbering according to the Ballschmiter and Zell is: PCB 11, 15, 77, 80, and 169—see Scheme 1 for the corresponding molecular structures.
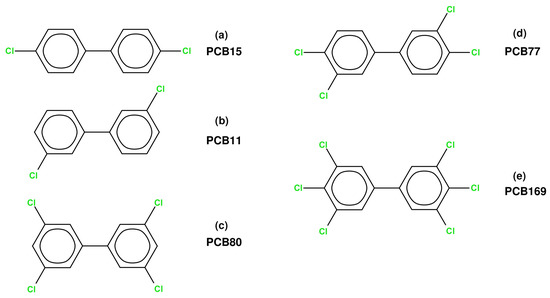
Scheme 1.
Structures of dioxin-like PCBs included in this study, together with their numerical designations according to the Ballschmiter & Zell system, and shorthand labeling (a–e) used in the text.
Among the oxidizing gases for water treatment, chlorine, ozone, and chlorine dioxide, the latter is the least common, despite some interesting properties. Chlorine dioxide, ClO2, is a gaseous oxidant used in water treatment as an alternative to Cl2 [13]. It possesses some advantages over Cl2, e.g., it is effective not only below neutral pH, but also in moderately alkaline waters, and its action on water impurities generates lesser amounts of (possibly carcinogenic) halomethanes [14]. On the other hand, ClO2 can undergo disproportionation into ClO and ClO, which limits its use in various jurisdictions [15]. PCBs are resistant to oxidation with either Cl or ClO; however, there is a possibility of the formation of halogen bonds between these species. Halogen bonding with PCB chlorine atoms acting as donors has been implicated in the modulation of enzymatic activity of iodothyronine deiodinases, with possible result of thyroid activity disruption [8]. As already noted in the first paragraph of the Introduction, investigation of halogen-bonded (as competitive to hydrogen-bonded) systems involving PCBs would shed light on the environmental fate of these persistent organic pollutants in a variety of environments, including contaminated water and wastewaters, and thereby contribute to improving the sustainable management of water resources.
Modeling of PCB distribution, transport, and environmental fate has been carried out from diverse points of view. From the macroscale, they focused on the distribution of PCBs in water, sediments, and organisms [16,17], including phytoremediation techniques [18]. Models of interactions between PCBs and soil, as well as attempts to determine the efficiency of PCB removal using steam, use water/organic phase partition coefficients [19,20]. Such partition coefficients and Henry law constants can be subjected to the quantitative structure-activity relationship investigations [21], and theoretical chemistry approaches have been used to assess these parameters linking molecular structure with macroscopic properties [22,23]. A quantum-chemical study of atmospheric oxidation of PCB-47 has shown the potential of theoretical methods in elucidating the fate of PCBs in the gaseous phase [24]. On the other hand, the role of weak hydrophobic (dispersion) interactions between a PCB molecule and a fluorescent sensor molecule, benzopyrene, was successfully applied in a new approach to PCB detection in a water environment [25]. Moreover, PCBs, regarded as relatively inert compounds, nevertheless have been shown to undergo metabolism in human cell lines leading to dechlorinated species [26]. This overview of the literature shows that the molecular-level description of the PCBs intermolecular interactions has a profound impact on their environmental fate, but quantum-chemical investigations have not yet deeply addressed this subject. In the current study, aimed to tackle this issue, PCBs interactions with water, chlorine, and chlorine dioxide are discussed based on quantum chemistry approaches. The Atoms in Molecules (AIM) theory [27] and Non-Covalent Interactions (NCI) index [28,29] were employed for non-covalent interactions characteristics and electron density distribution and estimation of the hydrogen/halogen bond energy. Symmetry-Adapted Perturbation Theory (SAPT) [30] was applied for the energy decomposition to give insight into energy components and the strength of the interactions.
Our studies will provide an overview of the nature and energy scale of interactions between PCBs and water, as well as chlorine and chlorine dioxide, which will enable the rational design of water purification substances. The scientific value of this study is contained in the detailed description of the differences in the interaction of PCBs with water and chlorine-containing species. The molecular-level explanation of the propensity of persistent organic pollutants to accumulate in a hydrophobic environment is a step toward a broader understanding of the problem of water pollutants. The current society is searching for new forms of water treatment in view of green chemistry. Therefore, our study indicates perspectives on the use of computational chemistry to this effect. The design of catalysts and scavengers capable of handling relatively inert POP molecules will benefit from the employment of computational strategies.
2. Computational Methodology
2.1. Structure Description and Energy Partitioning
Initial structures of selected PCBs, water, chlorine, and chlorine dioxide were drawn with the Avogadro 1.2.0 program [31] and optimized using the default MMFF94 force field. Further quantum-chemical calculations on the PCBs and the small molecules were carried out at the RI-MP2/def2-TZVP level of theory [32,33,34] using the ORCA 5.0.3 (Max-Planck Institut für Kohlenforschung, Mühlheim an der Ruhr, Germany) software [35,36]. The geometry optimization was followed by vibrational spectrum calculation with the numerical finite-difference method at the RI-MP2/def2-TZVP level of theory as well to confirm the nature of the located stationary points; in all cases, no imaginary wavenumbers were found.
Microsolvated models were generated using the classical molecular force-field (GAFF) [37] and atomic charges from the AM1-BCC model [38] based on the Amber-Tools2021 and Amber20 software (University of California, San Francisco, USA) [39]. Each PCB molecule was then solvated using the TIP3P water model [40] with 8 Å solute–cell boundary buffer distance, resulting in five cubic simulation boxes of 33 Å edge. Each solvated system underwent the following procedure: 1000 steps of steepest descent minimization, 20 ps of NVT thermalization at 300 K, 80 ps of NpT equilibration at 300 K and 1 atm, and finally, the NVT production run of 5 ns. The NpT equilibration phase led to the final density of the simulation cells varying from 0.987 to 0.991 g cm. The time step of 1 fs and non-bonded cutoff of 10 Å were used in the classical MD runs. The classical MD trajectories were used solely to generate the microsolvation models and their results were not further analyzed. Post-processing of these trajectories was performed with the use of the VMD 1.9.3 program (University of Illinois at Urbana-Champaign, Urbana, IL, USA) [41]. The final frames of each of the classical MD production runs were then used to extract 1:1 PCB-water complexes, two for each PCB: one with a water molecule along the line provided by the C–Cl bond (in later sections denoted by the number 1 in the abbreviated designation of the complexes), and one with a water molecule above the aromatic ring (denoted with the number 2). A simple atom substitution (chlorine in place of the oxygen atom in water) was then used to construct PCB–Cl and PCB–ClO complexes manually. These three series of structures were subjected to structure optimization at the RI-MP2 level, as described in the first paragraph of this section. After confirming the correctness of the nature of the stationary points (no imaginary wavenumbers in the vibrational spectrum), wavefunction files (WFX format) of non-radical singlet ground state complexes were generated for further analysis using RI-MP2 relaxed electron densities. The RI-MP2/def2-TZVP supramolecular binding energies were corrected for the Basis Set Superposition Error using the counterpoise scheme [42]. The nature of interactions in the complexes 1:1 PCB-water and PCB-Cl was investigated using the Symmetry-Adapted Perturbation Theory (SAPT) method [30]. The structures optimized previously at the RI-MP2/def2-TZVP level of theory, as described above, were taken and subjected to the density-fitting accelerated SAPT [43] interaction energy calculation at two levels: SAPT2 level with the same def2-TZVP basis set (reported in the Supplementary Materials only) and SAPT2+ level with Dunning aug-cc-pVDZ basis set (reported in the main text). The SAPT energy terms are defined in detail in the original SAPT review article [30] as well as in the paper providing implementation details in the PSI4 package (see Ref. [43], Equation (8) for SAPT2 and Equation (9) for SAPT2+); in particular, SAPT2+ contains corrections to the dispersion term resulting from the first- and second-order treatment of intramonomer electron correlation. The energy partitioning used in the SAPT framework consists of the following specific terms of well-defined physical meaning:
- electrostatic energy defined as Coulombic force between the molecular skeletons and electron densities of the non-interacting, unperturbed monomers, without polarization effects,
- Pauli repulsion exchange energy, which is a purely quantum-mechanical effect related to the orbital overlap, calculated using the unperturbed wavefunctions of the monomers,
- induction term gathering the effects of mutual polarization of the monomers on the electron density distribution within them, including corrections to the electrostatic and exchange terms,
- dispersion energy related to the instantaneous multipoles—fluctuations of the electron density—between the monomers.
These four terms, when combined, provide the fifth value of the total interaction energy at the SAPT2 level. The interaction energy is calculated by definition using the structures of the monomers taken from the dimer so that the effects of structural relaxation are not present. The SAPT calculations were prepared with PSI4 1.3.2 program [44]. The last considered approach to the structural investigations was to generate larger microsolvation models by including the water shell of molecules closer than 3.5 Å to the solvated PCB molecule in five snapshots taken (at regular intervals of 1 ns starting at 0.5 ns of the production run) from classical molecular dynamics for each of the five PCBs, obtaining 25 microsolvated models. An example of such a shell is shown in Figure 1. This post-processing step and preparation of the corresponding figure were carried out with the VMD 1.9.3 program [41]. The PCB–water interaction energy for the generated microsolvation models was then calculated at the RI-MP2/def2-TZVP level. These quantum-chemical calculations were performed with the ORCA 5.0.3 package [35,36].
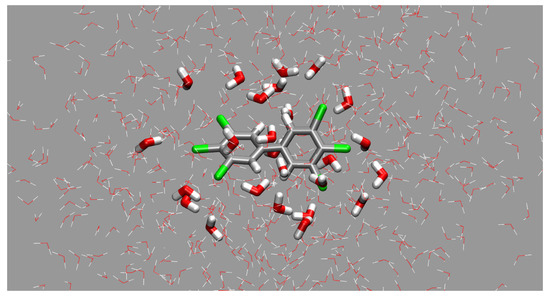
Figure 1.
An example of the microsolvation shell of PCB169 as a solute—snapshot from the classical MD run. Thicker lines denote the PCB and water molecules closer to the solute than 3.5 Å. Color coding for atoms: gray—carbon, white—hydrogen, red—oxygen, green - chlorine.
2.2. Non-Covalent Interactions (NCI) Description
Atoms in Molecules (AIM) theory [27] was applied in the study to investigate electron density distribution and molecular features derived from it. The electron density and its Laplacian were computed at Bond Critical Points (BCPs) involved in the non-covalent interactions. Additionally, the potential electronic energy density was calculated to give an insight into the strength of the interaction. Finally, to estimate interaction energy the Espinosa equation [45]: = (r) was used, where (r) is the potential energy density at the relevant BCP. The AIM analysis was performed with the assistance of the MultiWFN program [46,47]. Intermolecular, non-covalent interactions are manifested by bringing the atoms in closer than expected contact, which is usually assessed on the basis of the conventional van der Waals atomic radii [48]. This approach is well established, especially in crystal diffraction studies, where the accurate determination of the hydrogen atoms’ positions can often be challenging. Computational approaches provide a unique opportunity to appeal to the properties of electron density itself. This forms the basis for the Atoms in Molecules (AIM) theory [27], and this framework is employed in the current study for the 1:1 PCB complexes with water and chlorine.
As a complementary method to the AIM, the well-known Reduced Density Gradient (RDG) analysis was performed [28,29] using the MultiWFN 3.8.dev program (Beijing Kein Research Center for Natural Sciences, Beijing, China) [46,47]. It is a visualization index showing interatomic interactions based on the electron density and its reduced gradient. It is possible to estimate the strength of the non-covalent interactions in three-dimensional space. Non-Covalent Interactions Index (NCI) was employed to detect all possible secondary bonds in the studied complexes. The main building block of this method is the RDG, s(r) [49], a dimensionless quantity which was introduced in the context of generalized gradient approximation (GGA) to the exchange energy in DFT and serves as a correction to the electron uniform gas model [50]. The properties of RDG have been thoroughly tested and, on the basis of small values of it and electronic density, it is possible to easily separate non-covalent interactions occurring in the studied system from covalent ones. A further distinction of the NCIs is performed using the sign of —non-bonded and bonded interactions are characterized by positive and negative values of , respectively. The pictorial representation is built upon this idea and while repulsive interactions are presented using red color, the attractive ones can be discerned by its characteristic green to blue (when stronger) RDG isosurfaces.
The proposed theoretical approaches offer the advantage of deeper insight into the nature of the intermolecular interactions of the PCBs. A classical supramolecular approach to calculating the intermolecular energies provides only a general information on the stability of a given structure, while the SAPT methodology allows for obtaining physical partitioning of the interaction energy into terms that can be interpreted from the physico-chemical point of view. The AIM theory is a conceptual framework to analyze the strength and nature of the bonding interactions present in the system using an observable quantity—electron density. The NCI index adds the possibility of three-dimensional visualization of regions involved in diverse types of interactions, expanding the AIM capability so that not only the existing, but also possible interactions can be investigated. The advantages of these methods are also their accuracy and relatively low computational complexity coupled with the possibility of using freely available software tools.
3. Results and Discussion
3.1. Non-Covalent Bonding Analysis of the Studied 1:1 PCB Complexes
The AIM theoretical framework detects interatomic interactions by locating Bond Critical Points (BCPs) and associated bond paths linking the interacting atoms through the BCPs. Properties of bonding are revealed in the values of electron density and related parameters at the BCP. Pictorial representation of the electron density topology, including the BCPs as small green spheres, is shown in Figure 2 for the PCB-water complexes, and the parameters of the relevant intermolecular BCPs are provided in Table 1. For PCB-chlorine complexes, similarly arranged Figure 3 and Table 2 are also presented and discussed. The Figures and Tables use a shorthand labeling of the PCB complexes: letters from a to e denote the PCB according to Scheme Scheme 1, the digit 1 or 2 differentiates between two variants of the complex.
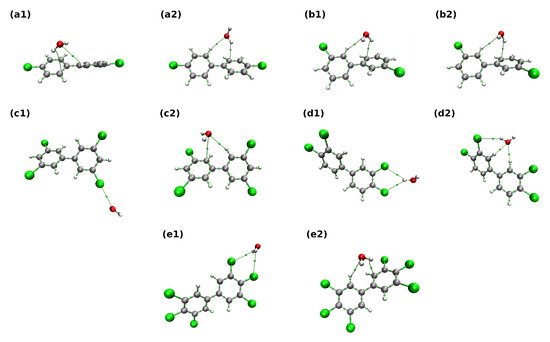
Figure 2.
Topology of the electron density in the 1:1 PCB–water complexes according to AIM theory. Subfigure labels (a–e) identify the PCB compound according to Scheme 1, while numbers 1 and 2 differentiate between two initial structures subjected to optimization. Color coding for atoms: gray—carbon, white—hydrogen, red—oxygen, green—chlorine. Bond critical points are labeled as small green spheres. Intermolecular bond paths are drawn as grey lines.

Table 1.
AIM-derived properties at BCPs of the investigated 1:1 complexes of chosen PCBs and water molecules. E1 is a bond energy computed using the Espinosa equation. The dimensions of given quantities are as follows: electron density, , is given in atomic units and the Laplacian of electron density, , is in units. VCP denotes potential energy density.
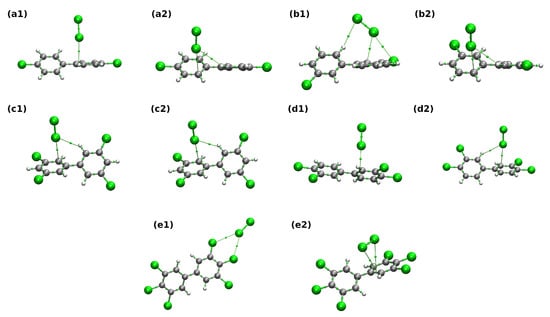
Figure 3.
Topology of the electron density in the 1:1 PCB–chlorine complexes according to the AIM theory. Subfigure labels (a–e) identify the PCB compound according to Scheme 1, while numbers 1 and 2 differentiate between two initial structures subjected to optimization. Color coding for atoms: gray—carbon, white—hydrogen, green—chlorine. Bond critical points are labeled as small green spheres. Intermolecular bond paths are drawn as gray lines.

Table 2.
AIM-derived properties at BCPs of the investigated 1:1 complexes of chosen PCBs and chlorine molecules. E1 is a bond energy computed using the Espinosa equation. The dimensions of given quantities are as follows: electron density, , is given in atomic units and the Laplacian of electron density, , is in units. VCP denotes potential energy density.
The complexes of PCB15 and PCB11 (each ring has only one chlorine substituent) with water exhibit a preference of the water molecule to interact rather with –H than –Cl functions, even if the geometry optimization started from the O–HCl–C arrangement—see the structures a1 and b1 in Figure 2. The more chlorine-rich PCBs are more likely to form water–chlorine atom interactions, visible in the structures c1, d1, and e1. Systems with classical, medium, or strong hydrogen bonds (HBs) prefer arrangements in which the role of HBs is maximized; here, we observe that the competitive and alternative bond paths are formed, e.g., in the a2 structure: both O–HC and C–HO contacts are visible. Further, the presence of at least two closely positioned –Cl atoms in PCB77 and PCB169 leads to interesting bifurcated O–HCl–C contacts, where two chlorine atoms are engaged by the same hydrogen atom of the water molecule—see the structures d1 and e1 in Figure 2. The presence of BCPs and bond paths indicates, however, merely the existence of interaction, while more details can be inferred from the numerical values of the relevant BCP properties. Noteworthy is the fact that averaged sums of estimated energies for all complexes are equal to 1.222 kcal/mol for PCB–water and 1.539 kcal/mol for PCB–chlorine ones. As seen in Table 1, the electron density at the BCPs is very low and does not exceed 0.01 . In each case, however, the value of is larger than the lowest boundary, 0.002 , assumed in the criteria of Koch and Popelier [51]. The values of electron density Laplacian are positive, according to expectation, but in many cases are lower than the threshold of 0.024 given in [51]. The simple but effective approach of Espinosa [45] allowed us to estimate the contributions of individual interactions to the total interaction energy between the PCB and water molecule. The E1 values given in Table 2 are between 0.617 and 1.937 kcal mol, placing the intermolecular HBs at the lower (weaker) range of energies.
The PCB–chlorine complexes also require the PCB to be chlorine-rich to exhibit significant ClCl contacts, as shown in Figure 3 (see especially the structure e1). On the other hand, there is a specific class of interactions, labeled in Table 2 as H–CCl and indicated in Figure 3 by the bond path between a carbon atom of PCB and one of the Cl atoms of the Cl molecule. In these cases, the electron density and its Laplacian at the corresponding BCP are consistently higher than for the weak C–HCl hydrogen bonds—e.g., for the d2 structure, the corresponding values of are 0.014 and 0.005 . This also means that such interactions of electron clouds of the Cl atom and the aromatic ring contribute ca. 2.5 kcal mol to the interaction energy, according to the Espinosa model [45]. Returning to the structure e1, exhibiting bifurcated ClCl halogen bonds, these interactions are similar in strength and in topological parameters to the weak HBs noted for the PCB-water complexes. The contributions of the two halogen bonds, calculated with the Espinosa equation, combine to the value of 1.738 kcal mol, in a surprisingly good agreement with the SAPT2+ interaction energy of −1.732 kcal mol reported in the next section. To sum up, one can conclude that the overall picture of AIM investigations for 1:1 models reveals that the Cl molecules compare favorably to the HO when it comes to interacting with various PCBs.
Let us start the discussion regarding non-covalent bonds present in the studied systems in the context of the Non-Covalent Interaction index (NCI) method. It should be noted that this method lacks the quantitative treatment of the system—we cannot easily estimate the interaction energies of the studied interactions; thus, only qualitative discussion can be provided. For HO–PCB complexes (see Figure 4), the more diverse, although weaker in strength when compared to Cl–PCB systems, the pattern of non-covalent interactions can be seen. Aside from weak hydrogen (C–HO–H or H–CH–O) and halogen bonds that are present in a2, b1, b2, c2, d2, e1, e2, and c1, O–HCl interactions in c2, d2 systems can also be observed. Regarding Cl–PCB complexes, one can note that the vast majority of interactions presented in Figure 5 are of weak van der Waals type. In virtually every presented complex, the donor-acceptor interactions between Cl and the aromatic rings were present—on the other hand, hydrogen bonds of type R–C–HCl, were also detected in structures b1, c1, c2, d1, and d2. It is visible that the substitution of the aromatic rings with more than one chlorine substituent leads to the beefing up of the -Cl interactions—most probably via the change of the quadrupole moment of the aromatic motif from negative to positive value. Interesting, and unnoticed by AIM analysis, was the presence of repulsive intramolecular C–HH–C between benzene-like frameworks and ClCl interactions.
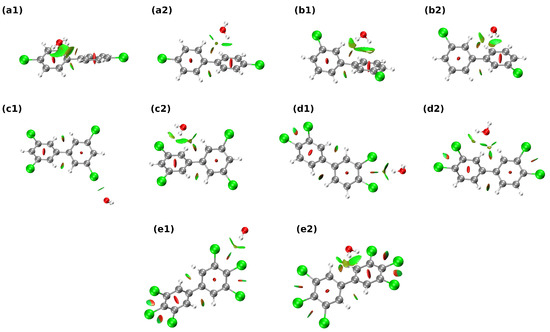
Figure 4.
Graphical representation of the Non-Covalent Interactions (NCI) index distribution in the 1:1 PCB–water complexes. Subfigure labels (a–e) identify the PCB compound according to Scheme 1, while numbers 1 and 2 differentiate between two initial structures subjected to optimization. Color coding for atoms: gray—carbon, white—hydrogen, red—oxygen, green—chlorine.
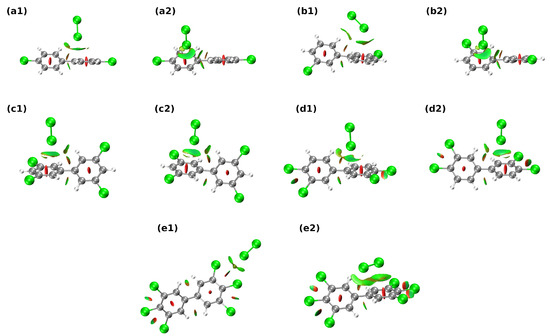
Figure 5.
Graphical representation of the Non-Covalent Interactions (NCI) index distribution in the 1:1 PCB-chlorine complexes. Subfigure labels (a–e) identify the PCB compound according to Scheme 1, while numbers 1 and 2 differentiate between two initial structures subjected to optimization. Color coding for atoms: gray—carbon, white—hydrogen, green—chlorine.
3.2. Interaction Energy Analysis in 1:1 PCB Complexes with Water, Chlorine, and Chlorine Dioxide
Bonding and interaction energies of the singlet spin state 1:1 complexes of PCBs with water and Cl molecules are reported in Table 3. Bonding energies obtained at the RI-MP2/def2-TZVP level are calculated with respect to the optimized monomers, while the SAPT2+/aug-cc-pVDZ interaction energies do not include structural relaxation. Additional results from the SAPT2/def2-TZVP level are provided in Table S1 of the Supplementary Material, and they follow the same trends as the values in Table 3. The most general observation related to these energy values concerns the comparison of HO and Cl as the interaction donors/acceptors. It is seen that, in general, complexes of the studied PCBs with chlorine are stronger than the corresponding PCB–water systems. SAPT2+, besides similar treatment of electrostatics, induction and exchange terms (at the second-order perturbational level with respect to intramonomer electron correlation) to SAPT2, treats dispersion at the level similar to MP4 and, thus, provides a more accurate estimation of that contribution. The importance of the more thorough level is especially visible when one considers results for chlorine complexes, where dispersion contributions are definitely the most important part of the interaction energy. Providing a more robust discussion of the presented complexes, let us start with the comparison of obtained sums of interaction energies with the binding energy provided by the supramolecular method. It can be seen that for the PCB–water series of the complexes, the RI-MP2 based approach systematically underestimates binding energy when compared to SAPT2+/aDZ level, while for the PCB–Cl series, both under- and overestimation occurs. Moreover, when one considers E+E as the antisymmetrized reference state electrostatic energy, it will be evident that its sum is certainly not attractive but even repulsive. Thus, as one may observe in Table 3, the most important contributions to the interaction energy stem from the dispersion and the induction energy for both investigated series of complexes. It is especially noticeable for Cl complexes, where, due to significantly larger van der Waals radii of chlorine atoms (and, thus, larger intermonomer charge density overlaps), the short-range exchange interactions dominate above all other terms. The same argument can be put forward when the dispersion contributions will be taken into consideration—generally, their contribution to the interaction energy of Cl complexes is almost twice larger in magnitude than its counterpart of HO complexes. For c1, d1, and e1 water complexes, one can observe significantly smaller values of exchange energy—in these cases, water molecules are located in the plane with the associated PCBs and form hydrogen (c1, d1) and halogen bonds (e1), respectively. Similar findings were obtained for e1, Cl–PCB complex, where also the halogen bond is formed and, due to lower overlap of atomic densities, the exchange and dispersion contributions are significantly lower in magnitude.

Table 3.
Binding or interaction energies in kcal mol−1 between PCBs and water, chlorine or chlorine dioxide in the studied 1:1 complexes optimized at the MP2/def2-TZVP level of theory. Results of supramolecular MP2/def2-TZVP (binding energy with counterpoise correction) and perturbational SAPT2+/aug-cc-pVDZ (interaction energy) approaches. The contributions summing up to the total SAPT2+ energy are: Elst = electrostatics; Exch = Exchange; Ind = Induction; Disp = Dispersion.
A final remark is necessary for the PCB–ClO complexes, which are spin doublets. For this reason, only their binding energies, evaluated at the RI-MP2/def2-TZVP level, are reported. Severe difficulties in localizing the minima on the potential energy surface have emerged, and only five structures were finally optimized. Their binding energies, grouped at the bottom of Table 3, are negative (unfavorable interactions) and on the order of 25–30 kcal mol. Such values indicate that the ClO molecules are not forming stable structures with the PCBs. The spin density, according to Mulliken and Löwdin population analysis schemes, stays totally on the ClO molecule. One cannot, therefore, hope for effective contact of PCBs with the oxidizing agent, chlorine dioxide.
3.3. Interactions between PCBs and Their Solvation Shells
High persistence of PCBs in the environment and their ability to bioaccumulate are attributed, among other factors, to their hydrophobicity and generally weak interactions with water. The latter fact was investigated in detail with the combination of classical MD, serving as the source of a representative ensemble of PCB solvation shell structures, and RI-MP2/def2-TZVP interaction energy calculations. As already noted in the Computational Methodology, the extent of the microsolvation shell was chosen to encompass water molecules with the nearest distance to the PCB less or equal to 3.5 Å. This ensured that the shell covered the first solvation sphere of the PCB, without additional water molecules not in direct interaction with the solute. For each of the five PCBs, five classical MD snapshots were analyzed—their structures are presented in Figure S1 of the Supplementary Material. As seen in Table 4, the number of water molecules surrounding a given PCB was between 21 and 35, with a median of 29. No obvious correlation between the number of chlorine atoms in the PCB molecule and the size of the microsolvation shell is visible in the gathered data. While the total interaction energies at a given snapshot are relatively large, between −7.8 and −18.3 kcal mol (with one outlier, an exceptionally weak interaction of −0.52 kcal mol), very low values of the interaction energy “per molecule” are seen, i.e., Eint/n, where n is the number of water molecules in the microsolvation shell. Such an average provides an estimate of the contribution of each single water molecule when the shell is built around the solute. The contributions gathered in Table 4 are indeed small, ca. 0.5 kcal mol stability gain for each attached water molecule, in comparison to the electronic energies (no zero point and temperature effects included) of classical water dimer structure (−5.0 kcal mol [52]) and a set of other possible diverse (HO) structures (from −5.0 to −2.4 kcal mol [53]). The reported interaction energy values explain the hydrophobicity of PCBs—preparation of a cavity for the solute molecule, together with the associated breakup of the water–water hydrogen bonding network, is energetically more costly than the stability gain due to the PCB–water interactions. The value of interaction energy per one water molecule is also consistently several times smaller than most of the values reported in the SAPT study where optimized structures were employed (see Table 3). This indicates that interaction “hot spots” are scarce on the boundary of the PCB molecules—thus, most of the microsolvation shell water molecules are passive towards the solute. The net result is high hydrophobicity and inertness of the PCB molecules in a water environment, a molecular-scale origin of the macroscopic behavior of PCBs as persistent organic pollutants.

Table 4.
Interaction energies in kcal mol−1 between PCBs and water microsolvation shells, sampled at the specified time from the classical MD runs and evaluated at the RI-MP2/def2-TZVP level with counterpoise correction. E—interaction energy, n—number of HO molecules in the microsolvation shell, E/HO—interaction energy per one water molecule.
4. Conclusions
We examined five PCBs interactions with the water molecule, chlorine, and chlorine dioxide. Subsequently, the models with solvation shells were constructed to reproduce the water environment. SAPT method has allowed the energy decomposition giving insight into the energy components. It was found that the dispersion is the most significant stabilizing factor in the studied complexes. The use of AIM and NCI methods enabled us to look at the strength and type of interactions on the basis of electron density. A variety of weak non-covalent interactions have been detected and their molecular features have been determined at BCPs. The strength of the interactions was estimated using Espinosa equations as well. The applied methodologies consistently show that the PCB–Cl complexes are slightly, but unmistakably stronger than the PCB–HO systems; the average binding energy of the former is equal to 1.539 kcal/mol and for the latter equals 1.222 kcal/mol.
The theoretical findings of the current study provide a quantitative description of the PCBs interactions with various compounds, and highlight the molecular scale origins of the persistence of PCBs in the natural environment. The results of the research can be used in the design of new compounds and methods for water purification. Such methods must tackle two problems:
- PCBs do not interact with water and accumulate in non-polar environments,
- the relatively inert C–Cl bonds must be activated.
It will hopefully be possible in near future to carry out a de novo design or directed evolution aimed at artificial enzymes recognizing aromatic molecules with halogen functions, activating the C–Cl bonds, and transforming the PCBs into hydrocarbons and chloride ions. Such enzymes will probably employ halogen bonding as one of the PCB recognition techniques in its active site. A currently available alternative is a two-phase system, in which the PCBs are washed out from the aqueous phase into the organic hydrophobic medium, and catalysts carry out the PCB degradation. The design of such catalysts should take into account the fact that PCBs interact via weak non-covalent interactions.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/su141912529/s1, Table S1: Binding or interaction energies in kcal mol between PCBs and water or chlorine in the studied 1:1 complexes. Results of supramolecular MP2 (binding energy) and perturbational SAPT2 (interaction energy) approaches with def2-TZVP basis set; Figure S1: Microsolvation shells—snapshots from the classical MD runs of the studied PCBs in water, used in the solvation shell interaction energy study at the RI-MP2/def2-TZVP level; Archive file: atomic coordinates of the investigated stable complexes optimized at the RI-MP2/def2-TZVP level.
Author Contributions
Conceptualization, K.W., J.J.P., and A.J.; methodology, K.W., J.J.P., and A.J.; investigation, K.W., J.J.P.; writing—original draft preparation, K.W., J.J.P., and A.J.; writing—review and editing, K.W., J.J.P., and A.J.; visualization, K.W. and J.J.P.; supervision, A.J.; project administration, A.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in the article itself.
Acknowledgments
The authors gratefully acknowledge generous grants of computer time provided by the Academic Computing Centre Cyfronet-Kraków (Prometheus supercomputer, part of the PL-Grid infrastructure) as well as by the Poznań Supercomputing and Networking Center (PSNC). Additionally, A.J. and J.J.P. acknowledge the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk, accessed on 5 March 2022) for generous CPU time and facilities within the framework of the DECI-17 access programme.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AIM | Atoms In Molecules |
| BCP | Bond Critical Point |
| GGA | Generalized Gradient Approximation |
| HB | Hydrogen Bond |
| MD | Molecular Dynamics |
| NCI | Non-Covalent Interactions |
| PCB | Polychlorinated Biphenyl |
| POP | Persistent Organic Pollutant |
| RDG | Reduced Density Gradient |
| RI-MP2 | Second-order Møller-Plesset perturbation theory with Resolution of Identity acceleration |
| SAPT | Symmetry-Adapted Perturbation Theory |
References
- United Nations Stockholm Convention on Persistent Organic Pollutants. 2001. Available online: http://chm.pops.int/Portals/0/Repository/convention_text/UNEP-POPS-COP-CONVTEXT-FULL.English.PDF (accessed on 19 August 2022).
- The 12 Initial POPs under the Stockholm Convention. Available online: http://chm.pops.int/TheConvention/ThePOPs/The12InitialPOPs (accessed on 19 August 2022).
- Alkorta, I.; Elguero, J.; Frontera, A. Not Only Hydrogen Bonds: Other Noncovalent Interactions. Crystals 2020, 10, 180. [Google Scholar] [CrossRef]
- Erickson, M.D.; Kaley, R.G. Applications of polychlorinated biphenyls. Environ. Sci. Poll. Res. 2010, 18, 135–151. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Dong, J.; Huang, Z.; Liu, C.; Qiao, X.; Wang, X.; Zhao, X.; Zheng, B.; Shen, J. Polychlorinated biphenyls in the drinking water source of the Yangtze River: Characteristics and risk assessment. Environ. Sci. Eur. 2020, 32, 29. [Google Scholar] [CrossRef]
- Ergül, H.A.; Erdem, T.; Pelin, E.G.; Tonay, A.M.; Aksan, S.; Öztürk, B. Assessment of Pesticide, Dioxin-like Polychlorinated Biphenyl, and Polycyclic Aromatic Hydrocarbon Existence around Galindez Island, and Comparison with the Organic Pollution Bibliography of the Antarctic Peninsula. Sustainability 2022, 14, 3994. [Google Scholar] [CrossRef]
- European Food Safety Authority. Results of the monitoring of dioxin levels in food and feed. EFSA J. 2010, 8, 1385. [Google Scholar] [CrossRef]
- Marsan, E.S.; Bayse, C.A. Halogen Bonding Interactions of Polychlorinated Biphenyls and the Potential for Thyroid Disruption. Chem. Eur. J. 2020, 26, 5200–5207. [Google Scholar] [CrossRef] [PubMed]
- Datta, S.; Limpanuparb, T. Quantum Chemical Investigation of Polychlorinated Dibenzodioxins, Dibenzofurans and Biphenyls: Relative Stability and Planarity Analysis. Molecules 2020, 25, 5697. [Google Scholar] [CrossRef] [PubMed]
- Landeros-Rivera, B.; Jancik, V.; Moreno-Esparza, R.; Martínez Otero, D.; Hernández-Trujillo, J. Non-Covalent Interactions in the Biphenyl Crystal: Is the Planar Conformer a Transition State? Chem. Eur. J. 2021, 27, 11912–11918. [Google Scholar] [CrossRef] [PubMed]
- Chana, A.; Concejero, M.A.; de Frutos, M.; González, M.J.; Herradón, B. Computational Studies on Biphenyl Derivatives. Analysis of the Conformational Mobility, Molecular Electrostatic Potential, and Dipole Moment of Chlorinated Biphenyl: Searching for the Rationalization of the Selective Toxicity of Polychlorinated Biphenyls (PCBs). Chem. Res. Toxicol. 2002, 15, 1514–1526. [Google Scholar] [CrossRef]
- Ballschmiter, K.; Zell, M. Analysis of polychlorinated biphenyls (PCB) by glass capillary gas chromatography. Fresenius Zeit. Anal. Chem. 1980, 302, 20–31. [Google Scholar] [CrossRef]
- Gan, W.; Ge, Y.; Zhong, Y.; Yang, X. The reactions of chlorine dioxide with inorganic and organic compounds in water treatment: Kinetics and mechanisms. Environ. Sci.: Water Res. Technol. 2020, 6, 2287–2312. [Google Scholar] [CrossRef]
- Sorlini, S.; Collivignarelli, C. Trihalomethane formation during chemical oxidation with chlorine, chlorine dioxide and ozone of ten Italian natural waters. Desalination 2005, 176, 103–111. [Google Scholar] [CrossRef]
- Hofmann, R.; Andrews, R.C.; Ranger, G. Water quality and disinfection impact of ClO2 contamination by free chlorine: A case study. J. Environ. Eng. Sci. 2004, 3, 75–80. [Google Scholar] [CrossRef]
- Butcher, J.; Garvey, E.; Bierman, V. Equilibrium partitioning of PCB congeners in the water column: Field measurements from the Hudson River. Chemosphere 1998, 36, 3149–3166. [Google Scholar] [CrossRef]
- Axelman, J.; Broman, D.; Näf, C. Field Measurements of PCB Partitioning between Water and Planktonic Organisms: Influence of Growth, Particle Size, and Solute-Solvent Interactions. Environ. Sci. Technol. 1997, 31, 665–669. [Google Scholar] [CrossRef]
- Urbaniak, M.; Kiedrzyńska, E.; Wyrwicka, A.; Zieliński, M.; Mierzejewska, E.; Kiedrzyński, M.; Kannan, K.; Zalewski, M. An ecohydrological approach to the river contamination by PCDDs, PCDFs and dl-PCBs—concentrations, distribution and removal using phytoremediation techniques. Sci. Rep. 2019, 9, 19310. [Google Scholar] [CrossRef]
- Hawthorne, S.B.; Grabanski, C.B.; Miller, D.J.; Arp, H.P.H. Improving Predictability of Sediment-Porewater Partitioning Models using Trends Observed with PCB-Contaminated Field Sediments. Environ. Sci. Technol. 2011, 45, 7365–7371. [Google Scholar] [CrossRef]
- Di, P.; Chang, D.P.Y.; Dwyer, H.A. Modeling of Polychlorinated Biphenyl Removal from Contaminated Soil Using Steam. Environ. Sci. Technol. 2002, 36, 1845–1850. [Google Scholar] [CrossRef]
- Fang, F.; Chu, S.; Hong, C.S. Air-Water Henry’s Law Constants for PCB Congeners: Experimental Determination and Modeling of Structure-Property Relationship. Anal. Chem. 2006, 78, 5412–5418. [Google Scholar] [CrossRef]
- Chen, J.; Harner, T.; Schramm, K.W.; Quan, X.; Xue, X.; Kettrup, A. Quantitative relationships between molecular structures, environmental temperatures and octanol—Air partition coefficients of polychlorinated biphenyls. Comput. Biol. Chem. 2003, 27, 405–421. [Google Scholar] [CrossRef]
- Phillips, K.L.; Sandler, S.I.; Greene, R.W.; Di Toro, D.M. Quantum Mechanical Predictions of the Henry’s Law Constants and Their Temperature Dependence for the 209 Polychlorinated Biphenyl Congeners. Environ. Sci. Technol. 2008, 42, 8412–8418. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Zhang, Q.; Wang, H.; Wang, W. Quantum chemical investigation on the mechanism and kinetics of OH radical-initiated atmospheric oxidation of PCB-47. Chemosphere 2015, 133, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, I.; Weng, J.; Stromberg, A.J.; Hilt, J.Z.; Dziubla, T.D. Fluorescence based detection of polychlorinated biphenyls (PCBs) in water using hydrophobic interactions. Analyst 2019, 144, 677–684. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.Y.; Li, X.; Flor, S.; Ruiz, P.; Kruve, A.; Ludewig, G.; Lehmler, H.J. Metabolism of 3-Chlorobiphenyl (PCB 2) in a Human-Relevant Cell Line: Evidence of Dechlorinated Metabolites. Environ. Sci. Technol. 2022, 56, 12460–12472. [Google Scholar] [CrossRef] [PubMed]
- Bader, R. Atoms in Molecules: A Quantum Theory; International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Pastorczak, E.; Corminboeuf, C. Perspective: Found in translation: Quantum chemical tools for grasping non-covalent interactions. J. Chem. Phys. 2017, 146, 120901. [Google Scholar] [CrossRef] [PubMed]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
- Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analys is platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Hellweg, A.; Hättig, C.; Höfener, S.; Klopper, W. Optimized accurate auxiliary basis sets for RI-MP2 and RI-CC2 calculations for the atoms Rb to Rn. Theor. Chem. Acc. 2007, 117, 587–597. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general Amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Jakalian, A.; Bush, B.L.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. Method. J. Comput. Chem. 2000, 21, 132–146. [Google Scholar] [CrossRef]
- Case, D.; Aktulga, H.; Belfon, K.; Ben-Shalom, I.; Brozell, S.; Cerutti, D.; Cerutti, T.; Cisneros, G.A., III; Cruzeiro, V.; Darden, T.; et al. Amber 2021; University of California: San Francisco, CA, USA, 2021. [Google Scholar]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Boys, S.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Hohenstein, E.G.; Sherrill, C.D. Density fitting of intramonomer correlation effects in symmetry-adapted perturbation theory. J. Chem. Phys. 2010, 133, 014101. [Google Scholar] [CrossRef]
- Smith, D.G.A.; Burns, L.A.; Simmonett, A.C.; Parrish, R.M.; Schieber, M.C.; Galvelis, R.; Kraus, P.; Kruse, H.; Di Remigio, R.; Alenaizan, A.; et al. PSI4 1.4: Open-source software for high-throughput quantum chemistry. J. Chem. Phys. 2020, 152, 184108. [Google Scholar] [CrossRef]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Quantitative analysis of molecular surface based on improved Marching Tetrahedra algorithm. J. Molec. Graph. Model. 2012, 38, 314–323. [Google Scholar] [CrossRef] [PubMed]
- Bondi, A. van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Boto, R.A.; Contreras-García, J.; Tierny, J.; Piquemal, J.P. Interpretation of the reduced density gradient. Mol. Phys. 2015, 114, 1406–1414. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Koch, U.; Popelier, P.L.A. Characterization of C-H-O Hydrogen Bonds on the Basis of the Charge Density. J. Phys. Chem. 1995, 99, 9747–9754. [Google Scholar] [CrossRef]
- Feyereisen, M.W.; Feller, D.; Dixon, D.A. Hydrogen Bond Energy of the Water Dimer. J. Phys. Chem. 1996, 100, 2993–2997. [Google Scholar] [CrossRef]
- Ghosh, S.R.; Debnath, B.; Jana, A.D. Water dimer isomers: Interaction energies and electronic structure. J. Mol. Model. 2020, 26, 20. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).