A Multiscale Cost–Benefit Analysis of Digital Soil Mapping Methods for Sustainable Land Management
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Soil Sampling Data
2.2. Spatial Interpolation and Prediction Methods
2.3. Environmental Covariates
2.4. Cost–Benefit Analysis of Evaluated Soil Prediction Methods
3. Results
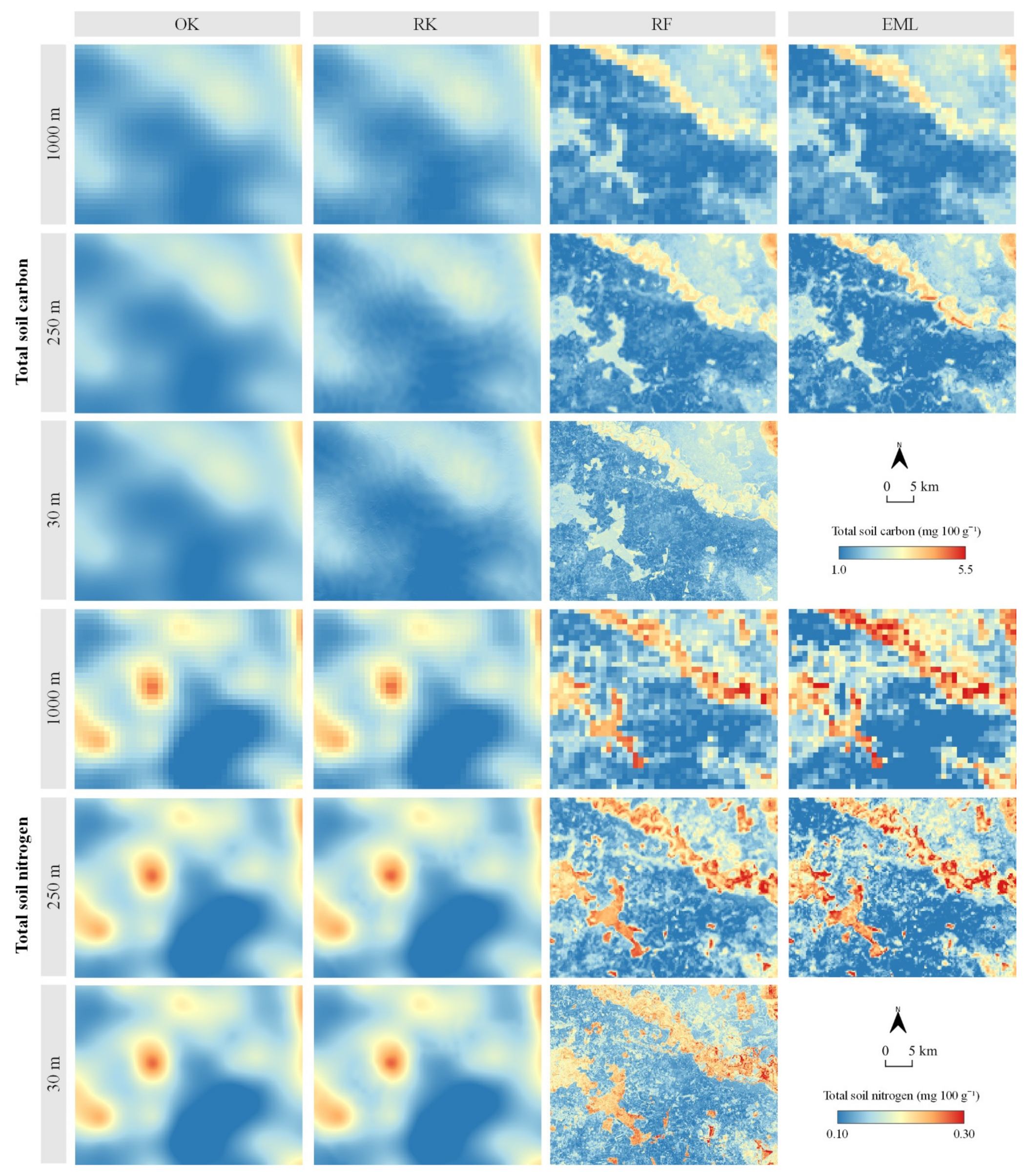
Predicted Soil TC and TN Values with Accuracy Assessment
4. Discussion
- As was the case in various applications of AHP in previous suitability and decision-making studies [69], the process of pairwise comparison was almost entirely subjective. While this property can be mitigated by the application of the objective, deterministic approach of the linear scaling standardization method, final cost–benefit values are still, to some degree, affected by the subjectivity of the user. An unsupervised classification of the cost–benefit components might be a more suitable solution for objective assessment, but the ranking of classes still has to be performed according to arbitrary, subjective criteria [11]. Nevertheless, the subjective component of the AHP could also be an advantage due to its flexibility relating to the needs of the specific study area and demands from a decision-making standpoint;
- Further optimization of the prediction process for the soil mapping in 30 m spatial resolution can be performed. This was successfully solved by prediction in blocks [46], but this approach prevents full automation of the procedure or includes further complexity of the prediction. In addition to RF, SVM, xgboost, nnet and cvglmnet implemented in the “landmap” package for EML, the addition of methods, such as RK [20] or geoadditive modeling and cubist [38], could ensure additional accuracy and robustness of the EML;
- Downscaling of the environmental covariates with lower native spatial resolution than 30 m inevitably includes a degree of data interpolation. While this approach could reduce the reliability of input data, downscaled data might actually be slightly more accurate when compared to the ground-truth data than those in native resolution [56]. For a more robust approach, negating the effects of downscaling, a two-scale EML approach is potentially more suitable [46]. In addition to soil mapping, this approach could enable accurate prediction of similar spatial components of the environment, such as erosion susceptibility [58], cropland suitability [56] and habitats of endangered flora species, in high spatial resolution.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cabrini, S.M.; Calcaterra, C.P. Modeling Economic-Environmental Decision Making for Agricultural Land Use in Argentinean Pampas. Agric. Syst. 2016, 143, 183–194. [Google Scholar] [CrossRef]
- Ellison, D.; Morris, C.E.; Locatelli, B.; Sheil, D.; Cohen, J.; Murdiyarso, D.; Gutierrez, V.; van Noordwijk, M.; Creed, I.F.; Pokorny, J.; et al. Trees, Forests and Water: Cool Insights for a Hot World. Glob. Environ. Change 2017, 43, 51–61. [Google Scholar] [CrossRef]
- Radočaj, D.; Jurišić, M.; Gašparović, M. A Wildfire Growth Prediction and Evaluation Approach Using Landsat and MODIS Data. J. Environ. Manag. 2022, 304, 114351. [Google Scholar] [CrossRef]
- Pelorosso, R.; Gobattoni, F.; Geri, F.; Monaco, R.; Leone, A. Evaluation of Ecosystem Services Related to Bio-Energy Landscape Connectivity (BELC) for Land Use Decision Making across Different Planning Scales. Ecol. Indic. 2016, 61, 114–129. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. Digital Soil Mapping: A Brief History and Some Lessons. Geoderma 2016, 264, 301–311. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.M.; Heuvelink, G.B.M.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global Gridded Soil Information Based on Machine Learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef]
- McBratney, A.B.; Mendonça Santos, M.L.; Minasny, B. On Digital Soil Mapping. Geoderma 2003, 117, 3–52. [Google Scholar] [CrossRef]
- Meena, V.S.; Mondal, T.; Pandey, B.M.; Mukherjee, A.; Yadav, R.P.; Choudhary, M.; Singh, S.; Bisht, J.K.; Pattanayak, A. Land Use Changes: Strategies to Improve Soil Carbon and Nitrogen Storage Pattern in the Mid-Himalaya Ecosystem, India. Geoderma 2018, 321, 69–78. [Google Scholar] [CrossRef]
- Pellegrini, A.F.A.; Ahlström, A.; Hobbie, S.E.; Reich, P.B.; Nieradzik, L.P.; Staver, A.C.; Scharenbroch, B.C.; Jumpponen, A.; Anderegg, W.R.L.; Randerson, J.T.; et al. Fire Frequency Drives Decadal Changes in Soil Carbon and Nitrogen and Ecosystem Productivity. Nature 2018, 553, 194–198. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Hu, X.; Ma, J.; Ye, J.; Sun, W.; Wang, Q.; Lin, H. Effects of Long-Term Organic Material Applications on Soil Carbon and Nitrogen Fractions in Paddy Fields. Soil Tillage Res. 2020, 196, 104483. [Google Scholar] [CrossRef]
- Radočaj, D.; Jurišić, M.; Antonić, O. Determination of Soil C:N Suitability Zones for Organic Farming Using an Unsupervised Classification in Eastern Croatia. Ecol. Indic. 2021, 123, 107382. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Stein, A. A Generic Framework for Spatial Prediction of Soil Variables Based on Regression-Kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Shen, Q.; Wang, Y.; Wang, X.; Liu, X.; Zhang, X.; Zhang, S. Comparing Interpolation Methods to Predict Soil Total Phosphorus in the Mollisol Area of Northeast China. Catena 2019, 174, 59–72. [Google Scholar] [CrossRef]
- Radočaj, D.; Jurišić, M.; Gašparović, M. The Role of Remote Sensing Data and Methods in a Modern Approach to Fertilization in Precision Agriculture. Remote Sens. 2022, 14, 778. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. A Tutorial Guide to Geostatistics: Computing and Modelling Variograms and Kriging. Catena 2014, 113, 56–69. [Google Scholar] [CrossRef]
- Bogunovic, I.; Kisic, I.; Mesic, M.; Percin, A.; Zgorelec, Z.; Bilandžija, D.; Jonjic, A.; Pereira, P. Reducing Sampling Intensity in Order to Investigate Spatial Variability of Soil PH, Organic Matter and Available Phosphorus Using Co-Kriging Techniques. A Case Study of Acid Soils in Eastern Croatia. Arch. Agron. Soil Sci. 2017, 63, 1852–1863. [Google Scholar] [CrossRef]
- Gia Pham, T.; Kappas, M.; Van Huynh, C.; Hoang Khanh Nguyen, L. Application of Ordinary Kriging and Regression Kriging Method for Soil Properties Mapping in Hilly Region of Central Vietnam. ISPRS Int. J. Geo Inf. 2019, 8, 147. [Google Scholar] [CrossRef]
- Radočaj, D.; Jug, I.; Vukadinović, V.; Jurišić, M.; Gašparović, M. The Effect of Soil Sampling Density and Spatial Autocorrelation on Interpolation Accuracy of Chemical Soil Properties in Arable Cropland. Agronomy 2021, 11, 2430. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists. Geoscience: Canberra, Australia, 2008. [Google Scholar]
- Mishra, U.; Gautam, S.; Riley, W.J.; Hoffman, F.M. Ensemble Machine Learning Approach Improves Predicted Spatial Variation of Surface Soil Organic Carbon Stocks in Data-Limited Northern Circumpolar Region. Front. Big Data 2020, 3, 528441. [Google Scholar] [CrossRef] [PubMed]
- Song, J.J.; Kwon, S.; Lee, G. Incorporation of Parameter Uncertainty into Spatial Interpolation Using Bayesian Trans-Gaussian Kriging. Adv. Atmos. Sci. 2015, 32, 413–423. [Google Scholar] [CrossRef]
- Sahu, B.; Ghosh, A.K. Seema Deterministic and Geostatistical Models for Predicting Soil Organic Carbon in a 60 Ha Farm on Inceptisol in Varanasi, India. Geoderma Reg. 2021, 26, e00413. [Google Scholar] [CrossRef]
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; R Core Team. Package ‘caret’. R J. 2020, 223, 7. [Google Scholar]
- Wright, M.N.; Ziegler, A. Ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. arXiv 2015, arXiv:150804409. [Google Scholar] [CrossRef]
- Hengl, T.; de Jesus, J.M.; MacMillan, R.A.; Batjes, N.H.; Heuvelink, G.B.M.; Ribeiro, E.; Samuel-Rosa, A.; Kempen, B.; Leenaars, J.G.B.; Walsh, M.G.; et al. SoilGrids1km—Global Soil Information Based on Automated Mapping. PLoS ONE 2014, 9, e105992. [Google Scholar] [CrossRef]
- Chen, S.; Arrouays, D.; Leatitia Mulder, V.; Poggio, L.; Minasny, B.; Roudier, P.; Libohova, Z.; Lagacherie, P.; Shi, Z.; Hannam, J.; et al. Digital Mapping of GlobalSoilMap Soil Properties at a Broad Scale: A Review. Geoderma 2022, 409, 115567. [Google Scholar] [CrossRef]
- User Guides-Sentinel-2 MSI-Sentinel Online-Sentinel Online. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-2-msi (accessed on 10 September 2022).
- Landsat 8 Data Users Handbook|U.S. Geological Survey. Available online: https://www.usgs.gov/media/files/landsat-8-data-users-handbook (accessed on 10 September 2022).
- User Guides-Sentinel-1 SAR-Sentinel Online-Sentinel Online. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-1-sar (accessed on 10 September 2022).
- User Guides-Sentinel-3 OLCI-Sentinel Online-Sentinel Online. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-3-olci (accessed on 10 September 2022).
- Landsat 9 Data Users Handbook|U.S. Geological Survey. Available online: https://www.usgs.gov/media/files/landsat-9-data-users-handbook (accessed on 10 September 2022).
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Climatologies at High Resolution for the Earth’s Land Surface Areas. Sci. Data 2017, 4, 170122. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-Km Spatial Resolution Climate Surfaces for Global Land Areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- EU-DEM v1.1—Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/imagery-in-situ/eu-dem/eu-dem-v1.1 (accessed on 21 April 2021).
- Wulder, M.A.; Loveland, T.R.; Roy, D.P.; Crawford, C.J.; Masek, J.G.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Belward, A.S.; Cohen, W.B.; et al. Current Status of Landsat Program, Science, and Applications. Remote Sens. Environ. 2019, 225, 127–147. [Google Scholar] [CrossRef]
- Phiri, D.; Simwanda, M.; Salekin, S.; Nyirenda, V.R.; Murayama, Y.; Ranagalage, M. Sentinel-2 Data for Land Cover/Use Mapping: A Review. Remote Sens. 2020, 12, 2291. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Baltensweiler, A.; Walthert, L.; Hanewinkel, M.; Zimmermann, S.; Nussbaum, M. Machine Learning Based Soil Maps for a Wide Range of Soil Properties for the Forested Area of Switzerland. Geoderma Reg. 2021, 27, e00437. [Google Scholar] [CrossRef]
- Nussbaum, M.; Spiess, K.; Baltensweiler, A.; Grob, U.; Keller, A.; Greiner, L.; Schaepman, M.E.; Papritz, A. Evaluation of Digital Soil Mapping Approaches with Large Sets of Environmental Covariates. SOIL 2018, 4, 1–22. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random Forest as a Generic Framework for Predictive Modeling of Spatial and Spatio-Temporal Variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef]
- Belgiu, M.; Dragut, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. Isprs J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- CORINE Land Cover User Manual. Available online: https://land.copernicus.eu/user-corner/technical-library/clc-product-user-manual (accessed on 10 September 2022).
- Data Europa, 2021. Changes in Soil Carbon Stocks and Calculation of Trends in Total Nitrogen and Organic Carbon in Soil and C: N Ratios. Available online: Https://Data.Europa.Eu/Data/Datasets/Zaliha-Ugljika-u-Tlu-Izracun-Trendova-Ukupnog-Dusika-i-Organskog-Ugljika-Te-Odnosa-c-n?Locale=en (accessed on 16 February 2022).
- Attorre, F.; Alfo, M.; De Sanctis, M.; Francesconi, F.; Bruno, F. Comparison of Interpolation Methods for Mapping Climatic and Bioclimatic Variables at Regional Scale. Int. J. Climatol. 2007, 27, 1825–1843. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable Geostatistics in S: The Gstat Package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Hengl, T.; Miller, M.A.E.; Križan, J.; Shepherd, K.D.; Sila, A.; Kilibarda, M.; Antonijević, O.; Glušica, L.; Dobermann, A.; Haefele, S.M.; et al. African Soil Properties and Nutrients Mapped at 30 m Spatial Resolution Using Two-Scale Ensemble Machine Learning. Sci. Rep. 2021, 11, 6130. [Google Scholar] [CrossRef]
- Seo, D.-J. Conditional Bias-Penalized Kriging (CBPK). Stoch. Environ. Res. Risk Assess. 2013, 27, 43–58. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Rossiter, D.G. About Regression-Kriging: From Equations to Case Studies. Comput. Geosci. 2007, 33, 1301–1315. [Google Scholar] [CrossRef]
- Santra, P.; Das, B.S.; Chakravarty, D. Spatial Prediction of Soil Properties in a Watershed Scale through Maximum Likelihood Approach. Environ. Earth Sci. 2012, 65, 2051–2061. [Google Scholar] [CrossRef]
- Hengl, T.; MacMillan, R.A. Predictive Soil Mapping with R; Lulu.com: Morrisville, NC, USA, 2019; ISBN 978-0-359-30635-0. [Google Scholar]
- Poggio, L.; de Sousa, L.M.; Batjes, N.H.; Heuvelink, G.B.M.; Kempen, B.; Ribeiro, E.; Rossiter, D. SoilGrids 2.0: Producing Soil Information for the Globe with Quantified Spatial Uncertainty. SOIL 2021, 7, 217–240. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.; Irons, J.R.; Johnson, D.M.; Kennedy, R.; et al. Landsat-8: Science and Product Vision for Terrestrial Global Change Research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Büttner, G. CORINE Land Cover and Land Cover Change Products. In Land Use and Land Cover Mapping in Europe: Practices & Trends; Manakos, I., Braun, M., Eds.; Remote Sensing and Digital Image Processing; Springer: Dordrecht, The Netherlands, 2014; pp. 55–74. ISBN 978-94-007-7969-3. [Google Scholar]
- Hengl, T. Finding the Right Pixel Size. Comput. Geosci. 2006, 32, 1283–1298. [Google Scholar] [CrossRef]
- Radočaj, D.; Jurišić, M.; Gašparović, M.; Plaščak, I.; Antonić, O. Cropland Suitability Assessment Using Satellite-Based Biophysical Vegetation Properties and Machine Learning. Agronomy 2021, 11, 1620. [Google Scholar] [CrossRef]
- Dedeoğlu, M.; Dengiz, O. Generating of Land Suitability Index for Wheat with Hybrid System Aproach Using AHP and GIS. Comput. Electron. Agric. 2019, 167, 105062. [Google Scholar] [CrossRef]
- Domazetović, F.; Šiljeg, A.; Lončar, N.; Marić, I. Development of Automated Multicriteria GIS Analysis of Gully Erosion Susceptibility. Appl. Geogr. 2019, 112, 102083. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with the Analytic Hierarchy Process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
- Saaty, T.L.; Ozdemir, M.S. Why the Magic Number Seven plus or Minus Two. Math. Comput. Model. 2003, 38, 233–244. [Google Scholar] [CrossRef]
- Dong, W.; Wu, T.; Luo, J.; Sun, Y.; Xia, L. Land Parcel-Based Digital Soil Mapping of Soil Nutrient Properties in an Alluvial-Diluvia Plain Agricultural Area in China. Geoderma 2019, 340, 234–248. [Google Scholar] [CrossRef]
- Radočaj, D.; Jurišić, M.; Gašparović, M.; Plaščak, I. Optimal Soybean (Glycine Max L.) Land Suitability Using GIS-Based Multicriteria Analysis and Sentinel-2 Multitemporal Images. Remote Sens. 2020, 12, 1463. [Google Scholar] [CrossRef]
- Panday, D.; Maharjan, B.; Chalise, D.; Shrestha, R.K.; Twanabasu, B. Digital Soil Mapping in the Bara District of Nepal Using Kriging Tool in ArcGIS. PLoS ONE 2018, 13, e0206350. [Google Scholar] [CrossRef]
- Meng, Y.; Cave, M.; Zhang, C. Comparison of Methods for Addressing the Point-to-Area Data Transformation to Make Data Suitable for Environmental, Health and Socio-Economic Studies. Sci. Total Environ. 2019, 689, 797–807. [Google Scholar] [CrossRef]
- Fu, C.; Zhang, H.; Tu, C.; Li, L.; Luo, Y. Geostatistical Interpolation of Available Copper in Orchard Soil as Influenced by Planting Duration. Environ. Sci. Pollut. Res. 2018, 25, 52–63. [Google Scholar] [CrossRef]
- Mondejar, J.P.; Tongco, A.F. Estimating Topsoil Texture Fractions by Digital Soil Mapping-a Response to the Long Outdated Soil Map in the Philippines. Sustain. Environ. Res. 2019, 29, 31. [Google Scholar] [CrossRef]
- Gavilán-Acuña, G.; Olmedo, G.F.; Mena-Quijada, P.; Guevara, M.; Barría-Knopf, B.; Watt, M.S. Reducing the Uncertainty of Radiata Pine Site Index Maps Using an Spatial Ensemble of Machine Learning Models. Forests 2021, 12, 77. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Boehner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Ren, C.; Li, Z.; Zhang, H. Integrated Multi-Objective Stochastic Fuzzy Programming and AHP Method for Agricultural Water and Land Optimization Allocation under Multiple Uncertainties. J. Clean. Prod. 2019, 210, 12–24. [Google Scholar] [CrossRef]
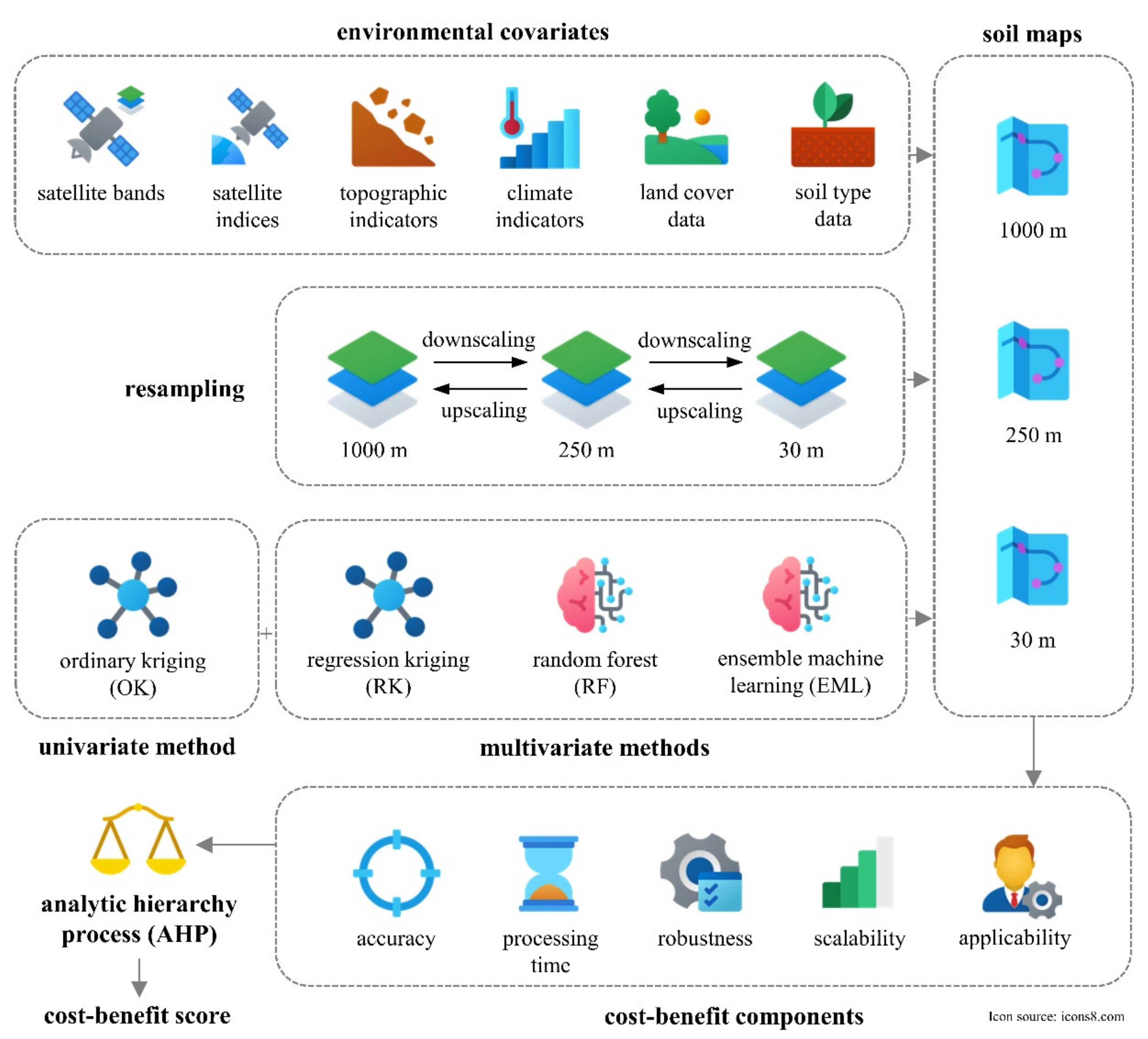



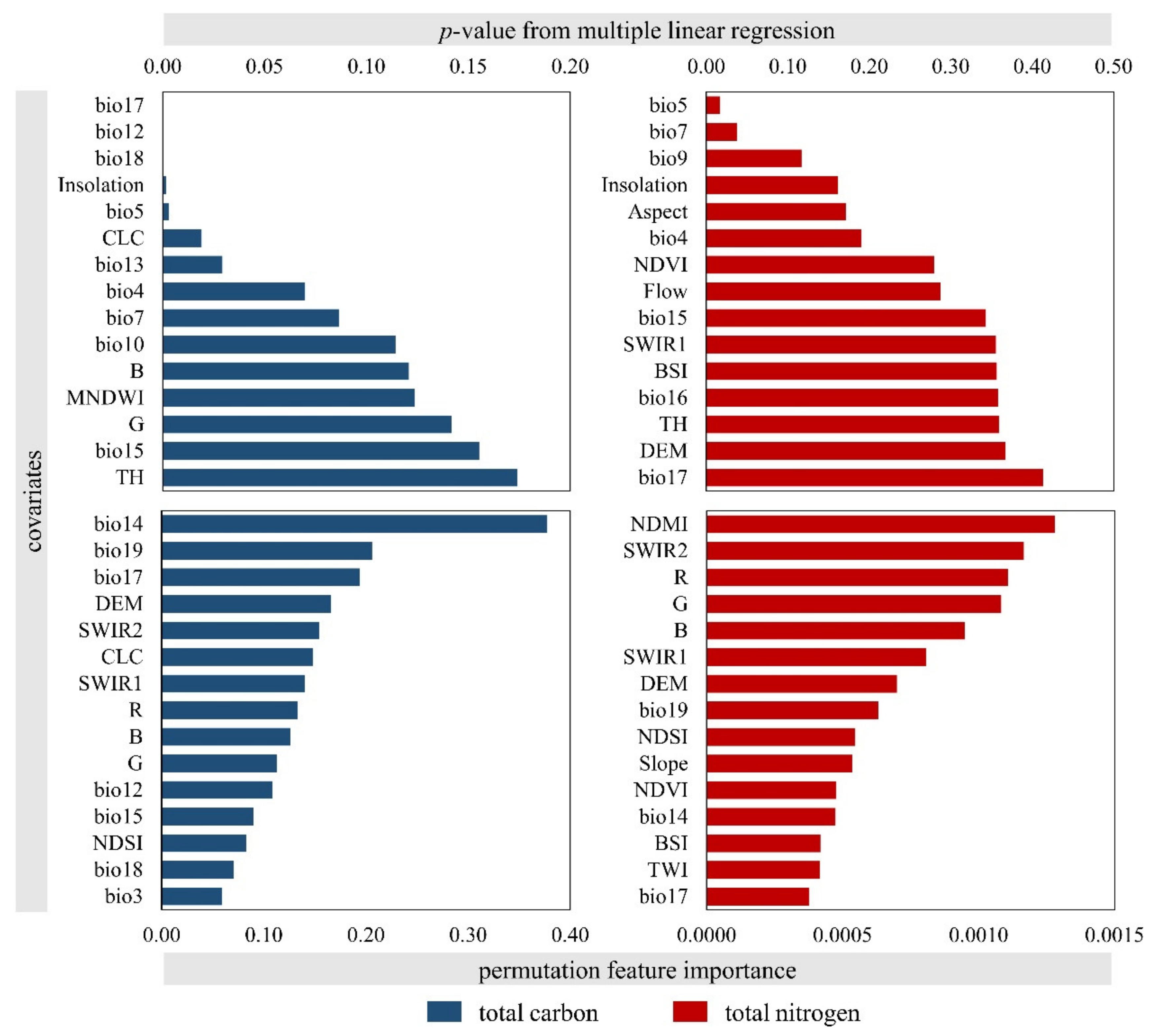
| Covariates | Description (Abbreviations) | Data Source (Native Spatial Resolution) | Reference |
|---|---|---|---|
| satellite multispectral bands | blue, green, red, near-infrared, shortwave infrared and thermal satellite multispectral bands (B, G, R, NIR, SWIR1, SWIR2, TH) | Landsat 8 (30 m) | [52] |
| satellite multispectral indices | vegetation (NDVI, EVI), soil (NDSI, BSI) and water (MNDWI, NDMI) spectral indices | Landsat 8 (30 m) | [52] |
| topographic indicators | digital elevation model (DEM), terrain morphometric (slope, aspect), hydrological (TWI, flow accumulation) and lightning parameters (insolation) | SRTM 1 arc-second DEM (30 m) | [53] |
| climate indicators | bioclimatic variables derived from the monthly air temperature and precipitation values (bio01–bio19) | CHELSA (1000 m) | [32] |
| land-cover data | CORINE Land Cover 2012 classes (CLC) | CORINE 2012 (vector) | [54] |
| soil-type data | soil-type classes based on the basic pedologic map of Croatia (soil map) | CAEN (vector) | [43] |
| Criterion Name | Description |
|---|---|
| “accuracy” | prediction accuracy of soil parameters at unknown locations |
| “time” | processing time required for computing of predicted soil parameters after preprocessing |
| “robustness” | resistance to properties of input soil sample data, including data normality, stationarity, sample count and spatial autocorrelation |
| “scalability” | ability of prediction method to improve accuracy and retain local heterogeneity on larger scales |
| “applicability” | the number of necessary steps in the preprocessing, including downloading, reprojection and resampling of environmental covariates |
| Soil Property | n | Mean (mg 100 g–1) | CV | Shapiro–Wilk Test | Moran’s I | |
|---|---|---|---|---|---|---|
| W-Value | p-Value | |||||
| TC | 178 | 2.161 | 0.671 | 0.878 | <0.001 | 0.536 |
| TN | 178 | 0.164 | 0.563 | 0.871 | <0.001 | 0.041 |
| Soil Property | Spatial Resolution | Value | OK | RK | RF | EML |
|---|---|---|---|---|---|---|
| TC | 1000 m | R2 | 0.537 | 0.527 | 0.718 | 0.748 |
| RMSE | 0.984 | 0.994 | 0.768 | 0.521 | ||
| NRMSE | 0.455 | 0.460 | 0.355 | 0.241 | ||
| 250 m | R2 | 0.537 | 0.527 | 0.722 | 0.848 | |
| RMSE | 0.984 | 0.994 | 0.763 | 0.319 | ||
| NRMSE | 0.455 | 0.460 | 0.353 | 0.148 | ||
| 30 m | R2 | 0.537 | 0.527 | 0.719 | - | |
| RMSE | 0.984 | 0.994 | 0.767 | - | ||
| NRMSE | 0.455 | 0.460 | 0.355 | - | ||
| TN | 1000 m | R2 | 0.189 | 0.174 | 0.331 | 0.498 |
| RMSE | 0.079 | 0.080 | 0.072 | 0.062 | ||
| NRMSE | 0.480 | 0.486 | 0.437 | 0.381 | ||
| 250 m | R2 | 0.189 | 0.174 | 0.327 | 0.626 | |
| RMSE | 0.079 | 0.080 | 0.072 | 0.054 | ||
| NRMSE | 0.480 | 0.486 | 0.438 | 0.328 | ||
| 30 m | R2 | 0.189 | 0.174 | 0.318 | - | |
| RMSE | 0.079 | 0.080 | 0.072 | - | ||
| NRMSE | 0.480 | 0.486 | 0.441 | - |
| Hardware | Soil Property | Spatial Resolution | Processing Time (ms) | |||
|---|---|---|---|---|---|---|
| OK | RK | RF | EML | |||
| Workstation | TC | 1000 m | 5329 | 5241 | 983 | 11,856 |
| 250 m | 10,919 | 9213 | 6947 | 40,276 | ||
| 30 m | 363,380 | 368,729 | 780,941 | - | ||
| TN | 1000 m | 4932 | 5120 | 1000 | 11,897 | |
| 250 m | 11,121 | 10,992 | 6672 | 40,574 | ||
| 30 m | 361,700 | 364,715 | 739,155 | - | ||
| Laptop | TC | 1000 m | 6127 | 5690 | 957 | 11,441 |
| 250 m | 11,322 | 10,607 | 8720 | 40,085 | ||
| 30 m | 381,159 | 379,951 | - | - | ||
| TN | 1000 m | 5715 | 5537 | 1054 | 14,739 | |
| 250 m | 11,430 | 9842 | 10,606 | 36,431 | ||
| 30 m | 378,083 | 376,846 | - | - | ||
| Criterion Name | Accuracy | Time | Robustness | Scalability | Applicability | Weight |
|---|---|---|---|---|---|---|
| accuracy | 1 | 3 | 4 | 6 | 8 | 0.493 |
| time | 1 | 2 | 4 | 5 | 0.232 | |
| robustness | 1 | 3 | 4 | 0.153 | ||
| scalability | 1 | 3 | 0.079 | |||
| applicability | 1 | 0.042 |
| Method | Standardized Values | Cost–Benefit Score | ||||
|---|---|---|---|---|---|---|
| Accuracy | Time | Robustness | Scalability | Applicability | ||
| OK | 0.032 | 0.898 | 0.272 | 0.000 | 1.000 | 0.308 |
| RK | 0.000 | 0.936 | 0.243 | 0.000 | 0.000 | 0.255 |
| RF | 0.455 | 1.000 | 0.000 | 0.026 | 0.500 | 0.480 |
| EML | 1.000 | 0.000 | 1.000 | 1.000 | 0.500 | 0.747 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radočaj, D.; Jurišić, M.; Antonić, O.; Šiljeg, A.; Cukrov, N.; Rapčan, I.; Plaščak, I.; Gašparović, M. A Multiscale Cost–Benefit Analysis of Digital Soil Mapping Methods for Sustainable Land Management. Sustainability 2022, 14, 12170. https://doi.org/10.3390/su141912170
Radočaj D, Jurišić M, Antonić O, Šiljeg A, Cukrov N, Rapčan I, Plaščak I, Gašparović M. A Multiscale Cost–Benefit Analysis of Digital Soil Mapping Methods for Sustainable Land Management. Sustainability. 2022; 14(19):12170. https://doi.org/10.3390/su141912170
Chicago/Turabian StyleRadočaj, Dorijan, Mladen Jurišić, Oleg Antonić, Ante Šiljeg, Neven Cukrov, Irena Rapčan, Ivan Plaščak, and Mateo Gašparović. 2022. "A Multiscale Cost–Benefit Analysis of Digital Soil Mapping Methods for Sustainable Land Management" Sustainability 14, no. 19: 12170. https://doi.org/10.3390/su141912170
APA StyleRadočaj, D., Jurišić, M., Antonić, O., Šiljeg, A., Cukrov, N., Rapčan, I., Plaščak, I., & Gašparović, M. (2022). A Multiscale Cost–Benefit Analysis of Digital Soil Mapping Methods for Sustainable Land Management. Sustainability, 14(19), 12170. https://doi.org/10.3390/su141912170












