Research on Automatic Driving Trajectory Planning and Tracking Control Based on Improvement of the Artificial Potential Field Method
Abstract
:1. Introduction
2. Trajectory Planning Algorithm Based on Improvement of the Artificial Potential Field Method
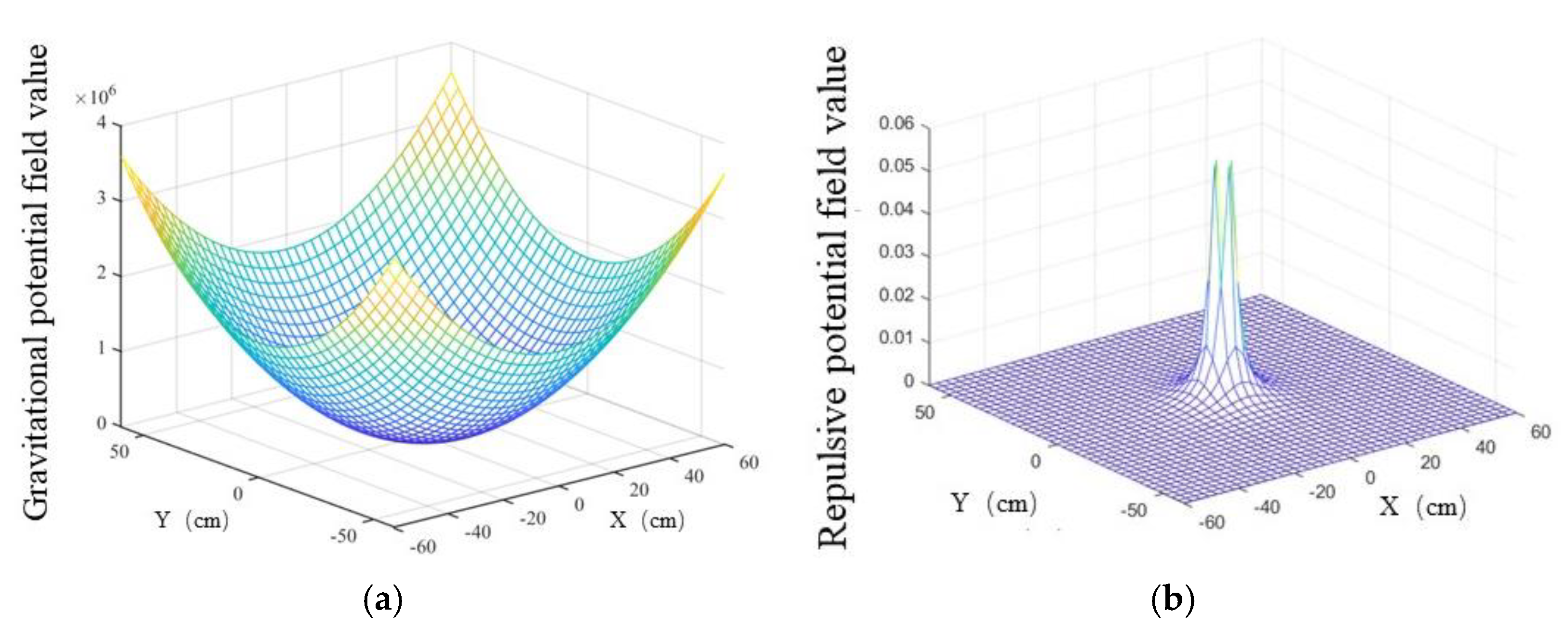
2.1. Traditional Artificial Potential Field Method
2.1.1. Gravitational Field
- is the gravitational potential field at the target point;
- is the gain coefficient of the gravitational potential field, which is positive real number;
- is the position vector of autonomous vehicle;
- is the target position vector of the autonomous vehicle.
2.1.2. Repulsive Force Field
- is the repulsive force field of the obstacle vehicle;
- is the gain coefficient of the repulsive potential field, and is a positive real number;
- is the shortest distance in space between the car and the obstacle vehicle;
- is the maximum range of impact that an obstacle vehicle can have.
2.2. Improved Artificial Potential Field Method
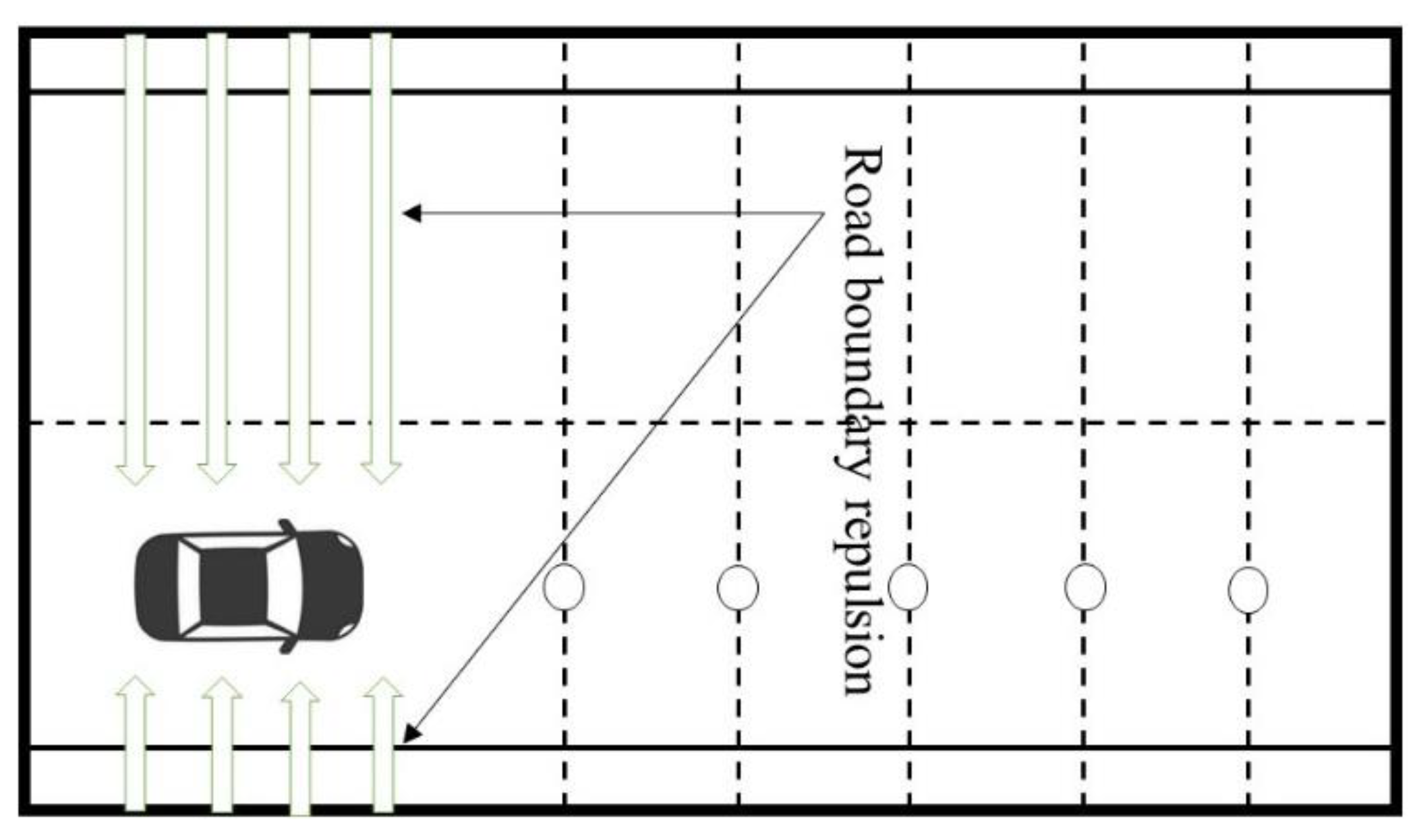
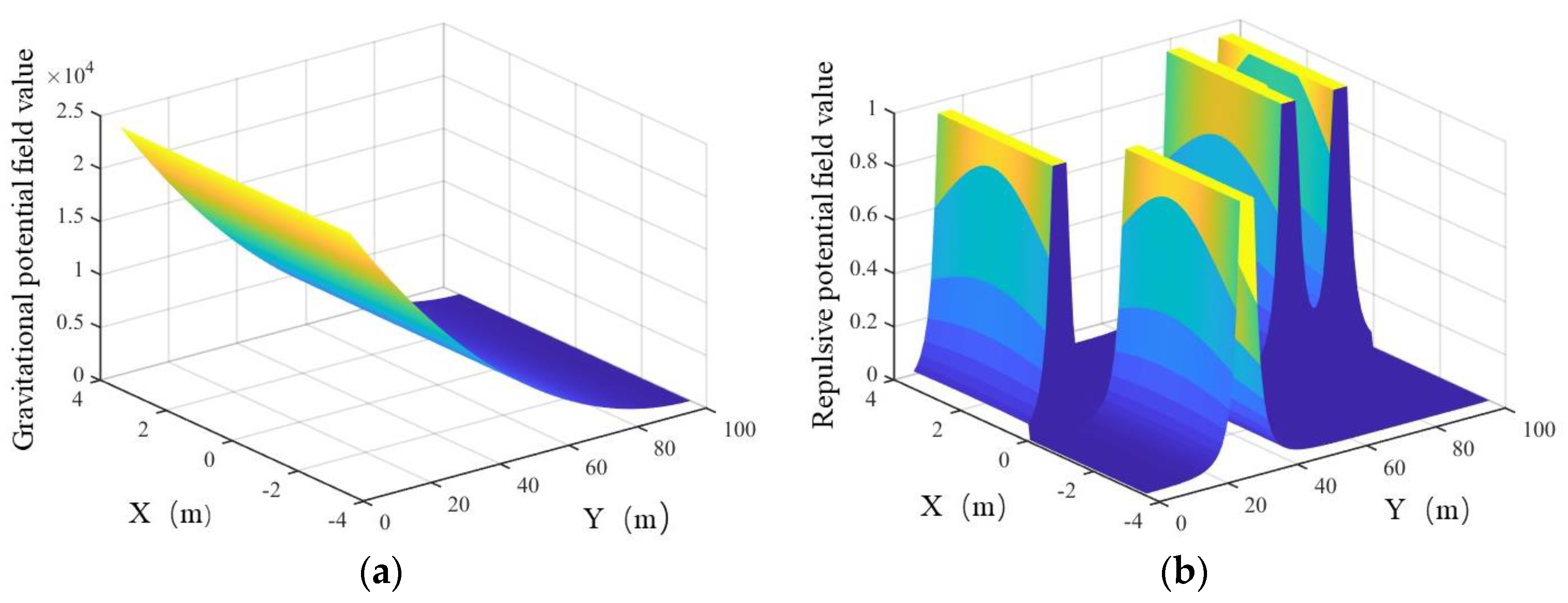
2.2.1. Improved Repulsive Potential Field
- is the real-time coordinate point of autonomous driving vehicle;
- is the coordinates of the target point;
- is the radius of the autonomous driving vehicle.
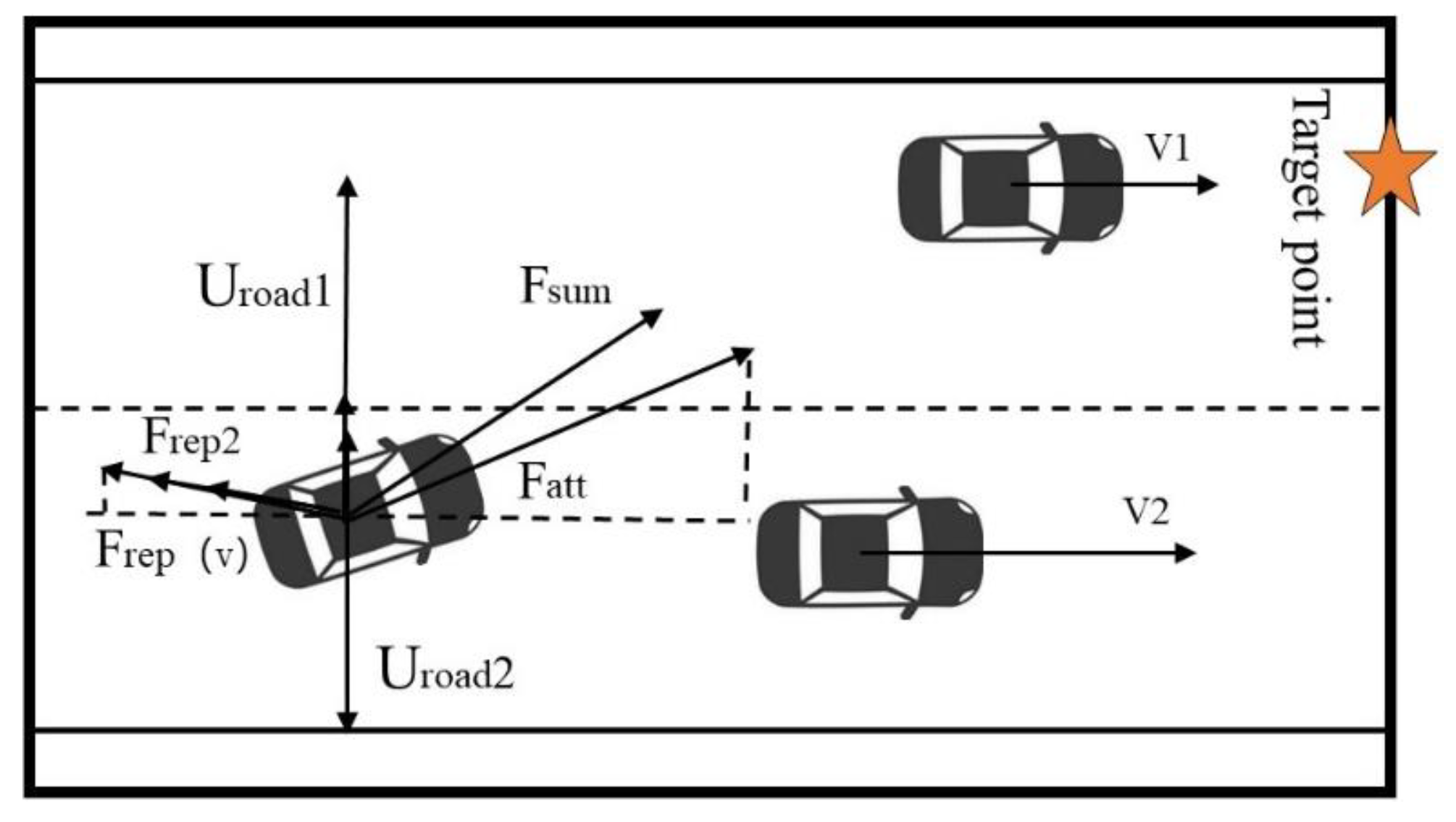
2.2.2. Establish Velocity Repulsion Field and Acceleration Repulsion Field
- is the gain coefficient of velocity repulsion field;
- is the controlled vehicle speed;
- is the velocity of the obstacle;
- is gravitational velocity component;
- is the repulsive velocity component;
- is the quality of the car.
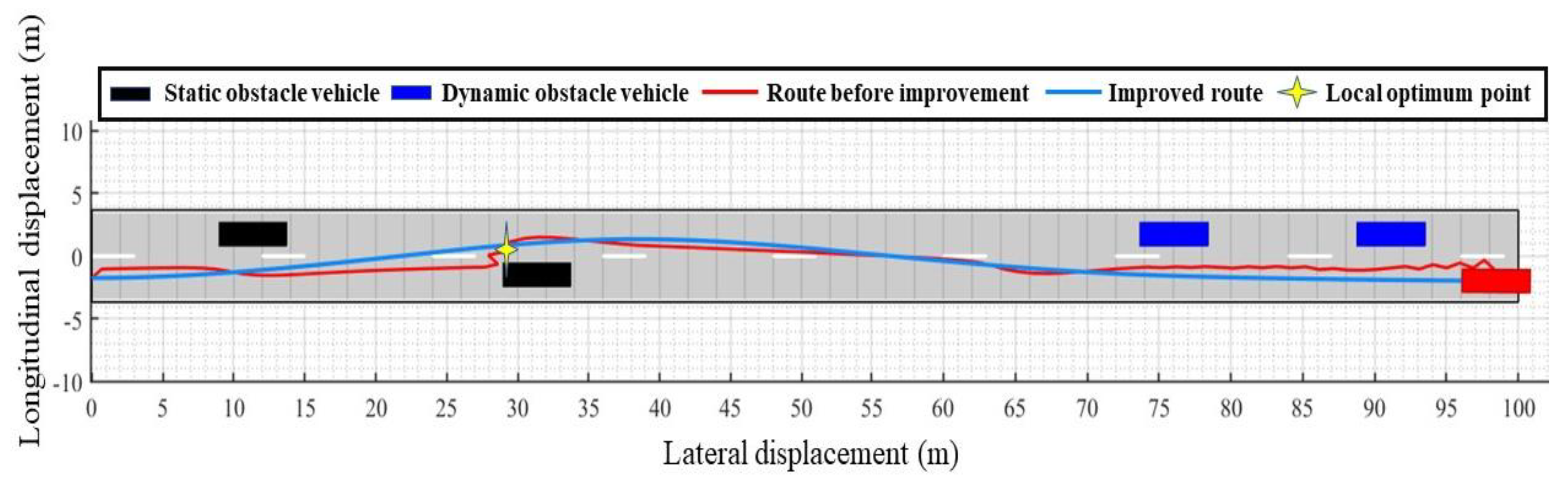
2.3. Trajectory Planning Analysis of Invasive Weed Algorithm
- It is necessary to determine whether the car has reached the target point;
- It is necessary to determine whether the vehicle has fallen into the local optimal solution trap at the current moment;
- Repulsion force is redistributed by selecting the optimal subdestination;
- It is necessary to determine whether the local optimal solution trap has been avoided at the current moment.
- is the destination;
- is the optimal sub-destination;
- is the local optimal solution point;
- is the initial position after escaping the local optimal solution.
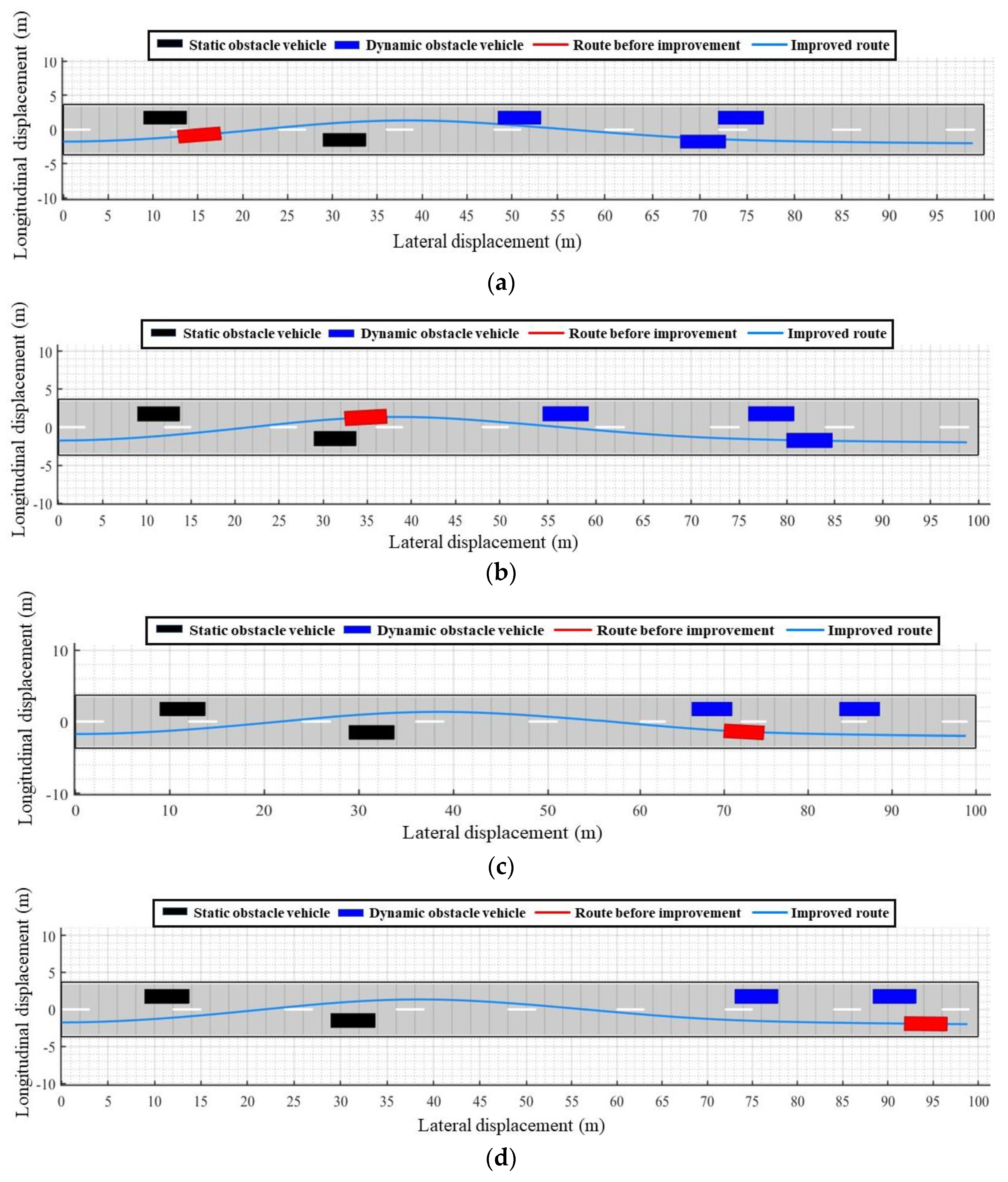
2.4. Simulation Experiment of Improved Artificial Potential Field Method
3. Vehicle Dynamics Model
3.1. Vehicle 3-DOF Dynamics Model
- The driving condition of the environmental road surface is superior, the vehicle only undergoes planar two-dimensional movement parallel to the road surface;
- The vehicle is rigid, and there is no consideration of the impact of the vehicle suspension system;
- The vehicle turns with the front wheel, and the angle changes of the left and the right wheels remain the same;
- The transverse and longitudinal coupling relationship of automobile tires is not considered;
- The influence of aerodynamics is ignored;
- The situation of vehicle load transfer is not considered;
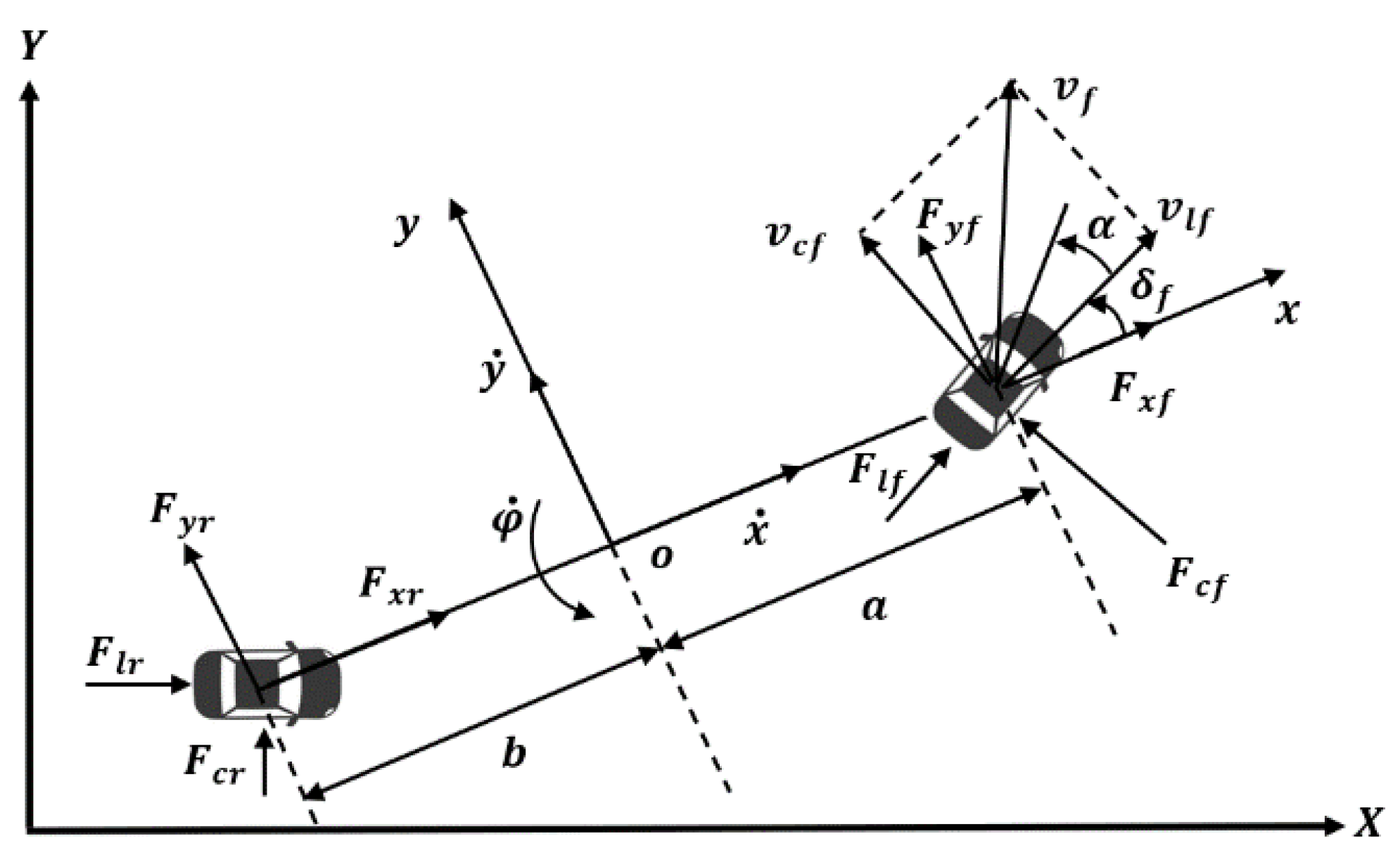
- Derived from the simplified model, the monorail model of the vehicle is established, and the stress analysis is shown in Figure 8.
- is the vehicle’s own coordinate system;
- is the ground coordinate system;
- -axial upward is the positive direction, and the judgment rule is the right-hand rule.
- is the vehicle quality;
- is the distance from the vehicle center of mass to the front axle;
- is the distance from the vehicle center of mass to the rear axle;
- is the moment of inertia of the z-axis;
- is the yaw rate;
- is the X-axis component force of front and rear tires;
- is the y-axis component force of front and rear tires;
- is the longitudinal force of front and rear tires;
- is the lateral force of front and rear tires;
- is the front and rear wheel angle.
- is the positive force on the tire;
- is the lateral force on the tire.
- is the state quantity of nonlinear system;
- is the control quantity of nonlinear system;
- is the output of the nonlinear system.
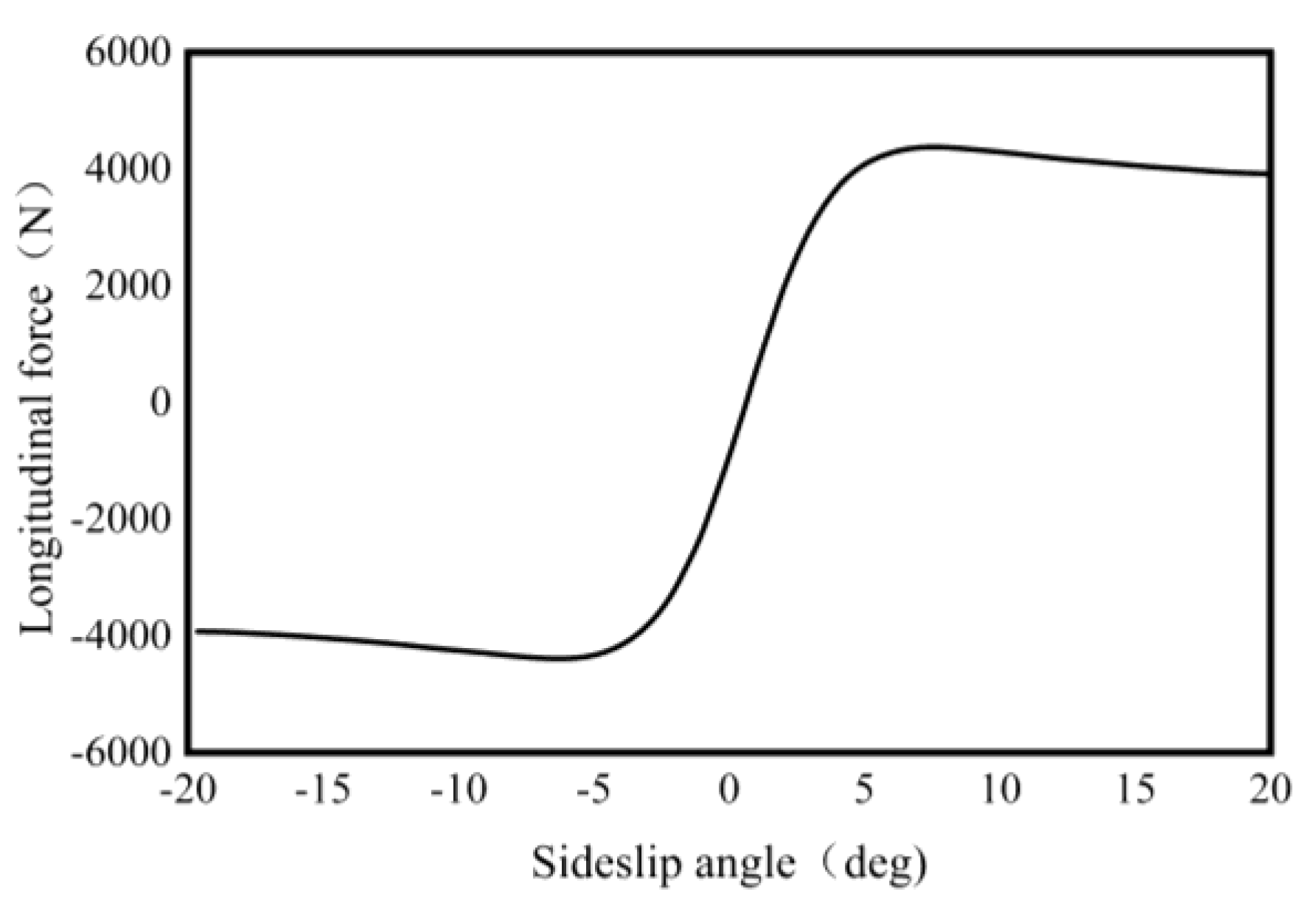
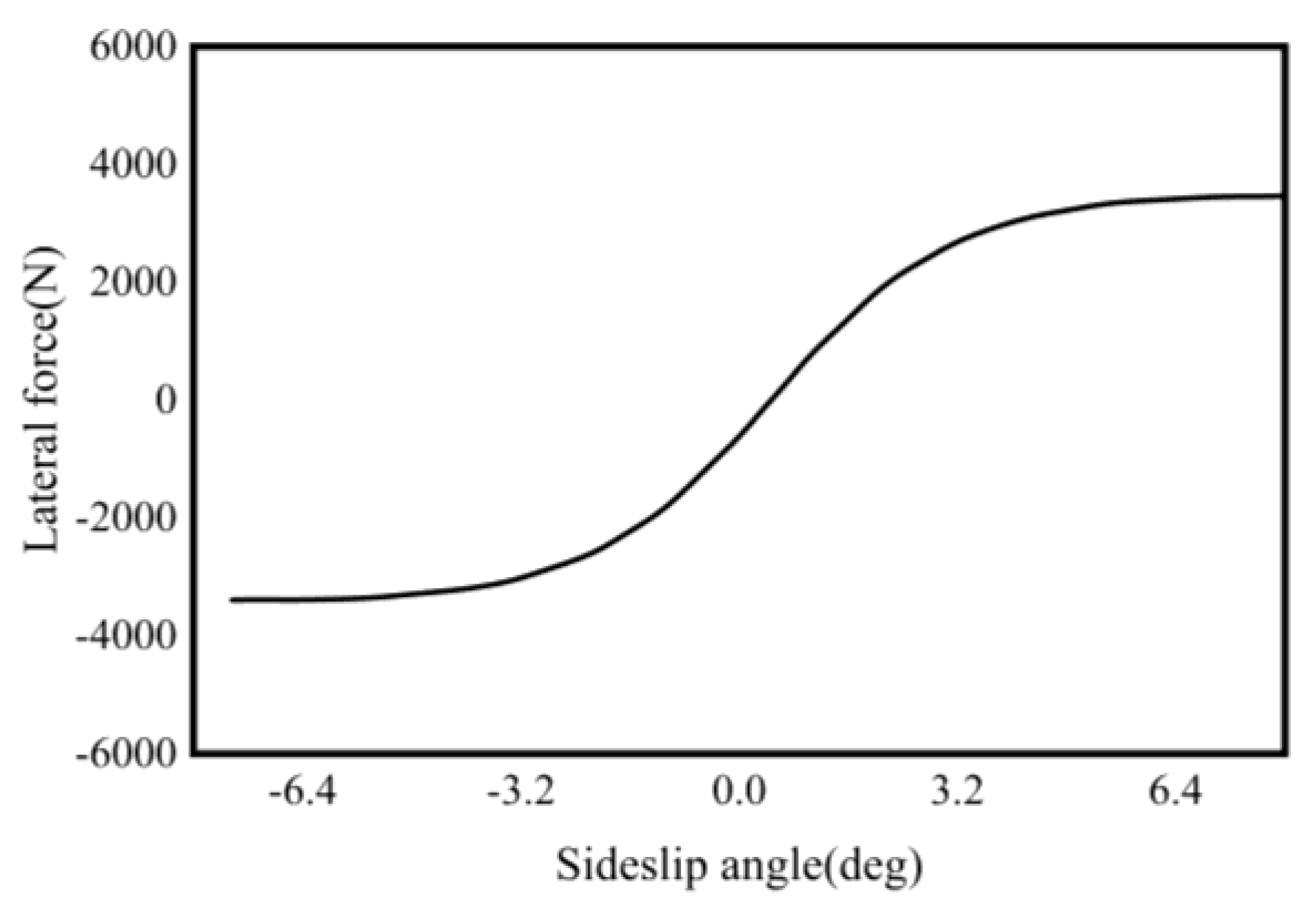
3.2. Tire Model
- is the output variable;
- is the input variable;
- is the stiffness factor;
- is curve shape factor;
- is the curve peak factor;
- is the curve curvature factor.
- is the drift in the horizontal direction;
- is drift in the vertical direction.
- is the tire sideslip angle;
- is the camber angle of the tire.
3.3. Vehicle Model Simplification
- is the system state quantity;
- is the system control quantity.
4. Trajectory Tracking Control Based on Model Predictive Control Algorithm
4.1. Model Predictive Control
4.1.1. Linear Time-Varying Prediction Model
- Prediction model
- is the current state quantity of the system;
- is the increment for system control.
- 2.
- Rolling optimization
- is the system state quantity;
- is the system control quantity;
- is the predicted value of the state quantity at the next time by the system at time K.
- is the weight coefficient matrix.
- is the control quantity constraint of the system;
- is the control increment constraint of the system;
- is the output constraint of the system.
- is the weight coefficient;
- is the relaxation factor.
- is a positive real number.
- 3.
- Feedback correction
4.1.2. System Linearization
- is the state constraint quantity;
- is the control constraint quantity.
4.2. Design of Model Predictive Controller
4.2.1. Linear Error Model
4.2.2. Objective Function Optimization
- is the weight coefficient;
- is the relaxation factor;
- is the weight factor.
- is a hard constraint;
- is a soft constraint;
- is the hard constraint minimum;
- is the maximum value of the hard constraint;
- is the soft constraint minimum;
- is the maximum value of the soft constraint.
4.2.3. Constraint Solving
- Centroid sideslip constraint
- 2.
- Vehicle attachment constraints
- is longitudinal acceleration;
- is the lateral acceleration.
- is the minimum constraint of acceleration;
- is the maximum constraint of acceleration.
- 3.
- Tire sideslip restraint
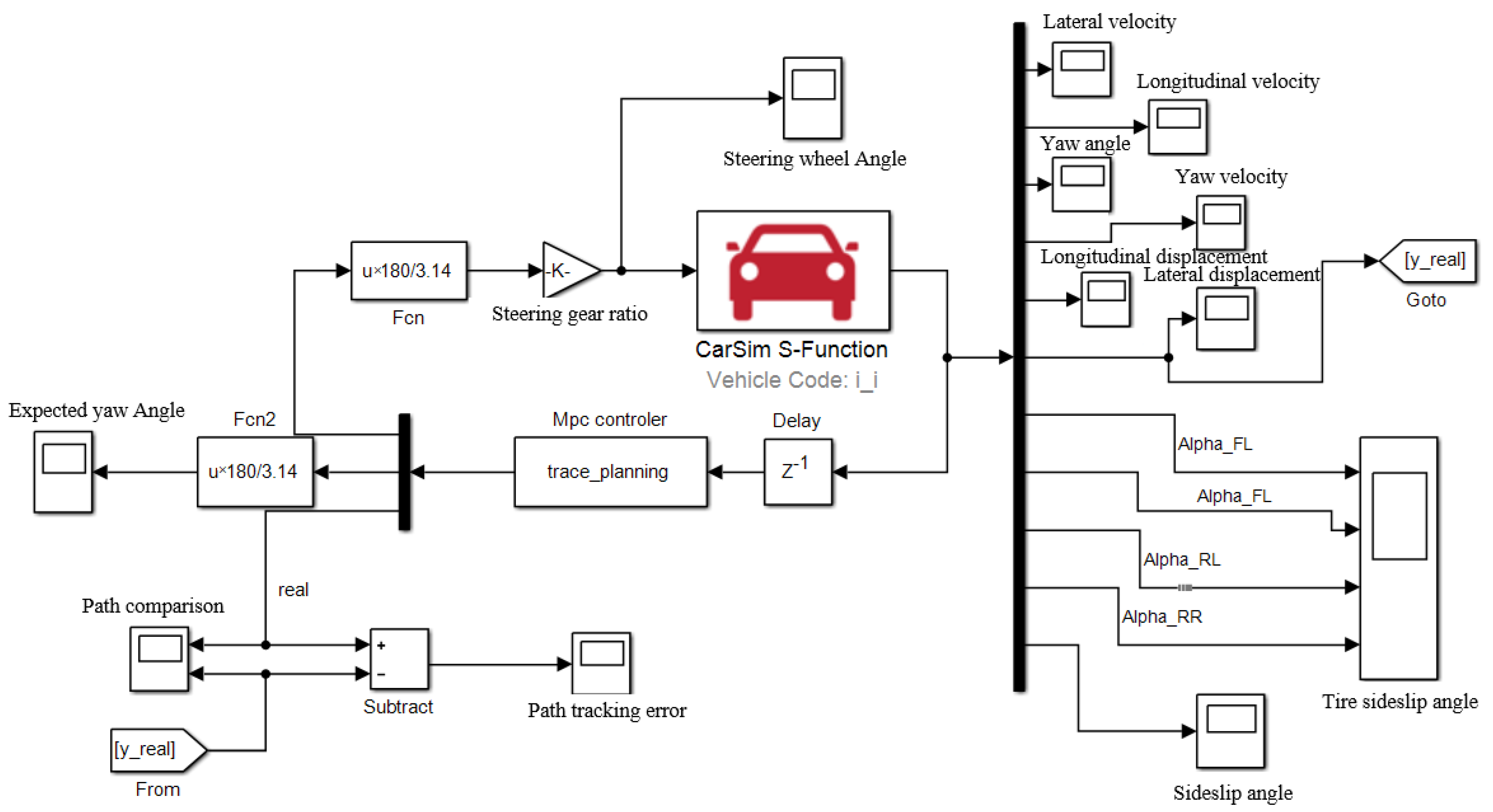
5. Joint Simulation Experiment Based on MATLAB and CarSim
5.1. Co-Simulation Platform
5.2. Controller Parameter Setting
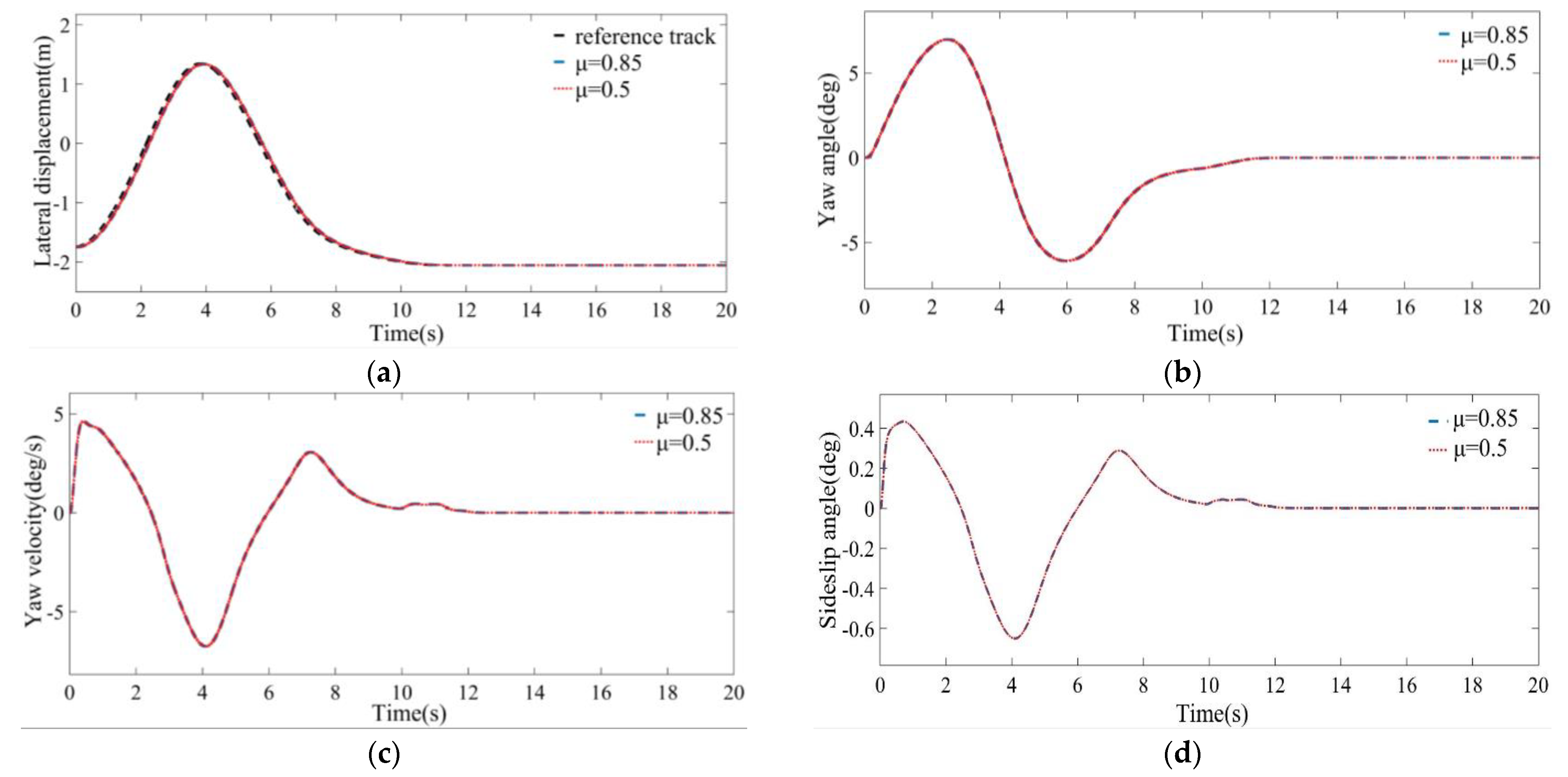
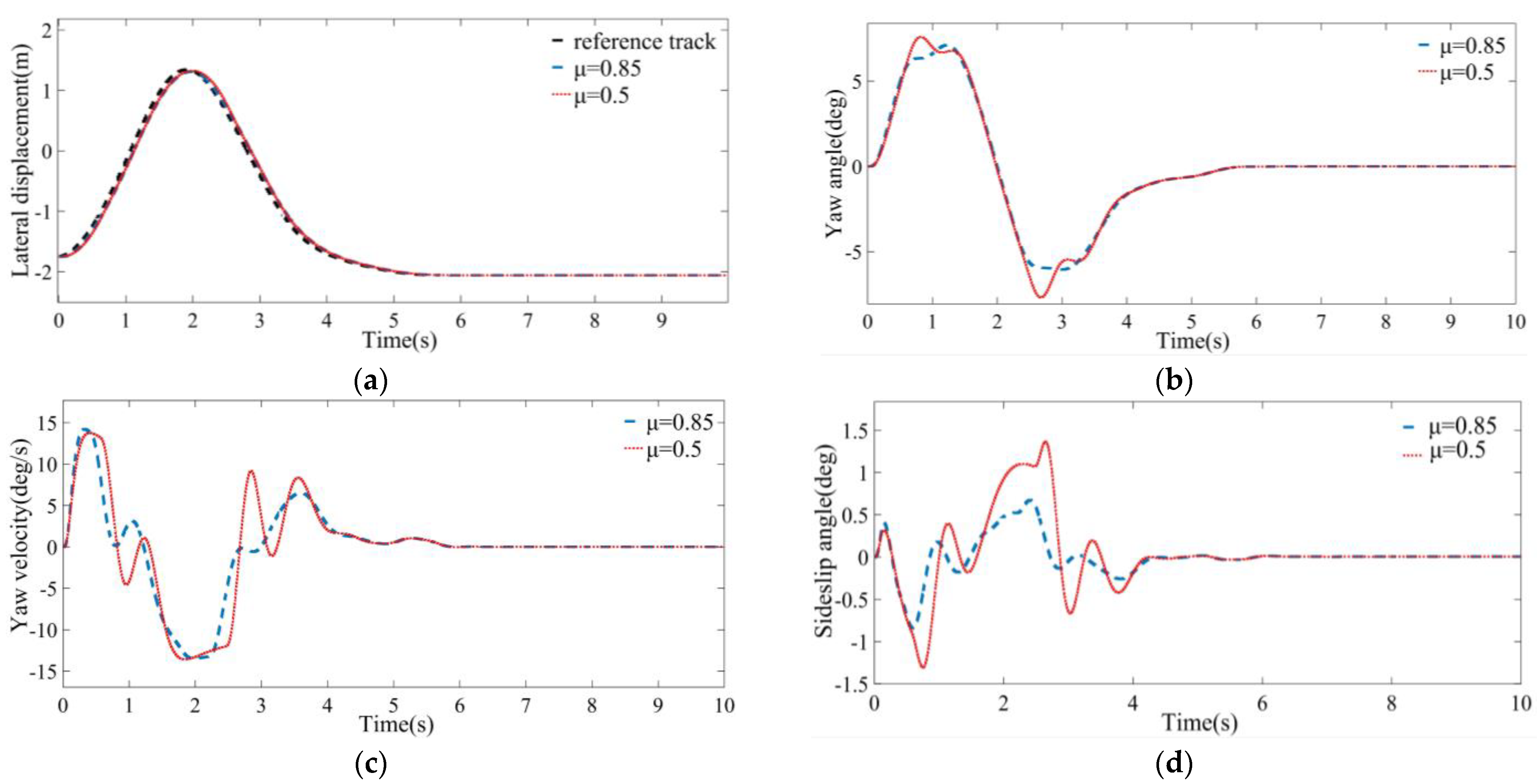
5.3. Simulation Analysis of Different Pavement Adhesion Coefficients
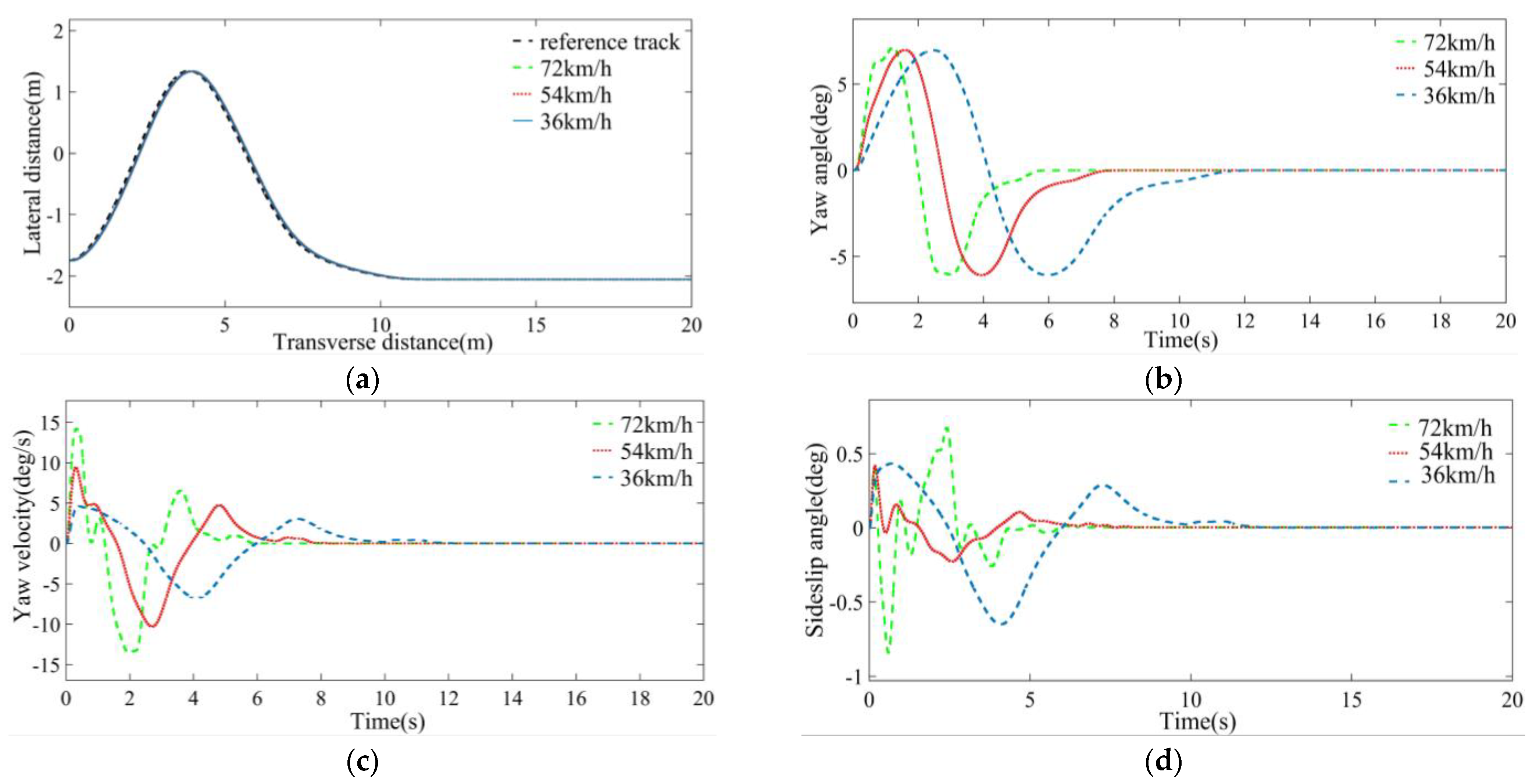
5.4. Simulation Analysis of Different Vehicle Speeds
6. Conclusions
- In the study, through increasing the target distance adjustment factor to solve the problem of inaccessible targets, the invasive weeds algorithm produces an optimal sub-destination, and the repulsive force redistribution problem is converted into a local optimal solution to establish the dynamic road repulsion field, velocity repulsion field, and acceleration repulsion field by relying on the change in speed to realize trajectory planning in a dynamic environment.
- An MPC model predictive controller was built to establish a vehicle dynamics model and tire model based on a “magic formula”, with the simplification of the vehicle dynamics model.
- A co-simulation platform was built, and two different road adhesion coefficients and three different vehicle speeds were selected for simulation. With the increase in the vehicle speed from 36 to 72 km/h, the values of the sideslip angle of the vehicle center of mass at the three speeds do not exceed the range of 4 deg. At the same time, the maximum tracking error is 0.134 m, and the tracking accuracy exceeds 98%, which indicates that the driving stability is excellent.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- J3016_201401; Taxonomy and Definitions for Terms Related to On-Road Motor Vehicle Automated Driving Systems. SAE International: Warrendale, PA, USA, 2014.
- Xu, X.; Hu, W.; Dong, H. Review of Key Technologies for Autonomous Vehicle Test Scenario Construction. Automot. Eng. 2021, 43, 610–619. [Google Scholar]
- Man, J. Research on Intelligent Vehicle Path Tracking Control. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2021. [Google Scholar]
- Drubin, C. Sensor Data Sharing, Driverless Vehicle Remote Control to Boost Cellular V2X Technologies. Microw. J. 2018, 61, 73. [Google Scholar]
- Xie, H. Research on Path Planning and Motion Control Algorithm for Unmanned Vehicles on Structured Roads. Ph.D. Thesis, Hunan University, Changsha, China, 2019. [Google Scholar]
- Tang, Z.; Ji, J.; Wu, M. Vehicles Path Planning and Tracking Based on an Improved Artificial Potential Field Method. J. Southwest Univ. (Nat. Sci. Ed.) 2018, 6, 180–188. [Google Scholar]
- An, L.; Chen, T.; Cheng, A. A Simulation on the Path Planning of Intelligent Vehicles Based on Artificial Potential Field Algorithm. Qiche Gongcheng/Automot. Eng. 2017, 39, 1451–1456. [Google Scholar]
- Xiu, C.; Chen, H. A Research on Local Path Planning for Autonomous Vehicles Based on Improved APF Method Automotive engineering. Automot. Eng. 2013, 35, 808–811. [Google Scholar] [CrossRef]
- Lee, J.; Nam, Y.; Hong, S. Random force based algorithm for local minima escape of potential field method. In Proceedings of the 2010 11th International Conference on Control Automation Robotics & Vision, Singapore, 7–10 December 2010; pp. 827–832. [Google Scholar]
- Taheri, E.; Ferdowsi, M.H.; Danesh, M. Fuzzy greedy RRT path planning algorithm in a complex configuration space. Int. J. Control. Autom. Syst. 2018, 16, 3026–3035. [Google Scholar] [CrossRef]
- Ci, Y.; Wu, H.; Sun, Y.; Wu, L. A Prediction Model with Wavelet Neural Network Optimized by the Chicken Swarm Optimization for On-ramps Metering of the Urban Expressway. J. Intell. Transp. Systems. 2022, 26, 356–365. [Google Scholar] [CrossRef]
- Boroujeni, Z.; Goehring, D.; Ulbrich, F.; Neumann, D.; Rojas, R. Flexible unit A-star trajectory planning for autonomous vehicles on structured road maps. In Proceedings of the 2017 IEEE International Conference on Vehicular Electronics and Safety (ICVES), Vienna, Austria, 27–28 June 2017; pp. 7–12. [Google Scholar]
- Yang, D.C.; Wen, C.L. Multiple Targets Robot Path Planning Based on Ant Colony and Improved Probabilistic Road Map. J. Hangzhou Dianzi Univ. (Nat. Sci.) 2017, 37, 63–67. [Google Scholar]
- Lei, W.; Ming, L. Application of improved adaptive genetic algorithm in mobile robot path planning. J. Nanjing Univ. Sci. Technol. 2017, 41, 327–633. [Google Scholar]
- Song, X.; Pan, L.; Cao, H. Local path planning for vehicle obstacle avoidance based on improved intelligent water drops algorithm. Automot. Eng. 2016, 38, 185–191. [Google Scholar]
- Wang, X.; Liu, M.; Ci, Y.; Yang, Y. Effectiveness of driver’s bounded rationality and speed guidance on fuel-saving and emissions-reducing at a signalized intersection. J. Clean. Prod. 2021, 325, 129343. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Y.; Liu, H.; Di, P.; Gao, M. Robot global path planning based on ant colony optimization with artificial potential field. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2015, 46. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.G.; Li, G.W. Study on path planning based on improved PRM method. Jisuanji Yingyong Yanjiu 2012, 29. [Google Scholar] [CrossRef]
- Zhang, L.X.; Wu, G.Q.; Guo, X.X. Path tracking using linear time-varying model predictive control for autonomous vehicle. J. Tongji Univ. Nat. Sci. 2016, 44, 1595–1603. [Google Scholar]
- Marino, R.; Scalzi, S.; Netto, M. Nested PID steering control for lane keeping in autonomous vehicles. Control. Eng. Pract. 2011, 19, 1459–1467. [Google Scholar] [CrossRef]
- Zeng, S. The Intelligent V ehicle Motion Research Based on LinearActive Disturbance Rejection Control. Ph.D. Thesis, Xiamen University, Xiamen, China, 2019. [Google Scholar]
- Li, T.; Hu, J.; Gao, L.; Liu, X.; Bai, X. Agricultural machine path tracking method based on fuzzy adaptive pure pursuit model. Trans. Chin. Soc. Agric. Mach. 2013, 44, 205–210. [Google Scholar]
- Lee, S.H.; Lee, Y.O.; Kim, B.A.; Chung, C.C. Proximate model predictive control strategy for autonomous vehicle lateral control. In Proceedings of the American Control Conference(ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 3605–3610. [Google Scholar]
- Gong, J.; Jiang, Y.; Xu, W. Model Predictive Control for Self-Driving Vehicles; Beijing Institute of Technology Press: Beijing, China, 2014. [Google Scholar]
- Zhou, L.H.; Shi, P.L.; Jiang, J.X.; Zhang, L.; Liang, M.L.; Hou, J.W. Simulation research on vehicle stability control based on collision avoiding trajectory tracking. J. Shandong Univ. Technol. (Nat. Sci. Ed.) 2021, 35, 75–81. [Google Scholar]
- Wu, L.; Ci, Y.; Sun, Y.; Qi, W. Research on Joint Control of On-ramp Metering and Mainline Speed Guidance in the Urban Expressway based on MPC and Connected Vehicles. J. Adv. Transp. 2020, 2020, 7518087. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Q.; Chen, W.; Zhao, L.; Tan, D. Path tracking based on model predictive control with variable predictive horizon. Trans. Inst. Meas. Control. 2021, 43, 2676–2688. [Google Scholar] [CrossRef]
- Morales, S.; Magallanes, J.; Delgado, C.; Canahuire, R. LQR trajectory tracking control of an omnidirectional wheeled mobile robot. In Proceedings of the 2018 IEEE 2nd Colombian Conference on Robotics and Automation (CCRA), Barranquilla, Colombia, 1–3 November 2018; pp. 1–5. [Google Scholar]
- Chen, J.; Li, L.; Song, J. A study on vehicle stability control based on LTV-MPC. Automot. Eng. 2016, 38, 308–316. [Google Scholar]
- Wu, L.; Ci, Y.; Wang, Y.; Chen, P. Fuel Consumption in the Oversaturated Signalized Intersection Considering Queue Effects: A Case Study in Harbin, China. Energy 2020, 192, 116654. [Google Scholar] [CrossRef]
- Ci, Y.; Wu, L.; Zhao, J.; Sun, Y.; Zhang, G. V2I-based Car-Following Modeling and Simulation on the Signalized Intersection. Phys. A Stat. Mech. Its Appl. 2019, 525, 672–679. [Google Scholar] [CrossRef]
- Pan, L.B. The Research about Path Planning and Tracking Control of the Intelligent Vehicle. Ph.D. Thesis, Hunan University, Changsha, China, 2016. [Google Scholar]
- Zhang, H.J.; Gong, J.W.; Jiang, Y.; Xiong, G.M.; Chen, H.Y. An iterative linear quadratic regulator based trajectory tracking controller for wheeled mobile robot. J. Zhejiang Univ. Sci. C 2012, 13, 593–600. [Google Scholar] [CrossRef]
- Zhou, D.S. Study on the Path Tracking of Driverless Cars Based on Preset Rolling Time Domain LQR. Ph.D. Thesis, Chongqing Jiaotong University, Chongqing, China, 2018. [Google Scholar]
- Samuel, M.; Hussein, M.; Mohamad, M.B. A review of some pure-pursuit based path tracking techniques for control of autonomous vehicle. Int. J. Comput. Appl. 2016, 135, 35–38. [Google Scholar] [CrossRef]
- Lin, F.; Lin, Z.; Qiu, X. LQR controller for car-like robot. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 2515–2518. [Google Scholar]
- Bian, W.; Gong, J.; Wen, A.; Chen, L.; Liu, Y. Two Levels of Parameter Identification of Magic Formula Tire Model Based on Genetic Algorithm. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2017, 36, 115. [Google Scholar]
- Xu, R.; Guo, Y.; Han, X.; Xia, X.; Xiang, H.; Ma, J. OpenCDA: An open cooperative driving automation framework integrated with co-simulation. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021. [Google Scholar]
- Li, Y.; Zhang, M.; Ding, Y.; Zhou, Z.; Xu, L. Real-Time Travel Time Prediction Based on Evolving Fuzzy Participatory Learning Model. J. Adv. Transp. 2022, 2022, 2578480. [Google Scholar] [CrossRef]

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| A1 | −34 | B0 | 2.37272 |
| A2 | 1250 | B1 | −9.46 |
| A3 | 3036 | B2 | 1490 |
| A4 | 128 | B3 | 130 |
| A5 | 0.00501 | B4 | 276 |
| A6 | −0.02103 | B5 | 0.0886 |
| A7 | 0.77394 | B6 | 0.00402 |
| A8 | 0.002289 | B7 | 0.0615 |
| A9 | 0.013442 | B8 | 1.2 |
| A10 | 0.0037 | B9 | 0.0299 |
| A11 | 19.1656 | B10 | −0.176 |
| A1 | 1.21356 | ||
| A1 | 6.2606 | ||
| A0 | 1.65 |
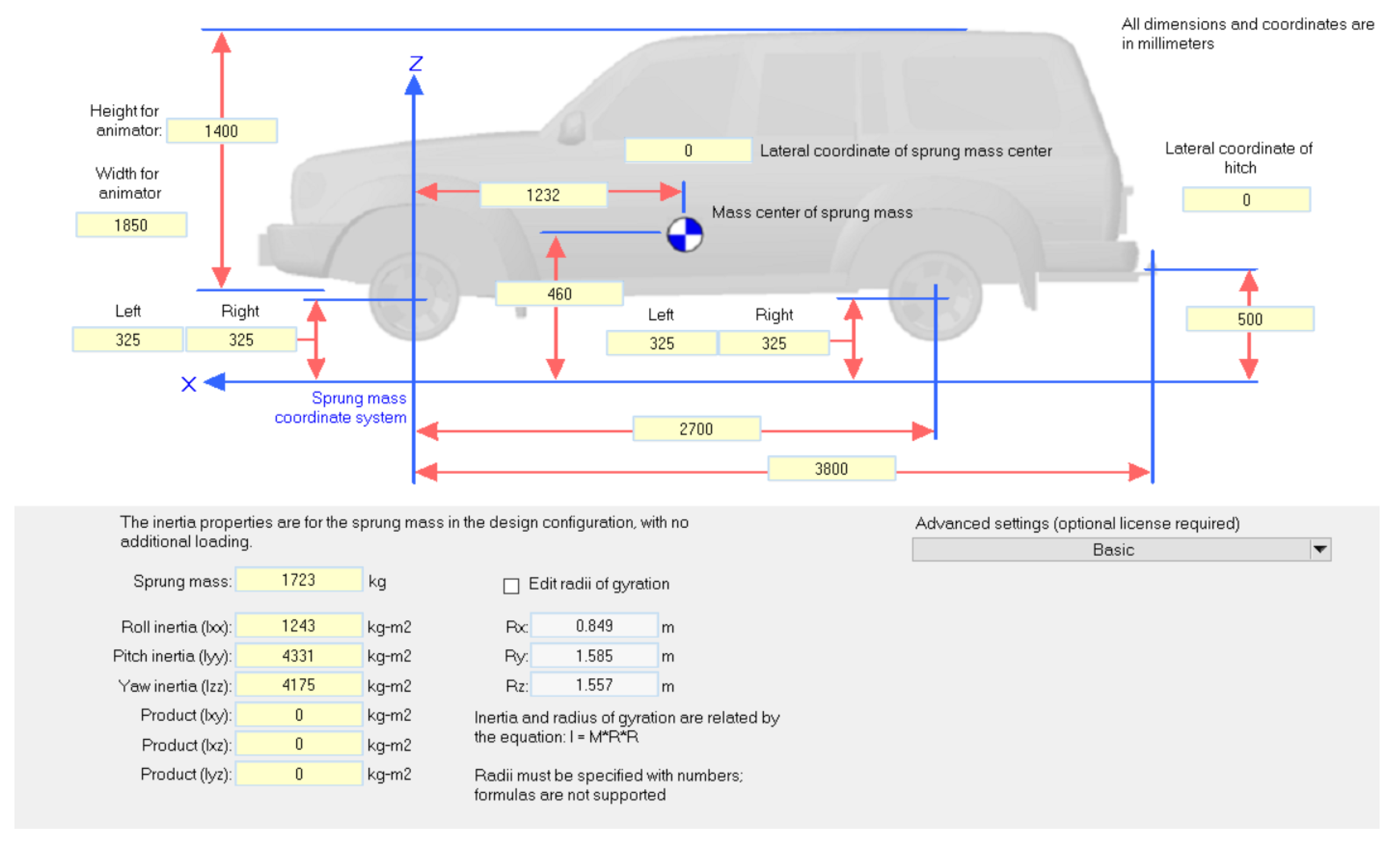
| Parameter | Value | Unit |
|---|---|---|
| Sprung mass | 1723 | kg |
| Width for animator | 1850 | mm |
| Yaw inertia | 4175 | kg·m2 |
| Axle base | 2700 | mm |
| Height of wheel center | 325 | mm |
| Height of the center of mass | 460 | mm |
| Parameter | Nomenclature | Value |
|---|---|---|
| Np | Prediction step length | 15 |
| Nc | Control step size | 8 |
| T | Sampling period | 0.02 |
| Q | Weight matrix | |
| R | Weight factor | 110,000 |
| ρ | Weight coefficient | 1000 |
| Speed (km/h) | Adhesion Coefficient of Pavement | Tracking Lateral Error (m) | Tracking Accuracy |
|---|---|---|---|
| 36 | 0.85 | 0.095 | 98.6% |
| 0.5 | 0.102 | 98.5% | |
| 72 | 0.5 | 0.134 | 98.1% |
| 0.85 | 0.121 | 98.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yang, W.; Zhang, X.; Kang, X.; Li, M. Research on Automatic Driving Trajectory Planning and Tracking Control Based on Improvement of the Artificial Potential Field Method. Sustainability 2022, 14, 12131. https://doi.org/10.3390/su141912131
Li Y, Yang W, Zhang X, Kang X, Li M. Research on Automatic Driving Trajectory Planning and Tracking Control Based on Improvement of the Artificial Potential Field Method. Sustainability. 2022; 14(19):12131. https://doi.org/10.3390/su141912131
Chicago/Turabian StyleLi, Yongyi, Wei Yang, Xiaorui Zhang, Xi Kang, and Mengfei Li. 2022. "Research on Automatic Driving Trajectory Planning and Tracking Control Based on Improvement of the Artificial Potential Field Method" Sustainability 14, no. 19: 12131. https://doi.org/10.3390/su141912131
APA StyleLi, Y., Yang, W., Zhang, X., Kang, X., & Li, M. (2022). Research on Automatic Driving Trajectory Planning and Tracking Control Based on Improvement of the Artificial Potential Field Method. Sustainability, 14(19), 12131. https://doi.org/10.3390/su141912131








