Towards Incompressible Laminar Flow Estimation Based on Interpolated Feature Generation and Deep Learning
Abstract
1. Introduction
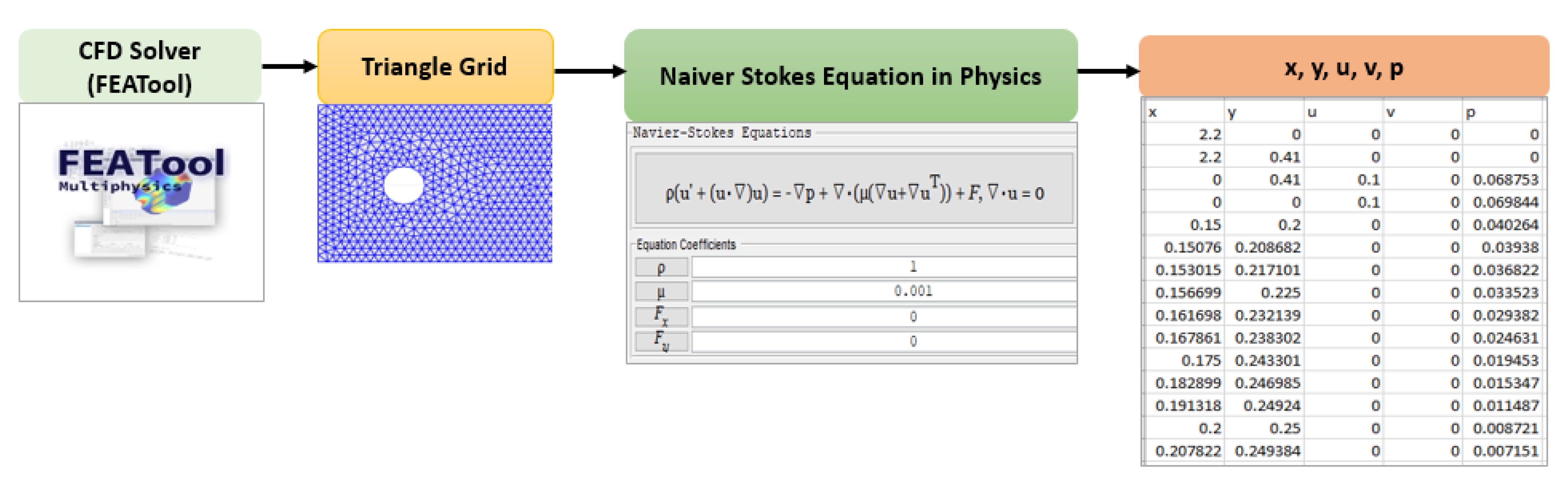
- Firstly, we create the raw laminar flow datasets around different obstacles using the CFD solver FEATool [19]. Then, we generate novel learning input and output interpolated CFD features using the mesh-grid and grid-data computations on these raw simulated datasets.
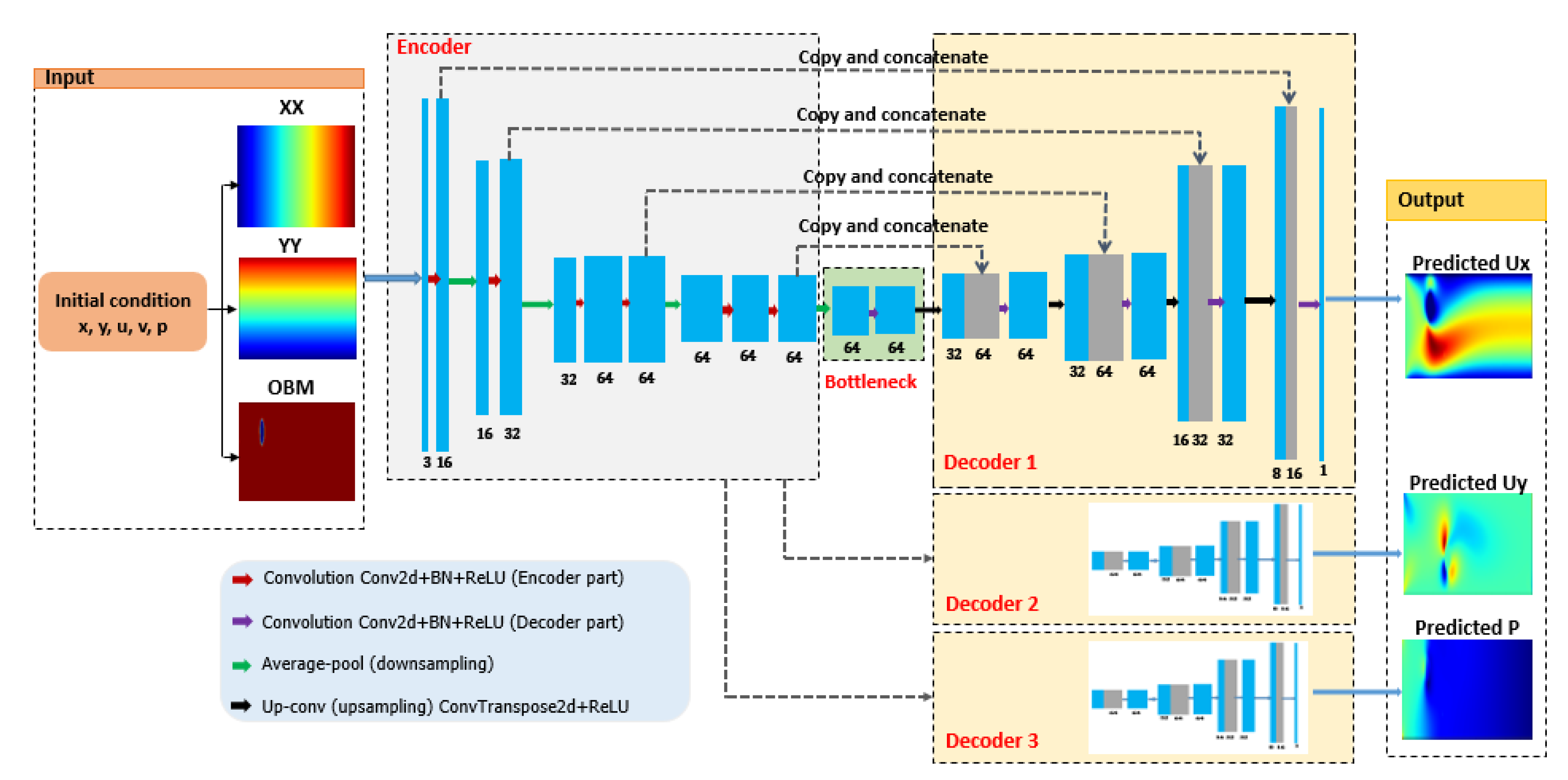
- Second, we build a deep U-Net model comprising an encoder and three decoders to predict three output classes corresponding to three different flow fields, respectively. This deep U-Net model estimates fluid flow fields by learning from preprocessed data, that is, interpolated features data.
- Lastly, we evaluate the proposed method by measuring the learning and testing loss metrics. The experimental results show the competition and promise of the proposed method with other baseline models on the same dataset.
2. Related Work
3. The Proposed Method
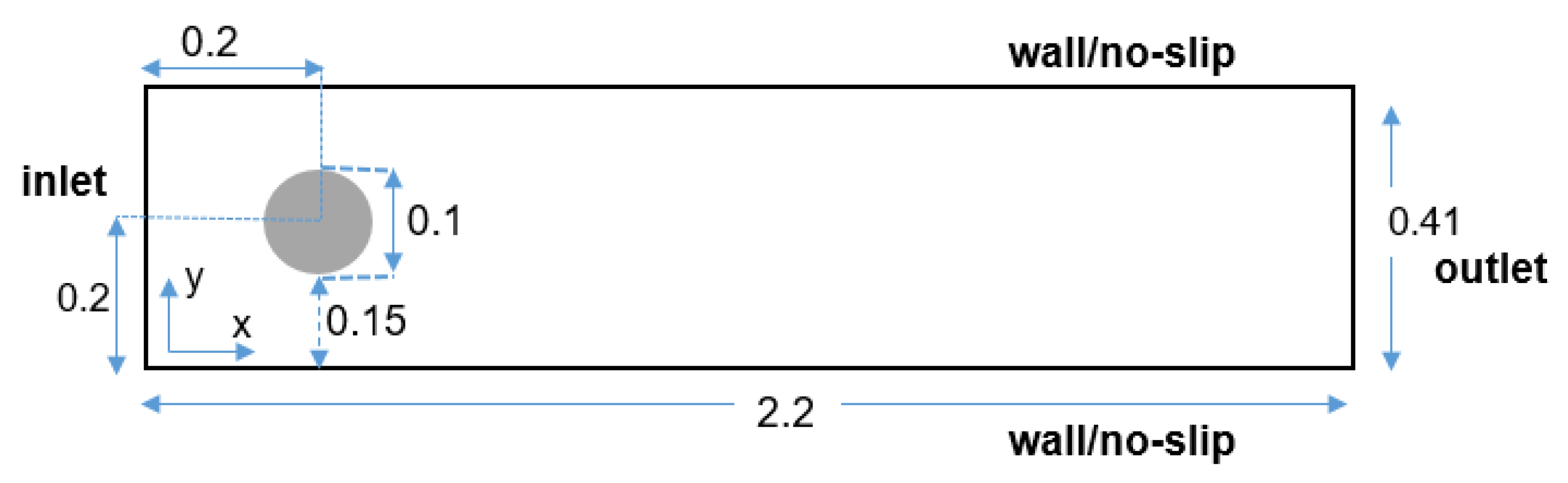
3.1. Data Generation and Preprocessing
3.1.1. Random Shape Generation and Numerical Resolution of the Naiver–Stokes Equation
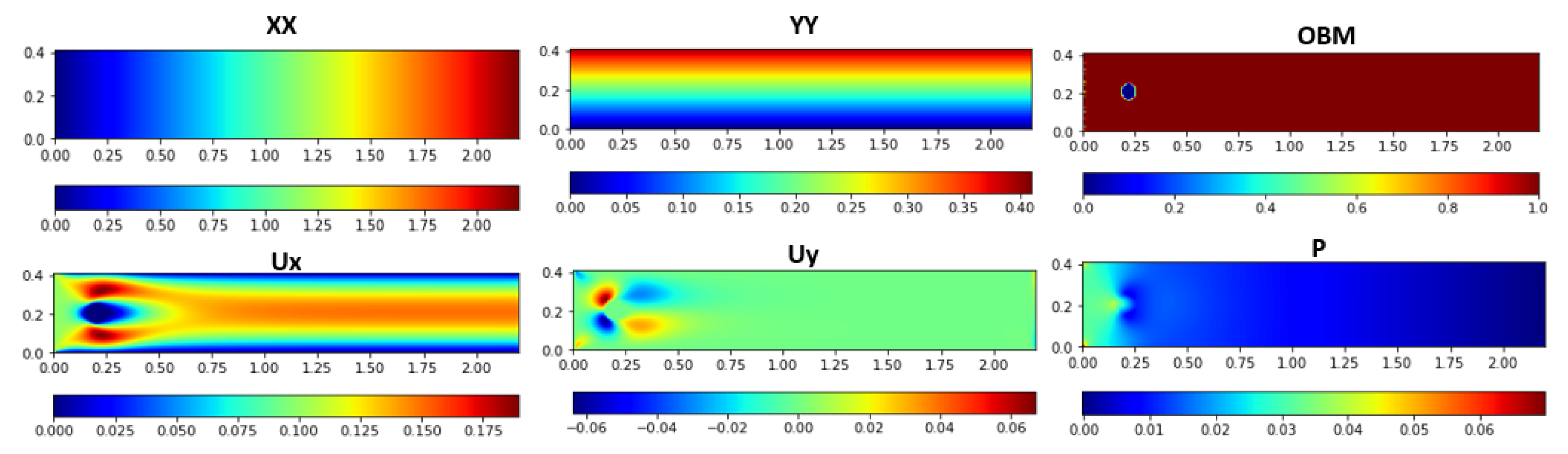
3.1.2. Learning Features Generation
| Algorithm 1: Interpolated Input and Output Features Generation |
input: x-coordinate x, y-coordinate y, horizontal velocity u, vertical velocity v, pressure p, width m, height n output: 2D array of horizontal mesh-grid , 2D array of vertical mesh-grid , object binary map , interpolated horizontal velocity , interpolated vertical velocity , interpolated pressure P 1 // Create two 1D array following x, y coordinates 2 3 4 // Generate 2D numpy arrays are horizontal and vertical of mesh-grids using and 5 6 // Generate obstacle binary mapping 7 8 9 10 11 12 13 14 15 // Generate output features 16 17 18 19 return |
3.2. The Proposed CFD Based Deep U-Net Model
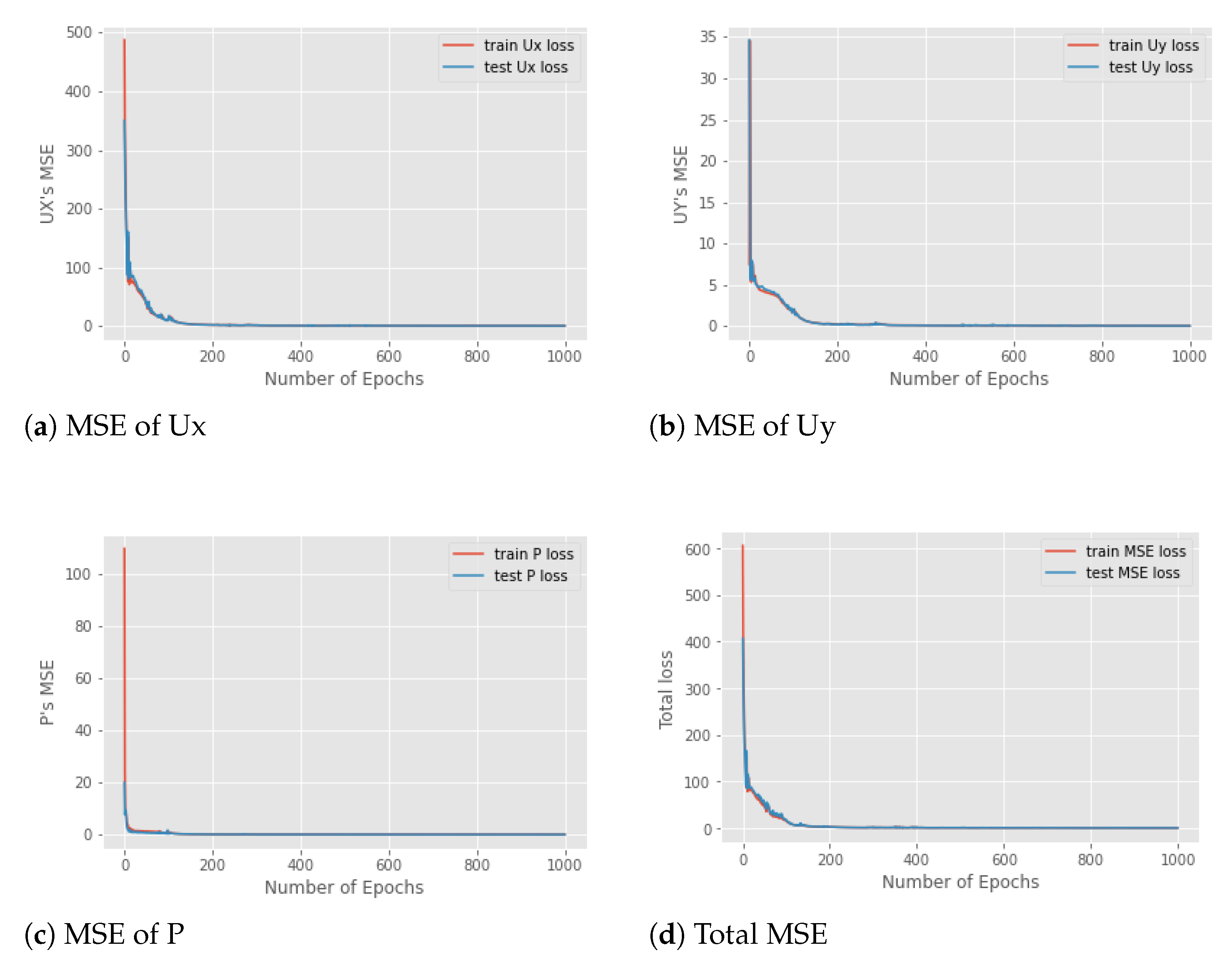
3.3. Model Evaluation and Optimization
| Algorithm 2: Deep U-Net-based CFD Prediction Model |
 |
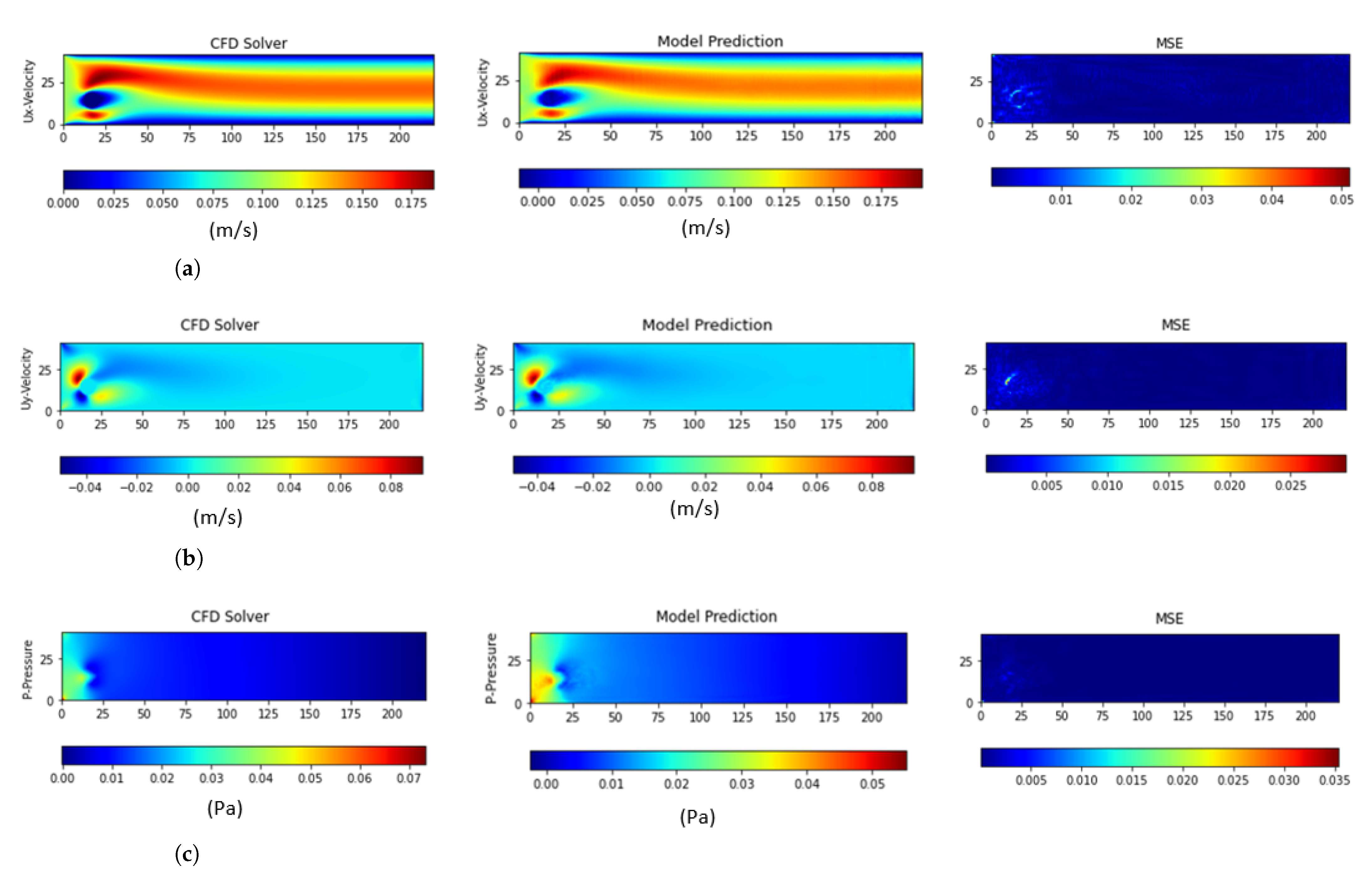
4. Experimental Results and Discussion
4.1. Effectiveness of Hyper-Parameters
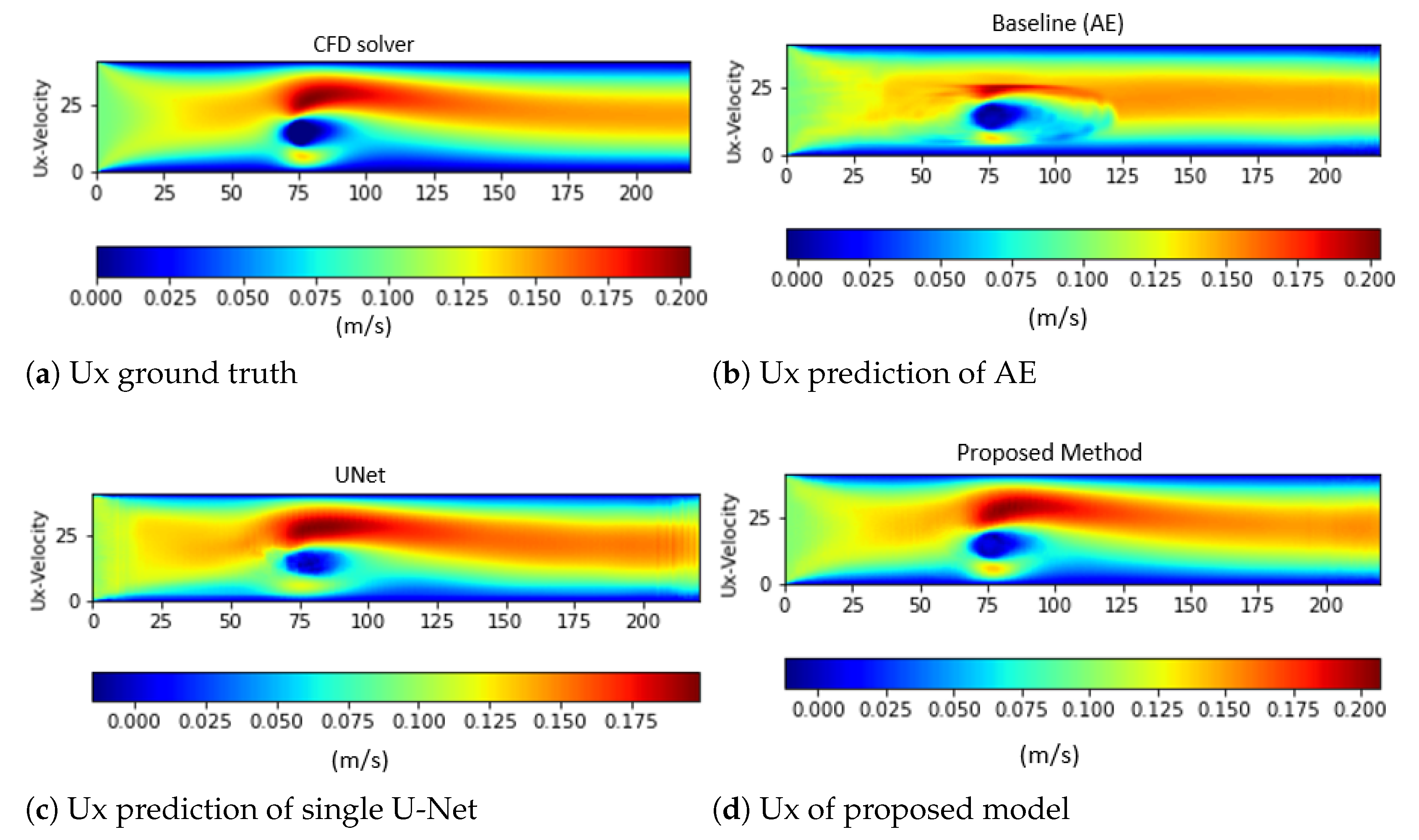
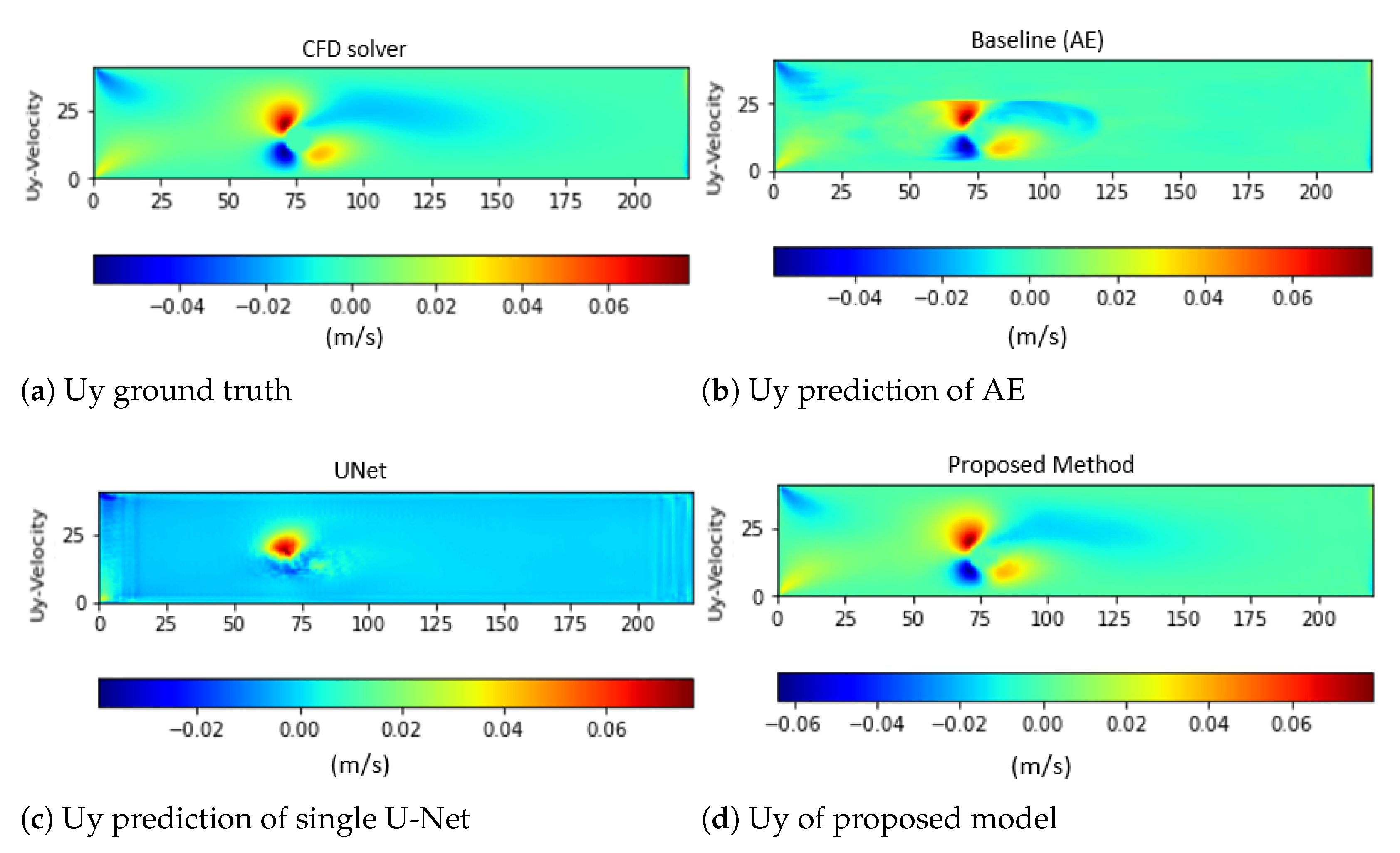
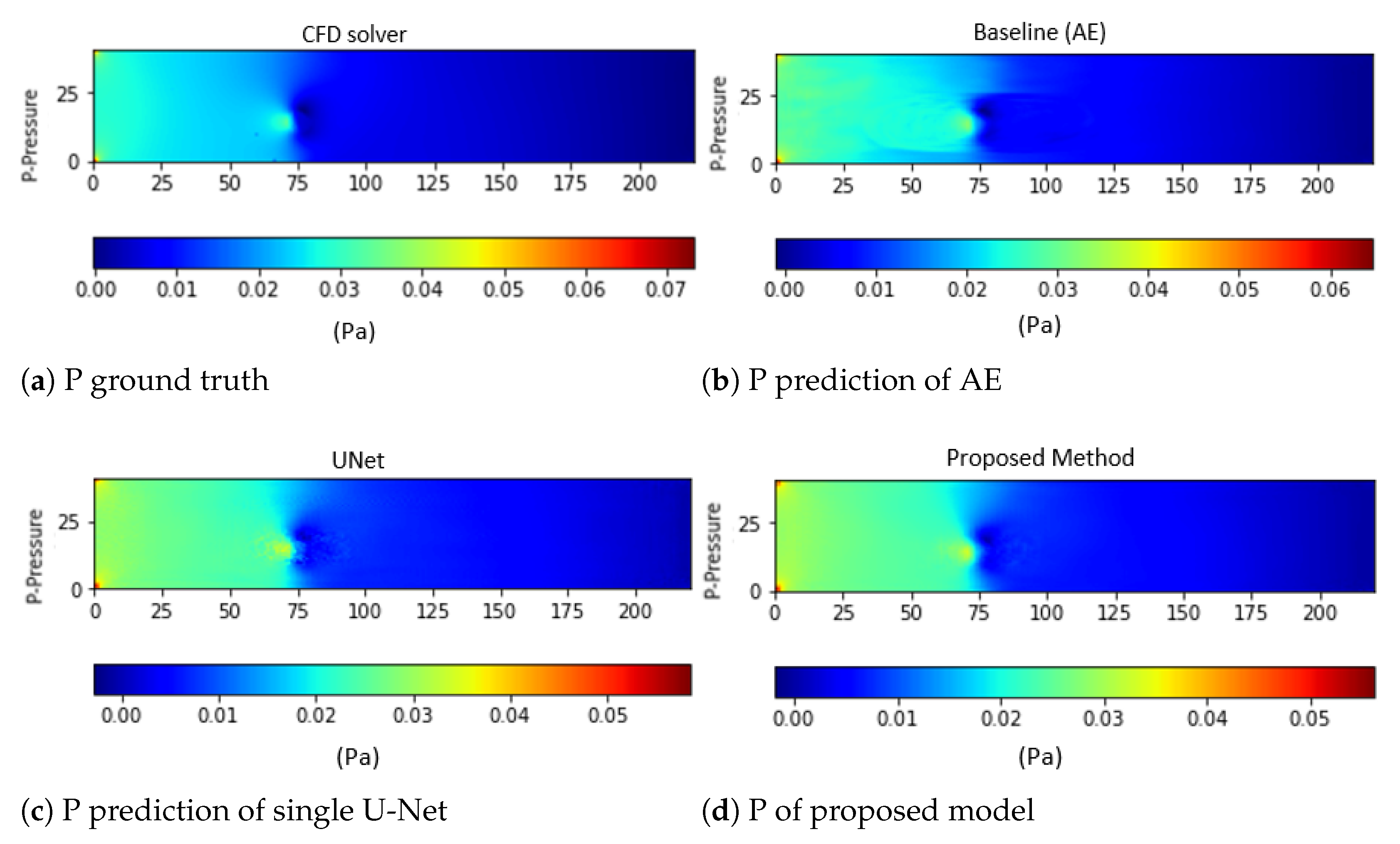
4.2. Performance Evaluation and Comparison to Other Deep Learning Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamic |
| DNNs | Deep Neural Networks |
| CNNs | Convolution Neural Networks |
| LES | Large Eddy Simulation |
| RANDS | Reynolds Averaged Navier–Stokes |
| ROM | Reduced Order Model |
| POP | Proper Orthogonal Decomposition |
| DL | Deep Learning |
| PDEs | Partial Different Equations |
| AE | Autoencoder |
| SDF | Signed Distance Function |
| MCR | MATLAB Compiler Runtime |
References
- Portwood, G.D.; Mitra, P.P.; Ribeiro, M.D.; Nguyen, T.M.; Nadiga, B.T.; Saenz, J.A.; Chertkov, M.; Garg, A.; Anandkumar, A.; Dengel, A.; et al. Turbulence Forecasting via Neural Ode. 2019. Available online: https://arxiv.org/abs/1911.05180 (accessed on 22 February 2022).
- Beck, A.D.; Flad, D.G.; Munz, C. Deep neural networks for data-driven turbulence models. CoRR 2018, abs/1806.04482. Available online: http://arxiv.org/abs/1806.04482 (accessed on 25 February 2022).
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Tracey, B.D.; Duraisamy, K.; Alonso, J.J. A machine learning strategy to assist turbulence model development. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; Jesús, O.D. Neural Network Design; PWS Publishing Co.: Cambridge, MA, USA, 2014. [Google Scholar]
- Wang, Z.; Xiao, D.; Fang, F.; Govindan, R.; Pain, C.C.; Guo, Y. Model identification of reduced order fluid dynamics systems using deep learning. Int. Numer. Methods Fluids 2017, 86, 255–268. [Google Scholar] [CrossRef]
- Fukami, K.; Fukagata, K.; Taira, K. Superresolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 2019, 870, 106–120. [Google Scholar] [CrossRef]
- Fresca, S.; Dedè, L.; Manzoni, A. A comprehensive deep learning-based approach to reduced order modeling of nonlinear time-dependent parametrized PDEs. J. Sci. Comput. 2021, 87, 61. [Google Scholar] [CrossRef]
- Fresca, S.; Manzoni, A. POD-DL-ROM: Enhancing deep learning-based reduced order models for nonlinear parametrized PDEs by proper orthogonal decomposition. Comput. Methods Appl. Mech. Eng. 2022, 388, 114181. [Google Scholar] [CrossRef]
- Fresca, S.; Manzoni, A. Real-Time Simulation of Parameter-Dependent Fluid Flows through Deep Learning-Based Reduced Order Models. Fluids 2021, 6, 259. [Google Scholar] [CrossRef]
- Pant, P.; Doshi, R.; Bahl, P.; Barati, F.A. Deep learning for reduced order modelling and efficient temporal evolution of fluid simulations. Phys. Fluids 2021, 33, 107101. [Google Scholar] [CrossRef]
- Kang, H.; Tian, Z.; Chen, G.; Li, L.; Wang, T. Application of POD reduced-order algorithm on data-driven modeling of rod bundle. Nucl. Eng. Technol. 2022, 54, 36–48. [Google Scholar] [CrossRef]
- Gao, H.; Sun, L.; Wang, J.-X. Phygeonet: Physicsinformed geometry-adaptive convolutional neural networks for solving parametric pdes on irregular domain. J. Comput. Phys. 2021, 428, 110079. [Google Scholar] [CrossRef]
- San, O.; Maulik, R.; Ahmed, M. An artificial neural network framework for reduced order modeling of transient flows. Commun. Nonlinear Sci. Numer. Simul. 2019, 77, 271–287. Available online: https://www.sciencedirect.com/science/article/pii/S1007570419301364 (accessed on 18 March 2022). [CrossRef]
- Sekar, V.; Khoo, B.C. Fast flow field prediction over airfoils using deep learning approach. Phys. Fluids 2019, 31, 057103. [Google Scholar] [CrossRef]
- Jin, X.; Cheng, P.; Chen, W.-L.; Li, H. Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder. Phys. Fluids 2018, 30, 047105. [Google Scholar] [CrossRef]
- Guo, X.; Li, W.; Iorio, F. Convolutional Neural Networks for Steady Flow Approximation; ser. KDD ’16; Association for Computing Machinery: New York, NY, USA, 2016; pp. 481–490. [Google Scholar] [CrossRef]
- Ribeiro, M.D.; Rehman, A.; Ahmed, S.; Dengel, A. Deepcfd: Efficient Steady-State Laminar Flow Approximation with Deep Convolutional Neural Networks. 2020. Available online: https://arxiv.org/abs/2004.08826 (accessed on 13 March 2022).
- Featool Multiphysics. FEATool Multiphysics. 2013–2022. Available online: https://www.featool.com/doc/quickstart.html (accessed on 12 January 2022).
- Sarghini, F.; de Felice, G.; Santini, S. Neural networks based subgrid scale modeling in large eddy simulations. Comput. Fluids 2003, 32, 97–108. Available online: https://www.sciencedirect.com/science/article/pii/S0045793001000986 (accessed on 16 March 2022). [CrossRef]
- Lee, S.; You, D. Data-driven prediction of unsteady flow over a circular cylinder using deep learning. J. Fluid Mech. 2019, 879, 217–254. [Google Scholar] [CrossRef]
- Kashefi, A.; Rempe, D.; Guibas, L.J. A point-cloud deep learning framework for prediction of fluid flow fields on irregular geometries. Phys. Fluids 2021, 33, 027104. [Google Scholar] [CrossRef]
- Lui, H.F.S.; Wolf, W.R. Construction of reducedorder models for fluid flows using deep feedforward neural networks. J. Fluid Mech. 2019, 872, 963–994. [Google Scholar] [CrossRef]
- Tompson, J.; Schlachter, K.; Sprechmann, P.; Perlin, K. Accelerating Eulerian Fluid Simulation with Convolutional Networks. 2016. Available online: https://arxiv.org/abs/1607.03597 (accessed on 28 March 2022).
- Ribeiro, M.D.; Portwood, G.D.; Mitra, P.; Nyugen, T.M.; Nadiga, B.T.; Chertkov, M.; Anandkumar, A.; Schmidt, D.P.; Team, N.; Team, U.; et al. A data-driven approach to modeling turbulent decay at non-asymptotic Reynolds numbers. In Proceedings of the APS Division of Fluid Dynamics Meeting Abstracts 2019, Provided by the SAO/NASA Astrophysics Data System, Seattle, WA, USA, 23–26 November 2019; p. G16.002. [Google Scholar]
- Gupta, S.; Girshick, R.; Arbeláez, P.; Malik, J. Learning Rich Features from Rgb-D Images for Object Detection and Segmentation. 2014. Available online: https://arxiv.org/abs/1407.5736 (accessed on 27 March 2022).
- Socher, R.; Huval, B.; Bhat, B.; Manning, C.D.; Ng, A.Y. Convolutional-recursive deep learning for 3d object classification. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Harrahs and Harveys, NV, USA, 3–8 December 2012; ser. NIPS’12. Curran Associates Inc.: Red Hook, NY, USA, 2012; Volume 1, pp. 656–664. [Google Scholar]
- Georgiou, T.; Schmitt, S.; Olhofer, M.; Liu, Y.; Bäck, T.; Lew, M. Learning fluid flows. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Zhang, Y.; Sung, W.-J.; Mavris, D. Application of Convolutional Neural Network to Predict Airfoil Lift coefficient. 2017. Available online: https://arxiv.org/abs/1712.10082 (accessed on 16 March 2022).
- Viquerat, J.; Hachem, E. A supervised neural 10 VOLUME, 2021Author Le et al.: Towards Incompressible Laminar Flow Estimation Based on Interpolated Feature Generation and Deep Learning network for drag prediction of arbitrary 2d shapes in laminar flows at low reynolds number. Comput. Fluids 2020, 210, 104645. Available online: https://www.sciencedirect.com/science/article/pii/S0045793020302164 (accessed on 2 April 2022). [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. Unet: Convolutional Networks for Biomedical Image Segmentation. 2015. Available online: https://arxiv.org/abs/1505.04597 (accessed on 4 April 2022).
- Thuerey, N.; Weißenow, K.; Prantl, L.; Hu, X. Deep learning methods for reynolds-averaged navier–stokes simulations of airfoil flows. AIAA J. 2020, 58, 25–36. [Google Scholar] [CrossRef]
- Kamrava, S.; Tahmasebi, P.; Sahimi, M. Physics and image-based prediction of fluid flow and transport in complex porous membranes and materials by deep learning. J. Membr. Sci. 2021, 622, 119050. [Google Scholar] [CrossRef]
- Wang, Y.D.; Chung, T.; Armstrong, R.T.; Mostaghimi, P. Ml-lbm: Machine Learning Aided Flow Simulation in Porous Media. 2020. Available online: https://arxiv.org/abs/2004.11675 (accessed on 5 March 2022).
- Chen, J.; Viquerat, J.; Heymes, F.; Hachem, E. A Twin-Decoder Structure for Incompressible Laminar Flow Reconstruction with Uncertainty Estimation around 2D Obstacles. 2021. Available online: https://arxiv.org/abs/2104.03619 (accessed on 7 April 2022).
- Peng, J.-Z.; Liu, X.; Aubry, N.; Chen, Z.; Wu, W.-T. Data-driven modeling of geometryadaptive steady heat conduction based on convolutional neural networks. Case Stud. Thermal Eng. 2021, 28, 101651. Available online: https://www.sciencedirect.com/science/article/pii/S2214157X21008145 (accessed on 10 April 2022). [CrossRef]
- Eichinger, M.; Heinlein, A.; Klawonn, A. Stationary flow predictions using convolutional neural networks. In ENUMATH, Lecture Notes in Computational Science and Engineering; Springer: Berlin/Heidelberg, Germany, 2019; Volume 139. [Google Scholar]
- Li, K.; Li, H.; Li, S.; Chen, Z. Fully convolutional neural network prediction method for aerostatic performance of bluff bodies based on consistent shape description. Appl. Sci. 2022, 12, 3147. [Google Scholar] [CrossRef]
- Nabh, G. On High Order Methods for the Stationary Incompressible Navier-Stokes Equations, ser. Interdisziplinäres Zentrum für Wissenschaftliches Rechnen der Universität Heidelberg. IWR. 1998. Available online: https://books.google.co.kr/books?id=cx4-HAAACAAJ (accessed on 15 April 2022).
| Kernel Size | Filter | Training Loss | Testing Loss | Ux’s MSE | Uy’s MSE | P’s MSE |
|---|---|---|---|---|---|---|
| (4, 8, 16, 16) | 8.043 | 8.585 | 4.740 | 3.465 | 0.379 | |
| 5 | (8, 16, 32, 32) | 15.556 | 17.438 | 14.349 | 1.795 | 1.293 |
| (16, 32, 64, 64) | 3.473 | 3.069 | 2.066 | 0.602 | 0.400 | |
| (4, 8, 16, 16) | 3.016 | 3.315 | 2.531 | 0.711 | 0.073 | |
| 11 | (8, 16, 32, 32) | 3.016 | 3.315 | 2.531 | 0.711 | 0.073 |
| (16, 32, 64, 64) | 0.309 | 0.452 | 0.404 | 0.033 | 0.014 |
| Obstacle | Train Loss | Test Loss | Ux’s MSE | Uy’s MSE | P’s MSE |
|---|---|---|---|---|---|
| Triangle | 0.524 | 1.198 | 0.903 | 0.236 | 0.058 |
| Rectangle | 0.541 | 3.366 | 3.366 | 0.081 | 0.253 |
| Pentagon | 3.255 | 4.855 | 3.559 | 0.474 | 0.821 |
| Model | Training Loss | Testing Loss | Ux’s MSE | Uy’s MSE | P’s MSE |
|---|---|---|---|---|---|
| AE | 11.183 | 11.183 | 12.688 | 1.125 | 1.408 |
| Single U-Net | 4.599 | 5.017 | 1.127 | 3.861 | 0.027 |
| Proposed method | 0.335 | 0.345 | 0.294 | 0.294 | 0.015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.-T.-H.; Kang, H.; Kim, H. Towards Incompressible Laminar Flow Estimation Based on Interpolated Feature Generation and Deep Learning. Sustainability 2022, 14, 11996. https://doi.org/10.3390/su141911996
Le T-T-H, Kang H, Kim H. Towards Incompressible Laminar Flow Estimation Based on Interpolated Feature Generation and Deep Learning. Sustainability. 2022; 14(19):11996. https://doi.org/10.3390/su141911996
Chicago/Turabian StyleLe, Thi-Thu-Huong, Hyoeun Kang, and Howon Kim. 2022. "Towards Incompressible Laminar Flow Estimation Based on Interpolated Feature Generation and Deep Learning" Sustainability 14, no. 19: 11996. https://doi.org/10.3390/su141911996
APA StyleLe, T.-T.-H., Kang, H., & Kim, H. (2022). Towards Incompressible Laminar Flow Estimation Based on Interpolated Feature Generation and Deep Learning. Sustainability, 14(19), 11996. https://doi.org/10.3390/su141911996








