Cooperative Operation Model of Wind Turbine and Carbon Capture Power Plant Considering Benefit Distribution
Abstract
:1. Introduction
2. Literature Review
3. Operation Optimization Model of Wind Turbine and CCPP Considering Deviation Penalty
3.1. Wind Turbines Operation Model
3.2. Thermal Power Unit Operation Model
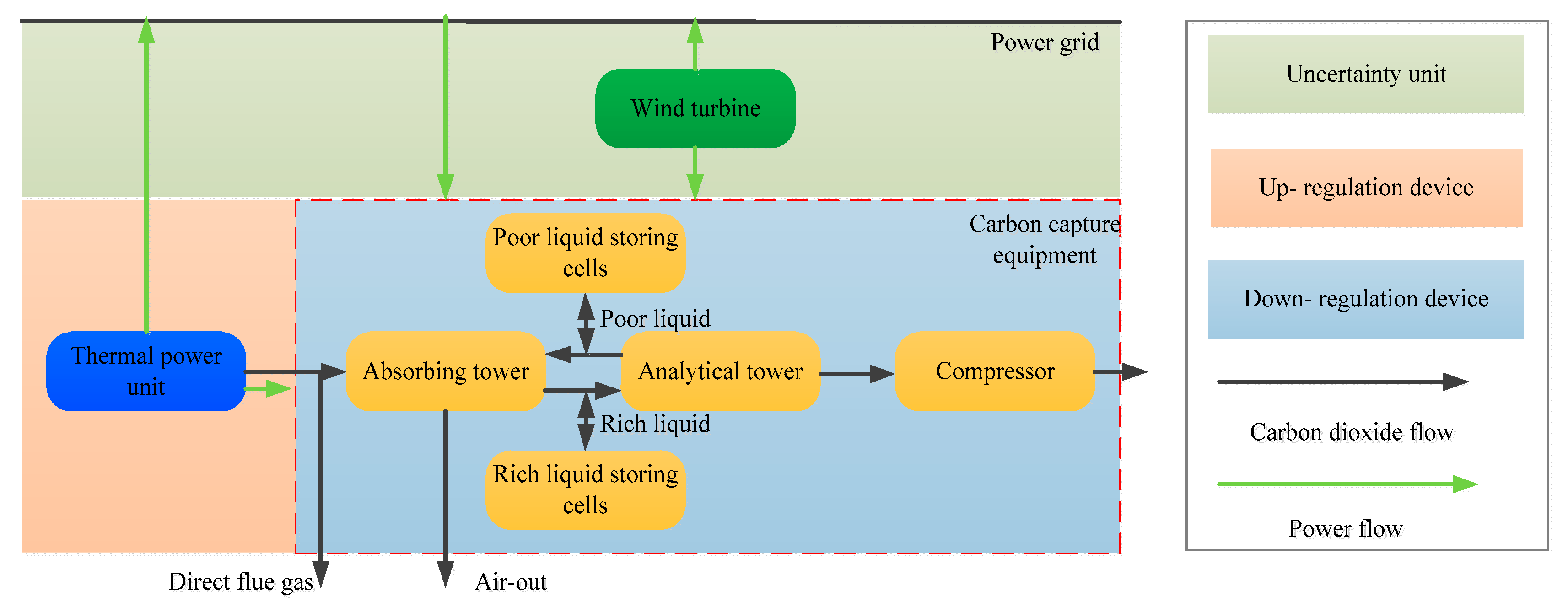
3.3. Carbon Capture Equipment Operation Model
4. Multi-Agent Cooperative Nash Bargaining Model of Wind Turbine and CCPP
4.1. The Basic Principle of Nash Bargaining
4.2. Wind Turbine and CCPP Cooperative Operation Nash Bargaining Model
4.3. Equivalent Conversion of Cooperative Operation Nash Bargaining Model
5. Solution of Wind Turbine and CCPP Cooperative Nash Bargaining Model
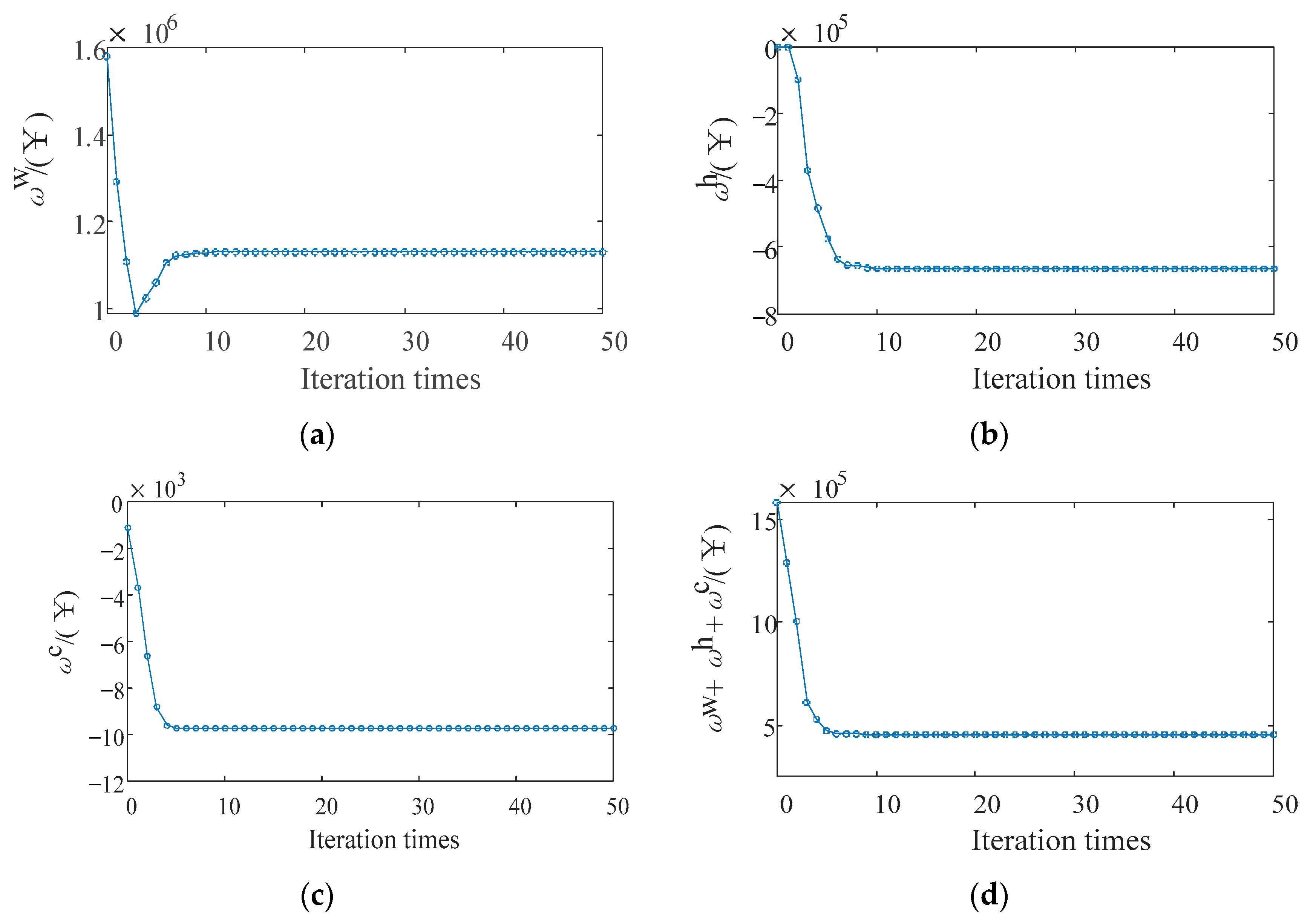
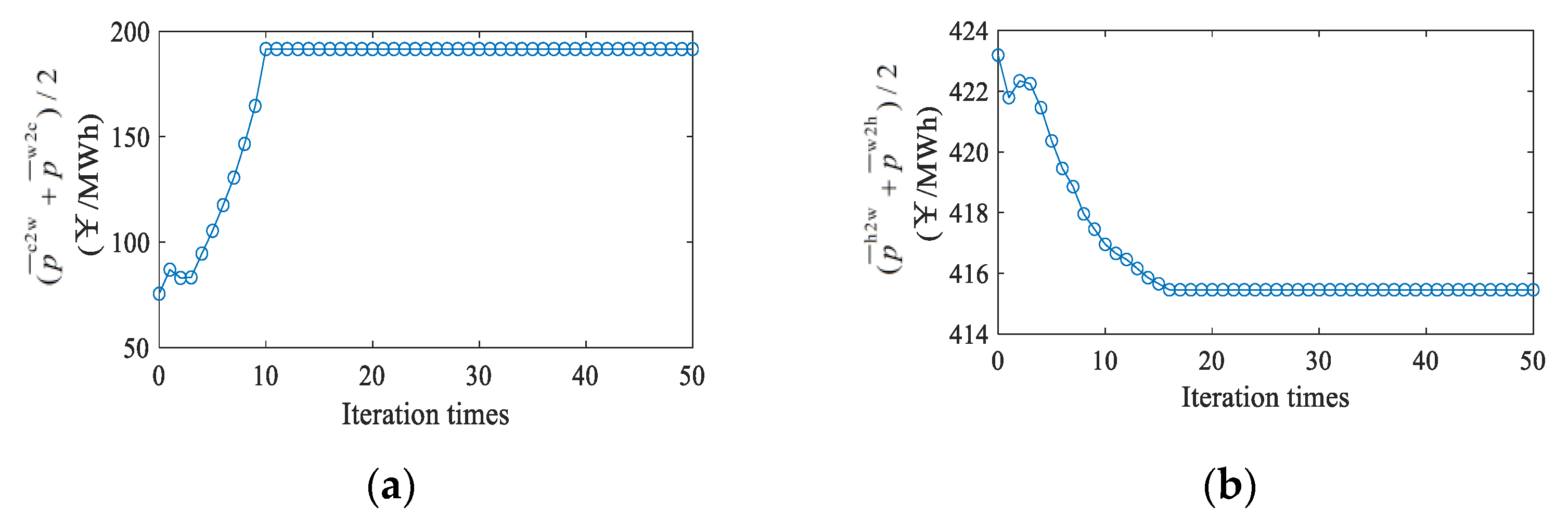
5.1. Solution of Operation Optimization Sub-Problem Based on ADMM
- (1)
- Distributed optimal operation model of wind turbine
- (2)
- Distributed optimal operation model of thermal power unit
- (3)
- Distributed optimal operation model of carbon capture equipment
5.2. Solution of Benefit Distribution Sub-Problem Based on ADMM
- (1)
- Distributed optimal operation model of wind turbine
- (2)
- Distributed optimal operation model of thermal power unit
- (3)
- Distributed optimal operation model of carbon capture equipment
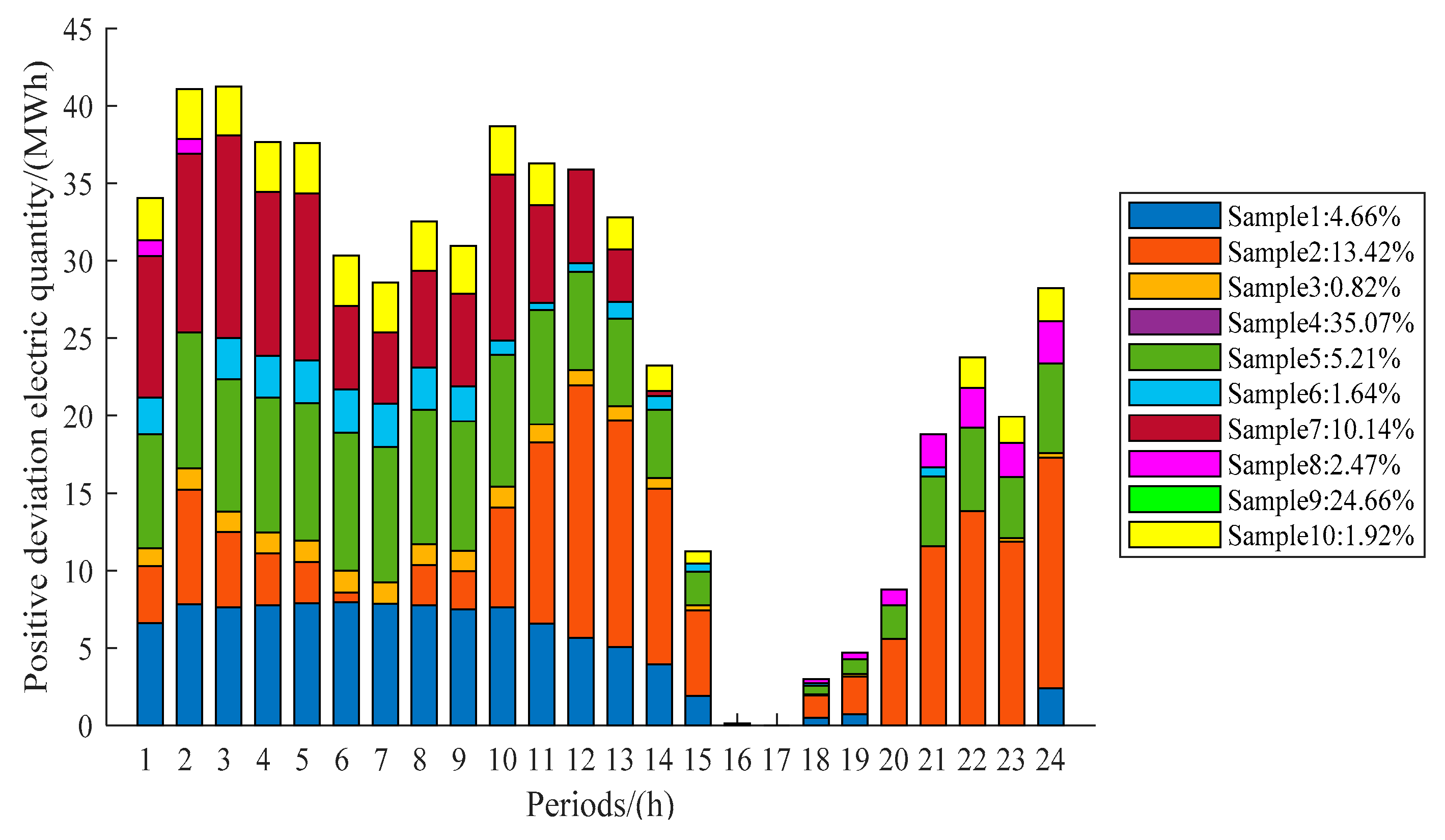
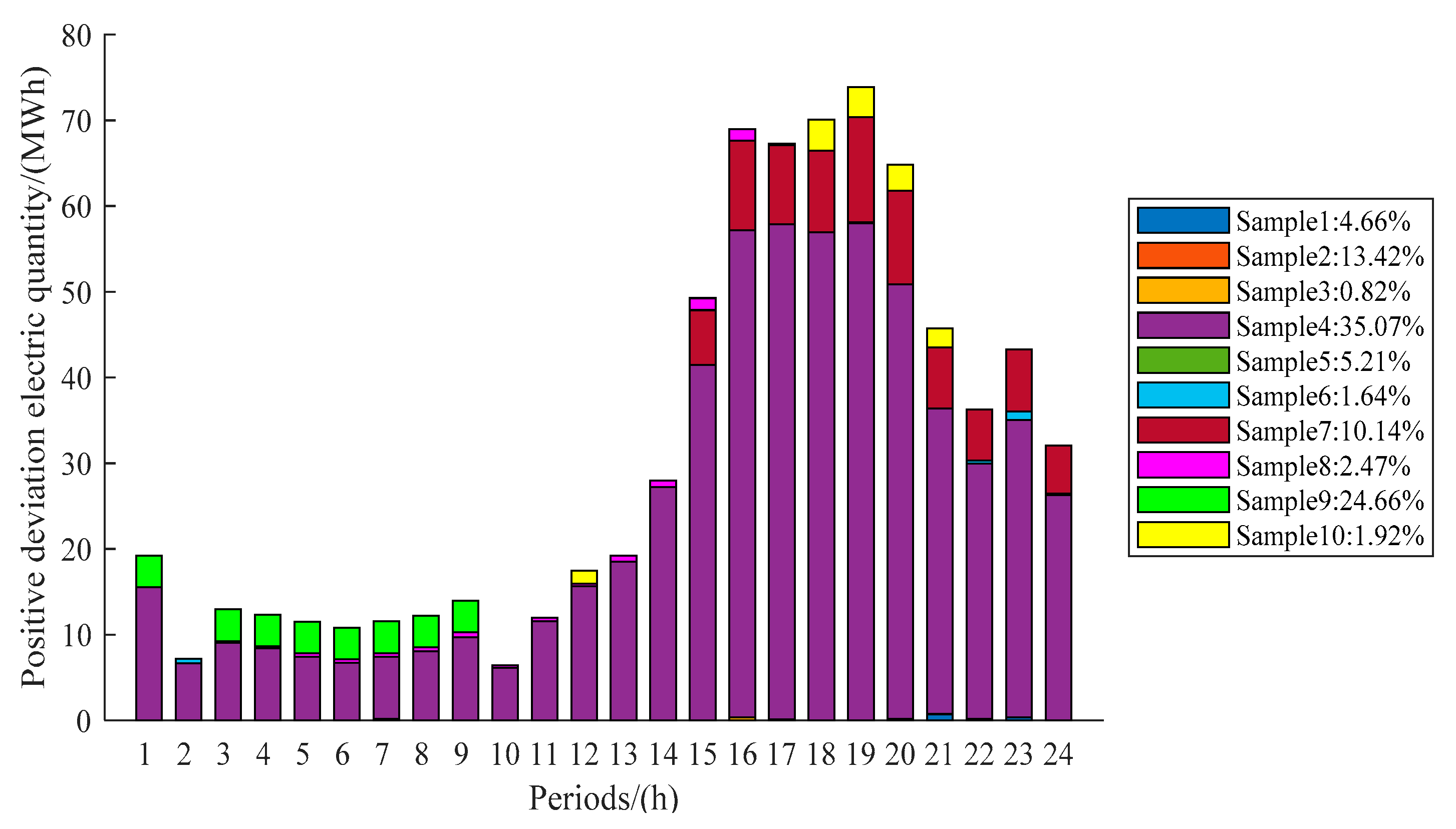
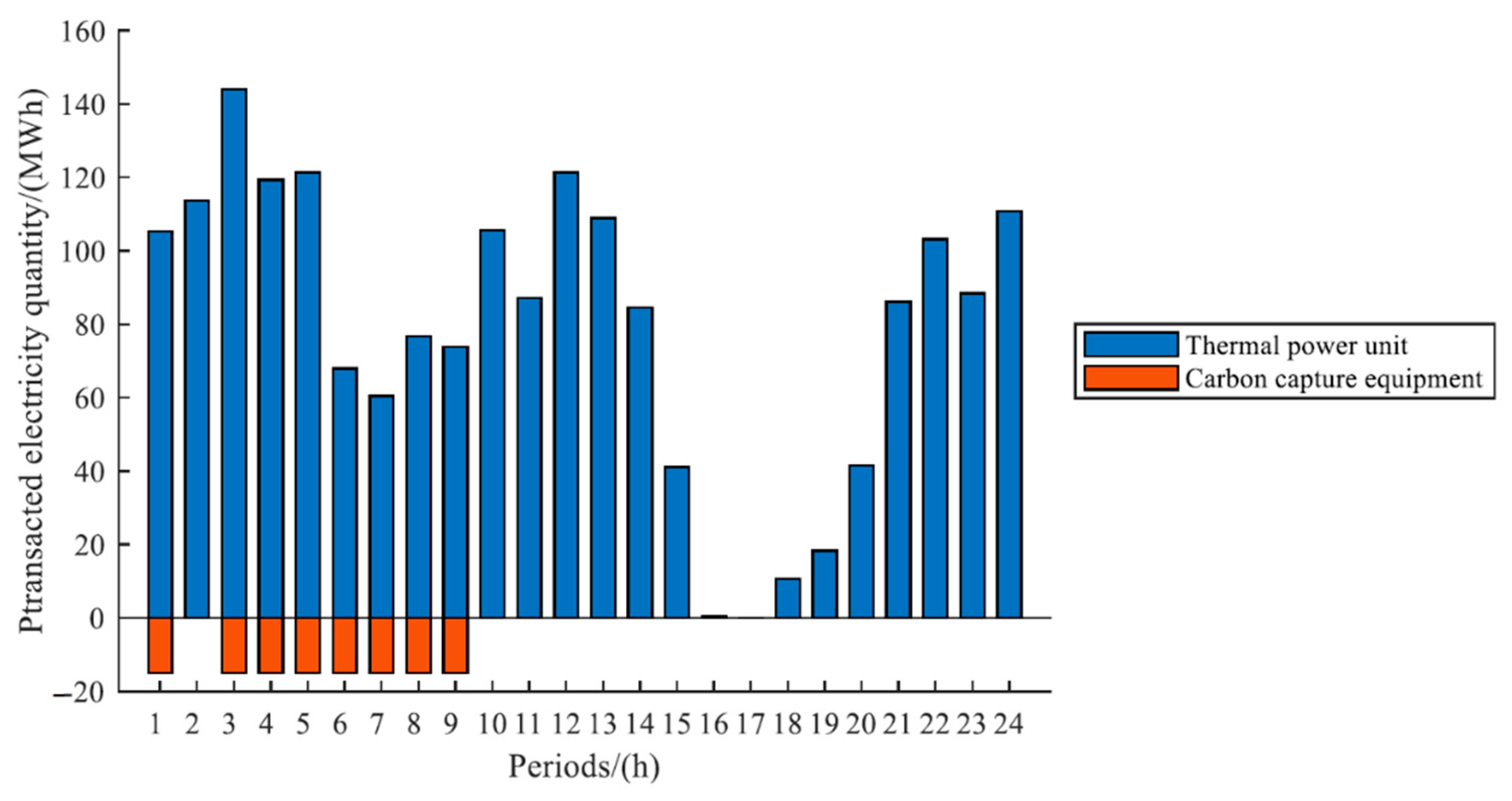
6. Case Analysis
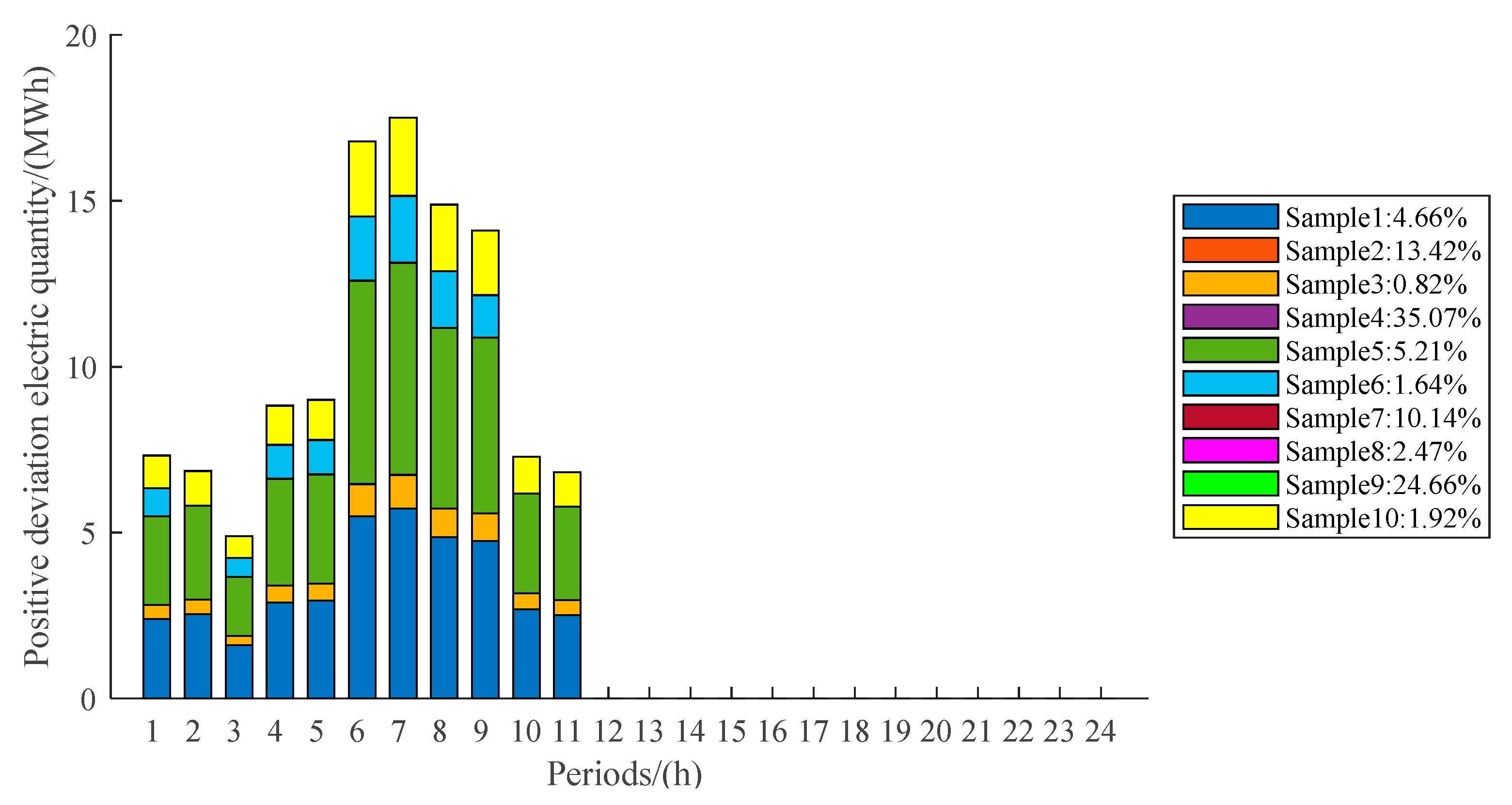
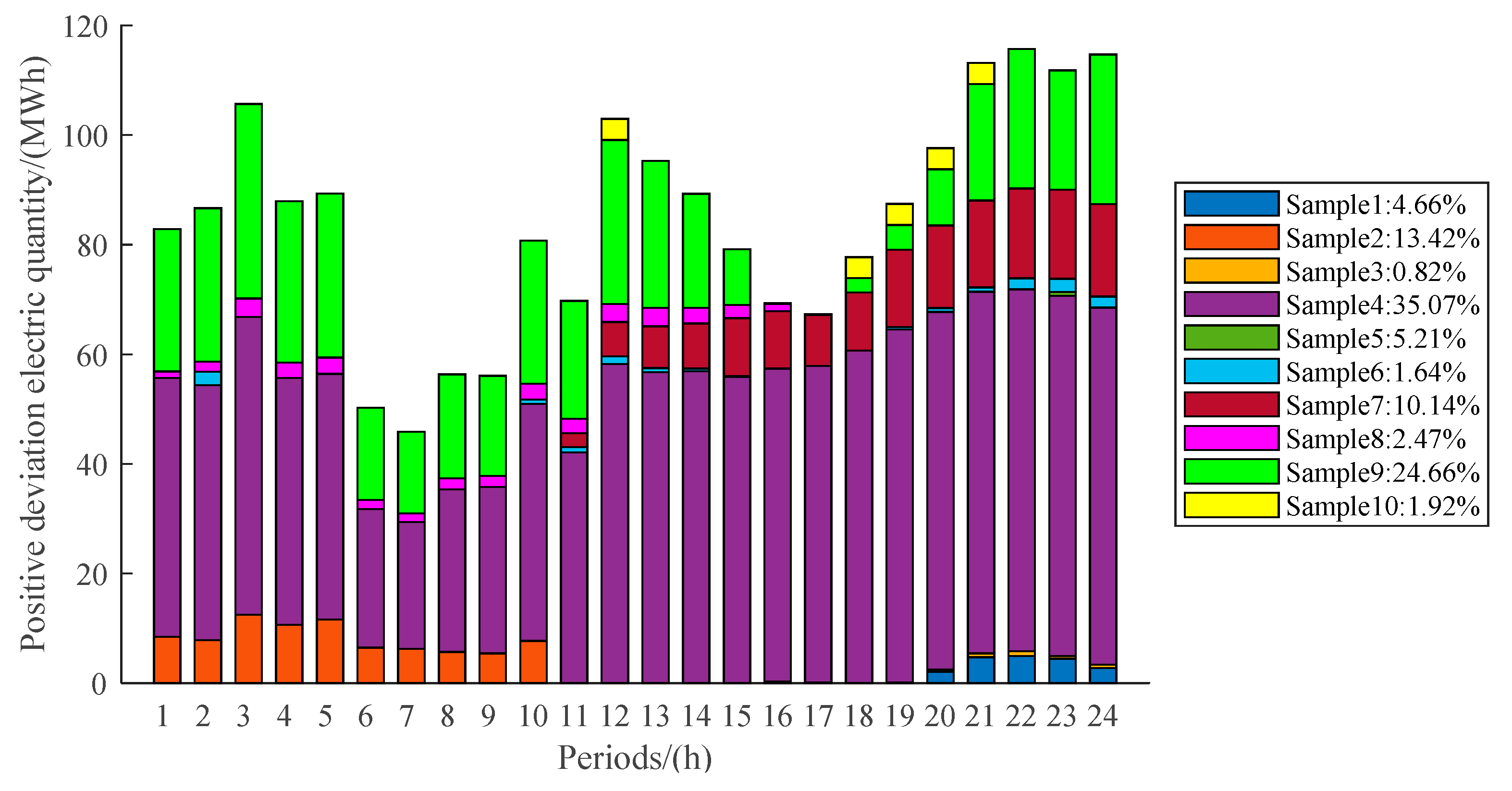
6.1. Optimization Results of Independent Operation
6.2. Optimization Results of Cooperative Operation
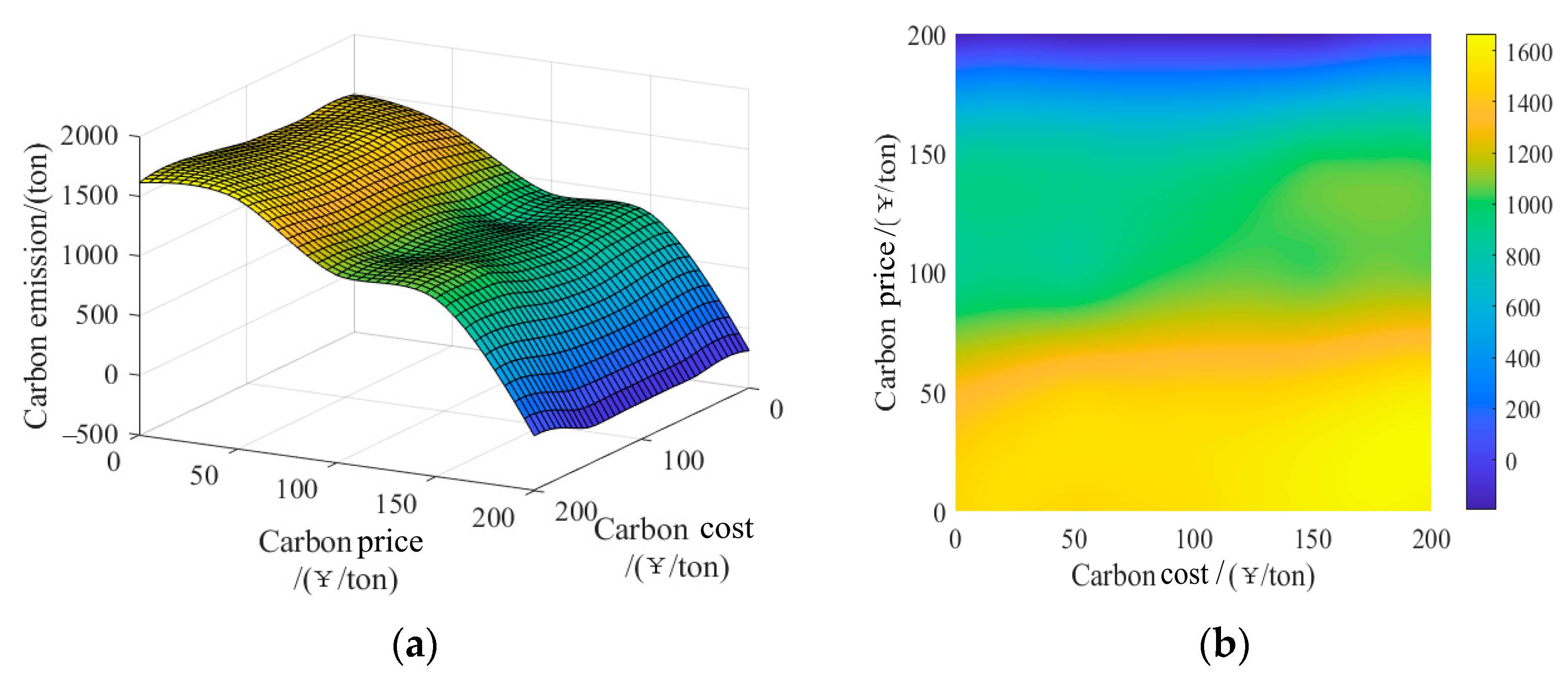
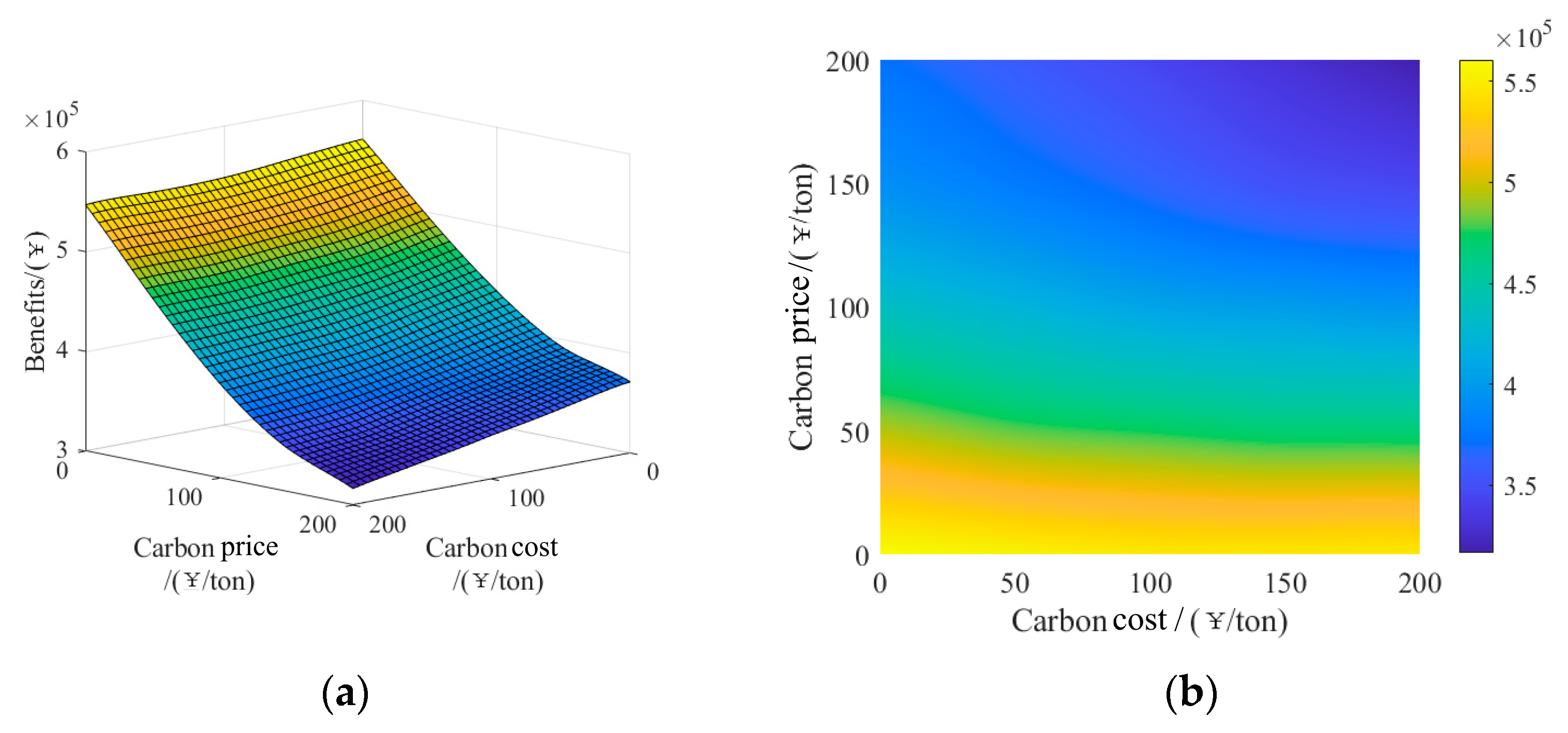
6.3. Sensitivity Analysis
7. Conclusions
- (1)
- In this paper, the cooperative operation model of wind turbine and CCPP is converted into the operation optimization sub-problem and the benefit distribution sub-problem. The proposed distributed algorithm, based on the ADMM, has good convergence characteristics for solving above problems and can make the distributed and efficient solution of the two sub-problems realized while protecting the privacy information of each participant.
- (2)
- Under the deviation punishment mechanism, there are a lot of positive and negative deviations between the declared electricity and the actual electricity generation of wind turbine. By providing up and down regulation services to wind turbine, thermal power unit and carbon capture equipment can obtain ancillary service income and reduce the declaration deviation of wind turbine, which realizes multi-win-win situation.
- (3)
- Carbon price affects both thermal power unit and carbon capture equipment. So, compared with carbon cost, the carbon emission and the alliance benefit are both more sensitive to carbon price. Thus, for alliance of wind turbine and CCPP, the policy-based emission-reducing effect by simply subsidizing to increase carbon sinks is worse than the market-based emission-reducing effect by improving carbon price.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Rated Power/(MW) | Cut-in Wind Speed/(m/s) | Cut-out Wind Speed/(m/s) | Rated Wind Speed/(m/s) | Climbing Limit/(MW/h) | |
|---|---|---|---|---|---|
| Value | 200 | 2.8 | 22.8 | 12.5 | 60 |
| Period | Power Output of the Wind Turbine/(MW) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sample1 | Sample2 | Sample3 | Sample4 | Sample5 | Sample6 | Sample7 | Sample8 | Sample9 | Sample10 | |
| 1 | 200 | 86 | 200 | 14 | 200 | 200 | 149 | 99 | 43 | 200 |
| 2 | 200 | 87 | 200 | 13 | 200 | 0 | 146 | 71 | 32 | 200 |
| 3 | 200 | 73 | 200 | 11 | 200 | 200 | 166 | 29 | 22 | 200 |
| 4 | 200 | 59 | 200 | 10 | 200 | 200 | 138 | 23 | 19 | 200 |
| 5 | 200 | 50 | 200 | 9 | 200 | 200 | 137 | 15 | 15 | 200 |
| 6 | 200 | 34 | 200 | 10 | 200 | 200 | 82 | 13 | 14 | 200 |
| 7 | 200 | 31 | 200 | 11 | 200 | 200 | 77 | 14 | 17 | 200 |
| 8 | 200 | 53 | 200 | 11 | 200 | 200 | 96 | 14 | 19 | 200 |
| 9 | 200 | 58 | 200 | 12 | 200 | 176 | 98 | 16 | 24 | 200 |
| 10 | 200 | 85 | 200 | 19 | 200 | 91 | 142 | 24 | 37 | 200 |
| 11 | 200 | 146 | 200 | 26 | 200 | 86 | 121 | 40 | 59 | 200 |
| 12 | 200 | 200 | 200 | 34 | 200 | 113 | 138 | 66 | 79 | 0 |
| 13 | 200 | 200 | 200 | 38 | 200 | 156 | 125 | 65 | 91 | 200 |
| 14 | 200 | 200 | 200 | 38 | 200 | 169 | 119 | 85 | 115 | 200 |
| 15 | 200 | 200 | 200 | 41 | 200 | 192 | 96 | 101 | 159 | 200 |
| 16 | 200 | 200 | 161 | 37 | 200 | 200 | 96 | 146 | 200 | 200 |
| 17 | 200 | 200 | 188 | 35 | 200 | 200 | 109 | 195 | 200 | 200 |
| 18 | 200 | 200 | 200 | 27 | 200 | 200 | 96 | 200 | 189 | 0 |
| 19 | 197 | 200 | 200 | 16 | 200 | 173 | 61 | 200 | 182 | 0 |
| 20 | 155 | 200 | 154 | 14 | 200 | 158 | 51 | 200 | 158 | 0 |
| 21 | 99 | 200 | 110 | 12 | 200 | 151 | 44 | 200 | 114 | 0 |
| 22 | 94 | 200 | 94 | 12 | 200 | 77 | 38 | 200 | 97 | 200 |
| 23 | 104 | 200 | 141 | 13 | 187 | 51 | 40 | 200 | 112 | 200 |
| 24 | 141 | 200 | 125 | 14 | 200 | 77 | 34 | 200 | 89 | 200 |
| Sample1 | Sample2 | Sample3 | Sample4 | Sample5 | Sample6 | Sample7 | Sample8 | Sample9 | Sample10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Probability | 4.66% | 13.42% | 0.82% | 35.07% | 5.21% | 1.64% | 10.14% | 2.47% | 24.66% | 1.92% |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| /(¥/MWh) | 400 | /(MWh) | 300 |
| /(¥/MWh) | 600 | /(MWh) | 125 |
| /(¥MWh) | 600 | /(MWh) | −125 |
| /(MWh) | 200 | /(ton/MWh) | 0.76 |
| /(MWh) | 60 | /(¥/ton) | 105 |
| /(MWh) | −60 | /(¥/ton) | 270 |
| /(ton/MWh) | 0.841 | /(MWh) | 30 |
| /(¥/MWh) | 302.4 | /(MWh) | 30 |
| /(¥/ton) | 58.5 | /(MWh) | −30 |
References
- China’s Long-term Low-Carbon Development Strategies and Pathways. Available online: https://www.efchina.org/Reports-zh/report-lceg-20210711-zh (accessed on 7 November 2021).
- China 2050: A Fully Developed Rich Zero-Carbon Economy. Available online: https://www.energy-transitions.org/publications/china-2050-a-fully-developed-rich-zero-carbon-economy/ (accessed on 1 January 2022).
- Wang, J.; Feng, L.; Palmer, P.I. Large Chinese land carbon sink estimated from atmospheric carbon dioxide data. Nature 2020, 586, 720–723. [Google Scholar] [CrossRef] [PubMed]
- Morales, J.M.; Conejo, A.J.; Pérez-Ruiz, J. Short-term trading for a wind power producer. IEEE Trans. Power Syst. 2010, 25, 554–564. [Google Scholar] [CrossRef]
- Poplavskaya, K.; Lago, J.; Vries, L.D. Effect of market design on strategic bidding behavior: Model-based analysis of European electricity balancing markets. Appl. Energy 2020, 270, 115130. [Google Scholar] [CrossRef]
- Johannes, V.; Stefan, L.; Raimund, M. Multi-unit multiple bid auctions in balancing markets: An agent-based Qlearning approach. Energy Econ. 2021, 93, 105035. [Google Scholar]
- Edenhofer; Pichs, M. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Abdilahi, A.M.; Mustafa, M.W.; Abujarad, S.Y. Harnessing flexibility potential of flexible carbon capture power plants for future low carbon power systems: Review. Renew. Sustain. Energy Rev. 2018, 81, 3101–3110. [Google Scholar] [CrossRef]
- Saboori, H.; Hemmati, R. Considering Carbon Capture and Storage in Electricity Generation Expansion Planning. IEEE Trans. Sustain. Energy 2016, 7, 1371–1378. [Google Scholar] [CrossRef]
- Kvamsdal, H.; Jakobsen, J.; Hoff, K. Dynamic modeling and simulation of a CO2 absorber column for post-combustion CO2 capture. Chem. Eng. Process. 2009, 48, 135–144. [Google Scholar] [CrossRef]
- Lawal, A.; Wang, M.; Stephenson, P. Dynamic modeling of CO2 absorption for post combustion capture in coal-fired power plants. Fuel 2009, 88, 2455–2462. [Google Scholar] [CrossRef]
- Wu, X.; Wang, M.; Liao, P.; Shen, J.; Li, Y. Solvent-based Post combustion CO2 Capture for Power Plants: A Critical Review and Perspective on Dynamic Modelling, System Identification, Process Control and Flexible Operation. Appl. Energy 2020, 257, 113941. [Google Scholar] [CrossRef]
- Chalmers, H.; Gibbins, J. Initial evaluation of the impact of post combustion capture of carbon dioxide on supercritical pulverized coal power plant part load performance. Fuel 2007, 86, 2109–2123. [Google Scholar] [CrossRef]
- Chalmers, H.; Lucquiaud, M.; Gibbins, J.; Leach, M. Flexible operation of coal fired power plants with post-combustion capture of carbon dioxide. J. Environ. Eng. 2009, 135, 449–458. [Google Scholar] [CrossRef]
- Zhou, R.J.; Liu, Y.S.; Cheng, T.L.; Pan, Z. Carbon Capture Level Optimization Modeling Considering Sensitive Internals of Carbon Emission Allowance. Autom. Electr. Power Syst. 2013, 37, 46–50. [Google Scholar]
- Zhang, X.H.; Yang, L.; Li, X.P.; Lu, Z.G. Analysis on Relative Capture Degree Based Multi-objective Optimization Decision of Flexible Operation of Carbon Capture Plan. Autom. Electr. Power Syst. 2014, 38, 143–149. [Google Scholar]
- Chen, D.P.; Wang, J.; Jing, Z.X. Decision model of carbon capture power plant to provide reserve service under flexible operation. Autom. Electr. Power Syst. 2017, 41, 138–145. (In Chinese) [Google Scholar]
- Lou, S.; Lu, S.; Wu, Y.; Kirschen, D.S. Optimizing spinning reserve requirement of power system with carbon capture plants. IEEE Trans. Power Syst. 2015, 30, 1056–1063. [Google Scholar] [CrossRef]
- Akbari-Dibavar, A.; Mohammadi-Ivatloo, B.; Zare, K.; Khalili, T.; Bidram, A. Economic-Emission Dispatch Problem in Power Systems With Carbon Capture Power Plants. IEEE Trans. Ind. Appl. 2021, 57, 3341–3351. [Google Scholar] [CrossRef]
- Lu, S.; Lou, S.; Wu, Y.; Yin, X. Power system economic dispatch under low-carbon economy with carbon capture plants considered. IET Gener. Transm. Distrib. 2013, 7, 991–1001. [Google Scholar] [CrossRef]
- Ji, Z.; Kang, C.; Chen, Q.; Xia, Q.; Jiang, C.; Chen, Z.; Xin, J. Low-carbon power system dispatch incorporating carbon capture power plants. IEEE Trans. Power Syst. 2013, 28, 4615–4623. [Google Scholar] [CrossRef]
- Lu, Z.; He, S.; Feng, T.; Li, X.; Guo, X.; Sun, X. Robust Economic/emission Dispatch Considering Wind Power Uncertainties and Flexible Operation of Carbon Capture and Storage. Int. J. Electr. Power Energy Syst. 2014, 63, 285–292. [Google Scholar] [CrossRef]
- Zhang, R.F.; Jiang, T.; Bai, L.Q. Adjustable robust power dispatch with combined wind-storage system and carbon capture power plants under low-carbon economy. Int. J. Electr. Power Energy Syst. 2019, 113, 772–781. [Google Scholar] [CrossRef]
- Qadir, A.; Manaf, N.A.; Abbas, A. Analysis of the integration of a steel plant in Australia with a carbon capture system powered by renewable energy and NG-CHP. J. Clean. Prod. 2017, 168, 97–104. [Google Scholar] [CrossRef]
- Shirmohammadi, R.; Aslani, A.; Ghasempour, R.; Romeo, L.M.; Petrakopoulou, F. Techno-economic assessment and optimization of a solar-assisted industrial post-combustion CO2 capture and utilization plant. Energy Rep. 2021, 7, 7390–7404. [Google Scholar] [CrossRef]
- Chen, X.H.; Wu, X.; Lee, K.Y. The mutual benefits of renewables and carbon capture: Achieved by an artificial intelligent scheduling strategy. Energy Convers. Manag. 2021, 233, 113856. [Google Scholar] [CrossRef]
- Li, J.; Zhao, J. Low carbon unit commitment for power system with wind farms and carbon capture devices based on DE-BBO algorithm. In Proceedings of the International Conference on Renewable Power Generation (RPG 2015), Beijing, China, 17 October 2015. [Google Scholar]
- He, L.; Lu, Z.; Zhang, J.; Geng, L.; Zhao, H.; Li, X. Low-carbon economic dispatch for electricity and natural gas systems considering carbon capture systems and power-to-gas. Appl. Energy 2018, 224, 357–370. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, N.; Cheng, Y.; Kang, C.; Xia, Q. Modeling the operation mechanism of combined P2G and gas-fired plant with CO2 recycling. IEEE Trans. Smart Grid 2019, 10, 1111–1121. [Google Scholar] [CrossRef]
- Ma, T.F.; Pei, W.; Xiao, H.; Li, D.X.; Lv, X.Y.; Hou, K. Cooperative Operation Method for Wind-solar-hydrogen Multi-agent Energy System Based on Nash Bargaining Theory. Proc. CSEE 2021, 41, 25–39+395. [Google Scholar]
| Period | Electricity Quantity Declaration/(MWh) | Period | Electricity Quantity Declaration/(MWh) | Period | Electricity Quantity Declaration/(MWh) |
|---|---|---|---|---|---|
| 1 | 149 | 9 | 98 | 17 | 200 |
| 2 | 146 | 10 | 142 | 18 | 200 |
| 3 | 166 | 11 | 146 | 19 | 200 |
| 4 | 138 | 12 | 200 | 20 | 200 |
| 5 | 137 | 13 | 200 | 21 | 200 |
| 6 | 82 | 14 | 200 | 22 | 200 |
| 7 | 77 | 15 | 200 | 23 | 200 |
| 8 | 96 | 16 | 200 | 24 | 200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Z.; Yang, J.; Li, F.; Zhao, H.; Li, X. Cooperative Operation Model of Wind Turbine and Carbon Capture Power Plant Considering Benefit Distribution. Sustainability 2022, 14, 11627. https://doi.org/10.3390/su141811627
Tan Z, Yang J, Li F, Zhao H, Li X. Cooperative Operation Model of Wind Turbine and Carbon Capture Power Plant Considering Benefit Distribution. Sustainability. 2022; 14(18):11627. https://doi.org/10.3390/su141811627
Chicago/Turabian StyleTan, Zhongfu, Jiacheng Yang, Fanqi Li, Haochen Zhao, and Xudong Li. 2022. "Cooperative Operation Model of Wind Turbine and Carbon Capture Power Plant Considering Benefit Distribution" Sustainability 14, no. 18: 11627. https://doi.org/10.3390/su141811627
APA StyleTan, Z., Yang, J., Li, F., Zhao, H., & Li, X. (2022). Cooperative Operation Model of Wind Turbine and Carbon Capture Power Plant Considering Benefit Distribution. Sustainability, 14(18), 11627. https://doi.org/10.3390/su141811627





