Abstract
Information is the basis for the sustainable and stable development of financial markets. Advanced internet technology has accelerated the dissemination of information. To investigate the impacts of private information dissemination on the sustainability of the financial market, we construct a rational expectation equilibrium (REE) model. The dissemination of private information favors noise traders who receive private information and weakens the advantage of informed traders who have direct access to private information, thus reducing noise-driven volatility and increasing fundamental-driven volatility, which is not conducive to the sustainability and stability of the financial market. Private information dissemination increases information asymmetry, reduces the number of noise traders in the market, decreases market liquidity, and hurts price efficiency for both exogenous and endogenous information acquisition, which is harmful to the sustainability of the financial market. Additionally, we numerically analyze the effects of private information on noise traders, market liquidity, and price efficiency. The numerical results are consistent with the theoretical analysis. The findings highlight the potential of private information dissemination to noise traders in financial market analysis. This study contributes to the analysis of financial market sustainability.
1. Introduction
Information is an important issue in financial market research. Improvements in information technology allow information to be disseminated faster and the dissemination range to be wider. In such an environment, information dissemination efficiency is improved. Information disseminates among traders, including noise traders [1], which creates a challenge for the financial market supervision authorities and for the sustainability of the financial market. Price volatility, market liquidity, and price efficiency are important factors affecting the sustainability of financial markets ([2,3,4,5]). An in-depth study of those issues could help to formulate effective regulatory policies for the sustainable development of financial markets.
Starting with Grossman and Stiglitz [6], most research in this area is based on a prior assumption that noise traders are irrational and that all noise traders make the same trading decisions with information unrelated to fundamental value ([6,7,8]). However, in the real economy, noise traders are unwilling to pay a cost to acquire information or falsely think that they have unique special sources of useful information. Noise traders will not refuse free private information. Private information will be considered in the trading decision when a noise trader receives private information without cost ([9,10,11,12]). Thus, noise trading may be influenced by private information dissemination. In this paper, we aim to improve our understanding of how noise traders affect financial markets. To this end, we take the influence of private information dissemination on noise traders into account.
We construct a REE model to explore the implications of private information dissemination for the financial market. Two assets exist in a competitive market: a risky asset and a risk-free asset. The risky asset is of limited supply, while the risk-free asset is infinitely supplied. Private information is only available to some traders. Informed traders are traders who own private information. They make trading based on the public information and private information that they own. Noise traders make their trading decisions via an optimal trade-off between the expected loss from trading against informed traders and the liquidity benefit of market participation. Private information may be disseminated between close family and friends. When an informed trader owns private information, they might share it with some noise traders. In this way, these uninformed noise traders will change state to being informed. All the noise traders are divided into two groups. The first group of noise traders are senior noise traders. Senior noise traders are noise traders receiving disseminated private information from informed traders. The second group are the remaining uninformed noise traders; we call them junior noise traders. Direct interpersonal communication is important in traders’ decision-making [13]. As a result of receiving private information, the demand functions of such noise traders will be different from those who have not received any private information. With different demand functions, senior noise traders and junior noise traders have different effects on the market. A trading fluctuation will be caused by the change of noise traders from junior to senior.
In summary, we find that private information dissemination has implications for price volatility, price efficiency, and market liquidity. Indeed, private information dissemination increases information asymmetry, leads fewer noise traders to be active, and lowers market liquidity, which impedes the sustainable development of the financial market ([3,4]). Private information is one of the factors behind price volatility [14]. Private information dissemination aggravates price volatility and harms price efficiency by attracting uninformed trading, which has a negative impact on the sustainable development of the financial market ([5,15]). Therefore, the dissemination of private information to noise traders is disadvantageous to the sustainability of the financial market.
Our findings on market liquidity and price efficiency contrast with those of Han et al. [8], who report the influence of public information on price efficiency and market liquidity. The study analyzed the impacts of public information precision on financial markets under the assumption that there is no private information dissemination. The normal state of the economy, involving information asymmetry and private information dissemination, should be used to truly reflect the information and efficiency of the financial market. Private information can be disseminated from informed traders to some noise traders for various reasons, such as emotional motivations, social information, etc. In our research, we take this private information dissemination into account and find that Han et al. [8] overestimate the influence of public information on noise traders’ number and market liquidity, as well as underestimating the influence of public information on price efficiency.
The financial markets relate to sustainable development [16]. The sustainability of the financial market relates to its ability to retain its identity or its capability to perform its functions. The sustainable and stable development of the financial market provides a financial guarantee for the sustainable development of the society and the environment. A better understanding of the drivers behind the price volatility and market liquidity in financial markets will contribute to a better analysis of financial market sustainability. In this sense, our study contributes to the analysis of sustainability.
The remainder of this paper is organized as follows. Section 2 provides related studies. Section 3 is the model description and assumptions. The equilibrium and implications of private information dissemination are discussed in Section 4. Section 5 extends the economy to the case where private information is endogenously acquired. Section 6 presents a simulation to verify the theoretical analysis. Section 7 concludes this work.
2. Literature Review
Our study relates to literature that examines the effect of information dissemination on the financial market. Information dissemination improves price efficiency when information is obtained exogenously ([17,18]) but reduces it when information is acquired endogenously ([7,19]). The dissemination of information between rational traders improves market liquidity ([1,20]). Colla and Mele [17] propose an equilibrium model for the impacts of public and private information on financial markets. Van Ness et al. [21] analyze the relationship between private information in trades and fluctuations in stock prices and demonstrate that trading-conveyed private information reduces stock return synchronicity. Grego [22] finds that the dissemination of information about price volatility decreases price efficiency. A better understanding of the liquidity risk leads to sustainable trading for traders [4]. Noise traders, as liquidity providers and price volatility drivers, play an important role in the sustainable and stable development of financial markets ([3,4]). However, existing studies have not examined the effect of private information dissemination on noise traders, and our study can fill this gap.
There are studies that have analyzed the way information is disseminated in financial markets. Starting with Admati and Pfleiderer [23], private information is disseminated from informed traders to uninformed traders through price in a great deal of research. Thus, price is not only an aggregator of information but also a transmitter ([24,25]). The price acts as a linker connecting traders’ own information with the information already contained in the price. Several studies investigate the way in which information disseminates among traders through more direct channels ([7,9,20,26,27], etc.). Bowden and McDonald [28] research information sharing with social networks and find that expected social learning relates to the experts. Han and Yang [7] study the implications of social communication for market efficiency and liquidity. Hong et al. [9] prove that social interaction helps to increase stock market participation. Ahern [20] uses hand-collected data, finding that inside information flows through strong ties based on family, friends, and geographic proximity. In Foerster [27] and Andrei and Cujean [29], private information is disseminated through social networks through talking. Information dissemination in the above studies only takes place between rational traders. However, none of these studies consider the channel of private information dissemination to noise traders.
Private information being widely disseminated among families and friends who have intimate relationships is a pervasive phenomenon. Thus, it is possible that private information disseminates from an informed trader to some noise traders who are intimate. With different expectations, the demand functions of noise traders who receive private information should be different from those who do not receive private information. We take the influence of information dissemination on noise trading into consideration and build a REE model to study its impact on the financial market. Previous studies suggest that private information dissemination among rational traders increases market liquidity [20] and price efficiency ([17,18]). Our study on private information dissemination comes to different conclusions, indicating that the dissemination of private information to noise traders decreases market liquidity and price efficiency. Our paper adds to the growing body of literature on information dissemination in financial markets.
Noise makes financial markets possible [30]. An increase in noise trading can improve market liquidity ([8,23,31,32]) but may reduce price efficiency ([8,31,32,33]). However, most studies adopt the definition of noise traders given by Kyle [34] and Black [30]. In these studies, noise trading is based on information that is unrelated to fundamental value ([35,36]). Yuan et al. [37] define noise traders as traders who trade based on incomplete information. Noise traders are not completely irrational traders, but rather bounded rational traders with a low degree of rationality ([38,39,40]). A trader profits not because they have better information but because they have some information that has not been discounted by the market [41]. A trader’s expected trading profit depends on the information that they own and information reflected in the price. As private information has not been absorbed by the price, when a noise trader receives private information for some reason, the private information will affect the noise trader’s expecting trading profit. However, the influence of private information dissemination on noise traders has not been considered in the existing studies. We shed light on the role that private information plays in the decision-making process of noise traders.
Grossman and Stiglitz [6] developed a REE model that is widely used to study the motivations for acquiring costly information and its impact on the financial market. Traders’ trading decisions are made based on a trade-off depending on all available information, whereas Grossman and Stiglitz [6] ignore information outside the price channel. Following this, a growing body of literature has used the REE model to analyze the impact of information on the financial market ([42,43,44,45]). However, none of these researchers considered the impact of the dissemination of private information to noise traders. We study the impact of private information transfer on noise traders and further analyze the impact of private information dissemination on price volatility, market liquidity, and price efficiency. We revise the model in Han et al. [8] and consider information dissemination in it. Colla and Mele [17] and Han N.O. [18] prove that social communication improves price efficiency when information is exogenous. However, our results show that, in both endogenous and exogenous cases, information dissemination negatively affects price efficiency. Therefore, our paper complements Colla and Mele [17] and Han N.O. [18].
3. Model Description and Assumptions
Suppose there are two assets in a competitive market: a risky asset and a risk-free asset. The risky asset has an endogenous price and a fixed supply. Simply, the risky asset supply is normalized as one share. The risk-free asset is unlimited and supplied with a constant value of 1. Traders who decide to participate in the emerging trading market are called active traders, and those who do not participate in the market are called inactive traders. The active traders will be divided into three types: informed traders, senior noise traders, and junior noise traders.
All traders can observe public signal and asset price , where
is the precision of public signal ; a larger means that contains more information regarding future payoff.
Suppose that the informed traders are continuous in . All the informed traders have a constant absolute risk aversion (CARA) utility; the risk aversion coefficient is denoted by . An informed trader i not only can observe the public information from a public signal and the price , but they also have access to private information from a private signal . satisfies the following form:
Informed traders trade on public information and their private information to maximize their expected utility.
Noise traders have mastered some information irrelevant to future payoff, but they believe they have all of the information regarding the future payoff of the risk asset. Noise traders are unlikely to acquire private information actively, but they will not refuse free information. Noise traders trade on all of the information they own to maximize their benefit. Therefore, if a noise trader receives private information disseminated from informed traders, the trading of the noise trader will be affected. Noise traders are not perfectly rational traders, and their learning and analysis abilities are weaker than informed traders. Hence, though they receive disseminated private information, noise traders have a different demand function from informed traders.
The time is divided into three periods. At , noise traders can only obtain public information from and . Between and , private information can be disseminated from informed traders to parts of the noise traders for some reasons, such as emotional motivations and social information, etc. Noise traders make trading decisions at . Suppose that the private information dissemination between and has no effects on noise traders’ decisions. After the dissemination of private information during the first half period, a part of the noise traders become informed with a probability q . These noise traders are named senior noise traders. They are different from informed traders in demand functions. Noise traders who have not received private information until are called junior noise traders. At , noise traders trade-off between the costs and benefits, and then make decisions regarding whether to participate in the trading and how much to trade. At , active traders trade their assets competitively. Cash flows are realized at .
In Admati and Pfleiderer [23], noise trader l who decides to trade must trade a fixed amount of risk asset. In our analysis, demands are different for junior and senior noise traders. Junior noise traders trade like the noise traders in Admati and Pfleiderer [23]. However, for the senior traders, the private information leads them to trade more units of a risk asset; can be both positive or negative.
By participating in the market, active noise traders can enjoy the exogenous liquidity benefit . Assuming that the expected utility of a noise trader is W, then W can be positive or negative, since there are endogenous trading costs.
The number of active noise traders in the market is defined as L. Let be the share of risk assets traded by a noise trader l, . Then, has the following form:
where .
Supposing that random variances are mutually independent. The total trading of active noise traders is
Obviously, private information dissemination causes more noise trading. The precise of is defined as , then
4. The Equilibrium
This study is based on the Grossman and Stiglitz [6] concept of REE. At the trading time , informed traders make their trading to maximize their expected utility, and senior noise traders and junior noise traders trade an amount of asset to maximize their benefit net of expected trading loss. The demand functions of these three types of traders are different. The following subsections present a discussion of the equilibrium.
4.1. Financial Market Equilibrium
Assuming that every trader believes that price function has the following form:
All coefficients in the above price function are endogenous. Following the spirit of Kyle [34], market liquidity, .
As informed traders are CARA, the demand function for a informed trader is
where is an informed trader i’s conditional mean of , and is the variance.
Given public signal , the information in price equivalent to signal is
Suppose that the precise value of is ; then, . reflects how much private information can be inferred from the price; that is, it reflects the level of price informativeness.
By Bayes’ rule, the following expression of and can be obtained:
and
Then, it is easy to obtain
The parameters and are functions of q. In the market-clearing state, the following condition holds:
In equilibrium, the expressions of have the following form:
where is a function of q.
4.2. Price Volatility
To analyze how private information dissemination affects price volatility through noise traders, we decompose it as Ozsoylev et al. [1]:
where is the fundamental-driven volatility driven by the volatility of future payoff , and is the noise-driven volatility caused by noise traders. We obtain the expressions as follows:
Obviously, and are related to private information dissemination q.
Theorem 1.
Private information dissemination reduces noise-driven volatility but increases fundamental-driven volatility. That is, , .
The dissemination of private information diminishes the advantages of informed traders with private information and creates greater fundamental-driven volatility. The trading volume of informed traders will be decreased due to the weakening of the advantages of having private information; therefore, less fundamental value is reflected in the market, leading to more fundamental-driven price volatility. The dissemination of private information weakens noise-driven volatility. On the one hand, the dissemination of private information favors senior noise traders. As private information is disseminated, the proportion of senior noise traders in the market increases, and their trading decisions become more rational than when they do not receive private information. On the other hand, the private information dissemination increases information asymmetry and leads to fewer noise traders being active in trading. As a result, the price volatility driven by them decreases. Price volatility may adversely affect the sustainable development of the financial market.
4.3. The Equilibrium under an Endogenous L
In this part, we analyze noise traders’ decisions. All noise traders participating in the trading can acquire an exogenous liquidity gain, . The expected return of noise trader l is . A positive means that noise trader l buys units of a risky asset at a price at and then sells them at with a payoff .
Similarly, a negative means that noise trader l shorts units of a risky asset and obtains payoffs at , and then produces an obligation of at .
For a given number of noise traders L, the expected utility of a noise trader is
The equilibrium is defined by
It is easy to prove that , . As is a continuous function, by the intermediate value theorem, there exists at least one equilibrium . Since and , it is obvious that L affects in two opposite ways, and q affects positively.
As and , this shows that a larger q leads to a stronger liquidity.
Theorem 2.
(i) For any given , there exists an equilibrium , where is determined by
(ii) If and , there exist three equilibria ; otherwise, there is a unique equilibrium except for a parameter set of Lebesgue measure zero.
Proof.
See Appendix A. □
4.4. The Property of the Equilibrium
Following Crego [22], an equilibrium is stable when , and unstable when Since and , if there is a unique equilibrium, it must be a stable one, and if there are three equilibria, denoted by , then has two extreme points: the one between and is negative, and the other one between and is positive. With the definition of stability above, it is obvious that and are stable and that is unstable.
4.5. Implication of Information Dissemination
We discuss the influence of private information dissemination on the market liquidity and price efficiency in this part. Private information dissemination increases the information asymmetry. Some active noise traders will choose to be inactive. The faster the private information spread, the more noise traders will exit the market, i.e., . The existing active noise traders who receive the disseminate information will adjust their trading volumes. Good (bad) private information dissemination helps senior noise traders to increase (decrease) their trading volumes. We know that an equilibrium is stable if and only if From (12), it is easy to obtain that
For any , always holds. Using an implicit theorem for (12), it can be obtained that
The liquidity is a function of , where is with respect to q, so
The first term is an indirect effect, and the second is a direct effect. Since , , , , we find that the negative impact of the first term outweighs the positive impact of the second term in . Thus, private information dissemination affects the market liquidity negatively. Private information dissemination leads to a smaller volume of noise trading, which hinders the market liquidity. The price efficiency decreases with private information dissemination. As private information dissemination results in a lower proportion of informed trading, less fundamental information is revealed in price. With the expression , then
By the implicit theorem,
Thus, , information dissemination has a negative effect on price efficiency.
Theorem 3.
Private information dissemination increases the information asymmetry and reduces the the number of noise traders; formally, . The market liquidity is decreased through private information dissemination; formally, . The price efficient is reduced by private information dissemination; formally, .
The work by Han et al. [8] is a special case in our study. This paper generalizes the research of the literature.
5. Endogenous Information Acquisition
Information acquisition is taken into account in this section. Assume that informed trader i acquires private information at with a cost function . is a monotonous increase and convex.
5.1. The Equilibrium
Suppose that informed trader i believes the precisions of other informed trader’ private signals are . Just like Grossman and Stiglitz [6], informed trader i’s expected net benefit of the private signals is
The informed trader i is arbitrary above, so is established. Using the first order condition , the following equation can be obtained via direct calculation:
is implicitly determined, . Distinctly, the equilibrium condition for is
where is implicitly determined; .
Theorem 4.
There exists an overall equilibrium where the precision of informed traders’ private information is determined by
where is uniquely determined by
the equilibrium mass of noise traders who choose to take part in the market is
The equilibrium price function is , with . If , the overall equilibrium is unique.
Proof.
See Appendix B. □
5.2. The Effect of Information Dissemination
For price efficiency , the following expression can be obtained via direct calculation:
where , ( is a convex function). when .
Theorem 5.
Assuming that . In equilibrium with endogenous information acquisition, private information dissemination weakens price efficiency. Formally, in the overall equilibrium.
Proof.
See Appendix C. □
Informed traders are the main contributors to price efficiency. The dissemination of private information to noise traders will seriously dilute the information advantages of informed traders, leading to a significant reduction in their trading volume. This negative effect overcomes the positive effect caused by a decrease in the number of noise traders. Thus, the dissemination of private information reduces price efficiency.
6. Numerical Results
In this section, several economic situations are analyzed to intuitively observe the influence of information dissemination on the number of equilibrium noise traders, market liquidity, and price efficiency. The parameter q controls the speed of information dissemination. Following Han et al. [8], we define that , where is constant. Set , .
Figure 1 displays the trend of the equilibrium noise traders’ number, market liquidity, and price efficiency with information dissemination in economics with different information costs. The number of noise traders L decreases with the increase of information dissemination q in Figure 1a. According to economic theory, individuals’ behavioral decisions are more inclined to deterministic results and are averse to uncertain results. Information dissemination increases information asymmetry among traders and leads fewer junior noise traders to participate in the market trading. We know that the information cost coefficient c may affect informed traders’ information acquisition. In order to observe whether changes in the value of c will cause different results, we observe the three curves of the equilibrium values of the noise traders number L in Figure 1a. We find that the trend of the equilibrium noise traders’ numbers decrease with the information costs c. In an economy with a higher information cost, the advantages of information become more apparent. Moreover, with information dissemination, more senior noise traders become active. However, when the information disseminates more widely, the information advantage of senior noise traders is weakened; thus, a faster decreasing rate of the equilibrium noise traders arises.
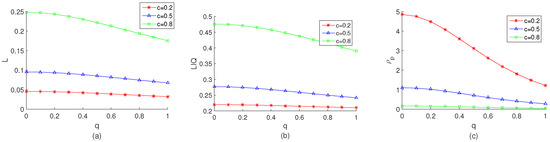
Figure 1.
(a): the effect of information dissemination on the number of equilibrium noise traders in economics. (b): the effect of information dissemination on market liquidity in economics. (c): the the effect of information dissemination on price efficiency in economics. Information acquisition costs in the three economics are set: , , . Parameter .
Because the information cost affects informed traders’ information acquisition, it may make an impact on the market liquidity. Figure 1b is the the equilibrium values of market liquidity with an increase of information dissemination in situations where the information acquisition costs are different: , , . It is obvious that the market liquidity decreases with information dissemination for all of the three situations. Comparing the situation where and , we find that the equilibrium market liquidity increases with the information costs c. When the information cost is higher, the advantages of traders who know the private information are highlighted. The information advantage attracts traders who have the private information to trade more, which leads to better market liquidity. Furthermore, the advantages become stronger with a higher information cost. From a comprehensive comparison of all curves in Figure 1b, we obtain the same conclusion.
Figure 1c plots the influence of information dissemination on price efficiency. In consideration of the effects of the information cost coefficient c on information acquisition, we plot three cases with different information cost values to make a comparative analysis. It shows that price efficiency decreases with q. By analyzing the three curves, we discover that the higher the information cost, the lower the price efficiency. On the one hand, when the information cost is higher, the informed trading volume will be reduced. Therefore, less fundamental information is reflected in the price. On the other hand, higher information costs reduce the information acquisition, which leads to weaker information dissemination impacts. Thus, a higher information cost results in lower price efficiency.
Han et al. [8] study the influence of public information on the number of noise traders, market liquidity, and price efficiency, but they have not considered information dissemination. Figure 2 shows the effect of public information on the number of noise traders, market liquidity, and price efficiency under different degrees of information dissemination, such as the case where equals the situation in Han et al. [8] In Figure 2a, private information dissemination weakens the effect of public information on the number of noise traders. Figure 2b displays that private information dissemination weakens the impact of public information market liquidity. The reinforcement increases with public information precision. Thus, there is a significant overestimation in Han et al. [8] In Figure 2c, the effect of public information on price efficiency is enhanced by information dissemination, and this effect decreases with the information dissemination. Therefore, effects of public information on noise traders’ number and market liquidity are overestimated and that on price efficiency is underestimated in Han et al. [8].
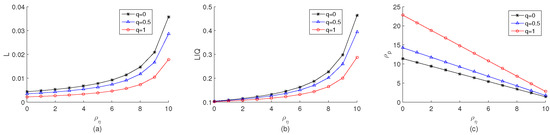
Figure 2.
(a): the effect effect of public information on the equilibrium number of noise traders; (b): the effect effect of public information on the equilibrium number of market liquidity; (c): the The effect effect of public information on the equilibrium number of price efficiency. The information dissemination speeds are set: , , . The information acquisition cost parameter is .
7. Conclusions
Information is a significant issue in financial market research. In this paper, we take private information dissemination into account and establish a REE model to study its impacts on price volatility, the number of noise traders, market liquidity, and price efficiency. The results show that private information dissemination expands fundamental-driven volatility, cuts down the number of noise traders in the market, reduces market liquidity, and decreases price efficiency. Moreover, when extending our economy to the situation where information is acquired endogenously, the same results are obtained.
This paper contributes to the analysis of the sustainability of financial markets. The numerical results verify that the parameters’ value can affect the size but not the direction or trend that the impact of information dissemination has on the financial markets. It can be seen from the figures that an increase in information cost strengthens the influence of information dissemination on noise traders’ number and market liquidity and weakens the impact of information dissemination on the price efficiency. The number of noise traders, market liquidity, and price efficiency all decrease with the increase in information dissemination. In addition, we find that information dissemination negatively affects the impact of public information on the number of noise traders and market liquidity but positively affects the public information price efficiency.
The dissemination of private information to noise traders plays a role as a driver of the non-sustainability of the financial market. Regulators should strengthen the supervision of information disclosure, provide traders with continuous fundamental information to weaken the negative impact of private information dissemination on the financial market, and contribute to the sustainable development of the financial market.
We would also like to point out that this topic needs further research. First, the heterogeneity of the noise traders is not considered in this study. In practice, the probability of receiving private information varies with the social networks of noise traders. Second, further empirical analysis is needed.
Author Contributions
Conceptualization, H.L. and W.L.; Methodology, H.L.; Writing—original draft, H.L.; Writing—review & editing, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The Shanxi Province youth talent support program (grant number 20190705); Humanities and Social Sciences Foundation of Ministry of Education, China (grant number 20YJA910004); National Statistical Science Research Project of China (grant number 2022LZ14); Scientific Activities of Selected Returned Overseas Professionals in Shanxi Province (grant number 20220025); National Natural Science Foundation of China (grant number 71971131).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proof of Theorem 1
The equilibrium expected profit of a noise trader is
is equivalent to
Let
Then, .
We can easily obtain
The discriminant of is
If , then for any . Thus, when , monotonically increases with L. Thus, there exists a unique solution to (15). If , then . In this case, there are two positive solutions to , which are denoted by and :
Using direct calculation, we obtain
As and , increases on , and decreases on . There are two equilibria if one of and is zero. Otherwise, there will be a unique equilibrium . is equivalent to
is equivalent to
The two above inequalities are equivalent to and .
Thus, if and , there exist three equilibria .
Similarly, we can prove that if and , there will be two equilibria .
If the values of are in the space but none of the above two conditions are satisfied, the equilibrium is unique.
Appendix B. Proof of Theorem 3
We know the equilibrium is determined by joining (20) and (21). Equation (20) can be rewritten as the following: .
Taking the expression of into (21), we have
Equation (A17) can be rewritten as
Appendix B.1
Define
then,
Since is convex, we have and . Thus, and is monotonous. Calculating directly, , so there is a unique that satisfies . For all , we have
Appendix B.2
Appendix B.3
Define
where
It is easy to acquire that
When , there is . Thus, when , , is decreasing. When , is increasing in . Using the intermediate theorem, there is a unique that satisfies the following equation:
Appendix C. Proof of Theorem 4
Appendix C.1
In the overall equilibrium, ; thus,
The above (A24) can be arranged as
Since is convex, , the numerator of is equivalent to . Using Bayes’ rule, we have . Therefore,
By calculating directly, when . The denominator of equals to
Thus, is always established.
Appendix C.2
Let
and
Obviously,
By calculating the derivation of both sides of (25), we have
Let ; that is,
It is easy to know that
Thus,
Based on the above analysis, when .
Appendix C.3
When , as
By calculating directly, we have
Since is convex, and . Furthermore, when . Therefore, Theorem 4 is proven.
References
- Ozsoylev, H.N.; Walden, J.; Yavuz, M.D.; Bildik, R. Investor Networks in the Stock Market. Rev. Financ. Stud. 2013, 27, 1323–1366. [Google Scholar] [CrossRef]
- Ruan, L. Research on sustainable development of the stock market based on VIX index. Sustainability 2018, 10, 4113. [Google Scholar] [CrossRef]
- Jeong, S.H.; Lee, H.S.; Nam, H.; Oh, K.J. Using a genetic algorithm to build a volume weighted average price model in a stock market. Sustainability 2021, 13, 1011. [Google Scholar] [CrossRef]
- Hur, S.K.; Chung, C.Y.; Liu, C. Is liquidity risk priced? Theory and evidence. Sustainability 2018, 10, 1809. [Google Scholar] [CrossRef]
- Truong, T.T.T.; Kim, J. Premiums for non-sustainable and sustainable components of market volatility: Evidence from the Korean stock market. Sustainability 2019, 11, 5123. [Google Scholar] [CrossRef]
- Grossman, S.J.; Stiglitz, J.E. On the impossibility of informationally efficient markets. Am. Econ. Rev. 1980, 70, 393–408. [Google Scholar]
- Han, B.; Yang, L. Social networks, information acquisition, and asset prices. Manag. Sci. 2013, 59, 1444–1457. [Google Scholar] [CrossRef]
- Han, B.; Tang, Y.; Yang, L. Public information and uninformed trading: Implications for market liquidity and price efficiency. J. Econ. Theory 2016, 163, 604–643. [Google Scholar] [CrossRef]
- Hong, H.; Kubik, J.D.; Stein, J.C. Social Interaction and Stock-Market Participation. J. Financ. 2004, 59, 137–163. [Google Scholar] [CrossRef]
- Ivkovi, Z.; Weisbenner, S. Information Diffusion Effects in Individual Investors’ Common Stock Purchases: Covet thy Neighbors’ Investment Choices. Rev. Financ. Stud. 2007, 20, 1327–1357. [Google Scholar] [CrossRef]
- Cohen, L.; Frazzini, A.; Malloy, C. The small world of investing: Board connections and mutual fund returns. J. Political Econ. 2008, 116, 951–979. [Google Scholar] [CrossRef]
- Pool, V.K.; Stoffman, N.; Yonker, S.E. The people in your neighborhood: Social interactions and mutual fund portfolios. J. Financ. 2015, 70, 2679–2732. [Google Scholar] [CrossRef]
- Shiller, R.J. Comovements in stock prices and comovements in dividends. J. Financ. 1989, 44, 719–729. [Google Scholar] [CrossRef]
- French, K.R.; Roll, R. Stock return variances: The arrival of information and the reaction of traders. J. Financ. Econ. 1986, 17, 5–26. [Google Scholar] [CrossRef]
- Xie, J.; Xia, W.; Gao, B. The sustainability of stock price fluctuations: Explanation from a recursive dynamic model. PLoS ONE 2021, 16, e0255081. [Google Scholar] [CrossRef] [PubMed]
- Waygood, S. How do the capital markets undermine sustainable development? What can be done to correct this? J. Sustain. Financ. Investig. 2011, 1, 81–87. [Google Scholar] [CrossRef]
- Colla, P.; Mele, A. Information linkages and correlated trading. Rev. Financ. Stud. 2010, 23, 203–246. [Google Scholar] [CrossRef]
- Ozsoylev, H.N.; Walden, J. Asset pricing in large information networks. J. Econ. Theory 2011, 146, 2252–2280. [Google Scholar] [CrossRef]
- Halim, E.; Riyanto, Y.E.; Roy, N. Costly information acquisition, social networks, and asset prices: Experimental evidence. J. Financ. 2019, 74, 1975–2010. [Google Scholar] [CrossRef]
- Ahern, K.R. Information networks: Evidence from illegal insider trading tips. J. Financ. Econ. 2017, 125, 26–47. [Google Scholar] [CrossRef]
- Van Ness, B.; Van Ness, R.; Yildiz, S. Private information in trades, R2, and large stock price movements. J. Bank. Financ. 2021, 131, 106194. [Google Scholar] [CrossRef]
- Crego, J.A. Why does public news augment information asymmetries? J. Financ. Econ. 2020, 137, 72–89. [Google Scholar] [CrossRef]
- Admati, A.R.; Pfleiderer, P. A Theory of intraday patterns: Volume and price variability. Rev. Financ. Stud. 1988, 1, 3–40. [Google Scholar] [CrossRef]
- Hayek, F.A. The use of knowledge in society. Knowl. Manag. Organ. Des. 1996, 35, 7–15. [Google Scholar]
- Verrecchia, R.E. Information acquisition in a noisy rational expectations economy. Econometrica 1982, 50, 1415–1430. [Google Scholar] [CrossRef]
- Duffie, D.; Manso, G. Information percolation in large markets. Am. Econ. Rev. 2007, 97, 203–209. [Google Scholar] [CrossRef]
- Foerster, M. Dynamics of Strategic Information Transmission in Social Networks. Theor. Econ. 2019, 14, 253–295. [Google Scholar] [CrossRef]
- Bowden, M.; McDonald, S. The Impact of interaction and social learning on aggregate expectations. Comput. Econ. 2008, 31, 289–306. [Google Scholar] [CrossRef]
- Andrei, D.; Cujean, J. Information percolation, momentum and reversal. J. Financ. Econ. 2017, 123, 617–645. [Google Scholar] [CrossRef]
- Black, F. Noise. J. Financ. 1986, 41, 528–543. [Google Scholar] [CrossRef]
- Subrahmanyam, A. Risk aversion, market liquidity, and price efficiency. Rev. Financ. Stud. 1991, 4, 417–441. [Google Scholar] [CrossRef]
- Bloomfield, R.; O’Hara, M.; Saar, G. How noise trading affects markets: An experimental analysis. Rev. Financ. Stud. 2009, 22, 2275–2302. [Google Scholar] [CrossRef]
- Shefrin, H.; Statman, M. Behavioral capital asset pricing theory. J. Financ. Quant. Anal. 1994, 29, 323–349. [Google Scholar] [CrossRef]
- Kyle, A.S. Continuous auctions and insider trading. Econometrica 1985, 53, 1315–1335. [Google Scholar] [CrossRef]
- Dongwei, S. Noise trading and market quality in chinese stock markets. Econ. Res. J. 2008, 43, 82–95. [Google Scholar]
- Chen Junhua, N.J. Stock index futures, noise trading and risk asset pricing. Rev. Investig. Stud. 2014, 33, 133–144. [Google Scholar]
- Yuan, Y.; Qi, Z.; Jia, Z. Noise trading, momentum effect and momentum strategy. Manag. Rev. 2021, 33, 44–54. [Google Scholar]
- Ben-Rephael, A.; Da, Z.; Israelsen, R.D. It depends on where you search: Institutional investor attention and underreaction to news. Rev. Financ. Stud. 2017, 30, 3009–3047. [Google Scholar] [CrossRef]
- Weiqi Liu, Y.R. Is institutional investor noise really small? Econ. Theory 2018, 37, 91–103. [Google Scholar]
- Weiqi Liu, Y.D. Information advantage, limited attention and informed traders compete for trading. J. Appl. Stat. Manag. 2020, 39, 162–173. [Google Scholar]
- Figlewski, S. Information diversity and market behavior. J. Financ. 1982, 37, 87–102. [Google Scholar] [CrossRef]
- Waters, G.A. The many faces of the taylor rule for advanced undergraduate macroeconomics. Int. Rev. Econ. Educ. 2022, 41. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhang, Q.; Liu, S.; Yang, Y. Illiquidity comovement and market crisis. J. Syst. Sci. Complex. 2022, 35, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Zhao, S.; Zhang, J. Multi-asset pricing modeling using holding-based networks in energy markets. Financ. Res. Lett. 2022, 46, 102483. [Google Scholar] [CrossRef]
- Miao, J.; Su, D. Asset market equilibrium under rational inattention. Econ. Theory 2022, 32, 1–30. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).