Abstract
Predicting household vehicle ownership (HVO) is a crucial component of travel demand forecasting. Furthermore, reliable HVO prediction is critical for achieving sustainable transportation development objectives in an era of rapid urbanization. This research predicted the HVO using a support vector machine (SVM) model optimized using the Bayesian Optimization (BO) algorithm. BO is used to determine the optimal SVM parameter values. This hybrid model was applied to two datasets derived from the US National Household Travel Survey dataset. Thus, two optimized SVM models were developed, namely SVMBO#1 and SVMBO#2. Using the confusion matrix, accuracy, receiver operating characteristic (ROC), and area under the ROC, the outcomes of these two hybrid models were examined. Additionally, the results of hybrid SVM models were compared with those of other machine learning models. The results demonstrated that the BO algorithm enhanced the performance of the standard SVM model for predicting the HVO. The BO method determined the Gaussian kernel to be the optimal kernel function for both datasets. The performance of the SVM#1 model was improved by 4.27% and 5.16% for the training and testing phases, respectively. For SVM#2 model, the performance of this model was improved by 1.20% and 2.14% for the training and testing phases, respectively. Moreover, the BO method enhanced the AUC of the SVM models used to predict the HVO. The hybrid SVM models also outperformed other machine learning models developed in this study. The findings of this study showed that SVM models hybridized with the BO algorithm can effectively predict the HVO and can be employed in the process of travel demand forecasting.
1. Introduction
When it comes to developing a more sustainable transportation system, it is important to keep a close eye on the rapid growth in private motorized vehicle ownership and use, which is a major source of air pollution in metropolitan areas, as well as a major contributor to traffic congestion. Although the emergence of shared mobility has contributed to a global decline in vehicle ownership [1], this effect is minimal [2]. The average number of automobiles owned by a household in the United States is 1.88 [3]. Nearly 9% of households lacked a car in 2017, indicating that nearly nine out of ten people in those households had accessibility to one or more light vehicles [3]. Traffic congestion, pollution, and deteriorating health are just a few of the negative effects of an increasing number of people taking to the roads in their own vehicles [4,5]. The issue of how to curb the growth in automobile ownership in the United States has become a real challenge. Transport policies explain the formation of a collection of agreements and recommendations aimed at achieving particular socioeconomic and environmental goals, in addition to improving the efficacy and reliability of the transportation system. The primary goal is to make sound judgments about how to distribute transportation resources, as well as to manage and control present transportation operations [6,7]. To satisfy the objectives of sustainability goals and minimize the adverse effects of a high rate of vehicle ownership, it is required to accurately predict motorized vehicle ownership and design an efficient allocation system for city transport systems.
Traditional statistical methods, such as regression models, have been frequently used to predict household vehicle ownership (VO). Nonetheless, it is difficult to utilize these models to investigate the predictors of household vehicle ownership (HVO) owing to the vast quantity of complex data on vehicle ownership. Regression models have to follow a number of strict statistical assumptions in order to be valid for data on vehicle ownership. These assumptions include the requirement for linearity in association modeling and the absence of outliers [8,9]. Detecting the predictors using cross-product terms may also be challenging, given that the interaction might take several forms [10].
In recent years, machine learning (ML) algorithms have progressively been utilized instead of or in addition to statistical models, especially in light of the advancements in artificial intelligence (AI). ML models, unlike statistical models, do not need a preexisting connection between the target and input variables; rather, they discover complicated connections between the dependent and independent variables by repeatedly generating a transformation matrix based on input data. There is no need to predetermine the mathematical structure of the algorithm, which is a major advantage of machine learning. With ML algorithms, the target variable may be predicted by spotting broad trends and patterns in a set of data. It can also handle incomplete information, extreme values, and multicollinearity among variables [11,12,13].
Typically, HVO datasets consist of a large number of parameters, each of which could have many classes. In addition, these datasets may be regularly updated as new data becomes available or is requested. In addition, it is quite common for HVO datasets to be incomplete or include missing information [14]. Such multivariate and under-sampling data, as well as incomplete, erroneous, or ambiguous knowledge or data, can be effectively managed by a Support Vector Machines (SVM) model [15,16,17,18]. Because of its ability to quickly update its network based on given or inputted data, SVM is regarded as ideal for transport-related learning and dynamic behavior (e.g., household vehicle ownership and travel mode choice) [6,19,20].
Using SVM models in previous transport-related studies, particularly for HVO prediction, was not without issues. SVM has three important hyperparameters, including kernel function, penalty factor (C), and Gamma (γ), that impact the model’s capacity to generalize and its accuracy [21,22]. The previous studies mostly employed software or tools with predefined hyperparameters, which yielded less-than-optimal results.
Typically, hyperparameter optimization of SVM can be performed using random search, grid search, and genetic algorithms (GA). However, there are apparent flaws in these optimization approaches that might impair HVO prediction and, in turn, travel demand forecasting. Because both random and grid searches are blind, they take a long time to complete. Because GA is inclined to fall into local optimality, this makes them less effective in the long run.
In recent years, the Bayesian Optimization (BO) method has been developed as a rapid optimization technique for computation-intensive functions. It has been shown to be a very successful method for managing several machine learning models, especially SVM (e.g., [19,20]). Consequently, this prompted the authors to use the BO method, which offers an accurate and efficient prediction of household vehicle ownership, in this work. This BO optimization approach is used to optimize the SVM hyperparameters. The BO algorithm can also remedy the shortcomings of existing optimization techniques to optimize the SVM hyperparameters by using Bayesian machine learning and Gaussian process regression. This technique has not yet been used to optimize the SVM hyperparameters for HVO prediction. In this work, the SVMBO model is used on two different sets of data from the 2017 US National Travel Survey (NHTS). This study shows how the application of the BO algorithm can improve the performance of the SVM model for predicting the HVO. This research mainly contributes to the investigation of artificial intelligence approaches in predicting vehicle ownership to achieve a more sustainable society. In addition, another contribution of this study is to suggest a new framework for decision-making in urban transport management to predict household vehicle ownership.
The following is the order in which the paper is presented: Section 2 includes a review of the literature on factors that influence HVO and methods for predicting HVO. Section 3 presents the issues that led to this study as well as the main research question. Section 4 presents the background of models used in this study, including the SVM, BO, and evolutionary random forest (ERF). The data utilized in this study is also shown in this section. Section 5 presents the results of input selection and optimized SVM models. These results are discussed in Section 6. Finally, the paper has been summarized in Section 7.
2. Literature Review
2.1. Factors Influencing HVO
Previous studies have demonstrated that some components of the built environment are linked to automobile ownership. Several studies have shown that areas with a higher density of walking and cycling facilities or higher population density have a lower rate of vehicle ownership [23,24,25,26,27,28]. It was also shown that higher levels of urbanization result in a higher level of private vehicle ownership [29].
Generally, vehicle ownership is considered as a consequence of a household’s demographic and socioeconomic characteristics [30]. It has been shown in several studies that people with higher socioeconomic status tend to have more vehicles. In addition, family size, the number of children, adults, and workers in a household all have a positive relationship with the rate of household vehicle ownership [30,31,32,33,34,35,36].
2.2. Methods Used for HVO Prediction
The negative implications of private car ownership have prompted several studies to simulate the variables that influence vehicle ownership (VO) and use. Furthermore, obtaining an accurate prediction of vehicle ownership to achieve sustainability goals attracts a lot of attention. The statistical approaches used in these investigations are mostly aggregate and disaggregate approaches. Individual or household variables are used in the disaggregate model to predict vehicle ownership at the individual or household level (HVO), whereas the aggregate model includes district-level features [37,38]. VO patterns and use patterns are often predicted using these models. A downside to these statistical models is that the dependent and independent variables must have a predetermined connection. The performance of statistical models is significantly impacted by extreme values, multicollinearity among independent variables, and incomplete information. Furthermore, these models are unable to accurately estimate VO in order to evaluate future policy options [39,40].
To date, several studies have employed ML algorithms to predict the HVO (e.g., [6,36,41,42,43,44,45]). Table 1 shows a summary of these studies. The most common ML techniques that have been employed by these studies were gradient boosting trees (GBT), neural networks (NNs), decision trees (DT), random forest (RF), support vector machines (SVM), k-nearest neighbors (kNN), and Naïve Bayesian (NB). Most of these models showed better performance compared to the traditional statistical techniques. It also should be noted that most of these studies used the default values for applying the ML models, which may yield less-than-optimal results. Among those studies that employed an optimization technique to fine-tune the hyperparameters, most studies used grid or random search, each of which has its own shortcomings.
The support vector machine (SVM) algorithm was employed in several studies to analyze vehicle ownership and showed promising performance [41,42,46]. Abdul Muhsin Zambang, Jiang, and Wahab [42] compared the performance of SVM with other ML techniques in Greater Tamale. However, their study did not employ any algorithm to optimize the SVM or other techniques’ hyperparameters. Basu and Ferreira [41] also conducted a comparative study in Singapore to understand the VO. They used a grid search method to optimize the hyperparameters of several ML models. Pineda-Jaramillo [46] investigated the major factors that impact travel behavior among people with restricted mobility to promote autonomous, healthy lives and healthy active transport modalities using ML and several other ML techniques. He used a random search strategy to fine-tune the hyperparameters. Despite the fact that these two last studies employed grid and random search to optimize the hyperparameters of SVM, each of these methods has their own drawbacks that will be explained in the Methodology section. Thus, it is necessary to apply efficient optimization techniques to fine-tune the hyperparameters of ML models and improve the performance of ML techniques in general and SVM in particular.

Table 1.
Recent studies on the use of ML techniques for predicting the vehicle ownership.
Table 1.
Recent studies on the use of ML techniques for predicting the vehicle ownership.
| Study | Study Aim | Model(s) Used | Hyperparameter Optimization |
|---|---|---|---|
| Chaipanha and Kaewwichian [47] | To provide a way for balancing the data using over- and under-sampling strategies. | kNN, NB, DTs | No |
| Manjushree, GH, Swamy and Giridharan [6] | To apply ML models to forecast the household characteristics that influence car ownership. | DTs, RF, MNL | No |
| Shao et al. [48] | To evaluate the nonlinear and interaction impacts of the built environment and motorcycles/E-bikes on automobile ownership using GBDT. | GBDT | Grid search |
| Pineda-Jaramillo [46] | To investigate the major factors that impact travel behavior among persons with restricted mobility to promote autonomous, healthy lives and healthy active transport modalities. | NB, kNN, DTs, SVM, RF, AdaBoost, NN, GBDT, CatBoost | Random search |
| Kaewwichian [14] | To remedy the imbalanced data problem in automobile ownership datasets. | DT, kNN, NB | No |
| Abdul Muhsin Zambang, Jiang and Wahab [42] | To approximate automobile ownership in Greater Tamale. | SGD, SVM, DT, RF, NB, kNN, | No |
| Wang et al. [49] | To anticipate ownership of electric vehicles. | AdaBoost | No |
| Sabouri, Brewer and Ewing [36] | To investigate the association between ride-sourcing services and household vehicle ownership. | DT, RF | No |
| Basu and Ferreira [41] | Through a comparison of econometric and machine learning models, to comprehend household automobile ownership in Singapore. | DT, RF, NN, SVM, LR, SGD, OLC | Grid search |
| Ha, Asada and Arimura [43] | To identify the variables that affect household car ownership trends in Phnom Penh. | RF, NN, MNL | No |
| Tanwanichkul et al. [50] | To approximate automobile ownership using ML methods. | DT, NN, MNL | No |
ML techniques: k-Nearest Neighbors = kNN; Naïve Bayes = BB; Decision Trees = DT; Random Forest (RF); Multinomial Logistic Regression = MNL; Gradient boosting decision trees = GBDT; support vector machines (SVM); Neural Networks = (NN); Stochastic Gradient Decent = SGD.
3. Research Motivations and Aims
The issues that motivated this research can be explained as follows: (1) a high rate of vehicle ownership has a negative effect on traffic and air pollution; (2) it is required to predict private vehicle ownership accurately to manage its adverse effects; (3) traditional statistical methods are unable to accurately predict vehicle ownership; (4) SVM can be considered an effective method to predict private vehicle ownership; and (5) BO is an efficient optimization algorithm, but it is not sufficiently examined for optimizing the SVM hyperparameters in the field of transportation research. In light of the problems that led to this study, the analysis of the collected data focused on answering the following research questions: (1) how does BO improve the performance of the SVM model to predict household vehicle ownership? (2) How does the optimized SVM model help decision makers to mitigate the adverse effects of vehicle ownership?
4. Methodology
This study employed the BO algorithm to optimize the parameters of SVM to predict the HVO. A flow diagram of this investigation can be found in Figure 1. To test our approach first, two datasets from the US National Household Survey were employed. Second, the data were split into training and testing subsets. Third, a feature selection using evolutionary random forest was applied to the data in each dataset. Fourthly, SVM and SVMBO models were trained and evaluated for each dataset. Finally, the best model in terms of performance was identified and introduced.
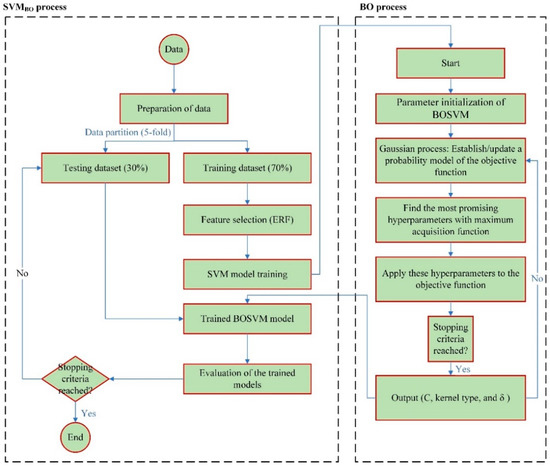
Figure 1.
Flow diagram of this study.
4.1. Data
This research chose two datasets at random from the US 2017 National Household Travel Survey (NHTS). These datasets are from two US states: Maine (ME) and Nevada (NV). The NHTS is one of the most important sources of transportation research in the United States, and numerous studies have used it to analyze transportation issues (e.g., [51,52,53,54,55]). The NHTS tracks daily non-commercial travel across all modalities, as well as the characteristics of the travelers, their households, and their vehicles. This dataset contains more than 400 variables. The authors selected household vehicle ownership (HVO) as the dependent variable and 14 additional factors as the independent variables for this research. The selection of these input variables was based on a comprehensive literature study. Two classes comprise the target variable (HVO): households with one vehicle and households with more than one vehicle. Table 2 provides a list of the variables utilized in this investigation. The distribution of the target variable’s classes is shown in Figure 2.

Table 2.
Variables utilized in this research.
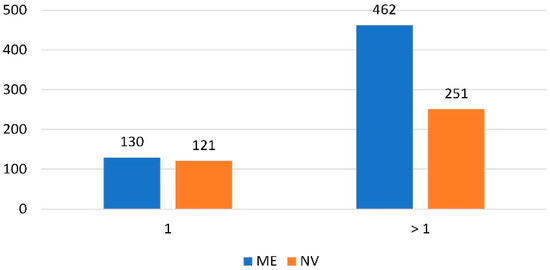
Figure 2.
The distribution of target variable classes.
4.2. Support Vector Machines (SVM) and Bayesian Optimization (BO) Algorithm
SVM is a statistically based machine learning methodology that combines many methodologies, including relaxing variables, maximum interval hyperplane, and kernel function. It is appropriate for solving classification issues involving limited samples, inhomogeneity, and high dimensions [56]. SVM was increasingly used in the area of transportation planning and engineering as interdisciplinary integration developed. A non-linear transformation is utilized to convert the input space samples into a high-dimensional feature space, and then an optimum classification plane is found that divides the characteristic space samples in a linear fashion. This is the main idea [57,58]. In investigations of HVO, the likelihood of having one or more vehicles corresponds well to the features of the method for handling binary classification issues.
The space from the hyperplane to the closest sample point is known as the margin. The broader the margin, the greater the classifier’s capacity for generalization. The objective of SVM is, thus, to identify the hyperplane that maximizes the margin, namely the optimum hyperplane. Every spot on the hyperplane on either side of the margin is termed a support vector, and the categorization border is decided exclusively by the support vectors, not additional data or the quantity of data. Because of this, optimizing SVM’s hyperparameters is very essential. SVM’s kernel type, C, and gamma are the most important hyperparameters. The kernel, as previously said, transforms the raw data into a feature space representation. Adding a penalty for each incorrectly categorized data point, hyperparameter C regulates the exchange between the decision boundary and correctness. In some kernel types, gamma is a parameter that is connected to C. Gamma has no influence on C if it is huge. It is comparable to a linear model if the gamma is small. C influences the model in the same manner.
The adjustment of learning parameters and model hyperparameters is often a consideration in the implementation of ML algorithms [59]. Model or training process qualities are defined by hyperparameters, which have a substantial impact on the model’s ultimate outcome [60]. Many machine learning algorithms use BO as a technique for selecting the best hyperparameters. Clearly, BO outperforms many optimization techniques, including GAs, particle swarm optimization algorithms, and other advanced AI algorithms [60,61].
In order to optimize noisy black-box functions, BO is used as a global optimization technique. When used for hyperparameter optimization, BO creates a probabilistic model of the function, translating hyperparameter values to the objective as assessed by the testing set. By repeatedly assessing a feasible hyperparameter combination based on the present model and then modifying it, BO seeks to collect samples that reveal as much information about this function and, more specifically, the position of the ideal. It maintains a balance between exploration and exploitation.
Using Bayesian machine learning and Gaussian process regression, this parameter optimization strategy employs a proxy for the objective and assesses the uncertainty in that proxy before determining the location of the sample using an acquisition function produced from the proxy. Typically, the issues that the BO algorithm encounters are:
where V shows the candidate set of d.
At each iteration of the sequential optimization problem, BO is required to choose the most optimum observation value. Using the Gaussian Process (GP), it is possible to tackle this critical issue according to the following equation:
The kernel function is denoted by , while the mean function is denoted by . The Gaussian kernel function has the following form:
Instead of using the original value, the BO algorithm returns a new value for each hyperparameter. This was followed by the development of a new hybrid model (SVMBO).
4.3. Models’ Performance Assessment
This study employed a confusion matrix, accuracy, receiver operating characteristics (ROC) curve, and area under the ROC curve (AUC) to evaluate the performance of the models developed in this study. The confusion matrix, which is also called the matrix of error, is used to figure out how well a classifier works. The approach can statistically represent the accurate rate of 0-value forecasts, the correct rate of 1-value forecasts, and the total forecast rate in the model’s findings. The ROC curve is an exhaustive measure of response sensitivity and particular factors. The greater the accuracy of the model, the nearer the curve is to the top left corner. AUC has a range of [0, 1]. In general, the closer AUC gets to 1, the more accurate the model is.
5. Results
This section presents the results of optimizing the SVM models to predict household vehicle ownership using the Bayesian Optimization (BO) algorithm and two distinct datasets (corresponding to steps 1 and 2 in the Methodology section). The results of using ERF to select inputs are shown in the first sub-section (corresponding to step 3 in the Methodology section). The results of the SVM and optimized SVM models are shown in the second sub-section (corresponding to steps 4 and 5 in the Methodology section). In the second sub-section, these models were also evaluated on their performance using different criteria (corresponding to step 5 in the Methodology section).
5.1. Input Selection
This study employed an evolutionary random forest model for input selection. Several previous studies successfully implemented this technique for input selection in other research domains (e.g., [62,63]). ERF selected the most relevant predictors of HVO in each dataset. Eight inputs were selected by the ERF model in each dataset (Figure 3). Some parameters have been tuned and used to develop the ERF model. These parameters, along with the selected inputs in both datasets, are shown in Figure 3. There are some common variables that have emerged as important in both models, including home ownership (HOMEOWN), household income (HHFAMINC), count of drivers in the household (DRVRCNT), and population density category (HBPPOPDN). For the NV and ME datasets, model accuracy was 94.45%, and for the ME dataset, it was 95.10%.
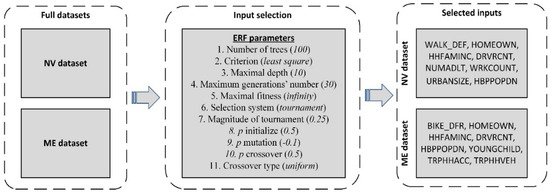
Figure 3.
ERF parameters and selected inputs by ERF.
The emergence of four aforesaid inputs in both datasets shows the importance of these variables in predicting HVO. This finding confirms that of previous studies that reported the importance of home ownership [44], household income [30], number of drivers in the household [44], and population density category [23,24,25,26] for HVO forecasting.
5.2. SVM and SVMBO Models’ Development and Assessment
In this work, two SVM models were used to predict the HVO across two datasets. The first SVM model, designated SVM#1, was applied to the ME dataset, while the second SVM model, designated SVM#2, was applied to the NV dataset. The author developed the models by using 414 and 260 training data points (representing 70% of the total data in each dataset) from the ME and NV datasets, respectively. In addition, 5-fold cross-validation was implemented at this stage. Subsequently, the SVM models were evaluated utilizing 178 and 112 datasets (representing 30% of the total data in each dataset), respectively, of ME and NV datasets. It should be noted that the authors developed SVM models and their optimized variants using different common proportions, including 70:30, 80:20, and 90:10. However, in both datasets, the 70:30 ratio yielded the highest improvement in models’ accuracy. Figure 4 shows how the SVM model’s ability to predict the HVO in two datasets became better after the BO algorithm was added. The linear kernel was used to develop these models. Table 3 displays the training and testing accuracy of these models. The accuracy (%) of both training and testing for these two models is fairly similar.
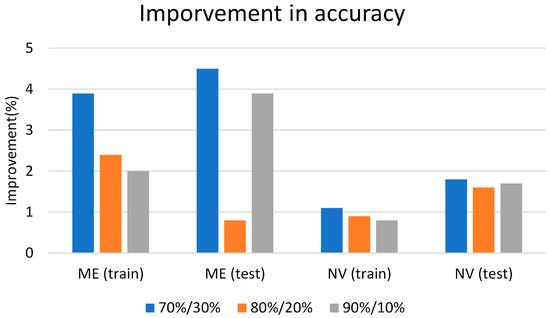
Figure 4.
Improvement in accuracy of SVM models after incorporating the BO algorithm to predict the HVO.

Table 3.
Confusion matrix and accuracy (%) of training and testing phases.
The Bayesian Optimization (BO) approach was used to enhance the performance of two SVM models that predict the HVO using identical training and testing datasets. The goal of the BO method for SVM-based hybrid models is to find the best values for the SVM model’s hyperparameters “C” and “gamma”. These parameter ranges were set between 0.001 and 1000. The following is the primary procedure for optimizing SVM parameters utilizing BO optimization techniques:
- Processing and preparing data: randomly dividing the dataset into a training set and a testing set with an appropriate ratio (70:30).
- Assessment of fitness: before optimizing the target parameter value, estimate, and assess the fitness function.
- Adjustment of parameters: update the optimization criteria satisfied by the parameters based on every iteration’s finding.
- Halt condition inspection: once the optimization stop condition is fulfilled, the optimal parameters are determined.
It should be mentioned that 100 iterations were used to train the models. Figure 5 depicts the progress of optimization of the SVM hyperparameters, as well as the mini-mum classification error. At 92 iterations, SVMBO#1 achieved a minimum classification error of 0.051, while SVMBO#2 obtained a minimum classification error of 0.077 at 77 iterations. SVMBO#1’s greater iteration rate than SVMBO#2 may be attributed to this model’s larger data size.
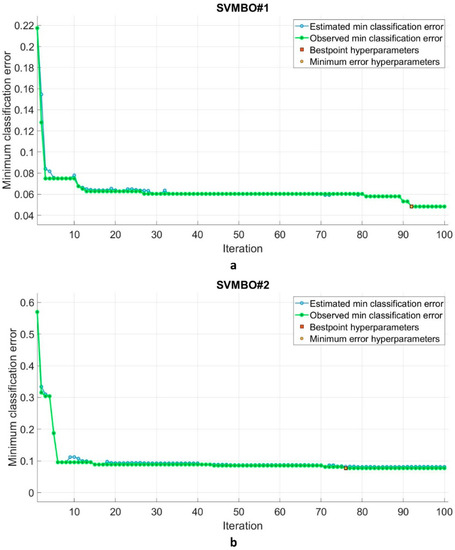
Figure 5.
Convergence curves of SVMBO#1 (a) and SVMBO#2 (b) models.
Table 4 shows the hyperparameters for the two SVM-optimized models that provide the best evaluation value of BO for each model. As can be seen, the Gaussian kernel was chosen as the best kernel function for developing SVMBO models to predict the HVO. The gamma values of these two models are quite similar. Moreover, the average training time for these two models is 375.55 s. Clearly, training an optimized SVM model requires more time compared to training a standard SVM model.

Table 4.
Models’ parameters and training times.
Table 2 shows the confusion matrix and accuracy (%) of the developed standard and hybrid SVM models. In both the training and testing stages, the BO technique enhanced the predictive accuracy of the SVM models for HVO in both datasets of this study. These results illustrate the efficacy of the BO approach in enhancing the HVO prediction performance of the SVM model.
Figure 6 and Figure 7 show the ROC and AUC for all models developed in this research. Figure 6 illustrates the dispersion of the AUC values of the two models (SVM#1 and SVMBO#1) applied to the ME dataset during the course of the iterative procedure, while Figure 7 shows the AUC values of the two models (SVM#2 and SVMBO#2) applied to the NV dataset. AUC values greater than 0.9 are commonly regarded as excellent [64]. Both optimized SVM models achieved an AUC higher than 0.9. Additionally, the BO algorithm made the AUC of SVM models that predict the HVO better for both datasets (ME and NV) and training and testing phases.
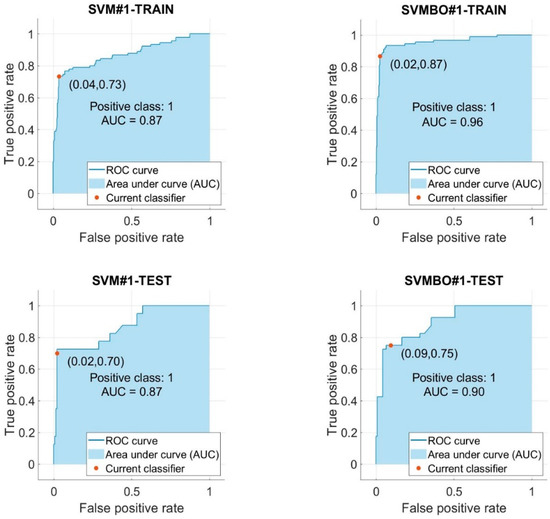
Figure 6.
ROC curves of SVM#1 and SVMBO#1.
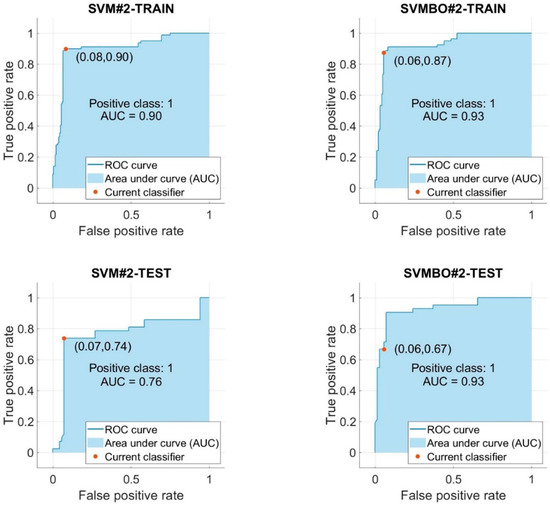
Figure 7.
ROC curves of SVM#2 and SVMBO#2.
The testing accuracy of the SVMBO#1 and SVMBO#2 models was compared to that of several machine learning approaches, such as artificial neural networks (ANN), single DT, bagged DT, boosted DT, and KNN. The outcome of this comparison is shown in Figure 8. The improved SVM models built in this work to predict the HVO outperformed other ML models for both datasets. This demonstrates the effectiveness of the model created for this research in predicting the HVO.
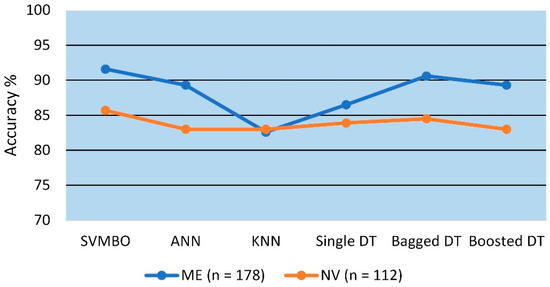
Figure 8.
Models’ accuracy in the testing phase.
6. Discussions
The superior performance of SVMBO models over other ML approaches and the regular SVM model may be credited to the technique’s ability to completely use information from previous iterations to identify the next possible parameter choice [65,66]. This study’s results corroborate those of prior research that indicated satisfactory outputs for other variations of the SVM model for different datasets to predict vehicle ownership (e.g., [20,42,51]). This investigation revealed, however, that the Gaussian kernel is the most effective kernel function for forecasting the HVO. This finding is unique, according to the authors’ best knowledge. Compared to other studies that employed SVM optimized by an optimization method, the SVMBO model achieved greater training and testing accuracy than that of Basu and Ferreira [41] (training accuracy = 86.91% and testing accuracy = 66.89%), which utilized a grid search strategy. This shows that the BO approach can be a better way to improve the performance of the SVM model for predicting the HVO than traditional optimization algorithms, such as grid search.
Implications for Academic and Policy-Making
Concerning the academic contributions, this research for the first time investigated Bayesian Optimization algorithms to improve the performance of a machine learning algorithm to predict household vehicle ownership. The findings of this study can be a starting point for other researchers to apply the BO to improve other ML algorithms to solve other transportation problems. In addition, this research proposes a novel framework for decision-making in urban mobility management in order to anticipate household car ownership. Our study also has a wide range of practical applications, including more effective policymaking.
It is significantly necessary to answer both casual and predictive inquiries in order to offer policy formulations. For example, a transportation policymaker in a metropolitan area who wishes to combat traffic congestion may need to determine if limiting the number of private automobiles would provide the intended outcomes. This is just an illustration of a causal question. However, other decision-making that may contribute to lower usage of private vehicles, such as whether it is essential to establish infrastructure to accommodate walking, biking, and public transit usage in areas where it does not exist, whether it is critical to enhance the existing facilities, and how to develop those that must be created, only requires a reliable forecast for the likelihood of lower usage of private vehicles. This example illustrates Kleinberg et al. [67] definition of “policy prediction problem”.
Researchers in the area of transportation may use ML techniques to forecast future travel trends and identify previously unknown passenger behavior patterns. These results and forecasts may aid decision-makers in locating ideal solutions that improve the reliability and efficiency of transport systems. In a way that no other algorithms could, ML algorithms could analyze a person’s travel history, determine their habits, and provide suggestions for how they can improve their travel habits in the future.
The current research confirms the benefits of the suggested SVMBO model, which might be used by transportation and vehicle ownership policymakers. The SVMBO algorithm can assure transport decision-makers and researchers that their predictions using this approach are among the most accurate possible, since the BO’s strong characteristics are utilized to determine the optimal SVM’s hyperparameters.
7. Conclusions
Fine-tuning of the SVM hyperparameters to obtain the highest possible predictive accuracy has been a common challenge for researchers in several fields of research. However, the successful use of BO to optimize the SVM hyperparameters in a number of research areas led to this method being used to find the best value for the SVM hyperparameters.
To address the need for an accurate prediction of household vehicle ownership while also meeting the objectives of sustainability goals, this study investigated how the BO algorithm can improve the performance of the SVM model in predicting household vehicle ownership. The findings of this study may assist decision-makers in fairly predicting motorized vehicle ownership and designing an efficient allocation system for urban transportation systems in order to reduce issues, such as traffic congestion and major air pollution.
This research is among the rare studies in the field of transportation that improve the performance of ML techniques using the BO algorithm. The results of this study may serve as a benchmark for future work on improving other ML algorithms for use in research in this field. The results of our research can be used in many ways, such as to improve policymaking.
The SVMBO model was applied to two distinct datasets from the US National Household Travel Survey (NHTS) to obtain a more comprehensive assessment. As a result, two optimized SVM models, SVMBO#1 and SVMBO#2, were developed. The results of these two hybrid models were analyzed using the confusion matrix, accuracy, ROC, and AUC. The outcomes of hybrid SVM models were also compared to the outcomes of other ML models. The findings of this research can be summarized as follows:
- These two models took 375.55 s on average to train.
- The SVMBO approach outperformed the traditional SVM model in predicting the HVO.
- The BO technique concluded that the Gaussian kernel was the best kernel function for both datasets.
- The BO method enhanced the performance of the SVM#1 model by 4.27% and 5.16%, respectively, throughout the training and testing phases.
- For the SVM#2 model, the performance of this model was improved by 1.20% and 2.14% for the training and testing phases, correspondingly.
- The AUC of the SVM models used to predict the HVO was improved by using the BO technique.
- In this study, the optimized SVM models did better than the other machine learning models that were applied.
This study concludes that the performance of an SVM model to predict household vehicle ownership can be enhanced by employing robust optimization methods such as BO. This study lends support to prior research that attempted to demonstrate the efficacy of artificial intelligence algorithms in predicting vehicle ownership for a more sustainable society. Next, we will look at how more complex optimization strategies affect the fine-tuning of hyperparameters in different machine learning models to predict vehicle ownership.
The study has limitations in addition to its contributions to the literature. The effectiveness of the SVMBO model to predict the HVO was tested using two datasets in this research. Although the authors believe that these two datasets are sufficient for this assessment, future studies might include other datasets from the same or alternative data sources to appraise the SVMBO model’s capacity to forecast HVO. The SVMBO was developed for the binary classes of HVO in this research. Future studies may use this approach to forecast when HVO has more classes.
Author Contributions
Conceptualization, Z.X., M.A. (Mahdi Aghaabbasi), and M.A. (Mujahid Ali); methodology, M.A. (Mahdi Aghaabbasi), M.A. (Mujahid Ali), and E.M.; formal analysis, M.A. (Mahdi Aghaabbasi), M.A. (Mujahid Ali); investigation, M.A. (Mahdi Aghaabbasi), M.A. (Mujahid Ali); writing—original draft preparation, Z.X., M.A. (Mahdi Aghaabbasi), and M.A. (Mujahid Ali). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors would like to thank everyone who helped with this study for their insightful remarks. We would especially want to thank the Transportation Institute, Chulalongkorn University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jain, T.; Rose, G.; Johnson, M. Changes in private car ownership associated with car sharing: Gauging differences by residential location and car share typology. Transportation 2022, 49, 503–527. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Zheng, Z.; Whitehead, J.; Perrons, R.K.; Washington, S.; Page, L. Examining the impact of car-sharing on private vehicle ownership. Transp. Res. A Policy Pract. 2020, 138, 322–341. [Google Scholar] [CrossRef]
- Bureau of Transportation Statistics. National Household Travel Survey Daily Travel Quick Facts. Available online: https://www.bts.gov/statistical-products/surveys/national-household-travel-survey-daily-travel-quick-facts (accessed on 1 April 2022).
- Handy, S.L.; Boarnet, M.G.; Ewing, R.; Killingsworth, R.E. How the built environment affects physical activity: Views from urban planning. Am. J. Prev. Med. 2002, 23, 64–73. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, Y. Travel behaviour and life course: Examining changes in car use after residential relocation in Beijing. J. Transp. Geogr. 2018, 73, 41–53. [Google Scholar] [CrossRef]
- Manjushree, N.; GH, S.G.; Swamy, S.C.; Giridharan, A. Household Vehicle Ownership Prediction Using Machine Learning Approach. In Proceedings of the 2022 International Conference for Advancement in Technology (ICONAT), Goa, India, 21–22 January 2022; pp. 1–8. [Google Scholar]
- Golroudbary, S.R.; Zahraee, S.M.; Awan, U.; Kraslawski, A. Sustainable Operations Management in Logistics Using Simulations and Modelling: A Framework for Decision Making in Delivery Management. Procedia Manuf. 2019, 30, 627–634. [Google Scholar] [CrossRef]
- Rashidi, S.; Ranjitkar, P.; Hadas, Y. Modeling bus dwell time with decision tree-based methods. Transp. Res. Rec. 2014, 2418, 74–83. [Google Scholar] [CrossRef]
- Stylianou, K.; Dimitriou, L.; Abdel-Aty, M. Big data and road safety: A comprehensive review. In Mobility Patterns, Big Data and Transport Analytics; Elsevier: Amsterdam, The Netherlands, 2019; pp. 297–343. [Google Scholar]
- Yan, X.; Richards, S.; Su, X. Using hierarchical tree-based regression model to predict train–vehicle crashes at passive highway-rail grade crossings. Accid. Anal. Prev. 2010, 42, 64–74. [Google Scholar] [CrossRef]
- Wahab, L.; Jiang, H. A comparative study on machine learning based algorithms for prediction of motorcycle crash severity. PLoS ONE 2019, 14, e0214966. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, Y.; Xue, Y. Travel Time Estimation of a Path Using Sparse Trajectories. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 25–34. [Google Scholar]
- Asif, M.T.; Mitrovic, N.; Dauwels, J.; Jaillet, P. Matrix and tensor based methods for missing data estimation in large traffic networks. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1816–1825. [Google Scholar] [CrossRef]
- Kaewwichian, P. Multiclass Classification with Imbalanced Datasets for Car Ownership Demand Model–Cost-Sensitive Learning. Promet-Traffic Transp. 2021, 33, 361–371. [Google Scholar] [CrossRef]
- Nowicki, R.K.; Grzanek, K.; Hayashi, Y. Rough support vector machine for classification with interval and incomplete data. J. Artif. Intell. Soft Comput. Res. 2020, 10, 47–56. [Google Scholar] [CrossRef]
- Brand, L.; Baker, L.Z.; Wang, H. A Multi-Instance Support Vector Machine with Incomplete Data for Clinical Outcome Prediction of COVID-19. In Proceedings of the 12th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics, Gainesville, FL, USA, 1–4 August 2021; pp. 1–6. [Google Scholar]
- Mohamed, M.; Cheffena, M. Received Signal Strength Based Gait Authentication. IEEE Sens. J. 2018, 18, 6727–6734. [Google Scholar] [CrossRef]
- Harrison, L.R.; Legleiter, C.J.; Overstreet, B.T.; Bell, T.W.; Hannon, J. Assessing the potential for spectrally based remote sensing of salmon spawning locations. River Res. Appl. 2020, 36, 1618–1632. [Google Scholar] [CrossRef]
- Qian, Y.; Aghaabbasi, M.; Ali, M.; Alqurashi, M.; Salah, B.; Zainol, R.; Moeinaddini, M.; Hussein, E.E. Classification of Imbalanced Travel Mode Choice to Work Data Using Adjustable SVM Model. Appl. Sci. 2021, 11, 11916. [Google Scholar] [CrossRef]
- Zhang, X.-H.; Hu, M.-Q.; Peng, X.-Y.; Gan, J.; Xiang, Q.-J. Prediction of Motor Vehicle Ownership in County Towns Based on Support Vector Machine. In Proceedings of the 2019 4th International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 5–7 September 2019; pp. 311–315. [Google Scholar]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Han, Z.; Pham, B.T. Improved landslide assessment using support vector machine with bagging, boosting, and stacking ensemble machine learning framework in a mountainous watershed, Japan. Landslides 2020, 17, 641–658. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, W. Optimization of computational intelligence models for landslide susceptibility evaluation. Remote Sens. 2020, 12, 2180. [Google Scholar] [CrossRef]
- Li, J.; Walker, J.L.; Srinivasan, S.; Anderson, W.P. Modeling private car ownership in China: Investigation of urban form impact across megacities. Transp. Res. Rec. 2010, 2193, 76–84. [Google Scholar] [CrossRef]
- Song, S.; Diao, M.; Feng, C.-C. Effects of pricing and infrastructure on car ownership: A pseudo-panel-based dynamic model. Transp. Res. A Policy Pract. 2021, 152, 115–126. [Google Scholar] [CrossRef]
- Dargay, J.M.; Madre, J.-L.; Berri, A. Car ownership dynamics seen through the follow-up of cohorts: Comparison of France and the United Kingdom. Transp. Res. Rec. 2000, 1733, 31–38. [Google Scholar] [CrossRef]
- Yang, Z.; Jia, P.; Liu, W.; Yin, H. Car ownership and urban development in Chinese cities: A panel data analysis. J. Transp. Geogr. 2017, 58, 127–134. [Google Scholar] [CrossRef]
- Ruas, E.B. The Influence of Shared Mobility and Transportation Policies on Vehicle Ownership: Analysis of Multifamily Residents in Portland, Oregon. Ph.D. Dissertation, Portland State University, Portland, OR, USA, 2019. [Google Scholar]
- Cirillo, C.; Liu, Y. Vehicle ownership modeling framework for the state of Maryland: Analysis and trends from 2001 and 2009 NHTS data. J. Urban Plan. Dev. 2013, 139, 1–11. [Google Scholar] [CrossRef]
- Chu, M.Y.; Law, T.H.; Hamid, H.; Law, S.H.; Lee, J.C. Examining the effects of urbanization and purchasing power on the relationship between motorcycle ownership and economic development: A panel data. Int. J. Transp. Sci. Technol. 2020, 11, 72–82. [Google Scholar] [CrossRef]
- Dargay, J.; Hanly, M. Volatility of car ownership, commuting mode and time in the UK. Transp. Res. A Policy Pract. 2007, 41, 934–948. [Google Scholar] [CrossRef]
- Bhat, C.R.; Paleti, R.; Pendyala, R.M.; Lorenzini, K.; Konduri, K.C. Accommodating Immigration Status and Self-Selection Effects in a Joint Model of Household Auto Ownership and Residential Location Choice. Transp. Res. Rec. 2013, 2382, 142–150. [Google Scholar] [CrossRef]
- Li, S.; Zhao, P. Exploring car ownership and car use in neighborhoods near metro stations in Beijing: Does the neighborhood built environment matter? Transp. Res. D Transp. Environ. 2017, 56, 1–17. [Google Scholar] [CrossRef]
- Huang, X.; Cao, X.J.; Yin, J.; Cao, X. Effects of metro transit on the ownership of mobility instruments in Xi’an, China. Transp. Res. D Transp. Environ. 2017, 52, 495–505. [Google Scholar] [CrossRef]
- Matas, A.; Raymond, J.-L.; Roig, J.-L. Car ownership and access to jobs in Spain. Transp. Res. A Policy Pract. 2009, 43, 607–617. [Google Scholar] [CrossRef]
- Tyrinopoulos, Y.; Antoniou, C. Factors affecting modal choice in urban mobility. Eur. Transp. Res. Rev. 2013, 5, 27–39. [Google Scholar] [CrossRef]
- Sabouri, S.; Brewer, S.; Ewing, R. Exploring the relationship between ride-sourcing services and vehicle ownership, using both inferential and machine learning approaches. Landsc. Urban Plan. 2020, 198, 103797. [Google Scholar] [CrossRef]
- Jong, G.D.; Fox, J.; Daly, A.; Pieters, M.; Smit, R. Comparison of car ownership models. Transp. Rev. 2004, 24, 379–408. [Google Scholar] [CrossRef]
- Anowar, S.; Eluru, N.; Miranda-Moreno, L.F. Alternative modeling approaches used for examining automobile ownership: A comprehensive review. Transp. Rev. 2014, 34, 441–473. [Google Scholar] [CrossRef]
- Karlaftis, M.G.; Vlahogianni, E.I. Statistical methods versus neural networks in transportation research: Differences, similarities and some insights. Transp. Res. C Emerg. Technol. 2011, 19, 387–399. [Google Scholar] [CrossRef]
- Aghaabbasi, M.; Shekari, Z.A.; Shah, M.Z.; Olakunle, O.; Armaghani, D.J.; Moeinaddini, M. Predicting the use frequency of ride-sourcing by off-campus university students through random forest and Bayesian network techniques. Transp. Res. A Policy Pract. 2020, 136, 262–281. [Google Scholar] [CrossRef]
- Basu, R.; Ferreira, J. Understanding household vehicle ownership in Singapore through a comparison of econometric and machine learning models. Transp. Res. Procedia 2020, 48, 1674–1693. [Google Scholar] [CrossRef]
- Abdul Muhsin Zambang, M.; Jiang, H.; Wahab, L. Modeling vehicle ownership with machine learning techniques in the Greater Tamale Area, Ghana. PLoS ONE 2021, 16, e0246044. [Google Scholar] [CrossRef]
- Ha, T.V.; Asada, T.; Arimura, M. Determination of the influence factors on household vehicle ownership patterns in Phnom Penh using statistical and machine learning methods. J. Transp. Geogr. 2019, 78, 70–86. [Google Scholar] [CrossRef]
- Ma, T.; Aghaabbasi, M.; Ali, M.; Zainol, R.; Jan, A.; Mohamed, A.M.; Mohamed, A. Nonlinear Relationships between Vehicle Ownership and Household Travel Characteristics and Built Environment Attributes in the US Using the XGBT Algorithm. Sustainability 2022, 14, 3395. [Google Scholar] [CrossRef]
- Mohammadian, A.; Miller, E.J. Nested logit models and artificial neural networks for predicting household automobile choices: Comparison of performance. Transp. Res. Rec. 2002, 1807, 92–100. [Google Scholar] [CrossRef]
- Pineda-Jaramillo, J. Travel time, trip frequency and motorised-vehicle ownership: A case study of travel behaviour of people with reduced mobility in Medellín. J. Transp. Health 2021, 22, 101110. [Google Scholar] [CrossRef]
- Chaipanha, W.; Kaewwichian, P. Smote vs. Random Undersampling for Imbalanced Data-Car Ownership Demand Model. Communications 2022, 24, D105–D115. [Google Scholar] [CrossRef]
- Shao, Q.; Zhang, W.; Cao, X.J.; Yang, J. Nonlinear and interaction effects of land use and motorcycles/E-bikes on car ownership. Transp. Res. D Transp. Environ. 2022, 102, 103115. [Google Scholar] [CrossRef]
- Wang, X.; Pan, Z.; Wang, H.; Lu, Z.; Huang, J.; Yu, X. Forecast of Electric Vehicle Ownership Based on MIFS-AdaBoost Model. In Proceedings of the 2021 IEEE 4th International Conference on Automation, Electronics and Electrical Engineering (AUTEEE), Shenyang, China, 19–21 November 2021; pp. 4–8. [Google Scholar]
- Tanwanichkul, L.; Kaewwichian, P.; Pitaksringkarn, J. Car ownership demand modeling using machine learning: Decision trees and neural networks. GEOMATE J. 2019, 17, 219–230. [Google Scholar]
- Bas, J.; Cirillo, C.; Cherchi, E. Classification of potential electric vehicle purchasers: A machine learning approach. Technol. Forecast. Soc. Chang. 2021, 168, 120759. [Google Scholar] [CrossRef]
- Kash, G.; Mokhtarian, P.L. What Counts as Commute Travel? Identification and Resolution of Key Issues around Measuring Complex Commutes in the National Household Travel Survey. Transp. Res. Rec. 2021, 2676, 03611981211051346. [Google Scholar] [CrossRef]
- Sadeghvaziri, E.; Tawfik, A. Using the 2017 National Household Travel Survey Data to Explore the Elderly’s Travel Patterns. In Proceedings of the International Conference on Transportation and Development 2020, Seattle, WA, USA, 26–29 May 2020; pp. 86–94. [Google Scholar]
- Esekhaigbe, E.O.; Bills, T. Examining the Travel Behavior of Transport Disadvantaged Communities Using the 2017 National Household Travel Survey. In Proceedings of the Transportation Research Board 100th Annual Meeting, Washington, DC, USA, 5–29 January 2021. [Google Scholar]
- Kickhöfer, B.; Bahamonde-Birke, F.J.; Nordenholz, F. Dynamic modeling of vehicle purchases and vehicle type choices from national household travel survey data. Transp. Res. Procedia 2019, 41, 2–5. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 27. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 1–9. [Google Scholar]
- Greenhill, S.; Rana, S.; Gupta, S.; Vellanki, P.; Venkatesh, S. Bayesian optimization for adaptive experimental design: A review. IEEE Access 2020, 8, 13937–13948. [Google Scholar] [CrossRef]
- Kobliha, M.; Schwarz, J.; Očenášek, J. Bayesian optimization algorithms for dynamic problems. In Proceedings of the Workshops on Applications of Evolutionary Computation, Budapest, Hungary, 10–12 April 2006; pp. 800–804. [Google Scholar]
- Yu, Q.; Monjezi, M.; Mohammed, A.S.; Dehghani, H.; Armaghani, D.J.; Ulrikh, D.V. Optimized Support Vector Machines Combined with Evolutionary Random Forest for Prediction of Back-Break Caused by Blasting Operation. Sustainability 2021, 13, 12797. [Google Scholar] [CrossRef]
- Ke, B.; Khandelwal, M.; Asteris, P.G.; Skentou, A.D.; Mamou, A.; Armaghani, D.J. Rock-Burst Occurrence Prediction Based on Optimized Naïve Bayes Models. IEEE Access 2021, 9, 91347–91360. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Shawky, L.A. Flower pollination algorithm: A comprehensive review. Artif. Intell. Rev. 2019, 52, 2533–2557. [Google Scholar] [CrossRef]
- Kleinberg, J.; Ludwig, J.; Mullainathan, S.; Obermeyer, Z. Prediction policy problems. Am. Econ. Rev. 2015, 105, 491–495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).