A Heuristic Algorithm Based on Travel Demand for Transit Network Design
Abstract
1. Introduction
- (1)
- A simultaneous optimization model is formulated for the transit network structure and frequency problem considering flow assignment and vehicle capacity.
- (2)
- A heuristic algorithm is developed to solve the transit network design problem, in which routes are generated based on accumulated flow, and the frequency for each route is set according to flow share. A new concept of vehicle difference is also introduced to reflect the difference between actually assigned vehicles and required vehicles for guiding the process of regulating frequencies.
- (3)
- The model and algorithm are applied to different scale networks. The properties of the proposed model and algorithm are examined, and the different performances for various scenarios through different parameter values are discussed.
2. Problem Formulation
2.1. Assumptions
2.2. Model Setting
2.2.1. Objective Function
2.2.2. Constraints
- (i)
- Calculations of variables
- (ii)
- Constraints for route structure
- (iii)
- Constraints for frequencies
- (iv)
- Constraints for capacity
- (v)
- Constraint of flow assignment
3. Solution
3.1. General Scheme of the Proposed Algorithm
- (a)
- The parameters, including those for the planning area, such as number of stops, number of routes, maximum available fleet size, bus capacity, maximum number of stops for a planning route, shortest path matrix, travel demand matrix, and those for the algorithm, such as stopping criteria, are initialized.
- (b)
- The initial route structure is generated according to the predefined parameters.
- (c)
- The vehicles for each determined route are allocated with the limit of maximum available fleet size.
- (d)
- After determining the route structure and corresponding frequencies, the travel demand can be assigned to each route in terms of the principle presented by the flow assignment.
- (e)
- The efficiency of the solution to meet the capacity constraint (14) is evaluated; if the answer is yes, the next step is performed; otherwise, the vehicles are regulated among routes until the solution satisfies the constraint.
- (f)
- The objective function value for the feasible solution is calculated according to Equation (1).
- (g)
- The frequencies of the determined transit network are optimized.
- (h)
- The stop criterion is checked; if the algorithm meets the stop criterion (the iteration reaches 500 generations), then the algorithm procedure is terminated, and the best solution is the output; otherwise, the next step is performed.
- (i)
- The route structure is optimized by adding and deleting stops in the routes.

3.2. Procedure of Initial Route Generation
3.2.1. Stop Selection
3.2.2. Combination and Sequence
| For each selected stop Combine the selected stop with an unformed route to form a new unformed route , set the selected stop as the first stop for the new unformed route, and set as the optimal structure . Calculate the length of and define the length as Calculate the number of stops of the unformed route Set = 1 While Change the sequence of and set the selected stop as the -th stop in the new unformed route to form a different new unformed route Calculate the length of and define the length as If Make as and as endif endwhile output the optimal structure and the shortest path for the new combined unformed route Next selected stop |
3.3. Allocating Vehicles for the Initial Routes
3.4. Flow Assignment
3.5. Judgment of Constraints
3.6. Vehicle Regulation
| For each route if the for route is negative define a new variable while with maximum as sum of and if move vehicles from route to route and update for all routes else move vehicles from route to route and update for all routes endif endwhile endif next route in the proposed solution |
3.7. Objective Calculation
3.8. Frequency Optimization
3.9. Termination
3.10. Route Structure Optimization
3.10.1. Operation of Stop Removal
3.10.2. Operation of Stop Insertion
4. Numerical Examples
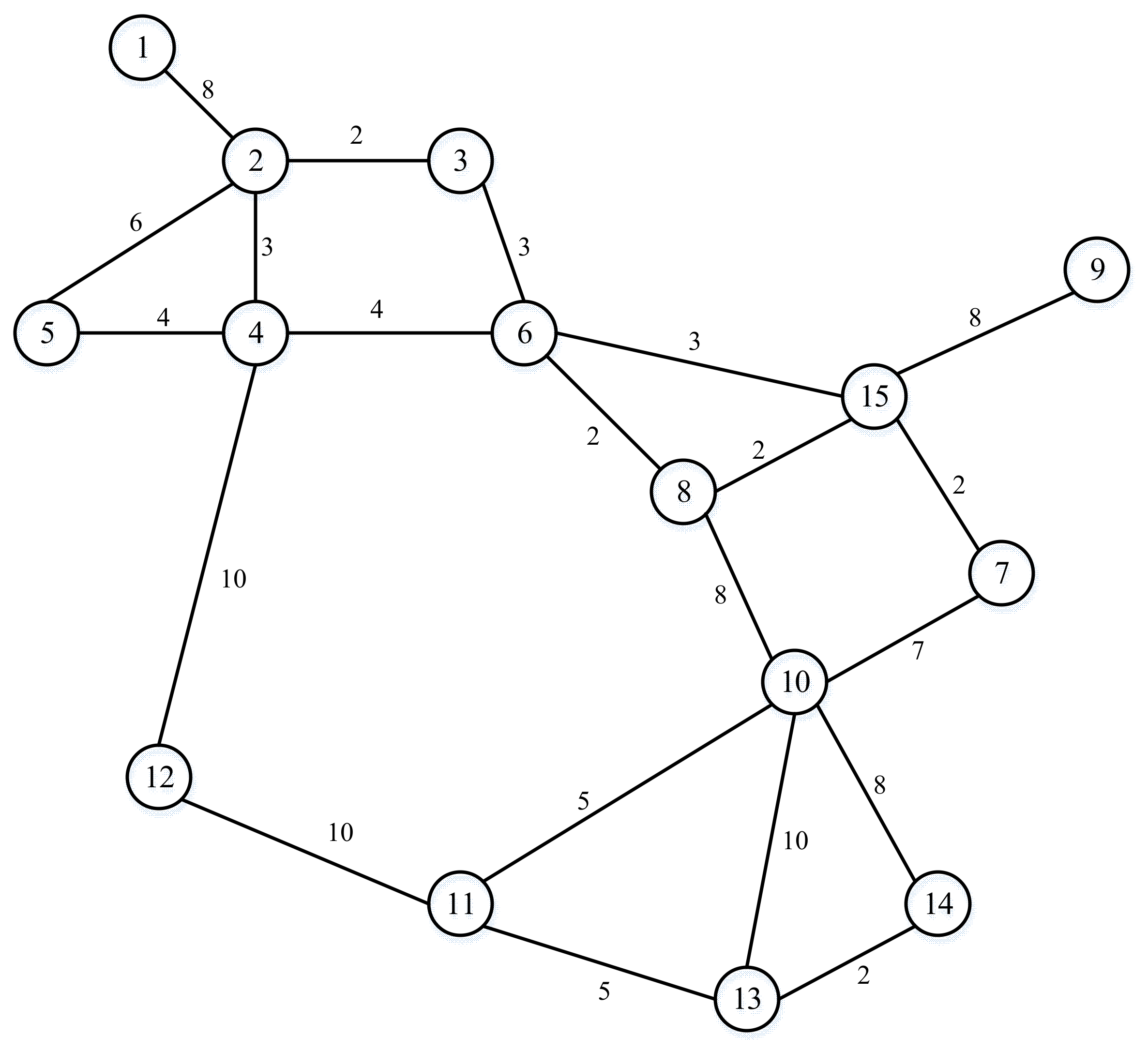
4.1. Small-Scale Network
4.1.1. Data
4.1.2. Parameters
4.1.3. Results
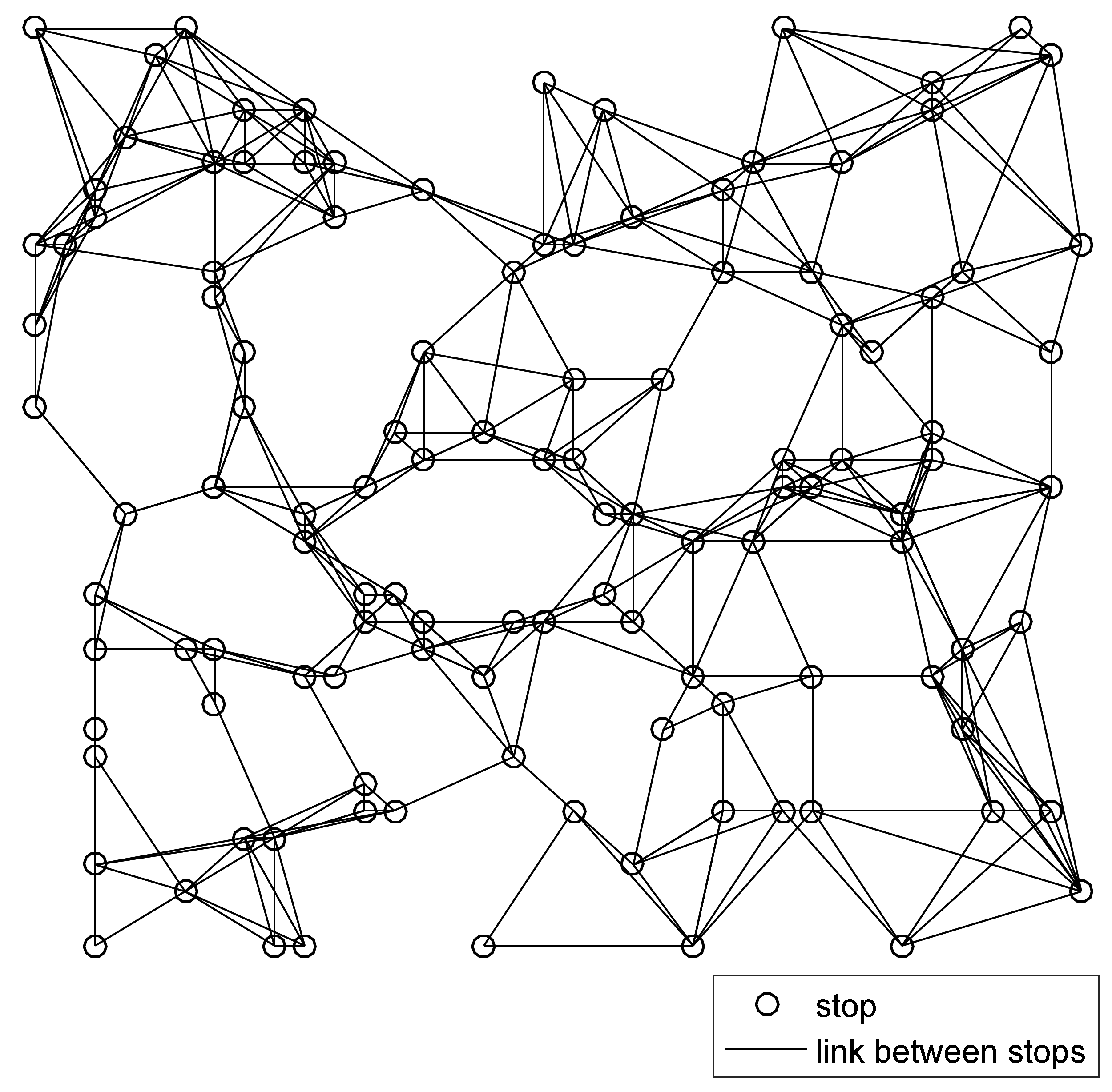
4.2. Medium-Scale Network
4.2.1. Data
4.2.2. Parameters
4.3. Analysis of the Proposed Algorithm
4.3.1. Initial Route Structure
4.3.2. Initial Frequencies
4.3.3. Computation Time
4.3.4. Comparison with Genetic Algorithm
4.4. Analysis of Results
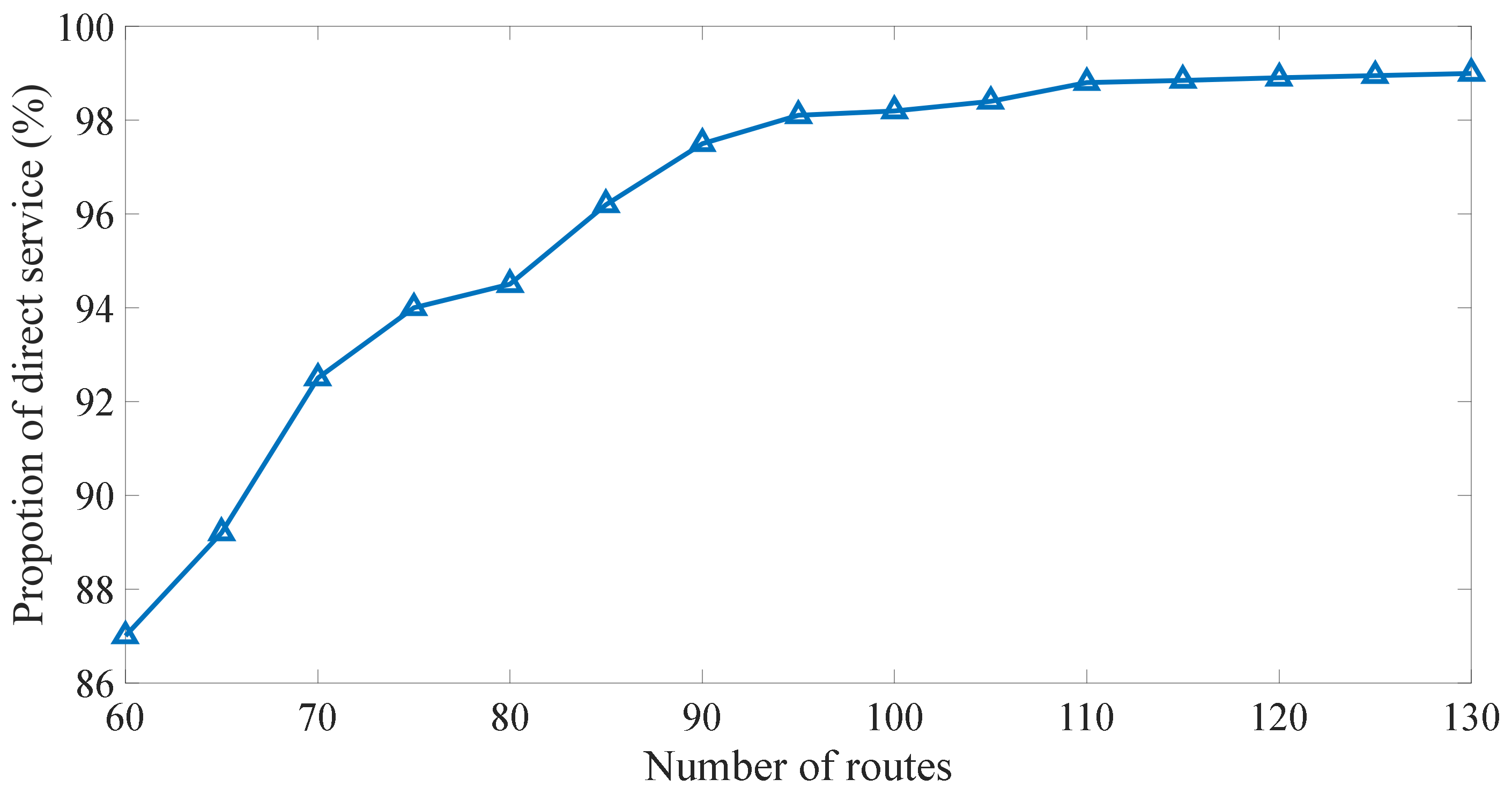
- (i)
- The proportion of direct service is high because the route generation is based on the changing matrix of travel demand.
- (ii)
- The route is the shortest path because of the sequential optimization for route structure.
- (iii)
- The initial frequency setting is close to the optimal solution for the determined transit network by the principle of vehicle assignment, which is based on the flow share.
- (iv)
- Computation time can be saved by setting a bus difference to determine the direction and step size and reassigning the vehicles to routes.
- (v)
- The proportion cannot be increased to 100% because of the following reasons: (1) the number of routes is insufficient to accomplish the goal, and (2) the distances are too long and the flow is limited for some pairs of OD, leading to inefficiency in the design of direct service for these OD.
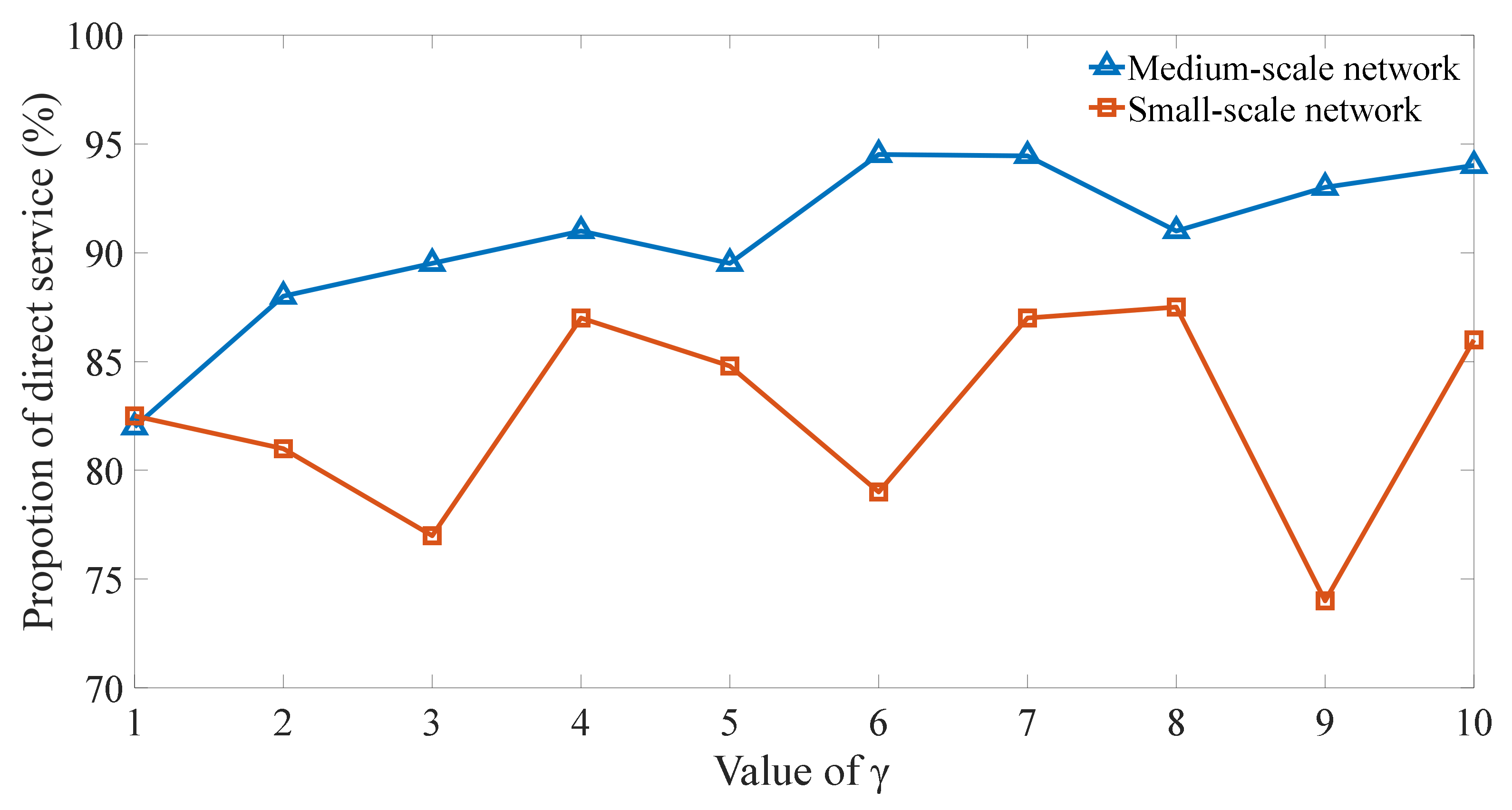
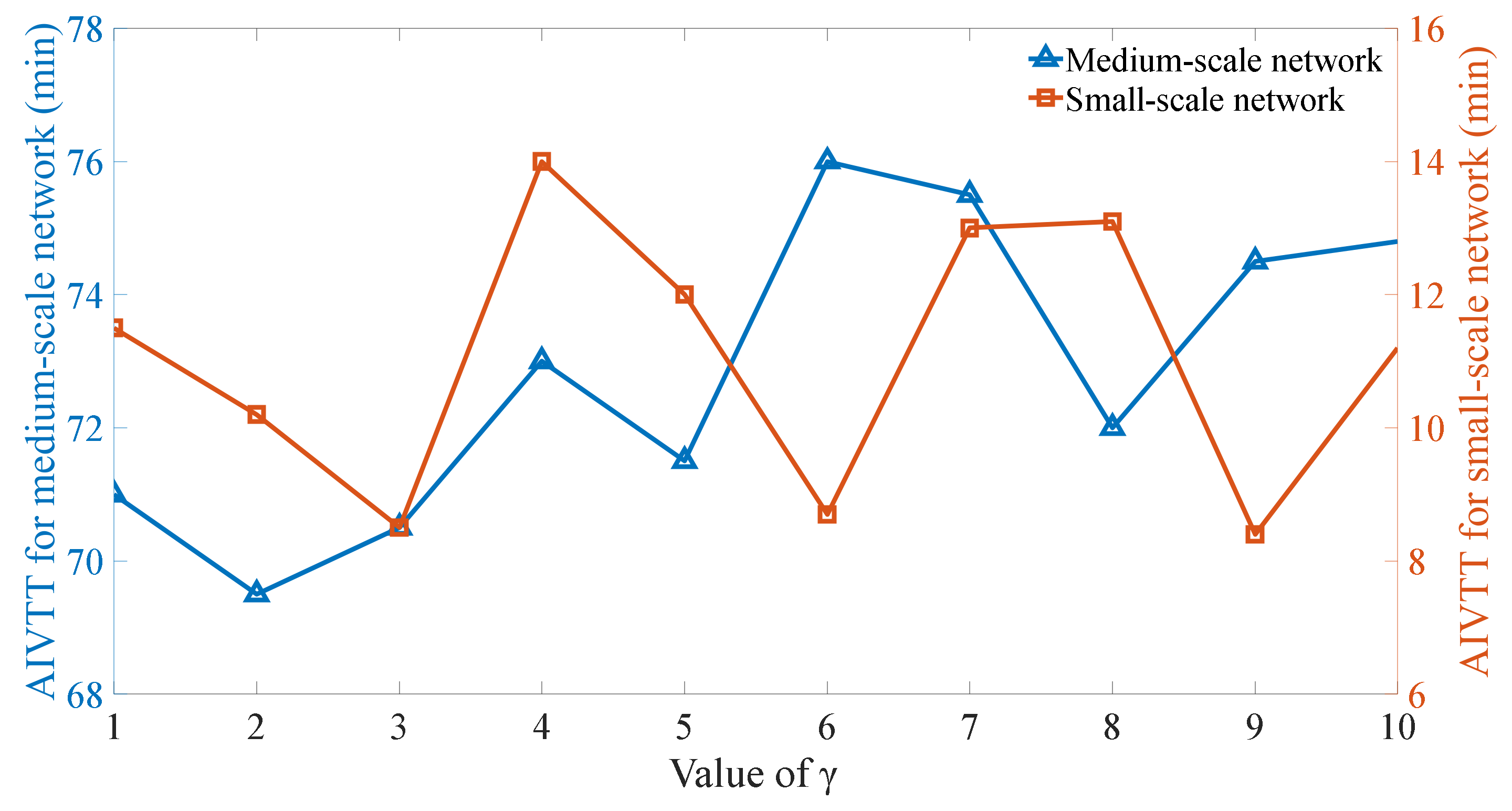
4.5. Analysis of Parameters
5. Conclusions
- (i)
- The proposed model and heuristic algorithm can simultaneously optimize the route structure and its corresponding frequencies with minimum travel time and transfer for different scale networks.
- (ii)
- Although the neighborhood search method is used to improve the route structure with the predefined number of routes, the proportion of direct service cannot reach 100%. An absolute direct service for all travel demands is consequently unreasonable to pursue. Providing direct service for the OD pairs with long distances and limited flow is inefficient and costly when the resource is limited.
- (iii)
- The introduction of an upper bound can improve the algorithm. For a medium-scale network, the upper bound is a useful parameter to balance the two contradictory sub-objectives in the objective function. However, a small-scale network has a minimal response to the parameter, thus suggesting that different performances may appear with the same model and algorithm.
- (iv)
- The proportion of direct service is not only sensitive to the upper bound but is also related to the number of routes. Direct service can be improved by increasing the number of routes if the subsidy is sufficient.
- (v)
- This algorithm currently tests an ideal hypothetical network. In the actual network, the algorithm can be applied to practice in combination with GIS tools.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| set of stops in the network; | |
| set of stops of route ; | |
| starting stop of route ; | |
| ending stop of route ; | |
| intermediate stops of route ; | |
| induces of stops; | |
| induces of routes; | |
| set of routes; | |
| objective function of the problem; | |
| weight of the travel without direct service; | |
| weight of the travel time; | |
| travel demand from stop to stop per unit time; | |
| binary variable, in which = 0 if the passengers from stop to stop can complete their travels without transfer and = 1 otherwise; | |
| sum of AIVTT and waiting time from stop to stop ; | |
| average waiting time from stop to stop ; | |
| AIVTT from stop to stop ; | |
| in-vehicle travel time from stop to stop through route ; | |
| frequency of route during the planning period; | |
| proportion of the travel demand assigned to route from stop and stop per unit time; | |
| binary variable, in which = 1 if the route passes through stop and stop continuously and = 0 otherwise; | |
| in-vehicle travel time from stop to stop by the shortest path; | |
| binary variable, in which = 1 if the route passes through stop and stop , that is, passengers from stop to stop can complete their travels without transfer by route ; and = 0 otherwise; | |
| average dwell time at each intermediate stop for all routes; | |
| set of routes that can provide the direct service from stop to stop | |
| number of routes for the network; | |
| maximum number of stops for a route; | |
| single-trip time of route ; | |
| time conversion unit in this study, in which = 60 min/h; | |
| maximum given fleet size for the planning network; | |
| flow on the segment from stop to stop for route per unit time; | |
| maximal load of a bus; | |
| number of passengers who board a bus at stop through route after assignment per unit time; | |
| number of passengers who alight from a bus at stop through route after assignment per unit time; | |
| flow assignment to route r from stop to stop ; | |
| section from stop to stop ; and | |
| maximum number of stops for a route. |
References
- Ceder, A.; Wilson, N.H. Bus network design. Transp. Res. Part B Methodol. 1986, 20, 331–344. [Google Scholar] [CrossRef]
- Kılıç, F.; Gök, M. A demand based route generation algorithm for public transit network design. Comput. Oper. Res. 2014, 51, 21–29. [Google Scholar] [CrossRef]
- Li, Z.C.; Lam, W.H.; Wong, S. On the allocation of new lines in a competitive transit network with uncertain demand and scale economies. J. Adv. Transp. 2011, 45, 233–251. [Google Scholar] [CrossRef]
- Mandl, C.E. Evaluation and optimization of urban public transportation networks. Eur. J. Oper. Res. 1980, 5, 396–404. [Google Scholar] [CrossRef]
- Murray, A.T. A coverage model for improving public transit system accessibility and expanding access. Ann. Oper. Res. 2003, 123, 143–156. [Google Scholar] [CrossRef]
- Wan, Q.K.; Lo, H.K. A mixed integer formulation for multiple-route transit network design. J. Math. Model. Algorithms 2003, 2, 299–308. [Google Scholar] [CrossRef]
- Xiong, Y.; Schneider, J.B. Transportation network design using a cumulative genetic algorithm and neural network. Transp. Res. Record. 1992, 1364, 37–44. [Google Scholar]
- Furth, P.G.; Wilson, N.H. Setting frequencies on bus routes: Theory and practice. Transp. Res. Record. 1981, 818, 1–7. [Google Scholar]
- Hadas, Y.; Shnaiderman, M. Public-transit frequency setting using minimum-cost approach with stochastic demand and travel time. Transp. Res. Part B Methodol. 2012, 46, 1068–1084. [Google Scholar] [CrossRef]
- Huang, Z.; Ren, G.; Liu, H. Optimizing bus frequencies under uncertain demand: Case study of the transit network in a developing city. Math. Probl. Eng. 2013, 2013, 375084. [Google Scholar] [CrossRef]
- LeBlanc, L.J. Transit system network design. Transp. Res. Part B Methodol. 1988, 22, 383–390. [Google Scholar] [CrossRef]
- Ceder, A.; Golany, B.; Tal, O. Creating bus timetables with maximal synchronization. Transp. Res. Part A Policy Pract. 2001, 35, 913–928. [Google Scholar] [CrossRef]
- De Palma, A.; Lindsey, R. Optimal timetables for public transportation. Transp. Res. Part B Methodol. 2001, 35, 789–813. [Google Scholar] [CrossRef]
- Hassold, S.; Ceder, A. Multiobjective approach to creating bus timetables with multiple vehicle types. Transp. Res. Rec. J. Transp. Res. Board 2012, 2276, 56–62. [Google Scholar] [CrossRef]
- Wong, R.C.; Yuen, T.W.; Fung, K.W.; Leung, J.M. Optimizing timetable synchronization for rail mass transit. Transp. Sci. 2008, 42, 57–69. [Google Scholar] [CrossRef]
- Bunte, S.; Kliewer, N. An overview on vehicle scheduling models. Public Transp. 2009, 1, 299–317. [Google Scholar] [CrossRef]
- Castelli, L.; Pesenti, R.; Ukovich, W. Scheduling multimodal transportation systems. Eur. J. Oper. Res. 2004, 155, 603–615. [Google Scholar] [CrossRef]
- Salzborn, F.J. Optimum bus scheduling. Transp. Sci. 1972, 6, 137–148. [Google Scholar] [CrossRef]
- Shrivastava, P.; Dhingra, S.; Gundaliya, P. Application of genetic algorithm for scheduling and schedule coordination problems. J. Adv. Transp. 2002, 36, 23–41. [Google Scholar] [CrossRef]
- Desrochers, M.; Soumis, F. A column generation approach to the urban transit crew scheduling problem. Transp. Sci. 1989, 23, 1–65. [Google Scholar] [CrossRef]
- Lam, W.; Zhou, J. Optimal fare structure for transit networks with elastic demand. Transp. Res. Rec. J. Transp. Res. Board 2000, 1733, 8–14. [Google Scholar] [CrossRef]
- Li, Z.-C.; Lam, W.H.; Wong, S. The optimal transit fare structure under different market regimes with uncertainty in the network. Netw. Spat. Econ. 2009, 9, 191–216. [Google Scholar] [CrossRef]
- Aguiléra, V.; Allio, S.; Benezech, V.; Combes, F.; Milion, C. Using cell phone data to measure quality of service and passenger flows of Paris transit system. Transp. Res. Part C Emerg. Technol. 2014, 43, 198–211. [Google Scholar] [CrossRef]
- Barry, J.; Freimer, R.; Slavin, H. Use of entry-only automatic fare collection data to estimate linked transit trips in New York City. Transp. Res. Rec. J. Transp. Res. Board 2009, 2112, 53–61. [Google Scholar] [CrossRef]
- Ceder, A. Bus frequency determination using passenger count data. Transp. Res. Part A Gen. 1984, 18, 439–453. [Google Scholar] [CrossRef]
- Cui, A. Bus passenger origin-destination matrix estimation using automated data collection systems. Mass. Inst. Technol. 2006, 21, 15–26. [Google Scholar]
- Kumar, A.; Nguyen, V.A.; Teo, K.M. Commuter cycling policy in Singapore: A farecard data analytics based approach. Ann. Oper. Res. 2014, 236, 57–73. [Google Scholar] [CrossRef]
- Tétreault, P.R.; El-Geneidy, A.M. Estimating bus run times for new limited-stop service using archived AVL and APC data. Transp. Res. Part A Policy Pract. 2010, 44, 390–402. [Google Scholar] [CrossRef]
- Zhao, J.; Rahbee, A.; Wilson, N.H. Estimating a Rail Passenger Trip Origin-Destination Matrix Using Automatic Data Collection Systems. Comput.-Aided Civil Infrastruct. Eng. 2007, 22, 376–387. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Z.; Zhu, S.; Wang, W. Design of limited-stop bus service with capacity constraint and stochastic travel time. Transp. Res. Part E Logist. Transp. Rev. 2015, 83, 1–15. [Google Scholar] [CrossRef]
- Szeto, W.; Jiang, Y. Hybrid artificial bee colony algorithm for transit network design. Transp. Res. Rec. J. Transp. Res. Board 2012, 2284, 47–56. [Google Scholar] [CrossRef]
- Szeto, W.; Jiang, Y. Transit route and frequency design: Bi-level modeling and hybrid artificial bee colony algorithm approach. Transp. Res. Part B Methodol. 2014, 67, 235–263. [Google Scholar] [CrossRef]
- Szeto, W.; Wu, Y. A simultaneous bus route design and frequency setting problem for Tin Shui Wai, Hong Kong. Eur. J. Oper. Res. 2011, 209, 141–155. [Google Scholar] [CrossRef]
- Constantin, I.; Florian, M. Optimizing Frequencies in a Transit Network: A Nonlinear Bi-level Programming Approach. Int. Trans. Oper. Res. 1995, 2, 149–164. [Google Scholar] [CrossRef]
- Fernandez, E.; Marcotte, P. Operators-users equilibrium model in a partially regulated transit system. Transp. Sci. 1992, 26, 93–105. [Google Scholar] [CrossRef][Green Version]
- Gao, Z.; Sun, H.; Shan, L.L. A continuous equilibrium network design model and algorithm for transit systems. Transp. Res. Part B Methodol. 2004, 38, 235–250. [Google Scholar] [CrossRef]
- Bagloee, S.A.; Ceder, A.A. Transit-network design methodology for actual-size road networks. Transp. Res. Part B Methodol. 2011, 45, 1787–1804. [Google Scholar] [CrossRef]
- Baaj, M.H.; Mahmassani, H.S. TRUST: A LISP program for the analysis of transit route configurations. Transp. Res. Rec. 1990, 1283, 265–275. [Google Scholar]
- Cortés, C.E.; Jara-Moroni, P.; Moreno, E.; Pineda, C. Stochastic transit equilibrium. Transp. Res. Part B Methodol. 2013, 51, 29–44. [Google Scholar] [CrossRef]
- De Cea, J.; Fernández, E. Transit assignment for congested public transport systems: An equilibrium model. Transp. Sci. 1993, 27, 133–147. [Google Scholar] [CrossRef]
- Lam, W.H.-K.; Gao, Z.; Chan, K.; Yang, H. A stochastic user equilibrium assignment model for congested transit networks. Transp. Res. Part B Methodol. 1999, 33, 351–368. [Google Scholar] [CrossRef]
- Nguyen, S.; Pallottino, S. Equilibrium traffic assignment for large scale transit networks. Eur. J. Oper. Res. 1988, 37, 176–186. [Google Scholar] [CrossRef]
- Szeto, W. Routing and scheduling hazardous material shipments: Nash game approach. Transp. B Transp. Dyn. 2013, 1, 237–260. [Google Scholar] [CrossRef]
- Chew, J.S.C.; Lee, L.S.; Seow, H.V. Genetic algorithm for biobjective urban transit routing problem. J. Appl. Math. 2013, 9, 411–421. [Google Scholar] [CrossRef]
- Fonzone, A.; Schmöcker, J.-D.; Liu, R. A model of bus bunching under reliability-based passenger arrival patterns. Transp. Res. Part C Emerg. Technol. 2015, 59, 164–182. [Google Scholar] [CrossRef]
- Newell, G.F. Dispatching policies for a transportation route. Transp. Sci. 1971, 5, 91–105. [Google Scholar] [CrossRef]
- Yu, B.; Yang, Z.; Yao, J. Genetic algorithm for bus frequency optimization. J. Transp. Eng. 2009, 136, 576–583. [Google Scholar] [CrossRef]
- Fan, W.; Machemehl, R.B. Using a simulated annealing algorithm to solve the transit route network design problem. J. Transp. Eng. 2006, 132, 122–132. [Google Scholar] [CrossRef]
- Zhao, F.; Zeng, X. Simulated annealing-genetic algorithm for transit network optimization. J. Comput. Civil Eng. 2006, 20, 57–68. [Google Scholar] [CrossRef]
- Baaj, M.H.; Mahmassani, H.S. Artificial intelligence-based system representation and search procedures for transit route network design. Transp. Res. Rec. 1992, 1358, 67–70. [Google Scholar]
- Baaj, M.H.; Mahmassani, H.S. An AI-based approach for transit route system planning and design. J. Adv. Transp. 1991, 25, 187–209. [Google Scholar] [CrossRef]
- Mumford, C.L. New heuristic and evolutionary operators for the multi-objective urban transit routing problem. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 939–946. [Google Scholar]
- Amiripour, S.M.; Ceder, A.A.; Mohaymany, A.S. Designing large-scale bus network with seasonal variations of demand. Transp. Res. Part C Emerg. Technol. 2014, 48, 322–338. [Google Scholar] [CrossRef]
- Lam, W.H.; Cheung, C.; Poon, Y. A study of train dwelling time at the Hong Kong mass transit railway system. J. Adv. Transp. 1998, 32, 285–295. [Google Scholar] [CrossRef]
- Yin, Y.; Lam, W.H.; Miller, M.A. A simulation-based reliability assessment approach for congested transit network. J. Adv. Transp. 2004, 38, 27–44. [Google Scholar] [CrossRef]
| (a) | (b) | (c) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stops | N1 | N2 | N3 | N4 | Stops | N1 | N2 | N3 | N4 | Stops | N1 | N2 | N3 | N4 |
| N1 | 0 | 1 | 2 | 3 | N1 | 0 | 1 | 2 | 3 | N1 | 0 | 1 | 2 | 3 |
| N2 | 1 | 0 | 4 | 5 | N2 | 1 | 0 | 4 | 5 | N2 | 1 | 0 | 0 | 0 |
| N3 | 2 | 4 | 0 | 6 | N3 | 2 | 4 | 0 | 0 | N3 | 2 | 0 | 0 | 0 |
| N4 | 3 | 5 | 6 | 0 | N4 | 3 | 5 | 0 | 0 | N4 | 3 | 0 | 0 | 0 |
 |  | |||||||||||||
| Stops | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 400 | 200 | 60 | 80 | 150 | 75 | 75 | 30 | 160 | 30 | 25 | 35 | 0 | 0 |
| 2 | 400 | 0 | 50 | 120 | 20 | 180 | 90 | 90 | 15 | 130 | 20 | 10 | 10 | 5 | 0 |
| 3 | 200 | 50 | 0 | 40 | 60 | 180 | 90 | 90 | 15 | 45 | 20 | 10 | 10 | 5 | 0 |
| 4 | 60 | 120 | 40 | 0 | 50 | 100 | 50 | 50 | 15 | 240 | 40 | 25 | 10 | 5 | 0 |
| 5 | 80 | 20 | 60 | 50 | 0 | 50 | 25 | 25 | 10 | 120 | 20 | 15 | 5 | 0 | |
| 6 | 150 | 180 | 180 | 100 | 50 | 0 | 100 | 100 | 30 | 880 | 60 | 15 | 15 | 10 | 0 |
| 7 | 75 | 90 | 90 | 50 | 25 | 100 | 0 | 50 | 15 | 440 | 35 | 10 | 10 | 5 | 0 |
| 8 | 75 | 90 | 90 | 50 | 25 | 100 | 50 | 0 | 15 | 440 | 35 | 10 | 10 | 5 | 0 |
| 9 | 30 | 15 | 15 | 15 | 10 | 30 | 15 | 15 | 0 | 140 | 20 | 5 | 0 | 0 | 0 |
| 10 | 160 | 130 | 45 | 240 | 120 | 880 | 440 | 440 | 140 | 0 | 600 | 250 | 500 | 200 | 0 |
| 11 | 30 | 20 | 20 | 40 | 20 | 60 | 35 | 35 | 20 | 600 | 0 | 75 | 95 | 15 | 0 |
| 12 | 25 | 10 | 10 | 25 | 15 | 15 | 10 | 10 | 5 | 250 | 75 | 0 | 70 | 0 | 0 |
| 13 | 35 | 10 | 10 | 10 | 5 | 15 | 10 | 10 | 0 | 500 | 95 | 70 | 0 | 45 | 0 |
| 14 | 0 | 5 | 5 | 5 | 0 | 10 | 5 | 5 | 0 | 200 | 15 | 0 | 45 | 0 | 0 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Route Label | Route Structure | Vehicles | Trip Time | Headway |
|---|---|---|---|---|
| 1 | 13-11-10-7-6 | 17 | 60 | 3.53 |
| 2 | 10-8-6-3-4-2-1 | 22 | 82 | 3.73 |
| 3 | 1-5-12-11-10-14-13 | 15 | 130 | 8.67 |
| 4 | 11-7-8-3-2-4-5 | 6 | 84 | 14.00 |
| Methods of Generation | Proportion of Direct Service | Total Trip Time |
|---|---|---|
| Random generation | 70.26% | 27,695 |
| Proposed generation | 94.86% | 11,919 |
| Initial Frequencies Scenario | Optimized Frequencies Scenario | |
|---|---|---|
| Objectives value (mins) | 33,250,015.89 | 33,153,646.8 |
| With Bus Difference | Without Bus Difference | |
|---|---|---|
| Computation time (s) | 0.09 | 0.14 |
| Genetic Algorithm | Proposed Alogrithm | |
|---|---|---|
| Computation time (s) | 150 s | 90 s |
| Objective values (min) | 353,000 | 333,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, H.; Xu, T.; Chen, Y. A Heuristic Algorithm Based on Travel Demand for Transit Network Design. Sustainability 2022, 14, 11097. https://doi.org/10.3390/su141711097
Liu Y, Zhang H, Xu T, Chen Y. A Heuristic Algorithm Based on Travel Demand for Transit Network Design. Sustainability. 2022; 14(17):11097. https://doi.org/10.3390/su141711097
Chicago/Turabian StyleLiu, Yuan, Heshan Zhang, Tao Xu, and Yaping Chen. 2022. "A Heuristic Algorithm Based on Travel Demand for Transit Network Design" Sustainability 14, no. 17: 11097. https://doi.org/10.3390/su141711097
APA StyleLiu, Y., Zhang, H., Xu, T., & Chen, Y. (2022). A Heuristic Algorithm Based on Travel Demand for Transit Network Design. Sustainability, 14(17), 11097. https://doi.org/10.3390/su141711097






