Abstract
Using the data of 23 industrial sectors in China, this paper constructs an industrial spatial weight matrix based on an input–output table and employs a spatial model to distinguish the spillover effects among industrial sectors and find sectors’ heterogeneity and connectivity on the decoupling system, to explore the specific driving power source for stable and deeper industrial decoupling. The results show that unstable industrial growth decoupling from energy consumption appears and differs in the capital–labor–resource-intensive sectors. Decoupling effects spill over from the neighboring sectors and act as a warning on decoupling in the local sector. Both technical progress and scale efficiency except technical efficiency play a driving role in deepening industrial decoupling in the local sector and spill out positive effects on the green development of the neighboring sector. Capital, as the substitute for energy both intra and inter sectors, facilitates decoupling as a driving factor, while obvious resistant force against decoupling is brought by foreign direct investment (FDI) and energy structure. Decoupling in resource-intensive sectors has great potential due to the positive effects from technology and scale efficiency improvement, which are substitute effects. Industrial decoupling in the labor-intensive sector, where low-skilled labor forms obstruction force against green decoupling, only benefits from the technological progress. FDI and scale efficiency dominate as driving sources for decoupling in the capital-intensive sector.
1. Introduction
Greenhouse gas emission leads to climate changes such as sandstorms, tornados, heavy rain, high-temperature heatwaves, and other extreme events. Extreme weather threatens human survival on earth and calls the global governments to take action immediately. While most are yet to realize the promise of the Paris Agreement emission reduction targets, they are far from satisfactory achievements. Much more work for less energy consumption and more economic output remains to be achieved. As is known, continuous fossil fuel consumption in economic growth is a major source of increased carbon emissions [1] and is responsible for environmental problems. As the International Energy Agency (IEA) predicts, if the traditional economic growth pattern is not changed, fossil energy consumption will cause global greenhouse gas emissions to increase by 57% until 2030, meaning that the earth’s surface temperature will increase by 3 °C and, consequently, cause the death of 6 million individuals, 90% of which will occur in developing countries (IEA, Paris, France, 2017). The effective measure for climate mitigation is to leave most of the fossil resources underground [2], and to use decouple economic growth from energy consumption to control the emission and release the climate burden. Decoupling material and energy throughput from economic growth is widely advertised by many countries as a great achievement towards the fight against climate change and other environmental impacts, and it has attained a renewed focus as the core for the new Sustainable Development Goals (SDGs) [3]. As one of the largest energy consuming countries in the world, seeking stable and strong decoupling economic growth from energy consumption matters a lot for the blue-sky protection fight in China. Strong decoupling indicates that energy consumption decreases while economic output grows, which should be attained by nations and industries for the climate targets. Being the main contributor to the national economy, the rapid development of industry, especially five sectors of high emission, accompanied with a dramatic increase in energy consumption, cause an increase in carbon dioxide emissions, which has put a lot of pressure on emission-reduction efforts in China. The implementation of decoupling with energy consumption reducing without costing the industrial production is imminent, especially for green development in the context of high-quality transformation.
2. Literature Review
Since being introduced into the environmental issue, decoupling has featured widely in discussions related to the relationship between resource conservation, pollution reduction, and economic growth. Many studies have focused on identifying an indicator with which to diagnose the occurrence of decoupling in the field of economic growth and environmental quality. Indeed, the study of decoupling between economic growth and energy consumption is fundamental, as energy consumption is the source of greenhouse gas emissions.
Economic growth may overcome the limited energy stock constraint due to technological progress, showing that the increasing returns of knowledge and the energy substitution of other factors lead to the decoupling of economic growth from energy consumption [4]. Most research has found decoupling or even strong decoupling. Roman [5] found that decoupling between economic growth and energy consumption in Colombia was unstable and often changed into a negative status. Negative decoupling or unstable temporary pseudo decoupling in certain countries also exists [6]. Energy efficiency improvement and low-carbon technology introduction are useful for decoupling realization [7]. Compared to the different countries, stable decoupling in developed countries tends to be deeper than that in low-income countries with heavy energy consumption for transportation in industrial sectors’ development [8,9,10,11]. Decoupling in China changes in an inverted U-shaped curve, and it is always overestimated in the developed regions [12]; meanwhile, China always performs better in energy saving than India [13]. Some studies try to thoroughly examine decoupling using samples of some specific regions, industries, or energy types. Decoupling from coal consumption and electricity consumption, measured by energy intensity, has also been identified in China’s different regions [14]. Four kinds of decoupling in Liao Ning have been found, and energy intensity is taken as a positive factor for decoupling [15]. The decoupling between power consumption and economic development in 100 cities in China forms an inverted-N shape, and it has entered into a downward regime in which the decoupling is continuously strengthened [16]. The transport sector in Japan and England, and the construction sectors in China and India, all show unstable decoupling and even coupling [17,18,19,20]. Moreover, in the agricultural sector in 18 of 89 countries, strong decoupling between agricultural energy consumption and production have been found [21]. Decoupling fluctuates and is unstable with the different regions, energy types, and industries. For specific industries, more attention has been given to the decoupling between economic growth and greenhouse gas rather than energy consumption. In addition to the evolution and identification of decoupling, more studies have been carried out on power sources or influencing factors.
Extant research generally adopts the decomposition methods performing a single decoupling indicator, which is composed of economic growth rate and energy consumption rate. Most focus on the internal aspect of the economic system, and a small group has begun to explore the influence of external factors. Technological progress, structure adjustment, energy intensity, and economic scale are widely known as contributors to decoupling [22,23]. Arto [24] used the bipolar decomposition method and found that the effects of substitution, clean energy, and primary energy have an impact on decoupling from fossil energy consumption; Schymura [25] used the same method to study 40 economies and found that the heterogeneous technology among countries contributed more than industrial structure change, while the industrial structure in the countries with a relatively small difference increased decoupling more than technology, and technology acted as the most important factor to improve energy efficiency regardless of whether it was energy intensive or not. Zhang [26] pointed out that only the energy intensity effect, rather than the economic activity effect, played a positive role in the decoupling development. Wu [11] used the Grey Correlation method and found that technological progress has played a significant driving role in developed countries, while the industrial structure and economic growth pattern in developing countries contributed more than technical factors. From China’s experience, the decoupling status between economy and energy consumption were determined largely by the secondary industry [27]. As energy footprint linked within countries, products’ trade or energy import affect national energy intensity [28]. Sanye [29] extracted the effects of import and export from local factors on energy consumption and found a relation, namely that the effects derived from regions or countries through international or internal trade will affect the economic operation, as well as energy consumption.
The studies on decoupling are from an independent perspective, and the decomposition methods used are relatively simple and easy to operate, which can measure the contribution of influencing factors. Following the geographic rules, industrial dependence is established through the input–output linkage, where resource flow and knowledge spilled from upstream and downstream supply chains help build the connectivity among sectors. However, the interaction and correlation among regions and sectors is always missed in the extant decoupling research, and such ignorance of the industrial spillover effects on decoupling will lead to the uncertainty of factors’ respective contribution. A spatial model can help identify the spillover power from neighboring regions or sectors, in which spatial dependence is the special case where the dependent variable or error term in one location that is correlated with those in another location [30]. Therefore, the contribution of this paper is the construction of a spatial model to explore the spillover effects of an industrial decoupling system, considering the sectors’ heterogeneity and connectivity, distinguishing the different power of impact factors intra and extra industry, and providing more specific references for stable and balanced industrial decoupling. Moreover, this paper is organized as follows: Section 2 depicts the decoupling status of 23 industrial sectors; Section 3 establishes a spatial model to estimate the spillover impact and marginal contribution of total factor productivity (TFP) on decoupling; Section 4 analyzes the results and provides some discussion; Section 5 draws several conclusions and puts forward suggestions.
3. Data and Method
3.1. Variables Selection and Data Source
Elasticity originated from physics is widely used in economics to measure the changes in sensitivity from one variable to another variable. Based on this, the decoupling elasticity index (Di), calculated by the proportion of the energy consumption growth rate(gE) and economic growth rate (gY) with a fixed first base period, is performed to assess the decoupling state, which can be categorized into five types, as shown in Table 1, including strong decoupling (Di < 0), active decoupling (Di < 0.5) when Di approaches the strong decoupling regime, passive decoupling (Di > 0.5) when Di approaches the negative decoupling regime, and negative decoupling (Di > 1). The larger the Di value is, the worse decoupling becomes.

Table 1.
Decoupling types.
Economic growth and a high-quality environment can coexist if there is significant technological progress in the industrial sectors [31]. Total factor productivity (TFP), used to represent technological progress [32], is calculated based on the DEA Malmquist index and decomposed into the technical progress index (tech), technical efficiency index (pech), and scale efficiency index (sech). Input factors include capital and labor, and output is the industrial output. Capital is estimated using depreciation rate and investment amount. To avoid the drawback of the fixed depreciation rate used in the existing research, this paper calculates different depreciation rates by dividing the original value of the previous year’s fixed assets from the current year’s depreciation. Then, industrial capital stock = comparable investment amount + (1-depreciation rate) × the lagged-term capital stock, where the comparable investment amount is the adjusted net value of the fixed-asset investment reduced by the fixed assets investment price index. Industrial employees represent labor.
Efficient technologies and newer vintages of capital equipment or the changes in the structural composition help improve energy efficiency [33]. The fixed assets value is chosen as an index for Capital equipment (K). Human capital could either be a substitute or a complement for energy inputs during the production process [34]. Employees of enterprises above designated size in various industries at the end of the year are chosen for human capital. Renewable energy consumption or its share of the total energy mix is positive and statistically significant on economic growth [35]. Energy conversion in power sources reflects the gradual switch from traditional fossil energy to renewable energy, and the growth rate of electricity consumption (eners) is used to represent it. As an important source of external technology and capital, foreign direct investment (FDI) plays an important role in green development. FDI facilitates technology diffusion and raises energy productivity in the Chinese economy [36], while FDI inflows in carbon-intensive sectors also stimulate energy demand.Then, the effects on decoupling industrial growth from energy consumption become complicated. The actual total amount of foreign investment from industrial enterprises above the designated size is chosen for FDI. All the data during 2004–2017 are collected from the China Industrial Statistical Yearbook, energy statistics, and China Statistical Yearbook. Only the data of industrial output, accumulated depreciation, and original fixed assets value are picked from the industrial enterprises above designated size (Table 2).

Table 2.
Descriptive statistics of variables.
3.2. Empirical Model
According to the tradition growth model, a classic model is established to explore the influence of technology, labor, capital, FDI, and energy structure on decoupling between industrial growth and energy consumption. The equation is presented as follows:
Then we take K, L, and FDI into logarithmic form and transform the basic model into a semi-logarithmic linear equation to discuss the relationship. The semi-log-linear can be presented as follows:
where subscript i, t denotes industrial sector and time period, respectively, and represents the coefficients of different variables. is the stochastic error term. indicates industry fixed effect and the time-fixed effects.
In order to find the industrial spillover effects in the decoupling system, we extend the linear model into an industrial spatial model. The industrial spillover effects mean that the factors of the neighboring sector will influence the decoupling of the local sector, which is an exogenous factor compared to the endogenous one from the local variables. SDM is a more general model, which can not only estimate the spillover effects through the dependent and independent variables, but also by the error terms. Then, the above-mentioned model can be extended as:
where wij represents the industrial spatial weights’ matrix and is constructed based on the 2010 industrial input–output matrix; is the coefficients matrix of spatially lagged terms. The estimated process can be referred to by Elhorst.
4. Results and Discussion
4.1. Decoupling Status of Industrial Sectors
To identify the industrial decoupling status, 23 industrial sectors accounting for nearly all of the industrial production output are chosen and then divided into capital-intensive sectors, including petroleum processing coking and nuclear fuel processing industry (PPCNF), chemical industry (CI), non-metallic mineral products industry (NMMP), metal smelting and calendering industry (MSC), transportation equipment manufacturing industry (TEM), general equipment and special equipment communication, labor-intensive sectors, including food and tobacco industry (FAT), textile industry (TXT), textile clothing leather industry (TCLI), wood processing and furniture industry (WPF), paper making, printing, culture, education and sports industry (PPCES), metal products industry (MPI), instrument and culture, office machinery manufacturing industry (ICOM), electrical machinery and equipment manufacturing industry (EMEM), resource-intensive sectors, including coal mining and washing industry (CMW), oil and gas extraction (OGE), metal mining and dressing industry (MMD), non-metallic ore mining and dressing industry (NMOD), electricity and heat Production and supply (EHPS), gas production and supply (GPS), and water production and supply (WPS).
As shown in Figure 1, active decoupling in the industry has been identified, with Di changing among the 0.5–0.2 interval during 2004–2017, increasing and decreasing in the unstable trace. TEA (total energy consumption) increases, except for in 2013–2014, where it shows a slight decrease. Continual energy consumption is the potential risk endangering the stability of industrial decoupling. Three sectors have also achieved decoupling and become close to the active decoupling regime. Changing the trace of Di in the capital-intensive and labor-intensive sector increases concentration more than in the resource-intensive sector. The Di of all the labor-intensive sectors change around interval 0.9–0.1, and most center between 0.6 and 0.2, approaching the active and passive decoupling regime. The positive decoupling of some sectors (FAT, MPI, PPCES) remains for a short time and worsens with an increase in Di, indicating that there is unstable decoupling in the labor-intensive sector (Figure 2). Di in all the sectors sharply declines to a lower point, while Di in WPF ranks the highest of all and decreases down to the starting point of around 0.5, indicating much potential for WPF decoupling. In China, the small enterprises in WPF are scattered, disordered, and polluted, and need more regulations in the production process. The Di in ICOM remains at the bottom, a sign of active decoupling.
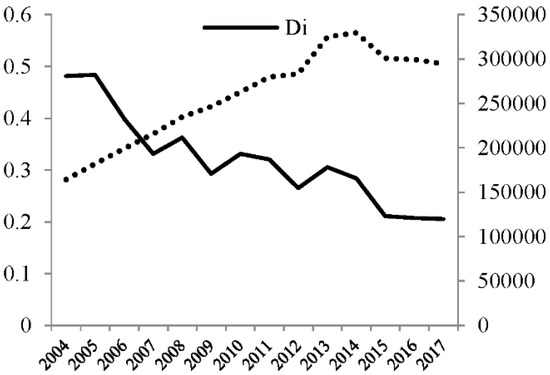
Figure 1.
Industry Di and energy consumption.
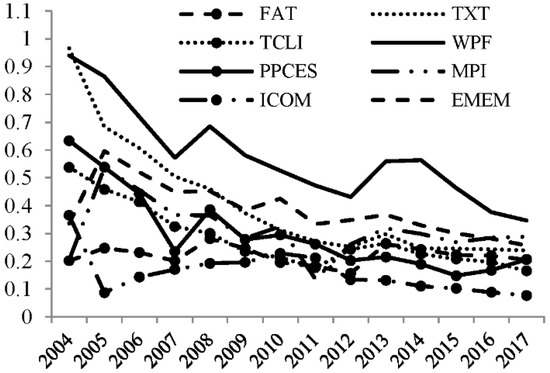
Figure 2.
Labor-intensive sector’s Di.
As Figure 3 shows, Di in the capital-intensive sectors center around 0.5–0.2 and shows a deeper status than in the labor-intensive sectors, indicating much more positive effects from capital than from labor. Technology intensive capital goods can help lower energy intensity and shift energy consumption patterns. Di in the most capital-intensive sectors experienced a steady decline, representing the achievements of industrial upgrading, while the communication and information technology industry (CECO) remained in passive decoupling for a short time, with Di changing around 0.7–0.6 and then gradually declining to around 0.5–0.4, which is relatively higher compared to the others. To prevent the coupling due to energy consumption rebound, the focus should be put on the CECO sector. Di in the TEM (transportation industry) of heavy energy consumption shows a completely different changing trace, and decoupling instability brings potential risks to the green development of capital-intensive sectors. As shown in Figure 4, Di in resource-intensive sectors hovers between 0.3 and 0.2, which is far lower than that of the other two industries, indicating that the decoupling degree is deeper and stable. Most of the sub-sectors changed in the same direction, decreasing firstly and then flattening to the low level. The renewable energy sector’s water production and supply (WPS) is the exception, with an increasing Di at around 0.5–0.6, indicating that passive decoupling has been found and that there is great potential. Di in NMOD (Nonmetallic mineral products industry) is constantly increasing, which needs the driving force pushing decoupling; Di in EHPS (production and supply of electricity and heat) dramatically declines to the bottom, a sign of achievement from the energy power source and electricity system reform.
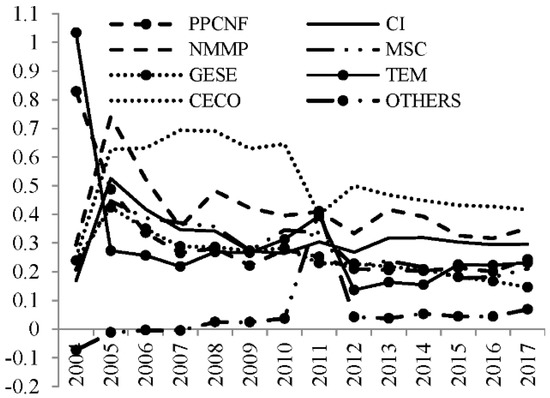
Figure 3.
Capital-intensive sector’s Di.
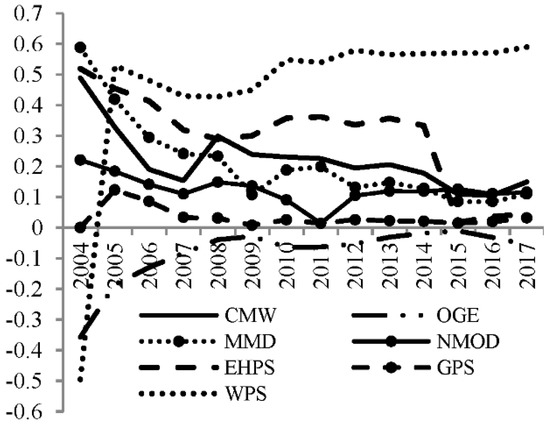
Figure 4.
Resource-intensive sector’s Di.
With the wide application of energy saving technologies in production and service-oriented industry upgrading, industrial growth mode has been changed, which can be reflected in the decoupling status of subdivided sectors. However, due to the control of quantitative changes rather than structural optimization, the decoupling in different industries has been unstable and fluctuates. Therefore, in order to tap into the potential of stable decoupling, it is necessary to explore the driving factors of industrial decoupling.
4.2. Results of Model Estimation
4.2.1. Panel Unit Root and Co-Integration
The results of panel stationery can be concluded from the unit root test. As shown in Table 3, all LLC, IPS, ADF, and PP tests reject the null hypothesis with a unit root and provide consistent conclusions that all the variables are stable at level, which is fundamental to the model’s construction and estimation.

Table 3.
Unit root result.
4.2.2. Industrial Spatial Correlation
In the traditional spatial model, Moran’s I is used to identify the similarity among adjacent areas and is generally calculated by the spatial weight matrix wij. Moran’s I at interval [0, 1] means that the adjacent regions are positively correlated, and that there are many more similarities. Two regions achieve higher-degree homogeneity when approaching 1. The closer the two regions become, the easier the high–high or low-–ow agglomeration will form. When the value is between [0, −1], there is a negative correlation, indicating much difference between regions, and great heterogeneity means that the regions tend to form high–low or low–high agglomeration. The industrial spatial weight index wij is calculated based on the 2010 and 2015 input–output table and is used for the Moran’s I value to diagnose the industrial correlation. As found, the mean value of Di Moran’s I is 0.1219 and 0.1424, respectively, and is significant at the 10% level (p = 0.0721) and the 5% level (p = 0.0433). The results are comparatively robust, and both reject the null hypothesis of “no spatial auto-correlation”, implying that there is a significant industrial spatial spillover effect in the decoupling system.
4.2.3. Industrial Spatial Model Selection Evidence
As in the spatial model, the Lagrange multiplier test (LM) and Robust LM are carried out to diagnose the existence of industrial spatial dependence in OLS residuals. As shown in Table 4, both LMs for the industrial spatial error and industrial spatially lagged models based on 2010 input–output weights’ metrics are significant at the 1% level, rejecting the null hypothesis of no spatial dependence. The robust test corrects for asymptotic interdependence between LM error and lag tests [37]. The RLM test of spatial lag and error are both significant at the 1% level, indicating that the spatial model is much fitter than the panel one. Moreover, the omission of the spatial term in the spatial model will cause an omission bias problem. The Spatial Dubin model, rather than SLM with spatially lagged explanatory variables or SEM with the spatially lagged error term, will not present a biased estimation, even if the data generation process calls for other spatial econometric models [38]. Wald and LR are used to test whether SDM could be simplified to one of its nested models. Both the results are significant at the 1% level, indicating that SDM is preferable. The Hausman test is significant at the 1% level, suggesting fixed-individual effects in the model, and the maximum likelihood method is therefore employed.

Table 4.
Spatial tests result.
4.3. The Spatial–Temporal Effects of Industrial Decoupling System
The goodness for the spatial models can rely on the Log-Likelihood and other indicators except R2 [39]. As shown in Table 5, Log-Likelihood value increases from 253.0103 (in the panel model) to 272.588 or 259.798 in SDM, indicating that SDM is better. The coefficients of the main explanatory variables in the models are relatively stable. The column 5–6 in Table 5 include the results estimated based on the weight matric calculated from the 2015 input–output table, which are similar to column 3–4 using the 2010 weight matric, implying the robustness of the variables’ effects on decoupling. Column β includes the coefficients of industrial spatially lagged terms, reflecting the industrial spillover effects.

Table 5.
The whole industry estimation result.
As shown in Table 5, the industrial decoupling system shows obvious spatial correlation. Some factors, such as driving force, facilitate decoupling, while others are inhibiting, and most of them spill among industries. The spatially lagged coefficient of Di is negative and significant at the 1% level, indicating that the exogenous effects on decoupling spilling from upstream and downstream industries. Specifically, an 1% increase in Di from the neighboring sectors will lead to a 0.314% decrease in Di from the local sector. The penalties on the green growth of shallow or negative decoupling arouse alarm to others. “Learning from the neighbors” leads to the construction of a demonstration model, and lessons from the neighboring industries teach others to reduce, energy consumption and improve efficiency in the process of production, transportation, and other links. Technical progress and the substitution effect can improve energy efficiency by changing the industrial structure and production input factors’ formation, which effectively deepen decoupling. Coefficients of tech and sech except pech are negative and significant at the 5% level, showing that technical progress and scale efficiency help deepen industrial decoupling. With the introduction of new processing, new skills, and new equipment, industrial output has been improved without any more energy input. The number of technological skills and industrial output have been increased, and specialized production, transaction, and cost-saving have been intensified, leading to a reduction in the energy consumption in the departments. The negative coefficients of industrial tech and sech spatially lagged terms are also significant, indicating the positive spillover effects on decoupling in the local sector. The greater proportion of departments in the advanced stage that achieve higher technical level in the industry, the more conducive scale effect and professional production is, and the more easily channels will be built for the flows of products, factors, or services. Through the platform, technology and knowledge spill with the flows of workers, capital, or machines. Then, a positive influence on decoupling is rapidly absorbed and diffused, while the insignificant pech coefficient indicates that the green reform of the industry is still in the stage of scale, rather than the stage of efficiency improvement.
As a substitute for energy, the capital’s positive effect is found not only from the local sector, but also from the neighboring sectors. On the contrary, the complementary effects of labor on energy have been identified only from the neighboring sectors. The flows of resources among the similar industries often produce strong spills and result in overall energy saving. As shown, FDI and eners from the local and neighboring sectors impose inhibiting power on decoupling. Both the coefficients of FDI and its spatially lagged term are significantly positive, indicating that decoupling is affected not only by FDI inflows in the local sector, but also by that in the connected neighboring sectors. FDI plays an important role in economic growth and energy consumption [40], in which the transfer of knowledge and technology with FDI flows may stimulate energy demand both for theeners in local and neighboring sectors’ present inhibiting force on decoupling. Although the power source gradually transfers to renewable energy, the proportion of fossil energy is still large enough to decide the industrial growth mode.
4.4. Industrial Heterogeneity Effects
The evolving path and driving source of decoupling differs due to industrial heterogeneity. Capital-, labor-, and resource-intensive sectors have been divided based on some similarities. Then, the models based on the three sectors can help identify the specific influence of different factors. As Table 6 shows, the coefficients of the Di industrial spatially lagged term are all significantly negative in all three sectors, implying that the robustness of warning spillover effects in the decoupling system. In resource-intensive sectors, most factors play positive roles in driving decoupling. Technical progress, scale efficiency, technical efficiency, and substitute effects are the main drivers for decoupling, as well as FDI. FDI “Pollution halo” plays a leading role, which is different from the impacts in the whole industry. Technology and capital dominate in deepening decoupling energy consumption from resource-intensive sectors’ growth, while knowledge, capital, and other resource flows have not built an effective bridge for the spillover of driving factors. In the labor-intensive sectors, the driving mode of decoupling is similar. Technical efficiency and substitute effects of capital are the driving source. However, the scale efficiency of technological progress has no significant impact, which means that green development has entered the efficiency seeking stage instead of the quantity control stage, which is different from the situation of the whole industry. Both capital and FDI drive decoupling in the local sector and in the adjacent sectors, acting as a stable positive, and pushing in and out power. The green labor-intensive sector can benefit much more from structural optimization, capital replacement, and technology spillover from FDI. As for capital-intensive sectors, only scale efficiency and FDI can drive decoupling, indicating that resource investment leading to scale efficiency improvement can be a potential field for deeper decoupling.

Table 6.
Different industries estimation results.
5. Conclusions and Suggestions
This paper attempts to trace the decoupling status of 23 industrial sectors and incorporates the industrial spatially lagged terms in the employed model to distinguish endogenous and exogenous effects. The conclusions and suggestions for sustainable decoupling can be summarized as:
Firstly, industrial sectors have attained unstable decoupling during the sample period, and the decoupling changing trace of different industries varies greatly. Three sectors have gradually transferred from a passive decoupling regime to a positive decoupling regime. Decoupling in the capital-intensive and labor-intensive sector is more concentrated and unstable. Di values in most sectors fluctuate on the same path, which decreases greatly and then increases slightly and tries to recover. For example, see the decoupling changes in the transportation sector and communication and information technology sector. Decoupling in the resource-intensive sector, with much greater heterogeneity, reflects the reform implementation achievements of the “energy efficiency doubling” plan in the mining sector and improvement of the “green smelting” management mode. Decoupling in the resource-intensive sector needs more care to be stabilized.
Secondly, the stability of industrial decoupling is not only affected by endogenous factors, but also by the spillover power from upstream and downstream industries. The obvious indirect influence among industries on decoupling have been identified as a greater power source than the direct effects from endogenous factors. The industrial decoupling in the neighboring sectors compete against that in the local sector. Technology progress and scale efficiency, except for technical efficiency, play positive roles in pushing industrial decoupling. The effects of efficiency improvement are vague due to some energy rebound. Capital can be a substitute rather than complementary to energy and is another driving factor. These driving factors also spill positive effects on decoupling in other sectors, facilitating Di reduction and decoupling deepening. To explore the potential for deeper and stable decoupling in the industry, we should focus on the power source spilled from the neighboring sectors. The effective cooperation arrangements between the upstream and downstream can help stimulate the gains of industrial agglomeration to achieve stable decoupling.
Finally, the driving mechanisms of decoupling in the three different sectors vary due to the sectors’ heterogeneity. Decoupling in the resource-intensive sector has greater potential and enters into a full-driven period with more pushing factors. The improvement of technology and scale efficiency and substitute effects are all driving sources. Increasing capital investment, expanding production scale, bringing in new technology, and modifying processes are effective measures to deepen decoupling. In the labor-intensive sector, technology driven decoupling, rather than scale efficiency improvement decoupling, is dominant. Due to the greater proportion of low-skilled and low-income workers in these sectors, inhibiting power-hindering decoupling comes from labor rather than capital. Accelerating technological innovation, improving the production skills of enterprises, and optimizing the labor structure are critical for deeper decoupling in the labor-intensive sector. Unlike the other two sectors, decoupling in the capital-intensive sector faces many more difficulties and mainly relies on FDI inflows and scale improvement. Optimizing FDI and expanding the production scale are important areas for tapping into the decoupling potential in the capital-intensive sector.
The trace of industrial decoupling and the diverse driving mechanism of industrial decoupling have been identified, testified, and explored, and can provide specific guidance for policymakers. Moreover, as transport or the ICT sector, accounting for the large share of the total energy consumption in the industry, has been classified into one, which means that the studies still hang on a general industrial sample, future research can be executed in a certain sector to grasp the individual causes of decoupling instability.
Author Contributions
Conceptualization and methodology: L.Z. (Lanting Zeng); validation: X.Z.; writing—original draft preparation: L.Z. (Lanting Zeng); paper language checking: L.Z. (Liping Zhang). All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by Natural Science Foundation of Fujian Province (Grant No.2021J05269); Middle-aged and young teacher’s education research project of Fujian (Grant No. JAS20221)).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The research data presented in this study are available on request from the corresponding author and are available from China provincial Statistical Yearbook.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhao, X.; Zhang, X.; Shao, S. Decoupling CO2 emissions and industrial growth in China over 1993–2013: The role of investment. Energy Econ. 2016, 60, 275–292. [Google Scholar] [CrossRef]
- McGlade, C.; Ekins, P. The geographical distribution of fossil fuels unused when limiting global warming to 2 °C. Nature 2015, 517, 187–190. [Google Scholar] [CrossRef] [PubMed]
- Bizikova, L.; Schandl, H.; Pinter, L.; Offerdahl, K. Sustainable Consumption and Production (SCP) Targets and Indicators and the SDG’s; UNEP: Ottawa, ON, Canada, 2014. [Google Scholar]
- Williams, M.; Laumas, P. The relation between energy and non-energy inputs in India’s manufactures industries. J. Ind. Econ. 1981, 30, 264–270. [Google Scholar] [CrossRef]
- Roman, C.R.; Cansino, J.M.; Botia, C. How far is Colombia from decoupling? Two-level decomposition analysis of energy consumption changes. Energy 2018, 148, 687–700. [Google Scholar] [CrossRef]
- Bithas, K.; Kalimeris, P. Unmasking decoupling: Redefining the Resource Intensity of the Economy. Sci. Total Environ. 2018, 338, 619–620. [Google Scholar] [CrossRef]
- Chovancoya, J.; Vavrek, R. Decoupling analysis of Energy Consumption and Economic Growth of V4 Countries. Probl. Ekorozw. 2019, 14, 159–165. [Google Scholar]
- Moreau, V.; Vuille, F. Decoupling energy use and economic growth: Counter evidence from structural effects and embodied energy in trade. Appl. Energy 2018, 215, 54–62. [Google Scholar] [CrossRef]
- Burke, P.J.; Csereklyei, Z. Understanding the energy-GDP elasticity: A sectoral approach. Energy Econ. 2016, 58, 199–210. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, B. Decoupling analysis on energy consumption, embodied GHG emissions and economic growth—The case study of Macao. Renew. Sustain. Energy Rev. 2017, 67, 662–672. [Google Scholar]
- Wu, Y.; Zhu, Q.; Zhu, B. Comparisons of decoupling trends of global economic growth and energy consumption between developed and developing countries. Energy Policy 2018, 116, 30–38. [Google Scholar] [CrossRef]
- Wei, W.D.; Cai, W.Q. Decoupling Relationship between Energy Consumption and Economic Growth in China’s Provinces from the Perspective of Resource Security. Energy Policy 2020, 68, 101693–101702. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, R.; Zhan, L. Is Decoupling Economic Growth from Fuel Consumption Possible in Developing Countries?—A Comparison of China and India. J. Clean. Prod. 2019, 229, 806–817. [Google Scholar] [CrossRef]
- Zhang, M.; Bai, C.; Zhou, M. Decomposition analysis for assessing the progress in decoupling relationship between coal consumption and economic growth in China. Resour. Conserv. Recycl. 2016, 129, 454–462. [Google Scholar] [CrossRef]
- Dong, B.; Zhang, M.; Mu, H.; Su, X. Study on decoupling analysis between energy consumption and economic growth in Liaoning Province. Energy Policy 2016, 97, 414–420. [Google Scholar] [CrossRef]
- Hao, Y.; Zhang, T.; Jiang, L. Would the Decoupling of Electricity Occur Along with Economic Growth? Empirical Evidence from the Panel Data Analysis for 100 Chinese cities. Energy 2019, 180, 615–625. [Google Scholar] [CrossRef]
- Lin, S.J.; Rogers, R. Decoupling Effects Among Energy Use, Economic Growth and CO2 Emission from the Transportation Sector. WIT Trans. Ecol. Environ. 2007, 105, 227–235. [Google Scholar]
- Steve, S.; Markku, L. Decoupling of road freight energy use from economic growth in the United Kingdom. Energy Policy 2012, 41, 84–97. [Google Scholar]
- Jiang, R.; Li, R. Decomposition and Decoupling Analysis of Life-Cycle Carbon Emission in China’s Building Sector. Sustainability 2017, 9, 793. [Google Scholar] [CrossRef]
- Gokarakona, S.; Shrestha, S. Decoupling in India’s Building Construction Sector: Trends, Technologies and Policies. Build. Res. Inf. 2019, 47, 91–107. [Google Scholar] [CrossRef]
- Chen, X.; Shuai, C.; Zhang, Y.; Wu, Y. Decomposition of energy consumption and its decoupling with economic growth in the global agricultural industry. Environ. Impact Assess. Rev. 2020, 81, 106364–106367. [Google Scholar] [CrossRef]
- Chung, W.; Kam, M.S. A study of residential energy use in Hong Kong by decomposition analysis, 1990–2007. Appl. Energy 2011, 88, 5180–5187. [Google Scholar] [CrossRef]
- Rojas, J.C.; Hasanbeigi, A.; Sheinbaum, C. Energy efficiency in the Mexican iron and steel industry from an international perspective. J. Clean. Prod. 2017, 158, 335–348. [Google Scholar] [CrossRef]
- Arto, I.; Dietzenbacher, E. Drivers of the Growth in Global Greenhouse Gas Emissions. Environ. Sci. Technol. 2014, 48, 5388–5394. [Google Scholar] [CrossRef] [PubMed]
- Schymura, M. What Drives Changes in Carbon Emissions? An Index Decomposition Approach for 40 Countries. Zew Discuss. Pap. 2014, 40, 14–38. [Google Scholar] [CrossRef][Green Version]
- Zhang, M.; Song, Y.; Su, B. Decomposing the Decoupling Indicator between the Economic Growth and Energy Consumption in China. Energy Effic. 2015, 8, 1231–1239. [Google Scholar] [CrossRef]
- Lin, B.; Wang, M. Possibilities of decoupling for China’s energy consumption from economic growth: A temporal-spatial analysis. Energy 2019, 185, 951–960. [Google Scholar]
- Wood, R.; Stadler, K. Growth in Environmental Footprints and Environmental Impacts Embodied in Trade. Resource efficiency indicators from EXIOBASE3. J. Ind. Ecol. 2018, 22, 553–564. [Google Scholar] [CrossRef]
- Sanye, M.; Secchi, S.; Corrado, A. Assessing the Decoupling of Economic Growth from Environmental Impacts in the European Union: A Consumption-Based Approach. J. Clean. Prod. 2019, 236, 117535–117541. [Google Scholar] [CrossRef]
- Anselin, L. Space and applied econometrics. Reg. Sci. Urban Econ. 1992, 22, 307–316. [Google Scholar] [CrossRef]
- Adom, P.K.; Kwakwa, P.A. Effects of changing trade structure and technical characteristics of the manufacturing sector on energy intensity in Ghana. Renew. Sustain. Energy Rev. 2014, 35, 475–483. [Google Scholar] [CrossRef]
- Solow, R.A. Contribution to the theory of economic growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Cian, E.D.; Verdolini, E. Energy Intensity Developments in 40 Major Economies: Structural Change or Technology Improvement? Electron. J. 2014, 5, 442–451. [Google Scholar]
- Perobelli, F.S.; Vinicius, D.A. The increase in Brazilian household income and its impact on CO2 emissions: Evidence for 2003 and 2009 from input-output tables. Energy Econ. 2015, 7, 197–207. [Google Scholar] [CrossRef]
- Inglesi, L.R. The impact of renewable energy consumption to economic growth: A panel data application. Energy Econ. 2016, 53, 58–63. [Google Scholar] [CrossRef]
- Hubler, M. Technology diffusion under contraction and convergence: A CGE analysis of China. Energy Econ. 2011, 33, 131–142. [Google Scholar] [CrossRef]
- Anselin, L. Technical Report S-92-1 of the National Center for Geographic Information and Analysis; University of California: Los Angeles, CA, USA, 1992. [Google Scholar]
- Lei, J. On the ineffectiveness of LM Test and the choice of spatial econometric model—Taking the socio-economic influencing factors of China’s air quality index as an example. Financ. Theory Res. 2018, 184, 40–53. [Google Scholar]
- Anselin, L. Exploring Spatial Data with GeoDa: A Workbook, Revised Version; University of Illinois Urbana-Champaign: Champaign, IL, USA, 2005. [Google Scholar]
- Lee, J.W. The contribution of foreign direct investment to clean energy use, carbon emissions and economic growth. Energy Policy 2013, 55, 483–489. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).