Numerical Simulation to Determine the Largest Confining Stress in Longitudinal Tests of Cable Bolts
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
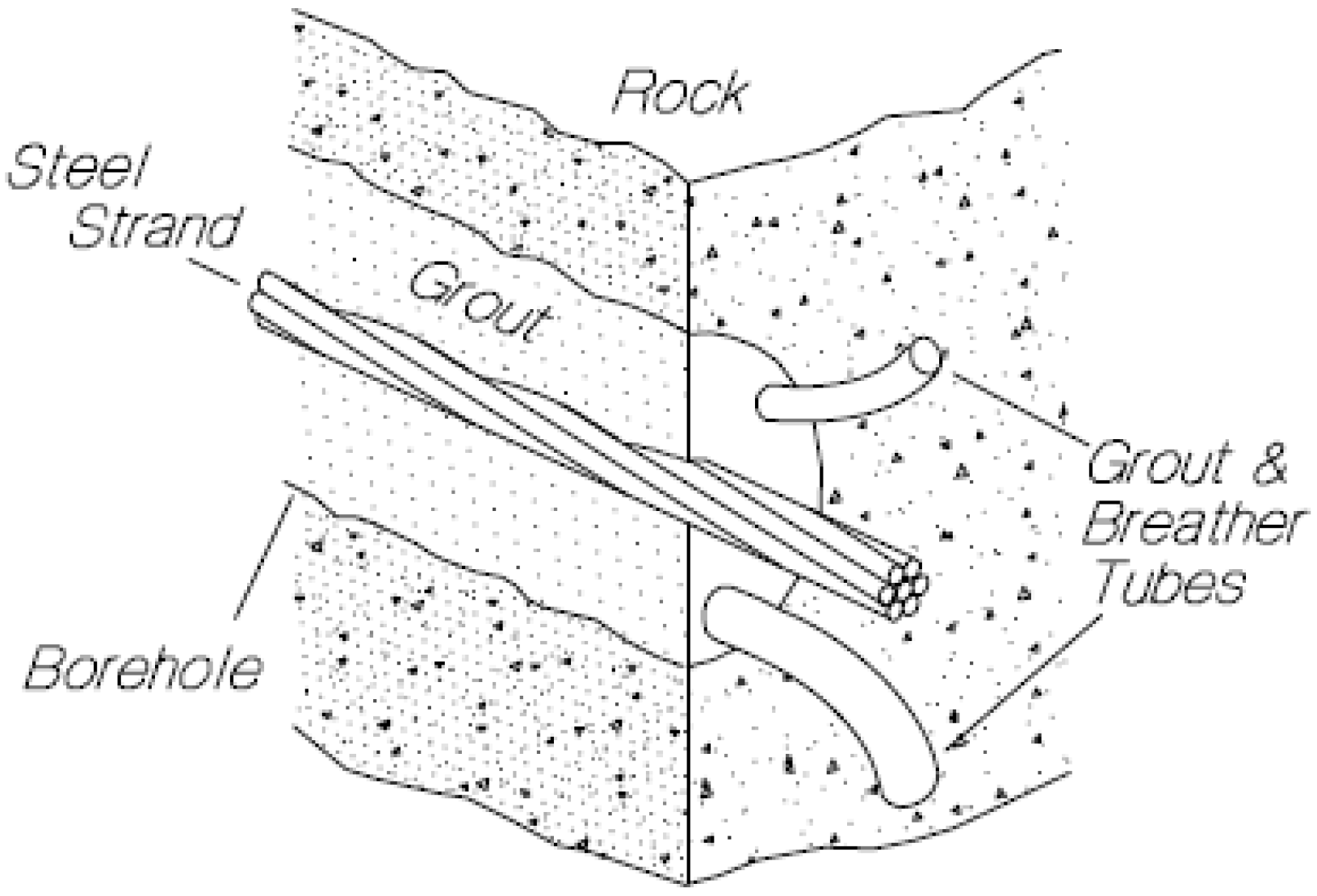
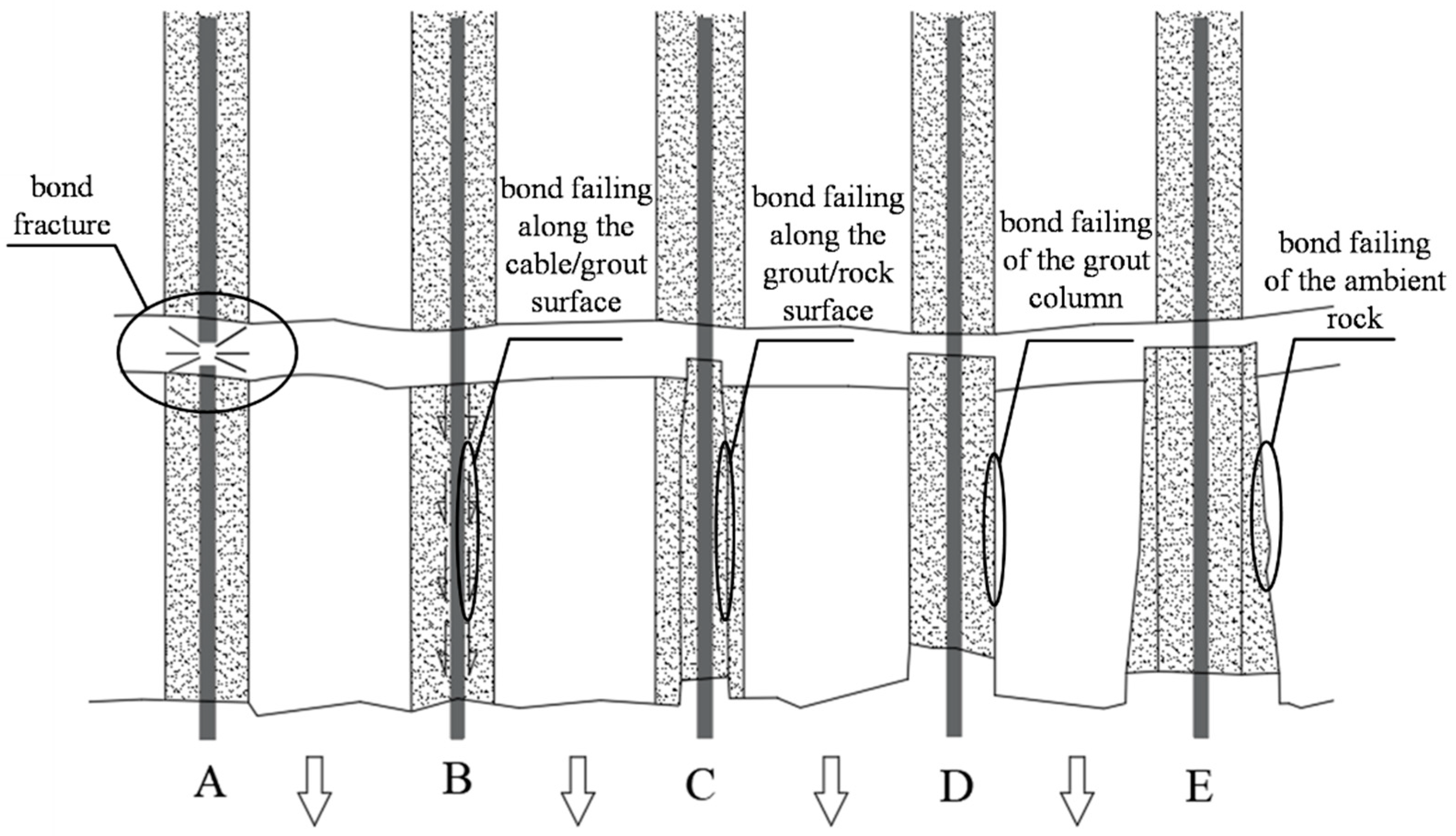
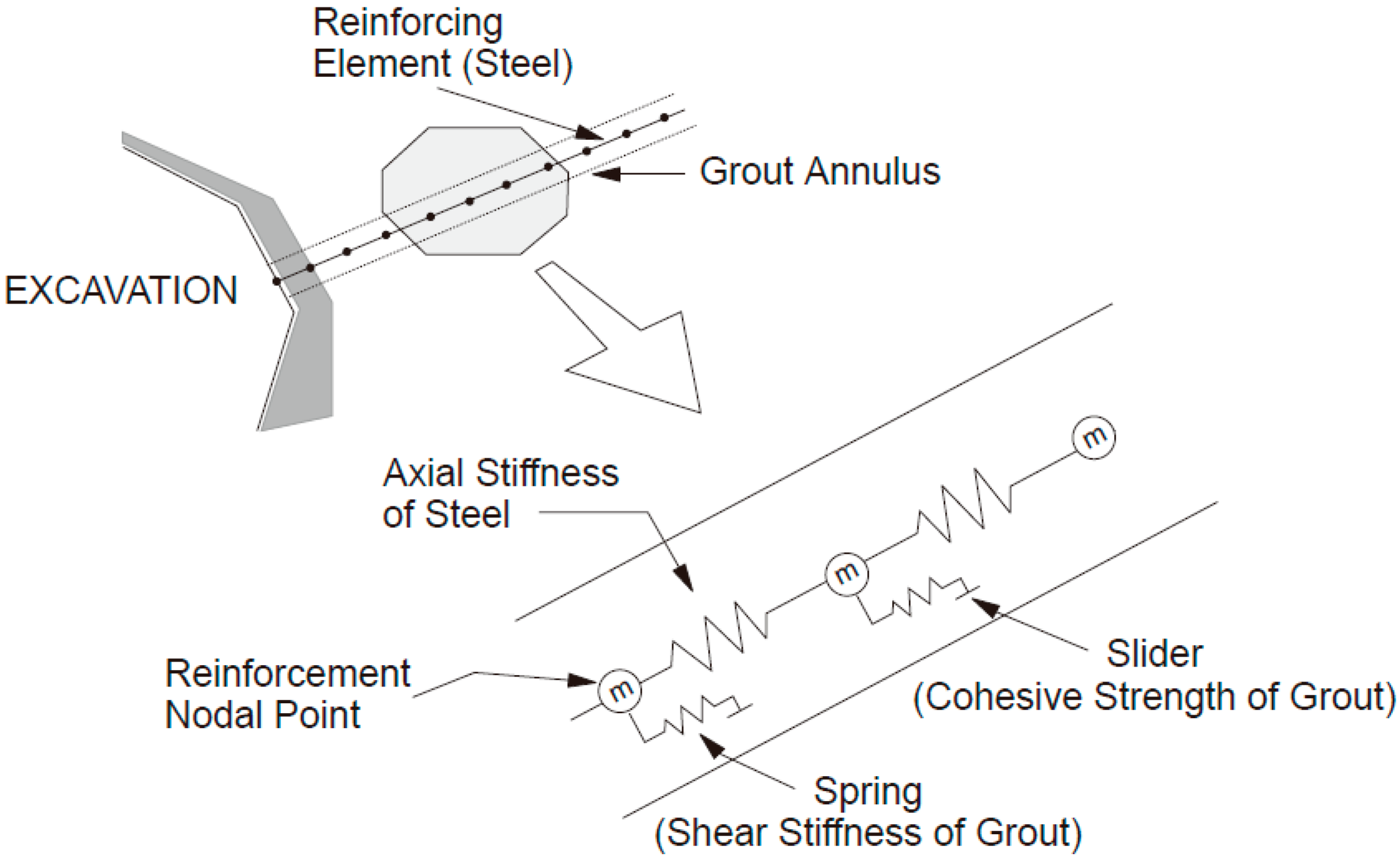
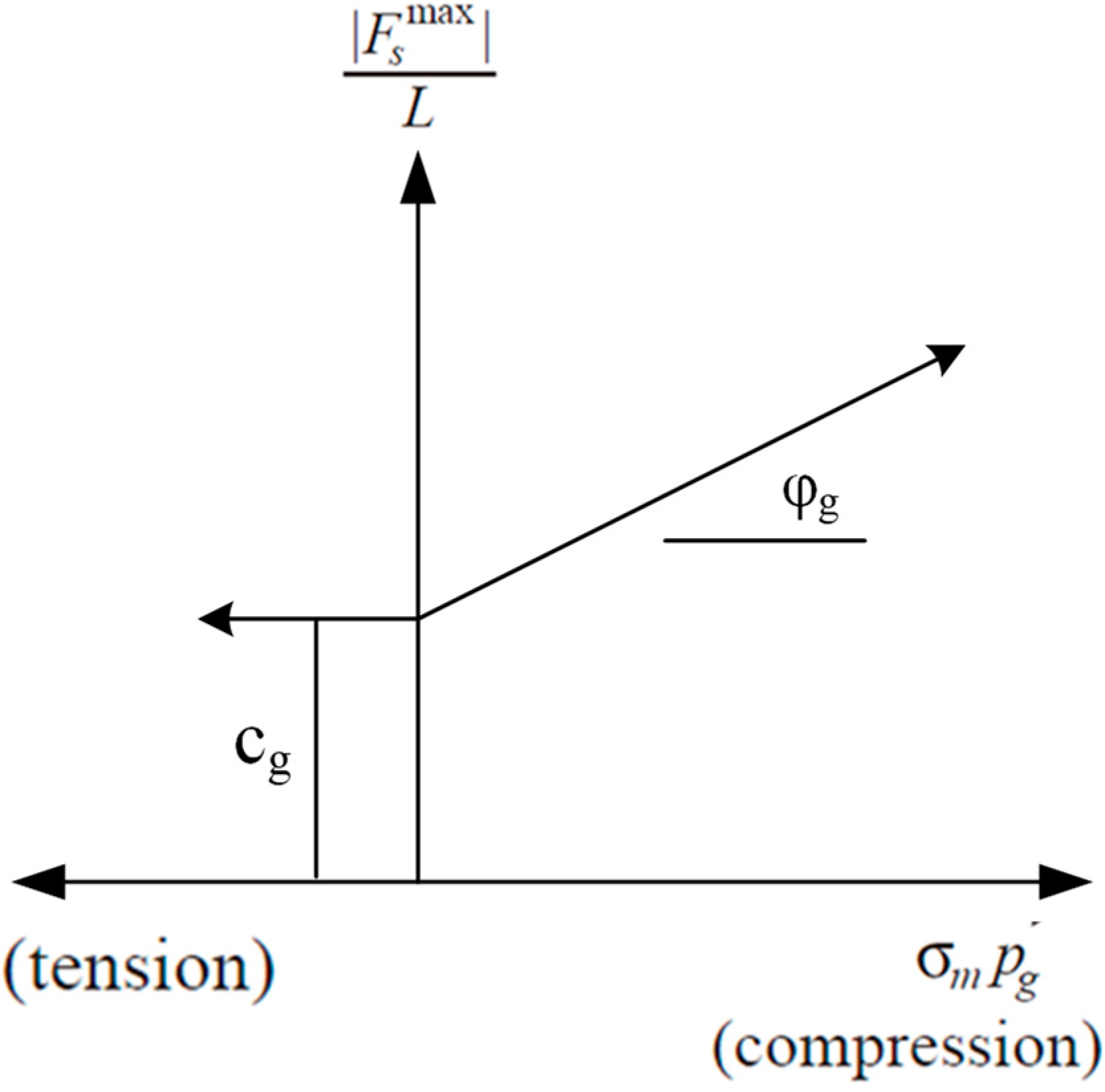
2.2.1. Theoretical Background
2.2.2. Numerical Pulling Test on a Normal Cable Tendon
2.2.3. Numerical Pulling Test on an Improved Cable Tendon
3. Results and Discussion
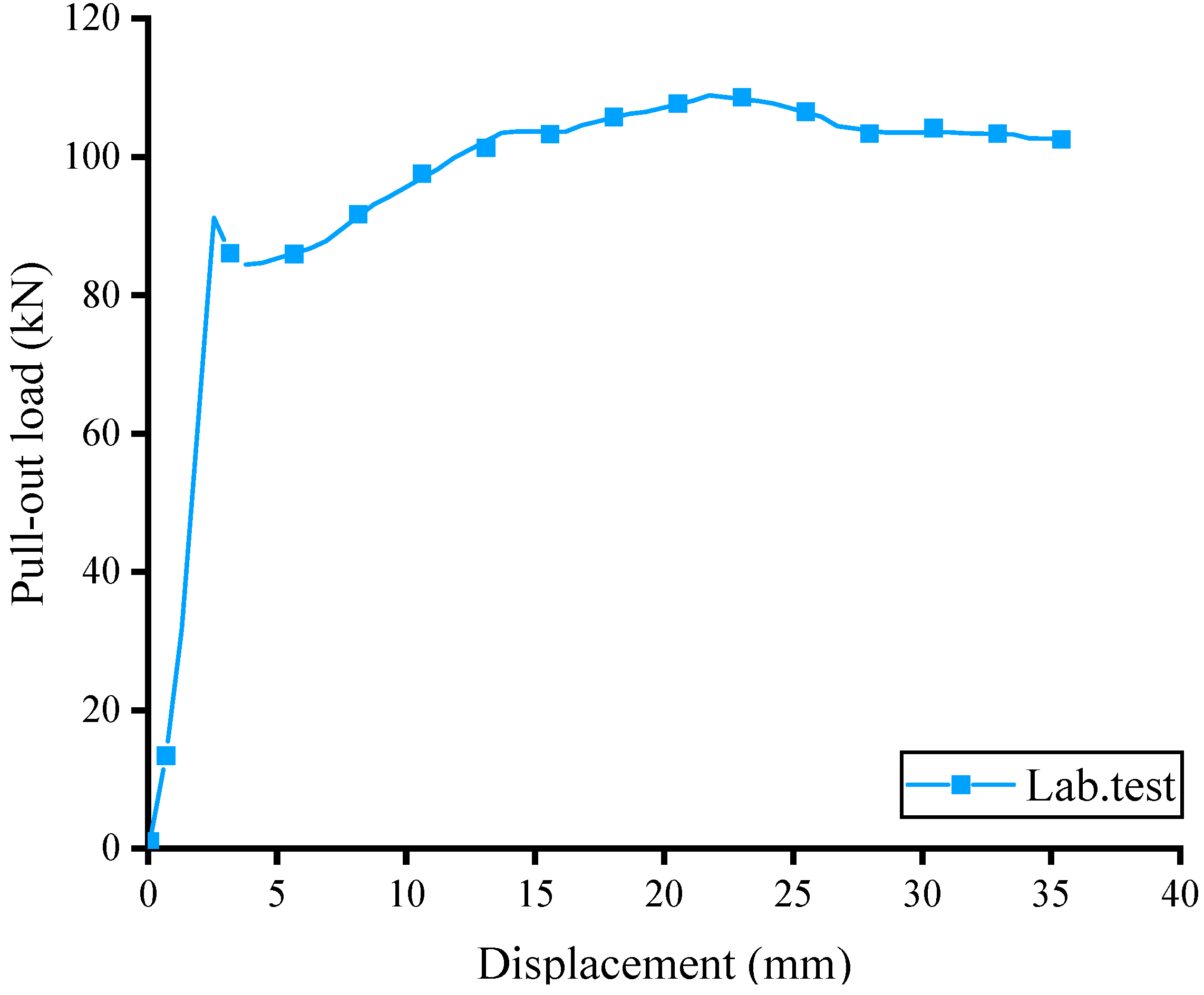
3.1. Pulling Test Results of the Normal Cable Tendon
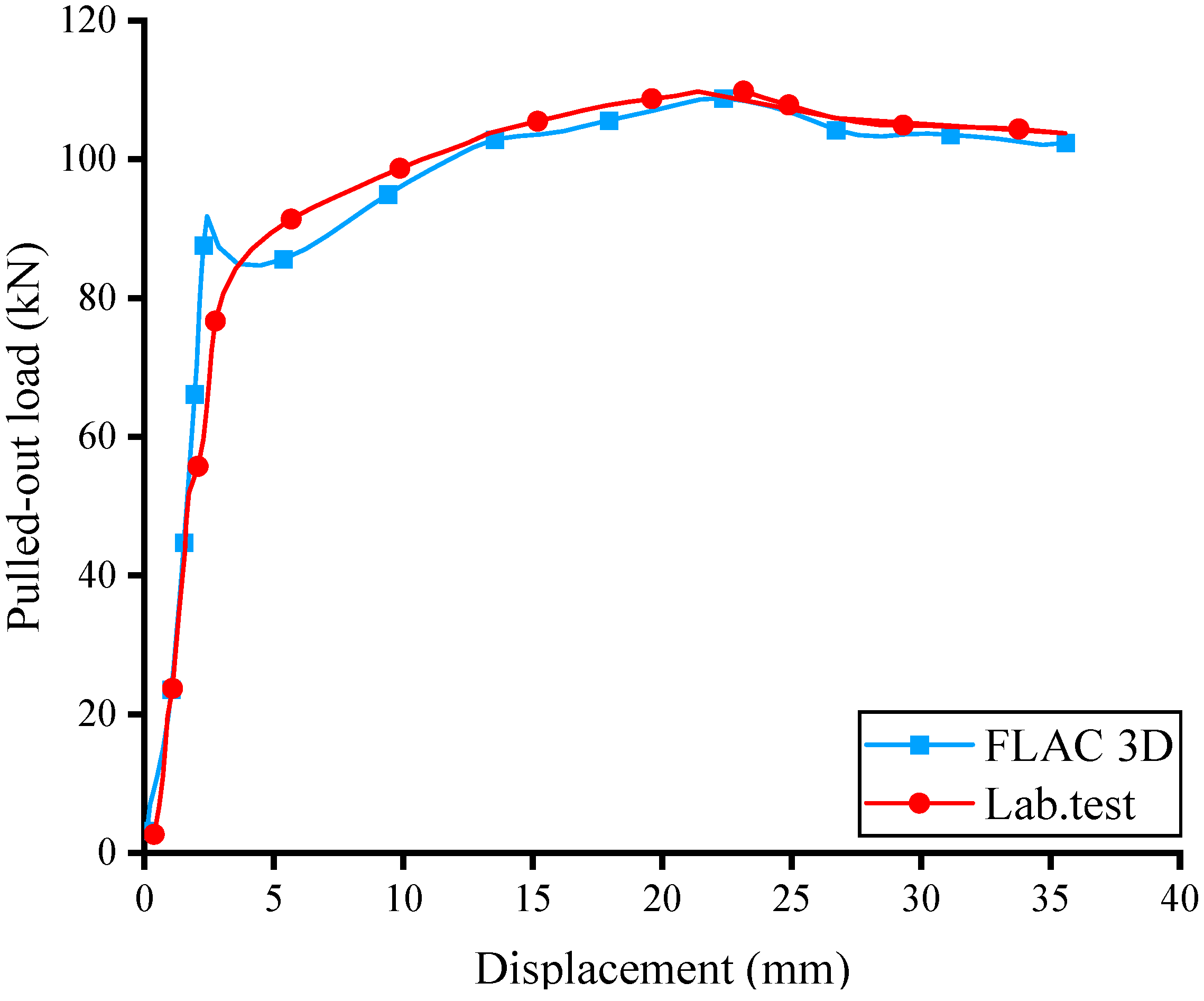
3.2. Pulling Test Results of the Improved Cable Tendon
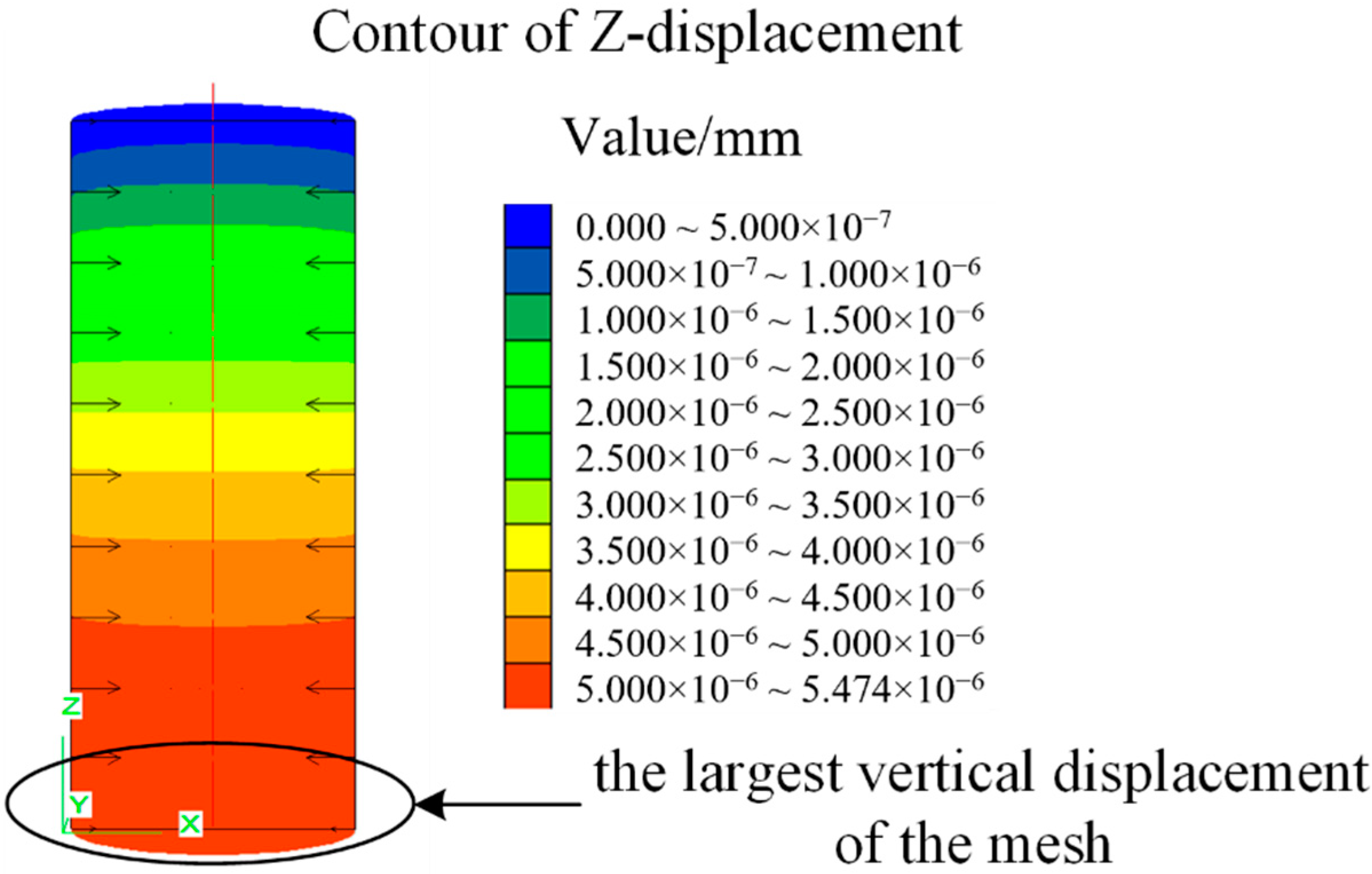
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, C.; Zhao, Y.; Han, P.; Bai, Q. Coal pillar failure analysis and instability evaluation methods: A short review and prospect. Eng. Fail. Anal. 2022, 138, 106344. [Google Scholar] [CrossRef]
- Hutchinson, D.J.; Diederichs, M.S. Cablebolting in Underground Mines; BiTech Publishers Ltd.: Richmond, BC, Canada, 1996. [Google Scholar]
- Li, D.; Masoumi, H.; Ming, C. A constitutive model for modified cable bolts exhibiting cone shaped failure mode. Int. J. Rock Mech. Min. Sci. 2021, 145, 104855. [Google Scholar] [CrossRef]
- Wang, M.; Bai, J.; Li, W.; Wang, X.; Cao, S. Failure mechanism and control of deep gob-side entry. Arab. J. Geosci. 2015, 8, 9117–9131. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, N.; Zheng, X. Experimental study of axial stress distribution and transfer along the bolt rods in an underground coal mine. Arab. J. Geosci. 2016, 9, 30. [Google Scholar] [CrossRef]
- Chen, J.; Liu, P.; Liu, L.; Zeng, B.; Zhao, H.; Zhang, C.; Zhang, J.; Li, D. Anchorage performance of a modified cable anchor subjected to different joint opening conditions. Constr. Build. Mater. 2022, 336, 127558. [Google Scholar] [CrossRef]
- Fuller, P.G.; Cox, R.H.T. Mechanics of load transfer from steel tendons to cement based grout. In Proceedings of the Fifth Australasian Conference on the Mechanics of Structures and Materials, Melbourne, Australia, 25–26 August 1975; pp. 189–203. [Google Scholar]
- Thenevin, I.; Martín, L.B.; Hadj-Hassen, F.; Schleifer, J.; Lubosik, Z.; Wrana, A. Laboratory pull-out tests on fully grouted rock bolts and cable bolts: Results and lessons learned. J. Rock Mech. Geotech. Eng. 2017, 9, 843–855. [Google Scholar] [CrossRef]
- Sakhno, I.; Sakhno, S.; Isaienkov, O.; Kurdiumow, D. Laboratory studies of a high-strength roof bolting by means of self-extending mixtures. Min. Miner. Depos. 2019, 13, 17–26. [Google Scholar] [CrossRef]
- Krykovskyi, O.; Krykovska, V.; Skipochka, S. Interaction of rock-bolt supports while weak rock reinforcing by means of injection rock bolts. Min. Miner. Depos. 2021, 15, 8–14. [Google Scholar] [CrossRef]
- Goris, J.M. Laboratory Evaluation of Cable Bolt Supports (in Two Parts) 1. Evaluation of Supports Using Conventional Cables; Bureau of MINES: Washington, DC, USA, 1990; pp. 1–23. [Google Scholar]
- Hyett, A.J.; Bawden, W.F. The 25mm Garford Bulb Anchor for Cable Bolt Reinforcement Part 1: Laboratory Results; Queen’s University: Kingston, ON, Canada, 1994; pp. 1–16. [Google Scholar]
- Satola, I.S. Testing of the yielding cable bolt achieved by debonding. In Proceedings of the Congress of the International Society for Rock Mechanics, Paris, France, 25–28 August 1999; pp. 1467–1470. [Google Scholar]
- Mosse-Robinson, S.; Sharrock, G. Laboratory experiments to quantify the pull-out strength of single strand cable bolts for large boreholes. In Proceedings of the Second Australasian Ground Control in Mining Conference 2010, Sydney, Australia, 23–24 November 2010; pp. 201–209. [Google Scholar]
- Tadolini, S.C.; Tinsley, J.; McDonnell, J.P. The next generation of cable bolts for improved ground support. In Proceedings of the 31st Internatioanl Conference on Ground Control in Mining, Morgantwon, WV, USA, July 31–August 2012; pp. 1–7. [Google Scholar]
- Moosavi, M. Load Distribution along Fully Grouted Cable Bolts Based on Constitutive Models Obtained from Modified Hoek Cells; Unpublished; Queen’s University: Kingston, ON, Canada, 1997. [Google Scholar]
- Hyett, A.J.; Bawden, W.F.; Reichert, R.D. The effect of rock mass confinement on the bond strength of fully grouted cable bolts. Int. J. Rock Mech. Min. Sci. 1992, 29, 503–524. [Google Scholar] [CrossRef]
- Aoki, T.; Maeno, Y.; Shibata, K.; Obara, Y. Laboratory pull-out tests of cablebolts. In Proceedings of the ISRM International Symposium-EuRock 2002, Madeira, Portugal, 25–27 November 2002; pp. 599–606. [Google Scholar]
- Chekired, M.; Benmokrane, B.; Mitri, H.S. Laboratory evaluation of a new cable bolt tension measuring device. Int. J. Rock Mech. Min. Sci. 1997, 34, 203.e1–203.e13. [Google Scholar] [CrossRef]
- Liu, H.Y.; Small, J.C.; Carter, J.P. Full 3D modelling for effects of tunnelling on existing support systems in the Sydney region. Tunn. Undergr. Space Technol. 2008, 23, 399–420. [Google Scholar] [CrossRef]
- Gale, W.J.; Mark, C.; Oyler, D.C.; Chen, J. Computer simulation of ground behaviour and rock bolt interaction at Emerald Mine. In Proceedings of the International Conference on Ground Control in Mining, Morgantown, WV, USA, 3–5 August 2004; pp. 27–34. [Google Scholar]
- Itasca. FLAC3D Fast Lagrangian Analysis of Continua in 3 Dimensions; Consulting Group Incorporation: Minneapolis, MN, USA, 2016. [Google Scholar]
- Chen, J.; Zhao, Y.; Zhao, H.; Zhang, J.; Zhang, C.; Li, D. Analytic study on the force transfer of full encapsulating rockbolts subjected to tensile force. Int. J. Appl. Mech. Eng. 2021, 13, 2150097. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, B.; Liu, L.; Tao, K.; Zhao, H.; Zhang, C.; Zhang, J.; Li, D. Investigating the anchorage performance of full-grouted anchor bolts with a modified numerical simulation method. Eng. Fail. Anal. 2022, 141, 106640. [Google Scholar] [CrossRef]
- Chen, J.; Saydam, S.; Hagan, P.C. Numerical simulation of the pull-out behaviour of fully grouted cable bolts. Constr. Build. Mater. 2018, 191, 1148–1158. [Google Scholar] [CrossRef]
- Moosavi, M.; Bawden, W.F. Shear strength of Portland cement grout. Cem. Concr. Compos. 2003, 25, 729–735. [Google Scholar] [CrossRef]
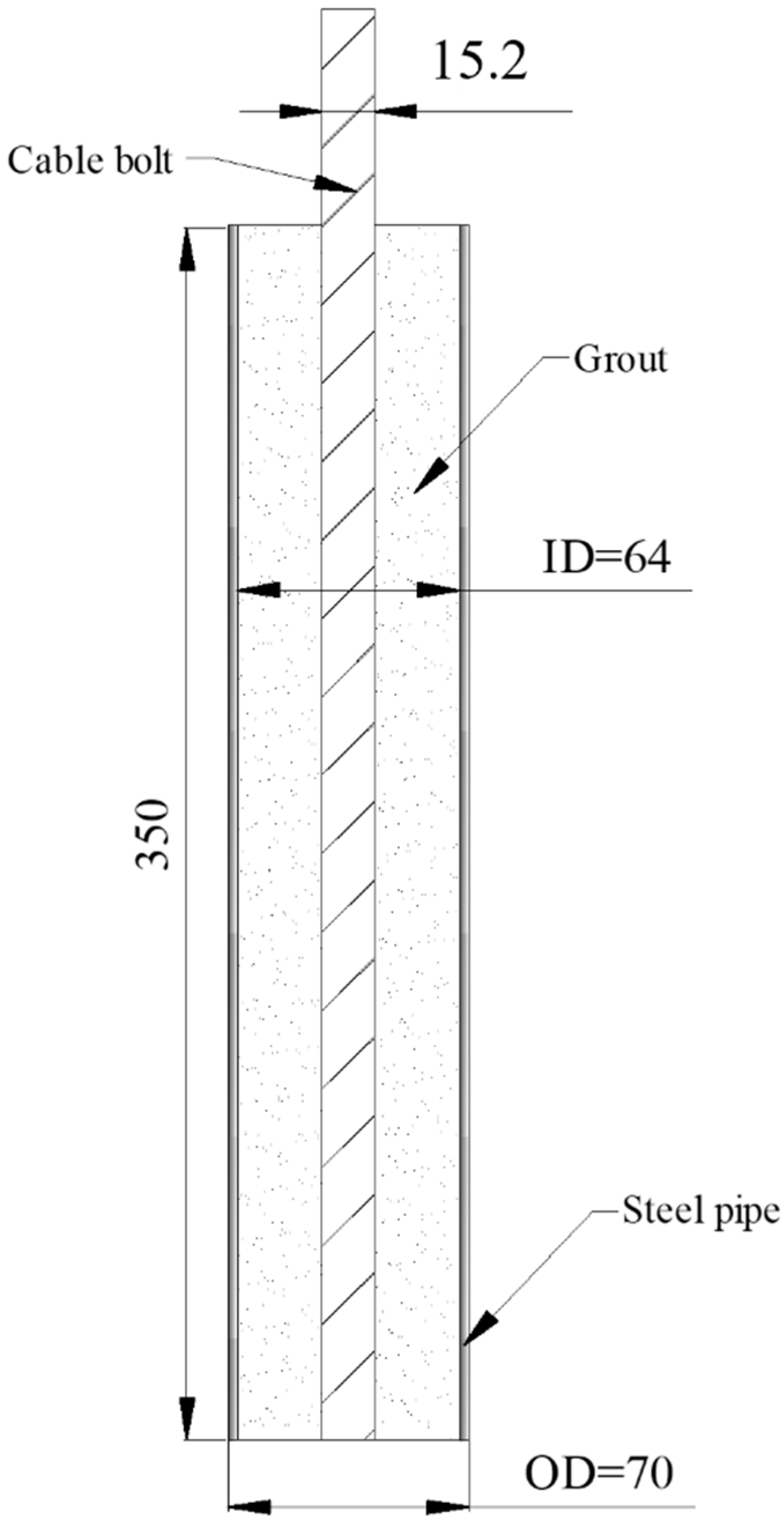
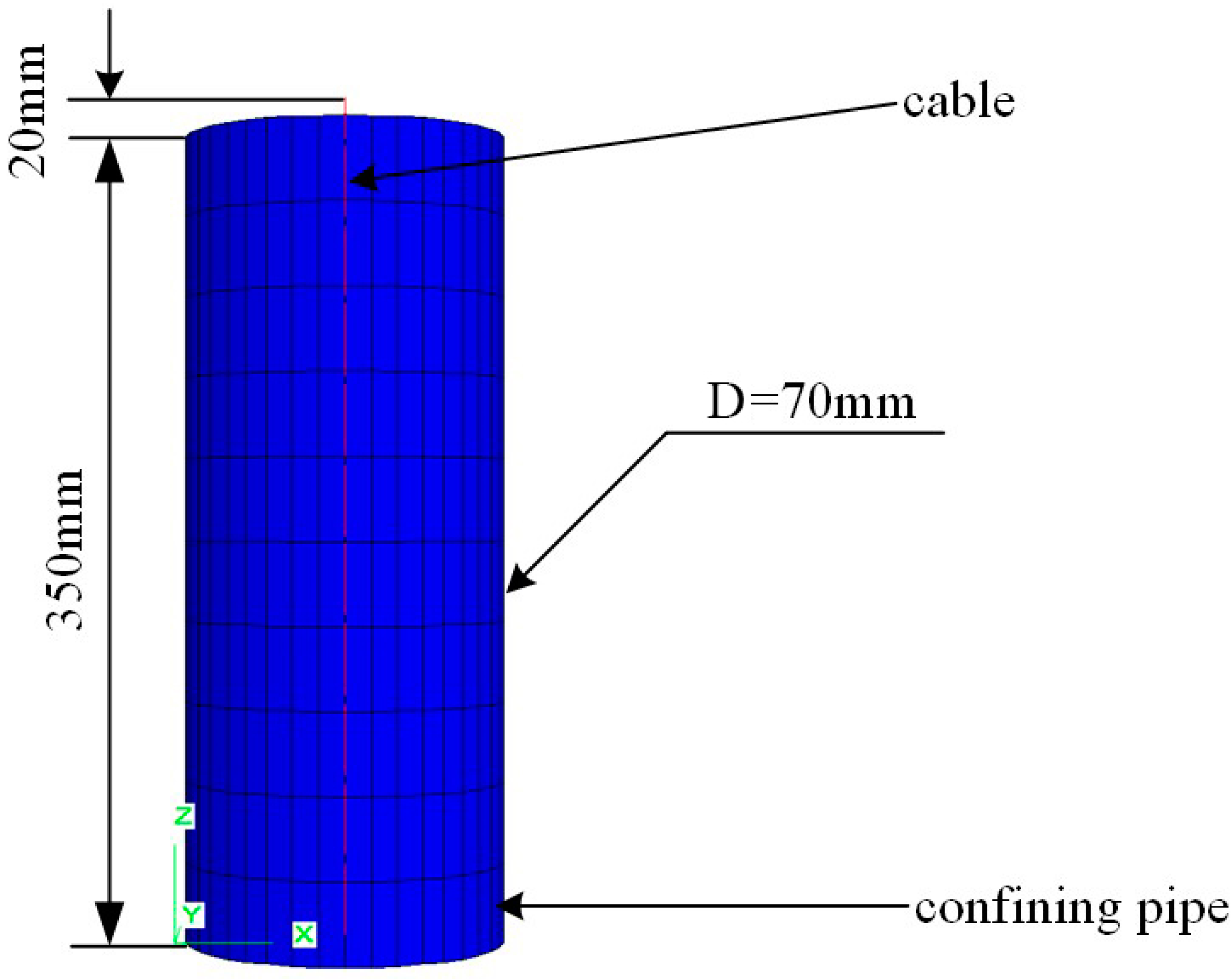
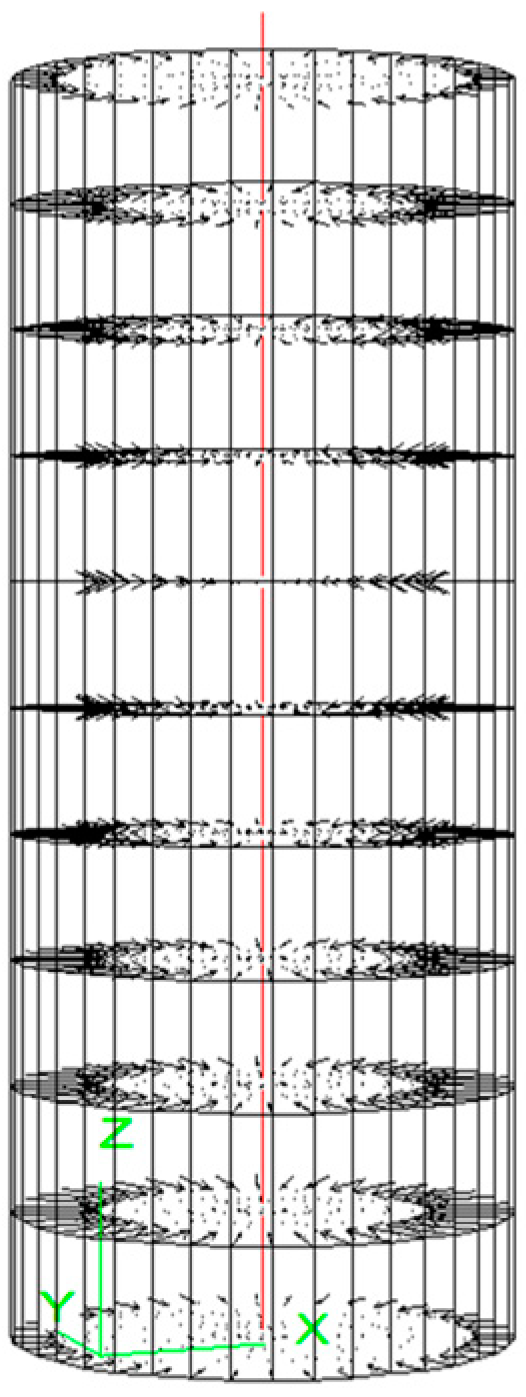
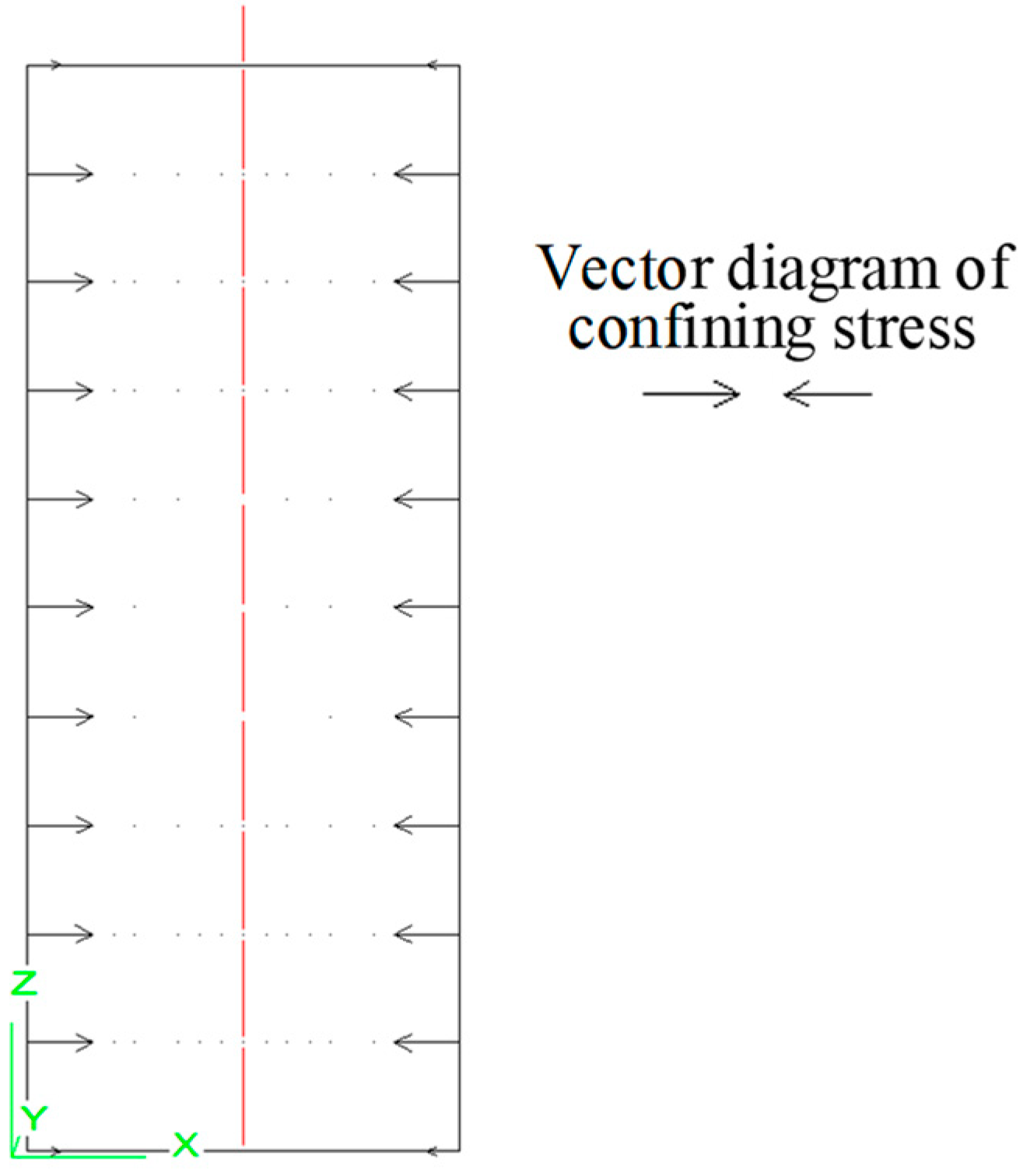

| Type | Index | Symbol | Value |
|---|---|---|---|
| Cable | Young’s modulus (MPa) | E | 190 |
| Diameter (mm) | - | 15.2 | |
| Embedment length (mm) | - | 350 | |
| Steel pipe | Young’s modulus (MPa) | E | 210 |
| Poisson’s ratio | μ | 0.3 | |
| Grout | Bond quality | - | 0.17 |
| Cohesive strength (MPa) | C | 12.4 | |
| Friction angle (°) | φ | 42 |
| Type | Index | Symbol | Value |
|---|---|---|---|
| Cable | Young’s modulus (MPa) | E | 190 |
| Diameter (mm) | - | 15.2 | |
| Embedment length (mm) | - | 350 | |
| Steel pipe | Young’s modulus (MPa) | E | 210 |
| Poisson’s ratio | μ | 0.3 | |
| Grout | Bond quality | - | 0.35 |
| Cohesive strength (MPa) | C | 12.4 | |
| Friction angle (°) | φ | 42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Q.; Leng, Q.; Yao, X.; Shao, S.; Qin, J.; Shi, X.; Zhang, B. Numerical Simulation to Determine the Largest Confining Stress in Longitudinal Tests of Cable Bolts. Sustainability 2022, 14, 10871. https://doi.org/10.3390/su141710871
Chang Q, Leng Q, Yao X, Shao S, Qin J, Shi X, Zhang B. Numerical Simulation to Determine the Largest Confining Stress in Longitudinal Tests of Cable Bolts. Sustainability. 2022; 14(17):10871. https://doi.org/10.3390/su141710871
Chicago/Turabian StyleChang, Qingliang, Qiang Leng, Xingjie Yao, Sihua Shao, Jianzhuang Qin, Xianyuan Shi, and Biao Zhang. 2022. "Numerical Simulation to Determine the Largest Confining Stress in Longitudinal Tests of Cable Bolts" Sustainability 14, no. 17: 10871. https://doi.org/10.3390/su141710871
APA StyleChang, Q., Leng, Q., Yao, X., Shao, S., Qin, J., Shi, X., & Zhang, B. (2022). Numerical Simulation to Determine the Largest Confining Stress in Longitudinal Tests of Cable Bolts. Sustainability, 14(17), 10871. https://doi.org/10.3390/su141710871









