Abstract
A serious problem faced by the metal mineral mining industry is the challenge to the sustainable development of resource mining due to the continuous decline of ore geological grade. In the case of producing concentrates of the same quality, compared with using only high-grade raw ore, ore blending is a way to slow down the decline of ore geological grade by combining high- and low-grade raw ore. There are many ore blending models considering cost minimization or profit maximization as the target value, ignoring the fact that ore blending is intended to obtain a homogenized product. Moreover, the ore blending model cannot be solved by traditional operational research methods when blended grade stability of multiple elements is considered in the ore blending program. In this paper, a multi-objective ore blending optimization model is constructed for the comprehensive utilization of associated resources in ores. It minimizes the deviation of the grade of each metallic element in the blended associated ore from the beneficiation grade and the percentage of different types of rocks at the unloading point. To solve this multi-objective optimization model, an intelligent optimization method is proposed that is an improved multi-objective optimization algorithm based on the Non-dominated Sorting Genetic Algorithm III (NSGA-III). The case study shows that the proposed model and algorithm can effectively solve the mixing problem of polymetallic ores and obtain a satisfactory ore blending solution.
1. Introduction
The global metal mining industry is currently facing the situation that the geological reserve grade of ore is constantly reduced because of the continuous consumption of high-grade ore [1,2]. Therefore, how to utilize low-grade ore and reduce the consumption of high-grade ore for mining sustainability is a great challenge in metal mines. There are many efforts for the rational utilization of low-grade ore to extend the life of mines and obtain considerable profits, such as the optimization of cut-off grade [3,4,5], production schedule optimization of mining [2,6,7,8,9], exploitation of beneficiation agent [10,11]. One of the important tasks in medium- and short-term production scheduling optimization is the blending of ore that aims to mix high-grade and low-grade ore according to the demand before crushing and beneficiation. The nature of the ore blending problem is due to uncertainty and the uneven distribution of minerals in geology. The benefits of ore blending are extending the ore reserve base by utilization of low-grade, minimizing the need for selective mining hence reducing mining costs and increasing mine production, contributing to the grade control process to increase the recovery rate of the beneficiation [6,12].
In China, ore blending is especially important in mining because the characteristics of metal mineral resources in the geology are more low-grade ore, less high-grade ore, rich in associated ore, and distributed unevenly. This makes the mining company have to strengthen ore blending to increase the utilization of high-grade ore, improve the quality of ore sent to the process plant and reduce the production cost. In the majority, the formulation of the blending problem is a classical linear programming model with only one objective function for one metal mineral [13]. In practice, especially for polymetallic mines, the comprehensive ore blending and utilization of polymetallic ores can get more benefits than that of only one main metal ore in associated metal resource, such as the cost of mining only one mineral but benefits of multi-mineral, no waste of associated resources and increase the reserves of resources. In addition, it has been confirmed that others should be considered for crushing and beneficiation in ore blending, such as grindability of the ore [14], and oxidation rate [11]. It makes the ore blending problem more and more complex.
The polymetallic ore blending problem is to blend the ore so that each metal in the mixed ore meets the requirements of the concentrator. It is a multi-objective problem because of the competition between each objective [15]. Thus, the traditional operational research methods for a single-objective problem are unable to solve the existing problem of polymetallic ore blending. In this paper, a multi-objective model considering grinding and ore dressing for polymetallic ore blending is established. To solve the model, a novel evolutionary optimization algorithm which is based on the NSGA-III classical evolutionary algorithm is proposed. The main contributions in this paper are as follows:
- (1)
- A multi-objective ore blending mathematical model for the polymetallic mineral is established. The grade of several metals and the grindability of the ore are considered objectives. The oxidation rate and harmful substances that affect the recovery rate of the mineral beneficiation are considered the constraints. These factors are not considered by the existing traditional ore blending model, but they are a confirmed impact on beneficiation [11,14].
- (2)
- A novel algorithm is proposed. To solve the multi-objective ore blending mathematical model, a novel algorithm is proposed based on the NSGA-III algorithm which is improved by using a mating pool mechanism, a general normalization process, and the reference-point generation method, named as constrained NSGA-III algorithm based on a matching mechanism (CM-NSGA-III).
- (3)
- The model and CM-NSGA-III are applied to obtain a daily ore blending plan for a large open-pit mine in China. We analyze the overall situation of the calculated target values, the target demand of each unloading point, and the finally obtained planning. The results show that the CM-NSGA-III scheme can obtain a satisfactory ore blending plan.
The remaining sections complete the presentation of this paper. Section 2 provides a review of the work related to ore blending. Section 3 describes the multi-objective optimization problem of ore blending and its mathematics model. Our proposed CM-NSGA-III algorithm and its details are explained in Section 4. In Section 5, we introduce a case of ore blending and describe in detail how to solve this case using our proposed ore blending model and CM-NSGA-III. Finally, a conclusion is drawn in Section 6 along with pertinent observations.
2. Literature Review of Ore Blending
The blending problem is a common research problem in mining and smelting industry. The expression of the blending problem is that different components need to be determined in proportion or quantity and then mixed to meet the demand, such as the production of the ore [2,6,7,16,17], filling materials for tailings (or concrete) [18,19], flotation agent [10], ore smelting [20,21]. The ore blending problem often occurs in the production of ore and ore smelting. Although these two scenarios are similar in the purpose that they are all for the desired product, only the first scenario will be considered in the literature review.
The existing research on the ore blending problem can be divided into two aspects. The first one is to make the schedule to achieve the quality and quantity for blending the run-of-mine materials. The method widely used to solve this problem is classical linear programming, but it suffers from the fact that only one objective function is permitted at a time and the objective and constraints should be linear [6]. Therefore, there are many different models that have been proposed to solve the problem with other conditions in the past several decades.
Chanda and Dagdelen [6] described a linear goal programming model of the blending problem in short-term mine planning. The model added the deviation variables for quality and quantity in constraints and minimize the deviation in the objective; and then, discussed the capabilities of the model in comparison to a CAD interactive graphics-based system, in terms of minimizing the deviation from set targets for tonnage and given quality parameters. Kumral [13] proposed a chance constraint linear programming model taking account of the random nature of ore variables. The model is solved by the simulated annealing (SA) algorithm to find the so-called best result. In addition to this, the method is extended to solve the multi-objective mineral blending problem [15]. Xu, Yang and Liu [22] proposed a modified two-step fuzzy optimization algorithm for multi-objective ore blending. Gholamnejad, Azimi and Teymouri [23] treated the ore dump elements as normally distributed random variables and formulated a stochastic programming model to solve the ore homogenization problem in an iron ore mine. The stochastic model was then converted to its equivalent non-linear model using the chance-constrained programming approach. Ulger, Ozer and Akkaya [24] developed a blending model and GIS-based software to provide the specific ore to the glass industry. Gholamnejad and Kasmaee [25] developed a linear goal programming (GP) model to determine the optimum iron ore blend in terms of quality from low-grade and high phosphorous stockpiles of the Choghart mine.
Despite the purpose of the above research is to blend the run-of-mine materials and obtain homogenization productions, it seems to take more attention to the cost or profit because most of the established optimization models are considering the quality of ore blending as a constraint, and the cost or profit as the optimizing objective. This situation is more common in mine scheduling studies, for example, the research of [7,8,9,16,17,26,27,28,29,30,31]. It is flexible to establish a model which is consistent with the needs of producers for the situation that there is one ore unloading point or one determined product that needs to be blended. In the situation that there are several ore unloading points or different products that need to be blended at the same time, using ore blending as the model constraints maybe occur with no feasible solutions. In addition, the influence of ore blending on ore dressing is reported in some of the research [10,12,14,32]. It is difficult to treat the ore blending target as a constraint to meet the requirements of the concentrator because the constraints are range values, but we expect the ore blended to be as close to the required value as possible.
The second one is research on the effects of ore blending. The purpose of these studies is to determine the impacts of ore blending on subsequent processes and solve the problems of uneven mixing during the implementation of the ore blending schedule.
Van Tonder, Deglon and Napier-Munn [10] investigated whether blends of platinum ores display linear grinding and flotation characteristics or whether non-linear effects occur, i.e., synergistic/antagonistic effects. Mkurazhizha [14] studied the quantitative influence of comminution characteristics of the individual ores as well as the behavior of the different blend combinations. Bicak [11] evaluated the determination of the presence of secondary copper minerals and surface oxidation of sulphide minerals by using of Oxidation Index methodology based on the EDTA extraction technique. This technology is able used to determine the ore blending and dressing strategies. Nwaila, Ghorbani, Becker, Frimmel, Petersen and Zhang [1] applied a geometallurgical approach to investigate mineralogical and metallurgical factors that influence the leaching of blended ores in a set of bottle shaker and reactor column tests. These studies can be regarded as determining ore blending schedule objectives or beneficiation parameters. It is the premise for the formulation of the ore blending schedule. However, the problem is that many parameters affect the beneficiation recovery rate, and the existing technology cannot identify and determine how some parameters affect the beneficiation recovery rate. Liu, Zhang and Gao [12] proposed an ABC-BP neural network algorithm that is used to fit the relationship between the properties of ore blending products and the total concentrate recovery and taken it as the optimization goal to guarantee the quality of ore dressing products at the source. It is a way to solve the above problem.
In addition, the implementation of the ore blending and the evaluation of the blended ore quality is also important in the ore production process. Gu, Lu, Guo and Jing [33] designed and developed a dynamic management system based on GIS/GPS/GPRS for the daily production plan of ore blending and monitors in an open-pit mine. Marques and Costa [34] proposed an algorithm to simulate ore grade variability in blending and homogenization piles that a blending (or homogenization) simulator for longitudinal stockpiles has been developed, where the input to the algorithm consists of the pre-defined mining sequence. The algorithm has been applied to several simulated scenarios of the mineral deposit. Zhao, Lu, Koch and Hurdsman [35] developed an innovative modeling approach to estimate the quality of a stockpile during the blending process, and the quality of the stockpile is calculated with a high degree of accuracy when the chemical analysis is completed. Ilic, Lavrinec and Orozovic [36] presented a method to quantify the physical blending process at a particle level through simulation in a conveyor transfer system. Ma [37,38] studied the impact of rock blasting on ore blending practices. The contents of these studies do not directly influence the formulation of the ore blending schedule, but they can ensure the implementation of the ore blending schedule successfully and the quality of the final blended product.
Although there are many studies on the topic of ore blending, it is unfortunate that there is rarely research on the topic of the polymetallic ore blending problem.
3. Mathematical Model of Polymetallic Ore Blending Schedule Problem
The purpose of this section is to introduce the proposed multi-objective model of the polymetallic ore blending schedule problem. Firstly, the ore blending schedule problem is introduced by problem assumption and description. Secondly, the mathematical model of the problem is built, and the formulations and parameters in the formulations are explained, respectively.
3.1. Problem Assumption and Description
In this study, we only consider the problem and solution of the formulation of the polymetallic ore blending schedule. Therefore, to simplify the establishment and solution of the model, the following three assumptions are made:
- In a mining face (or a loading point), the various components in the geology are uniform distribution. We can get the average value of each component through laboratory tests and calculations. The type of rock at a mining face (or a loading point) is unique.
- The implementation of the ore blending is strictly in accordance with the ore blending schedule.
- The relationship between the beneficiation recovery rate and the homogeneous ore has been established by laboratory tests. As long as the ore is blended to the required quality, the best beneficiation recovery rate can be obtained.
The problem of the polymetallic ore blending schedule can be described as the polymetallic associated ore from different mining faces (or loading points) to be transported to several crushing stations (or unloading points) and blended into homogeneous ore products (or after grinding). In addition to the grade of the metal, the oxidation rate and the percentage of different ore types, which affect beneficiation and grinding, are also with consideration in the ore blending schedule when the run-of-mine materials are sent to the crushing station.
3.2. Mathematical Formulation of Polymetallic Ore Blending Schedule Problem
The presented mathematical model for the polymetallic ore blending schedule problem is based on the assumption and description mentioned above. This formulation uses the target deviation as the objective so that it can clearly understand the gap between the optimal result and the goal in reality. In other words, whether the goal can be achieved. The parameters, and the variables considered in the mathematical model as shown in Table 1. The formulation of the problem is as follows:

Table 1.
Parameters and variables are considered in the mathematical model, respectively.
Subject to:
The multi-objective functions are represented as Equations (1) and (2). It considers the deviation for the grade of multiple metals and the percentage of different types of rocks, respectively. In this study, the percentage deviation of rocks is minimized when there is only one rock type at an unloading point. Equations (3) and (4) ensure that the oxidation rate of minerals and harmful substances that affect the beneficiation recovery is below a certain level. Equation (5) ensures that the ore blending schedule meets the short-term production schedule of the mine, that is, the current mining face schedule will not delay the mining schedule of the mining face under it. Equation (7) ensures that the minimum crushing capacity of the crushing plant is met. Equations (6) and (8)–(10) represent the production capacity for loading points (or mining faces), crushing, stockpiling, shovel and truck, respectively. Equation (11) ensures that the quantity of ore willing to transport from the i-th loading point (or mining face) to the j-th unloading point (crushing station or stockpiling station). If the quantity is too small, it will mean that no trucks will be sent for transportation.
4. The Proposed CM-NSGA-III Algorithm
The purpose of this section is to introduce the proposed CM-NSGA-III algorithm. It is used to solve the polymetallic ore blending schedule mathematical model. First, we introduce the process and framework of the CM-NSGA-III algorithm. Then, the mating-pool mechanism and normalization, the generation and transformation of reference points, and the processing of constraints of the mathematical optimization model in the CM-NSGA-III algorithm are introduced in detail, respectively.
4.1. The Framework of the Proposed CM-NSGA-III Algorithm
NSGA-III is a well-known evolutionary algorithm proposed by Deb and Jain [39]. In the NSGA-III, the random crossover and mutation method cannot guarantee the generation of high-quality offspring, a novel NSGA-III is proposed. Based on the NSGA-III algorithm, Achievement Scalarizing Function (ASF) mating mechanism and general normalization process are used to ensure the quality of offspring for improving the efficiency of the algorithm. In addition, to obtain as many feasible solutions as possible for the reasonable ore blending plan selection, the generation mode of reference points is optimized. The ore blending model has multiple targets and multiple constraints, while the original NSGA-III algorithm is used to deal with unconstrained or box-constrained problems. Thus, we introduce the constraint-violation degree in [40] to the CM-NSGA-III algorithm for dealing with constraints. The algorithm flowchart is shown in Figure 1. We improve the mating-pooling mechanism, reference point generation and transformation method of the original NGSA-III algorithm, and add the normalization process and constraint processing method for the algorithm. The framework of the CM-NSGA-III algorithm and the NSGA-III algorithm is similar, as shown in Algorithm 1. The modified parts are described one by one.
| Algorithm 1. Framework of CM-NSGA-III |
| Input: N (population size) Output: approximated Pareto-optimal front
Repeat ∪ and i = i + 1 until || ≥ N, Last front to be included: if || = N then, , break else
Normalize objectives: = Normalization () Association: () = Associate (W, ) %: closest reference point, d: distance between s and π(s) Compute niche count: , j ∈ W Choose K members one at a time from to construct : Niching (K, , π, d, W, , ) Transformation reference point set W: W = Reference-Point-Transformation (W) end if |
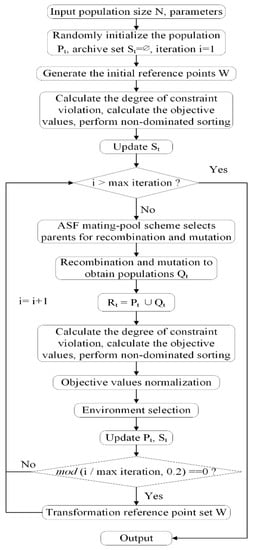
Figure 1.
The CM-NSGA-III algorithm flowchart.
4.2. ASF Mating-Pool Scheme and Normalization
4.2.1. ASF Mating-Pool Scheme
The mating-pool scheme mechanism is used during recombination and mutation. Mating selection is a part of the process of producing offspring. High-quality offspring will be produced by high-quality parents [41]. So, a mating mechanism is proposed based on this idea. In the ASF mating mechanism, the quality of offspring is improved by two principles. The first is the convergence principle. If both solutions converge well, the distance between solutions is not too far; and then, the parent with a smaller ASF value will be selected to join the mating selection. The second is the diversity principle. If both solutions have good diversity, they are not too close to each other. Their combination ensures the diversity of offspring. Ultimately, mating selection selects the largest solution from the smallest Euclidean distance.
We first calculate the ASF value and minimum angle of each solution, where ASF values are computed using the achievement scalarizing function and the minimum Euclidean distance is the minimum value of the angle between the solution and other solutions [42]. Then picking the solutions i, j at random, if ASF(i) < ASF(j) and dist_min(i) > dist_min(j), select i, otherwise, select j; if either of the above conditions is satisfied, one of the solutions i, j is randomly selected. Later, we will calculate the acceptable probability p of the solution obtained in step 5. Last, a random number between 0 and 1 is generated, if rand (1) < p, the solution is selected as the parent solution to generate a new child solution, otherwise, randomly select a solution from the population as the parent. The specific steps of the ASF mating-pool mechanism are shown in Algorithm 2.
| Algorithm 2. ASF Mating-Pool () |
%: the maximum ASF value of solution i,
|
4.2.2. Normalization
The purpose of normalization is to make the objective values of different dimensions in the same dimension. In the CM-NSGA-III algorithm, the normalized result is used for environment selection. For the M-objective problem, the objective value of solution x in the population is normalized by Zmin = (,…,) and Zmax = (,…,). Equation (12) calculates the normalized objective (x):
4.3. Reference-Point Generation and Transformation
We use the reference point generation method proposed by Jiang and Yang [43]. For generating k-layer reference points, the first is to define a unit simplex. The central reference point is defined as C = (1/M, …, 1/M) and the dimension is the number of objectives. The i extreme reference point is defined as = (, …, ), where = 1 and = 0, for all I ≠ j, 1 ≤ i ≤ M, 1 ≤ j ≤ M. The unit simplex eventually can be divided into M sub-simplex. Each sub-simplex is bounded by C, , . The sub-simplex A(i) explains how the proposed method generates reference points in a sub-simplex, the rest sub-simplex is calculated in the same way. The generation of reference points on line C and C as well as points on the lines of and as shown in Figure 2. Equation (13) computes the r reference point on line C. Equation (14) shows the calculation of the t reference point on the lines of and . Equation (15) calculates the total number of reference points , which generated by M objectives and k layer.
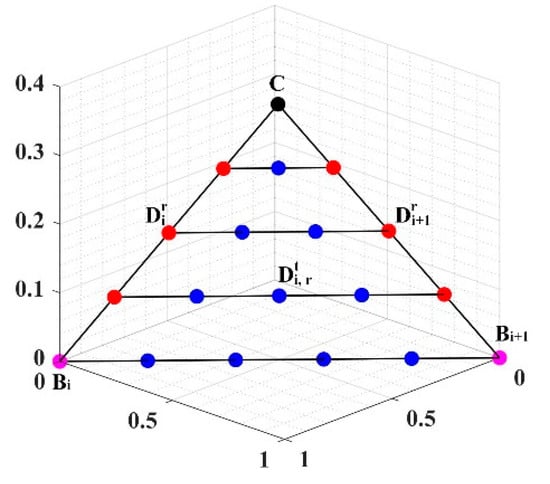
Figure 2.
The generation of reference points in sub-simplex A(i).
For the reference points to better guide the search process for solutions, the idea of transforming the reference point’s location is considered. The reference point set W is updated with the following Equation (16) when :
where gen is the current iteration and is the maximum iteration. p is the conversion frequency and mod means take the remainder. and represent the maximum objective value and minimum objective value in the current generation. During the process of updating the reference points, conversion frequency p = 0.2 is used by trying and testing, because there is no need to update the reference point in each iteration. The frequent transformation will reduce the level of good reference points participating in guiding solution search. Nonetheless, for an unknown Pareto front, we want to generate reference points that conform to the shape of its Pareto front, so we choose to transform reference points every few generations.
4.4. Constraints Handling
The following is a brief introduction to the degree of constraint violation. Equation (17) calculate the constraint violation value (CV (x)) of a solution x:
where represents the normalized constraint function. For example, inequality constraint , then . The normalized constraint function works in a similar way. The difference is with the equality constraints. The bracket operator returns the negative of α, if α < 0; and returns zero, otherwise [40]. The smaller CV value represents a better solution. This is used in the process of finding the minimum between the reference points and the objective values, then the minimum is taken as the ideal value, which is used in the environment selection of the algorithm to restrict the solutions within the constraints.
5. Case Study
5.1. The Situation of the Polymetallic Open-Pit Mine and Experimental Data
The polymetallic open-pit mine in the case study is located in Luoyang, Henan province. The geological situation of the mine is shown in Figure 3a. The ores are mainly molybdenum (blue in Figure 3a) and tungsten (purple in Figure 3a) and contain a small amount of copper (red in Figure 3a). In addition, there is very little pyrite. The current situation of mining is shown in Figure 3b. Due to the ongoing consumption of high-grade molybdenum ore, mining companies began in 2016 to beneficiate tungsten and copper as well as molybdenum. In fact, the work also brought significant benefits to the company and extended the life of the mine by 20 years in theory. Some efforts have been made, such as reducing molybdenum grade fluctuations from more than 15% to around 4.5-10% through strict management practices. However, the current challenge for the mine is how to mix raw ore from different sources to an acceptable quality for each metal and maintain balance.

Figure 3.
The situation of the open-pit mine. (a) 3D model of geological; (b) Production management system for the mine.
In the open-pit mine, there are 10 to 20 loading points that can supply raw ore to 5 crushing stations. The minimum transport volume from each loading point to each unloading point is 300 tons. In addition, the rock type of ore at each unloading point should be the same type as much as possible. There are more than 200 trucks involved in the production of the mine, and the mass of each truck is about 50 tons in single transportation. There are 4 shovels and 28 diggers used for loading. The bucket capacity of the shovel is 3 m3. The average bucket capacity of the digger is 1.5 m3. The experimental data comes from the open-pit mine at one shift, as shown in Table 2 and Table 3.

Table 2.
Parameters of loading points.

Table 3.
Parameters of unloading points.
5.2. Parameter Settings and Experimental Environment
In order to test the performance of the CM-NSGA-III algorithm, the NSGA-III algorithm is selected as the benchmark. The parameters setting for NSGA-III and CM-NSGA-III algorithms as shown in Table 4. From Table 2 and Table 3, there are 14 loading points and 4 unloading points, so the number of decision variables is 56. The parameters of population size and maximum iterations are set by trying to test the principle of computational efficiency. The number of reference points is calculated by Equation (15). Crossover probability, mutation probability, and distribution index are determined according to the literature [40].

Table 4.
Parameters used in algorithms.
These two algorithms are used to solve the ore blending problem with the population of individuals (or chromosomes) encoded as real numbers, as shown in Figure 4. is denoted as the quantity of the ore from loading point 1 to 1# unloading point. The quantity of ore from all loading points to all unloading points forms a chromosome. In addition, to make the NSGA-III algorithm solve the constraint problem, we added the same constraint processing method as CM-NSGA-III in the NSGA-III algorithm. The environment of the computer for the experiment is Intel-11800H@ 2.30 GHz (8 cores) with 16 GB of RAM. The software used is MATLAB with version 9.11.0 (R2021b). In addition, the CM-NSGA-III algorithm is run with the help of the platEMO platform developed by [44].

Figure 4.
Chromosome encoding.
5.3. Results
These two algorithms for the problem formulated in Section 3.2 is operated thirty times. After each run, 84 optimized feasible solutions can be obtained. It means that a total of 84 ore blending schemes are generated. Figure 5a,b show the running results of the CM-NSGA-III and NSGA-III algorithms, respectively. Coordinate axes f1, f2, f3, and f4 represent the sum of the target deviations for molybdenum grade, tungsten grade, copper grade and the sum of the rock percentages for all unloading points, respectively. It should be noted that when the value of f4 is zero, it means that the rock properties of the raw ore supplied to all unloading points are of the same type. In theory, the minimum value of these four objectives is zero when considering a single optimization objective. However, when multiple objectives are considered for simultaneous optimization, there is a conflict between the individual objective values.
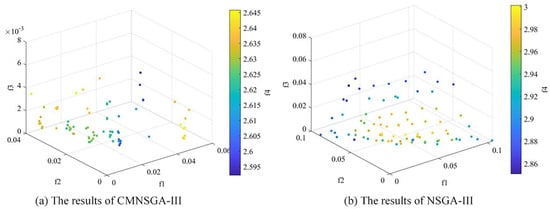
Figure 5.
The optimization result of four objectives.
Comparing Figure 5a,b, from the overall results of the four unloading points, the results obtained by the CM-NSGA-III algorithm are better than those obtained by the NSGA-III algorithm. In the results obtained by the CM-NSGA-III algorithm, the deviation of molybdenum grade is less than 0.06, the deviation of tungsten grade is less than 0.04, the deviation of copper grade is less than 0.004, and the percentage deviation of rock type is between 2.595 and 2.645. The results obtained by the NSGA-III algorithm are no better than the CM-NSGA-III algorithm.
Based on the optimization results shown in Figure 5, the optimization results of ore blending at each unloading point were calculated, as shown in Figure 6, Figure 7 and Figure 8. From the data in Figure 6, it is obvious that most of the optimized feasible solutions of CM-NSGA-III correspond to grades that are consistent with the target value for each metal at 1# and 4# unloading points. At 2# and 3# unloading points, the results obtained by CM-NSGA-III do not as well as 1# and 4# unloading points. Whatever CM-NSGA-III or NSGA-III algorithms, the most interesting aspect of Figure 6b,c is that for a given amount of raw ore at the #2 and #3 unloading sites the calculated grade of molybdenum is higher than the target value and the grade of tungsten is lower than the target value. It implies that it is to be more difficult to get the grades of the various metals to the target values by ore blending. Fortunately, however, the deviations in the grades of the various metals are within 5% of the target.
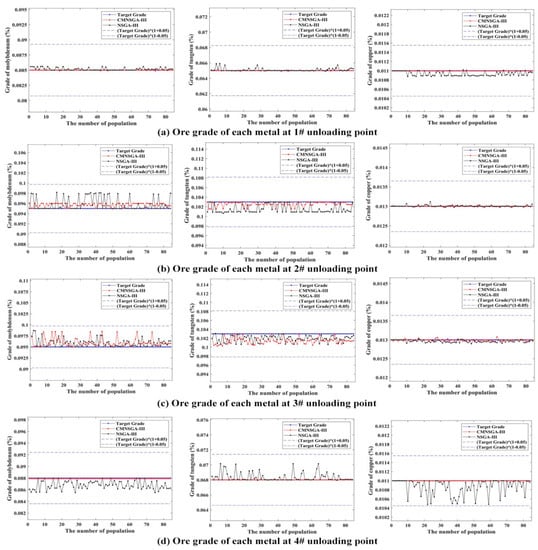
Figure 6.
Obtained grade of each metal at each unloading point.
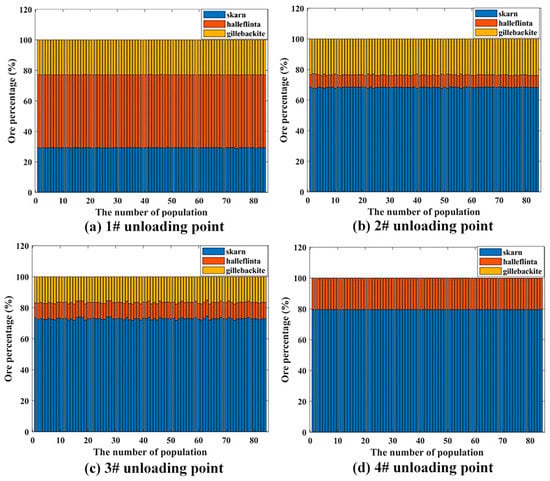
Figure 7.
The percentage of rock type at each unloading point by CM-NSGA-III.
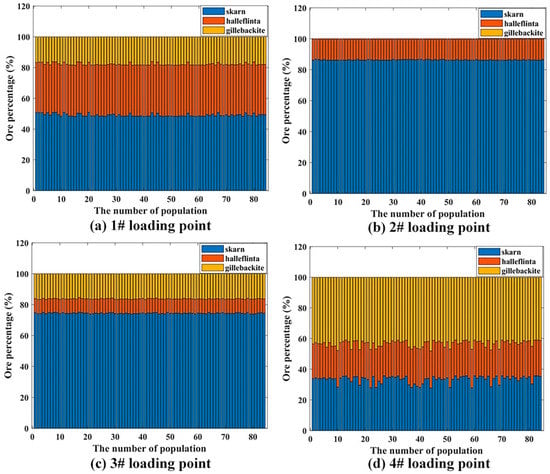
Figure 8.
The percentage of rock type at each unloading point by NSGA-III.
Comparing the results of NSGA-III and CM-NSGA-III algorithms at each unloading point, except that the tungsten results of NSGA-III at the 3# unloading point 3 are better than CM-NSGA-III on the whole, the ore blending results obtained by CM-NSGA-III algorithm are better than NSGA-III algorithm in most cases. It shows that the improvement taken on NSGA-III is effective. However, it does not mean that the NSGA-III algorithm cannot solve the polymetallic ore blending schedule problem. Because among the results shown in Figure 6, some of the 84 results obtained by NSGA-III are not much different from those of CM-NSGA-III. Moreover, the 84 results obtained by the CM-NSGA-III algorithm shown in Figure 6 have a small difference. It is due to the small difference between the obtained decision variables (for example, the difference of the same decision variable corresponding to two different results is 1 ton), and the difference is even smaller when reflected in the objective value.
From the data in Figure 7 and Figure 8, the rock type of the ore varies for each unloading point. In the results obtained by the CM-NSGA-III algorithm, the ore supplied to the 1#, 2# and 3# unloading point consist of three rock types and supplied to the 4# unloading point consist of two rock types. The largest percentage of the rock in the 1# unloading site is halleflinta, which reaches more than 40%. At 2#, 3# and 4# unloading points, the main rock is skarn, which reaches 70~80%. In the results obtained by the NSGA-III algorithm, the ore supplied to the 1#, 3# and 4# unloading point consist of three rock types and supplied to the 2# unloading point consist of two rock types. The largest percentage of the rock in the 1# unloading site is skarn, which reaches more than 40%. At 2# and 3# unloading points, the main rock is skarn, which reaches more than 80% and 70%, respectively. At the 4# unloading point, the main rock is gillebackite, which reaches more than 40%. It is noteworthy that there is no case of a single type of rock in the unloading points 1~4#. Therefore, it is impossible to try to make a single type of rock for the ore supplied at a particular unloading point.
Combining the optimization results shown in Figure 6, Figure 7 and Figure 8, it can be observed that the different grades of various metals in the same ore lead to the fact that it is more difficult to achieve the established ore blending targets for polymetallic ore within one shift, especially after considering the type of rock. However, the CM-NSGA-III algorithm can optimally solve the multi-objective ore blending model in Section 3.2 to reduce the grade deviation of each metal to within a suitable percentage of the target grade. Such results are sufficient to improve the existing ore blending schedule of the mine. Of these 84 ore blending schemes, one scheme is selected based on the principle of minimizing the relative deviation in grade for each metal, shown in Table 5. The selected method is to set a maximum grade deviation value for the grades of molybdenum, tungsten, and copper, respectively, and then gradually reduce the deviation value, so that there is only one result that satisfies the deviation value. The ore oxidation rates for the 1#~4# unloading point are 0.0944, 0.147, 0.1469, and 0.104, respectively, which meet the established requirements.

Table 5.
The scheme of ore blending.
5.4. Discussion
The main aim of the present study is to solve the problem of blending polymetallic ore. Specifically, it is to increase the utilization of ore by developing an ore blending shift scheme so that the grade of various metals in the ore can reach the required quality for the processing plant. For the polymetallic ore blending schedule problem, a multi-objective optimization model is developed and the CM-NSGA-III algorithm is proposed to solve the model in this research. By conducting experiments and using the NSGA-III algorithm as the benchmark. The results of the experiments show that, compared with the NSGA-III algorithm, CM-NSGA-III can solve the daily ore blending requirements of the mine and can achieve various metal grades within a suitable percentage deviation of the target grade. In addition to this, it is important to study the conflict between various objectives in polymetallic ore blending, which is directly related to whether the purpose of the blending can be achieved. The results of the study also provide some evidence for the existence of conflicts between targets in polymetallic ore blending.
Based on the CM-NSGA-III algorithm results shown in Figure 6, the deviation of the various metal grade ratios for each unloading point is calculated, as shown in Figure 9. In Figure 9a, as the deviation in grade for molybdenum and tungsten increases, the deviation in grade for copper decreases. In Figure 9b,c, there is a clear conflict between molybdenum and tungsten, when the grade deviation of molybdenum increases, the grade deviation of tungsten decreases; when the grade deviation of molybdenum decreases, the grade deviation of tungsten increases. This phenomenon is caused by the uneven distribution of various metals in the ore, for example, a piece of ore with a high content of one metal and a low content of another, which can easily occur during ore blending. This conflict is exacerbated when more factors are considered. Therefore, it is not appropriate to use the weighted approach in [15] to convert the multi-objective into a single objective and then perform the optimization solution when performing the optimization of polymetallic ore allocation. When the multi-objective optimization problem cannot be converted into a single-objective problem, the multi-objective optimization problem needs to be solved using a multi-objective optimization algorithm. The CM-NSGA-III optimization method proposed in this paper can effectively solve the multi-objective ore blending optimization problem for polymetallic ores by comparing it with the NSGA-III algorithm.
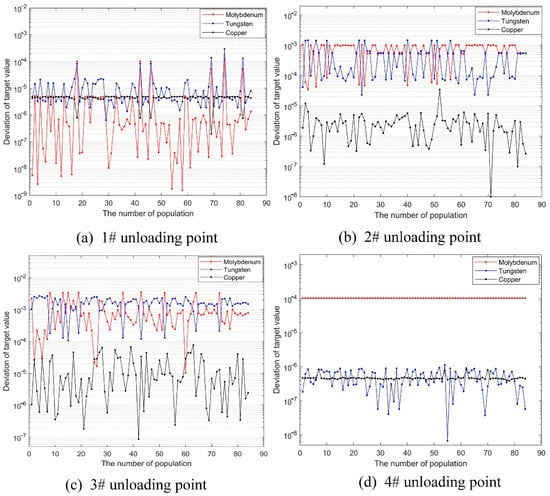
Figure 9.
Ore grade deviation value of each metal at four unloading points.
In addition to that, in the study of [6,12,30,45,46], the deviation of grade between the blended ore and the target required by the concentrator is usually used as a constraint. However, these studies do not explain how the upper and lower bounds of the constraint are determined, leading to the following problems: when the range of the constraint is small, the uncertainty of the geology may make the original optimization model has no feasible solution to satisfy the ore blending constraint; when the range of the constraint is large, the final blending of the ore may with a large fluctuation and not satisfy the requirements of the concentrator plant. Therefore, in practice, this study can be used to determine the minimum deviation value between the ore mixing and the target required by the ore processing plant, and then to develop a reasonable range of ore quality constraints.
6. Conclusions
Ore blending schemes can provide stable grade raw material for the beneficiation process, reduce the production cost, increase ore recovery rate and mine resource reserves, which is an effective way to improve the economic efficiency of mining enterprises. Putting the rock type and oxidation rate considered in beneficiation into the ore mixing process for consideration, the traditional ore mixing model will not be able to meet the requirements. Moreover, to make the grade of various metals in the associated ore reach or close to the beneficiation grade, the mixing of the raw associated metal will be more complex and challenging. In this paper, a multi-objective optimization model for the blending of associated metal ores is developed for the utilization of associated resources in associated ores, which is used to optimize the grade fluctuation of each associated metal in the blended ore, i.e., to make the grade of each metal in the blended ore close to the respective target grade. To solve this multi-objective optimization model, an improved constrained multi-objective algorithm based on the NSGA-III algorithm is proposed. The main conclusions that can be drawn are that:
- There is a conflict between the various metals in the ore when the associated metal ores are blended, i.e., for the grade of one metal in the blended ore to meet its beneficiation grade, the grade of the other metal in the ore will deviate from its beneficiation grade. So, the blending of associated ores is a multi-objective optimization problem, and it cannot be converted into a single-objective optimization problem by assigning weights to each objective. If it is transformed into a single-objective optimization problem, the optimal result will be a Pareto local optimum solution.
- Through the experiment, compared with the NSGA-III algorithm, the result obtained by the CM-NSGA-III algorithm is better. It shows that the CM-NSGA-III algorithm has better optimization solving performance. Moreover, the proposed model and algorithm can provide different optimal ore blending schemes available for the production of the mine and ensure a relatively minimal deviation from the required target by testing on the case.
- When the quality of the ore is not strictly required, i.e., it is allowed to fluctuate within a certain range, the method proposed in this paper can provide a theoretical basis for determining the fluctuation range of various metals in the ore.
It should be noted that the method proposed in this paper obtains a set of decision schemes, which cannot be directly used for the blending practice of the associated ores, and requires the decision maker to select a most satisfactory scheme for the practice through decision preferences or some rules. It is a limitation of this paper. These things considered, in the future, the ore blending optimization scheme can be considered by developing an integer multi-objective planning optimization model because the transportation process of ore is not continuous. The blending problem of associated ore can also be studied in combination with short-term production planning and production scheduling.
Author Contributions
Conceptualization, Q.G.; Data curation, C.Z.; Formal analysis, Z.F.; Funding acquisition, Q.G. and Z.F.; Investigation, L.C. and Z.F.; Methodology, L.C. and R.W.; Project administration, Q.G.; Software, L.C. and R.W.; Supervision, Q.G.; Validation, C.Z.; Visualization, Rui Wang; Writing—original draft, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52074205; National Natural Science Foundation of China, grant number 51774228; China Postdoctoral Science Foundation, grant number 2019M662505.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
The authors would like to thank Dianbo Liu (China Molybdenum Co., Ltd., Hong Kong, China) for his help in origin data collection. In addition, the authors thank the editors and reviewers for their help to this article.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
References
- Nwaila, G.T.; Ghorbani, Y.; Becker, M.; Frimmel, H.E.; Petersen, J.; Zhang, S. Geometallurgical Approach for Implications of Ore Blending on Cyanide Leaching and Adsorption Behavior of Witwatersrand Gold Ores, South Africa. Nat. Resour. Res. 2020, 29, 1007–1030. [Google Scholar] [CrossRef]
- Sotoudeh, F.; Nehring, M.; Kizil, M.; Knights, P.; Mousavi, A. Production scheduling optimisation for sublevel stoping mines using mathematical programming: A review of literature and future directions. Resour. Policy 2020, 68, 101809. [Google Scholar] [CrossRef]
- Yu, S.; Zhu, K.; He, Y. A hybrid intelligent optimization method for multiple metal grades optimization. Neural Comput. Appl. 2012, 21, 1391–1402. [Google Scholar] [CrossRef]
- Githiria, J.; Musingwini, C. A stochastic cut-off grade optimization model to incorporate uncertainty for improved project value. J. South Afr. Inst. Min. Metall. 2019, 119, 217–228. [Google Scholar] [CrossRef]
- Khan, A.; Asad, M.W.A. An optimal cut-off grade policy under diverse stockpile handling strategies in open-pit mining operations. Int. J. Min. Reclam. Environ. 2021, 35, 141–151. [Google Scholar] [CrossRef]
- Chanda, E.K.C.; Dagdelen, K. Optimal blending of mine production using goal programming and interactive graphics systems. Int. J. Surf. Min. Reclam. Environ. 1995, 9, 203–208. [Google Scholar] [CrossRef]
- Prasojo, T.S.; Yulianto, A.; Hindarto, A.; Parinussa, B.; Arifien, A. Ore Blending as Mine Scheduling Strategy to Accommodate Resources Conservation at Pakal Nickel Mine, PT ANTAM (Persero) Tbk. Procedia Earth Planet. Sci. 2013, 6, 24–29. [Google Scholar] [CrossRef][Green Version]
- Danish, A.A.K.; Khan, A.; Muhammad, K.; Ahmad, W.; Salman, S. A simulated annealing based approach for open pit mine production scheduling with stockpiling option. Resour. Policy 2021, 71, 102016. [Google Scholar] [CrossRef]
- Armstrong, M.; Lagos, T.; Emery, X.; Homem-de-Mello, T.; Lagos, G.; Sauré, D. Adaptive open-pit mining planning under geological uncertainty. Resour. Policy 2021, 72, 102086. [Google Scholar] [CrossRef]
- Van Tonder, E.; Deglon, D.A.; Napier-Munn, T.J. The effect of ore blends on the mineral processing of platinum ores. Miner. Eng. 2010, 23, 621–626. [Google Scholar] [CrossRef]
- Bicak, O. A technique to determine ore variability in a sulphide ore. Miner. Eng. 2019, 142, 105927. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, D.; Gao, X. A Method of Ore Blending Based on the Quality of Beneficiation and Its Application in a Concentrator. Appl. Sci. 2021, 11, 5092. [Google Scholar] [CrossRef]
- Kumral, M. Solution of Ore Blending Problem by Stochastic Approach. In Proceedings of the 10th International Mining Congress and Exhibition of Turkey-IMCET; Available online: https://www.maden.org.tr/resimler/ekler/18c255f89434eab_ek.pdf (accessed on 23 August 2022).
- Mkurazhizha, H. The Effects of Ore Blending on Comminution Behaviour and Product Quality in a Grinding Circuit-Svappavaara (LKAB) Case Study. Master’s Thesis, Luleå University of Technology, Luleå, Sweden, 2018. [Google Scholar]
- Kumral, M. Application of chance-constrained programming based on multi-objective simulated annealing to solve a mineral blending problem. Eng. Optimiz. 2003, 35, 661–673. [Google Scholar] [CrossRef]
- Askari-Nasab, H.; Pourrahimian, Y.; Ben-Awuah, E.; Kalantari, S. Mixed integer linear programming formulations for open pit production scheduling. J. Min. Sci. 2011, 47, 338–359. [Google Scholar] [CrossRef]
- Blom, M.L.; Burt, C.N.; Pearce, A.R.; Stuckey, P.J. A Decomposition-Based Heuristic for Collaborative Scheduling in a Network of Open-Pit Mines. INFORMS J. Comput. 2014, 26, 658–676. [Google Scholar] [CrossRef]
- Onuaguluchi, O.; Eren, O. Recycling of copper tailings as an additive in cement mortars. Constr. Build. Mater. 2012, 37, 723–727. [Google Scholar] [CrossRef]
- Ma, L.; Liu, C.D.; Bi, Y.L.; Peng, S.P.; Jiang, K.S.; Zhang, H.; Luo, Q.; Xue, F.; Xu, T.X.; Li, T.X.; et al. Experimental Study on Impermeability Law of Aquiclude Reconstructed by Mudstone of External Dump in Arid Zone. Adv. Civ. Eng. 2021, 2021, 5561794. [Google Scholar] [CrossRef]
- Singh, V.; Biswas, A.; Tripathy, S.K.; Chatterjee, S.; Chakerborthy, T.K. Smart ore blending methodology for ferromanganese production process. Ironmak. Steelmak. 2016, 43, 481–487. [Google Scholar] [CrossRef]
- Liu, X.; Liu, C.; Wang, B.; Ye, F. Optimization of iron ore blending in the COREX shaft furnace. J. S. Afr. Inst. Min. Metall. 2019, 119, 445–452. [Google Scholar] [CrossRef]
- Xu, T.J.; Yang, P.; Liu, Z.Q. Mine Ore Blending Planning and Management Based on the Fuzzy Multi-objective Optimization Algorithm. In Proceedings of the 2008 International Seminar on Business and Information Management, Wuhan, China, 19 December 2008. [Google Scholar]
- Gholamnejad, J.; Azimi, A.; Teymouri, M. Application of stochastic programming for iron ore quality control. J. Min. Environ. 2018, 9, 331–338. [Google Scholar]
- Ulger, N.E.; Ozer, U.; Akkaya, U.G. Determination of quality of a quartzite deposit, model of pre-blending, and the developing software-boss. J. Min. Sci. 2011, 47, 483–492. [Google Scholar] [CrossRef]
- Gholamnejad, J.; Kasmaee, S. Optimum blending of iron ore from Choghart stockpiles by using goal programming. J. Cent. South Univ. 2012, 19, 1081–1085. [Google Scholar] [CrossRef]
- Letelier, O.R.; Espinoza, D.; Goycoolea, M.; Moreno, E.; Munoz, G. Production Scheduling for Strategic Open Pit Mine Planning: A Mixed-Integer Programming Approach. Oper. Res. 2020, 68, 1425–1444. [Google Scholar] [CrossRef]
- Singh, G.; Garcia-Flores, R.; Ernst, A.; Welgama, P.; Zhang, M.M.; Munday, K. Medium-Term Rail Scheduling for an Iron Ore Mining Company. Interfaces 2014, 44, 222–240. [Google Scholar] [CrossRef]
- Blom, M.L.; Pearce, A.R.; Stuckey, P.J. A Decomposition-Based Algorithm for the Scheduling of Open-Pit Networks Over Multiple Time Periods. Manag. Sci. 2016, 62, 3059–3084. [Google Scholar] [CrossRef][Green Version]
- Moreno, E.; Rezakhah, M.; Newman, A.; Ferreira, F. Linear models for stockpiling in open-pit mine production scheduling problems. Eur. J. Oper. Res. 2017, 260, 212–221. [Google Scholar] [CrossRef]
- Jamshidi, M.; Osanloo, M. Reliability analysis of production schedule in multi-element deposits under grade-tonnage uncertainty with multi-destinations for the run of mine material. Int. J. Min. Sci. Technol. 2019, 29, 483–489. [Google Scholar] [CrossRef]
- Rezakhah, M.; Moreno, E.; Newman, A. Practical performance of an open pit mine scheduling model considering blending and stockpiling. Comput. Oper. Res. 2020, 115, 12. [Google Scholar] [CrossRef]
- Samatova, L.A.; Shepeta, E.D.; Gvozdev, V.I. Poor scheelite ores from Primorye deposits: Mineralogy and processing characteristics and dressing flowsheets. J. Min. Sci. 2012, 48, 565–573. [Google Scholar] [CrossRef]
- Gu, Q.; Lu, C.; Guo, J.; Jing, S. Dynamic management system of ore blending in an open pit mine based on GIS/GPS/GPRS. Min. Sci. Technol. 2010, 20, 132–137. [Google Scholar] [CrossRef]
- Marques, D.M.; Costa, J.F.C.L. An algorithm to simulate ore grade variability in blending and homogenization piles. Int. J. Miner. Process. 2013, 120, 48–55. [Google Scholar] [CrossRef]
- Zhao, S.; Lu, T.F.; Koch, B.; Hurdsman, A. Automatic quality estimation in blending using a 3D stockpile management model. Adv. Eng. Inform. 2015, 29, 680–695. [Google Scholar] [CrossRef]
- Ilic, D.; Lavrinec, A.; Orozovic, O. Simulation and analysis of blending in a conveyor transfer system. Miner. Eng. 2020, 157, 11. [Google Scholar] [CrossRef]
- Ma, L.; Lai, X.P.; Zhang, J.G.; Xiao, S.S.; Zhang, L.M.; Tu, Y.H. Blast-Casting Mechanism and Parameter Optimization of a Benched Deep-Hole in an Opencast Coal Mine. Shock Vib. 2020, 2020, 1396483. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, J.G.; Xu, C.; Lai, X.P.; Luo, Q.; Liu, C.D.; Li, K.M. Comprehensive Evaluation of Blast Casting Results Based on Unascertained Measurement and Intuitionistic Fuzzy Set. Shock Vib. 2021, 2021, 8864618. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Comput. 2014, 18, 602–622. [Google Scholar] [CrossRef]
- He, Z.; Yen, G.G. Many-Objective Evolutionary Algorithms Based on Coordinated Selection Strategy. IEEE Trans. Evol. Comput. 2017, 21, 220–233. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H.; Wang, B.; Zhang, B.; Yao, X. Balancing Convergence and Diversity in Decomposition-Based Many-Objective Optimizers. IEEE Trans. Evol. Comput. 2016, 20, 180–198. [Google Scholar] [CrossRef]
- Jiang, S.; Yang, S. A Strength Pareto Evolutionary Algorithm Based on Reference Direction for Multiobjective and Many-Objective Optimization. IEEE Trans. Evol. Comput. 2017, 21, 329–346. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization [Educational Forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Hou, J.; Li, G.Q.; Wang, H.; Hu, N.L. Genetic algorithm to simultaneously optimise stope sequencing and equipment dispatching in underground short-term mine planning under time uncertainty. Int. J. Min. Reclam. Environ. 2020, 34, 307–325. [Google Scholar] [CrossRef]
- Yang, H.; Hu, N.L.; Xu, Z.; Chen, L. A Real-Time Ore Proportioning System in a Large Open-Pit Copper-Molybdenum Mine. Appl. Mech. Mater. 2013, 336–338, 2124–2129. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).