Abstract
Installed wind power has significantly grown in recent years to synchronize with the ever-increasing demand for environment-friendly and renewable energy. However, wind energy has significant uncertainty or random futures, and will give rise to destructive effects on the safety operations of the power system. In this respect, an accurate and reliable wind power prediction is of great significance for improving the power system stability and optimizing the dispatch plan. Compared with traditionally deterministic point forecast techniques, probabilistic forecasting approaches can provide more stochastic information to quantify the random characteristics of wind power and to estimate its impacts on the power system. Moreover, the interval of the output power is a key stochastic information on wind power. In general, an interval prediction needs to compromise the calibration and the average width of the predicted interval. To find the best combination of these two metrics, a methodology based on a kernel extreme learning machine (KELM) and an improved universal tabu search algorithm is proposed. In the proposed methodology, to eliminate the inherent randomness on the weights between the input and hidden lays in the commonly used extreme learning machine, a radial-basis-function-based kernel extreme learning machine is proposed, and an improved tabu search method is introduced to optically compromise the calibration and the average width of the predicted interval to overcome the deficiency of existing algorithms, such as the insufficient global search ability of a particle swarm optimization. A prototype wind farm is utilized as a case study to verify the efficiency and advantage of the proposed methodology.
1. Introduction
As the most environment-friendly and renewable energy, wind energy has an ever-increasing demand in the new century [1]. As a result, installed wind power has significantly grown in recent years. However, compared with the traditional thermal power, wind energy has significant uncertainty or random futures and will give rise to a destructive effect on the operation of the power system [1,2]. These uncertainties come mainly from the chaotic weather conditions. In this respect, accurate and reliable wind power prediction is of great significance for improving the power system stability and optimizing the dispatch plan [3].
The existing prediction methods for wind power are mostly point-forecasting approaches. In these forecasting models and methods, the wind power at a future moment is predicted. Since wind power is inherently uncertain at a moment, these traditional point predictions will inevitably introduce errors on the prediction results, and they cannot reveal and model fully the uncertainty natures of the wind power output. Consequently, in the face of the access of a high proportion of wind power energy and with an ever-increasing capacity of the installed wind energy, a wealth of efforts has been devoted to developing probabilistic prediction methods. Compared with traditionally deterministic point forecast techniques, a probabilistic forecasting approach can provide more stochastic information to quantify the random characteristics of the wind power and to estimate its impacts on the power system. Consequently, different probabilistic forecasting models and methods have been proposed and applied to two-stage robust optimizations [4], multistage robust dispatch [5], unit commitment [6], stochastic control [7], and energy trading [8], to name but a few. Moreover, the interval of the output power is a key stochastic performance parameter in a wind power prediction model and method. For example, in the adaptive robust optimization for the security-constrained unit commitment problem [5], a two-stage robust optimization methodology is utilized to find the worst case in the wind power uncertainty set in order to develop the most economical unit commitment to deal with the worst conditions of the wind power. In the two-stage robust optimization, the total scheduling costs can be divided into two parts, that is, the unit start-up/shutdown costs and the dispatch costs. The decision variables of the first stage are the operation condition of a thermal power unit in 24 h, which can provide the domain of the “max–min” function in the second stage [4,5,6]. Dispatching cost is the most economical way to deal with the worst case of the wind power interval. It should be noted that the worst case of wind power and the dispatching cost are functions of the first-stage decision variables. However, according to the nature of a stochastic process, the wind power at a specific time is essentially a continuous random variable [9]. In this point of view, the worst case of the wind power will rarely occur [9]. That means that the results of the robust optimization are extremely conservative [4,6,9]. If the intervals of the wind power are set too widely, the resulting set of the unit commitment will also be conservative excessively. To conclude, the wind power interval is vital to the operation plan of a unit commitment [1,2]. Therefore, it is advisable to develop an effective algorithm for rational interval predictions of the wind power.
In the literature, different methods have been proposed for reliable wind power interval predictions. These methods can be divided into two categories, that is, the parametric estimation and the nonparametric estimation methods. The parametric estimation method often assumes that the error of the forecasted wind power obeys a special distribution, and then uses some samples to estimate this distribution. In this direction, Wan et al. [10] proposed a new algorithm based on the extreme learning machine (ELM) and bootstrap method for the probabilistic forecasting of wind power generation. However, the assumption on the special distribution of the prediction errors may not be appropriate and applicable for other wind farms. Therefore, researchers have paid more attention to nonparametric interval predictions of the wind power. In this respect, Wan et al. [11] developed a hybrid intelligent algorithm by combining ELM and particle swarm optimization (HIA) to predict the wind power interval directly. However, the particle swarm optimization algorithm used in this approach is easy to be trapped in local optimal solutions. Wan et al. [12] introduced some auxiliary variables in the quantile regression model to obtain a more reliable interval prediction result. Zhao et al. [13] used an adaptive bilevel programming model (ABP) to calculate the best quantile at a certain confidence level, which can minimize the average width of the predicted intervals. Since the slave problem is a linear programming one in the ABP model, the strong dual condition is satisfied, and the KKT theorem can be used to transform the bilevel programming into a single-level problem. However, the transformed model includes a bilinear item, which is an NP-hard problem. Wan et al. [14] developed an empirical distribution function to approximate the quantile interval via the similar historical power series data at a specific forecasting time. However, the procedures of repeated validations are required in the algorithm to determine the appropriate parameter for measuring the similarity, which will take a large amount of solution times. To conclude, a reliable and robust wind power interval prediction technique is still demanding.
In general, the interval forecasting of wind power is formulated as an optimization problem to optimize the calibration and the average width of the wind power interval. To address the interval forecasting of wind power, this paper proposed a combined universal tabu search algorithm and the KELM methodology. The ELM is trained as a regression model for the interval prediction of wind power. To compromise both the calibration and the average width of the wind power interval, the weights from the single hidden layer to the output layer are optimized. To eliminate the inherent randomness on the weights between the input and hidden lays in the commonly used extreme learning machine, a radial-basis-function-based kernel extreme learning machine is proposed instead of the commonly used extreme learning machine. Since the objective function is a nonconvex and multimodal one, a universal tabu search method is improved to overcome the deficiencies of existing algorithms, such as the insufficient global search ability of a particle swarm optimization, to optically compromise the calibration and the average width of the predicted interval. To verify the effectiveness of the proposed methodology, it is used to predict the power interval of a prototype wind farm with promising results.
The rest of this paper is organized as follows: The prediction model KELM is given in Section 2. The improved universal tabu search algorithm is explained and numerically validated in Section 3. The case study and numerical results are reported in Section 4. Finally, conclusions are presented in Section 5.
2. Kernel Extreme Learning Machine
The probabilistic prediction model for the interval of wind power in this paper is based on the extreme learning machine. An extreme learning machine (ELM) is a feedforward neural network with a single hidden layer [15]. The weights and biases connecting the input layer and the hidden layer nodes are randomly assigned or given by a designer, and are not updated during the training and learning process. The weights between the hidden layer and the output layer will be updated in the training process. An extreme learning machine has a strong generalization ability and a high computational efficiency, and its computational speed is faster than that of the neural network trained by a back-propagation algorithm. Consequently, an extreme learning machine can be used for classification, regression, clustering, sparse approximation, compression, and feature learning. Now ELM has been widely employed in face recognition, image classification, wind speed, and wind power prediction.
In the following discussion, one will consider a case where there are N training samples , where is the ith input node, n is the number of the total input nodes in ELM, and is a sampled value of the trained function, which presents the training target, that is, the output power in this study. If the number of hidden layer neurons of the extreme learning machine is Nh, and its activation function is g(x), the relationship between input and output can be expressed as Equation (1):
where is the output of the extreme learning machine, is the weight vector connecting the ith hidden layer neuron and all input nodes, is the weight vector connecting the ith hidden layer neuron and all output nodes, is the ith bias of the hidden layer neurons, and is the inner product of these two vectors. If one defines as the vector of , the above N equations can be written in a matrix form as Equation (2):
where is given by:
If the input weights and hidden layer biases are randomly assigned, the matrix will not change in the training process. If the number of neurons in the hidden layer is equal to the number of training samples, is an invertible square matrix, and the trained neural network can accurately approximate and fit all the training samples. However, the number of neurons in the hidden layer is generally much smaller than the number of training samples. Consequently, is a nonsquare matrix, and a generalized inverse matrix is used to solve the output weight. Moreover, can be reformulated as Equation (4):
where H+ is the Moore–Penrose generalized inverse matrix of the matrix H. After is determined, if the new sample is used as the input of the ELM, the output can be calculated from Equation (5):
where is a matrix obtained by the new sample and the input weight.
Since the weights between the input and hidden lays in the extreme learning machine have inherent randomness characteristics, the kernel extreme learning machine (KELM) is used in this paper [16]. KELM combines the ELM and the kernel function to eliminate the inherent randomness characteristics and to enhance the adaptability and stability of an ELM.
Generally, the hidden nodes are more than the features of input data in the ELM, so the data transformation from the input layer to the hidden layer can be equivalent to a dimension ascension. Therefore, KELM uses a kernel function to map all input samples from an n-dimensional input space to a high-dimensional hidden layer feature space. In this study, a radial basis function (RBF) kernel function is used and given by Equation (6):
where is the bandwidth of the kernel function.
According to Equation (6), the kernel matrix can be obtained as:
where is defined as:
The can be regarded as a high-dimensional mapping of the ith sample through the weights of the input and the hidden layers. Note that one does not need to have the information of the matrix, and the output weights can be gained via the RBF kernel function.
In order to increase the stability of the ELM, a regularization coefficient C and a unit matrix E are introduced, and the output weight is then calculated from Equation (9):
The matrix can be calculated via Equation (7). In the proposed ultra-short-term forecasting of wind power, we use the historical wind power data as input variables for KELM instead of using the numerical weather prediction (NWP) information. It is better to use the historical wind power data as input variables for KELM than to use the numerical weather prediction (NWP) information. Consequently, the input data are the historical wind power series, and the output is the wind power at a further instant.
3. Interval Prediction Methodology
To evaluate the qualities of the forecasted wind power interval, two indicators to quantify, respectively, reliability and sharpness, are used. Reliability is defined as the ratio of the number of observing samples falling within the interval to that of the total samples, and it can be expressed as Equation (10):
In (10), I represents an indicator function. When the real value of the wind power of the ith sample at time t falls within the interval, I(yi) is assigned to be 1; otherwise, it is set to be 0. The value of the reliability should be as close as possible to the predefined confidence level . Under the same reliability, a narrower interval is more helpful and preferred in applications to power system scheduling. Although randomly increasing or decreasing the distance between the upper and lower boundaries of the interval can easily meet the reliability requirements, it will cause a sharpness deterioration. In this respect, one defines the width of the predicted interval as Equation (11):
where and are, respectively, the upper bound and lower bound of the predicted wind power. At a certain confidence level , the score of the interval as defined in [10] can be used as an indicator for evaluating the width of the forecasted interval:
It is clear that the score of a narrow interval will be higher, and the interval whose true value falls outside the interval will be weighted by a penalty term in its score.
In order to ensure both the reliability and the sharpness of the predicted interval, one will optimize the following objective function in this paper:
where is the reliability as defined in (10), and is the average score for the interval.
In training KELM, the weights from the single hidden layer to the output layer are optimized to find the best solution of Equations (13) and (14). As explained previously, the objective function as defined in Equation (13) is a nonconvex and multimodal one, and the universal tabu method as introduced in [17] is improved and used to solve this optimization problem to overcome the deficiency of existing ones.
A tabu search algorithm (TS) is a heuristic algorithm proposed by F. Glover et al. [18,19]. Compared with other stochastic algorithms, a tabu search method is featured for its simpleness in concept and easiness in algorithm structure and numerical implementation. Consequently, tabu search has been widely used in optimization problems [20,21]. However, the balance between the exploration and exploitation searches in exiting tabu searches is still unsatisfactory. In this regard, the universal tabu search method as proposed in [17] is improved to find the optimal solution of Equations (13) and (14).
For space limitations, details about a tabu search algorithm are referred to in [17,18,19,20,21], and only the improvements made in this paper will be explained in the following paragraphs. To compromise the exploration and exploitation searches, the searching procedures of the proposed tabu search algorithm are divided into two different phases: the intensification phase and the diversification.
In the diversification phase, to guarantee the diversity of the algorithm, for each current state, x, a series of neighborhood solutions are generated first. Moreover, a neighborhood solution, y, of x will be generated using the following mechanism as Equation (15):
where j presents the jth dimension, hi is the step size of the neighbor i, r is a random number that is uniformly distributed in [−1, 1], and pj is half of the dimension size of the jth variable.
Once all of the neighborhood solutions are generated, the search procedure will move to the best one of all the neighborhood solutions to start a new cycle of iterations.
In the intensification phase, to guarantee the exploiting search ability of the algorithm, for each current state, x, a series of neighborhood solutions are also generated first but using a different generating mechanism. For example, a neighborhood solution, y, of x will be generated using the following equation as Equation (16):
where r is a random number that is generated using a Gaussian distribution.
Once all of the neighborhood solutions are generated, the search procedure will move to the best one of all the currently available solutions, including x and all neighborhood solutions, as well as the so far searched best one to start a new cycle of iterations.
The proposed algorithm starts from the diversification phase to explore uniformly the whole searching space. If the so far searched best solution in this phase will not change for a given number of consecutive iterations, the procedure will move to the intensification phase to start exploiting searches until the number of consecutives iterations for no improvement in the so far searched best solution exceeds a predefined value.
To help readers to implement the proposed tabu search method to develop the corresponding codes, its detailed iterative procedures are given below. In the below explanation, Nd, Ni, and Ng are three stop criteria to terminate the algorithm.
Step 0: Initialize the algorithm parameters;
Step 1: Start the diversification searching phase until the number of consecutive iterations without any improvement on the so far searched best solution exceeds Nd;
Step 2 Start the intensification searching phase until the number of consecutive iterations without any improvement on the so far searched best solution exceeds Ni;
Step 3: N = N + 1. If N ≤ Ng, go to step 1;
Step 4: Terminate the iterative procedures of the method.
To demonstrate and test the performances of the proposed improved tabu search algorithm, an extremely high multimodal function having about 105 local optima is selected as a case study. This benchmark mathematical function is given by
The global optimal solution and the cost function value are, respectively, xi = 1, (I = 1, 2, …, 5) and fglobal = 0. To compare the performances of different algorithms, this case study is solved by the proposed tabu search method and the original tabu search algorithm [12]. In the numerical study, the parameters of the proposed tabu search method are set as: Nd = 10, Ni = 5, and Ng = 3. The other parameters for the two tabu search algorithms are the same for a fair comparison. To obtain the stochastic information on the averaged performances of a method, each algorithm is run 100 times by starting from different randomly initialized points. Table 1 gives the averaged performance comparison of the aforementioned two methods for solving this test mathematical function.

Table 1.
Performance comparisons of different algorithms.
In Table 1, finding the global optimal solution for a run means that the errors between the searched solutions of the algorithm and the exact ones in view of both the function value and the decision variables are smaller than 10−6 in absolute values. From the numerical results in Table 1, it is observed that all the 200 independent and random runs of the two algorithms converge to the exact global optimal solution of this test function. In other words, the proposed algorithm and the original one can escape from the nearly infinite local optima of this extremely multimodal test function and converge on the global optimum with 100% probability. However, the iterative number used by the proposed algorithm is extremely reduced as compared with the original version of the tabu search algorithm, that is, reduced from 3281 to 2045. Consequently, the improved tabu search algorithm is computationally efficient in finding the global optimal solution of a multimodal objective function with continuous variables.
4. Case Study
A prototype wind farm is selected as the case study of the proposed method to demonstrate its performances. As explained previously, the forecasted wind power result using NWP as the input variables is usually less accurate as compared with that using the historical wind power series since the correlation between forecasted points and historical data plays a more important role as compared with the NWP data. In this regard, the historical wind power series are used in this case study. Generally, the weather in the time period from winter to spring of the following year is windy, while that from summer to autumn is breezy. In this point of view, the wind power forecasting for different seasons should use different historical wind power data. More specifically, in the presented work, the interval prediction of the wind power is divided into the following four phases:
- (1)
- The winter period interval prediction. In this phase, the historical wind power data in November to December will be used.
- (2)
- The summer period interval prediction. In this phase, the historical wind power data from June to July will be used.
- (3)
- The autumn period interval prediction. In this phase, the historical wind power data from September to October will be used.
- (4)
- The spring period interval prediction. In this phase, the historical wind power data from March to April will be used.
The historical wind power data of a complete year for the prototype wind farm are obtained by recording the wind power every 1 h. Since the wind turbines are generally located in an open-air field and work in a chaotic environment, the historical wind power data are easily disturbed by weather conditions. As a consequence, abnormal data will be inevitably recorded in the initial historical wind power. Accordingly, one will first eliminate the abnormal data from the raw historical wind power data before the forecasting. In this regard, a wealth of methods is readily available [22,23,24,25,26,27,28,29]. However, the approach as introduced in [30] is used in this study. The finally used v-p wind power curve is given in Figure 1. In the implementation of a wind power forecasting methodology, the first 70% of the total data are used as the training data, and the remaining 30% as the testing data. The target of the training data will be expanded 1.2 times into the upper training data, and reduced 0.8 times into the lower training data, respectively. The initialization of the output weights (the decision variables) of the upper bound and the low bound is conducted in the two training datasets via KELM. One will then set a neighborhood (or variation) range for each output weight by adding 2 and subtracting 2 from the initial weights to construct the ranges of weights. The domain of the optimization function is then determined. The confidence level of intervals is set to be 100(1−0.1)%.
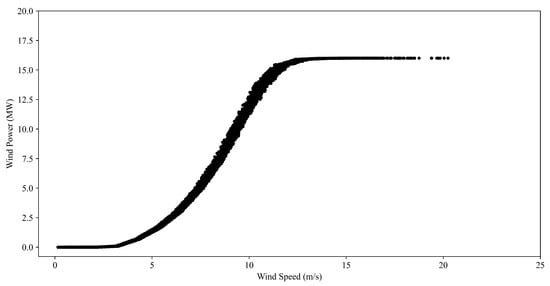
Figure 1.
Power curve of the prototype wind farm.
Under the previous implementation and parameter conditions, the forecasted results of very short intervals (e.g., 15 min–6 h) for the wind power for 1 h look-ahead time in December, July, April, October, and July with 1 h look-ahead time using the proposed model and method are given in Figure 2, Figure 3, Figure 4 and Figure 5. It should be pointed out that the interval for the look-ahead time can be set flexibly. Following the common practice in the literature, one sets them from 15 min to 6 h in this article. However, one could also set them from 10 min to 6 h, for example.
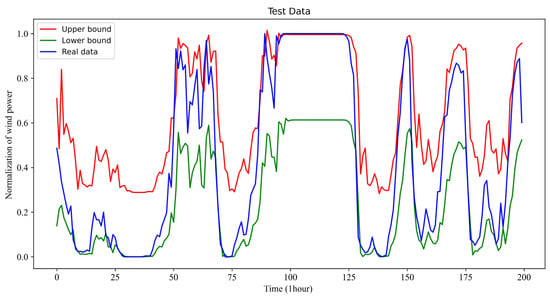
Figure 2.
One-hour look-ahead of wind power interval prediction results in December.
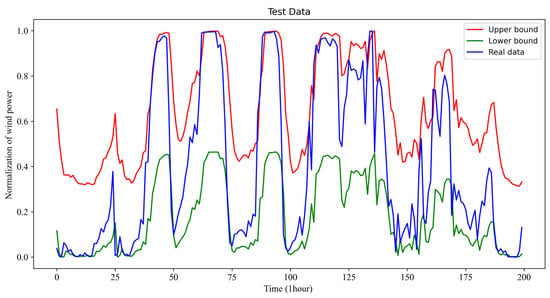
Figure 3.
One-hour look-ahead of wind power interval prediction results in July.
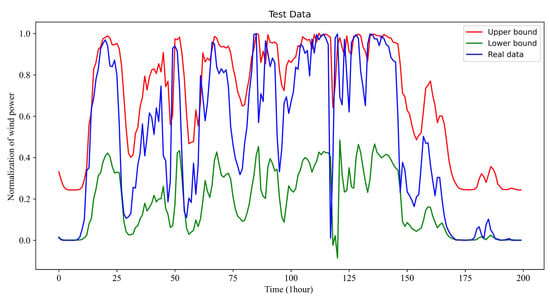
Figure 4.
One-hour look-ahead of wind power interval prediction results in October.
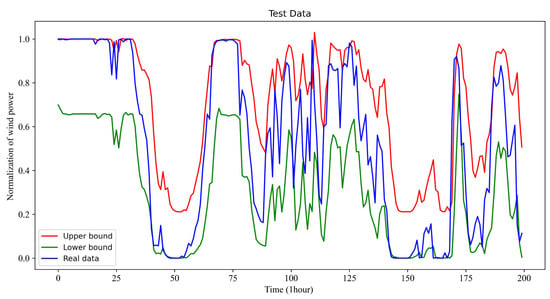
Figure 5.
One-hour look-ahead of wind power interval prediction results in April.
Observing the results of Figure 2, Figure 3, Figure 4 and Figure 5, it is clear that the real wind power curve (the blue-colored curve) is nearly exact in the forecasted interval between the forecasted upper bound and forecasted lower bound for all of the forecasted seasons. Consequently, the proposed method can reliably predict the interval of the wind power for power system scheduling.
To compare the performances of the proposed interval prediction model and existing ones, the hybrid intelligent algorithm (HIA) as introduced in [11] is also used for the short-term interval prediction of this prototype wind farm. In numerical comparisons, the reliability performance parameter P (%) and the sharpness of the predicted interval W are used. The performance parameter P (%) is the percentage of the actual power values that fall within the forecasted intervals, while the performance parameter W is the average width of each interval in each season. In view of the metric P (%), the deviation between P (%) and the confidence level is smaller, and a more reliable interval is predicted by the method. In view of the metric W, under a certain confidence level, a narrower interval (i.e., a smaller W) is more promising in engineering application. The performance parameters of HIA and the proposed method under 90% confidence level are compared in Table 2. From these performance parameter results, it is naturally concluded that:

Table 2.
Experimental results of two algorithms with 90% confidence level.
- (1)
- In view of the metric W, the proposed algorithm outperforms HIA since the values of the metric W of the predicted interval for December, July, and April using the proposed algorithm are smaller than the corresponding values using HIA;
- (2)
- In view of the metric P (%), the two methods behave almost similarly, since the proposed method performs better in the predicted interval for December and October, while HIA performs better for July and April;
- (3)
- It should be noted that the robustness of the proposed algorithm is stronger than that of HIA since the values of the metric P (%) for the four seasons of the former are always larger than that of the predefined 90% confidence level, while the values of the same metric for only July and April of the latter are larger than that of the predefined 90% confidence level.
5. Conclusions
Interval prediction is an effective tool to quantify the uncertainty of wind power. In order to have a high-quality forecasting interval of wind power, a combined methodology based on KELM and an improved universal tabu search method is proposed. First, the compromise between the reliability and the average width of the interval prediction is formulated as the optimization of the weights from the single hidden layer to the output layer of KELM. This nonconvex optimization problem is then solved by introducing an improved tabu search algorithm. The numerical prediction results on the intervals of a prototype wind farm under a 90% confidence level confirm that:
- (1)
- In view of the sharpness of the predicted interval, the proposed algorithm outperforms the existing approach, HIA;
- (2)
- In view of the robustness on the reliability of the predicted interval, the proposed algorithm behaves extremely well over the existing approach, HIA.
As regards the further direction of the authors, we will explore the relevance of the implications to BRICS countries.
Author Contributions
Formal analysis, Q.L.; Funding acquisition, S.Y.; Investigation, Y.M.; Methodology, Q.Z. and R.Z.; Software, W.W. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Science and Technology Project of SGCC under grant no. 52272220004H.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data can be requested from the corresponding author by email.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhao, C.; Wan, C.; Song, Y. Chance constrained extreme leaning machine for nonparametric prediction intervals of wind power generation. IEEE Trans. Power Syst. 2020, 35, 3869–3884. [Google Scholar] [CrossRef]
- Zhao, C.; Wan, C.; Song, Y. Operating reserve quantification using prediction intervals of wind power: An integrated probabilistic forecasting and decision methodology. IEEE Trans. Power Syst. 2021, 36, 3701–3714. [Google Scholar] [CrossRef]
- Zhao, Y.; Ye, L.; Pinson, P.; Tang, Y. Correlation-constrained and sparsity-controlled vector autoregressive model for spatiotemporal wind power forecasting. IEEE Trans. Power Syst. 2018, 33, 5029–5040. [Google Scholar] [CrossRef]
- Bertsimas, D.; Litvinov, E.; Sun, X.A.; Zhao, J.; Zheng, T. Adaptive Robust Optimization for the Security Constrained Unit Commitment Problem. IEEE Trans. Power Syst. 2013, 28, 52–63. [Google Scholar] [CrossRef]
- Shi, Y.H.; Dong, S.F.; Guo, C.X.; Chen, Z.; Wang, L.Y. Enhancing the Flexibility of Storage Integrated Power System by Multi-Stage Robust Dispatch. IEEE Trans. Power Syst. 2021, 36, 2314–2322. [Google Scholar] [CrossRef]
- Lorca, Á.; Sun, X.A.; Litvinov, E.; Zheng, T. Multistage adaptive robust optimization for the unit commitment problem. Oper. Res. 2016, 64, 32–51. [Google Scholar] [CrossRef]
- Jiang, Y.; Wan, C.; Wang, J.; Song, Y.; Dong, Z.Y. Stochastic receding horizon control of active distribution networks with distributed renewables. IEEE Trans. Power Syst. 2019, 34, 1325–1341. [Google Scholar] [CrossRef]
- Li, G.; Li, Q.; Yang, X.; Ding, R. General Nash bargaining based direct P2P energy trading among prosumers under multiple uncertainties. Int. J. Electr. Power Energy Syst. 2022, 143, 108403. [Google Scholar] [CrossRef]
- Wan, C.; Cui, W.K.; Song, Y.H. Probabilistic forecasting for power systems with renewable energy sources: Basic concepts and mathematical principles. Proc. CSEE 2021, 41, 6493–6509. [Google Scholar]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Probabilistic forecasting of wind power generation using extreme learning machine. IEEE Trans. Power Syst. 2014, 29, 1033–1044. [Google Scholar] [CrossRef]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Optimal prediction intervals of wind power generation. IEEE Trans. Power Syst. 2014, 29, 1166–1174. [Google Scholar] [CrossRef] [Green Version]
- Wan, C.; Lin, J.; Wang, J.; Song, Y.; Dong, Z.Y. Direct quantile regression for nonparametric probabilistic forecasting of wind power generation. IEEE Trans. Power Syst. 2017, 32, 2767–2778. [Google Scholar] [CrossRef]
- Zhao, C.; Wan, C.; Song, Y. An adaptive bilevel programming model for nonparametric prediction intervals of wind power generation. IEEE Trans. Power Syst. 2020, 35, 424–439. [Google Scholar] [CrossRef]
- Wan, C.; Cao, Z.; Lee, W.J.; Song, Y.; Ju, P. An Adaptive Ensemble Data Driven Approach for Nonparametric Probabilistic Forecasting of Electricity Load. IEEE Trans. Smart Grid 2021, 12, 5396–5408. [Google Scholar] [CrossRef]
- Huang, G.B.; Wang, D.H.; Lan, Y. Extreme learning machines, a survey. Int. J. Mach. Learn. Cybern. 2011, 2, 107–122. [Google Scholar] [CrossRef]
- Huang, G.B. An insight into extreme learning machines: Random neurons, random features and kernels. Cogn. Comput. 2014, 6, 376–390. [Google Scholar] [CrossRef]
- Yang, S.Y.; Ni, G.Z. An universal tabu search algorithm for global optimization of multimodal functions with continuous variables in electromagnetics. IEEE Trans. Magn. 1998, 34, 2901–2904. [Google Scholar] [CrossRef]
- Glover, F. Tabu search-Part 1. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Glover, F. Tabu search-Part 2. ORSA J. Comput. 1990, 2, 4–32. [Google Scholar] [CrossRef]
- Hu, N. Tabu search method with random moves for globally optimal design. Int. J. Numer. Methods Eng. 1992, 35, 1055–1070. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, A.; Ai, Y.; Tian, B.; Chen, L. Real-time scheduling of autonomous mining trucks via flow allocation-accelerated tabu search. IEEE Trans. Intell. Veh. 2022. [Google Scholar] [CrossRef]
- Long, H.; Sang, L.; Wu, Z.; Gu, W. Image-based abnormal data detection and cleaning algorithm via wind power curve. IEEE Trans. Sustain. Energy 2020, 11, 938–946. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Huang, C. A fast abnormal data cleaning algorithm for performance evaluation of wind turbine. IEEE Trans. Instrum. Meas. 2021, 70, 5006512. [Google Scholar] [CrossRef]
- Liang, G.; Su, Y.; Chen, F.; Long, H.; Song, Z. Wind power curve data cleaning by image thresholding based on class uncertainty and shape dissimilarity. IEEE Trans. Sustain. Energy 2021, 12, 1383–1393. [Google Scholar] [CrossRef]
- Shen, X.; Fu, X.; Zhou, C. A combined algorithm for cleaning abnormal data of wind turbine power curve based on change point grouping algorithm and quartile algorithm. IEEE Trans. Sustain. Energy 2019, 10, 46–54. [Google Scholar] [CrossRef]
- Zhao, Y.; Ye, L.; Zhu, Q. Characteristics and processing method of abnormal data clusters caused by wind curtailments in wind farms. Autom. Electr. Power Syst. 2014, 38, 39–46. [Google Scholar]
- Zhao, Y.; Hu, Q.; Srinivasan, D.; Wang, Z. Data-driven correction approach to refine power curve of wind farm under wind curtailment. IEEE Trans. Sustain. Energy 2018, 9, 95–105. [Google Scholar] [CrossRef]
- Hu, Y.; Qiao, Y.; Liu, J.; Zhu, H. Adaptive confidence boundary modeling of wind turbine power curve using SACADA data and its application. IEEE Trans. Sustain. Energy 2018, 10, 1330–1341. [Google Scholar] [CrossRef]
- Fen, C.; Zhu, S.; Zhu, Z.; Sun, M. Comparative study on detection methods of abnormal wind power data. Adv. Technol. Electr. Eng. Energy 2021, 40, 55–61. [Google Scholar]
- Wang, W.; Yang, S.; Yang, Y. An improved data-efficiency algorithm based on combining isolation forest and mean shift for anomaly data filtering in wind power curve. Energies 2022, 15, 4918. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).