On the Performance of a Modified Triple Stack Blade Savonius Wind Turbine as a Function of Geometrical Parameters
Abstract
1. Introduction
2. Problem Description
3. Numerical Method
4. Governing Equations
4.1. Continuity
4.2. Momentum
5. Results and Discussion
5.1. Grid Independence and Validation Analyses
5.2. Impact of Adding Secondary Blades to the Main Blades
5.3. Impact of the Distance between the Main and Secondary Blades
5.4. Impact of Adding Secondary Blades with Slots in the Centerline of the Main Blades
5.5. Impact of the Angular Position (β) of the Secondary Blades and Slots
5.6. Impact of the Secondary Blade’s Profile (Secondary Blade’s Radius (R))
6. Conclusions and Future Scope
- A 50 mm-diameter simple triple-blade Savonius turbine with a wind velocity of 5 m/s was tested at various wind velocities of 3, 4, and 6 m/s. The results show that as the wind velocity increases, the output torque improves.
- For a wind velocity of 5 m/s, the maximum output torque, unlike the simple triple-blade Savonius rotor obtained at 30 and 60 degrees, was obtained at zero and 90 degrees. Furthermore, the results showed that the best performance of the turbine was achieved when the secondary blade was located at a distance of 6 mm.
- The output torque curve and the numerical results show that the area below the output torque diagram increased and turbine performance was enhanced despite the secondary blade. For example, at a velocity of 5 m/s and an angle of zero degrees, the output torque increased from about 0.009 to 0.088 Nm, and at an angle of 30 degrees, an improvement of about 33% was achieved. However, at 60 degrees, the values are different, and despite the secondary blade, the output torque decreases by nearly 125%. For a 90-degree angle, about 550% improvement was achieved.
- Due to the best position and the distance between the main and the auxiliary blade, which is equal to 6 mm, the effects of a slot on the main blade with different values of d = 4, 8, 12, and 16 mm to varying velocities of 3 to 6 m/s were investigated. The results showed that with increasing the width of the slot on the main blade from d = 4 mm to 16 mm, the output torque also increased. However, this increase has a positive effect only at a 90-degree angle.
- The best output torque curve is related to the effect of creating a slot on the main blade with a slot width of 16 mm and at different wind velocities of 3 to 6 m/s; a simple triple-blade Savonius rotor and a triple-blade Savonius rotor with the secondary blade were compared at four angles. The results showed that by creating a slot on the main blade, the surface below the output torque diagram is not improved, and creating a slot on the main blade reduces the performance of the turbine rotor.
- The output torque at the angle β = 130 degrees is higher than other angles. After that, the maximum torque is obtained at angles of β = 110 degrees, β = 70 degrees, and β = 50 degrees, respectively.
- By increasing the radius of the additional blade from R = 25 mm to 43 mm, the torque is improved, and the area below the output torque curve is increased.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Honarbari, A.; Najafi-Shad, S.; Saffari Pour, M.; Ajarostaghi, S.S.M.; Hassannia, A. MPPT Improvement for PMSG-Based Wind Turbines Using Extended Kalman Filter and Fuzzy Control System. Energies 2021, 14, 7503. [Google Scholar] [CrossRef]
- Olfian, H.; Ajarostaghi, S.S.M.; Ebrahimnataj, M.; Farhadi, M.; Arıcı, M. On the thermal performance of evacuated tube solar collector integrated with phase change material. Sustain. Energy Technol. Assess. 2022, 53, 102437. [Google Scholar] [CrossRef]
- Ajarostaghi, S.S.M.; Mousavi, S.S. Solar energy conversion technologies: Principles and advancements. In Solar Energy Advancements in Agriculture and Food Production Systems; Academic Press: Cambridge, MA, USA, 2022; pp. 29–76. [Google Scholar]
- Javadi, H.; Ajarostaghi, S.S.M.; Mousavi, S.S.; Pourfallah, M. Thermal analysis of a triple helix ground heat exchanger using numerical simulation and multiple linear regression. Geothermics 2019, 81, 53–73. [Google Scholar] [CrossRef]
- Mousavi Ajarostaghi, S.S.; Javadi, H.; Mousavi, S.S.; Poncet, S.; Pourfallah, M. Thermal performance of a single U-tube ground heat exchanger: A parametric study. J. Cent. South Univ. 2021, 28, 3580–3598. [Google Scholar] [CrossRef]
- O’Neill, S. Giant Turbines Poised to Claim Offshore Wind; Elsevier: Amsterdam, The Netherlands, 2021; pp. 894–896. [Google Scholar]
- Alipour, R.; Alipour, R.; Fardian, F.; Koloor, S.S.R.; Petrů, M. Performance improvement of a new proposed Savonius hydrokinetic turbine: A numerical investigation. Energy Rep. 2020, 6, 3051–3066. [Google Scholar] [CrossRef]
- Greig, C. Contemporary Research in Energy Science and Engineering. Engineering 2017, 3, 436–438. [Google Scholar] [CrossRef]
- Luhmann, T.; Wieben, E.; Treydel, R.; Stadler, M.; Kumm, T. An approach for cost-efficient grid integration of distributed renewable energy sources. Engineering 2015, 1, 447–452. [Google Scholar] [CrossRef][Green Version]
- Alipour, R.; Alipour, R.; Rahimian Koloor, S.S.; Petrů, M.; Ghazanfari, S.A. On the performance of small-scale horizontal axis tidal current turbines. Part 1: One single turbine. Sustainability 2020, 12, 5985. [Google Scholar] [CrossRef]
- Roy, S.; Saha, U.K. Review on the numerical investigations into the design and development of Savonius wind rotors. Renew. Sustain. Energy Rev. 2013, 24, 73–83. [Google Scholar] [CrossRef]
- Gao, X.; Li, B.; Wang, T.; Sun, H.; Yang, H.; Li, Y.; Wang, Y.; Zhao, F. Investigation and validation of 3D wake model for horizontal-axis wind turbines based on filed measurements. Appl. Energy 2020, 260, 114272. [Google Scholar] [CrossRef]
- Energy, G.W. Global Wind Energy Market Report Wind Energy Industry Grows at Steady Pace, Adds over 8,000 MW in 2003. Available online: https://www.osti.gov/biblio/836859-global-wind-energy-market-report-wind-energy-industry-grows-steady-pace-adds-over-mw (accessed on 23 May 2022).
- Anup, K.C.; Whale, J.; Urmee, T. Urban wind conditions and small wind turbines in the built environment: A review. Renew. Energy 2019, 131, 268–283. [Google Scholar]
- Lipian, M.; Dobrev, I.; Massouh, F.; Jozwik, K. Small wind turbine augmentation: Numerical investigations of shrouded-and twin-rotor wind turbines. Energy 2020, 201, 117588. [Google Scholar] [CrossRef]
- Menegozzo, L.; Dal Monte, A.; Benini, E.; Benato, A. Small wind turbines: A numerical study for aerodynamic performance assessment under gust conditions. Renew. Energy 2018, 121, 123–132. [Google Scholar] [CrossRef]
- Reinauer, T.; Hansen, U.E. Determinants of adoption in open-source hardware: A review of small wind turbines. Technovation 2021, 106, 102289. [Google Scholar] [CrossRef]
- Eriksson, S.; Bernhoff, H.; Leijon, M. Evaluation of different turbine concepts for wind power. Renew. Sustain. Energy Rev. 2008, 12, 1419–1434. [Google Scholar] [CrossRef]
- Savonius, S. The S-Roter and Its Applications. Mech. Eng. 1931, 53, 333–338. [Google Scholar]
- Morshed, K.N.; Rahman, M.; Molina, G.; Ahmed, M. Wind tunnel testing and numerical simulation on aerodynamic performance of a three-bladed Savonius wind turbine. Int. J. Energy Environ. Eng. 2013, 4, 1–14. [Google Scholar] [CrossRef]
- Ali, M.H. Experimental comparison study for Savonius wind turbine of two three blades at low wind speed. Int. J. Mod. Eng. Res. IJMER 2013, 3, 2978–2986. [Google Scholar]
- Debnath, P.; Gupta, R. Flow Physics Analysis of Three-Bucket Helical Savonius Rotor at Twist Angle Using CFD. Int. J. Mod. Eng. Res. 2013, 3, 739–746. [Google Scholar]
- Deb, B.; Gupta, R. Fluid flow analysis of Savonius rotor at different rotor angle using CFD. ISESCO J. Sci. Technol. 2012, 8, 35–42. [Google Scholar]
- Yoshida, Y.; Kawamura, T. Numerical simulations of two-dimensional flows around a Savonius rotor with various curvature of the blade. Nat. Sci. Rep. Ochanomizu Univ. 2012, 63, 11–21. [Google Scholar]
- McTavish, S.; Feszty, D.; Sankar, T. Steady and rotating computational fluid dynamics simulations of a novel vertical axis wind turbine for small-scale power generation. Renew. Energy 2012, 41, 171–179. [Google Scholar] [CrossRef]
- Brown, K.A.; Brooks, R. Design and analysis of vertical axis thermoplastic composite wind turbine blade. Plast. Rubber Compos. 2010, 39, 111–121. [Google Scholar] [CrossRef]
- Abdi, B.; Koloor, S.S.R.; Abdullah, M.R.; Amran, A.; Yahya, M.Y. Effect of strain-rate on flexural behavior of composite sandwich panel. Appl. Mech. Mater. 2012, 229, 766–770. [Google Scholar] [CrossRef]
- Kashyzadeh, K.R.; Koloor, S.S.R.; Bidgoli, M.O.; Petrů, M.; Asfarjani, A.A. An optimum fatigue design of polymer composite compressed natural gas tank using hybrid finite element-response surface methods. Polymers 2021, 13, 483. [Google Scholar] [CrossRef]
- Armstrong, S.; Fiedler, A.; Tullis, S. Flow separation on a high Reynolds number, high solidity vertical axis wind turbine with straight and canted blades and canted blades with fences. Renew. Energy 2012, 41, 13–22. [Google Scholar] [CrossRef]
- Armstrong, S.; Tullis, S. Power performance of canted blades for a vertical axis wind turbine. J. Renew. Sustain. Energy 2011, 3, 013106. [Google Scholar] [CrossRef]
- Chan, C.M.; Bai, H.L.; He, D.Q. Blade shape optimization of the Savonius wind turbine using a genetic algorithm. Appl. Energy 2018, 213, 148–157. [Google Scholar] [CrossRef]
- Ferrari, G.; Federici, D.; Schito, P.; Inzoli, F.; Mereu, R. CFD study of Savonius wind turbine: 3D model validation and parametric analysis. Renew. Energy 2017, 105, 722–734. [Google Scholar] [CrossRef]
- Kothe, L.B.; Möller, S.V.; Petry, A.P. Numerical and experimental study of a helical Savonius wind turbine and a comparison with a two-stage Savonius turbine. Renew. Energy 2020, 148, 627–638. [Google Scholar] [CrossRef]
- Mauro, S.; Brusca, S.; Lanzafame, R.; Messina, M. CFD modeling of a ducted Savonius wind turbine for the evaluation of the blockage effects on rotor performance. Renew. Energy 2019, 141, 28–39. [Google Scholar] [CrossRef]
- Bethi, R.V.; Laws, P.; Kumar, P.; Mitra, S. Modified Savonius wind turbine for harvesting wind energy from trains moving in tunnels. Renew. Energy 2019, 135, 1056–1063. [Google Scholar] [CrossRef]
- Mereu, R.; Federici, D.; Ferrari, G.; Schito, P.; Inzoli, F. Parametric numerical study of Savonius wind turbine interaction in a linear array. Renew. Energy 2017, 113, 1320–1332. [Google Scholar] [CrossRef]
- Sahim, K.; Santoso, D.; Puspitasari, D. Investigations on the effect of radius rotor in combined Darrieus-Savonius wind turbine. Int. J. Rotating Mach. 2018, 2018, 3568542. [Google Scholar] [CrossRef]
- Roshan, A.; Sagharichi, A.; Maghrebi, M.J. Nondimensional parameters’ effects on hybrid Darrieus–Savonius wind turbine performance. J. Energy Resour. Technol. 2020, 142, 011202. [Google Scholar] [CrossRef]
- Storti, B.A.; Dorella, J.J.; Roman, N.D.; Peralta, I.; Albanesi, A.E. Improving the efficiency of a Savonius wind turbine by designing a set of deflector plates with a metamodel-based optimization approach. Energy 2019, 186, 115814. [Google Scholar] [CrossRef]
- Calautit, K.; Aquino, A.; Calautit, J.K.; Nejat, P.; Jomehzadeh, F.; Hughes, B.R. A review of numerical modelling of multi-scale wind turbines and their environment. Computation 2018, 6, 24. [Google Scholar] [CrossRef]
- Zemamou, M.; Aggour, M.; Toumi, A. Review of savonius wind turbine design and performance. Energy Procedia 2017, 141, 383–388. [Google Scholar] [CrossRef]
- Ansys, F. 18.1 User Guide. Knowledge Resources: Online Documentation. Available online: https://www.ansys.com/academic/learning-resources (accessed on 23 May 2022).
- Saedodin, S.; Zaboli, M.; Ajarostaghi, S.S.M. Hydrothermal analysis of heat transfer and thermal performance characteristics in a parabolic trough solar collector with Turbulence-Inducing elements. Sustain. Energy Technol. Assess. 2021, 46, 101266. [Google Scholar] [CrossRef]
- Ajarostaghi, S.S.M.; Zaboli, M.; Nourbakhsh, M. Numerical evaluation of turbulence heat transfer and fluid flow of hybrid nanofluids in a pipe with innovative vortex generator. J. Therm. Anal. Calorim. 2021, 143, 1583–1597. [Google Scholar] [CrossRef]
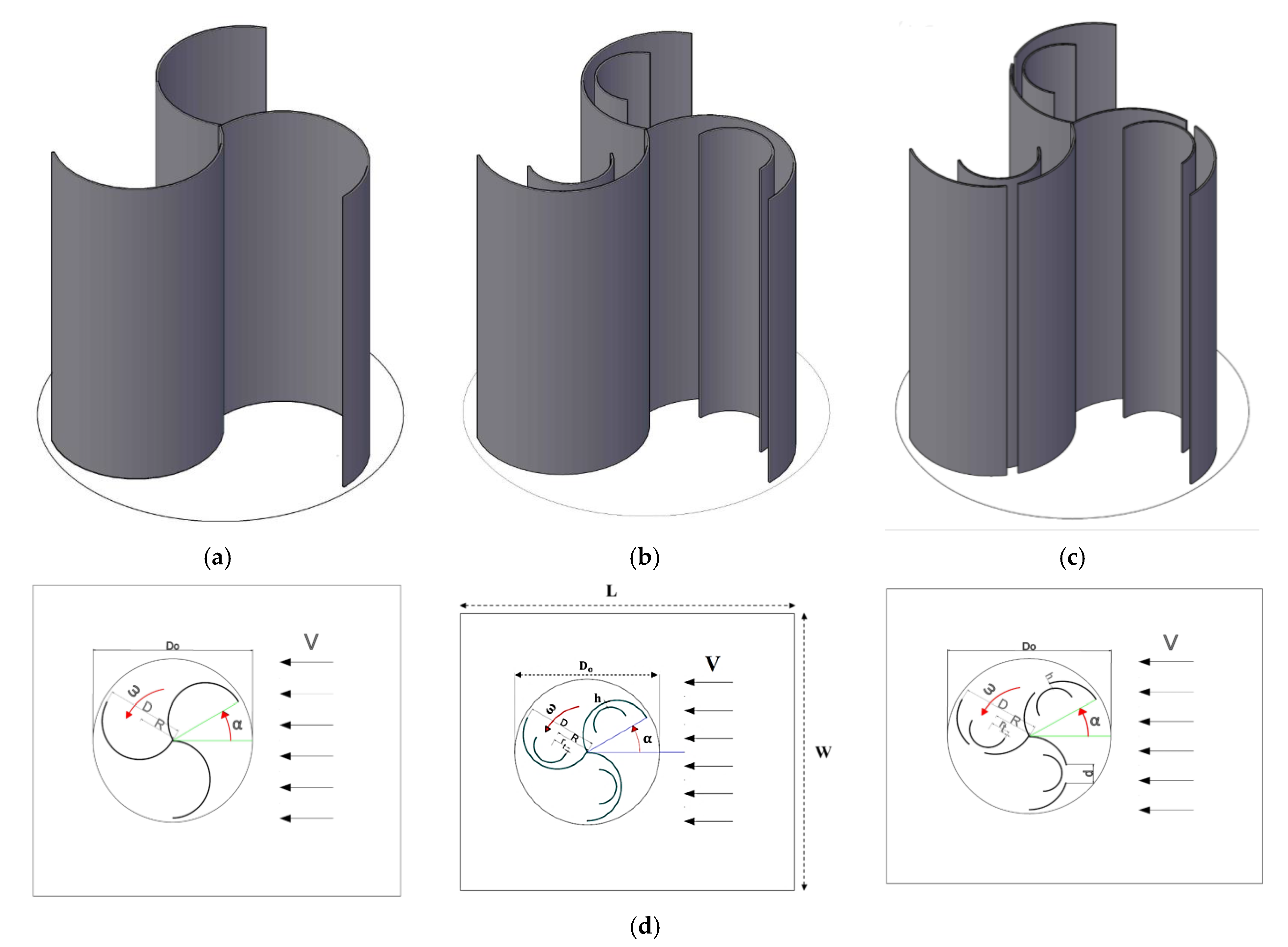



























| Parameters | Value | |
|---|---|---|
| Length of the computational domain | L | 1700 mm |
| Width of the computational domain | W | 1000 mm |
| Inlet velocity of the wind | V | 3-4-5-6 m/s |
| The rotation angle of blades | α | 0-30-60-90 degrees |
| Angular velocity | 16-32-44-52 rad/s | |
| Diameter of rotating area | 210 mm | |
| The outer diameter of the main blades | D | 100 mm |
| The outer radius of the main blades | R | 50 mm |
| The outer radius of secondary blades | r | 25 mm |
| Thickness of blades | t | 1 mm |
| Distance between the two blades | h | 6-12-18-24 mm |
| Width of the slot | d | 4-8-12-16 mm |
| Angle of Attack (α) | Cts Experimental [21] | Cts Numerical | Error [%] | Ts Experimental [21] | Ts Numerical | Error [%] |
|---|---|---|---|---|---|---|
| 0 degree | 0.18 | 0.1805 | 0.2 | 0.0108 | 0.0107 | −0.9 |
| 30 degrees | 0.48 | 0.4827 | 0.5 | 0.0285 | 0.0286 | 0.3 |
| 60 degrees | 0.55 | 0.5451 | −0.8 | 0.0326 | 0.0323 | −0.9 |
| 90 degrees | 0.22 | 0.2161 | −1.7 | 0.013 | 0.0128 | −1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Norouztabar, R.; Mousavi Ajarostaghi, S.S.; Mousavi, S.S.; Nejat, P.; Rahimian Koloor, S.S.; Eldessouki, M. On the Performance of a Modified Triple Stack Blade Savonius Wind Turbine as a Function of Geometrical Parameters. Sustainability 2022, 14, 9816. https://doi.org/10.3390/su14169816
Norouztabar R, Mousavi Ajarostaghi SS, Mousavi SS, Nejat P, Rahimian Koloor SS, Eldessouki M. On the Performance of a Modified Triple Stack Blade Savonius Wind Turbine as a Function of Geometrical Parameters. Sustainability. 2022; 14(16):9816. https://doi.org/10.3390/su14169816
Chicago/Turabian StyleNorouztabar, Reza, Seyed Soheil Mousavi Ajarostaghi, Seyed Sina Mousavi, Payam Nejat, Seyed Saeid Rahimian Koloor, and Mohamed Eldessouki. 2022. "On the Performance of a Modified Triple Stack Blade Savonius Wind Turbine as a Function of Geometrical Parameters" Sustainability 14, no. 16: 9816. https://doi.org/10.3390/su14169816
APA StyleNorouztabar, R., Mousavi Ajarostaghi, S. S., Mousavi, S. S., Nejat, P., Rahimian Koloor, S. S., & Eldessouki, M. (2022). On the Performance of a Modified Triple Stack Blade Savonius Wind Turbine as a Function of Geometrical Parameters. Sustainability, 14(16), 9816. https://doi.org/10.3390/su14169816









