Carbon Emission Reduction Cost Assessment Using Multiregional Computable General Equilibrium Model: Guangdong–Hong Kong–Macao Greater Bay Area
Abstract
:1. Introduction
2. Methods and Data
2.1. Guangdong Province IO Table Decomposition
2.1.1. Data Sources and Industry Breakdown
2.1.2. Data Decomposition
2.2. Model Building
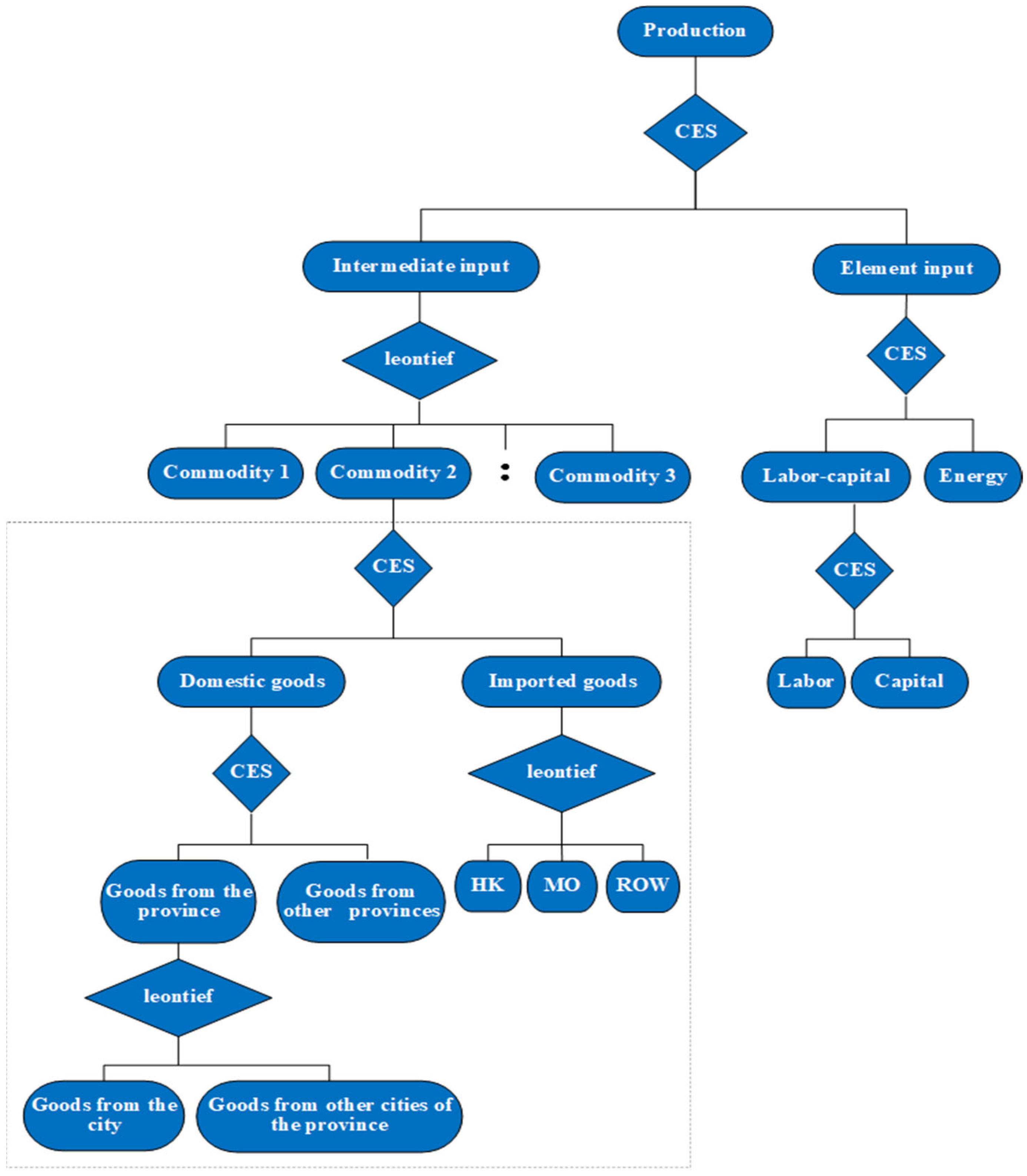
2.2.1. Basic Modules
Production Modules
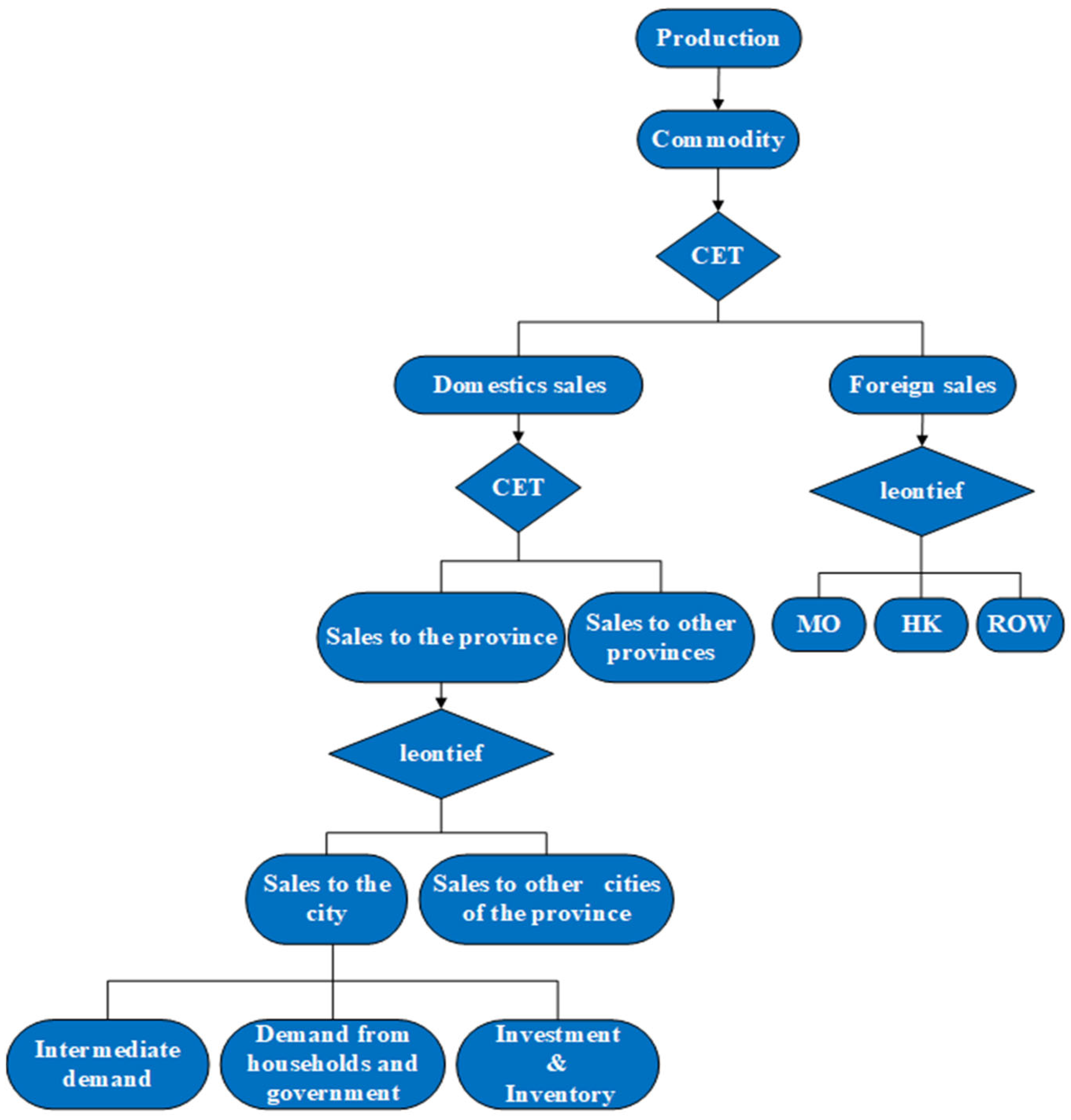
Trade Module
Income and Expense Module
Balance and Macro-Closure Modules
2.2.2. Carbon Tax/Trading Policy Module
2.3. Parameter Setting and Model Validation
3. Analysis and Discussion
3.1. Scheme Settings
3.2. Analysis of Results
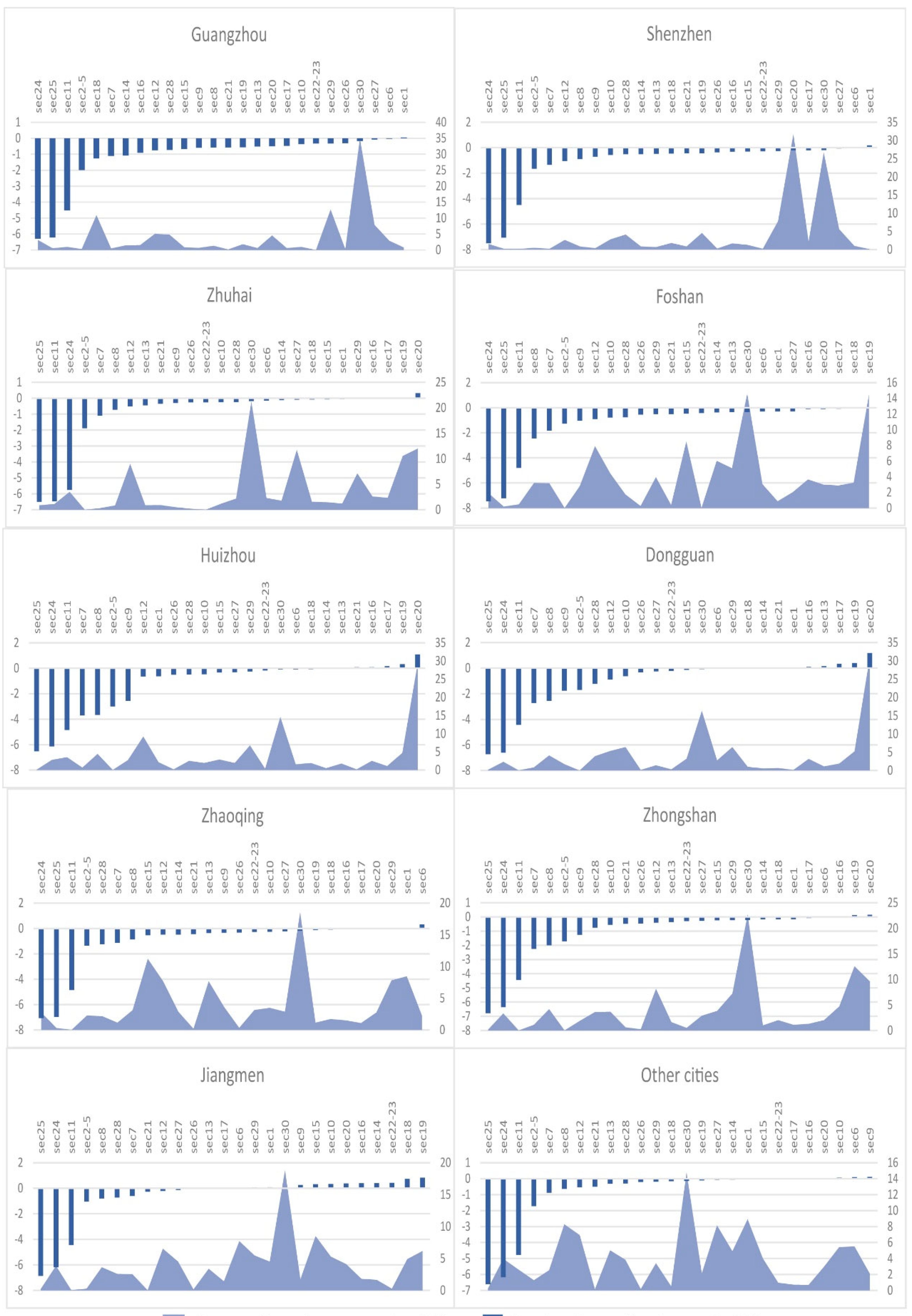
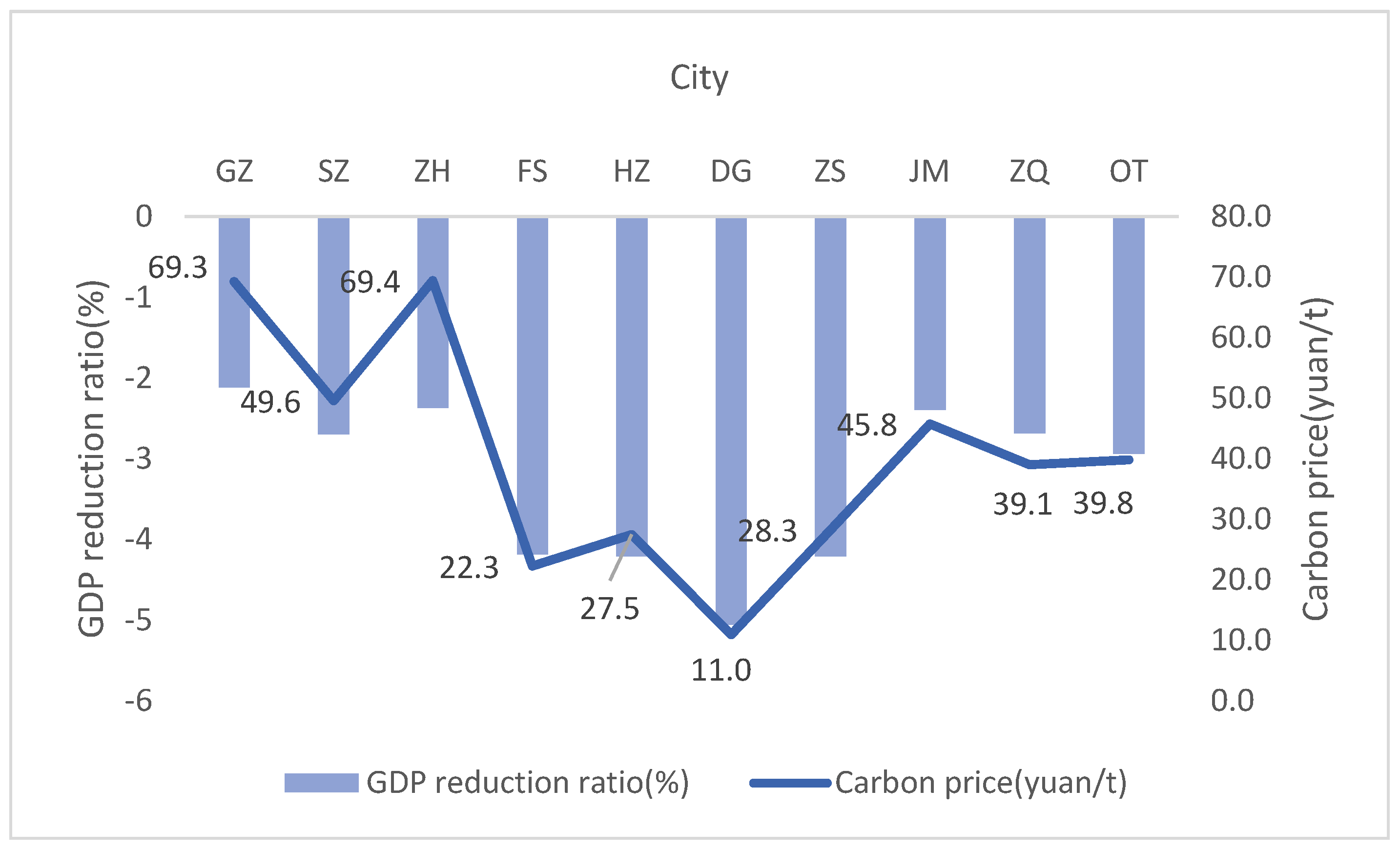
3.2.1. Characteristics of Carbon Emissions Reduction Costs (i.e., Carbon Prices) in Each City
3.2.2. Economic Impact of Carbon Emissions Reduction on Each City
Macroeconomic Impact
Microeconomic Impact
Guangzhou (GZ)
Shenzhen (SZ)
Zhuhai (ZH)
Foshan (FS)
Huizhou (HZ)
Dongguan (DG)
Zhongshan (ZS)
Jiangmen (JM)
Zhaoqing (ZQ)
3.2.3. Comparison with Related Studies
3.3. Uncertainty Analysis
3.3.1. Impact of Energy–Labor and Capital Substitution Elasticity
3.3.2. Analysis of the Influence of Macroscopic Closure Conditions
4. Conclusions and Suggestions
- The carbon price of each city is positively correlated with the intensity of emissions reduction but is negatively correlated with the carbon intensity. Meanwhile, the carbon price of each city is affected by its own industrial and trade structure. Cities with high carbon intensity (e.g., Zhaoqing, Jiangmen, and Foshan) are sensitive to carbon prices (i.e., low carbon prices lead to low direct emissions reduction costs). Otherwise, cities with low carbon intensities (e.g., Guangzhou, Shenzhen, Zhuhai, Huizhou, Dongguan, and Zhongshan) are relatively insensitive to carbon prices (i.e., relatively high carbon prices lead to high direct emissions reduction costs when the same emissions reduction is reached). Additionally, the intensity of trade also has a certain impact on carbon prices. Cities with large trade volumes are more sensitive to carbon prices because they increase the cost of products and have a greater impact on supply and demand (e.g., Shenzhen and Dongguan).
- Increasing the substitution elasticity of energy–labor and capital reduces the carbon price and the opportunity cost of carbon reduction. Carbon prices are also affected by macro-closure conditions. Under Keynesian closure conditions, carbon prices are negatively correlated with the degree of economic impact on cities, and those with greater impact are more sensitive to carbon prices with lower carbon prices at the same emissions reduction rate.
- The economic impacts of carbon emissions reduction on cities have similarities and differences. Under neoclassical conditions, owing to the influence of carbon prices, the production costs of most sectors increase, and demand decreases accordingly. Thus, the total social output value, GDP, import and export, government income, and household consumption of most cities decrease. A few cities (e.g., Dongguan and Jiangmen) enjoy GDP increases because carbon emissions reduction causes labor and capital to transfer to low-carbon industries, and those sectors play a role in supporting the main industries of the city. Thus, the overall GDP increases. Under Keynesian conditions, all industries are generally impacted, with carbon- and trade-intensive sectors being the most affected. No industry benefits from emissions reductions, but sectors with less trade are relatively less affected.
- The allocation of city-level carbon quotas should consider the current energy and industrial structural characteristics of cities, while considering the emissions reduction costs of each. Cities sensitive to carbon prices should not aim too high (e.g., Foshan).
- Moderate subsidies and support should be given to high-carbon energy industries, which are greatly affected during carbon emissions reduction, to ensure the stability and orderly optimization of their economic structures.
- For trade-oriented cities, because they are relatively sensitive to carbon prices, special attention should be paid to the low-carbon support and guidance of the leading trade industries (e.g., Shenzhen and Dongguan).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Values | Description |
|---|---|---|
| 0.3 | Substitution elasticity of intermediate input and labor-capital bundle | |
| 0.2 | Substitution elasticity of labor-capital bundle | |
| 0.2 | Substitution elasticity of energy&labor-capital bundle | |
| 0.6 | Substitution elasticity of domestic commodity and import commodity under the Armington condition. | |
| 1.4 | Substitution elasticity of domestic commodity and export commodity in the CET function. |
| GDP | Government Revenue | Resident Income | Enterprise Income | Imports | Transfer-in | Provincial Supply | Exports | Transfer-out | ||
|---|---|---|---|---|---|---|---|---|---|---|
| G Z | simulated | 19,957 | 3099 | 9374 | 5200 | 3921 | 11,221 | 4173 | 5792 | 8240 |
| real | 19,955 | 3099 | 9373 | 5200 | 3923 | 11,226 | 4166 | 5794 | 8249 | |
| S Z | simulated | 21,621 | 3176 | 10,643 | 5402 | 11,512 | 16,656 | 5133 | 16,590 | 13,781 |
| real | 21,581 | 3170 | 10,622 | 5392 | 11,473 | 16,621 | 5131 | 16,528 | 13,744 | |
| Z H | simulated | 2594 | 413 | 1245 | 667 | 1109 | 2334 | 252 | 1887 | 1609 |
| real | 2590 | 413 | 1243 | 666 | 1107 | 2331 | 251 | 1883 | 1606 | |
| F S | simulated | 9633 | 1563 | 4382 | 2635 | 1214 | 9509 | 545 | 3196 | 8408 |
| real | 9579 | 1554 | 4357 | 2620 | 1204 | 9459 | 559 | 3155 | 8338 | |
| H Z | simulated | 3884 | 648 | 1925 | 933 | 1187 | 4211 | 1300 | 2238 | 4084 |
| real | 3871 | 646 | 1918 | 930 | 1183 | 4201 | 1297 | 2233 | 4064 | |
| D W | simulated | 8276 | 1258 | 4105 | 2036 | 5297 | 6323 | 130 | 6984 | 7020 |
| real | 8324 | 1266 | 4129 | 2047 | 5328 | 6354 | 125 | 7027 | 7073 | |
| Z S | simulated | 3076 | 464 | 1477 | 790 | 529 | 3790 | 88 | 2074 | 2523 |
| real | 3059 | 462 | 1469 | 786 | 526 | 3768 | 87 | 2056 | 2505 | |
| J M | simulated | 2504 | 381 | 1250 | 612 | 308 | 3494 | 664 | 1068 | 2751 |
| real | 2514 | 383 | 1255 | 615 | 309 | 3509 | 669 | 1076 | 2770 | |
| Z Q | simulated | 2173 | 304 | 1146 | 513 | 135 | 2650 | 230 | 223 | 2344 |
| real | 2172 | 304 | 1145 | 513 | 136 | 2649 | 229 | 222 | 2341 | |
| O T | simulated | 15,006 | 2236 | 8014 | 3313 | 7124 | 8620 | 7448 | 4837 | 9420 |
| real | 15,002 | 2235 | 8011 | 3312 | 7122 | 8619 | 7448 | 4836 | 9416 | |
Appendix B
Appendix B.1. Equations
Appendix B.2. Parameters and Variables Symbol Description
| Activity department | |
| Commercial department | |
| No-energy commercial department | |
| Energy commercial department | |
| Regions | |
| The region whose labor price is taken as the “price base” | |
| Regions other than nn1 | |
| Share parameter of CES function of QA | |
| Share parameter of CES function of QEVA | |
| Share parameter of CES function of QVA | |
| Share parameter of CET function of QQ | |
| Share parameter of CET function of QDAT | |
| Share parameter of Armington function of QQ | |
| Share parameter of Armington function of QDC | |
| Government expend | |
| Investment | |
| Enterprise saving | |
| Exchange rate | |
| Foreign saving | |
| Real gross domestic product | |
| Government saving | |
| Consumption coefficient of non-energy product | |
| Consumption coefficient of energy product | |
| Marginal propensity to consume | |
| Price of product a | |
| Price of commodity for domestic use | |
| Price of commodity for use in the region | |
| Price of commodity for use out of the province | |
| Price of commodity for use in other regions of the province | |
| Price of commodity from domestic product | |
| Price of commodity from provincial product | |
| Price of commodity from out of the province | |
| Price of commodity for export | |
| Price of import commodity | |
| Price index of GDP | |
| Price of intermediate input | |
| Price of commodity in the market | |
| Price of the added value | |
| Price of the bundle of energy and added value | |
| World price of commodity for out-port | |
| World price of commodity for in-port | |
| Quantity of product a | |
| Quantity of product trading among the regions | |
| Quantity of commodity for export | |
| Demand of energy bundle | |
| Total supply of energy | |
| Demand of government for commodity c | |
| Demand of habitant for commodity c | |
| Department quantity of intermediate input | |
| Total quantity of intermediate input | |
| Final demand of investment for commodity c | |
| Quantity of commodity for domestic use | |
| Quantity of commodity for regional use | |
| Quantity of commodity for use out of the province | |
| Quantity of commodity for use in other regions of the province | |
| Quantity of commodity from domestic product | |
| Quantity of commodity from the province | |
| Quantity of commodity from other provinces | |
| Demand for capital | |
| Supply of capital | |
| Demand for labor | |
| Supply of labor | |
| Quantity of commodity import | |
| Quantity of commodity in the market | |
| Quantity of added value | |
| Quantity of the bundle of energy and added-value | |
| Power parameter of CES function of QA | |
| Power parameter of CES function of QEVA | |
| Power parameter of CES function of QVA | |
| Power parameter of Armington function of QQ | |
| Power parameter of Armington function of QDC | |
| Power parameter of CET function of QA | |
| Power parameter of CET function of QDAT | |
| Scale parameter of CES function of QA | |
| Scale parameter of CES function of QEVA | |
| Scale parameter of CES function of VA | |
| Scale parameter of CET function of QA | |
| Scale parameter of CET function of QDAT | |
| Scale parameter of Armington function of QQ | |
| Scale parameter of Armington function of QDC | |
| Share of capital revenue to enterprise | |
| Share of capital revenue to habitant | |
| Expanding share of habitant revenue to commodity c | |
| Export subsidy rate | |
| Income tax of enterprise | |
| Income tax of habitant | |
| Tariff of commodity c | |
| Transferred revenue from government to enterprise | |
| Transferred revenue from government to habitant | |
| Trade matrix among the regions | |
| Indirect tax for department a | |
| Energy tax for department a | |
| Price of fixed energy | |
| Price of capital | |
| Price of labor | |
| Enterprise revenue | |
| Government revenue | |
| Habitant revenue |
References
- Kyoto Protocol to the United Nations Framework Convention on Climate Change. Available online: https://unfccc.int/process-and-meetings/the-kyoto-protocol/history-of-the-kyoto-protocol/text-of-the-kyoto-protocol (accessed on 24 July 2022).
- Paris Agreement. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement (accessed on 24 July 2022).
- EU Emissions Trading System (EU ETS). Available online: https://icapcarbonaction.com/en/ets/eu-emissions-trading-system-eu-ets (accessed on 24 July 2022).
- He, X. Regional differences in China’s CO2 abatement cost. Energy Policy 2015, 80, 145–152. [Google Scholar] [CrossRef]
- Jiang, J.; Xie, D.; Ye, B.; Shen, B.; Chen, Z. Research on China’s cap-and-trade carbon emission trading scheme: Overview and outlook. Appl. Energy 2016, 178, 902–917. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Feng, C. Marginal abatement costs of carbon dioxide emissions and its influencing factors: A global perspective. J. Clean. Prod. 2018, 170, 1433–1450. [Google Scholar] [CrossRef]
- China’s Achievements in Implementing National Independent Contributions and New Goals and Measures. Available online: http://us.china-embassy.gov.cn/zt_1/ydqhbh/202111/P020211106160885316810.pdf (accessed on 24 July 2022). (In Chinese)
- Outline of the 14th Five-Year Plan for National Economic and Social Development of Guangdong Province and the Long-term Goals for 2035. Available online: https://www.gd.gov.cn/zwgk/wjk/qbwj/yf/content/post_3268751.html (accessed on 24 July 2022). (In Chinese)
- Zhou, J.-F.; Wu, D.; Chen, W. Cap and Trade Versus Carbon Tax: An Analysis Based on a CGE Model. Comput. Econ. 2021, 59, 853–885. [Google Scholar] [CrossRef]
- Van den Bergh, K.; Delarue, E. Quantifying CO2 abatement costs in the power sector. Energy Policy 2015, 80, 88–97. [Google Scholar] [CrossRef]
- Kong, L.; Hasanbeigi, A.; Price, L.; Liu, H. Energy conservation and CO2 mitigation potentials in the Chinese pulp and paper industry. Resour. Conserv. Recycl. 2017, 117, 74–84. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Wu, J.-H. Bottom-up analysis of energy efficiency improvement and CO2 emission reduction potentials in the cement industry for energy transition: An application of extended marginal abatement cost curves. J. Clean. Prod. 2021, 296, 126619. [Google Scholar] [CrossRef]
- Wang, K.; Wei, Y.-M. China’s regional industrial energy efficiency and carbon emissions abatement costs. Appl. Energy 2014, 130, 617–631. [Google Scholar] [CrossRef]
- Yang, L.; Tang, K.; Wang, Z.; An, H.; Fang, W. Regional eco-efficiency and pollutants’ marginal abatement costs in China: A parametric approach. J. Clean. Prod. 2017, 167, 619–629. [Google Scholar] [CrossRef]
- Huang, S.K.; Kuo, L.; Chou, K.-L. The applicability of marginal abatement cost approach: A comprehensive review. J. Clean. Prod. 2016, 127, 59–71. [Google Scholar] [CrossRef]
- Wang, P.; Dai, H.-c.; Ren, S.-y.; Zhao, D.-q.; Masui, T. Achieving Copenhagen target through carbon emission trading: Economic impacts assessment in Guangdong Province of China. Energy 2015, 79, 212–227. [Google Scholar] [CrossRef]
- Wu, R.; Dai, H.; Geng, Y.; Xie, Y.; Masui, T.; Tian, X. Achieving China’s INDC through carbon cap-and-trade: Insights from Shanghai. Appl. Energy 2016, 184, 1114–1122. [Google Scholar] [CrossRef]
- Cui, L.; Fan, Y.; Zhu, L.; Bi, Q. How will the emissions trading scheme save cost for achieving China’s 2020 carbon intensity reduction target? Appl. Energy 2014, 136, 1043–1052. [Google Scholar] [CrossRef]
- Tang, B.-J.; Ji, C.-J.; Hu, Y.-J.; Tan, J.-X.; Wang, X.-Y. Optimal carbon allowance price in China’s carbon emission trading system: Perspective from the multi-sectoral marginal abatement cost. J. Clean. Prod. 2020, 253, 119945. [Google Scholar] [CrossRef]
- Wu, J.; Fan, Y.; Timilsina, G.; Xia, Y.; Guo, R. Understanding the economic impact of interacting carbon pricing and renewable energy policy in China. Reg. Environ. Chang. 2020, 20, 74. [Google Scholar] [CrossRef]
- Kim, E.; Kim, K. Impacts of regional development strategies on growth and equity of Korea: A multiregional CGE model. Ann. Reg. Sci. 2002, 36, 165–180. [Google Scholar] [CrossRef]
- Development Prospects Group (DECPG). Linkage Technical Reference Document, Version 6.0; The World Bank: Washington, DC, USA, 2005. [Google Scholar]
- Hertel, T.W. Global Trade Analysis: Modeling and Applications. Master’s Thesis, Cambridge University Press, Cambridge, UK, 1997. [Google Scholar]
- Horridge, M.; Madden, J.; Witter, G. Using a highly disaggregated multiregional single-country model to analyze the impacts of the 2002-03 drought on Australia. J. Policy Model. 2005, 27, 285–308. [Google Scholar] [CrossRef]
- Yuan, Y.-N.; Li, N.; Shi, M.-J. Construction of China’s multi regional CGE model and its application in carbon trading policy simulation. Math. Pract. Theory 2016, 46, 106–116. (In Chinese) [Google Scholar]
- Pang, J.; Timilsina, G. How would an emissions trading scheme affect provincial economies in China: Insights from a computable general equilibrium model. Renew. Sustain. Energy Rev. 2021, 145, 111034. [Google Scholar] [CrossRef]
- Hou, H.-P. Research on the Construction and Influencing Factors of High-Quality Development Evaluation Indicators in the Guangdong-Hong Kong-Macao Greater Bay Area. Master’s Thesis, Guangdong University of Foreign Studies, Guangzhou, China, 2020. (In Chinese). [Google Scholar]
- The State Council’s Proposal on Printing and Distributing the 13th Five-Year Plan Notification of the Work Programme for the Control of Greenhouse Gas Emissions. Available online: http://www.gov.cn/zhengce/content/2016-11/04/content_5128619.htm (accessed on 24 July 2022). (In Chinese)
- Bian, Y. The Guangdong-Hong Kong-Macao Greater Bay Area Can Take the Lead in Achieving carbon neutrality. China Open. J. 2021, 3, 105–112. (In Chinese) [Google Scholar] [CrossRef]
- Progress, Challenge and Trend of Carbon Market in Guangdong. Available online: https://www.efchina.org/Reports-zh/report-lceg-20220427-zh (accessed on 24 July 2022). (In Chinese).
- China—Guangdong Pilot ETS. Available online: https://icapcarbonaction.com/en/ets/china-guangdong-pilot-ets (accessed on 24 July 2022).
- China—Shenzhen Pilot ETS. Available online: https://icapcarbonaction.com/en/ets/china-shenzhen-pilot-ets (accessed on 24 July 2022).
- Liu, L.; Sun, X.; Chen, C.; Zhao, E. How will auctioning impact on the carbon emission abatement cost of electric power generation sector in China? Appl. Energy 2016, 168, 594–609. [Google Scholar] [CrossRef]
- Schmidt, R.C.; Heitzig, J. Carbon leakage: Grandfathering as an incentive device to avert firm relocation. J. Environ. Econ. Manag. 2014, 67, 209–223. [Google Scholar] [CrossRef]
- Yi, W.-J.; Zou, L.-L.; Guo, J.; Wang, K.; Wei, Y.-M. How can China reach its CO2 intensity reduction targets by 2020? A regional allocation based on equity and development. Energy Policy 2011, 39, 2407–2415. [Google Scholar] [CrossRef]
- Zetterberg, L.; Wrake, M.; Sterner, T.; Fischer, C.; Burtraw, D. Short-run allocation of emissions allowances and long-term goals for climate policy. Ambio 2012, 41 (Suppl. S1), 23–32. [Google Scholar] [CrossRef]
- Data Reading Bay Area: Analysis on the Proportion of Import and Export Trade in Guangdong-Hong Kong-Macao Greater Bay Area. Available online: https://www.sohu.com/a/361857235_120303032 (accessed on 24 July 2022). (In Chinese).
- Analysis Report on the Statistical Indicator System for the Moderate and Diversified Development of Macao’s Economy in 2018. Available online: http://www.dsec.gov.mo/Statistic/General/SIED/2018.aspx?lang=zh-CN (accessed on 24 July 2022). (In Chinese)
- Chen, W.; Zhou, J.-F.; Li, S.-Y.; Li, Y.-C. Effects of an Energy Tax (Carbon Tax) on Energy Saving and Emission Reduction in Guangdong Province-Based on a CGE Model. Sustainability 2017, 9, 681. [Google Scholar] [CrossRef]
- Zhang, M.; Fan, J.; Zhou, Y.-H. Compilation and updating of input-output tables for multiple regions within a province: A case study of Jiangsu Province. Stat. Res. 2008, 7, 74–81. (In Chinese) [Google Scholar] [CrossRef]
- Zhou, J.; Liu, L.; Chen, W.; Wu, D. Study on implied carbon transfer in Guangdong Hong Kong Macao Great Bay Area. In Research Report on Ecological Civilization and Low Carbon Development in Guangdong Province; Fu, J., Ed.; Sun Yat-sen University: Guangzhou, China, 2020; pp. 113–123. (In Chinese) [Google Scholar]


| Sector | Code | Carbon Intensity | Sector | Code | Carbon Intensity |
|---|---|---|---|---|---|
| Farming, Forestry, Animal Husbandry and Fisheries (AGRI) | 1 | 0.28 (LC) | Manufacture of General-purpose (GEP) | 16 | 0.31 (LC) |
| Mining and Washing of Coal (COAL) | 2 | 2.54 (HC) | Manufacture of Special-purpose (SPP) | 17 | 0.33 (LC) |
| Extraction of Petroleum and Natural Gas (GAS) | 3 | 0.63 (MC) | Manufacture of Transport Equipment (TRE) | 18 | 0.33 (LC) |
| Mining and Dressing of Metal Ores (MDM) | 4 | 0.64 (MC) | Manufacture of Electrical Machinery and Equipment (EME) | 19 | 0.38 (LC) |
| Mining and Dressing of Nonmetal Ores (MDNM) | 5 | 0.46 (LC) | Manufacture of Communication Equipment/Computers (CEC) | 20 | 0.36 (LC) |
| Manufacture of Food and Tobacco (FOOD) | 6 | 0.48 (LC) | Manufacture of Instruments and Meters (I&M) | 21 | 0.46 (LC) |
| Textile Industry (TXT) | 7 | 1.63 (HC) | Other Manufactures and Waste (O&M) | 22 | 0.18 (LC) |
| Manufacture of Textile Garments (TXTG) | 8 | 0.39 (LC) | Manufacture of Metal Products, Machinery (M&M) | 23 | 0.19 (LC) |
| Manufacture of Furniture, Timber Processing (FUTI) | 9 | 0.42 (LC) | Production and Supply of Electric Power and Heat Power (EPHP) | 24 | 2.73 (HC) |
| Papermaking, Printing, and Manufacture of Cultural (PPC) | 10 | 1.43 (MC) | Production and Supply of Gas (SGAS) | 25 | 0.56 (MC) |
| Petroleum Refining, Coking, and Nuclear Fuel (PCN) | 11 | 4.13 (HC) | Production and Supply of Water (SWAT) | 26 | 1.27 (MC) |
| Manufacture of Chemical Products (CMC) | 12 | 1.21 (MC) | Construction (CNS) | 27 | 0.55 (MC) |
| Nonmetal Mineral Products (NMM) | 13 | 4.75 (HC) | Transport, Storage, and Post (TSP) | 28 | 2.11 (HC) |
| Smelting and Pressing of Metals (SPM) | 14 | 3.24 (HC) | Wholesale, Retail Trade and Hotel, Restaurants (WRHR) | 29 | 0.32 (LC) |
| Metal Products (MPR) | 15 | 0.63 (MC) | Others (OTS) | 30 | 0.09 (LC) |
| Reduction intensity | s1: The emissions reduction rate of each city is 3%, representing the average annual emissions reduction intensity under the emissions reduction target. s2: The emissions reduction rate of each city is 5%, representing the situation of high emissions reduction intensity in a year. s3: The emissions reduction rate of each city is 10%, representing a situation in which the intensity of emissions reduction is very high in a year. |
| Substitution elasticity | ρ1 = 0.1; ρ2 = 0.2; ρ3 = 0.3. |
| Macro-closure | c1: Neoclassical macro-closure: The quantity of labor and capital is exogenous, and the price is endogenous; the quantity of energy is exogenous, and the price is endogenous. c2: Keynes closure; labor and capital prices are exogenous, set to 1, and the quantity is endogenous; The quantity of energy is exogenous, and the price is endogenous. |
| City | QA | GDP | QDAL | QDAP | QE | QDCL | QDCP | QM | YG | QH |
|---|---|---|---|---|---|---|---|---|---|---|
| GZ | −0.69 | −0.22 | −0.65 | −1.05 | −0.72 | −0.77 | −0.60 | −0.62 | −0.49 | −0.08 |
| SZ | −0.42 | −0.11 | −0.47 | −0.44 | −0.40 | −0.46 | −0.54 | −0.27 | −0.32 | −0.31 |
| ZH | −0.45 | −0.10 | −0.43 | −0.38 | −0.42 | −0.43 | −0.14 | −0.99 | −0.52 | −0.28 |
| FS | −0.66 | −0.24 | −0.66 | −0.66 | −0.11 | −0.68 | −0.48 | −0.20 | −0.56 | −0.51 |
| HZ | −0.42 | −0.16 | −0.39 | 0.15 | −1.36 | −0.33 | −0.80 | 0.40 | −0.76 | −0.27 |
| DG | −0.09 | 0.14 | −0.16 | 0.20 | −0.50 | −0.11 | −0.42 | −0.10 | −0.09 | −0.07 |
| ZS | −0.51 | −0.12 | −0.53 | −0.55 | 0.08 | −0.53 | −0.31 | −0.02 | −0.37 | −0.35 |
| JM | −0.15 | 0.28 | −0.22 | 0.21 | 0.22 | −0.13 | 0.02 | 0.13 | −0.10 | 0.00 |
| ZQ | −0.53 | −0.05 | −0.51 | −0.42 | −0.36 | −0.52 | −0.41 | −0.20 | −0.41 | −0.28 |
| OT | −0.58 | −0.07 | −0.51 | −0.42 | −0.11 | −0.50 | −0.37 | −0.39 | −0.77 | −0.29 |
| City | Output | Trade | Most Affected | Less Affected | ||||
|---|---|---|---|---|---|---|---|---|
| Sector | Ratio (%) | Sector | Ratio (%) | Sector | Ratio (%) | Sector | Ratio (%) | |
| GZ | OTS | 34.86 | TRE | 29.01 | EPHP | −6.3 | SWAT | −0.3 |
| WRHR | 12.63 | WRHR | 17.46 | SGAS | −6.21 | OTS | −0.17 | |
| TRE | 10.91 | CEC | 6.79 | PCN | −4.52 | CNS | −0.07 | |
| CNS | 7.84 | NMM | 6.4 | MINE | −1.99 | FOOD | −0.03 | |
| CMC | 5.11 | MPR | 4.6 | TRE | −1.26 | AGRI | 0.05 | |
| SZ | CEC | 31.69 | CEC | 43.84 | EPHP | −7.51 | SPP | −0.2 |
| OTS | 26.65 | CMC | 11.34 | SGAS | −7.07 | OTS | −0.2 | |
| WRHR | 7.78 | WRHR | 9.35 | PCN | −4.5 | CNS | −0.07 | |
| CNS | 5.57 | EME | 5.45 | MINE | −1.66 | FOOD | 0.03 | |
| EME | 4.54 | FOOD | 4.3 | TXT | −1.35 | AGRI | 0.18 | |
| ZH | OTS | 21.17 | EME | 23.44 | SGAS | −6.5 | WRHR | −0.05 |
| CEC | 11.99 | CEC | 22.7 | PCN | −6.47 | GEP | 0 | |
| CNS | 11.7 | WRHR | 10.06 | EPHP | −5.77 | SPP | 0.01 | |
| EME | 10.53 | PCN | 6.55 | MINE | −1.88 | EME | 0.04 | |
| CMC | 8.97 | NMM | 6.37 | TXT | −1.1 | CEC | 0.31 | |
| FS | OTS | 14.56 | EME | 36.98 | EPHP | −7.46 | GEP | −0.12 |
| EME | 14.41 | CEC | 10.8 | SGAS | −7.22 | CEC | −0.11 | |
| MPR | 8.45 | MPR | 9.71 | PCN | −4.81 | SPP | −0.08 | |
| CMC | 7.87 | PPC | 8.79 | TXTG | −2.46 | TRE | −0.07 | |
| SPM | 6.02 | TRE | 5.84 | TXT | −1.83 | EME | 0.01 | |
| HZ | CEC | 29.06 | CEC | 29.62 | SGAS | −6.52 | I&M | 0.08 |
| OTS | 14.57 | OTS | 16.22 | EPHP | −6.14 | GEP | 0.08 | |
| CMC | 9.19 | TXTG | 13.28 | PCN | −4.85 | SPP | 0.16 | |
| WRHR | 6.76 | EME | 6.78 | TXT | −3.71 | EME | 0.32 | |
| EME | 4.69 | FOOD | 6.21 | TXTG | −3.66 | CEC | 1.08 | |
| DG | CEC | 30.91 | CEC | 25.44 | SGAS | −6.73 | GEP | 0.1 |
| OTS | 16.31 | EME | 10.27 | EPHP | −6.61 | NMM | 0.15 | |
| WRHR | 6.43 | GEP | 9.94 | PCN | −4.42 | SPP | 0.33 | |
| PPC | 6.4 | TSP | 8.45 | TXT | −2.72 | EME | 0.39 | |
| CMC | 5.32 | CMC | 6.84 | TXTG | −2.58 | CEC | 1.18 | |
| ZS | OTS | 22.63 | EME | 41.44 | SGAS | −6.79 | SPP | −0.08 |
| EME | 12.57 | CEC | 10.17 | EPHP | −6.36 | FOOD | −0.04 | |
| CEC | 9.63 | TXTG | 5.4 | PCN | −4.44 | GEP | 0 | |
| CMC | 8.12 | FOOD | 4.85 | TXT | −2.25 | EME | 0.14 | |
| WRHR | 7.24 | WRHR | 4.8 | TXTG | −1.99 | CEC | 0.16 | |
| JM | OTS | 18.79 | CEC | 19.92 | SGAS | −6.86 | GEP | 0.4 |
| MPR | 8.49 | MPR | 11.06 | EPHP | −6.18 | SPM | 0.41 | |
| FOOD | 7.71 | EME | 10.38 | PCN | −4.45 | MNF | 0.42 | |
| CMC | 6.53 | AGRI0 | 8.58 | MINE | −1.04 | TRE | 0.74 | |
| EME | 6.18 | GEP | 7.1 | TXTG | −0.8 | EME | 0.84 | |
| ZQ | OTS | 18.5 | MPR | 18.98 | EPHP | −7.06 | SPP | −0.04 |
| MPR | 11.2 | GEP | 16.74 | SGAS | −6.96 | CEC | −0.04 | |
| AGRI | 8.44 | FOOD | 12.89 | PCN | −4.86 | WRHR | −0.03 | |
| WRHR | 7.81 | TSP | 10.15 | MINE | −1.36 | AGRI | −0.02 | |
| NMM | 7.66 | WRHR | 7.62 | TSP | −1.24 | FOOD | 0.31 | |
| City | ρ = 0.2 | ρ = 0.3 | ρ = 0.1 | |||
|---|---|---|---|---|---|---|
| GDP (108 yuan) | Carbon Price (yuan/t) | GDP Change (%) | Carbon Price Change (%) | GDP Change (%) | Carbon Price Change (%) | |
| GZ | 19,907.72 | 57.02 | 0.026 | −8.26 | −0.024 | 7.66 |
| SZ | 21,578.51 | 34.96 | 0.001 | −7.75 | −0.001 | 7.24 |
| ZH | 2589.13 | 56.63 | 0.003 | −9.48 | −0.003 | 8.93 |
| FS | 9576.98 | 25.00 | 0.001 | −8.21 | −0.001 | 7.72 |
| HZ | 3868.37 | 47.21 | 0.004 | −9.49 | −0.003 | 8.89 |
| DG | 8322.83 | 34.45 | 0.001 | −9.27 | −0.001 | 8.60 |
| ZS | 3059.12 | 40.27 | 0.001 | −8.93 | −0.001 | 8.39 |
| JM | 2513.42 | 18.59 | 0.001 | −10.99 | −0.001 | 10.36 |
| ZQ | 2171.55 | 15.99 | 0.001 | −5.40 | −0.001 | 5.05 |
| OT | 14,992.86 | 24.71 | 0.003 | −7.67 | −0.003 | 7.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.-F.; Wu, J.; Chen, W.; Wu, D. Carbon Emission Reduction Cost Assessment Using Multiregional Computable General Equilibrium Model: Guangdong–Hong Kong–Macao Greater Bay Area. Sustainability 2022, 14, 10756. https://doi.org/10.3390/su141710756
Zhou J-F, Wu J, Chen W, Wu D. Carbon Emission Reduction Cost Assessment Using Multiregional Computable General Equilibrium Model: Guangdong–Hong Kong–Macao Greater Bay Area. Sustainability. 2022; 14(17):10756. https://doi.org/10.3390/su141710756
Chicago/Turabian StyleZhou, Jin-Feng, Juan Wu, Wei Chen, and Dan Wu. 2022. "Carbon Emission Reduction Cost Assessment Using Multiregional Computable General Equilibrium Model: Guangdong–Hong Kong–Macao Greater Bay Area" Sustainability 14, no. 17: 10756. https://doi.org/10.3390/su141710756
APA StyleZhou, J.-F., Wu, J., Chen, W., & Wu, D. (2022). Carbon Emission Reduction Cost Assessment Using Multiregional Computable General Equilibrium Model: Guangdong–Hong Kong–Macao Greater Bay Area. Sustainability, 14(17), 10756. https://doi.org/10.3390/su141710756





