Abstract
To address the problem of low-carbon, optimal operation of AC–DC hybrid microgrids, a carbon trading mechanism is introduced and the impact of multiple uncertainties on system optimization is considered. Firstly, a two-layer model with the comprehensive economy of the hybrid microgrid as the upper layer and the respective optimal operation of the AC and DC sub-microgrids as the lower layer is established and the demand-side response is introduced, based on which the uncertainty of the scenery load is simulated using the multiscenario analysis method. Then, the baseline method is used to allocate carbon emission allowances to the system without compensation, and the actual carbon emissions of diesel engines, microcombustion engines, and fuel cells are considered to construct a hybrid microgrid. Finally, the model is solved using the CPLEX solver in conjunction with the calculation example, and the simulation verifies the effectiveness and feasibility of the proposed strategy in coordinating and optimizing the economy and low carbon of the system. The results show that when the carbon trading mechanism is considered, the carbon emission of the hybrid microgrid is reduced by 4.95%, the output power of the diesel generator is reduced by 5.14%, the output power of the fuel cell is reduced by 18.22%, but the electricity purchase from the power grid is increased by 38.91%. In addition, the influence degrees of the model considering the uncertainty of renewable energy and load are simulated. Furthermore, the impact of different electricity price models on optimal operation is evaluated, and the results show that electricity price will affect electricity purchase from the power grid and further affect carbon emissions.
1. Introduction
In recent years, the excessive use of fossil fuels has led to energy depletion and environmental pollution, and the world is suffering greatly from the current and future demands of energy. The efficient use of renewable energy for power generation is one of the keys to alleviating this problem [1,2]. AC–DC hybrid microgrid technology combines the advantages of AC microgrids and DC microgrids, providing a reliable way to connect various types of distributed power sources to the grid on a large scale, and is also an effective way to achieve the “low carbon” goal. Therefore, the optimal operation of AC–DC hybrid microgrids has become a hot spot and a difficult area for microgrid research [3,4,5].
When the AC–DC hybrid microgrid is under operation, the most important part is its optimal operation. Targeting system operating costs is no longer a good option, and carbon emissions are necessary as a limiting measure. How to coordinate the utilization of various resources in the hybrid microgrid and achieve the best effect in the operating cost and carbon emissions at the same time is a problem worth studying. Considering the zoning structure characteristics and multiple constraints of AC–DC hybrid microgrids, it is a huge problem with many decision variables. Therefore, it is very important to establish a suitable model and choose a solution method. In addition, based on the uncertainty of renewable resources and load forecasting, the optimal operation of the system faces many uncertainties, which is also the main aspect of this research.
The optimization objective of the traditional microgrid optimization operation problem is mainly based on economic benefits. In [6], the authors focused on the maximization of renewable energy usage and the minimization of the operational cost of an AC–DC hybrid microgrid. They stress the need for load coordination of the source network and use an improved memetic algorithm (IMA) that gives a shorter running time and improved results compared to the basic memetic algorithm. In [7], a distributed, finite-step consensus algorithm was proposed for the dynamic economic dispatch problem of an AC–DC hybrid microgrid, which can be converted to the optimal value in finite steps. In [8], a time-coordinated energy management strategy for an AC–DC hybrid microgrid considering the dynamic conversion efficiency of a bidirectional AC/DC converter was proposed.
Recent literatures on mathematical optimization techniques have used mixed integer linear programming (MILP). In [9], given the uncertainty of spinning reserves, which provided by energy storage is modeled by probabilistic constraints, the operating cost of an isolated microgrid (MG) is minimized by using chance-constrained programming, and the model is converted to solve a MILP problem. By setting the confidence level of the spinning reserve probability constraint appropriately, the operation of MG can achieve a trade-off between reliability and economy. In [10], a new framework is proposed for the day-ahead energy dispatch problem of a residential microgrid that comprises interconnected smart users, each owning individual renewable energy sources (RESs), noncontrollable loads (NCLs), energy- and comfort-based CLs, and individual plug-in electric vehicles (PEVs). When the constraints of device/comfort/contract are satisfied, in order to minimize the expected energy cost, the feasibility constraints on energy transfer between users and the grid under RES generation and users’ demand uncertainties are considered. Finally, the min-max problem is transformed into a mixed-integer quadratic programming problem to solve the scheduling problem. In [11], a mixed-integer conic optimization formulation for the design of generator droop control is presented. The convexity of the mixed-integer problem’s continuous relaxation gives global optimality guarantees for the design problem.
Compared with the traditional power grid, a hybrid microgrid has the advantages of a high energy utilization rate and environmental friendliness. However, the high penetration of RES connected with the public power grid can cause stability concerns because of their intermittent and uncertain nature related to climatic conditions [12,13,14]. In [15], a multitimescale rolling optimization scheduling framework was developed. Based on the predicted mean, deviation, and confidence probability of the source and load power, the conservatism of adaptive robust optimization was reduced. In [16], a new risk-based uncertainty set optimization method was proposed for energy management of a typical AC–DC hybrid microgrid. In [17], the novel Copula method was introduced to model the uncertainties associated with the solar panels and wind energy units in the AC–DC hybrid microgrid.
For the economic optimization of hybrid microgrids, in order to improve the environmental friendliness of the system, it is necessary to study the impact of resource utilization on carbon emissions. In [18], introducing peak load price and CO2 tax, evaluation criteria were converted into cost. In [19], a closed-loop hierarchical operation (CLHO) algorithm was proposed that potentially helps the real-time optimal operation of the microgrids, showing that a low emissions allowance (EA) and a high emissions trading price reduced the total amount of carbon emissions. In [20], a novel collaborative coordination scheme was proposed for facilitating electricity and heat interaction among multistakeholder distributed energy systems. The total cost and carbon dioxide emissions were reduced obviously. In [21], a mathematical model was created that allows the user to arrive at an optimal trade-off between energy generation and carbon production in each scenario.
Table 1 includes the main features of the literature on optimal operation of a microgrid. Therefore, the current paper develops a two-layer optimization model for AC–DC hybrid microgrids that considers the carbon trading mechanism and coordinates the relationship between economic and low-carbon microgrid operation, a hybrid microgrid, and sub-microgrids for participation in an AC–DC hybrid microgrid in the carbon trading market. In addition, it considers the operation mode and characteristics of the AC–DC hybrid microgrid [22,23]. First, the paper simulates the uncertainty of scenic load based on scenario analysis; then, it constructs a carbon trading mechanism for an AC–DC hybrid microgrid. Finally, it verifies that the proposed optimization operation method improves the economic efficiency of the AC–DC hybrid microgrid, ensures low-carbon operation of the system, and has better adaptability to the random fluctuation of scenic load through simulation. Therefore, the main contributions of this work can be summarized as follows:

Table 1.
The main features of literatures on the optimal operation of microgrid.
- A two-layer optimization model has been established considering the benefits of each part of the hybrid microgrid.
- The carbon trading mechanism has been integrated into the upper layer optimization model. Moreover, the different carbon trading prices on carbon emissions and operation costs have been investigated.
- The demand response and dynamic conversion efficiency have been taken into account.
- The uncertainties of WT power and PV power output and AC and DC load have been evaluated.
- The effect of different electricity price models on total operating costs and carbon emissions and power output have been evaluated.
2. The Structure and Operation Method of the AC–DC Hybrid Microgrid
The grid structure of the AC–DC hybrid microgrid studied in this paper is shown in Figure 1, which mainly consists of distributed generations (DG), load, and a current converter. The AC bus is connected to a wind turbine (WT), diesel generator (DEG), microturbine (MT), and AC load, forming an AC sub-microgrid, which is also connected to the larger grid through the point of common coupling (PCC). The DC bus is connected to a photovoltaic cell (PV), fuel cell (FC), storage battery (SB), and the DC load, forming a DC sub-microgrid. The AC sub-microgrid and the DC sub-microgrid are connected via an interlinking converter (ILC) for bidirectional power flow.
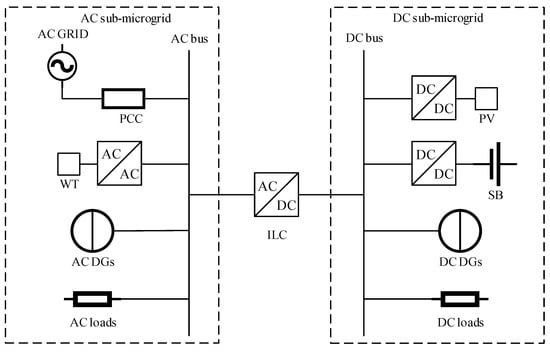
Figure 1.
The structural chart of the AC/DC hybrid microgrid.
In the normal operation of the microgrid, the first step is to determine whether the renewable energy in the AC/DC sub-microgrid can meet the corresponding AC/DC load to avoid the phenomenon of wind and light abandonment, and then to reasonably allocate the power output of each distributed power source according to the real-time situation in the sub-microgrid. At the same time, the operation of energy storage devices in the DC sub-microgrid is also an important way of power balancing, enabling peak-to-valley regulation of the entire hybrid microgrid. Therefore, compared with the traditional AC microgrid or DC microgrid dispatch, the optimal dispatch of the AC–DC hybrid microgrid needs to cope with the uncertainty of new energy generation in addition to the comprehensive consideration of the characteristics of AC/DC source–load partition operation, which objectively constitutes multiple uncertainties of optimal operation.
The carbon trading mechanism is also considered in the hybrid microgrid optimization problem. On the one hand, the determination of the carbon trading model depends on the operation of the individual microsources of the AC/DC sub-microgrid, and at the same time, the AC/DC sub-microgrid is influenced by the interaction of the hybrid microgrid with the larger grid and the switching strategy when formulating the operation. On the other hand, the carbon trading model and the overall economy of the hybrid microgrid are mutually influenced from the perspective of economic interests and comprehensive benefit. The calculation also requires the operation of each microsource of the AC/DC sub-microgrid, so the problem cannot simply be converted into a single-layer model to solve.
3. Mathematical Model for AC–DC Hybrid Microgrid Double Layer Optimization
Hierarchical optimization is suitable for coordinating the interests of individuals with different optimization objectives and different decision variables. In order to consider the economic and low-carbon aspects of the AC–DC hybrid microgrid, as shown in Figure 2, coordinate the operational benefits between the whole grid and the sub-grids, and optimize the power allocation for each time period under multiple objectives, the following two-layer model is used: an upper layer for the comprehensive economic optimization of the AC–DC hybrid microgrid and a lower layer for the optimization of the power output within the sub-microgrid. The upper layer optimizes the power allocation between the main network and the AC and DC sub-microgrids and the purchase and sale of power from the grid according to the power allocation of each distributed power source obtained from the lower layer. Meanwhile, the lower layer optimizes the specific power output of each distributed power source and adjusts the load for each time period according to the power allocation of the upper layer.
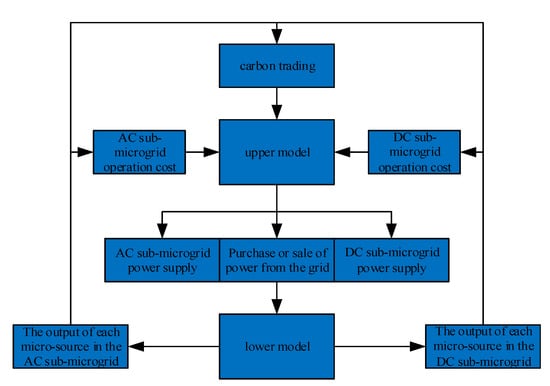
Figure 2.
The flow chart for two-layer optimization.
3.1. Upper Layer Model
The upper layer optimization model of the AC–DC hybrid microgrid has the objective of minimizing the overall operating cost and carbon trading cost of the entire hybrid microgrid . The decision variables are the amount of power supplied by the AC sub-microgrid, the amount of power supplied by the DC sub-microgrid, and the amount of power purchased and sold from the larger grid. The upper optimization problem is transformed into the following:
3.1.1. Comprehensive Operating Cost Model
The total upper layer operating costs include the AC sub-microgrid operating costs , the DC sub-microgrid operating costs , and the microgrid purchase and sale costs to the larger grid . The AC sub-microgrid operating costs and DC sub-microgrid operating costs are given by the lower layer optimization results. The specific model is shown as follows:
where and are the buying and selling prices from grid power at the time , respectively. The is exchange power with the large grid over time period .
The total power balance constraint is as follows:
where and represent the total DG power generated by the upper layer model allocated to the lower layer AC and DC sub-microgrids over time period , respectively, and and are the AC and DC loads after the demand response of the microgrid over time period , respectively. The is the converting power of the AC sub-microgrid and the DC sub-microgrid over time period .
Grid-connected transmission power constraint: the active change power of the microgrid and large grid must be kept between the upper and lower limits as follows:
where and are the lower and upper limit of , respectively.
3.1.2. Carbon Trading Mechanism
The carbon trading mechanism is a mechanism for trading CO2 emission rights based on the carbon emission allowances allocated by the government. In order to simulate the motivation of players of interest to save energy and reduce emissions, the baseline method is used to determine the unpaid carbon emission quotas of each interest player. For the AC–DC hybrid microgrid optimization model established in this paper, the carbon emission distributing power sources are diesel generators, microcombustion engines, and fuel cells [24,25,26]. The carbon emission cost model under the carbon trading mechanism is as follows [20]:
where is the total cost of carbon emissions, is the carbon unit price in the carbon trade market, represents the actual carbon emissions, represents the free carbon trading allowances allocated to the microgrid by the carbon trade market, and is the carbon factor. includes all distributed generations in microgrid, and , , and will be accompanied by varying degrees of carbon emissions.
3.2. Lower Layer Model
The AC–DC hybrid microgrid lower-level optimization model takes the minimization of the AC sub-microgrid operating cost , DC sub-microgrid operating cost , demand response cost and converter loss cost as the optimization objectives, and the decision variables are the DGs’ output, demand response load, and ILC converter power of each AC and DC sub-microgrid. The upper optimization problem is transformed into the following:
Demand response (DR) means that customers adjust their energy consumption behavior according to tariffs or incentives and participate in grid interaction, thus optimizing the load curve and improving the operational efficiency of the system while enhancing the two-way interaction between the supply side and the use side [27,28,29].
This paper considers both load uncertainty and demand response and models the load within the microgrid based on the nature of the load and the ability of the load to participate in the response as follows:
where represents the random load, which is the load that naturally occurs and starts randomly according to the needs of the user’s life and work style and is also the load value for scenario analysis in the upper model; represents the controllable load, which is the load whose power can be adjusted or even intermittently interrupted, and the user can adjust the time of use according to the change in the price of electricity. This is the key to the price-based demand response model and is also the load value for regulation in the lower model.
The cost of demand response is given by the following:
where is the factor of demand response cost, and represents the adjusted load powers based on demand response.
The customer satisfaction is given by the following:
where is the customer satisfaction factor after demand response. It decreases as the demand response load increases. is the customer satisfaction factor lower limit.
The cost of AC/DC conversion loss can be modeled as follows [8]:
where and are the powers and loss of ILC, respectively; is the dynamic conversion efficiency of the interconnection converter, and and take values of −0.01 and 0.95, respectively.
The powers of ILC limits can be obtained as follows:
where represents the powers of the ILC upper limit.
3.2.1. AC Sub-Microgrid Optimization Model
The combined operating costs of the AC sub-microgrid consist of the operation and maintenance costs of the individual devices , fuel costs , and environmental costs . The specific model is shown as follows:
where denotes the type of AC sub-microgrid power supplies, consisting of a WT, MT and DEG; is the operation and maintenance factor of the DG; is the power generated by the DG at time ; and are the unit price and lower heating value of the fuel, respectively; is the fuel efficiency of the MT; and are the fuel factors of the DEG; denotes the type of pollutant emitted by the DG during operation, consisting mainly of CO2, SO2, and NO2; denotes the emission factor of the pollutant for the DG; and denotes the discounted cost factor of the pollutant.
The AC sub-microgrid power balance constraint is given by the following:
where is the power transferred from the DC sub-microgrid to the AC sub-microgrid. denotes the AC sub-microgrid load after demand response.
The limits and climb power of the MT and DEG are constrained as follows:
where and are the climbing rates of the MT and DEG, respectively, and , , , and are the upper and lower limits of the MT and DEG, respectively.
3.2.2. DC Sub-Microgrid Optimization Model
The combined operating costs of the DC sub-microgrid consist of the operation and maintenance costs of the individual devices , fuel costs , and environmental costs . The specific model is shown as follows:
where denotes the types of DC sub-microgrid power supplies, consisting of a PV, FC, and BS; the rest of the formula types are similar to the AC sub-microgrid and will not be described individually.
The DC sub-microgrid power balance constraint is given by the following:
where is the power transferred from the AC sub-microgrid to the DC sub-microgrid. denotes the DC sub-microgrid load after demand response.
The limits and climb power of the FC are constrained as follows:
where is the climbing rate of the MT, and and denote the range of output power of the FC.
The limits and SOC limits of the SB are constrained as follows:
where is the upper limit of SB, is the battery charging and discharging efficiency, is the battery rated capacity, and represent the range of SOC, and and are the initial value and the final value of SOC, respectively, taking a value of 0.3.
4. Scenario Analysis Method
Compared to conventional microgrids, AC–DC hybrid microgrids require more complex uncertainty issues to be considered. In general, robust optimization or scenario analysis is often used to cope with the effects of multiple uncertainties on the system. Robust optimization is computationally inefficient because it requires large-scale sampling to simulate stochasticity, whereas scenario analysis converts the uncertainty problem into a deterministic problem under several typical scenarios, which reduces the difficulty of model building while ensuring model accuracy. The scenario analysis method mainly consists of two steps: scenario generation and scenario reduction. In scenario generation, Latin hypercube sampling (LHS) is more concise and efficient than Monte Carlo simulation; in scenario reduction, cluster analysis is generally used to simplify the sample and improve computational efficiency [30,31,32].
4.1. Scene Generation
The multiple uncertainties considered in this paper include wind and PV power output prediction errors, AC and DC load prediction errors, and time-sharing tariffs. The prediction errors of wind and PV load power are all considered to obey Gaussian distributions. Different variance sizes are set according to historical data, and the initial set of scenarios S for wind, PV, and load power is generated using the Latin hypercube sampling technique. The time-sharing tariff uncertainty is determined by using historical data in a different strategy consideration.
where is the predicted error power of resource , is the variance, and is the different scenarios value of uncertain resource predicted value in time period .
4.2. Scene Reduction
After the optimal discretization of the continuous distribution of the random variables at each time interval, the full scenario set formed by combining the entire scheduling interval is huge in size and has a dimensional explosion problem. The basic idea of clustering is to partition a dataset into different classes or clusters according to a specific criterion, so that the similarity of data objects within the same cluster is as high as possible, while the difference of data objects not in the same cluster is as large as possible. In other words, after clustering, data from the same class are clustered together as much as possible and different data are separated as much as possible.
This paper uses a subspace clustering algorithm to reduce the initial scenario, considering the relevance of scenery output as well as AC and DC loads, clustering wind and PV together and AC and DC loads together to obtain a typical scenario, thus reducing the amount of computation under the condition of meeting the accuracy requirements. The simple and efficient subspace clustering algorithm has better high dimensionality. Compared with the K-means clustering algorithm, the results obtained from the scenery load prediction data in this paper, after scenario generation, using the subspace clustering algorithm are better under the CH evaluation index and can better characterize the randomness of the data.
5. Case Study
5.1. System Structure and Data
The operating data of the AC–DC hybrid microgrid system in this paper are modified from the demonstration project in [33], and the structure of the tested system is depicted briefly in Figure 1. The operating period was set to be 1 day (24 h), and the unit running time was 1 h. The operating parameters of the microsource part in the hybrid microgrid are shown in Table 2: the battery equipment capacity is 250 kW·h, the battery state of charge varies from 0.3 to 0.9, the maximum interaction power between the microgrid and the main network is 100 kW, the interaction power of the bidirectional power converter between the AC and DC sub-microgrids is limited to 50 kW, and the transmission efficiency is taken as 95%. The respective pollutant emission factors of the dispatchable resources MT, DEG, and FC; the environmental discounted costs of different pollutants; and the unit price of fuel and the low calorific value of fuel gas are referenced in the literature [34,35], and the carbon trading price in this paper is CNY 30/t, ignoring the power losses in the converter connected to the microsource and on the line.

Table 2.
The part operating parameters of microgrid system.
The following three strategies are set for comparative analysis to verify the effectiveness of this paper’s treatment of the uncertainty optimization running problem. A comparison of the results of the three strategies for the runs is shown in Table 3.

Table 3.
The effect of prediction error on optimization results.
Strategy 1: The operational strategy proposed in this paper only considers power prediction scenarios for wind power, PV power, and load—i.e., optimal dispatching according to the determined power of wind power, PV power, and load—with the objective of minimizing basic operating costs in each layer.
Strategy 2: A different carbon trading mechanism strategy that considers the effect of the size setting of the carbon trading weights on the optimization results; the rest of the conditions are the same as for Strategy 1.
Strategy 3: Different time-of-use tariff strategies. This develops multiple time-of-use tariff strategies with the remaining conditions the same as Strategy 1.
The main problem of optimization in this paper can be converted into a mixed integer linear programming problem. In this paper, we use the YALMIP toolbox to invoke the CPLEX 12.8.0 optimization solver on the MATLAB R2018b platform to solve the day-ahead optimization runtime problem under the above three strategies.
5.2. Comparison Analysis of Different Scenarios and Strategies
In order to verify the rationality of the model proposed in this paper, a scenario analysis method was used to select five typical scenarios, as shown in Figure 3 and Figure 4, based on the optimization model proposed in Strategy 1 and to compare and analyze the impact of uncertainty on the strategy proposed in this paper.
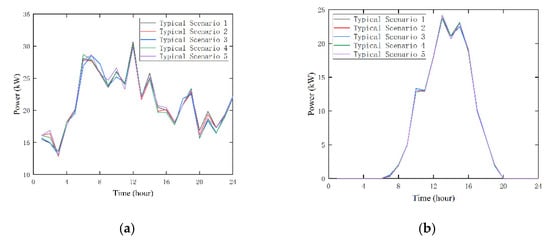
Figure 3.
Five typical scenarios. (a) Typical WT scenarios; (b) typical PV scenarios.
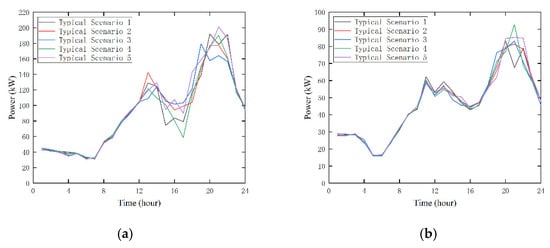
Figure 4.
Five typical scenarios. (a) Typical AC load scenarios; (b) typical DC load scenarios.
Strategy 1 is the result of the simulation using the predicted values of scenic loads, and Scenarios 1–5 are typical scenarios after considering the prediction error of scenic loads. As can be seen from Table 3, through the simulation of the five typical scenarios, the fluctuation range of the comprehensive operating cost is 97.87–104.46%, and the fluctuation range of the actual carbon emission is 98.54–100.41%. The results show that Strategy 1 has good flexibility in the scenic load and better flexibility under multiple scenarios of uncertainty.
The following is a further comparison of the impact of different strategies on operating costs and carbon emissions. The upper tier target was used as the study target. Strategy 2 was selected without carbon trading and increasing the carbon trading price for comparison, and Strategy 3 was selected with different time share tariffs for peak and valley periods; the time share tariff strategy is shown in Figure 5.
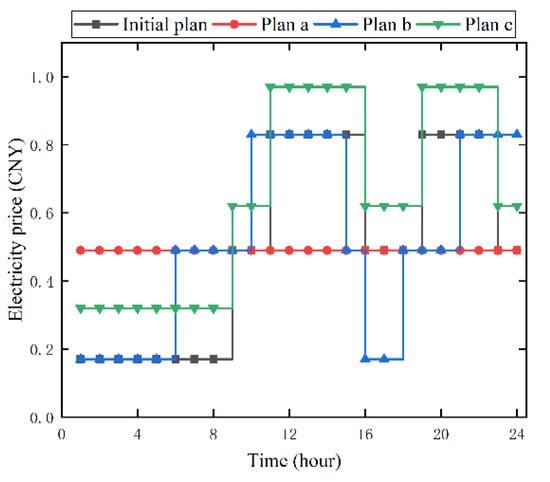
Figure 5.
Electricity price plan.
As can be seen from Table 4, comparing Strategy 2, the integrated operating cost without carbon trading is CNY 84.38 less than in Strategy 1, whereas the actual carbon emission is 132.7 kg more than in Strategy 1; meanwhile, the integrated operating cost and the actual carbon emission keep the same trend after increasing the carbon trading price. Comparing the objective function in the upper model, it can be concluded that the increase in carbon trading price makes the system adjust the energy allocation and the cost of electricity purchase and the cost of the DC sub-microgrid increase, whereas the cost of the AC sub-microgrid decreases, indicating that the AC sub-microgrid has a larger share in carbon emissions. Comparing Strategy 3, the combined operating costs and actual carbon emissions are greater under a constant tariff than in Strategy 1. Time-sharing Tariff 2 changes the peak and trough periods of the tariff, which in turn changes the microsource output for each period, while time-sharing Tariff 3 changes the size of the tariff for each period, causing the microsource output to increase and both the combined operating costs and actual carbon emissions to increase. The difference in operating costs between the different time-sharing tariff strategies chosen is mainly reflected in the cost of purchasing electricity. The uncertainty of the time-sharing tariff mainly affects the operating profit in the hybrid AC–DC microgrid model, whereas a large amount of historical information and reliable and publicly available data sources exists.

Table 4.
The influence of different operation strategies on optimization results.
In addition to studying the economics of AC–DC hybrid microgrids, this paper also analyzes their flexibility. The upward and downward flexibility are used to characterize the flexibility of the microgrid system and to reflect the ability of the microgrid system to use the existing schedulable resources to respond to source–load uncertainty. The upward and downward flexibility are shown in Figure 6. The upward flexibility adjustment reaches the maximum value of 200kW in hours 1–7, whereas the downward flexibility adjustment reaches the maximum value in hours 19–21, and the remaining period has a sufficient margin.
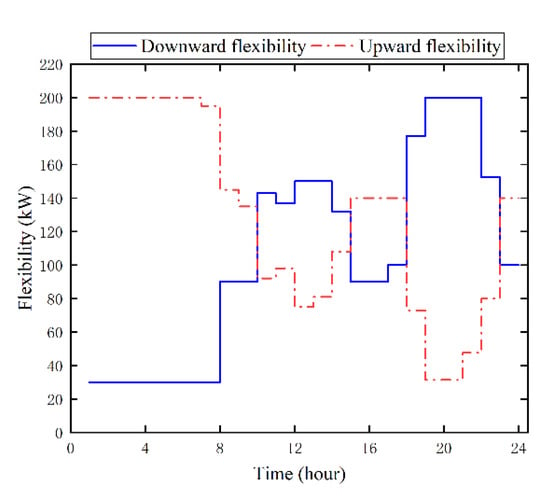
Figure 6.
The upward and downward flexibility.
In summary, the operation scheme developed according to Strategy 1 has more obvious economic benefits and higher flexibility and is more adaptable to fluctuations in scenic load power, thus verifying the effectiveness of this paper’s scenario-analysis-based AC–DC hybrid microgrid operation optimization method on a one-hour time scale.
5.3. Day-Ahead Forecast Optimization Results Analysis
The results of the AC–DC hybrid microgrid operation using Strategy 1 are shown in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. The composition of the AC/DC load before and after the demand response is shown in Figure 7, from which it can be seen that load in the peak and valley hours before and after the demand response has a more obvious change. The load curve is smoothed out and the effect of peak and valley reduction is achieved. Figure 12, Figure 13, Figure 14 and Figure 15 show the optimized operation results of the AC and DC sub-microgrids without considering the carbon trading mechanism and without considering the time-of-use electricity price, i.e., Strategy 2a and Strategy 3a.
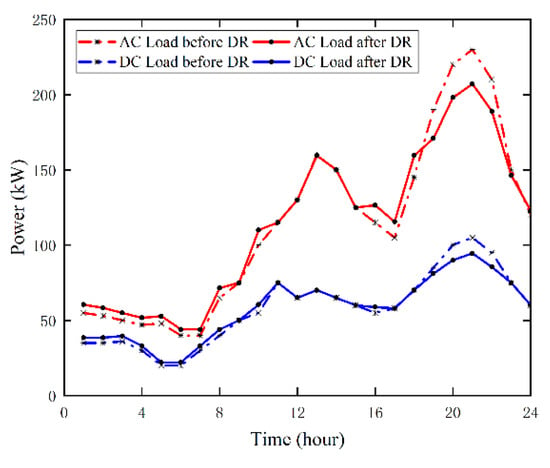
Figure 7.
Consequence of demand response.
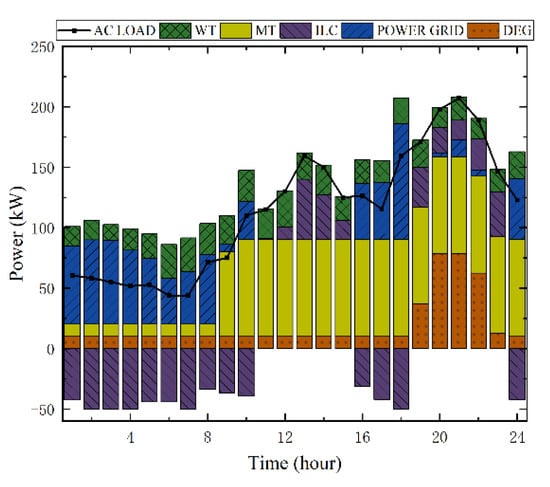
Figure 8.
Power output curves of AC sub-microgrid under Strategy 1.
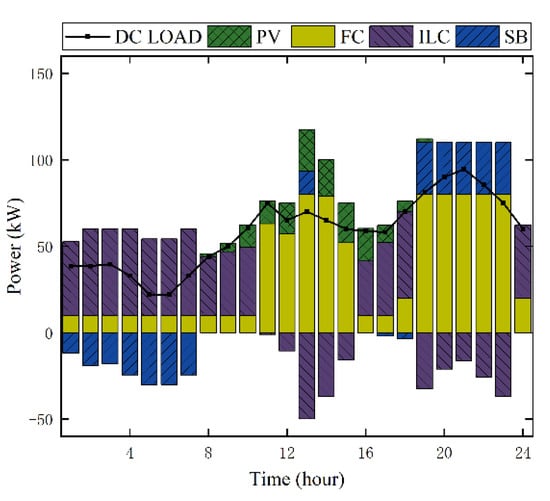
Figure 9.
Power output curves of DC sub-microgrid under Strategy 1.
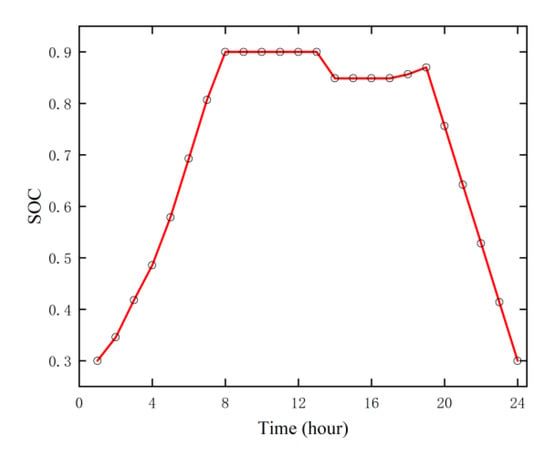
Figure 10.
SOC curves of SB.
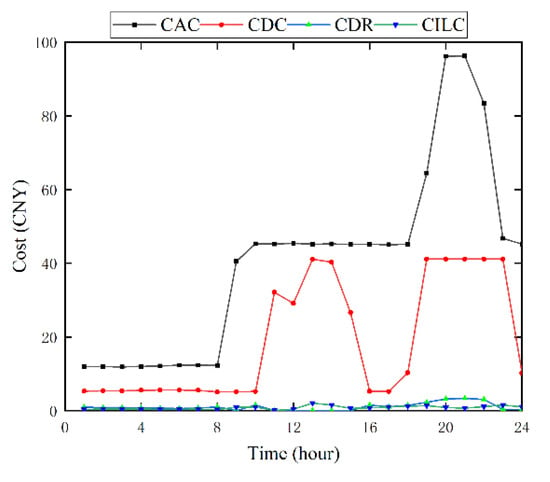
Figure 11.
The lower layer operating cost.
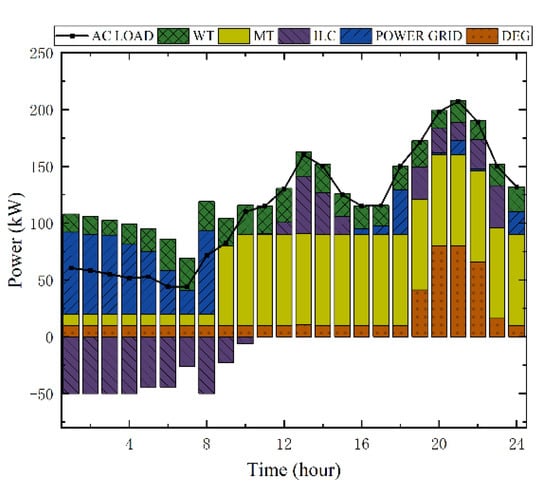
Figure 12.
Power output curves of AC sub-microgrid under Strategy 2a.
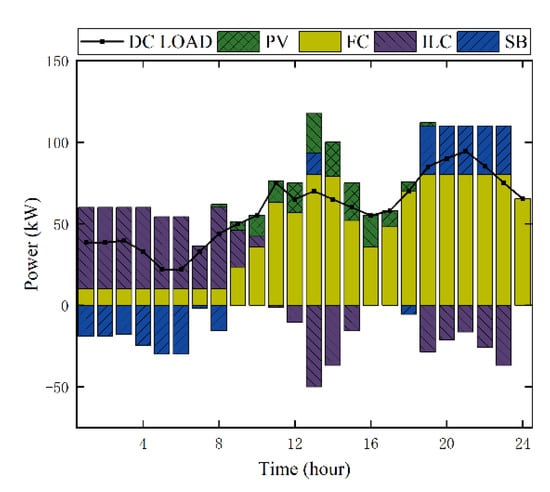
Figure 13.
Power output curves of DC sub-microgrid under Strategy 2a.
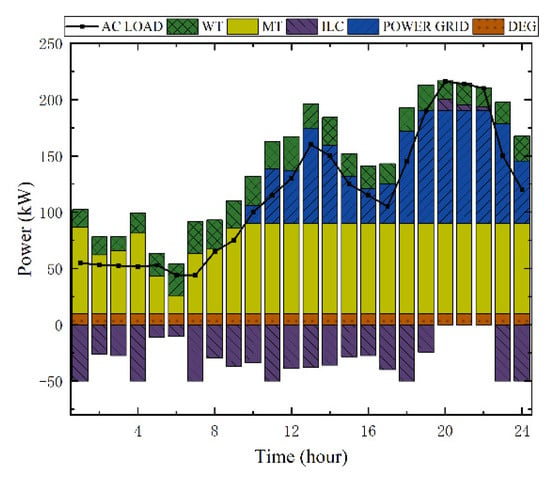
Figure 14.
Power output curves of AC sub-microgrid under Strategy 3a.
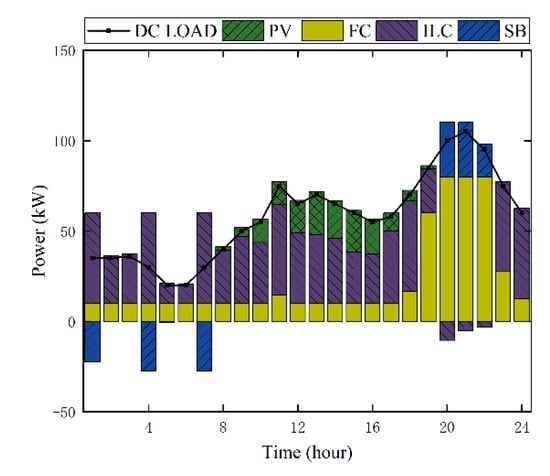
Figure 15.
Power output curves of DC sub-microgrid under Strategy 3a.
The power output of each DG of the AC and DC sub-microgrids is shown in Figure 8 and Figure 9, respectively. The wind power generation power is basically at a more average level within 24 h. The controllable microsources in the AC sub-microgrid include diesel generators and microcombustion turbines. The diesel generators are basically at their lowest power generation state due to their high-power generation cost and only play a backup role when the AC load is high (19:00~22:00). Microgas turbines, with their lower power generation costs, give full play to their power generation advantages during the hours when the gap between wind power and AC load is too large (9:00~24:00), thus meeting the demand, and the power generated by them in 24 h accounts for about 49.31% of the AC load. The AC sub-microgrid purchases power from the grid at a lower price during the valley load hours (24:00 to 08:00) and continues to purchase power from the grid during the peak load hours (16:00 to 18:00) to meet the load demand.
PV power generation increases and then decreases from 8:00 to 18:00. The controllable microsource in the DC sub-microgrid is the fuel cell. During the period from 9:00 to 24:00, the load demand starts to gradually increase, and the fuel cell output also starts to gradually increase, becoming the main source of electricity for the DC sub-microgrid. The power generated by it in 24 h accounts for about 64.15% of the DC load, and due to the emergence of PV, the fuel cell does not reach its maximum power at first. The battery is charged during the valley tariff and when the load level is not high (1:00 to 7:00) and discharged during the higher load hours (13:00, 19:00 to 23:00), if it meets the requirements of the charge state. Figure 10 shows the charge state of the battery as a function of time. The battery acts as an energy buffer link to complement other distributed energy sources, playing a role in peak and valley reduction while also increasing the flexibility of the system.
The AC sub-microgrid and the DC sub-microgrid exchange power through a bidirectional power converter. The figure shows the interactive power between the sub-microgrids, setting the input sub-microgrid as positive. Combining the two diagrams, it can be concluded that during the period from 1:00 to 7:00, the PV power is 0, the AC sub-microgrid delivers power to the DC sub-microgrid, and the DC sub-microgrid uses the resulting power to balance the load and charge the battery. During the period from 12:00 to 15:00, the PV output is larger, while the AC sub-microgrid experiences a peak load, and the DC sub-microgrid delivers power to the AC sub-microgrid to satisfy the power balance. During the hours of 19:00~23:00, the AC and DC loads come to the peak hours of the day, the battery starts to discharge under the premise of meeting the requirements of the charge state, and the DC sub-microgrid transmits power to the AC sub-microgrid due to the overload of the AC sub-microgrid. The time curve of each cost in the lower layer objective function is shown in Figure 11.
In contrast, as illustrated in Figure 12, Figure 13, Figure 14 and Figure 15, Strategy 2a has a big difference in the output period of the MT and FC, whereas Strategy 3a has a significant decrease in the output of the FC due to the increase in electricity purchased from the grid, and the BS is not fully utilized.
5.4. The Impact of Carbon Trading Price on System Operation
The carbon trading price can be regarded as the weight of the objective function, so the change of the carbon trading price will affect the carbon emission, carbon trading cost, and energy purchase cost and thus affect the total operating cost of the system. In order to further study the impact of carbon trading price on system operation, the relationship between total operating cost and actual carbon emissions with carbon price was drawn, as shown in Figure 16.
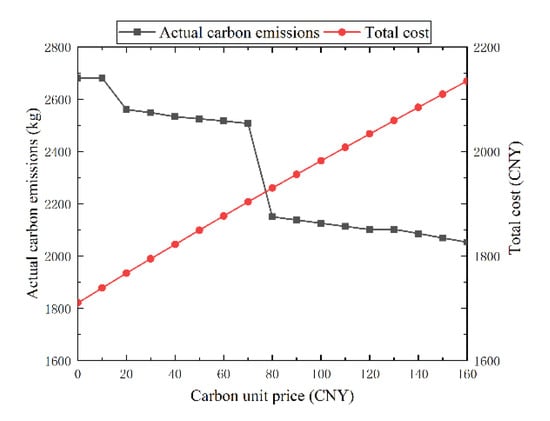
Figure 16.
Carbon price relationship curve.
The actual carbon emission generally decreases with the increase in the carbon trading price. A carbon trading price between CNY 10–20 and 70–80 leads to a large change in the actual carbon emission, and the rest of the changes are basically the same. The total operating cost increases with the increase in the carbon trading price, and the growth rate is basically the same. From the above analysis, setting a reasonable carbon trading price can promote the synergy of system economy and low carbon.
6. Conclusions
In this paper, a two-layer optimization model has been designed for AC–DC hybrid microgrid, which considers the carbon trading mechanism and the prediction uncertainties of renewable energy and load. Through the analysis of three strategies considering the uncertainties in multiple scenarios, the following conclusions can be drawn up:
- (1)
- The optimization model proposed in this paper has good results in terms of the economic benefits of microgrids as well as carbon emissions, realizing a reasonable allocation and use of resources and effectively coordinating the economy and low carbon of system operation.
- (2)
- In this paper, the impact of various uncertainties on the system was verified by simulating and analyzing the uncertainties of wind, PV, load, and tariff. A reasonable time-sharing tariff strategy can not only reduce system operating costs but also reduce carbon emissions to a certain extent.
- (3)
- By comparing the impact of the price of carbon trading costs on the optimized operation results, this paper concludes that the total operating cost of the system steadily increases with the increase in carbon trading price, and the carbon emissions show a phased decrease with the change of carbon trading price; furthermore, setting a reasonable carbon trading price can synergize low carbon and economy.
Follow-up work will consider the feasibility of optimizing the operation on a time scale of minutes and conduct a more in-depth study of the impact of a stepped carbon trading mechanism on the operation of the system.
Author Contributions
L.Y. and Y.Z. conceived the research. Y.Z. participated in the analysis of the data and in writing the initial manuscript. T.X., N.M., Z.L. and Z.Y. revised the manuscript and adjusted the data presentation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kumar, P.P.; Saini, R.P. Optimization of an off-grid integrated hybrid renewable energy system with different battery technologies for rural electrification in India. J. Energy Storage 2020, 32, 101912. [Google Scholar] [CrossRef]
- Zhu, L.; Tong, Q.; Yan, X.; Liu, Y.; Zhang, J.; Li, Y.; Huang, G. Optimal design of multi-energy complementary power generation system considering fossil energy scarcity coefficient under uncertainty. J. Clean. Prod. 2020, 274, 122732. [Google Scholar] [CrossRef]
- Zahraoui, Y.; Alhamrouni, I.; Mekhilef, S.; Basir Khan, M.R.; Seyedmahmoudian, M.; Stojcevski, A.; Horan, B. Energy Management System in Microgrids: A Comprehensive Review. Sustainability 2021, 13, 10492. [Google Scholar] [CrossRef]
- Wang, K.; Niu, D.; Yu, M.; Liang, Y.; Yang, X.; Wu, J.; Xu, X. Analysis and Countermeasures of China’s Green Electric Power Development. Sustainability 2021, 13, 708. [Google Scholar] [CrossRef]
- Azeem, O.; Ali, M.; Abbas, G.; Uzair, M.; Qahmash, A.; Algarni, A.; Hussain, M. A Comprehensive Review on Integration Challenges, Optimization Techniques and Control Strategies of Hybrid AC/DC Microgrid. Appl. Sci. 2021, 11, 6242. [Google Scholar] [CrossRef]
- Li, P.; Zheng, M. Multi-objective optimal operation of hybrid AC/DC microgrid considering source-network-load coordination. J. Mod. Power Syst. Clean Energy 2019, 7, 1229–1240. [Google Scholar] [CrossRef] [Green Version]
- Jiang, K.; Wu, F.; Zong, X.; Shi, L.; Lin, K. Distributed Dynamic Economic Dispatch of an Isolated AC/DC Hybrid Microgrid Based on a Finite-Step Consensus Algorithm. Energies 2019, 12, 4637. [Google Scholar] [CrossRef] [Green Version]
- Wei, B.; Han, X.; Wang, P.; Yu, H.; Li, W.; Guo, L. Temporally Coordinated Energy Management for AC/DC Hybrid Microgrid Considering Dynamic Conversion Efficiency of Bidirectional AC/DC Converter. IEEE Access 2020, 8, 70878–70889. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Li, G.; Zhao, D.; Tian, W. Optimal Scheduling of an Isolated Microgrid With Battery Storage Considering Load and Renewable Generation Uncertainties. IEEE Trans. Ind. Electron. 2018, 66, 1565–1575. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, S.M.; Carli, R.; Dotoli, M. Robust Optimal Energy Management of a Residential Microgrid Under Uncertainties on Demand and Renewable Power Generation. IEEE Trans. Autom. Sci. Eng. 2021, 18, 618–637. [Google Scholar] [CrossRef]
- Jabr, R.A. Mixed-Integer Convex Optimization for DC Microgrid Droop Control. IEEE Trans. Power Syst. 2021, 36, 5901–5908. [Google Scholar] [CrossRef]
- Deng, X.; Lv, T. Power system planning with increasing variable renewable energy: A review of optimization models. J. Clean. Prod. 2019, 246, 118962. [Google Scholar] [CrossRef]
- Jiang, Y.; Kang, L.; Liu, Y. The coordinated optimal design of a PV-battery system with multiple types of PV arrays and batteries: A case study of power smoothing. J. Clean. Prod. 2021, 310, 127436. [Google Scholar] [CrossRef]
- Mbungu, N.T.; Naidoo, R.M.; Bansal, R.C.; Vahidinasab, V. Overview of the Optimal Smart Energy Coordination for Microgrid Applications. IEEE Access 2019, 7, 163063–163084. [Google Scholar] [CrossRef]
- Qiu, H.; Gu, W.; Xu, Y.; Zhao, B. Multi-Time-Scale Rolling Optimal Dispatch for AC/DC Hybrid Microgrids with Day-Ahead Distributionally Robust Scheduling. IEEE Trans. Sustain. Energy 2018, 10, 1653–1663. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, H.; Wang, X.; Chen, S.; Zhang, C. Risk-Based Uncertainty Set Optimization Method for Energy Management of Hybrid AC/DC Microgrids with Uncertain Renewable Generation. IEEE Trans. Smart Grid 2020, 11, 1526–1542. [Google Scholar] [CrossRef]
- Li, Q.; Li, A.; Wang, T.; Cai, Y. Interconnected hybrid AC-DC microgrids security enhancement using blockchain technology considering uncertainty. Int. J. Electr. Power Energy Syst. 2021, 133, 107324. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Y.; Li, Q.; Gao, W.; Qian, F.; Song, L. Economic optimization of microgrids based on peak shaving and CO2 reduction effect: A case study in Japan. J. Clean. Prod. 2021, 321, 128973. [Google Scholar] [CrossRef]
- Li, F.; Qin, J.; Kang, Y. Closed-Loop Hierarchical Operation for Optimal Unit Commitment and Dispatch in Microgrids: A Hybrid System Approach. IEEE Trans. Power Syst. 2020, 35, 516–526. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Yu, S. Optimal management of multi-stakeholder distributed energy systems in low-carbon communities considering demand response resources and carbon tax. Sustain. Cities Soc. 2020, 61, 102230. [Google Scholar] [CrossRef]
- Su, J.; Li, Z.; Jin, A.J. Practical Model for Optimal Carbon Control with Distributed Energy Resources. IEEE Access 2021, 9, 161603–161612. [Google Scholar] [CrossRef]
- Saeed, M.H.; Wang, F.; Salem, S.; Khan, Y.A.; Kalwar, B.A.; Fars, A. Two-stage intelligent planning with improved artificial bee colony algorithm for a microgrid by considering the uncertainty of renewable sources. Energy Rep. 2021, 7, 8912–8928. [Google Scholar] [CrossRef]
- Kharrich, M.; Kamel, S.; Hassan, M.H.; ElSayed, S.K.; Taha, I.B.M. An Improved Heap-Based Optimizer for Optimal Design of a Hybrid Microgrid Considering Reliability and Availability Constraints. Sustainability 2021, 13, 10419. [Google Scholar] [CrossRef]
- Lu, H.; Ma, X.; Huang, K.; Azimi, M. Carbon trading volume and price forecasting in China using multiple machine learning models. J. Clean. Prod. 2020, 249, 119386. [Google Scholar] [CrossRef]
- Zakeri, A.; Dehghanian, F.; Fahimnia, B.; Sarkis, J. Carbon pricing versus emissions trading: A supply chain planning perspective. Int. J. Prod. Econ. 2015, 164, 197–205. [Google Scholar] [CrossRef] [Green Version]
- Cao, K.; Xu, X.; Wu, Q.; Zhang, Q. Optimal production and carbon emission reduction level under cap-and-trade and low carbon subsidy policies. J. Clean. Prod. 2017, 167, 505–513. [Google Scholar] [CrossRef]
- Zhu, L.; Zhou, X.; Zhang, X.; Yan, Z.; Guo, S.; Tang, L. Integrated resources planning in microgrids considering interruptible loads and shiftable loads. J. Mod. Power Syst. Clean Energy 2018, 6, 802–815. [Google Scholar] [CrossRef] [Green Version]
- Wu, N.; Wang, H.; Yin, L.; Yuan, X.; Leng, X. Application Conditions of Bounded Rationality and a Microgrid Energy Management Control Strategy Combining Real-Time Power Price and Demand-Side Response. IEEE Access 2020, 8, 227327–227339. [Google Scholar] [CrossRef]
- Hu, M.; Xiao, F.; Wang, S. Neighborhood-level coordination and negotiation techniques for managing demand-side flexibility in residential microgrids. Renew. Sustain. Energy Rev. 2021, 135, 110248. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, S.; Li, Q.; Zhang, Y.; Deng, W.; Zhou, L. Optimal Day-ahead Scheduling of Islanded Microgrid Considering Risk-based Reserve Decision. J. Mod. Power Syst. Clean Energy 2021, 9, 1149–1160. [Google Scholar] [CrossRef]
- Faraji, J.; Hashemi-Dezaki, H.; Ketabi, A. Optimal probabilistic scenario-based operation and scheduling of prosumer microgrids considering uncertainties of renewable energy sources. Energy Sci. Eng. 2020, 8, 3942–3960. [Google Scholar] [CrossRef]
- Cen, B.; Cai, Z.; Liu, P.; Chen, Y.; Sun, Y.; Hu, K.; Zeng, X. Characteristic matching of stochastic scenarios and flexible resource capacity optimisation for isolated microgrids. IET Gener. Transm. Distrib. 2020, 14, 6009–6018. [Google Scholar] [CrossRef]
- Li, P.; Xu, D.; Zhou, Z.; Lee, W.; Zhao, B. Stochastic optimal operation of microgrid based on chaotic binary particle swarm optimization. IEEE Trans. Smart Grid 2016, 7, 66–73. [Google Scholar] [CrossRef]
- Mohamed, F.A.; Koivo, H.N. System modelling and online optimal management of microgrid using mesh adaptive direct search. Int. J. Electr. Power Energy Syst. 2010, 32, 398–407. [Google Scholar] [CrossRef]
- Pipattanasomporn, M.; Willingham, M.; Rahman, S. Implications of on-site distributed generation for commercial/industrial facilities. IEEE Trans. Power Syst. 2005, 20, 206–212. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).