Abstract
As the largest ecological background system and basic economic unit in China, counties are of great significance to China’s carbon emission reduction targets. This article conducts theoretical model construction and empirical test research from a contraction perspective, using population and built-up area change as variables and combining indicators of county scale structure in an attempt to find key scale structure elements and representative indicators that affect the carbon emission intensity of counties. By using data from 140 counties in Northeast China during the period of 2015–2020, an empirical study was conducted on population shrinkage clustering, county size structure, and carbon emission intensity. The results show that: (1) population shrinkage significantly increases the carbon intensity of counties, but the contribution of population shrinkage to carbon intensity is scale-heterogeneous, the contribution effect decreases with population size, and the effect on large counties is minimal; (2) population size and industrial structure are the main factors influencing carbon intensity in counties, both have a negative linear elasticity relationship, and GDP per capita is not included in the overall model and is only significant in large counties; (3) the relationship between total construction land and carbon intensity is an inverted U-shaped Kuznets curve, with a critical value of 30 km2, and the total construction land in most counties is below or close to the critical value.
1. Introduction
The sprawling expansion of global cities and towns, the significant increase in urban population size, and the dramatic changes in the spatial structure of the economy have led to a significant increase in carbon emissions [1,2]. As a developing country with rapid urbanization, China’s total carbon emissions have reached a quarter of the world’s total, making it the world’s largest emitter of carbon dioxide [3]. Research on the evolution of the spatial pattern of carbon emissions in large- and medium-sized cities and the factors influencing them has yielded comparatively abundant results [4,5,6], but research on the mechanisms of carbon emissions in small- and medium-sized towns has not yet been fully carried out. As the most basic administrative and economic unit in China, counties account for 80% of the country’s land area and over 70% of the population and connect the urban and rural areas of China [7]. Thus, the study and clarification of the spatial and temporal evolution of their carbon emissions are conducive to the comprehensive layout of low-carbon planning and the efficient achievement of carbon control and emission reduction targets [8].
Carbon intensity, i.e., carbon dioxide emissions per unit of GDP, is a measure of the relationship between carbon emissions and economic development in a country or region. For developing countries, it is more relevant to use carbon intensity to quantify emission reduction targets than total carbon emissions or per capita carbon emission indicators [9], and for counties with imperfect statistics, using carbon intensity to measure carbon emission efficiency is the easiest to achieve.
In terms of the scale of research, current research on carbon emissions intensity mainly covers the measurement and decomposition of carbon emissions intensity [4,10], spatial and temporal evolution characteristics and patterns [11], and the exploration of driving factors [8,11]. The research scales cover national [11,12], provincial [13], and municipal [14]. The applicability of the existing findings on the impact relationship has not been fully demonstrated for the county level, which has a smaller size class and more differentiated stages of development.
In terms of exploring the drivers, the main methods used by scholars can be classified into five categories: index decomposition analysis (IDA), which mainly includes the logarithmic mean Divisia index (LMDI) [15], and the adaptive weighting Divisia (AWD) [16]; structure decomposition analysis (SDA) [17], which is more applied to carbon emissions as an input–output approach; the KAYA equation and its deformations [18], mainly the application of the IPAT model and the STIRPAT model [13,19]; the environmental Kuznets curve (EKC) [20]; and the econometric approach. Studies have attributed the factors affecting carbon efficiency to growth in population size, rapid economic levels [19], urbanization levels, increased industrialization [21], and the resulting changes in population affluence levels, consumption levels, and expenditure structures [13]. The results of the above studies suggest that the size and structure of the urban population, economy, and land use system all have an impact on the growth of carbon intensity to some extent and by different mechanisms.
Urban shrinkage is an objective stage in the life cycle of a city, typically characterized by a continuous outflow of population from densely populated urban areas [22]. According to a sample of 660 Chinese cities studied from 2007 to 2016, 80 cities experienced varying degrees of population shrinkage, with the most severe reduction in total population in Northeast China [23]. The shrinkage of cities greatly reduces the operational efficiency of cities at the level of scale and agglomeration effects. Analyses of the mechanisms affecting urban energy efficiency under shrinking conditions have been published in the literature [24,25,26], but few quantitative analyses based on continuous, large samples have been conducted at the county scale, making it difficult to provide scientific and empirical evidence on the environmental effects of shrinkage in counties. In addition, in recent years, rapid urbanization has deeply affected the county space in China, and it has become common to model the construction of county cores on the model of large cities. Projections of the construction land and population scale of counties often exceed their actual development capacity, which also leads to a large number of structural changes and the agglomeration of carbon emission growth under the expansion of scale [27].
This article presents an empirical study on population shrinkage, county size structure, and carbon intensity using data from 140 county areas in the Northeast region for the period 2015–2020. The time span of the study is limited by the release of the China County Construction Statistical Yearbook (2015). Different from previous studies, this paper analyzes the impact of population shrinkage on the carbon emission intensity of counties of different scales from the perspective of population size. The objectives of the study are: (1) to study the impact of population shrinkage on carbon intensity, focusing on the heterogeneous effect of population contraction on carbon emission reduction in counties with different population sizes, where the impact of population contraction on carbon efficiency is different for cities with different population sizes, a heterogeneous effect that has received little attention in previous literature; (2) to construct regression models by population size to further explore the differences in the influence relationship between different sizes, with a view to identifying management objectives and important grips for structural carbon control in counties of different sizes; (3) to test the Kuznets curve relationship between construction land expansion and carbon intensity, and since the problem of population loss has become inevitable, we turn to investigate whether there is an optimal county size in Northeast China.
2. Materials and Methods
2.1. Study Area
In this article, the Northeast region of China refers to the provinces of Heilongjiang, Jilin, and Liaoning (Figure 1). The Northeast region is a traditional industrial city cluster in China and was the first to be established as a heavy industry production and processing base. However, since 1990, the depletion of resources, a single industrial structure, and institutional changes have led to a decline in population, economic decline, and the loss of competitiveness of industries in Northeast China [28].
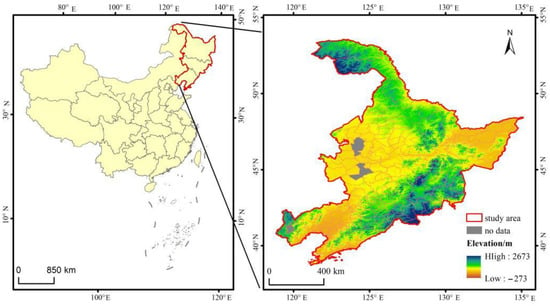
Figure 1.
The spatial location of the study area.
Northeast China has long been a heavy industrial base, rich in natural resources and high in energy consumption, a key area for reducing carbon emissions [29]. However, its unique natural resource conditions and historical development conditions have created a large number of unique town system structures built around the farming, forestry, coal, and oil systems. The spatial pattern of its towns is mostly too scattered, with many problems such as small-scale and inadequate infrastructure and living facilities, making it difficult to form a reasonable town system and failing to achieve agglomeration and scale effects, which seriously restricts low-carbon travel for residents and low-carbon development of towns. With the overall shrinkage of towns due to population loss in recent years, the above problems are particularly prominent [30].
The study was made on a county-by-county basis. In order to make the study feasible, the areas administered by each prefecture-level municipality were combined as a whole but were not counted in the analysis of county-level carbon emissions and carbon intensity. The missing county carbon emission data for one in each of the three provinces are Qianguolos Mongolian Autonomous County, Karachin Left Wing Mongolian Autonomous County, and Dulbert Mongolian Autonomous County; there are 140 county study units left.
2.2. Theoretical Analysis and Mechanisms
Although urban shrinkage has been defined in various dimensions in the literature [31], population loss remains a central feature of urban shrinkage, and its changes will inevitably have an impact on carbon emissions from energy use [32]. According to the previous section, carbon dioxide emissions per unit of GDP output is the main measure of the relationship between county economies and carbon emissions, so this article explains the direct pathways by which county shrinkage affects the intensity of carbon emissions in terms of both the energy saving effect and the economic output disincentive effect.
Specifically, as the population of the county decreases, carbon emissions from energy consumption, such as water, electricity, and gas, which are closely related to the lives of residents, will directly decrease. At the same time, population outflows are often accompanied by a reduction in the labor force, which in turn affects economic levels. According to the theory of agglomeration economy [33], the spatial agglomeration of population and economy contributes to the accentuation of effects such as resource sharing and knowledge spillover. The loss of labor factors and reduced economic density in shrinking cities are not conducive to the formation of agglomeration and economies of scale [34]. On the one hand, the decline of the economic aggregate of the shrinking counties will reduce the income level, thereby reducing the carbon emissions from production and life; on the other hand, when the decline in economic output is greater than the energy consumption, the carbon emission intensity will increase. Therefore, county shrinkage can directly affect carbon emission intensity, and the specific direction depends on the comparison between its impact on energy consumption and economic output.
2.3. Research Methodology
2.3.1. STIRPAT Model
The IPAT model was developed in the 1970s as a model for assessing environmental stress. This formula suggests that the environment is influenced by the interaction of three factors: population size (P), affluence (A), and technology level (T). The STIRPAT model [30] is an extension of the IPAT model and has been widely used to measure the impact of CO2 emissions since it reflects the development of energy, economic, and environmental systems under the goal of a low-carbon economy. The Kuznets hypothesis of the relationship between CO2 emissions and economic development can also be further tested. The expression of which is Equation (1):
In Equation (1), I represents the environmental impact, P represents the population factor, A represents the economic factor, and T represents the technological factor. i represents the country, t represents the year, a, b, c, and d represent the coefficients, and eit is a random perturbation term.
In the empirical analysis, the natural logarithm of both sides of the equation is generally taken to give Equation (2): According to previous studies, the population, economy, and land size of a county have a certain degree of influence on carbon emissions intensity to a certain extent and by different mechanisms. Thus, we construct an extended STIRPAT model of the influence factors of total carbon emissions intensity, which is expressed as Equation (2):
According to previous studies, the population, economy, and land size of a county have a certain degree of influence on carbon emission intensity to a certain extent and by different mechanisms. Thus, we construct an extended STIRPAT model of the influence factors of total carbon emission intensity, which is expressed as Equation (3):
where Tit denotes carbon intensity; i denotes county and t denotes year; shrink represents population shrinkage; POPit is the population size of the county; perGDP is GDP per capita; Tertiary represents the added value of the tertiary industry as a proportion of GDP. In order to test the Kuznets curve relationship between the expansion of construction land and carbon emission intensity, this study adds a Kuznets curve model including primary, secondary, and tertiary terms according to the Kuznets curve theory; different values of β5, β6, and β7 can reflect the possible relationship between construction land and its composition and carbon emission intensity (Table 1). The four types of curves are U-shaped, inverted U-shaped, N-shaped, and inverted N-shaped.

Table 1.
Four curves between construction land rate and carbon emission intensity.
2.3.2. Analysis by Population Size of the County
Further, to explore the heterogeneity of the effect of population shrinkage on the carbon intensity of counties with different population sizes in order to discover the optimal population size under the low-carbon constraint, we develop Equation (4) based on Equation (3):
where D1 and D2 are dummy variables indicating the classification of the county’s population size. The impact of changes in carbon intensity due to population shrinkage in counties of different population size classes is estimated by introducing cross-terms between the dummy variables and population shrinkage. In model (4), coefficients β1, β8, and β9 are the focus of research attention, which measure the mechanism by which population contraction affects carbon intensity in counties of different population sizes.
The international standard for county population size is 100,000, but the difference in population between counties in China can be more than 1300 times, ranging from mega-counties with populations close to 2 million to ultra-small counties with populations of less than 10,000. We used household population data from the China County Statistical Yearbook 2020 for our analysis and found that over 50% of the population size was between 100,000 and 500,000. As the county population in the sample of counties in Northeast China is slightly lower than the average county population in China, this study divides the population size into three classes: small counties with a resident population of less than 150,000; medium-sized counties with a resident population of more than 150,000 and less than 400,000; and large counties with a resident population of more than 400,000. The effect of population shrinkage on the change in the carbon intensity of counties in different population classes was estimated by introducing dummy variables with cross-terms for population shrinkage (D1 × Shrink and D2 × Shrink).
2.4. Variable Selection and Data Source
2.4.1. Explained Variable
The explanatory variable is the carbon intensity of counties in Northeast China, which is calculated using the ratio of these carbon emissions to the GDP of the corresponding county. The time span of the study is 2015–2020. The carbon emission data in this paper are based on Chen et al. [35]. The study used the particle swarm optimization–back propagation (PSO-BP) algorithm to unify the scale of the US Air Force Defense Meteorological Satellite Program’s (DMSP) and the Visible Infrared Imaging Radiometer Suite’s (VIIRS) nighttime light data to estimate CO2 emissions for 2735 counties in China from 1997–2017. The carbon emissions data from 2017 onwards are extended using linear interpolation.
2.4.2. Core Explanatory Variables
The core explanatory variables are population shrinkage (Shrink), and the cross-terms of population shrinkage (D1 × Shrink and D2 × Shrink).
Population shrinkage (Shrink) is a measure of population shrinkage. Population shrinkage is a phenomenon in which the total population (or labor force, or households) of a region with a relatively independent socio-economic system continues to decline over a certain period of time [36]. From existing studies, the proportion and extent of population shrinkage are most pronounced at the county level [37]. In terms of measurement indicators, we choose the permanent population, which is more direct and easily accessible, and easy to study on a longer time scale. Considering the comparison of the degree of population shrinkage between counties, this paper uses the annual average population change rate for analysis [38], and as population change is characterized by geometric changes, the geometric mean is used in calculating the annual average population change rate:
where Shrinkit denotes the annual average rate of population change from period t0 to t; POPit0 and POPit denote the resident population in years t0 and t, respectively; t0 is the base year 2015; and n denotes the number of years between t0 and t. According to the concept of population contraction, Shrinkit means that the county is experiencing population shrinkage, and the larger the absolute value of Shrinkit, the higher the degree of shrinkage; conversely, it is not experiencing population shrinkage.
2.4.3. Other Explanatory Variables
- Population size (POP): Permanent population is used in this paper to represent the population size factor. According to relevant studies, an increase in population size leads to an increase in the number of basic consumption units, which inevitably leads to an increase in the scale of consumption and an increase in total household carbon emissions, but is not necessarily related to changes in carbon intensity [39,40]. This paper examines whether the population size of counties in Northeast China can generate sufficient scale and agglomeration effects to reduce carbon intensity. County population data are from the China County Statistical Yearbook—County and City Volume.
- Per capita income level (PerGDP): This index is used in this paper as a factor of affluence in the STIRPAT model. Higher levels of per capita income vary, leading to rising demands on the environment and material consumption, which in turn leads to rising carbon emissions. It has been shown that carbon emissions per capita are highly positively correlated with GDP per capita, and it has been shown that the carbon emissions curve increases with GDP per capita before reaching an inflection point to achieve a ‘carbon peak’ [41].
- The added value of the tertiary industry to the GDP (Tertiary): In terms of energy consumption and carbon emission intensity of the three industries, the energy consumption and carbon emission intensity of the primary industry are lower, but their proportion tends to decrease [42]. In previous studies, the term industrial structure (IS) is usually used: the proportion of the second industrial added value to the GDP or the secondary industry as a percentage of GDP. However, in Northeast China, after a continuous contraction of each county to a higher degree of de-industrialization, there are very few industries above the scale, so we use the added value of the tertiary industry to the GDP to represent the industrial structure.
- Area of urban construction land (S): As the most important natural resource input and the main carrier of carbon emissions in the process of urbanization and industrialization, the expansion of construction land will inevitably lead to a corresponding increase in carbon emissions, which is caused by the rough use of construction land at the early stage of development. After a certain stage of urbanization and industrialization, the effect of carbon emissions will gradually decrease due to changes in the industrial structure of the land, improvements in energy technology, and even the strengthening of environmental policies and public awareness. From a theoretical point of view, the relationship between the expansion of land for construction and carbon emissions follows an inverted U-shaped curve. However, as most counties in the Northeast are small and at different stages of development, the applicability of the existing relationship has not been fully demonstrated. Explained variables and explanatory variables mentioned above are presented in Table 2 in original units.
 Table 2. Variable definitions.
Table 2. Variable definitions.
3. Results
3.1. Analysis of the Carbon Emission Intensity in Northeast China’s Counties
Northeast China’s carbon emissions intensity showed a trend of first falling and then rising. From 2015 to 2016, it declined by 7.34%, from 2.83 tons to 2.63 tons per 10,000 Yuan. Between 2016 and 2020, carbon emission intensity gradually increased. The two years with the largest year-on-year increases are 2019 and 2020. They have carbon emission intensities of 3.6 and 3.93 t/ten thousand yuan respectively. They rose by 0.52 t/ten thousand yuan and 0.33 t/ten thousand yuan respectively relative to the previous year. Macroscopically, the carbon emission intensity in Northeast China is still higher compared to that of regional counties in China [43]. This indicates that there is still much room for carbon emission reduction in Northeast China. The carbon emission intensity of small-scale counties is greater than that of medium-scale counties and large-scale counties, and the trend is roughly the same, with both showing a decline before an increase. The change in carbon emission intensity is most obvious in small-scale counties.
3.2. Parameter Estimation Results of Panel Data Model
We first conducted a correlation analysis of these variables (Table 3) to see if there was any association between each of the independent variables and carbon intensity. The results showed that each of the independent variables passed the 1% significance test for association with carbon intensity, indicating that they were associated with carbon intensity. When considering the internal relationship, POP and shrink were negatively correlated, and Tertiary was positively correlated. POP, perGDP, and S were positively correlated but not significant. It shows that larger-scale counties may have lower population shrinkage and more reasonable industrial structures. Then, we conducted a collinearity test to see if there was significant collinearity between the variables. The results showed that the mean value of the variance inflation factor was 1.216 and the maximum value was 1.475, indicating that there was no serious collinearity.

Table 3.
Results of the correlation test.
In this study, the STIRPAT model was constructed using Shrink, POP, perGDP, Tertiary, S, S2, and S3 as the explanatory variables and T as the explanatory variable and was modeled using the robust standard error method. The models involved three models, namely the mixed POOL model, the fixed effects (FE) model, and the random effects (RE) model. The model test was first conducted to facilitate the identification of the optimal model, as can be seen from Table 4: the Fisher test presented a 5% level of significance F (139,693) = 105.489, p = 0.000 < 0.05, implying that the FE model was superior relative to the POOL model. The FE model was superior. The Breusch–Pagan test showed a 5% level of significance chi (1) = 1341.546, p = 0.000 < 0.05, implying that the RE model was superior relative to the POOL model. The Hausman test showed a 5% level of significance chi (5) = 13.493, p = 0.019 < 0.05, implying that the FE model was superior compared to the RE model. Combining the above analyses, the FE model was finally used as the final result.

Table 4.
Summary of test results.
Table 5 reports the estimation results of Equation (1), where the cross-term effects are not considered and the square and cube of the building land are added in turn. Models (1), (2), and (3) are the results of the fixed effects estimation. In this study, the FE model is used as the final result, and from the above table, it can be seen that for Shrink, it presents a significance at 0.05 level and the regression coefficient value is 0.803 > 0, indicating that Shrink can have a significant positive influence relationship on carbon intensity, which is not conducive to carbon emission reduction. The impact coefficient of the Shrink indicator is low, and the difference with the influence factors of prefecture-level cities is obvious [26]. For POP, it shows significance at the 0.01 level and the regression coefficient is −0.135 < 0, indicating that POP has a significant negative effect on carbon intensity. For perGDP, it is not significant, thus indicating that perGDP does not have an effect on carbon intensity. For Tertiary, it is significant at the 0.05 level and the regression coefficient is −0.297 < 0, suggesting that Tertiary has a dampening effect on carbon intensity. The s analysis results in an inverted U-shaped curve, so there is a critical value.

Table 5.
Estimation results of the panel data model based on Equation (3).
Table 6 reports the results of the estimation of Equation (4), which estimates the change in carbon intensity due to population shrinkage for counties of different population classes by introducing a cross-term of dummy variables and population contraction. Models (4), (5), and (6) are the results of fixed effects (FE) estimation. The results of model (4) show that the coefficient of Shrink is significantly negative, indicating that the degree of population contraction contributes to the carbon intensity of the county, with each 1% increase in Shrink increasing the carbon intensity of small counties by 0.674%. The cross-term D1 × Shrink has a coefficient of 0.145, implying that a 1% increase in Shrink is associated with a 0.529% (=0.674% − 0.145%) increase in carbon intensity for medium-sized counties with populations between 100,000 and 400,000. In contrast, a large county with a population above 400,000 has a 0.393% (=0.674% − 0.281%) increase in carbon intensity. It can be seen that the increase in carbon intensity due to population contraction is different for counties of different population classes. The effect of increased carbon intensity due to population shrinkage decreases as the population size increases incrementally. Depending on the internal relationship between the various variables, population size may affect the degree of population shrinkage and further influence the industrial structure.

Table 6.
Estimation results of the panel data model based on Equation (4).
Models (5) and (6) build on (4) by adding the squared and cubed terms of S as control variables to test for environmental Kuznets curve effects. In model (5), the coefficient of Shrink is negative and passes the significance test. For a 1% increase in population shrinkage, the carbon intensity increases by 0.578% in small counties, 0.681% in medium counties, and 0.301% in large counties. The results show that in large counties, the increase in carbon intensity caused by population shrinkage is less and more suitable for green and low-carbon construction in counties. The estimation results of model (6) show that the effect of construction land on carbon emission intensity is N-shaped: first rising, then falling, then rising again. Among the other explanatory variables, the coefficient of the structural variable Tertiary is significantly negative in all three models, indicating that the increase in the share of tertiary GDP has a suppressive effect on carbon intensity; the coefficient of POP is significantly negative, but its absolute value is small, and for every 1% increase in the resident population, carbon intensity decreases by 0.012% to 0.013%.
3.3. Heterogeneity Test
As the development levels of different counties in China vary greatly, there may be multiple carbon intensity impact mechanisms in counties of different development levels. Previous studies have mostly conducted differentiated studies by region or province, and there are few cases where studies have been classified by size. Since even counties in the same region or province have huge differences in development, the findings obtained by population size are more useful for the precise implementation of differentiated planning and construction. Therefore, on the basis of the total sample, regression models are constructed for large, medium, and small county samples, respectively, so as to explore the differential impact mechanisms of carbon intensity for different population sizes, and thus seek the optimal county size under low-carbon constraints. The overall sample, comprising 140 counties, was divided into three, with 59 large counties, 66 medium-sized samples, and 15 small samples, and regression analyses were conducted separately, with the regression results summarized in Table 7, Table 8 and Table 9.

Table 7.
Large counties’ estimation results.

Table 8.
Medium counties’ estimation results.

Table 9.
Small counties’ estimation results.
For POP, large and medium counties and the regression coefficient value is less than 0, indicating that POP will have a significant negative effect relationship on carbon intensity, whereas small counties are not significant. This indicates that there is a scale and agglomeration effect that inhibits the growth of carbon intensity when the population size exceeds 150,000. For large counties, perGDP is significant at the 0.1 level and the regression coefficient is −0.079 < 0, thus indicating that perGDP has a dampening effect on carbon intensity in larger counties. In medium and small counties, perGDP remains insignificant. For Tertiary, the regression coefficients for both medium and small counties are negative and larger than the coefficients for the overall model, suggesting that increasing Tertiary has a significant dampening effect on carbon intensity in small- and medium-sized counties. Compared with other indicators, the effect of urban construction land as an indirect factor on carbon emission intensity shows significant scale differences. From the analysis of the regression results of different size samples, the coefficients of small- and medium-sized counties are similar to other indicators; the regression model for large counties is that the impact of total construction land on carbon emission intensity even exceeds the significant degree of population and economic development.
Regarding the correlation between land use for construction and carbon intensity in large counties, it can be found that in the quadratic curve fitting model, although the constant and primary coefficients can pass the 5% significance level test, the quadratic coefficients can only pass the 10% significance level test, but the linear regression has good results in all tests, so the relationship between land use for construction and carbon intensity in large counties has a not very good relationship. The relationship between land use and carbon intensity in large counties is therefore not very clear, with an inverted U-shaped curve. The results of the regression between the total amount of land used for construction and carbon intensity in medium-sized counties show that both the secondary and tertiary curves do not pass the 5% significance level test, so there is not a Kuznets inverted U-curve relationship between land use and carbon intensity in established towns, but a positive linear relationship. Land use for construction contributes to carbon intensity. Smaller counties pass the 5% significance level test for all coefficients, showing a more significant inverted U curve.
3.4. Bivariate Fit Results
In order to explore a more accurate correlation, we further adopted a curve estimation model for the analysis, comparing the significance coefficient (sig.), coefficient of determination (R2), and test value (F) of the three parameters of the bivariate multiple curve fits for the overall sample, large, and small county samples, respectively. The best-fit results for the bivariate of the four samples are shown in Table 10.

Table 10.
Bivariate best-fit results.
In the overall sample model, an inverted U-shaped Kuznets curve was observed between the total amount of land used for construction and the carbon intensity index, with the inflection point of the Kuznets curve located at the critical point of 30 km2 of total land used for construction (Figure 2a). The majority of counties have a built-up land area of 5–25 km2 and as their population shrinks, these counties lose the opportunity to continue to expand beyond the threshold. There is an inverted U-curve relationship between large and small counties and carbon intensity, with the threshold for large counties being slightly greater than 30 km2 (Figure 2b) and for small counties around 10 km2 (Figure 2d). Similar to the overall sample findings, the vast majority of counties have total built-up land below the threshold. The regression results for medium-sized counties show that both the secondary and tertiary curves do not pass the 5% significance level, whereas the positive linear relationship is more pronounced, but with a smaller coefficient (Figure 2c). An increase in the total amount of land used for construction will lead to an increase in carbon intensity, which is not conducive to carbon reduction.
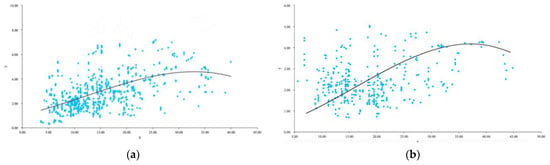
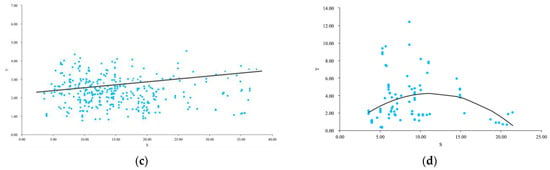
Figure 2.
Bivariate best-fit overall sample (a), large counties (b), medium counties (c), and small counties (d).
4. Discussion
4.1. Comparative Analysis of the Results
Studies have shown that at the national and provincial levels, the main influencing factors of carbon intensity are GDP per capita, consumption level per capita, and population size as typical representative indicators, which have been confirmed as consensus indicators at the macro level in national and different provincial experiments [11,44]. At the level of large- and medium-sized cities, carbon intensity is most closely related to population size, income levels, and consumption levels [14]. In addition to this, population contraction and sprawl of construction land have been shown to be correlated with carbon intensity as separate studies [26]. The results of this study, when combined with the national, provincial, and municipal levels, show the following differences.
(1) The first is that the coefficient of the effect of population contraction on carbon intensity is lower than that at the urban level. The possible reasons for this difference are: the industrial structures of the counties in the Northeast are more homogeneous, with the primary sector accounting for a larger share and less indirect effects from population loss.
(2) Secondly, the indicators characterizing population affluence have a low significance of impact and are significantly different from the prefecture-level city influences. GDP per capita reflects the affluence of the county population to some extent, but only in large counties and is not included in the model for the overall sample. Possible reasons for this variability are that GDP per capita in the counties of the Northeast is not high overall and the differences are relatively small and the small differences do not lead to technological advances or higher carbon emissions from living.
(3) Finally, the study shows that the land use factor is still a weak indirect influence relationship compared to the population and economic factors when analyzed from a national sample [45]. However, in the counties of the Northeast region, the relationship between the structural elements of land use size and carbon intensity is more or less the same as the significant degree of population and economic development. The reason for the difference is the small population size of counties in the Northeast compared to other counties in the region, which amplifies the impact of the land size factor. With a limited population, too much land for construction is not conducive to public transport, and facilities and energy supply will all increase accordingly.
4.2. Policy Implications
(1) In the construction and development of counties in Northeast China, differentiated treatment is required, and different county development paths should be taken in conjunction with the different effects of population contraction on the existence of counties of different population sizes. A scientific grasp of functional positioning and classification is needed to guide the direction of county development.
(2) For medium-sized and small counties subject to greater population contraction, attention should be paid to the low-carbon construction of the county. In addition, it is necessary to grasp the leading factors of high-carbon emissions, determine the main direction of carbon emission reduction program design, and the leading factors of high-carbon emission intensity. It is necessary to attach great importance to the role of economic development level and industrial structure in curbing carbon emission intensity, and guiding the transformation and development of population-depleted counties.
(3) Follow the changing trend of population movement in counties and prevent blind construction in depopulated counties. Strictly limiting the total amount of construction land rising close to the critical value of the Kuznets curve can solve the bottleneck of county and city construction by guiding the valued withdrawal of idle construction land indicators in rural areas and marketizing surplus construction land indicators and construction land in rural areas.
4.3. Uncertainties and Prospects
On the one hand, although the results of Chen et al. [35] are the most widely used and accurate dataset available, their core methodology is the downscaling of provincial energy carbon emissions data through nighttime lighting data. Nighttime lighting data has a limited ability to analyze areas of low population density, which includes vast rural areas. The drawbacks of DMSP data lie mainly in its fuzzy data and coarse resolution; although VIIRS can detect poorly lit areas better than DMSP, the crossing time when the satellite hosting VIIRS observes the Earth is around 1:30 am when household (or farm) lighting in rural areas is unlikely to be switched on, whereas street lights in cities are often on all night [46]. Since most counties in China currently lack statistics on carbon emissions from energy consumption, this is the best method that can be used at present. On the other hand, county-level data indicators and data quality still need to be improved due to administrative changes and lack of data. In the future, as data statistics are improved, more accurate data can be used to study the carbon intensity of county-level emissions in Northeast China.
Different counties will have different development patterns due to different geographical factors, resource conditions, and historical reasons. Counties can also be categorized into counties around major cities, specialized functional counties, counties in major agricultural production areas, and counties in key ecological functional areas. In future studies, more refined classifications can be added to analyze the future development direction and focus of counties.
5. Conclusions
We studied the characteristics and influencing factors of carbon emission intensity of counties in Northeast China by constructing the STIRPAT Model. By introducing a cross-term of dummy variables and population contraction, we estimated the non-linear effects of changes in carbon emissions in counties of different population classes due to population contraction. The following conclusions are presented:
(1) Since 2015, carbon emission intensity in the Northeast has decreased and then increased. The carbon emission intensity of small-scale counties is greater than that of medium-scale counties than large-scale counties, and the change in carbon emission intensity is most pronounced in small-scale counties.
(2) There is a general contribution to carbon intensity from population contraction in the counties of Northeast China. This effect decreases with population size and has the least effect on large counties. As for other impression factors, population size and industrial structure factors play a suppressive role in carbon intensity. The reason for this may be that, with a shrinking population, certain population size can ensure the operation of infrastructure and public transport within the county; the added value of the tertiary industry is higher in counties, which tends to mean that the county is moving away from the old pattern of development in the Northeast and creating new GDP growth points, thus reducing carbon intensity.
(3) A study of the Kuznets curve relationship between total construction land and carbon emission intensity shows that the relationship between total construction land and carbon emission intensity in counties in the Northeast region generally has an inverted U-shaped Kuznets curve relationship, with a critical point at about 30 km2. Only in medium-sized counties is the relationship insignificant and linear, with the critical point at 30 km2 for large counties and 10 km2 for small counties.
Author Contributions
Conceptualization, H.J., Z.K. and J.L.; Data curation, T.Z. and X.G.; Formal analysis, T.Z. and X.G.; Investigation, J.L.; Methodology, T.Z. and H.J.; Project administration, J.L.; Resources, Z.K.; Software, X.G.; Supervision, Z.K.; Validation, T.Z.; Writing—original draft, T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work research was funded by a project of the National Social Science Foundation of China (Grant No:51678178), a National Key Research and Development Program Topics (Grant No:2018YFC0704705), and a project of Natural Science Foundation of Heilongjiang Province (Grant No: E2015011).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dietz, T.; Rosa, E. Rethinking the environmental impacts of population, affluence and technology. Hum. Ecol. Rev. 1994, 1, 277–300. [Google Scholar]
- Oelkers, E.H.; Cole, D.R. Carbon dioxide sequestration a solution to a global problem. Elements 2008, 4, 305–310. [Google Scholar] [CrossRef]
- International Energy Agency. Available online: http://www.iea.org/ (accessed on 3 July 2022).
- Greening, L.A.; Davis, W.B.; Schipper, L. Decomposition of aggregate carbon intensity for the manufacturing sector: Comparison of declining trends from 10 OECD countries for the period 1971–1991. Energy Econ. 1998, 20, 43–65. [Google Scholar] [CrossRef]
- Knapp, T.; Mookerjee, R. Population growth and global CO2 emissions: A secular perspective. Energy Policy 1996, 24, 31–37. [Google Scholar] [CrossRef]
- Wang, P.; Wu, W.; Zhu, B.; Wei, Y. Examining the impact factors of energy-related CO2 emissions using the STIRPAT model in Guangdong Province, China. Appl. Energy 2013, 106, 65–71. [Google Scholar] [CrossRef]
- Ma, L.J.C. Urban administrative restructuring, changing scale relations and local economic development in China. Political Geogr. 2005, 24, 477–497. [Google Scholar] [CrossRef]
- Gao, Z.; Li, S.; Cao, X.; Li, Y. Carbon Emission Intensity Characteristics and Spatial Spillover Effects in Counties in Northeast China: Based on a Spatial Econometric Model. Land 2022, 11, 753. [Google Scholar] [CrossRef]
- Jotzo, F.; Pezzey, J.C.V. Optimal intensity targets for greenhouse gas emissions trading under uncertainty. Environ. Resour. Econ. 2007, 38, 259–284. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, Z.; Ye, X.; Wei, Y.D. Spatiotemporal dynamics of carbon intensity from energy consumption in China. J. Geogr. Sci. 2014, 24, 631–650. [Google Scholar] [CrossRef] [Green Version]
- Dong, F.; Yu, B.; Hadachin, T.; Dai, Y.; Wang, Y.; Zhang, S.; Long, R. Drivers of carbon emission intensity change in China. Resour. Conserv. Recycl. 2018, 129, 187–201. [Google Scholar] [CrossRef]
- Nag, B.; Parikh, J. Indicators of carbon emission intensity from commercial energy use in India. Energy Econ. 2000, 22, 441–461. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, Y. Spatial effects of carbon emission intensity and regional development in China. Environ. Sci. Pollut. Res. 2021, 28, 14131–14143. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Deng, X.; Phillips, F.; Fang, C.; Wang, C. Impacts of industrial structure and technical progress on carbon emission intensity: Evidence from 281 cities in China. Technol. Forecast. Soc. Chang. 2020, 154, 119949. [Google Scholar] [CrossRef]
- Li, H.; Wu, L. Analysis of Hubei province industry’s carbon emissions based on the LMDI. In Proceedings of the 2nd International Conference on Renewable Energy and Environmental Technology (REET), Dalian, China, 19–20 August 2014; pp. 1865–1868. [Google Scholar]
- Li, S.P.; Wang, Q.; Meng, Y. Analysis on the status and influencing factors of industrial carbon emissions in Northeast China. In Proceedings of the 3rd International Conference on Energy, Environment and Sustainable Development (EESD 2013), Shanghai, China, 12–13 November 2013; pp. 866–869. [Google Scholar]
- Dietzenbacher, E.; Los, B. Structural decomposition techniques: Sense and sensitivity. Econ. Syst. Res. 1998, 10, 307–324. [Google Scholar] [CrossRef]
- Zha, D.L.; Zhou, D.Q. The inequality about provincial energy efficiency and its related CO2 emission: Decomposition based on kaya. Syst. Eng. 2007, 25, 65–71. [Google Scholar]
- Wang, Y.; Yang, G.; Dong, Y.; Cheng, Y.; Shang, P. The Scale, Structure and Influencing Factors of Total Carbon Emissions from Households in 30 Provinces of China—Based on the Extended STIRPAT Model. Energies 2018, 11, 1125. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Wang, S.; Wang, J. Examining the influences of urbanization on carbon dioxide emissions in the Yangtze River Delta, China: Kuznets curve relationship. Sci. Total Environ. 2019, 675, 472–482. [Google Scholar] [CrossRef]
- Al-mulali, U. Factors affecting CO2 emission in the Middle East: A panel data analysis. Energy 2012, 44, 564–569. [Google Scholar] [CrossRef]
- Wolff, M. Understanding the role of centralization processes for cities–Evidence from a spatial perspective of urban Europe 1990–2010. Cities 2018, 75, 20–29. [Google Scholar] [CrossRef]
- Long, Y.; Wu, K. Shrinking cities in a rapidly urbanizing China. Environ. Plan. A 2016, 48, 220–222. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Wang, M.; Qiang, W.; Wu, K.; Wang, X. Urban form, shrinking cities, and residential carbon emissions: Evidence from Chinese city-regions. Appl. Energy 2020, 261, 114409. [Google Scholar] [CrossRef]
- Xiao, H.; Duan, Z.; Zhou, Y.; Zhang, N.; Shan, Y.; Lin, X.; Liu, G. CO2 emission patterns in shrinking and growing cities: A case study of Northeast China and the Yangtze River Delta. Appl. Energy 2019, 251, 113384. [Google Scholar] [CrossRef]
- Zeng, T.; Jin, H.; Geng, Z.; Kang, Z.; Zhang, Z. The Effect of Urban Shrinkage on Carbon Dioxide Emissions Efficiency in Northeast China. Int. J. Environ. Res. Public Health 2022, 19, 5772. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.Y. Revitalizing old industrial base of Northeast China: Process, policy and challenge. Chin. Geogr. Sci. 2008, 18, 109–118. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Y.; Ji, G.; Wang, Z. Residential carbon dioxide emissions at the urban scale for county-level cities in China: A comparative study of nighttime light data. J. Clean. Prod. 2018, 180, 198–209. [Google Scholar] [CrossRef]
- Liu, X.Y.; Duan, Z.Y.; Shan, Y.L.; Duan, H.Y.; Wang, S.; Song, J.N.; Wang, X.E. Low-carbon developments in Northeast China: Evidence from cities. Appl. Energy 2019, 236, 1019–1033. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Liu, L.C.; Wu, G.; Tsai, H.T.; Wei, Y.M. Changes in carbon intensity in China: Empirical findings from 1980–2003. Ecol. Econ. 2007, 62, 683–691. [Google Scholar] [CrossRef]
- Hartt, M. How cities shrink: Complex pathways to population decline. Cities 2018, 75, 38–49. [Google Scholar] [CrossRef]
- Großmann, K.; Bontje, M.; Haase, A.; Mykhnenko, V. Shrinking cities: Notes for the further research agenda. Cities 2013, 35, 221–225. [Google Scholar] [CrossRef]
- Schilling, J.; Logan, J. Greening the Rust Belt: A Green Infrastructure Model for Right Sizing America’s Shrinking Cities. J. Am. Plan. Assoc. 2008, 74, 451–466. [Google Scholar] [CrossRef]
- Glaeser, E.L.; Kahn, M.E. The greenness of cities: Carbon dioxide emissions and urban development. J. Urban Econ. 2010, 67, 404–418. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Gao, M.; Cheng, S.; Hou, W.; Song, M.; Liu, X.; Liu, Y.; Shan, Y. County-level CO2 emissions and sequestration in China during 1997–2017. Sci. Data 2020, 7, 391. [Google Scholar] [CrossRef] [PubMed]
- Rieniets, T. Shrinking cities: Causes and effects of urban population losses in the twentieth century. Nat. Cult. 2009, 4, 231–254. [Google Scholar] [CrossRef]
- Guan, D.; He, X.; Hu, X. Quantitative identification and evolution trend simulation of shrinking cities at the county scale, China. Sustain. Cities Soc. 2021, 65, 102611. [Google Scholar] [CrossRef]
- Thomas, L. Monitoring long-term population change: Why are there so many analysis methods? Ecology 1996, 77, 49–58. [Google Scholar] [CrossRef]
- Aldy, J.E. Divergence in state-level per capita carbon dioxide emissions. Land Econ. 2007, 83, 353–369. [Google Scholar] [CrossRef]
- Poumanyvong, P.; Kaneko, S. Does urbanization lead to less energy use and lower CO2 emissions? A cross-country analysis. Ecol. Econ. 2010, 70, 434–444. [Google Scholar] [CrossRef]
- Moomaw, W.R.; Unruh, G.C. Are environmental Kuznets curves misleading us? The case of CO2 emissions. Environ. Dev. Econ. 1997, 2, 451–463. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Lin, B. Impacts of urbanization and industrialization on energy consumption/CO2 emissions: Does the level of development matter? Renew. Sustain. Energy Rev. 2015, 52, 1107–1122. [Google Scholar] [CrossRef]
- Wenmeng, Y.; Tingting, Z.; Dajun, S. County-level spatial pattern and influencing factors evolution of carbon emission intensity in China: A random forest model analysis. China Environ. Sci. 2022, 1–10. Available online: https://kns.cnki.net/kcms/detail/11.2201.X.20220219.1311.002.html (accessed on 3 July 2022).
- Wei, Y.M.; Liu, L.C.; Fan, Y.; Wu, G. The impact of lifestyle on energy use and CO2 emission: An empirical analysis of China’s residents. Energy Policy 2007, 35, 247–257. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, H.; Wang, R. Influence Mechanism of County Scale and Structure on the Household Carbon Emissions and its Planning Strategies. IOP Conf. Ser. Earth Environ. Sci. 2019, 330, 032021. [Google Scholar] [CrossRef]
- Chen, X.; Nordhaus, W. A test of the new VIIRS lights data set: Population and economic output in Africa. Remote Sens. 2015, 7, 4937–4947. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).