Abstract
Modern photovoltaic (PV) systems have received significant attention regarding fault detection and diagnosis (FDD) for enhancing their operation by boosting their dependability, availability, and necessary safety. As a result, the problem of FDD in grid-connected PV (GCPV) systems is discussed in this work. Tools for feature extraction and selection and fault classification are applied in the developed FDD approach to monitor the GCPV system under various operating conditions. This is addressed such that the genetic algorithm (GA) technique is used for selecting the best features and the artificial neural network (ANN) classifier is applied for fault diagnosis. Only the most important features are selected to be supplied to the ANN classifier. The classification performance is determined via different metrics for various GA-based ANN classifiers using data extracted from the healthy and faulty data of the GCPV system. A thorough analysis of 16 faults applied on the module is performed. In general terms, the faults observed in the system are classified under three categories: simple, multiple, and mixed. The obtained results confirm the feasibility and effectiveness with a low computation time of the proposed approach for fault diagnosis.
1. Introduction
Renewable energy technology has advanced rapidly, and it now serves as a primary source of electricity in many countries. According to the latest reports, renewable energy produced of global electricity in 2016 [1]. PV faults have arisen as a result of the recent increase in PV generation and wide use of it around the world, attracting much attention. These faults have a significant impact on the PV system’s dependability and performance. Partial shading faults, temperature faults, module aging, cell damage, and short-circuit or open-circuit of PV modules are some of the causes of these faults [2,3,4]. Temperature faults are caused by the high temperature of the PV panels’ surface after sunlight absorption. The presence of clouds, fallen leaves, or dust causes partial shading faults. Due to module aging, both short- and open-circuit faults occur after a long period of PV operation. The notion of fault location in a PV system is extremely useful in preventing system degradation and ensuring system reliability.
PV system faults can be classified into three groups based on their duration: abrupt, intermittent, and incipient fault. Line-to-ground or line-to-line short circuits, open-circuit faults, connecter disconnection, and junction box faults are examples of permanent or abrupt faults that happen because the PV array is damaged. Permanent faults are defined as hot spots [5,6].
Partially shaded faults or environmental stress are examples of temporary or intermittent faults that clear or change over time (e.g., dust or contamination). The most difficult problems to discover are incipient faults, which are minor and change slowly over time, making them difficult to detect at first. If they are not detected early, they can cause delayed damage to PV cells, which can lead to serious difficulties. On both the DC and AC sides, incipient faults can occur. Examples of DC-side faults (PV module and DC/DC converter sides) include solar cell yellowing and browning, delamination, cracks, bubbles, and faults in the anti-reflective coating. Examples of AC-side faults (inverter side) include insulated-gate bipolar transistor (IGBT) faults, overheating, aging, and wiring degradation.
Several research works have recently focused on the FDD in PV systems utilizing computational intelligence and machine learning techniques, both of which are data-driven methodologies based on historical data collected during PV system operation [7,8,9]. Among them are those that make use of artificial neural networks (ANNs) and fuzzy logic. The artificial neural network [10,11,12] is a method for simulating the human brain’s problem-solving capabilities. For example, ref. [13] proposes a simple technique based on the wavelet transform that uses fewer resources. The standard deviations of the grid voltage wavelet coefficients are used in this method to detect PV faults.
Using a deep learning technique, ref. [14] introduces intelligent fault pattern recognition of aerial PV module images to fix low performance in a flexible and reliable manner. A convolutional neural network (CNN) is used to classify faults in this case.
In addition, in the outside operation conditions of the PV system, an FDD approach based on fuzzy classifiers for detecting a rise in series resistances has been devised [14]. A decision tree (DT) has been designed for the detection of numerous common faults in PV systems [15]. Reference [16] presented the random forest (RF) ensemble learning technique for the detection and diagnosis of PV early faults. Some fault features, such as the operating real-time voltage and current strings, are considered by the RF technique. It also employs a grid-search method to optimize the RF model parameters.
In the literature, many techniques are proposed to eliminate the correlations between the variables such as principal component analysis (PCA), which is applied to extract features by transforming the dataset variables into latent variables [17,18].
The main objective of this paper is to propose an FDD framework based on the GA and ANN paradigms that can diagnose GCPV faults. In the developed approach, the GA tool is applied for feature extraction and selection, and the ANN is used for fault classification. The implemented GA-based ANN paradigm is developed to monitor the GCPV system under various operating conditions. The diagnosis effectiveness is assessed using different indicators using data extracted from several working modes of the GCPV system. A thorough analysis of sixteen faults used on the module is presented. The faults occurring in the system are categorized into three classes: simple, multiple, and mixed. The obtained results show the performances of the proposed GA-based ANN in terms of classification accuracy and computation time during the fault diagnosis phase.
2. Models
2.1. Artificial Neural Network
The artificial neural network (ANN, for simplicity often abbreviated as NN only) is made up of an input layer of neurons, one or two hidden layers of neurons (or even three), and a final layer of output neurons. A typical architecture is depicted in Figure 1, which also includes lines connecting neurons. Weight is a numerical value assigned to each connection. In the hidden layer, the output of neuron i is .
where is the activation function, N is the number of input neurons, are the weights, are the input neurons’ inputs, and are the hidden neurons’ threshold terms. The objective of the activation function is to limit the value of the neuron so that the neural network is not paralyzed by divergent neurons, in addition to introducing nonlinearity into the neural network.
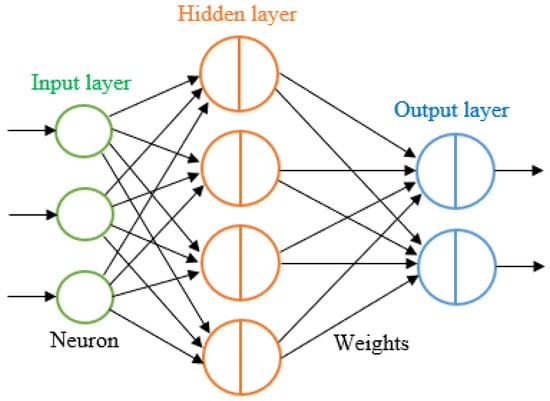
Figure 1.
Architecture of a neural network.
The sigmoid function is a prominent example of an activation function as defined in Equation (2). Other activation functions include the arc tangent and hyperbolic tangent. They have a similar response to inputs as the sigmoid function, but their output ranges are different.
It has been demonstrated that a neural network built in this manner may approximate any computable function to any precision. For the function being approximated by the neural network, the numbers given to the input neurons are independent variables, and the numbers returned from the output neurons are dependent variables. When data are suitably encoded, the inputs and outputs of a neural network can be binary (such as 0 or 1) or even symbols (red, blue, etc.). This property gives neural networks a wide range of applications.
Following the architecture, we go through training, which is an important part of every neural network application. A neural network is trained by giving it a collection of input data called a training set, similar to how humans learn by example. The target outputs of the training data are known; therefore, the goal of the training is to reduce an error function, which is generally the sum of the squared differences between the neural network outputs and the desired outputs, by modifying the weights of the connected neurons.
When experimenting with neural network architectures, a separate dataset known as the validation set can be used on the trained neural networks. The top performer is then chosen as the best choice. After validation, a separate dataset called the test set is utilized to establish the neural network’s performance level, which indicates how confident we are while utilizing the neural network. It is important to understand that a neural network cannot learn something that is not in the training set.
As a result, the training set must be large enough for the neural network to memorize the features included therein. On the other hand, if the training set contains too many irrelevant features, the neural network’s resources (weights) may be wasted fitting the noise. To deploy neural networks successfully, smart data selection and/or representation are required [19].
2.2. Genetic Algorithm
The genetic algorithm (GA) was first used by John Holland in Adaptation in Natural and Artificial Systems in 1975. Genetic algorithms are a group of computational models that are based on evolutionary principles. Although genetic algorithms have been used in a wide range of problems, they are frequently thought of as function optimizers.
The genetic algorithm is a highly optimized method based on natural selection mechanics and genetics. For extreme multivariable functions, the genetic algorithm is an adaptive heuristic search strategy. Figure 2 shows a procedural implementation of a genetic algorithm.
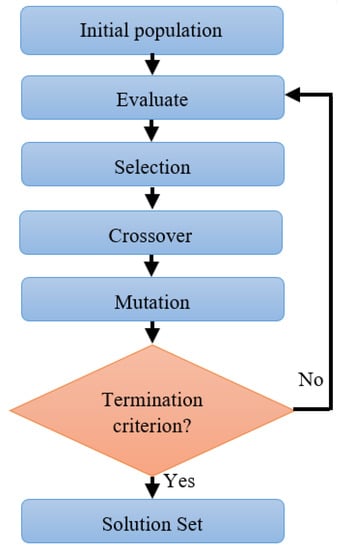
Figure 2.
Basic architecture of genetic algorithm.
The main steps in GA are the following:
- Initialization: The initial population is produced at random throughout the search space or by the user.
- Evaluation: After the population is initialized, the fitness values of the possible solutions are evaluated.
- Selection: The fittest chromosomes are more likely to be picked for the following generation after examination. We must first compute the fitness of each chromosome in order to calculate the fitness probability.
- Crossover: Crossover is the process of combining two or more parental solutions to create new, maybe better solutions. Crossover can be accomplished in a variety of ways. Select a point in the parent chromosome at random (single or several sites, depending on the crossover method) before exchanging sub-chromosomes.
- Mutation: After crossover on two or more parental chromosomes, mutation alters a solution at random. There are various types of mutation methods. The gen is replaced with a new value at random positions during the mutation process [20,21].
2.3. Proposed Method
PV systems consist of data collection, which is composed of many variables (…); since these data are correlated, many techniques are proposed to eliminate this limit such as principal component analysis (PCA), which is used to extract features by transforming the dataset variables into latent variables [17,18,22,23]. For this stage, the genetic algorithm (GA) is implemented. Figure 3 shows the model generation and testing phases in the classification of GCPV faults.
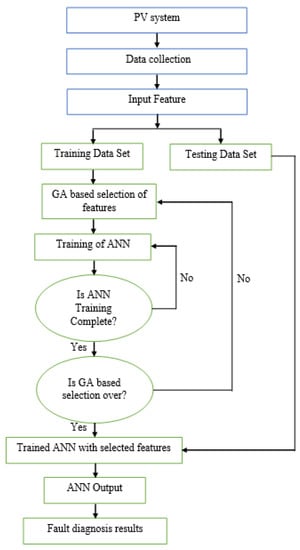
Figure 3.
GA-based NN strategy.
The GA-based ANN divides the input dataset into training and testing subsets in order to categorize the operating modes and discriminate between the classes. In the training phase, starting with randomly produced chromosomes, a population of ten individuals was employed. This size was designed to ensure a high level of interchange between various chromosomes and to limit the chance of population convergence. The most relevant features were selected using the GA tool. Then, an ANN was trained using arbitrary collections of final features. The estimated classification model is the last step. The GA approach selects the best features of the test sample data that belong to a certain class during the testing phase. Following that, the ANN classifies the selected features using the model that was computed during the training stage. The classification involves the consideration of the dataset before transferring the data to a classifier. It is recommended to consider only an important feature for selection. As a result, it is useful for choosing the relevant and pertinent features in fault diagnosis. In addition, the feature selection is used during the classification of 16 different faults (simple, multiple, and mixed) to decrease the workload of the classifier and reduce the computation time.
In Figure 4, the ANN-based GA reduces the redundancy within the input data and provides more relevance between input/output data. Then, in the evaluate step, we calculate the input feature subsets by applying the ANN, which maximizes the mutual data between features. Finally, the crossover and mutation steps are used to detect the best features by minimizing the redundancy-based evaluate step. The GA selects the subset of features sent to the ANN for computing the fitness value. At the final stage, the GA identifies an optimal subset of the feature. Next, to validate the robustness of the GA, the best features are fed to another proposed classifier, such as LSTM [24,25], CNN [26,27], FFNN [28,29], CFNN [30,31], or RNN [32,33]. The proposed technique (as well as other known methods for fault diagnosis in PV arrays) is presented in Figure 4 as a flow chart.
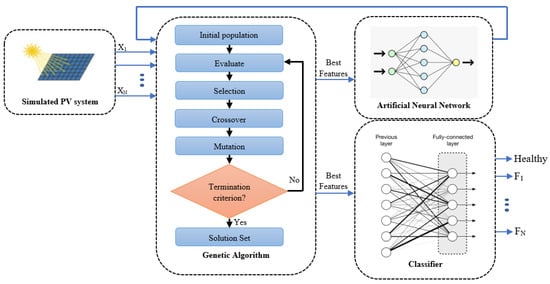
Figure 4.
Flow chart of diagnostic procedure.
3. Case Study Experiment
3.1. Application to Grid-Connected PV Systems
Figure 5 presents a PV system configuration with a DC bus voltage of 500 (V). The PV side consists of three PV arrays delivering a maximum power of 4 kW each. A single PV array set consists of 2 parallel strings where each string has 24 modules connected in series. Each module contains 20 cells (see Figure 6).
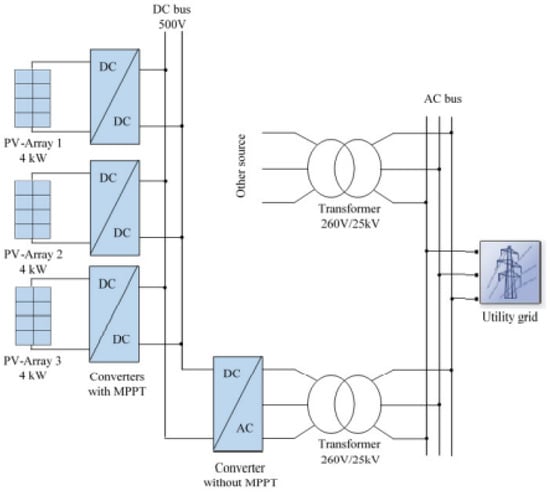
Figure 5.
Scheme of a parallel structure on a direct bus.
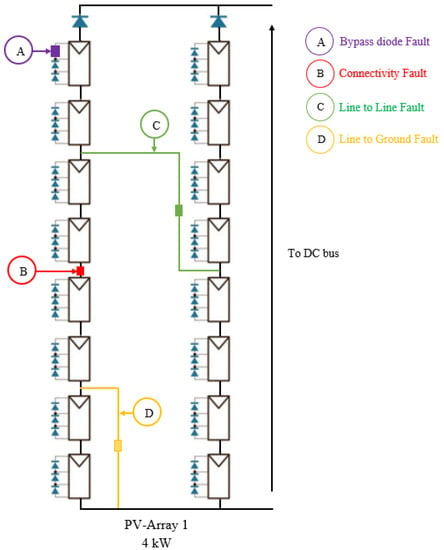
Figure 6.
Used structure to associate photovoltaic panels.
In this work, we injected different scenarios in the PV1 and PV2 systems, which included five types of faults, as indicated in Table 1:

Table 1.
Description and characteristic of the different labeled injected faults.
A simple fault in contains four scenarios of faults, A bypass diode fault (fault1) is emulated by varying the resistance. The connectivity fault (fault2) is considered in string 1, between two modules. fault2 is modeled by a serial variable resistance (Rf2) at one point. The resistance variation represents the state of the considered fault. The two faults line-to-line fault and line-to-ground fault (fault3 and fault4) are described by the variation in the resistances Rf3 and Rf4, respectively. Rf3 is located between two different points, and Rf4 is located between one point and the ground. Resistive faults with equal to 0 and infinity are considered for fault1 and fault2. In fault3 and fault4, resistive faults equal to 10 and 20 () are settled. As shown in Figure 6, 16 different scenarios can be generated from those four faults.
The same simple faults are injected in PV2.
The second scenario is about multiple faults, which present more than onefault in one PV, injected in PV1 and PV2.
Finally, mixed faults represent several faults in both PVs at the same time.
Experimental data variables were collected to prepare for the various tests performed for fault classification purposes. The PV healthy state is classified as class , whereas the other 16 operating modes are classified as classes , respectively. The dataset collected from the PV system was divided into two subsets; training (4000 samples) and testing (200 samples) (please refer to Table 2).

Table 2.
Construction of database for PV fault diagnosis system.
Table 3 contains a variety of simulated variables that are needed to carry out the various tests for FDD.

Table 3.
Variables’ description.
3.2. Performance Metrics
On a grid-connected PV system, the proposed fault diagnosis approaches were validated. Accuracy, precision, recall, and computation time (CT) were the adopted criteria. The accuracy was calculated by dividing the total number of input samples by the number of correct predictions.
Precision is defined as the ratio of the true positive results to the positive results predicted by the classifier.
Recall is the ratio of the number of accurate predictions to the total number of input samples.
Computation time (CT (s)) is the time it takes to run the algorithm.
The number of samples correctly identified (true positive), the number of samples incorrectly dismissed (false positive), and the number of samples incorrectly identified (false negative) are all represented by the symbols TP, FP, and FN.
3.3. Fault Classification Results
To obtain classification accuracy and demonstrate the efficacy of the presented methodologies for FDD purposes, a 10-fold cross-validation approach was adopted, and we chose 50 as the Maxepochs with 10 Hiddens. The healthy operation was assigned to class , while the 16 faulty modes (–) were assigned to classes –.
In the first stage, PV data were applied to collect and label the database in faulty mode. Then, we used the labeled data as inputs for the presented approaches. The main idea of the ANN-based GA is to decrease the computational time of the ANN model. A confusion matrix is offered to further highlight the diagnostic performance of the proposed approaches (see Table 4 and Table 5). The confusion matrix is a visual representation of the proposed algorithms’ performance. The columns represent instances in a predicted class, while the rows represent occurrences in an actual class. In addition, the confusion matrix shows which samples were correctly identified and which were misclassified for each condition mode ( to ) for the GCPV system. The two proposed algorithms identify 2000 samples among 2000 for the healthy case in the GCPV systems, which is attributed to class (true positive). Furthermore, the detection precision and recall are also . As a result, this class has no misclassification.

Table 4.
Confusion matrix ANN in testing phase.

Table 5.
Confusion matrix for ANN-based GA in testing phase.
Table 4, which presents the confusion matrix of the proposed ANN method in the GCPV system, shows that, for the faulty case (), the precision is and the recall is . In this case, 354 samples are identified as fault10 among 2000 assigned to class . For the faulty case (), the precision is and the recall is . In this case, 488 samples are identified as fault3 among 2000 assigned to class . For the faulty case (), the precision is and the recall is . In this case, 1566 samples are identified as fault1 among 2000 assigned to class . Finally, for the faulty case (), the precision is and the recall is . In this case, 2000 samples are identified as fault6.
Table 5m which presents the confusion matrix of the proposed NN-based GA in the GCPV system shows that for the faulty case (), the precision is and the recall is . In this case, 449 samples are identified as fault10 among 2000 assigned to class . For the faulty case (), the precision is and the recall is . In this case, 972 samples are identified as fault3 among 2000 assigned to class . For the faulty case (C10), the precision is and the recall is . In this case, 1299 samples are identified as fault1 among 2000 assigned to class . Finally, for the faulty case (), the precision is and the recall is . In this case, 164 and 1031 samples are identified as fault6 and fault7 among 2000 assigned to class and .
The performance of the proposed NN and NN-based GA approaches is shown in Table 6. Furthermore, as compared to the NN with the GA method, the computation time is decreased by more than while maintaining about the same accuracy. Applying the GA shows that the number of input features is decreased; from 8 features (variables), we obtain just 2 important ones (1,2), which presents the simple and multiple faults in PV1. Furthermore, we note that the computation time is decreased as well, from 0.28 s to 0.15 s, while it maintains almost the same accuracy from to . The next scenario in PV2, the number of features (3,4) and the computation time are reduced, although the accuracy keeps the same values. Regarding the third one, the number of features is decreased as well; it provides 4 variables (1,2,3,4) from 8 features. It provides the same accuracy, precision, and recall: ; at the same time, it minimizes the computation time from 0.30 s to 0.20 s. The last scenario looks like the previous one, reducing the number of variables from 8 to 4 features (1,2,3,4)f, which presents all faults, and the accuracy is almost the same: to . In addition, the computation time is reduced from 0.98 s to 0.40 s.

Table 6.
The performance of the proposed ANN and GA-based ANN approaches.
To validate the robustness and effectiveness of our method, we propose other classifiers such as the recurrent neural network (RNN), long short-term memory (LSTM), convolution neural network (CNN), feed forward neural network (FFNN), and cascade forward neural network (CFNN).
The architecture of the CNN developed in this work is composed of 26 layers: input layer, six convolution layers, five batch normalization layers, five max pooling layers, six ReLU layers, fully connected layer, sotfmax layer, and output layer. The number of filters used in the convolutional layers is 8, 16, 32, 64, 128, and 256, respectively. Each convolutional layer is followed by a batch normalization layer. A fully connected dense layer having six nodes with the softmax activation follows the max pooling block. We set 50 epochs and 250 as the miniBatchsize for our network. We used “ReLU” as the activation function.
The architecture of the proposed LSTM is composed of ten layers: an input layer, 3 LSTM hidden layers, 3 dropout layers, a fully connected layer, a softmax layer, and an output layer. The LSTM layers are composed of three hidden layers with 50 nodes in the first layer, 10 nodes in the second layer, and 6 nodes in the third layer. The fully connected layer is composed of six nodes.
In the architecture of the RNN, we chose 50 epochs as the Maxepochs with 10 Hiddens.
In the architecture of the FFNN, we chose 50 epochs as the Maxepochs with 10 Hiddens.
Finally, in the architecture of the FFNN, we chose 50 epochs as the Maxepochs with 10 Hiddens.
Table 7 summarizes the performances of the proposed method. The LSTM and CNN showed that the computation time is reduced and maintains almost the same accuracy, recall, and precision: 5.05 s to 2.84 s for LSTM, 6.2 s to 4.42 s for CNN, 0.85 s to 0.23 s for FFNN, and 0.64 s to 0.20 s for CFNN. In addition to the RNN, which provides an accuracy from 61.82% to 64.70%, it reduces the computation time by more than 50%.

Table 7.
Summary of the performances of the proposed methods.
4. Conclusions
This research examined the fault detection and diagnosis (FDD) issue for grid-connected PVs (GCPVs). The developed technique uses a genetic-algorithm (GA)-based artificial neural network (ANN) for FDD purposes. The primary objective is to decrease the number of input features, presenting different scenarios of faults (simple, multiple, and mixed) using GA. The number of selected features was reduced while retaining only the non-redundant information. Finally, the ANN classifier was used with the selected features to address the FDD issue. The results of the simulation demonstrated that the suggested techniques offer a good trade-off between low computing time and maintaining the same performance. The proposed GA-based ANN approach was developed to monitor the GCPV systems under normal and faulty conditions. Different cases were investigated in order to show the robustness and the efficiency of the developed approach. The proposed GA-based ANN method only uses available measurements (GCPV currents and voltages), which avoids extra hardware and costs.
Author Contributions
A.H. established the major part of the present work which comprises modeling, simulation and analyses of the obtained results. M.H., M.M., K.A., K.B., H.N., M.N. have earnestly contributed to verifying the work and finalizing the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Qatar National Research Fund (a member of the Qatar Foundation).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| FDD | Fault detection and diagnosis |
| FS | Feature selection |
| GA | Genetic algorithm |
| PV | Photovoltaic |
| GCPV | Grid-connected PV |
| PCA | Principal component analysis |
| KPCA | Kernel PCA |
| CT | Computation time |
| CM | Confusion matrix |
References
- Pablo-Romero, M.P.; Sánchez-Braza, A.; Galyan, A. Renewable energy use for electricity generation in transition economies: Evolution, targets and promotion policies. Renew. Sustain. Energy Rev. 2021, 138, 110481. [Google Scholar] [CrossRef]
- Appiah, A.Y.; Zhang, X.; Ayawli, B.B.K.; Kyeremeh, F. Review and performance evaluation of photovoltaic array fault detection and diagnosis techniques. Int. J. Photoenergy 2019, 2019, 6953530. [Google Scholar] [CrossRef]
- Ndjakomo Essiane, S.; Gnetchejo, P.J.; Ele, P.; Chen, Z. Faults detection and identification in PV array using kernel principal components analysis. Int. J. Energy Environ. Eng. 2022, 13, 153–178. [Google Scholar] [CrossRef]
- Gul, S.; Ul Haq, A.; Jalal, M.; Anjum, A.; Khalil, I.U. A unified approach for analysis of faults in different configurations of PV arrays and its impact on power grid. Energies 2019, 13, 156. [Google Scholar] [CrossRef] [Green Version]
- Aziz, F.; Haq, A.U.; Ahmad, S.; Mahmoud, Y.; Jalal, M.; Ali, U. A novel convolutional neural network-based approach for fault classification in photovoltaic arrays. IEEE Access 2020, 8, 41889–41904. [Google Scholar] [CrossRef]
- Chine, W.; Mellit, A.; Lughi, V.; Malek, A.; Sulligoi, G.; Pavan, A.M. A novel fault diagnosis technique for photovoltaic systems based on artificial neural networks. Renew. Energy 2016, 90, 501–512. [Google Scholar] [CrossRef]
- Ammiche, M.; Kouadri, A.; Halabi, L.M.; Guichi, A.; Mekhilef, S. Fault detection in a grid-connected photovoltaic system using adaptive thresholding method. Sol. Energy 2018, 174, 762–769. [Google Scholar] [CrossRef]
- Mekki, H.; Mellit, A.; Salhi, H. Artificial neural network-based modelling and fault detection of partial shaded photovoltaic modules. Simul. Model. Pract. Theory 2016, 67, 1–13. [Google Scholar] [CrossRef]
- Shrikhande, S.; Varde, P.; Datta, D. Prognostics and health management: Methodologies & soft computing techniques. In Current Trends in Reliability, Availability, Maintainability and Safety; Springer: Berlin/Heidelberg, Germany, 2016; pp. 213–227. [Google Scholar]
- Ghadami, N.; Gheibi, M.; Kian, Z.; Faramarz, M.G.; Naghedi, R.; Eftekhari, M.; Fathollahi-Fard, A.M.; Dulebenets, M.A.; Tian, G. Implementation of solar energy in smart cities using an integration of artificial neural network, photovoltaic system and classical Delphi methods. Sustain. Cities Soc. 2021, 74, 103149. [Google Scholar] [CrossRef]
- Marugán, A.P.; Márquez, F.P.G.; Perez, J.M.P.; Ruiz-Hernández, D. A survey of artificial neural network in wind energy systems. Appl. Energy 2018, 228, 1822–1836. [Google Scholar] [CrossRef] [Green Version]
- Garud, K.S.; Jayaraj, S.; Lee, M.Y. A review on modeling of solar photovoltaic systems using artificial neural networks, fuzzy logic, genetic algorithm and hybrid models. Int. J. Energy Res. 2021, 45, 6–35. [Google Scholar] [CrossRef]
- Kim, I.S. On-line fault detection algorithm of a photovoltaic system using wavelet transform. Sol. Energy 2016, 126, 137–145. [Google Scholar] [CrossRef]
- Spataru, S.; Sera, D.; Kerekes, T.; Teodorescu, R. Detection of increased series losses in PV arrays using Fuzzy Inference Systems. In Proceedings of the 2012 38th IEEE Photovoltaic Specialists Conference, Austin, TX, USA, 3–8 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 000464–000469. [Google Scholar]
- Zhao, Y.; Yang, L.; Lehman, B.; de Palma, J.F.; Mosesian, J.; Lyons, R. Decision tree-based fault detection and classification in solar photovoltaic arrays. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 93–99. [Google Scholar]
- Chen, Z.; Han, F.; Wu, L.; Yu, J.; Cheng, S.; Lin, P.; Chen, H. Random forest based intelligent fault diagnosis for PV arrays using array voltage and string currents. Energy Convers. Manag. 2018, 178, 250–264. [Google Scholar] [CrossRef]
- Hajji, M.; Harkat, M.F.; Kouadri, A.; Abodayeh, K.; Mansouri, M.; Nounou, H.; Nounou, M. Multivariate feature extraction based supervised machine learning for fault detection and diagnosis in photovoltaic systems. Eur. J. Control 2021, 59, 313–321. [Google Scholar] [CrossRef]
- Mohamed-Faouzi, H. Détection et Localisation de Défauts par Analyse en Composantes Principales. Ph.D. Thesis, Institut National Polytechnique de Lorraine, Nancy, France, 2003. [Google Scholar]
- Lissemore, L.; Ripley, B.; Kakuda, Y.; Stephenson, G. Sensitivity, specificity and predictive value for the analysis of benomyl, as carbendazim, on field-treated strawberries using different enzyme linked immunosorbent assay test kits. J. Environ. Sci. Health Part B 1996, 31, 871–882. [Google Scholar] [CrossRef]
- Sagar, V.; Kumar, K. A symmetric key cryptography using genetic algorithm and error back propagation neural network. In Proceedings of the 2015 2nd International conference on computing for sustainable global development (INDIACom), New Delhi, India, 11–13 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1386–1391. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Kouadri, A.; Hajji, M.; Harkat, M.F.; Abodayeh, K.; Mansouri, M.; Nounou, H.; Nounou, M. Hidden Markov model based principal component analysis for intelligent fault diagnosis of wind energy converter systems. Renew. Energy 2020, 150, 598–606. [Google Scholar] [CrossRef]
- Zhao, H.; Zheng, J.; Xu, J.; Deng, W. Fault diagnosis method based on principal component analysis and broad learning system. IEEE Access 2019, 7, 99263–99272. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Smagulova, K.; James, A.P. A survey on LSTM memristive neural network architectures and applications. Eur. Phys. J. Spec. Top. 2019, 228, 2313–2324. [Google Scholar] [CrossRef]
- Kattenborn, T.; Leitloff, J.; Schiefer, F.; Hinz, S. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS J. Photogramm. Remote Sens. 2021, 173, 24–49. [Google Scholar] [CrossRef]
- Alves, R.H.F.; de Deus Júnior, G.A.; Marra, E.G.; Lemos, R.P. Automatic fault classification in photovoltaic modules using Convolutional Neural Networks. Renew. Energy 2021, 179, 502–516. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Katuwal, R. On the origins of randomization-based feedforward neural networks. Appl. Soft Comput. 2021, 105, 107239. [Google Scholar] [CrossRef]
- Pati, Y.C.; Krishnaprasad, P.S. Analysis and synthesis of feedforward neural networks using discrete affine wavelet transformations. IEEE Trans. Neural Netw. 1993, 4, 73–85. [Google Scholar] [CrossRef] [PubMed]
- Hayder, G.; Solihin, M.I.; Mustafa, H.M. Modelling of river flow using particle swarm optimized cascade-forward neural networks: A case study of Kelantan River in Malaysia. Appl. Sci. 2020, 10, 8670. [Google Scholar] [CrossRef]
- He, Z.; Nguyen, H.; Vu, T.H.; Zhou, J.; Asteris, P.G.; Mammou, A. Novel integrated approaches for predicting the compressibility of clay using cascade forward neural networks optimized by swarm-and evolution-based algorithms. Acta Geotech. 2022, 17, 1257–1272. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef] [Green Version]
- Dhruv, P.; Naskar, S. Image classification using convolutional neural network (CNN) and recurrent neural network (RNN): A review. In Machine Learning and Information Processing; Springer: Singapore, 2020; pp. 367–381. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).