Abstract
This article investigates the significance of varying radius of copper nanoparticles for non-Newtonian nanofluid flow due to an extending sheet in the presence of a magnetic field and porous medium. The modern technological applications of non-Newtonian nanofluids have attracted researchers in the current era. So, the impacts of the radius of nanoparticles with micropolar fluid have been taken into consideration. Three-dimensional leading equations (PDEs) for momentum, concentration, and temperature are transformed into ODEs by applying the appropriate similarity transformation. The numerical approach bvp4c is applied to obtain the problem’s solution numerically. The influence of the nanoparticles’ radius and various physical parameters on the microrotation, velocity, and temperature profile are analyzed. The velocity profile decreases against the magnetic field (M), rotational parameter (), and Forchheimer number (Fr), but the temperature distribution has increasing behavior for these parameters, and the microrotation is augmented for rising inputs of the magnetic parameter and boundary parameter (). It is also observed that the temperature reduces against the material parameter (∇) and Forchheimer number (). The skin friction coefficients and Nusselt number decrease against the growing strength of the Forchheimer number . At the stretching surface, the skin friction factor and Nusselt number are numerically and graphically calculated.
1. Introduction
Micropolar fluids are non-Newtonian fluids that defy the Newtonian viscosity law. These liquids are stiff components that lie within a viscous or sticky channel. Micropolar theory has attained a lot of interest in recent years as a result of its many applications in various industrial processes such as polymer solutions, nuclear power plants, low concentration suspension flux, biological structures, and flows of turbulent shear, etc. Erigen [1] was the first to present the notion of simple micropolar liquids. Reddy et al. [2] explored the thermal radiation impact on the time-independent 3D MHD flux of micropolar liquid on a horizontal surface. Singh et al. [3] investigated the numerical solution of micropolar liquid flux on the stretching surface along the chemical reaction and melting heat transportation by using the Keller box method. Salahuddin et al. [4] illustrated the study of the mass and heat transfer micropolar liquid flux close to the stagnation region of an object. The heat transportation of 3D micropolar over a rigid plate was investigated by Nadeem et al. [5]. Ali et al. [6] described the significance of injection/suction, thermal radiation, gravity modulation, and MHD on the dynamics of micropolar fluid over an inclined sheet. The Darcy–Forchheimer porous media is very useful for fluid zones, and it has a wide range of applications in the design of heat exchangers, geophysics, under ground water systems, and crude oil recovery systems [7]. He et al. [8] examined the instability of two-superposed Walters’ B fluids moving through porous media.
Enhancement of the heat transfer in a flux of fluid has led specialists to accept the performance of nanofluids in thermal engineering. The previous development was based on the nature of nanoparticles and the host fluid. The concentration of nanoparticles and temperature impacts on the viscosity and the ratio of mass to density, as some of the physical attributes. Heat conductivity, nanoparticles’ specific size, the heat capacity of nanoparticles’ concentration at several levels, and temperature are some of the thermal characteristics. The pressure drop, nanoparticle concentration, nanoparticle radius, and the friction factor are also some of the outlined properties of nanofluids as pointed out by Lin and Yang [9] and Mohamoud Jama [10]. Magnetite’s intrinsic magnetic characteristics fluctuate as the diameter changes. The superparamagnetic property of magnetic nanoparticles varies as the size of nanoparticles decreases. The change in nanoparticles’ radius affects the attributes of both nanoparticles and the interphase, as reported by Ashraf et al. [11]. Vishal et al. [12] observed that nanofluid’s viscosity can be highly effected by the particle size and the nature of energy transmitted between the surface of particles and the fluid’s layer. The single wall and multiwall carbon nanotubes are a form of allotrope of carbon having a wide scope of practical applications such as optics, chemical production, cooling in microelectronics, and many other distinctive material sciences [13,14]. Yapici et al. [15] investigated the outcome of a comparative examination of ethylene glycol conveying ZnO (10–30 nm, 35–45 nm, and 80–200 nm), MgO (20 nm, 40 nm), CuO (40 nm, 80 nm), TiO (30 nm, 50 nm), and SiO (20–30 nm, 60–70 nm), demonstrating that the relative viscosity of these nanofluids was a reducing attribute of particle sizes. The analysis of Namburu et al. [16] showed that enhancing the diameter of the nanoparticles of SiO in water and ethylene glycol corresponded to a decrease in the viscosity of nanofluid. The noted decline in the viscosity of fluids was more significant when the nanofluid was cold. The decline in viscosity along with the particle size diminished at higher temperatures. Recently published research articles on nanofluids are mentioned in references [17,18,19,20].
MHD examines the flux of electrically conducting solutions when a magnetic field is present. The application of a magnetic field noticeably alters the heat transfer and transportation features of electrically conducting flows, according to a number of novel and anticipated studies. MHD fluxes are necessary in an extensive range of technical and industrial usage such as wire drawing, MHD flow meters, the extrusion process in aerodynamics, MHD generators, and the design of nuclear reactors and MHD pumps. Awan et al. [21] analyzed the MHD stagnation oblique stagnation point flow of second grade fluid on an oscillatory extending surface. Jang et al. [22] examined the experimental and theoretical analysis on MHD micropumps. Over the last few years, excellent analysis of the significance and applications of MHD has been conducted [23,24,25,26].
Rotational flows are extremely important because of their applications in engineering, science, and manufacturing industries. Many manufactured items rely on the physics of rotational flow for their modeling capabilities and foundations such as vacuum pumps, whirlpools, tropical cyclones, centrifugal pumps, jet engines, and tornadoes, etc. Since rotating flow is a complex phenomenon, researchers are working to understand the underlying science. Aziz et al. [27] investigated the numerical simulation on the three-dimensional rotational flux of a nanoliquid with entropy generation. Numerical investigation of a time-dependent MHD convective rotational flow past an infinite vertically moving permeable surface was studied by Krishna et al. [28]. Yacob et al. [29] reported the rotational flux in a nanoliquid with CNT nanoparticles with a stretching surface. Shahzad et al. [30] explained the heat transmission analysis of MHD rotational flux of by extending the surface. Sajid et al. [31] analyzed the MHD rotational flow of viscous fluid on a shrinking surface.
In the above mentioned investigations, less consideration was paid towards the significance of a nanoparticle’s radius on the dynamics of water-based micropolar nanofluid subject to the Darcy–Forchheimer law, Lorentz force, and rotating frame of reference. To the authors’ knowledge, the elaborated fluid flow model has not been addressed in previous research. The primary objective of this report is to optimize the heat transfer rate using nanoparticles’ radius, motivated by the wide scope of non-Newtonian fluids and nanoparticles’ extraordinary thermal characteristics such as thermal conductivity, etc. The novelties of the current examination are: (i) the significance of nanoparticles’ radius on the dynamics of micropolar fluid, (ii) the analysis of Lorentz and Coriolis forces on the dynamics of water-based non-Newtonian fluid, (iii) assimilation of the Darcy–Forchheimer law effect on the dynamics of micropolar fluid when Lorentz and Coriolis forces are dominant, (iv) the selection of Cu nanoparticles for this examination, and (iv) the observation of the variation in the skin friction coefficient and Nusselt number when the magnetic field, Darcy–Forchheimer law, rotating, and materials parameters are incremented. The formulated three-dimensional fluid problem is reduced to dimension ODEs via the similarity transformation, and the numerical computation is obtained via using a well-known Bvp4c with shooting approach, which is coded in a MATLAB tool. The present findings are confirmed by comparing them to already published results.
2. Mathematical Formulation
Let us analyze the 3D time-independent incompressible water-based non-Newtonian (micropolar) nanofluid conveying copper nanoparticles on a stretchable sheet with magnetic effect in the presence of a porous medium and a rotating frame. Two forces are inverse in direction and identically act in x-direction to extend the surface such that the x-component of velocity linearly varies along it, i.e., . denotes the uniformly magnetic strength and acting in the z direction. Under the assumption of a small magnetic Reynolds number, the induced magnetic field is negligible, moreover, the Ohmic dissipation and Hall current impacts are ignored, since the magnetic field applied is not excessively strong [32]. In addition, the viscous dissipation is ignored and isothermal conditions are sustained at the surface of sheet. Further, we consider that and are the ambient temperature and the superficial temperature. The thermo-physical features of water and Cu nanoparticles are shown in Table 1 and Table 2. The solid particles’ agglomeration is neglected because the nanofluid mixture is considered as a stable compound. The geometry of the problem is depicted in Figure 1.

Table 1.
Attributes of the nanoparticles and base fluid [36].

Table 2.
Properties of the nanoparticles and base fluid [38,39].
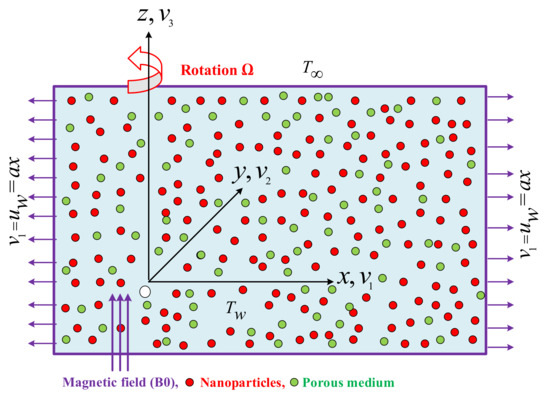
Figure 1.
Physical fluid flow configuration.
Considering the above assumptions, the governing equations are as follows [33,34,35]:
Here, , , and are the velocity components in the directions of the x, y, and z axes, respectively. T, N, , D, , and are the temperature of the nanofluid, microrotation, density, electric conductivity, kinematic viscosity, and heat diffusion, respectively. j, k, and are the micro-inertia per unit mass. The boundary conditions are as follows [33,34]:
The following similarity transformation was used for further examination [37]:
By the use of the similarity transformation, the first equation is satisfied identically, and Equations (2)–(6) are converted into the following nonlinear ODEs.
The boundary conditions are:
where
In Equations (9)–(13), ∇ is the material parameter, H is the microrotation, the rotating parameter is , denotes the porosity factor, and M, , and Pr are the magnetic strength, Forchheimer number, and Prandtl number, which are defined as:
The relations for the coefficient of skin friction and the Nusselt number are [40,41]:
Then
Finally, we have
where is the local Reynolds number that is defined as .
3. Solution Procedure
In this section, the ordinary nonlinear coupled differential flow expressions (8)–(11), subject to the conditions in (12), are addressed and solved numerically by utilizing the computational tool bvp4c, a built-in function in Matlab software. The nonlinear system of coupled flow equations is changed to first-order differential equations following refs [41,42]:
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- .
The corresponding boundary conditions are as follows:
To solve the above first order differential equations via the shooting technique, seven initial condition are required. The numerical computations were performed for various physical emerging parameters for the appropriate computational domain [0,10] instead of [0,∞], where was fixed at 10 because there is no more variation in the results after . Newton’s iterative scheme was applied to improve the accuracy of the initial guesses until the desired approximation was obtained. The stopping criteria for the iterative process was . Bvp4c is an effective solver for a system of ODEs as compared to other boundary value problem solvers. It is very easy to implement in Matlab and has low computational cost.
4. Results and Discussion
The influence of the nanoparticles’ radius and emerging parameters in the elaborated fluid flow problem on the dynamic of micropolar fluid is demonstrated in this section. For solving the problem graphically, the bvp4c technique was implemented to observe the impacts of the velocities (, ), microrotation distribution (), and temperature () with the radius of nanoparticles and the emerging physical parameters. Moreover, and (coefficients of skin friction) and (Nusselt number) are shown graphically. A comprehensive comparison of the consequences was conducted to check the validity of the bvp4c technique as displayed in Table 3 and Table 4 and clearly, there was a strong relationship between the consequences. For the skin friction factor, the results were compared with Wang et al. [43] and Ali et al. [38] in the presence of when other parameters are ignored, as shown in Table 3. The results for the Nusselt number in the presence of and are compared with Adnan et al. [44] and Ali et al. [45] in Table 4. Our computations had an excellent agreement with the already published results. The current computation was conducted by using these parameters’ values: , (water host fluid), , , , , and .

Table 3.
Comparison of the and values with various values of ignoring other involved parameters.

Table 4.
Comparison of the values of with various values of and Pr.
Figure 2a,b reveal the influence of the radius of nanoparticles and the rotating parameter on the primary velocity and the secondary velocity . With the enhancement of the nanoparticle radius , the primary velocity increased. With each increment in , the velocity curves were smooth and continuously growing in a symmetrical manner. An elaboration on this consequence can be seen in Figure 2a. However, the nanoparticles with radius showed the opposite behavior for the secondary velocity. decreased against the rising value of , as shown in Figure 2b. This can be associated with the fact that enhancing the diameter of the nanoparticles in water as pointed out by Namburu et al. [16] corresponds to a decline in the viscosity of the nanofluids. In addition, the consequence of an analysis of (i) the CuO and water nanoparticle mixture and (ii) the alumina and ethylene glycol nanoparticles mixture by Pastoriza-Gallego et al. [46,47] indicated that higher viscosity was bound to occur as the size of the particle diminished. Moreover, Figure 2a,b disclose the impact of the rotating parameter on and . Both velocities were lessened close to the surface and later encountered a fluctuation when was raised. When , obtained its maximum value. Extending the surface in the x direction caused the momentum to rise in this direction, which is worth noticing whereas the momentum in the y direction remained unsupported. Therefore, Figure 2a,b show that was swapped marginally, and was swapped significantly.
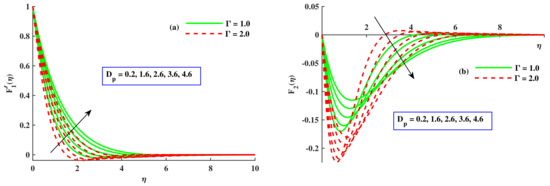
Figure 2.
Variation in and along and .
Figure 3a,b depicts the affect of the radius of nanoparticles and M on velocity. With the escalating values of the radius of nanoparticles , was boosted but decreased. However, there was depreciation in and with amplified values of M, which was related to the boundary layer thickness. This corroborated the general behavior of the magnetic impact. Physically, the growing value of M enhanced the opposing force that was called the Lorentz force, which produced a decline in the velocities. So, and were reduced. Figure 4a,b show the variation in and due to the radius of nanoparticles and (Fr). increased with a higher contribution of and Fr. Physically, due to the permeable medium, the fluid became thicker and the opposing force produced slowed down the velocities and . The effect of the radius of nanoparticles and the material parameter ∇ on the velocity profile is sketched out in Figure 5a,b. The components of velocity magnified with incremental inputs of ∇ and ; however, showed decreasing behavior against incremented values of both parameters. The material parameter’s larger value denoted a reduction in the viscous effects, enabling the flow to move more quickly, because it was inversely related to the dynamic viscosity coefficients. Figure 6a,b display the effects of the magnetic parameter, radius of nanoparticles , and the rotational parameter on the microrotation distribution profile. With the impact of the rising values of and M, the microrotation profile increased, but with the growing values of , decreased. Figure 7a,b portray the effect of the material parameter (∇), radius of nanoparticles (), and boundary parameter () on . With higher inputs of and , the microrotation profile increased but reduced against the amplified value of ∇. Figure 8a,b disclose the influence of , ∇, and . The temperature lowered conspicuously with developing values of and ∇. Physically, larger nanoparticles reduced the area of surface, which allowed for less heat transportation. So, for small-sized nanoparticles, the temperature of the nanoliquid was at a higher level. With incremented values of Fr, the temperature increased. Physically, opposing forces were produced due to the porous channel, so liquid dragged in the boundary layer zone, which led to heat dissipation to create further heat in this region. Therefore rose with the Fr. The impact of the rotating parameter, radius of nanoparticles, and the magnetic parameter on the temperature of the nanofluid is visualized in Figure 9a,b. It decreased with the rising values of , whereas, the development of heat by increasing inputs of was satisfied on the basis of larger diffusion processes. With amplified values of M, the temperature field increased. With magnified values of M, the flux of fluid stopped, and the dissipation appended to the thermal energy of liquid.
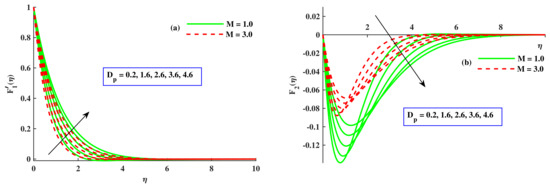
Figure 3.
Variation in and along M and .
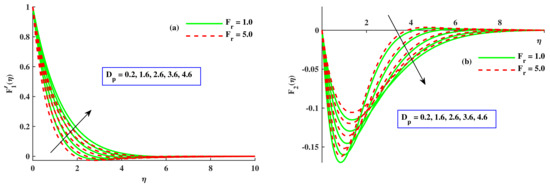
Figure 4.
Variation in and along and .
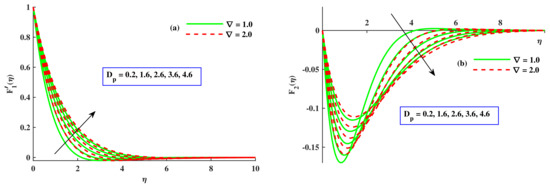
Figure 5.
Variation in and along ∇ and .
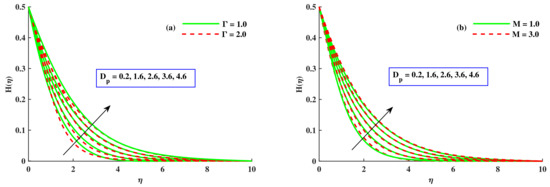
Figure 6.
Variation in and along , M, and .
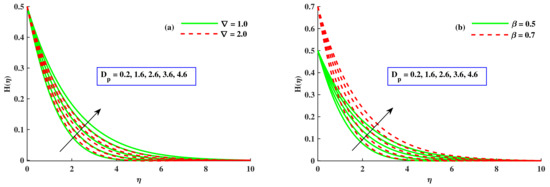
Figure 7.
Variation in and along ∇, , and .
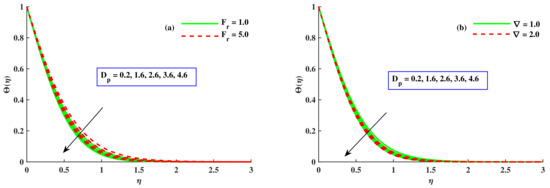
Figure 8.
Variation in along ∇, , and .
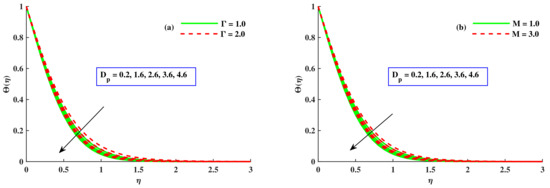
Figure 9.
Variation in along , M, and .
Figure 10a,b depict the variation in and when parameters M, , and ∇ were given different inputs. The skin friction coefficient increased when the radius of nanoparticles increased, but it had receding behavior with increased values of M and ∇; the skin friction coefficient underwent a notable increase with rising values of M, ∇, and . Figure 11a,b are drawn to show the fluctuation in the coefficients of skin friction with varying values of , Fr, and . Figure 11a presents the increment in with growing inputs of but a reduction with larger values of Fr and . Figure 11b shows that rose with amplified values of Fr and but decreased with varying values of . Figure 12a,b show that the Nusselt number was boosted along with elevated inputs of and ∇ but lessened with increasing values of M, Fr, and .
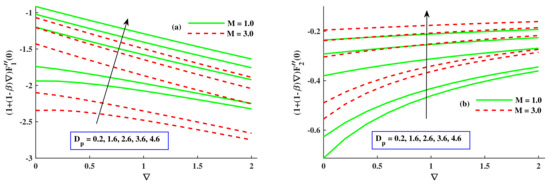
Figure 10.
Variation in and along , M, and ∇.
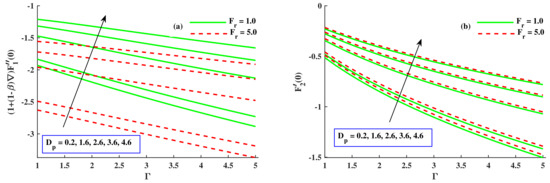
Figure 11.
Variation in and along , , and Fr.
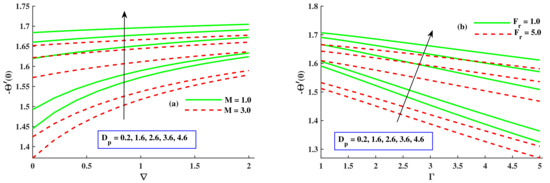
Figure 12.
Variation in along M, ∇, , , and Fr.
5. Conclusions
The fluctuation of the radius of copper nanoparticles for a non-Newtonian liquid flux due to a stretching sheet in the presence of a porous medium and magnetic field was investigated with fixed interparticle spacing. By using the bvp4c technique, the fluid velocity components, microrotation distribution, temperature, skin friction factor, and Nusselt number were examined. Some of the significant consequences are summarized as follows:
- The increase in the nanoparticle radius increased the velocity and microrotation H and
- Decreased the secondary velocity .
- Decreased the Cu-nanofluid’s temperature.
- Increased the skin friction factor.
- Increased the Nusselt number.
- The magnetic parameter M reduced the component of velocity , and
- Increased the microrotation of nanoparticles.
- Increased the temperature of the non-Newtonian fluid.
- Increased the skin friction coefficient but lessened the .
- Reduced the Nusselt number.
- The boundary concentration parameter increased the microrotation distribution.
- The rotational parameter lowered the , , and H and
- Enhanced the temperature profile.
- Decrease the skin friction coefficients and Nusselt number.
- The higher input of the Forchheimer number decreased the velocity , , and microrotation and
- Increased the temperature of the fluid.
- Increase the but reduced the and Nusselt number.
- The material parameter ∇ reduced the component of velocity , microrotation, and temperature and
- Enlarged the velocity component .
- Enlarged the but reduced the .
- Enlarged the Nusselt number.
By this computational endeavor, we successfully clarified the parametric effects on fluid dynamics. This study can be extended to Prandtl nanofluid, Carreau–Yasuda nanofluid, Maxwell nanofluid, viscoelastic Jeffrey’s nanofluid, and tangent hyperbolic.
Author Contributions
Conceptualization, B.A.; Methodology, A.U.A.; Software, E.M.T.-E., F.A.S. and S.M.; Validation, A.S.O. and F.A.S.; Formal analysis, A.S.O. and S.M.; Investigation, A.U.A.; Resources, N.A.A.; Data curation, N.A.A.; Writing—original draft, S.M.; Visualization, B.A.; Supervision, A.U.A.; Project Administration, B.A.; Funding acquisition, E.M.T.-E.; Revision, B.A., N.A.A., A.U.A., A.S.O. and F.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Reddy, S.; Reddy, P.B.A. Thermal radiation effect on unsteady three-dimensional mhd flow of micropolar fluid over a horizontal surface of a parabola of revolution. Propuls. Power Res. 2022, 11, 129–142. [Google Scholar] [CrossRef]
- Singh, K.; Pandey, A.K.; Kumar, M. Numerical solution of micropolar fluid flow via stretchable surface with chemical reaction and melting heat transfer using keller-box method. Propuls. Power Res. 2021, 10, 194–207. [Google Scholar] [CrossRef]
- Salahuddin, T.; Khan, M.; Al-Mubaddel, F.S.; Alam, M.M.; Ahmad, I. A study of heat and mass transfer micropolar fluid flow near the stagnation regions of an object. Case Stud. Therm. Eng. 2021, 26, 101064. [Google Scholar] [CrossRef]
- Nadeem, S.; Malik, M.; Abbas, N. Heat transfer of three-dimensional micropolar fluid on a riga plate. Can. J. Phys. 2020, 98, 32–38. [Google Scholar] [CrossRef]
- Ali, B.; Shafiq, A.; Siddique, I.; Al-Mdallal, Q.; Jarad, F. Significance of suction/injection, gravity modulation, thermal radiation, and magnetohydrodynamic on dynamics of micropolar fluid subject to an inclined sheet via finite element approach. Case Stud. Therm. Eng. 2021, 28, 101537. [Google Scholar] [CrossRef]
- Ali, B.; Rasool, G.; Hussain, S.; Baleanu, D.; Bano, S. Finite element study of magnetohydrodynamics (mhd) and activation energy in darcy–forchheimer rotating flow of casson carreau nanofluid. Processes 2020, 8, 1185. [Google Scholar] [CrossRef]
- He, J.-H.; Moatimid, G.M.; Sayed, A. Nonlinear ehd instabilitynonlinear ehd instability of two-superposed walters’ b fluids moving through porous media. Axioms 2021, 10, 258. [Google Scholar] [CrossRef]
- Lin, J.; Yang, H. A review on the flow instability of nanofluids. Appl. Math. Mech. 2019, 40, 1227–1238. [Google Scholar] [CrossRef]
- Jama, M.; Singh, T.; Gamaleldin, S.M.; Koc, M.; Samara, A.; Isaifan, R.J.; Atieh, M.A. Critical review on nanofluids: Preparation, characterization, and applications. J. Nanomater. 2016, 2016, 6717624. [Google Scholar] [CrossRef]
- Ashraf, M.A.; Peng, W.; Zare, Y.; Rhee, K.Y. Effects of size and aggregation/agglomeration of nanoparticles on the interfacial/interphase properties and tensile strength of polymer nanocomposites. Nanoscale Res. Lett. 2018, 13, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Vishal, C.C.; Kanala, R.K.; Raju, C.S.K.; Madathil, P.K.; Saha, P.; Rao, B.R.; Sriganesh, G.; Ramesh, K. Sub-micron sized metal oxides based organic thermic fluids with enhanced thermo-physical properties. Appl. Therm. Eng. 2019, 163, 114337. [Google Scholar] [CrossRef]
- He, J.-H.; Abd Elazem, N.Y. The carbon nanotube-embedded boundary layer theory for energy harvesting. Facta Univ. Ser. Mech. Eng. 2022, 20, 211–235. [Google Scholar]
- Ali, B.; Siddique, I.; Khan, I.; Masood, B.; Hussain, S. Magnetic dipole and thermal radiation effects on hybrid base micropolar cnts flow over a stretching sheet: Finite element method approach. Results Phys. 2021, 25, 104145. [Google Scholar] [CrossRef]
- Yapici, K.; Osturk, O.; Uludag, Y. Dependency of nanofluid rheology on particle size and concentration of various metal oxide nanoparticles. Braz. J. Chem. Eng. 2018, 35, 575–586. [Google Scholar] [CrossRef]
- Namburu, P.; Kulkarni, D.; Dandekar, A.; Das, D. Experimental investigation of viscosity and specific heat of silicon dioxide nanofluids. Micro Nano Lett. 2007, 2, 67–71. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Ahammad, N.A.; Din, E.M.T.E.; Gamaoun, F.; Awan, A.U.; Ali, B. Bio-convection effects on prandtl hybrid nanofluid flow with chemical reaction and motile microorganism over a stretching sheet. Nanomaterials 2022, 12, 2174. [Google Scholar] [CrossRef]
- Habib, D.; Salamat, N.; Abdal, S.H.S.; Ali, B. Numerical investigation for mhd prandtl nanofluid transportation due to a moving wedge: Keller box approach. Int. Commun. Heat Mass Transf. 2022, 135, 106141. [Google Scholar] [CrossRef]
- Wang, J.; Mustafa, Z.; Siddique, I.; Ajmal, M.; Jaradat, M.M.; Rehman, S.U.; Ali, B.; Ali, H.M. Computational analysis for bioconvection of microorganisms in prandtl nanofluid darcy–forchheimer flow across an inclined sheet. Nanomaterials 2022, 12, 1791. [Google Scholar] [CrossRef]
- Younis, O.; Alizadeh, M.; Hussein, A.K.; Ali, B.; Biswal, U.; Malekshah, E.H. Mhd natural convection and radiation over a flame in a partially heated semicircular cavity filled with a nanofluid. Mathematics 2022, 10, 1347. [Google Scholar] [CrossRef]
- Awan, A.U.; Abid, S.; Ullah, N.; Nadeem, S. Magnetohydrodynamic oblique stagnation point flow of second grade fluid over an oscillatory stretching surface. Results Phys. 2022, 18, 103233. [Google Scholar] [CrossRef]
- Jang, J.; Lee, S.S. Theoretical and experimental study of mhd (magnetohydrodynamic) micropump. Sensors Actuators A Phys. 2000, 80, 84–89. [Google Scholar] [CrossRef]
- Chabani, I.; Mebarek-Oudina, F.; Ismail, A.A.I. Mhd flow of a hybrid nano-fluid in a triangular enclosure with zigzags and an elliptic obstacle. Micromachines 2022, 13, 224. [Google Scholar] [CrossRef]
- Bhatti, M.; Arain, M.; Zeeshan, A.; Ellahi, R.; Doranehgard, M. Swimming of gyrotactic microorganism in mhd williamson nanofluid flow between rotating circular plates embedded in porous medium: Application of thermal energy storage. J. Energy Storage 2022, 45, 103511. [Google Scholar] [CrossRef]
- Al-Farhany, K.; Abdulkadhim, A.; Hamzah, H.K.; Ali, F.H.; Chamkha, A. Mhd effects on natural convection in a u-shaped enclosure filled with nanofluid-saturated porous media with two baffles. Prog. Nucl. Energy 2022, 145, 104136. [Google Scholar] [CrossRef]
- He, J.-H.; Moatimid, G.M.; Mostapha, D.R. Nonlinear instability of two streaming-superposed magnetic reiner-rivlin fluids by he-laplace method. J. Electroanal. Chem. 2021, 895, 115388. [Google Scholar] [CrossRef]
- Aziz, A.; Aziz, A.; Ullah, I.; Subhani, M. Numerical simulation for 3d rotating flow of nanofluid with entropy generation. Int. J. Model. Simul. 2022, 1–22. [Google Scholar] [CrossRef]
- Krishna, M.V.; Ahamad, N.A.; Chamkha, A.J. Numerical investigation on unsteady mhd convective rotating flow past an infinite vertical moving porous surface. Ain Shams Eng. J. 2021, 12, 2099–2109. [Google Scholar] [CrossRef]
- Yacob, N.A.; Dzulkifli, N.F.; Salleh, S.N.A.; Ishak, A.; Pop, I. Rotating flow in a nanofluid with cnt nanoparticles over a stretching/shrinking surface. Mathematics 2021, 10, 7. [Google Scholar] [CrossRef]
- Shahzad, F.; Jamshed, W.; Sajid, T.; Nisar, K.S.; Eid, M.R. Heat transfer analysis of mhd rotating flow of fe3o4 nanoparticles through a stretchable surface. Commun. Theor. Phys. 2021, 73, 075004. [Google Scholar] [CrossRef]
- Sajid, M.; Javed, T.; Hayat, T. Mhd rotating flow of a viscous fluid over a shrinking surface. Nonlinear Dyn. 2008, 51, 259–265. [Google Scholar] [CrossRef]
- Ali, B.; Siddique, I.; Ahmadian, A.; Senu, N.; Ali, L.; Haider, A. Significance of lorentz and coriolis forces on dynamics of water based silver tiny particles via finite element simulation. Ain Shams Eng. J. 2022, 13, 101572. [Google Scholar] [CrossRef]
- Rashid, S.; Hayat, T.; Qayyum, S.; Ayub, M.; Alsaedi, A. Three-dimensional rotating darcy–forchheimer flow with activation energy. Int. J. Numer. Methods Heat Fluid Flow 2018, 29, 935–948. [Google Scholar] [CrossRef]
- Javed, T.; Ahmad, I.; Abbas, Z.; Hayat, T. Rotating flow of a micropolar fluid induced by a stretching surface. Z. Naturforschung A 2010, 65, 829–843. [Google Scholar] [CrossRef][Green Version]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Ali, B.; Khan, S.A.; Hussein, A.K.; Thumma, T.; Hussain, S. Hybrid nanofluids: Significance of gravity modulation, heat source/sink, and magnetohydrodynamic on dynamics of micropolar fluid over an inclined surface via finite element simulation. Appl. Math. Comput. 2022, 419, 126878. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Mustafa, M.; Alsaedi, A. An optimal study for three-dimensional flow of maxwell nanofluid subject to rotating frame. J. Mol. Liq. 2017, 229, 541–547. [Google Scholar] [CrossRef]
- Ali, B.; Naqvi, R.A.; Ali, L.; Abdal, S.; Hussain, S. A comparative description on time-dependent rotating magnetic transport of a water base liquid H2O with hybrid nano-materials Al2O3-Cu and Al2O3-TiO2 over an extending sheet using buongiorno model: Finite element approach. Chin. J. Phys. 2021, 70, 125–139. [Google Scholar] [CrossRef]
- Graham, A.L. On the viscosity of suspensions of solid spheres. Appl. Sci. Res. 1981, 37, 275–286. [Google Scholar] [CrossRef]
- Lou, Q.; Ali, B.; Rehman, S.U.; Habib, D.; Abdal, S.; Shah, N.A.; Chung, J.D. Micropolar dusty fluid: Coriolis force effects on dynamics of mhd rotating fluid when lorentz force is significant. Mathematics 2022, 10, 2630. [Google Scholar] [CrossRef]
- Wei, Y.; Rehman, S.U.; Fatima, N.; Ali, B.; Ali, L.; Chung, J.D.; Shah, N.A. Significance of dust particles, nanoparticles radius, coriolis and lorentz forces: The case of maxwell dusty fluid. Nanomaterials 2022, 12, 1512. [Google Scholar] [CrossRef]
- Rehman, S.U.; Mariam, A.; Ullah, A.; Asjad, M.I.; Bajuri, M.Y.; Pansera, B.A.; Ahmadian, A. Numerical computation of buoyancy and radiation effects on mhd micropolar nanofluid flow over a stretching/shrinking sheet with heat source. Case Stud. Therm. Eng. 2021, 25, 100867. [Google Scholar] [CrossRef]
- Wang, C. Stretching a surface in a rotating fluid. Z. Angew. Math. Phys. 1988, 39, 177–185. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A.; Mehmood, A. Study of flow and heat transfer on a stretching surface in a rotating casson fluid. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2015, 85, 421–426. [Google Scholar] [CrossRef]
- Ali, B.; Nie, Y.; Hussain, S.; Manan, A.; Sadiq, M.T. Unsteady magneto-hydrodynamic transport of rotating maxwell nanofluid flow on a stretching sheet with cattaneo–christov double diffusion and activation energy. Therm. Sci. Eng. Prog. 2020, 20, 100720. [Google Scholar] [CrossRef]
- Pastoriza-Gallego, M.J.; Lugo, L.; Legido, J.L.; Piñeiro, M.M. Thermal conductivity and viscosity measurements of ethylene glycol-based Al2O3 nanofluids. Nanoscale Res. Lett. 2011, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Pastoriza-Gallego, M.J.; Casanova, C.; Legido, J.A.; Piñeiro, M.M. Cuo in water nanofluid: Influence of particle size and polydispersity on volumetric behaviour and viscosity. Fluid Phase Equilibria 2011, 300, 188–196. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).