Lane-Change Risk When the Subject Vehicle Is Faster Than the Following Vehicle: A Case Study on the Lane-Changing Warning Model Considering Different Driving Styles
Abstract
:1. Introduction
2. Methods
2.1. Participants and Test Routes
2.2. Apparatus
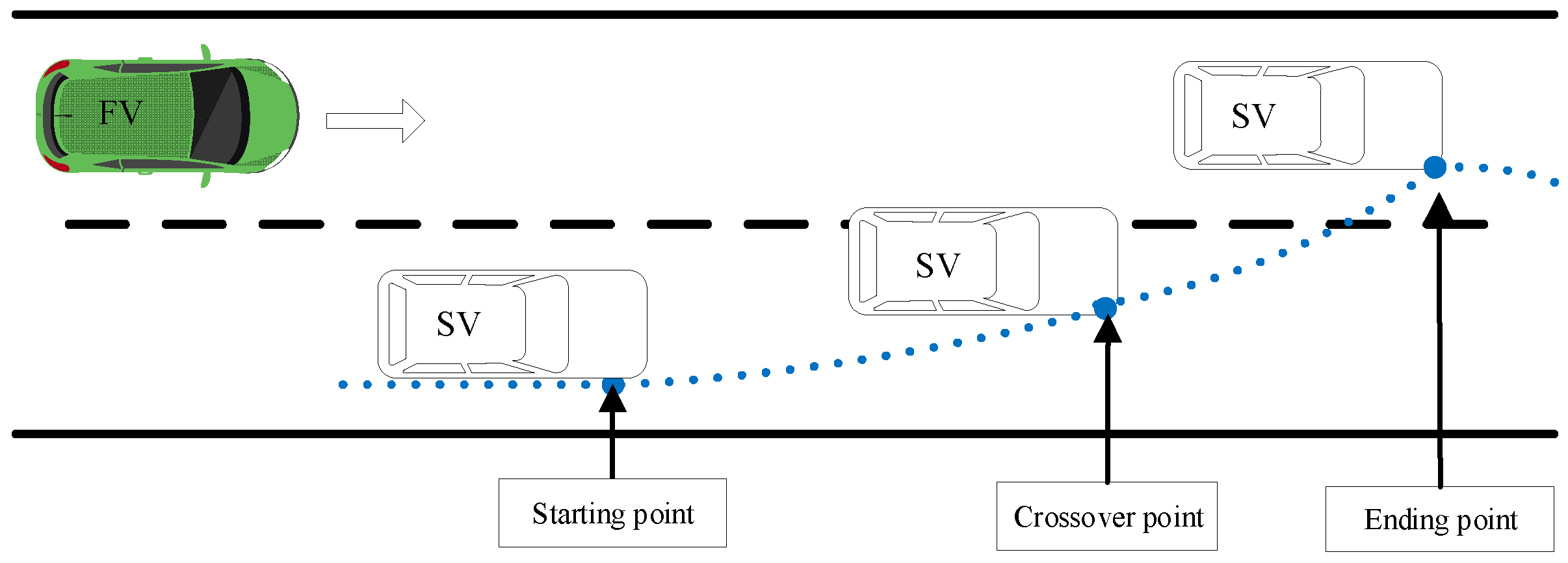
2.3. Extraction of Lane-Changing Events
3. Driving Style Classification in Lane-Changing Situations
3.1. Clustering Model Establishment
3.1.1. K-Means Algorithm
3.1.2. Gaussian Mixture Model with the Inputs of K-Means Algorithm
- Initialize centroids by first shuffling all data points and randomly selecting k data points as the cluster centers.
- Compute the sum of the squared distance between each data point and k centroids and assign each data point to the possible cluster based on the principle of the minimum distance.
- Update k centroids by iterating until there is no change to the centroids.
- Compute the proportion and the mean vector of the data points in each cluster determined by the k-means algorithm.
- Take the clustering result of the k-means algorithm as the initial input parameters of the GMM (i.e., mean vector and weight of a cluster and covariance matrix of clusters).
- Run the improved GMM algorithm to obtain the optimized clustering result.
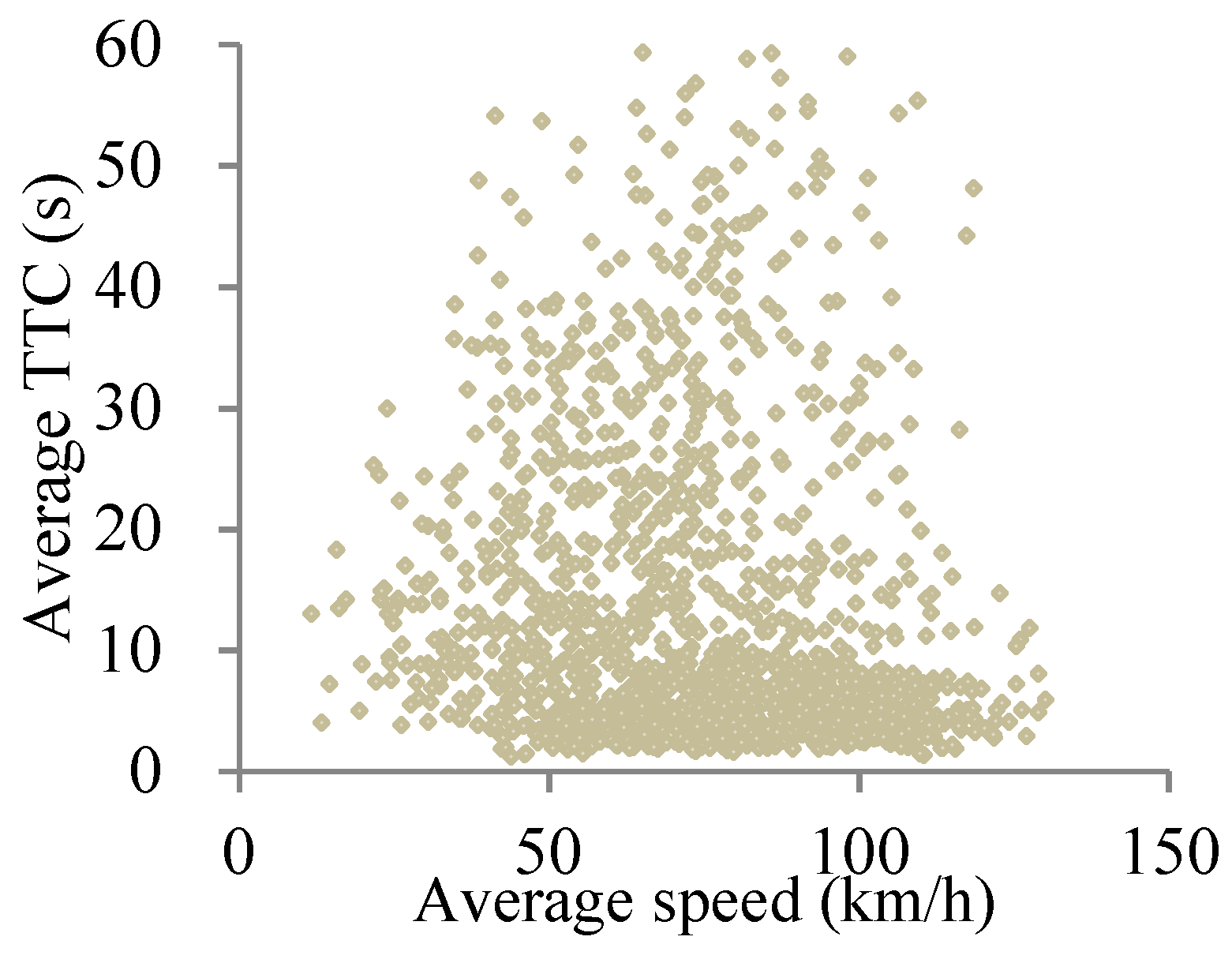
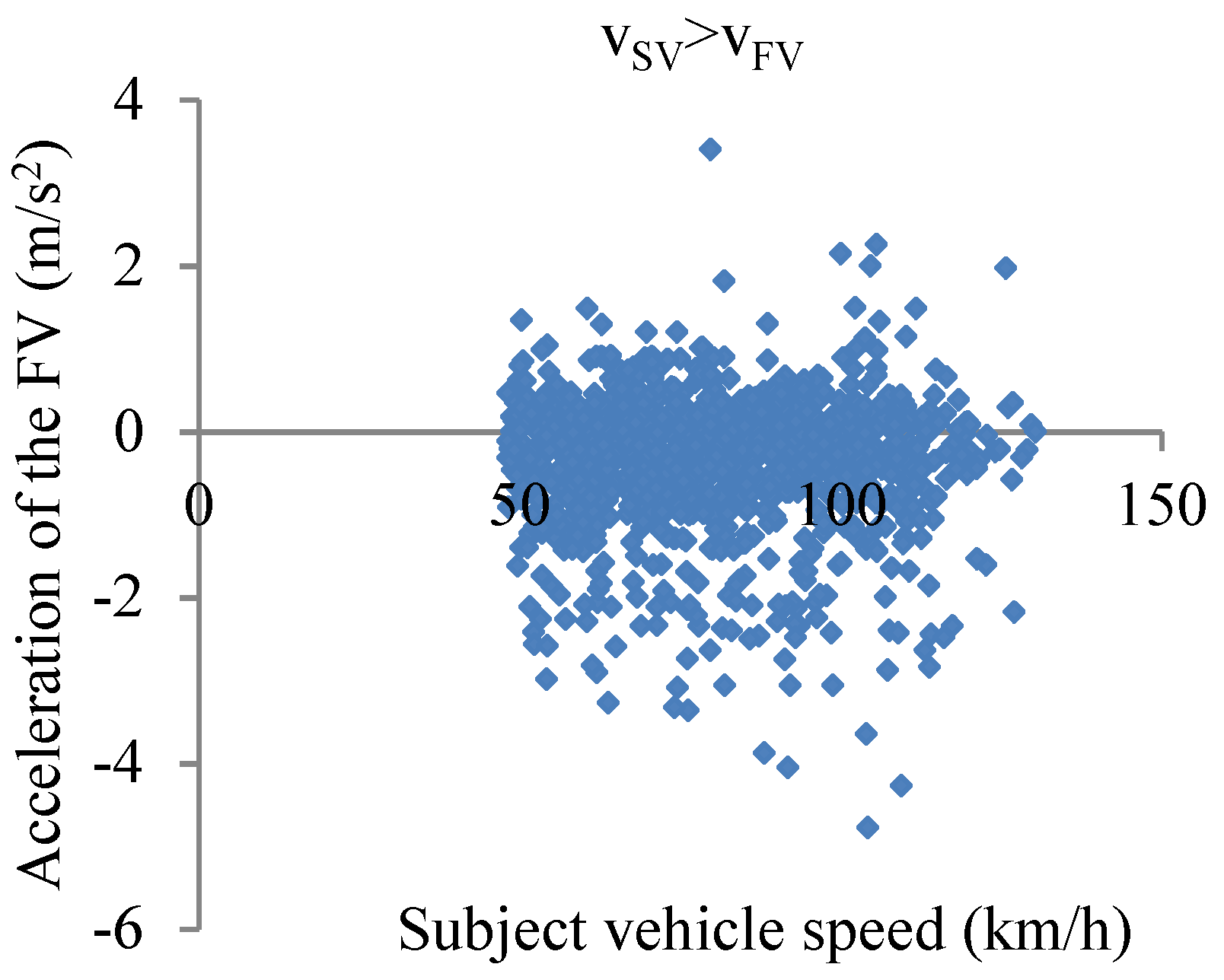
3.2. Lane-Changing Safety Indicator Selection
3.3. Clustering Results and Verification
4. Lane-Changing Warning Model Considering Different Driving Styles
4.1. Lane-Changing Safety Distance Model
- (1)
- Ensure that the SV is always in front of the FV during lane changes
- (2)
- Ensure a safety distance between the SV and the FV after entering the adjacent lane
4.2. Lane-Changing Warning Model
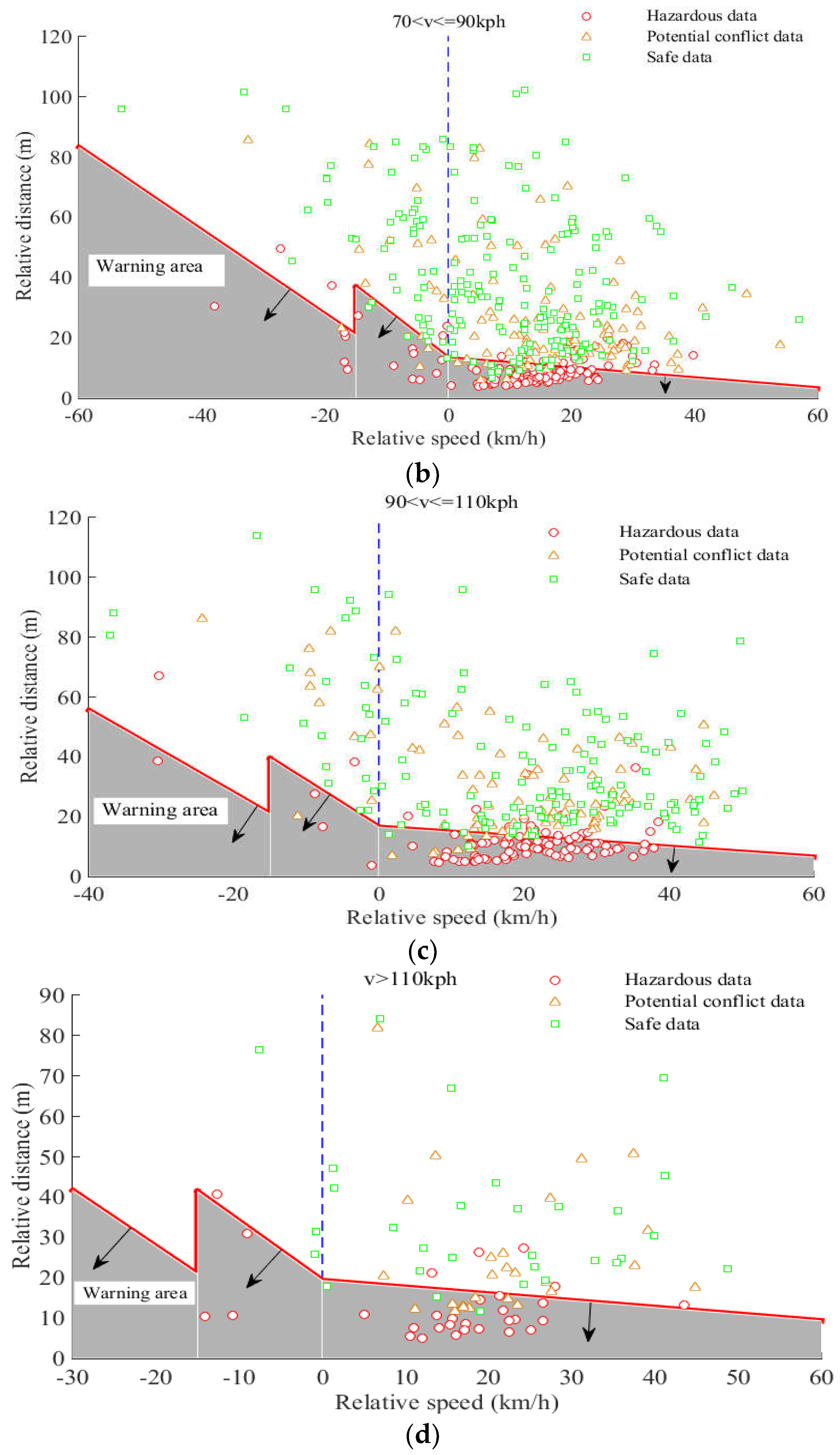
4.3. Recognition Results of Lane-Changing Warning Model
5. Conclusions
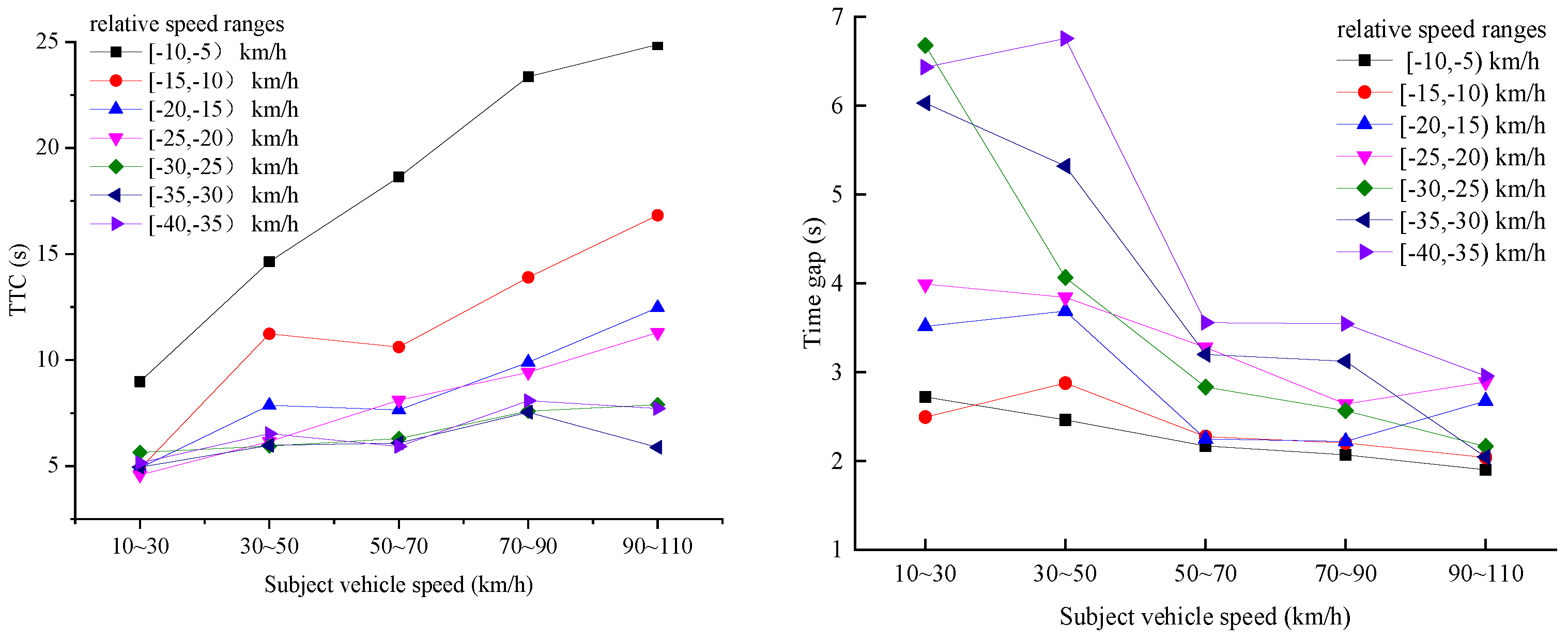
- For different speed ranges of the SV, the time to collision was relatively stable under high relative speed conditions (<−15 km/h), while the time gap was stable under low relative speed conditions (≥−15 km/h).
- A significant difference existed in the lane-changing durations for the three types of drivers, and the peak frequencies of the lane-changing duration for aggressive drivers, calm drivers, and conservative drivers were 3–4 s, 4–5 s, and 5–6 s, respectively.
- The overall recognition accuracy of the lane-changing warning model considering driving styles was 81%, and the overall recognition accuracy of the model for aggressive drivers was relatively higher at 84% when compared with the other two types of drivers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, D.; Lam, H.; Peng, H.; Bao, S.; LeBlanc, D.J.; Nobukawa, K.; Pan, C.S. Accelerated evaluation of automated vehicles safety in lane-change scenarios based on importance sampling techniques. IEEE Trans. Intell. Transp. Syst. 2017, 18, 595–607. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Wang, P.; Chan, C.Y. Understanding lane change behavior under dynamic driving environment based on real-world traffic dataset. In Proceedings of the 2019 5th International Conference on Transportation Information and Safety (ICTIS), Liverpool, UK, 14–17 July 2019; pp. 1092–1097. [Google Scholar]
- Queensland Transport. Road Traffic Crashes in Queensland: A Report on the Road Toll 2009; Customer Services, Safety & Regulation Division, Department of Transport and Main Roads: Brisbane, Australia, 2012.
- Traffic Management Bureau of the Public Security Ministry. Annual Statistic Year book of Road Traffic Accidents in China (2015); Traffic Management Bureau of the Public Security Ministry: Wuxi, China, 2016.
- Hou, Y.; Edara, P.; Sun, C. Situation assessment and decision making for lane change assistance using ensemble learning methods. Expert Syst. Appl. 2015, 42, 3875–3882. [Google Scholar] [CrossRef]
- Hang, L.; Chen, C.; Zhang, J.; Fang, S.; You, J.; Guo, J. Modeling lane-changing behavior in freeway off-ramp areas from the shanghai naturalistic driving study. J. Adv. Transp. 2018, 2018, 8645709. [Google Scholar]
- Ning, H.; Yu, Y.; Bai, L. Unsafe Behaviors Analysis of Sideswipe Collision on Urban Expressways Based on Bayesian Network. Sustainability 2022, 14, 8142. [Google Scholar] [CrossRef]
- Ponziani, R. Turn Signal Usage Rate Results: A Comprehensive Field Study of 12,000 Observed Turning Vehicles; SAE Technical Paper; SAE: Warrendale, PA, USA, 2012. [Google Scholar]
- Wang, X.; Yang, M.; Hurwitz, D. Analysis of cut-in behavior based on naturalistic driving data. Accid. Anal. Prev. 2019, 124, 127–137. [Google Scholar] [CrossRef]
- Fitch, G.M.; Hankey, J.M. Investigating improper lane changes: Driver performance contributing to lane change near-crashes. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2012, 56, 2231–2235. [Google Scholar] [CrossRef]
- Wang, C.; Song, D.; Fu, R.; Guo, Y.; Xu, Y. Identification of lane change safety characteristic of large commercial bus on expressway. China J. Highw. Transp. 2018, 31, 229–238. [Google Scholar]
- Alonso, J.D.; Vidal, E.R.; Rotter, A.; Muhlenberg, M. Lane-change decision aid system based on motion-driven vehicle tracking. IEEE T. Veh. Technol. 2008, 57, 2736–2746. [Google Scholar] [CrossRef]
- Khan, A.; Bacchus, A.; Erwin, S. Surrogate safety measures as aid to driver assistance system design of the cognitive vehicle. IET Intell. Transp. Syst. 2014, 8, 415–424. [Google Scholar] [CrossRef]
- Paul, A.; Chauhan, R.; Srivastava, R.; Baruah, M. Advanced Driver Assistance Systems (No. 2016-28-0223); SAE Technical Paper; SAE: Warrendale, PA, USA, 2016. [Google Scholar]
- Tijerina, L. Operational and behavioral issues in the comprehensive evaluation of lane change crash avoidance systems. Transp. Hum. Factors 1999, 1, 159–175. [Google Scholar] [CrossRef]
- Fu, R.; Ma, Y.; Guo, Y.; Yuan, W.; Sun, H. Lane change warning rules based on real vehicle test data. J. Jilin Univ. Eng. Technol. Ed. 2015, 45, 379–388. [Google Scholar]
- Mar, J.; Lin, H.T. The car-following and lane-changing collision prevention system based on the cascaded fuzzy inference system. IEEE Trans. Veh. Technol. 2005, 54, 910–924. [Google Scholar] [CrossRef]
- Kim, T.; Lovell, D.J.; Kim, H.; Oh, C. Empirical results of effects of various causal factors on car-Following behavior. Transp. Res. Rec. 2010, 2188, 174–186. [Google Scholar] [CrossRef]
- Sagberg, F.; Selpi Piccinini, G.F.B.; Engstrom, J. A review of research on driving styles and road safety. Hum. Factors 2015, 57, 1248–1275. [Google Scholar] [CrossRef] [PubMed]
- Bengler, K.; Dietmayer, K.; Farber, B.; Maurer, M.; Stiller, C.; Winner, H. Three decades of driver assistance systems: Review and future perspectives. IEEE Intell. Transp. Syst. Mag. 2014, 6, 6–22. [Google Scholar] [CrossRef]
- Liu, T.; Fu, R.; Ma, Y.; Li, Z.; Cheng, W. Car-following warning rules considering driving styles. China J. Highw. Transp. 2020, 33, 170–180. [Google Scholar]
- Lotfi, R.; Ghatee, M. Smartphone based Driving Style Classification Using Features Made by Discrete Wavelet Transform, Human-Computer Interaction. arXiv 2018, arXiv:1803.06213. [Google Scholar]
- Johnson, D.A.; Trivedi, M.M. Driving style recognition using a smartphone as a sensor platform. In Proceedings of the 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 1609–1615. [Google Scholar]
- Takamatsu, Y.; Takada, Y.; Kishi, N. A narrow road driving assistance system based on driving style. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 1669–1674. [Google Scholar]
- Zhang, Y.; Lin, W.C.; Chin, Y.K.S. A pattern-recognition approach for driving skill characterization. IEEE Trans. Intell. Transp. Syst. 2010, 11, 905–916. [Google Scholar] [CrossRef]
- Ren, G.; Zhang, Y.; Liu, H.; Zhang, K.; Hu, Y. A new lane-changing model with consideration of driving style. Int. J. Intell. Transp. Syst. Res. 2019, 17, 181–189. [Google Scholar] [CrossRef]
- Hou, H.; Jin, L.; Guan, Z.; Du, H.; Li, J. Effects of Driving Style on Driver Behavior. China J. Highw. Transp. 2018, 31, 18–27. [Google Scholar]
- Wang, C.; Sun, Q.; Guo, Y.; Fu, R.; Yuan, W. Improving the user acceptability of advanced driver assistance systems based on different driving styles: A case study of lane change warning systems. IEEE Trans. Intell. Transp. Syst. 2019, 21, 4196–4208. [Google Scholar] [CrossRef]
- Dang, R.; Ding, J.; Su, B.; Yao, Q.; Tian, Y.; Li, K. A lane change warning system based on V2V communication. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1923–1928. [Google Scholar]
- Satzoda, R.K.; Gunaratne, P.; Trivedi, M.M. Drive quality analysis of lane change maneuvers for naturalistic driving studies. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 654–659. [Google Scholar]
- Lee, S.E.; Olsen, E.C.; Wierwille, W.W. A Comprehensive Examination of Naturalistic Lane-Changes; National Highway Traffic Safety Administration: Washington, DC, USA, 2004.
- McLachlan, G.; Peel, D. Finite Mixture Models; Wiley-Interscience: Hoboken, NJ, USA, 2000. [Google Scholar]
- Sun, X.; Wu, Z.; Lv, X.; Chen, Z. Improved Gaussian Mixture Model Based Moving Target Detection. Comput. Eng. Des. 2014, 35, 914–917. [Google Scholar]
- Liu, T. Comparison of Car-Following Behavior in Terms of Safety Indicators Between China and Sweden. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3696–3705. [Google Scholar] [CrossRef]
- Doshi, A.; Trivedi, M.M. Examining the impact of driving style on the predictability and responsiveness of the driver: Real-world and simulator analysis. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, La Jolla, CA, USA, 21–24 June 2010; pp. 232–237. [Google Scholar]
- Aust, M.L.; Engström, J.; Viström, M. Effects of forward collision warning and repeated event exposure on emergency braking. Transp. Res. Part F 2013, 18, 34–46. [Google Scholar] [CrossRef]
- Feng, F.; Bao, S.; Sayer, J.R.; Flannagan, C.A.; Manser, M.; Wunderlich, R. Can vehicle longitudinal jerk be used to identify aggressive drivers? An examination using naturalistic driving data. Accid. Anal. Prev. 2017, 104, 125–136. [Google Scholar] [CrossRef]
- ISO 15623:2002-10; Transport Information and Control Systems-Forward Vehicle Collision Warning Contents. ISO: Geneva, Switzerland, 2002; Volume 10.
- Vadeby, A. Modeling of relative collision safety including driver characteristics. Accid. Anal. Prev. 2004, 36, 909–917. [Google Scholar] [CrossRef] [PubMed]
- Xiong, X.; Wang, M.; Cai, Y.; Chen, L.; Farah, H.; Hagenzieker, M.P. A forward collision avoidance algorithm based on driver braking behavior. Accid. Anal. Prev. 2019, 129, 30–43. [Google Scholar] [CrossRef]
- Jiang, R.; Zhu, S.; Chang, H.; Wu, J.; Ding, N.; Liu, B.; Qiu, J. Determining an Improved Traffic Conflict Indicator for Highway Safety Estimation Based on Vehicle Trajectory Data. Sustainability 2021, 13, 9278. [Google Scholar] [CrossRef]
- Ni, J.; Liu, Z.; Tu, X. Safety prediction model of lane changing based on driver assistance system. J. Transp. Syst. Eng. Inf. Technol. 2016, 16, 95–100. [Google Scholar]
- Fu, R.; Liu, T.; Guo, Y.; Zhang, S.; Cheng, W. A case study in China to determine whether GPS data and derivative indicator can be used to identify risky drivers. J. Adv. Transp. 2019, 2019, 9072531. [Google Scholar] [CrossRef]
- Mori, M.; Miyajima, C.; Hirayama, T.; Kitaoka, N.; Takeda, K. Integrated modeling of driver gaze and vehicle operation behavior to estimate risk level during lane changes. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems (ITSC 2013), Hague, The Netherlands, 6–9 October 2013; pp. 2020–2025. [Google Scholar]





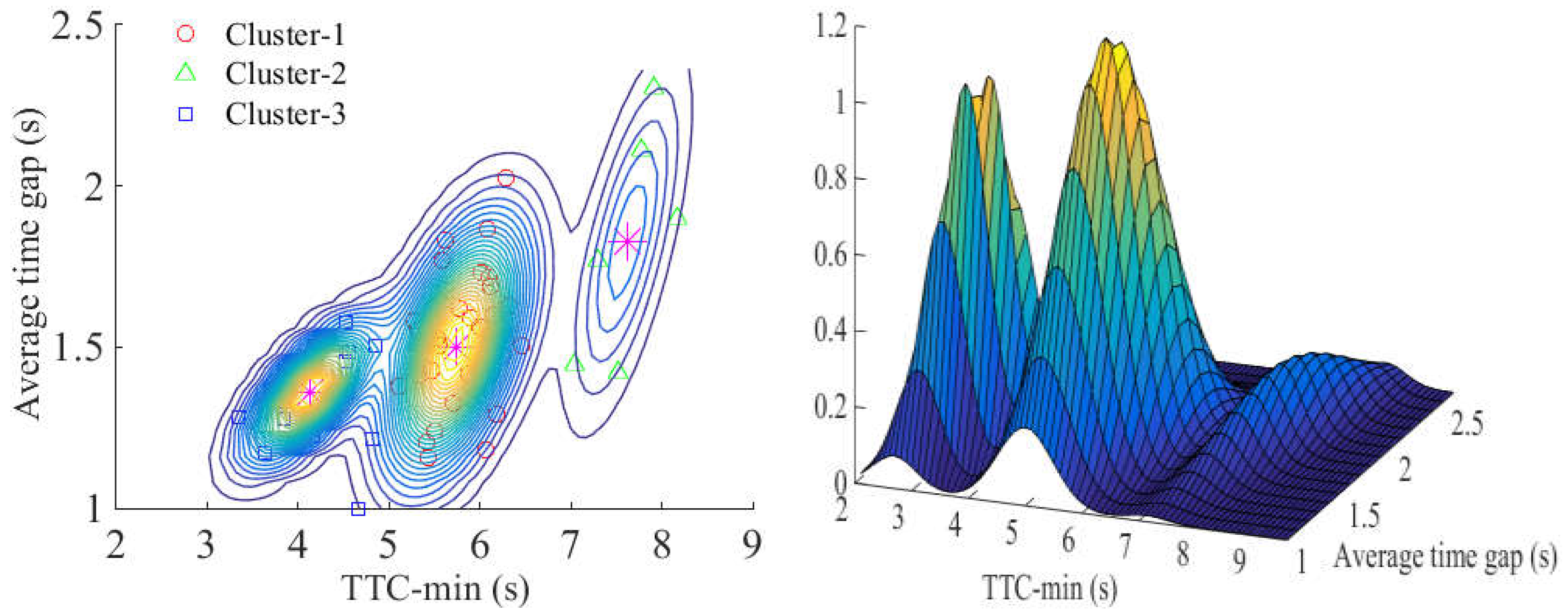

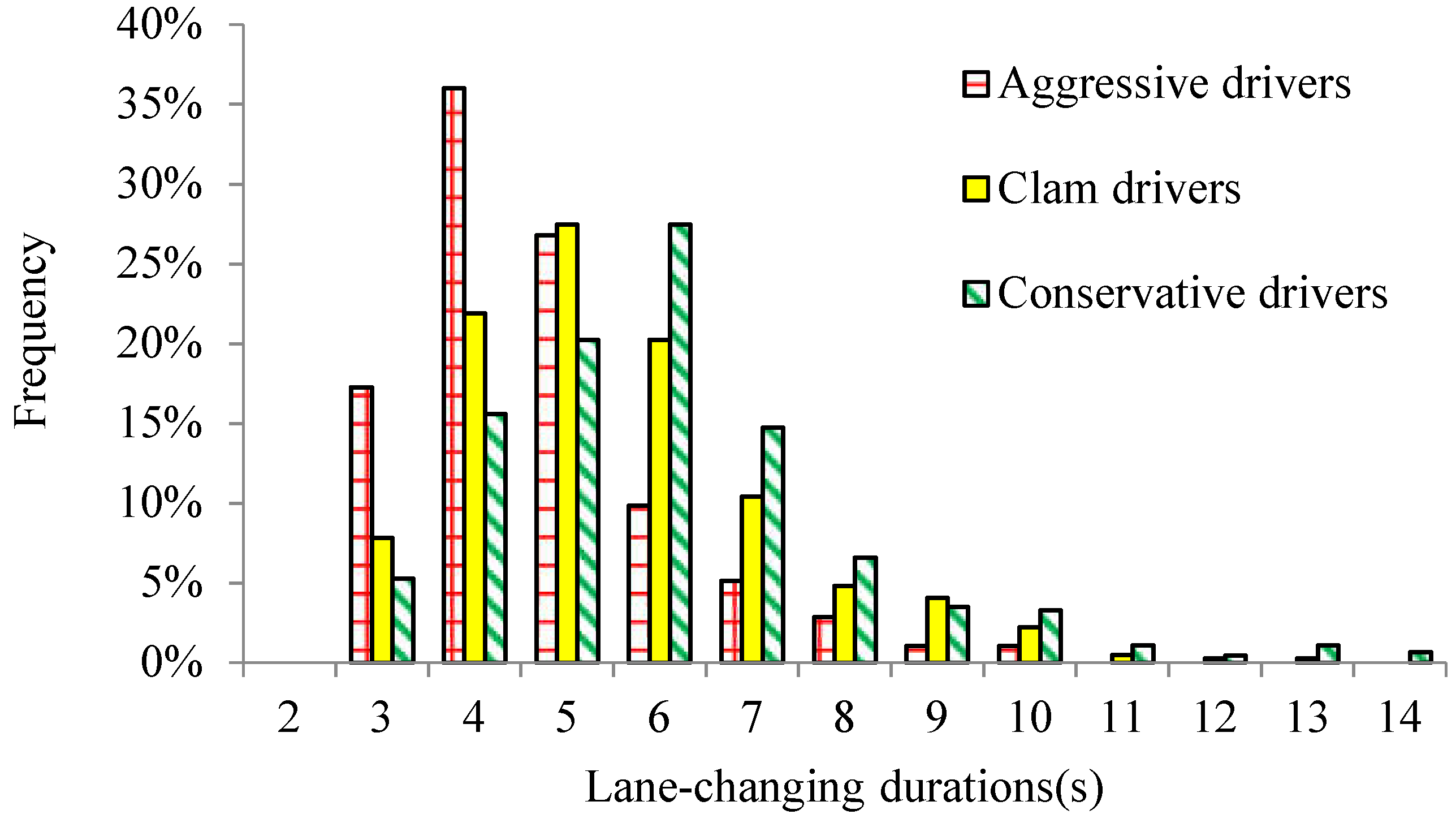
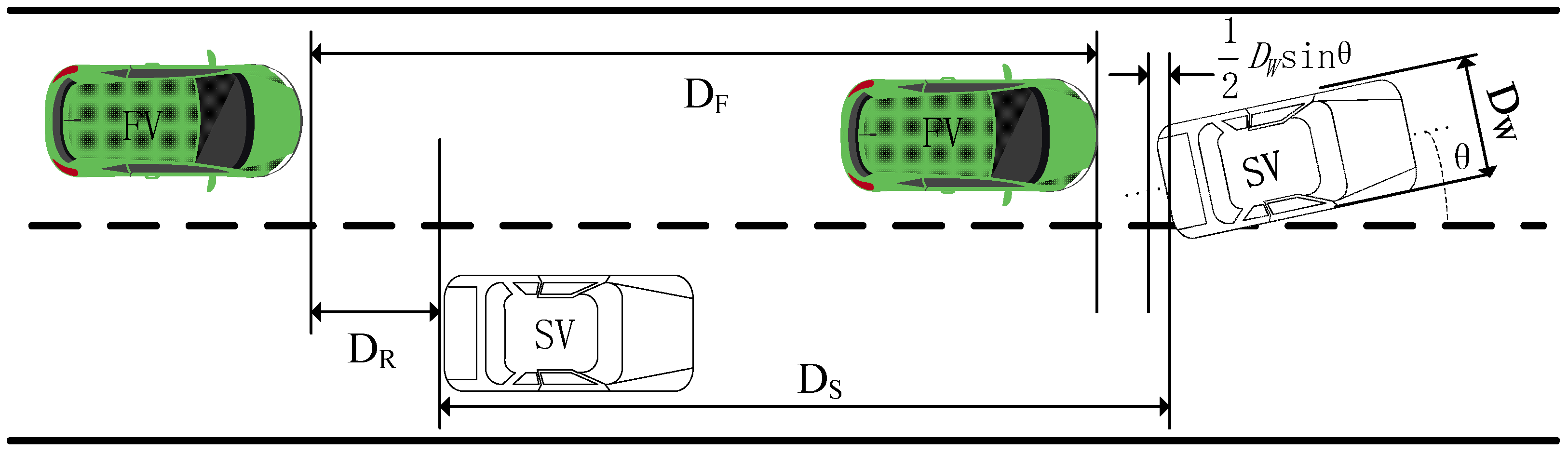

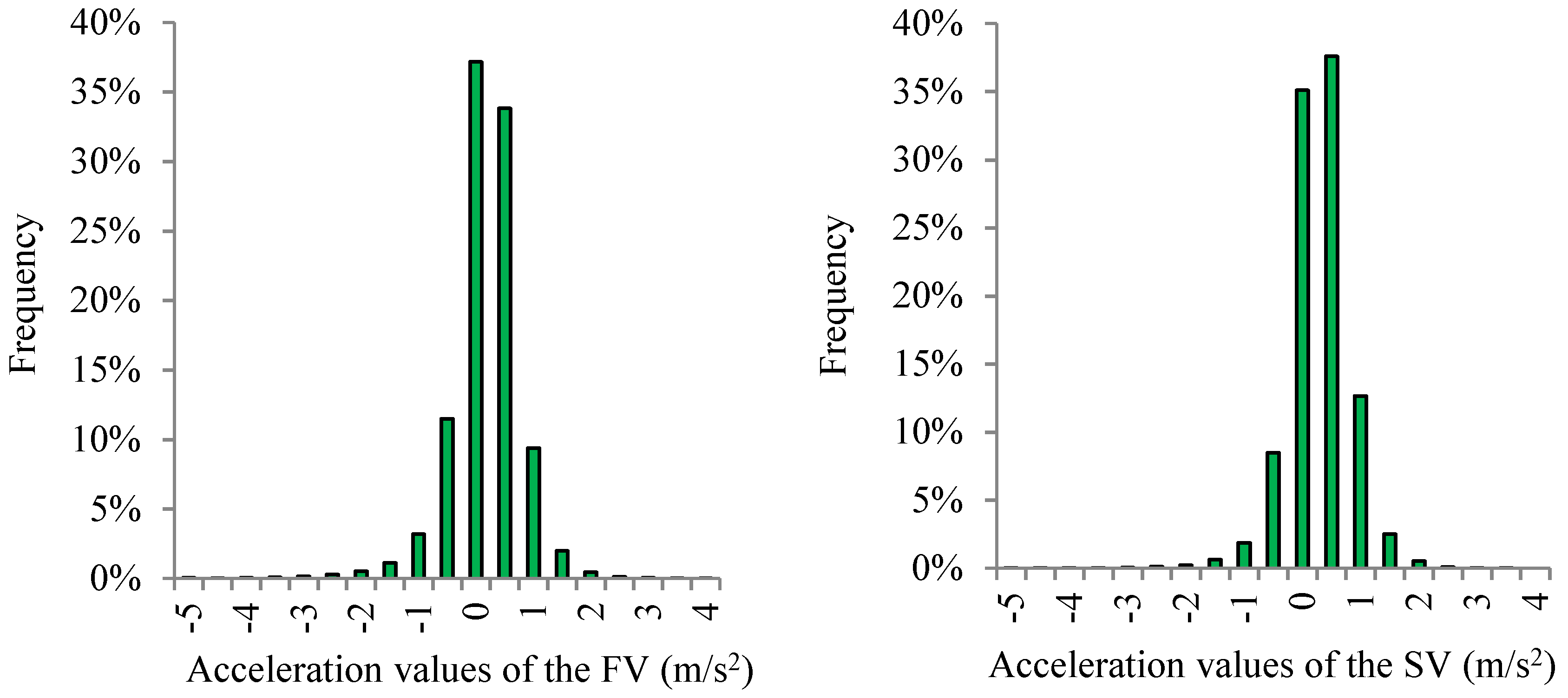
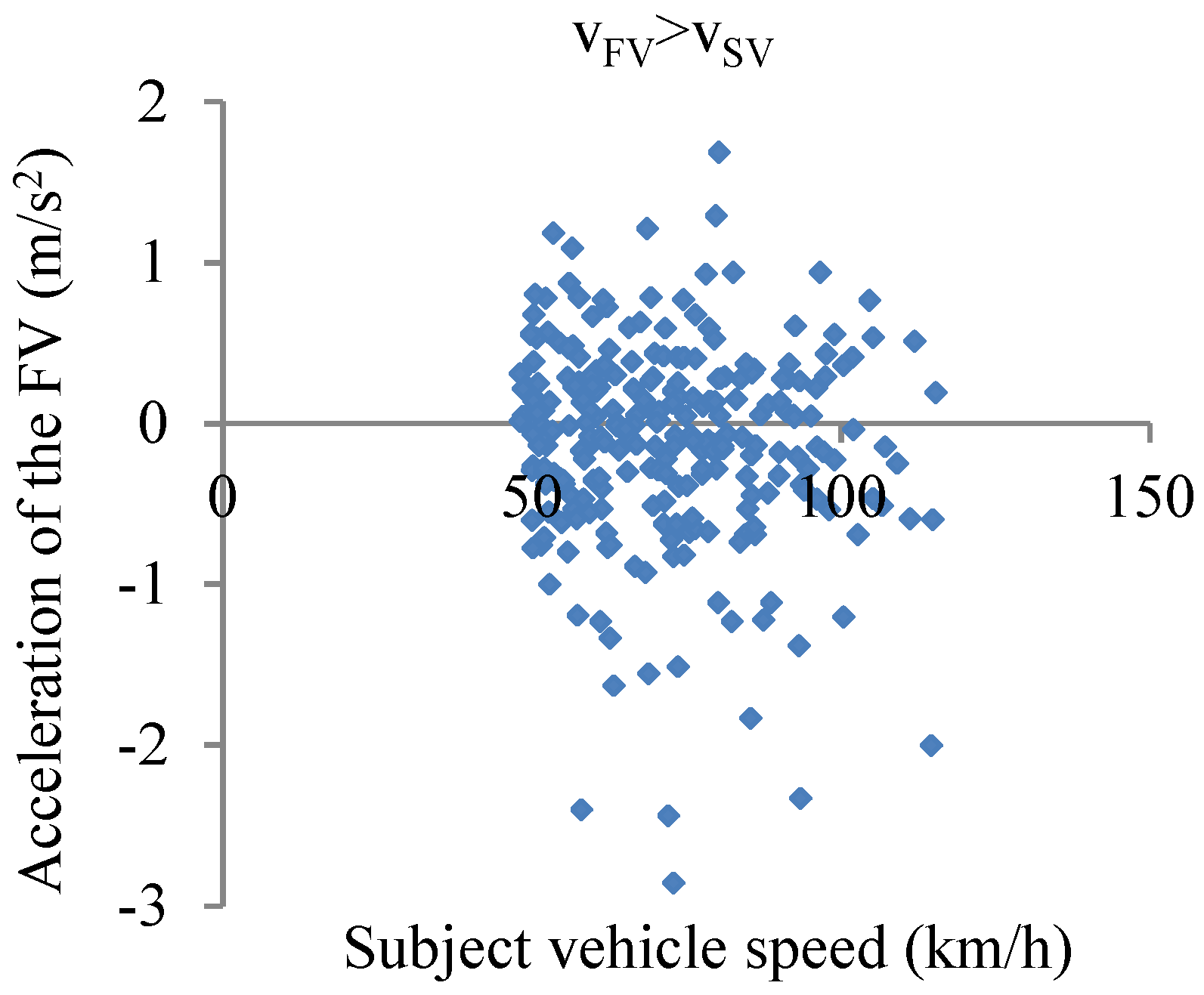



| Driving Styles | Driver #s | Average Time Gap (s) | Average TTC_Min (s) |
|---|---|---|---|
| Aggressive | 6, 7, 16, 17, 20, 22, 23, 26, 28, 40, 43, 50 | 1.36 | 4.21 |
| Calm | 3, 4, 5, 9, 12, 14, 18, 21, 30, 32, 34, 35, 39, 41, 44, 45, 46, 47 | 1.55 | 5.84 |
| Conservative | 2, 8, 15, 24, 25, 37 | 1.83 | 7.62 |
| Speed Ranges (km/h) | Lane-Changing Safety Distance Model |
|---|---|
| ≤ 70 | |
| ≤ 90 | |
| ≤ 110 | |
| > 110 |
| Speed Ranges (km/h) | Lane-Changing Warning Model |
|---|---|
| ≤ 70 | |
| ≤ 90 | |
| ≤ 110 | |
| > 110 |
| (a) vS ≤ 70 km/h | ||
| Warning Area | Safety Zone | |
| Hazardous data | 83 | 21 |
| Potential conflict/Safe data | 26 | 309 |
| (b) 70 km/h < v ≤ 90 km/h | ||
| Warning Area | Safety Zone | |
| Hazardous data | 96 | 28 |
| Potential conflict/Safe data | 25 | 277 |
| (c) 90 km/h < v ≤ 110 km/h | ||
| Warning Area | Safety Zone | |
| Hazardous data | 80 | 24 |
| Potential conflict/Safe data | 11 | 225 |
| (d) v > 110 km/h | ||
| Warning Area | Safety Zone | |
| Hazardous data | 24 | 6 |
| Potential conflict/Safe data | 11 | 45 |
| Warning Area | Safety Zone | |
|---|---|---|
| Hazardous data | 243 | 69 |
| Potential conflict/Safe data | 57 | 692 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Wang, C.; Fu, R.; Ma, Y.; Liu, Z.; Liu, T. Lane-Change Risk When the Subject Vehicle Is Faster Than the Following Vehicle: A Case Study on the Lane-Changing Warning Model Considering Different Driving Styles. Sustainability 2022, 14, 9938. https://doi.org/10.3390/su14169938
Liu T, Wang C, Fu R, Ma Y, Liu Z, Liu T. Lane-Change Risk When the Subject Vehicle Is Faster Than the Following Vehicle: A Case Study on the Lane-Changing Warning Model Considering Different Driving Styles. Sustainability. 2022; 14(16):9938. https://doi.org/10.3390/su14169938
Chicago/Turabian StyleLiu, Tong, Chang Wang, Rui Fu, Yong Ma, Zhuofan Liu, and Tangzhi Liu. 2022. "Lane-Change Risk When the Subject Vehicle Is Faster Than the Following Vehicle: A Case Study on the Lane-Changing Warning Model Considering Different Driving Styles" Sustainability 14, no. 16: 9938. https://doi.org/10.3390/su14169938
APA StyleLiu, T., Wang, C., Fu, R., Ma, Y., Liu, Z., & Liu, T. (2022). Lane-Change Risk When the Subject Vehicle Is Faster Than the Following Vehicle: A Case Study on the Lane-Changing Warning Model Considering Different Driving Styles. Sustainability, 14(16), 9938. https://doi.org/10.3390/su14169938






