Abstract
The traditional wave energy converters (WECs) use hydraulic or turbine-type power take-off (PTO) mechanisms which consist of many moving parts, creating mechanical complexity and increasing the installation and maintenance costs. Linear generator-based direct-drive WECs could be a solution to overcome this problem, but the efficiency of the single conventional linear generator is not high enough, and it cannot work satisfactorily in the low-frequency range. This article reviews the recent research developments of the linear permanent magnet (PM) generator-based WEC to harness maximum energy from ocean waves. It starts with a brief introduction and background of wave energy converters using linear generators. Following this, the working principle of the WECs with linear PM generators is briefly outlined. Subsequently, the analytical model of the linear PM generator-based WEC is studied. After that, the up-to-date developments of the linear PM generator-based PTO systems are studied. Despite some modifications resulting in complexity in the linear PM generator’s structure and a rise in manufacturing costs, the study shows the systems’ efficiencies increased by increasing magnetic flux and reducing cogging force. The key parameters and improvement issues that can increase the performances and efficiencies of the PTO systems are identified to help future researchers for further development. Moreover, the review discusses the numerical and experimental analysis tools, the typical control systems used by the researchers and the challenges of the linear generator-based wave energy conversion system. Finally, conclusions about the significant beneficial characteristics and design choice of the WEC linear generator structure are provided and related to the application conditions.
1. Introduction
Increased energy demand, environmental pollution, and fossil fuel costs push researchers to find new energy sources. Therefore, energy generation from ocean waves has been seen as an attractive research topic to solve the energy demand and environmental problems. Ocean waves are a significant unused promising renewable energy source that covers 70% of the world’s surface area. This energy source can be used for energy generation to fulfil the world energy demand. All the latest reviews show that there are several hundred WEC projects in different development stages around the world [1]. As new concepts and technologies are developing, this number is continuously increasing. Day et al. summarised that over 100 projects and more than 1000 patents worldwide had been developed in Europe, the USA, Japan, China and Asia since 2015 [2]. To evaluate the WEC’s performance, broad numerical and experimental studies have been carried out by different researchers all over the world. Although there are many devices and methods that have been proposed to harness wave energy, the designs are still in the early stages, as not a single commercial mature technological model has been developed. Thus, it can still be seen as an immature and expensive technology. However, currently, the largest portion of wave energy projects that have been installed is based on the oscillating bodies’ technology, especially the point absorber (PA) type [3].
The point absorber is an offshore-type device that generally utilises heave motion for energy generation and is very popular because of its advantages over other wave energy technologies. The point absorber-type device’s size is smaller than other WEC technologies, it contains decidedly less mechanical complexity, and it can generate energy from any direction of waves at one point of the ocean [4]. Two general types of electrical generators are used in the point absorber (PA)-type WEC system: the rotary generator and the linear generator. Generally, hydraulic motors, turbines, or gearboxes are used in the traditional rotary generator-based WEC to produce a high-speed rotating motion from slow-moving wave motions [5]. This design consists of many moving parts, which creates a comparatively very complex mechanical system and can pollute the ocean environment due to oil leakage of any moving part [6]. To overcome this mechanical complexity, electromagnetic-based linear generators can be used in WECs [7]. The advantages of this buoy type of linear generator set-up are that it has a simple mechanical design because it does not contain any gearbox or other mechanical or hydraulic conversion system.
Moreover, it has fewer environmental impacts and reduces the maintenance cost of the WEC due to reducing the need for maintenance [8]. So far, many linear generator-based WECs have been proposed, tested and deployed in the ocean. Among the well-known linear PM generator-based WECs, the Archimedes Wave Swing (AWS) was the first device deployed in the ocean for performance testing [9]. The second linear PM generator-based WEC was developed and tested by Uppsala University (UU). The third one was developed and tested by Oregon State University (OSU) in collaboration with industry partners. Uppsala University and Oregon State University developed several linear generator-based WEC prototypes and installed them in the ocean for performance analysis [10]. Uppsala University’s deployed prototypes showed promising results in developing linear PM generator-based WECs by simplifying assembly steps, grid connections and measuring stations, and modelling wave farms, in addition to comprehensive environmental-monitoring studies. Oregon State University deployed the prototype in the ocean testing of a 10-kW wave energy conversion system which was an interdisciplinary effort. bringing together researchers from electrical, mechanical and ocean engineering.
In contrast to traditional rotary generators, linear PM generators are powered at varying wave speeds, and the movement of the translator also varies in direction. The output voltage and current differ in frequency and amplitude; hence, the phase series is adjusted alternately, and the maximum/average power rate can be high. Therefore, the generator needs to be built to have an appreciation value significantly higher than the average output compared with other linear generators. Polinder, H., et al. evaluated the linear PM generator system, such as the AWS WEC and the WEC developed by Uppsala. They identified problems and potential solutions that require further study [11]. The drawbacks of these types of linear electromagnetic systems are that the magnetic attraction force is high due to the high volume of magnetic materials, the efficiency of every single device is smaller compared to other types of WEC, the manufacturing cost is high, the end effects are very significant, the size is large and, due to the unequal voltage generated by the irregular wave movement, the power transmission system is complicated [8].
To overcome the disadvantages and increase the efficiency of the linear PM generator for WECs, many design concepts have been proposed, developed and tested, as published in the literature. These design concept improvements are related to the design of the translator and stator, which are the two main parts of the linear PM generator. Many researchers have proposed different permanent magnet arrangements and stator designs to increase the output power and reduce the cogging force in the generator. Linear generators have been proposed to capture energy from the ocean and produce hydrogen using wave energy conversion systems [12]. The experimental studies of this research show the promising future for linear generators in the wave energy research field. Moreover, many control systems have been proposed and used in linear generator-based WECs for increasing the energy generation performances of the device and capturing the maximum power from ocean waves. The generator-side control system increases the power generation from power take-off systems, and the grid-side control system helps to provide suitable electrical power signals. Most of the proposed and used control systems include controlling the damping forces of the WEC [13].
So far, many research papers have been published based on electromagnetic direct-drive WECs. Therefore, this comprehensive review is essential to encourage the success of research and advancement of linear PM generator-based wave energy converters. So far, few review articles have been published in the field of WECs with linear PM. These previously published review papers were based on either wave energy conversion generator systems, the numerous design technologies and topologies or the research issues related to this. M.A. Mueller studied the design of linear generators for direct-drive wave energy converters by comparing the longitudinal flux permanent magnet generator with the transverse flux permanent magnet generator [14]. The size of these linear generators and the development of electromagnetic and circuit models of the transverse flux permanent magnet generators were studied to investigate the power output at typical device velocities. Jawad Faiz and Alireza Nematsaberi reviewed the specifics and assumptions of various proposed and tested linear generator technologies and topologies and their relevant problems three years ago [15]. Pooja Khatri and Xu Wang presented a comprehensive study and working principle of various linear generators investigated until 2019 for direct-drive ocean wave energy conversion systems [16]. Various PM generators, including linear and flat generators, were reviewed and discussed based on their design configuration for different magnet arrangements. Moreover, various linear PM generators have been compared with respect to the core type, flux path, and PM location, etc.
To identify the most promising kinds of linear generators that can be used in WEC direct-drive systems, this review provides a timely and comprehensive critical comment on the distinctive linear permanent magnet (PM)-based generator systems that have been studied and evaluated in recent years. Apart from the review mentioned above, no detailed review has been published recently that focusses on the direct-drive WEC with linear PM generator and the analysis of the different design concepts or methods, analytical modelling, control systems and performance analysis. It is hoped that this review can offer helpful guidance to assist the commercial production of wave energy converter systems and speed up new research activity in the wave energy field. The author’s recent paper [1] presented a brief review of the five major wave energy power take-off systems with their significant advances and challenges for wave energy technologies. In addition, this included details of the recent research and development and the current operational market of the WEC. This paper aims to specifically focus on and review the recent research developments of the WEC with the linear PM generator. Moreover, the control system and the linear generator’s performance analysis for WECs have also been reviewed.
2. WEC with Linear Generator-Based Direct Electric-Drive PTO System
The main components of the direct-drive linear generator-based WECs are the linear PM generator-type PTO system and the wave buoy. Usually, the linear PM generator consists of a translator which holds the permanent magnets (PMs) and the stator equipped with coil windings, or vice versa. The operating principle of the linear PM generator-based WEC has the translator connected to a floating or submerged buoy, and the stator is fixed, or vice versa [17]. With the hydrodynamic motion of the ocean waves, the translator goes up and down along with the buoy and produces the fluctuating magnetic field within the coil windings, generating electrical energy. Figure 1 displays the schematic diagram of the WEC with a linear PM generator, and the basic functional units of wave energy conversion are shown in Figure 2.
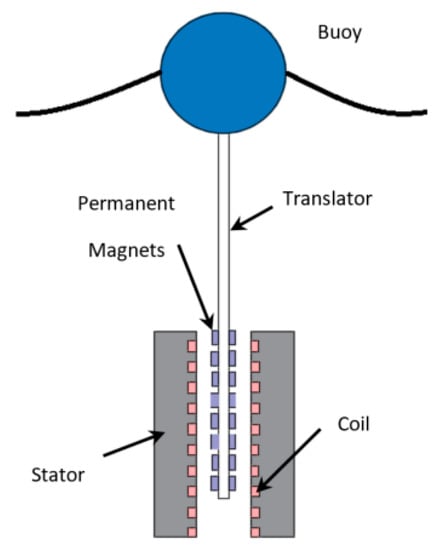
Figure 1.
Schematic diagram of the linear PM generator-based WEC [18].
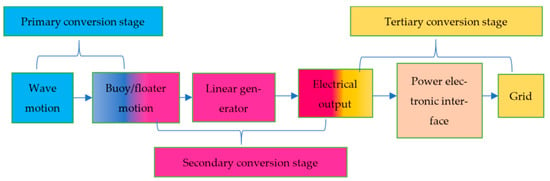
Figure 2.
Basic functional units of a linear generator-based WEC.
The wave energy conversion system can be divided into the primary, secondary and tertiary conversion stages [19]. In the primary conversion stage, the WEC captures the wave’s kinetic energy through the buoy. The secondary conversion stage transforms the buoy motion energy into electricity via the linear generator. Finally, the tertiary conversion stage adapts the characteristics of the generated power with power electronic interfaces to the grid requirements.
2.1. Different Topologies of WECs with Linear Generator-Based PTO Systems
The main focus of this section is to provide an overall perspective on the various common types of linear wave generator configurations, presenting their advantages and disadvantages. The multiple topologies of WECs with linear PM PTO can be classified depending on the applications employed and the underlying system principles. Some systems are based on a floating buoy on the sea surface, as shown in Figure 3a, or a fully submerged heaving system, as displayed in Figure 3b. However, when the wave energy converter is fully submerged into the water, then it is less vulnerable to storms, but cooling problems and hydraulic and pneumatic intermediaries tend to cause failures, requiring higher maintenance costs. To avoid these construction, operational and maintenance difficulties, the best practice is not to submerge the device in the water [20].
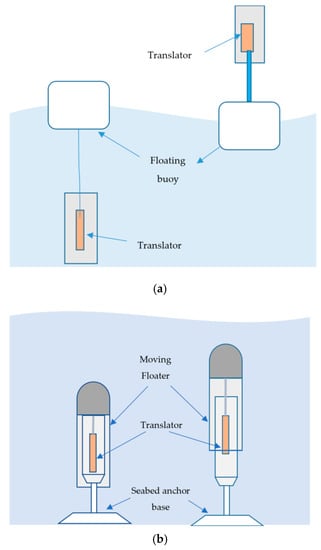
Figure 3.
(a) Floating buoy on the sea surface (b) Fully submerged heaving system.
2.1.1. Floating Buoy on the Sea Surface
The most straightforward design using a floating buoy on the sea surface involves having the buoy directly connected to the generator moving part with a tether, while the linear generator is fixed onto the seabed [21]. Another possibility is placing the linear generator above the ocean surface, which is mounted with or without a fixed structure, and the translator of the generator is attached to the floating buoy [6,22]. The other common design concept is to leave the linear generator floating underneath the ocean surface and the translator directly connected with the floating buoy on the sea surface by a tether [23]. A new concept has been presented where the whole linear generator system floats on the sea surface [24]. Different direct-drive linear generator WECs have been developed based on these concepts. Still, the most appropriate technique might be to have the overall system partially above the sea surface because the submerged systems create difficulties, such as problems related to moorings, seawater corrosion and access for maintenance.
Single-Body Heaving Buoy System
The single-body heaving system is the most common in the research field of direct-drive linear wave energy converters because of its simplicity. The well-known direct-drive linear generator-based WECs developed at Uppsala University and Oregon University were based on the single-body heaving system [25]. Uppsala University’s developed WEC contained a buoy and linear generator, where the translator moved up and down with the buoy inside the linear generator system, which was fixed to the seabed. The rectangular-shaped translator had several permanent magnets, and the wound coils were connected with the stator [26]. Springs were also used to connect the translator with the linear generator foundation to retract the translator in the wave troughs [8]. The moving part of the linear generator is driven by the buoy’s motion and counteracted by a fixed component at the bottom sea spring. End stops were also used at the top and bottom of the device to restrict the translator’s stroke length during extreme oceanic conditions [8]. The linear generator designed by Oregon State University contained a spar and a float where the spar was moored, and the float moved up and down with the wave motion. The spar was a central cylindrical design housing a bobbin wound with a three-phase armature, and the float was an outside cylinder that consisted of 960 magnets. The float’s inner surface faced the spar’s outer surface, and when the float moved up and down due to the wave motion, the voltage was directly produced inside the armature [27]. The device was around 3.3 m high and 1.2 m wide, with 10 kW of rated power [28].
Two-Body Heaving Buoy System
The single-body heaving system poses several challenges, such as constructing a large enough device with a natural frequency that coincides with the incoming waves’ low frequency to achieve resonance. The distance between the floater and the seabed can be significant, and due to this enormous distance, the single-body heaving system has reduced efficiency. To solve these problems, some researchers proposed two-body heaving systems [29]. The two-body heaving system consists of either a floating section that deals directly with the wave and a fully submerged section or two floating sections [5]. The passive buoy or submerge section creates inertia for damping, and combining the floating body and submerge bodies helps the buoy follow the wave frequencies more closely. The linear generator can be mounted between the two bodies to avoid the large linear generator connection distance between the seabed and the free surface. Both bodies move due to the wave motion and create relative movement between them, causing both the translator and stator of the linear generator system to move, which helps to increase the efficiency. Elie Al Shami et al., reviewed the studies of single and two-body heaving systems with their dynamics, hydrodynamics, advantages and disadvantages [30].
The power capture ratio of the two-body heaving system’s converter has been reported as approximately 80% when the waves are irregular. If a 14-ton translator was used, the coupling between the linear generator, submerged body (passive buoy), and floating buoy on the sea surface became rigid. In addition, if the submerged body (passive buoy) was placed at a depth of 40 m, the achieved power capture ratio was around 80%. The power capture ratio decreased to about 50% when the depth decreased by 30 m. The resonance behaviour of the two-body heaving system significantly affects the linear generators’ efficiency.
Moreover, another novel topology has been developed, which may be categorized as a fully floating two-body heaving direct-drive linear generator WEC [5]. The proposed system consists of a spar fixed on the sea floor and a floating system with two parts. The permanent magnets are mounted in the inner body, and the windings coils are mounted in the outer body. Both outer and inner bodies freely move up and down along the spar, and, during the movement, the outer body acts as a floating buoy to harness the wave energy, while the inner body experiences a forced oscillation.
2.1.2. Fully Submerged Heaving System
The Archimedes Wave Swing (AWS) is a fully submerged direct-drive device and was the first WEC device to utilise the linear permanent magnet generator as the PTO system [9]. The linear generator of the device is attached to a compressed air chamber fixed on the seabed. The linear generator’s translator is connected with the fully submerged floater (underwater). The working principle of the AWS is based on the oscillating movement of the sea waves, which increases and decreases pressure levels successively under the sea surface because of the wave motion. Due to the wave motion, the floater moves vertically up and down with respect to the fixed lower part and increases the wave pressure levels, forcing the air inside the chamber to be compressed. The volume inside the chamber expands when the air pressure becomes larger than that of the wave [7]. This reciprocating linear motion generates electrical energy from the wave motion. However, the wholly submerged system has the same advantages and disadvantages as the AWS. These fully submerged systems are not visibly gaining public acceptance, though they are less vulnerable to severe ocean weather conditions. On the other hand, because of the ocean’s environmental conditions, it requires higher maintenance costs. Moreover, the corrosion of metals, and the disturbance of the marine life are two drawbacks of the fully submerged systems.
2.1.3. Other Topologies of WECs with Linear Generator-Based PTO Systems
Other than the floating buoy on the sea surface and fully submerged heaving systems, there are other topologies of WECs with linear PM generators, such as the fully floating gyroscopic system and buoyant system, which have been proposed and tested experimentally [31]. The fully floating gyroscopic-based WEC consists of gyroscope systems and linear permanent magnet generators inside a fully sealed buoy [31]. The gyroscope’s inertial reactions are applied to the device (inertial sea wave energy converter (ISWEC)) as a floating buoy slack-moored to the ocean floor. The stroke of the linear generator is short, and the reciprocating motion between the gyroscopic system and the hull is used to drive the linear electrical generators. On the other hand, the buoyant electrical generator-based WEC is a point absorber-type device that consists of a linear generator, boat-shaped buoy and an electronic power section [12]. The linear generator is placed inside the buoyant system. The proposed device is claimed to provide a highly reliable wave energy conversion system that can produce hydrogen to store energy. Another new topology of WEC with a linear PM generator has been proposed, known as a surface riding WEC, where the magnet assembly slides inside the armature [32].
2.2. Linear Permanent Magnet (PM) Generator Topologies
So far, different types of linear generators have been used for WECs, which include linear permanent magnet (PM) synchronous generators [33], flux-switching permanent magnet linear generators [34], switched reluctance linear generators [35], vernier hybrid machines [36], and so on. Due to the low-cost power electronic converter’s availability and the permanent magnet (PM) material’s improvements in terms of remnant flux density, coercive force, magnetic flux leakage and copper losses of field windings, and operating temperature, PM-based linear generators are suitable for energy harvesting across the broadband frequency ranges [37]. Moreover, the exerted force and power density can be increased by using permanent magnet excitation. Therefore, up to now, the vast majority of the linear generators for wave energy conversion have been developed based on synchronous permanent magnet generators because of their efficiency at low speeds, price and robustness [34]. The PM-based linear generator’s geometry plays a significant role in the design development; its variation substantially affects the overall performance and efficiency. In the literature, various PM linear generator topologies have been proposed for wave energy conversion systems, shown in Figure 4.
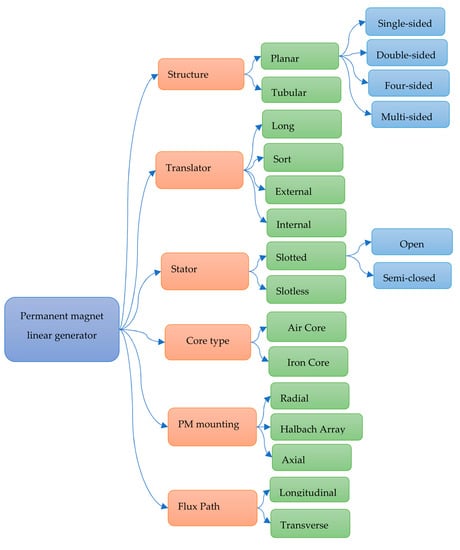
Figure 4.
Linear PM generator topologies.
The main components of the linear PM generator are permanent magnets and coils. The linear PM generator topologies can be classified according to various design methods, such as structure, translator size and location, stator shape, core type, location of the permanent magnet (PM), flux path and the installation method of the PM. The structure of the linear PM generator may be tubular or planar/flat [38]. It is easier to fabricate the planar-type linear generator for WECs. It can be constructed with different sides, such as two-sided, four-sided, octagonal or multisided-planar generators [39]. A hybrid generator concept has also been proposed using the double-sided planar layout and tubular layout, which creates higher force density due to more effective use of space [40]. Different translator sizes and positions have been used in linear PM generators for direct-drive WECs. Due to the reciprocating linear motion, the translator or the stator must be longer to maintain the system’s generation operation for the stroke’s larger fraction. Typically, the permanent magnet translator is longer than the stator to keep the whole stator winding active during the entire stroke and reduce the amount of series copper and conduction losses [41]. Moreover, the translator can be mounted internally or externally on the generator design for the direct-drive WEC [42].
There are three possible ways to attach the permanent magnets: axially aligned-buried, radially aligned-buried and radially aligned-surface [40]. In addition to that, to get the maximum magnetic flux density Halbach, quasi-Halbach arrays have been used in linear PM generators for WECs [42]. The linear generators can be classified as transverse and longitudinal according to the location of windings relative to translator motion [17]. Using both transverse and longitudinal flux, a new hybrid transverse/longitudinal flux linear PM generator has been developed for WECs [43]. The device’s translator was sandwiched between two stators carrying flux in the longitudinal direction, while the translator carried flux in the transverse direction. Both slotless and slotted stators have been used in research to develop and find the best generator design [44]. The linear PM generator can be classified as an iron-core or air-core generator based on a core. Iron-core and air-core generators have been used in direct-drive PTO-based WECs [45]. All linear generator topologies’ advantages and drawbacks have been discussed briefly in [16]. Other than these topologies, some new, innovative design concepts have been proposed for capturing the maximum energy from ocean waves [46,47].
Innovative Oscillator Design Concept
To date, most of the linear PM generator PTO systems have been developed based on linear oscillator systems (single-degree-of-freedom oscillator system) and traditional design concepts (all permanent magnets are mounted in the translator, with opposite poles facing each other with an iron core used between them, and with coil windings attached in the stator). Usually, the translator moves inside the stator, creating magnetic flux changes inside the winding coils, which generate electrical energy. The linear energy-harvesting technology has been compared with nonlinear systems based on actual data, where it was found that the linear energy harvester has the highest power output in most cases. Still, the nonlinear system has a broader harvesting frequency bandwidth, and the bistable system can harness more energy from random vibration [48]. Moreover, Owens et al. also found that the nonlinear oscillating system is better than linear oscillation for broadening the frequency response bandwidth [49].
To create maximum magnetic flux density inside the coil, several permanent magnets could be added outside the stator coil, and this system is known as the bistable system [50]. It has been found that the proposed bistable system can increase the magnetic flux density inside the winding coils [51]. The linear generator converter’s resonant power and efficiency with light damping and multi-degree of freedom oscillators are expected to be larger than those with a conventional single-degree-of-freedom oscillator [46].
The bandwidth problem of the existing PM linear generator can be overcome by widening the frequency bandwidth of the WEC. Light-damping nonlinear oscillators are expected to have larger operational frequency bandwidths than a conventional single-degree-of-freedom linear oscillator. The magnetic levitation system can be used in the translator design to make the oscillator nonlinear, which is more effective in the broadband frequency range, especially in the low-frequency ocean environment [52]. In the magnetic levitation system, the magnetic spring works like a physical spring and is created when two magnets face each other at the same poles (N–N or S–S), as presented in Figure 5. In addition, the light-damping multi-degree-of-freedom nonlinear oscillators are expected to develop larger operational frequency bandwidths than a single-degree-of-freedom nonlinear oscillator.
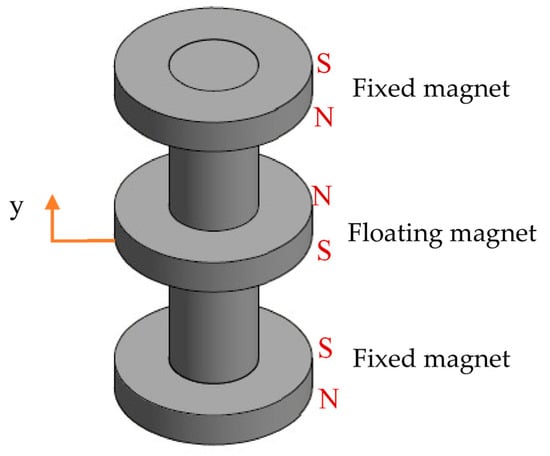
Figure 5.
Schematic diagram of a single-degree-of-freedom nonlinear oscillator system.
3. Mathematical Modelling
Dynamics of the WEC with Linear Permanent Magnet (PM)-Based PTO System
The hydrodynamic modelling of the system analyses the forces acting on the submerged rigid bodies, as well as the motion relative to them. Different theories, such as linear wave theory and Stokes theory, can be used to describe and solve the modelling related to wave–body interaction. The linear generator is connected to the floating buoy with a tether, and the schematic diagram of the typical WEC system is shown in Figure 6. The applicability of various wave theories can be found in [53].
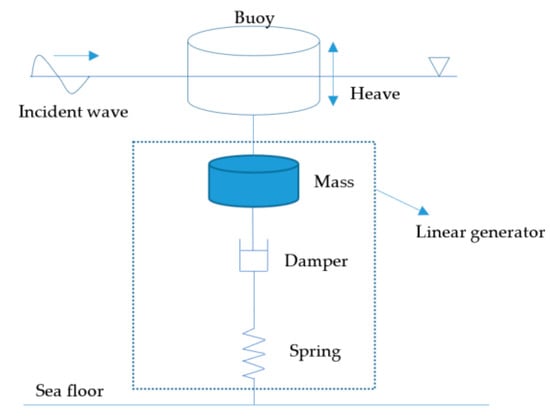
Figure 6.
Schematic diagram of a heaving direct-drive WEC with linear PM generator [54].
For this situation, the linear wave theory has been verified experimentally to be good enough to explain the wave–body interaction [55,56]. Thus, linear wave theory is accepted to find the hydrodynamic parameters and buoy force (wave forces) which help to develop the dynamic model of the WEC with a linear PM generator. In addition, it is assumed that the linear generator-based wave energy converter can be modelled using an equivalent spring-mass-damper system, in which the generator produces an opposing force proportional to acceleration, velocity and position [57]. Although the floating body has six degrees of freedom, only the heave motion has been considered for simplification, since the linear PM generator-based WEC (direct-drive) is a point absorber-type PTO system [5,54]. Based on Newton’s second law, the system’s (heaving buoy) force equation can be expressed by Equation (1) [5,58].
where is equal to the sum of the translator and buoy mass, and only the translator mass if there is slack in the line/rope, is the buoy force, is the generator force and is the electromagnetic force. Moreover, is the buoy acceleration, as well as translator acceleration under excitation from waves. The wave motion and acting spring drive the vertical motion of the translator. The motion of the translator induces an electromagnetic force . between the stator and translator of the generator. The buoy force is the () lift force due to the Archimedes principle, which is proportional to the amount of water displaced by the buoy. The buoy force () is the hydrodynamic force that is acting on the buoy, which can be expressed by Equation (2) where is the wave excitation force, is the wave radiation force and is the hydrostatic force, which can be stated based on the potential theory.
Moreover, z can be described as in harmonic form; then , . The system force can be stated as follows after adding the buoy force () in the frequency and time domains by Equations (3) and (4), respectively [54,59].
In Equation (3), is the frequency domain second derivative of the buoy heave vertical position. The device’s spring accelerates the translator at the second phase of the wave. The velocity of the translator motion from the wave top to the trough is increased by the spring force. The end stop force is not active in normal operation conditions and acts only when the translator stroke inside the stator becomes out of the limits due to the too-high wave heights. As expected, the movement of the translator of the linear generator follows the buoy, and the general generator force (. can be expressed in Equation (5) [54].
Here,
is the damping coefficient of the generator and is the spring constant of the generator system. From Equation (5), it can be simplified that the inner magnet and coil work as a damper system. In practice, many researchers in the WEC research field conducted their studies by regarding the linear generator as a constant damper [60]. Moreover, it can be said that the force provided by the linear generator () opposes the movement of the buoy, which means that the damping force of the generator is proportional to the translator speed with the damping coefficient. The wave radiation force (Fr) and hydrostatic force (Fh) can be expressed in frequency and time domains as,
where ρ is the density of the seawater, is the radius of the buoy and is the gravity acceleration. is the radiation damping and is the added mass. The electromagnetic force can be obtained from the FE calculation of the field in the generator. According to Faraday’s law, the electromagnetic force is created when the magnet oscillates through a coil. This moving magnet changes the magnetic flux and the current in the induction coil. The materials used in the stator, translator, and vibration frequency impact the generator’s efficiency and close relationship with the generator’s eddy current losses and hysteresis. The generator’s eddy current losses and hysteresis are generally ignored for general simplification because considering all uncontrollable variables becomes very complicated. For that reason, the generated current in the coil due to the magnet moving through the coil can be expressed by Equation (10) using Kirchoff’s voltage law [61].
where is the inductance of the coil itself, is the load resistance of the circuit, is the current inside the coil, is the coupling coefficient that couples the mechanical and electrical system and is the voltage inside the coil. and are the position and velocity of the magnets which attach with the translator. The item in Equation (10) represents the counter-electromotive force generated by the coil’s current change and denotes the electromotive force produced by coupling the coil and the moving magnet. The item of the coupling coefficient consists of the time-varying part of the inductance. The Laplace transform () of Equation (12) under the initial conditions
and can be given as
In the research area of wave energy converters, it is assumed that the electrical system behaves like a damper, which is a general simplification of the linear generator. It is also assumed that the resistance is relatively large, so then the voltage is expressed as
Due to the movement of the magnet through the coil, the electromagnetic force works on the magnets, which can be expressed as
By replacing V (Equation (13)) in Equation (14), the electromagnetic force can be written by Equation (15), which can be used directly to calculate the electromagnetic force between a coil and the oscillating magnet [62].
If the electromagnetic damping of the linear generator is defined by Equation (16), then the electromagnetic force can be calculated by Equation (17).
where is the generator electrical damping coefficient. After putting , , and into Equation (3), the system force can be stated in the frequency domain as
In Equation (19), the () is the sum of the mechanical and electrical damping of the generator. Moreover, after adding , , . and into Equation (4), the system force can be stated in the time domain by Equation (20).
However, the excitation force () is often simplified as a harmonic term or series. The excitation force on the heaving buoy can be described by Equation (21) [63] or Equation (22) [20].
where is the amplitude of the wave, is the wave force coefficient, is the frequency of the regular wave and is the phase of the regular wave.
Moreover, the governing equations for the electromagnetic mechanism of the linear permanent magnet generator-based WEC can be expressed by Equations (23) and (24), where Equation (23) is the dynamics equation of the WEC and Equation (24) is the dynamic equation of the current of the coils.
After adding and , Equations (23) and (24) can be expressed as
By considering the state variables and , the resulting state–space matrix form of the differential Equations (25) and (26) can be expressed as
Equations (27) and (28) can be used to calculate the position and velocity of the translator, as well as the output voltage of the generator. The MATLAB ODE file or Simulink can be used to solve these equations. From the above discussion, it can be seen that many parameters need to be considered to model the WEC, including the linear PM generator and buoy parameters. From theory, it can be stated that the generator’s excitation force and damping force are the control variables of the linear PM generator-based WEC. The typical structural parameters of the single-buoy linear PM generator-based WEC are presented in Table 1.

Table 1.
The structural parameters of the linear generator and the buoy.
4. Development of the Linear PM Generator-Based PTO System for WECs
The linear PM generator-based WEC has attracted interest worldwide since the linear PM generator was first proposed for wave energy conversion. Many different research techniques and prototype designs have been reported using the linear PM generator-based WEC concept, which can be seen in [16]. However, to date, although many devices and methods have been proposed to harness wave energy, the design can still be considered in the early stages, as not a single commercial, mature technological model has been developed.
H. Polinder et al. reviewed linear PM generator-based WECs, such as the AWS and the WEC developed at Uppsala University (UU), and their research issues [11]. Several research issues were addressed with potential solutions and some sensible directions, such as improving the WEC linear motion speed for future testing and exploring other generator forms with higher force densities and potentially better efficiencies. The linear PM generator-based WEC has inherent disadvantages, such as high attractive force, because of the large number of magnetic materials, large dimensions, static and dynamic effects, high cogging force, high cost and reduced performance due to its low speed [64]. Erik Lejerskpg et al. experimentally tested a prototype developed by UU at the Lysekil wave research site and found that the power generation of the WEC depends on parameters such as the translator, stator, buoy size, translator’s speed, the weight of the translator and damping of the generator, etc. [65]. Several technologies, methods and concepts have been proposed and modelled to solve these drawbacks. All these design parameters are essential for developing and increasing the efficiency of the direct-drive linear WEC. From the literature, previous work mainly focused on numerical modelling, design optimisation, prototype design and testing, and the control strategy [66]. This section discusses the recent development of the linear PM generator for WECs.
4.1. Reduction of Detent Force (Cogging Force and End Effect Force)
The relative motion between the stator and the translator generates cogging forces [67]. The cogging force creates an exciting force ripple that produces vibrations and acoustic noise, damaging the magnets and the stator teeth [68]. Cogging forces tend to keep the path between the translator and stator teeth at a minimum, inhibiting the translator’s movement. The generated cogging force can destabilise the system, shorten the device’s lifetime and increase the maintenance costs, so it is essential to decrease the cogging force for the linear PM generator [69]. On the other hand, the linear generator is open in both longitudinal ends, which is one of the main fundamental differences between the linear and rotating generators [70]. During the movement of the translator, the outmost magnets move in or out of the stator. Therefore, the magnets change their coupled partners and change the flux component in the translator, which does not exist in the rotor in a rotary generator. The end effect force is created because of the disconnection at the end of the two sides, and this end effect creates a nonlinear magnetic circuit.
Moreover, the electrical frequency, saturation and geometric parameters are strongly affected by the results of the longitudinal ends. Hence, making a common statement is problematic because those parameters differ from design to design and vary due to the mechanical frequency and electrical loading. As the longitudinal ends and their impact are unknown, the possible disadvantages leave the designer with an information gap in designing the specific linear PM generator. The longitudinal end effects have been studied based on numerical calculations to investigate the impact of the disadvantages of the longitudinal ends in the linear PM generator for WECs [71].
The cogging force and end effect force are known together as the detent force. The increased detent force can affect the mechanical design (increases the risk for fatigue), efficiency of the generator and energy absorption. Therefore, it is essential to accurately predict the magnetic field distribution and decrease the cogging force because it affects both the linear and nonlinear reluctance models and the electromagnetic performance of the generator. So far, many techniques have been used to reduce the cogging force. The notable ones are adjusting the PM length, magnetisation orientation, skewed PM, pole shifting, slotless generator, bulged stator and others [72].
On the other hand, several numerical and analytical methods have been proposed to solve the magnetic field problem of the linear generator recently. The finite element method (FEM), finite element analysis (FEA) and equivalent magnetic circuit (MEC) have been used to analyse the magnetic field and determine the related electromechanical parameters. The FEM method offers high accuracy and includes the impact of nonlinear factors, but this analysis method is comparatively slow and time-consuming. On the other hand, MEC analysis can find the nonlinearity, end effect and armature reaction. However, this method only analyses the magnetic field at several separate points of the structure, and its accuracy is not good enough. Moreover, the analytical model based on the subdomain method can be used to get more accurate predictions of the magnetic field distribution. The analytical model based on the subdomain method has already been used in various PM-based devices [73]. To predict the accurate air gap field distribution of the linear PM generator, the improved conformal mapping (ICM) method and slotless analytical model could be used as well, which have been used in various PM-based generators.
4.1.1. Permanent Magnet (PM) Modifications
The permanent magnets’ size and shape impact the performance efficiency of the linear generator significantly; often, larger magnets mean better results. O. Danielsson et al. studied the effects of the magnet size and shape, and found that increasing the permanent magnets’ size increases the generator’s performance and reduces the detent force [74]. Rectangular-shaped PMs were used for this study, which were found to increase the magnetic flux intensity and decrease the load angle but increase the normal force. Moreover, a study has been done reducing the PM length, and the optimised results show that it could reduce the cogging force [68]. However, reducing the PM length decreases the magnetic flux density and increases the load angle. There are different ways of installation that have been proposed to study the linear generator. Usually, PMs are attached to the outside diameter of the translator, but a study has been carried out by attaching PMs to the inside diameter of the translator [27]. A linear PM generator has been proposed by applying PMs skewed in the translator to reduce the detent force [75]. Although this effectively reduced the detent force, it needs more complex PM shapes and increased manufacturing costs. Moreover, pole shifting can reduce the harmonics of the detent force [76], though it can create an unbalanced voltage due to the PM asymmetric.
Moreover, to increase the magnetic flux density in a particular direction, Halbach arrays have been used in PM arrangements [77]. The Halbach PM array-based linear generator was compared with other typical designs, and it was found that Halbach PM arrays can reduce the overall detent force [78]. Chunyuan Liu et al. found that the detent force can be reduced by 82.56% by using the Halbach array in the PM arrangement [72]. To design the Halbach array-based linear generator, Yimin Tan et al. first used the Fourier decomposition to describe the Halbach arrays’ magnetisation components. Using specially treated boundary conditions, they extracted the magnetic field distribution based on the magnetic scalar potential method [44]. In the Halbach PM arrays, the magnetic flux can be cancelled on one side of the array, while the magnetic flux is enhanced on the other side. In reality, it is challenging and costly to manufacture magnets with the ideal Halbach magnetisation arrangement. Quasi-Halbach magnetisation concepts have been proposed to solve the problem and reduce the manufacturing cost [72]. The quasi-Halbach and Halbach magnetisation can boost the sinusoidal distribution of the magnetic field and increase magnetic flux density and the finite-element analysis solution is required to check them. However, the above proposed PM modifications have some advantages and disadvantages, which can be seen in Table 2.

Table 2.
Findings of the PM modifications.
4.1.2. Changing the Air Gap
According to the critical design point of view, the distance, i.e., the air gap, between the translator and stator should be stable. The magnitude of the magnetic field in the air gap is very dependent upon the width of the air gap. A small air gap results in high power density and large detent force [72]. Typically, the air gap magnetic flux density is for radial magnetisation, and the magnetic flux density can be increased by changing the design. The optimal values for the radially magnetised magnet’s ratio to the pitch of the pole and translator’s outer radius to the stator’s outer radius can be defined to achieve maximum efficiency and performance. Most of the linear generators have been studied with a fixed air gap, and it was found that a small gap can create demagnetization problems [80]. By changing the air gap, Omar Farrok et al. studied a permanent magnet linear generator (PMLG) and found that it had an essential role in increasing the generator’s efficiency [81]. However, reducing the attractive or frictional force between them is also crucial for preventing damage to the generator [82]. This attractive or frictional force can also create a demagnetisation problem with the generator.
The effects of changing the air gap design are shown in Table 3.

Table 3.
The results of changing the air gap design.
4.1.3. Modification of the Stator Design
Due to the low frequency and speed of the ocean wave, the detent force can be created in the linear PM wave energy generator. To raise the efficiency of the wave energy generator, it is essential to decrease this detent force [83]. Many techniques or methods have been used to reduce this detent force, such as stators with slots, without slots, U-shaped stators and the M-shaped stator [64]. To minimise the detent force, a slotless generator has been proposed. The analysis of the proposed generator showed that the detent force could be reduced, while the power density is merely one-fifth to one-tenth-lower than that of the slotted generator. Therefore, the slotless generator needs a larger volume than the slotted generator to generate the same wave energy. To decrease the detent force, Chunyuan Liu et al. used bulged stators and auxiliary slots [72]. Steel materials were used in the stator, and modular windings were used in the stator. Moreover, Haitao Yu et al. proposed a novel linear wave energy converter with an assistant tooth implemented with a 12-slotted stator to minimise the end and cogging effects [83].
It was found from the simulation results that by using the assistant tooth, more than 70% of the cogging force can be decreased compared with those without the assistant tooth. However, the core losses for the proposed linear generator were increased by 0.5% with the assistant tooth. Gargov, N.P., et al. used the shoe concept for the teeth arrangement of the semi-closed slot to optimise the flux distribution, and found that the use of shoes decreased both the power ripple and the air gap’s magnetic reluctance [84]. Furthermore, the cogging forces in linear machines can also be reduced. Table 4 presents the effects of the modification of the stator design.

Table 4.
The results of the modification of the stator design.
4.1.4. Magnetic Cores
Since the heave motion of the waves is prolonged (1–2 m/s peak), the linear generators in direct-drive WECs need to respond to considerable forces to produce a substantial amount of energy [45]. Hence, linear generators are becoming very large and costly. Many direct-drive WECs based on iron-cored linear generators have been developed and tested because of their performance. Lorand Szabo et al. showed that the iron core-based stator could generate three-times-higher voltage (RMS voltages) than the ironless stator (air core) because the magnetic flux inside the iron core is higher due to low reluctance [87].
Since the linear generators are so large, the attractive forces between the PM translator and the iron-core stators are also huge and present significant challenges regarding the bearing design and machine construction. The structural material to support these attractive forces often contributes considerably to the total expense of the WEC. Cogging forces cause problems, particularly due to the pairwise flux coupling and the longitudinal ends of iron-cored generators [88]. Moreover, iron-cored generators create copper losses and core losses, which decrease the generator’s efficiency by minimising the remanence magnetism of the PMs. To reduce the detent force and modular structure and increase the output efficiency, a linear generator-based WEC was proposed that uses hollow windings and a coreless iron structure [14]. The analysis results of the proposed design reduced the detent force, along with copper and core losses.
Air core-based linear generators are attracting increased attention for use in direct-drive WECs due to the above-discussed problems of the iron-cored device [45]. A longitudinal tubular air-cored generator was designed with a converter consisting of axially magnetised PMs of opposing polarity separated by pieces of steel [89]. The winding coils, called air gap windings, are wound around the translator. The air gap is therefore infinite, and the shear stress is around 10 kN/m2, which would be low in wave energy applications [90]. Another tubular-type linear generator for WECs based on an air-cored design was developed using more permanent magnets than a comparable iron-cored linear generator [91]. Removing the cogging forces and reducing the attraction forces between the stator and the translator makes the air-cored generators more suitable. A higher air gap flux density can be achieved using a linear double-sided permanent magnet converter instead of a single-sided air-cored unit [92].
Nevertheless, attractive forces are now being implemented between the two opposing sides of the translator, again generating the need for increased structural mass. Neil Hodgins et al. proposed an air-cored linear generator topology known as the core generator (C-Gen) for wave energy research [93]. The C-Gen is a double-sided arrangement consisting of air-cored windings and iron-cored permanent magnets. The analysis results of the proposed design topology show that there are no magnetic attraction forces between the stator and the PM translator, which reduces structural mass and simplifies the assembly process. To minimise the created magnetic forces between the stator and the translator, air-cored permanent magnet linear generator (PMLGs) designs have been proposed. Since the translator lacks stainless steel, the force of attraction between the stator and the translator is reduced. Lorentz forces, however, still exist. The Lorentz forces are radial in the direction of motion in the recently proposed air-cored generator design. A new air-cored tubular linear PM generator has been developed and simulated where it ‘sandwiches’ the windings between two sets of permanent magnets (PMs) inside the tubular structure [94]. The generator’s key benefit is that the Lorentz forces acting on the bearing are minimised by approaching the force parallel to the direction of the motion axis and removing the cogging forces. Moreover, a novel linear air core-based linear electromagnetic direct-drive WEC has been proposed by Rieghard Vermaak et al. that reduces most of the iron-cored device-related end effects and the attraction forces between iron-cored stators and magnet translators [92]. The attraction forces between the translator’s opposing sides of double-sided air-cored machines have been balanced. The analytical analysis of the model has shown the effectiveness of the proposed design.
On the other hand, the high-grade steel core can also be applied to reduce the core loss and detent force problem, significantly increasing power-generating ability [95]. Moreover, using high-grade steel in the core can solve the rising temperature problem. A linear PM generator has been developed using steel materials in the stator to investigate the benefits and drawbacks of using steel materials [17]. The analysed results show that the cogging force can be removed entirely with increasing electrical energy production.
4.2. Application of High-Grade PMs and Solving the Demagnetisation Problem
Maximum linear PM generators for WECs have been developed using conventional NdFeB N30 and N35, which have low remanence magnetism, coercive force and magnetic energy production [96]. It is known that high-grade NdFeB PMs offer high magnetic flux density and can retain their remanence magnetism even at high amounts of the reverse magnetic field. A comparative study was carried out using NdFeB and ferrite magnets in the translator to find their magnetic property differences [97]. The study results show they have similar magnetic properties, but the significant parameter could be the economic difference because of the high price of rare earth magnets (NdFeB). Moreover, it is difficult to handle the rare earth magnet (NdFeB), but using ferrite magnets increases the weight of the translator. With the increasing grade number of the NdFeB, the magnetic flux density increases and, therefore, the linear PM generator has been proposed for WEC by using high-grade NdFeB PMs. The simulation results show that the output-induced voltages could be increased by using high-grade NdFeB PMs. Due to the high price of the NdFeB and the environmental aspects, the alternative has been proposed to replace the NdFeB magnets [98]. The temperature rises during the operation of the linear generator, and this rising heat can demagnetise the magnets. High-grade permanent magnets can be used to solve the demagnetisation problem and keep the temperature low, but it is very costly. To prevent the demagnetisation problem, temperature control could be one of the effective methods. A cooling system-based linear generator has been proposed for WECs to reduce the rising temperature, which consists of a control unit, chiller, dehumidifier-based air handling unit and water pipes for circulating the chilled water. Although the proposed structure is very complex, the simulation results show that the proposed linear generator can minimise the temperature and increase the efficiency.
4.3. Design Concepts for Low-Frequency Wave Range
Much research has been done to increase the efficiency of the buoy-type linear PM generator-based WEC by changing many parameters. Still, very few studies have been done on changing the degree of freedom of the permanent magnet arrangement in the translator instead of the traditional method. All conventional arrangements used in the WEC were based on a single degree of freedom which cannot perform appropriately in the low-frequency range. Efficiency can be increased by arranging the translator based on a multi-degree-of-freedom system. Springs and magnetic springs can be used in the magnet arrangement for harvesting energy over a broadband frequency range [99,100].
Moreover, to increase the generator efficiency in the broadband frequency range, Masoud Masoumi and Ya Wang proposed a vibration-based generator for WECs known as the repulsive magnetic scavenger [52]. The generator consists of two fixed magnets with one placed at each end. The levitating magnets are lined around a threaded rod together, so that the same poles face one another. It delivers a collocated harvesting and braking mechanism in the face of high-amplitude vibrations. Usually, the concept has been used to generate energy from vibration in the low-frequency range [99,101].
Moreover, all existing linear WECs have used single translators to harvest energy, but the system cannot generate energy when the translator reaches either of the ends. A novel linear generator has been proposed to generate energy in that motion stage, consisting of two different translator bodies [102]. One translator works as a driver translator, while the other works as a driven translator. The driver translator is directly connected with the buoy, whereas the driven translator relates to the driver translator through a mechanical spring. The unique benefit of the proposed linear generator is that at the moment of zero vertical oceanic wave velocity, the driven generator generates acceptable voltage. Moreover, power is being produced by the driver generator, while the driven generator does not have any vertical velocity. Quite the opposite, when the driver generator has no velocity, the driven generator still generates power.
4.4. Using Magnetic Gearing to Increase the Speed of the Translator
The translator speed is also a significant parameter in increasing the efficiency of the WEC. Due to the low frequency of ocean waves, the existing linear generator cannot generate enough energy. Furthermore, the use of a linear magnetic gear has also been proposed by researchers, whose analytical and experimental results prove that the concept could increase the translator’s speed [59]. The linear magnetic gear consists of two movers and a field modulation core. The mover can consist of magnetising windings and permanent magnets (like aluminium–nickel–cobalt (AlNiCo)) [59]. One mover (mover 2 or low-speed mover) can be connected with the buoy, which moves due to the wave, and another mover (mover 1) is connected with the translator (high-speed mover). The motion of mover 2 increases the opposite motion of mover 1, increasing the translator’s speed. This means that the gear ratio variation only changes the motion speed of mover 1. This new translator speed and spring displacement are the original ones multiplied by the gear ratio . The corresponding relationships can be expressed by Equation (29) [103].
where and represent the speed of the mover 1 and 2, respectively. is the number of active PM pole pairs in mover 1 and is the number of active PM pole pairs in mover 2. The force transmission capability for the different gear ratios is displayed in Figure 7. Since the gear ratio variation only changes the linear generator’s movement speed, the linear generator’s new translator velocity and spring’s new displacement are the original ones multiplied by . In addition, the motion directions of the proposed linear magnetic gear movers are opposite each other. As a result, the spring force and the generator force are changed as
where and are the spring constant and damping coefficient of the generator; the natural frequency of the linear magnetic gear-based WEC can be measured by Equation (32) [59].
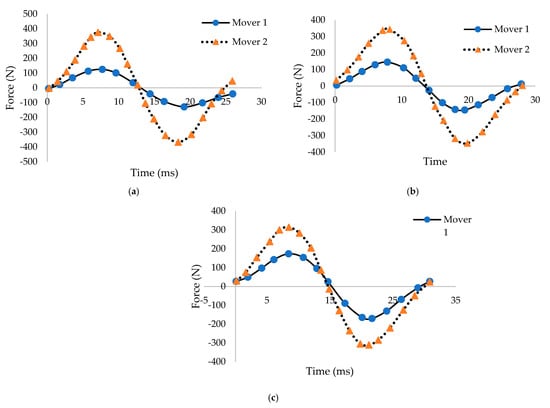
Figure 7.
Force transmission capability (a) gear ratio 13:4 (b) gear ratio 12:5, (c) gear ratio 11:6 [59].
In Figure 7a, the pole pair numbers of mover 1 and 2 are 4 and 13, respectively. The pole pair numbers of mover 1 and 2 are 5 and 12 for Figure 7b and 6 and 11 for Figure 7c, respectively. It can be seen in Figure 7 that the mover 1 and mover 2 pull-out forces under the ratios are 371.5 N and 114.2 N for 13:4, 343.8 N and 142.7 N for 12:5 and 314.2 N and 170.6 N for 11:6, respectively, which means the force of mover 1 can be increased or decreased by changing the gear ratio. From Figure 7, it also can be said that with the increase of the pole pair numbers of mover 1, the pull-out forces of mover 1 increase, and with the decrease of the pole pair numbers of mover 2, the pull-out forces of mover 2 decreases. That means the pull-out forces of the mover are directly proportional to the pole pair numbers. Therefore, it can be stated that increasing the pull-out forces of mover 1 decreases the velocity of mover 1, or vice versa. By using this relation, Equation (29) can be expressed as
where and are the pull-out forces of movers 1 and 2, respectively. Moreover, such findings show that the pole pair numbers of permanent magnets on the two movers are adjusted correctly, and it is possible to achieve the adjustable gear ratios. By selecting the proper gear ratio, it is possible to control the force and velocity of the mover 1 connected with the linear generator.
4.5. Other Design Concepts to Increase the Efficiency of the Generator
Many factors are related to the stator design that play an essential role in increasing the efficiency of the linear generator. Among them, proper lamination selection is an essential factor in increasing the efficiency of the linear generator [84]. The high magnetic flux density of the PMs can saturate the stator lamination materials in the teeth and back iron. N.P. Gargov et al. investigated the impact of the number of slots per pole, phase and the number of windings in the stator [84]. De Sousa Prado et al. showed that increasing the number of slots can lead to large pole pitches, and as a result, demagnetisation can be created, and due to the additional space harmonics, the decreasing number of slots causes eddy current losses [104]. Therefore, slot number selection is also an essential factor. To design the stator of the AWS, one slot per pole, per phase was selected [104]. To find the optimised design of the stator, the slot geometry, such as slot design and teeth design, is fundamental. It has been found that the stator tooth shape also affects power generation [102]. Omar Farrok et al. divided the stator into a main and supporting stator for increasing the output voltage of the WEC [105]. Lei Huang et al. used two stators, known as inner and outer primary, and a mover, which can move with the buoy between the inner and outer primary [34]. Jing Zhang added an asymmetric slot iron york structure and pie windings to increase the efficiency of the previous WEC design. Experimental results prove that the asymmetric slot structure increased efficiency [6].
A new concept known as the snapper generator has been proposed where the stator consists of permanent magnets, winding coils and a physical spring [86]. The physical spring connects the stator with the fixed seabed. Since both translator and stator consist of magnets and face each other, the magnetic attraction pulls the stator along with the translator due to the applied force on the translator. When the stator moves because of magnetic attraction, the physical spring extends and applies a reverse force to the stator. Finally, the spring forces are enough to resolve the magnetic attraction, where the stator accelerates quickly in the translator’s opposite direction. This high speed increases the power output efficiency and can decrease the size of the magnets needed and associated costs.
4.6. Using Advanced Numerical Simulation for Parameter Study
Finding all required parameters of the linear generator plays a significant part in numerical modelling and design optimisation. The parameters can be categorised as hydrodynamic parameters and electromechanical parameters. In modern engineering, simulation software has an important practical use. Many different solutions, new ideas and optimisations can be evaluated in the computer laboratory setting. Some calibrations are still required, so the need for experimental testing remains and should not be ignored after a simulation process. Furthermore, linear generator simulations boost the starting point for the next experiment and dramatically improve the speed of progress. M. Eriksson et al. studied a hydrodynamic model for the linear generator-based WEC [106]. This study aimed to evaluate different parameters, such as the radius of the floating buoy, spring constant and generator damping coefficient, to obtain the high-power capture ratio. In particular, the impact of resonance on the power generation ability of the entire system was investigated.
Researchers have used the WEC-Sim to calculate the , net buoyancy restoring, viscous damping and mooring forces differently for sinusoidal steady-state response scenarios and random sea simulations, which can be used for linear PM generator-based WEC designs [107]. The radiation and diffraction methods are used in WEC-Sim models to predict design optimisation and power performance. The radiation and diffraction method uses linear equations to solve device dynamics in the time domain to obtain the hydrodynamic forces from a frequency-domain boundary element method (BEM) solver. By solving the Laplace equation for velocity potential, the BEM solutions assume the flow is invisible, incompressible and irrotational. The time-domain simulations are performed by solving the governing equations of motion in six degrees of freedom. Dynamics can be simulated by solving the time-domain equations of motion (Equation (4)). The BEM can be indicated in the excitation and radiation forces by Equations (34) and (35), respectively.
4.7. Design Optimisation to Maximize the Performance
Recent design developments of the linear PM generator explain the need for optimal design. In recent years, many numerical optimisation techniques such as intelligent techniques and GSO have been developed and broadly applied to designing linear PM-based WECs [108]. For developing the high quasi-constant output voltage with minimum cogging force, a hybrid optimisation technique called GSO (based on Genetic Algorithm (GA) and Particle Swarm Optimisation (PSO)) has been proposed for linear PM generator-based WECs [109]. The proposed method was applied to the optimisation of the electromagnetic benchmark problem. In the proposed optimisation methods, a FEM engine-based simulation tool was built in the MATLAB environment as a numerical model linked to the GSO algorithm. The proposed simulation tool measured the cogging force and the fluxes generated by PMs, and evaluated the electromotive force (EMF), assuming a continuous velocity as the dynamic profile for translator motion.
Moreover, the prototype model’s analysis can be developed by trial-and-error design methods to get a good design, but it is time-consuming and costly [110]. For that reason, a thorough study of optimal design parameters of the linear PM generator is required to improve the intelligent design guidelines, because the fabrication technology of the linear PM generator-based WEC is improving. An intelligent optimal design technique based on Scatter Search and the article Swarm Optimisation has been proposed for the design optimisation of the linear PM generator [111]. The design optimisation analysis shows that the power losses of the active materials of the device could be minimised by using the Scatter search technique, and the volume of the active materials of the device can be minimised by using Particle Swarm Optimization.
Many design optimisations have been proposed to enhance magnetic field performance. The analytical design optimisation helps to find the relationship between critical design parameters and device performance. Still, it suffers from problems connected with model inaccuracy, mainly when the leakage flux is significant and the flux paths are complex. Moreover, the flux analysis of the linear PM generator becomes increasingly essential to increase the performance. The dynamic changes in the topological structure of the linear PM generator with time can be very complicated, so it is difficult to get accurate design optimisation using the traditional parametric equations. Hence, numerical analysis of the field distribution has been used to facilitate performance valuation [112]. Numerical analysis, such as the finite element method (FEM), provides accurate magnetic field distribution. However, they are still comparatively time-consuming and do not deliver as much insight as analytical studies into the impact of the design parameters on the generator behaviour [113].
An optimised linear PM generator design for wave energy conversion has been proposed using the level-set method to increase the energy-capturing efficiency from ocean waves [114]. It is known that the unbalanced back EMFs and the distortion of air gap flux density influence the performance and stability of the linear PM generator. The level-set method has increased the air gap’s magnetic field performance and decreased the back EMF’s unbalance. The optimisation study used topological evolution of the PM shape and yoke size, which were carried out based on the level-set equation after setting the optimal air gap magnetic field and picking the appropriate detection point. The study results show that the applied level-set method for the PM generator’s topology and size design consistently enhanced the magnetic field distortion.
5. Control Systems of the Linear PM Generator-Based PTO System
The power generation of linear PM-based WECs is affected by many parameters which can be optimised during the design stage or in the actual ocean operation. Dynamic control system optimisation analysis should be conducted during the actual ocean operation because it is not static compared with design-stage optimisation. The mechanical and electrical systems are essential for the controllers in real time, which can be used to attain progressive, dynamic control methods. To run the controllers, various timescales or different frequency ranges can be set up. The exact measurements and predictions of the incident sea waves and system parameters are essential because the controller performances depend on them. Commonly, to design a wave-to-wire model, the dynamic control approach is applied to the power chain’s various parts. The whole control system of the linear PM generator-based WEC can be separated into three control systems. The first one is the hydrodynamic control, the second is the PTO control (generator control) and the third is the grid-side control [13,115]. This section summarises the control systems proposed so far in the literature.
5.1. Hydrodynamic Control
The WEC system’s hydrodynamic characteristics consist of the buoy and the generator’s moving parts, which define the amount of energy harnessable from ocean waves. The study of the geometric structure configurations, such as the geometric size and shape, is significant because they impact the primary power-capturing system, which influences the energy generation and hydrodynamic performances of the WECs [116]. Based on geometric shape optimisation and efficiency maximisation, the hydrodynamic optimisations are typically performed during the design and fabrication stages. Moreover, during the actual ocean operation, the hydrodynamics of the device can be optimised by dynamic control because it helps to change according to the wave change [117].
The interaction between the mechanical structure and the sea wave’s motion creates the force (driving force) during the primary capturing system. The wave excitation force is also an essential parameter for optimising the WEC; therefore, it is necessary to control the excitation force. The excitation force can be controlled by changing the parameters, such as the area of the wetted surface and the pressure of the ocean states related to it. The control of the excitation force can influence the system’s performance so that optimal hydrodynamic conditions can be achieved [118]. In contrast, these systems increase the complexity of the WEC’s design and slow the response times. In addition, to increase the efficiency of the linear generator-based WEC, Ye Jun Oh et al. proposed a damping-control algorithm based on the heave motion mechanism of the buoy [119]. The study result shows that without using extra hardware, the proposed control strategy can increase the power. Moreover, the linear generator-type WEC also partially depends on the friction between the translator and the cylinder’s inner surface and the buoy’s damping loss.
5.2. Generator Control (PTO Control)
The PTO system is the heart of wave energy conversion; therefore, the control of the PTO system plays a vital role in increasing the efficiency and performance of capturing energy from ocean waves. Usually, the linear generator is used for the direct electric-drive PTO system. Various control strategies, such as fuzzy control, robust control, model predictive control and model-free control, have been proposed for PTO control to improve energy conversion efficiency [120,121]. They can be applied on the generator side, such as the various parts of the linear PM generator and the electronic power converter. Generally, the generator force control system can be classified into reactive and resistive control. The reactive control system is usually used to retain the velocity and the excitation in phase, so it needs some power back. The resistive control system controls the damping force and therefore does not need reactive power flow. It is known that heave motion is usually considered in the maximum power WEC design and can be used further to describe the changed behaviour of these two control systems. The heave force’s mathematical model of a linear PM generator-based PTO system is generally defined as follows
The generator force can be changed by controlling the generator damping and spring coefficient, which creates the variation of the phase and amplitude of the motion of the device along with the energy generation from the ocean waves. The method is known as reactive control. Reactive loading control has been used to increase the WEC’s efficiency range on either side of the resonant frequency [122]. This theoretically optimal control technique includes adjusting the primary converter’s dynamic parameters, such as the spring constant, energy absorbing damping and inertia, and allowing for maximum energy harvesting at all frequencies. Korde found that velocity feedback could be used to adjust the PTO system’s damping coefficient to balance the device’s radiation damping to maximise the allowable energy absorption [123]. The use of reactive control, which considers the linear generator’s copper losses, has also been proposed [124]. This reactive control method dramatically decreases the losses of the generator, increases the usable power and lowers the overall excursion and maximum speed the machine reaches. Nevertheless, this control strategy does not require device constraints to be considered. The generator damping coefficient changes linearly or nonlinearly in the resistive control system, but the changing principle for other modes is similar.
5.2.1. Latching Control
Latching control is a type of resistive control. Latching control was the first tested control system to stop the device’s motion at the limits of its movement (when velocity is zero) and release it when the wave forces are in phase to optimise the energy extraction [18]. This control strategy makes the system respond with a natural frequency higher than the exciting frequency of the wave (and may therefore have a smaller mass). Latching control is separate, very nonlinear and sub-optimal by definition.
The mass of the heaving buoy is so large that its natural frequency matches that of the wave (the ideal resonance condition). The body’s mass is small; therefore, its natural frequency is high, and it is latched at the excesses of travel.
5.2.2. Model Predictive Control (MPC)
Compared to other recently emerging control techniques, Model Predictive Control (MPC) provides a higher output and represents a promising advancement in wave energy extraction control techniques [125]. The goals of MPC are to optimise the generator force. Reactive control in the frequency domain is a linear method, while MPC in the time domain is a linear and nonlinear control technique that considers the hydrodynamic constraints. This technique includes an oscillating model of the system and a calculation of the excitation force over a time period to predict the next control action on the generator power. This behaviour is obtained by optimising an objective function proposed over the interval of predictions [126]. Gieske et al. first used the MPC in the AWS converter [127]. In the formulation of the objective function of MPC, Hals et al. proposed two alternatives [128]. The first optimises the velocity through a balance between excitation radiation forces.
Conversely, the second option optimises the power directly consumed by the PTO device. Ted K.A. Brekken proposed the MPC system to track the optimum speed achieved through a reactive control approximation that considers the radiation resistance as a constant value [129]. The prediction model is used to implement a System Predictive Control algorithm that tracks an optimum trajectory of velocity, while respecting system velocity, limits of position and limits of the generator’s power. Alternatively, the algorithm incorporates the prediction of excitation power. The simulation results indicate that the control method is in a position to produce power while preventing potentially harmful velocities and excursions. Mohammed Jama et al. designed a function-based continuous MPC to optimise the energy absorption of a single-body heaving system-based WEC [130]. The designed controller optimises the control effort to drive the WEC floater in resonance with respect to the physical limitations of the linear PM generator. The study showed decent reference signal-tracking capabilities, optimising the control effort to achieve maximum power transfer, while respecting the generator’s mechanical and electrical limitations.
Cretel et al. introduced triangular discretisation to obtain the discrete state system equations. They suggested various alternatives to model the objective function based on penalty terms that are applied to the objective function and depend on the force of the linear generator [131]. In this way, Cretel et al. proposed that losses can be considered by a term that considers the instantaneous weighted value of the generator force. Dan-El Montoya Andrade et al. proposed a Model Predictive Control (MPC) system which includes the copper losses in the point absorber control optimisation process incorporating linear generators [120]. Instead of optimising the power collected by the PTO system, this proposed MPC system maximises the power transferred from the linear generator to the power electronic converter.
Additionally, the device constraints at the maximum translator excursion and the maximum PTO force can be considered when implementing the MPC. Different MPC approaches have been studied for single- and two-body WECs based on the linear PM generator [132]. The linear MPC of a single-body WEC has been designed based on equation 25 [129]. The linear PM generator is equivalent to a spring-mass-damper system to find an optimal control law. Therefore, the system’s generator creates a force proportional to the floating buoy’s position, velocity and acceleration. The voltage is equivalent to force, and the current is equivalent to the velocity of the buoy. If the generator power’s imaginary component is nonzero, the generator provides power to the ocean at some points. As a result, to source the generator’s reactive components for a few seconds, external energy is required to be fed into the generator. Hence, energy storage is required for the WEC, which can be an essential obligation. That means the control law adjusts the system’s resonant frequency to resonate with the dominant wave frequency. This control law is also known as reactive control, or phase and amplitude control, because the velocity has to be in phase with the excitation force and the velocity amplitude has to equal. Moreover, it can be seen that the optimal generated power (theoretical) is precisely one-half of the incoming power, where the remaining half disperses back into the ocean. The power generation’s theoretical limit is 1 if allowing for the surge motion. It also has to be stated that the MPC control law needs significant energy storage due to the reactive components. The formulation of the MPC can be seen in [120,133].
5.2.3. Nonlinear Model Predictive Control (NMPC)
Nonlinear model predictive control (NMPC) has also been used to compensate for nonlinear dynamics from mooring lines [134], as well as time-varying PTO damper optimisation [135,136]. The findings of Edo Abraham et al. include an active control force, in addition to a time-varying PTO damper that enables reversal of the energy flow [136]. At the same time, Tom and Yeung depended on time-varying PTO damping as the only control input that prevented the reversal of the energy flow [135]. The performances of NMPC were compared with linear MPC. The results show that NMPC could optimise energy harvesting while satisfying the essential system limits. Tom and Yeung applied the nonlinear model predictive control (NMPC) to a linear PM generator to optimise power absorption in both normal and irregular ocean wave environments [137]. The NMPC system can evaluate the control input sequence, which maximises the WEC’s absorbed energy over a given time horizon. In the implementation of NMPC, the solver must seek to optimise the energy consumed over a finite time horizon by measuring the optimum at each phase of the period. The penalty term was included in the objective function to limit the change of the generator damping per time step. This penalty term offered more excellent numerical stability and can be used to represent losses associated with changing the configuration of the generator [131].
5.2.4. Other Control Systems
Many control systems have been implemented practically to develop the WEC and validate their effectiveness experimentally and numerically. The mechanical or electrical mechanisms are crucial for tracking whether the advanced control system delivers the reference signals. The physical components of the device can provide mechanical or electrical damping. The power take-off control logic is generally involved in the design or the analysis of the PTO system. The PTO system’s practical application and exact ability in physical models are significant concerns of the advanced control system [138].
The generated electromagnetic force on the translator influences the device and the preferred dynamic interaction between the generator and primary power-capturing systems. The optimised power extraction can be achieved by controlling it [139]. The current or power drawn from the coils can control the electromagnetic force. The electronic power converter has been used for generator side control by connecting the back-to-back converter with the common DC link. The generator side converter can be used to control the generator phase currents to maximise the power extracted from the sea waves. Simulation results show that the generator’s phase current could be controlled by using the rectifier. For arrays of direct-drive WECs, two control systems, such as optimum reactive control and sub-optimum damping force, have been studied with their impact from the electrical power point of view [140]. These control systems were taken from the hydrodynamic properties’ theoretical study of the oscillating body. The current control in the rectifier can be used on the generator side to obtain the reference PTO force. The study results show that the optimum reactive control system produces the highest power. Moreover, this proposed control system produced a low generator operating power factor, increasing the losses. However, the proposed control system requires high accuracy in predicting incoming waves before efficiently applying them to a WEC system.
Three different current controllers have been studied and implemented on linear PM generator-based WECs to emulate the optimal resistance, improving the device’s efficiency. The performances of the WEC were evaluated from the point of view of the overall conversion efficiency. Based on the speed control, a maximum power point tracking (MPPT) control system has been proposed for the AWS, which uses the back-to-back converter [141]. The performances of the direct-drive wave energy converter can be optimised by controlling the reaction force that increases the efficiency of the energy-capturing ability and decreases the mechanical complexity of the system. The reaction force control system has been studied and validated experimentally [142]. The experimental work was conducted with a linear PM generator test rig and a back-to-back power electronic converter. The generator side rectifier was used to control the current, which controlled the generator force effectively, as shown from validation studies. A solution has been proposed to collect the electric power extracted directly from each generator coil with various induced voltages and cannot simply be linked into a small number of phases [45]. To smooth the output electrical power and decrease the rating of the downstream inverter for grid interfacing, the local power storage was integrated. The unidirectional boost DC–DC converter was combined with the IGBT-controlled chopper placed between the IGBT-controlled inverter and the MOSFET-controlled rectifier [45]. The grid side DC link voltage was constant, while the generator side DC link voltage was controlled by changing the voltage. Moreover, a power smoothing control system was presented to control the chopper. Analysis results show that the proposed control system could decrease the effect on the grid and smooth the power flow.
Chung et al. were the first to use a Ferrofluid bearing in an electromagnetic harvester to reduce friction loss [143]. Advanced evolutionary techniques have been used to optimise the linear generator to refine the model for these networks, ensuring maximum energy production from the marine environment. To solve this problem, Sandra Eriksson proposed the Constant Torque Angle (CTA) control system [144].
Ean A. Amon et al. developed a control system known as Maximum Torque per Ampere (MTPA) control, which is very similar to CTA control, for control of a point-absorber WEC [145]. The authors proposed a novel WEC point absorber maximum power point-tracking (MPPT) algorithm [145]. The algorithm and control hardware has been tested numerically in the laboratory and ocean environments, showing that MPPT is an effective and promising control system for the WEC application. To that end, a fully coupled fluid-mechanical electric-magnetic electronic mathematical model and an optimisation routine were developed. This proposed time-domain wave-to-wire model was used to simulate the hydrodynamic and electric response of a wave energy converter connected to specific electric loads and was also used in an optimisation routine that searches for the optimal resistive load value for a wave energy converter under specific sea states. Sample results are presented for a point-absorber wave energy converter, showing that the electric power generation of a device under irregular waves can be significantly improved.
5.3. Grid Control (Load Side Control)
The power generation from ocean waves continuously fluctuates due to the different wave amplitudes and frequencies. Therefore, it is essential to convert this fluctuating power into stable power to connect directly to the grid [146]. In the earlier section, it has been shown that power electronic converters have been used to control the generator side, but they can also be used to control the grid or load side. Power electronic converters can be used to meet the grid codes of the system, as well as to decouple the generator side from the grid side. The main goal of the grid or load side controller is to freely control the reactive and the actual power added into the grid using a back-to-back converter, along with the DC link.
On the other hand, the main purpose of the generator side controller is to increase the energy-capturing capacity from the sea waves. Generally, the DC capacitor is used to decouple the generator side from the grid side. In power electronic converters, the control activities are performed using well-established switching techniques and controlling the electric power or current from the advanced control systems [147]. The load control has been used in WECs, where it was found to influence the generator and system performance. Experimental works have validated the impact of electric load resistance on the generator’s performance [60]. The effect of the nonlinear electrical load has also been validated for the linear generator coupled with a filter and rectifier [148].
Additionally, the control system can be electrically implemented as electrical damping circuits in various ways (unidirectional and bidirectional). The generator can either be attached to a passive or active rectifier [149]. The generator response can be improved with reactive power as needed for an active rectifier. However, this increases the generator voltage drop as the angle between the electromotive force (emf) and the current is reduced. A novel load control concept has been proposed to simulate the electric dynamics and the power conversion of linear PM generator-based WECs with optimal electric load, particularly for irregular wave cases [66]. The optimisation procedure is developed to find the optimal resistor load value for the WEC excited by irregular incident waves. Moreover, the proposed control system included the power losses of the electric power cable.
6. Performance Analysis of the Linear Generator-Based WEC
The primary purpose of this section is to review the features of the linear generator’s dynamic response and voltage performance through numerical simulations and experimental studies. Modelling linear generator-based WECs includes interaction between incident waves, system motion, generator and mooring. The linear electromagnetic generator-based WEC system performances can be validated by simulation, experimentation, or both, as shown in Table 5. The advancement of commercially available linear generator-based wave energy systems is challenging, slow and costly. The theoretical and computational models are developed first, and prototypes are evaluated after a time-consuming and expensive process under actual operating conditions. The challenge of setting up an experimental testing method affects the study of WEC systems. As a result, most research papers refer only to simulation validation methods. Testing the control methods used in the literature was primarily carried out with simulation works only. In linear generator WEC systems, some control methods were tested mainly with normal and irregular waves, although few controls were applied to only regular wave models. Few studies test the device in the literature for experimental conditions. Experimental works on the WEC system have rarely used the topologies of electronic converters and electrical side control. However, experimental tests have been done either in ocean test sites or wave tank environments. Moreover, experimental analyses have been done for load and without load.

Table 5.
Validation type of linear generator-based WEC systems in the literature.
6.1. Numerical Analysis
The numerical analysis aims to assess the performance of the WEC with a linear PM generator. Different simulation software has been used to analyse the magnetic field distribution, cogging force, electromagnetic force and eddy current losses. Moreover, numerical analysis and steady-state and dynamic analysis have been conducted. Usually, the simulation analysis results are compared with the theoretical results to validate the design. To find the electromechanical parameters, finite element methods (FEM) have been used by many researchers. Simulations of electromagnetic energy converters have been utilised during the total production of the world’s highest-voltage hydro, Turbo and many other designs, including the so-called powerformer [176]. This also used high-voltage motors called Motorformers and permanent high-voltage magnet devices. In all cases, the construction phase was preceded by device simulations. For a linear generator, Mats Leijon et al. proposed the simulations to model an arbitrarily selected wave function as input to the multiphysics solver [176]. Time variations are common, not restricted to a particular frequency. The simulations usually model many aspects of multiphysics effects of electromagnetics, thermodynamics and mechanics. Typically, the finite element method (FEM), finite element analysis (FEA) and others are used to find the flux linkage, magnetic flux density, cogging force, electromagnetic force, induced EMF or voltage and inductance. Overall, to have a finite element solution for a linear generator, work can be performed using existing software packages. However, there are no ready design resources available for non-traditional generator topologies where analytical and finite element approaches can work together, such as the design interface that could be formed using MATLAB—GUI and ANSYS MAXWELL.
The finite element solution was also used to calculate the cogging force and electromagnetic force, which are essential aspects of the linear generator [27]. Many generator designs have been proposed and tested numerically to reduce the cogging force or detent force [72]. The performance of the linear generator has been analysed by simulation at a constant speed and with sinusoidal motion [77]. The speed is not a constant value for the linear generator-based WECs. Still, constant speed is always helpful for analysing the low-speed translator of the linear generator, where a constant value of 0.4 m/s is often assumed [77,168]. In the practical WEC system, the device’s motion is very complicated. For analysis purposes, the translator speed in an ideal situation (ignoring inertia, wave reflection, friction and other effects) can be stated by Equations (37) and (38), where the wave amplitude is expected to be sinusoidal [42].
where A is the wavelength, T is the period, and is the phase angle. Moreover, the generator performances have been analysed in no-load and load conditions and for single-phase and 3-phase [93]. Moreover, the simulations have been performed for the no-load and load condition [177].
6.2. Experimental Analysis
Different experimental facilities have been used so far at varying stages of the design process. Usually, the linear generators based on WECs have been tested by the laboratory’s experimental setup to analyse the generator’s performances. Different models in the literature used different experimental setups. On the one hand, full WEC models have been tested in wave tanks and ocean basins. In Table 5, it can be seen that very few linear generator-based WECs have been tested in actual ocean environments.
6.2.1. Wave Tank Test
Experimental tests are usually used to validate the WEC linear generator to confirm the accuracy of the device settings and models. Wave tanks have been used to analyse the performance of the linear generator-based WEC [6,42,78,80,86,167,168,169]. Different waves can be generated in the wave tank, and the linear generator can be tested for regular and irregular waves. The full-time series from regular and irregular waves can be recorded with capacitance wave samples to have the most specific environment. The effects of the damping time series can be used to evaluate the times in the system when the system was active and disabled [137]. Before testing, the waves need to be calibrated using the reference wave probe and two additional wave probes (instead of the scaled model). As the wave field is non-uniform in the wave tank, the wave profile in the tank (where the model is located) is optimised for a “sweet spot”. The reference wave sample stays in position to ensure that the measurements match the configuration, while the model replaces the two new wave samples. The wave absorbers must be installed at the other end to decrease the reflected wave effect [163].
Two additional system characteristics were intensively utilised [178]. First, the software may store paddle movement during a test run and repeat it in additional test runs. This enables controllers to be tuned, tested and compared using the same wave height series. Second, the wave generator sends a trigger signal to the WEC model control hardware, which allows the testing to be precisely synchronised, as stated in the next section. To simulate actual ocean conditions, the wave maker system can be used to create different wave heights and periods. On the other hand, if the wave created by the wave maker is not sinusoidal, the wave velocity decreases due to the influence of the reflected waves [42]. Moreover, the numerical wave tank simulation has also been used to identify the wave tank’s important parameters [179].
6.2.2. Open Sea Test
Very few linear generator-based WECs have been tested experimentally in an open-sea test site, which can be seen in [1], because it is very challenging and expensive. The device can be deployed offshore or nearshore, depending on the design of the device. The linear generator developed by Oregon State University was deployed approximately 2.5 km from the shore and in about 40 m of water in 2007 [28]. The linear generators developed by Uppsala University were installed at the Lysekil wave research site at a water depth of 25 m and 2 km from the shore in 2002 [26]. Another linear generator-based WEC developed by SINN Power GmbH contained a variable number of buoys attached to a fixed steel frame. A single device was deployed nearshore at the Port of Heraklion, Crete (Greece) [1]. The AWS, developed by a UK-based wave energy developer company, was first deployed in Portugal in about 41 to 44 m water depth and tested [162]. The floating component of the AWS moves up and down due to the water pressure created as the wave passes over the AWS and generates energy from this relative motion. Finding suitable testing sites for the linear generator-based WEC has also been important in recent wave energy research. Table 6 presents various linear PM generator-based WECs with their rated power deployed in the ocean for open sea testing.

Table 6.
Linear PM generator-based WECs with their rated power.
7. Costs and Challenges of the Linear Generator-Type PTO System for Wave Energy Conversion Technology
The linear PM generator harvests energy directly from the linear movement between the fixed stator and the moving translator. Due to the translator’s motion, the resulting change of the magnetic field creates an induced voltage in the winding coils based on Faraday’s law. The whole system of this type of WEC is oscillating, meaning the waves act as a driving force, and the generator acts as a damper [182]. Therefore, damping is one of this type of device’s most critical factors, because the absorbed energy strongly depends on the damper. Moreover, another essential factor is reaction force, which needs to be big to get the same output power when the generator in the direct-drive system moves slowly. Another factor is the low power-to-weight ratio (very large machines are needed); due to the attractive forces between the stator and the translator, it needs a heavy structure [1]. The incoming ocean waves continuously vary, and their speeds are also different; therefore, the generator generates varying power. Due to this, extreme values are needed to be taken into account. As a result, overload is considered another important factor of the device [182]. The stroke length of the generator is also an essential factor of the device, because it should be set according to the wave heights. Due to different wave inputs, the output-induced voltage varies, so to connect the device with the commercial grid, the voltage level needs to be set, the current needs to be rectified and the frequency changed. Therefore, the grid connection is also an essential factor of this type of device, and the power transmission system is very complicated. Moreover, solving the complex electromechanical coupling issues, as reviewed in the literature, is also one of the important factors for the linear PM generator-type PTO system design. The advantages and disadvantages of the linear generator-based WEC are presented in Table 7.

Table 7.
Advantages and disadvantages of the linear generator-based WC.
Compared with other types of PTO systems, such as hydro, pneumatic, hydraulic and direct mechanical drive, it can generate electrical energy directly from mechanical energy and has reasonable efficiency (95%) [183,184]. The structure of the device is also simpler than other PTO systems and requires less maintenance, but overall manufacturing costs are expensive. It is known that the linear generator’s translator consists of magnets mounted on an iron or electrical steel plate between iron or aluminium spacers, and the stator is made of non-oriented laminated electrical steel or iron with a thin insulating coating to reduce eddy current losses. The magnet’s fluctuating price increases the overall cost, and the linear generator-type PTO system-based WEC is surely the relatively low distribution of the technology, resulting in the need for a tailored generator, which results in high investment costs and additional development risks. Generally, it is difficult to estimate the total cost of the generator because it depends on many different variables [144]. The translator’s height changes because of the stator and wave height, and the translator’s cost varies. The magnet weight can be changed due to the number of poles and the number of conductors per slot. Using heavy magnets increases the whole system’s mass, decreasing the efficiency because of the low velocity of wave oscillations [185]. The generator’s translator body with low electrical frequency can be made of solid steel. It has been found that the conductor (copper) cost per kg is higher than the cost per kg for stator steel and a translator cost of half of the stator cost for the original design. Copper wire or standard cables are typically used in the stator winding, which is a low-cost material on the international market. Moreover, the materials used in the concrete foundation are sea water-resistant materials. which are two-times higher than the one of ordinary materials used in the civil building sector. The manufacturing costs are also expensive, based on the average total pay for a specialised assembly. Based on a comprehensive analysis of current international market prices, Vincenzo Piscopo et al. measured the unit prices of the most significant item costs, as shown in Table 8, for the linear PM generator-type PTO system for WEC devices [186].

Table 8.
Materials costs [186].
It can be seen in Table 8 that the permanent magnets are the most expensive materials among all materials which are used to design the linear PM generator, and the price of the PM determines the total cost of a device. Moreover, the decommissioning costs should be considered because the linear generator and the floating buoy are not reusable, but recycled and sold for scrap. The annual operating costs are also a factor that adds to the total costs. A couple of simplified approaches have been proposed to calculate the relative cost of the generator design [144]. Considering these all-important factors, challenges and materials costs, they are relatively expensive, which raises a question for researchers on whether these types of PTO systems are economically viable or not. Few researchers addressed that the linear PM generator-based PTO system is not financially feasible, and much research is going on worldwide to make these devices economically viable [16]. Linear PM generator type PTO system-based WECs have been widely studied in different countries and universes worldwide. To optimize the whole system and decrease the unit production costs, many WEC devices were deployed in the ocean sea environment.Requirements of Linear Generators in Direct Electric-Drive PTO System for WECs.
To be able to harness the energy from ocean waves, many problems need to be overcome to build a robust system that is at the same time economically viable. The system needs to be tuned to the resource to work effectively because of the variation in wave amplitude, phase and direction [182]. The main challenge is achieving high energy conversion efficiency over various excitation parameters [18]. Compared to land-based structures, the design, construction and installation of the devices in the ocean environment are often challenging [185]. The case of the generator design is even more pronounced, as the generator is supposed to actively couple with the ocean waves to extract the power in the form of a reciprocating motion at a low speed [110]. Another challenge is to couple the irregular and slow motion (frequency 0.1 Hz) to drive the linear electromagnetic generator with an appropriate output quality for the utility network [187]. There are many ways to solve this problem: incorporate a WEC operating principle-based energy storage system within the device or use typical external energy storage [188]. To smooth the power, the device can connect to an array. However, due to the low speed, a large generator is required. How significant is an economical compromise between the size of the generator and the price and whether it is worth capturing the energy in larger, less common waves [144]? At a continuously different speed, a linear generator operates when the generator changes direction twice per wave period. Furthermore, with the wave variability the speed changes for each wave. A fixed speed is widely used when comparing different generator designs, but variable speed operation needs to be taken into account.
The linear electromagnetic generator design must be low-cost and harness maximum energy for low velocities and, if possible, with an irregular motion to be commercially viable. The linear electromagnetic generator driven by sea waves would oscillate at a peak velocity of 0.5 to 2 m/s [14]. Moreover, linear generators are considered hard-to-mount underwater, so they must be maintenance-free. They should also have high force density and as-low-as-possible mass volume [110]. For example, a direct-drive WEC can generate a peak of 100 kW at a peak velocity of 1 m/s, where the required peak reaction force is 100 kN. If a device provides shear stress of typically 20 kN/m2, it demands an active surface area of 5 m2 [14]. Using permanent magnets (Nd-Fe-B), some innovative generator topologies can boost the power density and shear stress in the air gap of the WEC. This requires the design of such a device that has the potential to produce the necessary thrusts in the WEC. Though each wave differs in frequency, an average of approximately 0.1 Hz can be considered a nominal baseline around which the output voltage of the WEC fluctuates according to the velocity or frequency of the incoming waves of the sea. Power electronic converters are required to interface the WEC to the grid. The linear electromagnetic converter should be a variable speed or permanent frequency system. It is expected that, other than using multi-MW WECs, several smaller devices (ratings might be 10–100 kW) can be used to make up a wave farm [91,93,165]. For this application, the generator required special types of design. The costs are likely to be high for larger devices, but by operating with smaller units, one may still be able to have the benefit of mass manufacturing, holding costs down.
8. Conclusions and Remarks
Ongoing improvements and progress of wave energy technologies continue to develop very fast. The energy from ocean waves is a largely untapped renewable energy source in the world, but harnessing this energy reliably and cost-effectively presents significant challenges. Different techniques have been used to harness this energy, and among them, the linear PM generator-based direct-drive WEC is very well known because of its mechanically simple structure. The working principles of the linear PM generator-based WEC have been discussed in this paper with the support of mathematical modelling.
Different WEC topologies with linear generator-based PTO systems have been outlined to provide a brief understanding of their design and working principles. Choosing the best WEC linear generator design concept is challenging because of the continuously increasing development of the WEC. The choice and design of the WEC linear generator structure depend on the application conditions, as to whether a high-power or low-power application is required. The outcome of the comparative studies can be concluded as follows:
- Linear generators are suitable for wave energy conversion if the devices are buoyant-moored with linear motion and operate with speeds of 1 m/s or more.
- Compared with other linear generator types, the linear PM synchronous generator is the most suitable for wave energy conversion because it has higher reliability and efficiency due to the more significant driving force.
- ○
- The planar/flat-type linear PM synchronous generators are preferred for high-power applications.
- ○
- The tubular-type linear PM synchronous generators are suitable for low-power applications because they offer high power or force density.
- ○
- Tubular-type linear PM generators with a long translator inside the generator perform better, with less cogging force.
- ○
- Three-phase generators are more efficient than single-phase generators due to their higher energy generation.
- ○
- Iron-cored generators are more suitable than air-cored generators because their power generation ability is higher.
- ○
- The most significant power is produced when the PMs are attached to the translator.
- ○
- Quasi-Halbach arrangements are preferred for improving the power generation efficiency with minimum losses.
- The force mainly determines the generator size it has to create. In wave energy conversion, the speeds are typically relatively low. The force should be high if the aim is to generate a large amount of power at a low speed. Therefore, the cost of the generator increases. The switched reluctance generators, variable reluctance generators, transverse flux PM machines and Vernier hybrid machines are suitable designs and have high force density. This limited force density does not influence the performances of these generator types and is suitable for low-power applications. However, they have disadvantages, such as complex construction structure, low power factor, complex iron losses and eddy current losses. Although they have some drawbacks, they can be viewed as an alternative to the typical linear PM generator in the future.
- Clever designs such as double-sided and cylindrical arrangements could decrease the cost.
- Superconducting linear generators are suitable for the WEC based on the linear generator in terms of low power application because it has a high current-carrying ability, producing much higher flux density with low-speed motion and lighter weight. However, it has a high manufacturing and material costs.
Many design concepts have been proposed to increase the performance efficiency and reduce the cost of the WEC with linear PM generators. This paper has summarised the developments of the WEC with linear PM generators, such as translator design, translator speed, stator design and others. The numerical and experimental analyses of the device have also been discussed. To increase the performance efficiency of the device, the control system has an enormous impact. Different types of control systems that have been proposed and used in linear electromagnetic wave energy converters have been reviewed. Overall, various WEC designs, working principles, design optimisation, advancements and control systems have been appraised in this paper.
Moreover, from the literature, it has been shown that all developed linear generator-based WECs still have some drawbacks, and very few have been deployed in the ocean. Further research is required to solve these existing problems and make the devices commercially mature.
The future research directions can be pointed out as follows:
- Innovative techniques for increasing the speed of the linear motion of the WEC.
- Study other types of generators with higher force densities and perhaps better performances.
- Study of air-cored generators in terms of their prospects for a practical combined electrical-mechanical structural design solution.
- Deployment in ocean environments for trials over the long term.
- Innovative designs for cutting down the cost of generator construction.
- Innovative designs for solving the low-frequency problem.
- Innovative systems for the transmission of the generated power to the grid.
- Implementation of control systems in the deployed WEC during sea trials.
Author Contributions
Conceptualization, R.A., I.H. and K.M.; methodology, R.A. and K.M.; software, R.A.; validation, R.A.; formal analysis, R.A.; investigation, R.A.; resources, R.A.; data curation, R.A.; writing—original draft preparation, R.A.; writing—review and editing, I.H. and K.M.; visualization, R.A. and K.M.; supervision, I.H. and K.M.; project administration, K.M.; funding acquisition, K.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The data presented in this article is available on request from the corresponding author.
Acknowledgments
The authors gratefully acknowledge the Australian Government Research Training Program Scholarship for Raju Ahamed’s study at Curtin University, Australia.
Conflicts of Interest
The authors declare no conflict of interest.
Acronyms
| Symbols | Abbreviations | Symbols | Abbreviations |
| AWS | Archimedes Wave Swing | Emf per phase | |
| BEM | Boundary element method | Wave force coefficient | |
| CTA | Constant Torque Angle Control | and | Pull-out forces of the mover 1 and 2 |
| EMF | Electromotive force | Buoy force | |
| FEA | Finite element analysis | Wave excitation force | |
| FEM | Finite element method | Electromagnetic force | |
| GA | Genetic Algorithm | Generator force | |
| ICM | Improved conformal mapping | Hydrostatic force | |
| MEC | Magnetic equivalent circuit | Wave radiation force | |
| MPC | Model Predictive Control | Gear ratio | |
| MPPT | Maximum power point tracking | Gravity acceleration | |
| MTPA | Maximum Torque per Ampere | Spring constant | |
| NMPC | Nonlinear model predictive control | Current inside the coil | |
| OSU | Oregon State University | Inductance of the coil | |
| PA | Point absorber | m | Sum of the translator and buoy mass |
| PM | Permanent magnet | Added mass | |
| PMLG | Permanent magnet linear generator | Number of active PM pole pairs in the mover 1 and 2 | |
| PSO | Particle Swarm Optimization | Natural frequency | |
| PTO | Power take-off system | Phase of the regular wave | |
| UU | Uppsala University | Load resistance of the circuit | |
| WEC | Wave energy converters | Radiation damping | |
| A and B | State or system matrix and input matrix | Density of the sea water | |
| Amplitude of the wave | Output phase voltage | ||
| Radius of the buoy | Density of the sea water | ||
| Coupling coefficient | Seed of the mover 1 and 2 | ||
| Magnetic flux density | Voltage inside the coil | ||
| Sum of the mechanical and electrical damping of the generator | , and | Acceleration, velocity and position of the translator or moving magnet, respectively | |
| Damping coefficient | Total damping ratio | ||
| Generator electrical damping coefficient | mechanical damping ratio | ||
| C and D | Output matrix and zero matrix |
References
- Ahamed, R.; McKee, K.; Howard, I. Advancements of wave energy converters based on power take off (PTO) systems: A review. Ocean Eng. 2020, 204, 107248. [Google Scholar] [CrossRef]
- Day, A.; Babarit, A.; Fontaine, A.; He, Y.-P.; Kraskowski, M.; Murai, M.; Penesis, I.; Salvatore, F.; Shin, H.-K. Hydrodynamic modelling of marine renewable energy devices: A state of the art review. Ocean Eng. 2015, 108, 46–69. [Google Scholar] [CrossRef]
- Xu, S.; Wang, S.; Soares, C.G. Review of mooring design for floating wave energy converters. Renew. Sustain. Energy Rev. 2019, 111, 595–621. [Google Scholar] [CrossRef]
- Hong, Y.; Waters, R.; Boström, C.; Eriksson, M.; Engström, J.; Leijon, M. Review on electrical control strategies for wave energy converting systems. Renew. Sustain. Energy Rev. 2014, 31, 329–342. [Google Scholar] [CrossRef]
- Gao, Y.; Shao, S.; Zou, H.; Tang, M.; Xu, H.; Tian, C. A fully floating system for a wave energy converter with direct-driven linear generator. Energy 2016, 95, 99–109. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, H.; Shi, Z. Design and Experiment Analysis of a Direct-Drive Wave Energy Converter with a Linear Generator. Energies 2018, 11, 735. [Google Scholar] [CrossRef]
- Polinder, H.; Mecrow, B.C.; Jack, A.G.; Dickinson, P.G.; Mueller, M.A. Conventional and TFPM linear generators for direct-drive wave energy conversion. IEEE Trans. Energy Convers. 2005, 20, 260–267. [Google Scholar] [CrossRef]
- Leijon, M.; Boström, C.; Danielsson, O.; Gustafsson, S.; Haikonen, K.; Langhamer, O.; Strömstedt, E.; Stålberg, M.; Sundberg, J.; Svensson, O. Wave energy from the North Sea: Experiences from the Lysekil research site. Surv. Geophys. 2008, 29, 221–240. [Google Scholar] [CrossRef]
- Polinder, H.; Damen, M.; Gardner, F. Design, modelling and test results of the AWS PM linear generator. Eur. Trans. Electr. Power 2005, 15, 245–256. [Google Scholar] [CrossRef]
- Chatzigiannakou, M.A.; Ulvgård, L.; Temiz, I.; Leijon, M. Offshore deployments of wave energy converters by Uppsala University, Sweden. Mar. Syst. Ocean Technol. 2019, 14, 67–74. [Google Scholar] [CrossRef]
- Polinder, H.; Mueller, M.; Scuotto, M.; Goden de Sousa Prado, M. Linear generator systems for wave energy conversion. In Proceedings of the 7th European Wave and Tidal Energy Conference, Porto, Portugal, 11–13 September 2007; IDMEC-Institute de Engenharia Mecânica: Lisbon, Portugal, 2007. [Google Scholar]
- Trapanese, M.; Boscaino, V.; Cipriani, G.; Curto, D.; Di Dio, V.; Franzitta, V. A permanent magnet linear generator for the enhancement of the reliability of a wave energy conversion system. IEEE Trans. Ind. Electron. 2018, 66, 4934–4944. [Google Scholar] [CrossRef]
- Saeed, O.; Wahyudie, A.; Susilo, T.B.; Shareef, H. Simple resonance circuit to improve electrical power conversion in a two-sided planar permanent magnet linear generator for wave energy converters. IEEE Access 2017, 5, 18654–18664. [Google Scholar] [CrossRef]
- Mueller, M. Electrical generators for direct drive wave energy converters. IEE Proc.-Gener. Transm. Distrib. 2002, 149, 446–456. [Google Scholar] [CrossRef]
- Faiz, J.; Nematsaberi, A. Linear electrical generator topologies for direct-drive marine wave energy conversion-an overview. IET Renew. Power Gener. 2017, 11, 1163–1176. [Google Scholar] [CrossRef]
- Khatri, P.; Wang, X. Comprehensive review of a linear electrical generator for ocean wave energy conversion. IET Renew. Power Gener. 2019, 14, 949–958. [Google Scholar] [CrossRef]
- Curto, D.; Viola, A.; Franzitta, V.; Trapanese, M.; Cardona, F. A New Solution for Sea Wave Energy Harvesting, the Proposal of an Ironless Linear Generator. J. Mar. Sci. Eng. 2020, 8, 93. [Google Scholar] [CrossRef]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. In Sage Publications; Sage UK: London, UK, 2009. [Google Scholar]
- Rusu, E.; Venugopal, V. Offshore Renewable Energy: Ocean Waves, Tides and Offshore Wind; MDPI: Basel, Switzerland, 2019. [Google Scholar]
- Rhinefrank, K.; Agamloh, E.; von Jouanne, A.; Wallace, A.; Prudell, J.; Kimble, K.; Aills, J.; Schmidt, E.; Chan, P.; Sweeny, B. Novel ocean energy permanent magnet linear generator buoy. Renew. Energy 2006, 31, 1279–1298. [Google Scholar] [CrossRef]
- Hai, L.; Svensson, O.; Isberg, J.; Leijon, M. Modelling a point absorbing wave energy converter by the equivalent electric circuit theory: A feasibility study. J. Appl. Phys. 2015, 117, 164901. [Google Scholar] [CrossRef]
- López, I.; Andreu, J.; Ceballos, S.; De Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Bastien, S.P.; Sepe, R.B.; Grilli, A.R.; Grilli, S.T.; Spaulding, M.L. Ocean wave energy harvesting buoy for sensors. In Proceedings of the IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 3718–3725. [Google Scholar]
- Panicker, P. The Vertical Axis Oscillating Wave Power Generator. Available online: https://contest.techbriefs.com/2012/entries/sustainable-technologies/2496 (accessed on 10 June 2022).
- Castellucci, V.; Eriksson, M.; Waters, R. Impact of tidal level variations on wave energy absorption at wave hub. Energies 2016, 9, 843. [Google Scholar] [CrossRef]
- Waters, R.; Stålberg, M.; Danielsson, O.; Svensson, O.; Gustafsson, S.; Strömstedt, E.; Eriksson, M.; Sundberg, J.; Leijon, M. Experimental results from sea trials of an offshore wave energy system. Appl. Phys. Lett. 2007, 90, 034105. [Google Scholar] [CrossRef]
- Prudell, J.; Stoddard, M.; Brekken, T.K.; von Jouanne, A. A novel permanent magnet tubular linear generator for ocean wave energy. In Proceedings of the Energy Conversion Congress and Exposition, ECCE 2009, San Jose, CA, USA, 20–24 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 3641–3646. [Google Scholar]
- Brekken, T.K.; Von Jouanne, A.; Han, H.Y. Ocean wave energy overview and research at Oregon State University. In Proceedings of the Power Electronics and Machines in Wind Applications, 2009, PEMWA 2009, Lincoln, NE, USA, 24–26 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–7. [Google Scholar]
- Amiri, A.; Panahi, R.; Radfar, S. Parametric study of two-body floating-point wave absorber. J. Mar. Sci. Appl. 2016, 15, 41–49. [Google Scholar] [CrossRef]
- Al Shami, E.; Zhang, R.; Wang, X. Point absorber wave energy harvesters: A review of recent developments. Energies 2019, 12, 47. [Google Scholar] [CrossRef]
- Boscaino, V.; Cipriani, G.; Di Dio, V.; Franzitta, V.; Trapanense, M. Experimental test and simulations on a linear generator-based prototype of a wave energy conversion system designed with a reliability-oriented approach. Sustainability 2017, 9, 98. [Google Scholar] [CrossRef]
- Jin, C.; Kang, H.; Kim, M.; Bakti, F.P. Performance evaluation of surface riding wave energy converter with linear electric generator. Ocean Eng. 2020, 218, 108141. [Google Scholar] [CrossRef]
- Seo, S.-W.; Shin, K.-H.; Koo, M.-M.; Hong, K.; Yoon, I.-J.; Choi, J.-Y. Experimentally Verifying the Generation Characteristics of a Double-Sided Linear Permanent Magnet Synchronous Generator for Ocean Wave Energy Conversion. IEEE Trans. Appl. Supercond. 2020, 30, 1–4. [Google Scholar] [CrossRef]
- Huang, L.; Yu, H.; Hu, M.; Liu, C.; Yuan, B. Research on a tubular primary permanent-magnet linear generator for wave energy conversions. IEEE Trans. Magn. 2013, 49, 1917–1920. [Google Scholar] [CrossRef]
- Di Dio, V.; Franzitta, V.; Milone, D.; Pitruzzella, S.; Trapanese, M.; Viola, A. Design of Bilateral Switched Reluctance Linear Generator to Convert Wave Energy: Case Study in Sicily; Advanced Materials Research; Trans Tech Publications: Zurich, Switzerland, 2014; pp. 1694–1698. [Google Scholar]
- Baker, N.J.; Raihan, M.A.; Almoraya, A.A. A cylindrical linear permanent magnet Vernier hybrid machine for wave energy. IEEE Trans. Energy Convers. 2018, 34, 691–700. [Google Scholar] [CrossRef]
- Mueller, M.; Baker, N.; Ran, L.; Chong, N.; Wei, H.; Tavner, P.; McKeever, P. Experimental Tests of an Air-Cored PM Tubular Generator for Direct Drive Wave Energy Converters; IET: Auburn Hills, MI, USA, 2008. [Google Scholar]
- Wahyudie, A.; Jama, M.; Susilo, T.B.; Mon, B.F.; Shaaref, H.; Noura, H. Design and testing of a laboratory scale test rig for wave energy converters using a double-sided permanent magnet linear generator. IET Renew. Power Gener. 2017, 11, 922–930. [Google Scholar] [CrossRef]
- Wahyudie, A.; Susilo, T.B.; Jama, M.; Mon, B.F.; Shaaref, H. Design of a Double-Sided Permanent Magnet Linear Generator for Laboratory Scale Ocean Wave Energy Converter; OCEANS 2017-Anchorage; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Joseph, D.M.; Cronje, W.A. Design and analysis of a double-sided tubular linear synchronous generator with particular application to wave-energy conversion. In Proceedings of the 2007 IEEE Power Engineering Society Conference and Exposition in Africa-PowerAfrica, Johannesburg, South Africa, 16–20 July 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–8. [Google Scholar]
- Prudell, J.; Stoddard, M.; Amon, E.; Brekken, T.K.; Von Jouanne, A. A permanent-magnet tubular linear generator for ocean wave energy conversion. IEEE Trans. Ind. Appl. 2010, 46, 2392–2400. [Google Scholar] [CrossRef]
- Liu, C.; Yu, H.; Hu, M.; Liu, Q.; Zhou, S.; Huang, L. Research on a permanent magnet tubular linear generator for direct drive wave energy conversion. IET Renew. Power Gener. 2013, 8, 281–288. [Google Scholar] [CrossRef]
- Vining, J.; Lipo, T.; Venkataramanan, G. Design and optimization of a novel hybrid transverse/longitudinal flux, wound-field linear machine for ocean wave energy conversion. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 3726–3733. [Google Scholar]
- Tan, Y.; Lin, K.; Zu, J.W. Analytical modelling of Halbach linear generator incorporating pole shifting and piece-wise spring for ocean wave energy harvesting. AIP Adv. 2018, 8, 056615. [Google Scholar] [CrossRef]
- Ran, L.; Mueller, M.; Ng, C.; Tavner, P.; Zhao, H.; Baker, N.; McDonald, S.; McKeever, P. Power conversion and control for a linear direct drive permanent magnet generator for wave energy. IET Renew. Power Gener. 2011, 5, 1–9. [Google Scholar] [CrossRef]
- Wang, X. Frequency Analysis of Vibration Energy Harvesting Systems; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Ahamed, R.; Howard, I.; McKee, K. Study of gravitational force effects, magnetic restoring forces and coefficients of the magnetic spring-based nonlinear oscillator system. IEEE Trans. Magn. 2022. [Google Scholar] [CrossRef]
- Beeby, S.P.; Wang, L.; Zhu, D.; Weddell, A.S.; Merrett, G.V.; Stark, B.; Szarka, G.; Al-Hashimi, B.M. A comparison of power output from linear and nonlinear kinetic energy harvesters using real vibration data. Smart Mater. Struct. 2013, 22, 075022. [Google Scholar] [CrossRef]
- Owens, B.A.; Mann, B.P. Linear and nonlinear electromagnetic coupling models in vibration-based energy harvesting. J. Sound Vib. 2012, 331, 922–937. [Google Scholar] [CrossRef]
- Xiao, X.; Xiao, L.; Peng, T. Comparative study on power capture performance of oscillating-body wave energy converters with three novel power take-off systems. Renew. Energy 2017, 103, 94–105. [Google Scholar] [CrossRef]
- Gao, M.; Wang, Y.; Wang, Y.; Wang, P. Experimental investigation of non-linear multi-stable electromagnetic-induction energy harvesting mechanism by magnetic levitation oscillation. Appl. Energy 2018, 220, 856–875. [Google Scholar] [CrossRef]
- Masoumi, M.; Wang, Y. Repulsive magnetic levitation-based ocean wave energy harvester with variable resonance: Modeling, simulation and experiment. J. Sound Vib. 2016, 381, 192–205. [Google Scholar] [CrossRef]
- Le Méhauté, B. An Introduction to Hydrodynamics and Water Waves; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cheng, Z.; Yang, J.; Hu, Z.; Xiao, L. Frequency/time domain modeling of a direct drive point absorber wave energy converter. Sci. China Phys. Mech. Astron. 2014, 57, 311–320. [Google Scholar] [CrossRef]
- Engström, J.; Kurupath, V.; Isberg, J.; Leijon, M. A resonant two body system for a point absorbing wave energy converter with direct-driven linear generator. J. Appl. Phys. 2011, 110, 124904. [Google Scholar] [CrossRef]
- Zurkinden, A.S.; Ferri, F.; Beatty, S.; Kofoed, J.P.; Kramer, M. Non-linear numerical modeling and experimental testing of a point absorber wave energy converter. Ocean Eng. 2014, 78, 11–21. [Google Scholar] [CrossRef]
- Wang, L.; Engström, J.; Göteman, M.; Isberg, J. Constrained optimal control of a point absorber wave energy converter with linear generator. J. Renew. Sustain. Energy 2015, 7, 043127. [Google Scholar] [CrossRef]
- Huang, L.; Hu, M.; Yu, H.; Liu, C.; Chen, Z. Design and experiment of a direct-drive wave energy converter using outer-PM linear tubular generator. IET Renew. Power Gener. 2016, 11, 353–360. [Google Scholar] [CrossRef]
- Li, W.; Chau, K.; Lee, C.H.; Ching, T.; Chen, M.; Jiang, J. A new linear magnetic gear with adjustable gear ratios and its application for direct-drive wave energy extraction. Renew. Energy 2017, 105, 199–208. [Google Scholar] [CrossRef]
- Stålberg, M.; Waters, R.; Danielsson, O.; Leijon, M. Influence of generator damping on peak power and variance of power for a direct drive wave energy converter. J. Offshore Mech. Arct. Eng. 2008, 130, 031003. [Google Scholar] [CrossRef]
- Mann, B.; Owens, B. Investigations of a nonlinear energy harvester with a bistable potential well. J. Sound Vib. 2010, 329, 1215–1226. [Google Scholar] [CrossRef]
- Williams, C.; Yates, R.B. Analysis of a micro-electric generator for microsystems. Sens. Actuators A Phys. 1996, 52, 8–11. [Google Scholar] [CrossRef]
- Zheng, Z.-Q.; Huang, P.; Gao, D.-X.; Chang, Z.-Y. Analysis of electromagnetic force of the linear generator in point absorber wave energy converters. J. Mar. Sci. Technol. 2015, 23, 475–480. [Google Scholar]
- Faiz, J.; Nematsaberi, A. Linear permanent magnet generator concepts for direct-drive wave energy converters: A comprehensive review. In Proceedings of the 2017 12th IEEE Conference on Industrial Electronics and Applications (ICIEA), Siem Reap, Cambodia, 18–20 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 618–623. [Google Scholar]
- Lejerskog, E.; Boström, C.; Hai, L.; Waters, R.; Leijon, M. Experimental results on power absorption from a wave energy converter at the Lysekil wave energy research site. Renew. Energy 2015, 77, 9–14. [Google Scholar] [CrossRef]
- Wang, L.; Lin, M.; Tedeschi, E.; Engstrm, J.; Isberg, J. Improving electric power generation of a standalone wave energy converter via optimal electric load control. Energy 2020, 211, 118945. [Google Scholar] [CrossRef]
- Youn, S.W.; Lee, J.J.; Yoon, H.S.; Koh, C.S. A new cogging-free permanent-magnet linear motor. IEEE Trans. Magn. 2008, 44, 1785–1790. [Google Scholar] [CrossRef]
- Kimoulakis, N.M.; Kladas, A.G.; Tegopoulos, J.A. Cogging force minimization in a coupled permanent magnet linear generator for sea wave energy extraction applications. IEEE Trans. Magn. 2009, 45, 1246–1249. [Google Scholar] [CrossRef]
- Faiz, J.; Ebrahimi-Salari, M.; Shahgholian, G. Reduction of cogging force in linear permanent-magnet generators. IEEE Trans. Magn. 2009, 46, 135–140. [Google Scholar] [CrossRef]
- Ekergård, B. Full scale applications of permanent magnet electromagnetic energy converters: From Nd2Fe14B to ferrite. Ph.D. Thesis, Boel Ekergård, Uppsala University, Uppsala, Sweden, 2013. [Google Scholar]
- Ekergård, B.; Leijon, M. Longitudinal End Effects in a Linear Wave Power Generator. Energies 2020, 13, 327. [Google Scholar] [CrossRef]
- Liu, C.; Yu, H.; Hu, M.; Liu, Q.; Zhou, S. Detent force reduction in permanent magnet tubular linear generator for direct-driver wave energy conversion. IEEE Trans. Magn. 2013, 49, 1913–1916. [Google Scholar] [CrossRef]
- Guo, R.; Yu, H.; Xia, T.; Shi, Z.; Zhong, W.; Liu, X. A simplified subdomain analytical model for the design and analysis of a tubular linear permanent magnet oscillation generator. IEEE Access 2018, 6, 42355–42367. [Google Scholar] [CrossRef]
- Danielsson, O.; Leijon, M.; Sjostedt, E. Detailed study of the magnetic circuit in a longitudinal flux permanent-magnet synchronous linear generator. IEEE Trans. Magn. 2005, 41, 2490–2495. [Google Scholar] [CrossRef]
- Viola, A.; Franzitta, V.; Curto, D.; Trapanese, M.; Di Dio, V.; Cipriani, G.; Boscaino, V.; Corpora, M.; Raimondi, F.M. Design of Wave Energy Converter (WEC): A Prototype Installed in Sicily; OCEANS 2015-Genova, 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Bianchi, N.; Bolognani, S.; Cappello, A. Reduction of cogging force in PM linear motors by pole-shifting. IEE Proc.-Electr. Power Appl. 2005, 152, 703–709. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, H.; Hu, M.; Huang, L.; Xia, T. Research on a PM Slotless Linear Generator Based on Magnet Field Analysis Model for Wave Energy Conversion. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, H.; Chen, Q.; Hu, M.; Huang, L.; Liu, Q. Design and experimental analysis of AC linear generator with Halbach PM arrays for direct-drive wave energy conversion. IEEE Trans. Appl. Supercond. 2013, 24, 1–4. [Google Scholar] [CrossRef]
- Molla, S.; Farrok, O. Vitroperm 500F and supermendur ferromagnetic cores used in a linear generator for oceanic wave energy conversion. In Proceedings of the 2019 International Conference on Robotics, Electrical and Signal Processing Techniques (ICREST), Dhaka, Bangladesh, 10–12 January 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 602–605. [Google Scholar]
- Vermaak, R.; Kamper, M.J. Experimental evaluation and predictive control of an air-cored linear generator for direct-drive wave energy converters. IEEE Trans. Ind. Appl. 2012, 48, 1817–1826. [Google Scholar] [CrossRef]
- Farrok, O.; Islam, M.R.; Sheikh, M.R.I.; Guo, Y.; Zhu, J.; Lei, G. A novel method to avoid degradation due to demagnetization of PM linear generators for oceanic wave energy extraction. In Proceedings of the 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Nilsson, K.; Danielsson, O.; Leijon, M. Electromagnetic forces in the air gap of a permanent magnet linear generator at no load. J. Appl. Phys. 2006, 99, 034505. [Google Scholar] [CrossRef]
- Yu, H.; Liu, C.; Yuan, B.; Hu, M.; Huang, L.; Zhou, S. A permanent magnet tubular linear generator for wave energy conversion. J. Appl. Phys. 2012, 111, 07A741. [Google Scholar] [CrossRef]
- Gargov, N.; Zobaa, A.; Pisica, I. Separated magnet yoke for permanent magnet linear generator for marine wave energy converters. Electr. Power Syst. Res. 2014, 109, 63–70. [Google Scholar] [CrossRef]
- Liu, C.-T.; Lin, C.-L.; Hwang, C.-C.; Tu, C.-H. Compact model of a slotless tubular linear generator for renewable energy performance assessments. IEEE Trans. Magn. 2010, 46, 1467–1470. [Google Scholar] [CrossRef]
- Crozier, R.; Bailey, H.; Mueller, M.; Spooner, E.; McKeever, P. Analysis, design and testing of a novel direct-drive wave energy converter system. IET Renew. Power Gener. 2013, 7, 565–573. [Google Scholar] [CrossRef]
- Szabo, L.; Oprea, C. Wave energy plants for the black sea possible energy converter structures. In Proceedings of the 2007 International Conference on Clean Electrical Power, Capri, Italy, 21–23 May 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 306–311. [Google Scholar]
- Danielsson, O.; Leijon, M. Flux distribution in linear permanent-magnet synchronous machines including longitudinal end effects. IEEE Trans. Magn. 2007, 43, 3197–3201. [Google Scholar] [CrossRef]
- Baker, N.J.; Spooner, E.; Mueller, M. Permanent Magnet Air-Cored Tubular Linear Generator for Marine Energy Converters; IEE Conference Publication, 2004; IET: London, UK, 2004; pp. 862–867. [Google Scholar]
- McDonald, A.; Mueller, M.; Jeffrey, J. Development of a novel permanent magnet linear generator topology for direct-drive wave energy converters. In Proceedings of the 2008 4th IET Conference on Power Electronics, Machines and Drives, York, UK, 2–4 April 2008; IET: London, UK, 2008; pp. 81–85. [Google Scholar]
- Clifton, P.; McMahon, R.; Kelly, H. Design and commissioning of a 30 kW direct drive wave generator. In Proceedings of the 5th IET International Conference on Power Electronics, Machines and Drives (PEMD 2010), Brighton, UK, 19–21 April 2010; IET: London, UK, 2010; pp. 1–6. [Google Scholar]
- Vermaak, R.; Kamper, M.J. Design aspects of a novel topology air-cored permanent magnet linear generator for direct drive wave energy converters. IEEE Trans. Ind. Electron. 2011, 59, 2104–2115. [Google Scholar] [CrossRef]
- Hodgins, N.; Keysan, O.; McDonald, A.S.; Mueller, M.A. Design and testing of a linear generator for wave-energy applications. IEEE Trans. Ind. Electron. 2011, 59, 2094–2103. [Google Scholar] [CrossRef]
- Gargov, N.; Zobaa, A. Multi-phase air-cored tubular permanent magnet linear generator for wave energy converters. IET Renew. Power Gener. 2012, 6, 171–176. [Google Scholar] [CrossRef]
- Farrok, O.; Kiran, M.R.; Islam, M.R.; Xu, W.; Zhu, J. Core loss minimization of the linear generator by using high graded magnetic materials for harvesting oceanic wave energy. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1762–1765. [Google Scholar]
- Rahman, A.; Farrok, O.; Islam, M.R.; Xu, W. Recent Progress in Electrical Generators for Oceanic Wave Energy Conversion. IEEE Access 2020, 8, 138595–138615. [Google Scholar] [CrossRef]
- Demenko, A.; Kulig, S.; Nowak, L.; Zawirski, K.; Parel, T.S.; Rotaru, M.D.; Sykulski, J.K.; Hearn, G.E. Optimisation of a tubular linear machine with permanent magnets for wave energy extraction. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2011, 30, 1056–1068. [Google Scholar] [CrossRef]
- Molla, S.; Farrok, O.; Islam, M.R.; Muttaqi, K.M. Application of iron nitride compound as alternative permanent magnet for designing linear generators to harvest oceanic wave energy. IET Electr. Power Appl. 2020, 14, 762–770. [Google Scholar] [CrossRef]
- Wang, W.; Cao, J.; Zhang, N.; Lin, J.; Liao, W.-H. Magnetic-spring based energy harvesting from human motions: Design, modeling and experiments. Energy Convers. Manag. 2017, 132, 189–197. [Google Scholar] [CrossRef]
- Chiu, M.-C.; Chang, Y.-C.; Yeh, L.-J.; Chung, C.-H. Optimal design of a vibration-based electromagnetic energy harvester using a simulated annealing algorithm. J. Mech. 2012, 28, 691–700. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Kim, E.S. Power generation from human body motion through magnet and coil arrays with magnetic spring. J. Appl. Phys. 2014, 115, 064908. [Google Scholar] [CrossRef]
- Farrok, O.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D.; Zhu, J. Design and Optimization of a Novel Dual-Port Linear Generator for Oceanic Wave Energy Conversion. IEEE Trans. Ind. Electron. 2019, 67, 3409–3418. [Google Scholar] [CrossRef]
- Chau, K.; Zhang, D.; Jiang, J.; Jian, L. Transient analysis of coaxial magnetic gears using finite element comodeling. J. Appl. Phys. 2008, 103, 07F101. [Google Scholar] [CrossRef]
- de Sousa Prado, M.G.; Gardner, F.; Damen, M.; Polinder, H. Modelling and test results of the Archimedes wave swing. Proc. Inst. Mech. Eng. A J. Power Energy 2006, 220, 855–868. [Google Scholar] [CrossRef]
- Farrok, O.; Islam, M.R.; Sheikh, M.R.I.; Guo, Y.; Zhu, J.G. A Split Translator Secondary Stator Permanent Magnet Linear Generator for Oceanic Wave Energy Conversion. IEEE Trans. Ind. Electron. 2018, 65, 7600–7608. [Google Scholar] [CrossRef]
- Eriksson, M.; Isberg, J.; Leijon, M. Hydrodynamic modelling of a direct drive wave energy converter. Int. J. Eng. Sci. 2005, 43, 1377–1387. [Google Scholar] [CrossRef]
- Yu, Y.-H.; Tom, N.; Jenne, D. Numerical analysis on hydraulic power take-off for wave energy converter and power smoothing methods. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Madrid, Spain, 17–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. V010T09A043. [Google Scholar]
- Pirisi, A.; Mussetta, M.; Gruosso, G.; Zich, R.E. An Optimized Three Phase TPM-LiG for Marine Applications; SPEEDAM 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1712–1717. [Google Scholar]
- Pirisi, A.; Mussetta, M.; Gruosso, G.; Zich, R.E. Optimization of a linear generator for sea-wave energy conversion by means of a hybrid evolutionary algorithm. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- Szabo, L.; Oprea, C.; Viorel, I.-A.; Biró, K.Á. Novel permanent magnet tubular linear generator for wave energy converters. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 983–987. [Google Scholar]
- Rao, K.R.; Sunderan, T.; Adiris, M.R.A. Performance and design optimization of two model based wave energy permanent magnet linear generators. Renew. Energy 2017, 101, 196–203. [Google Scholar] [CrossRef]
- Memon, A.H.; bin Ibrahim, T.; Nallagowden, P. Design optimization of linear permanent magnet generator for wave energy conversion. In Proceedings of the 2015 IEEE Conference on Energy Conversion (CENCON), Johor Bahru, Malaysia, 19–20 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 315–319. [Google Scholar]
- Wang, J.; Howe, D. Design optimization of radially magnetized, iron-cored, tubular permanent-magnet machines and drive systems. IEEE Trans. Magn. 2004, 40, 3262–3277. [Google Scholar] [CrossRef]
- Fang, H.-w.; Song, R.-n.; Xiao, Z.-x. Optimal design of permanent magnet linear generator and its application in a wave energy conversion system. Energies 2018, 11, 3109. [Google Scholar] [CrossRef]
- Wang, L.; Isberg, J.; Tedeschi, E. Review of control strategies for wave energy conversion systems and their validation: The wave-to-wire approach. Renew. Sustain. Energy Rev. 2018, 81, 366–379. [Google Scholar] [CrossRef]
- Goggins, J.; Finnegan, W. Shape optimisation of floating wave energy converters for a specified wave energy spectrum. Renew. Energy 2014, 71, 208–220. [Google Scholar] [CrossRef]
- Bachynski, E.E.; Young, Y.L.; Yeung, R.W. Analysis and optimization of a tethered wave energy converter in irregular waves. Renew. Energy 2012, 48, 133–145. [Google Scholar] [CrossRef]
- Santana, A.G.; Andrade, D.E.M.; Jaén, A. Control of Hydrodynamic Parameters of Wave Energy Point Absorbers Using Linear Generators and VSC-Based Power Converters Connected to the Grid. In Proceedings of the International 1st Conference on Renewable Energies and Power Quality, Granada, Spain, 23–25 March 2010. [Google Scholar]
- Oh, Y.J.; Park, J.S.; Hyon, B.J.; Lee, J. Novel Control Strategy of Wave Energy Converter Using Linear Permanent Magnet Synchronous Generator. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- de la Villa Jaén, A.; Santana, A.G. Considering linear generator copper losses on model predictive control for a point absorber wave energy converter. Energy Convers. Manag. 2014, 78, 173–183. [Google Scholar]
- Wahyudie, A.; Jama, M.; Susilo, T.; Saeed, O.; Nandar, C.; Harib, K. Simple bottom-up hierarchical control strategy for heaving wave energy converters. Int. J. Electr. Power Energy Syst. 2017, 87, 211–221. [Google Scholar] [CrossRef]
- Salter, S.H.; Taylor, J.; Caldwell, N. Power conversion mechanisms for wave energy. Proc. Inst. Mech. Eng. M J. Eng. Marit. Environ. 2002, 216, 1–27. [Google Scholar] [CrossRef]
- Korde, U.A. Control system applications in wave energy conversion. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition. Conference Proceedings (Cat. No. 00CH37158), Providence, RI, USA, 11–14 September 2000; IEEE: Piscataway, NJ, USA, 2000; pp. 1817–1824. [Google Scholar]
- de la Villa Jaén, A.; García-Santana, A.; Montoya-Andrade, D.E. Maximizing output power of linear generators for wave energy conversion. Int. Trans. Electr. Energy Syst. 2014, 24, 875–890. [Google Scholar] [CrossRef]
- Hals, J.; Falnes, J.; Moan, T. A comparison of selected strategies for adaptive control of wave energy converters. J. Offshore Mech. Arct. Eng. 2011, 133, 031101. [Google Scholar] [CrossRef]
- Rossiter, J.A. Model-Based Predictive Control: A Practical Approach; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Gieske, P. Model Predictive Control of a Wave Energy Converter: Archimedes Wave Swing; Delft University of Technology: Delft, The Netherlands, 2007. [Google Scholar]
- Hals, J.; Falnes, J.; Moan, T. Constrained optimal control of a heaving buoy wave-energy converter. J. Offshore Mech. Arct. Eng. 2011, 133, 011401. [Google Scholar] [CrossRef]
- Brekken, T.K. On Model Predictive Control for a Point Absorber Wave Energy Converter; 2011 IEEE Trondheim PowerTech, 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–8. [Google Scholar]
- Jama, M.; Wahyudie, A.; Assi, A.; Noura, H. In Controlling heaving wave energy converter using function-based model predictive control technique. In Proceedings of the 2013 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 2705–2710. [Google Scholar]
- Cretel, J.A.; Lightbody, G.; Thomas, G.P.; Lewis, A.W. Maximisation of energy capture by a wave-energy point absorber using model predictive control. IFAC Proc. Vol. 2011, 44, 3714–3721. [Google Scholar] [CrossRef]
- Richter, M. Different Model Predictive Control Approaches for Controlling Point Absorber Wave Energy Converters. Diploma Thesis, University Stuttgart, Stuttgart, Germany, 2011. [Google Scholar]
- Li, G.; Belmont, M.R. Model predictive control of sea wave energy converters–Part I: A convex approach for the case of a single device. Renew. Energy 2014, 69, 453–463. [Google Scholar] [CrossRef]
- Richter, M.; Magana, M.E.; Sawodny, O.; Brekken, T.K. Nonlinear model predictive control of a point absorber wave energy converter. IEEE Trans. Sustain. Energy 2012, 4, 118–126. [Google Scholar] [CrossRef]
- Tom, N.; Yeung, R.W. Nonlinear model predictive control applied to a generic ocean-wave energy extractor. J. Offshore Mech. Arct. Eng. 2014, 136, 041901. [Google Scholar] [CrossRef]
- Abraham, E.; Kerrigan, E.C. Optimal active control and optimization of a wave energy converter. IEEE Trans. Sustain. Energy 2012, 4, 324–332. [Google Scholar] [CrossRef]
- Tom, N.; Yeung, R.W. Experimental confirmation of nonlinear-model-predictive control applied offline to a permanent magnet linear generator for ocean-wave energy conversion. IEEE J. Ocean. Eng. 2015, 41, 281–295. [Google Scholar]
- Ferri, F. Wave-to-wire modelling of wave energy converters: Critical assessment, developments and applicability for economical optimisation; River Publishers: Aalborg, Denmark, 2014. [Google Scholar]
- Li, B.; Macpherson, D.; Shek, J. Direct Drive Wave Energy Converter Control in Irregular Waves; IET: London, UK, 2011. [Google Scholar]
- Annuar, A.; Macpherson, D.; Forehand, D.; Mueller, M. Optimum power control for arrays of direct drive wave energy converters. In Proceedings of the IET International Conference on Power Electronics, Machines and Drives 2012 (PEMD 2012), Bristol, UK, 27–29 March 2012; IET: London, UK, 2012. [Google Scholar]
- Marei, M.I.; Mokhtar, M.; El-Sattar, A.A. MPPT strategy based on speed control for AWS-based wave energy conversion system. Renew. Energy 2015, 83, 305–317. [Google Scholar] [CrossRef]
- Shek, J.; Macpherson, D.; Mueller, M. Experimental verification of linear generator control for direct drive wave energy conversion. IET Renew. Power Gener. 2010, 4, 395–403. [Google Scholar] [CrossRef]
- Cheung, J.T. Frictionless Linear Electrical Generator for Harvesting Motion Energy; Rockwell International: Thousand Oaks, CA, USA, 2004. [Google Scholar]
- Eriksson, S. Design of permanent-magnet linear generators with constant-torque-angle control for wave power. Energies 2019, 12, 1312. [Google Scholar] [CrossRef]
- Amon, E.A.; Schacher, A.A.; Brekken, T.K. A novel maximum power point tracking algorithm for ocean wave energy devices. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 2635–2641. [Google Scholar]
- Brooking, P.; Mueller, M. Power conditioning of the output from a linear vernier hybrid permanent magnet generator for use in direct drive wave energy converters. IEE Proc.-Gener. Transm. Distrib. 2005, 152, 673–681. [Google Scholar] [CrossRef]
- Ozkop, E.; Altas, I.H. Control, power and electrical components in wave energy conversion systems: A review of the technologies. Renew. Sustain. Energy Rev. 2017, 67, 106–115. [Google Scholar] [CrossRef]
- Bostrom, C.; Waters, R.; Lejerskog, E.; Svensson, O.; Stalberg, M.; Stromstedt, E.; Leijon, M. Study of a wave energy converter connected to a nonlinear load. IEEE J. Ocean. Eng. 2009, 34, 123–127. [Google Scholar] [CrossRef]
- Ekström, R.; Ekergård, B.; Leijon, M. Electrical damping of linear generators for wave energy converters—A review. Renew. Sustain. Energy Rev. 2015, 42, 116–128. [Google Scholar] [CrossRef]
- Farrok, O.; Islam, M.R.; Sheikh, M.R.I.; Guo, Y.; Zhu, J.G. Design and analysis of a novel lightweight translator permanent magnet linear generator for oceanic wave energy conversion. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Xia, T.; Yu, H.; Chen, Z.; Huang, L.; Liu, X.; Hu, M. Design and analysis of a field-modulated tubular linear permanent magnet generator for direct-drive wave energy conversion. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Wang, D.; Shao, C.; Wang, X. Design and performance evaluation of a tubular linear switched reluctance generator with low cost and high thrust density. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Lejerskog, E.; Leijon, M. Detailed study of closed stator slots for a direct-driven synchronous permanent magnet linear wave energy converter. Machines 2014, 2, 73–86. [Google Scholar] [CrossRef]
- Huang, L.; Chen, M.; Wang, L.; Yue, F.; Guo, R.; Fu, X. Analysis of a hybrid field-modulated linear generator for wave energy conversion. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Huang, L.; Liu, J.; Yu, H.; Qu, R.; Chen, H.; Fang, H. Winding configuration and performance investigations of a tubular superconducting flux-switching linear generator. IEEE Trans. Appl. Supercond. 2014, 25, 1–5. [Google Scholar] [CrossRef]
- Antipov, V.; Grozov, A.; Ivanova, A. A linear synchronous generator with a power of 30 kW for wave-power engineering. Russ. Electr. Eng. 2017, 88, 55–60. [Google Scholar] [CrossRef]
- Niu, X. Modeling and Design Analysis of a Permanent Magnet Linear Synchronous Generator; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2013. [Google Scholar]
- Almoraya, A.; Baker, N.; Smith, K.; Raihan, M. Development of a double-sided consequent pole linear vernier hybrid permanent-magnet machine for wave energy converters. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–7. [Google Scholar]
- Sun, Z.; Cheung, N.; Zhao, S.; Lu, Y.; Shi, Z. Design and simulation of a linear switched reluctance generator for wave energy conversion. In Proceedings of the 4th International Conference on Power Electronics Systems and Applications, Hong Kong, China, 8–10 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–5. [Google Scholar]
- Mendes, R.; Calado, M.; Mariano, S. Particle swarm and Box׳ s complex optimization methods to design linear tubular switched reluctance generators for wave energy conversion. Swarm Evol. Comput. 2016, 28, 29–41. [Google Scholar] [CrossRef]
- Elwood, D.; Yim, S.C.; Prudell, J.; Stillinger, C.; Von Jouanne, A.; Brekken, T.; Brown, A.; Paasch, R. Design, construction, and ocean testing of a taut-moored dual-body wave energy converter with a linear generator power take-off. Renew. Energy 2010, 35, 348–354. [Google Scholar] [CrossRef]
- Prado, M.; Polinder, H. Direct Drive in Wave Energy Conversion—AWS Full Scale Prototype Case Study. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–7. [Google Scholar]
- Kim, J.; Koh, H.; Cho, I.; Kim, M.; Kweon, H. Experimental study of wave energy extraction by a dual-buoy heaving system. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 25–34. [Google Scholar] [CrossRef]
- Vining, J.; Mundon, T.; Nair, B. Electromechanical design and experimental evaluation of a double-sided, dual airgap linear vernier generator for wave energy conversion. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 5557–5564. [Google Scholar]
- Elwood, D.; Schacher, A.; Rhinefrank, K.; Prudell, J.; Yim, S.; Amon, E.; Brekken, T.; von Jouanne, A. Numerical modeling and ocean testing of a direct-drive wave energy device utilizing a permanent magnet linear generator for power take-off. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009; pp. 817–824. [Google Scholar]
- Hong, Y.; Eriksson, M.; Castellucci, V.; Boström, C.; Waters, R. Linear generator-based wave energy converter model with experimental verification and three loading strategies. IET Renew. Power Gener. 2016, 10, 349–359. [Google Scholar] [CrossRef]
- Xia, T.; Yu, H.; Guo, R.; Liu, X. Research on the field-modulated tubular linear generator with quasi-halbach magnetization for ocean wave energy conversion. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Feng, N.; Yu, H.; Hu, M.; Liu, C.; Huang, L.; Shi, Z. A study on a linear magnetic-geared interior permanent magnet generator for direct-drive wave energy conversion. Energies 2016, 9, 487. [Google Scholar] [CrossRef]
- Son, D.; Yeung, R.W. Real-time implementation and validation of optimal damping control for a permanent-magnet linear generator in wave energy extraction. Appl. Energy 2017, 208, 571–579. [Google Scholar] [CrossRef]
- Du, Y.; Cheng, M.; Chau, K.T.; Liu, X.; Xiao, F.; Zhao, W. Linear primary permanent magnet vernier machine for wave energy conversion. IET Electr. Power Appl. 2015, 9, 203–212. [Google Scholar] [CrossRef]
- Huang, L.; Yu, H.; Hu, M.; Zhao, J.; Cheng, Z. A novel flux-switching permanent-magnet linear generator for wave energy extraction application. IEEE Trans. Magn. 2011, 47, 1034–1037. [Google Scholar] [CrossRef]
- Pan, J.; Li, Q.; Wu, X.; Cheung, N.; Qiu, L. Complementary power generation of double linear switched reluctance generators for wave power exploitation. Int. J. Electr. Power Energy Syst. 2019, 106, 33–44. [Google Scholar] [CrossRef]
- Pan, J.; Zou, Y.; Cheung, N.; Cao, G.-z. On the voltage ripple reduction control of the linear switched reluctance generator for wave energy utilization. IEEE Trans. Power Electron. 2013, 29, 5298–5307. [Google Scholar] [CrossRef]
- Mendes, R.; Calado, M.; Mariano, S. Electromagnetic design method for a TLSRG with application in ocean wave energy conversion. Int. J. Electr. Power Energy Syst. 2020, 121, 106097. [Google Scholar] [CrossRef]
- Huang, L.; Hu, B.; Hu, M.; Liu, C.; Zhu, H. Research on primary excitation fully superconducting linear generators for wave energy conversion. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Leijon, M.; Bernhoff, H.; Agren, O.; Isberg, J.; Sundberg, J.; Berg, M.; Karlsson, K.E.; Wolfbrandt, A. Multiphysics simulation of wave energy to electric energy conversion by permanent magnet linear generator. IEEE Trans. Energy Convers. 2005, 20, 219–224. [Google Scholar] [CrossRef]
- Feng, N.; Yu, H.; Zhao, M.; Zhang, P.; Hou, D. Magnetic field-modulated linear permanent-magnet generator for direct-drive wave energy conversion. IET Electr. Power Appl. 2020, 14, 742–750. [Google Scholar] [CrossRef]
- Kracht, P.; Perez-Becker, S.; Richard, J.-B.; Fischer, B. Performance improvement of a point absorber wave energy converter by application of an observer-based control: Results from wave tank testing. IEEE Trans. Ind. Appl. 2015, 51, 3426–3434. [Google Scholar] [CrossRef]
- Penalba, M.; Davidson, J.; Windt, C.; Ringwood, J.V. A high-fidelity wave-to-wire simulation platform for wave energy converters: Coupled numerical wave tank and power take-off models. Appl. Energy 2018, 226, 655–669. [Google Scholar] [CrossRef]
- Antonio, F.D.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar]
- Joubert, J.R.; van Niekerk, J.L.; Reinecke, J.; Meyer, I. Wave Energy Converters (WECs); CRSES: Matieland, South Africa, 2013. [Google Scholar]
- Czech, B.; Bauer, P. Wave energy converter concepts: Design challenges and classification. IEEE Ind. Electron. Mag. 2012, 6, 4–16. [Google Scholar] [CrossRef]
- Pecher, A.; Peter Kofoed, J. Handbook of Ocean Wave Energy; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Qiao, D.; Haider, R.; Yan, J.; Ning, D.; Li, B. Review of Wave Energy Converter and Design of Mooring System. Sustainability 2020, 12, 8251. [Google Scholar] [CrossRef]
- Aderinto, T.; Li, H. Ocean wave energy converters: Status and challenges. Energies 2018, 11, 1250. [Google Scholar] [CrossRef]
- Piscopo, V.; Benassai, G.; Della Morte, R.; Scamardella, A. Cost-based design and selection of point absorber devices for the mediterranean sea. Energies 2018, 11, 946. [Google Scholar] [CrossRef]
- Clément, A.; McCullen, P.; Falcão, A.; Fiorentino, A.; Gardner, F.; Hammarlund, K.; Lemonis, G.; Lewis, T.; Nielsen, K.; Petroncini, S. Wave energy in Europe: Current status and perspectives. Renew. Sustain. Energy Rev. 2002, 6, 405–431. [Google Scholar] [CrossRef]
- Ibrahim, H.; Ilinca, A.; Perron, J. Energy storage systems—Characteristics and comparisons. Renew. Sustain. Energy Rev. 2008, 12, 1221–1250. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).