Neighbor-Companion or Neighbor-Beggar? Estimating the Spatial Spillover Effects of Fiscal Decentralization on China’s Carbon Emissions Based on Spatial Econometric Analysis

Abstract

China’s rapid economic growth is associated with huge energy consumption and high carbon dioxide (CO₂) emissions. Although the environmental effect of fiscal decentralization (FD) has been widely reported, its impact on CO₂ is still a controversial subject. In this context, based on the panel data for China’s 30 provinces during 2003–2019, this paper uses a spatial autoregressive model to investigate the spatial spillover effects of revenue and expenditure decentralization on CO₂ emissions, respectively. The results show that: (1) CO₂ emissions exhibit spatial dependence, indicating that the rise of CO₂ emissions in the region can lead to the rise of it in neighboring regions. (2) Both revenue and expenditure decentralization have significant positive spatial spillover effects on CO₂ emissions, implying that higher FD in the province can significantly accelerate CO₂ emissions in neighboring provinces. (3) There exists regional heterogeneity in the spatial spillover effect of FD on CO₂ emissions. (4) Foreign direct investment (FDI) and technological innovation (R&D) can effectively mitigate the adverse effect of FD on CO₂ emissions. (5) Industrial structure and human capital can significantly inhibit CO₂ emissions, while economic development cannot. Therefore, it is important to optimize the system of fiscal decentralization and strengthen inter-regional cooperation on carbon emission reduction.

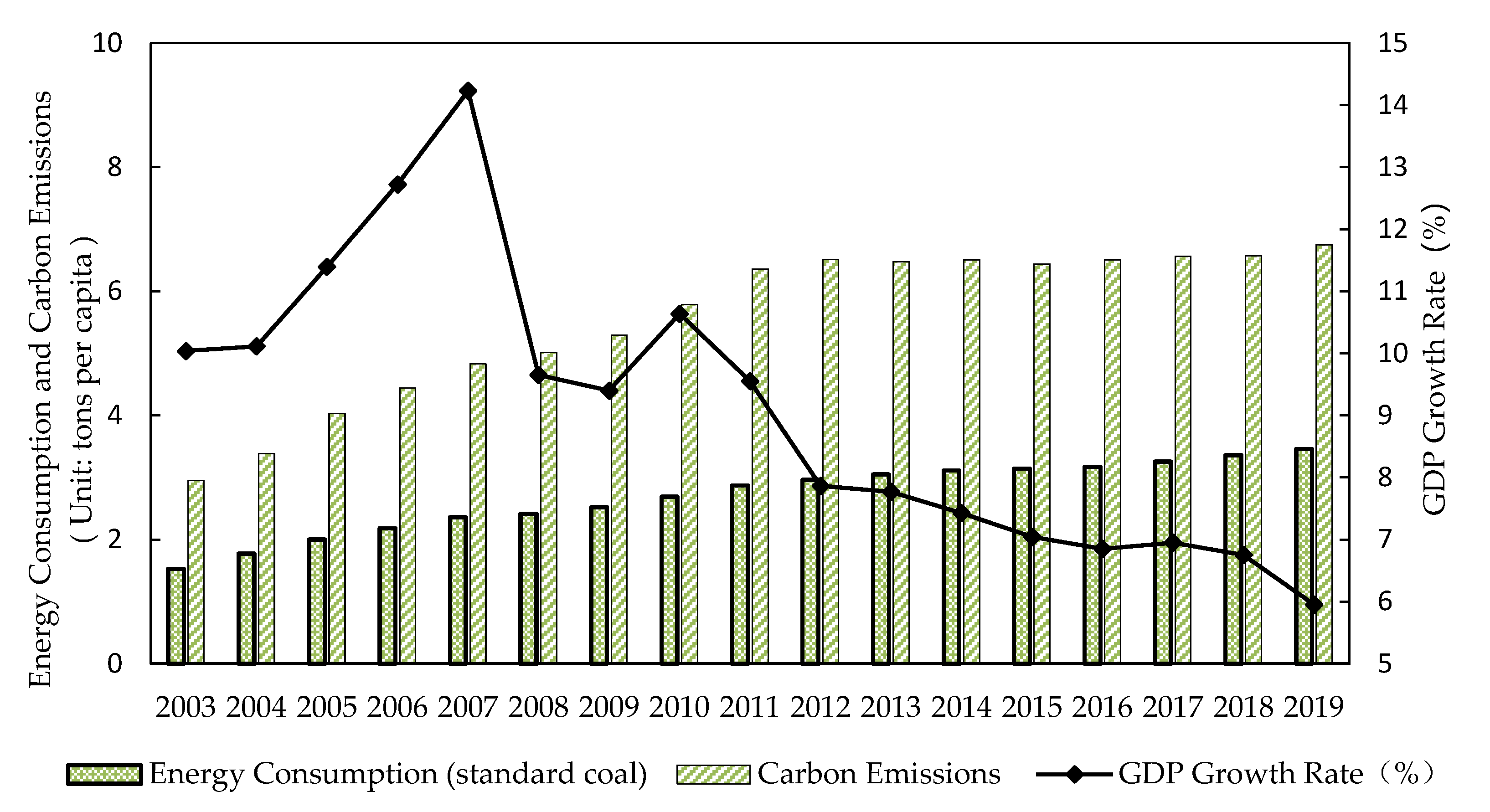
1. Introduction

In recent decades, as a result of excessive CO₂ emissions, the greenhouse effect, which has been leading to the melting of glaciers and rising of sea levels, has been recognized as one of the most challenging issues facing mankind [1,2]. Reducing CO₂ emissions and realizing low-carbon development have become the common goals around the world. As a large developing country, China has achieved a remarkable growth miracle which was mainly driven by industrialization and urbanization since the early 1980s [3]. During the period from 1980 to 2015, the annual growth rate of China’s GDP has averaged up to 9.5%. However, China’s extensive growth, which is marked by high pollution, high energy consumption, and low productivity, has resulted in massive CO₂ emissions (see Figure 1). In 2007, China became the largest carbon dioxide emitter worldwide, which has seriously affected China’s green and sustainable development [4]. Due to the global push to reduce CO₂ emissions and huge pressure from the carrying capacity of domestic resources and the environment, carbon reduction in China has become an international focus. As a responsible country, China has played a critical role in global climate governance and proposed a series of binding policies for emission reduction. Specifically, the Chinese government issued the Notice on Piloting Carbon Emissions Trading in October 2011, approving seven provinces to carry out pilot carbon trading, and issued the Air Pollution Prevention and Control Action Plan on 10 September 2013. In particular, in 2020, China announced that CO₂ emissions would peak around 2030 and achieve carbon neutrality by 2060, demonstrating China’s commitment to realizing its carbon-reduction targets. Now it is widely believed that high-quality development is not possible with the increase in input factors alone and that enhancing carbon productivity is the only way to maintain green and sustainable development. In this context, what is the effect of China’s CO₂ emissions reduction? What kind of path should be established to reduce CO₂ emissions? These questions have become the focus of academic research at home and abroad [5,6,7]!

Currently, many countries actively promote CO₂ emissions reduction under the condition that decentralized governance has made great progress, because local governments which have an information advantage about local preferences in a relatively decentralized fiscal system, can better meet the local needs for public goods [8,9]. It is undeniable that China’s CO₂ emissions are caused by the extensive development model, which stems from government behavior under the “Chinese style of decentralization” [10,11]. Specifically, in the early 1980s, because of the implementation of the “Fiscal Responsibility System”, the central government began to require fiscal revenue to be concentrated at the central level, and it gradually transferred some expenditure responsibilities including pollution governance to the local level. The system adjustment of “shifting financial power upward and decentralizing affairs” resulted in the persistently increasing expenditure pressure on local governments and severe fiscal imbalance [12,13]. Facing promotion incentives and fiscal pressure, local governments were willing to invest limited financial funds in high-return but high-pollution industries in pursuit of high economic growth, rather than environmental governance, which failed to achieve the direct benefits of political promotion in the short run. According to the data released by the National Bureau of statistics in 2019, China’s local government spending on energy conservation and environmental protection only accounted for 3.42% of the total expenditure, a decrease of 22.64% compared with 2003. Thus, local governments competing for growth may deregulate CO₂ emissions, resulting in the pattern of “racing to the bottom” at the local level [14]. Moreover, we ought not to ignore the reality of the tax-sharing reform implemented in 1994. Since then, local governments’ fiscal revenues showed a downward trend relative to their expenditures. For the sake of economic development and local governance, local governments will have to undertake most of the expenditures. And the more grass-roots governments are, the higher the mismatch between financial and administrative power is. Thus, does China’s fiscal decentralization (FD) affect regional CO₂ emissions? Will the inaction of local governments in environmental governance influence CO₂ emissions in their neighboring regions? In other words, is there a spatial spillover effect of FD on CO₂ emissions? Will there be “neighbor-beggar” or “neighbor-companion”? The answers to these questions will contribute to clarify the nexus between FD and CO₂ emissions and promote the reform of the environmental governance system, which deserves in-depth study [15,16].

This study aims to figure out how different types of FD affect CO₂ emissions in terms of spatial spillover effects. Specifically, we first build a two-sector growth model to analyze how revenue decentralization (FRD) and expenditure decentralization (FED) affect carbon emissions. And then we collect the provincial panel data from China during 2003–2019 and use a spatial panel econometric model to examine the effects of FRD and FED on CO₂ emissions, respectively. Compared with the existing literature, the contributions of this paper can be summarized as follows. Firstly, we incorporate FD and carbon emissions into a unified analytical framework, and establish a two-sector growth model including households and firms, then analyze the internal nexus between FD and carbon emissions, which makes up for the defects of the existing research. Secondly, based on the data of seven energy consumption and cement production for China’s 30 provinces over the period 2003–2019 and the emission coefficients issued by the Intergovernmental Panel on Climate Change, this paper calculates the carbon emissions at the province level, which is helpful in describing the spatiotemporal variation of regional carbon emissions. Thirdly, based on the spatial econometric model and effect decomposition, we confirm that FD, which is divided into FRD and FED, has significant positive spatial spillover effects on carbon emissions. The comprehensive evaluation of the environmental effects of FD from the spatial spillover perspective is of great significance. Finally, by introducing the interaction term of R&D and FD, as well as the interaction term of FDI and FD, this paper further investigates the influence mechanisms of FD on carbon emissions, which greatly enriches the existing studies.

The rest of this paper is structured as follows. Section 2 reviews the relevant literature and presents the gaps. Section 3 constructs a theoretical model to examine the link between FD and CO₂ emissions. Section 4 describes the methodology and data used in the empirical analysis. Section 5 discusses the estimation results. Section 6 summarizes the study and presents some policy implications.

2. Literature Review

After observing the previous studies, the literature related to this paper is divided into three streams: fiscal decentralization (FD) and economic development, factors influencing carbon emissions, and FD and environmental pollution. An overview of recent studies relating to these topics is summarized as follows.

The first stream studies the link between FD and economic development. As many countries gradually delegate fiscal powers to lower-level governments, the effect of FD on economic growth has been highly concern by many scholars worldwide. However, there is not yet a consensus in the existing literature on the link between FD and economic growth [8,17]. Some studies hold the view that FD grants local governments some fiscal autonomy, which stimulates their enthusiasm of them to develop the economy, promotes the healthy competition among regions and improves resource allocation efficiency, thus promoting economic growth eventually [9,18]. To be specific, Iimi [19] found that over the period 1997–2001, there is a positive effect of expenditure decentralization on per capita GDP growth in 51 developed and developing countries. It was found in the Buser [20] study that FD contributed positively to economic growth in 20 high-income OECD countries between 1972 and 2005. Chu and Zheng [3] asserted that FD remarkably promotes economic growth with provincial panel data of China for the period 1996 to 2005. Canavire-Bacarreza et al. [21] argued that over the period 1981–2012, FD showed an apparently positive impact on economic growth in 67 countries. Similarly, the positive correlation between FD and economic growth was demonstrated by Huynh and Tran [22] for 23 OECD countries during 2002–2016. In contrast, some scholars believed that in the decentralization system, due to the fragmentation of local interests, the coordinated ability among regions is weakened, which is unfavorable for the supply of some public goods. Meanwhile, FD widens the regional economic gap, which leads to macroeconomic instability, thus hindering economic growth [14,23]. Specifically, Davoodi and Zou [24] asserted that FD was negatively associated with economic growth in developing countries during 1970 to 1989. Rodríguez-Pose and Ezcurra [25] demonstrated that FD inhibited economic growth in 21 OECD countries covering 1990–2005. A similar conclusion is provided by Baskaran and Feld [26], who confirmed that between 1975 and 2008, revenue decentralization hindered economic growth in OECD countries. Furthermore, it is claimed by several people that the influence of FD on economic growth is indeterminate, because of the simultaneous existence of positive and negative externalities of local public goods caused by FD. Therefore, excessive FD or centralization will have a negative impact on economic growth [27]. For example, Thießen [28] examined the relationship between FD and economic growth for high-income OECD countries covering 1973–1998, and showed that the relationship is positive when the level of decentralization is low, but then reaches a peak and turns negative. Cantarero and Gonzalez [29] found that in Spain, the link between FD and economic growth is U-shaped covering 1985–2004. By studying panel data of 29 Chinese provinces during 1990–2012, Yang [4] pointed out that a non-linear relationship exists between FD and the secondary sector growth. Mauro et al. [30], who explored the influence of FD on economic growth covering 1975–2010, argued that by changing the rule of law, the growth effect of FD can vary from negative to positive.

The second stream that our paper related is factors influencing CO₂ emissions. As a key factor affecting the socio-economic and ecological benefits of a country or region, CO₂ emissions has become the focus of academic research worldwide. The existing studies on the factors influencing CO₂ emissions can be classified into two groups. The first group emphasizes the influence of economic factors on CO₂ emissions, including economic development, urbanization, foreign direct investment, and industrial structure. In terms of economic development, there is no consensus about its impact on CO₂ emissions. Many studies claimed that the rapid economic growth has substantially promoted energy consumption, thus causing a sharp increase in CO₂ emissions [31]. Nevertheless, other scholars acknowledged that economic development can reduce CO₂ emissions. For example, Asumadu-Sarkodie and Owusu [32], which investigated how economic development affected CO₂ emissions in Senegal during 1980 to 2011, found that every 1% increase in economic development was associated with about a 0.1% reduction in CO₂ emissions. Furthermore, some scholars support the existence of a U-shaped relationship between economic development and CO₂ emissions, that is, the EKC hypothesis is valid [33]. With respect to urbanization, the existing literature has mostly shown its impact on CO₂ emissions is uncertain. Several scholars hold the positive view that accelerated urbanization leads to increased CO₂ emissions [34]. Conversely, some studies exhibit an overall decreasing trend of CO₂ emissions with urbanization in recent years [35]. Furthermore, Other scholars have argued that the nexus is non-linear between urbanization and CO₂ emissions. For instance, Zhang et al. [36] confirmed the existence of an inverted U-shaped link between urbanization and CO₂ emissions by examining data for 141 countries, covering the period 1961–2011. With respect to foreign direct investment (FDI), two opposing views exist on how FDI affects CO₂ emissions. One is the pollution shelter hypothesis, indicating that the introduction of FDI leads to a regional CO₂ emissions increase [37]. Another is the pollution halo hypothesis, which presents that FDI brings clean technology and improves environmental standards. For instance, Zhou et al. [5] adopted the SYS-GMM method to study the data for China during 1995–2009, and verified that FDI can contribute to reducing CO₂ emissions. A similar conclusion is obtained by Adams [38]. With respect to industrial structure, many studies emphasize the importance of industrial structure for CO₂ emissions reduction and believe that the upgrading of industrial structure can help to improve environmental performance by enhancing energy efficiency [39]. However, there are still a few scholars who believe that their relationship is significantly nonlinear. To be specific, by using data from 30 Chinese provinces and a panel smoothed transition regression model for the period 2003–2015, Chen et al. [40] confirmed the existence of an inverted U-shaped relationship. The second group emphasizes the influence of non-economic factors on CO₂ emissions, including institutional quality, population factors, carbon emissions trading, and carbon tax. With respect to institutional quality, the existing literature focuses on corruption and how it affects CO₂ emissions. For instance, Liu et al. [41] found that corruption can promote CO₂ emissions in 33 Asian countries covering the period of 2000–2015, which is also verified by Wang et al. [42] for BRICS countries. However, based on a quantile regression model for China, Ren et al. [43] found that the nexus between corruption and CO₂ emissions is non-linear from 1998 to 2016. As for the population factor, the existing studies usually assumed that the expansion of population size positively affects CO₂ emissions [44]. Yet an increase in human capital will reduce CO₂ emissions. For example, Rahman et al. [45] argued that human capital improved environmental quality in newly industrialized countries from 1979 to 2017. With respect to the carbon trading system, many studies revealed that the carbon trading system can optimize the allocation of CO₂ emissions through market mechanisms, impel investment flows to low-carbon industries, and help enterprises to improve energy efficiency, thus reducing CO₂ emissions. For instance, Nguyen et al. [46] evaluated the economic feasibility and environmental efficiency of carbon trading schemes for Japan. Their outcomes indicated that carbon trading can significantly reduce CO₂ emissions. Likewise, Wang et al. [47] claimed that China’s ETS policy has significantly reduced CO₂ emissions over the period 2001–2017. With respect to the carbon tax, it is generally believed that carbon tax can facilitate CO₂ emissions reductions. For example, based on a numerical simulation analysis for Chile covering the period 2014–2024, Vera and Sauma [6] suggested that a carbon tax can be effective in reducing CO₂ emissions. A similar conclusion is obtained by Ma et al. [48] who state that carbon tax policies are also applicable to China.

The third stream of existing literature concentrates on the connection between FD and CO₂ emissions. After the mechanism of “vote with their feet” proposed by Tiebout [49], the environmental effects of FD have gained popularity worldwide. However, the connection between FD and CO₂ emissions has not been agreed upon. The first view believes in the validity of “racing to the top”, indicating that FD prompts local governments to improve resource allocation efficiency and environmental standards through the nimbyism effect, thus contributing to achieving pollution control and mitigating CO₂ emissions [50,51]. For instance, Hayek [15] argued that instead of the central government, local governments have an information advantage to develop environmental policies that are appropriate for their region, and suggests that FD has a negative impact on CO₂ emissions. He [10] found that an increase in FD significantly increased pollution control expenditures and emission fees in Chinese provinces between 1995 and 2010, which also supports the inhibition theory. By using panel data available for seven OECD countries covering 1990–2018, Khan et al. [16] argued that FD is negatively correlated with CO₂ emissions, implying that transferring authority to local governments could enhance environmental quality. The second view is that FD actively promotes CO₂ emissions and decreases environmental quality. Specifically, some scholars maintain that local governments are more willing to make way for economic development by relaxing local environmental regulations, and there is a “race to the bottom” of the environment, which result in an increase in CO₂ emissions [52]. For example, using panel data for 29 Chinese provinces, Zhang et al. [53] confirm that Chinese-style FD contributed significantly to CO₂ emissions from 1995 to 2012, resulting in a green paradox. Likewise, Iqbal et al. [54] explored the role of FD in curbing CO₂ emissions, using the augmented mean group approach for 37 OECD countries covering the period 1970–2019. Their outcomes indicated that FD accelerates CO₂ emissions. Xu and Li [7] surveyed data from 12 urban agglomerations in China from 1995–2019 and found that Chinese-style FD contributes to CO₂ emissions through channels such as investment bias, factor market distortions, and environmental regulation. The third view argues that a non-linear association exists between FD and CO₂ emissions because externalities of environmental public goods and inter-local government heterogeneity in environmental preferences coexist in decentralized states [55]. For instance, Liu et al. [56] concluded an inverted U-shaped curve between FD and CO₂ emissions in China during 2000–2012. Cheng et al. [57] also supported the argument by using dynamic panel regressions to analyze data for 29 provinces in China from 1997–2015. Similarly, Du and Sun [58] employed the panel smoothed transition regression model for 285 cities in China between 2003 and 2018, and concluded that the direction of the effect of FD on CO₂ emissions depends on technological progress.

According to the above literature review, we find that previous studies about the effects of FD on CO₂ emissions are relatively abundant (as can be seen in

Table 1. Summary diagram of the literature review.

Themes	Results		Authors
The link between fiscal decentralization and economic development	Positive relationship		Chu and Zheng [3]; Iimi [19]
	Non-linear relationship		Yang [4]; Thießen [28]
	Negative relationship		Davoodi and Zou [24]; Baskaran and Feld [26]
The factors influencing CO2 emissions	Economic factors	Positive relationship	Ma ei al. [31]; Hao et al. [37],
		Non-linear relationship	Heidari et al. [33]; Zhang et al. [36]; Chen et al. [40]
		Negative relationship	Asumadu-Sarkodie and Owusu [32]; Li et al. [39]
	Non-economic factors	Positive relationship	Liu et al. [41]; Wang et al. [42]
		Non-linear relationship	Ren et al. [43]
		Negative relationship	Rahman et al. [45]; Wang et al. [47]
The nexus between fiscal decentralization and CO2 emissions	Positive relationship		Zhang et al. [53]; Iqbal et al. [54]
	Non-linear relationship		Liu et al. [56]; Du and Sun [58]
	Negative relationship		He [10]; Hayek [15]

), but there are still some shortcomings. First, the theoretical nexus between the two has not been elucidated, especially, lacking for mathematical derivation in the analysis. Second, most studies have mainly focused on non-spatial panel models, and even when spatial models are involved, they have never explicitly demonstrated FD’s spatial spillover effects on CO₂ emissions. Finally, because of China’s vast size, the effect of FD on CO₂ emissions may vary in different areas, but the current literature rarely considers regional heterogeneity. Therefore, to fill these shortcomings, this study first constructs a two-sector growth model including households and firms, to investigate the internal link between FD and CO₂ emissions through mathematical derivation. Next, we use a spatial autoregressive (SAR) model and the effect decomposition technique to evaluate the spatial spillover effects of different types of FD on CO₂ emissions in the empirical analysis. Finally, we split the total sample into eastern, central, and western regions according to geographical location to further clarify the inter-regional differences in FD’s spatial spillover effects on CO₂ emissions.

3. Theoretical Model

Following Copeland and Taylor [59], this paper incorporates fiscal decentralization (FD), which is divided into fiscal revenue decentralization (FRD) and fiscal expenditure decentralization (FED), economic development, and CO₂ emissions into a unified analytical framework, and constructs a two-sector general equilibrium model including households and firms, and then explores the nexus between FD and CO₂ emissions.

3.1. Production Function

Assume that the production function of the representative firm can be expressed in Cobb-Douglas form, which exhibits the property of constant return to scale.

$${\mathrm{y}}_{\mathrm{i}}=\mathrm{f}\left({\mathrm{K}}_{\mathrm{i}},{\mathrm{L}}_{\mathrm{i}}\right)={\mathrm{AK}}_{\mathrm{i}}{}^{\mathsf{\alpha }}{\mathrm{L}}_{\mathrm{i}}{}^{1-\mathsf{\alpha }}$$

(1)

where A represents total factor productivity; K_i and L_i are the amounts of capital and labor inputs, respectively; α denotes the capital share of output, 0 < α < 1. When different degrees and types of FD affect the production decisions of firms, the existence of decentralization effects will make the total social production function no longer be the simple sum of the production functions of all individual firms, and thus the transforming effect of decentralization effects on production should be considered. Assuming that the decentralization effect on total social output is G(•), the social production function can be expressed as follows:

$$\mathrm{Y}=\mathrm{G}(•)\cdot {\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{y}}_{\mathrm{i}}=\mathrm{G}(•)\cdot \mathrm{F}\left(\mathrm{K},\mathrm{L}\right)=\mathrm{G}(•)\cdot {\mathrm{AK}}^{\mathsf{\alpha }}{\mathrm{L}}^{1-\mathsf{\alpha }}$$

(2)

where G(•) measures the decentralization effect of FD, K and L are the total social capital and labor, respectively. Suppose that FD affects the total social output through scale effect, technological progress, and crowding effect, and manifests itself in two types of FRD and FED. For simplicity, the social production function is treated in per capita form, and the expression for the per capital unit of potential output is obtained as follows:

$$\mathrm{y}=\frac{\mathrm{Y}}{\mathrm{L}}=\mathrm{G}\left(\mathrm{FRD},\mathrm{FED}\right)\cdot \mathrm{f}\left(\mathrm{k}\right)=\mathrm{G}\left(\mathrm{FRD},\mathrm{FED}\right)\cdot {\mathrm{Ak}}^{\mathsf{\alpha }}$$

(3)

where y is the per capital unit of potential output. It is assumed that the society produces a certain amount of carbon emissions while producing product. There are negative externalities to society as a result of increased carbon emissions, and when property rights are clearly defined, firms must pay a fee for CO₂ emissions, thus increasing production costs. Therefore, some elements of social production will be used for carbon emission governance. Under this assumption, the proportion of factor inputs used for carbon emission reduction in social production process is θ, then x which represent the per capita unit real output can be expressed as follows:

$$\mathrm{x}=\left(1-\mathsf{\theta }\right)\mathrm{y}=\left(1-\mathsf{\theta }\right)\mathrm{G}\left(\mathrm{FRD},\mathrm{FED}\right)\cdot \mathrm{f}\left(\mathrm{k}\right)$$

(4)

Theoretically, when θ = 0, it means that the society does not spend any factors to control carbon emissions, and the total social output equals to potential output. When θ = 1, it indicates that the society devotes all factor resources to control carbon emissions, which is obviously unrealistic. Usually, the value of θ ranges from 0 to 1. If the society devotes θ proportion of its factors to control carbon emissions, then the amount of the society’s carbon emissions e can be described as:

$$\mathrm{e}=\mathsf{\varphi }\left(\mathsf{\theta }\right)\mathrm{y}=\mathsf{\varphi }\left(\mathsf{\theta }\right)\cdot \mathrm{G}\left(\mathrm{FRD},\mathrm{FED}\right)\cdot \mathrm{f}\left(\mathrm{k}\right)$$

(5)

where the carbon emission function ϕ(θ) = A⁻¹ (1 − θ)^1⁄β is the decreasing function of θ, and ϕ′(θ) < 0, ϕ″(θ) > 0, β ∈ [0, 1]. Equation (5) shows that as technology improves and investment in CO₂ treatment increases, carbon emissions will decrease accordingly. By using Equations (4) and (5), the real social output function can be further deduced as:

$$\mathrm{x}=\mathrm{f}\left(\mathrm{k},\mathrm{e}\right)={(\mathrm{Ae})}^{\mathsf{\beta }}\cdot {\left[\mathrm{G}\left(\mathrm{FRD},\mathrm{FED}\right)\cdot \mathrm{f}\left(\mathrm{k}\right)\right]}^{1-\mathsf{\beta }}$$

(6)

where e means CO₂ emissions. Equation (6) shows that the real output of the society is a joint effect of potential output and CO₂ emissions.

3.2. Firms’ Production Decisions

In order to maximize profits, firm’s production process can be divided into two steps. First, given a labor wage and a capital cost, a firm minimizes the production cost of potential output by choosing the optimal ratio of capital to labor as follows:

$${\mathrm{C}}_{\mathrm{y}}\left(\mathsf{\omega },\mathsf{\gamma }\right)=\min \left\{\left(\mathsf{\omega }\mathrm{L}+\mathsf{\gamma }\mathrm{K}\right),\mathrm{G}\left(\mathrm{FRD},\mathrm{FED}\right)\cdot \mathrm{f}\left(\mathrm{k}\right)=1\right\}$$

(7)

where ω and γ represent a labor wage and a capital cost, respectively. To solve the above optimization problem, the first-order conditions (FOCs) are obtained as:

$$\left(\partial \mathrm{Y}/\partial \mathrm{K}\right)/\left(\partial \mathrm{Y}/\partial \mathrm{L}\right)=\mathsf{\omega }/\mathsf{\gamma }$$

(8)

Second, under the conditions of production cost per unit of potential output and carbon dioxide emission cost, the firm chooses the optimal combination of potential output and carbon emissions to minimize the production cost of actual output. That is:

$${\mathrm{C}}_{\mathrm{x}}\left({\mathrm{C}}_{\mathrm{e}},{\mathrm{C}}_{\mathrm{y}}\right)=\min \{\left({\mathrm{C}}_{\mathrm{e}}\mathrm{e}+{\mathrm{C}}_{\mathrm{y}}\mathrm{y}\right),\left(1-\mathsf{\theta }\right)\cdot \mathrm{G}\left(\mathrm{FRD},\mathrm{FED}\right)\cdot \mathrm{f}\left(\mathrm{k}\right)=1\}$$

(9)

where C_y is production cost per unit of potential output; C_e is carbon dioxide emission costs; and C_x is the production cost of actual output. By solving the above optimization problem, the following FOCs can be yielded:

$$\left(1-\mathsf{\beta }\right)\mathrm{e}/\left(\mathsf{\beta }\mathrm{y}\right)={\mathrm{C}}_{\mathrm{y}}/{\mathrm{C}}_{\mathrm{e}}$$

(10)

3.3. Carbon Dioxide Emission Decisions of Enterprises

Suppose that the market price p of real output x is exogenously determined, then firm’s total revenue is px, while the total cost of the firm consists of the potential output production cost C_yy and the carbon emissions cost C_ee. Under perfect competition, the long-run profit of firm’s production is zero, then we conclude:

$$\mathrm{px}={\mathrm{C}}_{\mathrm{y}}\mathrm{y}+{\mathrm{C}}_{\mathrm{e}}\mathrm{e}$$

(11)

Organized by Equations (10) and (11), the carbon emissions of the society in long-term equilibrium are:

$$\mathrm{e}=\mathsf{\beta }\mathrm{px}/{\mathrm{C}}_{\mathrm{e}}=\mathsf{\beta }\mathrm{p}\left(1-\mathsf{\theta }\right)\cdot \mathrm{G}\left(\mathrm{FRD},\mathrm{FED}\right)\cdot \mathrm{f}\left(\mathrm{k}\right)/{\mathrm{C}}_{\mathrm{e}}$$

(12)

3.4. Maximizing Social Welfare

Following Grimaud and Rouge [60], the social welfare function U(x,e) is supposed as follows:

$$\mathrm{U}\left(\mathrm{x},\mathrm{e}\right)={\mathrm{x}}^{1-\mathsf{\epsilon }}/\left(1-\mathsf{\epsilon }\right)-{\mathrm{e}}^{1+\mathsf{\rho }}/\left(1+\mathsf{\rho }\right)$$

(13)

In Equation (13), ε is the relative risk aversion coefficient, ρ reflects the degree of the society’s preference for carbon emissions, and ε > 0, ρ > 0. Suppose that there exists a social rule-maker that maximizes social welfare by choosing between output and carbon emissions. and then the FOCs of utility maximization are as follows:

$$\left(\partial \mathrm{U}/\partial \mathrm{x}\right)\cdot \left(\partial \mathrm{x}/\partial \mathrm{e}\right)={\mathrm{e}}^{\mathsf{\rho }}$$

(14)

According to new institutional economics, when the property rights are clear, the marginal cost of carbon emissions eventually equals to the marginal utility of real output, namely, ∂U/∂x = ∂x/∂e, which can be collapsed by substituting it into Equation (14) to obtain:

$${\mathrm{C}}_{\mathrm{e}}=\frac{\partial \mathrm{x}}{\partial \mathrm{e}}={\mathrm{e}}^{\mathsf{\rho }/2}$$

(15)

Finally, by combing Equation (15) with Equation (12), the amount of society’s carbon emissions in long-run equilibrium can be arranged as follows:

$$\mathrm{e}={\left[\mathrm{A}\mathsf{\beta }\mathsf{\rho }\left(1-\mathsf{\theta }\right)\right]}^{2/\left(\mathsf{\rho }+2\right)}\cdot \mathrm{G}{(\mathrm{FRD},\mathrm{FED})}^{2/\left(\mathsf{\rho }+2\right)}\cdot {\mathrm{k}}^{2\mathsf{\alpha }/\left(\mathsf{\rho }+2\right)}$$

(16)

Let μ = Aβp(1 − θ), π = 2/(ρ + 2), then Equation (16) can be further simplified as:

$$\mathrm{e}={\mathsf{\mu }}^{\mathsf{\pi }}\cdot \mathrm{G}\left(\mathrm{FRD},\mathrm{FED}{)}^{\mathsf{\pi }}\cdot {\mathrm{k}}^{\mathsf{\alpha }\mathsf{\pi }}={\mathsf{\mu }}^{\mathsf{\pi }}\cdot \exp ({\mathsf{\varphi }}_1\mathsf{\pi }\mathrm{FRD},{\mathsf{\varphi }}_2\mathsf{\pi }\cdot \mathrm{FED}\right)\cdot {\mathrm{k}}^{\mathsf{\alpha }\mathsf{\pi }}$$

(17)

After taking the logarithm of both sides of Equation (17), we can obtain:

$$\ln \mathrm{e}=\mathsf{\pi }\cdot \ln {\mathsf{\mu }}^{\mathsf{\pi }}+\left({\mathsf{\varphi }}_1\mathsf{\pi }\cdot \mathrm{FRD},{\mathsf{\varphi }}_2\mathsf{\pi }\cdot \mathrm{FED}\right)+\mathsf{\alpha }\mathsf{\pi }\cdot \ln \mathrm{k}$$

(18)

Equation (18) shows that FD affects carbon emissions mainly through knowledge spillover or resource congestion brought about by the externalities of FRD and FED.

4. Methodology, Variables and Data

4.1. The Specification of Econometric Model

From the above theoretical analysis, the nexus between FD and carbon emissions was preliminarily verified. To further investigate the influence and mechanism of FD on CO₂ emissions, we used a non-spatial panel econometric model, spatial econometric model, and spatial moderating effect model for the empirical test.

4.1.1. Non-Spatial Panel Econometric Model

To confirm the impact of FD on CO₂ emissions, we first used a non-spatial panel econometric model for empirical analysis. The formula is expressed as follows:

$${\mathrm{lnCE}}_{\mathrm{it}}={\mathsf{\alpha }}_0+{\mathsf{\alpha }}_1{\mathrm{FD}}_{\mathrm{it}}+{\mathsf{\alpha }}_2{\mathrm{X}}_{\mathrm{it}}+{\mathsf{\mu }}_{\mathrm{i}}+{\mathsf{\delta }}_{\mathrm{t}}+{\mathsf{\epsilon }}_{\mathrm{it}}$$

(19)

where i and t are province and year; lnCE_it reflects per capita carbon emissions; FD_it denotes fiscal decentralization, which is divided into FRD and FED; X_it stands for the control variables that affect CO₂ emissions, including the level of economic development (PGDP), foreign direct investment (FDI), industrial structure (IS), R&D intensity (RD) and human capital (HC); μ_i and δ_t represent regional and time fixed effect, respectively; ε_it means the random error term.

4.1.2. Spatial Econometric Model

The first law of geography indicates that neighboring regions will have similar characteristics and a wide range of inter-regional linkages, with no city or region being completely isolated [61]. Due to the negative externality of CO₂ emissions, it is reasonable to assume that CO₂ emissions from a certain area is typically related to the surrounding spatial area, and that neglecting the spatial correlation of CO₂ emissions will result in estimation bias. Therefore, according to the results of the LM test, Robust LM test, and Hausman test, this paper finally adopts the spatial autoregressive (SAR) model to verify the spatial spillover effects of FD on CO₂ emissions. The SAR model is expressed as follows:

$${\mathrm{lnCE}}_{\mathrm{it}}={\mathsf{\beta }}_0+{\mathsf{\rho }\mathrm{WlnCE}}_{\mathrm{it}}+{\mathsf{\beta }}_1{\mathrm{FD}}_{\mathrm{it}}+{\mathsf{\beta }}_2{\mathrm{X}}_{\mathrm{it}}+{\mathsf{\mu }}_{\mathrm{i}}+{\mathsf{\delta }}_{\mathrm{t}}+{\mathsf{\epsilon }}_{\mathrm{it}}$$

(20)

where ρ denotes the spatial autocorrelation coefficient; W is the spatial weight matrix; the definitions of other parameters and variables are the same as those in Equation (19). Following Chai et al. [62], the spatial weight matrix is defined as the spatial adjacent weight matrix (W1) in baseline regression analysis. When two regions are not adjacent at all, the value of the corresponding spatial weight is 0, otherwise, it is 1. Furthermore, the study uses the economic geographic distance weight matrix (W2) proposed by Bai et al. [63] for the robustness test. Each spatial weight matrix is normalized so that the sum of elements in each row of the weight matrix equals to 1.

Although many scholars currently choose to test the existence of spatial spillover effects using point estimates from spatial econometric models, LeSage and Pace [64] proposed that point estimates do not respond well to spatial spillover effects. Therefore, the direct and indirect effects of FD on CO₂ emissions in this study should be obtained after considering all loop feedback effects. The partial derivative matrix of CO₂ emissions with respect to FD in spatial unit 1 up to N is specified as follows:

$$\left[\frac{\partial \ln \mathrm{CE}}{\partial {\mathrm{FD}}_1},\cdots ,\frac{\partial \ln \mathrm{CE}}{\partial {\mathrm{FD}}_{\mathrm{N}}}\right]=\left[\begin{array}{ccc}\frac{\partial \ln {\mathrm{CE}}_1}{\partial {\mathrm{FD}}_1}& \cdots & \frac{\partial \ln {\mathrm{CE}}_1}{\partial {\mathrm{FD}}_{\mathrm{N}}}\\ \cdots & \cdots & \cdots \\ \frac{\partial \ln {\mathrm{CE}}_{\mathrm{N}}}{\partial {\mathrm{FD}}_1}& \cdots & \frac{\partial \ln {\mathrm{CE}}_{\mathrm{N}}}{\partial {\mathrm{FD}}_{\mathrm{N}}}\end{array}\right]={({\mathrm{I}}_{\mathrm{N}}-\mathsf{\rho }\mathrm{W})}^{-1}\left({\mathsf{\beta }}_1{\mathrm{I}}_{\mathrm{N}}\right)$$

(21)

where N is the total number of provinces, herein, N = 30. Consistent with LeSage and Pace [64], the direct effect of FD on CO₂ emissions can be measured by the average of the diagonal elements of the matrix on the left side of Equation (21), while its indirect effect (or spatial spillover effect) is calculated as the average of the row sums or column sums of the non-diagonal elements of the matrix.

4.1.3. Spatial Moderating Effect Model

To examine the transmission channels of FD on CO₂ emissions, we incorporated the interaction term of FD and R&D intensity (RD), as well as that of FD and foreign direct investment (FDI) into Equation (20) for empirical analysis, then the spatial moderating model is defined as follows:

$${\mathrm{lnCE}}_{\mathrm{it}}={\mathsf{\gamma }}_0+\mathsf{\rho }\mathrm{W}\ln {\mathrm{CE}}_{\mathrm{it}}+{\mathsf{\gamma }}_1{\mathrm{FD}}_{\mathrm{it}}+{\mathsf{\gamma }}_2{\mathrm{Z}}_{\mathrm{it}}+{\mathsf{\gamma }}_3\left({\mathrm{FD}}_{\mathrm{it}}\times {\mathrm{Z}}_{\mathrm{it}}\right)+{\mathsf{\gamma }}_4{\mathrm{X}}_{\mathrm{it}}+{\mathsf{\mu }}_{\mathrm{i}}+{\mathsf{\delta }}_{\mathrm{t}}+{\mathsf{\epsilon }}_{\mathrm{it}}$$

(22)

where Z_it represents the moderating variables, including RD and FDI; γ₃ denotes the parameter of the moderating effect.

4.2. Descriptions of Variables

4.2.1. Dependent Variable

In this paper, the dependent variable is the per capita carbon emissions at province level (CE). Since China has not issued official data on CO₂ emissions, referring to Du et al. [1], we selected seven energy sources including coal, coke, gasoline, kerosene, diesel, fuel oil, and natural gas, as well as cement production, and then converted them into standard coal units before multiplying them by the corresponding CO₂ emissions factors issued by the IPCC and summing them up, finally obtaining the total CO₂ emissions for each province. The following formula summarizes the calculation process:

$${\mathrm{CE}}_{\mathrm{i}}={\displaystyle \sum }_{\mathrm{j}=1}^7{\mathrm{EC}}_{\mathrm{i},\mathrm{j}}\times {\mathrm{NCV}}_{\mathrm{j}}\times {\mathrm{CEF}}_{\mathrm{j}}\times {\mathrm{COF}}_{\mathrm{j}}\times \frac{44}{12}+{\mathrm{Q}}_{\mathrm{i}}\times \mathrm{EF}$$

(23)

where CE_i denotes the total carbon emissions in province i; EC_i,j is the total consumption of the j-th energy in province i; NCV_j is the average low calorific value of energy j; CEF_j is the carbon emission factor of energy j; COF_j denotes the carbon oxidization rate of energy j; 44/12 is the molecular weight of carbon dioxide; Q_i denotes the output of cement production in province i; and EF represents the carbon dioxide emission coefficient during cement production.

4.2.2. Core Independent Variables

The existing research about FD is mainly focused on FRD or FED, and neglects the reality of “shifting financial power upward and decentralizing affairs” in China. Therefore, we investigated the effect of FD on CO₂ emissions from the perspectives of FRD and FED.

• Fiscal revenue decentralization (FRD). Referring to Jiménez-Rubio et al. [65], FRD is calculated as the ratio of per capita local government budget revenue to central government budget revenue. Higher FRD is associated with a higher share of tax revenue owned by the local government in the region.
• Fiscal expenditure decentralization (FED). Following Xia et al. [66], we used the ratio of per capita local government budget expenditure to central government budget expenditure to measure FED. A higher FED shows that more discretion is given to local governments in the allocation of public spending in their regions.

4.2.3. Moderating Variables

In order to clarify the influence mechanisms of FD on CO₂ emissions, we also incorporated R&D intensity and foreign direct investment as moderating variables.

• R&D intensity (RD). Theoretically, the increase in R&D investment can promote low-carbon technology progress and thus effectively reduce CO₂ emissions. Therefore, we adopt the ratio of R&D investment to GDP to reflect R&D intensity.
• Foreign direct investment (FDI). Previous studies have demonstrated that FDI can promote enterprises’ technological innovation through the effects of demonstration, competition, and input flow, which in turn improve resource allocation efficiency and thus promote CO₂ emissions reduction. Therefore, FDI is presented by the actual per capita FDI in each province.

4.2.4. Control Variables

To avoid the problems of estimation errors and omitted variables, based on the prior literature, this paper selected three control variables: the level of economic development (PGDP), industrial structure (IS), and human capital (HC). Specifically, PGDP is calculated using each province’s per capita GDP [67]. Industrial structure is calculated as the ratio of tertiary industry output to secondary industry output in each province [68]. Human capital is measured by the average years of education in each province [13].

4.3. Data Sources

Considering the availability of data and the actual needs of the research, we selected a balanced panel data for 30 Chinese provinces (excluding Tibet, Hong Kong, Macao, and Taiwan) from 2003 to 2019. The original data of CE was obtained from the China Energy Statistical Yearbook, and other indicators were obtained from the China Statistical Yearbook, China Industrial Economic Statistical Yearbook and relevant China Statistical Yearbook of Provinces. Some missing data in the yearbook was supplemented by the trend interpolation method. All monetary value data were deflated at constant prices in 2003 to remove the price effect. In order to eliminate the heteroscedasticity, we take the natural logarithm for some absolute variables including CO₂ emissions, FDI, and PGDP. Descriptive statistics for all variables are shown in

Table 2. Descriptive statistics of all variables.

Variable	Definition	Obs	Mean	Std. Dev	Min	Max	VIF
lnCE	Per capita carbon emissions	510	1.6681	0.5493	0.2660	3.3606	-
FRD	Fiscal revenue decentralization	510	1.1666	1.0068	0.3427	5.9256	3.38
FED	Fiscal expenditure decentralization	510	5.5143	2.9886	1.2910	14.8297	2.61
RD	R&D intensity	510	0.0148	0.0107	0.0017	0.0630	3.59
lnFDI	Foreign direct investment	510	5.9239	1.3907	1.0821	8.8097	2.25
lnPGDP	Economic development level	510	10.0412	0.6378	8.2141	11.6462	4.37
IS	Industrial structure	510	1.1572	0.6254	0.5271	5.2340	2.13
HC	Human capital	510	8.7721	1.0628	6.0405	13.2268	4.69

. Meanwhile, we found that the VIF values of all explanatory variables are smaller than 10, implying that there is no multicollinearity among variables.

5. Empirical Results and Analysis

5.1. Panel Unit Root Test and Cointegration Test

In order to overcome the problem of spurious regression, the stationarity of all variables was checked by performing unit root tests before model estimation. Specifically, given that using a single method is easy to lead to test bias, in this paper, three unit root tests comprising LLC, Fisher-ADF, and Fisher-PP tests are simultaneously used, The test results are illustrated in

Table 3. Results of unit root test for all variables.

Variable	Level			1st Difference
	LLC	ADF-Fisher	PP-Fisher	LLC	ADF-Fisher	PP-Fisher
lnCE	−9.5462 ***	152.89 ***	345.83 ***	−8.5433 ***	126.56 ***	126.94 ***
FRD	−4.2603 ***	53.282	35.511	−10.870 ***	194.46 ***	274.19 ***
FED	−6.2180 ***	48.430	50.371	−8.3063 ***	140.13 ***	197.76 ***
lnFDI	−3.4316 ***	92.041 ***	183.45 ***	−9.9681 ***	221.99 ***	356.77 ***
lnPGDP	−15.293 ***	154.85 ***	613.61 ***	−8.0416 ***	123.11 ***	121.51 ***
IS	−4.3829 ***	42.635	81.109 **	−6.7391 ***	137.27 ***	193.61 ***
HC	−1.3111 *	76.067 *	116.65 ***	−13.125 ***	234.95 ***	524.65 ***
RD	−0.2391	41.845	78.012 *	−9.2310 ***	193.60 ***	286.84 ***

Note: *, ** and *** indicate 10%, 5%, and 1% of significance levels, respectively.

.

Table 3 shows that all the variables passed more than one unit root test at levels, and they are stationary at the first difference. Since the variables have the same order differential stationarity, so the cointegration test can be employed to test the long-run equilibrium relationship among CO₂ emissions and its determinants, and the results of the cointegration test are reported in

Table 4. Results of cointegration test.

Test Method		FRD as the Core Independent Variable		FED as the Core Independent Variable
Pedroni test	common (within-dimension)	Weighted-statistic	Prob	Weighted-statistic	Prob
	Panel v-Statistic	−1.7881	0.9631	−3.3361	0.9996
	Panel rho-Statistic	6.4063	1.0000	6.7316	1.0000
	Panel PP-Statistic	−10.9000	0.0000	−9.9820	0.0000
	Panel ADF-Statistic	−2.5589	0.0053	−3.5392	0.0002
	individual (between-dimension)	Statistic	Prob	Statistic	Prob
	Group rho-Statistic	7.9555	1.0000	8.0436	1.0000
	Group PP-Statistic	−20.8197	0.0000	−18.8094	0.0000
	Group ADF-Statistic	−2.1451	0.0160	−2.4549	0.0070
Kao test		T-statistic	p value	T-statistic	p value
	ADF	−2.6868	0.0036	−3.2116	0.0007
	Residuals	0.0036	-	0.0036	-
	HAC variance	0.0049	-	0.0049	-

.

As can be seen in Table 4, the Panel v-Statistic, rho-Statistic, and Group rho-Statistic are insignificant. In contrast, the Panel (Group) PP-Statistic and Panel (Group) ADF-Statistic are statistically significant, and which is quite similar to the Kao test, indicating that strong statistical evidence supports a panel cointegration relationship between CO₂ emissions and its determinants. Örsal [69] point out that the influence of Panel ADF-Statistic is the most decisive in the Pedroni test. Therefore, the Panel ADF-Statistic reveals that all the variables are stationary, and can be used in model regressions.

5.2. Empirical Results and Analysis of Non-Spatial Panel Economic Model

To investigate the relationship between FD and CO₂ emission, we firstly conducted a regression analysis of Equation (19) using random effects (FE), fixed effects (RE), and feasible generalized least squares (FGLS). The regression results are shown in

Table 5. Full-sample regression results.

Variables	RE		FE		FGLS		DIFF-GMM		SYS-GMM
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
FRD	0.1508 ***		0.2846 ***		0.1619 ***		0.1059 ***		0.1621 ***
	(0.0310)		(0.0322)		(0.0316)		(0.0381)		(0.0515)
FED		0.0630 ***		0.0560 ***		0.0622 ***		0.0264 ***		0.0463 ***
		(0.0065)		(0.0075)		(0.0064)		(0.0102)		(0.0059)
RD	−13.545 ***	−13.328 ***	−23.277 ***	−18.518 ***	−13.056 ***	−13.211 ***	−23.437 ***	−28.352 ***	−5.2582 *	−6.2004 ***
	(2.3042)	(2.1527)	(2.3281)	(2.3470)	(2.2506)	(2.1134)	(4.0203)	(4.2825)	(2.8415)	(1.6605)
lnFDI	−0.0395 ***	−0.0169	−0.0365 ***	−0.0097	−0.0371 ***	−0.0158	−0.0141 *	−0.0184 **	−0.0652 ***	−0.0209 **
	(0.0116)	(0.0109)	(0.0109)	(0.0113)	(0.0112)	(0.0106)	(0.0084)	(0.0082)	(0.0131)	(0.0106)
lnPGDP	0.7377 ***	0.5975 ***	0.1220	0.2483 ***	0.7405 ***	0.6069 ***	0.0124	0.0793	0.0981	0.1397 ***
	(0.0304)	(0.0323)	(0.0756)	(0.0745)	(0.0296)	(0.0315)	(0.0911)	(0.0822)	(0.0684)	(0.0454)
IS	−0.2841 ***	−0.2812 ***	−0.3200 ***	−0.3566 ***	−0.2780 ***	−0.2767 ***	−0.2102 ***	−0.3182 ***	−0.4692 ***	−0.4342 ***
	(0.0284)	(0.0262)	(0.0346)	(0.0351)	(0.0278)	(0.0255)	(0.0492)	(0.0381)	(0.0526)	(0.0444)
HC	−0.0366	−0.0645 ***	−0.0822 ***	−0.1817 **	−0.0454 *	−0.0725 ***	−0.0446	−0.0719 ***	−0.0406	−0.0036
	(0.0255)	(0.0241)	(0.0311)	(0.0496)	(0.0248)	(0.0235)	(0.0380)	(0.0268)	(0.0337)	(0.0363)
L.lnCE							0.4455 ***	0.3708 ***	0.3876 ***	0.4035 ***
							(0.0753)	(0.0404)	(0.0395)	(0.0341)
R2	0.3217	0.4081	0.2873	0.2914	0.4257	0.4702
Hausman	25.35 ***	21.82 ***
AR (1)							0.0017	0.0107	0.0378	0.0146
AR (2)							0.8040	0.9666	0.8211	0.6389
Hansen							0.2676	0.4140	0.3632	0.4657
Obs	510	510	510	510	510	510	480	480	480	480

Note: *, ** and *** indicate 10%, 5%, and 1% of significance levels, respectively. The values in parentheses are the standard error of the coefficients.

, indicating that the FE model is better than the RE model according to the Hausman test. By comparing the results of FE and FGLS regressions, we found that the coefficients of the relevant variables had the same sign, but the regression results of FGLS were more significant than the fixed effects. According to Xu et al. [70], since the FGLS estimation method eliminates the effects of within-group autocorrelation, between-group heteroskedasticity, and contemporaneous correlation, its regression results are more reliable. However, the FGLS model does not consider the endogeneity problem, while the GMM is concerned with the persistence of the dependent variable, the omitted variable problem, measurement error, and endogeneity. When the number of cross sections is greater than the number of periods (namely N > T), GMM is valid. Therefore, we also use SYS-GMM and DIFF-GMM methods to test Equation (19), and the estimation results are presented in Table 5. the first-order lag coefficient of lnCE in Table 5 is significantly positive at the 1% level, indicating that carbon emissions are dynamically accumulative, and the AR (2) statistic in Table 5 indicates that the null hypothesis of no second-order autocorrelation should be accepted, satisfying the GMM estimation requirements. In addition, the Hansen statistic cannot decline the null hypothesis of over-identification through the overall validity of the instrument, which implies that the instrumental variables are valid. Therefore, the GMM estimation results are reasonable.

The significantly positive coefficients for FRD and FED in Table 5 imply that an increase in decentralization will significantly contribute to CO₂ emissions. Concerning FRD, the Chinese tax system creates distorted fiscal incentives for local officials. When available resources increase, they focus on economic development and local tax to seek for promotion advantages. In the short term, the local governments and energy-consuming firms are more likely to collude to circumvent environmental regulations, ultimately increasing CO₂ emissions. As for FED, facing a severe fiscal gap and pressure to promote economic development, local governments might then invest limited resources in more economically productive firms or infrastructure, rather than in environmental governance. RD, lnFDI, IS, and HC all significantly inhibit CO₂ emissions in general, and only the coefficient of lnPGDP is significantly positive, probably because economic development in China is still in a transition towards high-quality growth. However, because of the arbitrary drift and diffusion of CO₂, the impact of FD on CO₂ emissions will generally be biased if the spatial spillover effects were ignored. Therefore, it would be beneficial for us to use a spatial panel model in the next study.

5.3. Spatial Econometric Regression Results and Analysis

5.3.1. Spatial Correlation Test

Before performing spatial regression, we first conducted a test of spatial correlation to investigate whether the spatial dependence of CO₂ emissions exists. At present, various methods have been proposed to examine spatial correlation, including “Moran’s I”, “Geary GC”, and “Getis-Ord”. Following Huang et al. [71], in this paper, the global Moran’s I index is chosen to check the spatial correlation of provincial CO₂ emissions in China, which range from −1 to 1. The global Moran’s I statistic can be constructed as follows:

$$\mathrm{Global}\mathrm{Moran}’\mathrm{s}\mathrm{I}=\frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{W}}_{\mathrm{ij}}\left({\mathrm{CE}}_{\mathrm{i}}-\overline{\mathrm{CE}}\right)\left({\mathrm{CE}}_{\mathrm{j}}-\overline{\mathrm{CE}}\right)}{{\mathrm{S}}^2{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{W}}_{\mathrm{ij}}}$$

(24)

where ${\mathrm{S}}^2=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{CE}}_{\mathrm{i}}-\overline{\mathrm{CE}}\right)}^2/\mathrm{n}$; $\overline{\mathrm{CE}}=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{CE}}_{\mathrm{i}}/\mathrm{n}$; CE_i and CE_j represent the value of carbon emissions in province i and j, respectively; n denotes the number of provinces, herein n = 30; and W_ij is the i,j-th element of the spatial weight matrix. The first-order adjacent spatial weight matrix (W1) in the study is used for empirical analysis. The results of the Moran’s I test for regional carbon emissions in China are showed in

Table 6. Results of spatial correlation test based on W1.

Year	Moran’s I	Z-Stat Value	p-Value	Year	Moran’s I	Z-Stat Value	p-Value
2003	0.327 ***	2.945	0.002	2012	0.414 ***	3.699	0.000
2004	0.375 ***	3.324	0.000	2013	0.400 ***	3.573	0.000
2005	0.383 ***	3.380	0.000	2014	0.410 ***	3.656	0.000
2006	0.382 ***	3.376	0.000	2015	0.385 ***	3.457	0.000
2007	0.394 ***	3.481	0.000	2016	0.359 ***	3.231	0.001
2008	0.410 ***	3.631	0.000	2017	0.334 ***	3.047	0.001
2009	0.395 ***	3.518	0.000	2018	0.238 **	3.034	0.001
2010	0.422 ***	3.745	0.000	2019	0.332 ***	3.047	0.001
2011	0.413 ***	3.703	0.000

Note: ** and *** indicate 5%, and 1% of significance levels, respectively.

.

The global Moran’s I value in Table 6 is significantly positive during the period 2003–2019, and the specific geospatial distribution characteristics of CO₂ emissions are detailed in Figure 2. Therefore, it can be concluded that CO₂ emissions has a strong spatial dependence, that is, CO₂ emissions is influenced not only by the local factors but also by the factors from neighboring provinces. Thus, it is necessary to pay close attention to the spatial effects of CO₂ emissions.

5.3.2. Empirical Results and Analysis of Spatial Econometric Models

For the accuracy of the estimation, we focused on the SAR model results in this section. Meanwhile, to study the marginal effect of FD on CO₂ emissions and explore the impact of independent variables on CO₂ emissions in local and neighboring provinces, we decomposed the spatial effects with reference to Equation (21). The results are presented in

Table 7. Empirical results of SAR model with effect decomposition.

Variables	Coefficient	Direct	Indirect	Total	Coefficient	Direct	Indirect	Total
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
FRD	0.2908 ***	0.2944 ***	0.0784 ***	0.3728 ***
	(9.2768)	(9.5402)	(3.4622)	(8.2187)
FED					0.0546 ***	0.0551 ***	0.0109 ***	0.0659 ***
					(7.3481)	(7.0258)	(2.9854)	(6.6647)
RD	−20.028 ***	−20.350 ***	−5.3663 ***	−25.717 ***	−16.029 ***	−16.059 ***	−3.1413 ***	−19.200 ***
	(−8.5185)	(−8.7219)	(−3.8305)	(−8.7803)	(−6.7116)	(−6.9063)	(−3.1840)	(−7.0177)
lnFDI	−0.0378 ***	−0.0385 ***	−0.0103 **	−0.0488 ***	−0.0111	−0.0113	−0.0023	−0.0136
	(−3.5512)	(−3.5652)	(−2.4339)	(−3.4205)	(−0.9919)	(−0.9989)	(−0.9171)	(−0.9958)
lnPGDP	0.1500 **	0.1541 **	0.0409 *	0.1950 **	0.2726 ***	0.2767 ***	0.0549 **	0.3315 ***
	(2.0361)	(2.1054)	(1.8032)	(2.0898)	(3.7213)	(3.7396)	(2.3354)	(3.6246)
IS	−0.2754 ***	−0.2791 ***	−0.0739 ***	−0.3530 ***	−0.3237 ***	−0.3258 ***	−0.0639 ***	−0.3897 ***
	(−8.0595)	(−7.8663)	(−3.5752)	(−7.5772)	(−9.2308)	(−9.3339)	(−3.2765)	(−9.2026)
HC	−0.0896 ***	−0.0881 ***	−0.0236 **	−0.1116 ***	−0.0698 **	−0.0707 **	−0.0142 *	−0.0849 **
	(−2.9559)	(−2.8095)	(−2.1530)	(−2.7436)	(−2.2442)	(−2.3036)	(−1.7720)	(−2.2645)
ρ	0.2198 ***				0.1678 ***
	(4.7738)				(3.5792)
Log-Lik	404.47				389.96
Adj-R2	0.5371				0.5143
Obs	510				510

Note: *, ** and *** indicate 10%, 5%, and 1% of significance levels, respectively. The t-values of the coefficients are reported in parentheses.

.

In Table 7, columns (1) and (5) exhibit the effects of the independent variables on CO₂ emissions from FRD and FED perspectives, respectively. Statistical significance of ρ suggests that the spatial spillovers of CO₂ emissions exist. With respect to FRD, the coefficient of FRD is positive and significant, indicating that the increase in FRD promotes CO₂ emissions, the result is the same as the findings of Iqbal et al. [54] in OECD countries. It could be attributed to two reasons: the barriers of market segmentation and rent-seeking from corruption. To stabilize the tax base and protect large taxpayers, local governments often erect various trade barriers.

Such practice prevents enterprises from reaching the optimal size and leads to a lack of effective competition in the market, thus increasing CO₂ emissions. In terms of FRD, the discretionary power of local governments can easily lead to collusion between government and enterprise, which in turn breeds corruption and rent-seeking. When they focus investments on developing short-run projects, limited labor, capital, and other production factors fail to flow smoothly to emerging enterprises, thus inhibiting the free flow of innovative resources between regions, and leading to increased CO₂ emissions. Similarly, FED showed a significantly positive effect on CO₂ emissions, indicating that CO₂ emissions increases with FED, the result is consistent with Xu and Li [7]. For one thing, local governments usually invest their finite resources in productive enterprises and infrastructure under enormous fiscal spending pressure, but not in service-oriented fields such as science, education, culture, and health, and even less in green innovation. Ultimately, the supply of technologies such as clean production and pollution control is insufficient, which aggravate CO₂ emissions. For another thing, to promote economic development and achieve political promotion, local officials usually disregard the comparative advantages of the region and compete to develop key industries supported by higher-level governments. Unreasonable investment causes serious homogenization of industrial structure in each region and insufficient division of labor among regions, leading to duplicate construction and overcapacity, etc., which brings about serious CO₂ emissions. The coefficients for other variables are generally the same as in Table 5.

However, the point estimates of the SAR model cannot fully reflect the true relationship between the variables. Therefore, spatial effect decomposition is carried out in this paper, and columns (2)–(4) and columns (6)–(8) represent the results of effect decomposition from FRD and FED perspectives, respectively. The direct effect refers to how changes in independent variables in the province influence CO₂ emissions. The indirect effect, i.e., the spatial spillover effect, means the changes in CO₂ emissions of neighboring provinces caused by the changes in independent variable of this province. The total effect is the sum of the direct and indirect effects. In Table 7, FRD has significant positive spatial spillover effects on CO₂ emissions, showing that the increase in FRD results in a concomitant growth in CO₂ emissions from neighboring provinces. To increase tax revenue and attract foreign investment, local governments usually loosen environmental regulations. As a result, enterprises are willing to adopt low-cost and low-level emission reduction technologies for production, thus increasing CO₂ emissions, which in turn conduct spillover effects and will keep spreading to neighboring provinces. At the same time, to maintain a competitive advantage, adjacent provinces have a “race to the bottom” in terms of environmental protection, which eventually contributes to promote CO₂ emissions from neighboring provinces. Similarly, the spatial spillover effect of FED on CO₂ emissions is also significantly positive, it means that higher FED leads to higher CO₂ emissions in neighboring provinces. The large gap in fiscal expenditures will force the local governments to spend limited resources on intensive economic development and infrastructure construction to maximize benefits, which greatly reduces environmental governance investments, thus preventing low-carbon technology development. Meanwhile, emission reduction efforts have positive externalities, and the local governments are reluctant to be “free-riding”, which ultimately leads FED to exacerbate CO₂ emissions in neighboring provinces. The result is consistent with the conclusion drawn by Xia et al. [66]. As for the control variables, whether from FRD perspective or FED perspective, there are significant and negative spatial spillover effects for RD, FDI, HC, and IS, implying that under the condition of upgrading technology, accelerating industrial structure upgrading, attracting high-quality foreign investment, or bringing in high-end talent, CO₂ emissions in neighboring provinces can be reduced. Furthermore, the positive spatial spillover effect of PGDP on CO₂ emissions suggests that the higher level of economic development in the province, the higher it increases the CO₂ emissions in neighboring provinces.

5.3.3. Spatial Heterogeneity of Spillover Effects

Because of the variations in economic and social environments in different regions in China, we split the sample into eastern, central, and western regions to further explore the regional differences in the spatial spillover effects of FD on CO₂ emissions. The spatial heterogeneity in the indirect effects of independent variables is shown in

Table 8. Regional heterogeneity results of the spatial spillover effect.

Variables	The Spatial Spillover Effect Based on FRD Perspective			The Spatial Spillover Effect Based on FED Perspective
	Eastern	Central	Western	Eastern	Central	Western
FRD	0.0338 **	0.0024	0.0752
	(2.0274)	(0.1190)	(1.1831)
FED				0.0053	−0.0005	0.0139 **
				(1.4771)	(−0.1024)	(2.0571)
RD	−2.1688 *	0.3333	−2.8664	−1.5609 *	0.2509	−6.0738 *
	(−1.9032)	(0.3737)	(−1.1562)	(−1.6868)	(0.2822)	(−1.9484)
lnFDI	−0.0141 *	−0.0005	0.0007	−0.0086	−0.0007	0.0118
	(−1.9120)	(−0.1492)	(0.3801)	(−1.4228)	(−0.1965)	(1.5701)
lnPGDP	0.1656 **	−0.0797 *	−0.0820	0.1885 **	−0.0755 *	−0.1714 **
	(2.1642)	(1.6229)	(1.2066)	(2.0703)	(1.6372)	(−2.3810)
IS	−0.0282 **	−0.0219	−0.0259	−0.0342 *	−0.0221	−0.1022 **
	(2.0557)	(−1.2883)	(−1.0299)	(−1.9639)	(−1.2921)	(−2.0380)
HC	−0.0407 **	−0.0089	−0.0170	−0.0323 *	−0.0090	−0.0524 *
	(−2.0705)	(−0.9834)	(−1.0805)	(−1.8573)	(−1.0718)	(−1.7978)

Note: * and ** indicate 10% and 5% of significance levels, respectively. The t-values of the coefficients are in parentheses. This paper divide China’s provinces and regions according to China’s National Development and Reform Commission by their economic development levels.

.

From FRD perspective, the spatial spillover effect of FRD on CO₂ emissions in Table 8 is positive in different regions, while the degree of influence is different. In the east, it is significant, while it is not significant in the central and western regions. It can be attributed to the different incentives formed by the level of economic development in each region and the variations in resource endowment caused by the ecological environment conditions. In the east, higher levels of financial resources and economic development and higher competitive pressures on local governments have led local environmental authorities to continuously loosen environmental controls in exchange for economic growth, which caused the most significant spatial spillover effects. The central and western are lagging in terms of economic development, and local governments do not have enough tax revenue. Meanwhile, because the ecological environment in the central and western regions is more fragile, the central government will transfer more funds to them and pay more attention to their environmental problems, and give them enough incentives for environmental protection. Therefore, the behavior of sacrificing the environment for economic growth in the central and western regions is largely curbed, which makes the spatial spillover effect smaller and insignificant.

From FED perspective, the spatial spillover effect of FED on CO₂ emissions is positive in the east and west, but negative in the central region, and only significant in the west. In the east, local governments spend more fiscal expenditures on economic development but neglect environmental protection. but they have more FDI and developed clean technology, which makes the spatial spillover effect positive but insignificant. In the center, the local governments face severe spending gaps and insufficient transfer payments, but have abundant energy resources. The environment is sacrificed not only in terms of the failure to boost the economy significantly but also through the generation of excessive CO₂ emissions. Meanwhile, the central government is trying to incorporate environmental quality into the promotion system, to prevent demotion, and local officials are more inclined to protect the environment, thus making the spatial spillover effect negative but insignificant. As for the western region, local governments are most influenced by the incentive to develop the economy, but their energy and financial resources are limited, so they are willing to allocate financial resources to infrastructure and economic development. Meanwhile, since the central government will make transfer payments for its ecological protection, local governments in the western region will further occupy the expenditure on environmental protection to improve economic efficiency. Adjacent provinces make the same decision, which eventually results in a substantial increase in CO₂ emissions throughout the West.

5.3.4. Robustness Tests

To further ensure the credibility of the above conclusions, we used three methods to verify the robustness of the spatial spillover effect of FD on CO₂ emissions.

• Replacing the independent variables (Method 1). The denominator of the FD constructed in this paper is a deterministic value, which makes FD as a relative indicator. To ensure the accuracy of the FD index, following Chen et al. [72], we reconstructed the FD, and then estimated the Equation (20). The new FD indicator is as follows:

$$\mathrm{FRD}\left(\mathrm{FED}\right)=\frac{\mathrm{local}\mathrm{fiscal}\mathrm{revenue}\left(\mathrm{expenditure}\right)\mathrm{per}\mathrm{capita}}{\mathrm{local}\mathrm{fiscal}\mathrm{revenue}\left(\mathrm{expenditure}\right)\mathrm{per}\mathrm{capita}+\mathrm{central}\mathrm{fiscal}\mathrm{revenue}\left(\mathrm{expenditure}\right)\mathrm{per}\mathrm{capita}}$$

(25)

• Adjusting the sample interval (Method 2). Usually, the results will vary for different sample period. To verify the robustness of empirical results, we simply considered the sample data from 2005 to 2017 to see whether the estimation results will change.
• Replacing the spatial weight matrix (Method 3). The weight matrix of economic geographical distance (W2) was chosen to replace W1. Because W2 considers both the geographical distance and the variability of economic development among provinces, it may be more appropriate to estimate the SAR model. The regression results of spatial spillover effects for all robustness tests are presented in

  Table 9. Results of robustness test estimation.

  Variables	The Spatial Spillover Effect Based on FRD Perspective			The Spatial Spillover Effect Based on FED Perspective
  	Method 1	Method 2	Method 3	Method 1	Method 2	Method 3
  FRD	0.5230 ***	0.0565 ***	0.0906 ***
  	(3.1298)	(2.7882)	(3.3797)
  FED				0.4519 ***	0.0178 ***	0.0142 ***
  				(2.7374)	(3.3024)	(2.0571)
  RD	−3.4522 ***	−4.2807 ***	−7.1032 ***	−3.5179 ***	−4.6582 ***	−3.9701 ***
  	(−3.3075)	(−2.9052)	(−3.6291)	(−3.0762)	(−3.4939)	(−3.0499)
  lnFDI	−0.0095 **	−0.0079 **	−0.0119 **	−0.0102 **	−0.0038	−0.0012
  	(−2.5360)	(−2.2153)	(−2.2511)	(−2.3860)	(−1.0113)	(−0.3834)
  lnPGDP	−0.0254	0.0239	0.0378	0.0170	0.0718 **	0.0657 **
  	(−1.2209)	(1.3895)	(1.1305)	(0.7056)	(2.4677)	(2.1336)
  IS	−0.0626 ***	−0.0579 ***	−0.0698 ***	−0.0676 ***	−0.0932 ***	−0.0590 ***
  	(3.2771)	(−2.8680)	(−3.2745)	(−3.1852)	(−3.7049)	(−2.8375)
  HC	−0.0119	−0.0154 *	−0.0247 *	−0.0058	−0.0181 *	−0.0136
  	(−1.5811)	(−1.8606)	(−1.8474)	(−0.7146)	(−1.7253)	(−1.4687)

  Note: *, ** and *** indicate 10%, 5%, and 1% of significance levels, respectively. The t-values of the coefficients are reported in parentheses.

  .

Similarly, whether replacing the independent variables, adjusting the sample intervals, as well as replacing the spatial weight matrix, both FRD and FED have significant positive spatial spillover effects on CO₂ emissions in Table 9, indicating that the results in baseline SAR estimation are robust and reliable.

5.4. Further Discussion

5.4.1. Moderating Effect Analysis

From the above analysis, we find that the increase in FD not only significantly contributes to CO₂ emissions in the province, but also increases CO₂ emissions in neighboring provinces. According to theoretical analysis, we also discover that there may be two pathways, namely the technological innovation pathway (R&D) and the government resource allocation pathway (FDI), which can effectively mitigate the positive spatial spillover effect of FD on CO₂ emissions. To further confirm the effectiveness of the empirical results, this paper used Equation (22) to analyze the moderating effects of the two pathways from FRD and FED perspectives, respectively. The regression results of moderating effects from RD and FDI are shown in

Table 10. Results of moderating effects of FDI and RD from FRD perspective.

Variables	Technology Innovation Pathway (R&D)				Government Resource Allocation Pathway (FDI)
	Coefficient	Direct	Indirect	Total	Coefficient	Direct	Indirect	Total
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
FRD	0.3912 ***	0.3953 ***	0.1021 ***	0.4975 ***	1.0495 ***	1.0543 ***	0.2037 ***	1.2579 ***
	(9.8660)	(10.026)	(3.4843)	(8.7216)	(8.2407)	(8.3991)	(2.9596)	(7.9612)
RD	−10.255 ***	−10.376 ***	−2.6511 **	−13.027 ***	−15.845 ***	−16.097 ***	−3.0988 ***	−19.196 ***
	(−3.0634)	(−3.1210)	(−2.4860)	(−3.1325)	(−6.6319)	(−6.8211)	(−2.9105)	(−6.7355)
lnFDI	−0.0392 ***	−0.0399 ***	−0.0103 **	−0.0503 ***	0.0363 **	0.0363 **	0.0069 *	0.0432 **
	(−3.7455)	(−3.7988)	(−2.5739)	(−3.6819)	(2.2954)	(2.2744)	(1.8672)	(2.2856)
FRD * RD	−4.1818 ***	−4.2013 ***	−1.0802 ***	−5.2816 ***
	(−4.0361)	(−4.0895)	(−2.7981)	(−4.0266)
FRD * lnFDI					−0.0945 ***	−0.0947 ***	−0.0183 ***	−0.1130 ***
					(−6.1501)	(−6.2141)	(−2.8522)	(−6.1078)
lnPGDP	0.0955	0.0975	0.0251	0.1226	0.0348	0.0313	0.0060	0.0373
	(1.2980)	(1.2998)	(1.1800)	(1.2906)	(0.4759)	(0.4246)	(0.3914)	(0.4223)
IS	−0.2364 ***	−0.2390 ***	−0.0615 ***	−0.3005 ***	−0.2068 ***	−0.2094 ***	−0.0405 ***	−0.2499 ***
	(−6.7527)	(−6.8997)	(−3.3930)	(−6.6227)	(−5.8710)	(−6.0012)	(−2.7435)	(−5.7584)
HC	−0.0921 ***	−0.0921 ***	−0.0238 **	−0.1159 ***	−0.0764 ***	−0.0759 ***	−0.0148 *	−0.0908 **
	(−3.0894)	(−3.0292)	(−2.3017)	(−2.9807)	(−2.6096)	(−2.6016)	(−1.8703)	(−2.5480)
ρ	0.2124 ***				0.1682 ***
	(4.5624)				(3.6550)
Log-Lik	413.44				424.49
Adj-R2	0.5540				0.5757
Obs	510				510

Note: *, ** and *** indicate 10%, 5%, and 1% of significance levels, respectively. The t-values of the coefficients are reported in parentheses.

and

Table 11. Results of moderating effects of lnFDI and RD from FED perspective.

Variables	Technology Innovation Pathway (R&D)				Government Resource Allocation Pathway (FDI)
	Coefficient	Direct	Indirect	Total	Coefficient	Direct	Indirect	Total
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
FED	0.0945 ***	0.0949 ***	0.0110 *	0.1060 ***	0.0731 ***	0.0738 ***	0.0116 **	0.0855 ***
	(11.213)	(11.065)	(1.9023)	(9.8085)	(4.8566)	(4.6903)	(2.5607)	(4.9039)
RD	3.1841	3.0603	0.3617	3.4220	−14.520 ***	−14.606 ***	−2.3490 **	−16.955 ***
	(0.9844)	(0.9092)	(0.7416)	(0.9053)	(−5.4149)	(−5.5227)	(−2.3641)	(−5.4214)
lnFDI	0.0026	0.0020	0.0002	0.0023	0.0109	0.0113	0.0014	0.0127
	(0.2438)	(0.1921)	(0.1429)	(0.1885)	(0.5694)	(0.5629)	(0.4324)	(0.5502)
FED * RD	−2.1951 ***	−2.2017 ***	−0.2541 *	−2.4558 ***
	(−8.2543)	(−8.1475)	(−1.9155)	(−7.9450)
FED * lnFDI					−0.0032	−0.0033	−0.0005	−0.0037
					(−1.4149)	(−1.3697)	(−1.2097)	(−1.3787)
lnPGDP	0.2114 ***	0.2122 ***	0.0245	0.2368 ***	0.2622 ***	0.2588 ***	0.0418 **	0.3006 ***
	(3.0814)	(3.0690)	(1.6141)	(3.0477)	(3.5809)	(3.6026)	(2.1013)	(3.5449)
IS	−0.1750 ***	−0.1747 ***	−0.0203 *	−0.1950 ***	−0.3090 ***	−0.3117 ***	−0.0505 **	−0.3621 ***
	(−4.6443)	(−4.8028)	(−1.7670)	(−4.6890)	(−8.2471)	(−7.9620)	(−2.4390)	(−7.2740)
HC	−0.0398	−0.0410	−0.0048	−0.0458	−0.0649 **	−0.0664 **	−0.0110	−0.0773 **
	(−1.3633)	(−1.3889)	(−1.0356)	(−1.3824)	(−2.0786)	(−2.1266)	(−1.5288)	(−2.0878)
ρ	0.1050 **				0.1405 ***
	(2.1909)				(2.8992)
Log-Lik	426.29				391.27
Adj-R2	0.5772				0.5175
Obs	510				510

Note: *, ** and *** indicate 10%, 5%, and 1% of significance levels, respectively. The t-values of the coefficients are reported in parentheses.

.

Depending on the moderating effects regression results of R&D investment in Table 10, the coefficient and the spatial spillover effects of FRD*RD are statistically significant negative, which indicates that in the FRD context, enhancing R&D can effectively reduce CO₂ emissions, and engender the regional effect of “Neighbor-companion”. Through tax incentives and subsidies, the government can effectively promote the upgrading of enterprises’ R&D, accelerate technology innovation, and further promote the upgrading of industrial structure, thus reducing the promotion effect of FRD on CO₂ emissions. Considering the positive spillover of R&D technologies, efficient and clean technologies can be easily accepted and imitated by neighboring provinces, ultimately achieving the goal of regional joint emission reduction. Furthermore, these statistically significant and negative coefficients and spatial spillover effect of FDI confirm that FRD*lnFDI can generate neighborhood effects, which indicates that in the context of FRD, the effective allocation of government financial resources can also effectively reduce CO₂ emissions and bring about the regional effect of “Neighbor-companion”. The factor flow and spatial knowledge spillover, which caused by high-quality FDI, can improve the technology level and the regional innovation ability, which will inhibit CO₂ emissions. The “imitation effect” and “demonstration effect” among neighboring provinces can continuously improve environmental quality and form the pattern of “competition for green development”, thus playing a certain role in curbing CO₂ emissions of neighboring provinces.

It is noteworthy that the coefficients and spatial spillover effects of FED*RD had a significant negative effect on CO₂ emissions in Table 11. Local governments hold the autonomy of local fiscal expenditures, and by increasing R&D expenditures, they can encourage enterprises to upgrade technology, achieve scale effects, and carry out green competition. To cope with green competition, neighboring provinces will likewise increase R&D expenditures, thus achieving the common goal of emission reduction. Concerning government resource allocation, the coefficients and the spatial spillover effect of FED*lnFDI are both negative but insignificant. The possible reason can be concluded that China’s infrastructure development is not sufficient to support the development of clean technology brought by FDI. Furthermore, a part of FDI is ineffectively allocated out and the investment return obtained is not enough to offset the cost, leading to the waste of financial resources, which is detrimental to the development of clean technology and the effect of regional joint emission reduction, and thus the coefficient and spatial spillover effect is insignificant.

5.4.2. Environmental Policy Impact Analysis

Faced with the huge pressure of carbon emission reduction and green development, China has implemented some environmental policies to inhibit carbon emissions in recent years, including the Air Pollution Prevention and Control Action Plan (APPCAP) and the Notice on Piloting Carbon Emission Rights issued by the government in October 2011, which emphasize the importance of market mechanism to achieve the goals of controlling greenhouse gas. However, the impact of these policies has not been clearly reflected until today. In this context, the event of APPCAP, which was implemented in 2013, is used to assess the effectiveness of environmental policies. Specifically, we divide the sample period into two periods, 2003–2013 and 2014–2019, and apply the SAR model to regress Equation (20) in segments, and the results are presented in

Table 12. Air Pollution Prevention and Control Action Plan impact analysis.

Variables	2003–2013				2014–2019
	Coefficient	Indirect	Coefficient	Indirect	Coefficient	Indirect	Coefficient	Indirect
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
FRD	0.2631 ***	0.0306			0.0648	0.0227
	(8.0452)	(1.5878)			(1.5301)	(1.2474)
FED			0.0603 ***	0.0032			0.0086	0.0032
			(8.4119)	(0.8679)			(0.6458)	(0.5691)
RD	−14.605 ***	−1.6251	−8.4605 ***	−0.3986	−1.9108	−0.7000	−0.3306	−0.0942
	(−4.7732)	(−1.6337)	(−2.7742)	(−0.7771)	(−0.5901)	(−0.5373)	(−0.1078)	(−0.0719)
lnFDI	−0.0621 ***	−0.0073	−0.0242 *	−0.0014	−0.0137	−0.0047	−0.0125	−0.0047
	(−4.4337)	(−1.4737)	(−1.7151)	(−0.7174)	(−1.1188)	(−0.9441)	(−0.9858)	(−0.8229)
lnPGDP	0.3829	0.0445	0.6722 ***	0.0367	0.0585	0.0215	0.0776	0.0285
	(3.8459)	(1.4579)	(7.3373)	(0.8621)	(0.3932)	(0.3582)	(0.5178)	(0.4560)
IS	−0.2713 ***	−0.0305	−0.3017 ***	−0.0158	−0.2140 ***	−0.0765 *	−0.2100 ***	−0.0778 *
	(−5.8290)	(−1.6101)	(−6.5916)	(−0.8532)	(−3.8020)	(−1.9189)	(−3.5055)	(−1.9291)
HC	−0.0640 **	−0.0075	−0.0469	−0.0026	−0.0101	−0.0034	−0.0087	−0.0034
	(−1.9998)	(−1.1794)	(−1.4853)	(−0.6523)	(−l0.3342)	(−0.3040)	(−0.2855)	(−0.2682)
ρ	0.1024 *		0.0498		0.2638 ***		0.2763 ***
	(1.7183)		(0.8638)		(2.9457)		(3.0994)
Log-Lik	348.69		351.80		279.72		278.51
Adj-R2	0.5885		0.5972		0.1303		0.1165
Obs	330		330		180		180

Note: *, ** and *** indicate 10%, 5%, and 1% of significance levels, respectively. The t-values of the coefficients are reported in parentheses.

.

In Table 12, the results show that before the implementation of the APPCAP, both FRD and FED significantly promoted carbon emissions, and the spatial spillover effect was positive but not significant. After the implementation of the plan, the promotion effect of FRD and FED on carbon emissions is greatly reduced and insignificant, which indicates that the APPCAP is effective in reducing carbon emissions. Combined with Figure 2, the growth rate of carbon emissions in Zhejiang, Jilin and especially Beijing is much smaller than that of other provinces, implying that the introduction of the plan makes the local government endure the pressure of environmental protection, and even if it sacrifices part of the environmental benefits for growth, the cost is also limited. Among the ten specific measures proposed in the APPCAP, the requirements related to energy use account for five clauses. Under the combined effect of APPCAP and the supporting coal consumption control policies, coal consumption can not only achieve a gradual structural decline but also achieve the peak coal consumption target as soon as possible, thus achieving a carbon emission reduction.

6. Conclusions and Policy Recommendations

6.1. Conclusions

Since 1978, China’s extensive development model has resulted in a dramatic growth in carbon emissions, and behind the extensive growth, the model is the actions of local governments under the context of Chinese-style fiscal decentralization. Therefore, this paper selected the panel data of 30 provinces in China from 2003 to 2019 and used the spatial autoregressive model to investigate the spatial spillover effects of FD on CO₂ emissions from FRD and FED perspectives, respectively. The main conclusions of the study can be summarized as follows: (1) With statistically significant positive spatial correlation, CO₂ emissions has strong path dependence and certain positive feedback effects, implying that the increase in CO₂ emissions in this province will result in the increase in CO₂ emissions in neighboring provinces. (2) The significantly positive coefficients and spatial spillover effects of FRD and FED on CO₂ emissions show that revenue and expenditure decentralization not only promotes CO₂ emissions in the province but also exacerbates CO₂ emissions in neighboring provinces, forming a pollution pattern of neighbor-beggar. Meanwhile, the spatial spillover effects of FD on CO₂ emissions vary across provinces. Specifically, the impact of FRD on CO₂ emissions is significantly positive in the eastern region, while it is positive but insignificant in the central and western regions. Moreover, the effect of FED on CO₂ emissions is significantly positive in the west region, but it is not significant in the east and central regions. (3) The coefficients and the spatial spillover effects of FD*RD are all significantly negative from FRD and FED perspectives, indicating that increasing R&D inputs can effectively mitigate the adverse effect of FD on CO₂ emissions and reduce CO₂ emissions in neighboring provinces. Similarly, the coefficients and spatial spillover effects of FRD*lnFDI are significantly negative, implying that introducing high-quality FDI can effectively suppress CO₂ emissions not only in the province but also in the neighboring provinces, which eventually appears to be a pattern of “neighbor-companion”. However, as for FED, the coefficient and spatial spillover effect of FED*lnFDI are negative and insignificant, which can be attributed to the lack of local human capital, infrastructure, etc. (4) The spatial spillover effect of PGDP on CO₂ emissions is significantly positive, showing that PGDP aggravates CO₂ emissions in neighboring provinces, because China’s economy is still in a transition period towards high-quality development. In contrast, the spatial spillover effects of industrial structure and human capital are significantly negative.

6.2. Policy Recommendations

To implement the concept of green development and promote sustainable growth, Chinese government should play an active role in building a low-carbon economic development model. Therefore, based on the above findings, the following relevant policy recommendations are proposed:

• Strengthening regional collaborative governance. The central government should foster people’s awareness of carbon emission reduction, and accelerate to establish a cross-regional and cross-sectoral carbon emission management mechanism. First, the government should increase the publicity of carbon emission reduction, and enhance environmental law enforcement and investigation; second, China should develop differentiated emission reduction strategies in the east, central and west regions according to the difference of talents, technology, resource endowment, and economic development level. Finally, considering that reducing CO₂ emission is a public good, the central government needs to unify the planning to realize the integration and coordination of carbon emission governance in the whole region.
• Adjusting the tax system. The central government should improve the fiscal decentralization system, clarify the division of powers and responsibilities, optimize the structure of central and local financial and administrative powers, and implement positive interaction. Specifically, China should improve its tax system. Local governments should increase tax incentives for green production enterprises, accelerate the formulation and introduction of carbon tax nationwide, and implement policies such as environmental tax and emission permits to promote the R&D and innovation of green technologies. Meanwhile, through improving the system of budget revenue and expenditure supervision, China should fundamentally optimize the distribution of financial resources to promote carbon emission reduction.
• Improving the structure of fiscal expenditures. Firstly, it is essential to optimize the structure of local governments’ fiscal expenditures and change the spending preference of “emphasizing production over science and education”. Fiscal funds should be focused on scientific research, education development, and other aspects to promote low-carbon technological innovation. Secondly, the government should clarify the responsibility of spending on public services such as environmental protection at all levels, reduce common responsibilities, and avoid overlapping responsibilities. Thirdly, the local government should adjust the form of environmental protection investment by establishing a green development fund and building a low-carbon technology subsidy system to encourage enterprises to carry out green innovation spontaneously.
• Restructuring the promotion system for officials. The central government should improve the existing government performance assessment system. To be specific, China should strengthen the horizontal supervision of local officials and fully utilize the coordinated supervision role of the government, the media, and the public. In addition, a multi-dimensional assessment system, which will combine with an accountability regulatory and disciplinary system to gradually change from a GDP orientation to a people’s livelihood orientation, should be quickly established.

6.3. Limitations and Outlook

Although this paper helps to clarify the mechanism of FD on CO₂ emissions in terms of spatial spillover effects, there are still several shortcomings: Firstly, this paper adopts a static spatial econometric model, which may ignore the potential endogeneity problem. In the future, we will try to use a dynamic spatial GMM model so that spatial dependence and potential endogeneity can be controlled and dealt with simultaneously. Secondly, when exploring the spatial correlation nexus, only the spatial adjacency matrix is considered. In the subsequent study, we will try to introduce the weight matrix of geographic distance, economic distance, etc., and combine them with the spatial dynamic GMM method to obtain more reliable results. Thirdly, because Chinese provincial panel data is used for empirical analysis, the sample size is so small that sample bias may occur. It is generally believed that the intra-regional cooperation among the governments should be considered, especially as the lower the government is, the more fiscal pressure it faces. Therefore, we will try to obtain data at the municipal or even county level to greatly expand the sample size. Finally, considering that carbon emissions trading (CET) was piloted in seven Chinese provinces and cities in October 2011 and officially implemented in July 2021, it is difficult to obtain relevant data to assess the effect of CET on CO₂ emissions by using the SAR model. Therefore, in future research, we will adopt the multi-period DID method to comprehensively evaluate the effectiveness of CET on carbon emission reduction.