Climate Smart Pest Management
Abstract
:1. Introduction
2. Materials and Methods
2.1. The General Conceptual Framework
2.2. The Specific Case
3. Empirical Analyses
3.1. Objective Function
3.2. State Equations
3.3. Data and Model Parameters
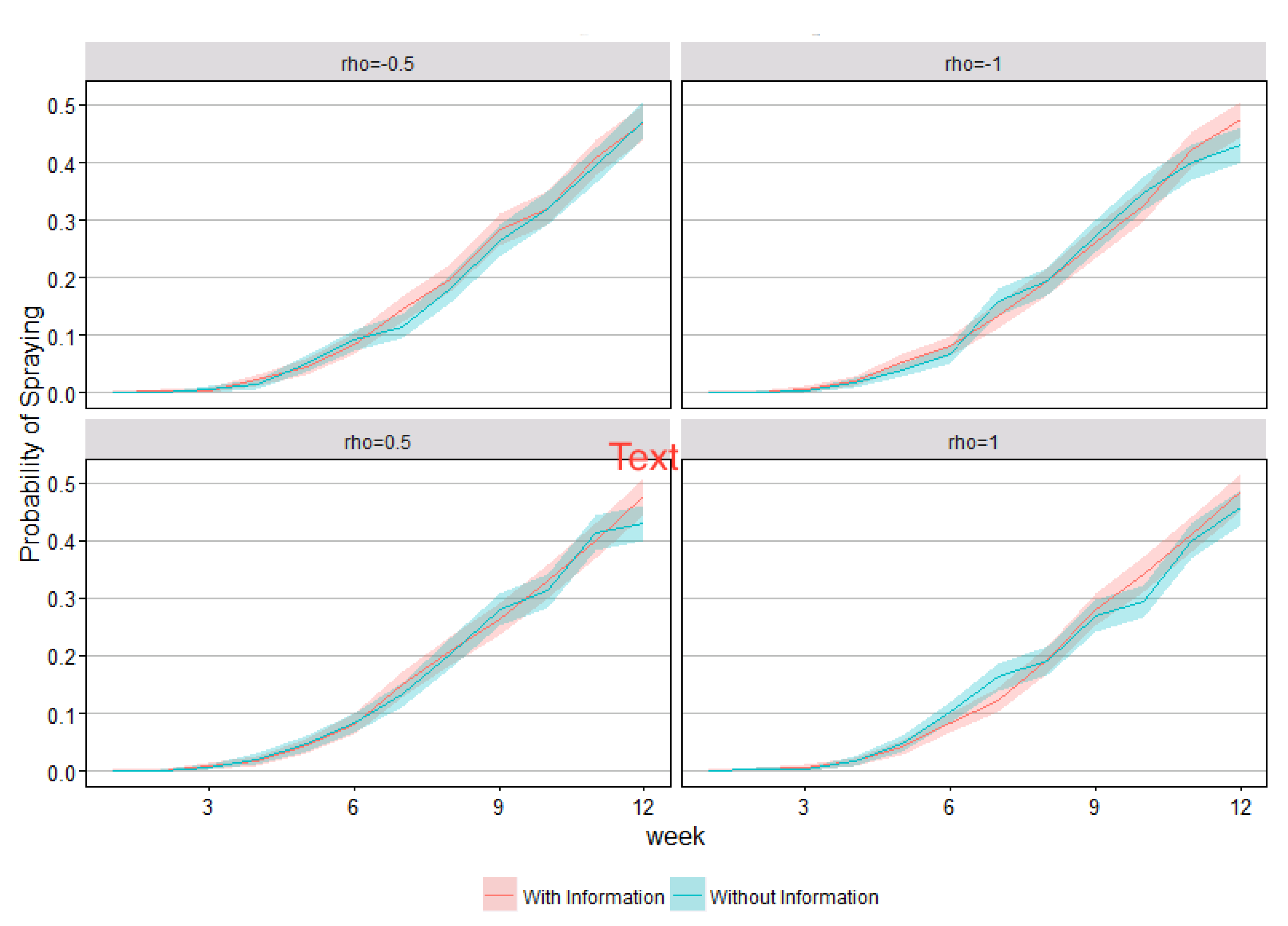
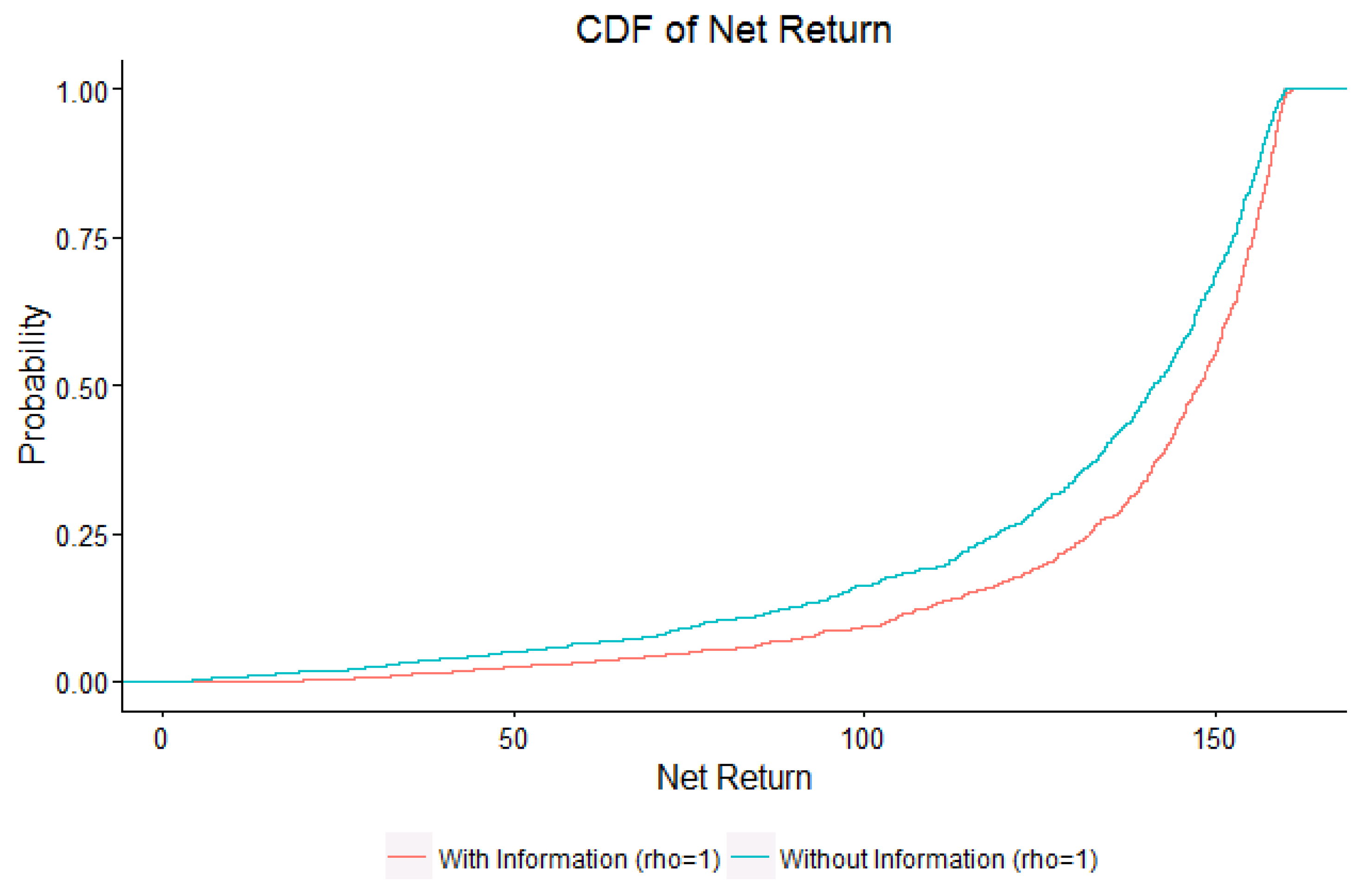
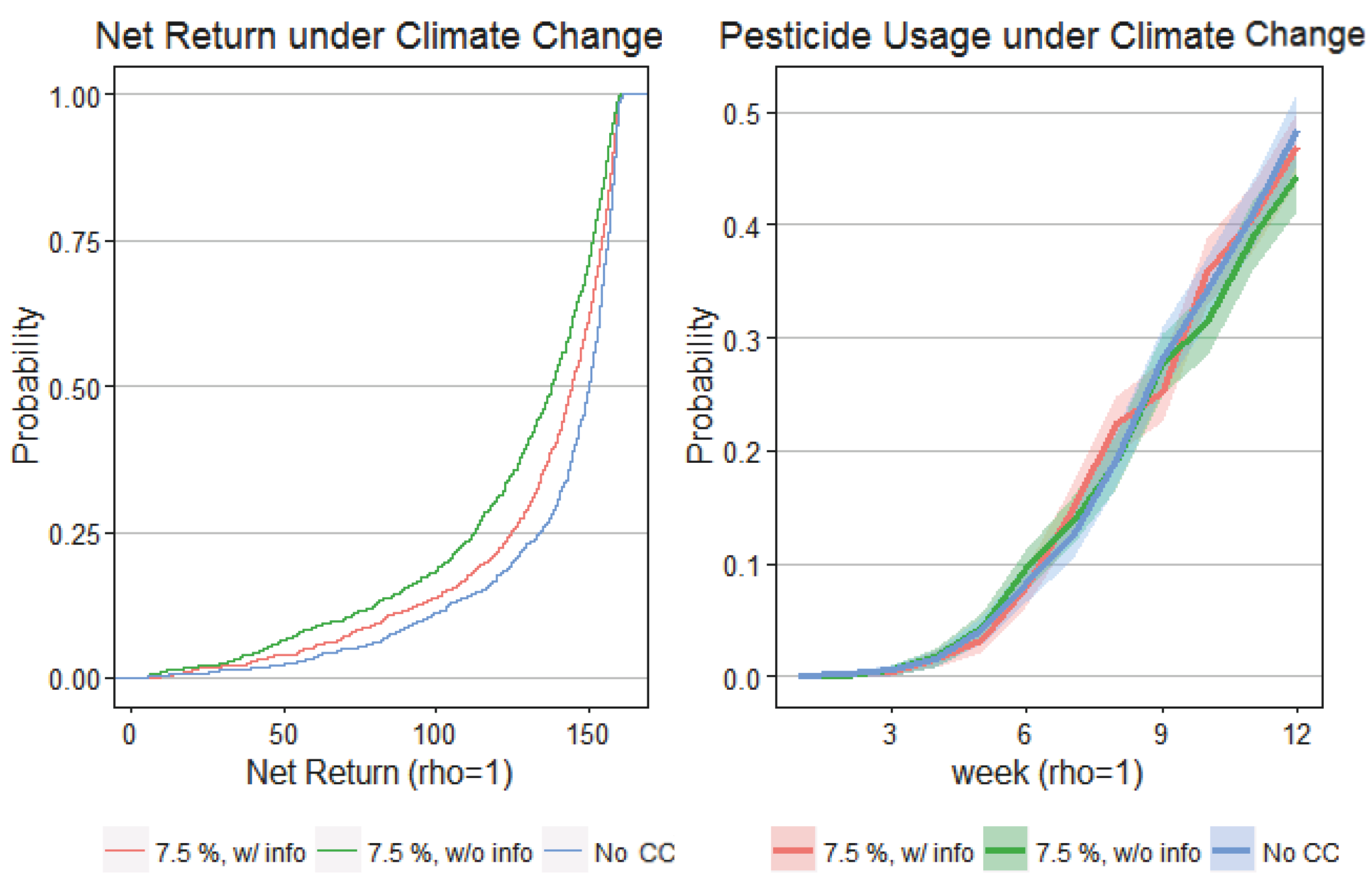
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Equation (3)
Appendix B. Proof of Equation (7)
Appendix C. Proof of Equation (13)
Appendix D. Proof of Equation (15)
Appendix E. Proof of Equation (19)
Appendix F. Proof of Proposition 1
| Par. | Value (Unit) | Source | Description |
|---|---|---|---|
| 0.351 | Regression Analysis | Standard deviation of aphid diffusion | |
| 0.121 | Regression Analysis | Standard deviation of weather diffusion | |
| 0.30 | Regression Analysis | Growth rate of aphid | |
| 0.137 | Regression Analysis | Growth rate of crop | |
| 0 | Regression Analysis | Correlation coefficient between weather | |
| and aphid variation () | |||
| T | 14 weeks | Oplinger et al. (1990) [48] | A full growing season |
| 0.25 | Regression Analysis | Marginal weather effect on aphid growth | |
| 0.85 | Elbakidze et al. (2011) [15] | Pesticide efficiency | |
| −0.074 | Regression Analysis | Marginal weather effect on biomass growth | |
| r | 0.0035 | Marsh et al. (2000) [16] | Discount rate |
| P | 0.295 $/lb | Painter (2011) [49] | Per pound lentil price |
| W | 4.84 $/Acre | Painter (2011) [49] | Per acre pesticide cost |
| A(0) | 1 | Assumed | Initial number of aphids |
| Oplinger et al. (1990) [48] | Carrying capacity of aphid per acre | ||
| 0.08 | Regression Analysis | Growth rate of weather index |
| SUR Formulation (31) | Equation (32) | ||
|---|---|---|---|
| VARIABLES | |||
| 0.0372607 *** | 0.0101419 *** | ||
| (0.0043546) | (0.0013303) | ||
| 0.2549528 | −0.0742 | ||
| (0.2343415) | (0.235) | ||
| A | −0.0568 * | ||
| (0.0316) | |||
| Constant | −2.493412 | 1.999086 | 7.751 *** |
| (1.999086) | (0.1346805) | (1.764) | |
| Observations | 137 | 137 | 23 |
| R-squared | 0.4678 | 0.2979 | 0.16 |
| Baseline Model | Climate Change Model | |||||
|---|---|---|---|---|---|---|
| Week | Usage w/o | Usage with | t-Test: | Usage w/o | Usage with | t-Test: |
| info: | info: | info: | info: | |||
| ( | () | |||||
| 1 | 0 | 0.001 | 0.316 | 0 | 0.001 | 0.874 |
| 2 | 0.001 | 0.001 | 1 | 0 | 0.002 | 0.900 |
| 3 | 0.004 | 0.009 | 0.166 | 0.006 | 0.004 | 0.766 |
| 4 | 0.018 | 0.018 | 1 | 0.017 | 0.015 | 0.974 |
| 5 | 0.04 | 0.044 | 0.655 | 0.044 | 0.032 | 0.433 |
| 6 | 0.067 | 0.082 | 0.2 | 0.095 | 0.079 | 0.250 |
| 7 | 0.158 | 0.15 | 0.627 | 0.137 | 0.148 | 0.588 |
| 8 | 0.194 | 0.208 | 0.438 | 0.191 | 0.223 | 0.047 ** |
| 9 | 0.273 | 0.263 | 0.621 | 0.277 | 0.252 | 0.095 * |
| 10 | 0.346 | 0.33 | 0.456 | 0.313 | 0.357 | 0.022 ** |
| 11 | 0.401 | 0.4 | 0.965 | 0.39 | 0.406 | 0.873 |
| 12 | 0.431 | 0.476 | 0.04 ** | 0.443 | 0.469 | 0.065 * |
| Expected | 113.24 | 122.103 | 0.000 *** | 94.25 | 106.49 | 0.008 *** |
| Net Return | ||||||
References
- Rose, S.K.; McCarl, B. Greenhouse gas emissions, stabilization and the inevitability of adaptation: Challenges for US agriculture. Choices 2008, 23, 15–18. [Google Scholar]
- Eigenbrode, S.; Capalbo, S.; Houston, L.; Johnson-Maynard, J.; Kruger, C.; Olen, B. Agriculture, Adaptation, and Mitigation. In Climate Change in the Northwest: Implications for Our Landscapes, Waters, and Communities; Chapter 6; Dalton, M., Mote, P.W., Snover, A.K., Eds.; Island Press: Washington, DC, USA, 2013; pp. 149–179. [Google Scholar]
- Kukal, M.S.; Irmak, S. Climate-driven crop yield and yield variability and climate change impacts on the US Great Plains agricultural production. Sci. Rep. 2018, 8, 3450. [Google Scholar] [CrossRef] [PubMed]
- Clement, S.L. Pea Aphid Outbreaks and Virus Epidemics on Peas in the U.S. Pacific Northwest: Histories, Mysteries, and Challenges. Plant Health Progress 2006, 7, 34. [Google Scholar] [CrossRef]
- Zilberman, D.; Schmitz, A.; Casterline, G.; Lichtenberg, E.; Siebert, J.B. The economics of pesticide use and regulation. Science 1991, 253, 518–522. [Google Scholar] [CrossRef]
- Carpentier, A.; Weaver, R.D. Damage Control Productivity: Why Econometrics Matters. Am. J. Agric. Econ. 1997, 79, 47–61. [Google Scholar] [CrossRef]
- Fox, G.; Weersink, A. Damage Control and Increasing Returns. Am. J. Agric. Econ. 1995, 77, 33–39. [Google Scholar] [CrossRef]
- Lichtenberg, E.; Zilberman, D. The Econometrics of Damage Control: Why Specification Matters. Am. J. Agric. Econ. 1986, 68, 261–273. [Google Scholar] [CrossRef]
- Saha, A.; Shumway, C.R.; Havenner, A. The Economics and Econometrics of Damage Control. Am. J. Agric. Econ. 1997, 79, 773–785. [Google Scholar] [CrossRef]
- Chen, C.C.; McCarl, B.A. Pesticide Usage as Influenced by Climate: A Statistical Investigation. Clim. Chang. 2001, 50, 475–487. [Google Scholar] [CrossRef]
- Chen, C.C.; McCarl, B.A.; Schimmelpfennig, D. Yield Variability as Influenced by Climate: A Statistical Investigation. Clim. Chang. 2004, 66, 239–261. [Google Scholar] [CrossRef]
- Costello, C.; Adams, R.; Polasky, S. The Value of El Niño Forecasts in the Management of Salmon: A Stochastic Dynamic Assessment. Am. J. Agric. Econ. 1998, 80, 765–777. [Google Scholar] [CrossRef]
- Rubas, D.J.; Mjelde, J.W.; Love, H.A.; Rosenthal, W. How Adoption Rates, Timing, and Ceilings Affect the Value of ENSO-based Climate Forecasts. Clim. Chang. 2008, 86, 235–256. [Google Scholar] [CrossRef]
- Cobourn, K.M.; Burrack, H.J.; Goodhue, R.E.; Williams, J.C.; Zalom, F.G. Implications of Simultaneity in A Physical Damage Function. J. Environ. Econ. Manag. 2011, 62, 278–289. [Google Scholar] [CrossRef]
- Elbakidze, L.; Lu, L.; Eigenbrode, S. Evaluating Vector-Virus-Yield Interactions for Peas and Lentils under Climatic Variability: A Limited Dependent Variable Analysis. J. Agric. Resour. Econ. 2011, 36, 504–520. [Google Scholar]
- Marsh, T.L.; Huffaker, R.G.; Long, G.E. Optimal Control of Vector-Virus-Plant Interactions: The Case of Potato Leafroll Virus Net Necrosis. Am. J. Agric. Econ. 2000, 82, 556–569. [Google Scholar] [CrossRef]
- Olson, L.; Roy, S. The Economics of Controlling A Stochastic Biological Invasion. Am. J. Agric. Econ. 2002, 84, 1311–1316. [Google Scholar] [CrossRef]
- Zhang, W.; Swinton, S.M. Incorporating Natural Enemies in An Economic Threshold for Dynamically Optimal Pest Management. Ecol. Model. 2009, 220, 1315–1324. [Google Scholar] [CrossRef]
- Zivin, J.; Hueth, B.M.; Zilberman, D. Managing a Multiple-Use Resource: The Case of Feral Pig Management in California Rangeland. J. Environ. Econ. Manag. 2000, 39, 189–204. [Google Scholar] [CrossRef]
- Hertzler, G. Dynamic Decisions under Risk: Application of Ito Stochastic Control in Agriculture. Am. J. Agric. Econ. 1991, 73, 1126–1137. [Google Scholar] [CrossRef]
- Richards, T.; Eaves, J.; Manfredo, M.; Naranjo, S.; Chu, C.; Henneberry, T. Spatial-Temporal Model of Insect Growth, Diffusion and Derivative Pricing. Am. J. Agric. Econ. 2005, 90, 962–978. [Google Scholar] [CrossRef]
- Saphores, J.D.M. The Economic Threshold with a Stochastic Pest Population: A Real Options Approach. Am. J. Agric. Econ. 2000, 82, 541–555. [Google Scholar] [CrossRef]
- Saphores, J.D.M.; Shogren, J.F. Managing Exotic Pests under Uncertainty: Optimal Control Actions and Bioeconomic Investigations. Ecol. Econ. 2005, 52, 327–339. [Google Scholar] [CrossRef]
- Sunding, D.; Zivin, J. Insect Population Dynamics, Pesticide Use, and Farmworker Health. Am. J. Agric. Econ. 2000, 82, 527–540. [Google Scholar] [CrossRef]
- Marten, A.L.; Moore, C.C. An options based bioeconomic model for biological and chemical control of invasive species. Ecol. Econ. 2011, 70, 2050–2061. [Google Scholar] [CrossRef]
- Sims, C.; Finnoff, D. When is a “wait and see” approach to invasive species justified? Resour. Energy Econ. 2013, 35, 235–255. [Google Scholar] [CrossRef]
- Clement, S.L.; Husebye, D.; Eigenbrode, S.D. Global Warming and Aphid Biodiversity: Patterns and Processes; Chapter Ecological factors influencing pea aphid outbreaks in the U.S. Pacific Northwest; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Gan, Y.; Hanson, K.G.; Zentner, R.P.; Selles, F.; McDonald, C.L. Response of Lentil to Microbial Inoculation and Low Rates Offertilization in the Semiarid Canadian Prairies. Canaian J. Plant Sci. 2005, 85, 847–855. [Google Scholar] [CrossRef]
- Richards, T.J.; Manfredo, M.R.; Sanders, D.R. Pricing weather derivatives. Am. J. Agric. Econ. 2004, 86, 1005–1017. [Google Scholar] [CrossRef]
- Kamien, M.I.; Schwartz, N.L. Dynamic Optimization: The Calculus of Variations and Optimal Control in Economics and Management, 2nd ed.; Elsevier Science: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Mbah, M.; Ndeffo, L.; Forster, G.A.; Wesseler, J.H.; Gilligan, C.A. Economically Optimal Timing for Crop Disease Control under Uncertainty: An Options Approach. J. R. Soc. Interface 2010, 7, 1421–1428. [Google Scholar] [CrossRef]
- Kao, E.P.C. An Introduction to Stochastic Processes; Duxbury Press: Belmont, CA, USA, 1996. [Google Scholar]
- USA Dry Pea And Lentil Council. U.S. Production Statistics; Technical Report; USA Dry Pea And Lentil Council: Moscow, ID, USA, 2007. [Google Scholar]
- Eigenbrode, S.; Bechinski, E.; Karasev, A.; Pappu, H.; Roberts, D.; Clayton, L.; McPhee, K.; Larsen, R.; Porter, L.; Stokes, B.; et al. Legume Virus Project. Technical Report. 2012. Available online: http://www.cals.uidaho.edu/aphidtracker/ (accessed on 7 June 2012).
- Siddiqui, W.H.; Barlow, C.A.; Randolph, P.A. Effects of some constant and alternating temperatures on population growth of the pea aphid, Acyrthosiphon pisum (Homoptera: Aphididae). Can. Entomol. 1973, 105, 145–156. [Google Scholar] [CrossRef]
- Ross, S.M. Introduction to Stochastic Dynamic Programming; Academic Press: Cambridge, MA, USA, 1995. [Google Scholar]
- EPA. Revised Interim Reregistration Eligibility Decisions for Dimethoate. Technical Report. 2011. Available online: http://www.epa.gov/oppsrrd1/REDs/dimethoate_ired_revised.pdf (accessed on 7 June 2012).
- EPA. Dimethoate 400. Technical Report. 2014. Available online: http://www.cdms.net/LDat/ld4PC014.pdf (accessed on 7 January 2014).
- Lu, L.; Winfree, J. Demand shocks and supply chain flexibility. In Proceedings of the NBER Conference “Risks in Agricultural Supply Chains”, Virtual Conference, 20–21 May 2021; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Lu, L.; Nguyen, R.; Rahman, M.M.; Winfree, J. Demand Shocks and Supply Chain Resilience: An Agent-Based Modelling Approach and Application to the Potato Supply Chain; NBER: Cambridge, MA, USA, 2021. [Google Scholar]
- Rahman, M.M.; Nguyen, R.; Lu, L. Multi-level impacts of climate change and supply disruption events on a potato supply chain: An agent-based modeling approach. Agric. Syst. 2022, 201, 103469. [Google Scholar] [CrossRef]
- Zilberman, D.; Reardon, T.; Silver, J.; Lu, L.; Heiman, A. From the laboratory to the consumer: Innovation, supply chain, and adoption with applications to natural resources. Proc. Natl. Acad. Sci. USA 2022, 119, e2115880119. [Google Scholar] [CrossRef]
- Lu, L.; Tian, G.; Hatzenbuehler, P. How agricultural economists are using big data: A review. China Agric. Econ. Rev. 2022, ahead-of-print. [Google Scholar] [CrossRef]
- Du, X.; Wang, X.; Hatzenbuehler, P. Digital technology in agriculture: A review of issues, applications and methodologies. China Agric. Econ. Rev. 2022, ahead-of-print. [Google Scholar] [CrossRef]
- Ma, C.S.; Zhang, W.; Peng, Y.; Zhao, F.; Chang, X.Q.; Xing, K.; Zhu, L.; Ma, G.; Yang, H.P.; Rudolf, V.H. Climate warming promotes pesticide resistance through expanding overwintering range of a global pest. Nat. Commun. 2021, 12, 5351. [Google Scholar] [CrossRef]
- Yong, J.; Zhou, X.Y. Stochastic Controls-Hamiltonian Systems and HJB Equations; Springer: New York, NY, USA, 1999. [Google Scholar]
- Chang, F. Stochastic Optimization in Continuous Time; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Oplinger, E.S.; Hardman, L.L.; Kaminski, A.R.; Kelling, K.A.; Doll, J.D. Lentil. Technical Report. 1990. Available online: http://www.hort.purdue.edu/newcrop/afcm/lentil.html (accessed on 30 June 2022).
- Painter, K. Crop Budgets. Technical Report. 2011. Available online: https://www.uidaho.edu/cals/idaho-agbiz/crop-budgets (accessed on 30 June 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, X.; Elbakidze, L.; Lu, L.; Taylor, R.G. Climate Smart Pest Management. Sustainability 2022, 14, 9832. https://doi.org/10.3390/su14169832
Du X, Elbakidze L, Lu L, Taylor RG. Climate Smart Pest Management. Sustainability. 2022; 14(16):9832. https://doi.org/10.3390/su14169832
Chicago/Turabian StyleDu, Xiaoxue, Levan Elbakidze, Liang Lu, and R. Garth Taylor. 2022. "Climate Smart Pest Management" Sustainability 14, no. 16: 9832. https://doi.org/10.3390/su14169832
APA StyleDu, X., Elbakidze, L., Lu, L., & Taylor, R. G. (2022). Climate Smart Pest Management. Sustainability, 14(16), 9832. https://doi.org/10.3390/su14169832






