A Multi-Objective Demand/Generation Scheduling Model-Based Microgrid Energy Management System
Abstract
:1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contributions
- This study proposed BOSA-based DSM of a SMG with a MOPSO-based DEED to improve economic and environmental issues. DSM improves the MG load pattern by adopting real-time pricing. MG operators can meet system demand with optimal management of WT, PV panel, DG, MT, and FC energy storage systems, and upstream networks.
- With the stochastic nature of the renewable resources units, a multi-objective supplier/consumer management system for a SMG based on PDFs has been presented to model the behavior of solar and wind systems, as well as a hybrid wind and solar system, in an effort to achieve the best possible results despite the uncertainty of the situation.
- The proposed optimal DSM is based on real-time dynamic pricing and the first-ever application of the BOSA optimization algorithm, which employs the load-shifting technique.
- Using a combination of the optimal DSM program, a multi-objective particle swarm optimizer with the Pareto criterion and fuzzy mechanism based nonlinear sorting was used to find the best MG management program.
- By utilizing algorithms for optimizing usage of the MG sources and loads, an economic dispatch can be achieved with optimally lower operation costs and pollution outcomes.
1.4. Paper Organization
2. Problem Statement
3. Distribution Energy Resources
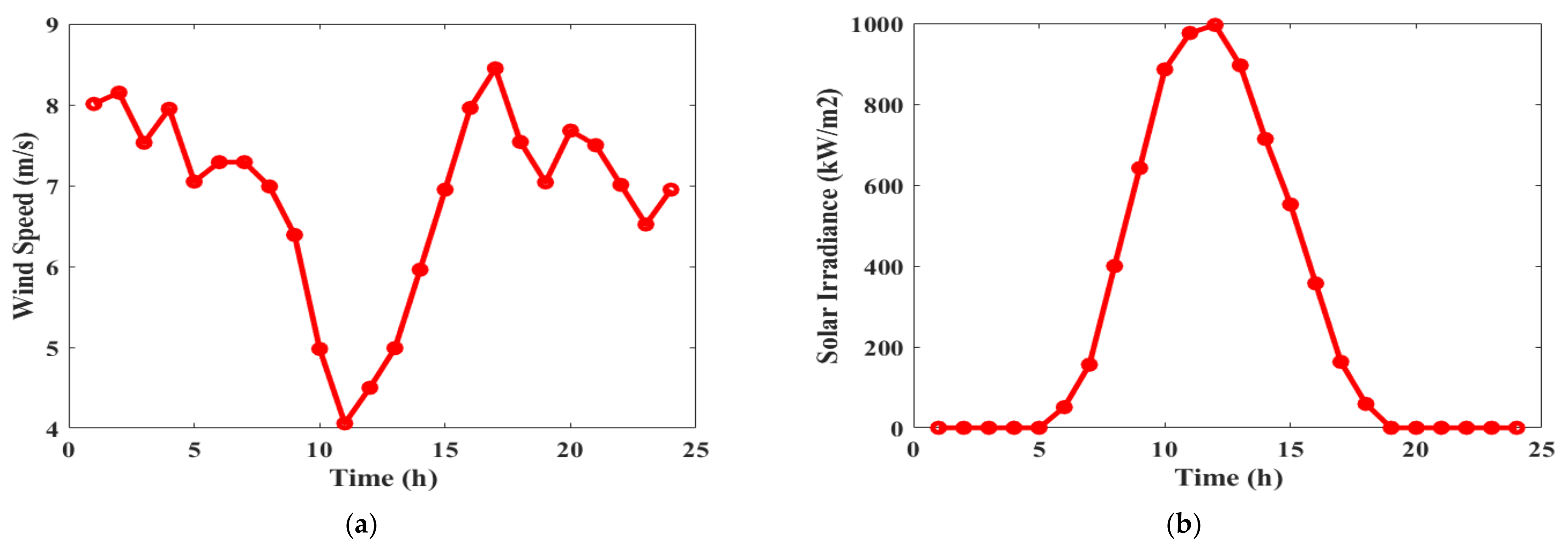
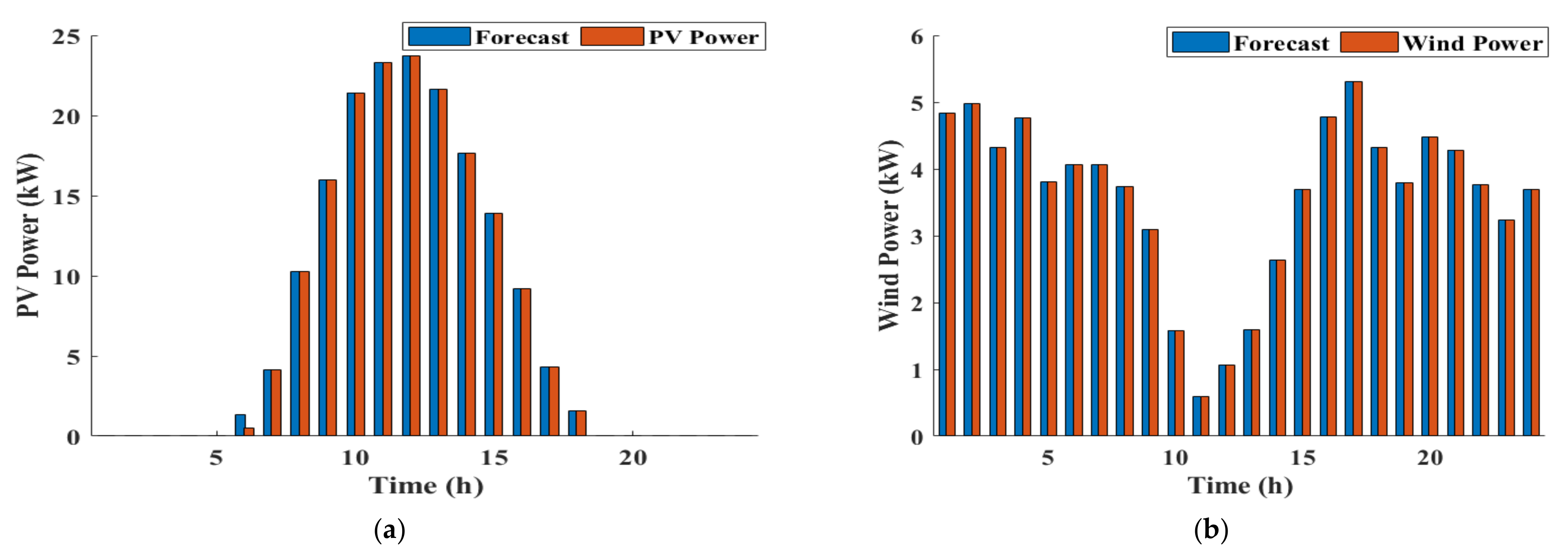
3.1. Renewable Units Stochastic Modeling
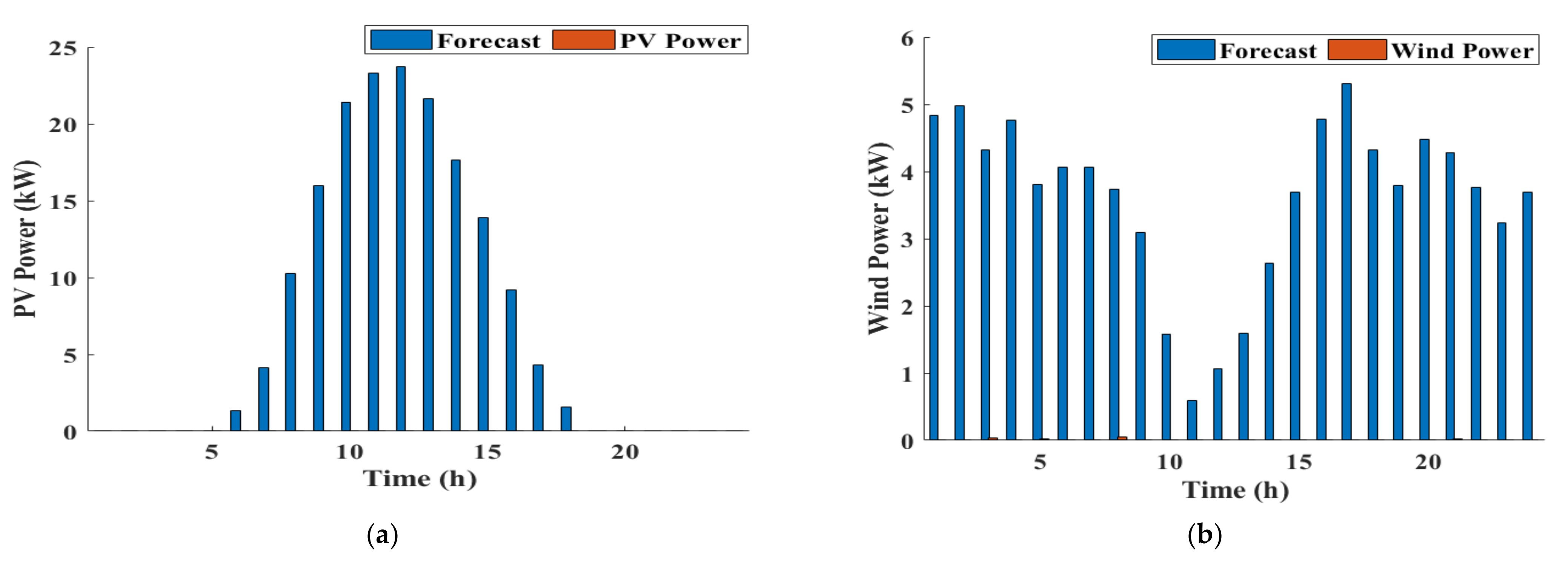
3.1.1. PV Panel
3.1.2. Wind Turbine
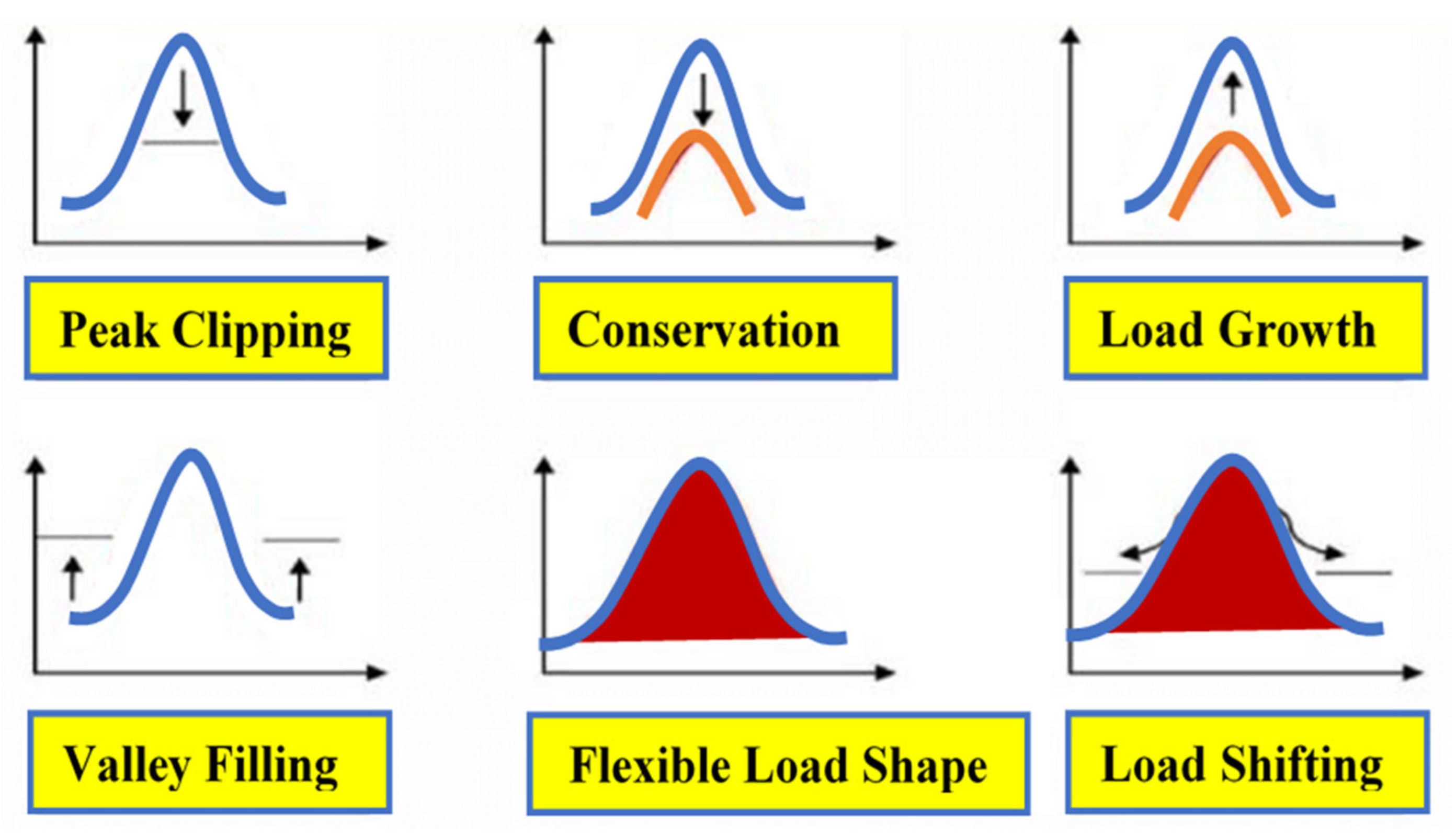
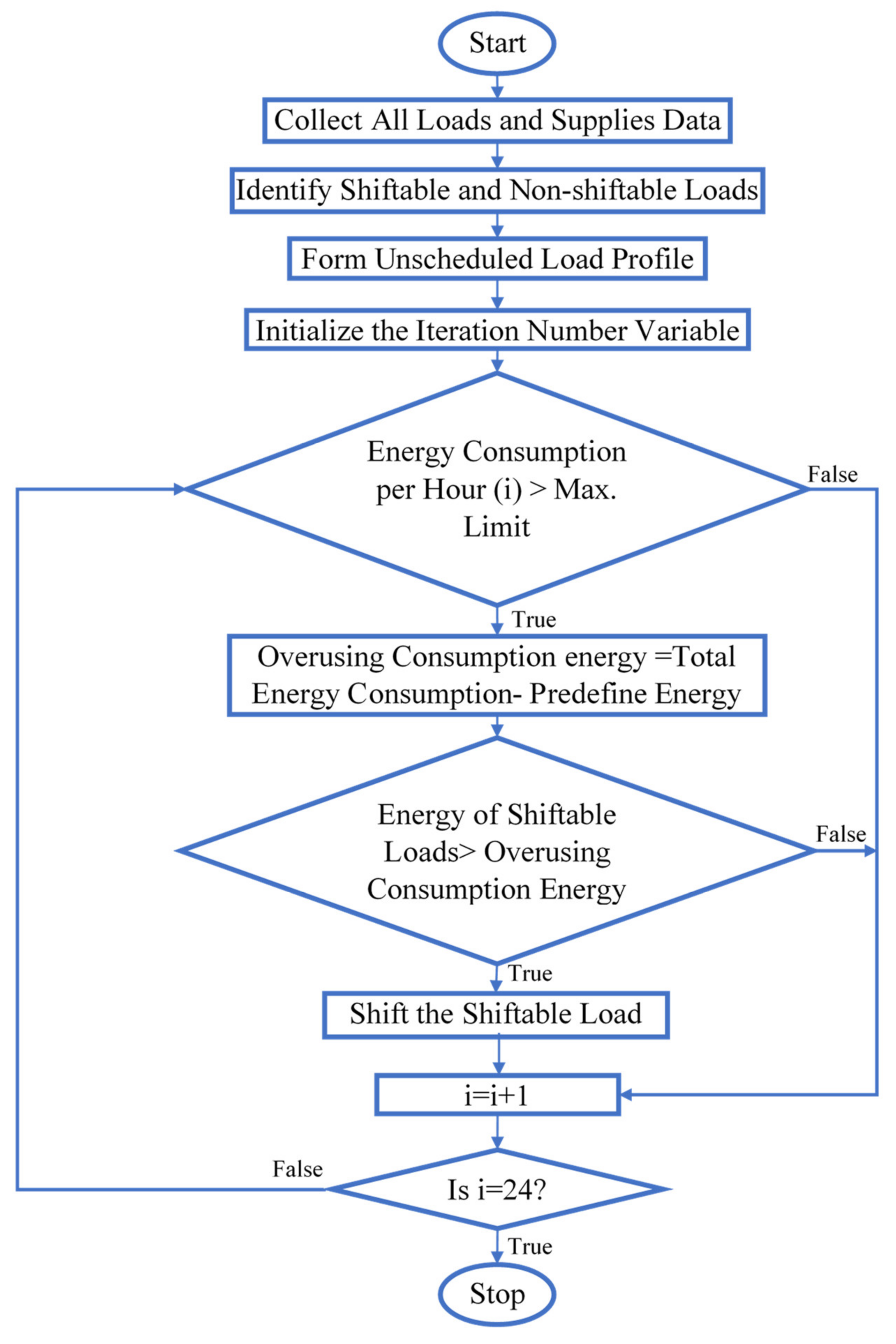
4. The Proposed DSM Program
4.1. DSM Objective Function
4.2. Constraints
4.3. Binary Orientation Search Optimization Algorithm
| BOSA Algorithm Steps |
|
5. Multi-Objective Optimization Model
5.1. Power Balance Constraint
5.2. DG Power Constraints
5.3. Battery Constraints
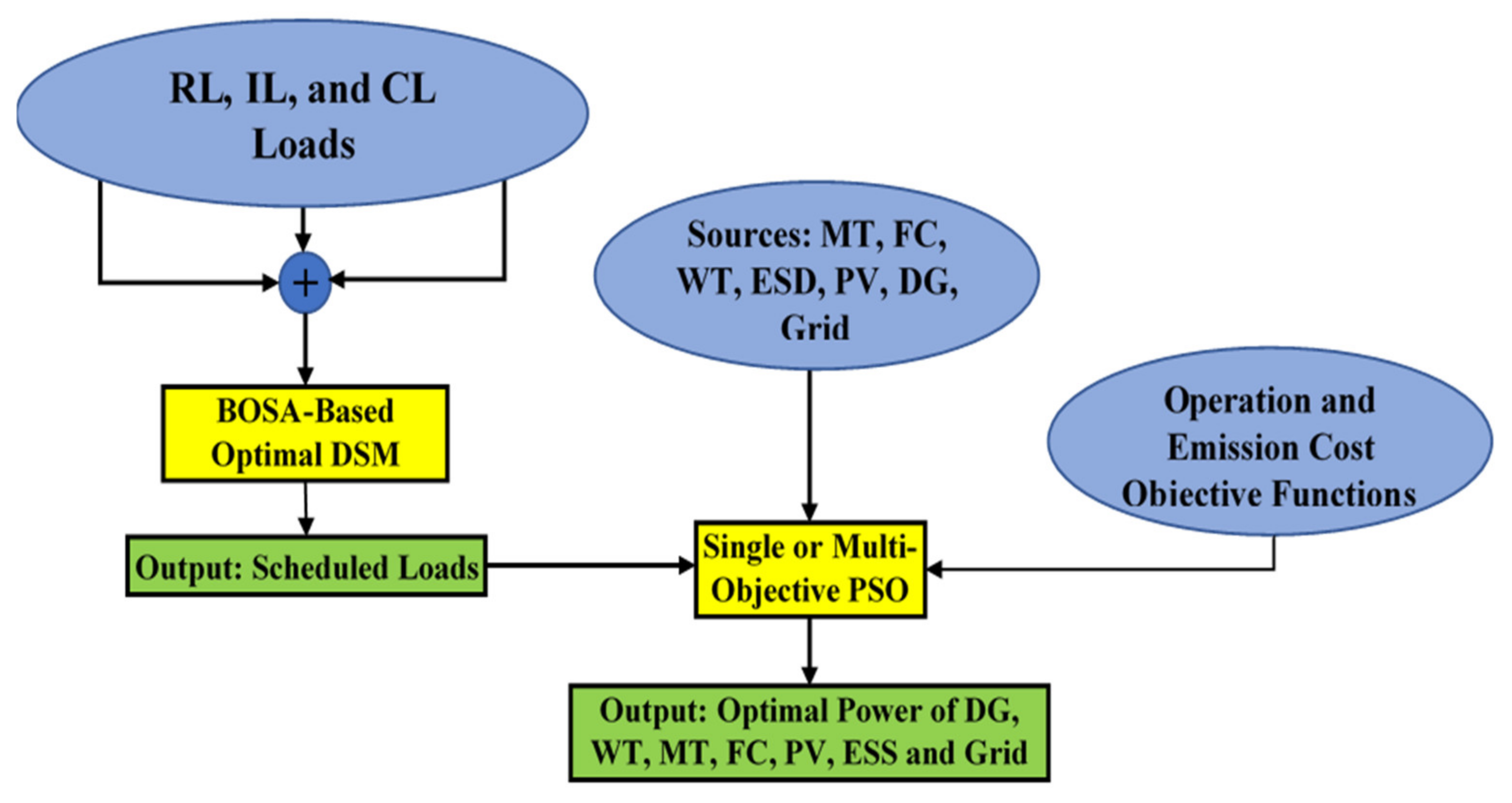
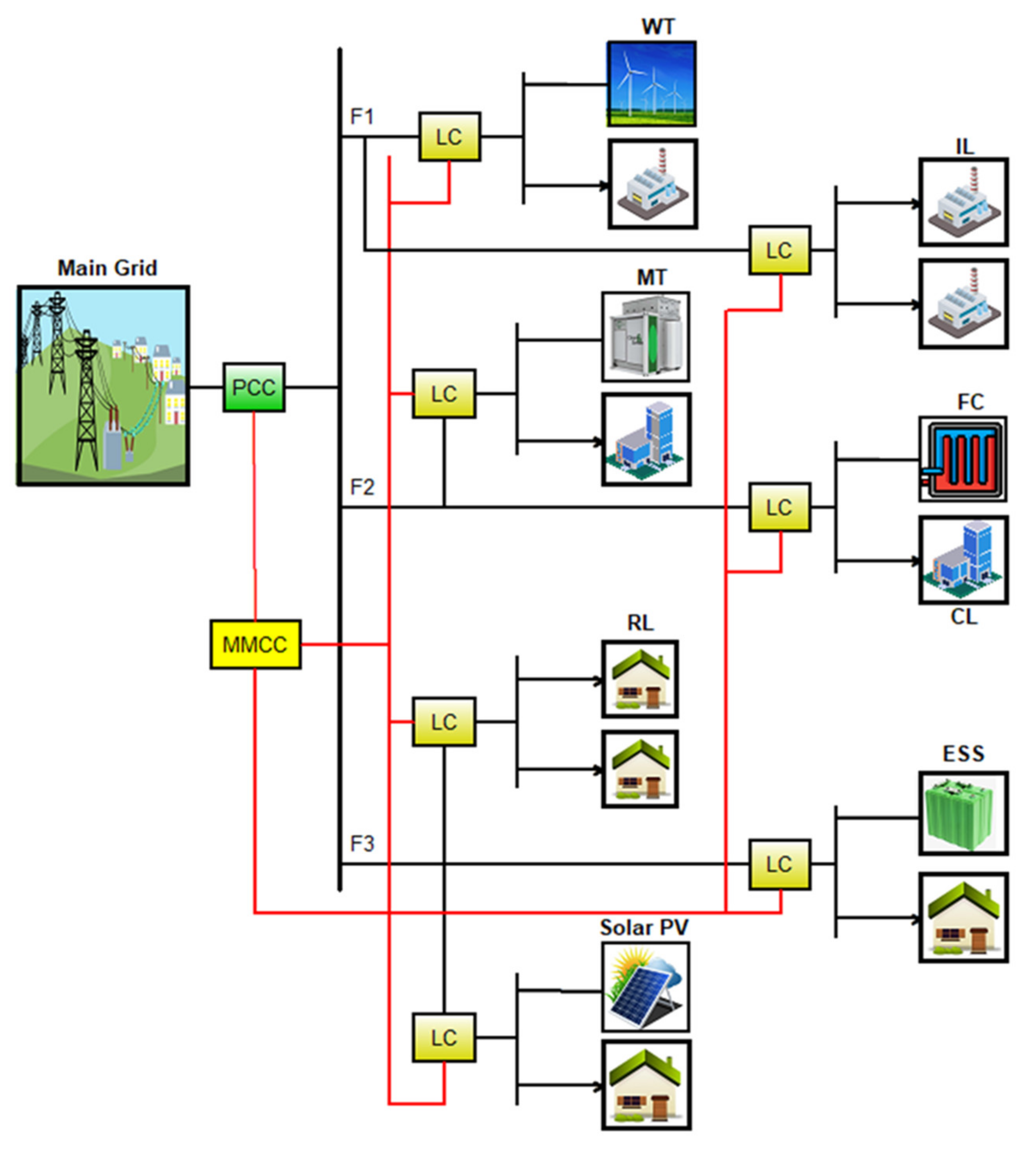
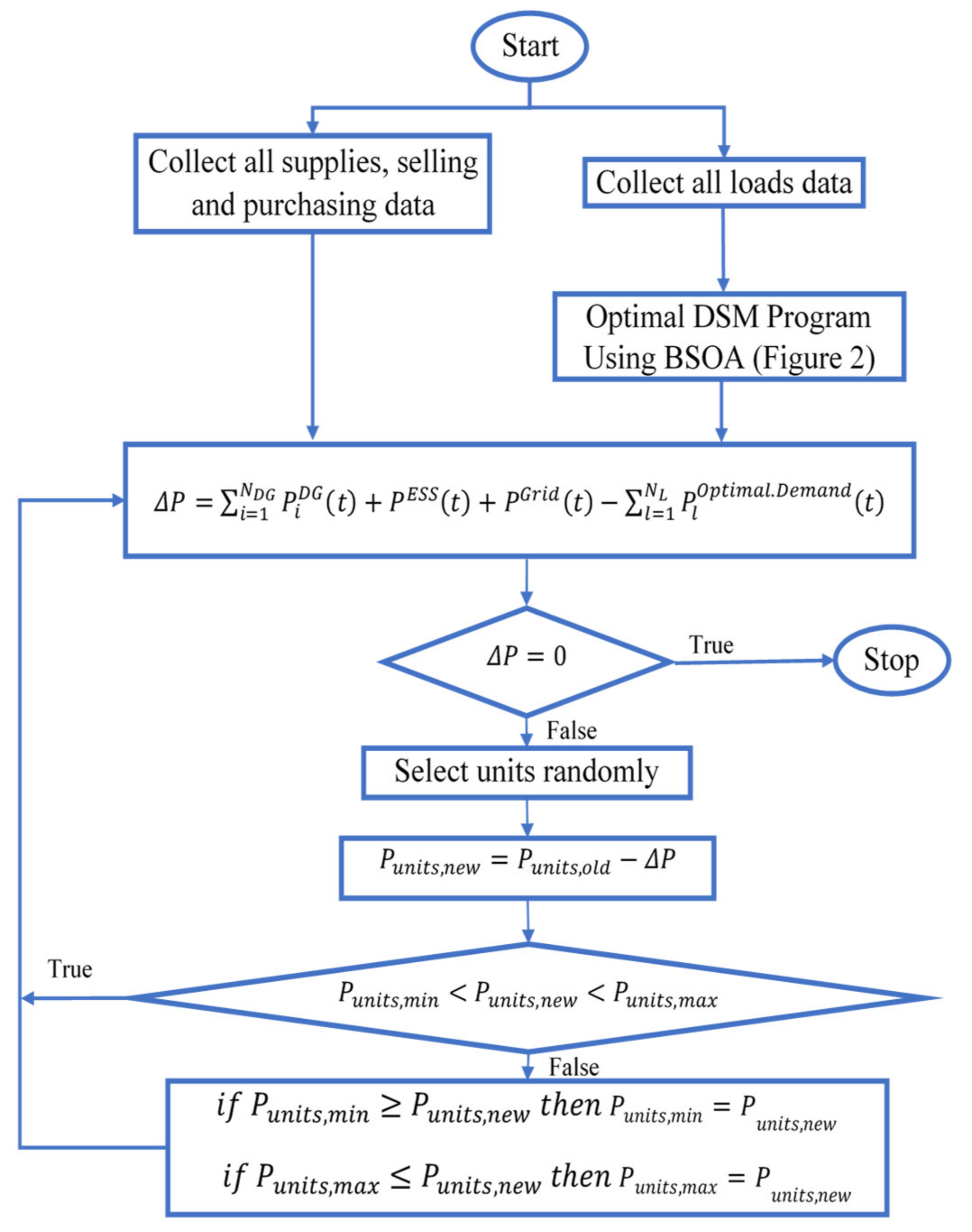
6. Proposed Smart MG System
7. BOSA-Based MOPSO Algorithm
- The required input data are collected at the start of the program, and include: MG structure, utility, and DG operating characteristics PV and WT forecasted output power for every time period under consideration, offering of the real-time price for DGs and utility, the daily demand curve, and pollutant emission coefficients.
- Set the values for all BOSA parameters.
- Randomize a population to minimize DSM objective (Equation (16)).
- For each population within the iteration range, Equations (29) and (30) are used to update positions.
- Check all the constraints for each population.
- Initial population of MOPSO, an initial population, is considered based on the problem’s limitations and the following relationship:where is regarded as the decision variable vector, which consists of the unit’s output generation power, the power exchange with the main grid, the amount of load reduction, and the on/off modes in the day ahead vision, which are stated as follows:where represents the number of decision variables, and represent the total number of generation units and storage units, respectively, and represents the total number of periods, , are the vectors of the active power that includes all DGs and storage units; utility grid power and load active power; and is the state vector that indicates whether all units are ON or OFF during period t.
- For each of the generated populations, the power dispatch algorithm is implemented as shown in Figure 5, and the fitness is calculated using (33) or (36).
- Defining non-dominant solutions.
- Creating a repository for non-dominated solutions.
- Choosing the best non-dominated solution particle as the leader: the best particle is chosen as the leader by apportioning the search area into equal sections, allocating probability distributions to each part of the identified search space, and finally using the roulette wheel to select the best particle as the leader.
- Each particle’s new velocity and position are calculated using (48) and (49).
- Modifying the optimal position of every particle:To update each particle’s optimal position, the new position of the particle is compared to the position of the particle before.
- Adding the repository’s current non-dominated solutions.
- The dominated solutions are being removed from the repository.
- Excessive members will be omitted if the number of individuals in the repository exceeds the pre-specified capacity.
- The optimization process will end if the maximum number of repetitions is reached; otherwise, return to Step 10.
- Choosing the best interactive solution: The membership function-based fuzzy logic can be used to select the optimal solution from the optimal Pareto responses. Here, is the objective function’s optimality amount in optimal Pareto response , which is calculated as follows:where and are the objective function’s upper and lower limits, respectively. In the method which is being proposed, these values are figured out by using the results of optimizing each objective function. is between 0 and 1, and a value of 0 indicates that the solution does not meet the designer’s objectives, while = 1 indicates that the solution meets the designer’s objectives.
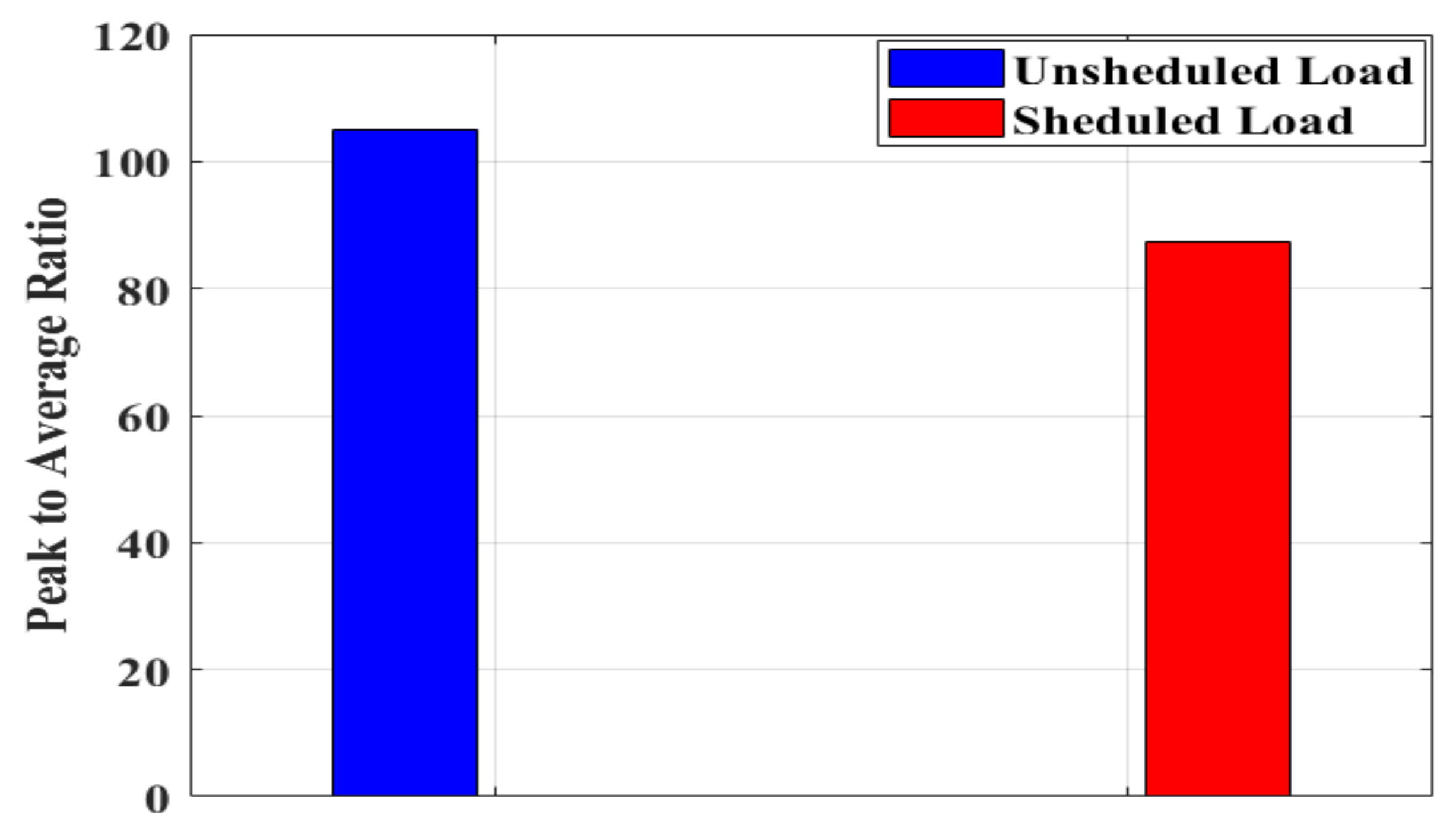
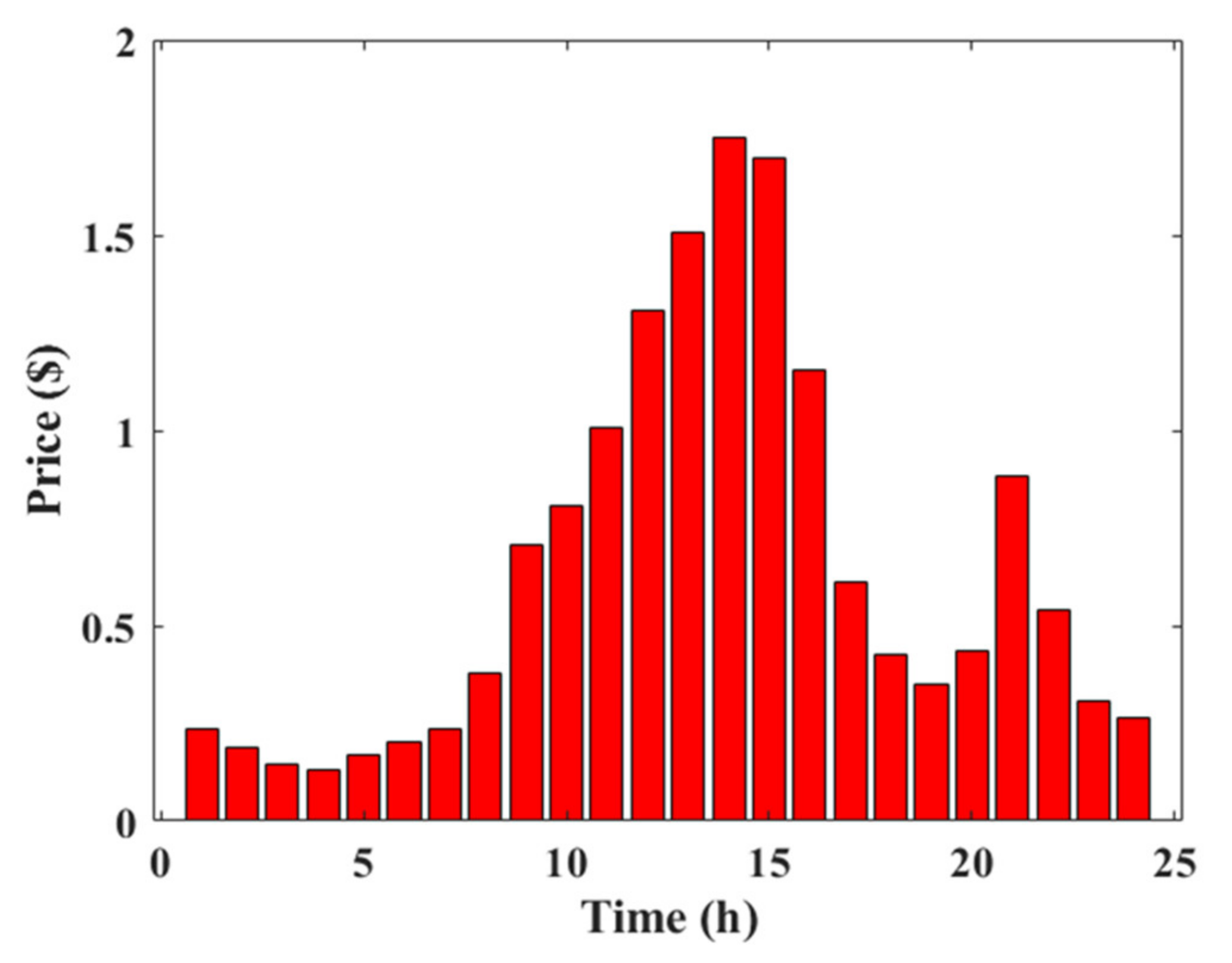
8. Results and Discussion
- Case #1: single-objective (emission function optimization only) without DSM.
- Case #2: single-objective (emission function optimization only) with DSM.
- Case #3: single-objective (considering operation cost function) without DSM.
- Case #4: single-objective (considering operation cost function) with DSM.
- Case #5: multi-objective (emission and operation cost functions) optimization without DSM.
- Case #6: multi-objective (emission and operation cost functions) optimization with DSM.
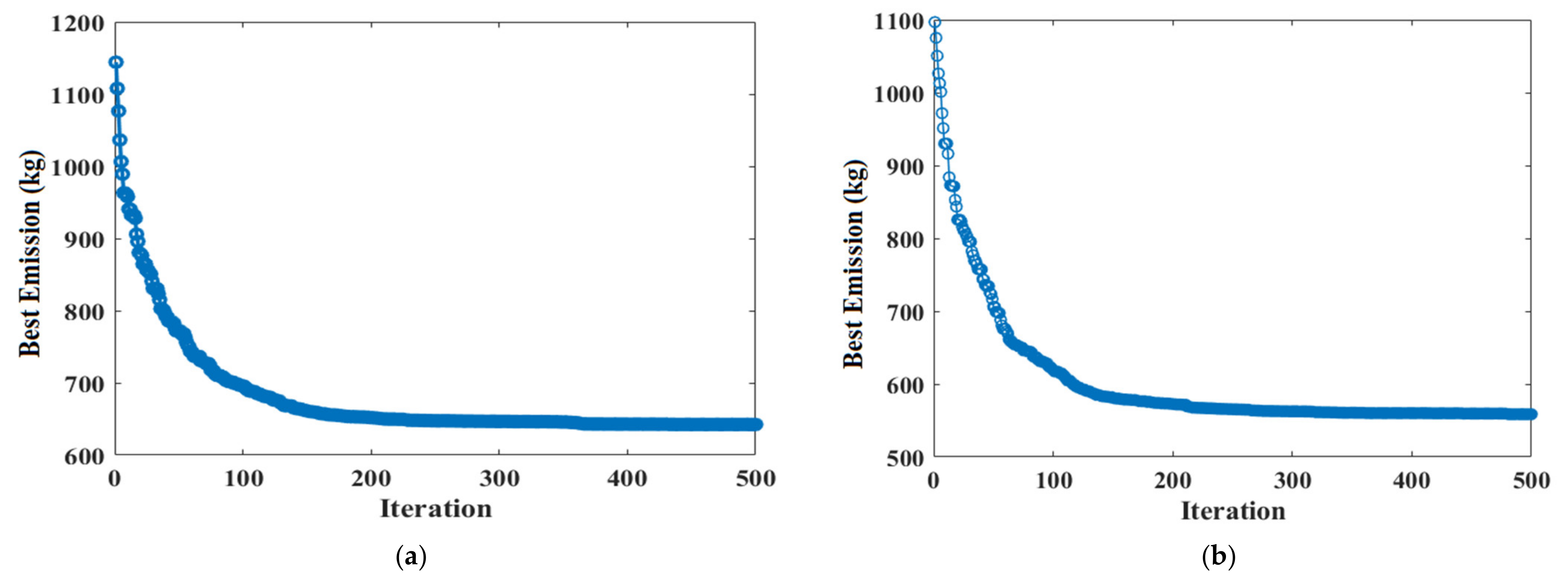
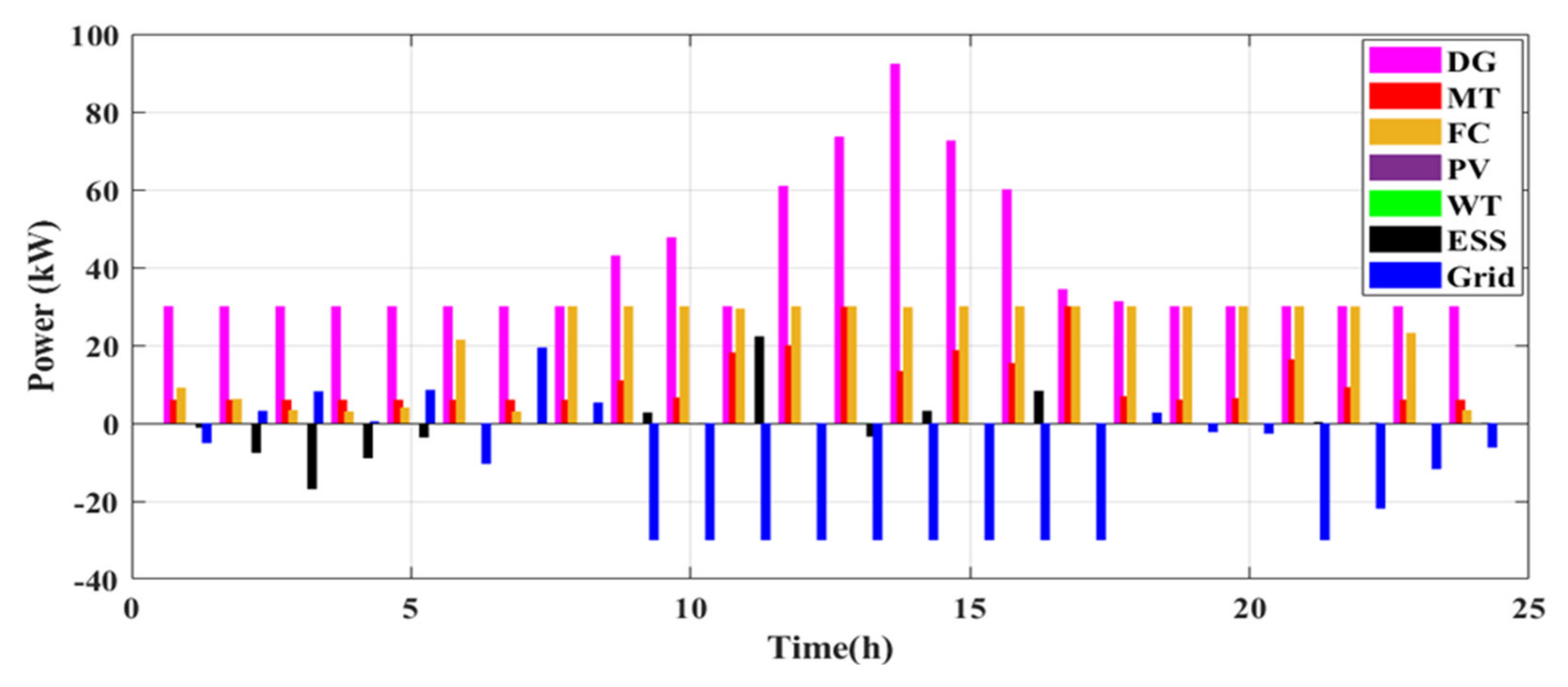
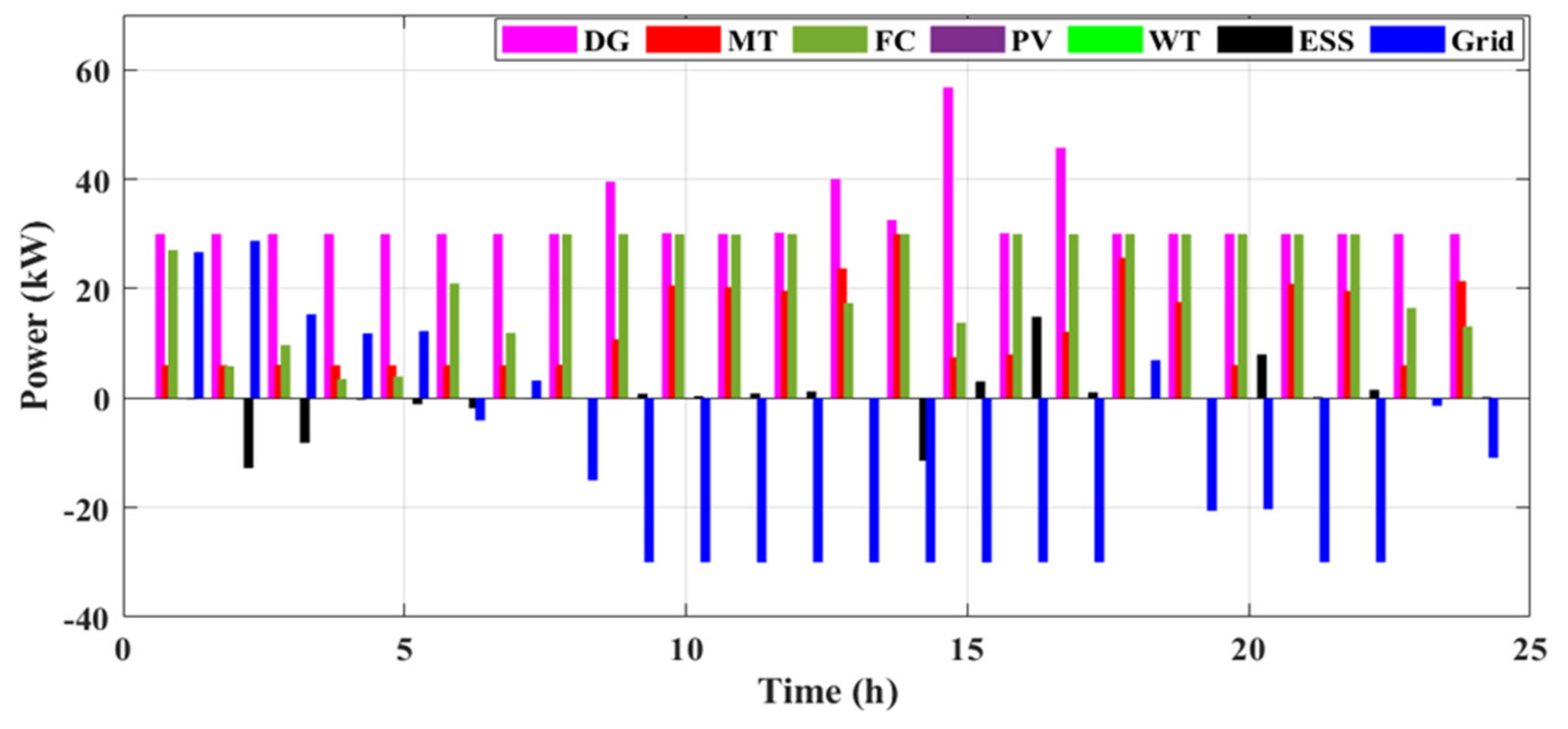
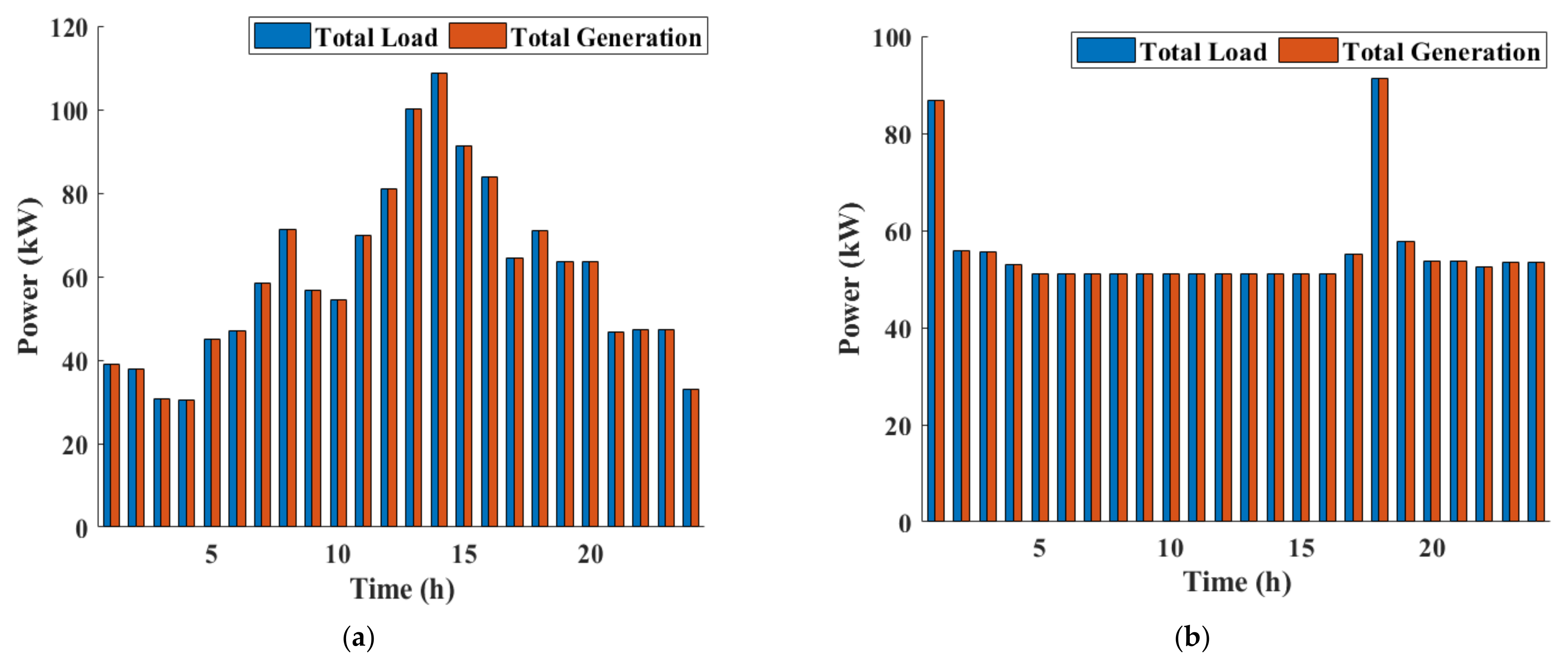
8.1. Cases #1 and #2: Emission Function Optimization Only without and with DSM
8.2. Cases #3 and #4: Operation Cost Function Optimization Only without and with DSM
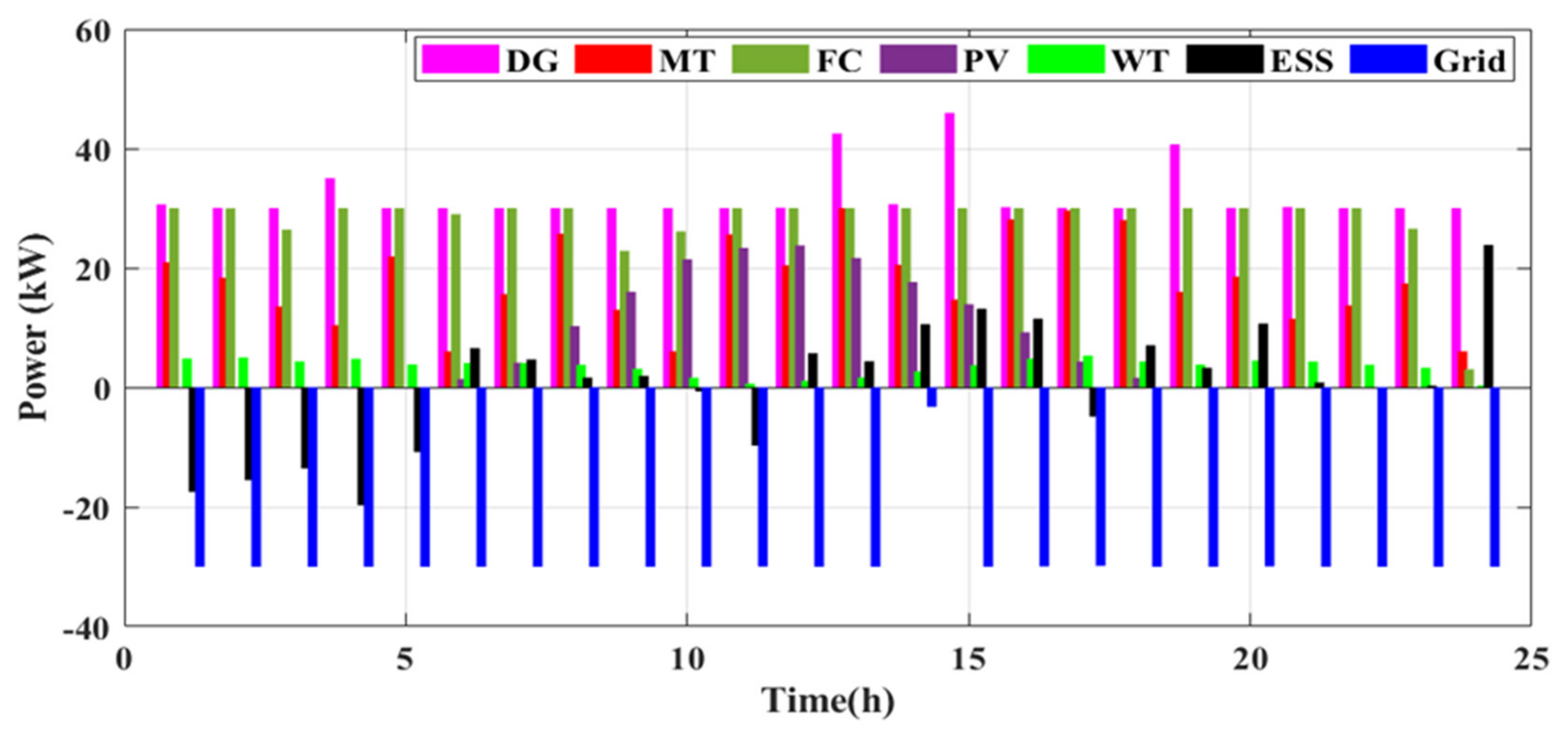
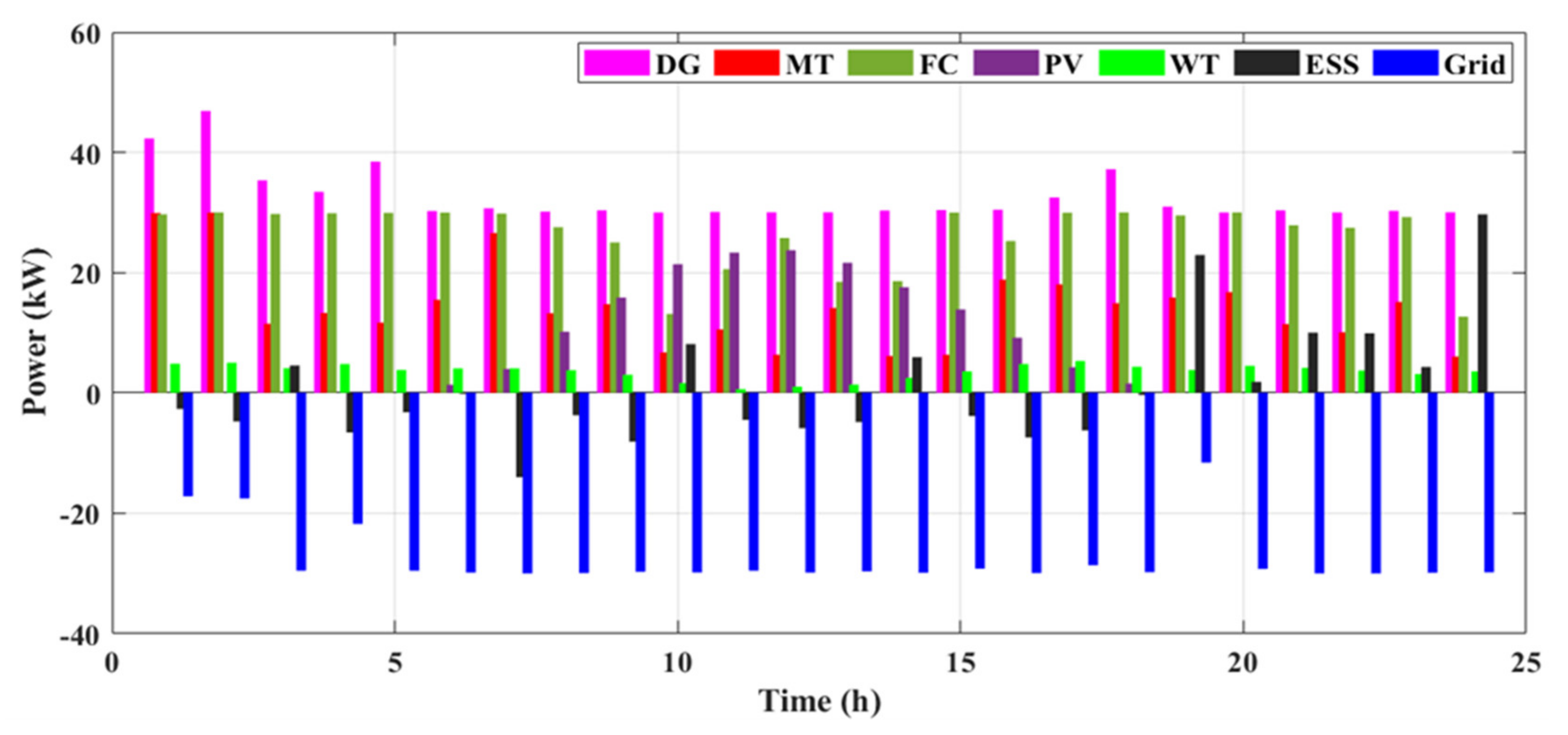
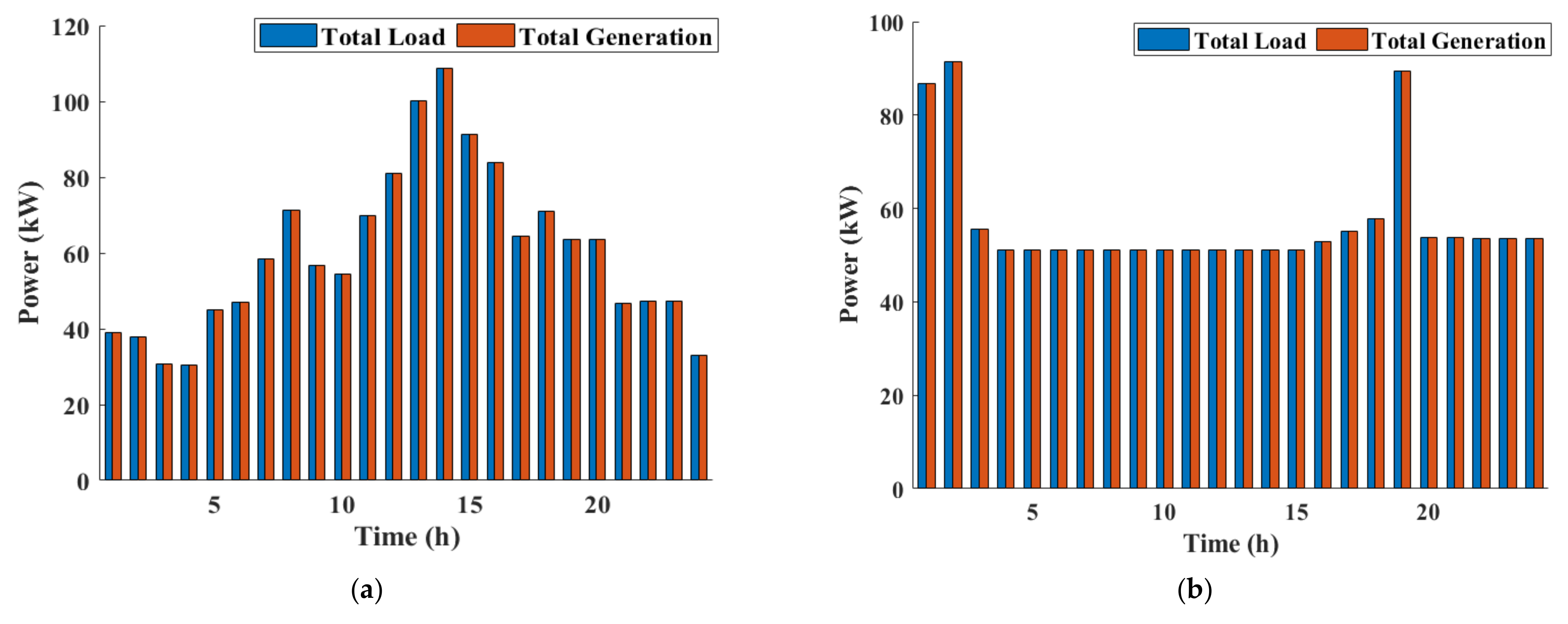
8.3. Cases #5 and #6: Emission and Operation Cost Functions Optimization without and with DSM
8.4. Time Testing Results
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Behrangrad, M. A review of demand side management business models in the electricity market. Renew. Sustain. Energy Rev. 2015, 47, 270–283. [Google Scholar] [CrossRef]
- Yan, X.; Ozturk, Y.; Hu, Z.; Song, Y. A review on price-driven residential demand response. Renew. Sustain. Rev. 2018, 96, 411–419. [Google Scholar] [CrossRef]
- Aghaei, J.; Alizadeh, M.; Abdollahi, A.; Barani, M. Allocation of demand response resources: Towards an effective contribution to power system voltage stability. IET Gener. Transm. Distrib. 2016, 10, 4169–4177. [Google Scholar] [CrossRef]
- Aghajani, S.; Kalantar, M. Operational scheduling of electric vehicles parking lot integrated with renewable generation based on bilevel programming approach. Energy 2017, 139, 422–432. [Google Scholar] [CrossRef]
- Akbaria, H.; Browne, M.C.; Ortega, A.; Huang, M.J.; Hewitt, N.J.; Norton, B.; McCormack, S.J. Efficient energy storage technologies for photovoltaic systems. Sol. Energy 2019, 192, 144–168. [Google Scholar] [CrossRef]
- Aydin, D.; Ozyon, S.; Yasar, C.; Liao, T. Artificial bee colony algorithm with dynamic population size to combined economic and emission dispatch problem. Int. J. Electr. Power Energy Syst. 2014, 54, 144–153. [Google Scholar] [CrossRef]
- Rajan, A.; Malakar, T. Optimum economic and emission dispatch using exchange market algorithm. Int. J. Electr. Power Energy Syst. 2016, 82, 545–560. [Google Scholar] [CrossRef]
- Nanjundappan, D.; Nanjundappan, D. Hybrid weighted probabilistic neural network and biogeography based optimization for dynamic economic dispatch of integrated multiple-fuel and wind power plants. Int. J. Electr. Power Energy Syst. 2016, 77, 385–394. [Google Scholar] [CrossRef]
- Zaman, M.; Elsayed, S.M.; Ray, T.; Sarker, R.A. Evolutionary algorithms for dynamic economic dispatch problems. IEEE Trans. Power Syst. 2016, 31, 1486–1495. [Google Scholar] [CrossRef]
- Zaman, F.; Elsayed, S.M.; Ray, T.; Sarker, R.A. Configuring two-algorithm-based evolutionary approach for solving dynamic economic dispatch problems. Eng. Appl. Artif. Intell. 2016, 53, 105–125. [Google Scholar] [CrossRef]
- Aghaei, J.; Niknam, T.; Azizipanah-Abarghooee, R.; Arroyo, J.M. Scenario-based dynamic economic emission dispatch considering load and wind power uncertainties. Int. J. Electr. Power Energy Syst. 2013, 47, 351–367. [Google Scholar] [CrossRef]
- Duan, J.; Chow, M. Robust Consensus-based Distributed Energy Management for Microgrids with Packet Losses Tolerance. IEEE Transactions Smart Grid 2019, 11, 281–290. [Google Scholar] [CrossRef]
- Tajalli, S.; Mardaneh, M.; Taherian-Fard, E.; Izadian, A.; Kavousi-Fard, A.; Dabbaghjamanesh, M.; Niknam, T. DoS-Resilient Distributed Optimal Scheduling in a Fog Supporting IIoT-Based Smart Microgrid. IEEE Trans. Ind. Appl. 2020, 56, 2968–2977. [Google Scholar] [CrossRef]
- Bilal, N.; Jasim, B.H.; Sedhom, B.E.; Guerrero, J.M. Consensus Algorithm-based Coalition Game Theory for Demand Management Scheme in Smart Microgrid. Sustain. Cities Soc. 2021, 74, 103248. [Google Scholar] [CrossRef]
- Pirouzi, S.; Zaghian, M.; Aghaei, J.; Chabok, H.; Abbasi, M.; Norouzi, M.; Shafie-Khah, M.; Catalão, J.P. Hybrid planning of distributed generation and distribution automation to improve reliability and operation indices. Electr. Power Energy Syst. 2022, 135, 107540. [Google Scholar] [CrossRef]
- Asl, S.A.F.; Bagherzadeh, L.; Pirouzi, S.; Norouzi, M.; Lehtonen, M. A new two-layer model for energy management in the smart distribution network containing flexi-renewable virtual power plant. Electr. Power Syst. Res. 2021, 194, 107085. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand side management in smart grid using heuristic optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Nadeem, J.; Ullah, I.; Akbar, M.; Iqbal, Z.; Khan, F.A.; Alrajeh, N.; Alabed, M.S. An Intelligent Load Management System With Renewable Energy Integration for Smart Homes. IEEE Access 2017, 5, 13587–13600. [Google Scholar] [CrossRef]
- Banala, V.; Sankaramurthy, P.; Chokkalingam, B.; Mihet-Popa, L. Managing the Demand in a Micro Grid Based on Load Shifting with Controllable Devices Using Hybrid WFS2ACSO Technique. Energies 2022, 15, 790. [Google Scholar]
- Sharma, A.; Saxena, A. A demand side management control strategy using Whale optimization algorithm. SN Appl. Sci. 2019, 1, 703–714. [Google Scholar] [CrossRef]
- Kumar, K.; Saravanan, B. Day ahead scheduling of generation and storage in a micro grid considering demand Side management. J. Energy Storage 2019, 21, 78–86. [Google Scholar] [CrossRef]
- Arif, A.; Javed, F.; Arshad, N. Integrating renewables economic dispatch with demand side management in micro-grids: A genetic algorithm-based approach. Energy Effic. 2014, 7, 271–284. [Google Scholar] [CrossRef]
- Chung, H.M.; Su, C.L.; Wen, C.K. Dispatch of generation and demand side response in regional grids. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC) IEEE, Rome, Italy, 10–13 June 2015; pp. 482–486. [Google Scholar] [CrossRef]
- Alham, M.; Elshahed, M.; Ibrahim, D.K.; El Zahab, E.E.D. A dynamic economic emission dispatch considering wind power uncertainty incorporating energy storage system and demand side management. Renew. Energy 2016, 96, 800–811. [Google Scholar] [CrossRef]
- Alham, M.; Elshahed, M.; Ibrahim, D.K.; El Zahab, E.E.D. Optimal operation of power system incorporating wind energy with demand side management. Ain Shams Eng. J. 2015, 8, 1–7. [Google Scholar] [CrossRef]
- Bilal, N.; Jasim, B.; Rahman, Z.-A.; Siano, P. A Novel Robust Smart Energy Management and Demand Reduction for Smart Homes Based on Internet of Energy. Sensors 2021, 21, 4756. [Google Scholar] [CrossRef]
- Shakouri, H.; Kazemi, A. Multi-objective cost-load optimization for demand side management of a residential area in smart grids. Sustain. Cities Soc. 2017, 32, 171–180. [Google Scholar] [CrossRef]
- Deyaa, A.; Ebeed, M.; Ali, A.; Alghamdi, A.; Kamel, S. Multi-Objective Energy Management of a Micro-Grid Considering Stochastic Nature of Load and Renewable Energy Resources. Electronics 2021, 10, 403. [Google Scholar] [CrossRef]
- Seshu, R.; Raghav, L.P.; Raju, D.K.; Singh, A.R. Impact of multiple demand side management programs on the optimal operation of grid-connected microgrids. Appl. Energy 2021, 301, 117466. [Google Scholar] [CrossRef]
- Faria, P.; Soares, J.; Vale, Z.; Morais, H.; Sousa, T. Modified particle swarm optimization applied to integrated demand response and DG resources scheduling. IEEE Trans. Smart Grid 2013, 4, 606–616. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Jadid, S.; Siano, P. Stochastic multi-objective operational planning of smart distribution systems considering demand response programs. Electr. Power Syst. Res. 2014, 111, 156–168. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Tan, R. Distributed model predictive control for onconnected microgrid power management. IEEE Trans. Control. Syst. Technol. 2018, 26, 1028–1039. [Google Scholar] [CrossRef]
- Maulik, A.; Das, D. Optimal power dispatch considering load and renewable generation uncertainties in an AC-DC hybrid microgrid. IET Gener. Transm. Distrib. 2019, 13, 1164–1176. [Google Scholar] [CrossRef]
- Yng, L.; Fan, X.; Cai, Z.; Bing, Y. Optimal active power dispatching of microgrid and DistributionNetwork based on model predictive control. Tsinghua Sci. Technol. 2018, 23, 266–276. [Google Scholar] [CrossRef]
- Atwa, Y.; El-Saadany, E.F.; Salama, M.M.A.; Seethapathy, R. Optimal renewable resources mix for distribution system energy loss minimization.,IEEE Transactions on. Power Syst. 2010, 25, 360–370. [Google Scholar] [CrossRef]
- Ettoumi, F.Y.; Mefti, A.; Adane, A.; Bouroubi, M. Statistical analysis of solar measurements in Algeria using beta distributions. Renew Energy 2002, 26, 47–67. [Google Scholar] [CrossRef]
- Deshmukh, M.; Deshmukh, S. Modeling of hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2008, 12, 235–249. [Google Scholar] [CrossRef]
- Athanasios, P.; Pillai, S. Probability, Random Variables and Stochastic Processes, 4th ed.; McGraw-Hill: New York, NY, USA, 2002; p. 852. [Google Scholar]
- Rahimi, E.; Rabiee, A.; Aghaei, J.; Muttaqi, K.M.; Nezhad, A.E. On the management of wind power intermittency. Renew. Sustain. Energy Rev. 2013, 28, 643–653. [Google Scholar] [CrossRef]
- Gen, B. Reliability and Cost/Worth Evaluation of Generating Systems Utilizing wind and Solar Energy. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2005. [Google Scholar]
- Owner’s Manual of the AIR403 Wind Turbine Made by Southwest Wind Power Inc. Available online: www.nooutage.com/pdf/swwp_air403_landman.pdf (accessed on 16 May 2022).
- Abouzahr, I.; Ramakumar, R. An approach to assess the performance of utilityinteractive wind electric conversion systems. Energy Conversion. IEEE Trans. 1991, 6, 627–638. [Google Scholar]
- Tina, G.; Gagliano, S.; Raiti, S. Hybrid solar/wind power system probabilistic modelling for long-term performance assessment. Sol. Energy 2006, 80, 578–588. [Google Scholar] [CrossRef]
- Awais, M.; Javaid, N.; Shaheen, N.; Iqbal, Z.; Rehman, G.; Muhammad, K.; Ahmad, I. An Efficient Genetic Algorithm Based Demand Side Management Scheme for Smart Grid. In Proceedings of the 2015 18th International Conference on Network-Based Information Systems, Taipei, Taiwan, 2–4 September 2015. [Google Scholar]
- Kothari, D. Modern Power System Analysis; Tata McGraw-Hill: New Delhi, India, 2003. [Google Scholar]
- Alessandro, A.; De Pascale, G.; Detti, P.; Vicino, A. Load Sceduling for Household Energy Consumption Optimization. IEEE Trans. Smart Grid 2013, 4, 2364–2373. [Google Scholar]
- Shengan, S.; Manisa, P.; Saifur, R. Demand Response as a Load Shaping Tool in an Intelligent Grid With Electric Vehicles. IEEE Trans. Smart Grid 2011, 2, 624–631. [Google Scholar]
- Yi, P.; Dong, X.; Iwayemi, A.; Zhou, C.; Li, S. Real-time Oppertunistic Scheduling for Residential Demand Response. IEEE Trans. Smart Grid 2018, 4, 227–234. [Google Scholar] [CrossRef]
- Mohammad, D.; Montazeri, Z.; Malik, O.P.; Dhiman, G.; Kumar, V. BOSA: Binary Orientation Search Algorithm. Int. J. Innov. Technol. Explor. Eng. (IJITEE) 2019, 9, 5306–5310. [Google Scholar]
- Amjad, A.; Seifi, A.; Niknam, T.; Pahlavani, M.R.A. Multi-objective operation management of a renewable MG (micro-grid) with back-up micro-turbine/fuel cell/battery hybrid power source. Energy 2011, 36, 6490–6507. [Google Scholar] [CrossRef]
- Ali, M.; Basil, H. Grid-Forming and Grid-Following Based Microgrid Inverters Control. Iraqi J. Electr. Electron. Eng. 2022, 18, 111–131. [Google Scholar] [CrossRef]
- Kiani, H.; Hesami, K.; Azarhooshang, A.; Pirouzi, S.; Safaee, S. Adaptive robust operation of the active distribution network including renewable and flexible sources. Sustain. Energy Grids Netw. 2021, 26, 100476. [Google Scholar] [CrossRef]
- Aghaei, J.; Bozorgavari, S.A.; Pirouzi, S.; Farahmand, H.; Korpås, M. Flexibility Planning of Distributed Battery Energy Storage Systems in Smart Distribution Networks. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 44, 1105–1121. [Google Scholar] [CrossRef]
- Bilal, N.; Jasim, B.H.; Sedhom, B.E. Distributed secondary consensus fault tolerant control method for voltage and frequency restoration and power sharing control in multi-agent microgrid. Int. J. Electr. Power Energy Syst. 2021, 133, 107251. [Google Scholar]
- Mahmoudi, C.; Flah, A.; Sbita, L. An Overview of Electric Vehicle Concept and Power Management Strategies. In Proceedings of the International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Tunis, Tunisia, 3–6 November 2014. [Google Scholar] [CrossRef]
- Mahmoudi, C.; Flah, A. A Novel Energy Optimization Approach for Electrical Vehicles in a Smart City. Energies 2019, 12, 929. [Google Scholar] [CrossRef]
- Mohamed, A.; Awwad, E.M.; El-Sherbeeny, A.M.; Nasr, E.A.; Ali, Z.M. Optimal scheduling of reconfigurable grids considering dynamic line rating constraint. IET Gener. Transm. Distrib. 2020, 14, 1862–1871. [Google Scholar] [CrossRef]
- Mohamed, A. A relaxed consensus plus innovation based effective negotiation approach for energy cooperation between smart grid and microgrid. Energy 2022, 252, 123996. [Google Scholar] [CrossRef]
- Mohamed, A.; Almalaq, A.; Abdullah, H.M.; Alnowibet, K.A.; Alrasheedi, A.F.; Zaindin, M.S.A. A distributed stochastic energy management framework based-fuzzy-PDMM for smart grids considering wind park and energy storage systems. IEEE Access 2021, 9, 46674–46685. [Google Scholar] [CrossRef]
- Bilal, N.; Jasim, B.H.; Issa, W.; Anvari-Moghaddam, A.; Blaabjerg, F. A New Robust Control Strategy for Parallel Operated Inverters in Green Energy Applications. Energies 2020, 13, 3480. [Google Scholar] [CrossRef]
- Alhasnawi, B.; Jasim, B.; Siano, P.; Guerrero, J. A Novel Real-Time Electricity Scheduling for Home Energy Management System Using the Internet of Energy. Energies 2021, 14, 3191. [Google Scholar] [CrossRef]
- Sonam, P.; Swarnkar, A.; Niazi, K.R.; Gupta, N. Multiobjective optimal sizing of battery energy storage in grid-connected microgrid. J. Eng. 2019, 18, 5280–5283. [Google Scholar] [CrossRef]
- Coello, C.A.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02, Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Kraiem, H.; Flah, A.; Mohamed, N.; Alowaidi, M.; Bajaj, M.; Mishra, S.; Sharma, M.K.; Sharma, S.K. Increasing Electric Vehicle Autonomy Using a Photovoltaic System Controlled by Particle Swarm Optimization. IEEE Access 2021, 9, 72040–72054. [Google Scholar] [CrossRef]
- The Solar Power Group Company. Available online: https://thesolarpowergroup.com.au (accessed on 8 April 2022).
- Chen, C.; Duan, S.; Cai, T.; Liu, B.; Hu, G. Smart energy management system for optimal microgrid economic operation. IET Renew. Power Gener. 2011, 5, 258–267. [Google Scholar] [CrossRef]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid. IEEE Trans. Power Syst. 2010, 25, 371–380. [Google Scholar] [CrossRef]

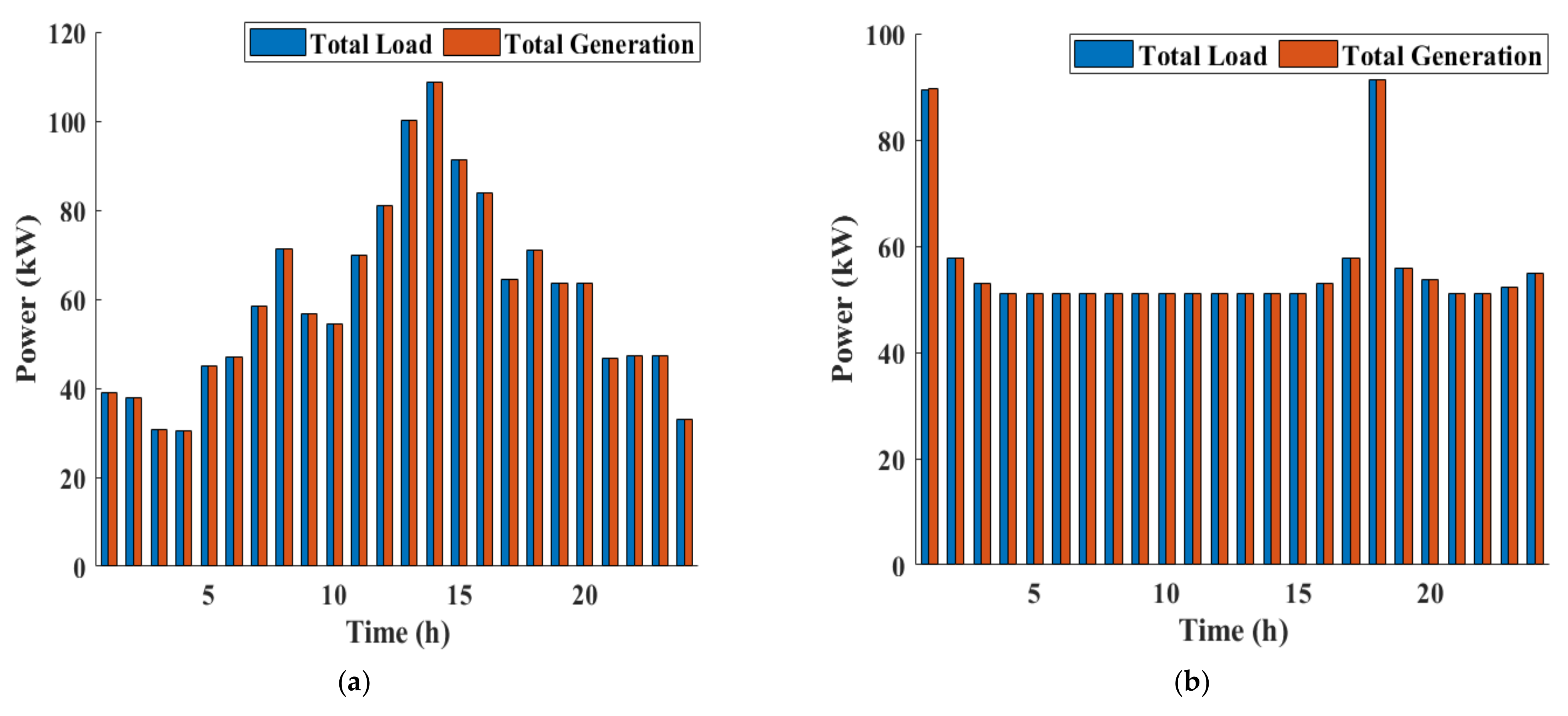
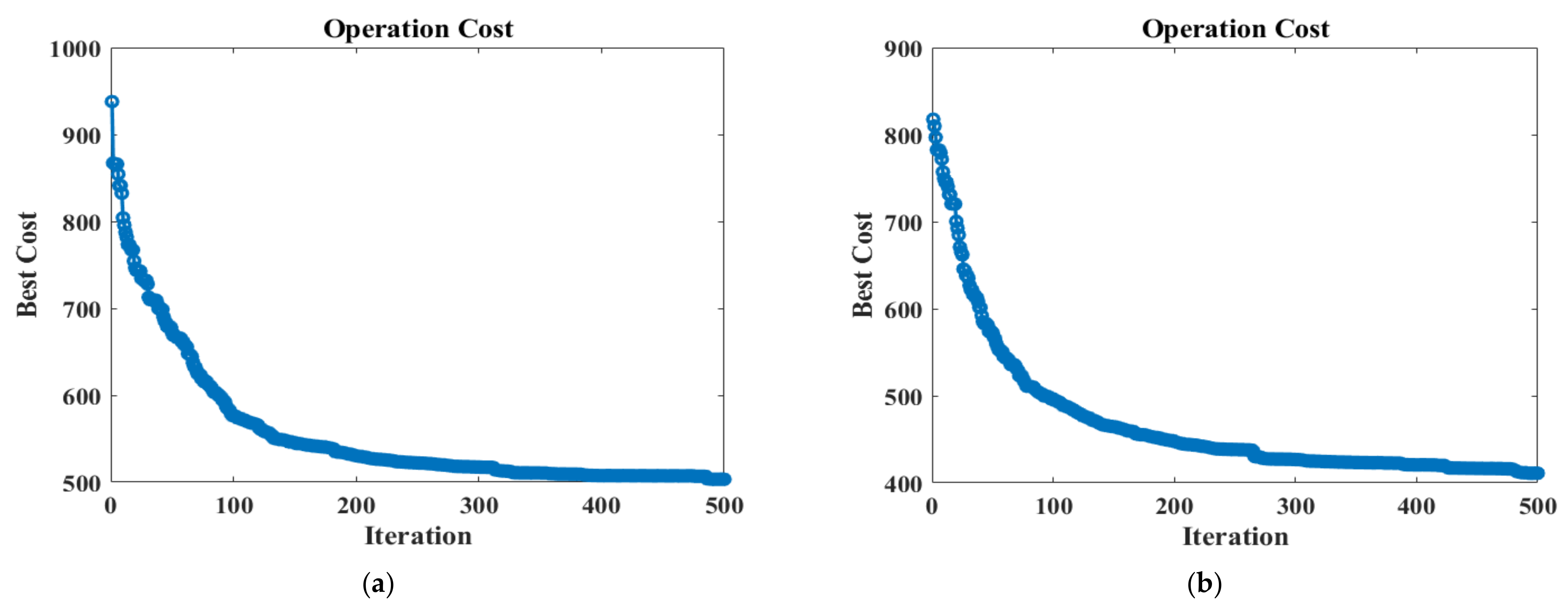

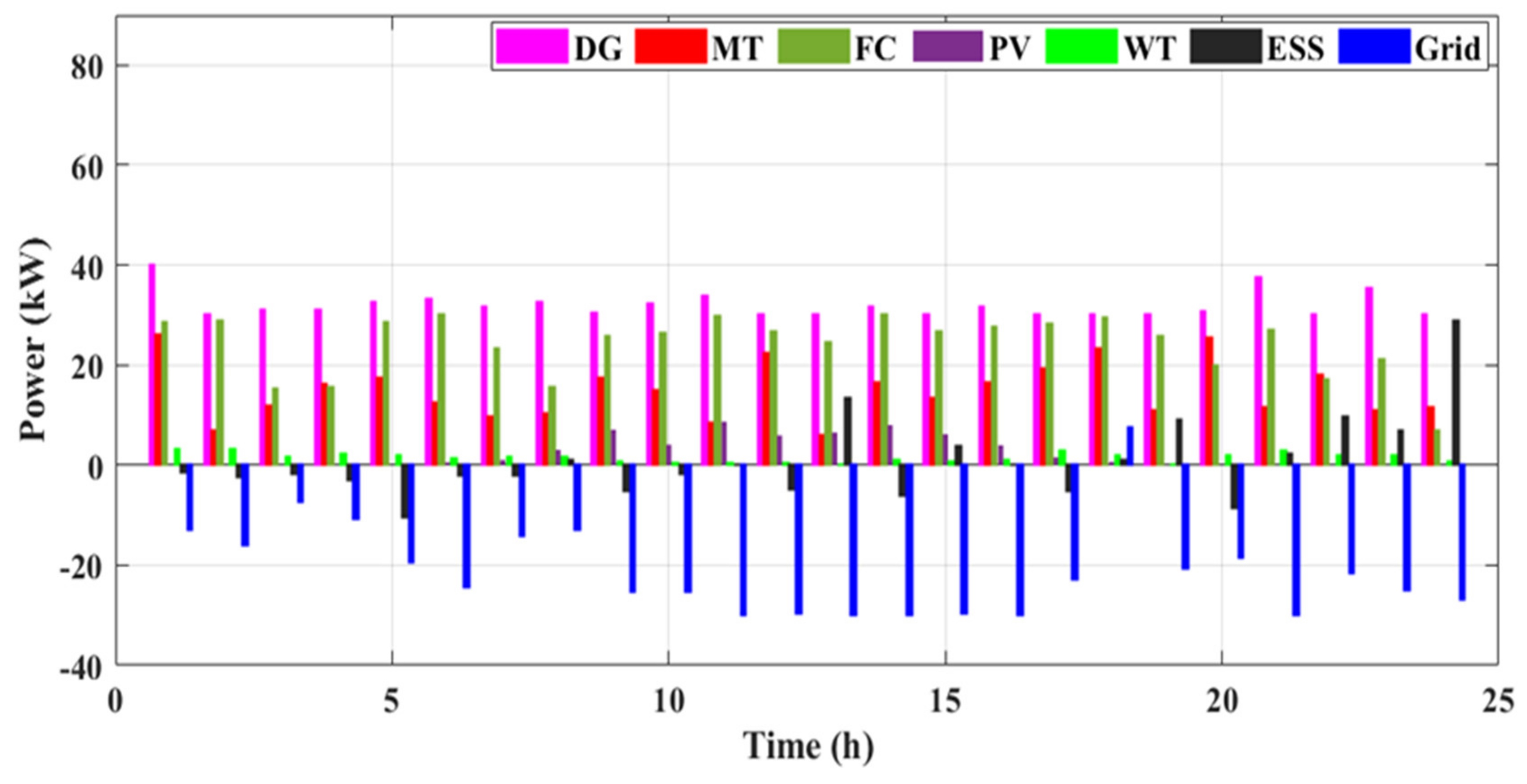
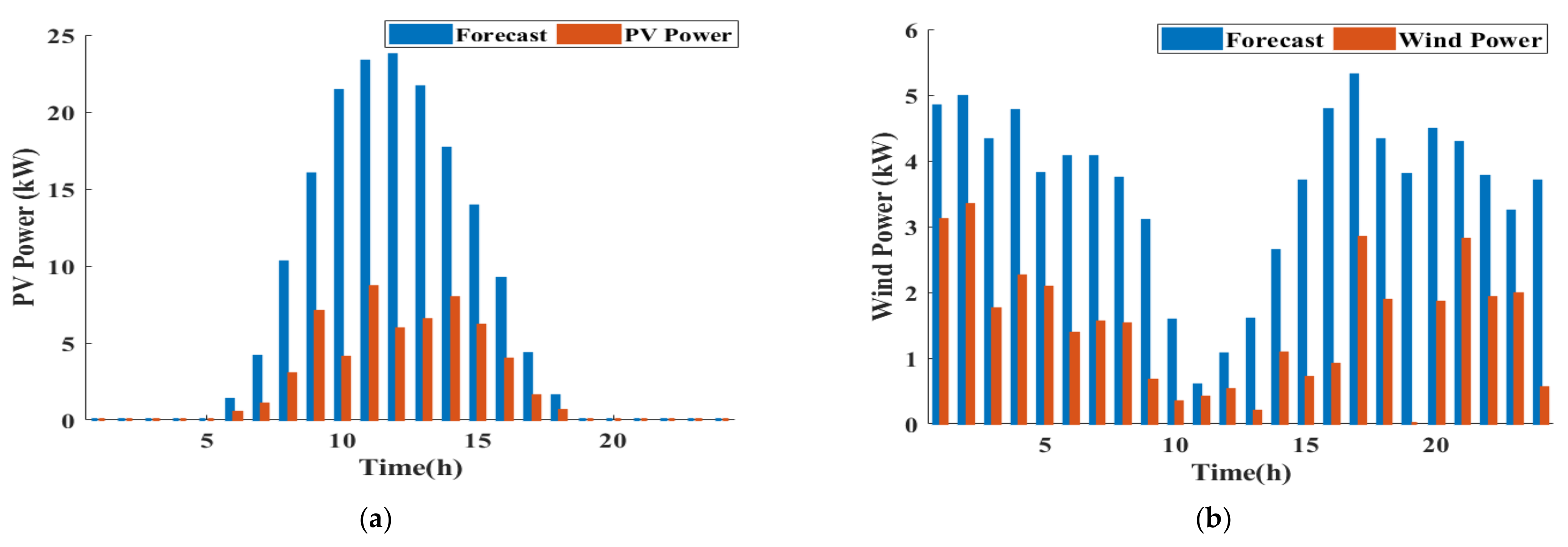

| Ref. | Resolved Problem(s) | Limitations |
|---|---|---|
| [9,10,11,12,13,14,15,16] | DEED | Demand-side scheduling was not optimized, and optimal multi-objective energy management was not applied. |
| [18,19,20,21] | DSM | DEED and multi-objective energy management were not applied. |
| [22,23,24,25,26,27,28,29,30,31,32,33,34] | DSM and DEED | In [24,25], the optimal DSM is not used. In [26,32,34], multi-objective optimization functions are not employed. The authors of [22,23,27,28,29,31,33] proposed multi-objective optimization with DR only, and load appliances scheduling based on intelligent DSM with a load-shifting program was not implemented. |
| Unit Type | Bid USD/kWh) | SU/SD (USD) | CO2 (kg/MWh) | SO2 (kg/MWh) | NOx (kg/MWh) | Pmin (kW) | Pmax (kW) |
|---|---|---|---|---|---|---|---|
| DG | 0.586 | 0.15 | 890 | 0.0045 | 0.23 | 30 | 300 |
| MT | 0.457 | 0.96 | 750 | 0.0036 | 0.1 | 6 | 30 |
| FC | 0.294 | 1.65 | 460 | 0.003 | 0.0075 | 3 | 30 |
| PV | 0.7 | 0 | 0 | 0 | 0 | 0 | 25 |
| WT | 0.65 | 0 | 0 | 0 | 0 | 0 | 15 |
| ESS | 0.38 | 0 | 10 | 0.0002 | 0.001 | −30 | 30 |
| Appliance Number | Appliance Type | Operating Time | IL Rated Power (kW) | CL Rated Power (kW) | RL Rated Power (kW) |
|---|---|---|---|---|---|
| 1 | Nonshiftable | 12 AM–12 PM | 4 | 4 | 2 |
| 2 | Shiftable | 7–9 AM, 11 AM–14 PM & 18 PM–22 PM | 0.6 | 0.6 | 0.3 |
| 3 | Shiftable | 7 AM–12 PM, 15 PM–20 PM | 0.4 | 0.4 | 0.2 |
| 4 | Shiftable | 1 AM–10 AM, 15 PM–24 PM | 4.8 | 4.8 | 2.4 |
| 5 | Shiftable | 7 AM–9 AM, 11 AM–14 PM, 18 PM–22 PM | 0.6 | 0.6 | 0.3 |
| 6 | Shiftable | 8 AM–18 PM | 0.4 | 0.4 | 0.2 |
| 7 | Shiftable | 10 AM–15 PM, 18 PM–22 PM | 0.4 | 0.4 | 0.3 |
| 8 | Nonshiftable | 12 AM–12 PM | 2 | 2 | 1 |
| 9 | Nonshiftable | 12 AM–12 PM | 1.6 | 1.6 | 0.8 |
| Operational Condition of MG | Case No. | BOSA (Elapsed Time) | MOPSO (Elapsed Time) | BOSA + MOPSO (Elapsed Time) |
|---|---|---|---|---|
| Optimal DEED without DSM | #1 | - | 43.99 s | 43.99 s |
| #3 | - | 36.92 s | 36.92 s | |
| #5 | - | 63.41 s | 63.41 s | |
| Optimal DEED with DSM | #2 | 3.77 s | 44.29 s | 49.06 s |
| #4 | 3.59 s | 37.26 s | 40.97 s | |
| #6 | 3.7 s | 63.72 s | 67.85 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasim, A.M.; Jasim, B.H.; Kraiem, H.; Flah, A. A Multi-Objective Demand/Generation Scheduling Model-Based Microgrid Energy Management System. Sustainability 2022, 14, 10158. https://doi.org/10.3390/su141610158
Jasim AM, Jasim BH, Kraiem H, Flah A. A Multi-Objective Demand/Generation Scheduling Model-Based Microgrid Energy Management System. Sustainability. 2022; 14(16):10158. https://doi.org/10.3390/su141610158
Chicago/Turabian StyleJasim, Ali M., Basil H. Jasim, Habib Kraiem, and Aymen Flah. 2022. "A Multi-Objective Demand/Generation Scheduling Model-Based Microgrid Energy Management System" Sustainability 14, no. 16: 10158. https://doi.org/10.3390/su141610158
APA StyleJasim, A. M., Jasim, B. H., Kraiem, H., & Flah, A. (2022). A Multi-Objective Demand/Generation Scheduling Model-Based Microgrid Energy Management System. Sustainability, 14(16), 10158. https://doi.org/10.3390/su141610158







