Abstract
To manage the environmental impact of logistics, we considered a logistics service supply chain consisting of a fourth-party logistics company (4PL) and a third-party logistics company (3PL), where the 4PL deputed the 3PL with the logistics tasks of a client. We examined the investment and pricing strategies adopted by the 4PL for the 3PL, and how factors such as logistics audits level and commitment to investment efforts affected the motivation of the 4PL’s strategy choice. The results showed that if the investment cost was low, the 4PL motivated the 3PL to make efforts by investment. Otherwise, the 4PL incentivized the 3PL by providing a high wholesale price or using a high investment level and medium wholesale price. In addition, when the rectification costs of the 3PL were sufficiently high, increasing the audit level could improve the probability of complying with environmental regulations.
1. Introduction
The supply chain accounts for more than 90% of the environmental impact of most consumer goods companies, according to McKinsey & Company [1]. Therefore, with the development of industry, the supply chain is the primary cause, for most companies, of their environmental impact [2,3]. The transportation industry has a great impact on global air and water pollution, accounting for about 28% of global greenhouse gas emissions [4]. To achieve sustainability in the logistics area, the concept of green logistics has been proposed. Green logistics refers to a set of sustainable policies and measures aimed at reducing environmental impact [5]. Reducing the impact of logistics and transportation is at the heart of green logistics.
Fourth-party logistics, as an integrator of the supply chain, has made some explorations in sustainability. To ensure the sustainability of the supply chain, a fourth-party logistics company (4PL) is more willing to cooperate with a green third-party logistics company (3PL) [6]. The 4PL leverages the combined capabilities of the 3PL and management consulting, to provide solutions, while the 3PL focuses on operational issues, such as implementation and execution. For example, Cainiao Network, founded by Alibaba in 2013, is a 4PL, and connects a network of logistics partners, warehouses, and merchants, by creating a logistics information platform. In 2016, Cainiao Network joined with 32 logistics partners to launch a “Go Green Campaign” to explore ways to mitigate the environmental impact of the logistics industry, aiming to reduce carbon emissions by 3.62 million tons by 2020, while replacing 50 percent of e-commerce packaging with biodegradable materials [7].
Green logistics is primarily concerned with environmental protection, and involves all attempts to reduce the ecological impact of regional and global supply chains [8,9]. Thus, green logistics seeks changes in all processes, from product design to transportation types and routes. Periodic environmental audits are the critical enablers for successfully achieving this transformation [10,11]. For example, PwC provides audit services for non-financial information, including carbon footprint and environmental information, in Corporate Social Responsibility reports [12]. The audit of sustainability covers the entire supply chain [13], and the process includes analysis of current production systems, data analysis and reporting, and determining the best alternative.
Investment in logistics is an incentive instrument to improve sustainability [14]. Logistics investment refers to the allocation of capital through infrastructure, operations (transportation modes and equipment), and human resources (labor, management, etc.), to increase integration with supply chains, make better use of transportation assets, and improve the efficiency of freight distribution [15]. Therefore, the 4PL can invest in infrastructure, such as process automation or more efficient handling equipment, that can enable the 3PL to deploy resources more effectively [16]. For example, the Cainiao Green Foundation, formed by Cainiao Network with six leading logistics providers in China, invested about $40 million toward sustainability initiatives [4]. Li & Fung Logistics has invested heavily in “efficient equipment, technologies, systems and vehicular fleets” to improve sustainable logistics [17].
The level of logistics compliance with environmental regulations also depends on the efforts made by the 3PL, including improvements to the logistics process, investment in the logistics and delivery system, and training of delivery personnel. Furthermore, the 4PL’s investment efforts and the 3PL’s efforts may interact and jointly affect the level of logistics compliance with environmental regulations. For example, the 4PL may provide education and training on environmental management to the 3PL’s employees, and such efforts made by the 4PL will complement the 3PL’s efforts to improve its compliance level, because the skills acquired enable the 3PL to deploy resources more efficiently. Therefore, the 4PL’s investment improves the probability of the 3PL’s efforts to pass the audit being successful.
To improve the level of compliance level with environmental regulations, we investigated the investment and pricing strategies of the 4PL compared to the 3PL, and analyzed the effect of the logistics audit level, and the 4PL’s commitment to the level of investment, on the choice of strategies. We considered a logistics service supply chain, in which the 4PL deputed the delivery task of the client to a 3PL by a wholesale price contract. The 3PL decided whether to make efforts, while the 4PL chose whether the investment level was high or low, and determined the wholesale price. The 4PL set the efforts standards that the 3PL should comply with, and audited the 3PL’s actual efforts during the delivery process after entering a contract [18]. The 3PL’s not making efforts would lead to the logistics not complying with environmental regulations, and the not-complying would be recognized by the public, resulting in the 4PL suffering from a cost in loss of public goodwill. The 4PL might not commit (base case) or might commit its investment level: in the case of non-commitment, the 3PL and the 4PL would move simultaneously in their respective efforts, while in the case of commitment, the 4PL’s efforts could be known before the 3PL decided. We summarize our main findings below.
- Strategies for the 3PL to make more efforts. The 4PL can use different strategies to motivate the 3PL to make efforts. Firstly, when the investment cost is lower, the 4PL can incentivize the 3PL to make efforts by investment. Secondly, when the investment cost is higher, the 4PL can incentivize the 3PL to make efforts by offering a high enough wholesale price that it incurs a potential loss if it loses the contract with the 4PL. Thirdly, the 4PL can use low investment and medium wholesale price to deter the 3PL from not making efforts, which should only be used in the commitment case, as the 3PL would like to adopt the medium wholesale price and make efforts only if it knows the 4PL’s investment.
- Factors affecting the 4PL’s strategies. Increasing the goodwill cost can improve the 3PL’s efforts. However, reducing the investment cost does not necessarily increase the 3PL’s efforts, as the 4PL may replace the price premium with an investment strategy. When the investment cost is higher, the 4PL is faced with high goodwill cost, and will offer a high wholesale price to increase the 3PL’s efforts. When the investment is lower, the 4PL may rely solely on the investment to improve the 3PL’s efforts, which could lead to a decrease in the 3PL’s efforts, since the investment strategy only partially increases the 3PL’s efforts. In addition, increasing the audit level can increase the 3PL’s effort level when its rectification costs are sufficiently high.
- The commitment to investment effort. Commitment to investment effort certainly improves the final logistics compliance level. The 4PL’s commitment to investment effort can help the 3PL make efforts by using a high-investment and medium wholesale price strategy. In addition, a commitment to investment effort enables the 4PL to use a high-investment strategy, which can complement the 3PL’s efforts.
The rest of this paper is organized as follows. Section 2 reviews the relevant literature. We discuss the modeling approach in Section 3. In Section 4, we provide the model for the 4PL of not committing to its investment effort. We then focus on the model for the 4PL committing to its investment effort in Section 5. We conclude this paper in Section 6. All proofs are provided in the Appendix A, Appendix B, Appendix C and Appendix D.
2. Literature Review
Our paper is related to three streams of research: sustainability supply chain management, audits in the supply chain, and logistics service supply chain management.
2.1. Sustainability Supply Chain Management
From the early 2000s, sustainable operations management developed as an area that incorporates environmental and social issues into the supply chain management framework [19]. The environment, society, and economics are the triple-bottom-line dimensions of sustainability [20]. In regard to 4PL operations management, Qian, et al. [6], studied a 4PL employing multi-attribute reverse auctions to purchase logistics services from green 3PLs. Qorri, et al. [21], developed a new approach to assessing the environmental, social, and economic sustainability of the entire supply chain. Compared to reverse logistics or closed-loop supply chains, there are fewer operations research methodologies and analytic approaches for forward sustainability supply chain management in the published research [22,23]. Niu and Mu [17] considered an original equipment manufacturer and a logistics service provider’s preferred outsourcing structures, by incorporating the logistics service provider’s sustainable efforts and the competition with the manufacturer. Using the environment impact index defined by Krass, et al. [24], and by Choi and Chiu [25], Niu, et al. [26], investigated how environmental sustainability in a logistics service supply chain, consisting of short-distance and long-distance logistics service providers, deteriorated when a Physical Internet-enabled operational model was adopted. For suppliers to follow sustainable practices, firms can invest in activities that help raise awareness and improve the sustainability practices of the suppliers, enabling them to deliver goods, in compliance with all regulatory requirements, on time [27]. Christmann [28] considered that firms investing in environmental management practices evolve complementary abilities that enable them to outperform in other fields of competitiveness. Sodhi and Tang [29] examined the effect of partnerships and stress on corporate investments in socially sustainable practices.
2.2. Audits in the Supply Chain
Morais, et al., performed audits in the food industry to evaluate the energy consumption of the equipment, and presented several measures and best practices for the improvement of energy efficiency [30]. In the literature on responsible supply chain management, Chen and Lee [16] found that when the supplier has responsibility risk, the buyer uses the process audit to identify penitential problems to reduce the sourcing risks. Caro, et al. [31], compared three types of audit mechanisms of buyers, including the buyers conducting their respective audits, buyers conducting audits jointly, and each buyer conducting audits independently and sharing their audit reports. Plambeck and Taylor [32] explored the phenomenon of the supplier’s evasion of a buyer’s audit, which is caused by the supplier’s hiding effort when the supplier has caused major harm to workers or to the environment. Process audits were also used to improve the supply and quality of agents. Nikoofal and Gümüş [33] examined the effectiveness of auditing the hidden actions of the supplier, in regard to the buyer, when the supplier was privately aware of the supply risk. Nikoofal and Gümüş [18] characterized the value of output- and action-based incentive mechanisms adopted by manufacturers to control the quality of suppliers when privately informed of the risk of failure.
2.3. Logistics Service Supply Chain Management
Logistics service demand management is critical to service supply chain management, as it significantly influences customer demand [34]. De and Singh [35] examined the impact of different channel leadership strategies to promote proper decision making on prices and logistics service quality in the fresh agri-product supply chain in the post-COVID-19 era. Zhang, et al. [36], investigated the attractiveness and effectiveness of the 4PL-driven and private lending-driven financing models when a capital-constrained 3PL seeks credit loans. Wu, et al. [37], considered that product survival rate and freshness level are functions of the level of logistics service, and examined the decisions of distributors and logistics service providers under different channel power structures with unit pricing contracts. To motivate 3PL providers to invest in developing their IT capabilities, Gong, et al. [38], studied the impact of IT investment on 3PL providers, in terms of supply chain profitability, under four logistics outsourcing contract structures. So [39] examined the impact of using time guarantees on price and time competition for service firms, and found that the monopoly situation was significantly different from the competition situation. Additionally, in their study of logistics service supply chain coordination, Huang, et al. [40], considered a fourth-party logistics company deputing a third-party logistics company with tasks received from clients: to address possible risks in the delivery process, different quality-based delivery contracts were proposed, to stimulate the 3PL to exert their best efforts. Liu, et al. [41], explored the supply chain coordination issues between a functional logistics service provider and a logistics service integrator, arising from the Belt and Road Initiative, and investigated the effects of the cost-sharing contract on the determinations for a mass-customized logistics services supply chain. Liu, et al. [42], examined scenarios in which the logistics service integrator and the functional logistics service provider had altruistic preferences; they proposed an ex-post payment contract and revenue sharing + franchise fee contract to coordinate the system. Liu, et al. [43], examined the quality game between a logistics service integrator and a functional logistics service provider in the presence of multi-period-oriented cooperation.
The features that set our paper apart from the aforementioned research are as follows. Firstly, we studied the impact of strategic choices on the probability of environmental compliance in logistics at the strategic level. Secondly, we audited the delivery process of green logistics, while the aforementioned research studied responsibility risks in the supply chain, and audited the compliance of suppliers with health and safety regulations. Thirdly, we introduced a logistics audit tool in logistics supply chain management, which was not considered in previous logistics papers.
3. The Model
A 4PL outsourced the client’s delivery tasks to a 3PL. The volume of goods transported was fixed and normalized to one. To improve the sustainability of the logistics, the 4PL set the standards that the 3PL’s efforts needed to meet, and carried out a logistics audit [33]; the probability that the 3PL’s efforts met the standards depended on both the 3PL’s efforts and the 4PL’s investment. The 3PL’s effort level was ; the corresponding costs were kt and 0, respectively. The investment level of the 4PL was , where evh(evl) denoted high (low) investment level, . For analytical tractability, we assumed that the investment cost was kv for the high investment, and 0 for the low investment.
The 3PL’s efforts and the 4PL’s investment may interact and jointly affect the probability that the 3PL’s efforts meet the standards. For example, the investment in education and training provided by the 4PL complements the 3PL’s efforts, as the information and skills gained enable the 3PL to deploy resources more effectively. The interaction of two actions with joint value has been widely studied in the economics and management literature [14,44,45,46]. When the 3PL’s efforts were et = 0, the probabilities of the 3PL’s efforts meeting the standards were related to the investment level of the 4PL, respectively γevl and γevh, in which represented the complement of the 4PL’s investment effort to the 3PL’s efforts; when the 3PL’s efforts were et = 1, with probability 1, the 3PL’s efforts met the standards. Table 1 presents the probabilities of the 3PL’s efforts meeting the standards.

Table 1.
The probabilities of the 3PL’s efforts meeting the standards.
The 4PL specified the standards of efforts in the contract, and conducted a logistics audit to verify the 3PL’s efforts. According to previous studies, the audit would be imperfect [16], so we assumed that the 4PL’s audit effort level was ea, which meant that the probability of the 3PL’s efforts not meeting the standards, and being detected, was 0 ≤ ea ≤ 1. If the 3PL did not make efforts, the 4PL would discover the 3PL’s violation through the audit, and the 3PL would incur a cost, φ, to rectify the problem. We assumed that the rectification was thorough, and that the final logistics service met environmental regulations. The probability of the 3PL’s not making efforts to be undetected was 1 − ea, and the probability that an undetected 3PL was found not to meet the environmental regulations after delivery was 1 − p, in which case the 4PL suffered from goodwill costs, g, and the 3PL would lose part of the future business from the 4PL [47].
The payment that the client paid to the 4PL for the delivery was . The 4PL offered a wholesale price contract to the 3PL, and determined the wholesale price, α, and the investment level, ev. When the 4PL’s investment level was high (low), the rate at which the 3PL lost future business was δh(δl). We assumed that the 3PL’s reservation profit normalized to zero. To simplify expressions, we let Pl = 1 − γevl, Ph = 1 − γevh, and we had Pl < Ph. Table 2 presents the strategies of the game, where the first expression in each cell was the expected profit of the 4PL, and the second expression was the expected profit of the 3PL. The model of the investment and auditing is shown in Figure 1, and the sequence of events is shown in Figure 2.

Table 2.
The 4PL’s (top expression) and 3PL’s (bottom expression) expected profits.
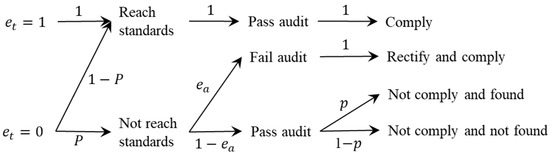
Figure 1.
Model of investment and auditing.
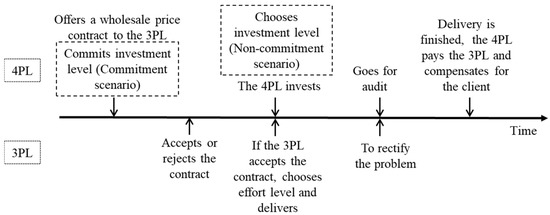
Figure 2.
Sequence of events.
We considered the following two scenarios: that the 4PL did not commit, and that the 4PL did commit the investment level. Throughout the paper, we let the superscript indicate results in the non-commitment scenario, and we let indicate results in the commitment scenario.
4. Base Model
In this section, the 4PL did not commit to the investment level, ev. Given the wholesale price, , the 4PL determined the investment level, ev, while the 3PL determined the efforts level, . The sequence of events in the non-commitment case were as follows:
- The 4PL provided a wholesale price contract to the 3PL;
- The 3PL accepted the contract if its expected profits were higher than the reservation profit;
- The 3PL chose the efforts level, , and delivered, whereas the 4PL chose its investment level, ev, and invested; we assumed that their decisions were simultaneous.
- The 4PL conducted the process audit.
- After the delivery was completed, the 4PL paid to the 3PL, and may have suffered from goodwill cost, .
We denoted the expected profits of 4PL and 3PL as and , respectively. In the expected that represented the equilibrium in the subgame, given , the 4PL solved the following problem to determine the wholesale price, :
s.t.
Inequality (2) represented the 3PL’s participation constraint. Constraints (3) and (4) represented the 4PL and the 3PL choosing the investment decision, , and efforts decision, , to maximize their profits for any given wholesale price, .
4.1. Equilibrium in a Subgame
For any fixed , the 3PL determined its best response, , to the 4PL’s decision on , then was determined as:
Then, we obtained as follows:
4.2. Subgame-Perfect Equilibrium
By substituting into (1) and (2) to find a subgame perfect equilibrium , we obtained:
Proposition 1.
In the non-commitment case, the subgame-perfect equilibrium is:
where ,
,
.
Proof.
See Appendix A. □
There were three possible equilibrium outcomes in Proposition 1. The first and second outcomes indicated that the 4PL did not pay a premium, and that the wholesale price covered only the 3PL’s rectification cost. Therefore, the 3PL made no efforts, and obtained a zero surplus. The 4PL’s investment level separated these two strategies. In the third equilibrium outcome, to incentivize the 3PL to make efforts, the 4PL offered the 3PL a wholesale price, , which was higher than his efforts cost, , and the 3PL received a positive surplus. This premium motivated the 3PL to make efforts, by imposing high opportunity costs on the 3PL.
Proposition 1 implied that in equilibrium the 4PL had three strategies in the non-commitment scenario: low-investment; high-investment; and low-investment-and-premium. Under the low-investment strategy, the 3PL made no efforts, and the probability of the logistics activity complying with environmental regulations was , where the 4PL’s investment and audit made the logistics activity comply with environmental regulations with probabilities and , respectively. From , under the low investment strategy, the probability of the logistics activity complying with environmental regulations was smaller than that under the high-investment strategy. Additionally, under the low-investment-and-premium strategy, the 3PL made efforts, and the probability of the logistics activity complying with environmental regulations was 1. Therefore, the low-investment-and-premium (low investment) strategy led to the best (worst) outcome.
Figure 3 shows the three strategies and threshold lines, , , and . From Figure 3, as increased, the 4PL preferred the low-investment strategy to the low-investment-and-premium strategy, when the investment cost, , was high, or changed from the low-investment strategy to the high-investment strategy, and then to the low-investment-and-premium strategy, when the investment cost, , was low. Thus, as the goodwill cost, , increased, the 4PL’s strategy choice increased the probability that the logistics activity complied with the environmental regulations.
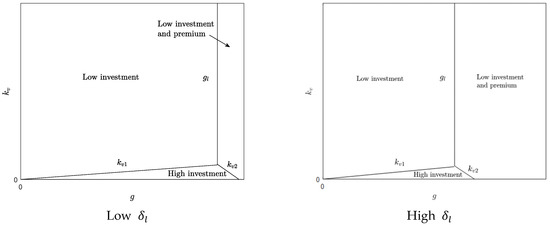
Figure 3.
Equilibrium outcomes in the non-commitment scenario.
From Figure 3, as the 4PL’s investment cost, , decreased, the 4PL could change its strategy from the low-investment strategy to the high-investment strategy when the goodwill cost, , was low, or from the low-investment-and-premium strategy to the high-investment strategy when the goodwill cost, , was high. In the former case, as the investment cost, , of the 4PL decreased, the 4PL could engage in a high investment. In the latter case, when the investment cost, , was lower, the 4PL could choose a high-investment strategy without paying a premium to the 3PL. This was because, by adopting a high-investment strategy, the 4PL could enhance the probability of the 3PL’s efforts meeting standards, and thus the compliance of logistics activities with environmental regulations, so that there was less motivation to pay premiums to promote the 3PL to make efforts. Therefore, as the investment cost, , decreased, the 3PL could be induced not to make efforts if the 4PL shifted from the low-investment-and-premium strategy to the high-investment strategy.
Figure 3 illustrates that the threshold lines, and , shifted to the left when the ratio of losing future orders, , increased. Thus, the 4PL preferred the low-investment-and-premium strategy. This was because when was higher, the 3PL suffered a higher loss, due to making no efforts, resulting in a higher premium, , that the 4PL paid to incentivize the 3PL to make efforts.
Proposition 2.
The variation of threshold lines, , with respect to are as follows:
- (i)
- is decreasing in;
- (ii)
- If , is increasing in ; if , is decreasing in ;
- (iii)
- If , is increasing in ; If , is decreasing in .
Proof.
See Appendix B. □
Note that from Proposition 2, when the rectification cost was small, and and were increasing in the audit level, then the likelihood of the low-investment strategy being the equilibrium strategy increased, while the likelihood of the low-investment-and-premium strategy being in equilibrium decreased. As the audit level increased, the cost for the 3PL rectifying increased, and the cost savings of the 3PL not making efforts decreased. Under the low-investment strategy, the 3PL made no efforts, and the 4PL paid a higher wholesale price to compensate for the loss of the cost savings for the 3PL not making efforts. As the goodwill cost reduced due to rectification then, when the reduction in goodwill cost was higher than the increase in wholesale price, the 4PL’s expected profit increased with the audit level. Under the low-investment-and-premium strategy, as the audit level increased, the cost savings of the 3PL for not making efforts decreased, and the 4PL incentivized the 3PL to make efforts by paying a premium. However, the premium given to the 3PL increased with the audit level, and thus the profit of the 4PL decreased. Therefore, the likelihood of the low-investment-and-premium strategy being in equilibrium decreased, while that of the low-investment strategy increased.
When the rectification cost was large, and and were decreasing at the audit level, then the likelihood of the low-investment-and-premium strategy being in equilibrium increased, while that of the low-investment strategy decreased. This was because, as the audit level increased, the cost savings of the 3PL not making efforts decreased. As the 3PL did not make efforts under the low-investment strategy, the 4PL paid a higher wholesale price to compensate for the loss of the cost savings for the 3PL not making efforts, and the goodwill cost decreased because of rectification, but the decrease in goodwill cost was less than the increase in the wholesale price, so the 4PL’s expected profit decreased with the audit level. Under the low-investment-and-premium strategy, as the audit level increased, the cost savings of the 3PL for not making efforts decreased, so that the 4PL could incentivize the 3PL to make efforts by paying a premium. However, when the cost of rectification was large, the premium given to the 3PL decreased with the audit level, and then the profit of the 4PL increased. Therefore, the likelihood of the low-investment-and premium-strategy being in equilibrium increased, while that of the low-investment strategy decreased.
5. Commitment to the 4PL Effort
In the commitment scenario, we considered the case in which the 4PL’s investment level, , was contractible or could be observed before the 3PL’s efforts decision. This process allowed the 4PL to commit to its investment effort before the 3PL chose its own efforts, resulting in a sequential move between the 4PL’s and the 3PL’s efforts decisions. After observing the 4PL’s decision on , the 3PL determined the effort level, . The sequence of events in the commitment scenario were as follows:
- The 4PL provided a wholesale price, , and committed the investment level, , to the 3PL;
- The 3PL accepted the contract if its expected profits were higher than the reservation profit;
- The 3PL chose the effort level, , and delivered, whereas the 4PL conducted its investment;
- The 4PL conducted a process audit;
- After the delivery was over, the 4PL paid to the 3PL, and could suffer from the goodwill cost, .
The 4PL’s contracting problem was:
s.t.
Inequality (6) represented the 3PL’s participation constraint. Constraint (7) represented that, given the 4PL’s decision , the 3PL chose to maximize its expected profit.
5.1. Subgame-Perfect Equilibrium
In this subsection, we derived the subgame perfect equilibrium of this program. Like the non-commitment scenario, the 3PL determined its best response, , to the 4PL’s decision on . The 3PL’s best response was as follows:
Next, by substituting into (5) and (6), we obtained:
Proposition 3.
If
- (i)
- When , the subgame-perfect equilibrium in the commitment scenario is:
- ii
- When , the subgame-perfect equilibrium in the commitment scenario is:
where , , ,
Proof.
See Appendix C. □
The four equilibrium results given in Proposition 3 corresponded to the low-investment, high-investment, low-investment-and-premium, and high-investment-and-premium strategies, respectively. Under the high-investment-and-premium strategy, the 3PL made efforts as in the low-investment-and-premium strategy. Unlike the high-investment strategy, under which the 3PL did not make efforts, under the high-investment-and-premium strategy, the 4PL did not face the risk of goodwill cost by paying a premium to the 3PL. In addition, by conducting investment, the premium given to the 3PL in the low-investment-and-premium strategy was lower than the low-investment-and-premium strategy; this was because the 4PL replaced some premium with investment efforts.
To investigate the factors affecting the equilibrium strategies, Figure 4 shows the four equilibrium strategies with the threshold lines , , , , , and defined in Proposition 3. As in the non-commitment scenario, the 4PL changed the strategy from low-investment to low-investment-and-premium as the goodwill cost, , increased. Moreover, in the commitment scenario, the 4PL changed the strategy from low-investment or high-investment to high investment-and-premium as increased.
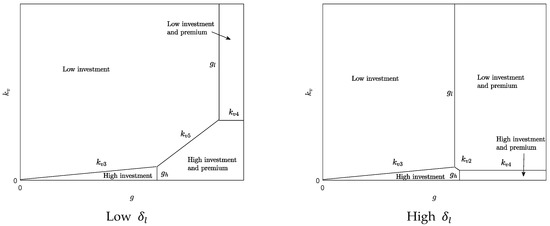
Figure 4.
Equilibrium outcomes in the commitment scenario.
The effect of the investment cost, , was different in the commitment and non-commitment scenarios. In the non-commitment scenario, as the investment cost, , decreased, the equilibrium strategy changed from the low-investment-and-premium strategy to the high-investment strategy, resulting in the 3PL not making efforts. In contrast, in the commitment scenario, when was low, as the investment cost decreased, it changed the equilibrium strategy from the low-investment-and-premium strategy to the high-investment-and-premium strategy, with the 3PL exerting efforts under both strategies. This suggests that the lower investment costs led the 3PL to make efforts in the commitment scenario in contrast to the non-commitment scenario. When was high, as the investment cost decreased, there was a range of goodwill costs, , that changed from the low-investment-and-premium strategy to the high-investment strategy, but it was much smaller compared to the non-commitment scenario.
As see in Figure 4, when was low, as the order loss rate, , increased, with the threshold line, , moving left, and moving down, so the likelihood of the low-investment-and-premium strategy being the equilibrium strategy increased. This was because, when was higher, the 3PL suffered a higher loss by not making efforts, resulting in lower premiums being paid by the 4PL to incentivize the 3PL to make efforts. Therefore, the 4PL was more likely to use the low-investment-and-premium strategy in this case. Similarly, in Figure 4, when was high, as the order loss rate, , increased, with the threshold, and , moving left, and moving down, so the likelihood of the low-investment-and-premium strategy being in equilibrium increased. Additionally, as increased, with the threshold lines, and , moving left, and moving up, so the likelihood of the high-investment-and-premium strategy being the equilibrium strategy increased.
Proposition 4.
The variation of threshold lines with respect to are as follows:
- (i)
- When , :
- (a)
- If the rectification cost , then and are increasing in the audit level, while ,, are decreasing in the audit level;
- (b)
- If the rectification cost , then and are decreasing in the audit level, while ,, are increasing in the audit level.
- (ii)
- When :
- (a)
- If the rectification cost , then , and are increasing in the audit level, while and are decreasing in the audit level;
- (b)
- If the rectification cost , then , and are decreasing in the audit level, while and are increasing in the audit level.
Proof.
See Appendix D. □
Proposition 4 shows that when if the rectification cost was small, with and increasing in the audit level, while , …, were decreasing in the audit level, then the likelihood of the low-investment strategy (high-investment-and-premium strategy) being the equilibrium strategy increased (decreased). If the rectification cost was large, with and decreasing in the audit level, while , …, were increasing in the audit level, then the likelihood of the high-investment-and-premium strategy (low-investment strategy) being the equilibrium strategy increased (decreased). For more information on this analysis, please refer to the analysis on Proposition 2. When we had similar findings as .
5.2. Effects of Commitment
We investigated the effects of the commitment to investment efforts by comparing the equilibrium outcomes in the non-commitment and commitment scenarios.
Figure 5 shows the overlap of Figure 3 and Figure 4 at low and high , respectively, illustrating four regions, A–D, where the equilibrium outcomes in the non-commitment scenario were different to those of the commitment scenario:
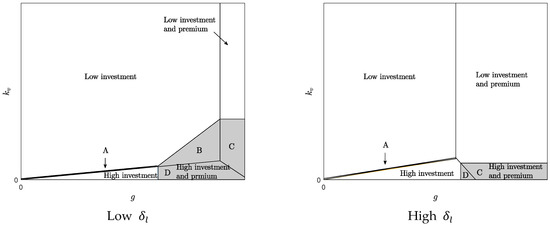
Figure 5.
Comparison of equilibrium outcomes in different scenarios.
- , low-investment high-investment.
- , low-investment high-investment-and-premium.
- , low-investment-and premium high-investment-and-premium.
- , high-investment high-investment-and-premium.
Comparing the two scenarios, we have the effects of commitment to investment efforts on the 4PL’s profits, the 3PL’s profits, and the 3PL’s efforts in Proposition 5.
Proposition 5.
Commitment to investment efforts will result in:
- (i)
- The 3PL’s profit remains unchanged in A, decreases in C, and increases in B and D.
- (ii)
- The 4PL’s profit increases in all regions.
- (iii)
- The efforts made by the 3PL increase in A, B, and D, and remain the same in C.
Proposition 5 (i) shows that the effect of commitment to investment efforts on 3PL’s profit depended on how the commitment to investment efforts changed the 4PL’s equilibrium strategy in each region. In region A, the 4PL did not pay premiums in both scenarios, and the 3PL’s profit remained unchanged. In region C, the 4PL reduced premiums, and the commitment to the investment efforts hurt the 3PL’s profit. In regions B and D, the 4PL changed the strategy, from not offering premiums to offering premiums, and the 3PL benefited from the commitment to investment efforts.
Proposition 5 (ii) states that the commitment to investment efforts always benefited the 4PL. This was because, if the 4PL committed to an investment level, then: (i) the new high-investment-and premium-strategy could lead to higher profits, (); (ii) the 3PL would accept a lower wholesale price, which would benefit the 4PL.
Proposition 5 (iii) indicates that, in B and D, the commitment to investment efforts increased the probability that the 3PL made efforts. In the commitment scenario, when the goodwill cost was high and the investment cost was low, the 4PL had an incentive to use the high-investment-and-premium strategy to induce the 3PL to make efforts. Yet, in the case of non-commitment, the 4PL did not use the strategy, because the premium of the high-investment-and-premium strategy was lower than that of the low-investment-and-premium strategy, and was insufficient to induce the 3PL to make efforts. In addition, in A, the commitment to investment efforts could prompt the 4PL to change the equilibrium strategy from a low-investment strategy to a high-investment strategy, such that the probability of 3PL’s efforts meeting the standards increased from to , due to investment and audit, when the goodwill cost and low-investment cost were low (i.e., and ). However, in the non-commitment scenario, the 4PL did not use the high-investment strategy because, without knowing the investment level, the 3PL would not accept the low wholesale price offered by the investment strategy.
Commitment to investment efforts led to increased compliance levels in all regions. For example, in region A, the commitment to investment efforts changed the equilibrium strategy from the low-investment strategy to the high-investment strategy, and the probability that the logistics service complied with environmental regulations increased from to . To improve the efforts level in region A, the cost of goodwill could be increased by raising consumers’ awareness of sustainability, as this would increase the potential loss to the 4PL due to non-compliance with regulations. Also, promoting industry cooperation could help the 4PL to reduce the investment cost, , so that the 4PL would then prefer to invest, to enhance the 3PL’s efforts.
6. Conclusions
As individuals become increasingly environmentally conscious, the logistics industry is becoming concerned with sustainability. We focused on the issue of complying with environmental regulations in a fourth-party logistics operating model, where the 4PL was the integrator of the supply chain, deputing the actual logistics delivery to the 3PL. To improve the level of logistics compliance with environmental regulations, we examined the investment and pricing strategies of the 4PL, and investigated the impact of the logistics audit level and the commitment of the 4PL to the logistics investment effort, on the choice of strategies. Specifically, we considered the 3PL’s efforts and the 4PL’s investment efforts, which could interact and jointly influence the probability of the 3PL’s efforts meeting the standards. Additionally, the 4PL used a logistics audit to evaluate the 3PL’s delivery process, so as to improve the visibility of the 3PL’s efforts and identify potential problems. The 4PL offered a wholesale price contract to the 3PL; the 3PL chose whether or not to make efforts and, if not, there was a probability of it failing the logistics audit, and incurring a cost to rectify the violation. Because the audit was not perfect, the 3PL, despite not making efforts, could still pass the audit while ending up with a lower compliance level; therefore, because there was a probability of being found to have not complied with the environmental regulations, the 4PL suffered a goodwill cost, and the 3PL was penalized by the reduction of its future business.
Our findings have the following implications. To improve the level of logistics compliance with environmental regulations, the 4PL can increase the 3PL’s efforts in the following ways: firstly, by offering the 3PL sufficiently high wholesale prices or high investment and medium wholesale prices; secondly, by changing the equilibrium strategy, by increasing the goodwill cost; thirdly, by reducing investment costs, although care would be needed, as reducing investment costs has the potential to reduce the probability of the 3PL making efforts when the 4PL suffers from high goodwill costs in the case of non-commitment; fourthly, by increasing the level of audit, when rectification costs are high enough; and fifthly, in that commitment to the investment is always advantageous to the environment.
This study may help 4PLs like Cainiao Network to manage environmental compliance, including the choice of logistics investment and pricing strategies, and the use of logistics audit tools. This research has the following implications for improving sustainability: firstly, the 4PL can effectively increase the probability of logistics compliance with environmental regulations, by choosing the appropriate level of penalties imposed on the 3PL and logistics audits; secondly, the government can help improve sustainability by reducing the investment costs of the 4PLs; thirdly, non-governmental organizations should help increase the goodwill cost of the 4PLs to increase the level of the 3PL’s efforts. There are some limitations to this paper that can be further investigated: firstly, as random factors were not considered, a possible extension would be to use random compliance levels to improve the analysis; secondly, the penalty mechanism for the 3PL in the paper was relatively simple, and other penalty schemes could be considered; thirdly, more effective contracts could be designed between the 4PL and the 3PL; fourthly, the impact of government policies on strategy choice could be studied.
Author Contributions
Conceptualization, H.W. (Hongyan Wang); methodology, H.W. (Hongyan Wang); validation, H.W. (Hongyan Wang) and M.H.; writing—original draft preparation, H.W. (Hongyan Wang); writing—review and editing, H.W. (Hongyan Wang) and H.W. (Hongfeng Wang); supervision, M.H. and H.W. (Hongfeng Wang); funding acquisition, M.H. and H.W. (Hongfeng Wang). All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China under Grant No. 2020YFB1708200; the NSFC Major International (Regional) Joint Research Project Grant No. 71620107003; the Fundamental Research Funds for State Key Laboratory of Synthetical Automation for Process Industries Grant No. 2013ZCX11; and the National Natural Science Foundation of China under Grant No. 62173076.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Proposition 1.
We made the following assumptions to rule out unrealistic cases:
- (i)
- From , we obtained , and from , we obtained , since , we obtained ;
- (ii)
- .
To simplify the expressions, we let:
From:
we obtained:
By solving ; s.t. , we obtained:
Next, we solved for the equilibrium wholesale price, :
- (i)
- If , the 4PL chooses when
- (ii)
- If , the 4PL chooses when
Then, the subgame-perfect equilibrium is:
□
Appendix B
Proof of Proposition 2.
Taking the derivatives of , and , we obtained:
From , we obtained ; From , we obtained , then is in the interval . We let .
From , we obtained ; From , we obtained .
Thus, if , is increasing in , and if , is decreasing in ;
If , is increasing in , and if , is decreasing in . □
Appendix C
Proof of Proposition 3.
To simplify the expressions, we let:
From
we obtained: ,
If , i.e., , from
- (i)
- , , for ;
- (ii)
- , , for .
- (iii)
- , , for .
We obtained:
We obtained if, and only if:
From , i.e., , and from , i.e., , we obtained . Thus, if , we obtained or .
- (a)
- If , program [21] can be simplified as follows:
- (i)
- is the equilibrium outcome if, and only if, and
- (ii)
- is the equilibrium outcome if, and only if, , and
- (iii)
- is the equilibrium outcome if, and only if, , and
- (iv)
- is the equilibrium outcome if, and only if, and .
- (b)
- If , we obtained:
- (i)
- is the equilibrium outcome if, and only if, and
- (ii)
- is the equilibrium outcome if, and only if, , and ;
- (iii)
- is the equilibrium outcome if, and only if, , and
- (iv)
- is the equilibrium outcome if, and only if, , and . □
Appendix D
Proof of Proposition 4.
Taking the derivatives of ,…,, and , we obtained:
- (i)
- When , from , we obtained ; From , if , i.e., , we obtained ; From , we obtained , then is in the interval . We let .
From , we obtained ; From , we obtained ; From , we obtained ;. From , we obtained ; From , we obtained .
Thus, if , is increasing in , if , is decreasing in ;
If , is increasing in , if , is decreasing in ;
If , is decreasing in , if , is increasing in ;
If , is decreasing in , if , is increasing in ;
If , is decreasing in , if , is increasing in .
- (ii)
- When , from , we obtained ; From , we had ; From , if , we obtained ; then is in the interval . We let .
From , we obtained ; From , we obtained ; From , we obtained ; From , we obtained ; From , we obtained ; From , we obtained .
Thus, if , is increasing in , if , is decreasing in ;
If , is increasing in , if , is decreasing in ;
If , is increasing in , if , is decreasing in ;
If , is decreasing in , if , is increasing in ;
If , is decreasing in , if , is increasing in . □
References
- Bové, A.-T.; Swartz, S. Starting at the Source: Sustainability in Supply Chains. Available online: https://www.mckinsey.com/business-functions/sustainability/our-insights/starting-at-the-source-sustainability-in-supply-chains (accessed on 30 May 2022).
- He, N.; Jiang, Z.-Z.; Wang, J.; Sun, M.; Xie, G. Maintenance optimisation and coordination with fairness concerns for the service-oriented manufacturing supply chain. Enterp. Inf. Syst. 2021, 15, 694–724. [Google Scholar] [CrossRef]
- Chau, K.-Y.; Tang, Y.M.; Liu, X.; Ip, Y.-K.; Tao, Y. Investigation of critical success factors for improving supply chain quality management in manufacturing. Enterp. Inf. Syst. 2021, 15, 1418–1437. [Google Scholar] [CrossRef]
- PLS Blog. Sustainable Supply Chain: 3 Benefits of Green Logistics. Available online: https://www.plslogistics.com/blog/sustainable-supply-chain-3-benefits-of-green-logistics (accessed on 30 May 2022).
- Interlake Mecalux. Green Logistics: Definition, Challenges and Solutions. Available online: https://www.interlakemecalux.com/blog/green-logistics (accessed on 30 May 2022).
- Qian, X.; Fang, S.-C.; Yin, M.; Huang, M.; Li, X. Selecting green third party logistics providers for a loss-averse fourth party logistics provider in a multiattribute reverse auction. Inf. Sci. 2021, 548, 357–377. [Google Scholar] [CrossRef]
- Alizila Staff. Cainiao Unveils ‘Green Logistics’ Master Plan. Available online: https://www.alizila.com/cainiao-unveils-green-logistics-master-plan/ (accessed on 30 May 2022).
- Zarbakhshnia, N.; Soleimani, H.; Goh, M.; Razavi, S.S. A novel multi-objective model for green forward and reverse logistics network design. J. Clean. Prod. 2019, 208, 1304–1316. [Google Scholar] [CrossRef]
- Aktas, E.; Bloemhof, J.M.; Fransoo, J.C.; Günther, H.-O.; Jammernegg, W. Green logistics solutions. Flex. Serv. Manuf. J. 2018, 30, 363–365. [Google Scholar] [CrossRef]
- Ecostars Europe Blog. Why and How Carry out a Logistics Audit. Available online: http://www.ecostars-europe.eu/en/logistics-audit (accessed on 30 May 2022).
- Orji, I.J.; U-Dominic, C.M.; Okwara, U.K. Exploring the determinants in circular supply chain implementation in the Nigerian manufacturing industry. Sustain. Prod. Consump. 2022, 29, 761–776. [Google Scholar] [CrossRef]
- PwC. Sustainability Assurance. Available online: https://www.pwccn.com/en/services/sustainability-and-climate-change/sustainability-assurance.html (accessed on 30 May 2022).
- Khalid, M.K.; Agha, M.H.; Shah, S.T.H.; Akhtar, M.N. Conceptualizing Audit Fatigue in the Context of Sustainable Supply Chains. Sustainability 2020, 12, 9135. [Google Scholar] [CrossRef]
- Lee, H.-H.; Li, C. Supplier Quality Management: Investment, Inspection, and Incentives. Prod. Oper. Manag. 2018, 27, 304–322. [Google Scholar] [CrossRef]
- Rodrigue, J.-P. The Benefits of Logistics Investments Opportunities for Latin America and the Caribbean. Available online: https://publications.iadb.org/publications/english/document/The-Benefits-of-Logistics-Investments-Opportunities-for-Latin-America-and-the-Caribbean.pdf (accessed on 1 October 2021).
- Chen, L.; Lee, H.L. Sourcing under supplier responsibility risk: The effects of certification, audit, and contingency payment. Manage. Sci. 2017, 63, 2795–2812. [Google Scholar] [CrossRef]
- Niu, B.; Mu, Z. Sustainable efforts, procurement outsourcing, and channel co-opetition in emerging markets. Transp. Res. Part E Logist. Transp. Rev. 2020, 138, 101960. [Google Scholar] [CrossRef]
- Nikoofal, M.E.; Gümüş, M. Quality at the source or at the end? Managing supplier quality under information asymmetry. M&SOM-Manuf. Serv. Oper. Manag. 2018, 20, 498–516. [Google Scholar] [CrossRef]
- Seuring, S.; Müller, M. From a literature review to a conceptual framework for sustainable supply chain management. J. Clean. Prod. 2008, 16, 1699–1710. [Google Scholar] [CrossRef]
- Elkington, J. Enter the Triple Bottom Line, 1st ed.; Earthscan: London, UK, 2004. [Google Scholar]
- Qorri, A.; Gashi, S.; Kraslawski, A. A practical method to measure sustainability performance of supply chains with incomplete information. J. Clean. Prod. 2022, 341, 130707. [Google Scholar] [CrossRef]
- Ilgin, M.A.; Gupta, S.M. Environmentally conscious manufacturing and product recovery (ECMPRO): A review of the state of the art. J. Environ. Manag. 2010, 91, 563–591. [Google Scholar] [CrossRef]
- Min, H.; Kim, I. Green supply chain research: Past, present, and future. Logist. Res. 2012, 4, 39–47. [Google Scholar] [CrossRef]
- Krass, D.; Nedorezov, T.; Ovchinnikov, A. Environmental taxes and the choice of green technology. Prod. Oper. Manag. 2013, 22, 1035–1055. [Google Scholar] [CrossRef]
- Choi, T.-M.; Chiu, C.-H. Mean-downside-risk and mean-variance newsvendor models: Implications for sustainable fashion retailing. Int. J. Product. Econ. 2012, 135, 552–560. [Google Scholar] [CrossRef]
- Niu, B.; Dai, Z.; Liu, Y.; Jin, Y. The role of Physical Internet in building trackable and sustainable logistics service supply chains: A game analysis. Int. J. Product. Econ. 2022, 247, 108438. [Google Scholar] [CrossRef]
- Gouda, S.K.; Saranga, H. Sustainable supply chains for supply chain sustainability: Impact of sustainability efforts on supply chain risk. Int. J. Product. Res. 2018, 56, 5820–5835. [Google Scholar] [CrossRef]
- Christmann, P. Effects of “Best Practices” of Environmental Management on Cost Advantage: The Role of Complementary Assets. Acad. Manag. J. 2000, 43, 663–680. [Google Scholar] [CrossRef]
- Sodhi, M.S.; Tang, C.S. Corporate social sustainability in supply chains: A thematic analysis of the literature. Int. J. Product. Res. 2018, 56, 882–901. [Google Scholar] [CrossRef]
- Morais, D.; Gaspar, P.D.; Silva, P.D.; Andrade, L.P.; Nunes, J. Energy consumption and efficiency measures in the Portuguese food processing industry. J. Food Processing Preserv. 2020, 2020, e14862. [Google Scholar] [CrossRef]
- Caro, F.; Chintapalli, P.; Rajaram, K.; Tang, C.S. Improving Supplier Compliance Through Joint and Shared Audits with Collective Penalty. M&SOM-Manuf. Serv. Oper. Manag. 2018, 20, 363–380. [Google Scholar] [CrossRef]
- Plambeck, E.L.; Taylor, T.A. Supplier Evasion of a Buyer’s Audit: Implications for Motivating Supplier Social and Environmental Responsibility. M&SOM-Manuf. Serv. Oper. Manag. 2016, 18, 184–197. [Google Scholar] [CrossRef]
- Nikoofal, M.E.; Gümüş, M. Value of audit for supply chains with hidden action and information. Eur. J. Oper. Res. 2020, 285, 902–915. [Google Scholar] [CrossRef]
- Wang, Y.; Wallace, S.W.; Shen, B.; Choi, T.-M. Service supply chain management: A review of operational models. Eur. J. Oper. Res. 2015, 247, 685–698. [Google Scholar] [CrossRef]
- De, A.; Singh, S.P. A resilient pricing and service quality level decision for fresh agri-product supply chain in post-COVID-19 era. Int. J. Logist. Manag. 2021; ahead-of-print. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Wang, L.; Zhao, X.; Gao, J. Financing capital-constrained third party logistic firms: Fourth party logistic driven financing mode vs. private lending driven financing mode. Int. J. Product. Res. 2021, 60, 2963–2982. [Google Scholar] [CrossRef]
- Wu, Q.; Mu, Y.; Feng, Y. Coordinating contracts for fresh product outsourcing logistics channels with power structures. Int. J. Product. Econ. 2015, 160, 94–105. [Google Scholar] [CrossRef]
- Gong, F.; Kung, D.S.; Zeng, T. The impact of different contract structures on IT investment in logistics outsourcing. Int. J. Product. Econ. 2018, 195, 158–167. [Google Scholar] [CrossRef]
- So, K.C. Price and time competition for service delivery. Manuf. Serv. Oper. Manag. 2000, 2, 392–409. [Google Scholar] [CrossRef]
- Huang, M.; Tu, J.; Chao, X.; Jin, D. Quality risk in logistics outsourcing: A fourth party logistics perspective. Eur. J. Oper. Res. 2019, 276, 855–879. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, K.; Chen, B.; Zhou, J.; Miao, L. Analysis of logistics service supply chain for the One Belt and One Road initiative of China. Transp. Res. Part E Logist. Transp. Rev. 2018, 117, 23–39. [Google Scholar] [CrossRef]
- Liu, W.; Yan, X.; Wei, W.; Xie, D.; Wang, D. Altruistic preference for investment decisions in the logistics service supply chain. Eur. J. Ind. Eng. 2018, 12, 598–635. [Google Scholar] [CrossRef]
- Liu, W.; Xie, D.; Xu, X. Quality supervision and coordination of logistic service supply chain under multi-period conditions. Int. J. Product. Econ. 2013, 142, 353–361. [Google Scholar] [CrossRef]
- Kremer, M. The O-Ring Theory of Economic Development. Q. J. Econ. 1993, 108, 551–575. [Google Scholar] [CrossRef]
- Schaefer, S. Product design partitions with complementary components. J. Econ. Behav. Organ. 1999, 38, 311–330. [Google Scholar] [CrossRef]
- Siggelkow, N. Misperceiving Interactions Among Complements and Substitutes: Organizational Consequences. Manag. Sci. 2002, 48, 900–916. [Google Scholar] [CrossRef]
- Cho, S.-H.; Fang, X.; Tayur, S.; Xu, Y. Combating Child Labor: Incentives and Information Disclosure in Global Supply Chains. M&SOM-Manuf. Serv. Oper. Manag. 2019, 21, 692–711. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).