Spatiotemporal Coupling Effect of Regional Economic Development and De-Carbonisation of Energy Use in China: Empirical Analysis Based on Panel and Spatial Durbin Models
Abstract
:1. Introduction
2. Indicator System Construction
3. Research Methodology
3.1. Global Entropy Method
- Construct the initial global evaluation matrix. Considering m provincial-level administrative regions, n evaluation indicators, and T years, the global idea is introduced to arrange the data in chronological order to form a global evaluation matrix .where denotes the j-th index data of the ith province in the t-th year.
- Standardise the indicator data. To eliminate the influence of inconsistencies in the evaluation indexes in terms of scale, order of magnitude, and units, the difference (Min-max) standardisation method is used to process the original data. The direction of positive indicators is consistent with the level of regional economic development and low-carbonisation of energy consumption in China evaluated in this study. That is, the larger the value, the better, while the direction of negative indicators is the opposite, and the smaller the value, the better.where
- Calculate the characteristic proportion of the i-th evaluation object under the j-th evaluation indicator in the t-th year for evaluation indicator :
- Calculate the information entropy value of each indicator :
- Calculate the coefficient of variation of each evaluation indicator . A lower entropy of an evaluation indicator corresponds to a higher coefficient of variation and higher weight of that indicator. Define the variability factor vector .
- Calculate the evaluation indicator weights :
- Calculate the overall evaluation score :
3.2. Coupling Coordination Model
3.3. Spatial Correlation Analysis
3.4. Spatial Durbin Model (SDM)
4. Empirical Analysis
4.1. Determination of Weights
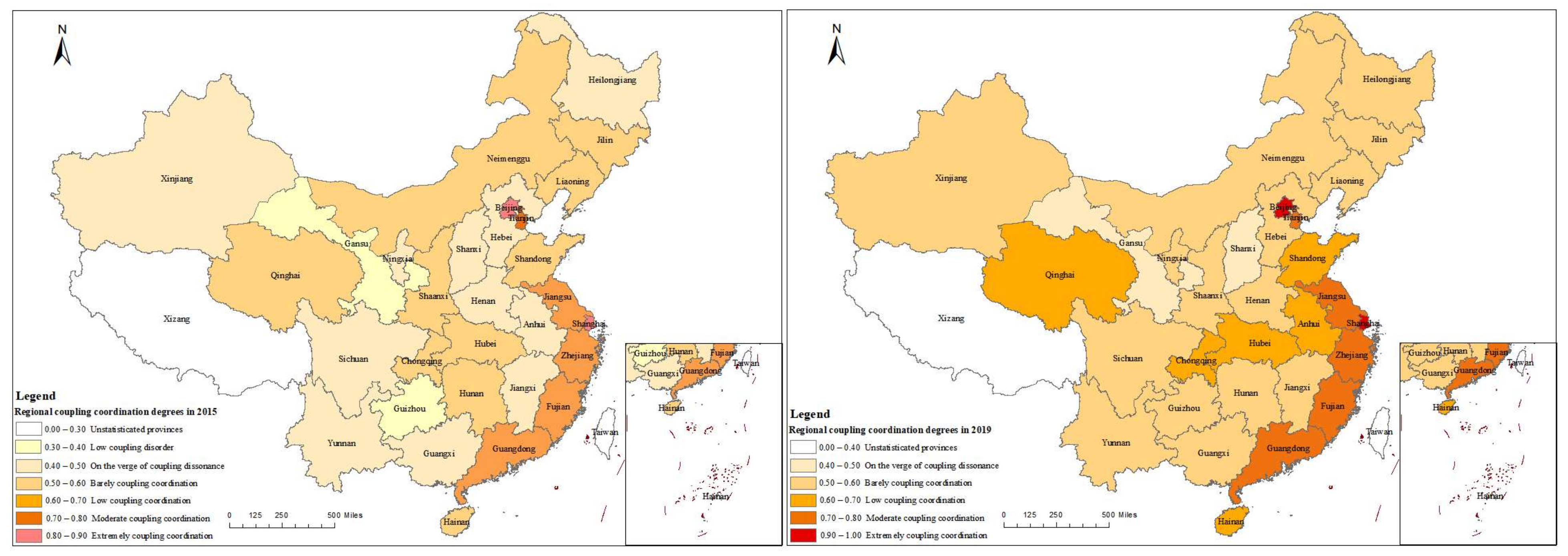
4.2. Calculation of the Coupling Coordination Degree
4.3. Spatial Correlation Analysis of Coupling Coordination
4.3.1. Global Spatial Correlation
4.3.2. Local Spatial Correlation
- H–H agglomeration: The H–H agglomeration area included economically developed regions such as Beijing, Shanghai, Jiangsu, and Zhejiang. The coupling coordination degrees of these provinces and neighbouring provinces were high, exhibiting a significant positive correlation, and the spatial association manifested as a diffusion effect that catalyses the economic development and low-carbonisation of energy consumption of the neighbouring regions. The number of H–H agglomeration provincial-level administrative regions increased from 7 in 2015 to 8 in 2019, and the newly added region was Shandong province. Under the background of the national maritime power strategy, Shandong Province, as a key area at the intersection of the Maritime Silk Road and the New Asia–Europe Continental Bridge Economic Corridor, is a critical juncture linking domestic and international markets, as well as an important pivot for major strategies such as the “Regional Comprehensive Economic Partnership” and “One Belt, One Road”. In recent years, positive progress has been made in Shandong Province regarding the upgrading of traditional industries, the development of high-tech industries, and the green and low-carbon transformation of energy sources, thereby contributing to the continuous enhancement of economic and sustainable development. In addition, although Hainan embraces relatively backward economic development, with the continuous promotion of policy strategies such as the strong maritime nation, Pan-Pearl River Delta economic circle, free trade port, and clean energy island construction, Hainan has made remarkable achievements in improving infrastructure construction, promoting industrial upgrading and optimization, giving full play to the advantages of marine resources, developing characteristic economy, and utilizing clean energy in recent years, accompanied by the continuous improvement in economic development and green and low-carbon level.
- L-H agglomeration: The L-H agglomeration area included three provinces: Anhui, Hebei, and Jiangxi Provinces. The coupling coordination in these provinces was low, whereas the coupling coordination in the neighbouring provinces was relatively high, suggestive of a negative correlation. The spatial association manifested as a transitional effect. In the context of the coordinated development of Beijing, the gradient transfer of industries from Beijing to Tianjin has occurred. Moreover, the proportion of energy-intensive production enterprises in the secondary industry in Hebei Province is high, with most of them being labour-intensive industries, with significant negative environmental effects [35]. Consequently, the coupling coordination is low, and Jiangxi Provinces’ relative backward regions in the Yangtze River Economic Zone and China’s southern Pan-Pearl River Delta region in terms of economic development. These regions must be integrated into the regional synergistic development strategy, and their practical cooperation with neighbouring provinces must be strengthened in domains such as infrastructure connectivity, industrial development layout planning, and ecological environmental protection, to promote high-quality regional economic and social development.
- L–L agglomeration: The L–L agglomeration area included western provinces such as Qinghai and Gansu, main coal-producing provinces such as Inner Mongolia and Shanxi, old industrial bases in northeast China such as Heilongjiang and Jilin, and relatively underdeveloped and densely populated provinces such as Henan and Sichuan. The degree of coordination in these provinces and neighbouring provinces was low, suggestive of a positive correlation, and the spatial correlation exhibited a trickle-down effect. China’s central and western regions are still dominated by traditional energy-intensive industries, and the overall economic development and technical levels are low. Although Inner Mongolia, Shanxi, and other provinces are rich in energy and mineral resources, the unbalanced industrial layout of coal resource-related industries and other heavy industries has led to critical problems associated with high energy consumption, high pollution, and high emissions. Jilin and other north-eastern provinces of China mainly use traditional heavy industries as the driver of economic growth. Consequently, these regions have failed to incorporate high-end manufacturing and high-tech industries, and are lagging in the process of economic development and low-carbonisation of energy consumption. Nevertheless, the huge population base of some provinces such as Henan has imposed relative difficulties on these areas in economic development and low-carbon energy transformation at the per capita level.
- H–L agglomeration: The H–L agglomeration area included Chongqing, Guangdong, and Hubei provinces. These provinces exhibited a high degree of coordination, but a low degree of coordination with their neighbouring provinces, suggestive of a negative correlation and polarisation effect in spatial correlation. Guangdong Province has undergone rapid economic development: In recent years, its high precision industries, advanced manufacturing industries, and high-end service industries have been growing in synergy, and the energy consumption and carbon emissions per unit of GDP have been decreasing. However, the spatial spillover effect has not been fully exploited, and the driving effect of this region on the neighbouring provinces is insufficient. Consequently, this region is considerably different from its neighbouring regions. In recent years, Hubei Province has embraced the rapid development in high-tech manufacturing and strategic emerging industries, with strong growth in the investment of infrastructure and manufacturing greatly driving the economic development to rank among the best. In addition, the process of low-carbonisation of energy consumption has been accelerating, standing out among the neighbouring provinces. In terms of the strategic promotion of the integrated economic development of Chengdu and Chongqing, the economic development rate and low-carbonisation level of energy use of Chongqing Municipality is high in the western region, leading to a significant difference in the coupling coordination with neighbouring provinces.
4.4. Analysis of Driving Factors
4.4.1. Selection of Explanatory Variables
4.4.2. Spatial Model Setting Tests
4.4.3. Analysis of Spatial Regression Results
- The direct effect coefficient of the real GDP per capita is 0.375, indicating that increased regional real GDP per capita promotes the coupling effect. If the other explanatory variables remain unchanged and the regional per capita real GDP increases by 1%, the coupling degree in the province can increase by 0.375 percentage points.
- The direct effect coefficient and total effect coefficient of the urbanisation rate are 0.228 and 0.155, respectively, indicating that increased urbanisation rate promotes the coupling effect. If the other explanatory variables remain unchanged and the urbanisation rate increases by 1%, the coupling degree in the province will increase by 0.228 percentage points under the direct effect. The impact of urbanization on the development of the low-carbon economy is mainly reflected in two aspects: economic development and carbon dioxide emissions. Based on empirical analysis, it has been concluded in previous studies that urbanisation promotes economic development [44], but there are divergences in the impact on carbon dioxide emissions [45,46], along with a “U” curve relationship between urbanisation and the development efficiency of the low-carbon economy [47]. Moreover, the implementation of urbanisation policies plays a significant role in promoting low-carbon technological innovation [48].
- The direct effect coefficient and total effect coefficient of the proportion of non-coal energy in the energy consumption are 0.291 and 0.465, indicating that the low coal consumption structure of the energy consumption promotes the coupling effect. If the other explanatory variables remain unchanged and the proportion of non-coal energy in the energy consumption increases by 1%, the coupling degree of economic development and energy low-carbon in the province will be increased by 0.291 percentage points in the direct effect. The coefficient of the spatial spillover effect of this explanatory variable is 0.174, indicating that an increase in the regional share of non-coal energy in energy consumption has a significant positive spatial spillover effect on the coupling degree in neighbouring provinces.
- The direct effect coefficient of the ratio of tertiary to secondary industry value added is −0.0977, and the total effect coefficient is −0.208, indicating that the advanced industrial structure negatively influences the coupling degree. In other words, the regional industrial structure and coupling effect present an unbalanced state of spatial mismatch. This phenomenon likely occurs because, first, the advanced industrial structure limits the economic growth, with this impediment being the weakest in the eastern region, less weak in the western region, and strongest in the central and western regions [49]. Second, there exist significant differences in the economic base, industrial layout, and innovation capacity of different provincial-level administrative regions in China, and the index of the advanced industrial structure does not reflect the synergistic development capacity and industrial maturity of various industries in the region. Third, an inverted-U type nonlinear relationship exists between the industrial structure transformation and energy consumption, and the inflection points of different regions are not consistent, exhibiting the heterogeneity and unevenness among regions [50,51].
- The direct effect coefficient and total effect coefficient of the R&D investment intensity are 0.205 and 0.520, indicating that the level of regional investment in science and innovation promotes the coupling degree. If the other explanatory variables remain unchanged and the intensity of R&D investment increases by 1%, the coupling degree in the region will increase by 0.205 percentage points under the direct effect. The coefficient of the spatial spillover effect of this explanatory variable is 0.315, indicating that an increase in the regional level of investment in science and innovation has a significant positive spatial spillover effect on the coupling degree in neighbouring provinces.
4.4.4. Robustness Tests
- Transforming the spatial weight matrix. The reciprocal spatial weight matrix of the geographical distance (W2) is used to construct the time fixed effect SDM of the to verify the robustness of the findings. The elements on the nondiagonal of W2 are the reciprocal of the geographic distance between the central locations of two provincial-level administrative regions, with the diagonal elements being zero [40,52,53]:
- 2.
- Replacing the explanatory variables: To verify the robustness and reliability of the empirical results, the disposable income of urban residents per capita is used as a substitute explanatory variable to replace GDP per capita. Table 12 presents the results of the decomposition of the effects of the SDM with the replacement of the explained variables. A comparison with Table 10 shows that the direction and significance of the regression coefficients of the explanatory variables do not change significantly, which verifies the robustness of the model and stability of the study results.
5. Conclusions and Suggestions
- The coupling coordination degree in each provincial-level administrative region increased in the period 2015–2019. The top five provinces in terms of the coupling coordination degree are Beijing Municipality, Shanghai Municipality, Tianjin Municipality, Jiangsu Province, and Zhejiang Province. In 2019, Guizhou, Guangxi, Ningxia, Gansu, and Shanxi ranked the bottom five provinces in terms of low-carbon economic development. Therefore, it is essential to strengthening policy formulation to promote economic development, industrial structure optimisation, energy structure adjustment, and low-carbon consumption reduction.
- The coupling coordination levels of the 30 provinces in 2015 included low coupling disorder, on the verge of coupling dissonance, barely coupled coordination, low coupling coordination, moderate coupling coordination, and highly coupling coordination. In 2019, two provinces upgraded to extremely coupling coordination. During the study period, the overall coupling coordination level increased, indicating that the coupling coordination degree between regional economic development and energy consumption low-carbonisation in China gradually increased over time. However, in 2019, the proportion of provinces with coupling coordination below the moderate coupling coordination level remains high at 76.56%. Therefore, in future policymaking, policymakers should take the imbalance and inadequacy of development between regions into account, giving more priority to enhancing the coordinated development of economic and low-carbon energy consumption in these provinces with a lower level of coupling.
- The global SAR results indicate that the global Moran’s I indices of the coupled coordination from 2015 to 2019 are significantly correlated within the 95% confidence interval, and the I values are greater than zero, indicating that the coupled coordination is positively correlated in terms of the spatial distribution and has significant spatial clustering characteristics. The global Moran’s I index value increased from 0.252 to 0.315 during the study period, indicating that the spatially positive correlation between the regional economic development and low-carbonisation of energy consumption became more significant. Therefore, in future policy formulation, the role of the spatial correlation effect of coupling coordination should be given full play to strengthen the complementary links and positive influence between provinces and neighbouring provinces in terms of economy, society, energy, industry, technology, and talent.
- The local SAR results show that the local Moran’s I indices of the 30 provincial-level administrative regions in China are distributed in the first and third quadrants during the study period, indicating that the coupling coordination of most provincial-level administrative regions exhibits a strong positive spatial correlation with the neighbouring provinces. The eastern and western provincial-level administrative regions are mainly distributed in the H–H and L–L agglomeration areas of the Moran’s scatterplot, respectively. In the study period, the spatial correlation pattern of the regional coupling coordination has a high stability, with most regions not leaping, and two of the 30 provincial-level administrative regions leaping to the first and third quadrants from 2015 to 2019. This finding indicates that the positive spatial correlation effect of the coupling and coordination of the system is strengthened. There are significant differences in the spatial distribution of the coupling coordination degree among provinces, as shown by the clustering characteristics of provinces with higher and lower levels of coupling, while the driving effects of some provinces with higher coupling levels on neighbouring provinces are limited. In this sense, there is no doubt that issues such as the uneven development of regional economies, societies, energy consumption, and the environment have hindered the smooth development of China’s low-carbon economy. Therefore, provincial districts should promote the process of low-carbon economic development based on the status quo and difficulties of local development, and strengthen inter-provincial policy interchange and mutual promotion, dynamic flow of production factors, emission as well as carbon reduction in energy consumption, industrial integration and development, and synergistic innovation in science and technology, in order to narrow regional differences comprehensively, and to advance the balanced development of China’s green, low carbon, and circular economic system.
- The results of the decomposition of the effects of the SDM show that the improvement in the regional economic level, advancement of urbanisation process, low coal consumption structure of energy, and increased level of investment in science and technological innovations promote the increase in the coupling degree. As the core of policy formulation and implementation, the factors elaborated above are critical to promoting the development of a high-quality low-carbon economy. The low coal consumption structure of regional energy and the investment level in science and innovation impose a significant positive spatial spillover effect on the coupling degree of neighbouring provinces. Therefore, it is crucial to step up in-depth cooperation between local governments in the fields of energy supply and demand, clean energy technologies, and scientific research and innovation, to give full play to synergy-driven effect. The advanced industrial structure adversely influences the coupling degree. This phenomenon occurs owing to the heterogeneity of regional industrial development in terms of coordination, balance, and maturity, and interactive relationship between industrial structure transformation, economic growth, and energy consumption in different regions. Given the differences in regional resource endowments and disparate stages of economic development, on the one hand, it is essential for provinces to implement the strategies of industrial structure transformation and upgrading in accordance with local conditions, and the enhancement of local government governance capacity and policy support are accelerated, to give full play to the positive role of local governments in energy conservation and emission reduction during industrial structure transformation [50]. On the one hand, in provinces dominated by heavy industries, it is necessary to accelerate the promotion of energy conservation and carbon reduction in traditional industries, contribute to technological innovation and equipment upgrading of advanced production capacity, and eliminate outdated production capacity with high energy consumption as well as pollution. Regarding the provinces with new technology-based industries as the primary driver of development, it is necessary to further integrate high-quality elements, reinforce the investment in scientific research, and step up the transformation efficiency of R&D and capabilities and achievements to encourage the green, low-carbon and high-quality development of technology-intensive industries.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dou, R.Y.; Liu, X.M. Study on the relationship between energy consumption and economic growth in typical resource-based regions of China. China Popul. Resour. Environ. 2016, 26, 164–170. [Google Scholar]
- He, Z.; Yang, Y.; Song, Z.Y.; Liu, Y. The mutual evolution and driving factors of China’s energy consumption and economic growth. Geogr. Res. 2018, 37, 1528–1540. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CJFD&dbname=CJFDLAST2018&filename=DLYJ201808006&uniplatform=NZKPT&v=jxZEPYyDYor_hoGHUq6HoF7XXjyjqJqm6e-uAfBIjfkwBb7tcvVy3Cqv44sne7nn (accessed on 3 December 2021).
- Bekun, F.V.; Emir, F.; Sarkodie, S.A. Another look at the relationship between energy consumption, carbon dioxide emissions, and economic growth in South Africa. Sci. Total Environ. 2019, 655, 759–765. [Google Scholar] [CrossRef] [PubMed]
- Shahbaz, M.; Hoang, T.H.V.; Mahalik, M.K.; Roubaud, D. Energy consumption, financial development and economic growth in india: New evidence from a nonlinear and asymmetric analysis. Energy Econ. 2017, 63, 199–212. [Google Scholar] [CrossRef]
- Mirza, F.M.; Kanwal, A. Energy consumption, carbon emissions and economic growth in pakistan: Dynamic causality analysis. Renew. Sustain. Energy Rev. 2017, 72, 1233–1240. [Google Scholar] [CrossRef]
- Li, G.Z.; Huang, Q.J. Study on the coordinated development of energy—Economy—Environment -technology system in Beijing-Tianjin-Hebei. Stat. Decis. 2021, 37, 129–131. [Google Scholar] [CrossRef]
- Lu, J.; Chang, H.; Wang, Y. Dynamic evolution of provincial energy economy and environment coupling in China’s regions. China Popul. Resour. Environ. 2017, 27, 60–68. [Google Scholar]
- Miao, Y.; Xing, W.J.; Bao, J.Q. Low-Carbon Index Evaluation System of the Urban Energy Structure and Its Attainment. Ecol. Econ. 2016, 32, 53–57. [Google Scholar]
- Fu, J.X.; Liu, Y.Q. A Study on China’s Low-Carbon Energy Development:A Case Study of Beijing. Macroeconomic 2020, 164–175. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, Q.S.; Li, S.Y.; Li, X.J. Measurement on China’s Urban Low-carbon Development Performance Index. Stat. Decis. 2021, 37, 75–79. [Google Scholar] [CrossRef]
- Meng, F.S.; Zou, Y. The Optimization Degree Evaluation of Energy Structure Base on the SPA-TOPSIS. Oper. Res. Manag. Sci. 2018, 27, 122–130. [Google Scholar]
- Jiang, W.J. Analysis of coupled population-regional economic-environmental development coordination. Stat. Decis. 2017, 15, 101–104. [Google Scholar] [CrossRef]
- Pang, S.L.; Wu, M.Y. Research on the coupled and coordinated development of higher education scale and regional economy in China. Stat. Decis. 2021, 37, 109–112. [Google Scholar] [CrossRef]
- Guo, H.X. The Coal Resources in Shanxi Province and Study on The Relationship between The Coupling of The Regional Economic Development. Master’s Thesis, Shanxi Agricultural University, Jinzhong, China, 2015. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?Dbname=CMFD201502&filename=1015635110.nh (accessed on 17 December 2021).
- Statistics Bureau of the People’s Republic of China. China Statistical Yearbook, 2016–2020. Available online: http://www.stats.gov.cn/ (accessed on 2 May 2022).
- Statistics Bureau of the People’s Republic of China. Statistical Yearbook of China’s Fixed Assets Investment (China’s Investment Field), 2016–2020. Available online: http://www.stats.gov.cn/ (accessed on 2 May 2022).
- Statistics Bureau of the People’s Republic of China. China Energy Statistical Yearbook, 2016–2020. Available online: http://www.stats.gov.cn/ (accessed on 2 May 2022).
- Statistics Bureau of the People’s Republic of China. China Census Yearbook, 2016–2020. Available online: http://www.stats.gov.cn/ (accessed on 2 May 2022).
- Carbon Emission Account & Datasets. Emission Inventories for 30 Provinces, 2015–2019. Available online: https://www.ceads.net.cn/ (accessed on 2 May 2022).
- Zhao, R.F.; Wang, X.N. Comparison of Regional Innovative Abilities in Bejing-Tianjin-Hebei Area Based on Overall Entropy Method. China Bus. Mark. 2017, 31, 114–121. [Google Scholar] [CrossRef]
- Luo, Y.S.; Lu, Z.N.; Zhao, X.C. Evaluation and spatial statistical analysis of the level of intellectual property resources in Chinese provinces. Stat. Decis. 2020, 36, 62–66. [Google Scholar] [CrossRef]
- Li, Y.J.; Zhang, L. Dynamic Evaluation of Industrial Ecologization Level in the Upper Reaches of the Yangtze River Base on Overall Entropy Method. Ecol. Econ. 2021, 37, 44–48.56. [Google Scholar]
- Zong, X.; Yang, H. Analysis on the Spatio temporal Coupling Relationship and Driving Forces of New Urbanization and Urban Low Carbon Development. Ecol. Econ. 2021, 37, 80–87. [Google Scholar]
- Miao, L.; Wen, B.X.; Wen, Q.Y. Coupling and Coordination Relationship Between Local Financial Investment in Education and Economic Development Level in China. Econ. Geogr. 2021, 12, 1–9. [Google Scholar] [CrossRef]
- Li, M.; Mao, C. Spatial-Temporal Variance of Coupling Relationship between Population Modernization and Eco- Environment in Beijing-Tianjin-Hebei. Sustainability 2019, 11, 991. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, Z.; Li, G.; Zhuo, Y.; Xu, Z. Spatial-Temporal Evolution of Sustainable Urbanization Development: A Perspective of the Coupling Coordination Development Based on Population, Industry, and Built-Up Land Spatial Agglomeration. Sustainability 2018, 10, 1766. [Google Scholar] [CrossRef]
- Yu, X.X. Spatio-temporal analysis of the coupled economic-social-technological-resource coordinated development. Stat. Decis. 2017, 9, 127–131. [Google Scholar] [CrossRef]
- Gao, H.G.; Luo, Y. Coupled measurement of urbanization and ecological environment quality in the Yangtze River Economic Zone. Stat. Decis. 2021, 37, 111–115. [Google Scholar] [CrossRef]
- Chen, Q. Advanced Econometrics and Stata Applications; Higher Education Press: Beijing, China, 2014; Volume 4, pp. 578–579. [Google Scholar]
- Liang, S.; Gao, X.L.; Wang, S.Y. Evaluation and Spatial Measurement Study of Energy Security, Energy Consumption and Pollutant Emissions; China Water Conservancy and Hydropower Press: Beijing, China, 2021; Volume 1, pp. 107–114. [Google Scholar]
- Anselin, L. Spatial Econometrics: Methods and Models; Kluwer Academic Press: Dordrecht, The Netherlands, 1988; pp. 223–239. [Google Scholar]
- Guo, Y.; Fan, B.N.; Long, J. Practical Evaluation of China’s Regional High-quality Development and Its Spatiotemporal Evolution Characteristics. Quant. Tech. Econ. 2020, 37, 118–132. [Google Scholar] [CrossRef]
- Rey, S.J. Spatial Empirics for Economic Growth and Convergence. Geogr. Anal. 2010, 33, 195–214. [Google Scholar] [CrossRef]
- Sun, Y.; Zheng, S.L.; Gan, K.Q. Research on Measurement and Spatial Pattern of National Quality Infrastructure Development in China. Sci. Technol. Manag. Res. 2021, 41, 191–198. [Google Scholar]
- Zhang, S.S. A few thoughts on undertaking industrial transfer in Hebei Province. West. Leather 2018, 40, 117. [Google Scholar]
- Fan, H.J.; He, S.J. Construction and Measurement of Evaluation System of Modern Industrial System. Reform 2021, 8, 90–102. [Google Scholar]
- Liu, B.; Wang, A. Study on the Evaluation and Construction Path of Modern Industrial System: Taking Shandong Province as an Example. Inq. Econ. Issues 2020, 5, 66–72. [Google Scholar]
- Elhorst, J.P. Matlab Software for Spatial Panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef]
- Zhong, R.Y.; Zeng, J.H. The Impact of Digital Economy on Household Consumption—Empirical Analysis Based on the Spatial Durbin Model. Inq. Econ. Issues 2022, 3, 31–43. [Google Scholar]
- Lu, T.T.; Zhu, Z.Y. The Influence of Artificial Intelligence on Labor Income Share from the Perspective of Space—Analysis Based on Static and Dynamic Space Durbin Model. Inq. Econ. Issues 2022, 5, 65–78. [Google Scholar]
- Mao, Z.G.; Wu, U.M.; Xie, C. Spatial Pattern and Influencing Mechanism of Consumption Level in Yangtze River Delta Urban Agglomeration. Econ. Geogr. 2020, 40, 56–62. [Google Scholar] [CrossRef]
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Xu, D.Y.; Liu, X.H. Impact of Infrastructure on the Real Exchange Rate: Evidence from China’s Provincial Data by Spatial Dubin Model. World Econ. Stud. 2022, 3, 33–53+134. [Google Scholar] [CrossRef]
- Brunt, L.; García-Pealosa, C.; Boucekkine, R. Urbanization and the onset of modern economic growth. Econ. J. 2021, 132, 512–545. [Google Scholar] [CrossRef]
- Poumanyvong, P.; Kaneko, S. Does urbanization lead to less energy use and lower CO2 emissions? A cross-country analysis. Ecol. Econ. 2010, 70, 434–444. [Google Scholar] [CrossRef]
- Sharma, S.S. Determinants of carbon dioxide emissions: Empirical evidence from 69 countries. Appl. Energy 2011, 88, 376–382. [Google Scholar] [CrossRef]
- Zhang, A.H.; Huang, J. An Empirical Study on the Effects of Urbanization on the Efficiency of Development of Regional Low-Carbon Economy. J. Shaanxi Norm. Univ. (Philos. Soc. Sci. Ed.) 2015, 44, 76–82. [Google Scholar]
- Xiao, Y.F.; Wu, Y.; Zhou, W.Q. Can new urbanization construction promte low-carbon technology innovation. J. Chongqing Univ. Technol. (Soc. Sci.) 2019, 33, 22–32. [Google Scholar]
- Cui, J.N.; Shi, L.Y.; Xie, B.J. Can the Convergence of Technology and Industry Drive the Development of Regional Economy—A Dynamic Spatial Durbin Model Based Studyl. J. Harbin Univ. Commer. (Soc. Sci. Ed.) 2022, 02, 15–25. [Google Scholar]
- Fu, Z.H.; Jing, P.Q. Local government governance capacity, industrial structure transformation and energy consumption. Stat. Decis. 2022, 10, 162–166. [Google Scholar] [CrossRef]
- Zhang, Z.Q.; Liu, J.P. Analysis on the inverted “U” relationship between advanced industrial structure and energy intensity. Coal Eng. 2021, 53, 189–192. [Google Scholar]
- Liu, Y.; Xiao, H.; Zikhali, P.; Lv, Y. Carbon Emissions in China: A Spatial Econometric Analysis at the Regional Level. Sustainability 2014, 6, 6005–6023. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, H.; Zhang, N. Industrial Carbon Emissions of China’s Regions: A Spatial Econometric Analysis. Sustainability 2016, 8, 210. [Google Scholar] [CrossRef]

| Coupled Evaluation Systems | Evaluation Dimensions | Indicator | Indicator Direction | Unit |
|---|---|---|---|---|
| Regional economic development | Economic aggregation and structure | GDP per capita | Positive | yuan |
| Proportion of added value of tertiary industry in GDP | Positive | % | ||
| Economic efficiency | Financial revenue per capita | Positive | yuan | |
| Disposable income of urban residents per capita | Positive | yuan | ||
| Economic and social development | Urbanisation rate | Positive | % | |
| Total retail sales of social consumer goods per capita | Positive | yuan | ||
| Total investment in fixed assets per capita | Positive | yuan | ||
| Regional low-carbonisation of energy consumption | Energy consumption | Increase or decrease in the energy consumption per 10,000 yuan of GDP | Negative | (±%) |
| Growth rate of total energy consumption | Negative | % | ||
| Increase or decrease in the electricity consumption per 10,000 yuan of GDP | Negative | (±%) | ||
| Energy structure | Proportion of coal consumption in energy consumption | Negative | % | |
| Proportion of electric energy in energy consumption | Positive | % | ||
| Scale of carbon emissions | carbon emissions per capita | Negative | tons | |
| Carbon emissions per 10,000 yuan of GDP | Negative | tons/10,000 yuan |
| Serial Number | Coupling Coordination | Coupling Coordination Level |
|---|---|---|
| 1 | (0.9, 1.0] | Extremely coupling coordination |
| 2 | (0.8, 0.9] | Highly coupling coordination |
| 3 | (0.7, 0.8] | Moderate coupling coordination |
| 4 | (0.6, 0.7] | Low coupling coordination |
| 5 | (0.5, 0.6] | Barely coupling coordination |
| 6 | (0.4, 0.5] | On the verge of coupling dissonance |
| 7 | (0.3, 0.4] | Low coupling disorder |
| 8 | (0.2, 0.3] | Moderate coupling disorder |
| 9 | (0.1, 0.2] | Highly coupling disorders |
| 10 | (0.0, 0.1] | Extreme coupling disorders |
| Regional Economic Development | ||||
| Evaluation Dimensions | Indicator Name | Entropy Value | Redundancy | Weighting |
| Economic Aggregation and Structure | GDP per capita (X1) | 0.9426 | 0.0574 | 0.1460 |
| Proportion of added value of tertiary industry in GDP (X2) | 0.9643 | 0.0357 | 0.0908 | |
| Economic Efficiency | Financial revenue per capita (X3) | 0.8886 | 0.1114 | 0.2833 |
| Disposable income of urban residents per capita (X4) | 0.9427 | 0.0573 | 0.1458 | |
| Economic and Social Development | Urbanisation rate (X5) | 0.9634 | 0.0366 | 0.0931 |
| Total retail sales of consumer goods per capita (X6) | 0.9306 | 0.0694 | 0.1765 | |
| Total investment in fixed assets per capita (X7) | 0.9746 | 0.0254 | 0.0645 | |
| Regional Low-Carbonisation of Energy Consumption | ||||
| Evaluation Dimensions | Indicator Name | Entropy Value | Redundancy | Weighting |
| Energy Consumption | Increase or decrease in the energy consumption per 10,000 yuan of GDP (Y1) | 0.9957 | 0.0043 | 0.0616 |
| Growth rate of total energy consumption (%) (Y2) | 0.9939 | 0.0061 | 0.0877 | |
| Increase or decrease in the electricity consumption per 10,000 yuan of GDP (Y3) | 0.9874 | 0.0126 | 0.1800 | |
| Energy Structure | Proportion of coal consumption in energy consumption (Y4) | 0.9707 | 0.0293 | 0.4191 |
| Electricity as a share of energy consumption (Y5) | 0.9978 | 0.0022 | 0.0309 | |
| Scale of Carbon Emissions | Carbon emissions per capita (Y6) | 0.9911 | 0.0089 | 0.1267 |
| Carbon emissions per 10,000 Yuan of GDP (Y7) | 0.9934 | 0.0066 | 0.0940 | |
| Province | 2015 | 2016 | 2017 | 2018 | 2019 |
|---|---|---|---|---|---|
| Beijing Municipality | 0.8799 | 0.8872 | 0.9117 | 0.9265 | 0.9464 |
| Tianjin Municipality | 0.7637 | 0.7858 | 0.7699 | 0.7606 | 0.7866 |
| Hebei Province | 0.4483 | 0.4652 | 0.4928 | 0.5172 | 0.5376 |
| Shanxi Province | 0.4408 | 0.4293 | 0.4217 | 0.4550 | 0.4751 |
| Inner Mongolia Autonomous Region | 0.5353 | 0.5564 | 0.5382 | 0.4825 | 0.5324 |
| Liaoning Province | 0.5702 | 0.5582 | 0.5754 | 0.5854 | 0.5953 |
| Jilin Province | 0.5278 | 0.5417 | 0.5521 | 0.5661 | 0.5666 |
| Heilongjiang Province | 0.4634 | 0.4793 | 0.5008 | 0.5199 | 0.5381 |
| Shanghai Municipality | 0.8409 | 0.8635 | 0.8915 | 0.9077 | 0.9180 |
| Jiangsu Province | 0.6861 | 0.6920 | 0.7136 | 0.7381 | 0.7500 |
| Zhejiang Province | 0.6940 | 0.7081 | 0.7349 | 0.7584 | 0.7806 |
| Anhui Province | 0.4937 | 0.5187 | 0.5557 | 0.5845 | 0.6043 |
| Fujian Province | 0.6480 | 0.6582 | 0.6717 | 0.6965 | 0.7207 |
| Jiangxi Province | 0.4670 | 0.4983 | 0.5277 | 0.5607 | 0.5833 |
| Shandong Province | 0.5710 | 0.6006 | 0.6314 | 0.6353 | 0.6512 |
| Henan Province | 0.4548 | 0.4911 | 0.5253 | 0.5552 | 0.5963 |
| Hubei Province | 0.5714 | 0.5794 | 0.6044 | 0.6276 | 0.6497 |
| Hunan Province | 0.5002 | 0.5233 | 0.5393 | 0.5665 | 0.5884 |
| Guangdong Province | 0.6628 | 0.6592 | 0.6997 | 0.7173 | 0.7324 |
| Guangxi Zhuang Autonomous Region | 0.4313 | 0.4591 | 0.4850 | 0.4928 | 0.5182 |
| Hainan Province | 0.5836 | 0.6081 | 0.6250 | 0.6373 | 0.6463 |
| Chongqing Municipality | 0.5946 | 0.6333 | 0.6453 | 0.6529 | 0.6786 |
| Sichuan Province | 0.4943 | 0.5229 | 0.5601 | 0.5759 | 0.5941 |
| Guizhou Province | 0.3887 | 0.4232 | 0.4579 | 0.5103 | 0.5262 |
| Yunnan Province | 0.4439 | 0.4703 | 0.4913 | 0.5173 | 0.5338 |
| Shaanxi Province | 0.5220 | 0.5208 | 0.5507 | 0.5887 | 0.5959 |
| Gansu Province | 0.3991 | 0.4481 | 0.4280 | 0.4599 | 0.4975 |
| Qinghai Province | 0.5337 | 0.5471 | 0.5569 | 0.5769 | 0.6148 |
| Ningxia Hui Autonomous Region | 0.4712 | 0.5085 | 0.4501 | 0.4774 | 0.5028 |
| Xinjiang Uyghur Autonomous Region | 0.4964 | 0.5037 | 0.5225 | 0.5407 | 0.5508 |
| Year | I | Z | p-Value |
|---|---|---|---|
| 2015 | 0.252 | 2.647 | 0.004 |
| 2016 | 0.254 | 2.673 | 0.004 |
| 2017 | 0.281 | 2.919 | 0.002 |
| 2018 | 0.329 | 3.373 | 0.000 |
| 2019 | 0.315 | 3.246 | 0.001 |
| Year | H–H (High–High) | L–H (Low–High) | L–L (Low–Low) | H–L (High–Low) |
|---|---|---|---|---|
| 2015 | Shanghai, Jiangsu, Zhejiang, Beijing, Tianjin, Fujian, Hainan | Anhui, Hebei, Jiangxi | Guizhou, Shanxi, Ningxia, Qinghai, Gansu, Jilin, Shaanxi, Yunnan, Heilongjiang, Inner Mongolia, Xinjiang, Guangxi, Henan, Sichuan, Hunan | Guangdong, Shandong, Hubei, Liaoning, Chongqing |
| 2016 | Shanghai, Jiangsu, Zhejiang, Beijing, Tianjin, Fujian, Hainan | Anhui, Hebei, Jiangxi | Guizhou, Shanxi, Ningxia, Qinghai, Gansu, Jilin, Shaanxi, Yunnan, Heilongjiang, Inner Mongolia, Xinjiang, Guangxi, Henan, Sichuan, Hunan, Liaoning | Guangdong, Shandong, Hubei, Chongqing |
| 2017 | Shanghai, Jiangsu, Zhejiang, Beijing, Tianjin, Fujian, Hainan | Anhui, Hebei, Jiangxi | Guizhou, Shanxi, Ningxia, Qinghai, Gansu, Jilin, Shaanxi, Yunnan, Heilongjiang, Inner Mongolia, Xinjiang, Guangxi, Henan, Sichuan, Hunan, Liaoning | Guangdong, Shandong, Hubei, Chongqing |
| 2018 | Shanghai, Jiangsu, Zhejiang, Beijing, Tianjin, Fujian, Hainan, Shandong | Anhui, Hebei, Jiangxi, Hunan | Guizhou, Shanxi, Ningxia, Qinghai, Gansu, Jilin, Shaanxi, Yunnan, Heilongjiang, Inner Mongolia, Xinjiang, Guangxi, Henan, Sichuan, Liaoning | Guangdong, Hubei, Chongqing |
| 2019 | Shanghai, Jiangsu, Zhejiang, Beijing, Tianjin, Fujian, Hainan, Shandong | Anhui, Hebei, Jiangxi | Guizhou, Shanxi, Ningxia, Qinghai, Gansu, Jilin, Shaanxi, Yunnan, Heilongjiang, Inner Mongolia, Xinjiang, Guangxi, Henan, Sichuan, Hunan, Liaoning, Hunan | Guangdong, Hubei, Chongqing |
| Driver Measurement Layer | Indicator Name | Variable Name | Average Value | Standard Deviation | Minimum Value | Maximum Value |
|---|---|---|---|---|---|---|
| Level of Coupling between the Two Systems | Degree of coupling between the two systems | Y | 0.589 | 0.122 | 0.389 | 0.946 |
| Regional Economic Level | Real GDP per capita | Z1 | 5.632 | 2.565 | 2.595 | 14.60 |
| Regional Urbanisation Level | Urbanisation rate | Z2 | 0.598 | 0.111 | 0.42 | 0.883 |
| Regional Energy Consumption Structure | Proportion of non-coal energy in energy consumption | Z3 | 0.634 | 0.143 | 0.363 | 0.984 |
| Regional Industrial Structure | Ratio of tertiary to secondary value added | Z4 | 1.452 | 0.749 | 0.801 | 5.234 |
| Regional Level of Investment in Science and Innovation | R&D investment intensity | Z5 | 1.776 | 1.126 | 0.454 | 6.315 |
| Test | Test Index | Statistic | Df | p-Value |
|---|---|---|---|---|
| LM Test | Spatial Error | |||
| Moran’s I | 86.249 | 1.000 | 0.000 | |
| Lagrange multiplier | 6.652 | 1.000 | 0.010 | |
| Robust Lagrange multiplier | 4.402 | 1.000 | 0.036 | |
| Spatial Lag | ||||
| Lagrange multiplier | 10.848 | 1.000 | 0.001 | |
| Robust Lagrange multiplier | 8.598 | 1.000 | 0.003 | |
| LR Test | Irtest SDM SAR | |||
| LR chi2 (5) | 5.11 | 0.403 | ||
| Irtest SDM SEM | ||||
| LR chi2 (5) | 6.73 | 0.242 | ||
| Wald Test | Wald Test for SEM | |||
| Sem chi2 (5) | 8.19 | 0.146 | ||
| Wald test for SAR | ||||
| Sar chi2 (5) | 10.53 | 0.062 | ||
| Hausman Test | LR chi2 (5) | 18.83 | 0.002 | |
| SDM (Spatial Fixed-Effects) | SDM (Time Fixed-Effects) | SDM (Spatial and Time Fixed-Effects) | |
|---|---|---|---|
| Z1 | 0.113 (0.95) | 0.380 *** (7.71) | 0.0954 (0.82) |
| Z2 | 0.664 *** (4.14) | 0.233 *** (6.00) | 0.746 *** (4.70) |
| Z3 | 0.296 *** (6.00) | 0.282 *** (12.63) | 0.310 *** (6.08) |
| Z4 | 0.540 *** (4.59) | −0.0922 ** (−3.11) | 0.601 *** (4.94) |
| Z5 | 0.251 *** (3.59) | 0.195 *** (4.56) | 0.234 *** (3.42) |
| W*Z1 | 0.139 (0.65) | −0.213 * (−1.94) | 0.350 (1.44) |
| W*Z2 | 0.00938 (0.04) | −0.104 * (−1.72) | 0.475 * (1.67) |
| W*Z3 | −0.0988 (−1.33) | 0.101 * (1.85) | 0.0495 (0.53) |
| W*Z4 | −0.535 ** (−2.07) | −0.0829 (−1.41) | −0.0897 (−0.29) |
| W*Z5 | 0.163 (1.15) | 0.235 *** (2.75) | 0.0215 (0.14) |
| rho | 0.0949 (0.87) | 0.176 * (1.66) | −0.0119 (−0.10) |
| Variance sigma2_e | 0.000365 *** (8.65) | 0.00130 *** (9.06) | 0.000345 *** (8.66) |
| R2 | 0.881 | 0.966 | 0.878 |
| N | 150 | 150 | 150 |
| Driver Measurement Layer | Explanatory Variables | SDM (Time Fixed-Effects) W1 | ||
|---|---|---|---|---|
| LR Direct | LR Indirect | LR Total | ||
| Regional Economic Level | Real GDP per capita (Z1) | 0.375 *** | −0.170 | 0.205 |
| (7.15) | (−1.45) | (1.43) | ||
| Regional Urbanisation Level | Urbanisation rate (Z2) | 0.228 *** | −0.0734 | 0.155 ** |
| (5.93) | (−1.06) | (2.09) | ||
| Regional Energy Consumption Structure | Proportion of non-coal energy in energy consumption (Z3) | 0.291 *** | 0.174 *** | 0.465 *** |
| (13.98) | (2.79) | (7.54) | ||
| Regional Industrial Structure | Ratio of tertiary to secondary value added (Z4) | −0.0977 *** | −0.110 | −0.208 ** |
| (−3.42) | (−1.56) | (−2.45) | ||
| Regional Level of Investment in Science and Innovation | R&D investment intensity (Z5) | 0.205 *** | 0.315 *** | 0.520 *** |
| (5.03) | (2.99) | (4.21) | ||
| Driver Measurement Layer | Explanatory Variables | SDM (Time Fixed-Effects) W2 | ||
|---|---|---|---|---|
| LR Direct | LR Indirect | LR Total | ||
| Regional Economic Level | Real GDP per capita (Z1) | 0.363 *** | −0.578 | −0.216 |
| (6.86) | (−1.19) | (−0.43) | ||
| Regional Urbanisation Levels | Urbanisation rate (Z2) | 0.133 *** | −1.024 | −0.891 |
| (2.95) | (−1.60) | (−1.34) | ||
| Regional Energy Consumption Structure | Proportion of non-coal energy in energy consumption (Z3) | 0.381 *** | 1.372 * | 1.754 ** |
| (10.14) | (1.96) | (2.40) | ||
| Regional Industrial Structure | Ratio of tertiary to secondary value added (Z4) | −0.107 *** | −0.802 * | −0.909 ** |
| (−3.04) | (−1.85) | (−1.99) | ||
| Regional Level of Investment in Science and Innovation | R&D investment intensity (Z5) | 0.275 *** | 1.738 * | 2.013 * |
| (5.11) | (1.67) | (1.86) | ||
| Driver Measurement Layer | Explanatory Variables | SDM (Time Fixed-Effects) W1 | ||
|---|---|---|---|---|
| LR Direct | LR Indirect | LR Total | ||
| Regional Economic Level | Real GDP per capita (Z1) | 0.266 *** | −0.156 | 0.110 |
| (3.60) | (−0.99) | (0.80) | ||
| Regional Urbanisation Level | Urbanisation rate (Z2) | 0.300 *** | −0.185 ** | 0.115 |
| (6.66) | (−2.06) | (1.33) | ||
| Regional Energy Consumption Structure | Proportion of non-coal energy in energy consumption (Z3) | 0.275 *** | 0.252 *** | 0.527 *** |
| (10.85) | (4.15) | (9.45) | ||
| Regional Industrial Structure | Ratio of tertiary to secondary value added (Z4) | −0.116 *** | −0.205 *** | −0.321 *** |
| (−3.07) | (−3.35) | (−4.90) | ||
| Regional Level of Investment in Science and Innovation | R&D investment intensity (Z5) | 0.290 *** | 0.411 *** | 0.701 *** |
| (6.94) | (4.45) | (7.56) | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Lu, C.; Ning, Y.; Wang, J. Spatiotemporal Coupling Effect of Regional Economic Development and De-Carbonisation of Energy Use in China: Empirical Analysis Based on Panel and Spatial Durbin Models. Sustainability 2022, 14, 10104. https://doi.org/10.3390/su141610104
Zhang X, Lu C, Ning Y, Wang J. Spatiotemporal Coupling Effect of Regional Economic Development and De-Carbonisation of Energy Use in China: Empirical Analysis Based on Panel and Spatial Durbin Models. Sustainability. 2022; 14(16):10104. https://doi.org/10.3390/su141610104
Chicago/Turabian StyleZhang, Xintong, Cuijie Lu, Yuncai Ning, and Jingtao Wang. 2022. "Spatiotemporal Coupling Effect of Regional Economic Development and De-Carbonisation of Energy Use in China: Empirical Analysis Based on Panel and Spatial Durbin Models" Sustainability 14, no. 16: 10104. https://doi.org/10.3390/su141610104
APA StyleZhang, X., Lu, C., Ning, Y., & Wang, J. (2022). Spatiotemporal Coupling Effect of Regional Economic Development and De-Carbonisation of Energy Use in China: Empirical Analysis Based on Panel and Spatial Durbin Models. Sustainability, 14(16), 10104. https://doi.org/10.3390/su141610104






